The Utility of Fisher’s Geometric Model in Evolutionary Genetics

Abstract

The accumulation of data on the genomic bases of adaptation has triggered renewed interest in theoretical models of adaptation. Among these models, Fisher Geometric Model (FGM) has received a lot of attention over the last two decades. FGM is based on a continuous multidimensional phenotypic landscape, but it is for the emerging properties of individual mutation effects that it is mostly used. Despite an apparent simplicity and a limited number of parameters, FGM integrates a full model of mutation and epistatic interactions that allows the study of both beneficial and deleterious mutations, and subsequently the fate of evolving populations. In this review, I present the different properties of FGM and the qualitative and quantitative support they have received from experimental evolution data. I later discuss how to estimate the different parameters of the model and outline some future directions to connect FGM and the molecular determinants of adaptation.

INTRODUCTION

With the rise of genomics and massive sequencing, the quantitative investigation of the genetic bases of adaptation seems finally at hand. Precise analysis of quantatitative trait loci (QTL), genome wide association studies and experimental evolution coupled to whole genome sequencing have provided new opportunities to identify individual mutations contributing to adaptation (Barrick & Lenski 2013) and to assess mutation fitness effects at large scale (Acevedo et al. 2014, Hietpas et al. 2011, Robins et al. 2013). As a consequence some fundamental questions in evolution can now be experimentally tackled. What is the type and effect of mutations that contribute most to adaptation? How do these mutations interact with one another? How do the rates and effects of beneficial and deleterious mutations vary among populations or among species? All these questions are indeed linked to the properties of the genotype to phenotype to fitness map that defines a fitness landscape.

The forces that shape these fitness landscapes have biochemical, physiological or ecological origins, and despite the progress being made to unravel them (Lewis et al. 2012), they may be difficult to apprehend other than empirically. Yet, this apparent complexity and diversity may not exclude the existence of some simplified models capturing their quantitative properties. Theoreticians have therefore tried over the last two decades to define some simplified abstract fitness landscape that may have some relevant mathematically tractable properties. The objective of such models is to define a minimal number of intelligible and measurable parameters that allow the model to capture the large body of experimental data being produced both on deleterious and beneficial mutations, the interactions between mutations and with the environment.

In his book the “Genetical theory of natural selection” (Fisher 1930), one of the 3 founding fathers of population genetics, RA. Fisher briefly outlined a geometrical model that synthetized his vision of adaptation. The description of the model took no more than a page, and though largely cited, the model was barely used until the 1990ies. Yet, during the last 20 years, it has been widely utilized to study the quantitative properties of adaptation and confront experimental data. The aim of this review is to present the specificity of the model, its emergent properties and the benefits and challenges of using such model for interpreting data on adaptation.

Fisher Geometric model

In Fisher’s Geometric Model (FGM) an organism is characterized by a set of independent phenotypic traits, each corresponding to an axis in an n-dimensional Euclidian space. The axes correspond to idealized traits; they are a combination of traits that produce an orthogonal bases of the space. A genotype is assumed to generate a single phenotype and is therefore characterized by a point in this space. The dimensionality of the space is referred to as phenotypic complexity: the number of independent and evolvable traits an organism is exposing to the action of natural selection in a given environment.

All phenotypes are supposed to be under stabilizing selection, i.e. there is an optimal value for each. As a result, an optimal combination of phenotypic values exists. Fitness decays as the distance to this optimum increases. Fisher used an isotropic model, meaning that fitness was supposed to decay similarly along all the axes. As a consequence, in the canonical FGM, fitness isoclines are hyper-spheres centered on the optimum (Figure 1A). Several functions can be used to describe how fitness declines with the distance to the optimum. For the sake of simplicity and similarity with multivariate quantitative genetics model (Lande & Arnold 1983), the following quadratic decay function has been used:

$$W\left(d\right)=e^{-\frac{d^2}{2}}$$ [1]

where d is the distance to the optimum (Table 1). It has sometimes been extended (Tenaillon et al. 2007) to

$$W\left(d\right)=e^{-\alpha d^Q}$$ [2]

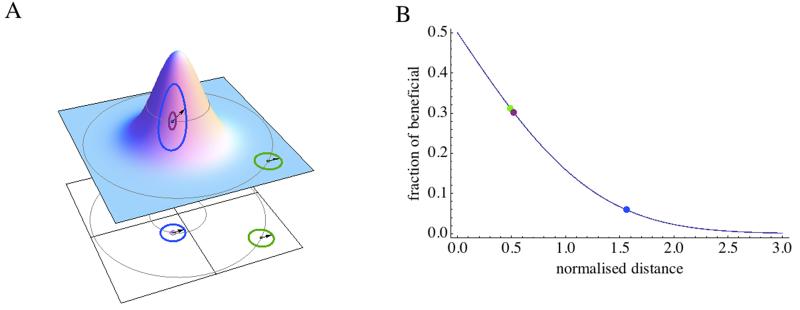
Figure 1.

A) FGM fitness landscape, with fitness on the vertical axes and below the projection on a 2D plot. Fitness decays as the phenotype moves away from the optimal phenotype. Mutation of phenotypic size r moves the phenotype on a hyper-sphere. The same mutation (arrow) may have different effects depending on the initial phenotype. B) Fraction of beneficial mutations as a function of the scaled effect of mutation $x=\frac{r\sqrt{n}}{2d}$. The points represent the situations illustrated in A, assuming a 100 dimensions. A large r (blue) is less likely to be beneficial than a small r from the same phenotype (purple) or a mutation of similar r affecting a less optimal phenotype (green). C) The distribution of mutation effects on fitness depends on the initial position of the phenotype. D) The distribution is presented for the points presented in C assuming n = 20, $\stackrel{‒}{s}=-0.01$ and initial log-fitness of −0.01 (purple), −0.1 (blue) and −0.5 (green). E) Ten adaptive walks moving log-fitness from −0.1 to −0.01 are presented. F) Different distribution of mutation effects produced from a phenotype of log-fitness −0.1 are presented (other parameters as in D): total mutations (Gray), beneficial mutations (Blue), beneficial mutations surviving drift (Purple), mutations fixed during adaptive walks starting from that phenotype (Black).

Table 1.

Parameters	Meaning
n	Phenotypic complexity, dimensionality of the phenotypic space
d	Phenotypic distance to the optimum of the reference genotype
α, Q	robustness and epistasis parameter influencing the decay rate and the curvature of the fitness function W(d) = e−αdQ
s0	Mal-adaptation of the reference genotype: s0 = −log(W(d)) = αdQ
r	Length of the mutational vector
σ	Standard deviation of normal deviates of the mutational vector on each axis : Δzi = N(0, σ)
x	Scaled distance to the optimum $x=\frac{r}{2d}\sqrt{n}$
e	Epistasis defined as $e=\log \left(\frac{w_{12}}{w_0}\right)-\log \left(\frac{w_1}{w_0}\right)-\log \left(\frac{w_2}{w_0}\right)$
m	Pleiotropy of mutations: number of phenotypes affected by mutations
N	Effective population size
μ	Mutation rate

In FGM, mutations are represented by a vector that moves an ancestral phenotype to the mutant’s phenotype. Mutations are classically supposed to be isotropic. This means that they have no preferred direction and affect all phenotypic axes similarly. This hypothesis coined “universal pleiotropy” (Paaby & Rockman 2013, Wagner & Zhang 2011), as most mutations affect all traits simultaneously, is not without consequences, but has been widely used for the sake of simplicity.

To summarize, FGM can be fully described with only three meta-parameters: phenotypic complexity, the fitness function and the way mutations affect the phenotype of an organism. This limited number of parameters is the great strength of FGM: once they have been defined, all the interesting properties of the fitness landscape that constrain adaptation emerge. Indeed, despite its apparent simplicity, FGM integrates a very rich model of mutation or epistatic interactions.

The first and only usage of FGM by Fisher, took indeed full benefit of the model’s strength. Fisher supported the micro-evolutive vision of evolution that stipulated that adaptations proceeded by mutations of very small effects. To support his vision, he showed that the fraction of beneficial mutation increased as the length of mutation vector decreased, and that mostly small effect mutations were beneficial when phenotypic complexity was large (Figure 1AB). In other words, for complex organisms adaptation would most likely proceed through small steps rather than large one. Though Fisher missed the major contribution of drift to the selective process (Kimura 1983), the full power of the model is illustrated here: FGM has emerging properties concerning mutation effects and their interactions that depend on the parameters chosen but are not the direct choice of the modeler. Moreover, intuitive and visual interpretation of these properties is possible (Figure 1).

FGM in the light of alternative models of evolution

FGM and quantitative genetics

Being a continuous model based on phenotype traits, FGM is clearly linked to quantitative genetics models (QGM), which also define fitness from a set of phenotypic traits, often under stabilizing selection (some work on disruptive selection has also been performed). Selection and mutation may affect the traits differentially and in most cases Gaussian deviates are used. So, in essence the multivariate landscaped defined in quantitative genetics and FGM are very similar.

FGM and QGM differ in the focus they give to the mutation process. FGM emphasizes mostly the role of de novo mutation in the process of an asexual population with no standing variation. Quantitative genetics is on the opposite mostly focusing on the adaptive process of sexual populations with some standing genetic variation. In that process, adaptation is not a single genotype moving in the phenotypic space but rather a population of recombining and mutating genotypes, which can be characterized in most conditions by a Gaussian cloud (Turelli & Barton 1994). A variance-covariance matrix, named the G matrix, identifies the populations in that landscape (Lande 1979, Walsh & Blows 2009). In that perspective, mutations are not studied independently but collectively through their contribution to standard genetic variation. The underlying idea being that mutations have small effects and are distributed among many loci. Interestingly, it is Fisher’s use of FGM that convinced scientists that beneficial mutations being of very small effects, there would be no experimental power to analyze them (Orr & Coyne 1992). As a consequence, the individual properties of mutations have rarely been the main focus of quantitative genetics which concentrated on mean traits and fitness evolution, and few studies have tried to connect quantitative genetics with the adaptive fate of a single mutation (but see Chevin & Hospital 2008). In contrast, in what we refer to as FGM, in the line of the early work of Fisher, de novo mutations are the center of attention. To unravel the properties of these mutations, most FGM studies use asexual populations with a low mutation rate such that the populations are monomorphic and can be described by a single point in the adaptive landscape.

Why has FGM perspective on de novo mutation been so popular in the recent years and not before? The recent success of FGM’s perspective on mutation came from the discrepancies between the small effect mutation hypothesis used in the models and the genetical information gathered in QTL analysis in the 80ies and 90ies (Orr & Coyne 1992): QTL analysis revealed the existence of large effect loci. So, a new formalism was needed to uncover the genetic bases of adaptations.

The rise of FGM as a genetic model of adaptation

Along with the observation of quantitative genetic variation, the rise of molecular evolution, the beginning of genomics and the coming of age of experimental evolution, the genetic bases of adaptation started to trigger more and more interest. Microbial experimental evolution played a particularly important role. Most experiments in that domain use asexual organisms, and initiate populations with a single individual. Therefore adaptation must result from de novo mutations. The existence of mutations providing resistance to phage and later on to antibiotics suggested that massive selective advantage were possible. As soon as 1951 (Atwood et al. 1951), using chemostat, it was shown that succession of selective sweeps were observed within a few hundreds of generations. In the 80ies and 90ies, the use of fitness assays through competitions, uncovered the effect of the mutations that were fixed. In particular, the long-term evolution of 12 replicate populations of Escherichia coli by R.E. Lenski unraveled succession of mutation fixations that reached up to 10% fitness effect (Lenski & Travisano 1994). Large effect mutations appeared therefore to be the drivers of adaptation. Consequently, microbial experimental evolution community favored genetic models of adaptation with mutations of large effects explicitly modeled and not just integrated through their effects on standing variation.

Multi-locus genetic models defining an adaptive landscape have been developed for a long time. For instance, Haigh developed the simplest genetic landscape (Haigh 1978) as a set of biallelic locus, each having similar contribution to fitness. This landscape has a single optimum, and the fitness of an individual carrying k mutations is simply w(k)=(1-s)^k, s being the selective effect of the non-optimal allele. The model was further modified in the 80ies to take into account epistasis: the impact on selection of mutation interactions (Charlesworth 1990, Kondrashov 1988). More elaborate models were further developed but in all cases all mutational parameters of the model were fully defined by the modeler. Consequently, the focus was more on mean fitness improvement or decay (Gordo & Charlesworth 2000) rather than on mutations themselves.

As experimental evolution unraveled some properties of adaptation, modelers turned to models with some emerging properties concerning adaptive mutations. The House of Card model (Gillespie 1983, Kingman 1978) is one of these models. Assuming mutations are sampled from a fixed distribution, a large population, through the action of natural selection, will move towards the high fitness tail of that distribution. Extreme value theory (EVT), which describes the properties of the tails of distribution, provided a theoretical framework to analyze the patterns of adaptation of populations (Gillespie 1991). EVT suggested for instance, that over a large range of conditions (Joyce et al. 2008), the distribution of fitness effects of substitutions fixed during adaptation should be exponential (Orr 2003). However the model being equivalent to single locus model with an infinite number of alleles, interactions among mutations could not be studied, while experimental data started to produce some results on epistasis (Visser et al. 2011).

In contrast, the NK model (Kauffman 1993) was built precisely upon the notion of genetic interactions between mutations. In this model, in which N loci are each in epistatic interaction with K others, the parameter K tuning the ruggedness of the landscape. A single peak exists with K=0, whereas the landscape is random (very rugged) with K=N. While the model has some rich properties, it suffers nevertheless from several drawbacks. Only a limited number of sites can be modeled and most importantly the statistical properties of the model are quite difficult to apprehend. The interesting domain in which multiple peaks of different heights are present seems incompatible with the convergence in fitness observed in most experimental evolution settings (Wiser et al. 2013).

With the latter models, the perspective on beneficial mutation became completely the opposite of the one of theoretical quantitative genetics. Adaptation was now envisioned as the result of a handful of large effect mutation and suggested that the use of discrete adaptive landscape was relevant. FGM, with its continuous space appeared first at odds with this perspective.

Yet, two highly influential papers uncovered the relevance and power of FGM. First, in a pioneer paper, Allen Orr (Orr 1998) showed that the FGM approach was relevant to study the genetics of adaptation. Rather than looking at the fraction of mutation that were beneficial or at the probability that these mutations would get fixed (Kimura 1983), he followed an adaptive path. He showed that the distribution of effects fixed in an adaptive walk was almost exponential and included large effect mutations. This observation matched some QTL analysis and showed that FGM could be used to study adaptation with a focus on individual beneficial mutations. Second, Burch and Chao showed (1999), using a bacteriophage hampered by a deleterious mutation, that small populations could adapt through the selection of numerous small effect beneficial mutations. They hence concluded that, as Fisher showed in his model, beneficial mutations of small effect were more numerous. This paper had two major impacts. It showed that FGM offered a reasonable framework to study microbial evolution, and in doing so it also suggested that the mutations were numerous enough for the continuous landscape used in FGM to be relevant.

Both papers revealed the quite paradoxical strength of FGM: despite being based on a continuous phenotypic landscape, it is relevant to study discrete genetic properties of the adaptive process. Over the last ten years, several studies have shown that the rate of beneficial mutations was high enough for a continuous approach to be relevant to study adaptation (Hietpas et al. 2013, Perfeito et al. 2007, Sanjuan et al. 2004a, Silander et al. 2007, Trindade et al. 2012). Moreover, the recent coupling of experimental evolution with whole genome sequencing has confirmed the idea that a large spectrum of beneficial mutations existed (Achaz et al. 2014). For instance, we evolved 114 populations of E. coli to a 42.2 °C (Tenaillon et al. 2012). The sequencing of the lineages revealed that a few functional units were the targets of selection, but that many alternative mutations could affect these targets. Up to hundreds of mutations could be selected for in a given gene, even when this one kept its function. Moreover, these mutations had slightly different selective effects as well as different pleiotropic side effects (Ostrowski et al. 2005, Rodríguez-Verdugo et al. 2013). The presence of hundreds or thousands of alternative beneficial mutations is enough to support a the shift from a discrete adaptive landscape to a continuous one.

Properties of the model

Now that the spirit of the model has been set up, I will describe in more details some of its emerging properties and their experimental support. All parameters are defined in table 1.

Mutational Properties of the model

Fraction of beneficial mutations

Let us first start by describing the bases of Fisher’s first use of the model (Figure 1AB). What is the fraction of beneficial mutation, P_ben, for an individual at a distance d from the optimum and a mutation vector of size r, with phenotypic complexity n? Though the model was initially derived by Fisher in 1930, the derivation was made much more explicit by Hartl and Taubes in 1996 (Hartl & Taubes 1996). For n >10, and $x=\frac{r}{2d}\sqrt{n}$

$$P_{\mathit{ben}}\left(x\right)\approx \sqrt{\frac{1}{2\pi }}{\int }_x^{\infty }{e}^{-\frac{u^2}{2}}\mathit{du}=\frac{1}{2}\mathit{erfc}\left(\frac{x}{\sqrt{2}}\right)$$

Several osbervations can be derived from this formula. First $\mathit{erfc}\left(\frac{x}{\sqrt{2}}\right)<1$, so P_ben(x) < 1/2; there is always an excess of deleterious mutations. This is in agreement with the common sense: mutations are more likely to disrupt things than to improve them. It also agrees with the mutation accumulation experiments done in microbes (Chao 1990, Kibota & Lynch 1996).

Second, when mutations have a small effect compared to the distance to the optimum (r/d<<1), P_ben can be close to 50%. It means that beneficial mutations can be extremely frequent when their effect is small. Geometrically, in these conditions, the curvature of the fitness isoclines at a distance d, is negligible compared to the curvature of the mutation radius. This was the initial point of Fisher, and was recovered in several experimental systems (Chao 1990, Maisnier-Patin et al. 2002).

Similarly, if r/d is small because d is large, or in other words, if the initial individual is extremely maladapted, then again the fraction of beneficial mutations will be high. The high rate of beneficial mutation in maladapted genotypes has been observed in many settings (Hietpas et al. 2013, Perfeito et al. 2007, Sanjuan et al. 2004a, Silander et al. 2007). First, it is a common experience among microbiologist that extremely debilitating genotypes can be compensated within a single colony growth. Moreover, using a more quantitative approach based on the evolution of bacteriophage, it was shown that as high as 20% of beneficial mutations could be found in extremely low fitness clones, while no beneficial mutations were detected in high fitness ones (Silander et al. 2007).

Finally, the higher the number of dimensions, the lower the fraction of beneficial mutations. This again complies with common sense intuition that mutation is more likely to disrupt a complex system than a simple one. In terms of mathematics it results from the fact that in high dimensions, the fraction of vectors that points towards the origin is vanishingly small.

Distribution of mutation effects

The evolutionary fate of populations is not only conditioned by the rate of beneficial mutations, but also based on the whole distribution of fitness effect of mutations (DFEM) that includes both beneficial and deleterious effects. To infer DFEM, the distribution of mutation sizes and the fitness decay function have to be further defined. In the canonical FGM, with isotropic mutations and circular fitness isoclines, if one uses the fitness function of equation 2, it can be shown that

$$p\left(s\right)=\frac{e^{-\frac{{\left(\frac{-s+s0}{\alpha }\right)}^{2∕Q}+{\left(\frac{s0}{\alpha }\right)}^{2∕Q}}{2{\sigma }^2}}}{\alpha Q{\sigma }^2}{\left(\frac{-s+s0}{\alpha }\right)}^{\frac{\frac{n}{2}+1-Q}{Q}}{\left(\frac{s0}{\alpha }\right)}^{(1-\frac{n}{2})∕Q}{I}_{\frac{n}{2}-1}\left(\frac{1}{{\sigma }^2}{\left(\frac{-s+s0}{\alpha }\right)}^{1∕Q}{\left(\frac{s0}{\alpha }\right)}^{1∕Q}\right)$$

with s0 being the mal-adaptation of the ancestor s0 = −log (W₀), σ² the variance of the Normal deviates used for mutations along each axes, I_k(y) the modified Bessel function of the first kind, and Q a parameter controlling the curvature of the fitness function (Table1). The moments are

$$\stackrel{‒}{s}=-\alpha {\sigma }^Q{2}^{\frac{Q}{2}}\frac{\Gamma \left(\frac{n+Q}{2}\right)}{\Gamma \left(\frac{n}{2}\right)}{}_{1}F_1\left(-\frac{Q}{2},\frac{n}{2},-\frac{1}{2{\sigma }^2}{\left(\frac{s0}{\alpha }\right)}^{\frac{2}{Q}}\right)-s0$$

$$\mathit{var}\left(s\right)={\alpha }^2{\sigma }^{2Q}{2}^Q\frac{\Gamma \left(\frac{n}{2}+Q\right)}{\Gamma \left(\frac{n}{2}\right)}{}_{1}F_1\left(-Q,\frac{n}{2},-\frac{1}{2{\sigma }^2}{\left(\frac{s0}{\alpha }\right)}^{\frac{2}{Q}}\right)-{(\stackrel{‒}{s}+s0)}^2$$

with ₁F₁ being the Kummer confluent hyper-geometric function. This simplifies in the case Q=2 to

$$\stackrel{‒}{s}=-\alpha n{\sigma }^2,$$

$$\mathit{var}\left(s\right)=2\alpha {\sigma }^2(-2s0-\stackrel{‒}{s})=-\stackrel{‒}{s}2\alpha {\sigma }^2(1+2\epsilon )$$

with $\epsilon =-\frac{s0}{\stackrel{‒}{s}}=\frac{s0}{an{\sigma }^2}>0$ as s0 > 0.

Using a moment matching approach, Martin and Lenormand (Martin & Lenormand 2006a) showed that with $\alpha =\frac{1}{2}$, Q=2, the distribution of effects was well approximated by a shifted negative gamma distribution:

$$p\left(s\right)=\frac{e^{-\left(\frac{s0-s}{a}\right)}}{\Gamma \left(b\right)}{(s0-s)}^{b-1}{a}^{-b}$$

$$a={\sigma }^2\frac{(1+2\epsilon )}{(1+\epsilon )},b=\frac{n}{2}\frac{{(1+\epsilon )}^2}{(1+2\epsilon )}$$

Which converges towards a normal distribution when n is large:

$$p\left(s\right)\sim \mathrm{N}\left(-\frac{{\sigma }^{2}n}{2},\sqrt{2\alpha {\sigma }^2\left(2s0+\frac{{\sigma }^{2}n}{2}\right)}\right)$$

This is quite similar to the distribution of effects found when the effect size of mutations is kept constant to r, as Waxman and Peck (1998) derived it (with r² = nσ²)

$$p(s,r)\sim \mathrm{N}\left(-\frac{r^2}{2},\sqrt{2\frac{r^2}{n}s0}\right)$$

Several observations can be made from these formulas. First, as long as selection is stabilizing as modeled by eq [2], the mean effect of mutations is always deleterious. Second, in the case Q=2, the average mutation effect is constant but the variance in effect increases with the distance to the optimum (Martin & Lenormand 2006b). In other words, in stressful environments, it is the variance in effects that should increase not the mean effect (Figure 1CD). This observation has found some experimental support (Martin & Lenormand 2006b). Third, the negative gamma distribution for the DFEM proposed has received strong experimental support (Hietpas et al. 2013, Jacquier et al. 2013, Martin & Lenormand 2006b, Sanjuan et al. 2004a, Trindade et al. 2012). Experiments in which single mutations were introduced into a gene (Hietpas et al. 2013, Jacquier et al. 2013), a virus (Sanjuan et al. 2004a) or a bacterial genome (Elena et al. 1998) have all produced this type of distribution when mutant fitness or proxies have been measured. Fourth and most importantly, these mathematical derivations suggest a highly dynamic DFME in the adaptive landscape. As mentioned before, the fraction of beneficial mutations does change, but also the overall shape of the distribution (Figure 1CD). This observation is also supported by some experiments. Using antibiotic resistance mutations (Trindade et al. 2012), or mutations centered in the active site of the chaperon HSP90 (Hietpas et al. 2013), it was shown that changes in the environment affected the variance of the distribution. Moreover, using two clones of beta-lactamase TEM-1, separated by a single stabilizing mutation, very different distribution of mutation effects on the enzyme efficiency were found (Jacquier et al. 2013). Finally, Barrick et al (2010) could also demonstrate that the distribution of beneficial mutations was changing among clones that differed in fitness due to a single point mutation. Clones with lower initial fitness had access to beneficial mutations of larger effects.

Distribution of epistasis

The change of the distribution of mutation effects with the position in the phenotypic space suggests that FGM has a built-in model of epistasis. Graphically this can be pictured by looking at the effect of a given mutation vector in different places of the space. The effect on fitness of a mutation may drastically change depending on its starting point (Figure 1A). For instance, a mutation that moves an individual phenotype closer to the optimum is beneficial, but the same change of phenotypes will be deleterious at the optimum. Epistasis can be defined as the difference in log-fitness between the double mutant (w₁₂/w₀) and the effects of the single mutant (w₁/w₀ and w₂/w₀):

$$e=\log \left(\frac{w_{12}}{w_0}\right)-\log \left(\frac{w_1}{w_0}\right)-\log \left(\frac{w_2}{w_0}\right)$$

Martin et al (2007) were the first to investigate the distribution of epistasis among pairs of mutations. If fitness is defined as in equation 1, then the average epistasis is null in the whole phenotypic space, $\stackrel{‒}{e}=0$, and is approximately distributed normally with a variance twice as large as the variance of mutation effects on fitness at the optimum, $V_m^{\ast }$. $\mathit{Var}\left(e\right)=2V_m^{\ast }$. Interestingly these results hold in the case of deviations from canonical FGM, with ellipsoids fitness isoclines and have found quantitative support with two datasets. Under fitness equation 2, the average epistasis at the optimum can be computed as $\stackrel{‒}{e}=(2-2^{Q^{∕}2})\stackrel{‒}{s}$ (Gros et al. 2009).

The fact that epistasis is distributed with both positive and negative values in FGM contrasts drastically with genetic models that studied the role of epistasis and allowed only positive or negative epistasis (Kondrashov 1988). Accordingly, experimental data on viruses (Sanjuan et al. 2004b), bacteria (Elena & Lenski 1997) and yeast (Costanzo et al. 2010) have all supported these broad distribution of epistasis and supported the prediction of the model.

When Q is different from 2, the mean epistasis can be shifted towards positive epistasis (Q<2) or negative epistasis (Q>2). Interestingly in that case, the intensity of epistasis is directly connected to the intensity of mutation effects, showing that epistasis and genetic robustness are intrinsically connected as it has been suggested in computational models (Wilke & Adami 2001).

When Q=2, the model also predicts that epistasis among beneficial mutations will be on average negative (Blanquart et al. 2014, Martin et al. 2007). The reason being that beneficial mutations tend to point toward the optimum, hence they tend to follow the curvature of the fitness function, which has a diminishing return. Once again this prediction fit quite well with experimental data (Chou et al. 2011, Khan et al. 2011).

The study of epistasis among beneficial mutations can be extended, to focus not only on pairs of mutations, but also on all possible combinations of mutations found in an adaptive walk. In several experimental systems, all possible combinations of 4 to 5 beneficial mutations were generated and an adaptive landscape build from their fitness effects (Chou et al. 2011, Khan et al. 2011, Weinreich et al. 2006). Despite its original continuity, similar landscapes can be obtained in FGM when focusing on a panel of mutations, for instance a set of mutations fixed in an adaptive walk (Blanquart et al. 2014). Interestingly, landscapes built from different realizations of stochastic adaptive walks in the same exact conditions were highly variable in terms of epistasis and accessible paths. Hence, FGM suggests, that despite their appealing simplicity, these small experimental landscapes contain limited information about the underlying architecture of the global adaptive landscape.

Distribution of dominance

FGM can also be used to study evolution in diploid populations (Manna et al. 2011). In that case, mutations will affect only one of the two copies of each gene. Assuming additivity on the phenotypic space between alleles at each locus, mutations generate heterozygotes, whose phenotype is intermediate between both homozygous. Dominance is then akin to the study of epistasis between two identical mutations in the haploid model.

The subsequent derivations that suggest an average dominance of 0.25 have found some global support in the experimental data available but will need more accurate testing (Manna et al. 2011). The benefit of FGM is that, contrary to other qualitative discussion on the emergence of dominance, it proposes a quantitative model that could be tested. Moreover any kind of dominance is present in the model, including over-dominance that occurs when a mutations overshoots the optimum. In that case, the heterozygous state is closer to the optimum than both homozygous and therefore over-dominance emerges (Sellis et al. 2011).

Adaptive Properties of the model

Distribution of substitutions

Once the distribution of mutation effects has been characterized, one can further study the mutations that will be fixed through adaptation from a given position in the landscape. To contribute to population adaptation, beneficial mutations need not only to appear, but also to survive genetic drift, a process that is directly coupled to the mutation’s impact on fitness. Kimura was the first study the problem and to moderate the micro-mutationist conclusions of Fisher (Kimura 1983). He showed that the frequent small effect mutations were mostly lost by drift and that mutations of intermediate size were the ones contributing most to adaptation.

Numerical solutions of the exact distribution, the gamma distribution, or analytical solutions for the normal approximation can be used to show that fixed mutations have larger effects than beneficials (Figure 1EF). When s0<<1, n is large and Q=2, the distribution of beneficial, s_b, and of fixed beneficials, s_f, can be described by a beta distribution $\frac{s_b}{\mid s0\mid }\sim \mathit{Beta}(1,n∕2)$ and $\frac{s_f}{\mid s0\mid }\sim \mathit{Beta}(2,n∕2)$ respectively (Martin & Lenormand 2008). If $x=\frac{r}{2d}\sqrt{n}=\sqrt{\frac{-n\stackrel{‒}{s}}{4s0}}=\frac{n\sigma }{2\sqrt{2s0}}>>1$ and n>>1, one finds $\frac{s_b}{s0}\sim \mathrm{\text{Exponential}}\left(\frac{n}{2s0}\right)$ and $\frac{s_f}{s0}\sim \mathrm{\text{Exponential}}\left(\frac{n}{4s0}\right)$, and $\overline{s_f}=\frac{4s0}{n}=2\overline{s_b}$. This approximation requires beneficial mutations to be very rare, such that EVT can be applied to the tail of the distribution. Note that the scaling by the overall mean mutation effects disappears in that case (Martin & Lenormand 2008, Orr 1998, 2006).

Adaptive walks

Adaptation is not only the process of a single beneficial substitution, but results from several substitutions. To study adaptive walks, one has yet to remember that the distribution of mutation effects is changing with position in the phenotypic space. Yet, Orr observed that there is some self-similarity in the process (Orr 1998). For instance, when x>>1, after a mutation is fixed with an average effect of $\frac{4s0}{n}$, the problem is similar with a new s0 of $s{0}_1=s0\left(1-\frac{4s0}{n}\right)$. The distribution of mutations fixed over an adaptive walk can then be studied and appears to be roughly exponential as suggested by some QTL analyses (Figure 1EF).

The rate of adaptation can also be computed (Orr 2000) when mutations are rare enough not to interfere. If one follows the log-fitness, the rate of improvement of log fitness is the production of beneficial mutation per generation, $N\mu {\int }_0^{+\infty }p\left(s\right)\mathit{ds}$, times the probability the beneficial mutation will survive drift $\frac{{\int }_0^{+\infty }2sp\left(s\right)\mathit{ds}}{{\int }_0^{+\infty }p\left(s\right)\mathit{ds}}$, times the selective effects of mutations surviving drift $\frac{{\int }_0^{+\infty }2s^{2}p\left(s\right)\mathit{ds}}{{\int }_0^{+\infty }2sp\left(s\right)\mathit{ds}}$. Hence, $\frac{d\ln \left(w\right)}{\mathit{dt}}=N\mathrm{\mu }{\int }_0^{+\infty }2s^{2}p\left(s\right)\mathit{ds}$, which can be numerically evaluated with exact or approximate solutions.

From this equation, a triple cost of complexity emerges (Orr 2000). As complexity increases, (i) there are fewer beneficial mutations, they have a smaller fitness effect, which (ii) diminishes their chance to survive drift and (iii) their influence on the rate of adaptation. At a given distance from the optimum, the rate of adaptation is maximal for an intermediate size of mutations (r or σ). However, this optimum effect size r does change with the distance to the optimum, so there is no mutational size that is optimal in the whole landscape: when far from the optimum, large mutations maximize the rate of adaptation, when close to the optimum small mutations do.

Here, I chose to focus only on models of asexual populations with a fixed optimum, however the model has also be used to analyze moving optimum (Gordo & Campos 2013, Kopp & Hermisson 2009) or even in some cases the impact of recombination (Peck et al. 1997). Moreover, recent developments have been made in which diploids rather than haploids have been studied. If mutations of large effects are common, then, regularly, some large effect mutations overshooting the optimum will be selected for. As a result the adaptive walk will recruit mutations with over-dominance effects (Sellis et al. 2011).

Equilibrium properties

If adaptation proceeds for long enough, what will be the fate of finite populations in FGM? The evolutionary fate of a finite population depends on the balance between the probability to produce and fix beneficial mutation and the probability to produce and fix deleterious ones. As we have seen in FGM, the distribution of mutation effects and the fraction of beneficial mutations are highly variable (Figure 2). The fact that fitness improvements are more likely as fitness decreases suggests the existence of fitness equilibriums (Hartl & Taubes 1998, Poon & Otto 2000, Tenaillon et al. 2007, Wagner & Gabriel 1990). In the limit of small mutation rate, if fitness is defined by equation 2, and effective population size is N, we could derive exact solution for the distribution of log fitness (Gros & Tenaillon 2009, McCandlish et al. 2014, Tenaillon et al. 2007).

$$p(-\log (w\left)\right)=\Gamma \left(-\log \left(w\right),\frac{n}{Q},2N-2\right)=\frac{{(2N-2)}^{n∕Q}}{\Gamma (n∕Q)}{(-\log (w\left)\right)}^{\frac{n}{Q}-1}{e}^{(2\mathrm{N}-2)\log \left(w\right)}$$

$$\overline{\log \left(w\right)}=-\frac{n}{Q(2N-2)}\approx -\frac{n}{2\mathit{QN}}$$

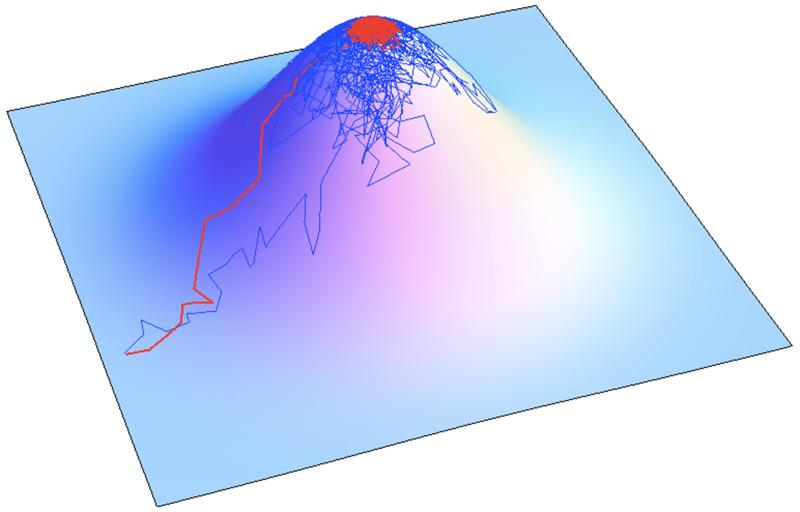
Figure 2.

Populations evolve toward some mutation-selection-drift-equilibrium depending on their population size. Here the adaptive walks are presented starting from a non-optimal phenotypes, one with a population size of 5 (Blue) and another one of 100 (Red).

The equilibrium represents the loss of fitness due to drift: the drift load. The contribution to drift load of the ratio between effective population size and phenotypic complexity, reveals that natural selection requires very large population sizes to be efficient enough to optimize many traits simultaneously. The epistasis parameter Q contributes also to the load. The higher the value of Q, the lower is the mean epistasis and the lower the load. Increasing Q leads to more and more drastic costs of deleterious mutations as they accumulate, and therefore an easier action of natural selection to filter them out. Finally, as long as the mutational process is symmetrical (mutating from phenotype A to phenotype B is as likely as going from B to A), it does not contribute to the load. The pleiotropy and size of mutations (see later), the existence of modules or the mutation rate have no impact, and each of the trait contribute an equal share of 1/4N to the load (Tenaillon et al. 2007). The existence of these equilibria is still debated, but some experiments suggest their existence. Fitness of populations with low and high fitness were found to converge toward similar fitness value when evolved with of similar sizes: high fitness populations decayed while low fitness populations adapted, suggesting convergence in fitness (Silander et al. 2007, Tenaillon et al. 2007).

Indeed, if the mutation rate is such that Nμ<<1 the contribution of recurrent mutations to the load, or mutation load, is −μ; it can be added to the drift load. When Nμ is larger than one, the mutation load can be computed as $-\sqrt{\frac{n}{2}\mathrm{\mu }\stackrel{‒}{s}}$ which is no longer independent of the mutation process (Lande 1980, Martin & Gandon 2010, Roze & Blanckaert 2014)

Molecular evolution

FGM can also be used to study molecular evolution. Interestingly, at MSDE, evolution is still going on and an equal share of beneficial or deleterious mutations are fixed (Hartl & Taubes 1996, Razeto-Barry et al. 2011, 2012; Sella & Hirsh 2005) (but see McCandlish et al. (2014) for an interesting perspective on mutations at equilibrium). MSDE can therefore be used to study molecular evolution and even the accumulation of incompatibilities between populations evolving independently (Chevin et al. 2014). Under simplifying assumptions, Gu suggested that the mean rate of evolution as well as its heterogeneity among sites could be linked to the parameters of the model (Gu 2007). Moreover using recurrent shifts of the optimum, it was shown that the rate of molecular evolution was more linked to phenotypic complexity than to population size (Lourenco et al. 2013).

Selective pressure on FGM parameters

As we have seen, the various parameters of the model influence the adaptive process. So, if these parameters show heritable variation, they could evolve by natural selection. In FGM formalism, these parameters are kept constant and their impact on the processes can be compared, but not the selective pressure controlling the evolution of the parameters themselves. This can however be done with the use of modifiers: an additional locus controlling the value of the parameters is added to FGM and its quantitative evolution followed.

This approach has been performed on the genetic robustness parameter, α (Gros & Tenaillon 2009), and on the epistasis parameter, Q (Gros et al. 2009), at equilibrium with low mutation rate. For instance, with some similarly to a previous genetic model (Krakauer & Plotkin 2002), it was shown that, if reducing the fitness consequences of mutation effects on traits (by reducing α) comes at a cost, two selective regimes exists. If the ratio of population size to phenotypic complexity is large, N/n >> 1, selection removes efficiently deleterious mutations and the cost of robustness is too much of a burden; minimal robustness evolves. However, in the opposite case, N/n << 1, the populations are loaded with deleterious mutations, there is consequently a short-term benefit to decrease the fitness consequences of mutations, and costly robustness is selected for. However, once the new robustness is selected, the population moves to the new equilibrium fitness, and its fitness decreases again. Hence in that regime the population is captured in a vicious circle in which ever increasing robustness is selected for and fitness keeps declining in the long-term, a situation coined the “paradox of robustness” (Frank 2007).

These observations are relevant in the context of protein repair by chaperons. The overexpression of chaperons, has been shown to decrease the effect of deleterious mutations (Fares et al. 2002), as chaperon enforce the folding of destabilized mutant proteins. Yet this repair comes at a cost: production of chaperons and use of ATP. Interestingly, the “paradox of robustness” seems to be at work in obligate endo-symbionts that have low effective population size, a very high production of chaperons and proteins of low stability (Gros & Tenaillon 2009).

Finally, from a theoretical point of view, these models show that robustness can be selected for by drift and not only by elevated mutation rate which is the commonly accepted hypothesis (de Visser et al. 2003).

So far these modifier approaches have been studied only at MSDE, it is also possible to study them in other regimes, for instance during adaptation or when mutation rate is high.

FGM parameters

FGM appears to be a relevant toy model giving some qualitative and quantitative facets of evolutionary genetics. It is now becoming a standard reference model on which any quantitative observations on mutations and adaptation should be projected. In that sense it is becoming similar to the idealized Wright Fisher population (WFP) in population genetics. This constant size population of hermaphrodite in pan-mixy has no biological reality. However, population with different demography and reproductive regime can be projected on that model and be attributed an effective population size which is the only parameter of the model. This allows for instance populations of farm-animals and Drosophila populations to be compared. FGM is more complex than WFP, but, as we have seen, can be characterised by three meta-parameters defining the landscape and one defining the initial fitness of the population. How can such parameters be estimated or chosen?

Fitness function

The fitness decay of the form W(d) = e^−αdQ has been mostly used. The parameter α, is a scaling factor that can be compensated by a change of scale in the phenotypic axis. However if some phenotypic measure are performed and linked to fitness then it can be fitted to the data. What should be the value of Q? Measures of epistasis strongly support an almost centered distribution of epistasis and therefore support a value of Q around 2. Moreover, when close to an optimum an FGM like model with Q=2 seems to emerge in a very large set of conditions (Martin 2014). A value of Q different from 2 should nevertheless be used only if the mean epistasis significantly deviates from 0, or if the mean effect of mutations does consistently change with the level of adaptation, which may be the case at the gene level (Jacquier et al. 2013).

The model used in FGM assumes that fitness isoclines are circular, yet the model can be extended to include anisotropy in the selection and mutation processes, leading to ellipsoidal fitness isoclines and mutational cloud (Martin & Lenormand 2006a, Waxman & Welch 2005). This can be done assuming a mutation matrix M and the fitness function $W\left(z\right)=e^{-\frac{z^{T}Sz}{2}}$, z being the position vector, and S being a selection matrix. Both in M and S, non-diagonal terms represent covariances among the different phenotypes. The model can nevertheless be reduced to an isotropic FGM having similar mutational properties and an effective number of dimensions equal to

$$n_e=\frac{n}{1+\mathit{CV}{\left({\sigma }_i^2\right)}^2}=\frac{nE{\left({\sigma }_i^2\right)}^2}{E\left({\sigma }_i^4\right)}\text{and}{\sigma }_e^2=E\left({\sigma }_i^2\right)(1+\mathit{CV}{\left({\sigma }_i^2\right)}^2)=\frac{E\left({\sigma }_i^4\right)}{E\left({\sigma }_i^2\right)}$$

with ${\sigma }_i^2$ being the Eigen values of the S.M matrix and CV standing for coefficient of variation and E for Esperance (Martin & Lenormand 2006a). This is a moment matching transformation. It computes n_e as the number of dimensions, each affected similarly (while the n-ne other dimensions are not affected), such that the mean and variance of ${\sigma }_{\mathit{i}}^2$ over all n traits are identical to the one observed. For instance, if there are large differences in the selective pressure acting on the different axes $(\mathit{CV}{\left({\sigma }_i^2\right)}^2>>1)$ then the mutational properties of the system will be equivalent to a FGM model with a very limited number of dimensions.

Mutations effect size

Mostly two theoretical approaches have been used for the effect size of the mutation vector: either a single value, r, (Fisher 1930, Orr 1998) or a distribution (Chi square) resulting from a multivariate Gaussians deviation of standard deviation, σ, along each phenotypic axis (Gros et al. 2009, Martin & Lenormand 2006a). In both cases, and especially when comparing with data, most authors maintain constant the effect size of the vector across phenotypic complexity. Hence, in the constant r model, r is fixed across dimensions and when r is drawn in a distribution,${\sigma }^2=-\frac{\stackrel{‒}{s}}{\alpha n}$ such that the mean effect of mutations is kept constant and can be fitted to experimental measurement of $\stackrel{‒}{s}$. Under this scaling, both models converge when n is large. Indeed in the Gaussian multivariate model, the square of the length of the vector r² has a chi-squared distribution with n degree of freedom and with mean – $\frac{\stackrel{‒}{s}}{\alpha }$ and variance $\frac{2{\stackrel{‒}{s}}^2}{{\alpha }^{2}n}$ which is roughly equivalent to a constant r when n is large.

When at the optimum, this scaling can give some non-biological distribution of effects in the case of large dimensions (Figure 1D). Indeed, the model then implies that all mutations have about the same deleterious effect and consequently suggests the absence of both large and small effect mutations. Consequently, either dimensionality is small, or the hypothesis of universal pleiotropy is wrong.

Pleiotropy

The concept of pleiotropy has been defined more than a century ago (Stearns 2010), and refers to the idea that a mutation affects several phenotypic traits simultaneously. Yet, in the different fields of biology, pleiotropy have slightly different meanings that only partially overlap (Paaby & Rockman 2013). With recent high-through-put methods (Nichols et al. 2011, Wang et al. 2010) and quantitative genomics approaches (Wagner et al. 2008) some large-scale analysis of pleiotropy have been performed. They suggest (using gene knock-down mostly) that only a few mutations affect many traits and seem to reject the idea of universal pleiotropy (Nichols et al. 2011, Wagner & Zhang 2011, Wagner et al. 2008, Wang et al. 2010). Moreover they suggest that pleotropic mutations have a larger effect than the less pleiotropic ones. However, there is still some debate on the extent of pleiotoropy due to some technical issues on the contribution of measurement error, the definition of the phenotypic traits that are sometimes measured in different environments, or the estimation of pleiotropy for lethal mutations (Paaby & Rockman 2013). The point here is not to discuss at length pleiotropy (see Wagner & Zhang 2011 for that purpose), but rather to see how departure from universal pleiotropy will affect the results we discussed previously and how could it be estimated from the data.

Restricted pleiotropy does not affect the drift load results (Tenaillon et al. 2007), but the distribution of mutation is fully dependent on it (Chevin et al. 2010, Lourenco et al. 2011). If all mutations have a pleiotropy of m, then at the optimum, the mean effect of mutation scales with m rather than with n (Lourenco et al. 2011) and could be used to infer pleiotropy. However, away from the optimum and even more if there is a distribution of pleiotropy, all derived formula can not be computed any more, though some quantitative predictions may still hold (Chevin et al. 2010).

The cost of complexity may be affected by pleiotropy, but it may depend on the scaling that is used between mutation effects and pleiotropy. In FGM, pleiotropy can be defined as the dimension of the hyper-space that mutations in a locus may reach (Chevin et al. 2010), and therefore be independent of size effects. Alternatively, it can be a directly linked to the length of the mutation vector (Lourenco et al. 2011): a more pleiotropic mutation affects more traits and has an overall increased length. In the later case, intermediate pleiotropy results in the higher adaptation rate (though as seen previously the optimal pleiotropy is changing with adaptation) (Wang et al. 2010). Yet there always seem to be a cost of complexity as the fraction of mutations (Welch & Waxman 2003) pointing toward the optimum is always limited when the number of dimension is high.

Phenotypic complexity

The final parameter of the model is the dimensionality of the phenotypic space. This parameter is quite important for its mathematical contribution to the previous results, but also for its biological interpretation. As for the case of pleiotropy, we tackle here a concept that extends further than its mathematical definition in FGM. Complexity is a widely mentioned concept in biology. Nevertheless it has a myriad of definitions most of them un-precise and subject to anthropocentrism. With FGM phenotypic complexity is a quantitative measure that reflects the number of variationally quasi independent traits an organism is exposing to the action of natural selection in a given environment. FGM’s definition of complexity is not only powerful as it is centered on the unifying concept of biology, natural selection, and can therefore be applied to all evolving organisms; but it also offers a full theoretical background to analyze it (Le Nagard & Tenaillon 2013, Le Nagard et al. 2011).

Based on mathematical derivations, FGM offers various ways to estimate an effective phenotypic complexity. Unfortunately they reveal different facets of the model and echoed in that sense some limitations of the concept of effective population size that depends on whether we want to focus on neutral, deleterious or beneficial mutations.

-The first derivation is an ideal one and corresponds to a statistical vision of FGM (Le Nagard et al. 2011). If all traits could be measured for thousands of genotypes then the dimensionality of the space could be derived through a principal component analysis. Though this is hard to perform on real organisms, it can be applied to artificial systems. Nevertheless some high throughput data make this approach more realistic in the near future.

-The second comes from fitting the distribution of mutation effects, including all mutations or only beneficials. Martin and Lenormand (2006a) showed that the moments of the distribution of mutation effects could be used to infer the phenotypic complexity: assuming a multivariate normal distribution of mutation effects on traits $n=\frac{\mathit{var}\left(s\right)}{{\stackrel{‒}{s}}^2}$ at the optimum. Applying this formula to some existing data revealed a surprisingly low phenotypic complexity ranging from 0.5 from bacteria, to 1 for yeast (Hietpas et al. 2013) and 3 for Caenorabditis elegans. Indeed, as we mentioned before, these estimates heavily rely on the hypotheses of universal pleiotropy and may be better interpreted as a proxy of pleiotropy (m) rather than the dimensionality of the space (n). Other methods have been derived based on beneficial mutations. Bataillon et al (2011), Sousa et al (2012) studied the distribution of beneficial mutations in various environments or genetic backgrounds (loaded with a deleterious mutation linked to antibiotic resistance) to compute a complexity ranging from about 3 in Pseudomonas fluorescence to 26 for E. coli. Later on (Perfeito et al. 2014), they used mutation accumulation and compensation to derive an estimate of 9 for E. coli. Finally, the precise distribution of epistasis between mutations has also been proposed to provide a proxy for complexity (Weinreich & Knies 2013) but experimental noise combined with the assumption that the initial genotype is at the fitness peak may limit the power of this method.

-The MSDE derivations provide some alternative estimates of complexity. As they are independent of the mutation process, they are not affected by pleiotropy or any scaling of the mutation processes (Tenaillon et al. 2007). However, these results hold only if the mutation rate is low, and they moreover require the evolution of populations for long enough to reach equilibrium, an approach that is only amenable to experiments in microbes or artificial systems. When applied on two viruses, it gave a complexity of 40 or 10.

Which complexity should the modeler use? It seem that under the hypothesis of universal pleiotropy, a low effective complexity should be utilized. Under these assumptions, the model will be mostly useful in terms of distribution of mutation effects and accumulation of random mutations or short-term adaptation. If one is interested in long-term adaptation, it is likely that a higher phenotypic complexity should be utilized presumably associated with some restricted pleiotropy but more theoretical developments are needed. Indeed the adaptive process as well as the drift load is affected by the total number of dimensions of the phenotypic space, which defines the fraction of mutations that points toward the optimum.

Perspectives on FGM and genetics

FGM is a quite powerful framework to study evolution, yet as we have seen with dominance, pleiotropy or estimation of dimensionality there is still some progress to be made. What is now needed is a deeper biological understanding of the model. In other words, how can the molecular determinants of an organism in an environment generate an evolutionary process that is largely compatible with FGM?

Taking into account the nature of mutations

Several aspects of the mutation process are still poorly studied in FGM. As we have seen much progress could be made to uncover the effects of restricted pleiotropy on the distributions of effects as well as on long-term adaptation. The impact of large mutation rate on equilibrium properties has been studied (Martin & Gandon 2010, Roze & Blanckaert 2014, Wagner & Gabriel 1990), but extending these results to analyse the adaptive process is another interesting perspective. It is worth noting that in that regime, returning to additive variance and a Gaussian cloud to describe the population may be an interesting alternative (Hallatschek 2011, Wagner & Gabriel 1990).

What is further required to compare FGM to real data is the integration of gene knock-outs. If one assumes that expression of a gene may be a trait under selection, then the FGM landscape does not incorporate appropriately the properties of gene knock-outs. These mutations are bringing the traits value to a minimum. As a consequence the context dependency of a gene knock-out mutations may differ quite drastically from FGM predictions and may lead to the existence of some boundaries in the space of accessible trait values. Incorporating the statistical properties of these knock-outs may make the model more realistic.

The meaning of complexity

Many progresses could be made if we gained a more biological understanding on phenotypic complexity and could infer it from the molecular constituents of an organism. First, the use of FGM to depict and eventually to predict organismal evolution could be extended to non-model organisms that are not amenable to evolutionary experiments in the laboratory. Second, the different organisms, or their system’s biology representation could be compared in an evolutionary perspective. Take a metabolic network for instance. From genome sequences, the topology of these networks can be built and subsequently quantitatively analyzed with Flux Balance Analysis (Lewis et al. 2012). It remains nevertheless quite hard to compare the evolutionary properties of different networks. Yet, if one could compute their complexity, networks could be ranked and compared in FGM framework. Third the selective pressures acting on phenotypic complexity could be studied through comparative approaches and the forces shaping the evolution of complexity could be studied. The emergence and evolution of complexity is an important question in biology and FGM offers an interesting framework to study it, yet so far complexity is only associated with a cost in FGM.

To proceed in that direction, we can use the phenotypic complexity estimates we have previously described but rather than applying them on real organisms for which we have no clear idea of the complexity, we can use them on artificial system with calibrated complexity. Le Nagard et al (2011) used that methodology; they compared various estimates of phenotypic complexity on artificial neural networks that evolved in a Darwinian way. The networks had different sizes and were asked to perform tasks constituting a gradient of complexity. While a simple task was to fit a polynomial of order 2, a complex task was to fit one of order 8. It was found that the phenotypic complexity correlated with the complexity of the task performed more than with the size of the evolving network. Moreover, this abstract computational model revealed both a mechanistic and a selective process that resulted in higher complexity. Mutations that decoupled the impact of further mutations on the various traits under-selection resulted in a higher complexity. They could be selected for as they allowed a fine-tuning of the different phenotypic values. Hence, complexity resulted mechanistically from the decoupling of mutation effects on the different phenotypes, and was selected for as it allowed fitness improvement that could not be reached if mutations affected all traits similarly. An intermediate complexity was selected for each task, reflecting the balance between the, afore mentioned, benefits of complexity and the costs that FGM predicts. Though based on a fully artificial system, these results provided some interesting insights on phenotypic complexity. When extrapolated to more real systems, they support the gene duplications vision of complexity proposed by Ohno (1970). After a duplication, mutations can affect the expression or function of only one of the two copy which can then perform a new task or be expressed in different tissues. This initial work opens on rich perspectives, but more biological models have now to be tested to confront the power of this approach and to give some further insights on the molecular determinants of phenotypic complexity.

The molecular bases of epistasis

Along the same lines, thanks to phenotyping methods, the molecular bases of epistasis could now be compared with the sources of epistasis in FGM. For instance, negative epistasis between beneficial mutations in FGM may come from optimum overshooting. When two highly beneficial mutations in the ancestral background are combined, they may overshoot the optimum resulting in a decline in fitness. Some recent work suggests that this pattern is sometimes found. Alternative mutations down-regulating the expression of an exogenous gene carried on a plasmid presented a strong pattern of negative epistasis (Chou et al. 2014). Tight control of the expression of the gene revealed that, while individual mutations improved fitness through a decreased cost of expression, the combination of mutations down regulated expression too much. Further experiments connecting the mutations involved in adaptation to phenotypes in the light of FGM will help us better understand the relevance of this phenotypic model.

Conclusion

FGM is an integrated model of adaptation in which many quantitative predictions emerge. These predictions concern many facets of evolutionary genetics: distribution of fitness effect, epistasis, dominance, distribution of fixed mutations, adaptive trajectories, equilibrium fitness. These quantitative predictions can be tested experimentally and as we have seen, many of them have found some experimental support and moreover allowed, in some cases, parameters of the model or effective parameters to be inferred. Therefore FGM can readily be used as a reference model of adaptation. Rather than developing new specific models, evolutionary biologist should use FGM in the set of models to be tested to confront any evolutionary genetics data.

Despite its apparent simplicity the model is extremely rich. Some of its properties such as the distribution of epistasis, or the existence of some non-null fitness equilibrium challenge some of the classical models of population genetics. They suggest revisiting the role of epistasis on the evolution of recombination or the process of Muller’s Ratchet (Wagner & Gabriel 1990). The pervasive role of epistasis in FGM, in agreement with observations in microbial experiments (Jacquier et al. 2013, Moore et al. 2000, Perfeito et al. 2014, Poon & Chao 2005, Silander et al. 2007) could now be used beyond the scope of microbes and its consequences investigated in other fields of biology such as conservation biology or medical human genetics in which the conceptual framework FGM offers could be very beneficial.

Glossary

Phenotypic complexity

the number of statistically independent phenotypic traits an organism is exposing to natural selection in a given environment.

Pleiotropy of a mutation

The number independent phenotypic traits a mutation is affecting

Universal pleiotropy

The fact that all mutations affect all phenotypic traits. In standard FGM, it is equivalent to the isotropy of mutations

Epistasis

The impact on fitness of mutation interactions, measured for pairs of mutation as the difference between double mutant log-fitness effect and the sum of single mutant log-fitness effects

Genetic robustness

The mean selective effect of mutations

Drift Load

The loss of fitness associated with the fixation of deleterious mutation caused by the inefficiency of selection in small populations

Mutation Load

The loss of fitness due to the recurrent production of deleterious mutations