High-Resolution Traction Force Microscopy

Abstract

Cellular forces generated by the actomyosin cytoskeleton and transmitted to the extracellular matrix (ECM) through discrete, integrin-based protein assemblies, that is, focal adhesions, are critical to developmental morphogenesis and tissue homeostasis, as well as disease progression in cancer. However, quantitative mapping of these forces has been difficult since there has been no experimental technique to visualize nanonewton forces at submicrometer spatial resolution. Here, we provide detailed protocols for measuring cellular forces exerted on two-dimensional elastic substrates with a high-resolution traction force microscopy (TFM) method. We describe fabrication of polyacrylamide substrates labeled with multiple colors of fiducial markers, functionalization of the substrates with ECM proteins, setting up the experiment, and imaging procedures. In addition, we provide the theoretical background of traction reconstruction and experimental considerations important to design a high-resolution TFM experiment. We describe the implementation of a new algorithm for processing of images of fiducial markers that are taken below the surface of the substrate, which significantly improves data quality. We demonstrate the application of the algorithm and explain how to choose a regularization parameter for suppression of the measurement error. A brief discussion of different ways to visualize and analyze the results serves to illustrate possible uses of high-resolution TFM in biomedical research.

INTRODUCTION

Cell contractile forces generated by the actomyosin cytoskeleton and transmitted to the extracellular matrix (ECM) through integrin-based focal adhesions drive cell adhesion, spreading, and migration. These forces allow cells to perform vital physiological tasks during embryo morphogenesis, wound healing, and the immune response (DuFort, Paszek, & Weaver, 2011). Cellular traction forces are also critical for pathological processes, such as cancer metastasis (Wirtz, Konstantopoulos, & Searson, 2011). Therefore, the ability to measure cellular traction forces is critical to better understand the cellular and molecular mechanisms behind many basic biological processes at both the cell and tissue levels.

Various experimental techniques for quantitative traction force mapping at spatial scales ranging from multicellular sheets to single molecules have been developed over the last 30 years. Traction force microscopy (TFM) was pioneered by Harris, Wild, and Stopak (1980), who showed that fibroblasts wrinkle an elastic silicone rubber substrate, indicating the mechanical activity. By applying known forces, Harris et al. were able to calibrate this technique and to assess the magnitude of traction forces. However, limitations of this approach include difficulty in force quantification due to the nonlinearity of the silicone rubber deformation and low spatial resolution (Beningo & Wang, 2002; Kraning-Rush, Carey, Califano, & Reinhart-King, 2012). Further development of this approach, which combined high-resolution optical imaging and extensive computational procedures, dramatically improved the resolution, accuracy, and reproducibility of traction force measurements and transformed TFM into a technique with relatively wide use in many biomedical research laboratories (Aratyn-Schaus & Gardel, 2010; Dembo & Wang, 1999; Gardel et al., 2008; Lee, Leonard, Oliver, Ishihara, & Jacobson, 1994; Ng, Besser, Danuser, & Brugge, 2012).

These days, plating cells on continuous, linearly elastic hydrogels labeled with fluorescent fiducial markers is the method of choice to visualize and to measure traction force exerted by an adherent cell. As a cell attaches to the surface of the substrate, it deforms the substrate in direct proportion to the applied mechanical force. These elastic deformations can be described quantitatively with high precision by continuum mechanics. Since the first introduction of this technique (Dembo, Oliver, Ishihara, & Jacobson, 1996), a variety of elastic materials and labeling strategies have been explored in order to improve measurement accuracy and to extend the number of biological applications where TFM can be applied (Balaban et al., 2001; Beningo, Dembo, Kaverina, Small, & Wang, 2001; Dembo & Wang, 1999).

Due to superior optical and mechanical properties, polyacrylamide hydrogels (PAAG) have become the most widely used substrates for continuous traction force measurements. PAAG are optically transparent, allowing a combination of TFM with either wide-field or confocal fluorescence microscopy to complement traction force measurements with the analysis of cytoskeletal or focal adhesion dynamics (Gardel et al., 2008; Oakes, Beckham, Stricker, & Gardel, 2012). The mechanical properties of polyacrylamide are also ideal for TFM since the gels are linearly elastic over a wide range of deformations and their elasticity can be tuned to mimic the rigidity of most biological tissues (Discher, Janmey, & Wang, 2005; Flanagan, Ju, Marg, Osterfield, & Janmey, 2002). Moreover, covalent cross-linking of PAAG with specific ECM proteins allows control of biochemical interactions between the cell and the substrate to activate distinct classes of adhesion receptors and, ultimately, to mimic the physiological microenvironment for various cell types.

Concurrent with development of TFM-optimized elastic materials, much effort was undertaken to improve the accuracy and spatial resolution at which the cell-induced substrate deformation is measured (Balaban et al., 2001; Beningo et al., 2001). Recently, TFM substrates labeled with a high density of fluorescent microspheres of two different colors have been developed (Sabass, Gardel, Waterman, & Schwarz, 2008), allowing analysis of the distribution and dynamics of traction forces within individual focal adhesions (Plotnikov, Pasapera, Sabass, & Waterman, 2012).

The protocols described in this chapter are geared toward setting up and performing high-resolution TFM to quantify cell-generated traction forces at the scale of individual focal adhesions. We discuss the fundamentals and experimental considerations important for designing a high-resolution TFM experiment. This background is particularly important for new users since high-resolution TFM is a highly interdisciplinary technique borrowing some of its key concepts from optical microscopy, polymer chemistry, soft matter physics, and computer sciences. Here, we target an advanced audience and assume high-level knowledge in cell biological lab procedures (including mammalian cell culture and transfection), light microscopy-based live-cell imaging (including DIC, epifluorescence, spinning-disk confocal imaging, and digital imaging), image processing, and mathematics (including differential calculus and programming in a high-level computer language, e.g., MATLAB). The chapter is designed to provide such readers with specific protocols that will allow them to perform high-resolution TFM.

BASIC PRINCIPLE OF HIGH-RESOLUTION TRACTION FORCE MICROSCOPY (TFM)

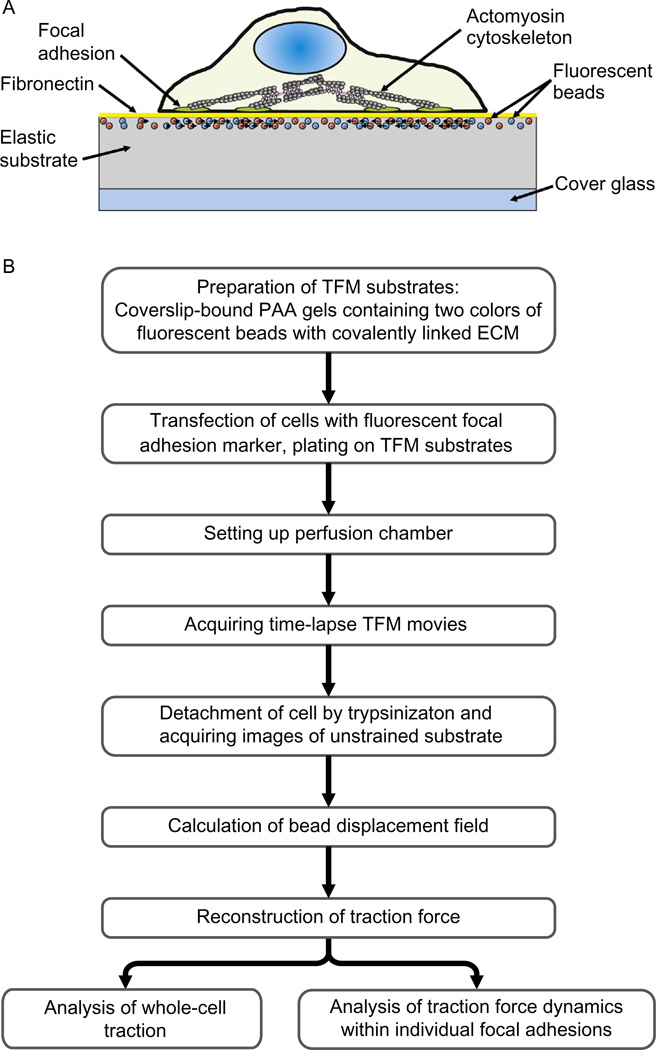
High-resolution TFM is an experimental technique that utilizes computational analysis of the direction and the magnitude of elastic substrate deformations to reconstruct cell-generated traction forces with submicrometer spatial resolution (Fig. 20.1). These deformations are detected by capturing the lateral displacement of fiducial markers, that is, fluorescent beads embedded in the substrate, due to mechanical stress applied by an adherent cell. Experimentally, the displacements are measured by comparing images of fluorescent beads in the strained gel, that is, when the cell exerts force on the substrate, with the unstrained state after the cell has been detached from the substrate either enzymatically or mechanically. Tracking displacement of individual beads followed by numerical modeling of the substrate displacement field based on elastic mechanics yields detailed two-dimensional vector maps of traction forces beneath the adherent cell.

FIGURE 20.1.

Schematic diagram of the procedure for performing high-resolution traction force microscopy (TFM) on a compliant PAA substrate. (A) Schematic of a TFM experiment depicting elastic substrate deformed by an adherent cell. (B) Flowchart for high-resolution TFM.

The spatial resolution of TFM is determined by the spatial sampling of the displacement field (Sabass et al., 2008), which is limited by the density of fiducial markers and the optical resolution of the microscope. Thus, labeling the elastic substrate with fiducial markers at the highest possible density is essential for high-resolution measurements. However, the necessity for resolving individual beads by the microscope to track their movement limits the density of fiducial markers and restricts spatial resolution of the displacement field. This holds true only if all fiducial markers are observed simultaneously. While this is applied for conventional TFM, recent studies have demonstrated that separation of fiducial markers in the wavelength domain by labeling the substrate with fluorescent beads of two different colors overcomes this limitation (Fig. 20.2), doubles the spatial resolution of the displacement field, and allows analysis of traction forces at the submicrometer scale (Plotnikov et al., 2012; Sabass et al., 2008). Using multiple colors of fiducial markers also improves accuracy and reliability of traction force measurements by decreasing the noise and irregularities in bead tracking. These improvements can only be achieved if the displacement fields for both channels are quantified with similar precision, which requires an integrated and automated workflow of cell experiments and image processing.

FIGURE 20.2.

Two colors of fluorescent beads in polyacrylamide (PAA) TFM substrates increase the effective bead density. Confocal images of the uppermost surface of a PAA gel containing red and far-red fluorescent nanobeads visualized by red (left panel, also shown in red on color overlay) and far-red (middle panel, also shown in green on color overlay) fluorescence imaging. Scale bar = 5 µm.

PRINCIPLES OF TRACTION RECONSTRUCTION

Almost all procedures for traction reconstruction are based on the theory of linear elastostatics (Landau & Lifshitz, 1959), providing a convenient and tractable mathematical framework. We employ a Cartesian coordinate system where the coordinates (x₁, x₂) lie in a plane parallel to the relaxed surface of the TFM hydrogel. The third, normal coordinate x₃ is positive above the gel. Deformations along the coordinate i are denoted by u_i. Variation of u_i in space causes strain, which is the relevant physics concept here because only relative deformations generate elastic restoring forces. In undeformed coordinates x_i, the strain tensor is given by

$${\epsilon }_{ij}=\frac{1}{2}(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j}+\sum _{k=1}^3\frac{\partial u_k}{\partial x_i}\frac{\partial u_k}{\partial x_j})\approx \frac{1}{2}(\frac{\partial u_j}{\partial x_i}+\frac{\partial u_i}{\partial x_j})$$ (20.1)

The approximate equality in the last term is necessary to make the theory linear since the quadratic term represents geometric nonlinearities. This approximation implies that the length scale x_A over which the displacement varies is larger than the scale u_i of the displacements. For TFM, x_A is determined by the typical size of a focal adhesion and is usually on the order of 1 µm. Therefore, for high-resolution TFM, the displacements of the gel should satisfy u_i < 1 µm.

For linearly elastic materials, the stress σ_ij is proportional to ε_ij (Hooke’s law). On further assuming a stress-free reference state and homogeneous, isotropic, memory-less gels,

$${\sigma }_{ij}=\frac{E}{1+s}({\epsilon }_{ij}+\frac{s}{1-2s}{\delta }_{ij}\sum _{k=1}^3{\epsilon }_{kk}),$$ (20.2)

where E is Young’s modulus, the determinant of the material rigidity, measured in pascal (N/m²). The dimensionless quantity s is Poisson’s ratio, a measure of the compressibility of the material. Incompressible materials are characterized by s = 0.5. Other quantities used to describe elastic behavior, such as the shear modulus or the Lamé coefficients, can be converted to the pair (E, s).

Adherent cells apply forces only to the surface of the elastic gel where x₃ = 0. Since spatial variations of the stress σ_ij inside the bulk of the gel would require forces where none are applied, we have 0 = ∂σ_ij/∂x_j for x₃ < 0. On the surface, the cell exerts a force per area, “traction,” denoted by f_k. The traction is balanced by the surface stress resulting in the deformations u_1,2 at x₃ = const. ≤ 0. Mostly, the vertical forces are negligible; thus, 0 = σ_zz(x₃ = 0). It is assumed frequently that the gel is infinitely extended in the (x₁, x₂) plane and extends from x₃ = 0 to x₃ = −∞, which determines the remaining boundary conditions. Due to the linearity of the problem, the solution can be generally written as

$$u_i(x_1,x_2,x_3)=\int \sum _{j=1}^2{G}_{ij}(x_1-x_1^{\prime },x_2-x_2^{\prime },x_3)f_j(x_1^{\prime },x_2^{\prime })\mathrm{d}{x}_1^{\prime }\mathrm{d}{x}_2^{\prime },$$ (20.3)

where Green’s function G_ij depends on the gel properties and on the boundary conditions discussed earlier. For an elastic half-space, the solution is well known (Boussinesq solution) (Landau & Lifshitz, 1959) and can be readily used for TFM.

OVERVIEW OF METHODS FOR RECONSTRUCTION OF TRACTION FORCES

Historically, the first approach to calculate traction from the measured displacement field was an inversion of the integral Eq. (20.3) in real space (Dembo&Wang, 1999). While being quite flexible, constructing the matrices and inverting them is computationally demanding (Herant & Dembo, 2010; Sabass et al., 2008). Considerable simplification can be achieved if the location and extension of the adhesion sites are known. Traction reconstruction with point forces (Schwarz et al., 2002) avoids numerical integration by assuming that the force in Eq. (20.3) is localized to small regions. This approach is particularly appropriate if the location of adhesion sites is prescribed by patterns of surface-coupled ligands.

Alternatively, the differential equations can be solved with a finite element method (FEM) (Yang, Lin, Chen, & Wang, 2006). FEM has the advantage that almost arbitrary geometries and nonlinear gel responses can be studied. However, the need to discretize the whole bulk inside the gel makes FEM computationally demanding. FEM approaches are especially suited for three-dimensional systems and recently have been used for traction force reconstruction for cells encapsulated in PEG hydrogels (Legant et al., 2010).

With Fourier transform traction cytometry (FTTC), Eq. (20.3) is solved in Fourier space, where the convolution integral becomes a matrix multiplication (Butler, Tolić-Nørrelykke, Fabry, & Fredberg, 2002). This method is efficient and reliable and has found wide popularity. Therefore, our method is also based on the idea of solving the pertinent equations in Fourier space (Sabass et al., 2008).

HIGH RESOLUTION AND REGULARIZATION

The resolution of TFM is strongly affected by errors in displacement measurements caused by inhomogeneity in substrate mechanics, optical aberrations, and lack of accuracy in the tracking routines. Errors can also result from violations of the assumption underlying the reconstruction. Since these error sources are all more or less local, the higher spatial frequency components of the reconstructed surface forces are most strongly affected. Obtaining good spatial resolution in TFM therefore requires a finely tunable and robust method for removing noise. For this purpose, we employ Tikhonov regularization of the traction field in Fourier space (Sabass et al., 2008). Here, f_i(x₁, x₂) is required to minimize the functional

$$\sum _{\{x_1{x}_2\}}({\Vert u_i-u_i(f_1,f_2)\Vert }^2+{\lambda }^2{\Vert f_i\Vert }^2),$$ (20.4)

where u_i are the measured displacements and u_i(f₁, f₂) are the displacements that result from the traction f_i. The 2-norm is written as ‖…‖ and the sum over {x₁, x₂} covers all positions on a spatial grid.

In Eq. (20.4), the difference between measurement and reconstruction is penalized by the first term. The second term constrains the magnitude of reconstructed forces and can be thought of as representing prior information about the uncertainty of the measurement. Increasing the regularization parameter λ leads to a “smoother” appearance of the traction field.

20.1 MATERIALS

The technique of high-resolution TFM relies on quantitative analysis of substrate deformation in response to cell-generated mechanical force. Depending on the substrate stiffness and cell contractility, the magnitude of the deformation varies from tens of nanometers to a micrometer. The necessity to capture such small deformations makes the imaging system the key component of the TFM setup and imposes several critical requirements on its optical performance. First, the imaging system should be equipped with a confocal scanner allowing for visualization of fluorescent beads located in the uppermost layer of the elastic substrate. This increases the signal-to-background ratio of the fluorescent beads and thus greatly improves the accuracy with which they can be tracked. Second, the system should be equipped with a highly corrected water-immersion objective lens with high numerical aperture. This decreases imaging artifacts, including severe spherical aberration, resulting from imaging through a thick layer of PAAG, which has a refractive index close to water. Using an objective with high numerical aperture also improves the sensitivity of the imaging setup, increases the signal-to-noise ratio, and eventually leads to more accurate measurement of the displacement field. Third, the spatial sampling rate, that is, pixel frequency, of the imaging system should conform to the Nyquist criterion (Pawley, 2006) to allow accurate location of subresolution fiducial markers with subpixel accuracy. This requirement is especially important if the TFM setup is based on a spinning-disk confocal microscope, as for any given objective lens, the pixel frequency of such a system is determined by the pixel size of the CCD camera and cannot be adjusted. Finally, since traction force measurements require imaging of live cells, a stage-top incubator or another device to maintain cells at physiological conditions while acquiring images is also required.

20.1.1 INSTRUMENTATION FOR HIGH-RESOLUTION TFM

A computer-controlled research-grade inverted epifluorescence microscope is required. It is critical for high-resolution TFM that the imaging system is fully integrated allowing to control transmitted and epifluorescent illumination and image acquisition settings for multiple fluorescence channels. For our experiments, we use a Nikon Eclipse Ti microscope system, and comparable systems from other major manufacturers would be suitable. We utilize the MetaMorph software package for controlling the microscope functions. However, other commercial (e.g., Nikon Elements) or freely available (e.g., Micro-Manager) software packages should be considered if cost is an important consideration. If time-lapse TFM is required, the microscope needs to be equipped with a focus drift correction system (e.g., Nikon Perfect Focus) to maintain focus at the substrate–cell interface. It is critical that the microscope is equipped with an intermediate magnification-changer module (the sliding insert type) so that the Nyquist sampling criterion can be satisfied with the objective lens and camera recommended in the succeeding text. To allow imaging of the cell position, the microscope should be equipped with differential interference contrast (DIC) imaging components. The following equipment is recommended:

1. Highly corrected, high-magnification water-immersion objective lens. We use a Nikon 60× Plan Apo NA 1.2 WI objective and DIC prisms. Using a water-immersion objective minimizes optical aberrations caused by imaging through a thick layer of PAA gel.

2. Spinning-disk confocal scanner (Yokogawa, CSU-X1-A3) equipped with quad-edge laser-grade dichroic beam splitter (Semrock, Di01-T405/488/568/647-13 × 15 × 0.5) and a set of emission filters (Chroma Technology, green, et525/50 m; red, et605/52 m; Semrock, far-red, LP02-647RU) in an electronic filter wheel. Spinning-disk confocal scanner is highly recommended for high-resolution TFM, as it allows visualization of fiducial markers located in the uppermost layer of the elastic substrate while rejecting fluorescence emitted by out-of-focus beads and, also allows use of a low-noise CCD camera as an imaging detector. Using a spinning-disk confocal scanner also minimizes cell photodamage and improves TFM temporal resolution. A laser-scanning microscope system could be utilized, although these systems tend to elicit greater photobleaching of fluorophores in living cells and the noise level of the photomultiplier tube detectors is detrimental to accurate localization of fluorescent fiducials by subpixel fitting.

3. Multiwavelength laser combiner allowing control of laser illumination wavelength and intensity modulation. Since high-resolution TFM requires imaging of three fluorescent channels in rapid succession, the laser combiner should provide at least three laser lines (two bead colors and a fluorescent-tagged protein expressed in the cell). For our experiments, we use the LMM5 laser combiner (Spectral Applied Research) equipped with solid-state lasers with the following wavelength and power: 488 nm (Coherent, 100 mW), 560 nm (MPB Communications, 100 mW), and 655 nm (CrystaLaser, 100 mW). Note that substantial saving on equipment cost can be achieved by replacing solid-state lasers with a moderate-power ion laser (e.g., Coherent Innova series).

4. Scientific-grade CCD camera with 6.45 µm pixel size (Roper Scientific, Photometrics CoolSNAP HQ2). Using a high-end digital camera with low noise and small pixels is critically important for high-resolution TFM. High quantum yield and low noise of the camera increase image signal-to-noise ratio and improve accuracy of bead tracking. However, the necessity to conform pixel frequency to the Nyquist criterion when using a 60× objective lens dictates that pixel size of the camera should not exceed 6.5 µm. Thus, EM-CCD cameras, which all have pixels over 10 µm, are not recommended for high-resolution TFM. Using a scientific CMOS camera is also not recommended, as these cameras can generate random “hot pixels” or periodic noise patterns that interfere with bead tracking software.

5. Airstream incubator (Nevtek, ASI 400). Many stage-top incubators and microscope enclosures are available on the market and can be purchased from major microscope manufacturers. However, for most of our TFM experiments, we prefer using a simple and inexpensive airstream incubator to maintain stable temperature on an unenclosed microscope stage.

6. Closed-loop XY-automated microscope stage with linear encoders (e.g., Applied Scientific Instrumentation, MS-2000). Using an automated microscope stage is optional but highly recommended as it substantially improves the efficiency of TFM data collection and allows imaging the cells and the substrate at multiple stage positions before and after trypsinization of the cells.

20.1.2 POLYACRYLAMIDE SUBSTRATES WITH TWO COLORS OF FIDUCIAL MARKERS

Since the mechanical properties of PAAG are easily tunable, these gels are the most commonly used substrates for traction force measurements. By changing the concentration of acrylamide and N,N′-methylenebisacrylamide, the building blocks of PAAG, the stiffness of PAAG can be adjusted to mimic the rigidity of most biological tissues (100 Pa to 100 kPa) without losing the elastic properties of the gel (Yeung et al., 2005). For most of our experiments, we use PAAG with a stiffness ranging from 4 to 50 kPa; gels softer than 4 kPa tend to inhibit cell spreading, while gels stiffer than 50 kPa usually cannot be deformed by most cell types. Different formulations of acrylamide/bisacrylamide can be used to produce PAAG with similar stiffnesses. The formulations described in this chapter have been adapted from Yeung et al. (2005) and their shear moduli have been confirmed by the Gardel group (Aratyn-Schaus, Oakes, Stricker, Winter, & Gardel, 2010). The volumes described herein will create a gel that has a thickness of ≈30 µm on 22 × 40 mm coverslips. Since the extent of polymer swelling varies with the PAAG formulation (Kraning-Rush et al., 2012) and cannot be easily predicted based on shear modulus alone, it is important to measure the height of the resulting TFM substrate. The gel must be sufficiently thick such that the gel can freely deform due to cellular forces without the influence of the underlying glass (Sen, Engler, & Discher, 2009). In the protocol in the succeeding text, we describe a method for preparing four coverslip-bound elastic PAAG that are labeled with fluorescent nanobeads of two different colors that serve to double the spatial resolution of traction force measurements.

20.1.2.1 Suggested equipment and materials

• Fume hood.

• Coverslip spinner. This is a custom-built device designed to remove the bulk of the water from the surface of the gel attached to the coverslip. Detailed description of the coverslip spinner has been published (Inoué & Spring, 1997) and is available online (http://www.proweb.org/kinesin/Methods/SpinnerBox.html).

• Vacuum chamber.

• Ultrasonic cleaning bath (e.g., Fisher Scientific FS140). An ultrasonic bath is required to prepare “squeaky clean” coverslips.

• Coverslips (#1.5, 22 × 40 mm). We use borosilicate coverslips supplied by Corning Inc. (#2940-224) due to their cleanliness, reliable optical properties, and low thermal expansion. It is strongly recommended not to buy low-grade coverslips as they can be variable in their amenability to surface chemistry and optical properties.

• (3-Aminopropyl) trimethoxysilane (APTMS, e.g., Sigma-Aldrich, #281778)

• 25% Glutaraldehyde solution. We use EM grade glutaraldehyde free of polymers packaged in 10 mL glass ampoules (Electron Microscopy Sciences, #16200).

• 40% Acrylamide solution (e.g., Bio-Rad, #161-0140).

• 2% Bisacrylamide solution (e.g., Bio-Rad, #161-0142).

• Ammonium persulfate (APS) (e.g., Sigma-Aldrich, #A3678).

• N,N,N′,N′-tetramethylethylenediamine (e.g., TEMED, Bio-Rad, #161-0800).

• Fluorescently labeled latex microspheres of two colors. We use red-orange (565/580 nm, #F8794) and dark-red (660/680 nm, #F8789) fluorescent microspheres (FluoSpheres, carboxylate-modified microspheres, 0.04 µm) supplied by Life Technologies due to their brightness and resistance to photodamage.

• Microscope slides. We use 3 × 1” Gold Seal precleaned microslides, as their superior cleanliness contributes to consistent results.

• Rain-X (ITW Global Brands, available at automotive parts suppliers).

• Molecular biology-grade water (ddH₂O).

20.1.2.2 Protocol

1. Prepare “squeaky clean” coverslips: For the measurements of traction force to be reliable, stringent cleaning of coverslips, which ensures tight attachment of the PAAG to the glass surface, is required. For our experiments, we use “squeaky clean” coverslips prepared as described in Waterman-Storer (2001). Briefly, sonicate coverslips for 30 min in hot water containing VersaClean detergent. Rinse the coverslips several times, and then sonicate for 30 min in each of the following solutions in the following order: tap water, distilled water, 1 mM EDTA, 70% ethanol, and 100% ethanol. Transfer coverslips to a 500-mL screw cap jar, cover them with 100% ethanol, and store at room temperature until use.

2. Prepare master mix of acrylamide/bisacrylamide: Mix up 40% acrylamide and 2% bisacrylamide stock solutions following Table 20.1. We maintain several stock solutions that are optimized for PAAG of different stiffness. Stock solutions can be kept for at least a year at 4 °C.

3. Prepare 50% (3-aminopropyl)trimethoxysilane (APTMS) solution: Transfer 2 mL of APTMS into 15 mL conical tube containing 2 mL ddH₂O and mix up by pipetting up and down. Be aware that dissolving APTMS in water is exothermic and produces a lot of heat—the solution may start boiling. Preparing fresh APTMS solution on the day of coverslip activation is recommended to ensure reliable binding of the PAAG to the glass surface.

4. Prepare 0.5% solution of glutaraldehyde: add 1 mL of 25% glutaraldehyde stock solution into 49 mL of ddH₂O.

5. Prepare 10% solution of APS: dissolve 10 mg APS in 100 µL ddH₂O by vortexing. Prepare fresh APS solution on the day of the experiment. Alternatively, APS solution can be stored at −20 °C for up to a month.

6. Activate coverslips: Place four “squeaky clean” coverslips (#1.5, 22 × 40 mm) into a 15-cm glass Petri dish and apply 0.5 mL of 50% APTMS on top of each coverslip. Incubate at room temperature for 10 min, add ddH₂O into the Petri dish to immerse the coverslips (≈30 mL ddH₂O), and incubate on an orbital shaker for another 30 min. Rinse the coverslips with ddH₂O multiple times, transfer to a Petri dish with 50 mL of 0.5% glutaraldehyde, and incubate 30 min with agitation. Rinse activated coverslips with ddH₂O several times, arrange them on a coverslip rack, and dry in the desiccator. Activated coverslips can be stored in vacuum desiccator for at least 2 weeks. Note that only the top surface of each coverslip is activated and is able to bind PAAG covalently. Make sure that you keep track of the top surface.

7. Prepare microscope slides with a hydrophobic surface: Use clean KimWipe tissue to coat one microscope slide for each 22 × 40 mm activated coverslip with Rain-X (ITW Global Brands). Allow the slides to dry for 5–10 min, remove excess of Rain-X with a KimWipe tissue, wash extensively with deionized water, and then rinse several times with ethanol. Make sure to remove all debris from the slides, since any remaining particles will be transferred to the polyacrylamide gel, interfering with polymerization and imaging. We usually prepare slides with hydrophobic surfaces in bulk and store them in the vacuum desiccator for several months.

8. Prepare polyacrylamide gel for TFM imaging: Prepare an acrylamide/bisacrylamide working solution by mixing the desired volume of stock solution, water, and fluorescent microspheres of two colors as listed in Table 20.1. To avoid bead agglomeration, sonicate the suspension of fluorescent microspheres in an ultrasonic bath for 30 s prior adding the beads to the working solution. Degas the working solution in a vacuum chamber for 30 min to remove oxygen, which prevents even polymerization of acrylamide. Remove the working solution from the vacuum chamber; add 0.75 µL of TEMED and 2.5 µL of 10% APS to initiate polymerization. Mix the solution by pipetting up and down several times. Avoid introducing air bubbles. Do not vortex. Apply 17 µL of acrylamide/bisacrylamide working solution on a hydrophobic microscope slide and cover with an activated coverslip. Make sure that activated surface is facing down (toward the solution). Let the gel polymerize for 20–30 min. After polymerization, lift the corner of the coverslip with a razor blade to detach the gel from the hydrophobic microscope slide, and immerse the gel attached to the coverslip in ddH₂O. Hydrated PAAG can be stored in ddH₂O at 4 °C for up to 2 weeks.

Table 20.1.

Composition of Acrylamide/Bisacrylamide Stock and Working Solutions Required for Preparation of Polyacrylamide Traction Force Microscopy (TFM) Substrates of Stiffness 2.3–55 kPa

	Polyacrylamide gel stiffness (G)
	2.3 kPa	4.1 kPa	8.6 kPa	16.3 kPa	30 kPa	55 kPa
Stock solution (can be stored up to a year at +4 °C)
40% Acrylamide (mL)	3.75	2.34	2.34	3.00	3.00	2.25
2% Bisacrylamide (mL)	0.75	0.94	1.88	0.75	1.40	2.25
dH2O (mL)	0.5	1.72	0.78	1.25	0.60	0.50
Total volume (mL)	5	5	5	5	5	5
Working solution (use immediately)
Stock solution (µL)	125	200	200	250	250	333
Red fluorescent beads (µL)	7.5	7.5	7.5	7.5	7.5	7.5
Far-red fluorescent beads (µL)	7.5	7.5	7.5	7.5	7.5	7.5
10% Ammonium persulfate (µL)	2.5	2.5	2.5	2.5	2.5	2.5
TEMED (µL)	0.75	0.75	0.75	0.75	0.75	0.75
ddH2O (mL)	357	282	282	232	232	163

Use indicated volumes of stock solution (upper half of table) to make the working solution (lower half of table) for preparing TFM substrates of the desired stiffness. Note that working solutions should be used immediately after adding ammonium persulfate and N,N,N′,N′-tetramethylethylenediamine (TEMED) as these chemicals induce rapid polymerization of acrylamide. In contrast, after preparation, the stock solutions can be kept for at least a year as long as maintained at +4 °C.

Note that shear modulus (G) is shown in the table as a measure of gel stiffness. The conversion between the shear modulus (G) and Young’s modulus (E) is given by the following formula:

$$G=\frac{E}{2(1+s)}$$

where s is Poisson’s ratio.

Data in this table were obtained from Yeung et al. (2005) and confirmed by Aratyn-Schaus et al. (2010).

20.1.3 FUNCTIONALIZATION OF POLYACRYLAMIDE SUBSTRATES WITH ECM PROTEINS

Since mammalian cells do not adhere to polyacrylamide, ECM proteins have to be covalently cross-linked to the surface of the TFM substrates. We routinely functionalize the gels with human plasma fibronectin, although other ECM proteins, such as collagen I, collagen IV, laminin, or vitronectin, can also be used. In the protocol in the succeeding text, we describe a method for chemical conjugation of fibronectin to the surface of PAAG by using the photoactivatable heterobifunctional cross-linker, Sulfo-SANPAH.

20.1.3.1 Suggested equipment and materials

• Orbital shaker (e.g., Thermo Scientific Lab Rotator).

• Coverslip spinner (see preceding text).

• Ultraviolet cross-linker (e.g., UVP CL-1000) equipped with long-wave (365 nm) tubes. Using a cross-linker with a built-in UV sensor is recommended to ensure consistent fibronectin cross-linking to the surface of PAAG.

• N-sulfosuccinimidyl-6-(4′-azido-2′-nitrophenylamino)hexanoate (Sulfo-SANPAH, Thermo Fisher Scientific, #22589). Although ordering Sulfo-SANPAH in bulk may seem efficient, we recommend purchasing 50 mg vials of this chemical to prevent its degradation due to hydrolysis.

• Dimethyl sulfoxide (DMSO, e.g., Sigma-Aldrich, #41647).

• Native fibronectin purified from human plasma (EMD Millipore, 1 mg/mL fibronectin dissolved in phosphate-buffered saline, #341635). Note that fibronectin dissolved in Tris-buffered saline has to be dialyzed prior cross-linking to the TFM substrate since the amine groups of Tris will react with the cross-linker.

• Dulbecco’s phosphate-buffered saline without calcium and magnesium (DPBS, e.g., Life Technologies, #14190-144).

20.1.3.2 Protocol

1. Prepare solution of Sulfo-SANPAH: Note that Sulfo-SANPAH undergoes rapid hydrolysis when dissolved in water. Prepare stock solution of Sulfo-SANPAH by dissolving 50 mg of Sulfo-SANPAH powder in 2 mL of anhydrous DMSO, aliquot in Eppendorf tubes (40 µL per tube), and freeze by immersing the tubes into liquid nitrogen. We store such stock solutions of Sulfo-SANPAH at −80 °C for several months.

2. Take an aliquot (40 µL) of Sulfo-SANPAH stock solution out of −80 °C freezer and thaw at room temperature for several minutes. One aliquot of Sulfo-SANPAH is sufficient to functionalize two 22 × 40 mm polyacrylamide gels.

3. Tape a piece of Parafilm in a square Petri dish (10 × 10 cm) and pipet one 50 µL drop of fibronectin solution (1 mg/mL) on the Parafilm for each cover glass.

4. While thawing Sulfo-SANPAH, spin two PAAGs quickly to remove excess of water. If coverslip spinner is not available, use KIMTECH Wipers (Kimberly-Clark) to remove excess water. Be careful not to touch gel surface in the center of the coverslip. Make sure that gels do not dry. Add 0.96 mL ddH₂O to the Sulfo-SANPAH aliquot, mix by pipetting, and apply 0.5 mL on top of each PAAG. Activate Sulfo-SANPAH by exposing gels to long-wavelength UV light (365 nm). To avoid decrease in Sulfo-SANPAH activation due to decline of UV lamp efficiency, we keep the expose energy constant (750 mJ/cm²), while the exposure time can change. During activation, the color of Sulfo-SANPAH solution will change from orange to brown.

5. Quickly wash PAAGs with ddH₂O, spin-dry, invert, and place the gel surface on the drop of fibronectin solution. Incubate at room temperature for 4 h, and then wash gels multiple times with DPBS with agitation on the shaker. Polyacrylamide substrates coated with ECM protein can be stored at 4 °C for up to a week.

20.2 METHODS

20.2.1 CELL CULTURE AND PREPARATION OF SAMPLES FOR HIGH-RESOLUTION TFM

Preparation of mammalian cells for TFM requires basic equipment for sterile tissue culture. For the purpose of this chapter, it will be assumed that the reader is familiar with sterile tissue culture techniques and has access to a tissue culture room. For choice of cell lines, it should be noted that the computational algorithm of traction force reconstruction discussed in this chapter relies on the assumption that deformation of the elastic substrate within the analyzed region is induced by a single cell and, thus, should be applied only to cell types which can be maintained in sparse culture conditions. Many different cell lines, including immortalized mouse embryo fibroblasts (MEFs), human foreskin fibroblasts, osteosarcoma cells U2OS, and mammary tumor epithelial cells MDA-MB-231, satisfy this requirement and have been previously used by us and others for TFM (Aratyn-Schaus & Gardel, 2010; Gardel et al., 2008; Kraning-Rush et al., 2012; Ng et al., 2012; Plotnikov et al., 2012; Sabass et al., 2008). In addition, for visualizing the location of focal adhesions, cells should be transfected with a cDNA expression construct that encodes a GFP fusion of a common focal adhesion protein.

20.2.1.1 Suggested equipment and materials

• Transfection reagents and apparatus. We perform electroporation with a Lonza Nucleofector 2b system and Nucleofector Kit V (#AAB-1001 and #VCA-1003, respectively). However, lipid-based transfection reagents such as Lipofectamine or FuGENE can also be used.

• cDNA expression construct(s) to visualize focal adhesions in live cells. For most experiments, we use a C-terminal fusion of eGFP to paxillin, since this construct labels focal adhesions in all stages of maturation (nascent adhesion, focal complexes, and focal adhesions) and has no significant effect on focal adhesion dynamics (Webb et al., 2004). The cDNA should be purified and should not contain endotoxins.

• Cells. We use immortalized MEFs (ATCC # CRL-1658).

20.2.1.2 Protocol

1. Culture the desired cell line in the appropriate medium and environmental condition. For example, we culture MEFs in DMEM media supplemented with 15% fetal bovine serum, 2 mM l-glutamine, 100 U/mL penicillin/streptomycin, and nonessential amino acids in a humid atmosphere of 95% air and 5% CO₂ at 37 °C.

2. Prepare media for live-cell imaging by adding fetal bovine serum (final concentration 15%) and l-glutamine (final concentration 2 mM) to DMEM lacking phenol red.

3. One day prior to measuring traction forces, transfect cells with the cDNA expression construct for visualizing focal adhesions in live cells.

4. The next day after cell transfection, preincubate polyacrylamide substrates for 30 min with media for live-cell imaging to equilibrate ion/nutrient concentration. Harvest transfected MEFs by trypsinization, resuspend in media for live-cell imaging, and plate on TFM substrates for 1–3 h. Plating time may vary substantially for different cell types: epithelial cells usually adhere and spread slower than fibroblasts. For most of the experiments, we plate the cells for just enough time to fully spread and polarize. This decreases ECM deposition and matrix remodeling by the cells and improves reproducibility of TFM measurements.

20.2.2 SETTING UP A PERFUSION CHAMBER FOR TFM AND ACQUIRING TFM IMAGES

In TFM experiments, images are acquired before and after detachment of the cell from the TFM substrate by perfusion of trypsin in order to allow visualization of the strained and unstrained substrate. This necessitates a very stable and reliable perfusion system that allows high-magnification, high-resolution imaging with an immersed objective lens, liquid perfusion of the cells while maintaining temperature, and reimaging the same position without loss of focus or movement of stage position.

20.2.2.1 Suggested equipment and materials

• Perfusion chamber for live-cell imaging with an appropriate microscope stage adapter. Using a commercial microscope perfusion chamber is required for high-resolution TFM, as it dramatically decreases the drift of the sample and improves the reliability of bead tracking. We suggest using an RC30 closed chamber system from Warner Instruments, as this perfusion chamber has been specifically designed for oil- or water-immersed objective lenses in confocal imaging applications and has the ability to use standard-size coverslips, providing high-quality images acquired in both epifluorescent and transmitted modes. The large viewing area of this chamber also increases the efficiency of TFM data collection, as several different cells per experiment can be imaged. Warner Instruments provides adapters to fit the stages of major microscope manufacturers, although if using an automated stage, custom-machined adapters may be needed. We utilize an automated stage made by Applied Scientific Instruments.

• Coverslips (#1.5, 22 × 30 mm, Corning, #2940-224).

• 12 mL disposable Luer-lock syringes and Luer-lock 3-way disposable stopcock (available from medical suppliers).

• Media for live-cell imaging prepared as described in previous section.

• Trypsin–EDTA, no phenol red (0.5%, Life Technologies, #15400-054).

• Vacuum grease.

20.2.2.2 Protocol

1. Prior to the experiment, warm up 10 mL aliquots of trypsin–EDTA and media for live-cell imaging and load them into 12 mL disposable syringes.

2. Assemble the perfusion chamber according the manufacture manual (http://www.warneronline.com/Documents/uploader/RC-30%20%20(2001.03.01).pdf). Connect the syringes loaded with trypsin–EDTA and media to the inlet line of the perfusion chamber via the three-way stopcock and fill the camber with media. Make sure that all air bubbles are removed from the chamber. Once the chamber is filled, use ddH₂O and ethanol to clean both top and bottom coverslips of the chamber. Make sure that the chamber is watertight and then mount it on the microscope, taking care to make sure that it is seated firmly in the stage. Immerse the 60× objective lens with water, and center the specimen over the lens.

3. Focus the 60× lens on the cells attached to the top surface of the PAAG by transmitted light mode, and then locate a candidate cell expressing moderate levels of the GFP-tagged focal adhesion marker for TFM by using epifluorescent imaging. Use transmitted light imaging to make sure that the candidate cell is isolated with no other untransfected cells within 10–20 µm from the cell edge. Since the distance of force propagation through the substrate scales linearly as substrate stiffness decreases, additional care should be taken when performing TFM on substrates softer than 4 kPa.

4. Insert the intermediate magnification module (1.5×) into the microscope optical path to increase spatial sampling frequency of the imaging system. When the 1.5× magnification is included, digital images acquired by a Nikon Ti microscope equipped with a 60× NA 1.2 water-immersed objective and CoolSNAP HQ2 CCD camera will satisfy the Nyquist criterion and are suitable for localizing positions of the fiduciary markers with subpixel accuracy.

5. Insert DIC components into the light path, and acquire a cell image by DIC mode for reference. This image is not required for TFM, but it can be used later to quantify the area of the cell.

6. Remove the DIC prism from the objective lens side of the optical path to improve images of fluorescent microspheres and increase spatial resolution of the substrate displacement field.

7. Focus the microscope on focal adhesions by epifluorescent mode. In the case of GFP-tagged focal adhesion marker, the focal adhesions can be observed in the green fluorescence channel.

8. Switch to laser illumination and spinning-disk confocal imaging mode, and obtain images in the GFP and bead channels (red and far-red). Adjust illumination intensity and camera exposure time settings to obtain images in all three channels with similar maximal fluorescence intensity of ~5 times higher than the background area that does not contain cells. This may take several images and testing several settings in each channel to get the settings right. During this procedure, minimize light exposure to the specimen, as this will contribute to bleaching and photodamage. Make sure to keep the specimen in precise focus (using the GFP-adhesion channel) because even very slight changes in focus with the high-NA lens will strongly affect the intensity in the image.

9. Acquire time-lapse TFM movies by capturing image triplets of fluorescently labeled focal adhesions and red and far-red fluorescent microspheres. It is important to acquire the images of fluorescent beads of different colors immediately after each other, as the deformation of the substrate changes rapidly due to focal adhesion turnover. If you have automated focus control, you may image the focal adhesions at their precise focal plane and image the beads at 0.4–1 µm deeper into the substrate, which will give higher contrast images of the beads. Furthermore, it allows bead tracking without the disturbance of cellular autofluorescence at the surface of the gel. However, the vertical position x₃ of the imaging plane must then be considered for the traction reconstruction as described in the succeeding text. If the imaging system is equipped with an automated microscope stage, memorize X and Y coordinates and repeat measurements for several cells. For time-lapse TFM, we acquire image triplets at ~15–60 s intervals.

10. Remove cells from the TFM substrate: Following imaging of the cells and the strained substrate, perfuse the cells with 5 mL 0.5% trypsin–EDTA solution and incubate it on the microscope stage for 10 min to detach the cells and to allow the substrate to relax from its cell-induced strained state. After incubation, remove the detached cells by perfusing the chamber with an additional 3–5 mL of trypsin–EDTA.

11. Image beads in the unstrained TFM substrate: Focus on the uppermost layer of the PAA gel and acquire z-stacks of bead images in the unstrained state with 100 nm increment. Later, one of these image planes will be selected in an automated and unbiased fashion as a reference (unstrained) image to quantify substrate deformation.

12. Move the stage to every memorized position, focus on the uppermost layer of PAA gel, and acquire z-stacks of bead images in the unstrained state as described.

20.2.3 QUANTIFYING DEFORMATION OF THE ELASTIC SUBSTRATE

Imaging multiple colors of fluorescent fiducials dramatically improves the accuracy and reliability of traction force measurement, since (1) it increases the density of the fiducial markers, which leads to better sampling of the substrate deformation, and (2) it decreases the noise and irregularities in bead tracking through averaging the displacement fields for the independent channels. In the protocol in the preceding text, we provide a step-by-step description of an algorithm that selects the reference (unstrained) images for each frame of a TFM image sequence, identifies fluorescent beads in the reference images, and tracks displacement of individual beads with subpixel accuracy. Although the initial image processing, for example, filtering, alignment, and image subtraction can be performed with a variety of software (e.g., ImageJ and MetaMorph), subsequent steps require the use of a high-level programming environment, for example, MATLAB:

1. Find reference images in a z-stack of images from the unstrained gel. The drift of the microscope stage makes it necessary to find a best-matching reference for each image of the TFM sequence and register the image and the reference. This can be done in an automated fashion by calculating the correlation coefficient between the images from deformed and shifted reference state. Correlation coefficients for whole images can be calculated efficiently by making use of the fast Fourier transform (FFT). MATLAB offers the “fft2()” function for this purpose.

2. Remove out-of-focus fluorescence and smooth each reference image by subtracting a median-filtered image from the original as $I_{\text{ref}}^{\prime }=I_{\text{ref}}-\text{medfilt}(I_{\text{ref}})$. The best results are mostly obtained with a filter window size larger than 2 µm². Subsequently, adjust the brightness of the new image as $I_{\text{ref}}^{″}=I_{\text{ref}}^{\prime }-\text{min}(I_{\text{ref}}^{\prime })$.

3. Find local maxima in reference images by locating pixels that are brighter than their neighbors and also brighter by a factor t than the average intensity of the whole image. When numbering the pixels in the (x₁, x₂) plane by (m₁, m₂), maxima at location $(m_1^{*},m_2^{*})$ are found from the conditions $I_{\text{ref}}^{″}(m_1*,m_2*)>I_{\text{ref}}^{″}(m_1^{*}\pm 1,m_2^{*}\pm 1)$ and $I_{\text{ref}}^{″}(m_1*,m_2*)>t\text{ mean}(I_{\text{ref}}^{″})$. The factor t should typically be set between 0.5 and 2.

4. Remove maxima that are too close to each other to avoid tracking similar features more than once. We exclude brightness peaks that are less than a pixels away from other peaks. Typically, we chose a = 4 … 10 pixels, depending on the bead density.

5. Improve quality of bead recognition. Fitting a two-dimensional parabola to an environment of a² pixels around $(m_1^{*},m_2^{*})$ helps to determine whether the local intensity maximum belongs to a fluorescent bead. This procedure is not essential, but highly improves the bead recognition. The target function $\Vert I_{\text{ref}}^{″}(m_1,m_2)-A_0-A_1{(m_1-m_1^{**})}^2-A_2{(m_2-m_2^{**})}^2\Vert$ can be minimized analytically to quickly yield the center of the parabola $(m_1^{**},m_2^{**})$. Individual brightness peaks are rejected if $(m_1^{**},m_2^{**})$ lies outside the region of a² pixels or if the fit fails. The results (A₁, A₂) also yield statistics about the width of the point-spread function.

6. Track displacement of fiducial markers: Use the unfiltered images (I_ref, I) for tracking. Place windows W_ref,ci(m₁, m₂) on top of each recognized bead in the reference images from the microscope channels c1 and c2. The size of the windows is usually on the order of 15 × 15 pixels or ≈1 µm². All windows are normalized individually as

   $${\tilde{W}}_{ci}(m_1,m_2)=(W_{ci}(m_1,m_2)-\text{mean}(W_{ci}))/\Vert W_{ci}(m_1^{\prime },m_2^{\prime })-\text{mean}(W_{ci})\Vert .$$

   Calculate the cross correlation between all reference windows W_ref,ci(m₁, m₂) and corresponding shifted windows W_ci(m₁ + b₁, m₂ + b₂) with

   $$cc(b_1,b_2)=\frac{1}{2}\sum _{i=1,2}\sum _{m_1,m_2}{\tilde{W}}_{ci}(m_1+b_1,m_2+b_2){\tilde{W}}_{\text{ref},ci}(m_1,m_2),$$ (20.5)

   where the sum over m₁, m₂ only covers the indices inside the windows. The location $(b_1^{*},b_2^{*})$ of the maximum in cc(b₁,b₂) is the average displacement in each window in units of pixels. The summation over the two channels leads to a significantly more robust tracking of substrate deformation. By averaging the correlation coefficients and not the windows themselves, we avoid mixing terms ~W_c1 W_c2 in the cross correlation.

7. Calculate subpixel displacements: Fitting a two-dimensional Gaussian to the maximum of the correlation matrix cc(b₁, b₂) yields a subpixel estimate of the position of the maximum. This position is taken as the displacement of the bead. The formulas for fitting two-dimensional Gaussians can be found elsewhere (Nobach & Honkanen, 2005).

20.2.4 CALCULATION OF TRACTION FORCES WITH REGULARIZED FOURIER–TRANSFORM TRACTION CYTOMETRY

The most common methods for traction reconstruction rely on the validity of several assumptions. While these assumptions are not a priori necessary, they render the computational procedure tractable. Experiments should be conducted with keeping the following points in mind:

1. The TFM substrate is infinitely thick and its lateral deformation is negligible compared to the gel thickness. In practice, this means that 30 µm or thicker PAA gels should be used for traction force measurements (Boudou, Ohayon, Picart, Pettigrew, & Tracqui, 2009; Merkel, Kirchgessner, Cesa, & Hoffmann, 2007). Bead displacement on the surface of the gel should not exceed 1 µm. Geometric and material nonlinearities, as well as the finite depth of the gel, may otherwise influence the result.

2. Forces normal to the surface of the substrate are very small. Although the vertical component of traction force is measurable (Delanoë-Ayari, Rieu, & Sano, 2010; Koch, Rosoff, Jiang, Geller, & Urbach, 2012; Legant et al., 2013), this assumption is valid for the majority of adherent cell types. However, since these forces are neglected, care should be taken that only well-spread and flat cells are analyzed.

3. The displacement field in the image is assumed to result only from the cell in the field of view. Disturbances out of the field of view should be negligible. To reconstruct traction forces exerted by a sheet of cells, other algorithms can be employed (Liu et al., 2010; Maruthamuthu, Sabass, Schwarz,&Gardel, 2011; Ng et al., 2012; Tambe et al., 2013).

20.2.4.1 Computational procedure

In the following, we explain step-by-step how to proceed to reconstruct traction with regularized Fourier–transform traction cytometry (Reg-FTTC). We encourage readers who are experiencing difficulties with the implementation to contact the authors:

1. The displacement field determined in the previous steps (Section 20.2.3) will consist of irregularly spaced bead locations and displacements of these beads. For subsequent use with FFT, the irregular field must be interpolated on to a rectangular, regular grid that covers the whole image. Use, for example, the function “griddata()” in MATLAB. The grid nodes at position (x₁, x₂) are numbered by a pair (n₁, n₂) of integers n_i ∈ [− (N_i/2 − 1) … N_i/2] where N_i is an even number of nodes.

2. Construct discrete wave vectors for the Fourier transform as k_i = 2πn_i/(dN_i). Here, d is the nodal distance of the grid in units of pixels.

3. Employ an FFT to obtain the discrete Fourier transform ${\tilde{u}}_i(k_1,k_2)$ of the displacement field u_i(n₁, n₂). All the data and results are real numbers. Since a discrete Fourier transform of any real quantity satisfies $\tilde{g}(k)={\tilde{g}}^{*}(-k)$, we only have N_i/2+1 independent Fourier modes in each of the two coordinates of the plane.

4. Construct a matrix of the Fourier-transformed Green’s function

   $${\tilde{G}}_{ij}(k_1,k_2,x_3)=\frac{2(1+s){\mathrm{e}}^{x_3\sqrt{k_1^2+k_2^2}}}{E{(k_1^2+k_2^2)}^{3/2}}((k_1^2+k_2^2){\delta }_{ij}-k_i{k}_j(s-\frac{x_3\sqrt{k_1^2+k_2^2}}{2}\left)\right).$$ (20.6)

   An overall displacement of the whole gel in the image corresponds to the mode (k₁ = 0, k₂ = 0). The assumption that all the sources of traction are in the field of view allows to avoid divergence of Green’s function by setting ${\tilde{G}}_{ij}(0,0,x_3)=0$. This Green’s function also depends on the vertical position x₃ of the imaging plane where the displacements were measured.
   Next, construct a matrix ${\tilde{M}}_{ij}(k_1,k_2)$ for any chosen regularization parameter λ as

   $${\tilde{M}}_{ij}(k_1,k_2)=\sum _l{(\sum _m{\tilde{G}}_{ml}(k_1,k_2){\tilde{G}}_{mi}(k_1,k_2)+{\lambda }^2{\delta }_{il})}^{-1}{\tilde{G}}_{jl}(k_1,k_2).$$ (20.7)

5. Calculate traction in Fourier space as ${\tilde{f}}_i(k_1,k_2)={\sum }_j{\tilde{M}}_{ij}(k_1,k_2){\tilde{u}}_j(k_1,k_2)$. A simple matrix multiplication determines the Fourier components of the traction.

6. Transform the result into real space with inverse FFT. In MATLAB, the command “ifft2(…, ‘symmetric’)” can be used here. The result, f_i(n₁, n₂), is a discrete field of traction values that extends over the whole image.

20.2.4.2 Choice of the regularization parameter

The Tikhonov regularization parameter λ in Reg-FTTC can be determined in the framework of Bayes theory (Gelman, Carlin, Stern, & Rubin, 2003) by comparison with a maximum a posteriori (MAP) estimator of the traction. The prior probability distribution for f_i, as well as the probability distribution for the noise in u_i, is a convex function that can be approximated by Gaussians with variances α² and ξ², respectively. The posterior probability distribution can be calculated with Bayes law as

$$P(\{f\}|\{u\})=\frac{P(\{u\}|\{f\})P(\{f\})}{P(\{u\})}~{\mathrm{e}}^{-{\sum }_{\{x_1,x_2\}}\left({\Vert u_i-u_i(\{f\})\Vert }^2\right)/{\zeta }^2}{\mathrm{e}}^{-{\sum }_{\{x_1,x_2\}}{\Vert f_i\Vert }^2/{\alpha }^2}.$$ (20.8)

Minimization of Eq. (20.4) corresponds to maximizing the posterior probability, Eq. (20.8); when

$$\lambda =\frac{\xi }{\alpha },$$ (20.9)

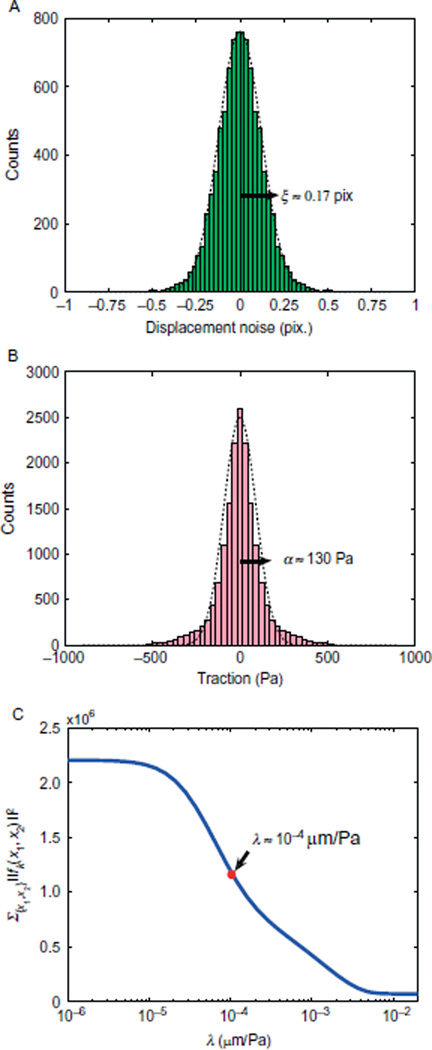
the MAP estimation of f_i therefore yields an estimate for the optimal regularization parameter λ. With a measurement standard deviation of ξ ≅ 0.17 pixels, a 90× effective magnification (60× objective and 1.5× intermediate magnification, pixel size is 70 nm), and typical traction magnitudes of α ≅ 130 Pa (Fig. 20.3A and B), we find λ ≅ 10⁻⁴ µm/Pa. Regularization parameters estimated with Eq. (20.9) usually yield a fairly smooth traction field with high resolution.

FIGURE 20.3.

Choice of the regularization parameter. (A) Histogram of the displacement error obtained by tracking beads in a region where no gel deformation occurs. Dotted line is a Gaussian fit. (B) Histogram of symmetrized traction in x₁ and x₂ directions. Data were collected from adhesion sites and their immediate proximity in one cell. A Gaussian fit (dotted line) allows to estimate the prior distribution of traction. (C) Example for the dependence of the overall traction magnitude on the regularization parameter.

Figure 20.3C demonstrates that the norm of the overall traction decreases sharply when the regularization parameter is ramped up. Heuristically, λ should be chosen as low as possible but from a range of parameters where the overall traction magnitude starts to become independent of the regularization parameter (L-curve criterion) (Schwarz et al., 2002). Alternatively, one can use advanced techniques that provide a value for λ from given assumptions about the underlying noise, such as the unbiased predictive risk estimator method (Mallows, 1973). It is advised to choose one value of λ and keep this value fixed when comparing different cells under similar conditions.

20.2.4.3 Alleviating spectral leakage due to the FFT

A frequently observed artifact is the formation of “aliases” at the edge of the image. Such artifacts result from spectral leakage, which occurs in discrete Fourier transformations when the data are nonperiodic. The problem can be effectively remedied by appending columns and rows of zeros around the measured two-dimensional field in (x₁, x₂) space. Such an artificial extension of the measurement window is called zero padding. However, we found that zero padding should not be used when x₃ ≠ 0.

20.2.5 REPRESENTING AND PROCESSING TFM DATA

20.2.5.1 Spatial maps of traction magnitude

Usually, the data sets are represented as a heat map of traction magnitude (Fig. 20.4). Here, the norm is plotted in varying colors. Alternatively, the traction norm can also be mapped linearly on the brightness of one color. This approach allows to directly plot fluorescence signal of cellular components together with the traction.

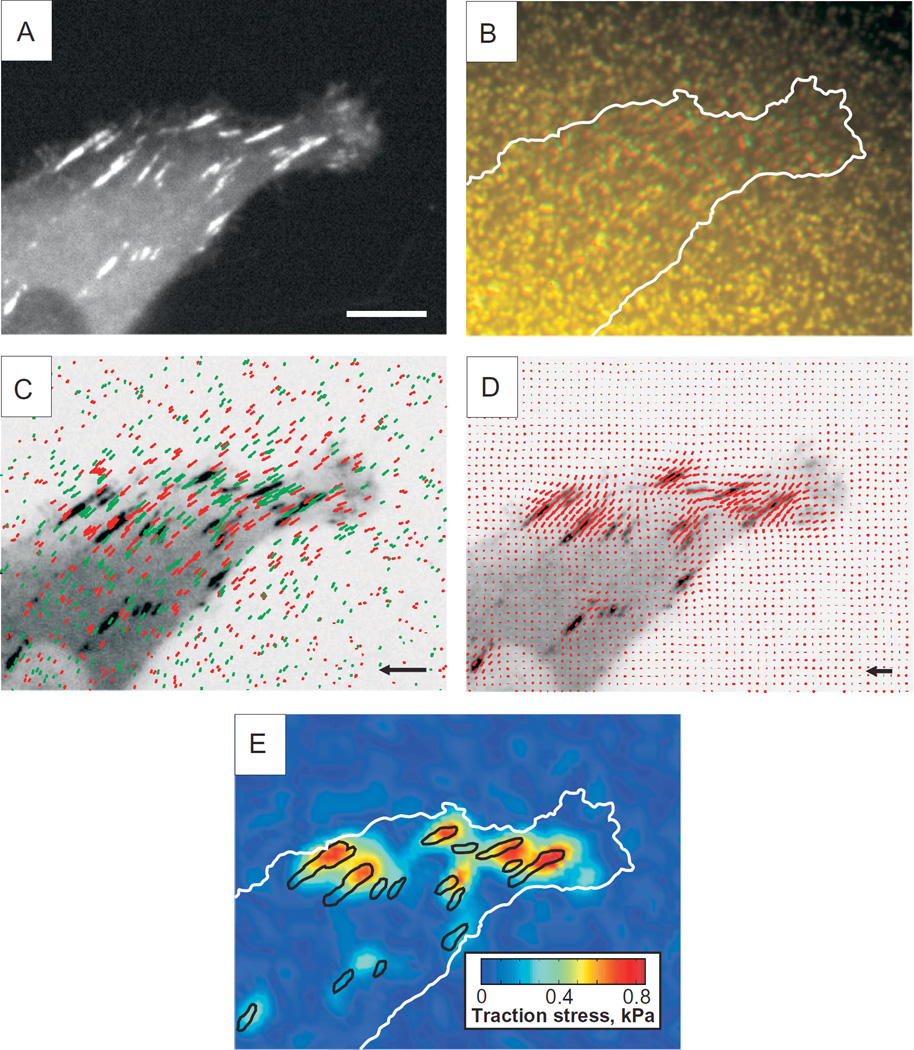
FIGURE 20.4.

Quantification of traction forces exerted by individual focal adhesions on a TFM substrate. Human breast adenocarcinoma cells (MDA-MB-231) were transfected with N-terminus-tagged eGFP–paxillin and seeded onto an 8.6 kPa TFM substrate labeled with red and far-red fluorescent nanobeads. (A) Confocal images of focal adhesions labeled with eGFP–paxillin. Scale bar = 5 µm. (B) Positions of far-red fluorescent nanobeads embedded in PAA gel in the strained (red) and unstrained (green) states. Cell edge is outlined in white. (C) Bead displacement field displayed as color coded vector plot overlaid on inverted-contrast image of eGFP–paxillin. Red and green vectors indicate lateral displacement of red and far-red fluorescent nanobeads from the unstrained position, respectively. Scale vector is 1 µm. (D) Traction stress vector field overlaid on inverted-contrast image of eGFP–paxillin. Scale vector is 1 pN. (E) Color-coded heat map of reconstructed traction stress on the ECM with focal adhesions outlined in black. Cell edge is outlined in white.

20.2.5.2 Whole-cell traction

The average of the whole traction is always zero by construction. However, the force dipole moment and higher force moments can be extracted from the traction field (Butler et al., 2002). The evolution of these moments can yield information about the dynamics of migrating cells.

The overall strength of a cell can be quantified through the median of the traction magnitude. Bar graphs of traction magnitude yield clear visual criteria for the strength of cells. An alternative measure for the overall strength of the cell is the total strain energy that is given by

$$U=\frac{l^2}{2}\sum _{n_1,n_2}\sum _{i=1}^2{f}_i(n_1,n_2)u_i(n_1,n_2),$$ (20.10)

where l² is the square of the nodal distance in the rectangular grid in µm². Strain energy also incorporates information on how much the cell is able to deform the substrate. Therefore, U can be useful if cell behavior on substrates with different stiffness is to be compared. However, in spite of being an integrated quantity, the quadratic dependence of U on the measurement data makes this quantity prone to measurement errors. This drawback can be somewhat mitigated by restricting the sum over n₁, n₂ to the area of the adherent cell and its immediate surroundings.

20.2.5.3 Traction along a predefined line

In analogy to the common kymograph, traction variation along prescribed one-dimensional coordinates can be plotted over time to quantify motion of the position of peak traction within individual adhesions (Plotnikov et al., 2012). These plots can be produced as follows: First, draw the lines along which traction is to be recorded by using MATLAB command “getline().” Next, partition the lines into segments of length d′ pixels. d′ can be chosen to be equal to the mesh size d. Finally, record the average traction and fluorescence in a region with area d′² at each segment.