Abstract
Pattern separation describes the orthogonalization of similar inputs into unique, non-overlapping representations. This computational process is thought to serve memory by reducing interference and to be mediated by the dentate gyrus of the hippocampus. Using ultra-high in-plane resolution diffusion tensor imaging (hrDTI) in older adults, we previously demonstrated that integrity of the perforant path, which provides input to the dentate gyrus from entorhinal cortex, was associated with mnemonic discrimination, a behavioral outcome designed to load on pattern separation. The current hrDTI study assessed the specificity of this perforant path integrity-mnemonic discrimination relationship relative to other cognitive constructs (identified using a factor analysis) and white matter tracts (hippocampal cingulum, fornix, corpus callosum) in 112 healthy adults (20–87 years). Results revealed age-related declines in integrity of the perforant path and other medial temporal lobe (MTL) tracts (hippocampal cingulum, fornix). Controlling for global effects of brain aging, perforant path integrity related only to the factor that captured mnemonic discrimination performance. Comparable integrity-mnemonic discrimination relationships were also observed for the hippocampal cingulum and fornix. Thus, whereas perforant path integrity specifically relates to mnemonic discrimination, mnemonic discrimination may be mediated by a broader MTL network.
Keywords: pattern separation, Perforant pathway, Dentate gyrus, Aging, mnemonic similarity task
Introduction
A fundamental component of memory is the ability to encode a given event as distinct from even highly similar events (e.g., where did you park your car today versus yesterday?). This type of mnemonic discrimination is thought to rely on pattern separation, in which unique representations are generated for each event (see Yassa & Stark, 2011). Computational models of hippocampal function have proposed that pattern separation is mediated by the dentate gyrus (McClelland, McNaughton, & O’Reilly, 1995; Treves & Rolls, 1994; Norman & O’Reilly, 2003). In support of this view, electrophysiological studies in rodents have revealed that neurons within the dentate gyrus alter their firing rates in response to minor changes in input events (i.e., the testing environment; Leutgeb, Leutgeb, Moser, & Moser, 2007; Neunuebel & Knierim, 2014). Similarly small changes in inputs (i.e., images of highly similar objects) have also elicited differential activity within the dentate gyrus in functional neuroimaging studies in humans, consistent with the role of the dentate in pattern separation (Bakker, Kirwan, Miller, & Stark, 2008; Lacy, Yassa, Stark, Muftuler, & Stark, 2011).
Importantly, the dentate gyrus operates within a broader network of medial temporal lobe (MTL) regions and their connections. The dentate gyrus primarily receives inputs (e.g., highly processed sensory information) from entorhinal cortex via the perforant path (Witter, 2007). Entorhinal cortex receives its input from neocortex via the cingulum bundle (Jones & Witter, 2007), whereas the hippocampus receives additional input from subcortical regions via the fornix (Swanson & Cowan, 1977; Amaral & Cowan, 1980). Thus, differences in pattern separation ability could be observed not only from a disruption of processing within dentate gyrus itself, but also from disrupted transfer of information via the perforant path and other MTL tracts (cingulum, fornix).
A noninvasive technique for assessing these white matter tracts in humans is diffusion tensor imaging (DTI), in which the rate of molecular water diffusion can be used to identify the orientation and “integrity” of white matter microstructure (e.g., axonal size and density, degree of myelination, coherence of fiber orientation; Beaulieu, 2002; Le Bihan, 2003). Using ultra-high in-plane resolution DTI (hrDTI), we previously calculated perforant path integrity as the amount of diffusion signal parallel to an anatomically-constrained prototypical perforant path within parahippocampal white matter (Yassa, Muftuler, & Stark, 2010b; Yassa, Mattfeld, Stark, & Stark, 2011). In healthy older adults, this measure of perforant path integrity was positively related to a behavioral index of pattern separation (i.e., mnemonic discrimination; Yassa et al., 2011), measured as the ability to discriminate highly similar lure objects from repeated objects in the Mnemonic Similarity Task (MST; Kirwan & Stark, 2007; Stark, Yassa, Lacy, & Stark, 2013). More recently, we used normal resolution DTI to show that integrity of the fornix (identified using traditional tractography methods) was also related to mnemonic discrimination (measured using the MST) in adults across the lifespan (Bennett, Huffman, & Stark, 2014).
The current study aimed to assess the specificity of the perforant path integrity-mnemonic discrimination relationship relative to other cognitive constructs and white matter tracts in 112 healthy adults (20–87 years). In addition to using measures of mnemonic discrimination from the MST for comparisons to our earlier work, mnemonic and executive functioning constructs were identified using a Principal Components factor analysis of thirteen MST and neuropsychological test measures. Furthermore, we introduce a novel method for assessing tract integrity, in which integrity metrics (diffusion, anisotropy) were calculated from fibers identified as running parallel to a prototypical tract orientation, after estimating multiple (two) fiber populations per voxel. This is especially important for the perforant path whose smaller fibers traverse parahippocampal white matter, which is primarily comprised of the hippocampal cingulum. It is predicted that perforant path integrity will be particularly sensitive to the factor capturing mnemonic discrimination. The mnemonic discrimination factor is also expected to relate to integrity of addition MTL tracts (fornix), but not the non-MTL control tract (corpus callosum).
Method
Participants
A lifespan sample of 112 healthy adults aged 20 to 87 years (51.7 ± 19.0 years, 69 female) were recruited from the University of California, Irvine and nearby Orange County communities. Prior to participation, all individuals were screened for health conditions that may interact with their neurological status (e.g., dementia, stroke, etc.), use of psychoactive medication (e.g., neuroleptics, sedatives, etc.), and contraindications for magnetic resonance imaging (MRI) scanning (e.g., having ferrous metal implants, being claustrophobic). All participants provided informed consent and were compensated for their time. The University of California, Irvine Institutional Review Board approved the experimental procedures.
Imaging Data Acquisition
Participants were scanned using a Philips Achieva 3.0 Tesla MRI system with an eight channel SENSE receiver head coil. Fitted padding was used to minimize head movements.
Twelve ultra-high in-plane resolution diffusion weighted echo planar imaging runs were acquired using the following parameters: TR/TE = 2,717/67 ms, flip angle = 90°, SENSE factor = 2.5, FOV = 59 × 170 × 170 mm, 15 coronal slices, and 0.664 × 0.664 × 3 mm spatial resolution with 1mm gap. Each run contained a single non-diffusion weighted volume (b = 0) and 32 volumes with diffusion weighting (b = 1,200 s/mm2) applied in non-collinear directions. An ultra-high in-plane resolution T2 weighted fast spin echo scan was also acquired using identical parameters, except TR/TE = 3,000/80 ms and no SENSE factor was applied. Both the DTI and T2 scans were centered and oblique oriented along the length of the hippocampus.
Imaging Data Analysis
Preprocessing
Diffusion weighted data were pre-processed separately for each participant. To correct for head movement, diffusion weighted volumes with the same gradient direction were aligned across runs and then aligned to the first non-diffusion weighted volume using Advanced Normalization Tools (ANTS; Avants, Tustison, & Song, 2009). A single diffusion tensor model, adjusted for slice angulation and other imaging settings (e.g., gradient overplus, slice orientation, patient orientation, etc.; Farrell et al., 2007), was then independently fit to each voxel using FMRIB Software Library’s (FSL) dtifit (Behrens et al., 2003), with a binary mask limiting tensor fitting to brain space. For each voxel, the modeled tensor was characterized by a primary, secondary, and tertiary diffusion direction. Dtifit provided separate output files for the vectors (eigenvectors: V1, V2, V3) and rates of diffusion (eigenvalues: L1, L2, L3) corresponding to these modeled tensor directions, as well a voxel-wise map of FA.
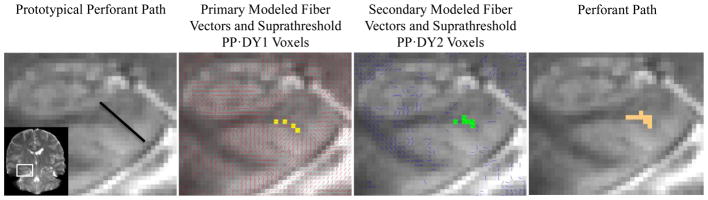
Given our interest in parahippocampal white matter that contained more than one fiber population (i.e., the perforant path and hippocampal cingulum), two diffusion tensor models were estimated for each voxel using FSL’s bedpostx (Behrens et al., 2003). The output of bedpostx included vectors indicating the mean diffusion direction of primary (dyads1, DY1) and secondary (dyads2_thr0.05, DY2) fibers within each voxel (see Figure 1).
Figure 1.
The prototypical perforant path was hypothesized to run at a 45° angle within coronal slices (i.e., from entorhinal cortex to the subiculum; black line). We separately calculated the dot product between the prototypical perforant path and the primary (red lines) and secondary (blue lines) modeled fiber vectors for each voxel. Fibers most consistent with the perforant path (yellow and green voxels) were isolated by thresholding PP·DY at 50% of the maximum value. The final perforant path estimation is presented on the far right (orange voxels).
Tract isolation
The likelihood that a modeled fiber was part of a given tract was assessed by calculating the dot product between the prototypical tract (PT) and the modeled fiber vectors (DY) for each voxel using the following equation: PT·DY = |(XPT × XDY) + (YPT × YDY) + (ZPT × ZDY)|. These calculations were conducted separately for each prototypical tract (perforant path, PP; hippocampal cingulum; fornix; corpus callosum), in the left (l) and right (r) hemisphere for bilateral tracts, and for the primary (DY1) and secondary (DY2) modeled fiber vectors (e.g., lPP·DY1, rPP·DY1, lPP·DY2, and rPP·DY2 for the perforant path).
The prototypical perforant path (PP) was hypothesized to run at a 45° angle within coronal slices (i.e., from entorhinal cortex to the subiculum; see Figure 1), which corresponds to XPP = 0.5, YPP = 0, and ZPP = 1 for the left perforant path, and XPP = 0.5, YPP = 0, and ZPP = −1 for the right perforant path. Fibers most consistent with the perforant path were isolated by thresholding PP·DY at 50% of the maximum value (0.56).
For bilateral hippocampal cingulum and fornix, the prototypical tracts were hypothesized to run through-plane within coronal slices (i.e., 0° angle from anterior to posterior MTL and fornix body, respectively), which corresponds to XPT = 0, YPT = 1, and ZPT = 0. The prototypical corpus callosum (CC) was hypothesized to run through-plane within sagittal slices (i.e., 0° angle from left to right), which corresponds to XCC = 1, YCC = 0, and ZCC = 0. Fibers most consistent with these larger tracts were isolated by thresholding PT·DY at 90% of the maximum value (0.90).
After identifying voxels that survived PT·DY thresholding, the tracts were further limited to standard anatomical masks (JHU-ICBM-labels-1mm) that were aligned to each participants’ diffusion space via the high-resolution T2 image. The same standard hippocampal cingulum mask was used for the perforant path and hippocampal cingulum. Non-white matter voxels were then excluded by thresholding FA maps at 0.2, as were the two most anterior and posterior slices (due to scanner-related distortions).
Integrity metrics
Two averaged integrity metrics were calculated for each tract. A diffusion metric, indicating the rate of diffusion in the modeled fiber vector direction, was calculated using the following equation: (L1 * (DY·V1)2) + (L2 * (DY·V2) 2) + (L3 * (DY·V3)2). An anisotropy metric was obtained from the output of bedpostx (i.e., mean_f1samples and mean_f2samples for DY1 and DY2, respectively). Each metric was calculated separately for each tract, in each hemisphere for bilateral tracts, and for each modeled fiber vector. Diffusion metrics were then averaged to yield a single value for each tract, whereas anisotropy metrics were averaged separately for the primary and secondary modeled fibers and then summed.
Mnemonic Similarity Task
The Mnemonic Similarity Task (MST) is a modified recognition memory task that consists of separate encoding and test phases (Kirwan & Stark, 2007; Stark et al., 2013). During an incidental encoding phase, participants viewed 128 common objects (i.e., the memory set) and indicated whether they were “indoor” or “outdoor” objects using a button press. During the test phase, participants were shown 192 objects that consisted of exact repetitions of memory set objects (64 targets), objects similar to those in the memory set (64 lures), and new objects not previously seen (64 foils). Participants judged whether each object was “old”, “similar”, or “new” using a keyboard press. For both task phases, each object is presented as a color photograph on a white background for 2 s with a 0.5 s inter-stimulus interval (see Stark et al., 2013 for additional details).
This version of the task also included a parametric manipulation of lure similarity. In a separate group of younger adults, we demonstrated that lure objects can be rank-ordered according to their degree of mnemonic similarity to target objects by using the probability of incorrectly responding “old” to each lure (Yassa et al., 2010a). These false alarm rates allowed us to divide the lure objects into five lure bins ranging from most (L1) to least (L5) mnemonically similar to targets.
Mnemonic discrimination indices
We can calculate several memory measures from the MST. One behavioral proxy for pattern separation is the lure discrimination index (LDI; formerly called the BPS index), which assesses whether the memory is highly detailed or exists in a gist-based form. The LDI score was calculated as the probability of correctly responding “similar” to similar lure objects minus the probability of incorrectly responding “similar” to novel foil objects (to correct for any bias in responding “similar” overall).
A potentially more refined LDI measure, the LDI-AUC, assesses mnemonic discrimination as a function of the lure similarity manipulation (i.e., the mnemonic similarity between target and lure objects). Previously, we computed an area under the curve (AUC) measure using the inverse of the probability of incorrectly responding “old” to similar lure objects across lure bins (aka the sum of the probability of calling these items “similar” and “new”; Stark et al., 2013). For the LDI-AUC, we refined this calculation (much akin to a “corrected recognition memory score”) by computing the area between the probability of correctly responding “similar” and incorrectly responding “new” to similar lure objects (to factor out any overall memory differences across lure bins).
Incorrect “old” responses to lure objects are not explicitly accounted for in either the LDI or LDI-AUC measures. However, we previously demonstrated a strong correlation (r = −0.93) between correct “similar” and incorrect “old” responses to lure objects, indicating that participants tradeoff between these responses (Bennett et al., 2014). Thus, higher LDI and LDI-AUC scores reflect better mnemonic discrimination, as measured by an increase in correct “similar” responses, and corresponding decrease in incorrect “old” responses, to lure trials.
Recognition
The MST task also provides a measure of traditional recognition memory (Recognition), calculated as the probability of correctly responding “old” to target objects (hits) minus the probability of incorrectly responding “old” to novel foil objects (false alarms). In contrast to the mnemonic discrimination indices, the Recognition memory measure is thought to place minimal demands on pattern separation because simple familiarity or gist-based memories can be used to dissociate repeated targets and novel foils from other dissimilar objects in the test phase.
Behavioral Factor Analysis
In addition to the MST, participants also completed a neuropsychological test battery that assessed recall memory using the Rey Auditory Verbal Learning Test (RAVLT Immediate and Delay; Rey, 1941) and Wechsler Memory Scale Logical Memory (LM Immediate and Delay; Wechsler, 1997b); executive functioning using Trails A and B (Reitan & Wolfson, 1985), Verbal and Category Fluency (Spreen & Benton, 1977), and Letter Number Sequencing (Wechsler, 1997a); and working memory using Digit Span (Wechsler, 1997a).
The three MST and 10 neuropsychological behavioral measures were entered into a Principal Components factor analysis with an Orthogonal/Varimax rotation, yielding a five factor solution that explained 77% of the variance across measures (see Table 1). The resulting factor scores for each participant were saved and used in subsequent analyses. Note that three participants were excluded from analyses involving factor scores due to one or more missing neuropsychological test scores.
Table 1.
Behavioral factor loadings
| Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 | |
|---|---|---|---|---|---|
| RAVLT Immediate | 0.88 | ||||
| RAVLT Delay | 0.91 | ||||
| MST LDI | 0.91 | ||||
| MST LDI-AUC | 0.95 | ||||
| Verbal Fluency | 0.88 | ||||
| Digit Span | 0.74 | ||||
| LN Sequencing | 0.45 | ||||
| MST Recognition | 0.54 | −0.75 | |||
| Trails A | 0.84 | ||||
| Trails B | 0.66 | ||||
| WMS LM Immediate | 0.89 | ||||
| WMS LM Delay | 0.76 | ||||
| Category fluency | 0.57 | ||||
|
| |||||
| Eigenvalues | 4.9 | 1.8 | 1.4 | 1.1 | 0.9 |
| % of total variance | 37.6 | 14.1 | 10.5 | 8.3 | 6.7 |
| Number of measures | 2 | 2 | 3 | 3 | 3 |
Notes. Obliquely rotated behavioral factor loadings (≥ 0.40) are shown for the three MST and 10 neuropsychological test measures. Bartlett’s test of sphericity was significant (χ2 (90) = 884.6, p < 0.001) and all communalities were above 0.5, indicating that the measures shared variance and were thus suitable for factor analysis. Rey Auditory Verbal Learning Test (RAVLT), Mnemonic Similarity Test (MST), Lure Discrimination Index (LDI), Lure Discrimination Index Area Under the Curve (LDI-AUC), Letter Number Sequencing (LN Sequencing), and Wechsler Memory Scale Logical Memory (WMS LM).
Results
Age-Related Declines in Tract Integrity
Because our study involved a lifespan sample, we first assessed the effect of age on tract integrity using separate simple regressions between chronological age and each integrity metric for each tract (perforant path, hippocampal cingulum, fornix, corpus callosum). Significant effects survived Bonferroni correction for multiple comparisons (p < .0125 across four tracts per integrity metric).
Results revealed significant age-related declines in perforant path diffusion (B = −0.31, t(110) = −3.5, p < 0.001) and fornix anisotropy (B = −0.29, t(110) = −3.2, p < 0.01). There was also a marginally significant age-related decline in perforant path anisotropy (B = −0.22, t(110) = −2.4, p < 0.02), but no other age effect attained significance (p’s > 0.16).
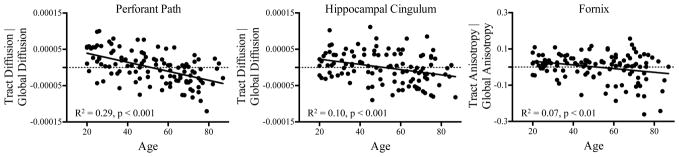
To assess whether the effect of age on perforant path and fornix integrity exceeded the more general effect of age on white matter integrity across the brain, we calculated global diffusion and anisotropy metrics within a scan-wide white matter mask (FA > 0.2) for each participant. Indeed, a multiple regression analysis revealed that the effect of age on perforant path diffusion (B = −0.75, t(110) = −7.3, p < 0.001) and fornix anisotropy (B = −0.26, t(109) = −2.9, p < 0.01) remained significant even after controlling for global integrity. Interestingly, a significant age-related decline in hippocampal cingulum diffusion was also observed, but only after controlling for global diffusion (B = −0.45, t(109) = −3.6, p < 0.001). However, a comparison of the standardized regression coefficients (Meng, Rosenthal, & Rubin, 1992) revealed that the effect of age on perforant path diffusion was significantly greater than the effect of age on the hippocampal cingulum diffusion (z = −3.72, p < 0.001). Significant effects are presented in Figure 2.
Figure 2.
Scatterplots show significant relationships between chronological age and tract integrity, after controlling for global integrity. Increased age was associated with decreased perforant path and hippocampal cingulum diffusion and fornix anisotropy, above and beyond the more general effect of age on global integrity.
Perforant Path Integrity Relates to Mnemonic Discrimination
Separate multiple regression models assessed whether perforant path integrity (diffusion metric, anisotropy metric) predicted each mnemonic discrimination measure (LDI, LDI-AUC), controlling for the more general effect of age on white matter integrity using the global integrity metrics (see Bennett et al., 2014). Significant effects survived Bonferroni correction for multiple comparisons (p < .025 across two behavioral measures per integrity metric).
Consistent with our previous findings in older adults (Yassa et al., 2010b), results revealed that perforant path diffusion significantly predicted both LDI (B = 0.40, t(109) = 3.3, p < 0.01) and LDI-AUC (B = 0.37, t(109) = 3.1, p < 0.01) measures, such that increased tract integrity was associated with better pattern separation performance. No effects for perforant path anisotropy attained significance (p’s > 0.47).
More importantly, we wanted to assess whether these perforant path integrity-performance relationships were specific to mnemonic discrimination. To identify a reduced number of mnemonic constructs from a larger set of correlated memory measures, we conducted a factor analysis on the three MST and 10 neuropsychological test scores. Five factors were identified: Both mnemonic discrimination measures (LDI, LDI-AUC) loaded onto Factor 2, whereas Factors 1 and 5 captured the recall memory measures (RAVLT and LM measures, respectively), and Factors 3 and 4 captured the remaining executive functioning and working memory measures. Separate multiple regression models assessed whether perforant path integrity (diffusion metric, anisotropy metric) predicted each of the five factors, controlling for the corresponding global integrity metric. Significant effects survived Bonferroni correction for multiple comparisons (p < .01 across five factors per integrity metric).
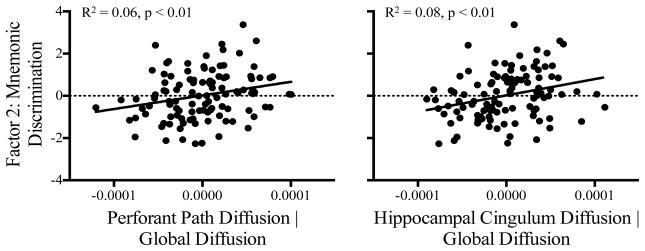
As expected, results revealed that perforant path diffusion significantly predicted the mnemonic discrimination factor (Factor 2; B = 0.33, t(106) = 2.7, p < 0.01). These data are presented in Figure 3. However, perforant path diffusion did not significantly predict any other factor (p’s > 0.08), and no effects for perforant path anisotropy approached significance (p’s > 0.16).
Figure 3.
Scatterplot show significant relationships between the mnemonic discrimination factor score and perforant path (left) and hippocampal cingulum (right) diffusion, controlling for global diffusion. Better mnemonic discrimination performance was associated with increased perforant path and hippocampal cingulum integrity.
Additional MTL Tracts Relate to Mnemonic Discrimination
To assess whether the integrity-mnemonic discrimination relationships were specific to the perforant path, two additional MTL tracts (hippocampal cingulum, fornix) and a control tract (corpus callosum) were also examined. For each tract, separate multiple regression models assessed whether tract integrity (diffusion metric, anisotropy metric) predicted each of the five factors, controlling for the corresponding global integrity metric. Significant effects survived Bonferroni correction for multiple comparisons (p < .01 across five factors per integrity metric).
As with the perforant path, hippocampal cingulum diffusion significantly predicted Factor 2 (B = 0.40, t(106) = 3.1, p < 0.01; see Figure 3), but not any other factor (p’s > 0.37). Hippocampal cingulum anisotropy was a marginally significant predictor of Factor 1 (B = 0.22, t(106) = 2.1, p < 0.04), which primarily captured the RAVLT recall memory measures.
For the fornix, neither integrity measure significantly predicted any factor (p’s > 0.42 for Factor 2, p’s > 0.05 for other factors, Bonferroni corrected α = 0.01). However, in line with our previous work (Bennett et al., 2014), there was a relationship between fornix anisotropy and mnemonic discrimination measured with the LDI, controlling for global anisotropy (B = 0.19, t(109) = 2.0, p < 0.05).
In contrast to the MTL tracts, integrity of the corpus callosum did not significantly predicted any factor score (p’s > 0.88 for Factor 2, p’s > 0.06 for other factors, Bonferroni corrected α = 0.01).
Discussion
The current study revealed three main findings. First, age-related integrity declines were observed for both local (perforant path) and large-scale (hippocampal cingulum, fornix) MTL tracts. Second, after controlling for white matter aging, perforant path integrity related only to mnemonic discrimination performance (LDI, LDI-AUC, Factor 2). Third, mnemonic discrimination was also related to integrity of the hippocampal cingulum (Factor 2) and fornix (LDI), but not the corpus callosum. Taken together, these data are consistent with the notion that the dentate gyrus and its direct inputs (perforant path) are specialized for behavioral pattern separation, but that behavioral pattern separation also depends on the transfer of information within a broader MTL network (hippocampal cingulum, fornix).
Increased age was associated with decreased perforant path and hippocampal cingulum diffusion and fornix anisotropy, but there was no effect of age on integrity of the corpus callosum. This finding is consistent with our previous DTI aging studies of MTL connectivity (Yassa et al., 2010b; Bennett et al., 2014), and with animal studies showing age-related degradation in these MTL tracts (Geinisman, deToledo-Morrell, Morrell, Persina, & Rossi, 1992; Rosenzweig & Barnes, 2003; Naranjo & Greene, 1977; Peters, Sethares, & Moss, 2010). Moreover, the age effects survived after controlling for the corresponding global integrity metric, indicating that the age-related decline in MTL tract integrity exceeded the more general effect of age on white matter integrity across the brain. However, additional research will be necessary to determine whether the effect of age on white matter integrity can be attributed to differences in specific underlying microstructural properties (e.g., axonal size and density, degree of myelination, coherence of fiber orientation).
After controlling for the global effect of age on white matter, increased perforant path diffusion was significantly related to better mnemonic discrimination (measured as LDI, LDI-AUC, and Factor 2). Importantly, perforant path integrity was not related to the factors capturing neuropsychological tests of recall memory, working memory, or executive functioning. In addition to extending our previous reports of significant perforant path integrity-mnemonic discrimination relationships in older adults (Yassa et al., 2010b; Yassa et al., 2011), these data support the conclusion that perforant path integrity is specifically sensitive to mnemonic discrimination in healthy adults across the lifespan.
Comparable integrity-mnemonic discrimination relationships (for Factor 2) were also observed for hippocampal cingulum diffusion. It is not surprising that results were similar for the perforant path and hippocampal cingulum, given that these tracts traverse the same parahippocampal white matter. And although values from different fiber populations and different voxels were used to calculate the integrity measures for these tracts, their diffusion metrics were significantly related (R2 = 0.74, p < 0.001). This highlights the difficulty in separating crossing fibers, even when advanced methodology is used, as was done here (e.g., employing hrDTI; calculating integrity metrics for distinct fiber populations; examining a large, lifespan sample). Importantly, results for the perforant path and hippocampal cingulum differ in at least two ways that indicate that discrete tracts were assessed, even if there is shared variance across the tract measures. First, the hippocampal cingulum revealed similar, yet significantly smaller, age-related declines in diffusion relative to the perforant path. Second, whereas no relationships between perforant path integrity and the non-mnemonic discrimination factors approached significance, hippocampal cingulum anisotropy was a marginally significant predictor of the RAVLT recall memory factor (Factor 1). This latter finding suggests that our initial examinations of perforant path integrity may have been contaminated by hippocampal cingulum fibers because relationships were observed between tract integrity and RAVLT Delay (Yassa et al., 2010b), yet perforant path integrity was also related to LDI in these older adults (Yassa et al., 2011).
In contrast to expectations, integrity of the fornix did not relate to the mnemonic discrimination factor. Comparable to our previous work (Bennett et al., 2014), however, fornix anisotropy did relate to mnemonic discrimination measured as LDI. A possible explanation for why perforant path and hippocampal cingulum integrity were more sensitive to mnemonic discrimination than fornix integrity is the degree of connectivity with the dentate gyrus. As stated in the Introduction, the primary input to the dentate gyrus is from entorhinal cortex via the perforant path (Witter, 2007). Further upstream, entorhinal cortex receives its input from neocortex via the cingulum, with the hippocampal aspect of the cingulum connecting entorhinal and parahippocampal cortices to retrosplenial and posterior cingulate cortices (Jones & Witter, 2007). In contrast, the fornix bypasses entorhinal cortex, and therefore the direct projections into the dentate via the perforant path. Instead the fornix projects directly into hippocampal subfields (Swanson & Cowan, 1977; Amaral & Cowan, 1980), presumably contributing smaller inputs to the dentate gyrus.
In summary, results of the current study support the conclusion that behavioral pattern separation can be attributed not only to information processing within dentate gyrus itself, but also to the transfer of information via the perforant path as well as a broader MTL network (hippocampal cingulum, fornix). In contrast to the MTL tracts, integrity of the corpus callosum did not vary with age or relate to any mnemonic factor. Whereas previous researchers have used hrDTI to reconstruct the perforant path in healthy adults (Zeineh, Holdsworth, Skare, Atlas, & Bammer, 2012), ex vivo human brain samples (Augustinack et al., 2010), and rats (Shepherd, Ozarslan, King, Mareci, & Blackband, 2006), the current hrDTI study adds to an emerging literature in which integrity of the perforant path has been used to discriminate patient populations (Solodkin et al., 2013) and to identify neuroanatomical substrates of behavioral pattern separation in healthy older adults (Yassa et al., 2010b; Yassa et al., 2011).
Highlights.
We assessed relationships between hippocampal tract integrity and mnemonic factors
Age-related declines were seen for perforant path, fornix, and cingulum integrity
Perforant path integrity related only to the mnemonic discrimination factor
But comparable relationships were seen for the other hippocampal tracts
Thus, mnemonic discrimination is likely mediated by a broad MTL network
Acknowledgments
This work was supported by the National Institutes on Aging R01 AG034613 (Stark) and K99 AG047334 (Bennett). We thank Shauna Stark and Samantha Rutledge for their assistance in data collection.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amaral DG, Cowan WM. Subcortical afferents to the hippocampal formation in the monkey. Journal of Comparative Neurology. 1980;189 (4):573–591. doi: 10.1002/cne.901890402. [DOI] [PubMed] [Google Scholar]
- Augustinack JC, Helmer K, Huber KE, Kakunoori S, Zollei L, Fischl B. Direct visualization of the perforant pathway in the human brain with ex vivo diffusion tensor imaging. Frontiers in Human Neuroscience. 2010;4:42. doi: 10.3389/fnhum.2010.00042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Tustison N, Song G. Advanced Normalization Tools, ANTS 1.0. Sourceforge 2009 [Google Scholar]
- Bakker A, Kirwan CB, Miller MI, Stark CEL. Pattern separation in the human hippocampal CA3 and dentate gyrus. Science. 2008;319:1640–1642. doi: 10.1126/science.1152882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system - a technical review. NMR in Biomedicine. 2002;15 (7–8):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Mathews PM, Brady JM, Smith SM. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnetic Resonance in Medicine. 2003;50 (5):1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- Bennett IJ, Huffman DJ, Stark CEL. Limbic Tract Integrity Contributes to Pattern Separation Performance Across the Lifespan. Cerebral Cortex. 2014 doi: 10.1093/cercor/bhu093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrell JAD, Landman BA, Jones CK, Smith SA, Prince JL, van Zijl P, Mori S. Effects of signal-to-noise ratio on the accuracy and reproducibility of diffusion tensor imaging–derived fractional anisotropy, mean diffusivity, and principal eigenvector measurements at 1.5 T. Journal of Magnetic Resonance Imaging. 2007;26 (3):756–767. doi: 10.1002/jmri.21053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geinisman Y, deToledo-Morrell L, Morrell F, Persina IS, Rossi M. Age-related loss of axospinous synapses formed by two afferent systems in the rat dentate gyrus as revealed by the unbiased stereological dissector technique. Hippocampus. 1992;2 (4):437–444. doi: 10.1002/hipo.450020411. [DOI] [PubMed] [Google Scholar]
- Jones BF, Witter MP. Cingulate cortex projections to the parahippocampal region and hippocampal formation in the rat. Hippocampus. 2007;17 (10):957–976. doi: 10.1002/hipo.20330. [DOI] [PubMed] [Google Scholar]
- Kirwan CB, Stark CEL. Overcoming interference: An fMRI investigation of pattern separation in the medial temporal lobe. Learning and Memory. 2007;14:625–633. doi: 10.1101/lm.663507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacy JW, Yassa MA, Stark SM, Muftuler LT, Stark CE. Distinct pattern separation related transfer functions in human CA3/dentate and CA1 revealed using high-resolution fMRI and variable mnemonic similarity. Learning and Memory. 2011;18 (1):15–18. doi: 10.1101/lm.1971111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Bihan D. Looking into the functional architecture of the brain with diffusion MRI. Nature Reviews Neuroscience. 2003;4 (6):469–480. doi: 10.1038/nrn1119. [DOI] [PubMed] [Google Scholar]
- Leutgeb JK, Leutgeb S, Moser MB, Moser EI. Pattern separation in the dentate gyrus and CA3 of the hippocampus. Science. 2007;315 (5814):961–966. doi: 10.1126/science.1135801. [DOI] [PubMed] [Google Scholar]
- McClelland JL, McNaughton BL, O’Reilly RC. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychological Review. 1995;102 (3):419–457. doi: 10.1037/0033-295X.102.3.419. [DOI] [PubMed] [Google Scholar]
- Meng XL, Rosenthal R, Rubin DB. Comparing correlated correlation coefficients. Psychological bulletin. 1992;111(1):172. [Google Scholar]
- Naranjo N, Greene E. Use of reduced silver staining to show loss of connections in aged rat brain. Brain research bulletin. 1977;2(1):71–74. doi: 10.1016/0361-9230(77)90029-6. [DOI] [PubMed] [Google Scholar]
- Norman KA, O’Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: a complementary-learning-systems approach. Psychological Review. 2003;110 (4):611–646. doi: 10.1037/0033-295X.110.4.611. [DOI] [PubMed] [Google Scholar]
- Peters A, Sethares C, Moss MB. How the primate fornix is affected by age. Journal of Comparative Neurology. 2010;518 (19):3962–3980. doi: 10.1002/cne.22434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reitan RM, Wolfson D. The Halstead-Reitan Neuropsychological Test Battery. Tuscon: Neuropsychology Press; 1985. [Google Scholar]
- Rey A. L’examen psychologique dans les cas d’encephalopathie traumatique. Archives Psychology. 1941;28:286–340. [Google Scholar]
- Rosenzweig ES, Barnes CA. Impact of aging on hippocampal function: plasticity, network dynamics, and cognition. Progress in Neurobiology. 2003;69 (3):143–179. doi: 10.1016/s0301-0082(02)00126-0. [DOI] [PubMed] [Google Scholar]
- Shepherd TM, Ozarslan E, King MA, Mareci TH, Blackband SJ. Structural insights from high-resolution diffusion tensor imaging and tractography of the isolated rat hippocampus. Neuroimage. 2006;32 (4):1499–1509. doi: 10.1016/j.neuroimage.2006.04.210. [DOI] [PubMed] [Google Scholar]
- Solodkin A, Chen EE, Hoesen GW, Heimer L, Shereen A, Kruggel F, Mastrianni J. In vivo parahippocampal white matter pathology as a biomarker of disease progression to Alzheimer’s disease. Journal of Comparative Neurology. 2013;521 (18):4300–4317. doi: 10.1002/cne.23418. [DOI] [PubMed] [Google Scholar]
- Spreen O, Benton AL. Neurosensory center comprehensive examination for aphasia: Manual of instructions. Vicoria, BC: Neuropsychology Laboratory, University of Victoria; 1977. [Google Scholar]
- Stark SM, Yassa MA, Lacy JW, Stark CEL. A task to assess behavioral pattern separation (BPS) in humans: Data from healthy aging and mild cognitive impairment. Neuropsychologia. 2013;51:2442–2449. doi: 10.1016/j.neuropsychologia.2012.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson LW, Cowan WM. An autoradiographic study of the organization of the efferet connections of the hippocampal formation in the rat. Journal of Comparative Neurology. 1977;172 (1):49–84. doi: 10.1002/cne.901720104. [DOI] [PubMed] [Google Scholar]
- Treves A, Rolls ET. Computational analysis of the role of the hippocampus in memory. Hippocampus. 1994;4 (3):374–391. doi: 10.1002/hipo.450040319. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Wechsler Adult Instelligence Scale (WAIS-III): Administration and scoring manual. San Antonio, TX: The Psychological Corporation; 1997a. [Google Scholar]
- Wechsler D. Wechsler Memory Scale. 3. San Antonio, TX: The Psychological Corporation; 1997b. WMS-III. [Google Scholar]
- Witter MP. The perforant path: projections from the entorhinal cortex to the dentate gyrus. Progress in Brain Research. 2007;163:43–61. doi: 10.1016/S0079-6123(07)63003-9. [DOI] [PubMed] [Google Scholar]
- Yassa MA, Lacy JW, Stark SM, Albert MS, Gallagher M, Stark CEL. Pattern separation deficits associated with increased hippocampal CA3 and dentate gyrus activity in nondemented older adults. Hippocampus. 2010a;21 (9):968–979. doi: 10.1002/hipo.20808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassa MA, Mattfeld AT, Stark SM, Stark CEL. Age-related memory deficits linked to circuit-specific disruptions in the hippocampus. Proceedings of the National Academy of Sciences. 2011;108 (21):8873–8878. doi: 10.1073/pnas.1101567108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassa MA, Muftuler LT, Stark CEL. Ultrahigh-resolution microstructural diffusion tensor imaging (msDTI) reveals perforant path degradation in aged humans in vivo. Proceedings of the National Academy of Sciences. 2010b;107 (28):12687–12691. doi: 10.1073/pnas.1002113107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yassa MA, Stark CEL. Pattern separation in the hippocampus. Trends in Neuroscience. 2011;34 (10):515–525. doi: 10.1016/j.tins.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeineh MM, Holdsworth S, Skare S, Atlas SW, Bammer R. Ultra-high resolution diffusion tensor imaging of the microscopic pathways of the medial temporal lobe. Neuroimage. 2012;62 (3):2065–2082. doi: 10.1016/j.neuroimage.2012.05.065. [DOI] [PMC free article] [PubMed] [Google Scholar]