Abstract
Purpose
Equations for blood oxyhemoglobin (HbO2) and carbaminohemoglobin (HbCO2) dissociation curves that incorporate nonlinear biochemical interactions of oxygen and carbon dioxide with hemoglobin (Hb), covering a wide range of physiological conditions, are crucial for a number of practical applications. These include the development of physiologically-based computational models of alveolar-blood and blood-tissue O2-CO2 transport, exchange, and metabolism, and the analysis of clinical and in-vitro data.
Method and Results
To this end, we have revisited, simplified, and extended our previous models of blood HbO2 and HbCO2 dissociation curves (Dash and Bassingthwaighte, Ann. Biomed. Eng. 38:1683–1701, 2010), validated wherever possible by available experimental data, so that the models now accurately fit the low HbO2 saturation (SHbO2) range over a wide range of values of PO2, PCO2, pH, 2,3-DPG, and temperature. Our new equations incorporate a novel PO2-dependent variable cooperativity hypothesis for the binding of O2 to Hb, and a new equation for P50 of O2 that provides accurate shifts in the HbO2 and HbCO2 dissociation curves over a wide range of physiological conditions. The accuracy and efficiency of these equations in computing PO2 and PCO2 from the SHbO2 and SHbCO2 levels using simple iterative numerical schemes that give rapid convergence is a significant advantage over alternative SHbO2 and SHbCO2 models.
Conclusion
The new SHbO2 and SHbCO2 models have significant computational modeling implications as they provide high accuracy under non-physiological conditions, such as ischemia and reperfusion, extremes in gas concentrations, high altitudes, and extreme temperatures.
Keywords: O2 and CO2 binding to hemoglobin, O2 and CO2 saturation of hemoglobin, Oxyhemoglobin and carbaminohemoglobin dissociation curves, Nonlinear O2-CO2 interactions, Bohr and Haldane effects, Mathematical modeling
Introduction
The delivery of oxygen to tissues for metabolism and energy production in parenchymal cells is regulated by a complex system of physicochemical processes in the microcirculation (Dash & Bassingthwaighte, 2006; Bassingthwaighte et al., 2012). In systemic capillaries, the release of oxygen from hemoglobin (Hb) inside red blood cells (RBCs) depends in part on the simultaneous release of carbon dioxide into the flowing blood. In the lungs, the loss of CO2 from RBCs increases O2 uptake, which in turn enhances CO2 dissociation from Hb. This interacting process also depends on the buffering of CO2 by bicarbonate ions (HCO3−), acid-base regulation, and the Hb-mediated nonlinear biochemical O2-CO2 interactions inside RBCs (Geers & Gros, 2000; Rees & Andreassen, 2005; Dash & Bassingthwaighte, 2006; Bassingthwaighte et al., 2012). In this regard, a decrease in pH or an increase in CO2 partial pressure (PCO2) in systemic capillaries decreases the affinity of O2 for Hb and HbO2 saturation (SHbO2), and increases the delivery of O2 to peripheral tissues (the Bohr effect). On the other hand, an increase in O2 partial pressure (PO2) in pulmonary capillaries results in the release of hydrogen ions (H+) from Hb, which in turn decreases the affinity of Hb for CO2, reducing HbCO2 saturation (SHbCO2) and aiding elimination of CO2 by the lungs (the Haldane effect). Thus, both the Bohr and Haldane effects are important in defining the Hb-mediated nonlinear biochemical O2-CO2 interactions inside RBCs (Siggaard-Andersen & Garby, 1973; Tyuma, 1984; Matejak et al., 2015). Raising blood temperature (T) also lowers the affinity of O2 for Hb, and increases the delivery of O2 to tissues. Consequently, the integrated computational modeling of O2 transport, exchange and metabolism in tissue-organ systems must account for the coupled transport and exchange of CO2, HCO3−, H+, and heat in the microcirculation (Dash & Bassingthwaighte, 2006). This is particularly important in highly metabolic tissue-organ systems such as heart and skeletal muscle during exercise (von Restorff et al., 1977), where arterio-venous (AV) temperature increases of 1 °C or so, PCO2 increases of nearly 10 mmHg, and pH decreases of about 0.1 pH unit, all combine to push the HbO2 dissociation curve to the right. Under these conditions, PO2 may decrease by as much as 80 mmHg and SHbO2 may decrease to less than 10% along capillaries which may be shorter than one millimetre in length. To properly account for the mass balance throughout the capillary-tissue exchange region, it is necessary to compute the changes associated with the nonlinear biochemical O2-CO2 interactions in blood as influenced by PO2, PCO2, pH, and T, thus the need for accurate and efficient forward and invertible SHbO2 and SHbCO2 equations.
In order to quantify the Bohr and Haldane effects as well as the synergistic effects of 2,3-DPG and T, Dash and Bassingthwaighte (2004; 2010) have developed new mathematical models of O2 and CO2 saturation of Hb (SHbO2 and SHbCO2) based on equilibrium binding of O2 and CO2 to Hb inside RBCs. They are in the form of an invertible Hill-type equation with apparent binding constants KHbO2 and KHbCO2 which depend on the levels of PO2, PCO2, pH, 2,3-DPG, and T in blood. The invertibility of these new equations enables analytical calculations of PO2 from SHbO2 and PCO2 from SHbCO2 and vice-versa. This is especially important for the integrated computational modeling of simultaneous transport and exchange of O2 and CO2 in alveolar-blood and blood-tissue exchange systems (Dash & Bassingthwaighte, 2006). The HbO2 dissociation curves computed from the SHbO2 model are in very good agreement with previously published experimental and theoretical curves in the literature over a wide range of physiological conditions (Kelman, 1966b; Severinghaus, 1979; Winslow et al., 1983; Siggaard-Andersen et al., 1984; Buerk & Bridges, 1986). However, as with any theoretical model, there are some limitations in the 2010 Dash and Bassingthwaighte SHbO2 and SHbCO2 models. In particular, the SHbO2 model is only accurate for values of SHbO2 lying between 0.3 and 0.98 (with a Hill coefficient nH of 2.7), even if accounting well in that range for the effects of pH, PCO2, 2,3-DPG and T. Furthermore, the SHbO2 and SHbCO2 models require complicated calculations of the indices n1, n2, n3, and n4 involved in the expression for the apparent equilibrium constant in a single-step O2-Hb binding reaction (Dash & Bassingthwaighte, 2010). These limitations are addressed here by simplifying the SHbO2 and SHbCO2 models further and extending the accuracy of the SHbO2 model to the whole SHbO2 range for the varied physiological conditions. The resulting SHbO2 and SHbCO2 models are also tested using diverse experimental data available in the literature on the HbO2 and HbCO2 dissociation curves for a wide range of physiological conditions (Joels & Pugh, 1958; Naeraa et al., 1963; Bauer & Schroder, 1972; Hlastala et al., 1977; Matthew et al., 1977; Reeves, 1980). This study does not include the buffering of CO2 in blood as that is covered in our previous work on blood-tissue gas exchange (Dash & Bassingthwaighte, 2006) and by Wolf (2013) for whole-body acid-base and electrolyte balance. Interested readers are referred to our previous article (Dash & Bassingthwaighte, 2010) for a historical perspective and details of the mathematical models of SHbO2 not covered in this paper.
Methods
Simple Mathematical Expressions for SHbO2 and SHbCO2
Based on the detailed nonlinear biochemical interactions of O2 and CO2 with Hb inside RBCs, Dash and Bassingthwaighte (2010) derived the following mechanistic mathematical expressions for the fractional saturation of Hb with O2 and CO2 (SHbO2 and SHbCO2, respectively):
| (1a,b) |
Here the concentrations are in moles per liter or M with respect to the water space of RBCs. The concentration of free O2 or free CO2 in the water space of RBCs may also be expressed in terms of the partial pressure of O2 or CO2 so that [O2] = αO2PO2 and [CO2] = αCO2PCO2, where αO2 and αCO2 are the solubilities of O2 and CO2 in water, computed from their measured values in plasma (Austin et al., 1963; Hedley-Whyte & Laver, 1964) and corrected for the effects of temperature (Kelman, 1966a; 1967; Dash & Bassingthwaighte, 2010):
| (2a) |
| (2b) |
Here Wpl = 0.94 is the fractional water space of plasma and T is in degrees centigrade (°C). Thus =αO21.46×10−6 M/mmHg and αCO2 = 3.27×10−5 M/mmHg at 37 °C (see Table 1). The expressions for [O2] and [CO2] in terms of PO2 and PCO2 and vice-versa are freely interchanged throughout this paper. The apparent equilibrium constants of Hb with O2 and CO2 (KHbO2 and KHbCO2 with units of M−1), based on single-step bindings of O2 and CO2 to Hb, are reproduced here from Dash and Bassingthwaighte (2010) in a simplified form, introducing the new variables Φ1 − Φ4:
| (3a,b) |
where the molar concentrations of the gases O2 and CO2 are used; the terms Φ1 − Φ4 involving the interactions of H+ with Hb-bound O2 and CO2 are given by:
| (4a–d) |
Table 1.
Model parameter values used in the simulations, most of which are as presented in the Dash and Bassingthwaighte (2010) paper; model parameters that are re-estimated based on fittings of the model to the experimental data in Figs. 1 and 3 are shown with footnotes. Unless otherwise noted, the kinetic parameter values are at T = 37 °C.
| Parameter | Definition | Value | Unit | |
|---|---|---|---|---|
|
|
Ionization constant of H2CO3 | 5.5×10−4 | M | |
|
|
Equilibrium constant for the CO2 hydration reaction: | 1.4×10−3 | Unitless | |
| K1 | Equilibrium constant for the overall CO2 hydration reaction: ; pK1 = −log10(K1) = 6.1 − 0.0434(pHpl−7.4) + 0.0014(T−37)(pHpl−7.4) | 7.94×10−7 (pHpl = 7.4; T = 37°C) | M | |
|
|
Ionization constant of HbNHCOOH | 1×10−6 | M | |
|
|
Equilibrium constant for the CO2-Hb binding reaction: | 21.5# 23.65* |
M−1 | |
| K2 | Equilibrium constant for the overall CO2-Hb binding reaction: | 21.5×10−6# 23.65×10−6* |
Unitless | |
|
|
Ionization constant of HbO2NHCOOH | 1×10−6 | M | |
|
|
Equilibrium constant for the CO2-HbO2 binding reaction: | 11.3# 14.7* |
M−1 | |
| K3 | Equilibrium constant for the overall CO2-HbO2 binding reaction: | 11.3×10−6# 14.7×10−6* |
Unitless | |
|
|
Equilibrium constant for the overall O2-Hb binding reaction: O2 + HbNH2 ↔ HbO2NH2 at standard physiological conditions (otherwise it is a function of PO2, PCO2, pHrbc, [DPG]rbc and T) | 2.03×105 | M−1 | |
|
|
Ionization constant of HbNH3+ | 2.4×10−8# 2.64×10−8* |
M | |
|
|
Ionization constant of HbO2NH3+ | 1.2×10−8# 1.56×10−8* |
M | |
| nH | Hill coefficient with variable cooperativity hypothesis for O2 binding to Hb: nH = α − β×10−PO2/γ (Eq. 11) | Variable | Unitless | |
| α | Parameter governing PO2-dependent variable Hill coefficient nH with variable cooperativity hypothesis for O2 binding to Hb | 2.82$ | Unitless | |
| β | Parameter governing PO2-dependent variable Hill coefficient nH with variable cooperativity hypothesis for O2 binding to Hb | 1.20$ | Unitless | |
| γ | Parameter governing PO2-dependent variable Hill coefficient nH with variable cooperativity hypothesis for O2 binding to Hb | 29.25$ | mmHg | |
| P50,S | Level of PO2 at which Hb is 50% saturated by O2 at standard physiological levels of PCO2, pHrbc, [DPG]rbc and T | 26.8$ | mmHg | |
| PO2,S | Standard partial pressure of O2 in blood | 100 | mmHg | |
| PCO2,S | Standard partial pressure of CO2 in blood | 40 | mmHg | |
| pHpl,S | Standard pH in plasma | 7.4 | Unitless | |
| pHrbc,S | Standard pH in RBCs, related to the standard plasma pH by: pHrbc,S = 0.795pHpl,S +1.357 | 7.24 | Unitless | |
| [DPG]rbc,S | Standard 2,3-DPG concentration in RBCs | 4.65×10−3 | M | |
| TS | Standard temperature of blood | 37 | °C | |
| pHrbc | pH in RBCs, related to plasma pH by: pHrbc = 0.795pHpl + 1.357) | Variable | Unitless | |
| Rrbc | Gibbs-Donnan ratio for electrochemical equilibrium of protons or bicarbonate ions across the RBC membrane (Rrbc = [H+]pl/[H+]rbc = [HCO3−]rbc/[HCO3−]pl; Rrbc = 10−(pHpl−pHrbc) = 10−(0.205·pHpl−1.357)) | Variable (0.692 at pHpl = 7.4) | Unitless | |
| αO2,S | Solubility of O2 in water at standard temperature (37 °C) | 1.46×10−6 | M/mmHg | |
| αCO2,S | Solubility of CO2 in water at standard temperature (37 °C) | 3.27×10−5 | M/mmHg | |
| HctS | Standard hematocrit (volume fraction of RBCs in blood) | 0.45 | Unitless | |
| [Hb]bl,S | Standard hemoglobin concentration in blood | 2.33×10−3 | M | |
| [Hb]rbc,S | Standard hemoglobin concentration in RBCs ([Hb]rbc=[Hb]bl/Hct) | 5.18×10−3 | M | |
| Wpl | Fractional water space of plasma | 0.94 | Unitless | |
| Wrbc | Fractional water space of RBCs | 0.65 | Unitless | |
| Wbl | Fractional water space of blood: Wbl = (1−Hct)·Wpl + Hct·Wrbc | 0.81 | Unitless | |
| [O2]tot | Total O2 concentration of whole blood: [O2]tot = Wbl·αO2·PO2 + 4·Hct·[Hb]rbc·SHbO2 | Variable | M | |
| [CO2]tot | Total CO2 concentration of whole blood: [CO2]tot = Wbl·αCO2·PCO2 + ((1−Hct)Wpl+Hct·Wrbc·Rrbc)(K1·αCO2·PCO2/[H+]pl) + 4·Hct·[Hb]rbc·SHbCO2 (parameter K1 defined above) | Variable | M |
Estimated based on model fittings to the data of Bauer and Schröder (1972) at T = 37 °C (see Fig. 3E)
Estimated based on model fittings to the data of Matthew et al. (1977) at T = 30 °C (see Fig. 3F)
Estimated based on model fittings to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) in normal human blood at standard physiological conditions
Here [H+] = 10−pH in RBCs. Given the pH of plasma, the pH of RBCs can be obtained using the simple relationship established by Siggaard-Andersen and colleagues (Siggaard-Andersen, 1971; Siggaard-Andersen & Salling, 1971): pHrbc = 0.795pHpl + 1.357, giving the Gibbs-Donnan ratio for electrochemical equilibrium of H+ and HCO3− across the RBC membrane as a function of pHpl: Rrbc = 10−(pHpl−pHrbc) = 10−(0.205pHpl−1.357) (see Table 1). In our previous SHbO2 and SHbCO2 models (Dash & Bassingthwaighte, 2010), Rrbc was considered as a constant: Rrbc = 0.69, a value corresponding to pHpl = 7.4 and pHrbc = 7.24 (see Table 1).
With these relationships (Eqs. 1–4), the total O2 and CO2 concentrations in whole blood can be calculated, as described in the Appendix of the Dash and Bassingthwaighte (2010) paper (see Table 1), and hence are not covered here in detail.
Dependency of on the Physiological Variables of Interest
Except for , the binding association/dissociation constants are all specified in Table 1. represents the single-step binding association constant of O2 with each heme chain of Hb (HmNH2) according to the following hypothetical reaction scheme (Dash & Bassingthwaighte, 2010):
| (5) |
The fundamental S-shape of the HbO2 dissociation curve results from the form of Eq. 1a and the values taken by the product KHbO2 [O2], which depends on . For any given range of [O2], the shifts in the HbO2 dissociation curve with respect to varying physiological conditions arise from the dependence of KHbO2 on [CO2], [H+] (via Φ1−Φ4), and . Similarly, the shape of the HbCO2 dissociation curve results from the form of Eq. 1b and the values taken by the product KHbCO2 [CO2], which also depends on . For any given range of [CO2], the shifts in the HbCO2 dissociation curve with respect to varying physiological conditions arise from the dependence of KHbCO2 on [O2], [H+] (via Φ1−Φ4), and . From the above description, it is clear that determining is a critical step in the application of Eqs. 1a and 1b. In our previous SHbO2 and SHbCO2 models (Dash & Bassingthwaighte, 2010), is expressed as a complicated function of [O2], [CO2], [H+], [DPG] and T involving the exponents n0, n1, n2, n3 and n4, which, except for n0 (a constant equal to 1.7), are themselves complicated functions of these physiological variables and P50 of O2. In the section below, we show how a very simple expression for can be obtained without involving the exponents n0−n4, significantly simplifying the SHbO2 and SHbCO2 models.
Derivation of Simple Mathematical Expression for
Hill’s exponent model for SHbO2 is based on an nth-order one-step binding of Hb with O2:
| (6) |
Here n = nH, the Hill coefficient, is approximately 2.7 for normal human blood; P50 is the value of PO2 at which Hb is 50 percent saturated by O2. In Eq. 6, the shifts of the HbO2 dissociation curve produced by varying physiological conditions arise because P50 is a function of PCO2, pH, [DPG] and T, as described below. If Eq. 1a and Eq. 6 are to give identical HbO2 dissociation curves, we must have KHbO2 αO2PO2= (PO2/P50)nH, which when simplified gives:
| (7) |
While it is simple to compute SHbO2 from Eq. 6, this is not true for SHbCO2. However, Eq. 7 provides an expression for in terms of PO2, PCO2, pH and P50, which along with Eq. 1b and Eq. 3b describes a simplified model for the HbCO2 dissociation curve. Note also that Eq. 7 can be written in the following alternative form:
| (8) |
so that as SHbO2 approaches 1, becomes infinitely large and KHbCO2 becomes equal to in Eq. 3b. If a “Division by Zero” error is to be avoided when calculating KHbCO2 in computer programs based on these equations, it is necessary to identify situations in which SHbO2 might equal 1 (at very high PO2), bypass Eq. 7, and immediately set .
Simple Mathematical Expression for P50 of O2
P50 is a function of PCO2, pH, [DPG] and T. Dash and Bassingthwaighte (2010) obtained a polynomial expression for P50 by varying one of these variables at a time, while keeping the other three fixed at their standard physiological values. The resulting polynomial expressions for P50,Δ pH, P50, ΔCO2, P50, ΔDPG, and P50, ΔT were fitted to the reported P50 data from the studies of Buerk and Bridges (1986) and Winslow et al. (1983). These polynomial expressions from Dash and Bassingthwaighte (2010) are further refined here based on additional experimental data from Joels and Pugh (1958), Naeraa et al. (1963), Hlastala et al. (1977), and Reeves (Reeves, 1980) that provide appropriate shifts in SHbO2 with varying pH, PCO2 and T:
| (9a) |
| (9b) |
| (9c) |
| (9d) |
Here the standard physiological values are denoted by the subscript “S” and are listed in Table 1. The accuracy of the expression for P50, ΔpH at extreme pH levels has been further improved in Eq. 9a by incorporating the cubic term. Previous researchers (Kelman, 1966b; Severinghaus, 1979; Siggaard-Andersen et al., 1984; Buerk & Bridges, 1986) have shown that for the calculation of P50 to be valid when multiple physiological variables are allowed to vary simultaneously, the contribution of each physiological variable to the resulting P50 is by multiplication of normalized individual P50’s. Consequently, the expression for P50 that best describes the simultaneous varying physiological conditions is given by:
| (10) |
Incorporation of the Variable Cooperativity Hypothesis
In our previous SHbO2 and SHbCO2 models (Dash & Bassingthwaighte, 2010), the Hill coefficient nH was fixed at 2.7 (or n0 was fixed at 1.7), making the SHbO2 accurate only between 30% and 98%. Next, we extend the accuracy of the modified SHbO2 model for the whole saturation range by incorporating an empirical PO2-dependent variable cooperativity hypothesis for O2 binding to Hb. Specifically, this is achieved by expressing the Hill coefficient nH at low PO2 as a simple exponential function of PO2:
| (11) |
where α, β and γ are parameters that govern an apparent cooperativity of O2 for Hb. Eq. 11 suggests that at low PO2, nH is close to α−β, but increases exponentially towards α with the rate γ as PO2 increases. These three parameters along with P50,S are estimated here based on fittings of the SHbO2 model to the available experimental data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) and Winslow et al. (1977) on normal human blood HbO2 dissociation curves at standard physiological conditions. With nH accurately defined by Eq. 11, suitable shifts in the HbO2 and HbCO2 dissociation curves are achieved through our new expressions for (Eqs. 9 and 10) and (Eq. 7).
Efficient Numerical Inversion of the SHbO2 and SHbCO2 Expressions for Practical Usage
Eq. 1a for HbO2 saturation (SHbO2) is not convenient for analytical inversion, because the apparent equilibrium constant KHbO2 for the binding of O2 to Hb depends on , which in turn depends on PO2 (see Eq. 7). However, since Eq. 1a is equivalent to Eq. 6, which depends on P50, which in turn is independent of PO2 and is only a function of pH, PCO2, [DPG] and T, Eq. 6 can be analytically inverted to compute PO2 from SHbO2, subject to the condition that the Hill coefficient nH is a constant. When nH is allowed to vary with PO2, Eq. 6 can no longer be inverted analytically. However, numerical inversion is possible using efficient iterative schemes such as those presented in the Appendix to this paper. These converge within 8 or less iterations when appropriate starting values are used for PO2. The same approach holds for the inversion of Eq. 1b in the computation of PCO2 from SHbCO2 (see Appendix), which may not be important clinically, but is of relevance in the integrated computational modeling of simultaneous transport and exchange of respiratory gases in physiological systems. Two efficient numerical methods are presented in the Appendix for the inversion of each gas, based on fixed-point and quasi-Newton-Raphson iteration methods. Similar iterative methods can be used to compute PO2 and PCO2 from the total [O2] and the total [CO2], respectively (these last two parameters are defined in Table 1).
Results
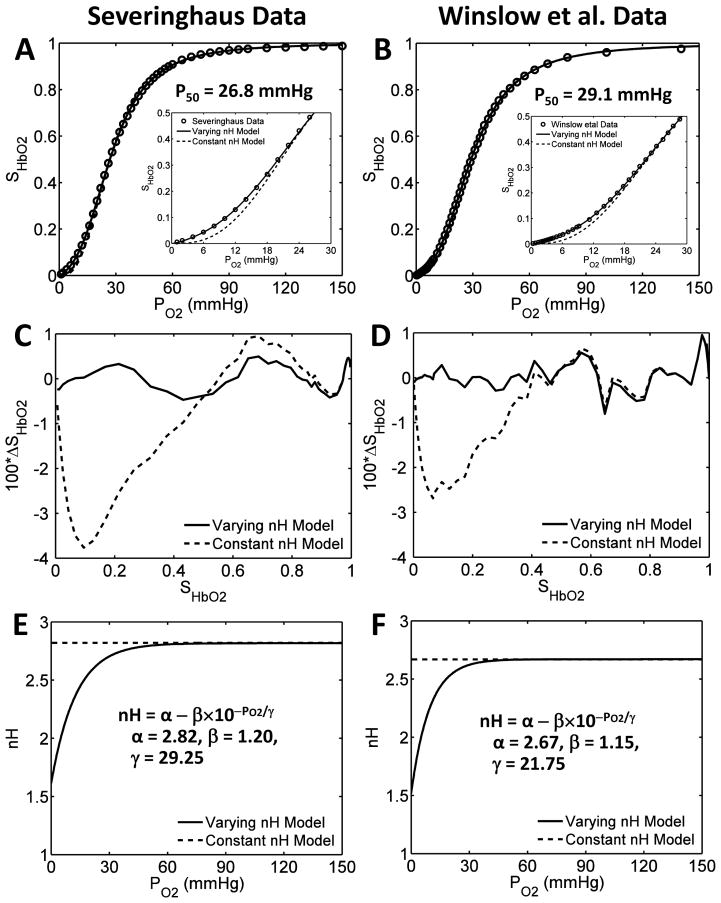
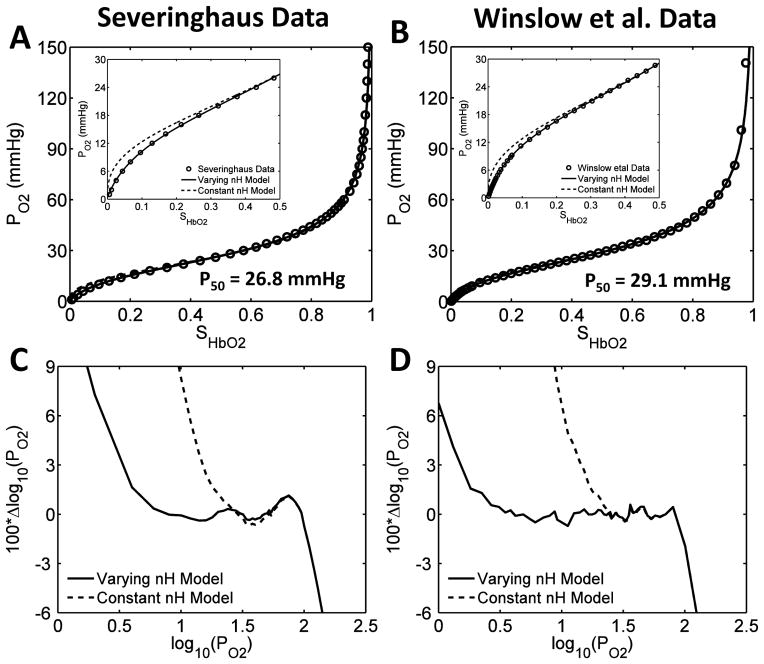
The effect of varying the Hill coefficient nH as a function of PO2 on the modified SHbO2 model simulations at standard physiological conditions is demonstrated through Fig. 1, in which Figs. 1(A,C,E) are based on the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979), while Figs. 1(B,D,F) are based on the data of Winslow et al. (1977). The first diagram in each set shows how the old and new SHbO2 models (constant and variable nH) fit the data in the PO2 range of 0–150 mmHg. The inset in each of these two figures shows the fit in the lower PO2 range of 0–30 mmHg. It is immediately apparent that the previous SHbO2 model, which does not incorporate the variable cooperativity hypothesis, produces a poor fit in the lower 40% saturation range. In Figs. 1(C,D), the residual error in the computed SHbO2 relative to the experimental SHbO2 is shown for each model for the range of values taken by SHbO2. When the saturation is less than 40%, the residual error is much improved for the new SHbO2 model (<0.05% for variable nH compared to ~3–% for constant nH), and the average residual error over the whole saturation range is virtually zero. Figs. 1(E,F) show how this improvement has been achieved by varying the Hill coefficient nH in the low PO2 range through the application of Eq. 11 (solid line), compared with the constant value used for nH in the old SHbO2 model (dashed line). We note here that the nH rate parameter γ is related to the P50,S value, which differs slightly for the two different data sets (26.8 mmHg vs. 29.1 mmHg). To achieve the best fit, the parameters α and β also differ slightly between the two different sets of data. This improved accuracy in SHbO2 at low PO2 may not be relevant clinically, but is important for the computational modeling and mechanistic understanding of in-vitro and in vivo blood gas data under non-physiological conditions, such as ischemia and reperfusion, extremes in gas concentrations, high altitudes, and extreme temperatures.
Figure 1. Illustration of the accuracy of the modified SHbO2 model under standard physiological conditions with PO2-dependent variable cooperativity hypothesis for O2-Hb binding.
(A,B) Comparison of the model-simulated HbO2 dissociation curves with constant and variable cooperativity hypotheses for O2-Hb binding (constant and variable Hill coefficient nH) to available experimental data in the literature, on normal human blood at standard physiological conditions. The simulations in panel A are compared to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979), and those in panel B are compared to the data of Winslow et al. (1977). The simulations in the main plots are compared to the data over the whole SHbO2 range, while those in the inset plots are compared to the data for SHbO2 ≤ 0.5, effectively demonstrating the improved accuracy of the modified SHbO2 model with variable nH in simulating the data in the lower SHbO2 range. (C,D) The percentage deviations (100 × ΔSHbO2) of the model-simulated SHbO2 values from the experimental SHbO2 values for the constant and variable nH models plotted as functions of SHbO2 for the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) and Winslow et al. (1977). The incorporation of the variable cooperativity hypothesis for O2-Hb binding (variable nH) has improved the accuracy of the SHbO2 model. (E,F) The PO2-dependent variation of nH corresponding to the constant and variable cooperativity hypotheses for O2-Hb binding that are obtained based on fittings of the modified SHbO2 model to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) and Winslow et al. (1977). The insets in plots (E,F) show the expressions for the variable nH and the governing parameter values for the two data sets.
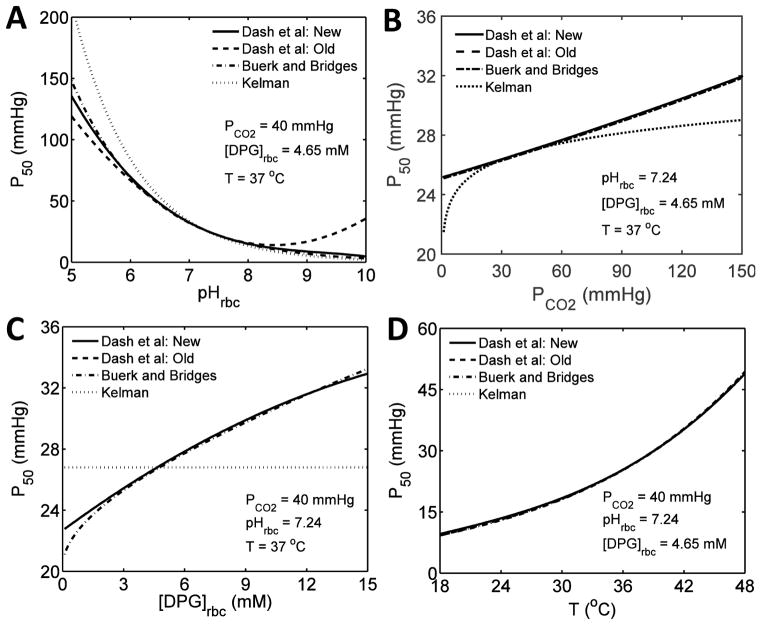
The P50 values computed from Eqs. 9 and 10 under varying physiological conditions are plotted in Figs. 2(A–D) and are compared to those computed from alternative models from the literature (Kelman, 1967; Buerk & Bridges, 1986; Dash & Bassingthwaighte, 2010). The alternative models do not include corrections based on the experimental data of Joels and Pugh (1958), Naeraa et al. (1963), Hlastala et al. (1977) and Reeves (1980); so for the purpose of this comparison, these corrections have been omitted from Eqs. 9(a–d) by applying appropriate scaling factors of 0.833, 0.588 and 1.02 for P50, ΔpH, P50, ΔCO2 and P50, ΔT, respectively. These simulations show that our scaled P50 values agree well with those computed from the model of Buerk and Bridges (1986), that are based on the studies of Winslow et al. (1983). However, they do differ from the P50 values computed from the model of Kelman (1966b), where it fails to fit the data at low pH and at either very low or very high PCO2. Our scaled P50 values are also improved from our old P50 values for pH > 8.5 with the incorporation of the cubic term in Eq. 9a. In addition, the inclusion of corrections based on the diverse experimental data sets of Joels and Pugh (1958), Naeraa et al. (1963), Hlastala et al. (1977), and Reeves (1980) in Eqs. 9(a–d) provides further improvement in the P50 values over a wide range of variation in the relevant physiological variables (see description below for Fig. 3). A new model recently published by Mateják et al. (2015), while this article was under preparation, also fits some of these experimental data well under altered physiological conditions. Their approach, a modification of Adair’s four-step algorithm (Adair, 1925), considers the problems in depth, and, like ours, relates the O2-Hb and CO2-Hb binding effects to the acid-base chemistry of blood based on pH and PCO2, as proposed by Siggaard-Andersen and others over the years (Rossi-Bernardi & Roughton, 1967; Forster et al., 1968; Siggaard-Andersen, 1971; Siggaard-Andersen & Salling, 1971; Bauer & Schroder, 1972; Siggaard-Andersen et al., 1972a; Siggaard-Andersen et al., 1972b; Siggaard-Andersen & Garby, 1973; Siggaard-Andersen et al., 1984; Siggaard-Andersen & Siggaard-Andersen, 1990). Specifically, they effectively express the four Adair coefficients in terms of the physiological variables of interest (i.e. pH, PCO2, and T they do not consider the effects of 2,3-DPG), providing appropriate shifts in the HbO2 dissociation curve with altered physiological conditions.
Figure 2. Comparison of P50 values under various physiological conditions based on simulations of different P50 models.
(A–D) Comparison of the modified P50 model (Eqs. 9 and 10) with the previous P50 models from the literature (Kelman, 1966b; Buerk & Bridges, 1986; Dash & Bassingthwaighte, 2010), in which the model-simulated P50 values are plotted as functions of one variable with the other variables fixed at their standard physiological values; i.e. P50 as a function of pHrbc (A), PCO2 (B), [DPG]rbc (C), and T (D). The P50 values have been computed from Eqs. 9 and 10 under varying physiological conditions with appropriate multiplicative factors (0.833, 0.588 and 1.02 for P50,ΔpH, P50,ΔCO2 and P50,ΔT, respectively) to allow a comparison with the previous models, which have not been adjusted to account for the data of Joels and Pugh (1958), Naeraa et al. (1963), Hlastala et al. (1977) and Reeves (1980).
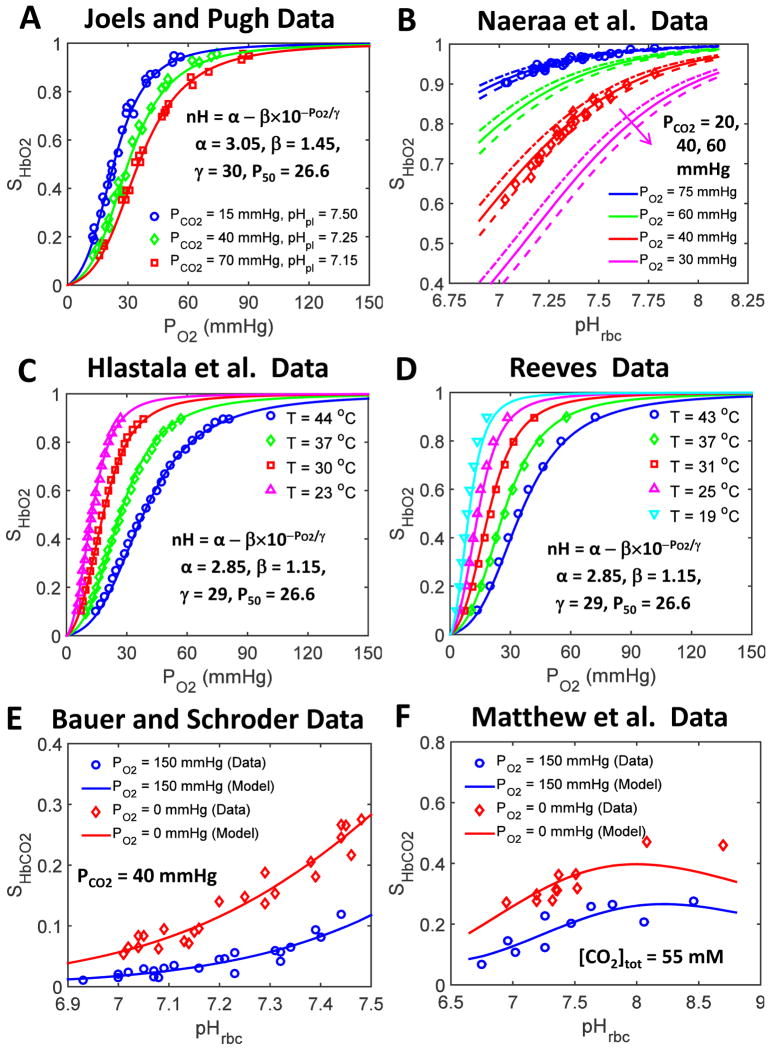
Figure 3. Comparison of our improved SHbO2 and SHbCO2 model simulations to the diverse experimental data available in the literature under non-standard physiological conditions.
(A) HbO2 dissociation curves obtained from our improved SHbO2 model (i.e. modified SHbO2 model with variable cooperativity hypothesis for O2-Hb binding (variable nH)) compared with the data of Joels and Pugh (1958) obtained at various pHpl and PCO2 levels with T = 37 °C. The inset shows the expression for the variable nH and the governing parameter values that produce the best fit of the model to these data sets. In addition, these model fittings characterize the pH and PCO2 dependencies of P50 in Eqs. 9a and 9b. (B) SHbO2 levels obtained from our improved SHbO2 model compared to the data of Naeraa et al. (1963) obtained as a function of pHrbc for different PO2 and PCO2 levels at 37 °C. Other details are as for panel A. (C,D) HbO2 dissociation curves obtained from our improved SHbO2 model compared with the data of Hlastala et al. (1977) and Reeves (1980) obtained for various values of T with pHpl and PCO2 fixed at 7.4 and 40 mmHg, respectively. The insets show the expression for the variable nH and the governing parameter values that enable best fits of the model to these data sets. In addition, these model fittings characterize the temperature dependency of P50 in Eq. 9d. (E,F) SHbCO2 levels obtained from our improved SHbCO2 model compared with the data of Bauer and Schröder (1972) and Matthew et al. (1977) obtained as a function of pHrbc in the oxygenated (high PO2) and deoxygenated (zero PO2) blood with PCO2 fixed at 40 mmHg (T = 37 °C) in the former experiments and total [CO2] fixed at 55 mM (T = 30 °C) in the latter experiments. These model fittings provide the estimates of the equilibrium constants associated with the binding of CO2 to oxygenated and deoxygenated Hb as well as the ionization constants of oxygenated and deoxygenated Hb.
The accuracy and robustness of our simplified and extended models of SHbO2 and SHbCO2 under varying physiological conditions (P50 defined by Eqs. 9 and 10, and variable nH defined by Eq. 11) has also been tested against diverse experimental data available from the literature (Joels & Pugh, 1958; Naeraa et al., 1963; Bauer & Schroder, 1972; Hlastala et al., 1977; Matthew et al., 1977; Reeves, 1980), and is illustrated in Fig. 3. Our refined SHbO2 model (i.e. the simplified SHbO2 model with variable nH) is able to reproduce the SHbO2 data of Joels and Pugh (1958) and Naeraa et al. (1963) obtained for a range of values of pH and PCO2 at 37 °C (Figs. 3A and 3B) as well as the SHbO2 data of Hlastala et al. (1977) and Reeves (1980) obtained over a range of values of T at fixed PCO2 and pH (Figs. 3C and 3D). These data allow a more accurate determination of the coefficients for use in the polynomial expressions for P50, ΔpH, P50, ΔCO2, P50, ΔDPG, and P50,ΔT, and hence characterize the dependence of P50 on pH, PCO2, [DPG] and T, and the corresponding shifts in the HbO2 dissociation curves. Similarly, our refined model of SHbCO2 is able to reproduce the SHbCO2 data of Bauer and Schröder (1972) and Matthew et al. (1977) obtained as a function of pHrbc in oxygenated and deoxygenated blood with either constant PCO2 of 40 mmHg at 37°C (Fig. 3E) or constant total [CO2] of 55 mM at 30 °C (Fig. 3F). These model fittings provide accurate estimates of the equilibrium constants associated with the binding of CO2 to oxygenated and deoxygenated Hb as well as the ionization constants of oxygenated and deoxygenated Hb at 30 °C and 37 °C (see Table 1). These estimates differ slightly from those used in our previous models of SHbO2 and SHbCO2 (Dash & Bassingthwaighte, 2010), but are in close agreement with those reported by Bauer and Schröder (1972) and Rossi-Bernardi and Roughton (1967). It can be noted here that the estimates of the parameters associated with the PO2-dependent variable nH for these different data sets are all similar, further signifying the importance of the variable cooperativity hypothesis in accurately simulating HbO2 dissociation curves in the whole saturation range under varying physiological conditions.
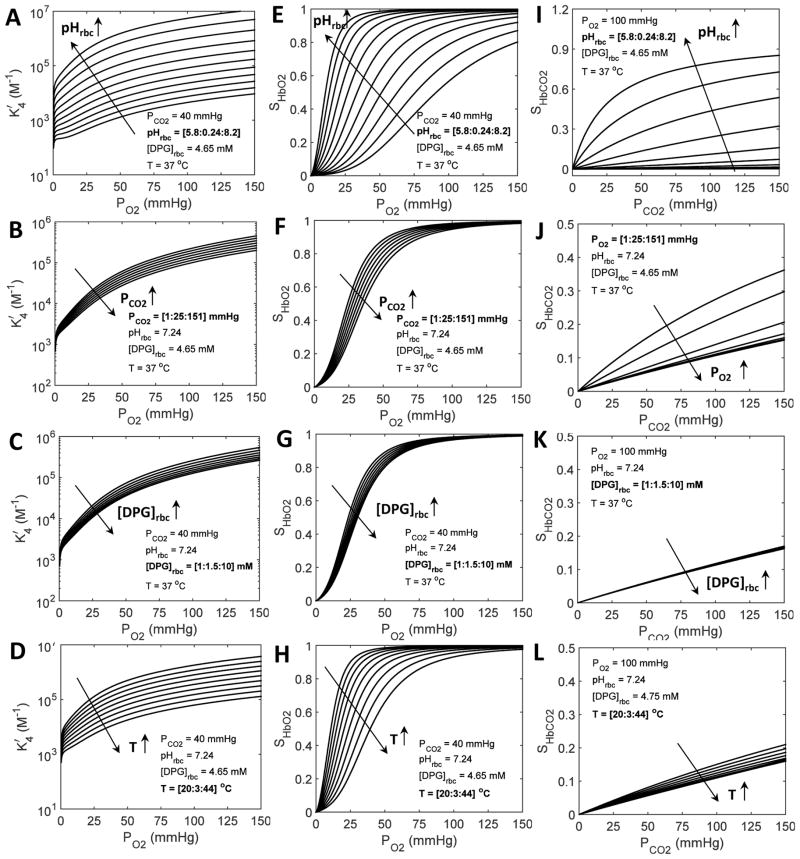
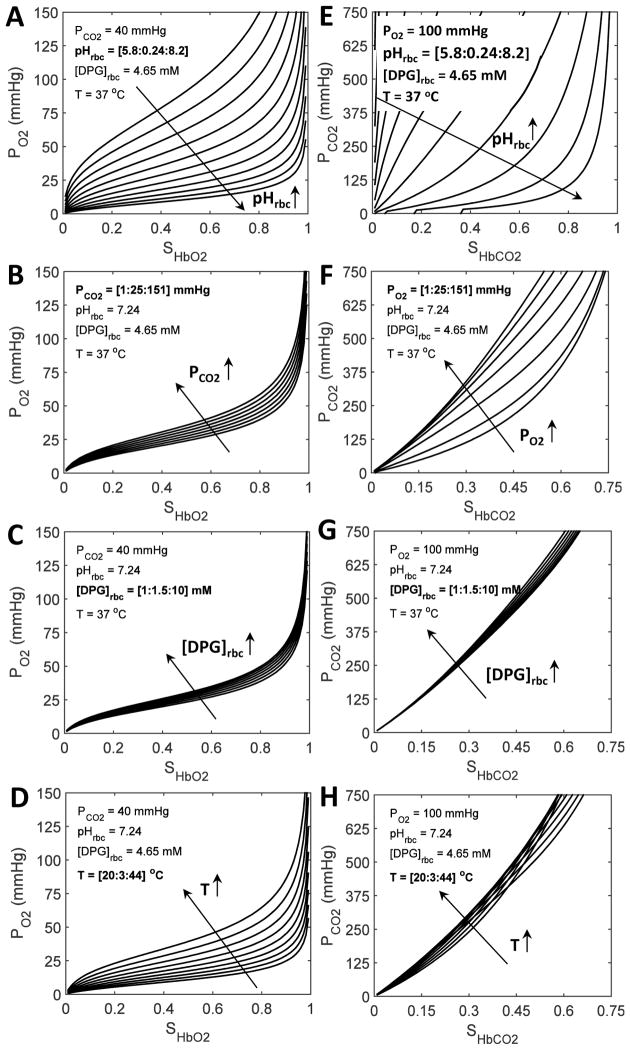
Simulations of the apparent HbO2 binding constant , HbO2 dissociation curves, and HbCO2 dissociation curves over a wide range of physiological conditions (PO2, PCO2, pH, [DPG], and T) are based on our refined models of , SHbO2 and SHbCO2 with the PO2-dependent variable cooperativity hypothesis for O2-Hb binding, and are shown in Fig. 4. The models of SHbO2 and SHbCO2 simulate the Bohr and Haldane effects, and the synergistic effects of 2,3-DPG and T on the HbO2 and HbCO2 dissociation curves. These simulations are consistent with the previous simulations by Dash and Bassingthwaighte (2010), except for their greater accuracy. The shifts in the HbO2 dissociation curves seen in Figs. 4(E–H) are correlated with the variations in the P50 values plotted in Figs. 2(A–D) (solid lines), as defined by Eqs. 9(a–d) and validated by diverse experimental data in Figs. 3(A–D). Similarly, the shifts in the HbCO2 dissociation curves seen in Figs. 4(I–L) are correlated with the extent of CO2 binding to Hb under stipulated physiological conditions, as validated by diverse experimental data in Figs. 3(E–F). These simulations clearly show the different effect of each variable on O2 and CO2 binding to Hb; pH is shown to significantly influence the O2 and CO2 binding, compared with the smaller effects of PCO2, 2,3-DPG, and T.
Figure 4. Simulations of the apparent HbO2 binding constant (A–D), HbO2 dissociation curves (E–H), and HbCO2 dissociation curves (I–L) under varying physiological conditions based on our modified models of , SHbO2 and SHbCO2 with the PO2-dependent variable cooperativity hypothesis for O2-Hb binding.
In plots (A–D) and (E–H), the simulations of and SHbO2 are shown as functions of PO2, respectively, while in plots (I–L), the simulations of SHbCO2 are shown as a function of PCO2. The values of the variables used in each simulation are shown as insets in each panel. Three of the variables are fixed at their standard physiological values, while the fourth one is allowed to increase from a low value to a high value by predetermined increments, shown by the sequence [low: increment: high]. Specifically, in plots (A,E,I), pHrbc varies, while either PCO2 or PO2, [DPG]rbc and T are fixed; in plots (B,F,J), either PCO2 or PO2 varies, while pHrbc, [DPG]rbc and T are fixed; in plots (C,G,K), [DPG]rbc varies, while pHrbc, either PCO2 or PO2, and T are fixed; in plots (D,H,L), T varies, while pHrbc, either PO2 or PCO2, and [DPG]rbc are fixed. In each plot, the long arrow shows the direction of the shift produced by increasing the value of the fourth variable. The shifts in the HbO2 dissociation curves seen in plots (E–H) are correlated with the variations in the P50 values plotted in Figs. 2(A–D) (solid lines), as defined by Eqs. 9(a–d) and validated by diverse experimental data in Figs. 3(A–D). Similarly, the shifts in the HbCO2 dissociation curves seen in plots (I–L) are correlated with the extent of CO2 binding with Hb under stipulated physiological conditions, as validated by diverse experimental data in Figs. 3(E–F).
The accurate and efficient numerical inversion of our refined SHbO2 model under standard physiological conditions is demonstrated in Fig. 5, based on the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) and Winslow et al. (1977). The inset plots in Figs. 5A and 5B clearly show the improved agreement between the inverted PO2 values and the experimental PO2 values at lower SHbO2 levels (<40%) when the Hill coefficient nH is allowed to vary as a function PO2 according to Eq. 11, rather than being held constant. A similar conclusion may be drawn from Figs. 5C and 5D. The results for the inverse problem are consistent with the results for the forward problem shown in Fig. 1. The comprehensive simulations of the numerical inversions under varying physiological conditions are shown in Fig. 6. These include the simulations of PO2 as a function of SHbO2 and the simulations of PCO2 as a function of SHbCO2 over a wide range of values of the relevant physiological variables. In each scenario, three variables are fixed at their standard physiological levels, while the fourth one is allowed to increase by predetermined increments over a large range, as in the simulations for the forward problem in Fig. 4. It is apparent that our iterative numerical inversion schemes are able to effectively simulate PO2 and PCO2 levels from the SHbO2 and SHbCO2 levels over a wide range of physiological conditions.
Figure 5. Illustration of the accurate numerical inversion of the modified SHbO2 model under standard physiological conditions with the PO2-dependent variable cooperativity hypothesis for O2-Hb binding.
(A,B) Comparison of the numerically-inverted PO2 values from the SHbO2 values with constant and variable cooperativity hypotheses for O2-Hb binding (constant and variable Hill coefficient nH) to available experimental data in the literature on normal human blood at standard physiological conditions. The numerical inversions in panel A are compared to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979), and those in panel B are compared to the data of Winslow et al. (1977). The numerical inversions in the main plots are compared to the data over the whole SHbO2 range, while those in the inset plots are compared to the data for SHbO2 ≤ 0.5, effectively demonstrating the accurate numerical inversion of the modified SHbO2 model with variable nH in simulating the data in the lower SHbO2 range. (C,D) The percentage deviations (100 × Δlog10(PO2)) of the numerically-inverted log10(PO2) values from the experimental log10(PO2) values for the constant and variable nH models plotted as functions of log10(PO2) for the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) and Winslow et al. (1977). The PO2 dependencies of nH for these two data sets are as shown in Figs. 1(E,F). The incorporation of the variable cooperativity hypothesis for O2-Hb binding (variable nH) has improved the accuracy of the numerically-inverted PO2 values from the SHbO2 values.
Figure 6. Illustration of the effective numerical inversion of our improved SHbO2 and SHbCO2 equations under varying physiological conditions.
In plots (A–D), the simulations of PO2 as a function of SHbO2 are shown, while in plots (E–H), the simulations of PCO2 as a function of SHbCO2 are shown. In each scenario, three variables are fixed at their standard physiological levels, while the fourth one is allowed to increase by predetermined increments over a large range, as described in detail in the legend to Fig. 4. The inversion computations were carried out using a variant of the Newton-Raphson method (i.e. quasi-Newton-Raphson method) with appropriate initial guesses that guaranteed convergence. These plots are the mirror-images of the corresponding plots in Fig. 4 (but with different scales), illustrating the accuracy of the numerical inversion schemes.
Discussion
We have shown here how shifts in the HbO2 dissociation curve due to variations in PCO2, pH, 2,3-DPG, and T (where the variations occur in one variable at a time or several variables simultaneously) may be handled easily in the Hill equation by using an equation of state for P50 which incorporates the contribution from each of these four variables. While other equations exist for P50, to the best of our knowledge, none incorporates contributions from all of the four variables under discussion or is as extensively validated using independent experimental data. Moreover, we believe that Eq. 10 is the most accurate equation of state for P50 currently available. Although standard versions of Hill’s two-parameter equation for SHbO2 (using only P50 and nH) have been widely used in the past, it is recognized that when nH is set equal to 2.7, as is common practice, the equation is inaccurate for SHbO2 below 30 per cent and above 98 per cent (Dash & Bassingthwaighte, 2010), thus stimulating the development of improved descriptions by Adair (1925), Kelman (1966b), Severinghaus (1979), Siggaard-Andersen et al. (1984), Buerk and Bridges (1986), and others. In this paper, we have addressed this important deficiency in the standard Hill equation by expressing the Hill coefficient nH as a simple exponential function of PO2 (Eq. 11), with P50 given by Eq. 10. Figures 1, 3, and 5 show that this change improves the agreement between the model and available experimental data at both standard physiological conditions and at other values of pH, PCO2, 2,3-DPG, and temperature that characterize pathophysiological states.
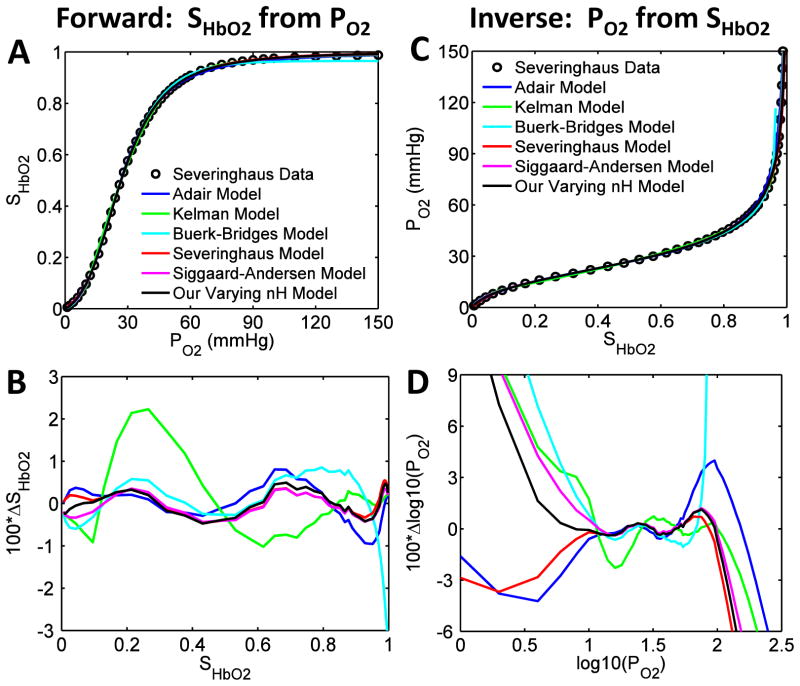
So the question that arises is this: Using these modifications, how does Hill’s equation compare with other commonly used mathematical models of the HbO2 dissociation curve? In Figs. 7A and 7C, we show the fit of our new refined Hill-based equation for SHbO2 to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) under standard physiological conditions and compare that to the fit obtained using the SHbO2 models of Adair (1925), Kelman (1967), Buerk and Bridges (1986), Severinghaus (1979), and Siggaard-Andersen et al. (1984; 1990) for both the forward (computation of SHbO2 from PO2) and inverse (computation of PO2 from SHbO2) situations. The associated residual errors are shown in Figs. 7B and 7D. Although all the models shown in Fig. 7A seem to provide a good fit to the data (except for Kelman (1966b) for some PO2 values and Buerk and Bridges (1986) for high PO2), the residual error shown in Fig. 7B is least for our present model and the models of Severinghaus (1979) and Siggaard-Andersen et al. (1984; 1990). Fig. 7C shows that all the models also produce a good fit to the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) on inversion, but the error plotted in Fig. 7D indicates that our model is the most accurate for PO2 greater than 100.5 (i.e. PO2 > 3) mmHg. Note that the distinction between the various models for the inverse problem is more apparent because of the use of a log-log scale. Apart from the two exceptions mentioned above, when compared with the data most of these models provide accuracy greater than 99.5% over the whole saturation range.
Figure 7. Comparison of our improved SHbO2 model with alternative SHbO2 models from the literature in simulating available experimental data at standard physiological conditions (both forward and inverse problems).
In each case, the model for comparison has first been parametrized to produce a “best fit” based on the experimental data. (A) HbO2 dissociation curves obtained from our improved SHbO2 model compared with those obtained from other commonly used SHbO2 models (Adair, 1925; Kelman, 1966b; Severinghaus, 1979; Siggaard-Andersen et al., 1984; Buerk & Bridges, 1986), in simulating the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) on normal human blood at standard physiological conditions. (B) The percentage deviations (100 × ΔSHbO2) of the model-simulated SHbO2 values from the experimental SHbO2 values based on our improved SHbO2 model and the alternative models, plotted as functions of SHbO2 for the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979). (C) Comparisons of the numerically-inverted PO2 values from the SHbO2 values obtained from our improved SHbO2 model and the alternative models, in simulating the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979) on normal human blood at standard physiological conditions. (D) The percentage deviations (100 × Δlog10(PO2)) of the numerically-inverted log10(PO2) values from the experimental log10(PO2) values based on our improved SHbO2 model and the alternative SHbO2 models, plotted as functions of log10(PO2) for the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979). The comparison may be repeated using the data of Winslow et al. (1977). This involves the re-parametrization of each model to obtain the best fit to the data. The result has not been shown here as it does not contribute anything further to the conclusions already drawn.
We also note here that the other SHbO2 models shown in Fig. 7 were parametrized based on the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979), and hence a comparison of the models with respect to the data of Winslow et al. (1977) cannot be made, unless they are re-parameterized. This is not the purpose of Fig. 7. Rather, the purpose of Fig. 7 is to illustrate how our new refined SHbO2 model is “at least” comparable in terms of accuracy to many other SHbO2 models used widely in the literature. Fig. 7 shows that this is indeed the case, yet our model is simpler than many others and efficiently invertible.
The recent model of Mateják et al. (2015), based on their version of the Adair equation (1925), is reported to fit well, the data of Severinghaus and colleagues (Roughton et al., 1972; Roughton & Severinghaus, 1973; Severinghaus, 1979), and is also shown to fit the temperature and pH-dependent SHbO2 data of Reeves (1980) and Naeraa (1963), and carbaminohemoglobin data of Bauer and Schröder (1972) and Matthew (1977). Our present SHbO2 and SHbCO2 models fit these diverse data sets as accurately, and also fit the PCO2, pH, and temperature-dependent data of Joels and Pugh (1958) and Hlastala et al. (1977), which were not used by Mateják et al. (18). Thus, the present SHbO2 and SHbCO2 models are well-validated based on a larger set of experimental data. More importantly, not only is our new refined SHbO2 model more accurate over the whole saturation range (important for the integrated computational modeling of alveolar-blood and blood-tissue O2-CO2 transport, exchange, and metabolism), it is also much simpler than our previous SHbO2 model, as there is no need to perform the complex computations to derive the indices n1, n2, n3, and n4.
The HbCO2 dissociation curve is obtained in our treatment from Eq. 1b. The expression for KHbCO2 is derived from Eq. 3b and Eq. 4. When SHbO2 equals 1, KHbCO2 equals . Otherwise is required and is given by Eq. 7. Fortuitously, all the information regarding the variables PCO2, pH, 2,3-DPG and T is contained in Eq. 10, the equation of state for P50. Thus, in our treatment, both SHbO2 and SHbCO2 rely on this equation for information about PCO2, pH, 2,3-DPG and T. Other authors incorporate this information in different ways. For example, Severinghaus (1979) provides one equation for the temperature coefficient of PO2 and another for the change in lnPO2 per unit change in pH. If instead of equating Eq. 6 with Eq. 1a, we equate the Severinghaus equation for SHbO2 with Eq. 1a, we obtain the following expression for :
| (12) |
The value for PO2 used in Eq. 12 is that obtained after correction for temperature and pH. A similar approach may be adopted in the case of the Adair equation (Adair, 1925) to transfer information regarding pH, 2,3-DPG and T to the CO2-Hb reaction system. Thus, Eq. 1b can be adapted for use with a variety of models of the HbO2 dissociation curve.
Inversion of SHbO2 and SHbCO2 equations is an essential feature in modeling of alveolar-blood and blood-tissue O2-CO2 exchange at a sophisticated level. Algebraic inversion is possible with the Severinghaus SHbO2 equation (1979), but not in our models, once the Hill coefficient nH is allowed to vary. Iterative approaches are generally used for this. The Appendix provides fixed-point and quasi-Newton-Raphson iterative methods that would also be applicable to the models of Mateják et al. (2015) and others that are not analytically invertible.
Conclusions
We have simplified and extended our previously developed mathematical models of blood HbO2 and HbCO2 dissociation curves (Dash & Bassingthwaighte, 2010) to make them accurate over the whole saturation range for a wide range of values of PO2, PCO2, pH, 2,3-DPG, and temperature. The extended SHbO2 model features a PO2-dependent variable Hill coefficient nH for the binding of O2 to Hb, and incorporates a modified P50 model that provides accurate shifts in the HbO2 dissociation curve over a wide range of physiological conditions, validated by diverse experimental data sets available in the literature. The information contained in this modified equation for P50 is transferred to the HbCO2 dissociation curve via , the apparent equilibrium constant in a single-step binding reaction of O2 and Hb. The coupling of the Hb dissociation curves for O2 and CO2 may also be accomplished using models of SHbO2 other than the Hill equation. Finally, the extended SHbO2 and SHbCO2 models are conveniently invertible for efficient computation of PO2 from SHbO2 and PCO2 from SHbCO2, using simple iterative numerical schemes with appropriate starting values that guarantee convergence. The calculations involved in our new SHbO2 and SHbCO2 models may be performed on handheld devices. More importantly, they can conveniently be used in the integrated computational modeling of alveolar-blood and blood-tissue O2-CO2 transport, exchange, and metabolism for analysis and mechanistic understanding of in-vitro and in-vivo blood gas data under physiological and non-physiological conditions, such as ischemia and reperfusion, extremes in gas concentrations, high altitudes, and extreme temperatures.
Acknowledgments
We thank the reviewers for helpful and insightful comments that have enhanced the overall quality of the manuscript. This work was supported by the National Institute of Health Grants U01-HL122199, P50-GM094503, and P01-GM066730. The extension of P50 model to extreme/wider physiological conditions (e.g. pH > 8.5) was motivated by RKD’s email correspondence with Stefan Kleiser (University Hospital Zurich), a user of the 2010 Dash and Bassingthwaighte SHbO2 and SHbCO2 models.
Frequently Used Abbreviations
- αO2
Solubility of oxygen
- αCO2
Solubility of carbon dioxide
- [O2]
Concentration of free oxygen
- [CO2]
Concentration of free carbon dioxide
- [H+]
Concentration of hydrogen ions (protons)
- [DPG]
Concentration of 2,3-diphosphoglycerate (2,3-DPG)
- T
Temperature
- pH
−log10([H+])
- PO2
Partial pressure of oxygen
- PCO2
Partial pressure of carbon dioxide
- P50
Partial pressure of oxygen for 50% HbO2 saturation
- Hb
Hemoglobin
- HbO2
Oxyhemoglobin
- HbCO2
Carbaminohemoglobin
- KHbO2
Apparent equilibrium constant of hemoglobin and oxygen binding
- KHbCO2
Apparent equilibrium constant of hemoglobin and carbon dioxide binding
- SHbO2
Saturation of hemoglobin with oxygen
- SHbCO2
Saturation of hemoglobin with carbon dioxide
Appendix: Efficient Iterative Schemes for Numerical Computations of PO2 from SHbO2 and PCO2 from SHbCO2
Two efficient numerical methods are presented below for the inversion of PO2 from SHbO2 and PCO2 from SHbCO2, based on fixed-point and quasi-Newton-Raphson iteration methods (Scheme-1 and Scheme-2, respectively) (Heath, 2002; Pozrikidis, 2008).
The iterative schemes for the computation of PO2 from SHbO2 are given by:
| (A-1a) |
| (A-1b) |
where is the input SHbO2 (given), is the value of SHbO2 evaluated at , and is the derivative of SHbO2 w.r.t. PO2 evaluated at . Either Eq. 1a or Eq. 6 can be used as the expression for SHbO2. In the second version of Eq. A-1b, it is only necessary to perform function evaluation, because has been estimated using a central-difference formula for first-order derivatives (Pozrikidis, 2008), which eliminates the need to differentiate the expression for SHbO2, which may be complicated. If the Hill coefficient nH is held constant, Eq. A-1a itself provides the analytical inversion for the computation of PO2 from SHbO2. For PO2-dependent nH (Eq. 11), the iteration scheme of Eq. A-1a converges within 3 to 5 iterations with 10−3 accuracy, using any starting value for PO2. For the same accuracy, the iteration scheme of Eq. A-1b converges within 5 to 8 iterations using P50 from Eq. 10 as the starting value for PO2.
The analogous iterative schemes for the computation of PCO2 from SHbCO2 are given by:
| (A-2a) |
| (A-2b) |
Similar iterative methods can be used to compute PO2 from total [O2] and PCO2 from total [CO2]. Note that the total [O2] and the total [CO2] are defined in Table 1.
Contributor Information
Ranjan K. Dash, Email: rdash@mcw.edu, Department of Physiology, Biotechnology and Bioengineering Center, Medical College of Wisconsin, 8701 Watertown Plank Road, Milwaukee, WI-53226, Phone: 414-955-4497
Ben Korman, Email: ben@korman.com.au, Department of Anaesthesia and Pain Medicine, Royal Perth Hospital, Perth, Western Australia, Australia
James B. Bassingthwaighte, Email: jbb2@u.washington.edu, Department of Bioengineering, Box 355061, N210G North Foege Bldg., University of Washington, Seattle, WA 9895-5061, USA, Phone: 206-685-2012
References
- Adair GS. The hemoglobin system VI. The oxygen dissociation curve of hemoglobin. J Biol Chem. 1925;63:529–545. [Google Scholar]
- Austin WH, Lacombe E, Rand PW, Chatterjee M. Solubility of carbon dioxide in serum from 15 to 38 C. Journal of Applied Physiology. 1963;18:301–304. doi: 10.1152/jappl.1963.18.2.301. [DOI] [PubMed] [Google Scholar]
- Bassingthwaighte JB, Beard DA, Carlson BE, Dash RK, Vinnakota K. Modeling to link regional myocardial work, metabolism and blood flows. Annals of biomedical engineering. 2012;40:2379–2398. doi: 10.1007/s10439-012-0613-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer C, Schroder E. Carbamino compounds of haemoglobin in human adult and foetal blood. The Journal of Physiology. 1972;227:457–471. doi: 10.1113/jphysiol.1972.sp010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buerk DG, Bridges EW. A simplified algorithm for computing the variation in oxyhemoglobin saturation with pH, PCO2, T and DPG. Chemical Engineering Communication. 1986;47:113–124. [Google Scholar]
- Dash RK, Bassingthwaighte JB. Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Annals of Biomedical Engineering. 2004;32:1676–1693. doi: 10.1007/s10439-004-7821-6. [DOI] [PubMed] [Google Scholar]
- Dash RK, Bassingthwaighte JB. Simultaneous blood-tissue exchange of oxygen, carbon dioxide, bicarbonate, and hydrogen ion. Annals of Biomedical Engineering. 2006;34:1129–1148. doi: 10.1007/s10439-005-9066-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dash RK, Bassingthwaighte JB. Erratum to: Blood HbO2 and HbCO2 dissociation curves at varied O2, CO2, pH, 2,3-DPG and temperature levels. Annals of Biomedical Engineering. 2010;38:1683–1701. doi: 10.1007/s10439-010-9948-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forster RE, Constantine HP, Craw MR, Rotman HH, Klocke RA. Reaction of CO2 with human hemoglobin solution. The Journal of biological chemistry. 1968;243:3317–3326. [PubMed] [Google Scholar]
- Geers C, Gros G. Carbon dioxide transport and carbonic anhydrase in blood and muscle. Physiol Rev. 2000;80:681–715. doi: 10.1152/physrev.2000.80.2.681. [DOI] [PubMed] [Google Scholar]
- Heath MT. Scientific Computing: An Introductory Survey. The McGraw-Hill Companies, Inc; Boston: 2002. [Google Scholar]
- Hedley-Whyte J, Laver MB. O2 Solubility in Blood and Temperature Correction Factors for PO2. Journal of Applied Physiology. 1964;19:901–906. doi: 10.1152/jappl.1964.19.5.901. [DOI] [PubMed] [Google Scholar]
- Hlastala MP, Woodson RD, Wranne B. Influence of temperature on hemoglobin-ligand interaction in whole blood. J Appl Physiol Respir Environ Exerc Physiol. 1977;43:545–550. doi: 10.1152/jappl.1977.43.3.545. [DOI] [PubMed] [Google Scholar]
- Joels N, Pugh LG. The carbon monoxide dissociation curve of human blood. The Journal of Physiology. 1958;142:63–77. doi: 10.1113/jphysiol.1958.sp005999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelman GR. Calculation of certain indices of cardio-pulmonary function, using a digital computer. Respir Physiol. 1966a;1:335–343. doi: 10.1016/0034-5687(66)90050-8. [DOI] [PubMed] [Google Scholar]
- Kelman GR. Digital computer subroutine for the conversion of oxygen tension into saturation. Journal of Applied Physiology. 1966b;21:1375–1376. doi: 10.1152/jappl.1966.21.4.1375. [DOI] [PubMed] [Google Scholar]
- Kelman GR. Digital computer procedure for the conversion of PCO2 into blood CO2 content. Respir Physiol. 1967;3:111–115. doi: 10.1016/0034-5687(67)90028-x. [DOI] [PubMed] [Google Scholar]
- Matejak M, Kulhanek T, Matousek S. Adair-based hemoglobin equilibrium with oxygen, carbon dioxide and hydrogen ion activity. Scand J Clin Lab Invest. 2015;75:113–120. doi: 10.3109/00365513.2014.984320. [DOI] [PubMed] [Google Scholar]
- Matthew JB, Morrow JS, Wittebort RJ, Gurd FR. Quantitative determination of carbamino adducts of alpha and beta chains in human adult hemoglobin in presence and absence of carbon monoxide and 2,3-diphosphoglycerate. The Journal of biological chemistry. 1977;252:2234–2244. [PubMed] [Google Scholar]
- Naeraa N, Petersen ES, Boye E. The influence of simultaneous, independent changes in pH and carbon dioxide tension on the in vitro oxygen tension-saturation relationship of human blood. Scand J Clin Lab Invest. 1963;15:141–151. doi: 10.1080/00365516309051325. [DOI] [PubMed] [Google Scholar]
- Pozrikidis C. Numerical Computations in Science and Engineering. Oxford University Press; New York: 2008. [Google Scholar]
- Rees SE, Andreassen S. Mathematical models of oxygen and carbon dioxide storage and transport: the acid-base chemistry of blood. Crit Rev Biomed Eng. 2005;33:209–264. doi: 10.1615/critrevbiomedeng.v33.i3.10. [DOI] [PubMed] [Google Scholar]
- Reeves RB. The effect of temperature on the oxygen equilibrium curve of human blood. Respir Physiol. 1980;42:317–328. doi: 10.1016/0034-5687(80)90122-x. [DOI] [PubMed] [Google Scholar]
- Rossi-Bernardi L, Roughton FJ. The specific influence of carbon dioxide and carbamate compounds on the buffer power and Bohr effects in human haemoglobin solutions. The Journal of Physiology. 1967;189:1–29. doi: 10.1113/jphysiol.1967.sp008152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roughton FJ, Severinghaus JW. Accurate determination of O2 dissociation curve of human blood above 98.7 percent saturation with data on O2 solubility in unmodified human blood from 0 degrees to 37 degrees C. Journal of Applied Physiology. 1973;35:861–869. doi: 10.1152/jappl.1973.35.6.861. [DOI] [PubMed] [Google Scholar]
- Roughton FJW, Deland EC, Kernohan JC, Severinghaus JW. Some recent studies of the oxyhemoglobin dissociation curve of human blood under physiological conditions and the fitting of the Adair equation to the standard curve. In: Rørth M, Astrup P, editors. Proceedings of the Oxygen Affinity of Hemoglobin and Red Cell Acid Base Status; Proceedings of the Alfred Benzon Symposium IV Held at the Premises of the Royal Danish Academy of Sciences and Letters; City. pp. 73–81. (Year) [Google Scholar]
- Severinghaus JW. Simple, accurate equations for human blood O2 dissociation computations. J Appl Physiol Respir Environ Exerc Physiol. 1979;46:599–602. doi: 10.1152/jappl.1979.46.3.599. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O. Oxygen-linked hydrogen ion binding of human hemoglobin. Effects of carbon dioxide and 2,3-diphosphoglycerate. I. Studies on erythrolysate. Scand J Clin Lab Invest. 1971;27:351–360. doi: 10.3109/00365517109080230. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Garby L. The Bohr effect and the Haldane effect. Scand J Clin Lab Invest. 1973;31:1–8. doi: 10.3109/00365517309082411. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Rorth M, Norgaard-Pedersen B, Andersen OS, Johansen E. Oxygen-linked hydrogen ion binding of human hemoglobin. Effects of carbon dioxide and 2,3-diphosphoglycerate. IV. Thermodynamical relationship between the variables. Scand J Clin Lab Invest. 1972a;29:303–320. doi: 10.3109/00365517209080246. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Salling N. Oxygen-linked hydrogen ion binding of human hemoglobin. Effects of carbon dioxide and 2,3-diphosphoglycerate. II. Studies on whole blood. Scand J Clin Lab Invest. 1971;27:361–366. doi: 10.3109/00365517109080231. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Salling N, Norgaard-Pedersen B, Rorth M. Oxygen-linked hydrogen ion binding of human hemoglobin. Effects of carbon dioxide and 2,3-diphosphoglycerate. Scand J Clin Lab Invest. 1972b;29:185–193. doi: 10.3109/00365517209081074. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Siggaard-Andersen M. The oxygen status algorithm: a computer program for calculating and displaying pH and blood gas data. Scand J Clin Lab Invest Suppl. 1990;203:29–45. doi: 10.3109/00365519009087489. [DOI] [PubMed] [Google Scholar]
- Siggaard-Andersen O, Wimberley PD, Gothgen I, Siggaard-Andersen M. A mathematical model of the hemoglobin-oxygen dissociation curve of human blood and of the oxygen partial pressure as a function of temperature. Clin Chem. 1984;30:1646–1651. [PubMed] [Google Scholar]
- Tyuma I. The Bohr effect and the Haldane effect in human hemoglobin. The Japanese journal of physiology. 1984;34:205–216. doi: 10.2170/jjphysiol.34.205. [DOI] [PubMed] [Google Scholar]
- von Restorff W, Holtz J, Bassenge E. Exercise induced augmentation of myocardial oxygen extraction in spite of normal coronary dilatory capacity in dogs. Pflugers Archiv : European journal of physiology. 1977;372:181–185. doi: 10.1007/BF00585334. [DOI] [PubMed] [Google Scholar]
- Winslow RM, Samaja M, Winslow NJ, Rossi-Bernardi L, Shrager RI. Simulation of continuous blood O2 equilibrium curve over physiological pH, DPG, and PCO2 range. J Appl Physiol Respir Environ Exerc Physiol. 1983;54:524–529. doi: 10.1152/jappl.1983.54.2.524. [DOI] [PubMed] [Google Scholar]
- Winslow RM, Swenberg ML, Berger RL, Shrager RI, Luzzana M, Samaja M, Rossi-Bernardi L. Oxygen equilibrium curve of normal human blood and its evaluation by Adair’s equation. The Journal of biological chemistry. 1977;252:2331–2337. [PubMed] [Google Scholar]
- Wolf MB. Whole body acid-base and fluid-electrolyte balance: a mathematical model. American journal of physiology. Renal physiology. 2013;305:F1118–1131. doi: 10.1152/ajprenal.00195.2013. [DOI] [PubMed] [Google Scholar]