Seeds of Locally Aligned Motion and Stress Coordinate a Collective Cell Migration

Abstract

We find how collective migration emerges from mechanical information transfer between cells. Local alignment of cell velocity and mechanical stress orientation—a phenomenon dubbed “plithotaxis”—plays a crucial role in inducing coordinated migration. Leader cells at the monolayer edge better align velocity and stress to migrate faster toward the open space. Local seeds of enhanced motion then generate stress on neighboring cells to guide their migration. Stress-induced motion propagates into the monolayer as well as along the monolayer boundary to generate increasingly larger clusters of coordinately migrating cells that move faster with enhanced alignment of velocity and stress. Together, our analysis provides a model of long-range mechanical communication between cells, in which plithotaxis translates local mechanical fluctuations into globally collective migration of entire tissues.

Introduction

Despite a recent flurry of articles that suggest the importance of mechanical cell-cell interactions during collective migration (1, 2, 3, 4, 5), very little is known about the rules by which local forces enable larger-scale coordination. Traction forces are distributed heterogeneously across a cell monolayer (6), implying single-cell self-propulsion. However, the magnitudes of these forces are not sufficient to drag neighboring cells to coordinate monolayer migration (6). Monolayer stress microscopy (1, 7) employed spatial force-balancing to infer combined forces within and between cells of the monolayer from traction force measurements. A combination of intra- and intercellular stresses at each position within the monolayer were represented by the orthogonal principal stresses, σ_max and σ_min, and revealed that the velocity of individual cells tends to align with the maximum principal stress orientation, a phenomenon referred to as “plithotaxis” (1, 2, 5, 8, 9). These findings led to the speculation that cellular coordination could be induced by local coupling of stress and motion that propagates throughout the monolayer in space and time.

Here we uncover evidence suggesting a simple mechanism for how local mechanical and cellular fluctuations guide emergence of global intercellular coordination. By designing and applying, to our knowledge, new analytical methods to previously published live-cell imaging data (2, 5), we find that cells at the monolayer edge transmit mechanical cues by inducing normal and shear strains on neighboring follower cells. Accumulation and propagation of these mechanical cues over time and space create groups of cells that migrate and exert forces in a coordinated manner. Such motion patterns direct cells from within the monolayer toward the sites of shear-strain-induced motion at the monolayer front. Altogether, our results provide direct insight into how collective migration emerges from active mechanical information transfer between cells, mediated by plithotaxis.

Materials and Methods

Monolayer expansion assay, and traction and monolayer stress microscopy using Madin-Darby canine kidney cells

Raw time-lapse image sequences were taken from the data originally published by Serra-Picamal et al. (2). Sequences were filmed at a rate of 9 min/frame with a pixel size in object space of 0.645 × 0.645 μm. All other experimental settings can be found in the original article. Time-lapse sequences of traction forces and derived monolayer stresses were also taken from the data in Serra-Picamal et al. (2). Traction force monolayer stress calculations are described in Trepat et al. (6) and Tambe et al. (1), respectively. Local stress is depicted by an ellipse (Fig. 1 b), with σ_max and σ_min denoting the magnitudes of the two principal stress components and their corresponding orthogonal principal orientations. The average normal stress within and between cells is defined as (σ_max + σ_min)/2 and the maximum intercellular shear stress or anisotropy is defined as (σ_max − σ_min)/2. The local stress magnitude was defined as $\sqrt{({\sigma }_{\text{max}}^2+{\sigma }_{\text{min}}^2)}$.

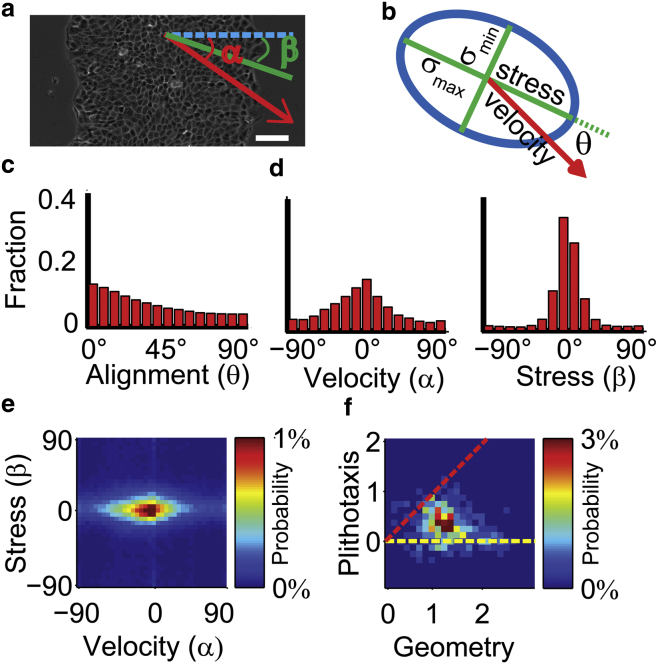
Figure 1.

The role of geometry and plithotaxis in inducing motion-stress alignment. (a) Velocity angle (α) and stress orientation (β), calculated in relation to the direction defined by the direction of monolayer expansion (blue line). Scale bar = 100 μm. (b) Velocity and stress representation. The values σ_max and σ_min define the principal axis of the stress tensor. θ is the motion-stress alignment angle. (c) Distribution of motion-stress alignment angle (θ). (d) Distribution of velocity angle (α, left), stress orientation (β, right), where 0° represents alignment with the x axis (equivalent to direction of monolayer expansion). (e) Joint distribution of velocity angles and stress orientations accumulated for all monolayer locations over time. (f) Joint distribution of plithotaxis index and geometry index for all time points (n = 96) in all experiments (N = 4), estimated corresponding angle in Fig. S2. See Fig. S1 and Materials and Methods for a definition of the indices.

Wound-healing assay using human bronchial epithelial cells

Human bronchial epithelial cells 16HBE14o- (HBEC) were cultured in modified Eagle medium with 10% fetal bovine serum (Cat. No. FB-11; Omega Scientific, Tarzana, CA), GlutaMAX (Invitrogen, Waltham, MA), and penicillin/streptomycin antibiotics (Cat. No. 15140; Gibco/Thermo Fisher Scientific/Invitrogen, Waltham, MA).

3 × 10⁶ HBEC were seeded into 6-well plate. After 48 h, cells were scratched by a pipette tip and removed by a scraper (Corning cell lifter; Sigma-Aldrich, St. Louis, MO) to generate empty space for cell migration. The migration of the cells from the edge of the wound was imaged by phase-contrast microscopy on an inverted Axiovert 200M (Carl Zeiss, Jena, Germany) equipped with an EC Plan-Neofluar 10× lens, motorized stage, temperature, and CO₂ controllers (37°C, 5% CO₂; Carl Zeiss). Time resolution was 5 min per frame, and the physical pixel size was 1.25 × 1.25 μm.

Velocity measurements

Velocity fields were computed using custom cross correlation-based particle image velocimetry using nonoverlapping image patches of size 13 × 13 μm (Madin-Darby canine kidney (MDCK) cell experiments) or 15 × 15 μm (HBEC experiments). The frame-to-frame displacement of each patch was defined by the maximal cross-correlation of a given patch with the subsequent image. The maximal search radius was set to 14 (MDCK) or 7 (HBEC) pixels, corresponding to an instantaneous velocity of 60 (MDCK) or 90 (HBEC) μm h⁻¹. Monolayer contours were computed by applying MultiCellSeg (10, 11) on each phase-contrast image.

Directionality, and strain rate

Every velocity vector is composed of two components, one in the direction toward the free edge, i.e., perpendicular, and one parallel to the monolayer boundary. Directionality is defined as the absolute value of the ratio perpendicular to parallel component. Strain rate was defined according to Blanchard et al. (12), as the spatial derivative of the velocity vector ∂|v|/∂x, where x is the local migration direction of each patch (Fig. 2 a). It was calculated as the difference between the velocities of the patches ahead and behind the patch of interest, according to its local direction. Assuming cellular cohesiveness and mass conservation, it is an implicit measure for cellular deformation rate (12), thus cell stretching was taken to be proportional to the strain rate along the trajectory. Note that this measure was considered to be only the normal component of strain rate, and ignores shear.

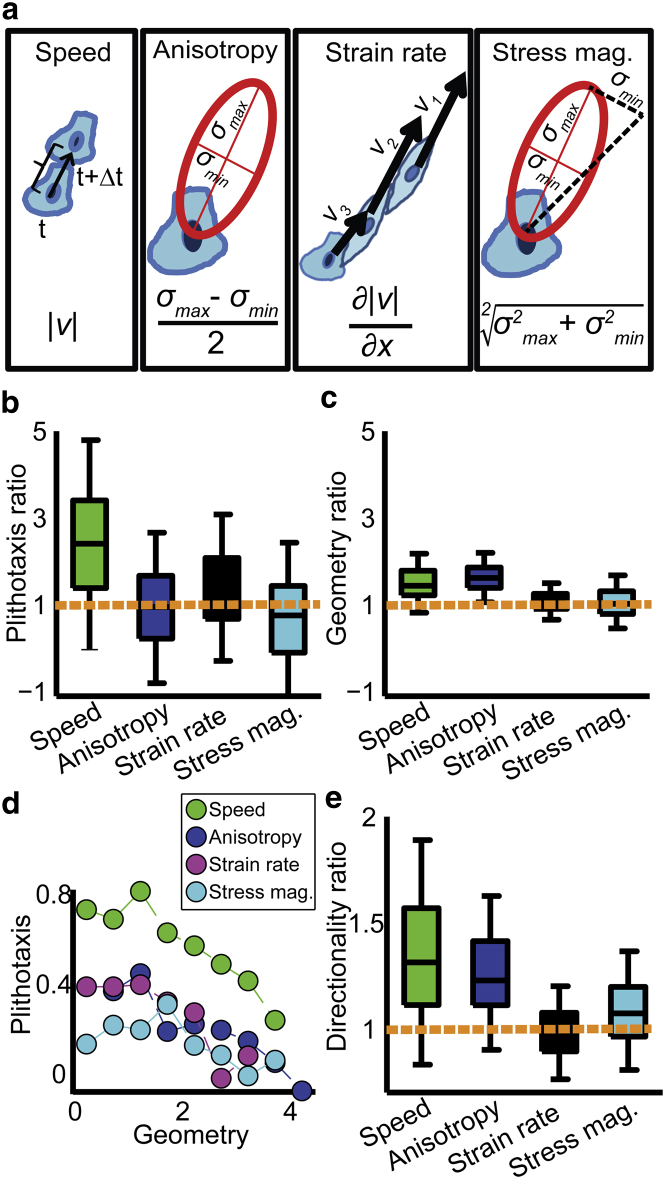
Figure 2.

Cell speed is associated with elevated plithotaxis. (a) The measured properties. Speed, t, t+Δt denote consecutive time points. Anisotropy, (σ_max − σ_min)/2. Strain rate, local spatial derivative of speed in the direction of cell motion (denoted x). Three adjacent cells in the monolayer are depicted with velocities v1, v2, and v3 at similar directions. Assuming that cells maintain cohesiveness, |v1| ≈ |v2| > |v3| imply that the middle cells are deformed in the direction of motion. This is an implicit measure of cell stretching. Stress magnitude, $\sqrt[2]{{\sigma }_{\text{min}}^2+{\sigma }_{\text{max}}^2}$. (b and c) Distributions of ratios between plithotaxis index (b) or geometry index (c) of the top 20% of cells for a given property and the full cell population. (d) Average plithotaxis index as function of the geometry index. (e) Distributions of ratios between the median directionality of the top 20% of cells according to a given property and the full cell population. Median is used because directionality may have extreme values. Note the difference in Y-axis scaling from (b) and (c). (b–e) Accumulated for all N = 4 independent experiments and n = 96 time points per experiment.

Geometry index and plithotaxis index

The resampled alignment distribution was constructed by random and independent resampling of velocity direction and stress orientation from their corresponding marginal distributions. By definition, this distribution is void of any local alignment of motion and stress, but only captures the general alignment of the two vector variables imposed by the monolayer geometry. The uniform alignment distribution is the expected resampled distribution from two uniform marginal distributions of velocity direction and stress orientation, where no bias is imposed by the monolayer geometry. The difference between the resampled and uniform distributions defines the geometry index determining how much of the observed motion-stress alignment is associated with the geometry of the monolayer (Fig. S1 in the Supporting Material). Differences between distributions were quantified by the earth movers distance (EMD) (13, 14), which is defined as the minimal cost to transform one distribution into the other:

$$EMD\left(x,y\right)=\sum _{i=1,..,\text{nbins}}\left|\sum _{j=1,..,i}{x}_j-\sum _{j=1,..,i}{y}_j\right|.$$

Accordingly, we define

$$geometryindex=EMD\left(\text{uniform},\text{resampled}\right).$$

The plithotaxis index determines how much of the observed motion-stress alignment is associated with local alignment of the two vector variables (Fig. S1). The index is calculated as

$$plithotaxisindex=EMD\left(\text{uniform},\text{observed}\right)-\text{geometry}\text{index}.$$

We prefer this definition to “EMD(observed, resampled)” for the reasons detailed in Data S1.

Coordination

Explicit detection of cells migrating or experiencing stress in coordinated clusters within the monolayer was performed by applying image segmentation on a dense grid of vectors as described in Zaritsky et al. (3). Image-patch velocities were inputs for segmentation of coordinated motion clusters. Stress vectors were defined by σ_max, σ_min, and the stress orientation:

$$\begin{array}{c}\mathit{dx}={\sigma }_{\text{max}}\times \text{cos}\left(\text{orientation}\right)-{\sigma }_{\text{min}}\times \text{sin}\left(\text{orientation}\right)\\ \mathit{d}\mathit{y}={\sigma }_{\text{min}}\times \text{cos}\left(\text{orientation}\right)-{\sigma }_{\text{max}}\times \text{sin}\left(\text{orientation}\right)\end{array}$$

A region-growing segmentation approach inspired by Nock and Nielsen (15) was used for the vector clustering. It starts with regions containing a single image patch. Clusters grow by iteratively merging spatially adjacent pairs of patches based on their vector similarity, defined as the magnitude of the difference vector normalized by the magnitude of the larger of the two considered vectors. The merging order is in ascending order of the similarity between adjacent patches. Two regions are merged if their similarity is lower than a given threshold. The merged region vector is updated to be the average of all contributing patch vectors. The same clustering algorithm was applied for stress-clustering (Fig. 3 a).

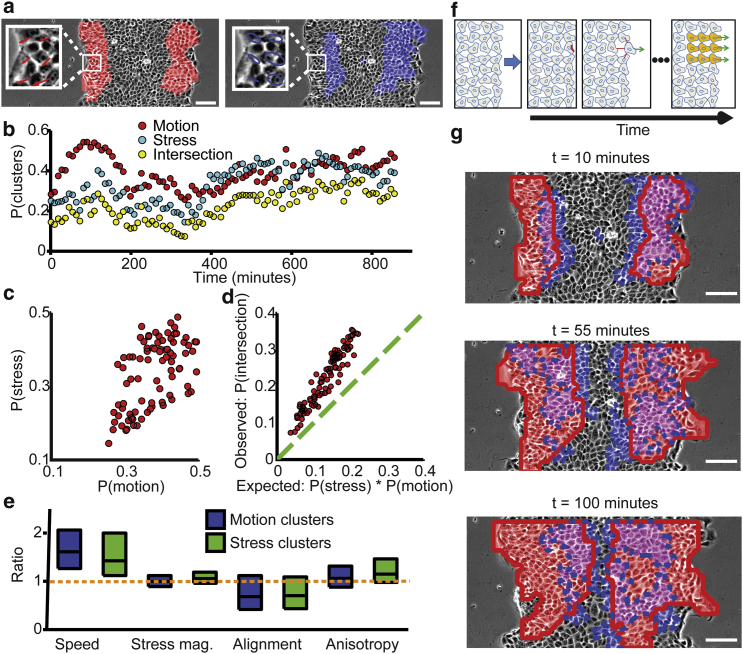
Figure 3.

Group plithotaxis: global alignment of stress and velocity drive intercellular coordination. (a) Motion clusters (left, red regions) derived from the velocity field (left inset, a magnified region from the main panel); stress clusters (right, blue regions) derived from the stress ellipse (right inset, a magnified region from the main panel). Scale bar = 100 μm. (b–d) Motion- and stress-coordinated clusters are interlinked. (b) Time course of probabilities for a cell to belong to either a motion cluster (red), or a stress cluster (light blue), or both (intersection, yellow). (c) Correlation between P(motion) and P(stress) for all time points (Pearson correlation: N = 96, R = 0.4, p < 0.00005). (d) Expected versus observed probability of the intersection between motion and stress clusters. Assuming that these clusters are spatially independent, the expected probability would be P(motion) ^∗P(stress). The observed probability is higher by 40% on average than the expected probability. (e) Comparison of cell dynamics inside and outside clusters. Distributions of ratios between properties of cells that participate in coordinated clusters (inside) and those that do not (outside). Distributions were generated from pooled ratios of averages over space and time (n > 5500; Fig. S4). (f) Proposed model, see text for discussion. (g) Stress coordination spatially precedes motion coordination. Motion clusters (red, solid line marks boundaries) and stress clusters (blue, dashed line marks boundaries) at three time points. Motion and stress clusters are spatially interlinked (magenta). Motion clusters are closer to the monolayer edge than stress clusters, implying that stress coordination precedes motion coordination. Over time, cells deeper in the monolayer first participate in stress clusters and later in motion clusters (Movie S1). Scale bar = 100 μm.

Protruding-cells kymograph

The monolayer edge was segmented and tracked over time. For each time point, we recorded the changes in the edge with respect to the previous time point. The protruding-cells kymograph was defined by a matrix with columns [1 …, t, …, T_max] representing all time points T_max of a movie, and rows [1, …, y, …, Y_max] representing Y_max constant sectors along the moving monolayer edge. The sector width was set to 13 μm (MDCK) and 15 μm (HBEC), the same as the side length of an image patch used to record velocity (see above). A nonzero value at (t,y) indicates that at time t, the cell in sector y moved forward. The color encodes the location of the cell in the direction perpendicular to the monolayer edge (x axis). Therefore, the protruding cells kymograph encodes the complete evolution of the monolayer edge over time. An example of a protruding cell kymograph can be found in Fig. 4 b, and the corresponding construction process is depicted in Movie S2 (for HBEC).

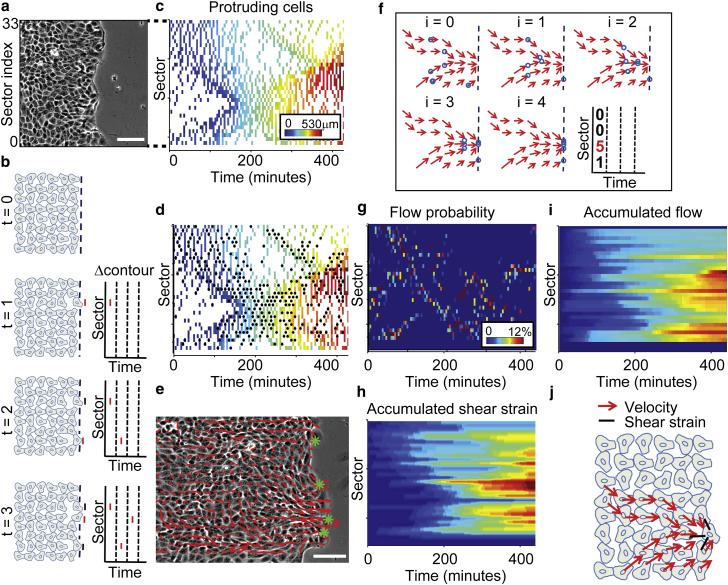
Figure 4.

Shear-strain events guide multicellular flow patterns. (a) First time frame of one side of a MDCK expansion assay. The monolayer edge moving along the x axis is divided into 33 sectors of 13 μm length. Scale bar = 100 μm. (b) Schematic construction of a protruding cells kymograph. (Left) Monolayer state at times 0–3. (Right) Stepwise recording of protrusion events in a kymograph (see Movie S2 for a step-by-step reconstruction). (c) Protruding cells kymograph. (Color encodes the position of the recorded protrusion event along the x axis.) (d) Detection of shear-strain events (black dots) in the protruding cells kymograph. (e) Snapshot of a frame taken 4 h after scratching. Velocity fields (red arrows) seem to converge onto shear-strain events (green asterisks). Scale bar = 100 μm. (f) Flow probability kymograph calculation. For each time point, tracers (blue circles) are placed randomly inside the monolayer and iteratively (labeled by i = 0–4) displaced along the snapshot of the motion field at that time point (red vectors). The final accumulation of tracers along the monolayer edge defines the flow probabilities (right). Note that this process repeats for each time-frame, freezing the corresponding velocity fields to repeatedly displace the tracers. (g) Flow probability kymograph. (Color encodes the probability of a tracer to reach the corresponding sector along the monolayer edge.) (h and i) Time-accumulated shear-strain events (h) and flow probabilities (i), p < 0.003 via permutation test (see Materials and Methods), Pearson R = 0.83, mean scrambled Pearson R = 0.73. (j) Shear-strain events guide long-distance multicellular dynamics.

Shear-strain events detection

A shear-strain event was defined as forward motion of one cell followed by forward motion of a neighboring cell along the monolayer edge, subject to the constraint that the position of the neighboring cell is not in front of the initiating protrusion event, in respect to the monolayer edge. To detect shear-strain events, we applied spatial binary pattern matching on the protruding cells kymographs. We matched templates that encode the initiation of a shear-strain event in a sector, such that at least three out of four sectors next to the protrusion initiating patch advanced within a time frame of four frames in the time lapse sequence (36 min for MDCK cells, 20 min for HBEC). The choice of three sectors as a minimal condition for a shear-strain event ensures that at least two adjacent cells are participating. We also enforced that a single cell will not be recorded twice by assigning the value of 0 to the patch adjacent to the protrusion initiating patch in every template. Under these assumptions, 18 templates fulfilled this definition (Fig. S12 a). The values of the corresponding bins in the protruding cells kymograph (represented as color) validate that the follower cell was not located before the leading cell in respect to the direction perpendicular to the monolayer edge (x axis) upon the initiation of a shear-strain event (Fig. S12 b). Last, we excluded the second detection of a sector in consecutive time points, to discard multiple detections for the same cells. There may still be ambiguous cases, due to the usage of subcellular patches instead of cells; however, these constraints capture the vast majority of possible scenarios, and subjective assessment suggests that it indeed effectively captures shear-strain events. Fig. S12 c illustrates a binary (i.e., ignoring the x-position constraint) shear-strain event representation in a protruding cells kymograph.

Flow probability analysis

Flow patterns were quantified by following the velocity vectors and quantifying the probability of a virtual tracer to be guided toward a particular sector along the monolayer front. For each time point, 500 virtual tracers were randomly distributed inside the monolayer up to a distance of 180 μm from the monolayer front. Next, the tracers were translocated for 500 iterations according to the local velocity vectors at the processed time point (Fig. 4 f). Importantly, the velocity fields remain constant for all iterations at a specific time point. The final positions of the tracers were used to record their distribution along the perimeter (Fig. 4 f, right panel). The distribution was sampled using the same 13/15-μm-wide sectors and attractor points identified as sectors with a high density of converging tracer paths. This process was repeated for every time point, each defining a column of the flow probability kymograph.

Correlating shear-strain events and flow probability

To correlate discrete shear-strain events to a flow probabilities kymograph, we integrated both over time (Fig. 4, h and i) and performed a permutation test in the time-accumulated kymographs. Specifically, each position (t,y) in the time-accumulated kymographs recorded the sum of shear-strain and flow probability events, respectively, over the period 1,…,t for sector y. To assess the association between shear-strain events and flow probabilities of a given experiment we performed a permutation test with the null hypothesis that shear-strain events at a specific sector are independent of flow probabilities events at the same sector. Under this null hypothesis, permutation of rows in the time-accumulated kymographs would not change their overall cross correlation. The rows of the time-accumulated flow probability kymograph were permuted 5000 times. For each permutation, the Pearson correlation coefficient between all bins of the permuted and of the time-accumulated shear-strain kymograph was recorded. The ranking of the Pearson correlation coefficient between the unpermutated time-accumulated kymographs determined the p-value. Reduced numbers of shear-strain events in the MDCK data resulted with less significant correlations. The flow tracers often arrived to adjacent sectors where shear-strain events occurred. Thus, for this analysis we reduced the resolution of the time-accumulated shear-strain and flow kymographs by combining two sectors as one (reducing the y axis resolution by factor of 0.5).

Results

Contributions of monolayer geometry and plithotaxis to motion-stress alignment

Plithotaxis is defined as the tendency of individual cells to migrate along the local orientation of the maximal principal stress (1). It has been proposed as a major organizational cue in collective cell migration (1, 8). The concept of plithotaxis has been formulated based on the observation that the distribution of alignment angles between velocity and maximal principal stress (denoted as motion-stress alignment) was leaning toward low angles (1, 2, 5, 8, 9) (Fig. 1, a–c). However, the marginal distributions of direction of velocity (Fig. 1 d, left) and stress orientation (Fig. 1 d, right) are biased to the direction of monolayer expansion. Therefore, the observed motion-stress alignment could be merely the consequence of a conjoint but independent preferential orientation of velocity and principal stress in the direction of the monolayer edge, driven by global mechanical constraints associated with the monolayer geometry. In agreement with this conjecture, the joint distribution of velocity direction and stress orientation shows that velocity and stress independently align very prominently with the direction toward the monolayer edge (Fig. 1 e). This analysis questions the existence of a true relation between motion and stress as predicted by plithotaxis.

To test whether the tendency for local motion-stress alignment underlies these distributions, the global contributions of monolayer geometry must be eliminated. We devised an approach to separate the global and local cues, which we denoted the “geometry index” and “plithotaxis index”, respectively (see Fig. S1 and the Materials and Methods). In brief, the method assumes that velocity and stress are each biased by the monolayer geometry and that this global cue is superimposed to a more local cue to cumulatively explain the observed alignment. To assess the magnitude of the global cue, we simulate motion-stress pairs by independent resampling of the marginal distributions of velocity direction and stress orientation. Deviation of this resampled distribution from a uniform distribution, which reflects the fully unbiased distribution, indicates how much global bias is present in the observed data. We quantify distance between the resampled and uniform distributions of motion-stress alignment angles based on the EMD metric (13, 14), and refer to it as the geometry index. The magnitude of the local cue, referred to as the plithotaxis index, was calculated accordingly as the EMD between the uniform distribution and the motion-stress distribution observed experimentally minus the geometry index (see Fig. S1 and Materials and Methods). Importantly, the plithotaxis index is a lower bound to the actual plithotaxis whereas the geometry index is an upper bound for the contribution of monolayer geometry. These bounds were empirically shown to be close estimates to the actual values (Data S1).

The joint distribution of the plithotaxis and geometry indices (Fig. 1 f) demonstrated that most data fall above the y = 0 line but below the y = x line (Fig. 1 f and Data S1). Hence, plithotaxis does contribute to the overall motion-stress alignment observed in experiments, but monolayer geometry plays the dominant role (Fig. S2).

Properties of cells exhibiting plithotaxis and motion-stress alignment

It has been hypothesized that enhanced plithotaxis enables more efficient migration during monolayer migration (8, 16, 17). We therefore asked whether there are specific physical properties that are amplified in cells that exhibit elevated motion-stress alignment. Four properties were considered: speed, stress anisotropy (henceforth denoted anisotropy), strain rate (which is an indirect measure for cellular stretching (2, 3, 12)), and stress magnitude (Fig. 2 a and Materials and Methods). For each property, the top 20% of cells for each time point were selected. Their plithotaxis and geometry indices were normalized in relation to all cells. For example, we calculated the normalized plithotaxis index of the fastest 20% of cells for time t as

$${\text{plithotaxis}}_{\mathit{ratio}\mathit{speed}20\%}^t=1+\frac{{\mathit{plithotaxis}\mathit{index}}_{\mathit{speed}20\%}^t-{\mathit{plithotaxis}\mathit{index}}_{\mathit{speed}\mathit{all}}^t}{\frac{1}{T}{\sum }_{t=1,\dots ,T}{\mathit{plithotaxis}\mathit{index}}_{\mathit{speed}\mathit{all}}^t}.$$

A value of 1 means that the subpopulation of the fastest 20% of cells behaves similarly in terms of plithotaxis compared to the full cell population. Values >1 indicate enhanced plithotaxis for this cell group. We found that fast cells were 2.5-fold enhanced in plithotaxis (Fig. 2 b), whereas anisotropy, strain rate, and stress magnitude had a minor or no association with plithotaxis. None of the four properties was associated on a similar scale to the geometry index (Fig. 2 c). Because of the correlation between plithotaxis and geometry indices (Data S1), we confirmed that the plithotaxis enhancement remained independent of the geometry index (Fig. 2 d). Spatial analysis demonstrated that cells closer to the monolayer edge displayed 1.2-fold increased plithotaxis and geometry indices (Fig. S3, a and b), the increase in plithotaxis index was independent of the increase in geometry index (Fig. S3 c), and front cells tended to migrate faster (Fig. S3 d). However, this spatially cued increase in plithotaxis is small compared to the fold-increase in plithotaxis of all fast cells (Fig. 2 b), suggesting that at least some of the fast and highly plithotactic cells reside deeper within the monolayer. Together, these analyses suggested that increased cell speed is a hallmark feature of plithotactic cells.

Next, we hypothesized that enhanced plithotaxis of fast cells originated from mechanical constraints imposed by the monolayer geometry, i.e., stresses aligned with the direction perpendicular to the monolayer boundary should translate more efficiently into unconstrained motion into the cell-free space. Indeed, fast cells, besides exhibiting more plithotaxis, also migrate with elevated directionality toward the monolayer edge (Fig. 2 e). Together, our results demonstrate that a subpopulation of cells better aligns motion with stress and migrates faster toward the direction of open space.

Intercellular coordination: global alignment of stress and velocity

Because the faster motion of a subpopulation of cells should lead to an increased strain in neighboring cells, which in turn could lead to elevated stress and motion alignment, we hypothesized that clusters of coordinated motion and stress form within the monolayer. The hypothesis was supported by data that showed spatial variation in plithotaxis (see Data S2). Thus, a small number of plithotactic cells may serve as seeds to induce multicellular coordination. To test this explicitly, we applied a spatial clustering algorithm to detect groups of cells that migrate or exert forces in a coordinated manner (3) (see Materials and Methods). These groups consist of cells with mutually correlative velocities or principal stresses.

For every time point, motion- and stress-coordinated clusters were detected independently and the fraction of cellular areas migrating/exerting forces coordinately was recorded (Fig. 3 a). This approximated the probabilities P(motion) and P(stress) of a cell to be part of a motion- or stress-coordinated cluster, respectively. The probability of a given cell to belong to both motion- and stress-clusters was denoted P(intersection). If stress- and motion-clusters were spatially independent, then P_expected(intersection) would be equivalent to the product P(motion) × P(stress). Fig. 3 b illustrates the temporal dynamics of the three probabilities. P(intersection) follows the trend of P(motion) and P(stress) and coordinated motion was found to be correlated to stress coordination (Fig. 3 c). For all time points, the observed intersection probability was higher than the expected one, i.e., P(intersection) > P_expected(intersection) (Fig. 3 d), indicating that motion- and stress coordination are interdependent.

To test the hypothesis that coordinated cells migrate more efficiently than other cells, we examined the characteristics of cells that participate in coordinated clusters compared to those that do not. Speed, stress magnitude, alignment of motion- and stress angles, and anisotropy were considered. For each property, the ratio between the spatiotemporal average values of cells inside- and outside clusters was recorded, e.g., speed_in/speed_out. Cells that migrated in coordinated clusters (motion or stress) were faster and maintained enhanced motion-stress alignment (smaller alignment angles) compared to cells outside clusters (Figs. 3 e and S4). Cells that migrated coordinately did not feature a significant increase in their plithotaxis index but a 2.5-fold increase in geometry index (Fig. S5, a and b). However, an increased plithotaxis index was observed also in clusters when we decoupled its dependency on the geometry index (Fig. S5 c), suggesting that a small increase in plithotaxis can lead to a significant increase in coordination. Careful examination of the distributions of stress orientation and velocity directions showed that the former remains almost stable inside and outside clusters while the velocity bias to the direction of the monolayer edge diminished for cells outside clusters (Fig. S5 d). These data provided an initial clue that stress may orient motion to induce multicellular coordination within the monolayer.

Altogether, these results enable us to formulate a model how single cell fluctuations lead to global coordination in the monolayer (Fig. 3 f). Some cells at the monolayer edge migrate more efficiently toward the monolayer edge, where the direction is less mechanically constrained by neighbors. Such cells migrate faster and with elevated directionality (Fig. 2 e). Consequently, they pull on their neighbors, which generate oriented stress that can, in turn, serve as a directional cue for neighboring cells. This process propagates spatially—we speculate by application of strain at cell-cell junctions—resulting in growth of coordinated cell clusters guided by so-called leader cells (18, 19, 20, 21).

According to the proposed model, fast moving leader cells would strain the neighbors located directly behind them and align orientation of stress. In turn, these neighboring follower cells would align motion axis with strain axis. To test this prediction directly in our data, we examined the spatial locations of coordinated clusters over time. Indeed, we found that stress-coordination spatially preceded motion-coordination (Fig. 3 g and Movie S1). Cells located deeper in the monolayer began migrating coordinately over time while coordinated stress propagated deeper into the monolayer over time (Fig. 3 g and Movie S1). Evidence for junctional transmission of the alignment signal was generated by reassessing data from a recent RNA_i-based mini-screen, which identified, in a wound healing assay using MDCK cells, the tight junction proteins Claudin-1, Patj, Angiomotin, and Merlin as implicated in collective migration (5). Close examination of these data revealed that the distribution of stress orientation remains stable upon depletion of these proteins, but the velocity direction distribution is much less biased toward the monolayer edge (Fig. S6). These results strongly suggest that motion does not align stress, but stress may align motion. Thus, we propose that intercellular coordination throughout the monolayer arises by cell-cell junctional propagation of strain from leader to follower cells amplified by local coupling of stress and motion.

Long-range mechanical guidance of cellular flow in the monolayer by leader cells

To establish further support for our model, we tested the prediction that cells from deep within the monolayer should be guided by the local strains induced by leader cells at the monolayer boundary.

We followed the advancing edge and visualized the cells that protrude into the open space at each time point along the monolayer edge in a protruding-cells kymograph (Fig. 4 b, Materials and Methods, and Movie S2). This representation revealed patterns of protrusion waves propagating along the monolayer edge (Fig. 4 c). Each wave was initiated by a single leader cell located at the monolayer front that moved toward the open space, and was followed by the motion of an adjacent follower cell in the next time point. These so-called shear-strain events were identified for each time-point in the protruding cells kymograph by detecting at least two adjacent cells, where one cell advances toward the open space while being followed by its neighbor(s) (Fig. 4 d and Materials and Methods). Intriguingly, the shear-strain events propagated over time to distant cells along the monolayer front. This suggests that, starting with a leader cell, protruding cells apply shear-strain and activate motion in their neighboring cells, leading to an overall transversal coordination of migration at the monolayer front.

Visual inspection of the movies also suggested the existence of long-range motion patterns that guide cells from within the monolayer to the location of shear-strain events at the edge (Fig. 4 e). We therefore quantified the relationships between local shear-strain events and the motion-field inside the monolayer: we placed virtual tracers in the motion field and iteratively tracked their paths to the monolayer front (Fig. 4 f). This generated a density distribution denoted flow probability, which indicated motion attractor points along the monolayer edge (Fig. 4 g, and see Materials and Methods). Qualitatively, the flow probability seemed to mirror the distribution of shear-strain events (Fig. 4 d versus Fig. 4 g). However, the frequency of discrete shear-strain events was too low for a direct analysis of this relationship. Instead, we integrated for each location along the monolayer edge shear-strain events and flow probabilities over time to define kymographs of time-accumulated shear-strain (Fig. 4 h) and flow (Fig. 4 i). Permutation-test analysis on the rows of these kymographs confirmed that the two properties are highly correlated in space (p < 0.003). Moreover, temporal cross correlation of the kymographs showed that the two properties are synchronized (Fig. S7).

To validate this long-range guidance, we used a wound-healing response of HBECs as a second model system instead of the MDCK cell-based expansion assay. HBECs were grown to confluence then scratched to introduce a wound, and wound closure was recorded via phase-contrast time-lapse microscopy (Fig. S8 a and Movie S3). Nearly identical to the MDCK expansion assay, the protruding cells kymograph showed waves spanning long distances (Fig. S8 b and Movie S2), and shear-strain events and flow probabilities seemed to be correlated (Fig. S8 c versus S8 d; additional examples in Fig. S9); this correlation was quantitatively validated with the corresponding accumulated kymographs (Fig. S8 e versus S8 f, p < 0.002; additional examples in Fig. S10, where p < 0.001). Temporal cross correlation showed that the two properties are synchronized (Fig. S11). Together, these analyses revealed that cellular flows tend to guide cells from deep within the monolayer toward the sites of shear-strain-induced motion at the monolayer front (Fig. 4 j) and thus suggest that cells within the monolayer transmit mechanical cues to guide their followers’ motion.

Discussion

Theoretical work suggested that single cells within the monolayer tend to align their traction forces with their velocity (16) and that cell-substrate traction may polarize neighboring cells in the same direction, eventually forming long-range polarization and intercellular coordination (22). Recent experiments correlated cell polarization along the direction of the maximal principal stress, maximum shear stress, and the cell aspect ratio and harnessed theoretical modeling to suggest that maximum shear stress is driving cell polarity (23). Other studies demonstrated that strain can induce a molecular response that correlates to long-range coordination and motion-stress alignment (5) and that elevation in strain rates precedes coordinated migration (3). Our findings now provide experimental and analytical insight into how local mechanical fluctuations can lead to spatially heterogeneous, yet coordinated migration. A subpopulation of leader cells transmits mechanical cues by inducing normal strain on follower cells in the rear and shear strain on adjacent cells on the side. This mechanism transforms local stress to coordinated traction forces and cell polarization, which finally results in coordinated motion (Fig. 3 g and Movie S1) using plithotaxis as the mediator of mechanical information transfer. Propagation of this cell-cell mechanical communication over time and space creates groups of cells that migrate and exert forces in a coordinated manner (Fig. 3 f), directing cells from within the monolayer toward the sites of strain-induced motion at the monolayer front (Fig. 4 j) to drive overall organization of the collective migration. We speculate that shear strain-induced motion propagation along the monolayer edge helps activating this inside-out migration over the whole monolayer front, while at the same time inhibiting the formation of multicellular fingerlike structures (18, 19).

Several molecular mechanisms are known to govern information transfer between cells, most prominently cadherin signaling (24, 25, 26) in conjunction with activation of contractility and cross-talk to cell-matrix adhesions (27). Other pathways such as Merlin-Rac1 may also be implicated (5). Nonetheless, very little is known about the molecular machinery underlying these coordinating mechanical events. Our findings in particular pose the questions: What is the molecular and cellular origin of plithotaxis? Are the molecular machineries propagating shear-strain (28) along the monolayer edge the same as those propagating normal strain (2, 3)? Are there cells that intrinsically exert elevated traction (21)? Are leader cells defined by particular molecular features (e.g., increased sensitivity to growth factor activation (20, 29, 30), or elevated RhoA activity (31))? Alternatively, coordination can be initiated via random force exertions and alternating leader cells (32). What is the role of local monolayer curvature in the formation of leader cells (33, 34, 35)? The image analysis and statistical methods introduced with this work will be enabling to upcoming studies addressing some of these molecular aspects as well as testing whether our observations can be quantitatively explained by previous theoretical models (16, 21, 34, 36).

Author Contributions

A.Z. conceived the study and analyzed the data; M.A.R. and Y.Y.T. performed wound-healing experiments with HBE cells; X.T. and X.S.-P. provided raw data and stress measurements for MDCK cells; and A.Z. and G.D. wrote the article. All authors read and edited the article and approved of its content.

Editor: Alissa Weaver.

Supporting Material

Movie S1. Propagating motion-induced coordination in stress

Time evolution of the probability of a cell to belong to a cluster of coordinated motion (red) or stress (blue), as a function of the distance from the monolayer front edge. Motion coordination spatially grows in time while the stress clusters propagate to deeper cells. This movie corresponds to the experiment displayed in Fig. 3 g.

Movie S2. Construction of protruding cells kymograph

(Left) Phase-contrast image overlaid by the detected contour. (Right) Construction of the corresponding protruding-cells kymograph. Note the motion waves propagating along the monolayer front edge (left), which are represented by diagonals in the protruding-cells kymograph. This movie corresponds to the protruding-cells kymograph in Fig. S8 b.

Movie S3. Phase-contrast imaging of a wound-healing experiment using HBECs

This movie corresponds to the experiment in Fig. S8. The raw data was recorded at 5 min per frame, and the replay is at 7 frames/s. The monolayer front migrates at ∼35 μm/h.