Selective refinement and selection of near-native models in protein structure prediction

Abstract

In recent years in silico protein structure prediction reached a level where fully automated servers can generate large pools of near-native structures. However, the identification and further refinement of the best structures from the pool of models remain problematic. To address these issues, we have developed (i) a target-specific selective refinement (SR) protocol; and (ii) molecular dynamics (MD) simulation based ranking (SMDR) method. In SR the all-atom refinement of structures is accomplished via the Rosetta Relax protocol, subject to specific constraints determined by the size and complexity of the target. The best-refined models are selected with SMDR by testing their relative stability against gradual heating through all-atom MD simulations. Through extensive testing we have found that Mufold-MD, our fully automated protein structure prediction server updated with the SR and SMDR modules consistently outperformed its previous versions.

Introduction

The knowledge of the three-dimensional (tertiary) structure of a protein is crucial in under- standing its biological function. While the amino acid (AA) sequences (primary structures) of proteins are routinely determined using high-throughput protein sequencing methods, the experimental determination of the corresponding secondary and tertiary structures¹, through X-ray crystallography and NMR spectroscopy, is expensive, slow and time consuming. As a result, computational protein structure prediction methods are becoming more and more prevalent.

The two main methods used in protein structure prediction are template-based (comparative) and ab initio modeling. While, in general, template-based modeling methods can successfully predict the structures of target proteins characterized by high (e.g., larger than 85%) sequence identity to other proteins of known structures², they often obtain poor models for targets with low (e.g., less than 25%) sequence identity. In the latter case, one needs to rely on much less accurate ab initio prediction methods³. In either case, after generating a large set of models, it is necessary to employ (i) an efficient refinement method for improving the quality of the models, and (ii) a proper selection strategy for identifying the best near native structure.

Although currently available protein structure prediction servers^4–7 are capable of generating high-quality models, their proper identification and eventual refinement remain problematic. To address this shortcoming, several groups have developed, implemented and tested a variety of methods for structure refinement and model selection. For example, Baker's group developed an all-atom refinement method using the Rosetta force field⁸ that was tested in the Critical Assessment of Techniques for Protein Structure Prediction (CASP) competition⁹. While for some targets the method led to improvements over the starting template-based models, in most cases the results were negative. Zhang and his colleagues proposed a Fragment-Guided Molecular Dynamics (FG-MD) algorithm¹⁰, which combines the physics-based force field AMBER99¹¹ with knowledge-based potentials, to refine predicted template-based models. In FG-MD, experimentally determined fragments extracted from the PDB are used as constraints to refine models through simulated annealing MD simulations. While the FG-MD method has potential for atomic-level model refinement, the obtained quality improvements appear to be limited. There was some new progress in model refinement as demonstrated in CASP10 and CASP11¹² ; however, it was based on very long-time MD simulations, which may not be generally applicable for routine structure prediction.

As of now, there is no available refinement method that works reliably for all targets. While a given refinement approach can improve models for certain targets, at the same time it can also reduce the structure quality for other targets. Based on this observation, here we propose a new selective refinement (SR) method that is applicable to a wide range of targets. In SR, the actual structure refinement is based on Rosetta Relax^8,13, an application that uses a conformational search algorithm to minimize the Rosetta full-atom energy scoring function¹⁴. What sets SR apart is that it first classifies targets (based on its size and secondary structure) into groups, and then refines the models by applying Rosetta Relax subject to constraints specific to each group of targets. SR utilizes both the local consensus information and the Rosetta full-atom energy function to refine the models and make them more native-like.

The selection of the best native-like models from a large pool of candidate structures is notoriously difficult when the actual crystal structure of the target is unavailable. The most common way of discriminating among predicted structures is by employing either knowledge- based or physics-based energy (scoring) functions^3,15. Knowledge based potentials that can be applied to reduced representations of proteins with either one center¹⁶, two centers¹⁷ or more centers (heavy atoms)¹⁸ of interaction per amino acid are widely used for identifying and ranking near-native models from a pool of generated decoys. The main difficulty in using any of these energy functions is to recognize both secondary and tertiary structure features that resemble to the native structure¹⁹. Scoring functions, such as Dfire^16,20, OPUS_Ca²¹ and OPUS_PSP²² are often used for model quality assessment. However, none of these methods make use of the dynamics features of proteins.

Recently, we have introduced an all-atom molecular dynamics (MD) based ranking method (MDR)^23,24 for evaluating and selecting the best models according to their stability against simulated heating. The main assumption of MDR is that near native models are always more stable against simulated heating than poor quality models. Originally, all MD simulations in MDR were carried out using the CHARMM²⁵ force field, and we have found that MDR worked rather well for β-sheets dominated targets but not so well for targets dominated by α-helices. This may be explained by the observation that the CHARMM (Amber) force field favors and over-stabilizes α-helical (β-sheet) motifs²⁶. Thus, here we extend and improve the reliability of the MDR method by selectively employing the CHARMM and Amber forces fields in the simulated heating MD simulations depending on whether the target has predominantly β-sheet or α-helical residues. We will refer to this approach as the selective MDR (SMDR) method.

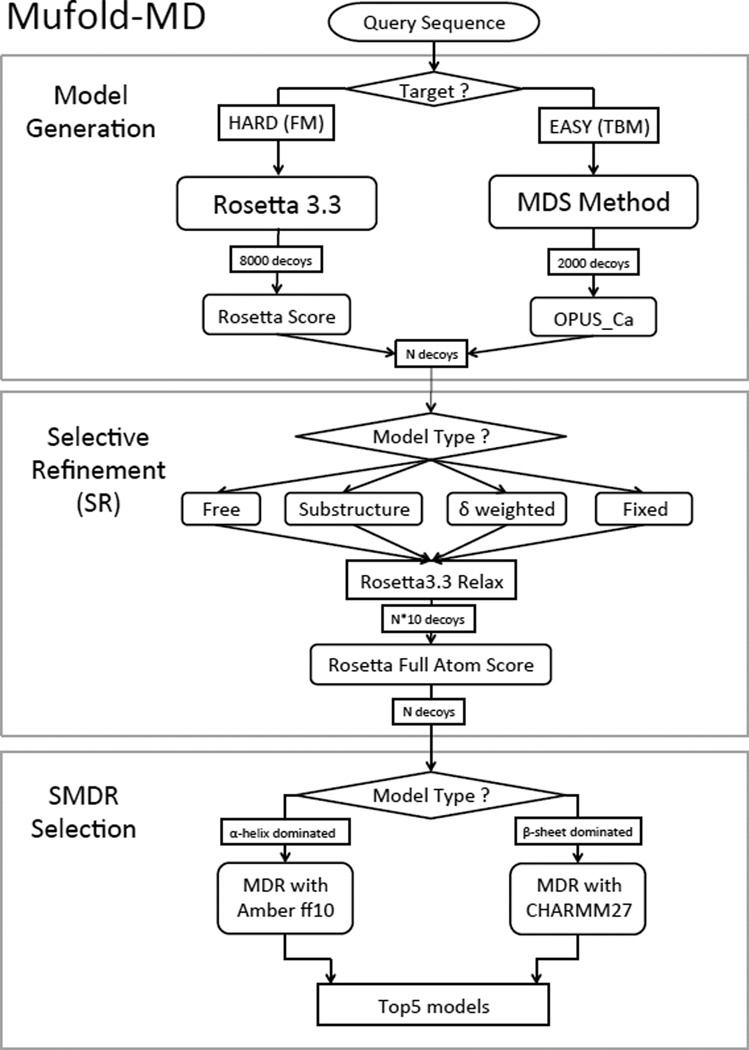
We have implemented the SR and SMDR methods as two modules in our fully automated Mufold-MD server that was successfully used during CASP10. The server consists of three sequential modules as shown in Figure 1. The first module is for generating models from the primary structure of the target. By using sequence-profile alignment (e.g., PSI-BLAST²⁷) and profile-profile alignment (e.g., HHSearch²⁸) methods, the query sequence is classified as either hard or easy target. For hard targets, models are generated using the Rosetta 3.3 software^29–31 (ab initio method) and then ranked by using their Rosetta energy score. For easy targets, models are generated with the Multi-Dimensional Scaling (MDS) method²³ and then ranked using the OPUS Ca scoring function²¹. Next, in the selective refinement (SR) module, the structures are refined selectively, subject to target specific constraints, by employing the relax mode in Rosetta 3.3. We have found that for most tested targets the SR protocol consistently improved the quality of the models in the pool. We emphasize that our goal in this paper is not to compare the performance of SR with other existing refinement methods but rather to explain how SR has been implemented in our Mufold-MD server, and to demonstrate that indeed, in general, SR improves the quality of the structures predicted by Mufold-MD. Also, in principle, the use of SR could benefit other refinement methods as well.

Figure 1.

Flowchart of Mufold-MD.

Finally, in the selective MDR selection (SMDR) module the MDR method is used to select the top 5 structures as the output of the server. SMDR, by using selectively CHARMM (Amber) for β-sheet (α-helices) dominated targets, provided significantly better results than the original MDR method that used exclusively the CHARMM force field for simulated heating. In all our tests, the new Mufold-MD server with the SR and SMDR modules provided better quality final output models than its predecessors.

Materials and Methods

Selective Refinement (SR)

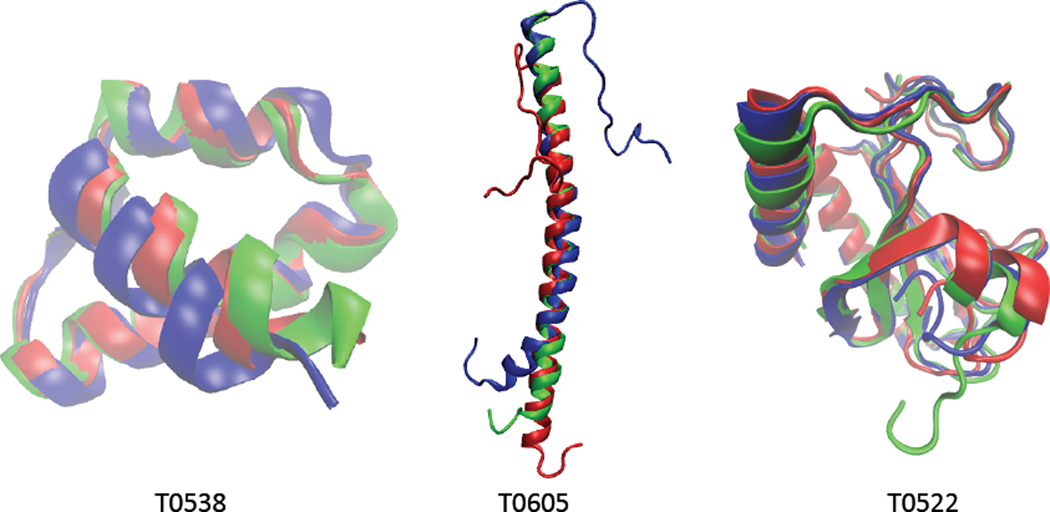
The refinement of previously generated models is becoming an increasingly important component of protein structure prediction. Here, we introduce a new selective refinement (SR) protocol based on Rosetta^29–31, an open source, library based object-oriented software suite, which provides a robust system for predicting and designing protein structures. Rosetta Relax^8,13 is an application provided in the Rosetta package for refining all-atom structures through searching conformational space guided by Rosetta full-atom energy scoring function¹⁴. Relax produces refined high-resolution full-atom 3D structures by minimizing the energy of the system in the conformational space in torsion angles and rotamers. It employs a combination of Monte Carlo sampling, discrete combinatorial optimization and quasi New- ton minimization⁸. However, biased energy scoring function and incomplete sampling of the search space may result in refined structures with worse quality than the input models. In some cases, the refining process may completely destroy the input structure. Three examples of refinement with Rosetta Relax are shown in Figure 2. The 54 AA long target T0538 has 36 helical residues. The GDT_TS of the input model is 82.4 while the GDT_TS of the refined model is 93.8. The second target T0605 (53 AA long) has 47 helical residues. The GDT_TS of the input and refined models are 69.8 and 88.2, respectively. The much longer third target T0522 (134 AA long) has 41 helical residues and 30 β-sheet residues. The GDT_TS of the input and refined models are respectively 92.5 and 82.4. These examples clearly show that Rosetta Relax can improve dramatically the structure quality of short targets with relatively simple structure, e.g., T0538 and T0605, while at the same time it may significantly reduce the structure quality of long and more complex targets like T0522. This suggests that to improve Relax's performance one needs to employ target specific constraints in order to aid and guide the refinement process.

Figure 2.

Examples of free refinement with Rosetta Relax. Cartoon representations of initial model (blue), refined model (red), and crystal structure (green). Images created with VMD³².

To address this issue, we have developed the SR protocol, which first identifies the type of the target and then applies specific constraints during refinement. To guide the refinement process we make use of (i) the Rosetta full-atom energy function, and (ii) a pool of previously generated models. As discussed before, the refinement effectiveness of Relax depends crucially on the size and structural complexity of the target protein. In general, for short and simple targets Relax can improve structure quality without the need to impose any constraints. On the other hand, the refinement of large and complex targets requires fixing their Cα atoms and leaving their sidechain atoms unconstrained. For moderately large and complex targets one identifies stable substructures and keep fixed the corresponding Cα atoms during refinement. Finally, for the rest of the targets the information derived from the available model pool is more reliable than the Rosetta energy function and, thus their refinement requires applying standard deviation weighted constraints to the corresponding Cα atom pair-distances. Thus, in the SR approach, based on their structure information, targets are divided into four different categories, and the models are subjected to the following, category-specific constraints. These rules and related thresholds are tuned and determined based on empirical training.

1) Free refinement

In general, ab initio methods, as implemented in Rosetta and other MD simulation based protein folding methods³³, can predict reasonably well the structures of small and simple targets. Structures of such targets should be subject to constraint- free refinement. To be specific, one defines as small target proteins with less than 110 residues, and simple targets that contain predominantly α-helices (i.e., more than 60% α-helical residues and less than 10% β-sheet residues) or only extended β-sheets. The residues of secondary structure elements can be identified by using the program STRIDE³⁴. Formally, the targets in this category are defined as

$$AA<110\text{ AND }[(\alpha >60\%\text{ AND }\beta <10\%)\text{ OR }(\alpha =0)],$$ (1)

where, AA = amino acid sequence length; α = percentage of α-helical residues; β = percentage of β-sheet residues.

2) Fixed backbone

In general, refinement through Rosetta Relax degrades the structure quality of targets that are too big or too complex. The right refinement protocol for such targets is to keep the backbone atoms fixed and refine only the sidechains. Targets assigned to this category are those that either have more than 400 residues, or have more than 200 residues and more β-sheet residues than α-helical residues, i.e.,

$$(AA>400)\text{ OR }(AA>200\text{ AND }\beta >\alpha ).$$ (2)

3) Substructure constraints

When regions of relatively large targets have structures that can be predicted with high degree of confidence (e.g., significant number of α-helical residues) refinement with Relax may give good results by constraining the corresponding backbone atoms. In general, such stable structural regions in proteins can be identified through the small standard deviation of the corresponding Cα pair distances in a prediction pool³⁵. Based on extensive testing, we have found that this refinement method can be applied for targets that have (1) more than 250 residues and more α-helical than β-sheet residues, and (2) more than 200 residues and more than 60% alpha-helical residues, i.e.,

$$(400>AA>250\text{ AND }\alpha >\beta )\text{ OR }(400>AA>200\text{ AND }\alpha >60\%).$$ (3)

4) Standard deviation, δ, weighted constraints

For all other targets, which do no fall in any of the previous three categories, one applies Rosetta Relax with constraints determined by the standard deviation of the Cα pair distances in the structural model pool. Specifically, the constraints are implemented as weighted harmonic potentials added to the Rosetta scoring function, i.e.,

$$f(x)=\sum _n\frac{{(x_n-x_{n0})}^2}{{\delta }_n^2},$$ (4)

where the sum goes over all Cα pair distances, δ_n is the standard deviation of the n^th pair distance in the input models, and x_n (x_n0) is the corresponding Cα pair distance in the refined (input) model. For a pool of N models, the standard deviation δ_n of the n^th pair distance is defined as

$${\delta }_n=\sqrt{\frac{1}{N}\sum _{i=1}^N{({\overline{x}}_n-x_{n,i})}^2},$$ (5)

where x_n,i is the pair distance of model i, (i = 1, …, N), and ${\overline{x}}_n=(1/N){\sum }_{i=1}^N{x}_{n,i}$ is the corresponding mean pair distance. Note that a bigger (smaller) standard deviation results in a smaller (larger) constraint energy contribution, thus making the corresponding pair distance more (less) flexible during refinement. Clearly, the effectiveness of this refinement constraint depends strongly on the quality of the models from the training set.

The SR target categories and the corresponding category-specific constraints have been fine-tuned and determined by employing a training set of 40 targets from the CASP9 competition. The targets, listed in Table 1, have diverse structures and complexity, with lengths ranging from 53 (T0538) to 567 (T0542) residues. The table also contains the relevant structural features of the targets, and their classification in SR categories (i.e., 5 targets in the free refinement, 8 in the fixed backbone, 4 in the substructure constraints, and 23 in the δ-weighted constraints categories.) For each target, we have used the 5 models submitted by the MUFOLD server in CASP9. The corresponding CASP9 models submitted by all other participating servers were used to generate the δ constraints given by Eq. (4). Then, applying individual SR constraints along with the SR protocol itself, we have used Rosetta Relax to generate 10 refined decoys for each of the 40 × 5 = 200 input models, leading to a total of 2, 000 structures. In addition, we have also tested SR on a set of 53 targets from CASP10. The SR procedure was the same as for the CASP9 targets. Out of the 53 CASP10 targets 4 were in the free refinement, 13 in the fixed backbone, 12 in the substructure constraints, and 24 in the δ-weighted constraints categories. This served as an independent test set, as neither the thresholds in defining categories nor category-specific constraints were tuned using this dataset. Finally, to assess the quality of the refined structures, we have used the Global Distance Test Total Score³⁶ (GDT_TS) of their Cα atoms relative to the target’s native crystal structure.

Table 1.

The 40 selected CASP9 targets. The columns from left to right are: 1) target name; 2) number of residues; 3) number and 4) percentage of α-helical residues; 5) number and 6) percentage of β-sheet residues; 7) used SR protocol.

Target	Sequence Length	α-helical residues	α	β-sheet residues	β	Protocol
T0538	53	36	67%	4	7%	Free refinement
T0569	78	0	0%	48	61%
T0605	52	47	90%	0	0%
T0612	108	0	0%	63	58%
T0619	100	67	67%	0	0%
T0524	321	28	8%	163	50%	Fix backbone
T0526	289	0	0%	151	52%
T0542	567	209	36%	125	22%
T0565	303	46	15%	126	41%
T0582	220	0	0%	129	58%
T0589	430	193	44%	83	19%
T0609	337	10	2%	170	50%
T0620	298	59	19%	99	33%
T0515	347	102	29%	85	24%	Substructure constraints
T0535	293	174	59%	44	15%
T0584	337	256	75%	6	1%
T0575	215	155	72%	2	0%
T0521	167	111	66%	10	5%	δ-weighted constraints
T0522	133	41	30%	30	22%
T0530	85	7	8%	44	51%
T0539	79	15	18%	18	22%
T0548	94	51	54%	13	13%
T0549	83	31	37%	18	21%
T0551	66	10	15%	35	53%
T0555	146	88	60%	2	1%
T0559	68	38	55%	14	20%
T0560	73	38	52%	13	17%
T0566	151	61	40%	59	39%
T0567	141	63	44%	22	15%
T0580	103	44	42%	22	21%
T0585	225	101	44%	42	18%
T0586	118	76	64%	10	8%
T0592	136	50	36%	20	14%
T0593	194	75	38%	36	18%
T0596	174	140	80%	0	0%
T0598	143	57	39%	34	23%
T0617	141	99	70%	8	5%
T0622	121	44	36%	30	24%
T0632	154	44	28%	55	35%
T0635	181	85	46%	28	15%

Selective MD-Ranking (SMDR)

MD-Ranking (MDR) is a dynamics based quality assessment method of near-native structures generated by any protein structure prediction method²⁴. MDR uses MD simulations to probe the stability of the models by monitoring the change of their cRMSD (RMSD of the Cα atoms) during simulated heating. The change in cRMSD (ΔRMSD), with respect to the initial structure, is calculated every picosecond (ps) during heating from 40 K to 140 K at a rate of 1 K/ps. The models are ranked according to the increasing order of their ΔRMSD at the end of the simulations. Thus, the best model corresponds to the smallest ΔRMSD.

The MD simulations reported in this paper were performed in the absence of solvent with the parallel MD program NAMD 2.8³⁷. The reason for the absence of solvent is to save computing time, as the simulation is for checking the stability of structural model instead of obtaining realistic dynamics of the protein. The van der Waals interactions were truncated at the cutoff distance 12 Å, with a smooth switching distance 10 Å. The SHAKE algorithm³⁸ was used for rigid bonds involving hydrogen atoms. The equations of motion were integrated with a time-step of 2 fs by using the velocity Verlet method. During the gradual heating the temperature was increased by 1 K each ps and was controlled by Langevin dynamics with a damping coefficient of 5 ps⁻¹. Before running the MD simulations all structures were optimized through the energy minimization feature of NAMD2. The energy minimization was carried out sequentially by: (1) keeping all heavy atoms fixed for 500 steps, (2) constraining only the Cα atoms for 2000 steps, and (3) removing all constraints for and additional 2000 steps. Each MDR simulation took less than 3 hours on a 2.8 GHz Intel Xeon CPU.

Based on extensive testing, using targets of known native structure, we have found that the simplest and most effective scoring function for MDR is the mean ΔRMSD during simulated heating for 100 ps from 40 K to 140 K. As an example, here we describe one of these tests. First, we have selected randomly 16 proteins from the July 2005 release of Astral database³⁹, and generated 15,000 low resolution structures (i.e., only backbone atoms) by using the MDS method. Next, from these models, we have selected five for each target using a filter based on a clustering method⁴⁰. The coordinates of the missing sidechain heavy atoms were determined by using the program PULCHRA⁴¹ and the hydrogen atoms were added by using PSFGEN, which is part of the VMD software package³². Then the all-atom models were subjected to MD heating from 40 K to 600 K, at a rate of 1 K/ps, and the ΔRMSD was recorded every ps. Examples of such heating curves for two targets and models of different quality (including the native structure) are shown in Figure 3. Next, we have calculated the average ΔRMSD, Δ_i, over five time intervals of increasing length Δt_i = i × 100 ps, i = 1, …, 5. Finally, the five models were ranked in increasing order of Δ_i, separately for each i = 1, …, 5. According to the MDR method, the best model (i.e., the one closest to the native structure) should be the one with the smallest Δ_i. The MDR results are displayed in Table 2. According to the results, the best MDR ranking was attained by using the scoring function Δ₁, i.e., corresponding to the heating interval from 40 K to 140 K. Indeed, using Δ₁, MDR had a 68.8% (81.3%) success rate in selecting the best (a structure within 0.5 Å of the best) model in the pool. The Δ₄ scoring function, corresponding to the heating interval from 40 K to 440 K, lead to a somewhat poorer MDR performance, i.e., a 62.5% (81.3%) success rate for identifying the best (a structure within 0.5 Å of the best) model in the pool.

Figure 3.

Change in cRMSD for four models corresponding to two different targets [a) and b)] during gradual heating from 40 K to 600 K. The black curves correspond to the native structure. The colored curves correspond to models with the following initial cRMSD values (in Å), with respect to the native structure: a) 2.5 (red), 4.5 (blue), 6.0 (orange); and b) 3.5 (red), 4.5 (blue), 6.0 (orange).

Table 2.

Ranking of 5 predicted models for 16 proteins using the scoring functions Δ_i, i = 1, … 5, described in the text. Columns 2 and 3 contain the cRMSD, with respect to the native structure, of the best and poorest models. Columns 4 through 8 contain the cRMSD of the models selected with MDR, using Δ_i, i = 1, … 5. The last two rows contain the percentage of cases in which MDR, with the corresponding Δ_i, identified the best model or a model within 0.5Å of the best.

No.	Smallest cRMSD	Largest cRMSD	Best Δ1	Best Δ2	Best Δ3	Best Δ4	Best Δ5
1	2.2	6.2	2.2	2.2	2.2	2.2	2.2
2	5.5	9.5	5.5	5.5	5.5	5.5	5.5
3	4.3	12	4.3	4.8	4.3	4.3	4.3
4	2.4	14.8	2.4	2.4	2.4	2.4	2.4
5	3.3	6.7	5.4	5.4	5.4	5.4	5.4
6	4.4	10.2	4.4	4.8	4.8	4.8	4.8
7	3	4.9	3	3	3	3	3
8	3.5	10.3	3.5	4.2	3.5	3.5	4.2
9	2.7	12.9	2.7	2.7	2.7	2.7	2.7
10	2.1	10.8	2.8	2.8	2.8	2.8	2.8
11	3.2	9.9	3.2	3.2	3.2	3.2	3.2
12	3.4	8.3	3.4	3.4	3.4	3.4	3.4
13	5.7	13.2	12.3	12.3	10.6	10.6	10.6
14	2.9	12.3	2.9	9.4	9.4	2.9	2.9
15	5	9.2	5.3	5.3	5.3	5.3	5.3
16	3.5	5.6	3.7	3.7	3.7	3.7	3.7
Best model (%)			68.8	43.8	56.3	62.5	56.3
0.5 Å to best model (%)			81.3	68.8	75	81.3	75

For certain targets, the performance of MDR can be enhanced by employing a target- specific force field in the corresponding MD simulations. Indeed, it is well documented in the literature (including recent MD simulations of the folding of small proteins²⁶) that the two most widely used force fields, CHARMM²⁵ and Amber¹¹ are biased towards forming and over-stabilizing α-helical and extended β-sheet secondary structures, respectively. Thus, because in MDR we are testing the structural stability of models against simulated heating, in our improved selective MDR (SMDR) method one employs selectively the CHARMM force field for targets dominated by extended β-sheets and the Amber force field for targets that contain mainly α-helices.

MUFOLD-MD server

We have implemented the SR and SMDR methods as two modules in our fully-automated server Mufold-MD. As shown in Figure 1, Mufold-MD consists of three sequential modules: (1) model generation, (2) selective refinement (SR), and (3) SMDR selection. The input to the model generation module is the query sequence of the target. A large pool of decoys is generated by using different prediction strategies depending whether the target is classified as easy or hard. By using sequence-profile alignment (e.g., PSI-BLAST) and profile-profile alignment (e.g., HHSearch) methods, the query sequence is classified as either easy (E-value < 10⁻³) or hard target (E-value > 10⁻³). For easy targets, models are generated with the MDS method and then filtered with the OPUS Ca scoring function. For hard targets, models are generated using the Rosetta 3.3 software (ab initio method) and then filtered using the Rosetta energy scoring function. After filtering, a limited number of models are forwarded to the refinement module. As explained above, the SR category of each target is identified based on its size, and its number of α-helical and β-sheet residues. Next, the proper SR protocol is applied to refine the models. Based on their Rosetta full-atom energy score, the top refined models are identified for final selection. Finally, the SMDR method, described above, is used to select the top 5 models as the output of the Mufold-MD server.

Results and Discussion

SR Module

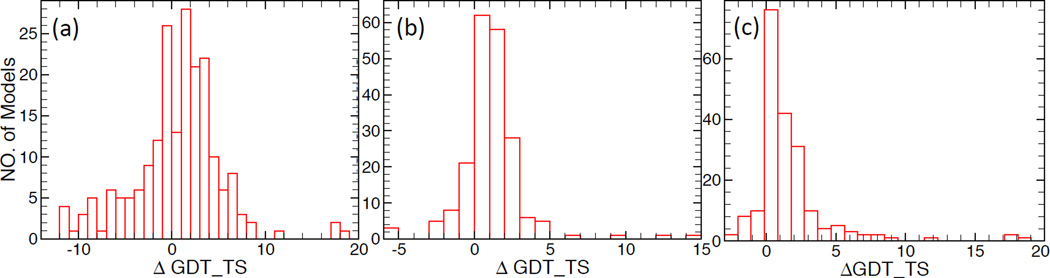
The premise of the SR method is that structure refinement through Rosetta Relax with target-specific constraints (as described in the Methods section) should provide more consistent and better results, reflected through higher GDT_TS scores, than applying indiscriminately a single type of constraint. To test this and assess the effectiveness of the SR method we have: (i) selected, for each of the 200 CASP9 input structures (described in the Methods section), the best of the 10 refined models (i.e., the one with the highest GDT_TS score with respect to the native structure) obtained using three different refinement protocols, and (ii) constructed histograms of the change, ΔGDT_TS, in the GDT_TS scores of the models as a result of refinement. The three refinement protocols used are: (a) free refinement, (b) δ-weighted constraint refinement, and (c) SR. The obtained histograms are shown in Figure 4, and the results are summarized in Table 3.

Figure 4.

Histogram of ΔGDT_TS for the considered CASP9 models by using: (a) free refinement; (b) δ (standard deviation) weighted constraint refinement; and (c) SR.

Table 3.

Comparison of the refinement results for 200 input models of 40 CASP9 targets, by using: (a) free refinement, (b) δ-weighted constraint refinement, and (c) SR. N₊ (N₊₂) denotes the number of models with ΔGDT_TS > 0 (ΔGDT_TS > 2) as a result of refinement.

Best of 10 refined models	Free refinement	δ-weighted constraints	SR
N+	122 (61%)	162 (81%)	177 (88.9%)
N+2	72 (36%)	43 (21.5%)	54 (27%)
〈ΔGDT_TS〉	0.5	1.12	1.5

In case of free refinement (Figure 4a), the broad ΔGDT_TS distribution, which extends on both sides of the origin, indicates that the numbers of models with increased and reduced quality through refinement were comparable. Indeed, out of the 200 input models only N₊ = 122 (i.e., 61%) had ΔGDT_TS > 0 (see Table 3). It should be noted, however, that more than half, N₊₂ = 72 (i.e., 36%), of these models underwent significant quality improvement with ΔGDT_TS > 2 (with a few structures gaining as much as ΔGDT_TS ≈ 20). Nevertheless, the fact that the qualities of about 40% of the models were degraded (in many cases significantly) during free refinement renders the straightforward use of this refinement method unreliable. On the other hand, in general for targets that meet criteria (1) free refinement seems to work very well, leading to much improved structures. Thus, in SR we use free refinement only for targets that satisfy condition (1).

A direct application of the δ-weighted constraint refinement to the CASP9 input models (Figure 4b) provided better overall results than free refinement. Indeed, in this case (see Table 3) N₊ = 162, i.e., the quality of 81% of the models were improved. This also means that the number of refined structures with ΔGDT_TS < 0 was less than half of those from free refinement (i.e., 19% vs 39%). However, the number of significantly improved models, N₊₂ = 43 (i.e., 21.5%), was smaller than in the case of free refinement. It should be emphasized that the performance of Δ-weighted constraint refinement depends crucially on the quality of the models used to generate the parameters in Eq. (4). Thus, in SR we apply this type of refinement to all targets whose models cannot be reliably refined by other methods (e.g., free refinement), and when a set of sufficiently high-quality models is available. Through this choice we seek to increase (decrease), as much as possible, the number of improved (reduced) quality models through refinement.

As expected, the SR protocol, which currently encompasses four target-specific refinement methods, provided the best overall refinement results for the CASP9 models (see Figure 4c and Table 3). For SR, N₊ = 177, i.e., the quality of almost 90% of the refined models has been improved. However, the number of targets with ΔGDT_TS> 2, N₊₂ = 54 (i.e., 27%), was somewhat smaller than for free refinement (i.e., 36%) but larger than for δ-weighted constraint refinement (21.5%). To quantify the overall performance of the considered refinement protocols, we have calculated 〈ΔGDT_TS〉, the average ΔGDT_TS for all refined models. The obtained values, in decreasing order, were (see Table 3): 1.5 for SR, 1.12 for δ-weighted constraint refinement, and 0.5 for free refinement. The success of SR is due to the fact that it selects and uses the best possible refinement method (including free and δ-weighted refinement) for each particular target. This way SR maximizes (minimizes) the number of refined structures of improved (reduced) quality.

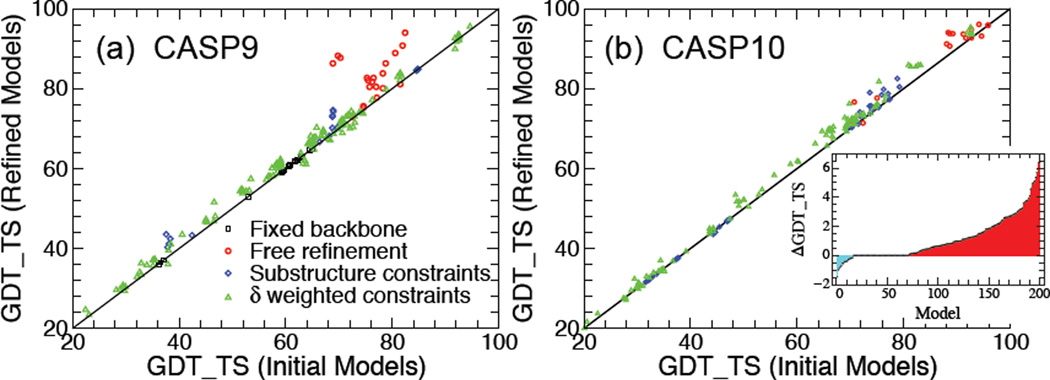
The results of SR applied to the considered CASP9 and CASP10 models (described in the Methods section) are shown in Figure 5. The data points in Figure 5a represent the GDT_TS of the best model obtained with SR vs GDT_TS of the corresponding input model for all 200 models of the 40 CASP9 targets. Clearly, the data points of the models for the 8 targets in the fixed backbone refinement category (black rectangle) lie on the diagonal because, during refinement, only the structures of the sidechains are affected. The best quality improvement is attained for the models corresponding to the 5 targets in the free refinement category (red circles). In most of these cases the improvement is significant (with 5 < ΔGDT_TS< 20), especially in one notice that the input models are of high quality, with GDT_TS> 75. The models belonging to the 4 targets in the substructure constraints category (blue rhomb) are also systematically improved during refinement. Finally, as expected, the refinement results for the bulk of the models corresponding to 23 models in the δ-weighted constraints category (green triangle) are relatively modest, with the corresponding data points clustered along and slightly above the diagonal. However, in agreement with the above analysis of δ-weighted constraint refinement, the number of improved quality models is significantly higher than the ones whose quality was slightly reduced during refinement.

Figure 5.

(a) GDT_TS of best SR model vs GDT_TS of the corresponding input model for the considered 40 CASP9 targets. Data points that lie above (below) the diagonal correspond to refined structures with improved (reduced) quality. (b) Same as (a) for the considered 53 CASP10 targets. Inset: ΔGDT_TS (increasing from left to right) vs target.

Next we applied the SR method to refine the 265 models of 53 CASP10 targets described in the Methods section. The results, similar to the CASP9 targets, are shown in Figure 5b. In this case, 13 targets fell in the fixed backbone SR category. For clarity, the data points (black rectangle) corresponding to these models, which should be located along the diagonal, have been omitted in Figure 5b. Out of the 200 non-fixed backbone models, SR resulted in 129 (i.e., 64.5%) improved quality structures. The largest ΔGDT_TS was a mere 6.5 (compared to 20 for the CASP9 models) and only 46 (i.e., 17%) models had significant quality improvement with ΔGDT_TS > 2. At the same time, however, there were only 16 (i.e., 8%) models whose quality decreased during refinement by less than ΔGDT_TS ≈ −1.5. Interestingly, for 55 CASP10 models SR led to ΔGDT_TS = 0, i.e., the backbone atom structure was left unchanged. Thus, for the CASP10 models, SR either improved or left unchanged the structure quality of 92% of the models. This success rate that is higher than for the considered CASP9 models is most likely attributed to better quality input models for the CASP10 targets. Indeed, out of the considered 53 CASP10 targets, only in two cases was the quality of the refined top input model reduced slightly (i.e., with |ΔGDT_TS| < 0:5). Furthermore, out of the 40 CASP10 targets belonging to the non-fixed backbone SR categories, in N₊ = 27 (67.5%) cases the top input model was improved through SR by ΔGDT_TS > 1, while for N₊₂ = 14 (35%) targets the quality improvement of the refined top model was ΔGDT_TS > 2. The results are summarized in Table 4.

Table 4.

Selective refinement (SR) results for 200 input models corresponding to 40 CASP10 targets in the non-fixed backbone SR categories. N₊ (N₊₂) denotes the number of models/targets with ΔGDT_TS > 0 (ΔGDT_TS > 2) as a result of refinement. 〈ΔGDT_TS〉 is the mean change in GDT_TS per model/target.

Best refined model	Out of 200 models	Out of 40 targets
N+	129 (64.5%)	27 (67.5%)
N+2	46 (17%)	14 (35%)
〈ΔGDT_TS〉	1.1	1.21

SMDR Module

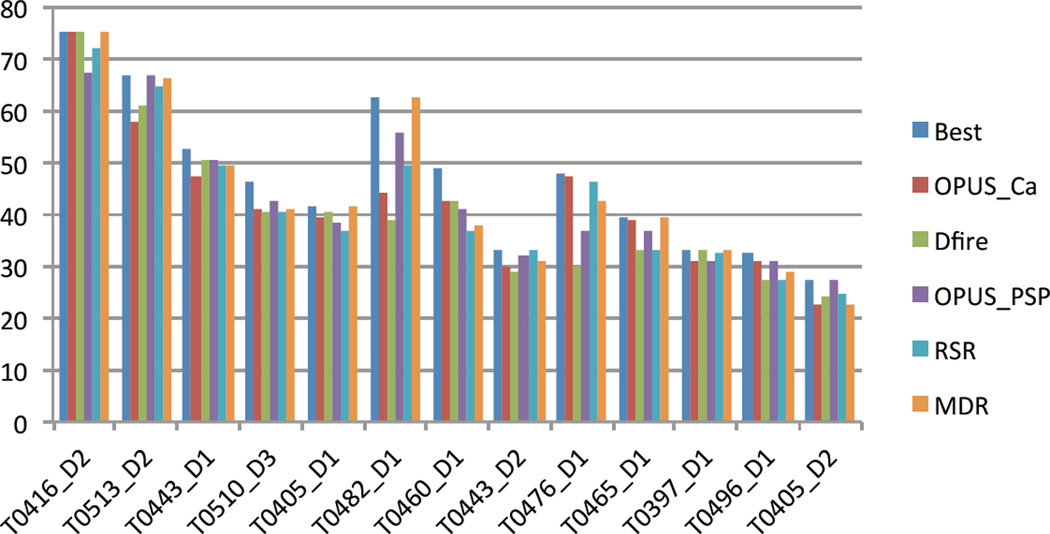
Extensive testing of the MDR method (with the CHARMM force field only) for selecting the best model from a pool of decoys provided consistently better or comparable results to commonly used (static) scoring function based selection methods. In general, MDR performed best when the pool of decoys contained high-quality models, with GDT_TS > 70. This point is eloquently shown in Figure 6 for the 13 CASP8 target domains from the template-free modeling category (so called “hard targets”). For each target, a set of 64 decoys was generated with Rosetta. Besides MDR, four other popular scoring functions, i.e., OPUS Ca, Dfire, OPUS PSP and RSR, were used to select the top candidate model. For the three targets with best-quality models (GDT_TS > 60) MDR was the only method that consistently identified the top model in the pool of decoys. In all other cases, MDR performed better or at least comparable to the other scoring functions.

Figure 6.

Comparison of the GDT_TS scores of the top models selected with MDR and four popular scoring functions (i.e., OPUS Ca, Dfire, OPUS PSP and RSR) for 13 CASP8 target domains from the template-free modeling category. For each target, the selections were made from the same set of 64 decoys generated with Rosetta. For reference, the GDT_TS of the best model in each pool of decoys is also included.

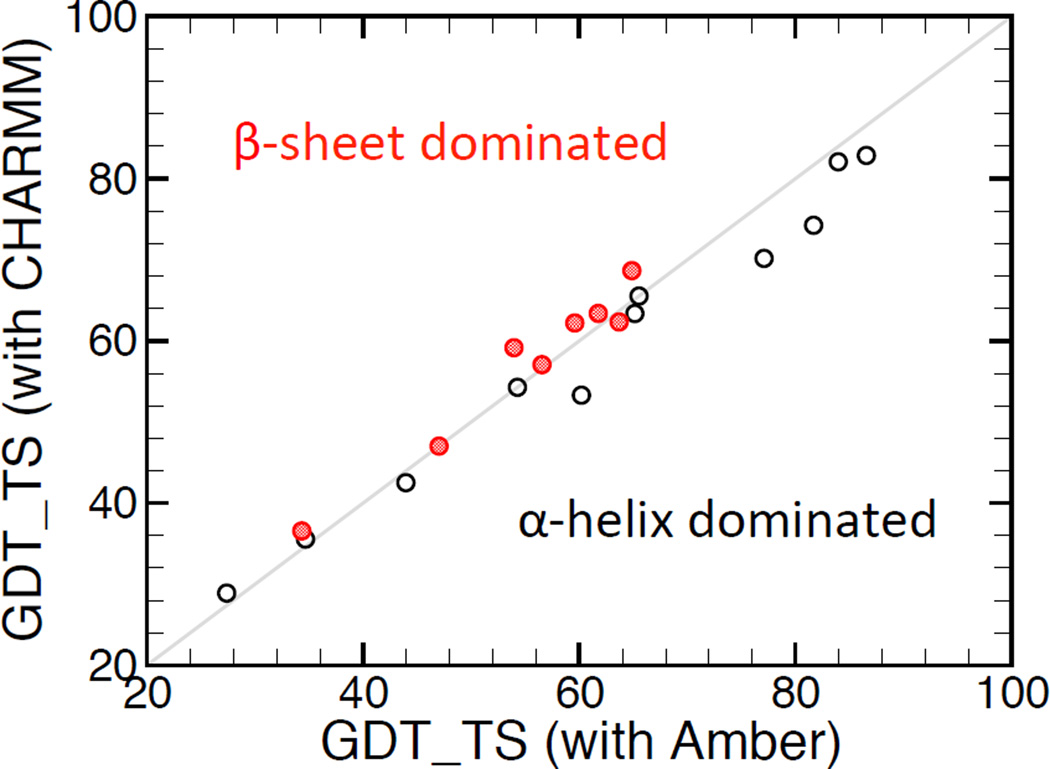
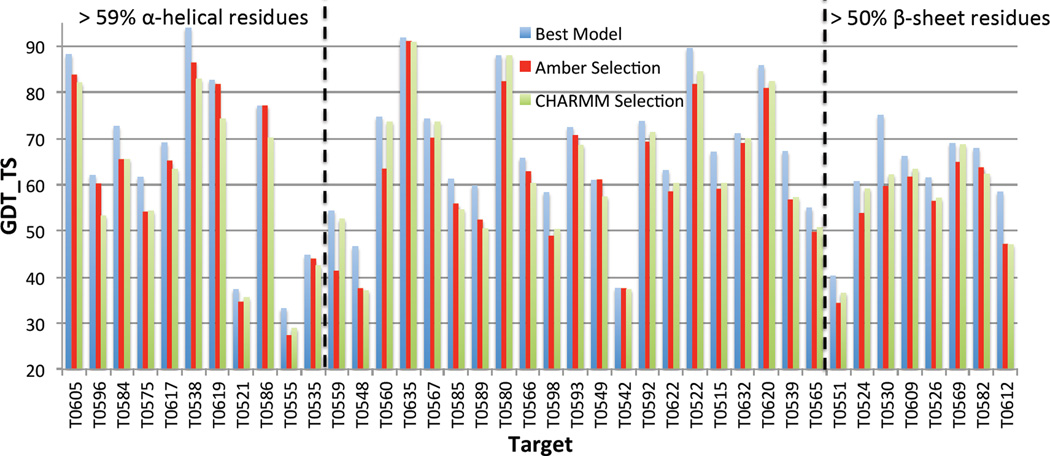
Unlike MDR, which uses a single force field (CHARMM), the proposed SMDR method employs selectively the CHARMM and Amber force fields depending whether the target in question has respectively more α-sheet or β-helical residues. In general, SMDR outperforms MDR, especially when the target is dominated either by α-helical or β-sheet residues. To demonstrate this, we have applied MDR with both CHARMM and Amber force fields to select the best quality structure from the pool of input models for the 40 CASP9 targets considered in this paper. Figure 7 clearly shows that for the 11 (8) targets, which contain more than 59% (50%) of α-helical (β-sheet) residues, the GDT_TS of the best model identified by MDR using Amber (CHARMM) is in general higher than the one using the other force field. For all other 21 targets, as shown in Figure 8, both force fields lead to similar MDR selection results. However, to maximize the success rate of SMDR, one should prefer Amber to CHARMM whenever the number of α-helical residues is larger than the number of β-sheet residues, and vice versa.

Figure 7.

Comparison between the GDT_TS of the best models selected by MDR using respectively CHARMM and Amber force fields for 8 β-sheet (filled circles) and 11 α-helix (open circles) dominated CASP9 targets.

Figure 8.

GDT_TS of the best models selected with MDR, by employing both CHARMM and Amber force fields, for all 40 CASP9 targets considered. For reference, for each target, the GDT_TS of the best model in the pool is also included. Targets on the left (right) contain predominantly α-helical (β-sheet) residues.

Combined SR and SMDR Modules

To assess the performance and reliability of the new Mufold-MD server, which incorporates both SR and SMDR modules (see the owchart in Figure 1), we have compared it with its CASP9 and CASP10 versions. The goal of the exercise was to determine whether, under the same conditions (i.e., by using the same set of targets and input models), the new Mufold-MD server would have out-performed (and if yes, by how much) its two previous versions.

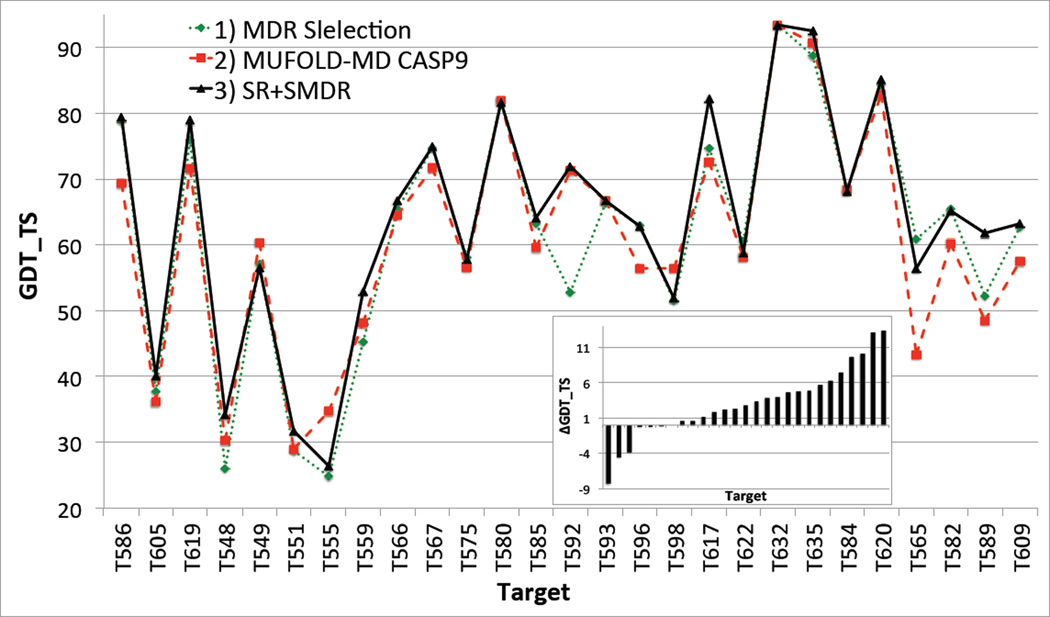
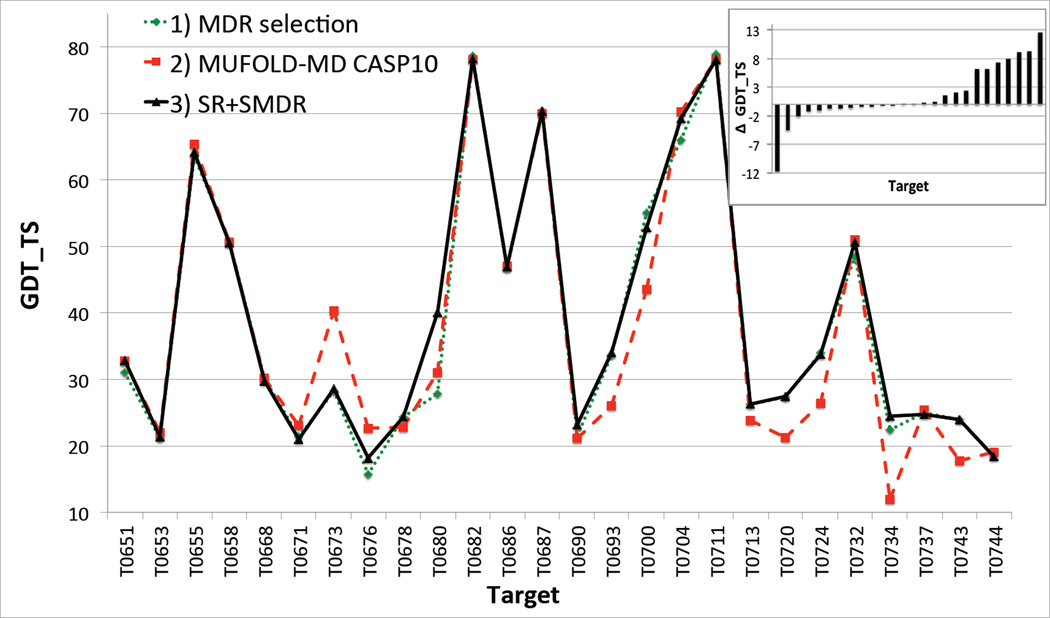
The model generation module of Mufold-MD used in CASP9 produced input models suitable for refinement only for 27 CASP9 targets considered in this paper. For each of these targets we have predicted the best-quality model (and the corresponding GDT_TS score with respect to the native structure) by employing three different refinement and selection protocols: 1) no refinement and MDR selection (i.e., using only the CHARMM force field); 2) free refinement and MDR selection (i.e., the actual Mufold-MD protocol used in CASP9); and 3) SR and SMDR (i.e., the new Mufold-MD server). The corresponding GDT_TS scores are plotted in Figure 9. The inset shows ΔGDT_TS, the difference between GDT_TS of the best model predicted with the new Mufold-MD server and the one used in CASP9. For 21 (16) targets the new Mufold-MD server would have (significantly) outperformed the old one, and only in 3 cases (i.e., 11%) would have made a noticeably lesser quality prediction.

Figure 9.

Comparison of GDT_TS scores (with respect to the native structures) of the best predicted models for 27 CASP9 targets, by using three different implementations of the Mufold-MD server, i.e., 1) no refinement and simple MDR selection; 2) free refinement and MDR selection; and 3) new Mufold-MD server with SR and SMDR. Inset: Change in GDT_TS, for each target, when switching from implementation 2) to 3). The targets are ordered in increasing order of ΔGDT_TS.

In case of CASP10, we have considered 26 hard targets from the human prediction category. The Mufold-MD server used in CASP10 had both SR and SMDR modules. However, in the CASP10 SR module, the δ-weighted constraint parameters x_n0 in Eq. (4) were calculated as an average over all input models of the corresponding Cα pair distances. By contrast, in the current SR module x_n0 are the Cα pair distances in the input model (subject to refinement). Figure 10 shows the comparison of the GDT_TS scores of the best models selected by the above described three protocols, with 2) being the CASP10 version of Mufold-MD. In this case, the new Mufold-MD would have (significantly) outperformed its CASP10 version for 14 (10) targets, while again for 3 targets would have predicted a noticeably worst quality structure. These results are similar to the CASP9 case, especially if we take into account that the qualities of the input structures were better than for CASP9, and the CASP10 Mufold-MD server included SMDR and an earlier version of SR.

Figure 10.

Comparison of GDT_TS scores (with respect to the native structures) of the best predicted models for 26 CASP10 targets from the human pre- diction category, by using three different implementations of the Mufold-MD server, i.e., 1) no refinement and simple MDR selection; 2) CASP10 implementation of Mufold-MD described in the text; and 3) new Mufold-MD server with SR and SMDR. Inset: Change in GDT_TS, for each target, when switching from implementation 2) to 3). The targets are ordered in increasing order of ΔGDT_TS.

Based on the above analysis (and other extensive testing not reported in this paper) one may conclude that the new Mufold-MD with SR and SMDR is more reliable and provides better quality protein structure predictions than previous versions of the server. In general, using SR and SMDR (with the present or further improved implementation) may improve the quality of any automated structure prediction server.

Conclusion

Motivated by the lack of availability of structure refinement and selection methods for fully automated protein structure prediction servers that work reliably for all targets, we have developed a target-specific selective refinement (SR) and a selective MD simulation based ranking (SMDR) method.

In the current version of SR, targets are divided in four categories based on their size and structural complexity. Models of easy targets, which satisfy condition (1), are subject to free refinement using Rosetta Relax. In general, the quality of these models increases significantly through refinement. Hard target models, identified through (2), are refined using fixed backbone constraints, leading only to modifications of the sidechains. While this does not change the quality of the model, measured by the GDT_TS of the Cα atoms, the refinement of the sidechains is important for the SMDR selection process, which involves all-atom MD simulations. Models for targets with regions whose structure can be predicted with high degree of confidence [identified through condition (3)], are refined by constraining the backbone atoms of these regions. Finally, for all other targets the corresponding models are refined with Rosetta Relax, using constraints determined by the standard deviation of the Cα pair distances in the input models [see Eq. (4)]. As we have demonstrated, the success of the SR method, which maximizes the positive outcome of the refinement process by choosing the best refinement method suitable for each individual target.

MDR is an all-atom MD simulation based ranking method used to identify the best quality model in a pool of decoys according to the stability of the model against simulated heating^23,24. The improvement of SMDR over MDR relies on the selective, target-specific use of the CHARMM and Amber force fields in the corresponding MD simulations. We have found that, in general, using Amber (CHARMM) is preferred whenever the target is dominated by α-helical (β-sheet) residues.

Finally, we have shown that Mufold-MD, our fully automated protein structure prediction server, updated with the SR and SMDR modules systematically outperformed previous versions of the server.