Abstract
A full understanding of RNA-mediated biology would require the knowledge of three-dimensional (3D) structures, structural flexibility, and stability of RNAs. To predict RNA 3D structures and stability, we have previously proposed a three-bead coarse-grained predictive model with implicit salt/solvent potentials. In this study, we further develop the model by improving the implicit-salt electrostatic potential and including a sequence-dependent coaxial stacking potential to enable the model to simulate RNA 3D structure folding in divalent/monovalent ion solutions. The model presented here can predict 3D structures of RNA hairpins with bulges/internal loops (<77 nucleotides) from their sequences at the corresponding experimental ion conditions with an overall improved accuracy compared to the experimental data; the model also makes reliable predictions for the flexibility of RNA hairpins with bulge loops of different lengths at several divalent/monovalent ion conditions. In addition, the model successfully predicts the stability of RNA hairpins with various loops/stems in divalent/monovalent ion solutions.
Introduction
In early years, RNA was considered to be an intermediary in transcription and translation (1). However, in the last two decades, RNA has been shown to perform other crucial functions, such as catalyzing biological reactions and controlling gene expression (2, 3). Understanding and utilizing these functions would require comprehensive knowledge of RNA structure and dynamics (4, 5, 6, 7). Although RNA sequences are being discovered rapidly, only limited three-dimensional (3D) RNA structures have been determined through experimental methods such as x-ray crystallography, NMR spectroscopy, and cryo-electron microscopy (4, 8). Simultaneously, for high efficiency and low cost, some computational models have been developed for predicting 3D structures or thermodynamics of RNA (8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18).
Some models based on fragment assembly, sequence alignment, and secondary structure, e.g., the MC-Fold/MC-Sym pipeline (19), are highly successful at predicting 3D structures even for large RNAs (19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39). However, these models are primarily designed to predict folded structures and would not give reliable predictions for the dynamic and thermodynamic properties of RNAs in three dimensions (16, 17, 18). Simultaneously, some other models have been developed that aim to predict RNA dynamics and thermodynamics. The Go-like coarse-grained (CG) three-interaction-site model can predict folding thermodynamics for hairpins and pseudoknots (40, 41). Another CG model of oxRNA can capture the thermodynamic and mechanical properties of RNA structures with pairwise interaction potentials (42). However, neither the three-interaction-site model nor the oxRNA model could give reliable predictions for 3D structures of RNAs from their sequences (16, 18). Although the three-bead CG model of iFoldRNA (43) and the six/seven-bead CG model of HiRE-RNA (16, 44) can predict 3D structures of small RNAs including pseudoknots, the parameters of the two models may need further validation or adjustment for predicting thermodynamic and dynamic properties of RNAs (18, 43, 44). Furthermore, since RNAs are highly charged polyanionic polymers, RNA structures can be sensitive to ion conditions and temperature (15, 45, 46, 47, 48, 49, 50, 51, 52, 53). However, none of the above models could predict 3D structures and thermodynamics of RNAs from their sequences over a wide range of ion concentrations and temperatures (16, 17, 18).
Very recently, to predict 3D structures and thermal stability of RNAs, we developed a CG model with three beads placed on the existing atoms P, C4′, and N9 for the purine (or N1 for the pyrimidine) (18, 54). Combined with an implicit-salt/solvent force field and the Monte Carlo (MC) simulated annealing algorithm, the model not only can predict native-like 3D structures of small RNAs from their sequences at high salt concentration (e.g., 1 M NaCl), but also can give reliable predictions about the stability of RNA hairpins over a wide range of sequences and monovalent ion concentrations that are comparable to the extensive experimental data (54). However, compared with monovalent ions (e.g., Na+), divalent ions such as Mg2+ can play a more special role in the stability and dynamics of RNA structures (55, 56, 57, 58, 59, 60). For example, Mg2+ is ∼1000 times more efficient in inducing the tertiary-structure folding of Tetrahymena thermophila ribozyme (45, 49). Although a recent structure-based model with an explicit treatment of Mg2+ and an implicit treatment of K+ can well capture the ion atmosphere around RNAs (61, 62, 63), there is still a need for a model that predicts 3D structures and stability of RNAs in divalent/monovalent ion solutions from their sequences. In this work, we further develop our previous model to enable it to predict the 3D structure and stability of RNAs in the presence of divalent ions.
In addition, the functions of RNAs may be not only related to the static 3D structures, but also influenced by the flexibility and stability of their structures (4, 5, 6, 7, 64, 65, 66). The flexibility of RNAs is rather important in the recognition of protein and in gene regulation (64, 65, 66, 67). For example, the transactivator response element (TAR) for the transactivator (TAT) protein of the human immunodeficiency virus (HIV) can undergo large conformational changes through the small bulge during the binding of TAT proteins (66, 67). Due to the polyanionic nature of RNAs, their flexibility would strongly depend on metal ions such as Mg2+ and loops (67, 68, 69). To examine the effects of metal ions (e.g., Mg2+) and loops on RNA flexibility, we select HIV-1 TAR and HIV-2 TAR variants as two paradigms in this work. To predict the 3D structures and flexibility of RNA hairpins with bulge loops, such as HIV TAR variants, in divalent/monovalent ion solutions, we introduce, to our knowledge, a new implicit electrostatic potential and an indispensable coaxial stacking interaction between two helices at the junction. With the model presented here, we predict the flexibility of HIV-1 TAR and HIV-2 TAR variants in divalent/monovalent ion solutions to understand the effects of salt and bulge loops.
In this work, we essentially develop the model to simulate RNA folding in divalent/monovalent ion solutions by improving the implicit-salt electrostatic potential and involving a parameterized coaxial stacking potential. Afterward, we first show that the CG model presented here can predict 3D structures of RNAs with bulges/internal loops at given ionic conditions with higher accuracy. Second, the model is employed to investigate the effects of divalent/monovalent salts and bulge length on the flexibility of HIV TAR variant RNAs. Finally, the model is used to quantitatively examine the stability of various RNA hairpins in divalent ion solutions. Throughout the article, all predictions are compared with the extensive experimental data.
Materials and Methods
CG structural model
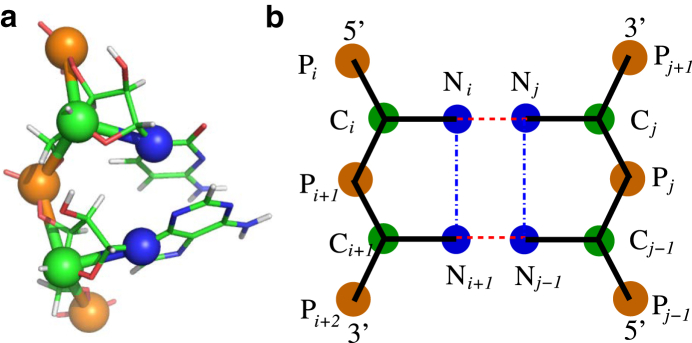
Since CG models generally allow considerable extension of the accessible size and timescale in simulations of biological systems (70, 71, 72, 73, 74), we have proposed a three-bead CG model for RNAs where the three beads stand for phosphate, sugar, and base (54). The backbone phosphate (P) bead and sugar (C) bead are placed at the P and C4′ atom positions, respectively, whereas the base (N) beads are placed at the N9 position for purine or the N1 position for pyrimidine (see Fig. 1). The P, C, and N beads are treated as spheres with van der Waals radii of 1.9 Å, 1.7 Å, and 2.2 Å, respectively (54, 75).
Figure 1.
(a) Our coarse-grained representation for one fragment of an RNA superposed on an all-atom representation. Specifically, three beads are located at the atoms of phosphate (P), C4′ (C), and N1 for pyrimidine or N9 for purine (N), respectively. The structure is shown with the PyMol (http://www.pymol.org). (b) The schematic representation for basepairing (dashed line) and base-stacking (dash-dotted line). To see this figure in color, go online.
Force field
In our CG model, the implicit-solvent/salt force field includes eight energy potentials (54):
| (1) |
The function forms for the eight energy potentials are described in detail in the Supporting Material, and we introduce them here only briefly, except in the case of the electrostatic interaction, Uel, and the coaxial stacking interaction, Ucs. The first three terms in Eq. 1 are the bonded potentials for covalent bonds (Ub), bond angles (Ua), and dihedral angles (Ud), respectively. The bonded potentials whose function forms have been described previously (54) were initially parameterized by the statistical analysis on the available 3D structures of RNA molecules in the Protein Data Bank (PDB; http://www.rcsb.org/pdb/home/home.do) (54, 75, 76, 77). Since lots of native structures in the PDB are mostly A-form helix, the statistical parameters from these structures would not be reasonable to describe the nature of RNA free chains (77). Therefore, for bonded potentials, two sets of parameters are calculated for single strands/loops and stems, referred to as Paranonhelical and Parahelical, respectively (see the Supporting Material and our previous work (54) for details). The former are used to describe the folding of an RNA from a free chain, and the latter are only used for stems during structure refinement after the folding process. The remaining terms of Eq. 1, namely the nonbonded potentials, describe various pairwise nonbonded interactions. The excluded volume, Uexc, between CG beads is modeled by a purely repulsive Lennard-Jones potential (54, 75). Ubp in Eq. 1 is employed to capture the basepairing interaction between Watson-Crick (G-C, A-U) and wobble (G-U) basepairs (43, 54, 78, 79, 80). Ubs in Eq. 1 is a temperature-dependent base-stacking potential that works between nearest-neighbor basepairs. The strength of Ubs was derived from the combined analysis of available sequence-dependent thermodynamic parameters (78, 79, 80) and the MC algorithm, and the details are shown in our previous work (54).
The electrostatic interaction, Uel, in Eq. 1, which is a newly refined term for the effect of divalent ions, is taken into account with the combination of the Debye-Hückel approximation and the concept of counterion condensation (CC) (78, 81, 82, 83):
| (2) |
The summation is over all the phosphate beads, and rij is the distance between two phosphate beads i and j. ε0 is the permittivity of vacuum. ε(T) is an effective temperature-dependent dielectric constant (40, 54, 58). lD is the Debye length of the ionic solution. Beyond our previous model (54), the effect of pure divalent ions and the competition between monovalent and divalent ions are also taken into account in the model presented here to study RNA folding in pure and mixed divalent ion solutions. Based on the CC theory (83), for a pure salt solution containing only one species of salt, such as NaCl or MgCl2, the reduced charge fraction, Q, could be written as Q = b/(vlB) (40, 54), where v is the cation valence, b is the phosphate-phosphate spacing of an RNA, and lB is the Bjerrum length (40, 54). For a mixed Na+/Mg2+ ion solution, we assume , where and represent the contribution fractions from Na+ and Mg2+, respectively. can be approximately calculated by the empirical formula previously derived from the tightly-bound-ion (TBI) model, which could account for the divalent-ion-RNA interactions (15, 60, 84, 85)
| (3) |
Here, (15, 60). [Na+] and [Mg2+] are the corresponding bulk concentrations in molar (M) and N is the chain length.
Ucs in Eq. 1 is newly introduced to model the coaxial stacking interaction at RNA junctions (4, 86, 87), and the coaxial stacking interaction between two discontinuous neighbor helices with interfaced basepairs i-j and k-l can be given by (86, 87)
| (4) |
where Gi-j,k-l is the sequence-dependent base-stacking strength. Gi-j,k-l is approximately taken as the stacking strength between the corresponding nearest-neighbor basepairs in an uninterrupted helix (79, 86, 87). rik (or rjl) is the distance between two interfaced bases, i(j) and k(l), of two stems, and a represents the extent of distance constraint. rcs is the optimum distance between two coaxially stacked stems. a and rcs are directly obtained from the statistical analysis of the known structures in the PDB database (see Fig. S1). Here, we only include the cases where there is one base or less in at least one of the single-stranded chains between two neighbor helices (see Fig. S1), since the noncanonical basepairs would generally be formed when there are more than one base in each side between two stems (3, 4, 86).
The detailed descriptions of the potentials in Eq. 1 and all the parameters for the potentials have been described in the Supporting Material; see also our previous work (54) for the process of building the force field.
Simulation algorithm
We use the MC simulated annealing algorithm, which can effectively avoid the trap in local energy minima (34, 54, 88), to search near-native conformations for an RNA at a given solution condition. Based on a random chain generated for an RNA sequence, the MC simulated annealing algorithm is performed from an initial high temperature to the target temperature (e.g., 298 K) at a fixed ion condition. In the folding process, the Paranonhelical of bonded parameters and the efficient pivot moves for the RNA chain, as well as the standard Metropolis algorithm, are used to sample conformations of a free RNA chain (54, 75, 78). With gradual cooling of the system, the initial 3D near-native structures would be folded at room temperature for RNAs.
After the MC annealing process with the bonded parameters of Paranonhelical for the whole RNA chain, the secondary structure and native-like 3D structures are predicted from a given sequence. To better capture the geometry of helical parts, further structure refinement is performed for higher accuracy of 3D structures as follows: based on the final 3D structure predicted by the preceding annealing process, another MC simulation (generally 1 × 106 steps) is performed at the corresponding ion condition and room temperature, with the bonded parameters of Parahelical and Paranonhelical for the basepairing regions (stems) and loops/single strands, respectively (54). As a result, an ensemble of refined 3D structures (∼8000 structures) would be obtained over the last ∼8 × 105 MC steps. The predicted 3D structures are evaluated by their RMSD values calculated over C beads from the corresponding C4′ atoms in the native structure in the PDB, though other parameters such as the template-modelling score and the base interaction network fidelity (89, 90) can also be used to evaluate the predicted structures. Since the model described here generally predicts a series of native-like structures during the refinement process, we will use the mean RMSD (the averaged value over the whole structure ensemble in the refinement process) and minimal RMSD (corresponding to the structure closest to the native one in the refinement process) to evaluate the reliability of predictions of 3D structures (30, 43, 54). Although RNA hairpins are mostly A-form helix, since helical stems may deform from the standard A-form helix (48) and the relative orientation between stems at a junction may change (67) with changes in ionic conditions, we still use the RMSD of the whole RNA, including stem and loop, to evaluate the performance of 3D structure prediction (89).
Results and Discussion
In this section, we employ the CG model to predict, from their sequences, the 3D structures of 32 RNA hairpins, most of which have bulges/internal loops (≤77 nucleotides (nt)), at the respective experimental ion (Na+/Mg2+) conditions. Afterward, the CG model is used to predict the flexibility and stability of RNA hairpins at extensive divalent/monovalent ion conditions. Our predictions will be compared with the extensive experimental data.
Predicting RNA 3D structures at the respective experimental ion conditions
Going beyond our previous work, which focused on predicting RNA structures at 1 M NaCl (54), we predict the 3D structures of 32 RNA hairpins, most of which have bulges/internal loops. The 3D structures of these RNAs have been determined by NMR at certain ion conditions (see Table 1). For each RNA hairpin, we make two separate predictions using the model presented here at the experimental ion condition and the previous version of the model at 1 M NaCl (54). Table 1 summarizes the major information about the RNA molecules, the corresponding experimental monovalent/divalent ion conditions, and the predictions from our model and the MC-Fold/MC-Sym pipeline (19).
Table 1.
The 32 RNA Molecules for 3D Structure Prediction in This Work
| RNAs | PDBa | Length (nt) | Typeb | [1+/2+]c (mM) | RMSDpred.d (Å) (mean/minimum) | RMSD0pred.e (Å) | RMSDMC-Symf (Å) |
|---|---|---|---|---|---|---|---|
| 1 | 2Y95g | 14 | H | 100/0 | 2.0/1.0 | 2.2 | 2 |
| 2 | 2LP9g | 16 | B | 65/0 | 2.6/1.1 | 2.7 | 2.8 |
| 3 | 1J4Yg | 17 | H | 20/0 | 3.9/1.9 | 4 | 4.6 |
| 4 | 1YN2g | 17 | H | 55/40 | 4.1/2.3 | 4.3 | 2.9 |
| 5 | 1Z30g | 18 | H | 50/0 | 1.7/0.9 | 1.9 | 2.6 |
| 6 | 1U2Ah | 20 | H | 75/0 | 2.1/1.1 | 2.6 | 3 |
| 7 | 1QWAg | 21 | B | 5/0 | 2.8/1.5 | 3 | 4.6 |
| 8 | 1D0Ug | 21 | B | 50/0 | 3.8/1.5 | 3.7 | 3.7 |
| 9 | 17RAh | 21 | B | 20/0 | 3.7/1.3 | 4 | 4.9 |
| 10 | 1JURg | 22 | B | 100/0 | 2.9/1.5 | 2.9 | 3.4 |
| 11 | 1OSWg | 22 | I | 25/0 | 3.7/1.5 | 4 | 4 |
| 12 | 2RO2g | 23 | H | 12.4/0 | 2.8/1.4 | 2.9 | 2.6 |
| 13 | 1BGZh | 23 | B&I | 20/0 | 3.4/2.1 | 4.6 | 4.8 |
| 14 | 1S34g | 23 | B | 35/0 | 3.5/1.7 | 4 | 2 |
| 15 | 1LC6g | 24 | I | 50/0 | 3.7/2.0 | 4.1 | 5.7 |
| 16 | 2KEZg | 24 | I | 50/0 | 3.4/1.5 | 3.6 | 2.9 |
| 17 | 1M82g | 25 | B | 20/0 | 2.1/1.2 | 2.4 | 2.2 |
| 18 | 2L5Zg | 26 | I | 50/5 | 4.0/2.6 | 4.6 | 5.2 |
| 19 | 2AHTg | 27 | B | 100/6 | 3.2/1.3 | 3.9 | 3.8 |
| 20 | 1F6Xg | 27 | B | 100/0 | 2.8/1.5 | 2.9 | 2.7 |
| 21 | 1XSHg | 27 | B | 100/0 | 3.4/1.7 | 3.6 | 2.9 |
| 22 | 1NBRg | 29 | B | 20/0 | 3.3/2.1 | 3.7 | 3.1 |
| 23 | 2JWVg | 29 | I | 50/0 | 4.5/2.0 | 5 | 4.9 |
| 24 | 1YNEg | 31 | B | 10/0 | 2.6/1.3 | 2.7 | 3.9 |
| 25 | 1JO7g | 31 | B&I | 10/0 | 4.0/2.3 | 4.6 | 4.9 |
| 26 | 2LWKg | 32 | B&I | 50/0 | 3.9/1.7 | 4.2 | 3.3 |
| 27 | 2JXVg | 33 | I | 20/0 | 3.2/1.9 | 3.9 | 4.9 |
| 28 | 2KPVg | 34 | B&I | 20/0 | 4.1/1.9 | 4.3 | 4.1 |
| 29 | 1ZC5g | 41 | B | 10/0 | 3.5/1.8 | 3.4 | 5.9 |
| 30 | 2KUUg | 48 | B | 20/0 | 4.5/2.3 | 5.1 | 5.5 |
| 31 | 2MQTg | 68 | B&I | 10/0 | 6.4/3.8 | 6.8 | 7.1 |
| 32 | 1P5Og | 77 | B&I | 100/5 | 11.0/8.7 | 13 | 10.8 |
The 3D structures of these RNA hairpins have been determined by NMR at certain ion conditions.
H, B, I, and B&I represent RNA hairpins without bulges/internal loops (H), with bulges (B), with internal loops (I), and with bulges and internal loops (B&I).
The salt conditions of solutions in which RNA structure were experimentally determined.
The mean/minimum RMSDs are calculated over C beads of the structures predicted by the model presented here from the corresponding C4′ atoms of the native structures.
The mean RMSD values are calculated over C beads of structures predicted by our previous model at 1 M NaCl from the corresponding C4′ atoms of the native structures.
The RMSD value is calculated over the C4′ atoms of the top single structure for each RNA predicted by the MC-Fold/MC-Sym pipeline (http://www.major.iric.ca/MC-Fold/) (19) from the native structure.
These hairpins were experimentally determined after the year 2000.
These hairpins were experimentally determined before the year 2000.
In monovalent solutions
First, we employ this model to predict 3D structures for RNA hairpins (with bulges/internal loops) at the corresponding monovalent ionic conditions listed in their PDB files. For example, the structure of stem loop IIa (PDB: 1U2A) is determined by NMR in a buffer consisting of 10 mM KH2PO4, 50 mM KCl, 15 mM NaCl, and 0.5 mM EDTA (91). We predict the 3D structures of stem loop IIa from its sequence in a solution of 75 mM monovalent salt. As shown in Table 1, the mean RMSD of the predicted 3D structures is ∼2.1 Å, which is obviously smaller than that (∼2.6 Å) of the structures predicted by the previous version of our model at 1 M NaCl. For the 28 tested RNA hairpins in the respective monovalent salt solutions, the overall mean RMSD between the structures predicted by this model at the respective experimental monovalent ionic conditions and the experimental structures is 3.37 Å, a smaller value than that (3.66 Å) predicted by the previous version of the model at 1 M NaCl (54); see Table 1.
In divalent solutions
In addition, one important feature of this model is that it combines CC theory and the results from the TBI model, and it can be employed to simulate RNA folding in mixed monovalent/divalent ion solutions. Four RNA hairpins with bulges/internal loops (PDB: 1YN2, 2L5Z, 2AHT, and 1P5O) were determined by NMR in solutions containing Mg2+, and the corresponding monovalent/divalent ion conditions are listed in Table 1. The mean RMSD values for these RNAs predicted by the model presented here in the corresponding experimental mixed ion solutions are 4.1 Å, 4.0 Å, 3.2 Å, and 11.0 Å, respectively, which are clearly smaller than the values (4.3 Å, 4.6 Å, 3.9 Å, and 13.0 Å) predicted by our previous model, regardless of the salt effect and the coaxial stacking interactions (54).
Salt versus coaxial stacking
As shown in Table 1, for the 32 hairpins, this model can make predictions with a visibly lower overall mean RMSD compared to our previous model (3.64 Å vs. 4.02 Å; p < 0.01 from the two-tailed Student’s t-test (12)), which suggests that the inclusion of monovalent/divalent salt and coaxial stacking in this model is effective for predicting RNA 3D structures in ion solutions. To clarify the contributions of the two improvements, we further perform two additional predictions for each hairpin using this model with coaxial stacking at 1 M NaCl and without coaxial stacking at the experimental ion conditions. We find that the two improvements both make positive contributions to the overall improved predictions and that the inclusion of the salt effect has a stronger contribution than that of coaxial stacking, as shown in Fig. S2. Due to the high charge density of the RNA backbone, the native-like structures of hairpins could be slightly stretched at low salt (48), and the difference between conformations at low and high salts should not be ignored (see Fig. S2). Although the coaxial stacking potential would only have a slight effect on hairpins with bulges/internal loops whose bases are stacking into neighbor helices (e.g., 1JUR and 1LC6), it would be indispensable for the formation of coaxially stacked states that are common in RNAs with bulges (e.g., 2KUU and 1P5O) and in the HIV-1 and HIV-2 TAR variants; see the subsection Flexibility of RNAs with bulges.
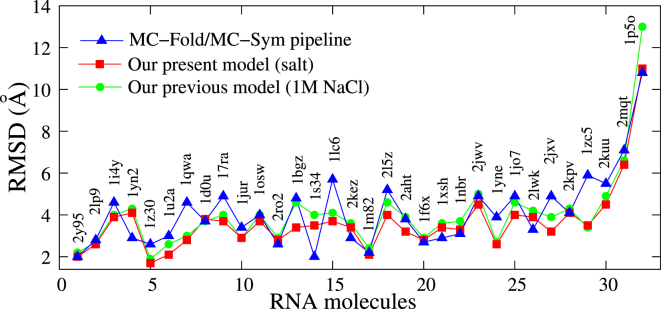
Comparisons with MC-Fold/MC-Sym pipeline
The MC-Fold/MC-Sym pipeline is a web service (http://www.major.iric.ca/MC-Pipeline/) for RNA secondary and tertiary structure predictions (19). To test the model presented here, we also make comparisons with the MC-Fold/MC-Sym pipeline. The RMSDs of the top 1 structures predicted by the pipeline online server (option: return the best 100 secondary structures and model_limit = 1000 or time_limit = 12 h) are calculated over C4′ atoms from the corresponding atoms in the experimental structures. As shown in Table 1 and Fig. 2, the overall predictions of 32 structures by this model (overall mean RMSD = 3.64 Å) appear visibly better than those from the MC-Fold/MC-Sym pipeline (overall mean RMSD = 4.12 Å), which is also suggested by the p-value of <0.01 from the two-tailed Student’s t-test (12). Table 1 and Fig. 2 also show that this model can give reliable predictions for relatively large RNAs (>45 nt (54)). For the 48-nt and 68-nt RNAs (PDB: 2KUU and 2MQT), this model gives much better predictions than those made by the MC-Fold/MC-Sym pipeline, whereas for the 77-nt RNA (PDB: 1P5O), the two models give similar predictions (see Table 1 and Fig. 2). This may be attributed to the fact that this model still ignores the possible noncanonical basepairs, which are abundant in the 77-nt RNA.
Figure 2.
Comparison of the RMSD values of RNA 3D structures predicted by the previous version of our model and that presented here and by the MC-Fold/MC-Sym pipeline. For each of the 32 tested RNAs, we use the MC-Fold/MC-Sym pipeline online tool (http://www.major.iric.ca/MC-Fold/) (19) to test the accuracy of MC-Fold/MC-Sym and calculate the RMSD for the top single predicted structure over the C4′ atom in the backbone. The RMSDs of structures predicted by the model described here at the experimental ion conditions (see Table 1) and by its previous version (54) at 1 M NaCl are calculated over C beads from the corresponding C4′ atoms in the native structures. To see this figure in color, go online.
Flexibility of RNAs with bulges
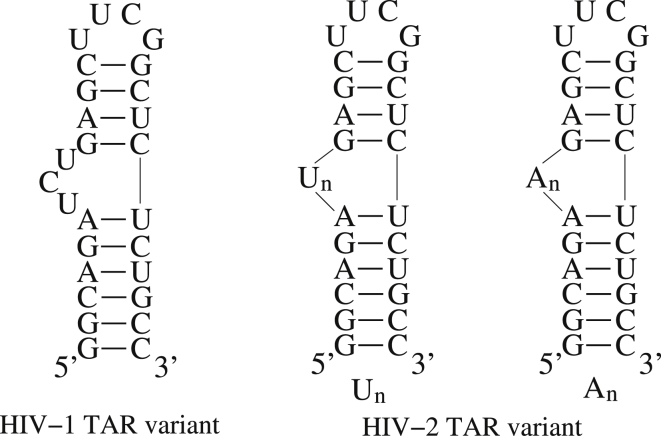
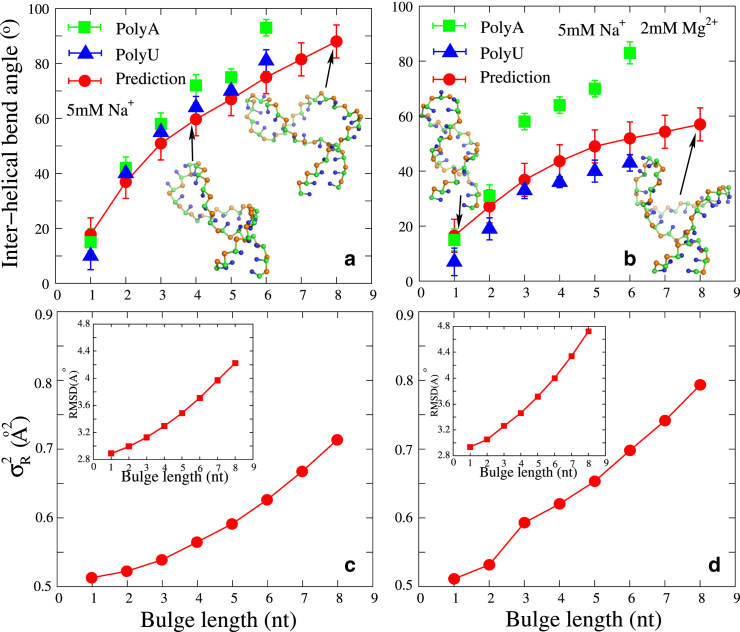
RNAs are highly flexible biomolecules that can undergo dramatic conformational changes to fulfill their diverse functions, e.g., the structural reorganization of riboswitches or the hammerhead ribozyme (2, 3). Generally, large conformational transitions of RNA structures are induced by the binding of ions, proteins, or ligands (45, 46, 47, 65, 66, 67). For example, HIV TAR RNAs, which can bind TAT protein through conformational changes during viral replication, have been important paradigms for studying RNA dynamics (66, 67). In this section, we employ the model presented here to study the flexibility of HIV-1/HIV-2 TAR variants at different ion conditions and make comparisons with the experimental data. The sequences of the HIV TAR variants and their secondary structures predicted by this model are shown in Fig. 3. The HIV-1 TAR variant with a 3-nt bulge is used to examine conformational changes at different ion conditions with this model, and HIV-2 TAR variants with different lengths of polyU (polyA) bulges are used to study conformational changes induced by various bulges. Our predictions are compared with results from the existing experiments for the HIV-1 TAR variant at extensive Na+/Mg2+ concentrations and for the HIV-2 TAR variant with various bulge lengths at 5 mM Na+ with/without 2 mM Mg2+, respectively (67, 68).
Figure 3.
The sequences and the secondary structures predicted by model presented here for the HIV-1 TAR variant with a 3-nt bulge and the HIV-2 TAR variants with different lengths of polyU (polyA) bulges, which are used to study the flexibility of RNAs.
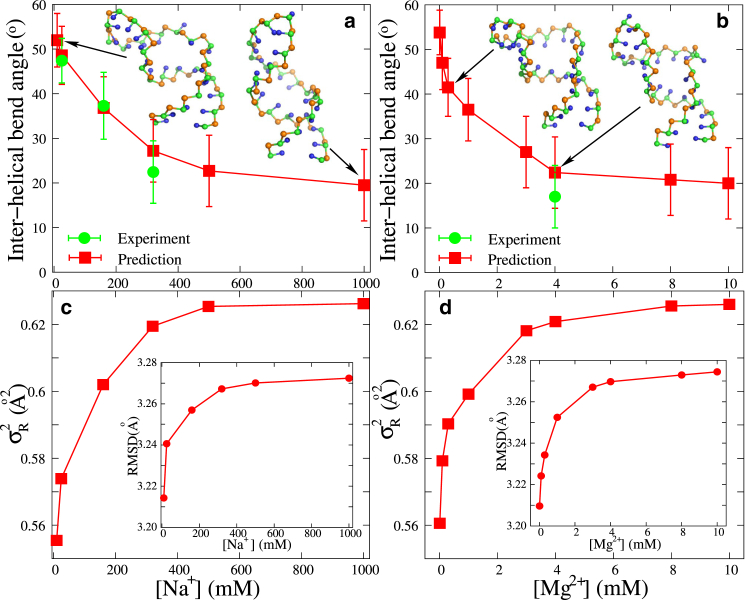
Bending versus monovalent/divalent salts
Recent studies have shown that RNA flexibility is strongly coupled to its ion condition (45, 46, 47, 67, 68, 69, 75, 92). As experimentally measured by Casiano-Negroni et al., the bending angle at the junction of the bulge is strongly dependent on salt (67). Here, we use our model to evaluate the bending at the bulge junction of the HIV-1 TAR variant (see Fig. 3) over a broad range of [Na+] as well as [Mg2+]. As shown in Fig. 4, a and b, the interhelical bend angle at the junction of the bulge decreases apparently with the increase of [Na+] (and [Mg2+]), and our predictions agree well with the corresponding experimental data (67). Such decrease of the bending angle with the increase of [Na+]/[Mg2+] is understandable. It comes from the competition between electrostatic repulsion, which plays a dominant role at low salt, and coaxial stacking interaction at the bulge, which plays a dominant role at high salt. A comparison between Fig. 4 a and Fig. 4 b shows that Na+ and Mg2+ induce a similar structural transition from a bent state at low ion concentrations to a coaxially stacked state at high salt, although Mg2+ is much more efficient at inducing such structure transition due to the higher ionic charge (55, 56, 57, 58).
Figure 4.
(a and b) The experimental (67) and predicted interhelical bend angle as functions of [Na+] (a) and [Mg2+] (b) for the HIV-1 TAR variant (see Fig. 3). The corresponding typical 3D structures predicted by the model presented here are shown with the PyMol (http://www.pymol.org). (c and d) The variances, , of the radius of gyration and the RMSD values from time-averaged reference structures as functions of [Na+] (c) and [Mg2+] (d) for the HIV-1 TAR variant (see Fig. 3). To see this figure in color, go online.
To further clarify the effect of coaxial stacking, we use the model presented here without coaxial stacking to predict the 3D structures for the HIV-1 TAR variant at extensive Na+/Mg2+ concentrations. A comparison of interhelical bend angles predicted by this model with and without coaxial stacking indicates that the inclusion of coaxial stacking can effectively capture coaxially stacked conformations that are closer to the experimental results, especially at high salt (67), as shown in Fig. S3.
Bending versus bulge length
Zacharias and Hagerman experimentally measured the bending angle for long RNA helices induced by bulges of various lengths (n = 1–6) and base compositions (An and Un series) (68). For simplicity, we predict the 3D structures of the HIV-2 TAR variant (see Fig. 3) with different bulge lengths at 5 mM NaPO4 in the absence and presence of 2 mM Mg2+ to study the bulge-induced bending of RNAs. As shown in Fig. 5, a and b, the bend angle at the bulge increases with an increase in the number of nucleotides in the bulge, which is in good accordance with the experimental data for the bulge of Un (68). As shown in Fig. 5 a, the severe interhelical bending and its sharp increase for longer bulges come from the more extended structures with larger end-to-end distance for longer bulges and from the strong electrostatic repulsion between helices, which can offset the interhelical stacking interactions at low salt concentrations. Higher salt (2 mM Mg2+) would reduce the electrostatic repulsion more strongly, and thus would promote interhelical stacking and reduce the bending angles (see Fig. 5 b). However, as shown in Fig. 5, a and b, the predictions on bending angle are apparently smaller than the experimental data for the HIV-2 TAR variant with an An bulge. This is because polyU behaves like a random coil, whereas polyA would exhibit strong intrachain self-stacking (69), which is not accounted for in the model presented here. Such self-stacking would enhance the rigidity of the single-stranded chain and consequently cause the large bending angle at the bulge.
Figure 5.
(a and b) The experimental (68) and predicted interhelical bend angles as functions of bulge length at 5 mM NaPO4 without (a) and with (b) 2 mM Mg2+ for the HIV-2 TAR variant (see Fig. 3). The corresponding typical 3D structures predicted by the model presented here are shown with the PyMol (http://www.pymol.org). (c and d) The variances, , of radius of gyration and RMSD values from time-averaged reference structures as functions of bulge length at 5 mM NaPO4 without (c) and with 2 mM Mg2+ (d) for the HIV-2 TAR variant (see Fig. 3). To see this figure in color, go online.
Recently, Mustoe et al. developed the CG model TOPRNA, which treats RNAs as collections of semirigid helices linked by freely rotatable single strands (74). Their model could nearly reproduce experimental bending angles of HIV-2 TAR with >2-nt bulges at low salt concentrations, whereas it did not give reliable predictions for HIV-2 TAR with a polyU bulge at high salt or for HIV-2 TAR with a 1-nt bulge, possibly because their model did not include the effects of salt and coaxial stacking and overestimated bulge rigidity for polyU (74).
Characterizing global structural fluctuation
The global size of an RNA can be characterized by its radius of gyration, Rg, the fluctuation of which can properly reflect RNA structural flexibility (64, 93). Based on the conformational ensemble of an RNA, we have calculated the variance, , of Rg by ; see Figs. S4 and S5, as well as the mean RMSD from the time-averaged reference structure. As shown in Fig. 4, c and d, and the RMSD of the HIV-1 TAR variant increase with the increase in salt concentration, and such increase becomes saturated at high salt. This is because the higher salt can reduce the electrostatic repulsion in the RNA and would favor conformational fluctuation. At high salt concentrations, the coaxial stacking between the two stems can be formed, and consequently, (and the RMSD) becomes saturated. Furthermore, as shown in Fig. 5, c and d, (and the RMSD) of the HIV-2 TAR variant increases for longer bulge length in 5 mM NaPO4 solution in the absence/presence of Mg2+. This is because RNA single-stranded loops are distinctly more flexible than duplexes (69, 75, 93).
Characterizing local structural fluctuation
Furthermore, we calculated the root-mean-square fluctuation (RMSF) of backbone beads to analyze the local flexibility along an RNA chain (64). The RMSF for the ith C-bead is calculated as
| (5) |
where the term within the square root symbol is the average over time t, ri(t) is the position of the ith C-bead at time t, and ri0 is the time-averaged reference position of the ith C-bead.
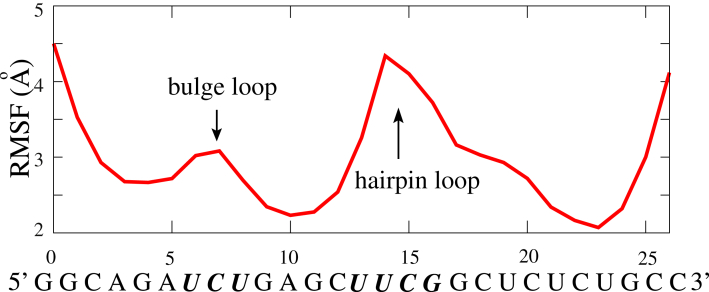
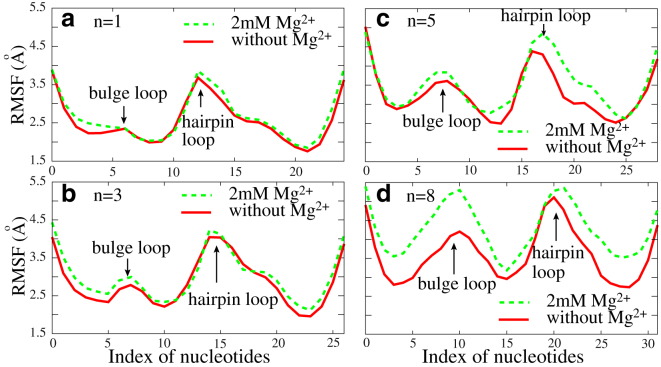
Fig. 6 shows the RMSF of each C-bead of the HIV-1 TAR variant at 1 M NaCl. The nucleotides near the 5′ and 3′ ends exhibit stronger conformational fluctuations, since the terminal basepairs have fewer spatial constraints (93). As shown in Figs. 6 and 7, the bulge and hairpin loops are more flexible than the stems, which comes from the significantly higher flexibility of unpaired single-stranded chains, since the previous theoretical and experimental studies have suggested that the persistence length of the stem is ∼60 times higher than that of the single-strand chain (64, 65, 66, 67, 68, 69, 75, 93). When the length of bulges increases from 1 to 8, the fluctuations of nucleotides, especially at the bulge, are apparently enhanced (see Fig. 7). This is because longer bulges have higher flexibility and naturally cause the higher flexibility of the whole RNA. Additionally, Fig. 7 shows that the addition of Mg2+ could increase the local flexibility of RNAs, especially for the HIV-2 TAR variant with a longer bulge. For RNAs with small bulges, the salt effect on local flexibility would not be very obvious (see also Fig. S6). This is reasonable, since the addition of Mg2+ would bring the strong electrostatic screening and consequently increase the flexibility of RNAs, especially at bulges. However, for RNAs with small bulges (≤∼3 nt), coaxial stacking would be formed between two stems and the addition of Mg2+ would only have a slight effect on their flexibility.
Figure 6.
The RMSF for C-beads along the HIV-1 TAR variant (see Fig. 3) in 1 M NaCl solution. The sequences of bulge and hairpin loops are in italics. To see this figure in color, go online.
Figure 7.
The RMSF for C-beads along the HIV-2 TAR variant (see Fig. 3) with different bulge length at 5 mM NaPO4 with and without 2 mM Mg2+. The lengths, n, of the bulge loop are 1 (a), 3 (b), 5 (c), and 8 (d), respectively. To see this figure in color, go online.
RNA hairpin stability in divalent ion solutions
The RNA folded structure is stabilized by the interplay of diverse interactions such as basepairing, base-stacking, and electrostatic interactions. RNA stability at high salt concentrations (e.g., 1 M NaCl) can be predicted with a relatively simple nearest-neighbor model (79, 80). However, the nearest-neighbor model cannot predict the 3D structure of RNAs at an arbitrary temperature and cannot predict RNA stability at ionic conditions departing from 1 M NaCl. However, due to its polyanionic nature, RNA stability is very sensitive to ionic condition (55, 56, 57, 58, 94, 95, 96, 97, 98, 99), and Mg2+ ions are particularly efficient at stabilizing RNA tertiary structure (55, 56, 57). To address the effect of Mg2+ in RNA stability, we employ the model present here to study the stability of various RNA hairpins in divalent and mixed divalent/monovalent ion solutions. Generally, a hairpin is either in a folded state at low T or an unfolded state at high T, or is bistable at middle T around the melting temperature Tm (50, 51, 52, 54). Based on the equilibrium value of the number of basepairs at each temperature, T, to obtain the Tm of a hairpin, the fraction of denatured basepairs, f(T), can be calculated and fitted to a two-state model (54, 79),
| (6) |
where dT is an adjustable parameter (54).
In pure divalent solutions
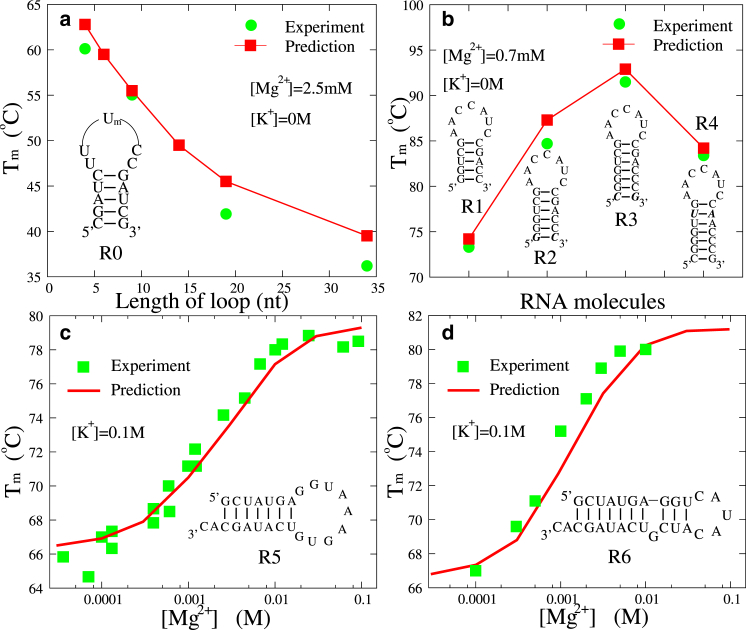
Recently, the loop-size dependence of the stability of an RNA hairpin (denoted as R0) was experimentally investigated in 2.5 mM Mg2+ (94). Fig. 8 a shows the sequences of hairpins R0, as well as the secondary structures predicted by the model presented here. Fig. 8 a also shows the predicted Tm for R0 in 2.5 mM Mg2+ as a function of the loop size (m = 4∼34 nt), which is in good accordance with the experimental data (94). Due to the larger conformational entropy for longer loops, the hairpin stability would decrease when the hairpin loop becomes longer. In addition, we have studied the stability of hairpins with the same loop but with different stems in 0.7 mM Mg2+ solutions. Hairpins R1–R4 are four similar RNAs whose stems are slightly different in length or sequence (see Fig. 8 b). As shown in Fig. 8 b, the Tm values of four hairpins predicted by the model presented here at 0.7 mM MgCl2 are in good agreement with the experimental data (95). The addition of a G-C or C-G basepair (from R1 to R2 and then to R3) can dramatically stabilize the RNA hairpins due to the strong basepairing/base-stacking interactions. The difference between the Tm values of R3 and R4 indicates that RNA stability is sensitive to sequence-dependent basepairing/base-stacking. The good agreement between our predictions and experiments (94, 95) suggests that our model can well describe the folding stability of small RNAs in pure Mg2+ solutions.
Figure 8.
(a) The experimental (94) and predicted melting temperature as functions of length of hairpin loop for RNA hairpin R0 at 2.5 mM [Mg2+]. (b) The experimental (95) and predicted melting temperatures of four RNA hairpins with different stems at 0.7 mM [Mg2+]. (c and d) The experimental (98, 99) and predicted melting temperatures, Tms, as functions of [Mg2+] for the two RNA hairpins R5 (c) and R6 (d) in the presence of 0.1 M [K+]. The sequences and the secondary structures predicted by the model presented here are also shown in (a)–(d). To see this figure in color, go online.
In mixed divalent/monovalent solutions
Using the model presented here, we also examined the stability of RNA hairpins R5 and R6 in mixed K+/Mg2+ solutions, and the secondary structures for R5 and R6 predicted by this model are shown in Fig. 8, c and d. As shown in Fig. 8, c and d, for Tm values of R5 and R6 at a fixed [K+] (100 mM), in addition to the general trend of increased stability for higher [Mg2+], the competition between K+ and Mg2+ also leads to the following behavior of RNA stability. At low [Mg2+] (≤0.1 mM), the stability of RNAs is dominated by (∼100 mM) K+ and the Tm values are close to that at the corresponding pure [K+]. As [Mg2+] is increased, Mg2+ ions begin to play a role and the stability of RNAs begins to increase markedly due to the efficient role of Mg2+ in stabilizing RNAs. At very high [Mg2+], Mg2+ would become dominant and the Tm would become saturated (60). As shown in Fig. 8, c and d, the agreement with experimental data (98, 99) indicates that the combination of CC theory and the results from the TBI model could give a good description of the competition between monovalent and divalent ions in stabilizing RNA hairpins, and the model presented here can give good predictions of the stability of RNA hairpins in mixed divalent/monovalent solutions.
Conclusions
In this work, we have developed our CG model to predict 3D structures and structural properties of RNAs with bulges/internal loops in the presence of divalent and monovalent ions. The major extensions of our CG model include improvement of the electrostatic potential to implicitly consider the effect of divalent ions and inclusion of coaxial stacking at the two-way junction. The improved CG model has been employed to examine the effects of divalent/monovalent salt on the 3D structure, flexibility, and stability of RNA hairpins with a two-way junction.
First, we employed this model to predict 3D structures for 32 RNAs (≤77 nt) at the respective monovalent/divalent salt conditions in which the RNA structures were experimentally determined by NMR, and the overall mean RMSD of 3.64 Å between the predictions and the experimental structures is visibly smaller than those from predictions by the MC-Fold/MC-Sym pipeline and by previous version of our model at 1 M NaCl. Second, we studied the flexibility of RNA hairpins with varying bulge loops at extensive Na+ and Mg2+ concentrations, and the predicted bending angles at the bulge for HIV-1 and HIV-2 TAR variants are in good agreement with the available experimental data for different salt conditions, as well as the different lengths of bulge loops. Third, we predicted the stability of RNA hairpins in divalent and mixed divalent/monovalent ion solutions, and the predictions agree well with the experimental data. Therefore, this improved model can provide the ensemble of probable 3D structures at extensive divalent/monovalent ion conditions and can make reliable predictions on structural properties such as flexibility and stability for small RNAs.
Despite the extensive agreement between our predictions and experiments, this model still involves some approximations and simplifications. First, in this model, the effect of divalent and monovalent salts is implicitly accounted for by the combination of CC theory and the TBI model. The good agreement with experimental data suggests that the combination of CC theory and TBI model can well capture the efficient role of divalent ions over monovalent ions, though more extensive experimental validation for larger RNAs is still required. Also, this model ignores the effect of specific ion binding, which might become important for large RNAs with complex structures (55, 56, 57). Of course, a more accurate treatment of salt is to explicitly consider the metal ions (75, 97), which would bring a huge computational cost. Very recently, Hayes et al. proposed a generalized Manning CC model in an alternative way that reproduces the ion atmosphere around RNAs through the explicit representation of Mg2+ and implicit treatment of K+ (61, 62, 63). Second, the CG model presented here only considers the canonical Watson-Crick (C-G, A-U) and wobble (G-U) basepairing, and ignores the possible noncanonical basepairs due to the lack of experimental thermodynamic parameters (79, 80). Noncanonical basepairing can be included in this model with the corresponding thermodynamic parameters, which would further improve the accuracy of structure prediction for RNAs with loops (19, 30). Third, although our model can predict 3D structures for RNAs beyond hairpins, e.g., small pseudoknots (54), it is still a challenge for the present version of the model to accurately and efficiently predict 3D structures of large RNAs with complex structures. Nevertheless, we are currently extending the model to predict 3D structures and stability for extensive RNA pseudoknots and complex structures, whereas 3D structure prediction for large RNAs from their sequences may require certain experimental constraints (34, 39). Finally, the 3D structure predicted by this model is at the CG level, and consequently, it is still necessary to develop this model to reconstruct all-atomistic structures based on CG predictions. Nevertheless, this model can be a reliable predictive model for 3D structure ensemble of small RNAs in divalent/monovalent solutions and at arbitrary temperatures.
Author Contributions
Z.J.T. and Y.Z.S. designed the research; Y.Z.S., L.J., and F.H.W. performed the research; Z.J.T., Y.Z.S., and X.L.Z. analyzed data; and Y.Z.S. and Z.J.T. wrote the article.
Acknowledgments
We are grateful to Professors Shi-Jie Chen (University of Missouri), Yang Zhang (University of Michigan), and Wenbing Zhang (Wuhan University) for valuable discussions.
This work was supported by grants from the National Key Scientific Program (973)-Nanoscience and Nanotechnology (2011CB933600), the National Science Foundation of China (11175132, 11374234, and 11575128), and the Program for New Century Excellent Talents (NCET 08-0408).
Editor: Nathan Baker.
Footnotes
Supporting Materials and Methods, six figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)01160-1.
Supporting Material
References
- 1.Crick F. Central dogma of molecular biology. Nature. 1970;227:561–563. doi: 10.1038/227561a0. [DOI] [PubMed] [Google Scholar]
- 2.Doherty E.A., Doudna J.A. Ribozyme structures and mechanisms. Annu. Rev. Biophys. Biomol. Struct. 2001;30:457–475. doi: 10.1146/annurev.biophys.30.1.457. [DOI] [PubMed] [Google Scholar]
- 3.Edwards T.E., Klein D.J., Ferré-D’Amaré A.R. Riboswitches: small-molecule recognition by gene regulatory RNAs. Curr. Opin. Struct. Biol. 2007;17:273–279. doi: 10.1016/j.sbi.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 4.Tinoco I., Jr., Bustamante C. How RNA folds. J. Mol. Biol. 1999;293:271–281. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
- 5.Hall K.B. Spectroscopic probes of RNA structure and dynamics. Methods Mol. Biol. 2012;875:67–84. doi: 10.1007/978-1-61779-806-1_4. [DOI] [PubMed] [Google Scholar]
- 6.Zhang W., Chen S.J. RNA hairpin-folding kinetics. Proc. Natl. Acad. Sci. USA. 2002;99:1931–1936. doi: 10.1073/pnas.032443099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gong S., Wang Y., Zhang W. Kinetic regulation mechanism of pbuE riboswitch. J. Chem. Phys. 2015;142:015103. doi: 10.1063/1.4905214. [DOI] [PubMed] [Google Scholar]
- 8.Sim A.Y., Minary P., Levitt M. Modeling nucleic acids. Curr. Opin. Struct. Biol. 2012;22:273–278. doi: 10.1016/j.sbi.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rother K., Rother M., Bujnicki J.M. RNA and protein 3D structure modeling: similarities and differences. J. Mol. Model. 2011;17:2325–2336. doi: 10.1007/s00894-010-0951-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Laing C., Schlick T. Computational approaches to RNA structure prediction, analysis, and design. Curr. Opin. Struct. Biol. 2011;21:306–318. doi: 10.1016/j.sbi.2011.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cruz J.A., Blanchet M.F., Westhof E. RNA-Puzzles: a CASP-like evaluation of RNA three-dimensional structure prediction. RNA. 2012;18:610–625. doi: 10.1261/rna.031054.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hajdin C.E., Ding F., Weeks K.M. On the significance of an RNA tertiary structure prediction. RNA. 2010;16:1340–1349. doi: 10.1261/rna.1837410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shapiro B.A., Yingling Y.G., Bindewald E. Bridging the gap in RNA structure prediction. Curr. Opin. Struct. Biol. 2007;17:157–165. doi: 10.1016/j.sbi.2007.03.001. [DOI] [PubMed] [Google Scholar]
- 14.Zhang Y. Progress and challenges in protein structure prediction. Curr. Opin. Struct. Biol. 2008;18:342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tan Z., Zhang W., Wang F. RNA folding: structure prediction, folding kinetics and ion electrostatics. Adv. Exp. Med. Biol. 2015;827:143–183. doi: 10.1007/978-94-017-9245-5_11. [DOI] [PubMed] [Google Scholar]
- 16.Cragnolini T., Derreumaux P., Pasquali S. Ab initio RNA folding. J. Phys. Condens. Matter. 2015;27:233102. doi: 10.1088/0953-8984/27/23/233102. [DOI] [PubMed] [Google Scholar]
- 17.Bailor M.H., Mustoe A.M., Al-Hashimi H.M. Topological constraints: using RNA secondary structure to model 3D conformation, folding pathways, and dynamic adaptation. Curr. Opin. Struct. Biol. 2011;21:296–305. doi: 10.1016/j.sbi.2011.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shi Y.Z., Wu Y.Y., Tan Z.J. RNA structure prediction: progress and perspective. Chin. Phys. B. 2014;23:078701. [Google Scholar]
- 19.Parisien M., Major F. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature. 2008;452:51–55. doi: 10.1038/nature06684. [DOI] [PubMed] [Google Scholar]
- 20.Massire C., Westhof E. MANIP: an interactive tool for modelling RNA. J. Mol. Graph. Model. 1998;16:197–205. doi: 10.1016/s1093-3263(98)80004-1. 255–257. [DOI] [PubMed] [Google Scholar]
- 21.Jossinet F., Ludwig T.E., Westhof E. Assemble: an interactive graphical tool to analyze and build RNA architectures at the 2D and 3D levels. Bioinformatics. 2010;26:2057–2059. doi: 10.1093/bioinformatics/btq321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Martinez H.M., Maizel J.V., Jr., Shapiro B.A. RNA2D3D: a program for generating, viewing, and comparing 3-dimensional models of RNA. J. Biomol. Struct. Dyn. 2008;25:669–683. doi: 10.1080/07391102.2008.10531240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rother M., Rother K., Bujnicki J.M. ModeRNA: a tool for comparative modeling of RNA 3D structure. Nucleic Acids Res. 2011;39:4007–4022. doi: 10.1093/nar/gkq1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Flores S.C., Altman R.B. Turning limited experimental information into 3D models of RNA. RNA. 2010;16:1769–1778. doi: 10.1261/rna.2112110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Popenda M., Szachniuk M., Adamiak R.W. Automated 3D structure composition for large RNAs. Nucleic Acids Res. 2012;40:e112. doi: 10.1093/nar/gks339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhao Y., Gong Z., Xiao Y. Improvements of the hierarchical approach for predicting RNA tertiary structure. J. Biomol. Struct. Dyn. 2011;28:815–826. doi: 10.1080/07391102.2011.10508609. [DOI] [PubMed] [Google Scholar]
- 27.Zhao Y., Huang Y., Xiao Y. Automated and fast building of three-dimensional RNA structures. Sci. Rep. 2012;2:734. doi: 10.1038/srep00734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Huang Y., Liu S., Xiao Y. A novel protocol for three-dimensional structure prediction of RNA-protein complexes. Sci. Rep. 2013;3:1887. doi: 10.1038/srep01887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang J., Zhao Y., Xiao Y. 3dRNAscore: a distance and torsion angle dependent evaluation function of 3D RNA structures. Nucleic Acids Res. 2015;43:e63. doi: 10.1093/nar/gkv141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Das R., Baker D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. USA. 2007;104:14664–14669. doi: 10.1073/pnas.0703836104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bida J.P., Maher L.J., 3rd Improved prediction of RNA tertiary structure with insights into native state dynamics. RNA. 2012;18:385–393. doi: 10.1261/rna.027201.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang J., Bian Y., Wang W. RNA fragment modeling with a nucleobase discrete-state model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:021909. doi: 10.1103/PhysRevE.85.021909. [DOI] [PubMed] [Google Scholar]
- 33.Zhang J., Dundas J., Liang J. Prediction of geometrically feasible three-dimensional structures of pseudoknotted RNA through free energy estimation. RNA. 2009;15:2248–2263. doi: 10.1261/rna.1723609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Seetin M.G., Mathews D.H. Automated RNA tertiary structure prediction from secondary structure and low-resolution restraints. J. Comput. Chem. 2011;32:2232–2244. doi: 10.1002/jcc.21806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tan R.K.Z., Petrov A.S., Harvey S.C. YUP: A molecular simulation program for coarse-grained and multiscaled models. J. Chem. Theory Comput. 2006;2:529–540. doi: 10.1021/ct050323r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jonikas M.A., Radmer R.J., Altman R.B. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA. 2009;15:189–199. doi: 10.1261/rna.1270809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cao S., Chen S.J. Physics-based de novo prediction of RNA 3D structures. J. Phys. Chem. B. 2011;115:4216–4226. doi: 10.1021/jp112059y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Xu X., Zhao P., Chen S.J. Vfold: a web server for RNA structure and folding thermodynamics prediction. PLoS One. 2014;9:e107504. doi: 10.1371/journal.pone.0107504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Xia Z., Bell D.R., Ren P. RNA 3D structure prediction by using a coarse-grained model and experimental data. J. Phys. Chem. B. 2013;117:3135–3144. doi: 10.1021/jp400751w. [DOI] [PubMed] [Google Scholar]
- 40.Denesyuk N.A., Thirumalai D. Coarse-grained model for predicting RNA folding thermodynamics. J. Phys. Chem. B. 2013;117:4901–4911. doi: 10.1021/jp401087x. [DOI] [PubMed] [Google Scholar]
- 41.Hyeon C., Thirumalai D. Mechanical unfolding of RNA hairpins. Proc. Natl. Acad. Sci. USA. 2005;102:6789–6794. doi: 10.1073/pnas.0408314102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Šulc P., Romano F., Louis A.A. A nucleotide-level coarse-grained model of RNA. J. Chem. Phys. 2014;140:235102. doi: 10.1063/1.4881424. [DOI] [PubMed] [Google Scholar]
- 43.Ding F., Sharma S., Dokholyan N.V. Ab initio RNA folding by discrete molecular dynamics: from structure prediction to folding mechanisms. RNA. 2008;14:1164–1173. doi: 10.1261/rna.894608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pasquali S., Derreumaux P. HiRE-RNA: a high resolution coarse-grained energy model for RNA. J. Phys. Chem. B. 2010;114:11957–11966. doi: 10.1021/jp102497y. [DOI] [PubMed] [Google Scholar]
- 45.Woodson S.A. Metal ions and RNA folding: a highly charged topic with a dynamic future. Curr. Opin. Chem. Biol. 2005;9:104–109. doi: 10.1016/j.cbpa.2005.02.004. [DOI] [PubMed] [Google Scholar]
- 46.Chen S.J. RNA folding: conformational statistics, folding kinetics, and ion electrostatics. Annu. Rev. Biophys. 2008;37:197–214. doi: 10.1146/annurev.biophys.37.032807.125957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lipfert J., Doniach S., Herschlag D. Understanding nucleic acid-ion interactions. Annu. Rev. Biochem. 2014;83:813–841. doi: 10.1146/annurev-biochem-060409-092720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Manning G.S. The response of DNA length and twist to changes in ionic strength. Biopolymers. 2015;103:223–226. doi: 10.1002/bip.22585. [DOI] [PubMed] [Google Scholar]
- 49.Takamoto K., He Q., Brenowitz M. Monovalent cations mediate formation of native tertiary structure of the Tetrahymena thermophila ribozyme. Nat. Struct. Biol. 2002;9:928–933. doi: 10.1038/nsb871. [DOI] [PubMed] [Google Scholar]
- 50.Zhang Y., Zhang J., Wang W. Atomistic analysis of pseudoknotted RNA unfolding. J. Am. Chem. Soc. 2011;133:6882–6885. doi: 10.1021/ja1109425. [DOI] [PubMed] [Google Scholar]
- 51.Bian Y., Zhang J., Wang W. Free energy landscape and multiple folding pathways of an H-type RNA pseudoknot. PLoS One. 2015;10:e0129089. doi: 10.1371/journal.pone.0129089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Xu X., Chen S.J. Kinetic mechanism of conformational switch between bistable RNA hairpins. J. Am. Chem. Soc. 2012;134:12499–12507. doi: 10.1021/ja3013819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chen J., Zhang W. Kinetic analysis of the effects of target structure on siRNA efficiency. J. Chem. Phys. 2012;137:225102. doi: 10.1063/1.4769821. [DOI] [PubMed] [Google Scholar]
- 54.Shi Y.Z., Wang F.H., Tan Z.J. A coarse-grained model with implicit salt for RNAs: predicting 3D structure, stability and salt effect. J. Chem. Phys. 2014;141:105102. doi: 10.1063/1.4894752. [DOI] [PubMed] [Google Scholar]
- 55.Pabit S.A., Sutton J.L., Pollack L. Role of ion valence in the submillisecond collapse and folding of a small RNA domain. Biochemistry. 2013;52:1539–1546. doi: 10.1021/bi3016636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Leipply D., Draper D.E. Effects of Mg2+ on the free energy landscape for folding a purine riboswitch RNA. Biochemistry. 2011;50:2790–2799. doi: 10.1021/bi101948k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Meisburger S.P., Pabit S.A., Pollack L. Determining the locations of ions and water around DNA from x-ray scattering measurements. Biophys. J. 2015;108:2886–2895. doi: 10.1016/j.bpj.2015.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tan Z.J., Chen S.J. Nucleic acid helix stability: effects of salt concentration, cation valence and size, and chain length. Biophys. J. 2006;90:1175–1190. doi: 10.1529/biophysj.105.070904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tan Z.J., Chen S.J. Predicting ion binding properties for RNA tertiary structures. Biophys. J. 2010;99:1565–1576. doi: 10.1016/j.bpj.2010.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tan Z.J., Chen S.J. RNA helix stability in mixed Na+/Mg2+ solution. Biophys. J. 2007;92:3615–3632. doi: 10.1529/biophysj.106.100388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hayes R.L., Noel J.K., Onuchic J.N. Generalized manning condensation model captures the RNA ion atmosphere. Phys. Rev. Lett. 2015;114:258105. doi: 10.1103/PhysRevLett.114.258105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hayes R.L., Noel J.K., Onuchic J.N. Reduced model captures Mg2+-RNA interaction free energy of riboswitches. Biophys. J. 2014;106:1508–1519. doi: 10.1016/j.bpj.2014.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hayes R.L., Noel J.K., Sanbonmatsu K.Y. Magnesium fluctuations modulate RNA dynamics in the SAM-I riboswitch. J. Am. Chem. Soc. 2012;134:12043–12053. doi: 10.1021/ja301454u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hagerman P.J. Flexibility of RNA. Annu. Rev. Biophys. Biomol. Struct. 1997;26:139–156. doi: 10.1146/annurev.biophys.26.1.139. [DOI] [PubMed] [Google Scholar]
- 65.Herschlag D., Allred B.E., Gowrishankar S. From static to dynamic: the need for structural ensembles and a predictive model of RNA folding and function. Curr. Opin. Struct. Biol. 2015;30:125–133. doi: 10.1016/j.sbi.2015.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mouzakis K.D., Dethoff E.A., Butcher S.E. Dynamic motions of the HIV-1 frameshift site RNA. Biophys. J. 2015;108:644–654. doi: 10.1016/j.bpj.2014.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Casiano-Negroni A., Sun X., Al-Hashimi H.M. Probing Na+-induced changes in the HIV-1 TAR conformational dynamics using NMR residual dipolar couplings: new insights into the role of counterions and electrostatic interactions in adaptive recognition. Biochemistry. 2007;46:6525–6535. doi: 10.1021/bi700335n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zacharias M., Hagerman P.J. Bulge-induced bends in RNA: quantification by transient electric birefringence. J. Mol. Biol. 1995;247:486–500. doi: 10.1006/jmbi.1995.0155. [DOI] [PubMed] [Google Scholar]
- 69.Chen H., Meisburger S.P., Pollack L. Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. USA. 2012;109:799–804. doi: 10.1073/pnas.1119057109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.de Pablo J.J. Coarse-grained simulations of macromolecules: from DNA to nanocomposites. Annu. Rev. Phys. Chem. 2011;62:555–574. doi: 10.1146/annurev-physchem-032210-103458. [DOI] [PubMed] [Google Scholar]
- 71.Zhou H.X. Theoretical frameworks for multiscale modeling and simulation. Curr. Opin. Struct. Biol. 2014;25:67–76. doi: 10.1016/j.sbi.2014.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kikot I.P., Savin A.V., Onufriev A.V. New coarse-grained DNA model. Biofizika. 2011;56:396–402. [PubMed] [Google Scholar]
- 73.Daily M.D., Olsen B.N., Baker N.A. Improved coarse-grained modeling of cholesterol-containing lipid bilayers. J. Chem. Theory Comput. 2014;10:2137–2150. doi: 10.1021/ct401028g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Mustoe A.M., Al-Hashimi H.M., Brooks C.L., 3rd Coarse grained models reveal essential contributions of topological constraints to the conformational free energy of RNA bulges. J. Phys. Chem. B. 2014;118:2615–2627. doi: 10.1021/jp411478x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Wang F.H., Wu Y.Y., Tan Y.Y. Salt contribution to the flexibility of single-stranded nucleic acid offinite length. Biopolymers. 2013;99:370–381. doi: 10.1002/bip.22189. [DOI] [PubMed] [Google Scholar]
- 76.Huang S.Y., Zou X.Q. A knowledge-based scoring function for protein-RNA interactions derived from a statistical mechanics-based iterative method. Nucleic Acids Res. 2014;42:e55. doi: 10.1093/nar/gku077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Huang S.Y., Zou X.Q. Statistical mechanics-based method to extract atomic distance-dependent potentials from protein structures. Proteins. 2011;79:2648–2661. doi: 10.1002/prot.23086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Zhang Y., Zhou H., Ou-Yang Z.C. Stretching single-stranded DNA: interplay of electrostatic, base-pairing, and base-pair stacking interactions. Biophys. J. 2001;81:1133–1143. doi: 10.1016/S0006-3495(01)75770-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Xia T., SantaLucia J., Jr., Turner D.H. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry. 1998;37:14719–14735. doi: 10.1021/bi9809425. [DOI] [PubMed] [Google Scholar]
- 80.Mathews D.H., Sabina J., Turner D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 81.Thomas D.G., Chun J., Baker N.A. Parameterization of a geometric flow implicit solvation model. J. Comput. Chem. 2013;34:687–695. doi: 10.1002/jcc.23181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Ren P., Chun J., Baker N.A. Biomolecular electrostatics and solvation: a computational perspective. Q. Rev. Biophys. 2012;45:427–491. doi: 10.1017/S003358351200011X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 84.Tan Z.J., Chen S.J. Electrostatic correlations and fluctuations for ion binding to a finite length polyelectrolyte. J. Chem. Phys. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Tan Z.J., Chen S.J. Salt contribution to RNA tertiary structure folding stability. Biophys. J. 2011;101:176–187. doi: 10.1016/j.bpj.2011.05.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Walter A.E., Turner D.H., Zuker M. Coaxial stacking of helixes enhances binding of oligoribonucleotides and improves predictions of RNA folding. Proc. Natl. Acad. Sci. USA. 1994;91:9218–9222. doi: 10.1073/pnas.91.20.9218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Walter A.E., Turner D.H. Sequence dependence of stability for coaxial stacking of RNA helixes with Watson-Crick base paired interfaces. Biochemistry. 1994;33:12715–12719. doi: 10.1021/bi00208a024. [DOI] [PubMed] [Google Scholar]
- 88.Kirkpatrick S., Gelatt C.D., Jr., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 89.Parisien M., Cruz J.A., Major F. New metrics for comparing and assessing discrepancies between RNA 3D structures and models. RNA. 2009;15:1875–1885. doi: 10.1261/rna.1700409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Zhang Y., Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 91.Stallings S.C., Moore P.B. The structure of an essential splicing element: stem loop IIa from yeast U2 snRNA. Structure. 1997;5:1173–1185. doi: 10.1016/s0969-2126(97)00268-2. [DOI] [PubMed] [Google Scholar]
- 92.Tan Z.J., Chen S.J. Electrostatic free energy landscapes for DNA helix bending. Biophys. J. 2008;94:3137–3149. doi: 10.1529/biophysj.107.122366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Wu Y.Y., Bao L., Tan Z.J. Flexibility of short DNA helices with finite-length effect: from base pairs to tens of base pairs. J. Chem. Phys. 2015;142:125103. doi: 10.1063/1.4915539. [DOI] [PubMed] [Google Scholar]
- 94.Kuznetsov S.V., Ren C.C., Ansari A. Loop dependence of the stability and dynamics of nucleic acid hairpins. Nucleic Acids Res. 2008;36:1098–1112. doi: 10.1093/nar/gkm1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Sehdev P., Crews G., Soto A.M. Effect of helix stability on the formation of loop-loop complexes. Biochemistry. 2012;51:9612–9623. doi: 10.1021/bi300481v. [DOI] [PubMed] [Google Scholar]
- 96.Tan Z.J., Chen S.J. Salt dependence of nucleic acid hairpin stability. Biophys. J. 2008;95:738–752. doi: 10.1529/biophysj.108.131524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Wu Y.Y., Zhang Z.L., Tan Z.J. Multivalent ion-mediated nucleic acid helix-helix interactions: RNA versus DNA. Nucleic Acids Res. 2015;43:6156–6165. doi: 10.1093/nar/gkv570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Nixon P.L., Theimer C.A., Giedroc D.P. Thermodynamics of stabilization of RNA pseudoknots by cobaltIII hexaammine. Biopolymers. 1999;50:443–458. doi: 10.1002/(SICI)1097-0282(19991005)50:4<443::AID-BIP9>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- 99.Nixon P.L., Giedroc D.P. Equilibrium unfolding (folding) pathway of a model H-type pseudoknotted RNA: the role of magnesium ions in stability. Biochemistry. 1998;37:16116–16129. doi: 10.1021/bi981726z. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.