Mechanics of Biomimetic Liposomes Encapsulating an Actin Shell

Abstract

Cell-shape changes are insured by a thin, dynamic, cortical layer of cytoskeleton underneath the plasma membrane. How this thin cortical structure impacts the mechanical properties of the whole cell is not fully understood. Here, we study the mechanics of liposomes or giant unilamellar vesicles, when a biomimetic actin cortex is grown at the inner layer of the lipid membrane via actin-nucleation-promoting factors. Using a hydrodynamic tube-pulling technique, we show that tube dynamics is clearly affected by the presence of an actin shell anchored to the lipid bilayer. The same force pulls much shorter tubes in the presence of the actin shell compared to bare membranes. However, in both cases, we observe that the dynamics of tube extrusion has two distinct features characteristic of viscoelastic materials: rapid elastic elongation, followed by a slower elongation phase at a constant rate. We interpret the initial elastic regime by an increase of membrane tension due to the loss of lipids into the tube. Tube length is considerably shorter for cortex liposomes at comparable pulling forces, resulting in a higher spring constant. The presence of the actin shell seems to restrict lipid mobility, as is observed in the corral effect in cells. The viscous regime for bare liposomes corresponds to a leakout of the internal liquid at constant membrane tension. The presence of the actin shell leads to a larger friction coefficient. As the tube is pulled from a patchy surface, membrane tension increases locally, leading to a Marangoni flow of lipids. As a conclusion, the presence of an actin shell is revealed by its action that alters membrane mechanics.

Introduction

The cell cortex is a thin shell of actin that lies underneath the plasma membrane. It is part of the cytoskeleton that controls cell shape. In mammalian cells, this cortex is ∼1 μm thick and is attached to the plasma membrane through specific protein links, but also through active proteins that polymerize actin locally (1). The cortex is a substrate for myosin attachment and tension buildup. The role of the cortex is to insure the mechanics of the cellular interface and adapt it to cell fate. For example, just before cell division, cells are able to round up through cortex rearrangements. Given the cell complexity, it is difficult to decipher the role of the different ingredients involved in insuring cell mechanics. Therefore, for the past two decades, simplified biomimetic systems of liposomes (or giant unilamellar vesicles) encapsulated with biological material that mimic cell content have been developed (2, 3). In certain experimental conditions in which the membrane tensions are of the order of 10⁻³ N/m, the elastic contribution of the membrane is found to be dominant, masking the role of the cortex on membrane mechanics (4, 5). Therefore, the specific contribution of the actin cytoskeleton on the global mechanics of plasma membrane needs to be unveiled in conditions other than pure elasticity measurements. Spreading dynamics of cell-sized liposomes (4) or tube-pulling dynamics (6) have revealed that the viscous contribution differs in the presence or absence of an actin shell grown from the inner leaflet of the membrane.

Here, we use hydrodynamic tube extrusion (7) to study the viscoelastic mechanics of a liposome, inside which an actin cortex has been produced on the model of the cell: an activator of actin polymerization is linked to the inner leaflet of the liposome, in which the actin machinery is incorporated. We show that the mechanics of such liposomes drastically depend on the presence of the actin shell. We explain that the actin cortex controls the mechanics of the entire cell-sized liposome through changing the mechanical properties of the membrane, both in the elastic and in the viscous regime. Our study confirms the subtle role of the actin cortex in controlling cell mechanics.

Materials and Methods

Liposome preparation

Liposomes were prepared using an inverted emulsion technique described by Pontani et al. (3). The lipids EPC, Cholesterol, DOGS-NTA-Ni, and DSPE-PEG(2000)-Biotin (Avanti Polar Lipids, Alabaster, AL) were dissolved in mineral oil (Sigma-Aldrich, St. Louis, MO) at a molar ratio EPC/Cholesterol/DOGS-NTA-Ni/Biotin of 52:37:10:1 at a total concentration of 0.5 mg/mL. The mix was sonicated for 2 h at 50°C and stored up to one week at 4°C. Bulk actin liposomes contained 3 μM actin, in internal buffer (“I-Buffer”). Cortex liposomes contained 3 μM actin, 7.8 μM VVCA-His, 0.45 μM Arp2/3, and 10 μM profilin in I-Buffer. The actin solution contained 10% fluorescently labeled actin from rabbit muscle (bulk, Alexa Fluor 488 conjugate; cortex, Alexa Fluor 568 conjugate) prepared in G-buffer (general actin buffer). Actin and Arp2/3 were purchased from Cytoskeleton (Denver, CO); the fluorescent actin was purchased from Invitrogen (Carlsbad, CA); and the VVCA-His and profilin were homemade, as previously described in Pontani et al. (3) and Carvalho et al. (8), respectively. The I-Buffer contained 10 mM HEPES (pH 7.5), 0.1 mM CaCl₂, 50 mM KCl, 2 mM MgCl₂, 5 mM ATP, 1 mM DTT (dithiothreitol), 0.5 mM Dabco (diazabicyclo[2,2,2]octane), 100 mg/mL dextran, and 180 mM sucrose to obtain a total osmolarity of 300 mOsm. The external buffer contained 10 mM HEPES (pH 7.5), 2 mM MgCl₂, 0.2 mM CaCl₂, 2 mM ATP, 1 mM DTT, 0.5 mM Dabco, 300 mM glucose, and 0.2 mg/mL casein to obtain a total osmolarity of 320 mOsm.

Hydrodynamic tube extrusion

The experimental chamber consisted of a single microfluidic channel made out of PDMS (poly-(dimethylsiloxane)), which was attached to a cover glass through plasma activation. One side of the channel was cut open to allow the introduction of the liposomes and the glass microstick. The other end was connected to an aspiration pump (MFCS-VAC-25 mbar; Fluigent, Villejuif, France), equipped with a debit meter. (A similar system has been previously used to study bare liposomes (7).) The size of the channel was 200 μm high, 600 μm wide, and 2 cm long. A coated glass microstick was used to attach the vesicles. Thin-tip microsticks were prepared by pulling borosilicate rods (1 mm; World Precision Instruments, Sarasota, FL) using a laser-based puller (P-2000; Sutter Instrument, Novato, CA). The rods were then forged to 2–3 μm using a microforge (MF-900; Narishige, Tokyo, Japan). To coat the microsticks, they were first cleaned in a plasma cleaner for 30 s, then incubated in 0.1% v/w PolyL-Lysin (Sigma-Aldrich) in PBS (phosphate-buffered saline) for 30 min, rinsed with PBS, and incubated in 1 mg/mL streptavidin (Sigma-Aldrich) in PBS solution for 1 h. The adhesion of the vesicles to the glass microsticks took place through the streptavidin and the biotinylated lipids in the vesicle membrane. Once the vesicle was attached to the rod, it was brought into the channel using a mechanical micromanipulator and raised to the middle of the channel. Using the aspiration pump, a fixed debit, D, ranging between 20 and 1000 nL/min, was applied. The velocity of the Poiseuille flow, U, at the midheight of the channel is related to D through U = 1.5 × D/A_c, where A_c is the cross section of the channel. For the dimensions of our channel, the flow velocities range between 4 and 200 μm/s.

Imaging and analysis

The imaging was performed using a charge-coupled device camera (CoolSNAP; Photometrics, Tucson, AZ) on an inverted microscope (Model No. IX70; Olympus, Tokyo, Japan). We used ×20 (NA = 0.5) and ×40 (NA = 0.6) objectives depending on the magnification required. The image acquisition rate was 0.5 or 1 frame/s controlled by the MetaMorph interface (Molecular Devices, Eugene, OR). The tracking of the liposomes were done using the MetaMorph software. Further analysis was performed using custom-made MATLAB routines (The MathWorks, Natick, MA).

To adjust the stepwise tube extrusion curves with Eq. 3 as explained in the Discussion section, we modified it as follows to leave the time corresponding to L = 0 of each step as a free parameter, t_n0. Considering that at time t_n (at which we change the force) that L = L_n, Eq. 3 becomes

$$L\left(t-t_{n0}\right)=L_n+L_{\text{cross}\_n}\left(e^{-\left(t_n-t_{n0}\right)/{\tau }_n}-e^{-\left(t-t_{n0}\right)/{\tau }_n}\right)+{\dot{L}}_{v\_n}\left(t-t_n\right).$$ (1)

This equation has four fitting parameters: L_{cross_n}, τ_n, t_n0, and ${\dot{L}}_{v\_n}$. We found that this fit is not very stable, sometimes giving erroneous values for L_{cross_n}. The parameter range for L_{cross_n} was therefore constrained to L_n < L_{cross_n} < L_n + 30 μm, where the initialization value for L_{cross_n} was obtained by fitting the beginning of the curve (first 10–15 s, corresponding to the elastic regime) with the first part of Eq. 1 $\left({\dot{L}}_{v\_n}=0\right)$. Once we have this length, we readjust the data with Eq. 1.

Results

Cortex and bulk liposome systems

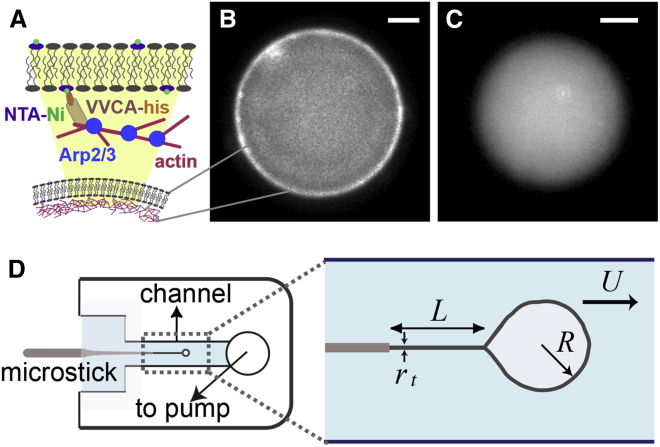
The actin machinery (the Arp2/3 complex, VVCA-His, profilin and actin; see Materials and Methods) is incorporated inside liposomes using the inverted emulsion technique as described in Pontani et al. (3), Murrell et al. (4), and Pautot et al. (9). Encapsulation is performed at 4°C, then liposomes are transferred into the experimental chamber and left at room temperature (23°C) to allow actin to polymerize into filaments. The way proteins assemble is shown schematically in Fig. 1 A. Actin nucleation is promoted by a fragment of N-WASP, a nucleation-promoting factor, known as VVCA-His, linked to nickel lipids at the membrane. Hence, actin polymerization takes place at the membrane and a branched actin network is formed through the Arp2/3-complex mechanism, building a branched actin cortex underneath the membrane (3). To prevent nucleation of filamentous actin from globular actin in the bulk, we use profilin (10) in a 3:1 proportion to actin monomers. Using 10% of fluorescent actin monomers, the actin cortex appears as a fluorescent shell inside the liposome within 5–20 min at 23°C, as shown in Fig. 1 B. We will refer to this system as “cortex” liposomes. In parallel, we use a cortex-free system, which we call “bulk” liposomes, where the liposome contains exclusively actin without the actin machinery that polymerizes actin into filaments. Indeed, in these conditions, actin does not polymerize at the membrane and remains in the bulk of the liposome, as seen in Fig. 1 C. This system is used as a reference to characterize the role of the biomimetic cortex on membrane mechanics.

Figure 1.

Experimental setup. (A) Schematic representation of protein assembly to form the biomimetic actin cortex. (B) Fluorescent image of an actin cortex, seen as a bright halo at the membrane of the liposome. (C) Liposome with actin in the bulk. Both scale bars are 5 μm. (D) Scheme of the experimental chamber and the principle of hydrodynamic tube-pulling technique. A constant flow U is applied inside the channel, applying a hydrodynamic force F_h = 6πηUR on the liposome (Movie S1). The length L is measured as a function of time for a given F_h.

For each trial, bulk and cortex liposomes are prepared separately with the exact same buffers except that the Arp2/3 complex, profilin, and VVCA-His are omitted from the bulk liposomes (see the Materials and Methods). Actin in both types of liposomes differs only by the fluorophore it carries. Liposomes are then introduced into the experimental chamber containing the external buffer. Tube-pulling measurements are performed on each type of liposome in random order. This approach allows us to have the two populations in the most comparable conditions.

Mechanical resistance of cortex liposomes revealed by tube-pulling assay

The mechanics of liposomes are characterized by pulling membrane tubes using a hydrodynamic flow. The scheme of the experiment is shown in Fig. 1 D: a liposome of radius R is attached to a microstick through biotin-streptavidin links and brought inside the microfluidic channel where a constant flow, U, is applied in the direction parallel to the stick, exerting a hydrodynamic force F_h = 6πηRU on the liposome, where η is the viscosity of the medium. The liposome in the flow feels a pulling force $F_p=6\pi \eta R\left(U-\dot{L}\right)$, where $\dot{L}$ is the tube elongation rate. In fact, the static force needed to pull a tube is given by $F=2\pi \sqrt{2\kappa \sigma }$, where σ is the membrane tension, and κ is the bending modulus of the membrane (11). The balance of forces during the pulling of the tube is thus given by

$$6\pi \eta R\left(U-\dot{L}\right)=2\pi \sqrt{2\kappa \sigma }.$$ (2)

In the presence of adhesion of the membrane to the underlying cytoskeleton, σ has to be replaced by σ + W, where W is the adhesion energy per unit area to detach the membrane from the cortex (12).

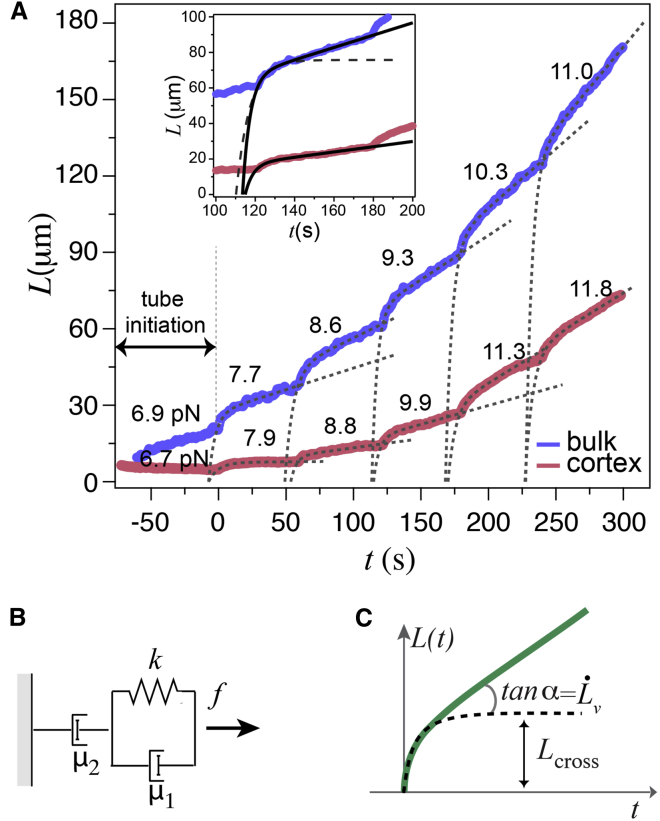
The tube dynamics are studied by analyzing tube length, L(t), as a function of time by video tracking. Fig. 2 A shows typical tube extrusion curves from cortex (red) and bulk (blue) liposomes, where the applied flow is increased in steps every 60–90 s (Movie S1 in the Supporting Material). Each step has the same feature: a rapid elongation during the first few seconds followed by a slow linear increase, as seen in the inset of Fig. 2 A. The characteristic time needed to change the value of the flow is <1 s, small compared to the characteristic time τ of the rapid elongation phase (∼10 s). We point out that the L(t) curves corresponding to cortex liposomes are visibly below the ones corresponding to bulk liposomes. At a given force and a given time, much shorter tubes are pulled from a cortex liposome than a bulk liposome, and at larger times the rate of elongation is reduced for cortex liposomes. We will analyze these two regimes by considering a mechanical model consisting of springs and dashpots.

Figure 2.

Tube dynamics of cortex and bulk liposomes. (A) Stepwise tube extrusion from liposomes with an actin cortex attached to the bilayer membrane (red) and with actin in bulk (blue). The numbers above each step indicate the hydrodynamic flow force, F_h = 6πηUR, in pN. At F_h = 6.7 pN (red curve), the tube initiated from the cortex liposome retracts itself, showing that 6.7 < F₀ < 7.9 pN, whereas for bulk liposome (blue curve), F₀ < 6.9 pN. The solid curves in the inset and the dotted lines in the main figure are adjustments to the extrusion curves with a modified KV body schematized in (B). The dashed line in the inset of (A) shows the case where μ₂ = ∞. The R² for the successive fits for the bulk liposomes are 0.97 for the first curve and 0.99 for the remaining, and for the cortex liposome, 0.97 for the first two, and 0.99 for the next three. (B) Modified KV body: a dashpot with a damping coefficient μ₂ is added in series to a KV body comprising a spring constant k and a dashpot with a damping coefficient μ₁ assembled in parallel and pulled by a force f. (C) L(t) curve corresponding to the mechanical model represented in (B). At short times, the tube elongates rapidly to a length L_cross, after which the elongation occurs at a constant speed ${\dot{L}}_v$.

Discussion

Kelvin-Voigt mechanical analog

Such a behavior of steep increase followed by a slow linear increase has a mechanical analog of a modified Kelvin-Voigt (KV) body made of a spring and a dashpot in parallel, with a spring constant k and a damping coefficient μ₁, connected in series to a second dashpot with a damping coefficient μ₂ as shown in Fig. 2 B. For a fixed force f, this model results in the following equation for the displacement L(t), shown schematically in Fig. 2 C:

$$L\left(t\right)=L_{\text{cross}}\left(1-e^{-t/\tau }\right)+{\dot{L}}_{v}t.$$ (3)

Here, τ = μ₁/k is the characteristic time of the elastic deformation, L_cross = f/k, and ${\dot{L}}_v=f/{\mu }_2$.

Mechanical parameters extracted from KV model

Equation 3 is valid for the first step when at t = 0, L = 0; however, for the consecutive steps, Equation 3 is modified as described in the Material and Methods. Therefore, we adjust Eq. 1 to deduce the following three mechanical parameters: the crossover length from the initial viscoelastic to viscous regime, L_cross; the characteristic time τ; and a long-term constant flow rate ${\dot{L}}_v$, which leads to μ₂.

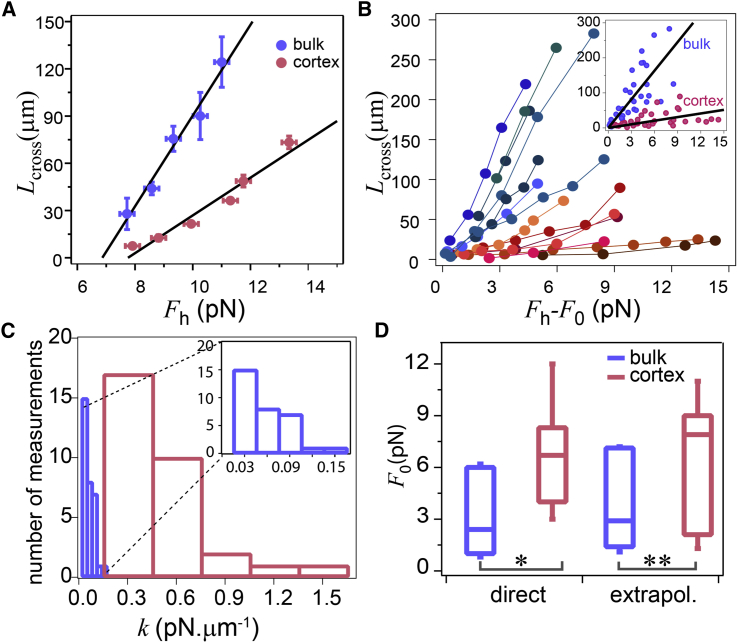
The solid lines in the inset of Fig. 2 A show an example of the adjustments of the L(t) curves with Eq. 1 for the two types of liposomes using the viscoelastic model in Fig. 2 B. An analysis of all the data is displayed in Fig. 3. We observe that 1) L_cross increases linearly with F_h and vanishes for a finite value F₀ (Fig. 3 A); and 2) the slope of L_cross (F) is much larger for bulk than for cortex liposomes (Fig. 3 B). Indeed, with f = F_h − F₀, the elastic coefficient is found to be k = (4 ± 1) × 10⁻⁸ N/m (mean ± SE) for bulk liposomes whereas it is ∼10 times higher, k = (32 ± 10) × 10⁻⁸ N/m (mean± SE), for cortex liposomes. This can also be seen from the histogram shown in Fig. 3 C, where k is obtained from each L_cross separately. We have also observed that the elastic coefficient k does not depend on the magnitude of the force increment (Fig. S1). The damping coefficient also shows a drastic difference between bulk, μ₂ = (1.4 ± 0.1) × 10⁻⁵ N.s/m (mean ± SE) and cortex, μ₂ = (15 ± 3) × 10⁻⁵ N.s/m (mean ± SE) liposomes. We have found little variation in the characteristic time, τ = 5.5 ± 0.5 s (mean ± SE) for bulk and τ = 4.5 ± 0.3 s (mean ± SE) for cortex liposomes, and that it does not vary with force (Figs. S2 and S3).

Figure 3.

Short-term viscoelastic deformation of the membrane tube as a function of pulling force. (A) Crossover length L_cross for bulk and cortex liposomes as the pulling force is increased in steps. Blue and red curves correspond to bulk and cortex liposomes, respectively. The radius of the bulk and the cortex liposomes is R₀ = 10 ± 0.5 μm. (B) L_cross for several liposomes as a function of F_h – F₀, where F₀ is the tube initiation force. (Inset) All data together. Linear regression demonstrates a mean slope for bulk and cortex liposomes proportional to the inverse of an effective bending modulus k (see text). (C) Histogram of k = f/L_cross for all data points, giving k = (4.4 ± 0.4) × 10⁻⁸ N/m (mean ± SE) for bulk and k = (38 ± 6) × 10⁻⁸ N/m (mean ± SE) for cortex liposomes; p < 10⁻¹⁴. (D) Critical extrusion force F₀ for bulk and cortex liposomes obtained by both direct (^∗p < 0.1) and extrapolation approaches (^∗∗p < 0.5).

Tube extrusion critical force

If σ₀ is the initial membrane tension before the tube is pulled, the critical force to extrude a tube is $F_0=2\pi \sqrt{2\kappa {\sigma }_0}$ for bulk liposomes and $F_0=2\pi \sqrt{2\kappa \left({\sigma }_0+W\right)}$ for cortex liposomes (see remarks above). Experimentally, the measurement of F₀ is not straightforward because to initiate the first tube, for an adhesion patch on the microstick as small as 1 μm in radius, a force threshold of ∼50 × F₀ needs to be overcome (13). Therefore, to initiate a tube, we momentarily increase the force by moving the microstick, with the liposome attached to it, back and forth in parallel to the flow direction (Movie S2). To determine F₀, we first increase F_h by small increments of 0.5–1 pN and we repeat the back-and-forth movement of the microstick until we succeed in pulling a tube. Once a tube is formed, we slightly vary the force until we get a stable short tube at a minimum force. This value corresponds to our direct estimate of F₀. We find an average value of F₀ = 3 ± 1 pN (mean ± SE) for bulk and F₀ = 6 ± 1 pN (mean ± SE) for cortex liposomes. A second way of estimating F₀ is by obtaining the intercept of L_cross versus F_h. As we show in Fig. 3 A, the intercept corresponds to F₀ for two liposomes, showing that F₀ for cortex liposomes is larger than for bulk liposomes. Note that F₀ may vary depending on the history of the tube. However, we do not have access to this variation in our experiments. Therefore, we consider F₀ to be constant for the consecutive steps.

On average, we find F₀ = 4 ± 1 pN (mean ± SE) for bulk and F₀ = 7 ± 1 pN (mean ± SE) for cortex liposomes, which is consistent with the estimated values for F₀ from the tube initiation approach (Fig. 3 D).

The value of the adhesion energy W between the membrane and the cortex can be derived from the ratio of $F_0^{\text{cortex}}/F_0^{\text{bulk}}=\sqrt{1+W/{\sigma }_0}$, which is ∼2 (Fig. 3 D). Therefore, in our experiments, W ≈ 3 × σ₀. Hence, both adhesion and membrane tension need to be taken into account for cortex liposomes. Note that for cells in nonadhering conditions, W is orders-of-magnitude larger than σ₀, thus the increase of σ₀ is masked by W entirely and the tube-pulling force is governed by cortex-membrane adhesion (14, 15). In adhering motile cells such as in keratocytes, σ₀ and W are comparable (16), and both contribute to the pulling force.

Model of viscoelastic tube extrusion

When a liposome is submitted to a flow above a threshold force F₀, and for times smaller than τ, the regime is elastic and tube length tends toward L_cross. However, for longer times, t > τ, a slow increase in L(t) corresponds to a viscous regime. We discuss here these two regimes of hydrodynamic tube extrusion for bulk and cortex liposomes.

Elastic regime

Let us first remind the reader of the elastic regime for bare liposomes as previously studied in the case of DOPC liposomes (7), taking into account the increase in membrane tension σ when a pulled tube unwinds membrane fluctuations. As shown by Helfrich and Servuss (17), when the area of a liposome is altered by an amount ΔA, its surface tension varies from σ₀ to σ according to the following relationship:

$$\frac{\Delta A}{A_p}=\frac{k_{\text{B}}T}{8\pi \kappa }\text{ln}\frac{\sigma }{{\sigma }_0}+\frac{\sigma -{\sigma }_0}{K_s}.$$ (4)

Here A_p = AπR₀² is the membrane projected area of the liposome with a radius R₀; k_BT is the thermal energy; κ is the bending modulus of the membrane already defined above; and K_s is the stretching coefficient. The first term on the right is the entropic term describing the increase of the membrane tension corresponding to smoothing of thermal membrane undulations, whereas the second term refers to the increase in the distance between lipid molecules resulting in membrane stretching in high tension regimes (σ > 10⁻³ N/m) (18).

Considering that the maximum pulling forces used in our experiments are ∼10 pN, the maximum tension can be estimated by taking κ = 5 k_BT from σ = F²/8π²κ = 6 × 10⁻⁵ N/m, showing that the contribution of the second term is small, and hence negligible; this is also confirmed by taking K_s = 0.1 N/m (7, 19), and the range of membrane tensions involved in our experiments. Therefore, we can simplify Eq. 4 to

$$\frac{\Delta A}{A_p}=\frac{k_{\text{B}}T}{8\pi \kappa }\text{ln}\frac{\sigma }{{\sigma }_0}.$$ (5)

When a tube of length L(t) is pulled, the change in the area of the liposome is ΔA = 2πr_tL(t), where $r_t=\sqrt{\kappa /2\sigma }=2\pi \kappa /F_p$ is the tube radius (11). Rewriting Eq. 5 in terms of L(t) and F_p $\left(F_p=6\pi \eta R\left(U-\dot{L}\right)\right)$, we obtain

$$L\left(t\right)=\frac{k_{\text{B}}T{R}_0^2}{4{\pi }^2{\kappa }^2}{F}_p\text{ln}\frac{F_p}{F_0}.$$ (6)

L_cross is derived from Eq. 6 for F_p = F_h, which corresponds to ${\dot{L}}_v=0$,

$$L_{\text{cross}}=\frac{1}{k}{F}_h\text{ln}\frac{F_h}{F_0},$$ (7)

where k = 4π²κ²/k_BTR₀² is the elastic modulus. For F_h close to F₀, we obtain a linear relationship between F_h and L_cross as

$$L_{\text{cross}}=\frac{1}{k}\left(F_h-F_0\right).$$ (8)

Integration of Eq. 6 leads to the general expression of L(t) in the elastic regime,

$$L\left(t\right)=L_{\text{cross}}\left(1-e^{-t/\tau }\right),$$ (9)

where τ = 3ηR₀³k_BT/2πκ². Note that Eq. 9 corresponds exactly to the first term of Eq. 3.

Data in Fig. 3, A and B, are approximated by a linear relationship (solid lines) using Eq. 8. The inverse of the slope gives k and the intercept gives an estimate for F₀. Such an analysis is correct for bulk liposomes (blue curve). However, the same linear behavior is also found for cortex liposomes (red curves, Fig. 3, A and B).

We first analyze k values for bulk liposomes. The distribution of k = (F_h – F₀)/L_cross is shown on the histogram of Fig. 3 C. From the slopes of the adjustments to Fig. 3 B, we obtain an average value of k = 4 ± 1 × 10⁻⁸ N/m for liposome radii ranging between 8.7 and 11.5 μm, which corresponds to κ = 5 ± 1 k_BT. The average critical pulling force is F₀ = 4 ± 1 pN, as shown on Fig. 3 D. Using σ₀ = F₀²/(8π²κ), we obtain the resting surface tension of the liposomes σ₀ = 9 ± 1 × 10⁻⁶ N/m. The values for κ and σ₀ are comparable to values reported previously for bare liposomes (7), implying that the mechanical properties of the membrane are not significantly affected by the presence of an encapsulated actin monomer solution. The characteristic time τ of Eq. 9 can be estimated by taking η = 10⁻³ Pa.s, and κ = 5 k_BT, which gives τ = 5 ± 2 s. This value compares well with the values obtained experimentally, justifying the use of the mechanical model introduced in the previous section.

For cortex liposomes, where the membrane is attached to the actin cortex with an adhesion energy W, the force modifies to $F_p=2\pi \sqrt{2\kappa \left(\sigma +W\right)}$ (12). Taking this into account, Eq. 5 becomes

$$L\left(t\right)=\frac{k_{\text{B}}T{R}_0^2}{8{\pi }^2{\kappa }^2}{F}_p\text{ln}\frac{F_p^2-8{\pi }^2\kappa W}{F_0^2-8{\pi }^2\kappa W}.$$ (10)

As for obtaining Eq. 8 from Eq. 6, L_cross is then derived for F_p = F_h, which corresponds to ${\dot{L}}_v=0$; for F_h close to F₀, L_cross reads

$$L_{\text{cross}}=\frac{1}{k_W}\left(F_h-F_0\right),$$ (11)

with $k_W=4{\pi }^2{\kappa }^2/k_{\text{B}}T{R}_0^2\left(1-(W/W+{\sigma }_0)\right)$. Equation 11 shows that for cortex liposomes, k_W should be smaller than the k for bulk liposomes. However, if we compare the values of L_cross versus F_h–F₀, we see a clear separation between the bulk (blue) and cortex (red) liposomes. For cortex liposomes, we find k_W = 32 ± 10 × 10⁻⁸ N/m, a much higher value than for bulk liposomes, where k = 4 ± 1 × 10⁻⁸ N/m, as can be seen on the histogram of Fig. 3 C. We note that k depends on two parameters: the membrane bending modulus κ, and the total available area, A_p = 4πR₀², for pulling a tube (see derivation of Eqs. 4 and 5). Because κ is the same for both types of liposomes (same lipid composition and no nonspecific interaction between filamentous actin and the membrane (2, 3)), the increase of the elastic coefficient suggests that the available surface for pulling a tube is no longer A_p but is reduced to α × 4πR₀², where α < 1. We can consider that the attachment of an actin cortex to the membrane creates patches that limit the available surface to pull a tube. This corral model was introduced to explain the confined motion of proteins in cell membranes (20) and applied to liposomes filled with polymer gels adhered to the lipid bilayer (21). A recent study (22) has put in evidence the influence of the plasma membrane compartmentalization by the cortical actin cytoskeleton on the diffusion of lipid molecules in the cell membrane. For cortex liposomes, the expression of k_W reads

$$k_W=\frac{k}{\alpha }\left(1-\frac{W}{W+{\sigma }_0}\right).$$ (12)

As estimated above, W ≈ 3σ₀, therefore, α ≈ 3%. The characteristic size of the patch is then given by $\sqrt{\alpha }{R}_0$ with α = 3% and R₀ ≈ 10 μm, and the corral size is of micron order, in agreement with Qian et al. (23). Note that the bending modulus of the cortex is higher than that of the membrane in our system, as in cells (24). Therefore, we consider here that the deformability of the cortex is negligible.

Viscous regime

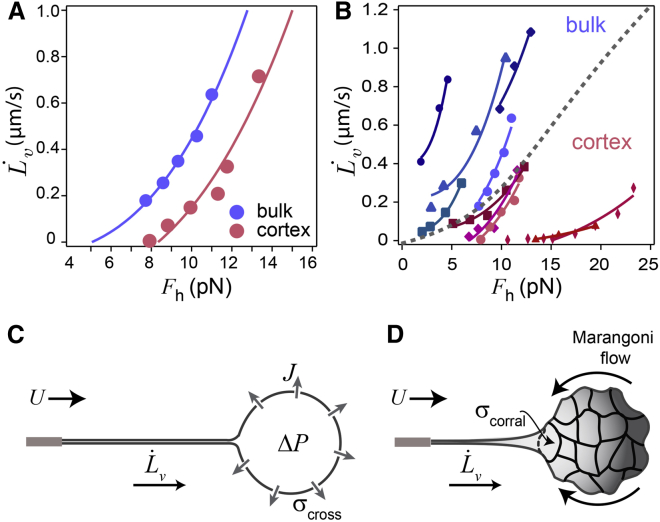
At longer times t > τ, corresponding to L > L_cross, the tube elongates with a constant velocity ${\dot{L}}_v$, as shown on Fig. 2 A. Fig. 4 shows our measured values for ${\dot{L}}_v$ as a function of the applied force F_h for both types of liposomes.

Figure 4.

Viscous response for bulk and cortex liposomes. (A) ${\dot{L}}_v$ versus F_h for bulk (blue) and cortex (red) liposomes for liposomes represented in Fig. 2A adjusted with a cubic function. The adjustment parameter gives the permeability, P_w, of the membrane for bulk liposomes and membrane viscosity for cortex liposomes. (B) ${\dot{L}}_v$ as a function of F_h for all liposomes (dashed line separates the two groups). (C) Sketch of a bulk liposome in the leakout regime; the tube elongates at a constant speed ${\dot{L}}_v$ when the membrane tension reaches a constant value σ_cross. (D) Sketch of a cortex liposome in the Marangoni regime. (Arrows) Marangoni flow from the floppy region toward the tense region at the tube neck.

Note that a long-term relaxation has been observed in a similar system from the dynamic-force relaxation experiments (6). The viscous regime corresponding to this condition was related to a putative diffusion process arising from the dynamic reorganization of the lipid molecules inside the membrane. Here, the long-term relaxation is observed at a constant pulling force. We address thoroughly which mechanism can give rise to a linear increase of tube length with time, observed in our experiments.

First we will consider the case of bulk liposomes. The elongation at constant velocity of the tube length is reminiscent of tube dynamics when pores are incorporated into the membrane of liposomes (25, 26). As a tube is pulled, the surface tension of the membrane increases. The Laplace pressure 2σ/R induces a slow leakout of the internal liquid. The radius of the liposome decreases, and the excess area increases. A stationary regime is reached, when the gain of the area due to liposome deswelling is transferred into the tube. Equation 2 shows that if ${\dot{L}}_v$ becomes constant, σ reaches a constant value σ_cross; this corresponds to the crossover between elastic and viscous regimes, corresponding to L ∼ L_cross.

The extrusion of tubes from porous liposomes decorated with n proteic pores of size a has been studied previously in Borghi et al. (25). The Poiseuille’s law for one pore can be written in a scaling approach as ηV/a² ≈ σ/aR, where V is the water velocity through the pore. The flux per pore is J_p = Va² ∼ σa³/ηR. The total flux is therefore J = nJ_p. Introducing Σ, the density of pores, and A, the area of the liposome, we get n = ΣA and the total flux J including the exact numerical coefficient (27), which is

$$J=\text{Σ}\frac{A}{3\eta }\frac{2\sigma }{R}{a}^3.$$ (13)

Equation 13 has been extended for the permeation of the water molecule through the lipid bilayer where a³ is the molecular volume of water v₀ ≈ 3 × 10⁻²⁹ m³. Therefore, J can be rewritten as

$$J=A{P}_w\frac{v_0}{k_{\text{B}}T}\frac{2\sigma }{R},$$ (14)

where P_w = Σk_BT/3η. Equation 14 holds for the intrinsic porosity of lipid bilayers, measured previously to be ∼P_w = 100 μm/s for a polyunsaturated phosphatidylcholine lipid membrane (28). However, as the tension of the membrane increases, transient pores open and close (29), leading to an increase of P_w. The leakout of the internal liquid leads to a deswelling of the liposome,

$$4\pi R^2\dot{R}=-A{P}_w\frac{v_0}{k_{\text{B}}T}\frac{2\sigma }{R};$$ (15)

then,

$$\dot{R}=-P_w\frac{v_0}{k_{\text{B}}T}\frac{2\sigma }{R}.$$ (16)

Combining Eqs. 2 and 16, and considering that the area decrease of the liposome is related to the increase of tube length through $-8\pi R\dot{R}=2\pi r_t{\dot{L}}_v$, we derive the following relationship between the tube elongation rate ${\dot{L}}_v$ and the hydrodynamic flow rate U as ${\left(U-{\dot{L}}_v\right)}^3=U_{p0}^2{\dot{L}}_v$, (17), where

$$U_{p0}\simeq \frac{\kappa }{{\left(3\eta R_0\right)}^{3/2}}{\left(\frac{k_{\text{B}}T}{4P_w{v}_0}\right)}^{1/2}.$$ (18)

We estimate U_p0 as the following, taking P_w = 100 μm/s for polyunsaturated phosphatidylcholine lipid membrane (28), with R₀ = 10 μm and κ = 5 k_BT, U_P0 ≈ 2 cm/s. This value is much larger than U, which is in the range of 10–100 μm/s. Hence for U_p0 >> U, Eq. 17 becomes

$${\dot{L}}_v\approx \frac{U^3}{U_{P0}^2}\approx C_l{F}^3,$$ (19)

where C_l = (4v₀P_w)/[(2π)³κ²k_BT]. The solid lines in Fig. 4, A and B, show the adjustments to the data with Eq. 19 for bulk liposomes, giving C_l = 1.1 ± 0.6 × 10²⁷ N⁻³.s.m⁻¹. We obtain P_w = 4300 ± 2300 μm/s. This large value of permeability compared to the values reported for liposomes at rest (28) confirms that at high membrane tension, the membrane becomes more permeable.

Let us now address the viscous regime observed for cortex liposomes. Due to the corral effect, the dissipation mechanism is different than in bulk liposomes. For cortex liposomes, the lipid mobility is strongly reduced and the membrane tension does not equilibrate rapidly because the tube is pulled from a small patch or corral domain. In this case, ${\dot{L}}_v$ is controlled by a Marangoni flow from the low tension region of the corral domain toward the tense region at the tube neck. The dynamics of membrane tube extrusion as a function of binder density, ν, has been studied before in the case of red blood cells (14). The relationship between F_h and ${\dot{L}}_v$ is given by

$$F_h^3-F_0^2{F}_h={\left(2\pi \right)}^{3}2{\kappa }^2\nu {\eta }_e{\dot{L}}_v\text{log}R/r_t,$$ (20)

where η_e is the membrane surface viscosity. Previous measures of η_e for cells show a variation between 10⁻⁴ and 10⁻⁹ Pa.s.m (14, 30, 31, 32, 33). Adjusting the curves for cortex liposomes shown in Fig. 4 by ${\dot{L}}_v=C_m\left(F_h^3-F_0^2{F}_h\right)$, where C_m = [(2π)³2κ²νη_elogR/r_t]⁻¹, we obtain C_m = 1.3 ± 0.5 × 10²⁶ N⁻³.s.m⁻¹, giving νη_e = 1.9 ± 0.9 × 10¹⁰ Pa.s/m. To evaluate η_e, we first estimate the binder density ν, which is related to the distance between binding sites ξ by ν ∼ 1/ξ². If we consider that all Arp2/3-complex molecules saturate the VVCA sites, for a liposome of radius 10 μm, and Arp2/3 concentration of 0.45 μM, we find ξ ≈ 30 nm, giving ν ≈ 10¹⁵ m⁻² and η_e ≈ 10⁻⁵ Pa.s.m, consistent with the membrane viscosity estimated for cells. Therefore, our experiments using stripped-down systems of cell-size liposomes mimicking cells are able to reproduce a cell behavior.

To summarize, the viscous regime of bulk and cortex liposome tube pulling can be explained by two different mechanisms. In the case of bulk liposomes, the viscous regime is explained by a leakout of the internal liquid through the permeable membrane. On the other hand, for cortex liposomes, the tension increases locally, due to the corral domains giving rise to a flow of lipids (Marangoni effect) from the floppy part toward the tube (see in Fig. 4, C and D). A surprising feature is that both phenomena give the same scaling law: ${\dot{L}}_v\sim F_h^3$ (Eqs. 19 and 20), but numerical coefficients differ by a factor of 10: C_l = 1.1 ± 0.6 × 10²⁷ N⁻³.s.m⁻¹ and C_m = 1.3 ± 0.5 × 10²⁶ N⁻³.s.m⁻¹ (p < 10⁻⁷), therefore explaining a slower velocity of extrusion in the presence of an actin cortex.

Conclusions

In this article, we study the mechanics of liposomes when an artificial actin cortex is reconstructed on the inner layer liposome. Using a lipid tube extrusion technique based on hydrodynamic flow, we show that the tube dynamics for liposomes with a cortex is significantly different compared to liposomes containing a nonpolymerizing actin solution. According to our data at comparable forces, cortex liposomes deform much less and the tube extrusion velocity is much smaller. We propose that polymerization of actin on the inner leaflet of the liposome creates patches that limit the size of the available area for pulling a tube. These patches are associated to a reduced lipid mobility that explains differences in the dynamics of the tube extrusion. Recently, a similar effect of cortical actin on lipid diffusion has been put in evidence in fibroblast cells (22). The presence of actin at the membrane drastically changes the classical laws of membrane elasticity and viscous dissipation.

Author Contributions

K.G., F. B.-W., and C.S. designed research; K.G. performed research; J.M. designed, purified, and characterized proteins; L.-L.P. prepared the liposome fabrication method; K.G., F. B.-W., and C.S. analyzed data; and K.G., F.B.-W., and C.S. wrote the article.

Editor: Margaret Gardel.

Supporting Material

Movie S1. Tube Extrusion from a Bulk Liposome Using the Hydrodynamic Tube Extrusion Technique

The extrusion force is 6.5 pN. Scale bar = 10 μm.

Movie S2. Tube Extrusion from a Cortex Liposome

The extrusion force varies as the following: 15, 12, 16, 18, 20, 23, 28, and 30 pN, at times 0, 30, 65, 115, 165, 215, 265, and 315 s. Scale bar = 10 μm.