Inference of Super-exponential Human Population Growth via Efficient Computation of the Site Frequency Spectrum for Generalized Models

Abstract

The site frequency spectrum (SFS) and other genetic summary statistics are at the heart of many population genetic studies. Previous studies have shown that human populations have undergone a recent epoch of fast growth in effective population size. These studies assumed that growth is exponential, and the ensuing models leave an excess amount of extremely rare variants. This suggests that human populations might have experienced a recent growth with speed faster than exponential. Recent studies have introduced a generalized growth model where the growth speed can be faster or slower than exponential. However, only simulation approaches were available for obtaining summary statistics under such generalized models. In this study, we provide expressions to accurately and efficiently evaluate the SFS and other summary statistics under generalized models, which we further implement in a publicly available software. Investigating the power to infer deviation of growth from being exponential, we observed that adequate sample sizes facilitate accurate inference; e.g., a sample of 3000 individuals with the amount of data expected from exome sequencing allows observing and accurately estimating growth with speed deviating by ≥10% from that of exponential. Applying our inference framework to data from the NHLBI Exome Sequencing Project, we found that a model with a generalized growth epoch fits the observed SFS significantly better than the equivalent model with exponential growth (P-value $=3.85\times {10}^{-6}$). The estimated growth speed significantly deviates from exponential (P-value $\ll {10}^{-12}$), with the best-fit estimate being of growth speed 12% faster than exponential.

SUMMARY statistics of genetic variation play a vital role in population genetic studies, especially inference of demographic history. In particular, the site frequency spectrum (SFS) is a vital summary statistic of genetic data and is widely utilized by many demographic inference methods applied to humans and other organisms (Marth et al. 2004; Gutenkunst et al. 2009; Excoffier et al. 2013; Bhaskar et al. 2015; Liu and Fu 2015). Some other demographic inference methods are based on the sequential Markov coalescent and utilize the most recent common ancestor ($T_{\mathrm{MRCA}}$) and linkage disequilibrium patterns (Li and Durbin 2011; Harris and Nielsen 2013; MacLeod et al. 2013; Sheehan et al. 2013; Schiffels and Durbin 2014). As another example, several studies used the average pairwise difference between chromosomes (Hammer et al. 2008; Gottipati et al. 2011; Arbiza et al. 2014) and the SFS (Keinan et al. 2009) to study the relative effective population sizes between the human X chromosome and the autosomes. The wide application of such genetic summary statistics stresses the need for their fast and accurate computation under any model of demographic history, instead of their estimations via simulations or approximations (e.g., Hudson 2002; Gutenkunst et al. 2009).

Several recent demographic inference studies showed evidence that human populations have undergone a recent epoch of fast growth in effective population size (Gutenkunst et al. 2009; Coventry et al. 2010; Gravel et al. 2011; Nelson et al. 2012; Tennessen et al. 2012; Gazave et al. 2014). However, the above studies assumed that the growth is exponential. The observation of a huge amount of extremely rare, previously unknown variants in several sequencing studies with large sample sizes (Nelson et al. 2012; Tennessen et al. 2012; Fu et al. 2013) and the recent explosive growth in census population size suggests that the human population might have experienced a recent super-expononential growth, i.e., growth with speed faster than exponential (Coventry et al. 2010; Keinan and Clark 2012; Reppell et al. 2012, 2014). Hence, recent studies presented a new generalized growth model that extends the previous exponential growth model by allowing the growth speed to be exponential or faster/slower than exponential (Reppell et al. 2012, 2014). Modeling the recent growth by this richer family of models holds the promise of a better fit to human genetic data and can also be applicable to other organisms that experienced growth. However, only simulation approaches are currently available for evaluating such a generalized growth demographic model (Reppell et al. 2012), which makes inference of demographic history computational intractable.

In this study, we first provide a set of explicit expressions for the computation of five summary statistics under a model of any number of epochs of generalized growth or decline: (1) the time to the most recent common ancestor ($T_{\mathrm{MRCA}}$); (2) the total number of segregating sites (S); (3) the SFS; (4) the average pairwise difference between chromosomes per site (π); and (5) the burden of private mutations (α), a summary statistic that has been recently introduced as sensitive to recent growth (Keinan and Clark 2012; Gao and Keinan 2014). We also introduce a new software package, Efficient computation of Generalized models’ Genetic summary Statistics (EGGS), which implements these expressions and facilitates fast and accurate generation of these summary statistics. We show that the numerically computed summary statistics match well with simulation results and facilitate computation that is orders of magnitude faster than simulations. By performing demographic inference on the SFS generated from simulated sequences, we then explore how many samples are needed for recovering parameters of a recent generalized growth epoch. Finally, we apply the software to investigate the nature of the recent growth in humans by inferring demographic models using the SFS of synonymous variants of 4300 European individuals from the National Heart, Lung, and Blood Institute (NHLBI) Exome Sequencing Project (Tennessen et al. 2012; Fu et al. 2013).

Materials and Methods

Generalized demographic models

A demographic model $N\left(T\right)$ describes the changes of effective population size N against time T. We consider time, measured in generations, as starting from 0 at present and increasing backward in time. Furthermore, we consider the families of demographic models that are constituted by any number of epochs of generalized growth or decline, along the lines of Bhaskar and Song (2014). More formally, there exists a minimal positive integer L such that the demographic history of a population can be split into a model with $L+1$ epochs that are split by L ordered different time points $T_1,T_2,\mathrm{\dots },T_L$ ($T_0=0<T_1<T_2<\dots <T_L<T_{L+1}=\mathrm{\infty }$), with the k^th epoch starting from $T_{k-1}$ and lasting through $T_k$ (thus the last epoch starts at time $T_L$ and continues into indefinite past, $T_{L+1}=\mathrm{\infty }$). Such a history is considered as a generalized model if the population size in each epoch $N\left(T_{k-1}\le T<T_k\right)$ can be described by the following differential equation regarding time T (Reppell et al. 2012, 2014),

$$\frac{dN}{dT}=-r_k{N}^{b_k},$$ (1)

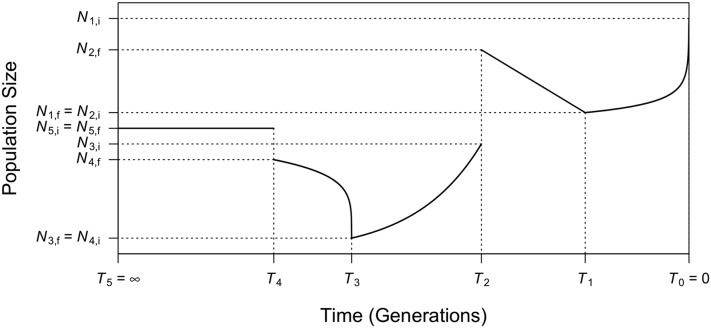
where $k=1,2,\mathrm{\dots },L+1.$ Each epoch can hence capture a variety of changing patterns in effective population size. Specifically, if $r_k=0$, this epoch is of constant population size. When $r_k\ne 0$, $b_k$ controls the growth or decline speed of this epoch: (1) if $b_k=1$, the epoch is of exponential growth ($r_k>0$) or decline ($r_k<0$) with rate $r_k;$ (2) if $b_k>1$, the epoch is of faster-than-exponential (super-exponential) growth ($r_k>0$) or decline ($r_k<0$); (3) if $b_k<1$, the epoch is of slower-than-exponential (sub-exponential) growth ($r_k>0$) or decline ($r_k<0$). Linear growth or decline is also a special case of generalized models when $b_k=0.$ An illustration of a generalized model with five epochs is provided in Figure 1, with more detailed explanation and illustrations in Supporting Information, File S1 and Figure S1.

Figure 1.

Illustration of an example of a generalized demographic model as introduced in the first section of Materials and Methods. This model consists of five epochs (starting from the present on the right): (1) faster-than-exponential ($b>1$) growth (forward in time) from $N_{1,\mathrm{f}}$ to $N_{1,\mathrm{i}}$ between $T_0=0$ and $T_1;$ (2) linear decline (a special case of generalized decline when $b=0$) from $N_{2,\mathrm{f}}$ to $N_{2,\mathrm{i}}$ between $T_1$ and $T_2;$ (3) exponential growth (a special case of generalized growth when $b=1$) from $N_{3,\mathrm{f}}$ to $N_{3,\mathrm{i}}$ between $T_2$ and $T_3;$ (4) slower-than-exponential ($b<1$) decline from $N_{4,\mathrm{f}}$ to $N_{4,\mathrm{i}}$ between $T_3$ and $T_4;$ and (5) constant population size (a special case of generalized growth when $r=0$) at $N_{5,\mathrm{i}}=N_{5,\mathrm{f}}$ starting from $T_4$, which lasts indefinitely backward in time ($T_5=\mathrm{\infty }$). The ending population size of the previous epoch is not necessarily the beginning population size of the next epoch (e.g., $N_{2,\mathrm{f}}\ne N_{3,\mathrm{i}}$, $N_{4,\mathrm{f}}\ne N_{5,\mathrm{i}}$), corresponding to an instantaneous population size change at that time.

The solution to Equation 1 is

$$N\left(T\right)=\{\begin{array}{ll}{\left(N_{k,\mathrm{i}}^{1-b_k}-r_k\left(T-T_{k-1}\right)\left(1-b_k\right)\right)}^{\frac{1}{1-b_k}},\hfill & b_k\ne 1\hfill \\ N_{k,\mathrm{i}}{e}^{-r_k\left(T-T_{k-1}\right)},\hfill & b_k=1\hfill \end{array}$$ (2)

(Reppell et al. 2012, 2014), where $N_{k,\mathrm{i}}$ is the initial population size of the k^th epoch. Each epoch k is defined by four parameters: the starting population size $N_{k,\mathrm{i}}$, the ending population size $N_{k,\mathrm{f}}$, the duration of the epoch $\left(T_k-T_{k-1}\right)$, and the growth speed parameter $b_k$. The growth rate parameter $r_k$ is an immediate function of these parameters, $r_k=r_k\left(N_{k,\mathrm{i}},N_{k,\mathrm{f}},b_k,T_k-T_{k-1}\right)$, and hence does not need to be provided as an independent variable in defining the changes in effective population size during an epoch. Note that $N_{k+1,\mathrm{i}}$, the starting population size of the ${\left(k+1\right)}^{\mathrm{th}}$ epoch, is not necessarily the same as $N_{k,\mathrm{f}}$, the ending population size of the k^th epoch. Specifically, if $N_{k+1,\mathrm{i}}\ne N_{k,\mathrm{f}}$, there is an instantaneous change in population size at time $T_k$.

Explicit expressions for summary statistics of demographic models under arbitrary population size functions

In this section, we briefly summarize the main results from previous studies that are used to evaluate the expected value of the summary statistics. Under Kingman’s standard coalescent (Kingman 1982a,b), given a demographic model $N\left(T\right)$, the expected time to the most recent common ancestor $\mathbb{E}\left[T_{\mathrm{MRCA}}^p\right]$ can be calculated by

$$\mathbb{E}\left[T_{\mathrm{MRCA}}^p\right]={\displaystyle \sum _{j=2}^p{A}_j^p{\psi }_j}$$ (3)

(Polanski and Kimmel 2003), where the superscript p is the number of chromosomes (i.e., twice the sample size for diploids), ${\psi }_j$ is the expected time to the first coalescent event when there are j chromosomes at present, and $A_j^p$ are constants (Tavare 1984; Takahata and Nei 1985; Polanski et al. 2003) provided in File S1. Without loss of generality, we consider the case of diploid individuals, where there are $2N\left(T\right)$ chromosomes at any generation T, and use the notation $\mathcal{N}\left(T\right)=2N\left(T\right)$. Then ${\psi }_j$ is expressed by the equation

$${\psi }_j={\displaystyle {\int }_0^{\mathrm{\infty }}T\frac{\left(\begin{array}{c}j\\ 2\end{array}\right)}{\mathcal{N}\left(T\right)}{e}^{-{\displaystyle {\int }_0^T\left(\left(\begin{array}{c}j\\ 2\end{array}\right)d\sigma /\mathcal{N}\left(\sigma \right)\right)}}dT}={\displaystyle {\int }_0^{\mathrm{\infty }}{e}^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T\right)}dT},$$ (4)

where $\mathrm{\Lambda }\left(T\right)={\displaystyle {\int }_0^T\left(d\sigma /\mathcal{N}\left(\sigma \right)\right)}$.

The expected full normalized SFS $\mathbb{E}\left[{\xi }^p\right]=\left(\mathbb{E}\left[{\xi }_1^p\right],\mathbb{E}\left[{\xi }_2^p\right],\mathrm{\dots },\mathbb{E}\left[{\xi }_{p-1}^p\right]\right)$ can be computed by the following set of equations (Polanski et al. 2003),

$$\mathbb{E}\left[{\xi }_i^p\right]=\frac{\mathbb{E}\left[{\ell }_i^p\right]}{\mathbb{E}\left[{\mathrm{ℒ}}^p\right]};\mathbb{E}\left[{\ell }_i^p\right]={\displaystyle \sum _{j=2}^p{W}_{i,j}^p{\psi }_j};\mathbb{E}\left[{\mathrm{ℒ}}^p\right]={\displaystyle \sum _{j=2}^p{V}_j^p{\psi }_j},$$ (5)

where ${\ell }_i^p$ is the length of branches in the genealogy that have i descendants ($i=1,2,\mathrm{\dots },p-1$) and ${\mathrm{ℒ}}^p={\displaystyle {\sum }_{i=1}^{p-1}{\ell }_i^p}$ is the total length of all branches in the coalescent tree. The quantities $V_j^p$ and $W_{i,j}^p$ are constants (Polanski et al. 2003), which we provide in File S1.

Naturally, the expected number of segregating sites is given by

$$\mathbb{E}\left[S\right]={\mu }_{0}L\mathbb{E}\left[{\mathrm{ℒ}}^p\right],$$ (6)

where ${\mu }_0$ is the mutation rate per site per generation and L is the length of the locus under consideration. The average pairwise difference between chromosomes per site $\mathbb{E}\left[\pi \right]$ can be calculated by

$$\mathbb{E}\left[\pi \right]=2{\mu }_0\mathbb{E}\left[T_{\mathrm{MRCA}}^{p=2}\right].$$ (7)

The expected burden of private mutations α at a diploid sample size of $\left(p/2-1\right)$, defined as the proportion of heterozygous sites in a new diploid individual that are homozygous in the previous $\left(p/2-1\right)$ individuals, $\mathbb{E}\left[{\alpha }_{p/2-1}\right]$ can be computed by

$$\mathbb{E}\left[{\alpha }_{p/2-1}\right]=\frac{2}{p\left[1+\delta \left(1,p-1\right)\right]}\frac{\mathbb{E}\left[{\ell }_1^p\right]+\mathbb{E}\left[{\ell }_{p-1}^p\right]}{\mathbb{E}\left[{\ell }_1^2\right]}$$ (8)

(Gao and Keinan 2014), where $\delta \left(\cdot ,\cdot \right)$ is Kronecker delta function.

The detailed description of the five summary statistics mentioned above is included in File S1.

Evaluation of the expected time to the first coalescent event under generalized models

The core of evaluating the summary statistics lies in finding feasible and numerically stable functions for calculating ${\psi }_j$, the expected time to the first coalescent event when there are j chromosomes at present. Previous studies give explicit expressions of ${\psi }_j$ for a demographic model constructed by exponential and constant-size epochs (Polanski et al. 2003; Bhaskar et al. 2015). In this study, we give a comprehensive set of formulas for ${\psi }_j$ under generalized models introduced above. Define ${\phi }_j^k:={\displaystyle {\int }_{T_{k-1}}^{T_k}{e}^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T\right)}}dT;$ then ${\psi }_j={\displaystyle {\sum }_{k=1}^{L+1}{\phi }_j^k}$, where $\left(L+1\right)$ is the total number of epochs. The quantity ${\phi }_j^k$ can be computed by the following set of equations:

1. If $r_k=0$ or $b_k=0,r_k\ne 0$,

   $${\phi }_j^k=\{\begin{array}{l}\begin{array}{l}\frac{1}{\left(\begin{array}{c}j\\ 2\end{array}\right)}\left[e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_k\right)}{\mathcal{N}}_{k,\mathrm{f}}\log {\mathcal{N}}_{k,\mathrm{f}}-e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_{k-1}\right)}{\mathcal{N}}_{k,\mathrm{i}}\log {\mathcal{N}}_{k,\mathrm{i}}\right],\\ r_k+\left(\begin{array}{c}j\\ 2\end{array}\right)=0\end{array}\hfill \\ \begin{array}{l}\frac{1}{r_k+\left(\begin{array}{c}j\\ 2\end{array}\right)}\left[e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_{k-1}\right)}{\mathcal{N}}_{k,\mathrm{i}}-e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_k\right)}{\mathcal{N}}_{k,\mathrm{f}}\right],\\ r_k+\left(\begin{array}{c}j\\ 2\end{array}\right)\ne 0.\end{array}\hfill \end{array}$$ (9)
2. If $b_k>0,r_k>0$ or $b_k=1,r_k<0$,

   $$\begin{array}{l}{\phi }_j^k=\frac{1}{\left(\begin{array}{c}j\\ 2\end{array}\right)}[{\mathcal{N}}_{k,\mathrm{i}}\mathcal{U}\left(2-\frac{1}{b_k},\frac{\left(\begin{array}{c}j\\ 2\end{array}\right)}{b_k{r}_k}{\mathcal{N}}_{k,\mathrm{i}}^{-b_k}\right)e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_{k-1}\right)}\\ -{\mathcal{N}}_{k,\mathrm{f}}\mathcal{U}\left(2-\frac{1}{b_k},\frac{\left(\begin{array}{c}j\\ 2\end{array}\right)}{b_k{r}_k}{\mathcal{N}}_{k,\mathrm{f}}^{-b_k}\right)e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_k\right)}].\end{array}$$ (10)
3. If $b_k<0,r_k>0$,

   $$\begin{array}{l}{\phi }_j^k=\frac{1}{\left(\begin{array}{c}j\\ 2\end{array}\right)}[{\mathcal{N}}_{k,\mathrm{f}}\mathrm{ℳ}\left(2-\frac{1}{b_k},\frac{\left(\begin{array}{c}j\\ 2\end{array}\right)}{b_k{r}_k}{\mathcal{N}}_{k,\mathrm{f}}^{-b_k}\right)e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_k\right)}\\ -{\mathcal{N}}_{k,\mathrm{i}}\mathrm{ℳ}\left(2-\frac{1}{b_k},\frac{\left(\begin{array}{c}j\\ 2\end{array}\right)}{b_k{r}_k}{\mathcal{N}}_{k,\mathrm{i}}^{-b_k}\right)e^{-\left(\begin{array}{c}j\\ 2\end{array}\right)\mathrm{\Lambda }\left(T_{k-1}\right)}].\end{array}$$ (11)

The expressions of function $\Lambda \left(T\right)$ are given in File S1. The function $U\left(b,x\right):=xU\left(1,b,x\right)=x{\displaystyle {\int }_0^{\mathrm{\infty }}{e}^{-xt}{\left(1+t\right)}^{b-2}}dt$, where $\mathcal{U}\left(a,b,x\right)$ is the confluent hypergeometric function of the second kind (Gradshteĭn et al. 2007). The function $M\left(b,x\right):=\left(x/\left(b-1\right)\right)M\left(1,b,x\right)=x{\displaystyle {\int }_0^1{e}^{xt}{\left(1-t\right)}^{b-2}}dt$, where $M\left(a,b,x\right)$ is the confluent hypergeometric function of the first kind (Gradshteĭn et al. 2007). The exponential growth or decline then becomes a special case of $\mathcal{U}\left(b,x\right)$ when $b=1,x\ne 0$,

$$\mathcal{U}\left(1,x\right)=x{e}^x{\displaystyle {\int }_1^{\mathrm{\infty }}\frac{e^{-t}}{t}dt}=x{e}^x{E}_1\left(x\right),$$ (12)

where $E_1\left(x\right)$ is the exponential integral (Gradshteĭn et al. 2007), which has been shown by previous studies (Polanski et al. 2003; Bhaskar et al. 2015). We could not find feasible and numerically stable closed-form formulas for ${\phi }_j^k$ when the population size decreases forward in time in a manner that is not linear or exponential (i.e., $r_k<0$ and $b_k\notin \left\{0,1\right\}$). In these scenarios, we used Gauss–Legendre quadrature (Kahaner et al. 1988) for efficient numerical evaluation of relevant functions (see File S1 for detailed description).

Software implementation

The above expressions are implemented in a software package, EGGS. The source code and compiled programs for Linux and Mac OS platforms are publicly available from our Web site (http://keinanlab.cb.bscb.cornell.edu). Source code was written in C++, with no external libraries needed for compilation. Additional information of implementation is included in File S1 and in the manual that accompanies the software online.

Demographic models assumed in this study

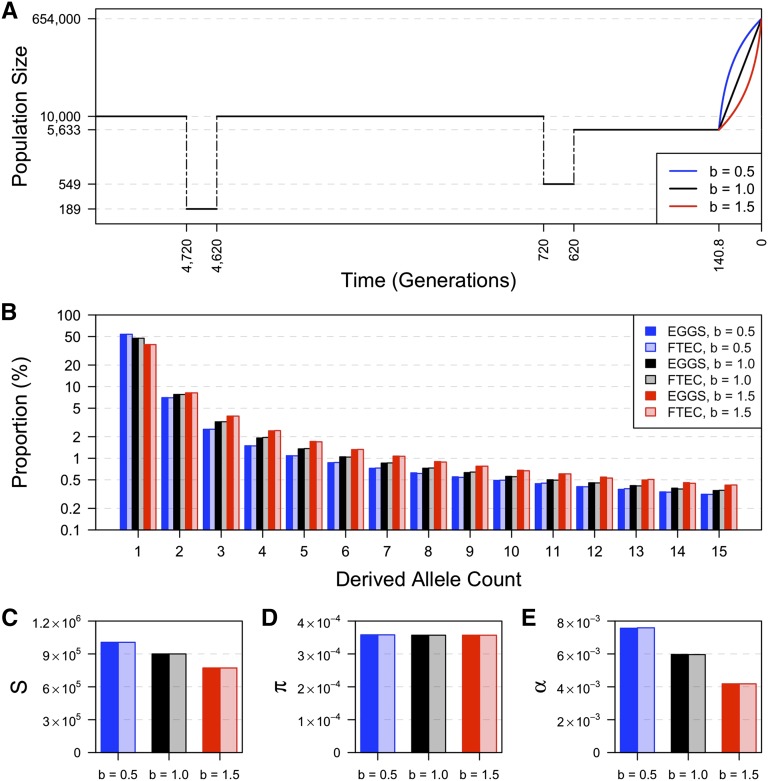
The demographic models used in this study are based on the inferred European history presented by Gazave et al. (2014) (Figure 2, in black), which contains two bottlenecks (Keinan et al. 2007) and a recent exponential growth epoch. Specifically, the Gazave et al. (2014) model inferred that the European population had a constant effective population size of 10,000 (diploid) individuals before 4720 generations ago and went through the ancient bottleneck between 4720 and 4620 generations ago with a population size of 189. The population size then recovered to 10,000 diploids until 720 generations ago, at which time the recent bottleneck started with a size of 549. At 620 generations ago, the population size recovered to 5633 individuals. The recent growth epoch started 140.8 generations ago and led to a population size of 654,000 at present. The parameters of the original recent growth epoch were varied to incorporate generalized growth effects.

Figure 2.

Comparison of four summary statistics estimated by FTEC simulation and computed by EGGS. (A) Demonstration of the demographic models considered for evaluating the accuracy of our calculations as implemented in EGGS (first section of Results). This two-bottleneck model has the same population size and time throughout history as in the inferred European history in Gazave et al. (2014), with the exception that we varied the growth speed parameter of the recent growth epoch to be $b=0.5$ (sub-exponential, blue), $b=1.0$ (exponential as in Gazave et al. 2014, black), and $b=1.5$ (super-exponential, red). The y-axis shows effective population size of diploid individuals on log scale. (B–E) The comparison of the first 15 entries of the SFS (B), the total number of segregating sites (S) across all 200,000 loci (each 1000 bp long) (C), the expected pairwise difference between chromosomes per base pair (D), and the burden of private mutations (α) as the percentage of heterozygous variants in one individual that are monomorphic in the rest of the sample of 999 individuals (E) computed numerically in EGGS (dark-colored bars) and simulated by FTEC (light-colored bars) for the demographic models shown in A: blue, $b=0.5;$ black, $b=1.0;$ red, $b=1.5;$ with a sample size of 1000 individuals (2000 chromosomes). The y-axis in B is on a log scale.

In addition to using the model mentioned above, we also applied an alternative model of ancient European history for inference. The model was first presented in Gravel et al. (2011) and later used in Tennessen et al. (2012). This model inferred that the European population had an ancient effective population size of 7300 diploid individuals until 6167 generations ago, when the population size expanded to 14,474 individuals. The first bottleneck took place 2125 generations ago, with the population size reducing to 1861 individuals. This first bottleneck lasted until 958 generations ago, at which time a second bottleneck took place with a decreased population size of 1032. We assumed 24 years per generation (Scally and Durbin 2012) to translate the year-based time presented in the original model. For compatibility with the Gazave et al. (2014) model, we considered that the population size had an instantaneous recovery after the second bottleneck lasted for 100 generations, instead of gradual recovery (Gazave et al. 2014). Figure S8 shows the schematic representation of the Gravel et al. (2011) model.

Demographic inference framework based on the site frequency spectrum

Demographic inference in this study was based on the observed allele frequency counts from the simulated or real data set. To determine the fitness of a model $N\left(T\right)$ to the observed data, we calculated the composite log likelihood by

$$\mathbb{L}\left[N\right]=\log \mathbb{E}\left[\xi |N\right]=C\cdot \mathbb{E}\left[\xi |N\right],$$ (13)

where C is a vector of the observed folded allele frequency counts and $\mathbb{E}\left[\xi |N\right]$ is the computed folded SFS under demographic model $N\left(T\right)$. More detailed description can be found in File S1.

To search for the maximum-likelihood point over the parameter space, we applied the ECM (Expectation/Conditional Maximization) method (Meng and Rubin 1993), which was previously used in the demographic inference study by Excoffier et al. (2013). One hundred ECM cycles were performed for each run of inference. We obtained 95% confidence intervals of parameter estimates via block bootstrapping of the data 200 times. Specifically, if the original data contained l loci, we randomly chose l loci from the original data with replacement in each bootstrap (see File S1 for details).

Processing of NHLBI Exome Sequencing Project data for demographic history inference

The NHLBI Exome Sequencing Project (ESP) data (Tennessen et al. 2012; Fu et al. 2013) contain deep sequencing of 4300 individuals of European ancestry. An important feature of these data is the high level of sequencing coverage, which allows the capture of very rare variants accurately. These variants constitute the part of the SFS that is most enriched for information on recent population growth (Keinan and Clark 2012; Tennessen et al. 2012; Gao and Keinan 2014). To reduce the effect of selection as much as possible while keeping a sufficient amount of data, we chose to use the SFS calculated from synonymous single-nucleotide variants (SNVs) only, as previously performed by Tennessen et al. (2012). To further improve the quality of the data, we filtered SNVs with average read depth ≤20 or with successful genotype counts <7740 (90%) and subsampled the remaining 233,134 SNVs to 7740 alleles, which is equivalent to 3870 diploid individuals (File S1).

Data availability

The NHLBI Exome Sequencing Project (ESP) data used in this study is publicly available at http://evs.gs.washington.edu/EVS/.

Results

Comparison with simulated results by FTEC

To validate that the expressions provided in Materials and Methods can correctly compute the summary statistics under generalized growth models, we compared the summary statistics calculated by our software EGGS to those simulated by the software FTEC (a coalescent simulator for modeling faster than exponential growth by Reppell et al. 2012) under the demographic models shown in Figure 2A. This model is the inferred European history in Gazave et al. (2014), except that we varied the growth speed parameter b (Equation 1), which corresponds to 1 in the original model (exponential growth), to also be 0.5 (corresponding to sub-exponential growth) and 1.5 (corresponding to super-exponential growth). The sample size is fixed at 1000 diploid individuals (2000 chromosomes). For FTEC simulation, we used a mutation rate of $1.2\times {10}^{-8}$ per base pair per generation (e.g., Kong et al. 2012) and simulated 200,000 independent loci, each of 1000 bp.

The comparison of the SFS, S (across all 200,000 loci), π, and α numerically computed by EGGS to those simulated by FTEC is shown in Figure 2, B–E. For each demographic model illustrated in Figure 2A, the values for all summary statistics from the numerical computation by EGGS are practically identical to those from the simulation results by FTEC. However, our software EGGS exhibits a huge speed improvement over FTEC. For each model considered in Figure 2A, EGGS takes <1 sec to generate the results, while it takes ∼5 hr for FTEC to simulate the sequences, due to the large number of independent loci required for accurate estimation (performed in the Ubuntu system with an Intel Xeon CPU at 2.67 GHz). For instance, when 2000 independent loci are simulated, which still takes ∼3 min, the summary statistics deviate considerably from the accurate results (Figure S2 and Table S1). Furthermore, our software works well over a wide range of values of the growth parameter b, even when $b=0$ (corresponding to linear growth or decline) or $b<0$ (Figure S3), conditions that are not handled by FTEC. We note, however, that as a simulation program FTEC provides the full sequences as output and can have a wider range of applications than facilitated by the SFS and other summary statistics that EGGS calculates.

Evaluating inference of generalized growth based on the site frequency spectrum

We next set out to test the accuracy (as a function of sample size) of inferring parameters in models with generalized growth from the SFS. Bhaskar and Song (2014) showed that in theory, an underlying generalized growth demographic model can be uniquely identified by the ideal, perfect expected SFS with a very small sample size generated from that model (34 haploid sequences for the models shown in Figure 2A). However, the SFS is estimated in practice from a limited amount of data from each individual (even in the case of whole-genome sequencing) and, as a result, the estimated SFS will fluctuate around the expected values, which limits its accuracy for inference (Terhorst and Song 2015). We aim to test such inference in practice and determine the power of generalized growth detection and the sample size needed for accurately recovering the growth speed parameter as well as other parameters of the demographic model. For it to be comparable with many practical applications, we considered sequence length that is about equivalent to that obtained from whole-exome sequencing (File S1).

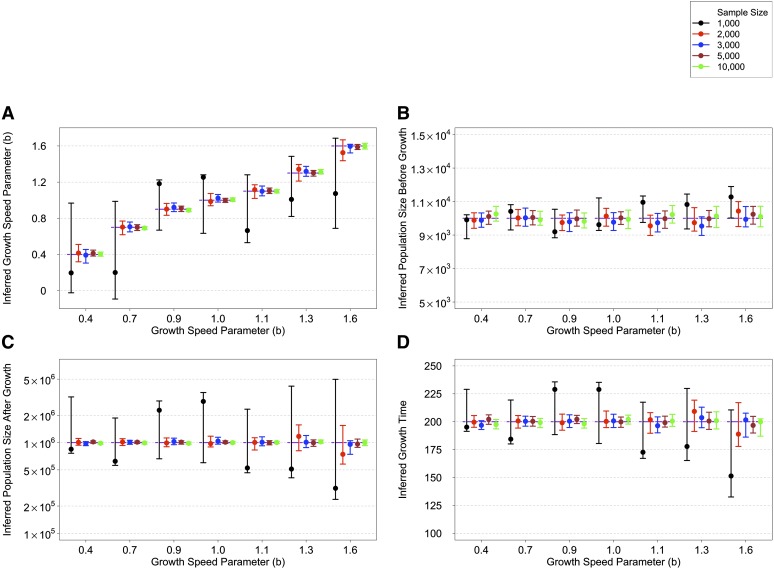
We performed inference on the SFS calculated from simulated sequences generated by FTEC. We simulated a demographic model with the same initial epochs as the model illustrated in Figure 2A. Starting 620 generations ago, the simulated model includes a constant population size of 10,000 until 200 generations ago, when the population starts a generalized growth epoch until the present. The generalized growth epoch starts with a population size of 10,000 that grows to an extant effective population size of 1 million individuals, with the growth speed parameter b taking each of the following values: 0.4, 0.7, 0.9, 1.0, 1.1, 1.3, and 1.6. We chose these values to represent a range of super-exponential and sub-exponential growth, with emphasis on values around the exponential rate ($b=1.0$) to test the detection power of generalized growth when the growth speed deviates slightly from exponential. We varied the sample size (number of diploid individuals sampled at present) to be 1000, 2000, 3000, 5000, and 10,000 (File S1). The first 15 entries of the site frequency spectra for these simulated scenarios are shown in Figure S4. From each set of simulations, we then inferred four parameters of the recent growth epoch, which can uniquely determine the epoch: (1) the growth speed parameter b; (2) the initial population size before growth, $N_{\mathrm{f}};$ (3) the ending population size after growth, $N_{\mathrm{i}};$ and (4) the onset time of growth T, which is equivalent to the growth duration since the simulated epoch ends at present.

As sample size increases, the accuracy of the point estimates generally improves and the confidence interval narrows (Figure 3). Specifically, when the SFS of only 1000 diploids is used for inference, the inference performs poorly for all parameters, exhibiting large confidence intervals (Figure 3). However, the confidence interval always includes the true simulated value. A sample size of 2000 already exhibits acceptable performance except when the growth speed becomes large ($b=1.3$ and 1.6). Larger sample sizes of 5000 and 10,000 are sufficient for inferring all parameters with very tight confidence intervals. For such sample sizes, the inference even significantly distinguishes between growth speeds ($b=0.9$ and $b=1.1$) that are close to exponential ($b=1.0$) from that of an exponential, thereby concluding that a sub-exponential (0.9) or super-exponential (1.1) growth has taken place. These observations suggest that a sample size of at least 3000 diploid individuals might be needed for inferring the parameters associated with the simulated recent generalized growth epoch, which is motivated by previous models of European demographic history. It remains to be explored how accurate the estimates are, and how their accuracy improves with sample size, across a more diverse set of models.

Figure 3.

Inference results on simulated data with a recent generalized growth epoch. The model parameters are as follows: Growth starts 200 generations before the present from an effective population size of 10,000 and ends with an effective population size of 1 million at present. The growth speed parameter b takes the following values in different simulations: 0.4, 0.7, 0.9, 1.0, 1.1, 1.3, and 1.6. Inference of these four parameters is based on the SFS estimated from a sample of individuals of one of five sizes (black, 1000; red, 2000; blue, 3000; brown, 5000; and green, 10,000). The point estimates with 95% confidence interval for these parameters are grouped by the growth speed parameter b (x-axis). The thick, dashed lines show the true values of the simulated model. The results are shown in the following order: (A) the inferred growth speed parameter, (B) the inferred population size before growth, (C) the inferred population size after growth, and (D) the inferred growth start time. The y-axis in C is on a log scale.

European demographic history inference

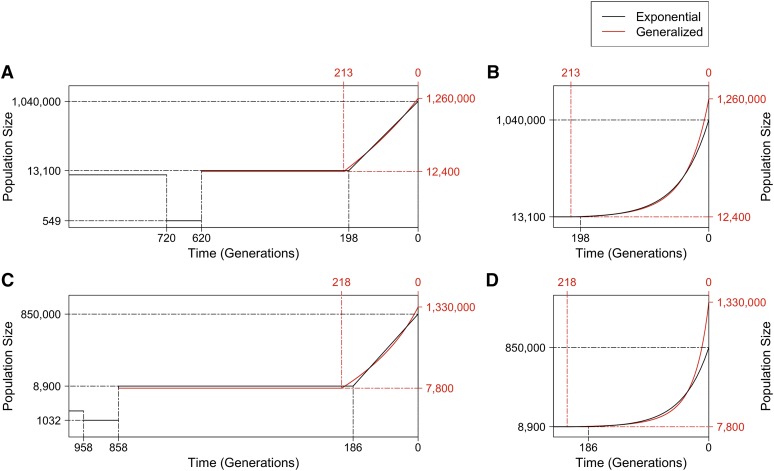
We next performed demographic inference on NHLBI ESP data (Tennessen et al. 2012; Fu et al. 2013). We applied our inference framework to these data while considering and comparing two models. Both models assume the ancient epochs before 620 generations ago to be the same as those in the Gazave et al. (2014) model illustrated in Figure 2A. We inferred the parameters only for the most recent epoch, which is of generalized growth in one model while limited to exponential growth in the other. The parameters for inference are as follows: for both models, (1) population size before growth ($N_{\mathrm{f}}$); (2) population size after growth ($N_{\mathrm{i}}$); and (3) growth onset time (T), which is equivalent to the duration of growth; and only for the generalized growth model (4) the growth speed parameter (b), which is fixed at $b=1$ for the exponential growth model. The point estimates and 95% confidence intervals are shown in Table 1 and the best-fit demographic models are illustrated in Figure 4, A and B (see also Figure S5, Figure S6 and Figure S7).

Table 1. Demographic inference results using ESP data for a model with a recent epoch of exponential growth and a model with a recent epoch of generalized growth.

Ancient history	Growth model	$N_{\mathrm{f}}\left({10}^4\right)$	$N_{\mathrm{i}}\left({10}^6\right)$	T	b
Gazave model	Exponential	1.31 (1.26–1.36)	1.04 (1.00–1.07)	198 (195–202)	NA
	Generalized	1.24 (1.18–1.30)	1.26 (1.16–1.37)	213 (206–220)	1.12 (1.07–1.15)
Gravel model	Exponential	0.89 (0.86–0.93)	0.85 (0.82–0.88)	186 (182–190)	NA
	Generalized	0.78 (0.74–0.83)	1.33 (1.22–1.46)	218 (211–228)	1.22 (1.18–1.26)

Shown are point estimates and 95% confident intervals (in parentheses) for the following parameters of the inferred recent growth epoch when the ancient history was assumed to be the same as that in the Gazave et al. (2014) model and the Gravel et al. (2011) model: population size before growth ($N_{\mathrm{f}}$); population size after growth ($N_{\mathrm{i}}$); time growth started in generations (T); and the growth speed parameter (b), which is fixed at $b=1$ in the exponential growth case.

Figure 4.

Demographic inference results based on ESP data. (A) Illustration of the effective population size (y-axis, on a log scale) over time for the best-fit models inferred based on ESP data, assuming the ancient history is the same as that in Gazave et al. (2014). Two models are shown: one restricted to recent growth being exponential (black) and one with a generalized recent growth epoch (red). Before 620 generations ago, the model was not inferred and all parameters were set to be the same as those shown in Figure 2A. Solid lines show the effective population size over time for each of the inferred models, with dashed lines indicating estimated parameter values on the x-axis or the y-axis. Only the most recent 1000 generations are shown to emphasize the difference between the two models. (B) A zoom-in to the most recent 240 generations of the inferred models in A to emphasize the acceleration pattern of the generalized growth model, with the y-axis on a linear scale. (C-D) Similar to A-B, except that the best-fit models presented are based on the assumption that the ancient history before 858 generations ago is fixed to that in Gravel et al. (2011) (see Figure S8).

Although the Gazave et al. (2014) model assumed a different ancient history before the recent growth epoch from that assumed in Tennessen et al. (2012), using ESP data and assuming exponential growth, the inferred growth epoch is generally consistent with that obtained in the latter study (Figure 4, A and B, and Table 1). Our study infers that recent growth started 198 (95% C.I.: 195–202) generations ago with an effective population size of ∼13,100 (12,600–13,600) and continued at a rate of 2.2% (2.15–2.26%) per generation (Table 1), while Tennessen et al. (2012) estimated that recent growth had an initial population size of ∼9500 individuals, a duration of 204 generations, and a growth rate of 2.0% per generation.

The inferred generalized growth model fits the data significantly better than that with exponential growth (P-value $=3.85\times {10}^{-6}$ by ${\chi }^2$ likelihood-ratio test with 1 d.f.). It estimates that growth started 213 (206–220) generations ago from an effective population size of 12,400 (11,800–13,000), both values consistent with those estimated in the exponential growth model. The extant effective population size following growth is estimated to be 1.26 (1.16–1.37) million. The inferred growth speed parameter $b=1.12$ (1.07–1.15) is significantly larger than the exponential speed of $b=1$ (P-value $\ll {10}^{-12}$, using a one-tailed z-test), which is the main difference between the two models. $b=1.12$ implies a growth rate acceleration pattern (File S1) that is super-exponential at 12% faster than exponential through the epoch (Figure 4): the super-exponential growth is relatively slow around the onset time, and it keeps accelerating as time approaches the present.

To test the sensitivity of the model to the assumption of ancient European history, we considered an alternate model of ancient history. We fixed the history before 858 generation ago to be that inferred by Gravel et al. (2011) for Europeans (Materials and Methods). We repeated inference of the same parameters, using the same ESP data. As above, the inferred parameters for exponential growth are similar to those obtained in Tennessen et al. (2012) that were based on the model of Gravel et al. (2011) (Table 1). However, the SFS from this model fits the data worse than that from the exponential model based on the ancient history of the Gazave et al. (2014) model (P-value $=1.59\times {10}^{-6}$ from ${\chi }^2$ goodness-of-fit test between the exponential Gravel model and ESP data; P-value = 0.97 for the corresponding exponential Gazave model; see File S1 and Table S3). By applying a generalized growth epoch to the Gravel et al. (2011) model, the inferred parameters are generally in line with those from the generalized model based on Gazave et al. (2014), although some differences exist (Table 1), indicating that the assumption of ancient history can affect the inference of recent growth to some extent. More importantly, the generalized Gravel model fits the data almost equally well as the generalized Gazave model, which is significantly better than the exponential model (P-value $\ll {10}^{-12}$ by ${\chi }^2$ likelihood-ratio test; also see Table S3). As with the generalized Gazave model, the inferred growth speed parameter from the generalized Gravel model, $b=1.22$ (1.18–1.26), is also significantly larger than the exponential speed $b=1$ (P-value $\ll {10}^{-12}$, using a one-tailed z-test; Figure 4, C and D).

Motivated by these results, we considered a third model with two recent exponential growth epochs, which still assumes the ancient epochs before 620 generations ago to be the same as those in the Gazave et al. (2014) model illustrated in Figure 2A. Five parameters were inferred (Table S2), with the first phase of growth estimated to start 219 (95–334) generations ago with a population size of 12,200 (11,700–13,200). This phase of growth lasts until 135 (25–157) generations ago and leads to a population size of 47,100 (30,200–540,900). The population size after the recent phase of growth is 1.12 (1.07–2.09) million. This model provides a significantly better fit than the model with a single exponential growth (P-value $=5.55\times {10}^{-6}$ by ${\chi }^2$ likelihood-ratio test with 2 d.f.), but is a worse model than the generalized growth model (based on the Bayesian information criterion, $\mathrm{BI}{\mathrm{C}}_{\text{two-epoch exponential}}-\mathrm{BI}{\mathrm{C}}_{\text{generalized}}=6.1$). However, this model exhibits some of the same accelerating patterns as in the generalized growth model, ascertained by the growth rate of the most recent exponential epoch being 2.4% (2.3–5.2%), larger than that of the first exponential epoch, 1.6% (1.3–2.1%). This acceleration pattern shown in both the generalized model and the model with two exponential epochs is consistent with evidence of growth in European census population size that has greatly accelerated in the modern era (Keinan and Clark 2012).

Discussion

In this study, we provide mathematical derivation and a software that can efficiently compute the expected values of five genetic data summary statistics given a generalized demographic model by evaluating the derived explicit expressions. These summary statistics include the time to the most recent common ancestor ($T_{\mathrm{MRCA}}$), the total number of segregating sites (S), the SFS, the average pairwise difference between chromosomes per site (π), and the burden of private mutations (α). The fast and accurate generation of these summary statistics under generalized models can provide a useful tool in the studies of human demographic inference. For instance, in addition to inference based on the SFS as in the present study, a recent study by Chen et al. (2015) presented an inference framework based on the total number of segregating sites. The results in this study can be easily incorporated into that framework. Furthermore, the source code of the software is freely available to allow extensions to compute other summary statistics of interest (for example, the joint SFS of samples from multiple populations under generalized models, by extending the work of Wakeley and Hey 1997 and Chen 2012). Such extensions can facilitate a variety of population genetic studies in humans and other organisms beyond the inference of demographic history.

It is also possible that other families of growth models may fit the pattern of human population size history. For instance, Eldon et al. (2015) considered the algebraic-growth model in the form of $N\left(T\right)=T^{\gamma }$. In reality, however, not all demographic models have numerically stable closed-form expressions for the expected time to the first coalescent event (${\psi }_j$). In these cases, fast and accurate numerical integration methods, such as the Gauss–Legendre quadrature used in this work, can be applied to evaluate ${\psi }_j$. This technique holds the promise of efficiently generating the expected value of population genetic summary statistics under arbitrary population size functions.

Bhaskar et al. (2014) pointed out that as sample size increases, the assumptions of standard Kingman’s coalescent are violated as multi-merger and simultaneous-merger events can become nonnegligible. Such events can distort the genealogies and potentially cause the values of summary statistics to be different from those under Kingman’s coalescent (Bhaskar et al. 2014). To explore such discrepancies, we compared the SFS from Kingman’s coalescent and the discrete-time Wright–Fisher (DTWF) model (Bhaskar et al. 2014) under the inferred demographic history in the generalized Gazave model with a sample size of 3870 diploids (File S1). We observed that the SFS from the DTWF model and Kingman’s coalescent are very similar (File S1 and Figure S9), which means that multi-merger and simultaneous-merger events should not have a significant effect on the inference carried out in this study. However, it remains valuable to systematically study the effect of multi-merger and simultaneous-merger events in the context of generalized growth, especially as sample size increases.

By applying inference of generalized growth based on the SFS generated from the synonymous variants of 4300 individuals of the NHLBI ESP data set (Tennessen et al. 2012; Fu et al. 2013), we found that the generalized growth model shows a better fit to the observed data than the exponential growth model that has been used by almost all previous demographic modeling studies (P-value $=3.85\times {10}^{-6}$). We also found that the European population experienced a recent growth in population size with speed modestly faster than exponential ($b=1.12$, P-value $\ll {10}^{-12}$ for difference from $b=1$). This result is consistent with previous speculations that the human population might have undergone a recent accelerated growth epoch based on the observation of very rare, previously unknown variants in several sequencing studies with large sample sizes (Nelson et al. 2012; Tennessen et al. 2012; Fu et al. 2013). It is also in line with the super-exponential growth in census population size during that time (Keinan and Clark 2012). In future studies, it will be valuable to incorporate gradient-based optimization techniques for the fast inference of demographic models containing generalized growth epochs, e.g., by extending the work of Bhaskar et al. (2015). Such an improvement will enable simultaneous inference of recent growth and more ancient epochs.

To minimize the impact of natural selection on our demographic inference, we considered only synonymous SNVs for demographic modeling, as in the original study of Tennessen et al. (2012). However, it is still a potential limitation that the data are affected by negative and background selection. Hence, it remains valuable to validate the result of super-exponential growth by conducting inference on SFS calculated from more neutral genomic regions (Gazave et al. 2014) or by modeling the effect of selection. One promising possibility is extracting genomic regions that are less subject to selection from whole-genome sequences in the UK10K project (The UK10K Consortium et al. 2015). More generally, with the increasing availability of high-quality whole-genome sequencing data with large sample sizes for humans and other species, more refined and realistic demographic histories can be estimated with generalized models.