A transversal approach for patch-based label fusion via matrix completion

Abstract

Recently, multi-atlas patch-based label fusion has received an increasing interest in the medical image segmentation field. After warping the anatomical labels from the atlas images to the target image by registration, label fusion is the key step to determine the latent label for each target image point. Two popular types of patch-based label fusion approaches are (1) reconstruction-based approaches that compute the target labels as a weighted average of atlas labels, where the weights are derived by reconstructing the target image patch using the atlas image patches; and (2) classification-based approaches that determine the target label as a mapping of the target image patch, where the mapping function is often learned using the atlas image patches and their corresponding labels. Both approaches have their advantages and limitations. In this paper, we propose a novel patch-based label fusion method to combine the above two types of approaches via matrix completion (and hence, we call it transversal). As we will show, our method overcomes the individual limitations of both reconstruction-based and classification-based approaches. Since the labeling confidences may vary across the target image points, we further propose a sequential labeling framework that first labels the highly confident points and then gradually labels more challenging points in an iterative manner, guided by the label information determined in the previous iterations. We demonstrate the performance of our novel label fusion method in segmenting the hippocampus in the ADNI dataset, subcortical and limbic structures in the LONI dataset, and mid-brain structures in the SATA dataset. We achieve more accurate segmentation results than both reconstruction-based and classification-based approaches. Our label fusion method is also ranked 1st in the online SATA Multi-Atlas Segmentation Challenge.

1. Introduction

Parcellation of the human brain structures is a key image processing step in many medical imaging studies related to computational anatomy and computer aided diagnosis (Li et al., 2014; Li et al., 2010; Nie et al., 2013; Nie et al., 2011). Manual annotation of anatomical structures is tedious and very time consuming, which makes it impractical in most of the current medical studies involving large amounts of imaging data. Therefore, high-throughput and accurate automated segmentation methods are highly desirable.

In the last two decades, multi-atlas segmentation (MAS) has emerged as a promising automated segmentation technique for segmenting a target image by propagating the labels from a set of annotated atlases. The use of multiple atlases makes MAS more capable of accommodating higher anatomical variability than using a single atlas. Moreover, as demonstrated in (Collins and Pruessner, 2009; Isgum et al., 2009; Rohlfing et al., 2004b), segmentation errors made by each individual atlas tend to be corrected when using multiple atlases. Generally, MAS consists of the following three steps: (1) the atlas selection step, where a subset of best atlases is first selected for a given target image based on a certain pre-defined measurement of anatomical similarity (Aljabar et al., 2009; Collins and Pruessner, 2009; Isgum et al., 2009; Rohlfing et al., 2004b; Sanroma et al., 2014a; Wu et al., 2007); (2) the registration step, where all selected atlases and their corresponding label maps are aligned to the target image (Klein et al., 2009; Shen and Davatzikos, 2002; Vercauteren et al., 2009; Wu et al., 2011); and finally (3) the label fusion step, where the registered label maps from the selected atlases are fused into a consensus label map for the target image (Artaechevarria et al., 2009; Cardoso et al., 2013; Coupe et al., 2011; Hao et al., 2013; Jia et al., 2012; Kim et al., 2013; Rousseau et al., 2011; Wang et al., 2011b; Warfield et al., 2004; Zikic et al., 2013). A great deal of attention has been put into the label fusion step, which is also the focus of the present paper, since it has a great influence on the final segmentation performance.

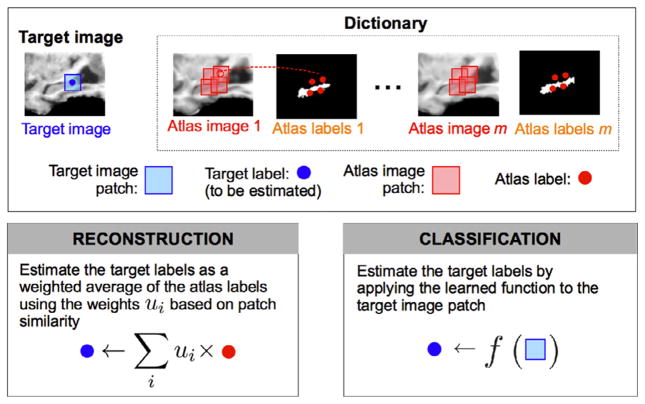
During the label fusion step, each target point is often independently labeled by using its own dictionary composed of the atlas patches and their labels selected from a neighborhood of the to-be-labeled target point (Coupe et al., 2011; Hao et al., 2013; Rousseau et al., 2011) (see the top panel in Fig. 1). Two recently popular label fusion approaches are the following: (1) reconstruction-based approaches, and (2) classification-based approaches. Reconstruction-based approaches are a particular type of weighted voting methods. As such, the target label is computed as a weighted average of the atlas labels (see the bottom-left panel in Fig. 1). Specifically, reconstruction-based approaches assign the weights based on the coefficients obtained by the linear reconstruction of the target patch using the dictionary of atlas patches (Tong et al., 2012; Zhang et al., 2012). This follows the idea of the image-similarity approaches, which assign higher weights to the atlas patches with more similarity to the target patch (Artaechevarria et al., 2009; Coupe et al., 2011; Rousseau et al., 2011). On the other hand, classification-based approaches use the dictionary of atlas image patches and their corresponding labels as the training set to learn the relationships between image appearance and anatomical labels (Hao et al., 2013) (Wang et al., 2011b). Then, in the labeling stage, the target label is estimated by directly applying the learned relationships to the target image patch (see the bottom-right panel in Fig. 1).

Fig. 1.

Illustration of reconstruction-based and classification-based label fusions. Top: a dictionary of atlas image patches (red squares) and their center labels (red circles) are used to estimate the target label (blue circle) in the center of the target image patch (blue square). Bottom-left: reconstruction-based approaches estimate the target label as a weighted average of the atlas labels, where atlas patches with higher similarity are assigned higher weights. Bottom-right: classification-based approaches estimate the target label by applying the relationships learned using the dictionary of atlas patches and labels. (See Sec. 3.1 for details about how the reconstruction and classification functions are computed.)

However, both reconstruction-based and classification-based approaches have their own limitations. Reconstruction-based approaches assume that the weights optimized based on patch-wise similarity are also optimal to fuse the labels. Unfortunately, as demonstrated in (Sanroma et al., 2014a), there is not always a clear relationship between appearance similarity and label consensus, and therefore similar atlas image patches could bear different labels. On the other hand, classification-based approaches overcome this limitation by specifically learning a mapping function from the image appearance domain to the label domain. However, all the atlas patches in the dictionary are given the same importance during the learning procedure, which may not be optimal since not all patches in the dictionary are equally representative for the target patch. Reconstruction-based approaches overcome this issue by adaptively weighting each atlas patch according to their estimated relevance in predicting the label of a particular target image point. In light of this, we present a novel label fusion method with the following contributions:

• We combine the advantages of both reconstruction-based and classification-based approaches by formulating label fusion as a matrix completion problem (but our method restricts to the linear sub-type of approaches). First, we build an incomplete matrix containing the target image patch as well as the atlas patches and their labels, where all the to-be-estimated target labels are missing. Based on the observation that there are high correlations among image patches and labels, we employ a low-rank constraint to estimate the missing elements in the above matrix. This entails taking full advantage of both row-wise and column-wise correlations (Candès and Recht, 2009), corresponding to the correlations in the vertical and horizontal directions of the matrix, respectively. As we will show, both reconstruction-based and classification-based approaches are particular cases where only row-wise (i.e., vertical) or column-wise (i.e., horizontal) correlations are exploited, respectively. By exploiting both types of correlations, our transversal method inherits the properties of both reconstruction-based and classification-based approaches, namely, (1) the property of the reconstruction-based approaches of representing the target patch as a weighted combination of the atlas patches, and (2) the discriminative ability of the classification-based methods in modeling the dependence of anatomical labels on the image appearance.

• We note that the labels at some parts of the image (e.g., deep inside the structures) can be determined more reliably than other parts (e.g., at boundaries of the structures), due to their anatomical characteristics and also due to their robustness to registration errors. However, most patch-based label fusion methods do not acknowledge this fact and label each target point independently. In this paper, we argue that it is more reasonable to let the high-confident points guide the labeling procedure of nearby less-confident points. Specifically, we embed our label fusion method into a sequential labeling framework that first labels the most confident target points and gradually labels those less-confident points iteratively. In this way, the anatomical labels estimated from the previous iterations can be used to help select more anatomically similar atlas patches to build the dictionary for improving the labeling.

We evaluate the label fusion performance of our proposed method on the ADNI, LONI, and SATA segmentation challenge datasets. We show that our proposed matrix completion based label fusion method outperforms both reconstruction-based and classification-based approaches. Moreover, we show that the sequential confidence-guided labeling scheme further improves our proposed method. Most importantly, our proposed method is ranked 1st in the online SATA Segmentation Challenge.

Note that a preliminary version of this work was presented in Sanroma et al., (2014b). The current paper (1) extends our previous work with the sequential confidence-guided labeling approach as described in Sec. 3.2, and ( 2) provides more exhaustive descriptions as well as illustrative examples of our extended method. We extensively (3) evaluate each component of our extended method by using additional datasets, and (4) compare it with the state-of-the-art methods.

2. Related work

With the advent of MAS, label fusion has become an increasingly active area of research. Label fusion is the key step that aims to segment the target image by finding a consensus among a set of registered atlas labels. The way in which the atlas information is used to derive the consensus segmentation has given rise to many different label fusion flavors. The simplest way, known as majority voting (MV), simply assigns each target point the label that appears most frequently among all corresponding atlas points (Heckemann et al., 2006; Rohlfing et al., 2005).

Another type of label fusion methods computes the target label as a weighted average of atlas labels, where weights are derived using local image similarity measurements. For example, local weighted voting (LWV) (Artaechevarria et al., 2009) is an example of this type of methods, which only uses the corresponding atlas points after registration to compute the label on each target point. Non-local weighted voting (Coupe et al., 2011; Rousseau et al., 2011) (NLWV) extends LWV by including all the atlas points within a small neighborhood, thus offering more flexibility to registration errors. Note that NLWV was originally inspired by image denoising ideas, where patches in the noisy image (i.e., target image) are reconstructed as a weighted average of patches in the database of images (i.e., atlas images). The only difference is that the label fusion methods reconstruct the target labels, instead of the target image. Motivated by the success of sparse representations in computer vision, sparse coding has also been studied in the context of label fusion (Tong et al., 2012; Zhang et al., 2012). The main idea is to reduce the number of contributing atlas labels to only a few relevant ones, thus offering better robustness to possible errors. The main idea behind all reconstruction-based methods is to first represent the target patch as a weighted combination of atlas patches, so that the target labels can be directly estimated using the ensemble of atlas labels according to the weights used in the representation.

On the other hand, Warfield et al. proposed a label fusion method, STAPLE (Rohlfing et al., 2004a; Warfield et al., 2004), that simultaneously estimates the target labels and the global performance of each atlas by means of the Expectation-Maximization algorithm (Dempster et al., 1977). Image appearance information has also been introduced into STAPLE to enhance the statistical modeling of the atlas performances. For example, non-local STAPLE (Asman and Landman, 2013) reformulates STAPLE to include priors based on the image similarity measurements. More recently, STEPS (Cardoso et al., 2013) introduces a local ranking strategy based on the image patch similarity into the STAPLE formulation.

Besides, there has been a wide interest in tackling the label fusion problem as a classification problem. In this case, the target label is computed as a function of the image features, where such a function models the dependency of atlas labels on the observed image patches. Different machine learning techniques have been used in this context of label fusion, such as support vector machines (Hao et al., 2013), polynomial regression (Wang et al., 2011b), random forests (Zhang et al., 2014; Zikic et al., 2013), and auto-context models (Kim et al., 2013). The main idea behind these methods is to learn a function that can discriminate among different possible labels based on the image appearance information.

Both reconstruction- and classification-based approaches follow a two-step approach, i.e., (1) the optimization step, where either the representation weights or the mapping functions are computed, and (2) the labeling step, where the target labels are estimated. Our method proposes a combination of reconstruction- and (linear) classification-based approaches by using matrix completion techniques (Candès and Recht, 2009), thus integrating the advantages of both approaches. Moreover, both optimization and labeling processes are carried out in a single step in our method.

However, in certain regions, the appearance information may be only weakly related to the underlying structural labels. In such case, it may be useful to rely on the putative anatomical information to reduce the ambiguity. For example, (Cardoso et al., 2013; Warfield et al., 2004) use Markov random fields (MRF) to enforce nearby target points to bear the same labels. Zhang et al. (Zhang et al., 2011) uses a similar assumption in a sequential labeling approach, where labels of more confident points are determined at earlier iterations and then the less confident points at later iterations are encouraged to bear the same labels as their neighboring more confident points.

Thus, we also embed our label fusion method into a sequential confidence-guided labeling framework by gradually labeling target points in decreasing order of confidence. However, instead of simply imposing neighboring points to bear the same labels, we use label information from previous iterations to select more meaningful atlas patches for labeling each target point.

3. Method

Our method is presented in two parts below. In Section 3.1, we present our label fusion method using matrix completion, and, in Section 3.2, we describe the sequential confidence-guided labeling framework. We denote images and label maps in bold capital letters, matrices in capital letters, vectors in lowercase letters with an overhead arrow, and scalars in lowercase letters.

3.1. Label fusion by matrix completion

3.1.1. Problem formulation

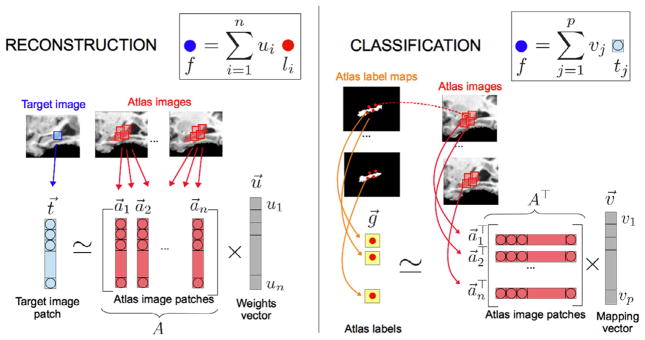
Suppose that we have a target image T and a set of m atlas images A_k along with their respective label maps L_k (k = 1 … m), which have been already registered to the target image. The conventional label fusion approaches estimate the target label f at each voxel x ∈ Ω of target image T in a patch-wise manner. Let t⃗ ∈ ℝ^{p × 1} denote a (column) vector containing the intensity values in the target image patch centered at voxel x, and matrix A = [a⃗₁, … a⃗_i, … , a⃗_n] ∈ ℝ^{p × n} denote a dictionary of n candidate atlas image patches with the highest similarity to the target image patch in a search neighborhood of x (See Appendix A.3 for the details about building the dictionary). Following the same column order as the matrix A, g⃗ = [l₁, … , l_i, … , l_n]^⊤ ∈ ℝ^{n × 1} is a (column) vector of ground-truth labels at the atlas patch centers, with each element l_i ∈ {−1, 1} indicating either the absence (i.e., background) or the presence (i.e., foreground) of a given structure at the center of the respective atlas image patch a⃗_i.

As mentioned, label fusion can be regarded as a reconstruction or classification problem. As said, the reconstruction case is a particular type of weighted voting methods. As such, each target label f is computed as a linear combination of the atlas labels (Artaechevarria et al., 2009; Coupe et al., 2011; Rousseau et al., 2011; Zhang et al., 2012) as follows:

$$f={\overrightarrow{u}}^{\top }\overrightarrow{g}$$ (1)

where u⃗ ∈ ℝ^{n × 1} is a weighing vector to combine the atlas labels. (Note that, the resulting continuous label can be discretized to {−1, 1} using the sign function). Weights in u⃗ encode the importance of each candidate atlas image patch in predicting the target label, and are computed so that the target patch t⃗ can be approximately reconstructed using the atlas patches in A (Tong et al., 2012; Zhang et al., 2012). This is,

$$\underset{\overrightarrow{u}}{min}\left\{C_{\text{rec}}\left(\left[\begin{array}{c}\overrightarrow{t}\\ 1\end{array}\right],\left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]\overrightarrow{u}\right)\right\}\Rightarrow \left[\begin{array}{c}\overrightarrow{t}\\ 1\end{array}\right]\approx \left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]\overrightarrow{u}$$ (2)

where C_rec( · ) is the data fitting term penalizing reconstruction errors of the target patch. Note that the trailing 1’s in the target and atlas patches encourage the weighting vector u⃗ to add up to one.

On the other hand, in the (linear) classification case, given a target image patch t⃗, its center label is determined based on the learned function, denoted as v⃗ ℝ^{p × 1}, aimed at mapping the appearance of the atlas image patch to its center label (Hao et al., 2013; Wang et al., 2011b). Assuming a linear function, the target label can be obtained by the following equation:

$$f={\left[\begin{array}{c}\overrightarrow{t}\\ 1\end{array}\right]}^{\top }\overrightarrow{v}$$ (3)

where the trailing 1 allows to include the bias term of the linear mapping in the last entry of v⃗ (as in the reconstruction case, the discrete label {–1,1} can be obtained using the sign function). The linear mapping function v⃗ encodes the relevance of each image feature in predicting the anatomical label and can be learned by minimizing the discrepancies between the predicted labels and ground-truth labels in the training set. This is,

$$\underset{\overrightarrow{v}}{min}\left\{C_{\text{cls}}\left(\overrightarrow{g},{\left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]}^{\top }\overrightarrow{v}\right)\right\}\Rightarrow \overrightarrow{g}\approx {\left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]}^{\top }\overrightarrow{v}$$ (4)

where C_cls( · ) is a term penalizing the atlas label prediction errors (i.e., training errors). The procedures of reconstruction-based and classification-based methods are illustrated in Fig. 2.

Fig. 2.

Illustrative example of how the weights u⃗ and the mapping function v⃗ are computed in the reconstruction-based and classification-based approaches, respectively. Note that the vectors of trailing ones have been omitted for simplicity.

3.1.2. Label fusion by matrix completion

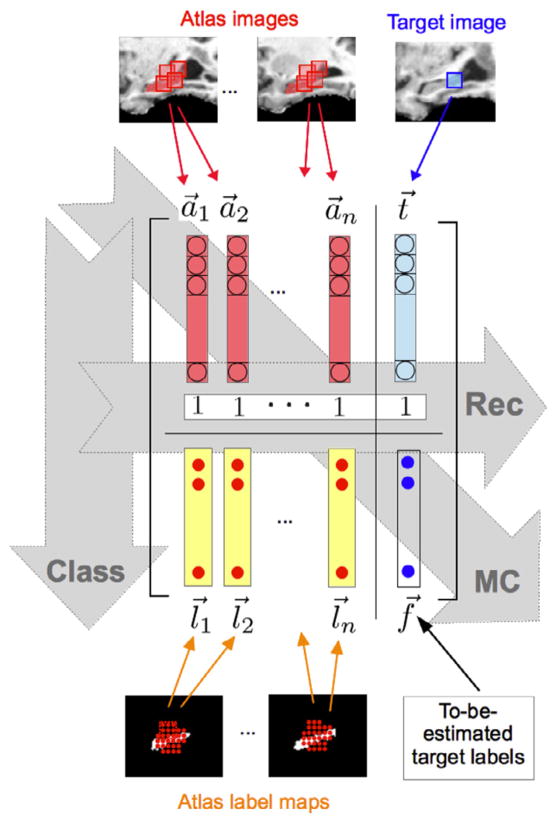
We pose label fusion as a matrix completion problem, where the labels of to-be-estimated target patches are the missing entries in a specially constructed matrix. Furthermore, instead of predicting only the label at the center of each target patch, we also estimate all labels in the entire target image patch. Following the same order as in the atlas image matrix A = [a⃗₁, … , a⃗_i, … , a⃗_n] ∈ ℝ^{p × n}, we arrange the label vector l⃗_i of each atlas patch a⃗_i into the atlas label matrix L = [l⃗₁, … , l⃗_i, … , l⃗_n] ∈ ℝ^{p × n}.

$$\text{Consider}\text{the}\text{four-quadrant}\text{matrix}Z=\left[\begin{array}{cc}\left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]& \left[\begin{array}{c}\overrightarrow{t}\\ 1\end{array}\right]\\ L& \overrightarrow{f}\end{array}\right],$$

where each quadrant is a sub-matrix consisting of: (1) the atlas image matrix A ∈ ℝ^{p × n}, (2) the atlas label matrix L ∈ ℝ^{p × n}, (3) the target image patch t⃗ ∈ ℝ^{p × 1}, and (4) the to-be-estimated target label patch f⃗ ∈ ℝ^{p × 1} (similarly defined as l⃗_i). The main idea of the reconstruction-based approaches implies that the target image patch can be expressed as a linear combination of the atlas image patches, whereas the main idea of the (linear) classification-based approaches implies that the label can be expressed as a linear combination of the image intensity values (with the vectors u⃗ and v⃗ in Fig. 2 containing the mixing coefficients in the reconstruction and classification cases, respectively). All these, in turn, imply that the four-quadrant matrix Z is highly correlated in both column-wise and row-wise fashions, and thus it is low-rank. We exploit this fact to recover the missing entries through rank minimization of the four-quadrant matrix (Candès and Recht, 2009). As we will see, this is equivalent to jointly using the properties of both reconstruction-based and classification-based approaches when estimating the target labels. In other words, we estimate the target labels by using both an ensemble of atlas labels and a learned discriminative function. Furthermore, by jointly estimating the labels for the whole target patch, we provide additional useful sources of correlation among the observed data to be leveraged by matrix completion. Fig. 3 illustrates the idea of our method.

Fig. 3.

Each quadrant of the four-quadrant matrix is a sub-matrix, consisting of (1) stacked vectors of the atlas image patches (red), (2) stacked vectors of atlas label patches (yellow), (3) target image patch (light blue), and (4) to-be-estimated target labels (dark blue circles), respectively. Reconstruction-based methods utilize the correlations along the columns of the four-quadrant matrix, whereas classification-based methods utilize the correlations along the rows, as indicated by the horizontal and vertical shaded arrows, respectively. By imposing the low-rank constraint on this four-quadrant matrix, our method can simultaneously leverages the full row-wise and column-wise correlations for estimating the target labels, as indicated by the transversal shaded arrow.

3.1.3. Optimization

As denoted in Eq. (2), reconstruction-based methods assume that each target-patch column can be represented as a linear combination of all atlas-patch columns. On the other hand, as denoted in Eq. (4), classification-based methods assume that each label-patch row can be represented as a linear combination of all image-patch rows. Such row- and column-wise dependences imply that the matrix Z is low-rank. This allows us to formulate the recovery of the missing target labels in f⃗ as a matrix rank minimization problem. By doing so, our method combines both reconstruction-based and classification-based methods, thus posing the recovery of target labels as a blend of row-wise and column-wise combinations. Since column-wise correlations describe the relationships between atlas image patches and target image patches, and row-wise correlations encode the dependence of the labels based upon the appearances of image patch, our MC-based label fusion method inherits the properties of both reconstruction-based and classification-based methods.

The key step in our approach is then finding the missing entries in f⃗ so that the rank of Z is minimized. Following Cabral et al., (2011), Goldberg et al., (2010), we seek a new matrix Ẑ which satisfies the following conditions: (1) the rank of Ẑ is low; and (2) the residue between the estimated and observed data in Ẑ and Z is small. Due to the different natures of the two types of data in the matrix, we use two different cost functions to evaluate the residues: one for the image appearance, and another for the anatomical labels. Therefore, we define Θ_I and Θ_L as the sets of indices pointing to the entries in Z (i.e., pairs of row and column coordinates), corresponding to the observed image and label data, respectively (note that the indices of the to-be-estimated target labels in f⃗ are excluded from Θ_L). Accordingly, z_a,b, (a, b) ∈ Θ_I, denotes the image-intensity value at position (a, b) in matrix Z (i.e., either red or blue quadrants of Fig. 3), and z_a,b, (a, b) ∈ Θ_L, denotes the label value at position (a, b) in matrix Z (i.e., yellow quadrant of Fig. 3). The above objectives for finding the missing target labels can be formulated into the following convex optimization problem:

$$\underset{\widehat{Z}}{min}\left\{\eta {\Vert \widehat{Z}\Vert }_{\ast }+\frac{1}{\mid {\mathrm{\Theta }}_1\mid }\sum _{(a,b)\in {\mathrm{\Theta }}_I}{c}_I({\widehat{z}}_{a,b},z_{a,b})+\frac{\lambda }{{\mathrm{\Theta }}_2}\sum _{(a,b)\in {\mathrm{\Theta }}_L}{c}_L({\widehat{z}}_{a,b},z_{a,b})\right\}$$ (5)

where || ·||_* denotes the nuclear norm (Candès and Recht, 2009) (i.e., the convex relaxation of the rank operator), | · | denotes the cardinality of the set, and c_I( · ) and c_L( · ) are the loss functions penalizing the estimation errors in the observed image and label entries, respectively. These two last terms follow the same idea as C_rec(· ) and C_cls(· ) of the reconstruction and classification approaches of Eqs. (2) and (4), respectively. We use the squared loss to penalize the error between the estimated image-intensity value Ẑ_{a ,b} and the observed one z_a,b ((a, b) ∈ Θ_I), i.e., c_I(Ẑ_a,b, Ẑ_a,b) = (Ẑ_a,b − Ẑ_a,b)²/2, since it is suitable for the continuous values in the intensity images, and the logistic loss to penalize the label estimation errors, i.e., c_L(Ẑ_a,b, z_a,b) = log(1 + exp(−z_a,b Ẑ_a,b)), ((a, b) ∈ Θ_L), since it is suitable for the binary values in the labels.

The first term in Eq. (5), which is controlled by the regularization parameter η, is responsible for decreasing the rank of the matrix Ẑ. Lower ranks tend to remove noisy variations in the matrix Z, thus improving the row-wise and column-wise correlations. This means that low rank minimization encourages each column to be represented as a linear combination of the other columns, and each row to be represented as a linear combination of the other rows, which correspond to the objectives of the reconstruction-based and classification-based approaches of Eqs. (2) and (4), respectively. Note that neither the weighting vector u⃗ nor the mapping function v⃗ are explicitly computed, as their computations are implicit in the minimization of the matrix rank. The second term in Eq. (5) is a feature error term which penalizes the discrepancy between the observed image data and the estimated image data in Ẑ. Having in mind that matrix Ẑ is low-rank and thus contains significant column-wise correlations, this term encourages that the target patch is represented as a weighted average of the atlas patches, and then the atlas labels are transferred to the target by following the same representation. The third term in Eq. (5), which is controlled by the regularization parameter λ, is a label error term that penalizes the discrepancy between the ground-truth atlas labels and the estimated ones in the matrix Ẑ. Considering that matrix Ẑ contains significant row-wise correlations, this term encourages that the dependencies between the atlas images and labels are effectively captured and, as consequence of the rank minimization, it also ensures that the missing target labels are filled-in following the same dependencies. We determine the values of and λ empirically.

The optimization of Eq. (5) can be solved by an iterative algorithm that alternates between a gradient step and a shrinkage step (Goldberg et al., 2010). Specifically, in the gradient step, the matrix is updated so as to decrease the residual error, while, in the shrinkage step, the rank of the matrix is reduced. Since it is a convex optimization problem, the convergence to global optimum is guaranteed.

3.1.4. Summary

The matrix-completion based label fusion method can be represented as a function f⃗ = MatComLF(t⃗, A, L) that estimates the labels of a target patch in f⃗ using the target image patch in t⃗ and the dictionary of atlas image patches and labels in A and L, respectively. Since we estimate the label for the entire image patch and there are overlaps between image patches, we end up with multiple estimations for each target point. Accordingly, we first combine the multiple overlapping patch estimations into a continuous label map F, as described in Appendix A.1, and then discretize the continuous label map to obtain the estimated target labels D, as described in Appendix A.2. Table 1 shows a summary of our proposed algorithm for labeling an entire image.

Table 1.

Algorithm for labeling one entire image using matrix-completion based label fusion.

Input: Target image T, along with the atlas images and label maps Ik and Lk, k = 1 … m

Output: Estimated continuous and discrete target label maps F and D, respectively

F = Ø #set for aggregating the overlapping estimations

For Each voxel x ∈ Ω in the target image domain, do

t⃗ = GetImgPatch(T, x)

(A, L) = BuildDictionary(Ik, Lk, t⃗, x), k = 1 … m #see Appendix A.3

f⃗ = MatComLF(t⃗, A, L)

F = F ∪ {f⃗}

End For

F = CombineOverlappingLabels(F) #see Appendix A.1

D = Discretize(F) #see Appendix A.2

3.2. Sequential confidence-based labeling

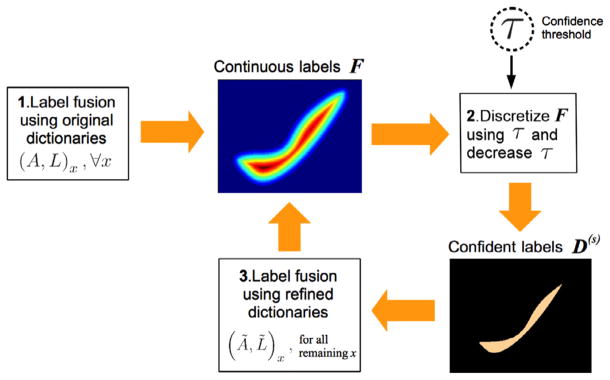
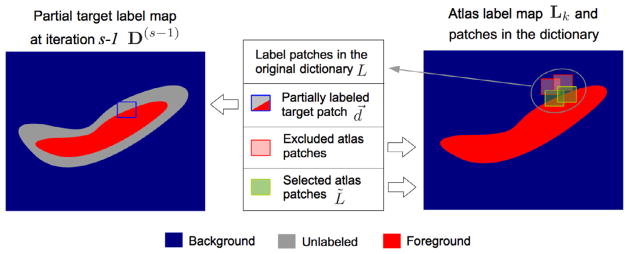
Selection of an appropriate dictionary is a key issue affecting the label fusion performance (Coupe et al., 2011; Hao et al., 2013). Recall that in f⃗ = MatComLF(t⃗, A, L), we obtain the dictionary (A, L) based on the image similarity between the target image patch and the neighboring atlas image patches (please refer to Appendix A.3). However, building the dictionary based solely on image similarity can undermine the label fusion performance, especially in challenging regions such as the boundaries of the structures, where similar atlas patches may bear different labels. To overcome this limitation we propose to use the prior knowledge about the labels on the target image to select the dictionary based on both image and label similarity with the target patch. Specifically, we adopt a sequential confidence-based labeling strategy where we first label the most confident target points (based on the magnitude of the continuous label values in F) and then use this partial label information to refine the dictionaries used for labeling the less confident points at later iterations. As result, for each target patch t⃗, we obtain a refined dictionary (Ã, L̃) ⊂ (A, L) containing a subset of atlas patches with both high image similarity and high label similarity. This process is summarized in Fig. 4.

Fig. 4.

Overview of the sequential confidence-guided labeling framework: (1) We label each target point x using the original dictionaries, denoted as (A, L)_x. Note that, instead of obtaining a discrete label map, we obtain a continuous label map F indicating the label confidence values. (2) We obtain a partial segmentation, consisting of the most confident labels by discretizing the continuous labels using a pre-defined threshold τ , and then decrease the threshold. (3) We label the remaining unlabeled target points x by using the refined dictionaries (Ã, L̃)_x obtained with the help of the confident labels from previous iterations. We repeat steps (2)–(3) until all the target points have been labeled.

3.2.1. Problem formulation

Assume that, at iteration s, we want to label a target image patch, denoted as t⃗, centered at x. We build the dictionary in a two-step approach: First, we build a dictionary of neighboring atlas image patches with high image similarity to the target image patch t⃗, denoted as A = [a⃗₁, … , a⃗_n] and L = [l⃗₁, … , l⃗_n]. Next, we refine it based on the label similarity with the target label patch.

Let us denote the partial target label map from the previous iteration as D^{(s − 1)}. We extract the partial labels for the target patch at iteration (s − 1), denoted as d⃗, consisting of a vector with entries in {−1, 1, ⊥}, where −1, 1 and ⊥ indicate background, foreground and unlabeled point, respectively. We then build the refined dictionary (Ã, L̃) using only the set of atlas patches with high label similarity to the partial target label patch, as defined in the following:

$$\{{\overrightarrow{a}}_i,{\overrightarrow{l}}_i\mid \text{sim}({\overrightarrow{l}}_i,\overrightarrow{d})\ge \rho \}$$ (6)

where 0 ≤ ρ ≤ 1 is a label similarity threshold and sim(l⃗_i, d⃗) measures the similarity between the atlas label patch l⃗_i and the partial target label patch d⃗. We define the label similarity measurement as the number of coincident labels in the atlas and target patches, normalized by the number labeled target points in the patch. More formally,

$$\text{sim}({\overrightarrow{l}}_i,\overrightarrow{d})=\mid \text{id}({\overrightarrow{l}}_i)\cap \text{id}(\overrightarrow{d})\mid /\mid \text{id}(\overrightarrow{d})\mid$$ (7)

where id(d⃗) is the indicator function denoting the set of indices in d⃗ containing foreground labels, and | · | denotes the cardinality of the set.

As result, the refined dictionary used to label the target image patch t⃗, denoted as (Ã, Ã), is composed by the atlas patches in the neighborhood of t⃗ satisfying both the image similarity criterion in Appendix A.3 (Eq. (A.2)) and the label similarity criterion of Eq. (6). Fig. 5 illustrates the dictionary refinement based on label similarity.

Fig. 5.

Partially labeled target patch (i.e., blue square in the left-hand side). Atlas patches in the original dictionary (i.e., red and green squares in the right-hand side). We exclude the atlas patches in the dictionary with low label similarity to the partially labeled target patch (i.e., those red squares in the right-hand side).

3.2.2. Summary

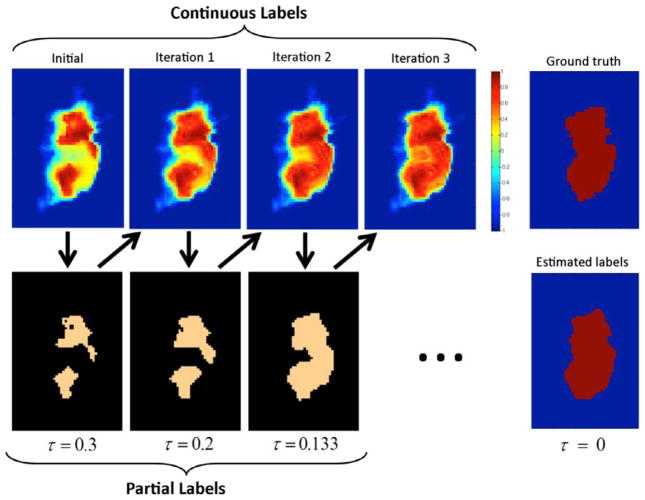
The whole iterative procedure is carried out as follows. At the first iteration, we compute the continuous label estimates F (which also represent the labeling confidence of the whole image) by using our proposed matrix-completion based label fusion method in Section 3.1. In the discretization step, we only assign labels to the most confident points according to a threshold τ , leaving the rest of points unlabeled. In the subsequent iterations, we re-compute the label confidences in the unlabeled parts by using the information of the labeled parts to refine the dictionary, as previously described. Note that we only need to re-compute the continuous labels in the unlabeled target points near to the labeled parts. In the end of each iteration, we discretize the new continuous estimates to obtain the partial label map D^(s), where we gradually decrease the confidence threshold τ across iterations. As result, we progressively estimate the labels for the less confident points with the guidance from labels of more confident points estimated in the previous iterations. This process has some similarity to simulated annealing (Sanroma et al., 2012a; 2012b), where a temperature parameter used to control the optimization process is gradually decreased and also the result from the previous iteration is used to initialize the next iteration. Fig. 6 shows an example of the evolution of the continuous label estimates across iterations, along with the resulting discrete confident labels. As we can see, the agreement of the continuous labels with the ground-truth labels improves across the iterations. In Table 2, we describe the algorithm of our full method.

Fig. 6.

Top-left: initial continuous label estimates of MC-based label fusion. Bottom-left: initial partial labels (with confidence threshold τ = 0.6). Top-middle: evolution of the continuous label estimates across iterations using the information from confident labels. Bottom-middle: partial labels with the decreasing confidence threshold across iterations. Top-right: ground-truth target labels. Bottom-right: estimated target labels in the end of the sequential confidence-based labeling procedure.

Table 2.

Algorithm of the sequential confidence-guided label fusion by matrix completion.

Input: Target image T, atlas images and label maps Ik and Lk, k = 1 … m, initial discretization threshold τini, and patch selection threshold ρ

Output: Estimated target label map D

D(0) = Initializetounlabeled

τ = τini

s = 0

While there are unlabeled points remaining in D(s), do

s = s + 1

F = Ø #set for aggregating the overlapping estimations

For Each voxel x ∈ Ω in the target image T, do

(t⃗, d⃗) = GetImg&LabelPatch(T, D(s−1), x)

(A, L) = BuildDictionary(Ik, Lk, t⃗, x), k = 1 … m #see Appendix A.3

(Ã, L̃) = RefineDictionary(A, L, d⃗, ρ) #Eq. (6)

f⃗ = MatComLF(t⃗, Ã, L̃) #Section 3.1

F = F ∪ {f⃗}

End For

F = CombineOverlappingLabels(F) #see Appendix A.1

D(s) = Discretize(F, τ) #see Appendix A.2

τ = τ /β , β ≥ 1

End While

D = D(s)

4. Experiments

We evaluate the performance of the proposed method by conducting human brain anatomical segmentation experiments in a variety of datasets. In Section 4.2, we present hippocampus segmentation experiments in the ADNI¹ dataset. In Section 4.3, we segment all 16 subcortical and limbical structures in the LONI LPBA40² dataset (Shattuck et al., 2008). Finally, in Section 4.4, we provide segmentation results in the online SATA³ Segmentation Challenge dataset, consisting of segmentations of 14 mid-brain structures.

In the ADNI and LONI-LPBA40 datasets, we conducted the following three pre-processing steps on all images before label fusion: (1) Skull stripping by a learning-based meta-algorithm (Shi et al., 2012); (2) N4-based bias field correction (Tustison et al., 2010); (3) ITK-based histogram matching for normalizing the intensity range. Prior to segmentation, we use FLIRT (Jenkinson et al., 2002) to perform linear (affine) alignment between each pair of images followed by non-rigid registration with diffeomorphic demons (Vercauteren et al., 2009). The images in the SATA dataset were already skull-stripped and the pairwise non-rigid registration was also performed.

4.1. Comparison methods

We compare our proposed label fusion method to a variety of related methods. As for the reconstruction-based methods, we compare with Sparse Patch-based Labeling (SPBL) (Tong et al., 2012; Zhang et al., 2012) and some related image-similarity based methods such as Local Weighted Voting (LWV) (Artaechevarria et al., 2009) and Non-Local Weighted Voting (NLWV) (Coupe et al., 2011; Rousseau et al., 2011) label fusion. Note that the only difference between LWV and NLWV is the use of the neighborhood radius ε to build the dictionary, i.e., with ε > 0 in NLWV while ε = 0 in LWV. As for the classification-based methods, we have implemented a method that uses multi-task logistic regression (termed LogReg) for learning the mapping function between the appearance and the labels of Eq. (4). See Appendix B for more details.

In both reconstruction-based and classification-based approaches, we have tried either estimating only the center label for each target patch, or the whole patch. In order to keep the results as concise as possible, we only report the best estimation result (point-wise or patch-wise) for both reconstruction- and classification-based approaches. In most cases, we have found little difference between point-wise and patch-wise label estimation. Note that SPBL, NLWV and LogReg use exactly the same dictionary as our proposed method, thus providing fair comparison for these different label fusion methods.

We also compare with the state-of-the-art method STEPS⁴ (Cardoso et al., 2013), which incorporates image similarity measurements into a statistical model of atlas performance to estimate the target labels. Moreover, it uses Markov Random field regularization to add spatial consistency by encouraging the neighboring target points to bear the same anatomical labels.

In order to assess each of our contributions, we further include two versions of our method in the comparison: (1) a degraded version (MCdeg) that uses only the matrix completion to label a target image in one-pass, as described in the algorithm of Table 1, and (2) the full version of our method (MCfull), as described in the algorithm of Table 2, which uses the sequential confidence-guided framework to refine the atlas dictionary.

Table 3 shows the values of the parameters used in all the comparison methods.

Table 3.

Parameter values used in all the comparison methods.

Parameter	Details
Number of atlases m	In all the methods, we use the best m = 15 atlases selected according to mutual information, as this number of atlases has achieved an optimal performance in similar studies (Aljabar et al., 2009).
Patch size	We tried with isotropic patch sizes of 3, 5 and 7 voxels, and found that 5 yielded the best results.
Neighborhood radius ε	We tried with radius of ε = 1, 2 and 3 and found that ε = 1 performed the best in all the cases. By definition, we adopted the value of ε = 0 for LWV.
LogReg and SPBL sparsity regularization α	We found that, the best amount of regularization for LogReg and SPBL was αc = 0.5 and αr = 0.01, respectively.
MCfull and MCdeg regularization parameters η, λ	We tried values in the range η = 10−5 … 1 and λ = 10−3 … 10, respectively, and we found that λ = 0.05 and η = 10−4 yielded the best results in all datasets.
Label similarity threshold ρ	In the full version of our method (MCfull), we found ρ = 0.9 was the best value for the label similarity threshold, suggesting that enforcing high anatomical similarities in selection of atlas patches is beneficial for the segmentation performance.
Initial confidence threshold and decay parameter τini, β	We set the value of the initial confidence threshold τini according to the experiments in the beginning of Section 4.2. The decay parameter is fixed to β = 1.5.
STEPS (Cardoso et al., 2013)	There are three parameters to be tuned in STEPS, namely (1) the kernel size to measure image similarity in the local region (related to image patch size), (2) the number of local labels, and (3) the amount of MRF regularization. We tried with a range of values around the recommended values, and we kept the ones performing the best, which are the kernel size of 1.5, the number of local labels equal to 11, and the amount of MRF regularization equal to 4. Regarding MRF regularization, STEPS authors recommended a value in the range 0 … 5, which suggests that, in the present experiments, the MRF regularization has an important role for improving performance.

4.2. ADNI dataset

The ADNI dataset is provided by the Alzheimer’s disease neuroimaging initiative and contains the segmentations of the left and right hippocampi which were obtained by a commercial brain mapping tool (Hsu et al., 2002). The size of each image is 256 × 256 × 256. We use 30 randomly selected subjects to test the performance of each of the segmentation methods. Due to the random selection, the prevalence of disease in our samples is similar to that in the original dataset, which is approximately 1/4 of Alzheimer’s disease patients, 1/4 of healthy subjects, and 1/2 of subjects with mild cognitive impairment. In each segmentation experiment, one image is regarded as the target subject and the remaining 29 as the atlases. This process is repeated 30 times by regarding each image as target image once. Segmentation performance is assessed by the Dice ratio between manual annotations and automatic segmentations.

4.2.1. Sensitivity study to the initial confidence threshold

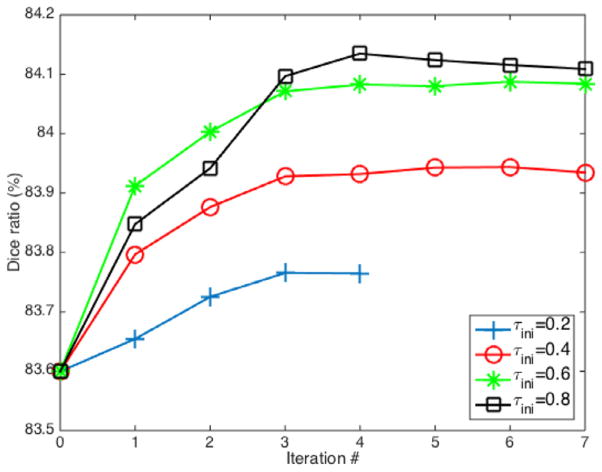
First of all, we evaluate the sensitivity of our method to the confidence threshold parameter τ_ini. In Fig. 7, we show the segmentation performance with iterations in the annealing procedure of MCfull, by using different initial values τ_ini = {0.2, 0.4, 0.6, 0.8} (See Appendix A.2 for details about the confidence-based discretization).

Fig. 7.

Evolution of Dice ratio with iterations of MCfull for different values of τ_ini. Intermediate segmentation results at each iteration are obtained by thresholding the continuous label map at τ = 0 in order to obtain a completely segmented image. Note that such completely labeled map is only used for obtaining the intermediate segmentation performance, while the partially labeled map according to the current value of the threshold is normally passed to the next iteration, as described in our method. Results at iteration 0 correspond to MCdeg, where the whole target image is labeled in one-pass without using any support from the high confident labels.

As we can see, segmentation performance increases w.r.t. the increase of the iteration number regardless the initial value of the confidence threshold, thus confirming the benefit of obtaining supports from the previously labeled points. Regarding the initial value of the threshold, results suggest to better start labeling only a few most confident points and then gradually labeling the rest of points in a supported way (i.e., τ_ini = 0.6 and 0.8) rather than taking a higher risk at the beginning by labeling a large number of points in an unsupported way (i.e., τ_ini = 0.2 and 0.4). On the other hand, using higher thresholds results in higher computational times because a larger number of points need to be considered at each iteration. The average computational times for completely labeling both left and right hippocampi in one subject for the confidence threshold values τ_ini = 0.2, 0.4, 0.6 and 0.8 are 134, 214, 291 and 370 s, respectively⁵. In the case of τ_ini = 0.2, the method usually completes the labeling of the subject before the 7th iteration. Taking into account both the performance and computational aspects, we choose the value τ_ini = 0.6 in the rest of experiments.

4.2.2. Quantitative comparison

In Table 4, we show the segmentation performance by all the comparison methods for the left and right hippocampi (HC). Each value in the table shows the mean Dice ratio (and standard deviation) across 30 leave-one-out cross-validation experiments.

Table 4.

Dice ratio (%) in the ADNI dataset. We denote with markers * and + the statistically best and second best results among all the methods, respectively (according to a paired t-test at 5% significance level).

	STEPS	LWV	NLWV	SPBL	LogReg	MCdeg	MCfull
Left HC	81.46 (2.27)	81.26 (2.35)	82.42 (1.98)	82.61 (1.91)	82.83 (2.13)	83.56 (2.01) +	84.02 (2.15)*
Right HC	81.99 (2.72)	81.67 (2.93)	82.86 (2.35)	82.75 (2.21)	83.13 (2.42)	83.64 (2.36) +	84.15 (2.31)*
Overall	81.73 (2.50)	81.47 (2.64)	82.64 (2.17)	82.68 (2.05)	82.98 (2.26)	83.60 (2.17) +	84.08 (2.22)*

As we can see from these results, our proposed method (MC-full) achieves the best performance among all the methods, followed by the degraded version (MCdeg) which outperforms the rest of competing methods (according to a paired t-test at 5% significance level). Specifically, our proposed method (MCfull) outperforms both the reconstruction-based (LWV, NLWV and SPBL) and the classification-based (LogReg) approaches by ~1.5% and 1.1%, respectively. Regarding the degraded version of our method (MCdeg), we can see that it also outperforms both SPBL and LogReg by ~1% and ~0.6%, respectively, thus confirming the superiority of our combined, matrix-completion based approach, compared to the separate reconstruction-based and classification-based approaches. By comparing the results of the two versions of our method, we can see that the sequential confidence-guided framework provides a further improvement of ~0.5% with respect to MCdeg. Another interesting observation is that NLWV outperforms LWV by >1%, thus confirming the advantage of including neighboring atlas patches in label fusion as already noted by Rousseau et al. (2011). This has to be taken into account when interpreting the results of STEPS, which, like LWV, does not include the neighboring atlas patches in the dictionary. Thus, the ~0.3% performance improvement of STEPS over LWV is due to both the superior statistical estimation technique and the MRF-based regularization. Regarding the comparison of SPBL and LogReg, we observe that the classification-based approach outperforms the reconstruction-based approach by an average of ~0.3%. Each column in Fig. 8 shows two consecutive slices with the typical segmentation results by each comparison method.

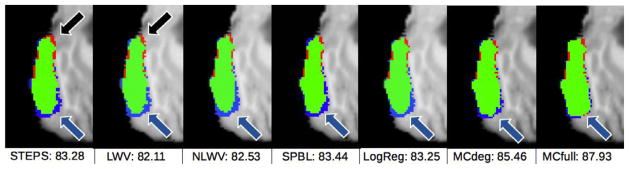
Fig. 8.

Each column shows two consecutive slices of a typical example of hippocampus segmentation result by each method. Green labels denote coincidence between manual and automated segmentations (i.e., true positives), blue labels denote the parts of manually-segmented structures not detected by the automated method (i.e., false negatives), and red labels denote the parts of the automated segmentation that do not appear in the manual segmentation (i.e., false positives).

The arrows point to the areas with the most significant differences among the methods. In general, the proposed methods, MCdeg and MCfull, show the highest true positives (green). Particularly, reconstruction-based methods tend to have more false negatives (blue). Comparing the results by STEPS and LWV, we can see that STEPS manages to reduce the false negatives in the area pointed by the purple arrow, probably due to the MRF regularization. LogReg obtains worse results than the proposed methods, MCdeg and MCfull, in the areas pointed by the black and purple arrows, respectively.

4.3. LONI dataset

The LONI LPBA40 dataset is provided by the Laboratory of Neuro-Imaging at UCLA and contains 40 brain images of size 220 × 220 × 184. Each image contains the annotations of 56 anatomical structures. We focus on the 16 subcortical and limbic structures, which consist of the left and right parts of the following structures: caudate nucleus (CN), gyrus rectus (GRe), hippocampus (HPC), putamen (PUT), lateral orbitofrontal gyrus (LOG), parahippocampal gyrus (PHG), insular cortex (IC), and middle orbitofrontal gyrus (MOG). As we did in the ADNI dataset, we compute the segmentation on each of the 40 images by using the remaining 39 as atlases, and this process is repeated for 40 times by leaving one different image out at each time. We assess the segmentation performance by using again the Dice ratio between manual annotations and automated segmentations by each method. In Table 5, we show the average Dice ratios (and standard deviations) across the 40 leave-one-out cross-validation experiments by each method in segmenting different structures.

Table 5.

Dice ratio (%) in the LONI database. We denote with markers * and + the statistically best and second best results among all the methods, respectively (according to a paired t-test at 5% significance level). Note that we omit the marker* when no single method is statistically superior to the rest.

	STEPS	LWV	NLWV	SPBL	LogReg	MCdeg	MCfull
CN	82.10 (5.17)	82.24 (5.20)	82.99 (5.15)	83.64 (4.79)	83.29 (5.04)	83.77 (4.71) +	83.78 (4.67) +
GRe	78.63 (5.16)	78.14 (4.51)	78.81 (4.48)	79.13 (4.52)	79.19 (4.39)	79.67 (4.34) +	80.32 (4.74)*
HPC	82.73 (2.82)	82.60 (2.74)	83.33 2.69	83.63 (2.55)	83.51 (2.68)	83.69 (2.46) +	83.93 (2.57)*
PUT	83.22 (3.13)	82.44 (3.10)	82.92 3.10	84.83 (2.91)	83.73 (2.95)	84.42 (2.83) +	84.88 (2.96)*
LOG	71.10 (8.16) +	69.80 (8.05)	70.48 (8.23)	69.94 (8.23)	70.34 (8.40)	70.33 (8.43)	71.54 (7.80)*
PHG	79.76 (3.49)	79.23 (3.22)	80.11 (3.22)	80.33 (3.33)	80.26 (3.22)	80.64 (3.24) +	81.25 (3.53)*
IC	85.30 (2.34)	85.19 (2.15)	85.88 (2.12)	86.30 (2.07)	86.10 (2.10)	86.47 (2.07) +	86.55 (2.26) +
MOG	77.76 (6.42)*	76.94 (6.30)	77.46 (6.41) +	77.27 (6.37)	77.29 (6.44) +	77.29 (6.47) +	77.69 (6.50) +
Overall	80.07 (6.43)	79.57 (6.55)	80.25 (6.58)	80.51 (6.79)	80.46 (6.70)	80.79 (6.77) +	81.24 (6.53)*

Overall, our full method (MCfull) outperforms the rest of the methods, followed by our degraded method (MCdeg) according to a paired t-test at the 5% significance level. Specifically, it obtains average Dice ratio improvements of ~1% with respect to NLWV and 0.7% with respect to LogReg and SPBL. The degraded version of our method (MCdeg) obtains average improvements of >0.5% with respect to NLWV and >0.3% with respect to LogReg and SPBL, demonstrating the advantages of the combined approach over the reconstruction-based or classification-based approaches. Furthermore, MCfull achieves an improvement of >0.4% with respect to MCdeg due to the sequential confidence-guided framework. Results across different structures show that our full method achieves the best results in all the structures except for MOG, where STEPS obtains the best performance followed by our full method. The degraded version of our method (MCdeg) also outperforms the remaining methods in all the structures, except for the LOG and MOG, where MCdeg is outperformed by STEPS. Similarly, as we observed in the ADNI dataset, STEPS is superior to LWV, partly due to the benefits of using MRF regularization. Also, similarly as in the ADNI dataset, NLWV outperforms LWV by >1%, thus showing the advantages of including the neighboring atlas patches in the dictionary. Here, there are no significant performance differences between reconstruction- and classification-based approaches, as evidenced by the results of SPBL and LogReg, respectively. The benefit of the linear reconstruction strategy with sparsity constraint compared to the image similarity measurement is evidenced by differences in performance between SPBL and NLWV.

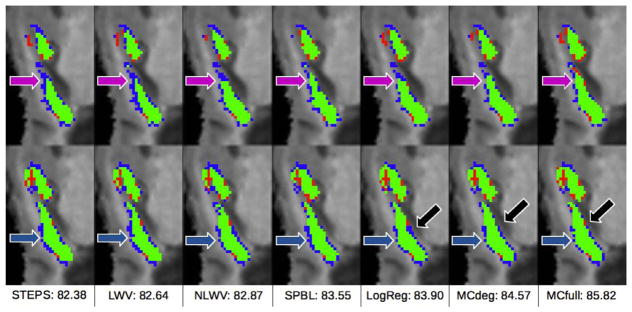
In Fig. 9, we further show one example of segmentation results of the right gyrus rectus by all the comparison methods.

Fig. 9.

Example segmentation results of the right gyrus rectus by all comparison methods. Green labels denote coincidence between manual and automated segmentations (i.e., true positives), blue labels denote the parts of the manually segmented structure not detected by the automated segmentation (i.e., false negatives), and red labels denote the parts of the automated segmentation that do not appear in manual segmentation (i.e., false positives).

Note the higher false negatives by all other methods in labeling the bottom part, except our proposed methods MCdeg and MCfull, as indicated by the blue regions pointed by the blue arrow. Both MCdeg and MCfull show improvement in this area with respect to other methods. Furthermore, MCfull shows the most accurate results, thus demonstrating the benefit of using the sequential confidence-guided framework. By comparing the segmentation results between STEPS and LWV as indicated by the black arrow, we can observe the increase in false positives perhaps due to the use of MRF regularization. We can also see that the MRF regularization is not able to correct the aforementioned false negatives as pointed by the blue arrow.

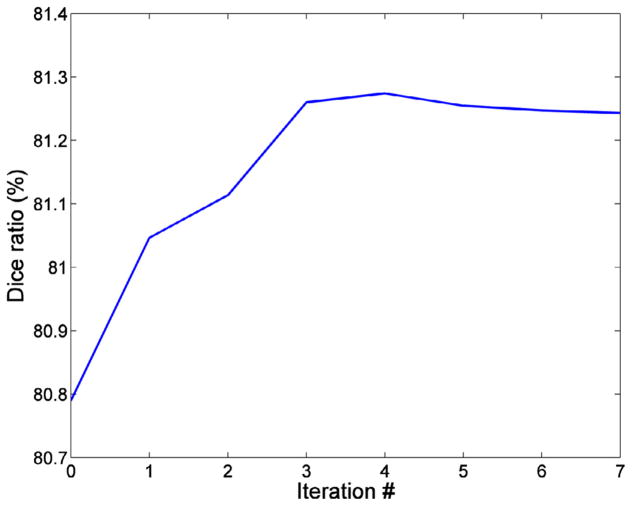
In order to give more insights on the performance of our full method, in Fig. 10, we further show the evolution of the segmentation performance with iterations. Similarly as in the ADNI dataset, we can see that the segmentation performance increases most significantly during the first 3 iterations, after which it stabilizes. The slight performance decrease at iterations 5 – 7 (although not statistically significant) is possibly due to the fact that the newly labeled points at these iterations have lower confidence values and thus introduce some ambiguity. Recall that our ‘annealing-like’ approach uses the support of previously labeled points in a decreasing order of their confidence values. Therefore, points at the early iterations provide a more reliable support than points at the latest iterations. Note also that the minority of ambiguous points at the latest iterations cannot undermine the dramatic performance improvement achieved during the early iterations.

Fig. 10.

Evolution of Dice ratio with iterations of our full method.

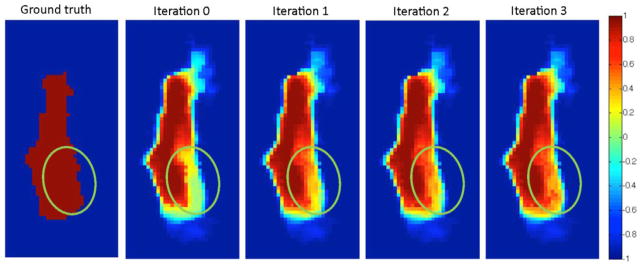
In order to give a visual insight of the proposed method, in Fig. 11 we also show the evolution of the continuous labels with iterations in labeling the right gyrus rectus. Our main purpose here is to show how the continuous label maps evolve with iterations after getting the supports from those confident labels of previous iterations.

Fig. 11.

From left to right: manual labels and the evolution of the continuous label maps obtained by the first 3 iterations of the sequential confidence-guided framework.

The green circles denote the area where the initial estimate of the continuous label map highly disagrees with the manual segmentation. As we can see in the label maps of further iterations, our proposed method automatically corrects the disagreement in the mentioned area, while leaving the practically unchanged values for the rest of the (correct) areas.

4.4. SATA dataset

The SATA Segmentation Challenge Dataset is a publicly available dataset composed of 35 training and 12 testing brain MR images, respectively. Our main goal here is to evaluate the performance of our methods in an online challenge. Training images contain the manual annotations of 14 mid-brain structures, including the left and right parts of the accumbens area, amygdala, caudate, hippocampus, pallidum, putamen and thalamus proper. Testing images do not contain any label, so the estimated segmentations were submitted to the SATA Challenge website, where the performance statistics were computed and published in the leaderboard⁶. Pairwise non-rigid registrations between the images are also provided.

Note that one of the methods participating in the challenge, denoted as PICSL, is the ensemble method, composed of Joint Label Fusion method by (Wang et al., 2013) and the learning-based post-processing step for systematic error correction by (Wang et al., 2011a).

In Table 6, we show the mean DR and the mean Hausdorff distance HD (in mm) obtained by the comparison methods.

Table 6.

Dice Ratio (%) and Hausdorff distance in the SATA challenge.

Method	Mean DR (std)	Mean HD (std)
MCfull	86.72 (2.83)	3.449 (0.650)
MCdeg	86.55 (2.88)	3.511 (0.718)
PICSL	86.43 (3.51)	3.458 (0.839)

As we can see, our proposed full method outperforms the rest of the methods in terms of both Dice ratio and Hausdorff distance. It is worth noting that our proposed full method (MCfull) achieves the 1st position in the overall ranking, whereas the degreaded version of our proposed full method (MCdeg) achieves the 3rd position (out of 14 methods). Specifically, our proposed full method obtains an improvement of ~0.3% with respect to the state-of-the-art ensemble method PICSL in both mean DR and HD, while having also lower standard deviations.

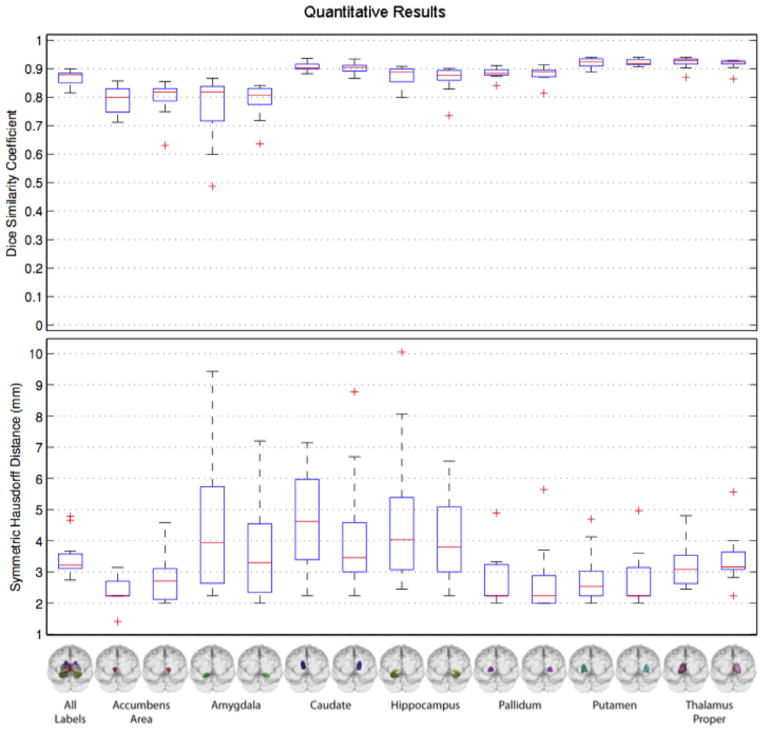
To give a further insight on the performance of our method, Fig. 12 shows the box plots across the different structures obtained by MCfull.

Fig. 12.

Dice ratio and Hausdorff distance (in mm) achieved by our full method (MCfull) across different structures in the SATA Challenge dataset.

As we can see, the segmentation results of our method are quite accurate with the mean results on all the structures above 80%, and on some structures above 90%.

5. Conclusions

We have presented a novel label fusion method that combines the reconstruction-based and classification-based approaches by formulating label fusion as a matrix completion problem. Latent labels on the target image are regarded as the missing entries in a four-quadrant matrix, which are estimated by imposing the low-rank constraint. Furthermore, we have presented a sequential confidence-guided framework that gradually estimates labels at each iteration in decreasing order of confidence, while leveraging the support from the more confident labels of previous iterations. This reduces the ambiguity in the dictionary, thus leading to a significant performance improvement as confirmed by the experimental results. Our full method outperforms all other comparison methods in all the experiments presented. Also importantly, it outperforms all the methods listed in the website of the online SATA Segmentation Challenge (MICCAI 2013). The proposed matrix-completion based approach outperforms both the purely reconstruction-based methods and the purely classification-based methods, thus confirming the benefit of our transversal approach. Another interesting conclusion is that including the neighboring atlas patches into the dictionary leads to performance improvements, as shown by the comparison between LWV and NLWV and also confirmed by other studies (Rousseau et al., 2011). Finally, both the statistical estimation and the MRF-based regularization implemented by STEPS have proven beneficial for label fusion, as deduced when comparing the results of STEPS and LWV.

Appendix A. Implementation details

In this section, we describe the following details of our method, namely, (A.1) computation of a continuous label map from the overlapping estimations, (A.2) discretization based on confidence threshold, and (A.3) construction of the initial tentative dictionary.

A.1. Computation of continuous label map from the overlapping estimations

As result of matrix-completion based label fusion, we obtain a low-rank matrix with continuous target labels. Such continuous labels can be interpreted as confidence values, such that the higher the values above zero, the more likely to represent a foreground voxel, and the lower the values below zero, the more likely to represent a background voxel. Since we predict the label values for the entire target patch, we end up with multiple estimations (from the neighboring patches) for each target image point. We average the multiple estimations of each point in order to obtain a single value. The fusion process described here corresponds to the function F = CombineOverlappingLabels(F) in the algorithms of Table 1 and Table 2, where F is the continuous label map obtained by averaging the overlapping estimations contained in F.

A.2. Confidence-based discretization

At the end of each iteration, we compute the discrete label map D^(s) by assigning labels to the most confident voxels according to a confidence threshold τ, which is decreased at each iteration. This procedure is denoted by the function D^(s) = Discretize(F, τ) in the algorithm of Table 2 and is carried out as follows:

$${\mathit{D}}^{(s)}(x)=\{\begin{array}{cc}1& \text{if}\mathit{F}(x)\ge \tau \\ -1& \text{if}\mathit{F}(x)<-\tau \\ \perp & \text{Otherwise}\end{array}$$ (A.1)

where F(x) denotes the confidence value at voxel x. Essentially, only the voxels with higher (in magnitude) confidence values above or below zero are assigned a label, whereas the voxels close to zero are left unassigned. As we decrease the confidence threshold, more ambiguous voxels are labeled. In the case of τ = 0, all voxels are assigned a label regardless of their confidence values.

A.3. Construction of the initial tentative dictionary

Recall that, matrix-completion based label fusion in Section 3.1 uses a dictionary of atlas patches, denoted as (A, L), to label a specific target patch centered at position x ∈ Ω. The sequential confidence-guided labeling framework in Section 3.2 further refines this initial tentative dictionary based on the label similarity. The dictionary building is denoted by the function (A, L) = BuildDictionary(I_k, L_k, t⃗, x) in algorithms in Table 1 and Table 2. Both spatial proximity and appearance similarity to the target patch have been demonstrated to be good criteria to build the dictionary (Coupe et al., 2011; Rousseau et al., 2011). According to spatial proximity, we select the patches in the neighborhood of the target patch from all the atlases. That is, we build the dictionaries A = [a⃗₁ … a⃗_qm] and L = [l⃗₁ … l⃗_qm] from q patches of each of all m atlases in the neighborhood of the target patch. According to image similarity, we exclude the neighboring atlas patches whose appearance similarity with the target patch is below a certain image similarity threshold γ. Using the same criterion as in (Coupe et al., 2011), we only keep the atlas patches a⃗_j satisfying the following equation:

$$\frac{2{\mu }_{\overrightarrow{t}}{\mu }_{{\overrightarrow{a}}_j}}{{\mu }_{\overrightarrow{t}}^2+{\mu }_{{\overrightarrow{a}}_j}^2}\times \frac{2{\sigma }_{\overrightarrow{t}}{\sigma }_{{\overrightarrow{a}}_j}}{{\sigma }_{\overrightarrow{t}}^2+{\sigma }_{{\overrightarrow{a}}_j}^2}>\gamma$$ (A.2)

where μ_t⃗ and σ_t⃗ denote the mean and standard deviation of image patch t⃗ and 0 ≤ γ ≤ 1 is the image similarity threshold.

Appendix B. Details of the classification-based method

As representative of the classification-based methods, we have implemented a label fusion variant closely related to our proposed method, i.e., using the logistic regression (LogReg) to learn the relationship between image appearance and anatomical labels of the atlas patches in the dictionary. The labels on each target patch, denoted as f⃗, are then computed as a mapping of its appearance vector, denoted as t⃗, by using the learned relationship, as follows:

$$\overrightarrow{f}=\text{logit}(V^{\top }\overrightarrow{t}+\overrightarrow{c})$$ (B.1)

where logit(·) is the logistic function (a smoothed sign function), and V and c⃗ are the relationship matrix and bias vector, respectively. We learn the relationship between atlas appearance and labels using multi-task logistic regression⁷ (Liu et al., 2009), where each label in the patch is encoded as an individual task. This corresponds to the following optimization problem:

$$\underset{V,\overrightarrow{c}}{min}{\mathrm{C}}_{\text{LL}}\left(L,V^{\top }\left[\begin{array}{c}A\\ {\overrightarrow{1}}^{\top }\end{array}\right]+\overrightarrow{c}\right)+\alpha {\Vert V\Vert }_{{\ell }_1/{\ell }_2}$$ (B.2)

where C_LL(·) is the element-wise logistic loss between two matrices, and ||V||_{ℓ1/ℓ 2} is the regularization enforcing sparsity across the rows of the matrix V and thus encouraging the sharing of features across different tasks (i.e., predictions of multiple labels in the target patch). The amount of regularization is controlled by the parameter α.