Evaluation of machine learning algorithms for treatment outcome prediction in patients with epilepsy based on structural connectome data

Abstract

The objective of this study is to evaluate machine learning algorithms aimed at predicting surgical treatment outcomes in groups of patients with temporal lobe epilepsy (TLE) using only the structural brain connectome. Specifically, the brain connectome is reconstructed using white matter fiber tracts from presurgical diffusion tensor imaging. To achieve our objective, a two-stage connectome-based prediction framework is developed that gradually selects a small number of abnormal network connections that contribute to the surgical treatment outcome, and in each stage a linear kernel operation is used to further improve the accuracy of the learned classifier. Using a 10-fold cross validation strategy, the first stage in the connectome-based framework is able to separate patients with TLE from normal controls with 80% accuracy, and second stage in the connectome-based framework is able to correctly predict the surgical treatment outcome of patients with TLE with 70% accuracy. Compared to existing state-of-the-art methods that use VBM data, the proposed two-stage connectome-based prediction framework is a suitable alternative with comparable prediction performance. Our results additionally show that machine learning algorithms that exclusively use structural connectome data can predict treatment outcomes in epilepsy with similar accuracy compared with “expert-based” clinical decision. In summary, using the unprecedented information provided in the brain connectome, machine learning algorithms may uncover pathological changes in brain network organization and improve outcome forecasting in the context of epilepsy.

Introduction

Improvements in computational analyses of neuroimaging data now permit the assessment of whole brain maps of structural connectivity. The combination of gray and white matter maps from anatomical magnetic resonance imaging (MRI) with white matter fiber tractography from the diffusion tensor imaging (DTI), MRI sequences enables the reconstruction of the architecture of medium and large connections in the brain, commonly referred to as the brain connectome (Sporns, 2013). The brain connectome provides unprecedented information about global and regional conformations of neuronal network architecture. This information is particularly relevant as it relates to neurological or psychiatric disorders such as epilepsy (Richardson, 2012; Engel et al., 2013; Taylor et al., 2014), schizophrenia (Rubinov and Bullmore, 2013; Crossley et al., 2014; Griffa et al., 2015), and Alzheimer's disease (Xie and He, 2011; Daianu et al., 2013; Zhu et al., 2014), which are believed to be directly associated with restructuring of complex neuronal networks.

In this context, epilepsy is a neurological disorder directly associated with pathological changes in brain network organization. Even though most forms of epilepsy are believed to arise from epileptogenic activity emerging from localized brain areas, there is a growing body of evidence suggesting that focal seizures are in reality the result of hyperexcitation of localized networks, rather than isolated cortical regions (Spencer, 2002; Richardson, 2012). Likewise, the propagation of seizures may be due to the abnormal rearrangement of networks adjacent to the seizure onset zone, which, instead of inhibiting the epileptogenic activity and aborting the seizure, provides the framework for anatomical dissemination of pathological excitability.

Temporal lobe epilepsy (TLE) is one of the most common forms of epilepsy. It is defined by seizures arising from the medial temporal lobe, and the proportion of patients with epilepsy who are, or become, clinically resistant to pharmacotherapy ranges from 30 to 40% (Sander, 1993; Hart and Shorvon, 1995; Devinsky, 1999; Brodie and Kwan, 2002;Kwan and Brodie, 2004). Surgery for TLE is a potentially curative form of treatment, but the presurgical diagnostics use expert clinical information (i.e., human knowledge, conventional imaging, and neurophysiology) and seizure freedom after surgery is only achieved approximately 70% of the time (Wiebe et al., 2001; Keller et al., 2007; Bien et al., 2013). Furthermore, other studies (Bonilha et al., 2012a; Bonilha et al., 2013) have demonstrated that refractory TLE is associated, on average, with connectome reorganization and the strengthening of temporal–extratemporal connectivity. Thus, the evaluation of the brain connectome in the context of epilepsy is of utmost importance, since it can provide unprecedented information regarding the organization of neuronal architecture that may be crucial to the neurobiology of the disease.

The development of automated algorithms that can select subtle tissue features capable of differentiating pathological conditions is a challenging problem in the medical image analysis community. Recently, classification methods based on voxel-based morphometry (VBM) (Ashburner and Friston, 2000) data have proposed the use of MRI white and/or gray matter tissue structures to predict TLE with hippocampal sclerosis (Focke et al., 2012) or predict the surgical treatment outcome of a patient with TLE (Feis et al., 2013). In general, methods that use VBM data have several limitations that include estimating the amount of noise in the gray scale pixel intensity values, accurately detecting relevant tissue structure patterns in regions with poor contrast differences, and the number of tissue features (i.e., number of dimensions) is typically much greater than the total number of samples (i.e., number of individual MRI images) in the study. Even though experts may debate (Bookstein, 2001; Ashburner and Friston, 2001) about the validity of VBM approaches, classification methods based on VBM data have been shown to perform well in Alzheimer's disease applications (Kloppel et al., 2008; Cuingnet et al., 2011; Casanova et al., 2011). To overcome some of these limitations in TLE classification applications, a ranked grid search approach (Feis et al., 2013) is proposed to pre-select the most important tissue features prior to model construction. However, this approach is based on a heuristic algorithm that requires human input to guide the pre-selection process so the resulting subset of selected tissue features can be sub-optimal (Gu et al., 2011). Hand-crafted local weighting maps (Focke et al., 2012) have also been proposed, however, this approach typically works well for localized tissue structures and not well for ones that are spatially distributed (Focke et al., 2011; Kloppel et al., 2009). In either case, the proposed tissue feature selection approaches may produce classifiers that are over-tuned to one particular neuroimaging training data set, and thus may perform poorly when applied to unseen neuroimaging data.

To complement conventional structural MRI analysis methods based on VBM data, a new connectome-based prediction framework is proposed that uses the elastic net (Zou and Hastie, 2005) regularization and feature selection algorithm to identify abnormal network connections, or network features, in connectomes reconstructed using white matter fiber tracts from presurgical DTI. In particular, elastic net is a supervised sparse learning technique that combines a least squares linear regression algorithm with a ℓ₁ regularization term (Tibshirani, 1994) and a ℓ₂ regularization term (Hoerl and Kennard, 2004). Over the last several years, sparse learning techniques have been successfully applied to several neuroimaging applications to improve the accuracy of the constructed model (Carroll et al., 2009; Ryali et al., 2010; Bunea et al., 2011; Ryali et al., 2012; Casanova et al., 2011, 2012; Mohr et al., 2015). Specifically, in Ryali et al. (2012) elastic net is used to better estimate partial correlations between brain regions in functional networks reconstructed from resting-state fMRI (rs-fMRI) time series data, and in Casanova et al. (2012) linear regression with ℓ₁ only regularization (i.e., lasso method, Tibshirani, 1994) is used to better identify gender associated differences in brain connectivity networks reconstructed from rs-fMRI time series data. Even though sparse learning techniques have been applied on brain connectivity networks reconstructed from fMRI data, such techniques have not been consistently applied to brain connectivity networks reconstructed from DTI white matter fiber tract data, epilepsy or epilepsy surgical outcome predictions. Unfortunately, our connectome-based prediction framework still suffers from one significant limitation, the number of subjects in the training population is much less than the number of network features defined in the connectome. To overcome this limitation, two new techniques are introduced: 1) A two-stage elastic net feature selection and regularization approach is proposed that gradually selects a small subset of presurgical network features that can be used to train an SVM classifier capable of predicting the surgical treatment outcome of patients with TLE, and 2) prior to SVM training a linear kernel operation is performed that creates a highly compact and symetric feature matrix. This operation ensures that the learned SVM decision boundary will have an exact solution.

In this study we evaluate whether these new sparse machine learning techniques can accurately differentiate patients with epilepsy from healthy controls and predict surgical treatment outcomes regarding seizure controls within the epilepsy group. We hypothesized that these methods would permit an accurate estimate of surgical outcome groups that is at least equal or superior to the current clinical standards. Importantly, we aimed to evaluate whether this accuracy in surgical outcome estimation could be derived from connectome data alone, and not in combination with other clinical or imaging data, thus implying a role of structure network organization in the pathophysiology of epilepsy.

Methods and materials

Participants

We retrospectively studied a cohort of 35 consecutive patients with refractory TLE who were treated at the Comprehensive Epilepsy Center at the Medical University of South Carolina (MUSC), and 35 patients with refractory TLE treated at the University of Bonn in Germany. The demographic information for these patients are provided in Table 1. All patients had medically refractory TLE due to hippocampal sclerosis, or with medical refractory lesional TLE. All patients were diagnosed according to the criteria defined by the International League Against Epilepsy (ILAE) (Commission on Classification Terminology of the International League Against Epilepsy, 1989), including a comprehensive neurological evaluation, ictal electroencephalography (EEG) recordings, diagnostic MRI, and, when appropriate, nuclear medicine studies. All cases exhibited unilateral temporal lobe seizure onset during ictal EEG monitoring. All patients had routine diagnostic MRI revealing unilateral hippocampal atrophy (concordant with the side of ictal EEG seizure onset). Patients with structural abnormalities on MRI other than hippocampal atrophy or T2 signal hyper-intensity were excluded from this study.

Table 1.

MUSC and Bonn patient and normal control demographics (note: age is measured in years).

Site	Total patients	Average age	Maximum age	Minimum age	Male	Female
Demographics of MUSC and Bonn patients with TLE
MUSC	35	41.4	68	19	11	24
Bonn	35	38.7	62	16	16	19
Demographics of MUSC and Bonn normal controls.
MUSC	18	38.6	67	20	8	10
Bonn	30	43.9	70	18	18	12

All patients were refractory to at least two first-line anti-epileptic medications. All MUSC patients underwent anterior temporal lobectomy, and all Bonn patients underwent amygdalohippocampectomy. We assessed surgical outcome based on the Engel Surgical Outcome scale (Engel et al., 2003) defined at least one year after surgery. Patients were classified into two groups: 1) free of disabling of seizures (i.e., seizure-free), equivalent to Engel Class I (including Class 1b patients with auras only) (18 MUSC patients and 23 Bonn patients); and 2) not seizure-free, equivalent to Engel Classes II, III or IV (17 MUSC patients and 12 Bonn patients).

As local control groups, we studied 18 healthy individuals at MUSC and 30 healthy individuals at Bonn. The demographic information for normal control group is provided in Table 1. All individuals in the control group had no significant past medical history of neurological or psychiatric problems.

The Medical University of South Carolina and the University Bonn Institutional Review Boards approved this study. Written informed consent was obtained from all control subjects. Data from patients was obtained retrospectively through chart review and MRI analysis. Patient data were obtained as standard of care for medication refractory epilepsy and were reviewed under the “waiver of consent” category.

MRI acquisition

The same imaging protocol was applied to all MUSC study participants (patients and controls). Images were acquired on a Siemens 3 T Verio MRI scanner equipped with a 12-channel head coil. The imaging protocol yielded a high-resolution T1-weighted image, with an isotropic voxel size of 1 mm (TR = 2250 ms, TE = 41 ms, FOV = 256 × 256 mm²). Diffusion-weighted images were obtained using two diffusion weightings (b = 0 and 1000 s/mm²) along 30 diffusion-encoding directions (TR = 10,600 ms, TE=100 ms, FOV=224 × 224 mm², parallel imaging factor of 2, slice thickness = 2 mm, and 60 axial slices, isotropic voxel size of 3 mm).

Similarly, the same imaging protocol was applied to all Bonn study participants (patients and controls). Images were acquired on a Siemens 3 T Trio scanner equipped with an 8-channel head coil. The imaging protocol yielded a high-resolution T1-weighted image, with an isotropic voxel size of 1 mm (TR = 1300 ms, TE = 3.97 ms, FOV = 256 × 256 mm²). Diffusion-weighted images were obtained using two different diffusion weightings (b = 0 and 1000 s/mm²) along 60 diffusion-encoding directions (TR = 12,000 ms, TE = 100 ms, FOV = 220 × 220 mm², parallel imaging factor of 2, slice thickness = 1.7 mm, and 72 axial slices, isotropic voxel size of 1.726 mm).

Image processing

DICOM images were converted to NIfTI format (with extraction of diffusion gradient directions) using dcm2nii in the MRIcron¹ software toolbox. The FMRIB Software Library (FSL) Diffusion Toolkit (FDT)² was used for preprocessing diffusion-weighted images and also for diffusion tensor estimation (Behrens et al., 2007; Heiervang et al., 2006). The images underwent eddy current correction through affine transformation of each DWI to the base b = 0, T2-weighted image.

White matter fiber tract reconstruction

Probabilistic tractography was used to define the number of white matter streamlines connecting each pair of cortical regions, which were defined according to an anatomical atlas. This step was iteratively performed until the connectivity between all possible pairs of cortical regions was determined. The connectivity information was then compiled in a brain connectome (i.e., symmetric two-dimensional connectivity matrix) using the steps outlined below.

Structural connectivity was obtained by applying FDT's probabilistic method for fiber tracking (Behrens et al., 2007; Ciccarelli et al., 2006; Behrens et al., 2003). Probabilistic tractography was performed on diffusion data after voxel-wise calculation of diffusion tensor. FDT's BEDPOST was used to build default distributions of diffusion parameters at each voxel. Probabilistic tractography was obtained using FDT's probtrackx with 5000 individual streamlines drawn through the probability distributions on the principal fiber direction. We chose to employ probabilistic tractography in this study, since it is theoretically capable of accommodating intra-voxel fiber crossings (Behrens et al., 2007; Nucifora et al., 2007).

Cortical seed regions for tractography were obtained from an automatic segmentation process, employing FreeSurfer³ on the T1weighted images. This process subdivides the human cerebral cortex into sulcogyral based cortical and subcortical regions of interest (ROIs) by automatically assigning a neuroanatomical label to each location on a cortical surface model, based on the probabilistic information estimated from a manually labeled training set (the Lausanne anatomical atlas, distributed as part of the Connectome Mapping Toolkit,⁴ yielding 82 ROIs in the subjects native T1-weighted space (41 regions in each hemisphere)). All processed images were visually inspected to ensure the cortical segmentation quality.

The ROIs were transformed into each subject's DTI space using an affine transformation obtained with FSL's FLIRT. Probabilistic tractography was performed using each of the 82 cortical ROIs in diffusion space as the seed region. Supplementary Table 1 provides an anatomical description of all ROIs employed in this study.

Presurgical connectome reconstruction

For each subject, a comprehensive presurgical neural connectivity map, or connectome, is calculated, where the connectivity is measured by the number of probabilistic white matter fiber tract streamlines arriving at ROI j when ROI i was seeded, averaged with the number of probabilistic white matter fiber tract streamlines arriving at ROI i when ROI j was seeded. The step is iteratively repeated to ensure all 82 cortical ROIs were treated as seed regions. Once all iterations are completed, a symmetric 82 × 82 density connectivity map D is constructed, where D_ij corresponds to the weighted network connection (or network connection for short) between ROIs i and j. Since the number of streamlines between i to j and j to i are averaged, D is symmetric with respect to the main diagonal, i.e., D_ij = 0 when i = j. Example connectomes using the described reconstruction procedure can be seen in Fig. 1. In particular, three different connectomes are shown: 1) normal control, 2) patient with TLE that is seizure-free after surgery is performed, and 3) patient with TLE who is not seizure-free (i.e., continue to experience seizures) after surgery.

Fig. 1.

Example symmetric 82 × 82 connectivity map constructed using method outlined in the Presurgical connectome reconstruction section for normal control, seizure-free, and not seizure-free patients, respectively. The brain structures are numbered from 1 to 82 in accordance with the atlas provided in Supplementary Table 1. Regions 1 to 42 represent the hemisphere contralateral to seizure onset, and 43 to 82 represent the hemisphere ipsilateral to seizure onset. Within each hemisphere, the regions are grouped as follows: frontal lobe, temporal lobe, basal nuclei, parietal lobe, and occipital lobe.

Two-stage connectome-based prediction framework

The block diagram shown in Fig. 2 illustrates the basic design and operation of the proposed two-stage connectome-based prediction framework. In particular, the proposed framework defines a Stage-1 prediction pipeline that is able to separate patients with TLE from normal controls, and a Stage-2 prediction pipeline that is able to predict the surgical treatment outcome of patients with TLE. It is important to point out that the Stage-2 prediction pipeline is dependent on the Stage-1 prediction pipeline. That is, the output of the Stage-1 connectome feature selection component is the input to the Stage-2 connectome feature selection component. Furthermore, each prediction pipeline defines three trained components, i.e., connectome feature selection, linear kernel operation, and linear SVM classifier, which are sequentially applied one after the other. The technical details describing how each of the three pipeline components are constructed and trained is provided in the Connectome feature selection pipeline component, Linear kernel operation pipeline component and Support vector machine classifier pipeline component sections.

Fig. 2.

Block diagram that illustrates the basic design and operation of the proposed two-stage connectome-based prediction framework. The framework defines two different prediction pipelines, specifically a Stage-1 prediction pipeline, and a Stage-2 prediction pipeline. Each prediction pipeline has three trained components: 1) connectome feature selection, 2) linear kernel operation, and 3) linear SVM classifier. Note that the superscript value identifies the stage.

The rationale behind the two-stage design is directly related to the number of network connections (i.e., features) defined in the connectome. Specifically, using only one stage to identify a small subset of features (less than a hundred) from thousands that contribute to the surgical treatment outcome is a very challenging feature selection problem for any machine learning algorithm. Instead, the proposed two-stage design takes a more controlled approach by gradually reducing a high-dimension connectome feature space to a lower-dimension one, thus making the problem more tractable.

In general, the three trained components in the Stage-1 prediction pipeline are sequentially applied as follows: Given a presurgical high-dimension connectome feature vector v not included in the training data set, the connectome feature selection component estimates a new sparse connectome feature vector s¹ by applying the learned binary mask to v. The binary mask used by the connectome feature selection component in this stage identifies network connections in v that are able to differentiate patients with TLE from normal controls (i.e., multiply these features by one), and connectome features that are not able to differentiate patients with TLE from normal controls (i.e., multiply these features by zero). Next, only the non-zero features output from the connectome feature selection component are input into the linear kernel operation component and a highly compact feature vector ŝ¹ using a well-known kernel transformation technique is created. Lastly, the output of the linear kernel operation component is input into linear two-class SVM classifier component to predict the group outcome y¹ (i.e., patient with TLE or normal control).

The three trained components in the Stage-2 prediction pipeline are sequentially applied as follows: Given the sparse connectome feature vector s¹ found in the first stage, the connectome feature selection component in the second stage estimates a new sparse connectome feature vector s² by applying a different learned binary mask to s¹. In particular, the binary mask used by the connectome feature selection component in the second stage identifies network connections in s¹ that are able to differentiate seizure-free from not seizure-free patients after surgery (i.e., multiply these features by one), and connectome features that are not able to differentiate seizure-free from not seizure-free patients after surgery (i.e., multiply these features by zero). Next, only the non-zero features output from the connectome feature selection component are input into the linear kernel operation component and a highly compact feature vector ŝ² using a well-known kernel transformation technique is created. Lastly, the output of the linear kernel operation is input into the linear two-class SVM classifier component to predict the surgical treatment outcome y² (i.e., seizure-free or not seizure-free).

Connectome feature selection pipeline component

Given a n × m training data matrix A = [a₁, a₂, …, a_i, …, a_n]^t of n subjects, where row vector a_i = (a_i1, …, a_im) is a m dimension presurgical connectome feature vector for subject i whose elements are the upper diagonal values of their connectivity map developed in the Presurgical connectome reconstruction section, and y = (y₁, y₂, …, y_n) is an n dimension vector whose values are the class labels (binary value indicating the clinical outcome) of subjects in the training data set, i.e., the class label for row vector a_i is y_i. Because m ≫ n, the elastic net (Zou and Hastie, 2005) technique is used to find a sparse m dimension weight vector x that minimizes

$$\underset{x}{\mathit{\text{min}}}\frac{1}{2}{\Vert Ãx-y\Vert }_2^2+\frac{\rho }{2}{\Vert x\Vert }_2^2+\lambda {\Vert x\Vert }_1,$$ (1)

where λ‖x‖₁ is the ℓ₁ regularization (sparsity) term, $\frac{\rho }{2}{\Vert x\Vert }_2^2$ is the ℓ₂ regularization (smoothness) term, and à is a n × m matrix with normalized training data. Specifically, Ã(i, j) = (a_ij − μ_j)/σ_j where a_ij is network connection j for subject i, μ_j is the mean value of column vector j in matrix A, and σ_j is the standard deviation of column vector j in matrix A.

After optimization, x has weight values in [0 1], where weight values equal to zero indicate network connections that do not contribute to the clinical outcome, and weight values greater than zero indicate network connections that do contribute to the clinical outcome. In general, x is referred to as the sparse representation of training data set. Lastly, each weight value in x greater than zero is set to one. Therefore, the resulting sparse representation can be perceived as a binary mask, i.e., the network connection is turned on (value of 1) or turned off (value of 0). A new sparse training data matrix S = [s₁, s₂, …, s_n]^t is created, where row vector s_i = (a_i1x₁, a_i2x₂, …, a_imx_m).

The cost function in Eq. (1) is optimized using the LeastR method in the sparse learning with efficient projections (SLEP) software package,⁵ and the λ and ρ values used by the sparse learning algorithm were set to 0.5 and 1.0, respectively, for each prediction pipeline in the proposed two-stage connectome-based framework.

Linear kernel operation pipeline component

Even though the learned sparse representation can greatly reduce the dimension of the input connectome feature vector, the number of non-zero features in the newly created sparse training data matrix will most likely not be equal to the number of training data subjects. This condition may result in an over-determined system of equations (with more subjects than features), or an under-determined system of equations (with more features than subjects). In both cases, there may be an infinite number of solutions, or no solution, to this system of linear equations, which in turn may severely impact the accuracy of the trained classifier. To overcome this limitation, a symmetric m̃ × m̃ Gramian (Lanckriet et al., 2004) matrix Ŝ is constructed using the linear transformation

$$Ŝ=S^{t}S,$$ (2)

where S^t is the matrix transpose and m̃ is the number of non-zero features in the sparse representation. It is important to note that these more compact features cannot be mapped back to a single network connection. In fact, each feature in this newly formed mathematical space is the inner product of two network connection vectors.

Support vector machine classifier pipeline component

Finally, Ŝ and y are used to train a linear two-class SVM classifier based on the LIBSVM library.⁶ Once the SVM classifier is trained, the surgical treatment outcome of an m dimension presurgical connectome feature vector, say v = (v₁, v₂, …, v_m), not included in the training data set, can be predicted using the sequence of steps provided below.

1. Normalize each value in v using the learned centering and magnitude scaling values for the j = 1, …, m network connection features, ṽ_i = (v_i − μ_j)/σ_j.

2. Create sparse connectome feature vector s = (ṽ₁x₁, ṽ₂x₂, …, ṽ_mx_m) by applying learned binary mask. All features that have a zero value are removed, resulting in a m̃ dimension connectome feature vector.

3. Apply learned linear transformation to obtain m̃-dimension feature vector s = (ŝ₁, ŝ₂, …, ŝ_m̃) where

   $${ŝ}_i=\sum _{j=1}^{\tilde{m}}{s}_jŜ(j,i),$$

   for i = 1, …, m̃.

4. Calculate the predicted class label

   $$y=\sum _{i=1}^{\tilde{m}}{\alpha }_{i}k({\varphi }_i,ŝ)+b,$$

where k(·) is the inner product of two vectors, and α_i is the weight, ϕ_i is the support vector, and b is the bias that defines the linear hyperplane (decision boundary) learned by the SVM classifier. The sign of the calculated prediction value (i.e., y ≥ 0 or y < 0 y < 0) determines the class label the testing subject is assigned to.

Prediction framework performance evaluation

The performance of the prediction framework is evaluated using a 10-fold cross-validation strategy. In particular, the Bonn and MUSC subjects are first combined into one data set, and then partitioned into 10 different folds, where each fold contains connectomes of randomly selected patients (i.e., a mixture of seizure free and not seizure free) and/or randomly selected normal controls. The prediction framework is iteratively trained using the connectome data in 9 of the 10 folds, and then tested using the connectome data in the remaining (or left-out) fold. This iterative process terminates when each fold has been selected as the test one. Using the combined confusion matrix (TP = true positive, FP = false positive, FN = false negative, and TN = true negative) results of each test fold, the prediction performance is reported using the specificity, sensitivity, positive predictive value, negative predictive value, and accuracy measures, where

• Sensitivity (SEN) = TP / (TP + FN),

• Specificity (SPE) = TP / (FP + TN),

• Positive predictive value (PPV) = TP / (TP + FP),

• Negative predictive value (NPV) = TN / (TN + FN), and

• Accuracy (ACC) = (TP + TN) / (TP + FN + FP + TN).

Feature selection using sparse canonical correlation analysis

For performance comparison purposes, SVM classifiers are also trained using presurgical connectome features selected by a sparse canonical correlation analysis (SCCA) method. This is accomplished by simply replacing the elastic net algorithm outlined in the Connectome feature selection pipeline component section with SCCA. Using the SCCA method described in Avants et al. (2010), the sparse representation x = x_β ∪ x_α was found that maximizes

$${\mathit{\text{max}}}_{{\mathrm{x}}_{\alpha },{\mathrm{x}}_{\beta }}{\mathrm{x}}_{\alpha }{Ā}_{\alpha }^t{Ā}_{\beta }{\mathrm{x}}_{\beta }-({\lambda }_{\beta }{\Vert {\mathrm{x}}_{\beta }\Vert }_1+{\lambda }_{\alpha }{\Vert {\mathrm{x}}_{\alpha }\Vert }_1),$$ (3)

where Ā_α is a normalized training data matrix that only contain subjects with class label α (e.g., disorder condition), Ā_β is a normalized training data matrix that only contain subjects with class label β (e.g., normal condition), and λ_β‖x_β‖₁ and λ_α‖x_α‖₁ are ℓ₁ regularization (sparsity) terms. In general, after the cost function in Eq. (3) is optimized, the canonical weight values in vectors x_α and x_β maximize the correlation between normalized training data matrices Ā_α and Ā_β. Like the approach in Avants et al. (2010),we took only the first component of the SCCA solution, however, we only selected the canonical weight values that were less than zero. In general, a negative value indicates that the same connectome feature is negatively correlated in the two normalized training data sets, which suggests that these connectome features are more likely to differentiate the disorder condition from the normal one. As a result, each canonical weight value in x_α and x_β that is less than zero is set to one, and the remaining ones are set to zero. Finally, the sparse representation x is found by finding the union of the binary values in x_α and xβ.

The SCCA cost function in Eq. (3) is optimized using a modified version of the LS_CCA method,⁷ and the λ_α and λ_β values used by the ℓ₁ regularization (sparsity) terms were both set to 0.5 for the prediction pipeline results reported in the Results section.

Feature selection using a deep non-linear hierarchical model

For performance comparison purposes, SVM classifiers are also trained using low dimension presurgical connectome feature codes found by a deep learning method (Hinton and Salakhutdinov, 2006; Lee et al., 2009; Le et al., 2011). Since elastic net and sparse canonical correlation analyses are both based on linear models, deep learning is an attractive machine learning alternative because it is capable of encoding latent, non-linear relationships in high dimension data. In particular, the basic concept is to learn the highly compact hierarchical feature representations by inferring simple ones first and then progressively building up more complex ones from the previous levels.

In general, a deep network is trained in two sequential steps: 1) an unsupervised step, i.e., training individual auto-encoders (AE) as illustrated in Figs. 3(a), and 2) a supervised step, i.e., stacking the initialized AEs (creating the deep network) and then fine-tuning by the known binary training labels as illustrated in Fig. 3(b). In the unsupervised step, each AE is trained separately producing weights and bias values that increase the likelihood of finding the global optimum, or at least a very good local minimum, during the supervised step. In the supervised step, one additional layer is added (a training label layer that include the binary class label), and the resulting deep network is treated like a traditional feed forward neural network that uses back propagation to fine-tune the initial weight values. Once the supervised step completes, the training label layer is removed, and the number of nodes in last hidden layer represents the final dimension of the output low dimension code (LDC). The resulting LDCs along with the binary class labels are then used to train a SVM classifier. Finally, the outcome of brain connectomes not included in the training data set can be predicted by first estimating the LDCs using the trained deep network, and then classifying the LDCs using the learned SVM classifier.

Fig. 3.

Training of deep learning (DL) network includes an unsupervised and a supervised training procedure. In particular, (a) in the unsupervised training step each auto-encoder (i.e., AE1 and AE2) is trained separately, and each AE only defines two layers (visible and hidden). Once training is completed, the hidden layer of the current auto-encoder (AE1) becomes the visible layer of the next auto-encoder (AE2), and the unsupervised training step repeats itself with AE2. (b)When each AE has been trained, they are stacked to form a deep network. At this point a training label layer (that defines the known diagnosis labels) is added and the supervised training step is initialed to create a fine-tuned deep network.

The deep networks were implemented using the DeepLearnToolbox software package.⁸ For both stages, the momentum and learning rate was set to 0.3 and 1.5, respectively. The architecture used to generate the prediction results in the Stage-1: TLE prediction pipeline section was set to [3321 1000 500 200 100] (i.e., 5 layers, with the first layer having 3321 nodes, the second layer having 1000 nodes, the third layer having 500 nodes, the fourth layer having 200 nodes, and the last layer having 100 nodes), where the output dimension of the LDC found by the deep learning network is 100. The architecture used to generate the prediction results in the Stage-2: surgical treatment outcome prediction pipeline was set to [383 100 50 15] (i.e., 4 layers, with the first layer having 383 nodes, the second layer having 100 nodes, the third layer having 50 nodes, and the last layer having 15 nodes), where the output dimension of the LDC found by the deep learning network is 15.

Single-stage surgical treatment prediction framework with optimal elastic net regularization parameters

For performance comparison purposes, a single-stage connectome-based framework with only one pipeline trained to predict the surgical treatment outcome is constructed as shown in Fig. 4. There are two significant differences between the trained connectome feature selection pipeline component in the single-stage framework, and the trained connectome feature selection pipeline component in the proposed two-stage framework shown in Fig. 2. Specifically, in the single-stage connectome feature selection pipeline component the elastic net feature selection and regularization algorithm is trained: 1) using all m connectome features, and 2) using the optimal ℓ₁ and ℓ₂ regularization parameter values.

Fig. 4.

Single-stage connectome-based prediction framework that only has one pipeline trained to predict the surgical treatment outcome of a patient with TLE. In general, the pipeline includes three trained components: 1) connectome feature selection, 2) linear kernel operation, and 3) linear SVM classifier.

In general, the three trained components in single-stage surgical outcome prediction pipeline are sequentially applied as follows: Given a presurgical m-dimension connectome feature vector v not included in the training data set, a new sparse connectome feature vector s is found by applying a learned binary mask to v, where the binary mask identifies only those presurgical network connections in v that are able to differentiate seizure-free patients from patients that continue to have seizures after surgery is performed. Only the non-zero features output from the connectome feature selection component are then input into the linear kernel operation component and a highly compact feature vector ŝ is created. Lastly, the output of the linear kernel operation is input into the linear two-class SVM classifier component to predict the surgical treatment outcome y (i.e., seizure-free or not seizure-free).

To estimate the optimal ℓ₁ regularization parameter (λ̃) value and ℓ₂ regularization parameter (ρ̃) value used by the elastic net algorithm in the single-stage feature selection pipeline component, a two-nested grid search scheme, similar to the scheme in Casanova et al. (2012), is executed. In particular, the external and internal cross-validation procedures both use the 10-fold cross-validation strategy described in Section 2.5. For each training step in the internal cross-validation procedure, the λ grid point is sequentially changed from 0.05 to 1.0 at increments of 0.05, the ρ grid point is sequentially changed from0.6 to 2.5 at increments of 0.1, and for each pair of (λ, ρ) grid points a single-stage surgical treatment outcome prediction pipeline is trained using connectome data in 9 of the 10 folds and then tested using the remaining fold. When an internal 10-fold cross-validation procedure completes the (λ̃, ρ̃) grid points that produce the maximum average PPV measure are selected. Lastly, for each training step in the external cross-validation procedure the optimal (λ̃, ρ̃) regularization values estimated in the corresponding internal step are then used to train a new single-stage surgical treatment outcome prediction pipeline using connectome data in 9 of the 10 folds and then tested using the remaining fold. Finally, when the external cross-validation procedure completes the average PPV, NPV, sensitivity, specificity, and accuracy are calculated.

Site differences and prediction framework over fitting

One common problem encountered during the training procedure is for the sparse machine learning technique to over fit the constructed model to connectome data acquired from the same MRI scanner at the same site. In the ideal environment, at training completion the sparse representation estimated by the elastic net algorithm should only keep network connections that contribute to the surgical treatment outcome, and remove network connections that are specific to the scanner or the scanning site. In the over fitting case, a significant number of these unwanted network connections will be included in the sparse representation. As a result, when given unseen connectome data derived from subjects scanned using a different scanner at a different site, the over fit sparse representation could be too specific and may adversely affect prediction performance. Additionally, the over fit sparse representation estimated in the first stage will likely be propagated to the second stage, which may limit the performance of the entire prediction framework.

Since the MRI data was collected at two different MRI scanners (Siemens Verio and Trio) at two different sites (MUSC and Bonn), there is a unique opportunity to evaluate whether the over fitting issue is occurring, and to what extent. In particular, experiments that evaluate the TLE prediction pipeline and the surgical outcome prediction pipeline were both repeated. However, this time a 10-fold cross validation was not used, and the train and test data sets did not combine subjects from the two different sites. Instead, the training data only included the connectomes from MUSC subjects, while the testing data only included the connectomes from Bonn subjects.

Results

The results reported in this section are obtained with prediction pipelines trained and tested only using presurgical structural brain connectome data (i.e., no demographic or EEG data was used).

Stage-1: TLE prediction pipeline

In this experiment, the total number of subjects in the connectome data set is 118, including 70 patients with TLE (35 MUSC and 35 Bonn), and 48 normal controls (18 MUSC and 30 Bonn). This data set was randomly partitioned into 10-folds, where 8 of the 10 folds have 12 subjects, and 2 of the 10 folds have 11 subjects. Furthermore, the outcome (patient/normal control) and the site (MUSC/Bonn) ratios were maintained across each fold. The number of subjects in the training population is approximately 106, and each training subject is defined by a (81 × 82) / 2 = 3321 dimension connectome feature vector. Lastly, the binary class labels used to train the prediction pipeline are 0 = patient with TLE and 1 = normal control.

Table 2 shows the 10-fold results for three different prediction pipelines, i.e., training a SVM classifier with the connectome features selected by 1) elastic net (proposed), 2) SCCA, and 3) deep learning machine learning algorithms. The best performance (PPV = 90%, NPV = 70%, and ACC = 80%) was achieved by the first prediction pipeline that uses elastic net for feature selection.

Table 2.

TLE vs. normal control 10-fold results for three different prediction pipelines. In particular, each prediction pipeline is trained using connectome features selected by a different machine learning algorithm. The highest performance measures are shown in bold font.

Connectome feature selection algorithm	SEN	SPE	PPV	NPV	ACC
Elastic net (proposed)	74%	88%	90%	70%	80%
SCCA	69%	78%	86%	56%	72%
Deep learning	67%	73%	79%	59%	69%

The total number of non-zero network connections |w_t| selected by the elastic net algorithm, which can, $w_t={\cup }_{f=1}^{10}{w}_f$ is the union of each learned sparse representation for each fold. Using a two-sample t-test with α = 0.05, a paired⁹ p-value is calculated for each non-zero network connection in w_t and then sorted in ascending order, where the null hypothesis represents data that are independent random samples from normal distributions with equal means and equal but unknown variances. The top 15 non-zero network connections with the smallest p-values, i.e., those with the greatest difference between the two groups, can be seen in Table 3 and are also visualized in Fig. 5 using the Brainnet viewer (Xia et al., 2013) software package. The complete list of network connections (i.e., all 383) are provided in Supplementary Table 2.

Table 3.

The top 15 connected regions in the brain with the smallest p-value (i.e., presurgical network connections with the greatest difference between patients with TLE and normal controls).

Region	–	Region
Ipsilateral insula	–	Ipsilateral putamen
Contralateral insula	–	Contralateral putamen
Ipsilateral precentral	–	Ipsilateral postcentral
Contralateral parsorbitalis	–	Contralateral parstriangularis
Ipsilateral superiorfrontal	–	Ipsilateral rostralanteriorcingulate
Ipsilateral caudate	–	Ipsilateral accumbensarea
Contralateral precentral	–	Contralateral postcentral
Ipsilateral medialorbitofrontal	–	Ipsilateral superiorfrontal
Contralateral lateralorbitofrontal	–	Contralateral parsorbitalis
Contralateral rostralanteriorcingulate	–	Ipsilateral rostralanteriorcingulate
Ipsilateral precentral	–	Ipsilateral insula
Ipsilateral temporal pole	–	Ipsilateral amygdala
Ipsilateral medialorbitofrontal	–	Ipsilateral rostralanteriorcingulate
Contralateral parahippocampal	–	Contralateral hippocampus
Contralateral superiorparietal	–	Contralateral precuneus

Fig. 5.

The top 15 connected regions with the smallest p-value (i.e., the network connections with the greatest difference between patients with TLE and normal controls). The p-values are calculated using a two-sample t-test. Note that the brain regions (defined using the Lausanne anatomical atlas) are represented by the red nodes, and the edge connecting two brain regions represents a network connection in the connectome.

Stage-2: surgical treatment outcome prediction pipeline

In this experiment, the total number of patients with TLE in the connectome data set is 70 (including 35 MUSC patients and 35 Bonn patients). This data set was partitioned into 10-folds, where each fold has 7 subjects. Furthermore, the outcome (seizure-free/not-seizure-free) and the site (MUSC/Bonn) ratios were maintained across each fold. The number of patients in the training population is 63, and each training subject is represented by a connectome feature vector that only includes the 383 connectome features found by the Stage-1 connectome feature selection pipeline component (see Fig. 2). Lastly, the binary class labels used to train the prediction pipeline are 0 = not-seizure-free and 1 = seizure-free.

Table 4 shows the 10-fold results for four different prediction pipelines, i.e., training a SVM classifier with the connectome features selected by 1) elastic net (proposed two-stage framework), 2) SCCA, 3) deep learning, and 4) elastic net (single-stage framework) machine learning algorithms. The best performance (PPV = 63%, NPV = 72%, and ACC = 70%) was achieved by the prediction pipeline that only use the 383 found by the Stage-1 connectome feature selection pipeline component and the elastic net algorithm. Note: the learned binary mask found by the elastic net algorithm in the single-stage framework uses all 3321 connectome features. Additionally, the reported performance measures for the single-stage framework are the average values found using a two-nested grid search scheme that also estimates the optimal elastic net regularization parameters.

Table 4.

Seizure-free vs. not-seizure-free 10-fold results by four different prediction pipelines. In particular, each prediction pipeline is trained using connectome features selected by a different machine learning algorithm. The highest performance measures are shown in bold font.

Connectome feature selection algorithm	SEN	SPE	PPV	NPV	ACC
Elastic net (proposed two-stage framework)	59%	76%	63%	74%	70%
SCCA	61%	59%	61%	59%	60%
Deep learning	55%	58%	55%	58%	57%
Elastic net (single-stage framework, see the Single-stage surgical treatment prediction framework with optimal elastic net regularization parameters section)	69%	44%	53%	50%	51%

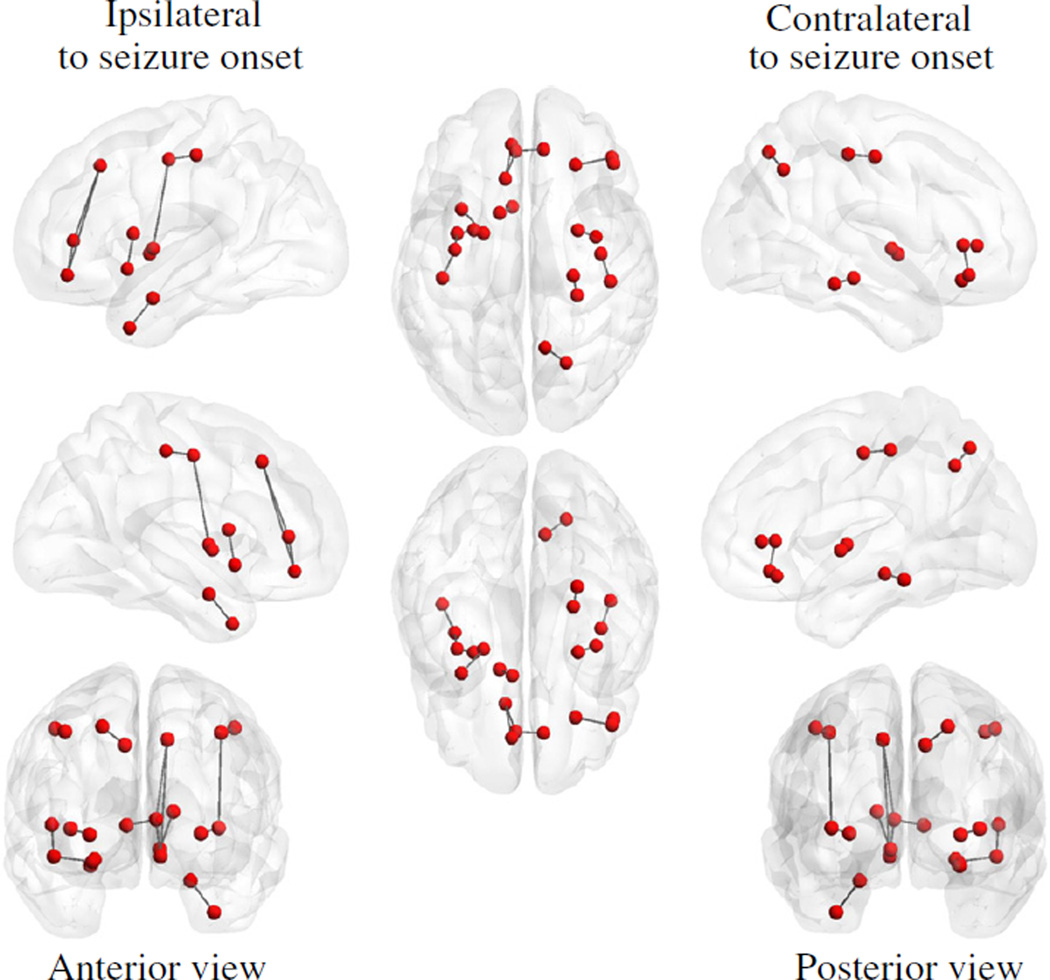
The total number of non-zero network connections |w_t| selected by the elastic net algorithm (in the second stage of the proposed two-stage framework), which can differentiate the seizure-free post-surgery group from the not-seizure-free post-surgery group, is 132. Using a two-sample t-test with α = 0.05, a paired p-value is calculated for each non-zero network connection in w_t and then sorted in ascending order, where the null hypothesis represents data that are independent random samples from normal distributions with equal means and equal but unknown variances. The top 15 non-zero network connections with the smallest p-values, i.e., those with the greatest difference between the two groups, can be seen in Table 5 and are also visualized in Fig. Fig. 6 using the Brainnet viewer (Xia et al., 2013) software package. The complete list of network connections (i.e., all 132) are provided in Supplementary Table 3.

Table 5.

The top 15 connected regions in the brain with the smallest p-value (i.e., presurgical network connections with the greatest difference between the seizure-free and not-seizure-free post-surgery groups).

Region	–	Region
Contralateral posterior cingulate	–	Ipsilateral frontal pole
Contralateral paracentral	–	Ipsilateral postcentral
Contralateral insula	–	Contralateral amygdala
Contralateral inferior temporal	–	Contralateral accumbens area
Ipsilateral medial orbitofrontal	–	Ipsilateral rostral anterior cingulate
Contralateral pericalcarine	–	Ipsilateral inferior temporal
Contralateral rostral anterior cingulate	–	Ipsilateral paracentral
Contralateral isthmus cingulate	–	Ipsilateral middle temporal
Contralateral parsorbitalis	–	Contralateral caudate
Contralateral pars triangularis	–	Contralateral inferior temporal
Contralateral rostral anterior cingulate	–	Contralateral entorhinal
Contralateral precentral	–	Contralateral postcentral
Contralateral caudate	–	Contralateral putamen
Ipsilateral rostral middle frontal	–	Ipsilateral caudal anterior cingulate
Contralateral isthmus cingulate	–	Ipsilateral insula

Fig. 6.

The top 15 connected regions with the smallest p-value (i.e., the network connections with the greatest difference between the patients that are seizure-free after surgery and the patients that are not seizure-free after surgery). The p-values are calculated using a two-sample t-test. Note that the brain regions (defined using the Lausanne anatomical atlas) are represented by the red nodes, and the edge connecting two brain regions represents a network connection in the connectome.

Site differences and prediction framework over fitting assessment

Table 6 shows the performance of the TLE prediction and surgical treatment outcome prediction pipelines trained using the connectomes of MUSC subjects, and tested using the connectomes of Bonn subjects. These results suggest that the proposed two-stage connectome-based prediction framework is robust to site and/or scanner differences. Furthermore, if an over fitting condition is indeed happening, this type of training error has a minimal impact on the performance of the proposed prediction framework.

Table 6.

Performances of connectome-based prediction framework by using MUSC subjects for training while Bonn subjects for testing. Note that only the proposed elastic-net based feature selection algorithm was used in these experiments.

SEN	SPE	PPV	NPV	ACC
Stage-1 TLE vs. normal control.
%	77%	79%	74%	77%
Stage-2 seizure-free vs. not-seizure-free.
%	58%	74%	54%	66%

Discussion

Using a 10-fold cross validation strategy, the performance of the two-stage connectome-based prediction framework is assessed using SVM classifiers trained with connectome features selected by the proposed elastic net learning algorithm, SVM classifiers trained with connectome features selected by a sparse conical correlation analysis algorithm, and SVM classifiers trained with connectome features selected by a deep learning algorithm. In each case, SVM classifiers trained with connectome features selected by elastic net were significantly more accurate than those trained with connectome features selected by sparse conical correlation analysis and by deep learning. Specifically, the connectome-based prediction framework is able to separate patients with TLE from normal control with 80% accuracy, and is able to predict the surgical treatment outcome of patients with TLE with 70% accuracy.

Surgical treatment outcome and model selection

In this study three different two-stage connectome-based prediction frameworks are evaluated, where each framework implements a different machine learning algorithm that is based on a particular mathematical model (or model for short). In general, two different types of models are compared in this study: 1) linear models such as elastic net and SCCA, and 2) a hierarchical non-linear model such as deep learning. Based on the 10-fold PPV, NPV, and accuracy results as reported in the Stage-2: surgical treatment outcome prediction pipeline section, a few important observations can be made:

• Compared to the classifiers trained using presurgical connectome features selected by a non-linear model, the classifiers trained using presurgical connectome features selected by a linear model are 1) approximately 8% more likely to recognize patients that are not seizure-free after surgery (PPV), 2) approximately 14% more likely to recognize patients that are seizure-free after surgery (NPV), and 3) approximately 13% more likely to correctly identify the surgical outcome (accuracy).

• Compared to the classifiers trained using presurgical connectome features selected by the SCCA model, the classifiers trained using presurgical connectome features selected by the elastic net model are 1) approximately 2% more likely to recognize patients that are not seizure-free after surgery (PPV), 2) approximately 13% more likely to recognize patients that are seizure-free after surgery (NPV), and 3) approximately 10% more likely to correctly identify the surgical outcome (accuracy).

The above observations suggest the relationship between the network connections in presurgical connectome and the surgical outcome are more linear than non-linear. Therefore, a linear model may be more suitable for surgical treatment outcome prediction in connectome-based classification applications.

Small sample size and high dimension data

One potential concern is that the number of subjects in the training population n is significantly less than the total number of network connections m defined in the brain connectome, i.e., m ≫ n. To mitigate this issue, the proposed connectome-based prediction framework employs the following two techniques:

• A two-stage feature selection approach. In the first stage, the elastic net algorithm selected 383 presurgical network connections from the original 3321 that are likely to differentiate patients with TLE from normal controls. This accounts for roughly an 88% reduction in network connections. In the second stage, the elastic net algorithm further selected 132 presurgical network connections from 383 that are now likely to differentiate patients that continue to have seizures from those that are seizure-free after surgery is performed. This accounts for roughly a 66% reduction in network connections. As also seen in Table 4, the two-stage feature selection approach is significantly more accurate than the single-stage feature selection approach with optimal elastic net regularization parameters. In general, breaking a larger feature selection problem into two smaller ones allows the elastic net algorithm to gradually and more accurately identify only those network connections that contribute most to the surgical treatment outcome.

• Linear kernel operation prior to classifier training. The two-stage feature selection approach outlined above can significantly reduce the number of features used to train a classifier, however, it is highly unlikely that the number of subjects in the training population will be equal to the number of non-zero features in the learned sparse representation. To ensure that the classification algorithm will converge to a unique solution, a linear kernel operation is performed. This mathematical operation produces the well known Gramian matrix (Lanckriet et al., 2004), which is widely used by machine-learning algorithms (Aizerman et al., 1964) that suffer from this same problem. As a result, the number of features used to train the classifier will be identical to the number of subjects in the training population.

Since the 10-fold accuracy, PPV, and NPV performance values reported in Tables 2 and 4 both show the reasonably good results, the linear kernel operation and two-stage feature reduction techniques used by the connectome-based prediction framework are very intuitive and sensible ones that help overcome this challenging problem.

Clinical interpretation of prediction results

The result from this study also support the notion that, epilepsy in general, and specifically TLE, are associated with temporal and extratemporal network architecture abnormalities (Bonilha et al., 2012b; Liu et al., 2014; Bonilha et al., 2013; DeSalvo et al., 2014). They also indicate that a pattern of network abnormalities may be relevant on an individual basis to guide the estimation of clinical outcomes. While most studies to date have demonstrated the average effects on TLE on the structural connectome, the application of machine learning to the connectome can disclose how the complexity of the connectome can be abridged to yield classifiers with clinical relevance. Importantly, the connectome is a rich and complex data set, and individuals with TLE may harbor abnormalities with inter-individual variability. Thus, the use of machine learning can overcome some of these challenges, while incorporating the crucial parameters in the connectome that are relevant to epilepsy management.

In this context, the connectome can be used not only to provide information about the neurobiology of the disease, but also to provide information about the personalized clinical trajectory. This trajectory cannot be accurately defined based on the existing clinical measures, and machine learning applied to the connectome may unveil a completely new avenue for additional clinical phenotyping and management planning.

One very interesting observation is that the two-stage connectome-based prediction framework can achieve roughly the same accuracy as the expert clinical opinion. Historically speaking, presurgical diagnostics using expert-based clinical information is approximately 70% accurate for patients that choose to have surgery. In this study, the prediction framework is also 70% accurate. This level of accuracy is achieved based on the connectome alone, which is pretty remarkable, and is an important clinical finding that may advance outcome prediction for patients with epilepsy.

Performance comparison to existing VBM-based methods

Compared to the white matter classification method developed in (Focke et al., 2012) that uses VBM data, and does not use local weights, the prediction accuracy of the two-stage connectome-based framework is consistently better. Specifically, our accuracy is 80%, while the reported mean accuracy of the DTI T2map is 75.3% (RHS vs. controls + LHS vs. controls divided by two), the reported mean accuracy of the T1 stream is 73.2%, and the reported mean accuracy of the T1 stream with hippocampal masking is 74.5%.

Compared to the white matter classification method developed in (Feis et al., 2013) that uses VBM data, the prediction accuracy of the two-stage connectome-based framework is considerably less. Specifically, our accuracy is 70%, while the reported accuracy in (Feis et al., 2013) is 95%. It is very difficult to compare our connectome-based method with a VBM-based method that uses heuristic grid-based search algorithm. In general, since this type of algorithm requires several iterations to finely tune different search parameters to one particular training data set acquired from a single site and/or MRI scanner, the resulting classifier may suffer from an over fitting condition. However, as shown in Section 3.3, our connectome-based prediction framework appears to be robust to this type of over fitting issue.

Additionally, the authors of these two VBM-based approaches did not report the amount of time needed to fully train their prediction models. In the proposed framework, only two parameters are required by the elastic net algorithm, namely the ℓ₁ regularization parameter (λ) and the ℓ₂ regularization parameter (ρ). Both regularization parameters produce stable performance results (approximately ± 1% variation in PPV, NPV, sensitivity, specificity, and accuracy) when values are independently or jointly changed. Lastly, the time needed to train both pipelines in the two-stage framework is approximately 5 s, which means the entire 10-fold cross validation requires approximately 1 min to complete.

Conclusion

In this study a sparse machine learning approach is used to select abnormal network connections defined in structural brain connectomes reconstructed using white matter fiber tracts from presurgical DTI data. The selected network connections were then used to train a classifier to predict the treatment outcome after anterior temporal lobectomy, or amygdalohippocampectomy, surgery is performed. Due to the large number of network connections defined in a connectome, and the small number of subjects in the training population, two new techniques are used to improve the accuracy of the connectome-based prediction framework. Specifically, a two-stage elastic net feature selection and regularization approach that gradually reduces the number of network connections is used to train a classifier capable of predicting the surgical treatment outcome, and a linear kernel operation is used to further improve the accuracy of the trained classifier. Using 10-fold cross validation, the first stage in the two-stage connectome-based framework is able to separate patients with TLE from normal controls with 80% accuracy, and the second stage in the two-stage connectome-based framework is able to correctly predict the surgical treatment outcome of patients with TLE with 70% accuracy. Compared to the existing state-of-the-art methods that use VBM data, our two-stage connectome-based framework provides a suitable alternative with comparable, or better, prediction performance. Lastly, our connectome-based prediction framework achieves roughly the same accuracy for predicting surgical treatment outcome as the expert clinical opinion.