Classical and all-floating FETI methods for the simulation of arterial tissues

Abstract

High-resolution and anatomically realistic computer models of biological soft tissues play a significant role in the understanding of the function of cardiovascular components in health and disease. However, the computational effort to handle fine grids to resolve the geometries as well as sophisticated tissue models is very challenging. One possibility to derive a strongly scalable parallel solution algorithm is to consider finite element tearing and interconnecting (FETI) methods. In this study we propose and investigate the application of FETI methods to simulate the elastic behavior of biological soft tissues. As one particular example we choose the artery which is – as most other biological tissues – characterized by anisotropic and nonlinear material properties. We compare two specific approaches of FETI methods, classical and all-floating, and investigate the numerical behavior of different preconditioning techniques. In comparison to classical FETI, the all-floating approach has not only advantages concerning the implementation but in many cases also concerning the convergence of the global iterative solution method. This behavior is illustrated with numerical examples. We present results of linear elastic simulations to show convergence rates, as expected from the theory, and results from the more sophisticated nonlinear case where we apply a well-known anisotropic model to the realistic geometry of an artery. Although the FETI methods have a great applicability on artery simulations we will also discuss some limitations concerning the dependence on material parameters.

1 Introduction

The modeling of hyperelastic materials is realized by using a strain–energy function Ψ. For a comprehensive overview and the mathematical theory on elastic deformations, see, e.g., [1, 2, 3, 4]. A well established model for arterial tissues was introduced by Holzapfel et al. [5, 6]. This model was further developed and enlarged to collagen fiber dispersion in [6, 7, 8]; see [9] for the modeling of residual stresses in arteries which play also an important role in tissue engineering. An adequate model for the myocardium can be found in [10]. The fine mesh structure to model cardiovascular organs normally results in a very large number of degrees of freedom. The combination with the high complexity of the underlying partial differential equations demands fast solution algorithms and, conforming to up–to–date computer hardware architectures, parallel methods. One possibility to achieve these specifications is to use domain decomposition (DD) methods which acquired a lot of attention in the last years and resulted in the development of several overlapping as well as non–overlapping DD methods, see [11]. They all work according to the same principle: the computational domain Ω₀ is subdivided into a set of (overlapping or non–overlapping) subdomains Ω_0,i. DD algorithms now decompose the large global problem into a set of smaller local problems on the subdomains, with suitable transmission or interface conditions. This yields a natural parallelization of the underlying problem. In addition to well established standard DD methods, other examples for more advanced domain decomposition methods are hybrid methods [12], mortar methods [13, 14, 15] and tearing and interconnecting methods [16].

In this paper we focus on the finite element tearing and interconnecting (FETI) method where the strategy is to decompose the computational domain into a finite number of non–overlapping subdomains. Therein the corresponding local problems can be handled efficiently by direct solvers. The reduced global system, that is related to discrete Lagrange multipliers on the interface, is then solved with a parallel Krylov space method to deduce the desired dual solution. This is, in the case of elasticity, the boundary stress and subsequentely, in a postprocessing step, we compute the primal unknown, i.e. the displacements, locally. For the global Krylov space method, such as the conjugate gradient (CG) or the generalized minimal residual (GMRES) method, we need to have a suitable preconditioning technique. Here we consider a simple lumped preconditioner and an almost optimal Dirichlet preconditioner, as proposed by Farhat et al. [17].

A variant of the classical FETI method is the all-floating tearing and interconnecting approach (AF-FETI) where, in contrast to the classical approach, the Dirichlet boundary acts as a part of the interface. It was introduced independently for the boundary element method by Steinbach and Of [18, 19] and as the Total-FETI (TFETI) method for finite elements by Dostál et al. [20]. This approach shows advantages in the implementation and, due to mapping properties of the involved operators, improves the convergence of the global iterative method for the considered problems. This behavior is illustrated with numerical examples, which are – to the best of our knowledge – the first application of all-floating FETI method to nonlinear and anisotropic biological materials.

An essential part of FETI methods is solving the local subproblems. Challenges occur with so-called floating subdomains which have no contribution to the Dirichlet boundary. These cases correspond to local Neumann problems and the solutions are – in the case of elasticity – only unique up to the six rigid body modes. For classical FETI it can happen that the kernel of the local operator is non-trivial and its dimension is lower than six. The problem to identify these kernels reliably causes trouble. One possibility to overcome this trouble is a modification of the classical approach, the dual-primal FETI (FETI-DP) method, cf. Farhat et al. [21] and Klawonn and Widlund [22]. In this variant some specific primal degrees of freedom are fixed. This yields solvable systems for all subdomains. Choosing the primal degrees of freedom may be very sophisticated [23]. This approach was already applied to model arterial tissues using FETI-DP by Klawonn and Rheinbach [24, 25], Brands et al. [26], Balzani et al. [28, 29] and Brinkhues et al. [27]. Note that for all-floating FETI the identification of the kernel of the local operators is no problem at all, since we treat all subdomains as floating subdomains, and hence have a kernel equal to six for all local operators. Moreover the resulting local systems are typically better conditioned than those arising in the FETI-DP approach, see Brzobohatỳ et al. [30]. All-floating FETI was used to model myocardial tissue in the preliminary work [31].

Both the classical FETI method, as well as all-floating FETI, need the construction of a generalized inverse matrix. This may be achieved using direct solvers with a sparsity preserving stabilization, see, e.g. [30], or stabilized iterative methods. For a mathematical analysis of FETI methods including convergence proofs for the classical one-level FETI method, see, e.g., [22, 32, 33].

2 Modeling Arterial Tissues

The deformation of a body $\mathcal{B}$ is described by a function ϕ : Ω₀ → Ω_t with the reference configuration ${\Omega }_0\subset {\mathbb{R}}^3$ at time t = 0 and the current configuration Ω_t at time t > 0. With this we introduce the displacement field U in the reference configuration and the displacement field u in the current configuration,

$$\mathbf{x}=\varphi \left(\mathbf{X}\right)=\mathbf{X}+\mathbf{U}\left(\mathbf{X}\right)\in {\Omega }_t,\mathbf{X}={\varphi }^{-1}\left(\mathbf{x}\right)=\mathbf{x}-\mathbf{u}\left(\mathbf{x}\right)\in {\Omega }_0,$$ (1)

and the deformation gradient as, see, e.g., [2],

$$\mathbf{F}=\text{Grad}\varphi \left(\mathbf{X}\right)=\mathbf{I}+\text{Grad}\mathbf{U}.$$ (2)

Moreover, we denote by J = det F > 0 the Jacobian of F and by C = F^⊤F the right Cauchy–Green tensor. For later use, to model the nearly incompressible behavior of biological soft tissues, we introduce the following split of the deformation gradient in a volumetric and an isochoric part, compare Flory [34], i.e.

$$\mathbf{F}=J^{1∕3}\overline{\mathbf{F}},\text{with det}\overline{\mathbf{F}}=1.$$ (3)

Consequently, this multiplicative split can be applied to other tensors such as the right Cauchy–Green tensor. Thus

$$\mathbf{C}=J^{2∕3}\overline{\mathbf{C}},\text{with}\overline{\mathbf{C}}={\overline{\mathbf{F}}}^{⊺}\overline{\mathbf{F}}\text{and det}\overline{\mathbf{C}}=1.$$ (4)

As a starting point for the modeling of biological soft tissues the stationary equilibrium equations in the current configuration are considered to find a displacement field u according to

$$\text{div}\sigma (\mathbf{u},\mathbf{x})+{\mathbf{b}}_t\left(\mathbf{x}\right)=0\text{for}\mathbf{x}\in {\Omega }_t,$$ (5)

where σ(u, x) is the Cauchy stress tensor and b_t(x) is the body force at time t.

In addition, we incorporate boundary conditions to describe displacements or normal stresses on the boundary Γ_t = ∂Ω_t, which is decomposed into disjoint parts such that $\partial {\Omega }_t={\overline{\Gamma }}_{t,\mathrm{D}}\cup {\overline{\Gamma }}_{t,\mathrm{N}}$. Dirichlet boundary conditions on Γ_t,D correspond to a given displacement field u = u_D(x), while Neumann boundary conditions on Γ_t,N are identified physically with a given surface traction σ(u, x) n_t(x) = g_t(x), where n_t(x) denotes the exterior normal vector at time t.

The equilibrium equations and the boundary conditions may also be formulated in terms of the reference configuration, i.e.

$$\text{Div}\mathbf{FS}(\mathbf{U},\mathbf{X})+{\mathbf{b}}_0\left(\mathbf{X}\right)=0\text{for}\mathbf{X}\in {\Omega }_0,$$ (6)

$$\mathbf{U}\left(\mathbf{X}\right)={\mathbf{U}}_{\mathrm{D}}\left(\mathbf{X}\right)\text{for}\mathbf{X}\in {\Gamma }_{0,\mathrm{D}},$$ (7)

$$\mathbf{FS}(\mathbf{U},\mathbf{X}){\mathbf{N}}_0\left(\mathbf{X}\right)={\mathbf{G}}_0\left(\mathbf{X}\right)\text{for}\mathbf{X}\in {\Gamma }_{0,\mathrm{N}},$$ (8)

where S is the second Piola–Kirchhoff tensor and b₀(X) is the body force at time t = 0. In order to formulate the boundary conditions we introduce a prescribed displacement field U_D(X), the exterior normal vector N₀(X) and the surface traction G₀(X) in the reference configuration.

Considering the study of the properties of soft biological soft tissues we have to deal with a nonlinear relationship between stress and strain, with large deformations and an anisotropic material. Since linear elasticity models are not adequate for treating such a complex behavior, we take a look at the more general concept of nonlinear elasticity.

The nonlinear stress-strain response is modeled via a constitutive equation that links the stress to a derivative of a strain-energy function Ψ, representing the elastic stored energy per unit reference volume. Derived from the Clausius–Duhem inequality, see [35, 36], we formulate the constitutive equations as

$$\sigma =2J^{-1}\mathbf{F}\frac{\partial \Psi \left(\mathbf{C}\right)}{\partial \mathbf{C}}{\mathbf{F}}^{⊺}\text{and}\mathbf{S}=2\frac{\partial \Psi \left(\mathbf{C}\right)}{\partial \mathbf{C}}.$$ (9)

We make use of the Rivlin–Ericksen representation theorem [37] and its extension to anisotropic materials, cf. [38], to find a representation of the strain-energy function Ψ in terms of the principal invariants of C.

Arteries are vessels that transport blood from the heart to the organs. In vivo the artery is a prestretched material under an internal pressure load. Healthy arteries are highly deformable composite structures and show a nonlinear stress-strain response with a typical stiffening effect at higher pressures. Reasons for this are the embedded collagen fibers which lead to an anisotropic mechanical behavior of arterial walls. We denote by a_{0, 1} and a_{0, 2} the predominant collagen fiber directions in the reference configuration. An important observation is that arteries do not change their volume within the physiological range of deformation, hence they are treated as a nearly incompressible material, see, e.g., [5]. In this work we focus on the in vitro passive behavior of the healthy artery, see Fig. 1. To capture the nearly incompressibility condition we remember the decomposition (3), which yields an additive split of the strain-energy function into a so-called volumetric and an isochoric part, i.e.

$$\Psi \left(\mathbf{C}\right)={\Psi }_{\text{vol}}\left(J\right)+\overline{\Psi }\left(\overline{\mathbf{C}}\right).$$ (10)

This procedure leads to constitutive equations in which the stress tensors are also additively decomposed into a volumetric and an isochoric part, i.e., cf. [2],

$$\sigma =p\mathbf{I}+2J^{-1}\mathbf{F}\frac{\partial \overline{\Psi }\left(\overline{\mathbf{C}}\right)}{\partial \mathbf{C}}{\mathbf{F}}^{⊺}\text{and}\mathbf{S}=\mathit{Jp}{\mathbf{C}}^{-1}+2\frac{\partial \overline{\Psi }\left(\overline{\mathbf{C}}\right)}{\partial \mathbf{C}}.$$ (11)

Here, the scalar-valued hydrostatic pressure is defined as

$$p≔\frac{\partial {\Psi }_{\text{vol}}\left(J\right)}{\partial J}.$$ (12)

To capture the specifics of this fiber-reinforced composite, Holzapfel and Weizsäcker [39] and Holzapfel et al. [5] proposed an additional split of the strain-energy function into an isotropic and an anisotropic part so that the complete energy function Ψ can be written as

$$\Psi \left(\mathbf{C}\right)={\Psi }_{\text{vol}}\left(J\right)+{\overline{\Psi }}_{\text{iso}}\left(\overline{\mathbf{C}}\right)+{\overline{\Psi }}_{\text{aniso}}(\overline{\mathbf{C}},{\mathbf{a}}_{1,0})+{\overline{\Psi }}_{\text{aniso}}(\overline{\mathbf{C}},{\mathbf{a}}_{2,0}).$$ (13)

Following the classical approach we describe the volume changing part by

$${\Psi }_{\text{vol}}\left(J\right)=\frac{\kappa }{2}{(J-1)}^2,$$ (14)

where κ > 0, comparable to the bulk modulus in linear elasticity, serves as a penalty parameter to enforce the incompressibility constraint.

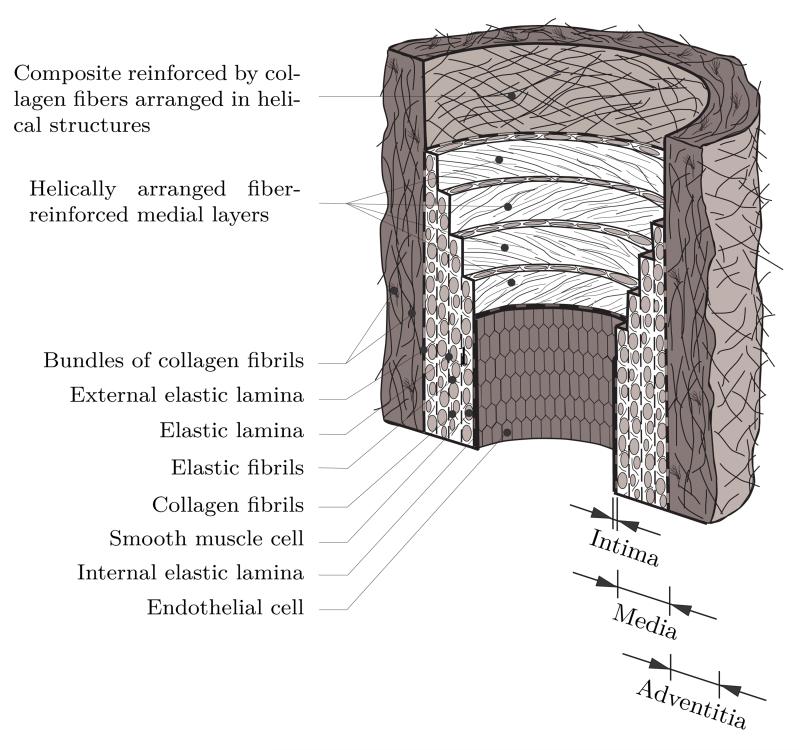
Figure 1.

Diagrammatic model of the major components of a healthy elastic artery, from [5]. The intima, the innermost layer is negligible for the modeling of healthy arteries, it plays a very important role in the modeling of diseased arteries, though. The two predominant directions of the collagen fibers in the media and the adventitia are indicated with black curves.

To model the isotropic non-collagenous matrix material the classical neo-Hookean model is used [2]. Thus

$${\overline{\Psi }}_{\text{iso}}\left(\overline{\mathbf{C}}\right)=\frac{c}{2}({\overline{I}}_1-3),$$ (15)

where c > 0 is a stress-like material parameter and ${\overline{I}}_1=\text{tr}\left(\overline{\mathbf{C}}\right)$ is the first principal invariant of the isochoric part of the right Cauchy–Green tensor. In (13), ${\overline{\Psi }}_{\text{aniso}}$ is associated with the deformation of the collagen fibers. According to [5], this transversely isotropic response is described by

$${\overline{\Psi }}_{\text{aniso}}(\overline{\mathbf{C}},{\mathbf{a}}_{1,0})=\frac{k_1}{2k_2}\left\{\exp \right[k_2{({\overline{I}}_4-1)}^2]-1\},$$ (16)

$${\overline{\Psi }}_{\text{aniso}}(\overline{\mathbf{C}},{\mathbf{a}}_{2,0})=\frac{k_1}{2k_2}\left\{\exp \right[k_2{({\overline{I}}_6-1)}^2]-1\},$$ (17)

with the invariants ${\overline{I}}_4≔{\mathbf{a}}_{1,0}\cdot \left(\overline{\mathbf{C}}{\mathbf{a}}_{1,0}\right),{\overline{I}}_6≔{\mathbf{a}}_{2,0}\cdot \left(\overline{\mathbf{C}}{\mathbf{a}}_{2,0}\right)$ and the material parameters k₁ and k₂, which are both assumed to be positive. It is worth to mention that for the anisotropic responses, (16) and (17) only contribute for the cases ${\overline{I}}_4>1$ or ${\overline{I}}_6>1$, respectively. This condition is explained with the wavy structure of the collagen fibers, which are regarded as not being able to support compressive stresses. Thus, the fibers are assumed to be active in tension (${\overline{I}}_i>1$) and inactive in compression (${\overline{I}}_i<1$). This assumption is not only based on physical reasons but it is also essential for reasons of stability, see Holzapfel et al. [40].

The material parameters can be fitted to an experimentally observed response of the biological soft tissue. Following [5] we use the material parameters summarized in Table 1.

Table 1.

Material parameters used in the numerical experiments; parameters taken from Holzapfel et al. [5].

c = 3.0 kPa

k1 = 2.3632 kPa

k2 = 0.8393 (−)

Similar models can also be used for the description of other biological materials, e.g., for the myocardium, cf. [10].

3 Finite Element Approximation

3.1 Variational formulation of nonlinear elasticity problems

In this section we consider the variational formulation of the equilibrium equations (5) and (6) with the corresponding Dirichlet and Neumann boundary conditions. In particular, using spatial coordinates, the boundary value problem (5) is formally equivalent to the variational equations

$${\langle {\mathcal{A}}_t\left(\mathbf{u}\right),\mathbf{v}\rangle }_{{\Omega }_t}≔{\int }_{{\Omega }_t}\sigma \left(\mathbf{u}\right):\epsilon \left(\mathbf{v}\right)\mathrm{d}\mathbf{x}={\int }_{{\Omega }_t}{\mathbf{b}}_t\cdot \mathbf{v}\mathrm{d}\mathbf{x}+{\int }_{{\Gamma }_{t,\mathrm{N}}}{\mathbf{g}}_t\cdot \mathbf{v}\mathrm{d}{s}_{\mathbf{x}}≕{\langle \mathcal{F},\mathbf{v}\rangle }_{{\Omega }_t},$$ (18)

valid for a smooth enough tensor field $\sigma \left(\mathbf{u}\right):{\overline{\Omega }}_t\mapsto {\mathbb{R}}^{3\times 3}$ and all smooth enough vector fields $\mathbf{v}:{\overline{\Omega }}_t\mapsto {\mathbb{R}}^3$, which vanish on Γ_t,D, see, e.g., [1, Theorem 2.4-1]. Additionally,

$$\epsilon \left(\mathbf{v}\right)=\frac{1}{2}(\text{grad}\mathbf{v}+{\left(\text{grad}\mathbf{v}\right)}^{⊺})$$ (19)

and ${\mathcal{A}}_t$ is the nonlinear operator in the current configuration which is induced by the stress tensor representation (11), and by using the related duality pairing ⟨·, ·⟩_Ωt. For later use, we introduce the corresponding terms in the reference configuration Ω₀ as ${\langle {\mathcal{A}}_0\left(\mathbf{U}\right),\mathbf{V}\rangle }_{{\Omega }_0}$ and ${\langle {\mathcal{F}}_0,\mathbf{V}\rangle }_{{\Omega }_0}$. Note that (18) formally corresponds to a variational formulation in linear elasticity. However, the integral and the involved terms have to be evaluated in the current configuration which comprises the nonlinearity of the system. If the test function v is interpreted as the spatial velocity gradient, then ε(v) is the rate of deformation tensor so that ${\langle {\mathcal{A}}_t\left(\mathbf{u}\right),\mathbf{v}\rangle }_{{\Omega }_t}$ has the physical interpretation of the rate of internal mechanical work.

In terms of the reference configuration, the boundary value problem (6), (8) is formally equivalent to the variational equations

$${\langle {\mathcal{A}}_0\left(\mathbf{U}\right),\mathbf{V}\rangle }_{{\Omega }_0}={\int }_{{\Omega }_0}\mathbf{S}\left(\mathbf{U}\right):\Sigma (\mathbf{U},\mathbf{V})\mathrm{d}\mathbf{X}={\int }_{{\Omega }_0}{\mathbf{b}}_0\cdot \mathbf{V}\mathrm{d}\mathbf{X}+{\int }_{{\Gamma }_{0,\mathrm{N}}}{\mathbf{G}}_0\cdot \mathbf{V}\mathrm{d}{s}_{\mathbf{X}}={\langle {\mathcal{F}}_0,\mathbf{V}\rangle }_{{\Omega }_0},$$ (20)

valid for a smooth enough tensor field $\mathbf{S}\left(\mathbf{U}\right):{\overline{\Omega }}_0\mapsto {\mathbb{R}}^{3\times 3}$ and all smooth enough vector fields $\mathbf{V}:{\overline{\Omega }}_0\mapsto {\mathbb{R}}^3$ with V = 0 on Γ_0,D, see, e.g., [1, Theorem 2.6-1]. In (20) we use the definition of the directional derivative of the Green–Lagrange strain tensor, i.e.

$$\Sigma (\mathbf{U},\mathbf{V})=\frac{1}{2}\left({\text{Grad}}^{⊺}\mathbf{V}\mathbf{F}\right(\mathbf{U})+{\mathbf{F}}^{⊺}(\mathbf{U}\left)\text{Grad}\mathbf{V}\right),$$ (21)

which is also known as the variation or the material time derivative of the Green–Lagrange strain tensor in the literature.

It is important to note that results on existence of solutions in nonlinear elasticity can be stated given a polyconvex strain-energy function Ψ, which holds true for the anisotropic model (13) discussed in Section 2. For more details we refer to the results of Ball [41, 42], see also [1, 43] and Balzani et al. [44].

3.2 Linearization and discretization

In the following we confine ourselves to the reference configuration Ω₀. The formulations in the current configuration Ω_t can be deduced in an analogous way.

For the solution of the nonlinear system (20) we apply Newton’s method to obtain the recursion

$${\langle \Delta \mathbf{U},{\mathcal{A}}_0^{\prime }\left({\mathbf{U}}^k\right)\mathbf{V}\rangle }_{{\Omega }_0}={\langle {\mathcal{F}}_0,\mathbf{V}\rangle }_{{\Omega }_0}-{\langle {\mathcal{A}}_0\left({\mathbf{U}}^k\right),\mathbf{V}\rangle }_{{\Omega }_0},{\mathbf{U}}^{k+1}={\mathbf{U}}^k+\Delta \mathbf{U},$$ (22)

with the tangential term ${\mathcal{A}}_0^{\prime }\left({\mathbf{U}}^k\right)$, the displacement field of the k-th Newton step U^k, the increment ΔU and a suitable initial guess U⁰.

For the computational domain ${\Omega }_0\subset {\mathbb{R}}^3$ we consider an admissible decomposition into N tetrahedral shape regular finite elements τℓ of mesh size hℓ, i.e. ${\overline{\Omega }}_0={\overline{\mathcal{T}}}_N={\bigcup }_{\ell =1}^N{\overline{\tau }}_{\ell }$, and we introduce a conformal finite element space X_h ⊂ [H¹ (Ω₀)]³, M = dimX_h, of piecewise polynomial continuous basis functions φ_i. Then the Galerkin finite element discretization of the linearized variational formulation (22) results in a system of algebraic equations to find ΔU_h ∈ X_h, ΔU_h = 0 on Γ_0,D such that

$${\langle \Delta {\mathbf{U}}_h,{\mathcal{A}}_0^{\prime }\left({\mathbf{U}}_h^k\right){\mathbf{V}}_h\rangle }_{{\Omega }_0}={\langle {\mathcal{F}}_0,{\mathbf{V}}_h\rangle }_{{\Omega }_0}-{\langle {\mathcal{A}}_0\left({\mathbf{U}}_h^k\right),{\mathbf{V}}_h\rangle }_{{\Omega }_0},{\mathbf{U}}_h^{k+1}={\mathbf{U}}_h^k+\Delta {\mathbf{U}}_h,$$ (23)

holds for all V_h ∈ X_h, V_h = 0 on Γ_0,D. Note that the initial guess ${\mathbf{U}}_h^0$ has to satisfy an approximate Dirichlet boundary condition ${\mathbf{U}}_h^0={\mathbf{U}}_{\mathrm{D},h}$ on Γ_0,D to fulfill condition (7), where U_D,h ∈ X_h∣Γ0,D denotes a suitable approximation of the given displacement U_D. For the computation of the tangential term ${\mathcal{A}}_0^{\prime }\left({\mathbf{U}}_h^k\right)$ we need to evaluate

$$\begin{array}{cc}\hfill {\langle \Delta {\mathbf{U}}_h,{\mathcal{A}}_0^{\prime }\left({\mathbf{U}}_h^k\right){\mathbf{V}}_h\rangle }_{{\Omega }_0}=& {\int }_{{\Omega }_0}\text{Grad}\left(\Delta {\mathbf{U}}_h\right)\mathbf{S}\left({\mathbf{U}}_h^k\right):\text{Grad}{\mathbf{V}}_h\mathrm{d}\mathbf{X}\hfill \\ \hfill & +{\int }_{{\Omega }_0}{\mathbf{F}}^{⊺}\text{Grad}\Delta {\mathbf{U}}_h:\mathbb{C}\left({\mathbf{U}}_h^k\right):{\mathbf{F}}^{⊺}\text{Grad}\left({\mathbf{V}}_h\right)\mathrm{d}\mathbf{X}.\hfill \end{array}$$ (24)

For a more detailed presentation how to compute the tangential term, in particular the forth-order elasticity tensor $\mathbb{C}\left({\mathbf{U}}_h^k\right)$ we refer to [46, 45].

Note that the convergence rate of the Newton method is dependent on the initial guess, on the parameters used in the model and on the inhomogeneous Dirichlet and Neumann boundary conditions which influence ${\mathcal{F}}_0$.

In a time-stepping scheme we use zero for the initial guess, and the result of the k-th time step as initial solution for the next step. The initial guess may also be the solution of a modified nonlinear elasticity problem such as the solution of the same nonlinear model but with modified parameters, e.g., a reduced penalty parameter κ, or modified boundary conditions, e.g., a reduced pressure on the surface. The latter is equivalent to an incremental load stepping scheme with a parameter τ ∈ (0, 1], τ → 1, so that

$${\langle \Delta {\mathbf{U}}_h,A^{\prime }\left({\mathbf{U}}_h^k\right){\mathbf{V}}_h\rangle }_{{\Omega }_0}={\langle \tau {\mathcal{F}}_0,{\mathbf{V}}_h\rangle }_{{\Omega }_0}-{\langle A\left({\mathbf{U}}_h^k\right),{\mathbf{V}}_h\rangle }_{{\Omega }_0},{\mathbf{U}}_h^{k+1}={\mathbf{U}}_h^k+\Delta {\mathbf{U}}_h.$$ (25)

Klawonn and Rheinbach [24] used a load stepping scheme of this kind, for more information on load stepping and global Newton methods, see [48, 47]. The standard finite element method (FEM) now yields a linear system of equations which is equivalent to the discretized variational formulation (23). Finally, we have to solve

$${\mathbf{K}}^{\prime }\left({\underset{¯}{U}}^k\right)\Delta \underset{¯}{U}=\underset{¯}{\mathcal{F}}-\underset{¯}{K}\left({\underset{¯}{U}}^k\right),{\underset{¯}{U}}^{k+1}={\underset{¯}{U}}^k+\Delta \underset{¯}{U},$$ (26)

with the solution vector U^k in the k-th Newton step and the increment ΔU. The tangent stiffness matrix K′ is calculated according to

$${\mathbf{K}}^{\prime }\left({\underset{¯}{U}}^k\right)[i,j]≔{\langle {\phi }_j,A^{\prime }\left({\mathbf{U}}_h^k\right){\phi }_i\rangle }_{{\Omega }_0},$$ (27)

and the terms of the right hand side are constructed by

$$\underset{¯}{\mathcal{F}}\left[i\right]≔{\langle {\mathcal{F}}_0,{\phi }_i\rangle }_{{\Omega }_0}\text{and}\underset{¯}{K}\left({\underset{¯}{U}}^k\right)\left[i\right]≔{\langle A\left({\mathbf{U}}_h^k\right),{\phi }_i\rangle }_{{\Omega }_0}.$$ (28)

The additive split of the stress tensors (11) and the introduction of the hydrostatic pressure (12) leads to the additional equation

$$p-\frac{\partial {\Psi }_{\text{vol}}\left(J\right)}{\partial J}=0,$$ (29)

which has to be satisfied in a weak sense. For this we use the idea of static condensation where this volumetric variable is eliminated element-wise, see, e.g., [46]. This may be achieved in using discontinuous basis functions; in this paper we will concentrate on piecewise constants. In the case of tetrahedral elements, this approach leads to ${\mathcal{P}}_k-{\mathcal{P}}_0$ elements. Here k is the order of the basis functions for the displacement field. It is known that linear finite elements are very prone to volumetric locking. Hence, for nearly incompressible materials piecewise quadratic elements (k = 2) are a better choice, see Simo [49]. The resulting P₂ – P₀ element is also the preferred choice to model nearly incompressible arterial materials in [24]–[29]. For the numerical results in this work (Section 5) we use both linear (P₁ – P₀ element) and quadratic (P₂ – P₀ element) ansatz functions for the displacement field and compare the results.

Note that due to the symmetry of the stress tensor S and the major and minor symmetry properties of the elasticity tensor $\mathbb{C}$ the operator $A_0^{\prime }\left({\mathbf{U}}^k\right)$ is self-adjoint. We can also show, using the positive definiteness of the elasticity tensor, see [4], and the polyconvexity of the strain-energy function (Section 3.1), that this operator is ${\left[H_0^1\right({\Omega }_0,{\Gamma }_{0,\mathrm{D}}\left)\right]}^3$-elliptic and bounded, see [4, 45]. With these properties of the operator $A_0^{\prime }\left({\mathbf{U}}_h^k\right)$ we can state that the linearized system (23),(24) admits a unique solution ΔU_h. Furthermore, the tangent stiffness matrix K′ is symmetric and positive definite.

Simulations with large deformations and the hence required derivative of the Neumann boundary conditions (8) would yield an additional non-symmetric mass matrix on the left hand side of (26). To stay with an symmetric system we neglect this matrix but compensate it with a surface update of the geometry after each Newton step. Thus, our whole system is symmetric and we can use the CG method as an iterative solver. Nonetheless, the FETI methods described in Section 4 also work for non-symmetric systems by using the GMRES method.

4 Finite Element Tearing and Interconnecting

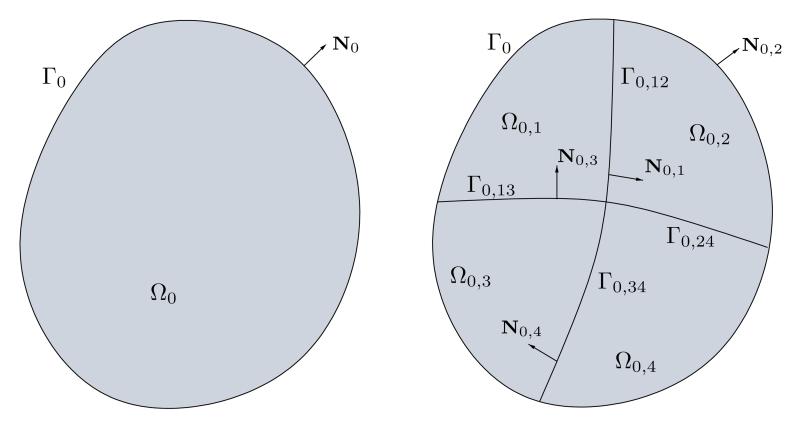
To solve the linearized equations (26) arising in the Newton method we apply the finite element tearing and interconnecting approach [16], see also [24, 50, 51], and references given therein. The derivation of the FETI system for nonlinear mechanics will be performed in the reference configuration. In an analogous way this is also valid for the formulation in the current configuration. For a bounded domain ${\Omega }_0\subset {\mathbb{R}}^3$ we introduce a non-overlapping domain decomposition

$${\overline{\Omega }}_0=\bigcup _{i=1}^p{\overline{\Omega }}_{0,i}\text{with}{\Omega }_{0,i}\cap {\Omega }_{0,j}=\varnothing \text{for}i\ne j,{\Gamma }_{0,i}=\partial {\Omega }_{0,i},$$ (30)

see Fig. 2. The local interfaces are given by Γ_0,ij := Γ_0,i ∩ Γ_0,j for all i < j. The skeleton of the domain decomposition (30) is denoted as

$${\Gamma }_{0,\mathrm{C}}≔\bigcup _{i=1}^p{\Gamma }_{0,i}={\Gamma }_0\cup \bigcup _{i<j}{\overline{\Gamma }}_{0,\mathit{ij}}.$$ (31)

We assume that the finite element mesh ${\mathcal{T}}_N$ matches the domain decomposition (30), i.e., we can reorder the degrees of freedom to rewrite the linear system (26) as

$$\begin{array}{cc}\hfill \left(\begin{array}{cccc}\hfill {\mathbf{K}}_{11}^{\prime }\left({\underset{¯}{U}}_1^k\right)\hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathbf{K}}_{1\mathrm{C}}^{\prime }\left({\underset{¯}{U}}_1^k\right){\mathbf{A}}_1\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\mathbf{K}}_{\mathit{pp}}^{\prime }\left({\underset{¯}{U}}_p^k\right)\hfill & \hfill {\mathbf{K}}_{p\mathrm{C}}^{\prime }\left({\underset{¯}{U}}_p^k\right){\mathbf{A}}_p\hfill \\ \hfill {\mathbf{A}}_1^{⊺}{\mathbf{K}}_{\mathrm{C}1}^{\prime }\left({\underset{¯}{U}}_1^k\right)\hfill & \hfill \cdots \hfill & \hfill {\mathbf{A}}_p^{⊺}{\mathbf{K}}_{\mathrm{C}p}^{\prime }\left({\underset{¯}{U}}_p^k\right)\hfill & \hfill \sum _{i=1}^p{\mathbf{A}}_i^{⊺}{\mathbf{K}}_{\mathrm{CC}}^{\prime }\left({\underset{¯}{U}}_i^k\right){\mathbf{A}}_i\hfill \end{array}\right)\left(\begin{array}{c}\hfill \Delta {\underset{¯}{U}}_{1,I}^k\hfill \\ \hfill ⋮\hfill \\ \hfill \Delta {\underset{¯}{U}}_{p,I}^k\hfill \\ \hfill \Delta {\underset{¯}{U}}_{\mathrm{C}}^k\hfill \end{array}\right)& \hfill \\ \hfill =-\left(\begin{array}{c}\hfill {\underset{¯}{K}}_1\left({\underset{¯}{U}}_1^k\right)\hfill \\ \hfill ⋮\hfill \\ \hfill {\underset{¯}{K}}_p\left({\underset{¯}{U}}_p^k\right)\hfill \\ \hfill \sum _{i=1}^p{\mathbf{A}}_i^{⊺}{\underset{¯}{K}}_{\mathrm{C}}\left({\underset{¯}{U}}_i^k\right)\hfill \end{array}\right)& ,\hfill \end{array}$$ (32)

where the increments $\Delta {\underset{¯}{U}}_{i,I}^k$, the stiffness matrices ${\mathbf{K}}_{\mathit{ii}}^{\prime }\left({\underset{¯}{U}}_i^k\right)$ and the terms on the right hand side ${\underset{¯}{K}}_i\left({\underset{¯}{U}}_i^k\right),i=1,\dots ,p$, are related to the local degrees of freedom within the subdomain Ω_0,i. All terms with an index C correspond to degrees of freedom on the coupling boundary Γ_0,C, see (31), while A_i denote simple reordering matrices taking boolean values.

Figure 2.

Decomposition of a domain Ω₀ into four subdomains Ω_0,i, i = 1, … , 4.

4.1 Classical FETI method

Starting from (32), the tearing is now carried out by

$$\Delta {\underset{¯}{U}}_i=\left(\begin{array}{c}\hfill \Delta {\underset{¯}{U}}_{i,I}^k\hfill \\ \hfill {\mathbf{A}}_i\Delta {\underset{¯}{U}}_{\mathrm{C}}^k\hfill \end{array}\right),{\mathbf{K}}_i^{\prime }=\left(\begin{array}{cc}\hfill {\mathbf{K}}_{\mathit{ii}}^{\prime }\left({\underset{¯}{U}}_i^k\right)\hfill & \hfill {\mathbf{K}}_{i\mathrm{C}}^{\prime }\left({\underset{¯}{U}}_i^k\right)\hfill \\ \hfill {\mathbf{K}}_{\mathrm{C}i}^{\prime }\left({\underset{¯}{U}}_i^k\right)\hfill & \hfill {\mathbf{K}}_{\mathrm{CC}}^{\prime }\left({\underset{¯}{U}}_i^k\right)\hfill \end{array}\right),{\underset{¯}{f}}_i=-\left(\begin{array}{c}\hfill {\underset{¯}{K}}_i\left({\underset{¯}{U}}_i^k\right)\hfill \\ \hfill {\underset{¯}{K}}_{\mathrm{C}}\left({\underset{¯}{U}}_i^k\right)\hfill \end{array}\right),$$ (33)

where ${\mathbf{A}}_i\Delta {\underset{¯}{U}}_{\mathrm{C}}^k$ is related to degrees of freedom on the coupling boundary Γ_0,iΓ₀. As the unknowns $\Delta {\underset{¯}{U}}_i$ are typically not continuous over the interfaces we have to ensure the continuity of the solution on the interface, i.e.

$$\Delta {\underset{¯}{U}}_i=\Delta {\underset{¯}{U}}_j\text{on}{\Gamma }_{0,\mathit{ij}},i,j=1,\dots ,p.$$ (34)

This is done by applying the interconnecting

$$\sum _{i=1}^p{\mathbf{B}}_i\Delta {\underset{¯}{U}}_i=\underset{¯}{0},$$ (35)

where the matrices B_i are constructed from {0, 1, −1} such that (34) holds. By using discrete Lagrange multipliers λ to enforce the constraint (35) we finally have to solve the linear system

$$\left(\begin{array}{cccc}\hfill {\mathbf{K}}_1^{\prime }\hfill & \hfill \hfill & \hfill \hfill & \hfill {\mathbf{B}}_1^{⊺}\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\mathbf{K}}_p^{\prime }\hfill & \hfill {\mathbf{B}}_p^{⊺}\hfill \\ \hfill {\mathbf{B}}_1\hfill & \hfill \dots \hfill & \hfill {\mathbf{B}}_p\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \Delta {\underset{¯}{U}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill \Delta {\underset{¯}{U}}_p\hfill \\ \hfill \underset{¯}{\lambda }\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\underset{¯}{f}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\underset{¯}{f}}_p\hfill \\ \hfill \underset{¯}{0}\hfill \end{array}\right).$$ (36)

4.2 all-floating FETI method

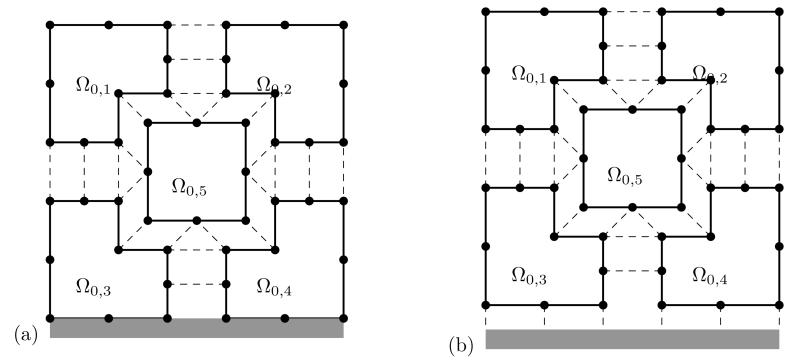
The idea of this special FETI method, cf., e.g., Of and Steinbach [19], is to treat all subdomains as floating subdomains, i.e. domains with no Dirichlet boundary conditions. In addition to the standard procedure of ‘gluing’ the subregions along the auxiliary interfaces, the Lagrange multipliers are now also used for the implementation of the Dirichlet boundary conditions, see Fig. 3. This simplifies the implementation of the FETI procedure since it is possible to treat all subdomains in the same way. In addition, some tests (Section 5) show more efficiency than the classical FETI approach and the asymptotic behavior improves. This is due to the mapping properties of the Steklov–Poincaré operator, see [19, Remark 1]. The drawback is an increasing number of degrees of freedom and Lagrange multipliers. Compare also to Dostál et al. [20] for the related Total-FETI method. If all regions are treated as floating subdomains the conformance of the Dirichlet boundary conditions is not given; they have to be enhanced in the system of constraints using the slightly modified interconnecting

$$\sum _{i=1}^p{\tilde{\mathbf{B}}}_i\Delta {\underset{¯}{U}}_i=\underset{¯}{b},$$ (37)

where ${\tilde{\mathbf{B}}}_i$ is a block matrix of the kind ${\tilde{\mathbf{B}}}_i={[{\mathbf{B}}_i,{\mathbf{B}}_{\mathrm{D},i}]}^{⊺}$ and the vector b is of the form b = [0, b_D]^⊤ such that B_D,i[j, k] = 1, if and only if k is the index of a Dirichlet node j of the subdomain Ω_i, while b[j] equals the Dirichlet values corresponding to the vertices X_k ∈ Γ_0,D, see also [19].

Figure 3.

Fully redundant classical FETI (a) and all-floating FETI (b) formulation: Ω_0,i, i = 1, … , 5, denote the local subdomains, the black dots correspond to the subdomain vertices and the dashed lines correspond to the constraints (34). The gray strip indicates Dirichlet boundary conditions. Note that the number of constraints for the all-floating approach rises with the number of vertices on the Dirichlet boundary.

For three-dimensional elasticity problems all subdomain stiffness matrices have now the same and known defect, which equals the number of six rigid body motions and which also simplifies the calculation of the later needed generalized inverse matrices ${\mathbf{K}}_i^{†}$. For all-floating FETI we finally get the linearized system of equations

$$\left(\begin{array}{cccc}\hfill {\mathbf{K}}_1^{\prime }\hfill & \hfill \hfill & \hfill \hfill & \hfill {\tilde{\mathbf{B}}}_1^{⊺}\hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\mathbf{K}}_p^{\prime }\hfill & \hfill {\tilde{\mathbf{B}}}_p^{⊺}\hfill \\ \hfill {\tilde{\mathbf{B}}}_1\hfill & \hfill \dots \hfill & \hfill {\tilde{\mathbf{B}}}_p\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \Delta {\underset{¯}{U}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill \Delta {\underset{¯}{U}}_p\hfill \\ \hfill \underset{¯}{\lambda }\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\underset{¯}{f}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\underset{¯}{f}}_p\hfill \\ \hfill \underset{¯}{b}\hfill \end{array}\right).$$ (38)

4.3 Solving the FETI system

To solve the linearized systems (36) and (38) we follow the standard approach of tearing and interconnecting methods. For convenience we outline the procedure by means of the classical FETI formulation (Section 4.1). However the modus operandi is analogous for the all-floating approach.

First, note that in the case of a floating subdomain Ω_0,i, i.e. ${\Gamma }_{0,i}\cap {\Gamma }_{0,\mathrm{D}}=\varnothing$, the local matrices ${\mathbf{K}}_i^{\prime }$ are not invertible. Hence, we introduce a generalized inverse ${\mathbf{K}}_i^{†}$ to represent the local solutions as

$$\Delta {\underset{¯}{U}}_i={\mathbf{K}}_i^{†}({\underset{¯}{f}}_i-{\mathbf{B}}_i^{⊺}\underset{¯}{\lambda })+\sum _{k=1}^6{\gamma }_{k,i}{\underset{¯}{r}}_{k,i}.$$ (39)

Here, r_k,i ∈ ker ${\mathbf{K}}_i^{\prime }$ correspond to the rigid body motions of elasticity and γ_k,i are unknown constants. For floating subdomains we additionally require the solvability conditions

$$({\underset{¯}{f}}_i-{\mathbf{B}}_i^{⊺}\underset{¯}{\lambda },{\underset{¯}{r}}_{k,i})=0\text{for}i=1,\dots ,6.$$ (40)

In the case of a non-floating subdomain, i.e. ker ${\mathbf{K}}_i^{\prime }=\varnothing$, we may set ${\mathbf{K}}_i^{†}={\mathbf{K}}_i^{-1}$. Note that it may happen that the kernel ker ${\mathbf{K}}_i^{\prime }$ is non-trivial and its dimension is lower than 6. This is the case if the set Γ_0,i ∩ Γ_0,D is either a vertex or an edge. For classical FETI methods this requires the implementation of an effective method to identify these kernels reliably. Note that this is a key advantage of the all-floating FETI approach because all subdomains are here treated as floating subdomains, and hence we know the kernel of each local operator ker ${\mathbf{K}}_i^{\prime }=6$. With these kernels the solution of the local problems to find the generalized inverse ${\mathbf{K}}_i^{†}$ can be reduced to sparse systems which are typically better conditioned as the systems arising from the FETI-DP method, see Brzobohatỳ et al. [30]. In Section 4.2 we comment on an all-floating approach where also Dirichlet boundary conditions are incorporated by using discrete Lagrange multipliers.

In general, the Schur complement system of (36) is constructed to obtain

$$\sum _{i=1}^p{\mathbf{B}}_i{\mathbf{K}}_i^{†}{\mathbf{B}}_i^{⊺}\underset{¯}{\lambda }-\sum _{i=1}^p\sum _{k=1}^6{\gamma }_{k,i}{\mathbf{B}}_i{\underset{¯}{r}}_{k,i}=\sum _{i=1}^p{\mathbf{B}}_i{\mathbf{K}}_i^{†}{\underset{¯}{f}}_i,({\underset{¯}{f}}_i-{\mathbf{B}}_i^{⊺}\underset{¯}{\lambda },{\underset{¯}{r}}_{k,i})=0.$$ (41)

This can be expressed as

$$\left(\begin{array}{cc}\hfill \mathbf{F}\hfill & \hfill -\mathbf{G}\hfill \\ \hfill {\mathbf{G}}^{⊺}\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \underset{¯}{\lambda }\hfill \\ \hfill \underset{¯}{\gamma }\hfill \end{array}\right)=\left(\begin{array}{c}\hfill \underset{¯}{d}\hfill \\ \hfill \underset{¯}{e}\hfill \end{array}\right),$$ (42)

with

$$\mathbf{F}=\sum _{i=1}^p{\mathbf{B}}_i{\mathbf{K}}_i^{†}{\mathbf{B}}_i^{⊺},\mathbf{G}=\sum _{i=1}^p\sum _{k=1}^6{\mathbf{B}}_i{\underset{¯}{r}}_{k,i},\underset{¯}{d}=\sum _{i=1}^p{\mathbf{B}}_i{\mathbf{K}}_i^{†}{\underset{¯}{f}}_i,$$ (43)

and e is constructed using e_k,i = (f_i, r_k,i for i = 1, … , p and k = 1, … , 6. For the solution of the linearized system (42) the projection

$${\mathbf{P}}^{⊺}≔\mathbf{I}-\mathbf{G}{\left({\mathbf{GG}}^{⊺}\right)}^{-1}{\mathbf{G}}^{⊺}$$ (44)

is introduced. It now remains to consider the projected system

$${\mathbf{P}}^{⊺}\mathbf{F}\underset{¯}{\lambda }={\mathbf{P}}^{⊺}\underset{¯}{d}.$$ (45)

This can be solved by using a parallel iterative method with suitable preconditioning of the form

$${\mathbf{M}}^{-1}≔\sum _{i=1}^p{\mathbf{B}}_{\mathrm{D},i}{\mathbf{Y}}_i{\mathbf{B}}_{\mathrm{D},i}^{⊺},$$ (46)

with modified jump operators B_D,i which are obtained by multiplicity scaling, see [24, 51]. Since the local subproblems all yield symmetric tangent stiffness matrices ${\mathbf{K}}_i^{\prime }$, i = 1, … , p, cf. Section 3, the matrix P^⊤F is also symmetric. This enables us to use the CG method as the global solver for (45). Be aware that the initial approximate solution λ⁰ has to satisfy the compatibility condition G^⊤ λ⁰ = e. A possible choice is

$${\underset{¯}{\lambda }}_0=\mathbf{G}{\left({\mathbf{G}}^{⊺}\mathbf{G}\right)}^{-1}\underset{¯}{e}.$$ (47)

In a post processing we finally recover the vector of constants

$$\underset{¯}{\gamma }={\left({\mathbf{G}}^{⊺}\mathbf{G}\right)}^{-1}{\mathbf{G}}^{⊺}(\mathbf{F}\underset{¯}{\lambda }-\underset{¯}{d}),$$ (48)

and subsequently the desired solution (39).

4.4 Preconditioning

Following Farhat et al. [17] we apply either the lumped preconditioner

$${\mathbf{M}}_{\mathrm{L}}^{-1}≔\sum _{i=1}^p{\mathbf{B}}_{\mathrm{D},i}{\mathbf{K}}_i^{\prime }{\mathbf{B}}_{\mathrm{D},i}^{⊺},$$ (49)

or the optimal Dirichlet preconditioner

$${\mathbf{M}}_{\mathrm{D}}^{-1}≔\sum _{i=1}^p{\mathbf{B}}_{\mathrm{D},i}\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{S}}_i\hfill \end{array}\right){\mathbf{B}}_{\mathrm{D},i}^{⊺},$$ (50)

where

$${\mathbf{S}}_i={\mathbf{K}}_{\mathrm{CC}}^{\prime }\left({\underset{¯}{U}}_i^k\right)-{\mathbf{K}}_{\mathrm{C}i}^{\prime }\left({\underset{¯}{U}}_i^k\right){\mathbf{K}}_{\mathit{ii}}^{\prime -1}\left({\underset{¯}{U}}_i^k\right){\mathbf{K}}_{i\mathrm{C}}^{\prime }\left({\underset{¯}{U}}_i^k\right)$$ (51)

is the Schur complement of the local finite element matrix ${\mathbf{K}}_i^{\prime }$. Alternatively, one may also use scaled hypersingular boundary integral operator preconditioners, as proposed in [52]. For comparison we employ an identity preconditioner which is constructed by using the identity matrix for Y_i in eq. (46).

5 Numerical Results

In this section some representative numerical examples for the finite element tearing and interconnecting approach for linear and nonlinear elasticity problems are presented. First, the FETI implementation is tested within linear elasticity. Here we are able to compare the computed results to a given exact solution. This enables us to show the efficiency of our implementation and also the convergence rates, as predicted from the theory. We compare the different preconditioning techniques and present differences between the classical FETI and the all-floating FETI approach.

Subsequently, we apply the FETI method to nonlinear elasticity problems. Thereby, we focus on the anisotropic model, as described in Section 2, and use a realistic triangulations of the aorta and a common carotid artery. As in the linear elastic case, different preconditioning techniques for the all-floating and for the classical FETI method are compared. In Section 5.3, we analyze the biomechanical behavior of an aorta up to an internal pressure of 300 mmHg and plot stress and displacement evolutions as a function of the internal pressure. Finally, in Section 5.4, we analyze our computational framework with respect to strong scaling properties.

The calculations were performed by using the VSC2-cluster (http://vsc.ac.at/) in Vienna. This Linux cluster features 1314 compute nodes, each with two AMD Opteron Magny Cours 6132HE (8 Cores, 2.2 GHz) processors and 8 × 4 RAM. This yields the total number of 21 024 available processing units. As local direct solver we use Pardiso [53, 54], included in Intel’s Math Kernel Library (MKL).

5.1 Linear elasticity

In this section of numerical benchmarks we consider a linear elastic problem with the academic example of a unit cube which is decomposed into a certain number of subcubes. Dirichlet boundary conditions are imposed all over the surface Γ_D = ∂Ω. The parameters used are Young’s modulus E = 210 GPa and Poisson’s ratio ν = 0.45. The calculated solution is compared to the fundamental solution of linear elastostatics

$$U_{1k}^{\ast }(\mathbf{x},{\mathbf{x}}^{\ast })=\frac{1}{8\pi }\frac{1}{E}\frac{1+\nu }{1-\nu }\left[(3-4\nu )\frac{{\delta }_{1k}}{\mid \mathbf{x}-{\mathbf{x}}^{\ast }\mid }+\frac{(x_1-x_1^{\ast })(x_l-x_l^{\ast })}{{\mid \mathbf{x}-{\mathbf{x}}^{\ast }\mid }^3}\right],k=1,2,3$$ (52)

for all $\mathbf{x}\in \Omega ,{\mathbf{x}}^{\ast }\in {\mathbb{R}}^3$ is an arbitrary point outside of the domain Ω, and δ_ij is the Kronecker delta, see [55]. The different strategies of preconditioning are compared and also the all-floating and classical FETI approaches. As global iterative method we use the CG method with a relative error reduction of ε = 10⁻⁸. Under consideration is a linear elasticity problem using linear tetrahedral elements (${\mathcal{P}}_1$ elements) with a uniform refinement over five levels (ℓ = 1, … , 5) given a cube with 512 subdomains.

Hence, the number of degrees of freedom associated with the coarsest mesh is 9 981 for the all-floating FETI approach and 6 621 for the classical FETI approach. The difference of the numbers is due to the decoupling of the Dirichlet boundary Γ_D. For the finest mesh we have 31 116 861 (all-floating) and 31 073 181 (classical) degrees of freedom. The number of Lagrange multipliers varies between 38 052 for level 1 and 2 908 692 for level 5. Again we have a higher number of Lagrange multipliers for the all-floating approach due to the decoupling of the Dirichlet boundary conditions. The computations were performed on VSC2 using 512 processing units.

First note in Table 2 that for all examined settings, the L2 error, i.e.

$${\Vert \mathbf{u}-{\mathbf{u}}_h\Vert }_{L_2\left(\Omega \right)},$$ (53)

where uh is the approximate and u the exact solution, and the estimated order of convergence

$${\text{eoc}}_{\ell }=\frac{\ln {\Vert \mathbf{u}-{\mathbf{u}}_{h,\ell }\Vert }_{L_2\left(\Omega \right)}-\ln {\Vert \mathbf{u}-{\mathbf{u}}_{h,\ell +1}\Vert }_{L_2\left(\Omega \right)}}{\ln 2}$$ (54)

behaves as predicted from the theory, i.e. it is of second order. As expected the least iteration numbers were observed for the optimal Dirichlet preconditioner. Nonetheless, since no additional time is required to compute the lumped preconditioner, in contrast to the more sophisticated Dirichlet preconditioner, this type of preconditioning yields comparable computational times for each level of refinement. As a comparison we also list the results of a very simple preconditioning technique, using the identity matrix for Y_i in (46), where almost no reduction of the condition numbers can be noticed.

Table 2.

Iteration numbers (it.), condition numbers and computational time (in s) for each preconditioning technique using ${\mathcal{P}}_1$ elements; ℓ is the level of uniform refinement. For the L2 error the definition is given in (53), while for the estimated error of convergence eoc the definition is given in (54).

all-floating
ℓ	identity prec.			lumped prec.			Dirichlet prec.			L2 error	eoc
1	61 it.	53.6	20.9 s	27 it.	10.3	19.7 s	21 it.	7.6	19.5 s	1.42E-04	-
2	71 it.	70.0	19.6 s	38 it.	19.7	18.8 s	26 it.	10.4	18.4 s	3.71E-05	1.94
3	88 it.	108.8	21.7 s	45 it.	26.1	22.3 s	27 it.	9.7	22.3 s	9.40E-06	1.98
4	119 it.	216.8	28.8 s	62 it.	53.2	26.4 s	32 it.	13.1	26.6 s	2.37E-06	1.99
5	160 it.	432.7	116.6 s	91 it.	126.2	99.0 s	37 it.	16.8	105.9 s	5.96E-07	1.99
classical
ℓ	identity prec.			lumped prec.			Dirichlet prec.			L2 error	eoc
1	80 it.	98.2	7.1 s	35 it.	14.1	5.9 s	29 it.	10.0	5.9 s	1.47E-04	-
2	105 it.	161.4	7.8 s	58 it.	41.9	6.1 s	37 it.	16.4	5.8 s	3.72E-05	1.98
3	140 it.	295.7	9.3 s	85 it.	105.9	7.9 s	46 it.	25.4	7.7 s	9.41E-06	1.98
4	188 it.	580.9	15.2 s	125 it.	252.1	13.1 s	54 it.	35.8	12.2 s	2.37E-06	1.99
5	251 it.	1150.3	103.4 s	179 it.	555.7	88.2 s	60 it.	46.3	83.6 s	5.96E-07	1.99

Moreover, we observe that all-floating FETI yields better condition numbers for all preconditioners, and hence better convergence rates of the global conjugate gradient method. Although the global iterative method converges in less iterations for this approach, we achieve lower computational time for the classical FETI method for the linear elastic case with ${\mathcal{P}}_1$ elements. This is mainly due to the larger expenditure of time to set up the all-floating FETI system, the larger coarse matrix GG^⊤, cf. (44), and due to the higher amount of Lagrange multipliers.

From level 4, with a maximum of 8 907 local degrees of freedom, to level 5, with a maximum of 66 195 local degrees of freedom, we observe an increase in the local assembling and factorization time from approximately 1.8 seconds up to about 13 seconds for all kinds of preconditioners. This is mainly due to the higher memory requirements of the direct solver. Note also that the factorization of the local stiffness matrices by the direct solver is unfeasible, if the number of local degrees of freedom gets too large. The reason for that are memory limitations on the VSC2 cluster. A possibility to overcome this problem is the use of fast local iterative solvers, e.g., the CG method with a multigrid or a BPX preconditioner. Summing it up seems that the simple lumped preconditioner and the classical FETI approach appear to be favorable for this academic example, with very structured subdomains and the boundary Γ_D = ∂Ω. The latter yields a large number of floating subdomains for all-floating FETI which are non-floating for the classical FETI approach, and hence a much larger coarse matrix GG^⊤ for all-floating FETI. The inversion of this matrix is the most time consuming part for the levels ℓ = 1, … , 4 that also results in the higher computational time for all-floating FETI in these cases.

Next, we consider a linear elastic problem by using tetrahedral elements and quadratic ansatz functions, i.e. ${\mathcal{P}}_2$ elements for the same mesh and parameter properties as above. The number of degrees of freedom now varies between 53 181 (level ℓ = 1) and 26 398 269 (level ℓ = 4) and the number of Lagrange multipliers between 77 700 and 2 908 692. Note that for all preconditioning types and for both the all-floating and the classical FETI method the L2 error compared to the fundamental solution behaves as predicted from the theory as we get a cubic convergence rate, see Table 3.

Table 3.

Iteration numbers (it.), condition numbers and computational time (in s) for each preconditioning technique using ${\mathcal{P}}_2$ elements; ℓ is the level of uniform refinement. For the L2 error the definition is given in (53), while for the estimated error of convergence eoc the definition is given in (54).

all-floating
ℓ	identity prec.			lumped prec.			Dirichlet prec.			L2 error	eoc
1	149 it.	444.7	23.3 s	73 it.	73.7	22.0 s	47 it.	36.7	18.7 s	1.13E-05	-
2	129 it.	330.8	21.9 s	75 it.	74.3	20.8 s	43 it.	27.7	19.3 s	1.44E-06	2.97
3	114 it.	210.3	30.3 s	73 it.	68.8	27.3 s	36 it.	16.6	28.5 s	1.81E-07	2.99
4	105 it.	167.8	99.8 s	69 it.	65.2	93.4 s	33 it.	14.4	90.2 s	2.26E-08	3.00
classical
ℓ	identity prec.			lumped prec.			Dirichlet prec.			L2 error	eoc
1	120 it.	405.0	7.5 s	65 it.	48.9	6.9 s	40 it.	21.0	6.5 s	1.17E-05	-
2	108 it.	302.6	7.5 s	69 it.	57.6	6.7 s	41 it.	20.6	7.5 s	1.46E-06	3.00
3	112 it.	253.4	12.6 s	91 it.	116.2	11.7 s	42 it.	21.0	12.3 s	1.82E-07	3.01
4	136 it.	273.1	76.3 s	128 it.	262.8	77.3 s	48 it.	27.7	79.1 s	2.26E-08	3.01

For all-floating FETI we have the very interesting case that the global CG iteration numbers remain almost constant for the lumped preconditioner, and it even seems to be a decay for the identity and the Dirichlet preconditioner, if we increase the local degrees of freedom, i.e. increase the refinement level ℓ.

For the classical FETI approach the iteration numbers stay almost constant for the Dirichlet preconditioner and increase marginally for the other two preconditioning techniques. Concerning the computational time we have an analogous result as in the previous case with linear ansatz functions: the classical approach with the lumped preconditioner seems to be the best choice for this particular example.

5.2 Arterial model on a realistic mesh geometry

In this section we present examples to show the applicability of the FETI approaches for biomechanical applications, in particular the inflation of an artery segment. We consider the mesh of an aorta and the mesh of a common carotid artery, see Figs. 4 and 5. The geometries are from AneuriskWeb [56] and Gmsh [57]. The generation of the volume mesh was performed using VMTK and Gmsh [57].

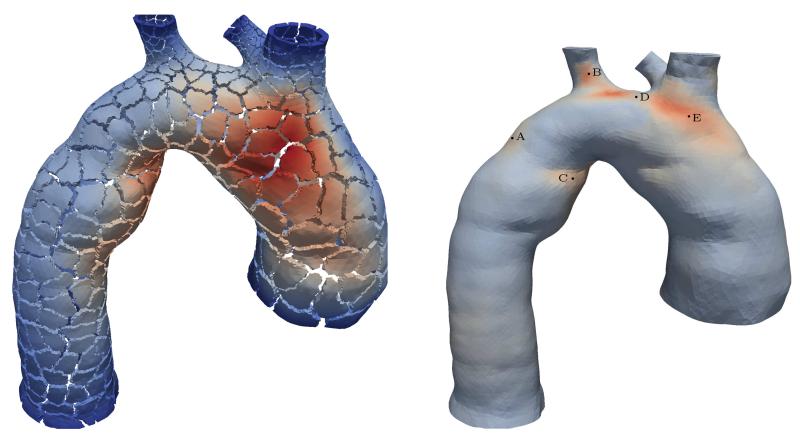
Figure 4.

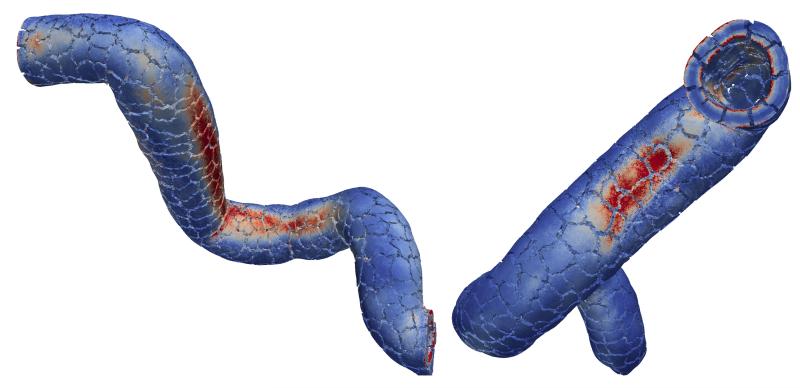
Mesh of an aorta seen from above showing the brachiocephalic artery, and the left common carotid and subclavian arteries. The fine mesh consists of 5 418 594 tetrahedrons and 1 055 901 vertices, while colors indicate the displacement field with an internal pressure of 1 mmHg. Additionally, the splits show the decomposition of the mesh into 480 subdomains (left). Coarser mesh consisting of 720 060 tetrahedrons and 150 725 vertices used in Section 5.3 with 5 selected vertices A–E (right); colors show the distribution of the stress magnitude σ_mag according to (56) with an internal pressure of 300 mmHg. For both images red indicates high and blue low values.

Figure 5.

Mesh of a segment of a common carotid artery from two different points of view. The mesh consists of 9 195 336 tetrahedrons and 1 621 365 vertices. Color indicates the distribution of the stress magnitude σ_mag according to (56) due to an internal pressure of 1 mmHg, red indicates high and blue low values. Additionally, the splits show the decomposition of the mesh into 512 subdomains.

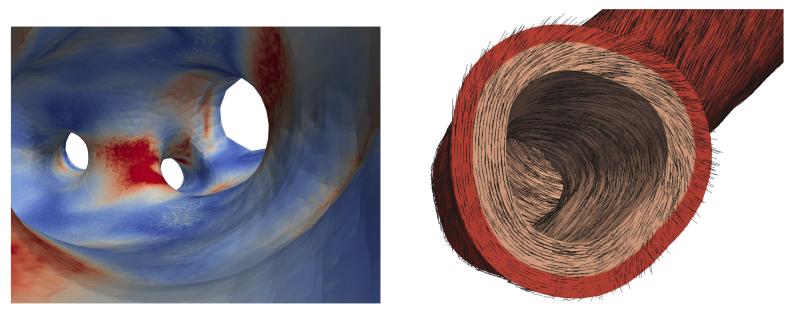
The fiber directions, see Fig. 6 (right), were calculated using a method described by Bayer et al. [58] for the myocardium. To adapt this method for the artery we first solved the Laplace equation on the domain Ω₀ with homogeneous Dirichlet boundary conditions on the inner surface and inhomogeneous Dirichlet boundary conditions on the outer wall. The gradient of the solution is used to define the transmural direction ${\widehat{\mathbf{e}}}_2$ in each element. As a second step we repeat this procedure using homogeneous Dirichlet boundary conditions on the inlet surface and inhomogeneous boundary conditions on the outlet surfaces which yields the longitudinal direction ${\widehat{\mathbf{e}}}_1$. The cross product of these two vectors eventually provides the circumferential direction ${\widehat{\mathbf{e}}}_0$. With a rotation we get the two desired fiber directions a_0,1 and a_0,2 in the media and the adventitia, respectively. Thus,

$$({\mathbf{a}}_{0,1}-{\mathbf{a}}_{0,2}{\widehat{\mathbf{e}}}_2)=\left({\widehat{\mathbf{e}}}_0{\widehat{\mathbf{e}}}_1{\widehat{\mathbf{e}}}_2\right)\left(\begin{array}{ccc}\hfill \cos \alpha \hfill & \hfill -\sin \alpha \hfill & \hfill 0\hfill \\ \hfill \sin \alpha \hfill & \hfill \cos \alpha \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\widehat{\mathbf{e}}}_0^{⊺}\hfill \\ \hfill {\widehat{\mathbf{e}}}_1^{⊺}\hfill \\ \hfill {\widehat{\mathbf{e}}}_2^{⊺}\hfill \end{array}\right)\left({\widehat{\mathbf{e}}}_0{\widehat{\mathbf{e}}}_1{\widehat{\mathbf{e}}}_2\right).$$ (55)

The value for the angle α are 29° for the media and 62° for the adventitia, taken from [5].

Figure 6.

Distribution of the stress magnitude σ_mag inside the aorta (left); values of high stress in red and of low stress in blue. To the right the fiber directions (black curves) and the two layers (adventitia in red and media in orange) of the carotid artery are shown.

To describe the anisotropic and nonlinear arterial tissue, we use the material model (13–17), with the parameters given in Table 1 and κ is varied. Dirichlet boundary conditions (7) are imposed on the respective intersection areas. We perform an inflation simulation on the artery segment where the interior wall is exposed to a constant pressure p. This is performed using Neumann boundary conditions (8). If not stated otherwise, we present the results of one load step applying a rather low pressure of 1 mmHg. This is necessary to have a converging Newton method. Nonetheless, the material model as used is anisotropic. To simulate a higher pressure, an appropriate load stepping scheme, see (25), has to be used. However, this does not affect the number of local iterations significantly. As already mentioned in Section 4 we use the CG method as global iterative solver. Experiments with a standard non-symmetric nonlinear elasticity system and the necessary GMRES method as an iterative solver showed similar results, as presented in the following with the symmetric system. However, the memory requirements of the GMRES solver are much higher.

The local generalized pseudo-inverse matrices are realized with a sparsity preserving regularization by fixing nodes, see, e.g., [30], and the direct solver package Pardiso. The global nonlinear finite element system is solved by a Newton scheme, where the FETI approach is used in each Newton step. For the considered examples the Newton scheme needed four to six iterations. Due to the non-uniformity of the subdomains the efficiency of a global preconditioner becomes more important. It may happen that the decomposition of a mesh results in subdomains that have only a few points on the Dirichlet boundary. This negatively affects the convergence of the CG method using classical FETI, but does not affect the global iterative method of the all-floating approach at all. This is a major advantage of all-floating FETI since here all subdomains are treated the same, and hence all subdomains are stabilized. This behavior is observed for almost all settings for preconditioners and the penalty parameter κ as well as for linear and quadratic ansatz functions, see Tables 4–7.

Table 4.

Iteration numbers (it.) per Newton step and computational time (in s) per Newton step for the all-floating and the classical FETI approach with linear ansatz functions comparing the three considered preconditioners. The penalty parameter κ was varied from 10 to 1000 kPa. Mesh: mesh of the aorta subdivided in 480 subdomains, computed with 480 cores.

all-floating
κ	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
10	1052 it.	57.6 s	160 it.	31.0 s	56 it.	22.8 s
100	1879 it.	94.6 s	305 it.	29.5 s	85 it.	25.4 s
1000	4122 it.	177.1 s	681 it.	48.8 s	209 it.	31.8 s
classical
κ	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
10	2056 it.	98.7 s	305 it.	35.5 s	117 it.	27.2 s
100	3711 it.	149.8 s	540 it.	35.5 s	144 it.	28.4 s
1000	8245 it.	327.8 s	1190 it.	60.9 s	263 it.	32.9 s

Table 5.

Iteration numbers (it.) per Newton step and computational time (in s) per Newton step for the all-floating and the classical FETI approach with linear ansatz functions comparing the three considered preconditioners. The penalty parameter κ was set to 1000 kPa. Mesh: mesh of the carotid artery with two layers (adventitia and media) subdivided in 512 subdomains, computed with 512 cores.

type	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
all-floating	> 10000 it.	− s	1084 it.	100.6 s	497 it.	85.5 s
classical	5130 it.	357 s	1794 it.	200.2 s	588 it.	97.7 s

Table 6.

Iteration numbers (it.) per Newton step and computational time (in s) per Newton step for the all-floating and the classical FETI approach with quadratic ansatz functions comparing the three considered preconditioners. The penalty parameter κ was varied from 10 to 1000 kPa. Mesh: mesh of the aorta subdivided in 480 subdomains, computed with 480 cores.

all-floating
κ	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
10	940 it.	491.1 s	283 it.	209.5 s	71 it.	157.3 s
100	1519 it.	1186.4 s	523 it.	332.0 s	105 it.	178.1 s
1000	3371 it.	2584.5 s	1372 it.	746.0 s	206 it.	282.7 s
classical
κ	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
10	1319 it.	654.2 s	333 it.	225.2 s	113 it.	188.4 s
100	2362 it.	1140.6 s	664 it.	402.6 s	110 it.	177.5 s
1000	5563 it.	4168.3 s	1742 it.	943.1 s	204 it.	280.1 s

Table 7.

Iteration numbers (it.) per Newton step and computational time (in s) per Newton step for the all-floating and the classical FETI approach with quadratic ansatz functions comparing the three considered preconditioners. The penalty parameter κ was set to 1000 kPa. Mesh: mesh of the carotid artery with two layers (adventitia and media) subdivided in 1024 subdomains, calculated with 1024 cores.

type	identity preconditioner		lumped preconditioner		Dirichlet preconditioner
all-floating	> 10000 it.	− s	2163 it.	1133.9 s	674 it.	994.6 s
classical	6006 it.	2672.6 s	4798 it.	2306.8 s	764 it.	771.2 s

For example, applying all-floating FETI with the Dirichlet preconditioner to the mesh of the aorta using a penalty parameter κ = 1000 kPa the global CG method converged in considerable less iterations (209) than the CG method using classical FETI (263), see Table 4. The advantage of the smaller number of iterations is not so significantly reflected in the computational time since, as for the linear case, we have higher set up times and a larger coarse system GG^⊤. Nonetheless, for the considered examples it shows that all-floating FETI yields lower iteration numbers of the global systems and it is also competitive or even advantageous with respect to the classical approach concerning the computational time.

In contrast to the academic example in Section 5.1 the more complex Dirichlet preconditioner is the best choice for all considered settings. Especially for k ⪢ 1 the iteration numbers with the lumped and the identity preconditioner escalate. Admittedly, the numbers in Table 4 also show that the convergence of the CG method, within all FETI approaches and preconditioner settings, is dependent on the penalty parameter κ.

Using quadratic ansatz functions we have a total number of 23 031 620 degrees of freedom for the aorta mesh and 36 527 435 degrees of freedom for the carotid artery mesh. In order to not infringe the memory limitations on the VSC2 cluster we have to use a decomposition into 1024 subdomains (instead of 512) for the carotid artery. For the aorta it was possible to stay with 480 subdomains. The number of Lagrange multipliers are then 1 552 665 (aorta) and 4 585 203 (carotid artery). Comparing the numbers in Table 6 and Table 7 show similar results as in the case with linear ansatz functions. The Dirichlet preconditioner is preferable for all test cases and the all-floating approach is competitive to the classical FETI approach. Albeit quadratic ansatz functions resolve the nearly incompressible elastic behavior better than linear ansatz functions we also notice a correlation between the global iteration numbers and the penalty parameter κ, see Table 6. Nonetheless, the iteration numbers do not increase as much as for the P₁ – P₀ element case and the values of J = det F in each element are much closer to 1 for the P₂ – P₀ elements.

5.3 Load stepping scheme

In this section we analyze the biomechanical behavior of the aorta up to an internal pressure of 300 mmHg. Higher pressures would induce damage and softening behavior which cannot be captured with the arterial model discussed in Section 2. For that purpose we consider a coarser version of the mesh of the aorta (see Fig. 4), which is subdivided into 32 subdomains since for this mesh the all-floating FETI method looks significantly advantageous. The reasons for that are as follows: (i) we have lower iteration numbers for the all-floating FETI approach, as already observed in Section 5.2; (ii) the matrix GG^⊤ in (44) is small, and hence less time is needed to compute the inverse of this coarse system, especially in comparison to the assembly time and the global solving time of the CG method.

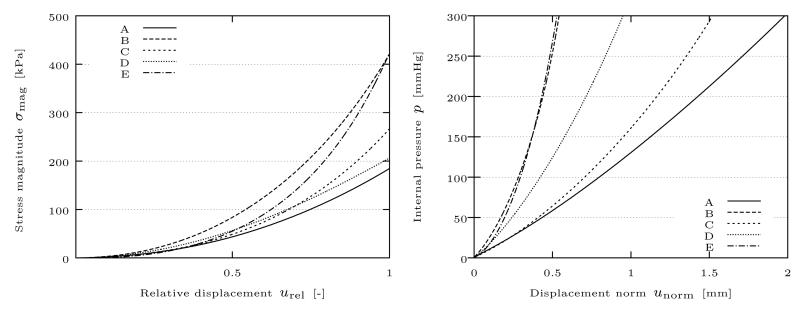
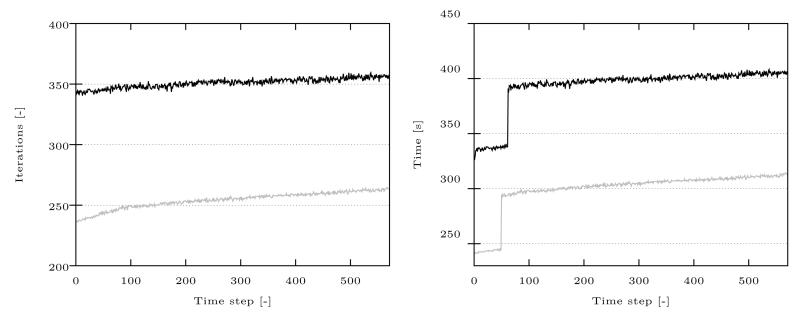
With this mesh we simulate an arterial model with the parameters from Table 1 and with c = 6 kPa and κ = 1000 kPa using the Dirichlet preconditioner. The results of a load stepping scheme, where we applied an internal pressure up to 300 mmHg over 572 loading steps, are found in the Figs. 7 and 8. Note that the average iteration number over one time step increased from 248 to 268 for all-floating FETI and from 340 to 358 for the classical FETI approach for higher pressures, and, consequently, a more anisotropic material behavior. The simulation needed four to five Newton steps and the solving times for all-floating FETI are significantly faster, see Fig. 8.

Figure 7.

Stress magnitude σ_mag versus relative displacement u_rel (left) and evolution of the displacement norm u_norm over the load steps up to an internal pressure p of 300 mmHg (right). The plots were generated using data at the specific points A–E, as shown in Fig. 4 (right).

Figure 8.

Comparison of all-floating FETI (gray) and classical FETI (black) for a time stepping scheme. Average iteration numbers of one time step (left) and solving times in seconds for one time step (right) over 572 load steps.

In our plots we used a stress magnitude σ_mag according to

$${\sigma }_{\text{mag}}=\sqrt{{\sigma }_{11}^2+{\sigma }_{22}^2+{\sigma }_{33}^2+2{\sigma }_{12}^2+2{\sigma }_{13}^2+2{\sigma }_{23}^2},$$ (56)

used as a measure to visualize our data. For advantages and disadvantages of certain stress values concerning the analysis of rupture and failure in aortic tissues, see, e.g., [59]. Other values used in Fig. 7 are the displacement norm u_norm and the relative displacement u_rel, i.e.

$$u_{\text{norm}}=\sqrt{u_1^2+u_2^2+u_3^2},u_{\text{rel}}=\frac{u_{\text{norm}}}{u_{\text{max}}},$$ (57)

for a point with the displacement vector u = (u₁, u₂, u₃) at the time step t, and u_max is the largest occurring displacement norm for that point over all time steps.

5.4 Strong scaling for nonlinear elasticity

Here we analyze our computational framework with respect to strong scaling efficiency, i.e.

$$\mathrm{eff}=\frac{t_{\mathrm{I}}}{P{t}_{\mathrm{P}}},$$ (58)

where t_I is the amount of time to complete a computation with the initial number of processing units I (in our case I = 16) and t_P is the amount of time to complete the same computation with P processing units. In particular, we consider the meshes of the carotid artery and the aorta as in Section 5.2, both subdivided into 512 subdomains. We apply the arterial model with the parameters from Table 1 and use a κ = 100 with the lumped preconditioner and linear ansatz functions. For the aorta we used all-floating FETI and needed an average of 324 global CG iterations to reach an absolute error of ε = 10⁻⁸ and 5 Newton steps to reach an absolute error of 10⁻⁶. In the case of the carotid artery and classical FETI we needed 674 global CG iterations and also 5 Newton steps to reach the same error limits as above.

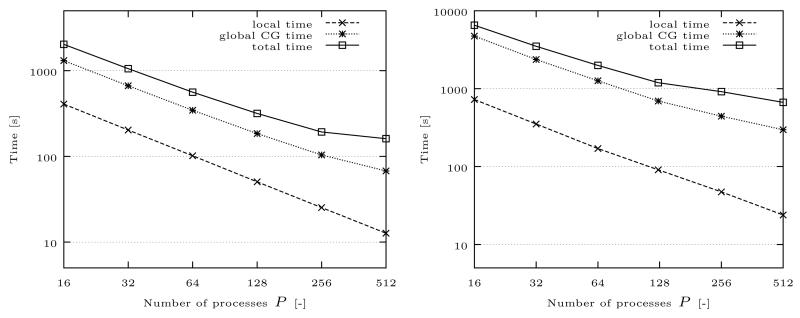
In the Tables 8 and 9 we present the following numbers: the local time is the sum of all assembling and local factorization times during the solution steps. The factorization of the local problems was performed with the direct solver package Pardiso. In most cases we observed a super-linear speedup, and hence an efficiency greater than 1 for this value. This is due to memory issues, mainly so-called cache effects. For more information on this well-known phenomenon, see, e.g., [60]. The global CG time is the duration of all CG solution steps together. We see that this value scales very well up to 256 cores for the aorta and up to 128 cores for the carotid artery. The total time is the total computational time including input and output functions. It also scales admissibly well up to 256 processing units for the aorta, and up to 128 cores for the carotid artery, see Tables 8 and 9, and Fig. 9. For a higher number of cores, at least for the specific examples, the speedup is rather low. Possibilities to overcome this problem are, for example, the usage of parallel solver packages such as hypre and a more efficient assembling of the coarse system of the FETI method. It also needs a more elaborate strategy with MPI and the memory management. Note that at some point the subdomains get too small and the increasingly dominant MPI communication impedes further strong scaling.

Table 8.

Computational time (in s) and efficiency (eff) according to (58) for a nonlinear elastic problem using a varying number of processing units P. The time is measured for 1 time step with 5 Newton steps for all-floating FETI and the lumped preconditioner.

P	local time	eff	global CG time	eff	total time	eff
16	407.7 s	1.000	1311.7 s	1.000	2028.6 s	1.000
32	203.1 s	1.004	666.4 s	0.984	1054.2 s	0.962
64	101.7 s	1.002	345.4 s	0.949	562.0 s	0.902
128	50.5 s	1.009	184.7 s	0.888	316.7 s	0.801
256	25.3 s	1.007	103.8 s	0.790	192.8 s	0.658
512	12.7 s	1.000	67.6 s	0.606	161.0 s	0.394

Table 9.

Computational time (in s) and efficiency (eff) according to (58) for a nonlinear elastic problem on the carotid artery mesh using a varying number of processing units P. The time is measured for 1 time steps with 5 Newton steps for classical FETI and the lumped preconditioner.

P	local time	eff	global CG time	eff	total time	eff
16	726.0 s	1.000	4725.8 s	1.000	6519.7 s	1.000
32	351.3 s	1.033	2368.2 s	0.998	3497.0 s	0.932
64	170.5 s	1.065	1262.9 s	0.936	1991.2 s	0.819
128	90.7 s	1.001	694.5 s	0.851	1194.1 s	0.682
256	47.3 s	0.960	443.6 s	0.666	914.4 s	0.446
512	23.9 s	0.949	297.2 s	0.497	667.4 s	0.305

Figure 9.

Computation times (in s) for a simulation of the anisotropic arterial model with the aorta mesh (left) and the carotid artery mesh (right) using a varying number of cores.

6 Discussion and Limitations

We have shown the application of the finite element tearing and interconnecting method to elasticity problems, in particular to the simulation of the nonlinear elastic behavior of cardiovascular tissues such as the artery. The main ideas of domain decomposition methods were summarized and the classical and the all-floating FETI approach were discussed in detail.

Illustrated by representative numerical examples we have shown certain advantages of the all-floating FETI method compared to the classical FETI approach. To the best of our knowledge the application of the all-floating approach to nonlinear anisotropic elasticity problems cannot be found in the literature. Certainly, the mentioned advantages are influenced by the mesh structure and the choice of the boundary conditions, and hence the method to choose depends on the specific problem.

We have presented and compared different techniques of preconditioning: the lumped preconditioner and the optimal Dirichlet preconditioner. Furthermore, the numerical examples exposed some instabilities of the global iterative method for nearly incompressible material parameters, i.e. for a very large penalty parameter κ. Here we were able to present, like it was also shown in earlier contributions, that quadratic ansatz functions resolve the incompressible elastic behavior better than linear ansatz functions.