Diagnosis of Prostatic Carcinoma on Multiparametric Magnetic Resonance Imaging Using Shearlet Transform

Abstract

This paper presents a method to diagnose prostate cancer on multiparametric magnetic resonance imaging (Mp-MRI) using the shearlet transform. The objective is classification of benign and malignant regions on transverse relaxation time weighted (T2W), dynamic contrast enhanced (DCE), and apparent diffusion coefficient (ADC) images. Compared with conventional wavelet filters, shearlet has inherent directional sensitivity, which makes it suitable for characterizing small contours of cancer cells. By applying a multi-scale decomposition, the shearlet transform captures visual information provided by edges detected at different orientations and multiple scales in each region of interest (ROI) of the images. ROIs are represented by histograms of shearlet coefficients (HSC) and then used as features in Support Vector Machines (SVM) to classify ROIs as benign or malignant. Experimental results show that our method can recognize carcinoma in T2W, DCE, and ADC with overall sensitivity of 92%, 100%, and 89%, respectively. Hence, application of shearlet transform may further increase utility of Mp-MRI for prostate cancer diagnosis.

I. Introduction

Aside from skin cancer, U.S. men are most frequently diagnosed with prostate cancer [1]. In 2014, an estimated 233,000 men will be diagnosed with prostate cancer and 29,480 will die from this disease [1]. Early diagnosis of this disease permits curative treatments. Undiagnosed prostate cancers are at high risk of spreading and metastasizing to other organs, particularly to the bone. Currently, there are no curative treatments available for metastatic prostate cancer [2]. Therefore, patient survival largely depends on early diagnosis.

Prostate cancer is diagnosed by histopathological evaluation of tissue cores taken during prostate biopsies [3]. Pathological evaluation includes assessment of histopathologic Gleason grade [4] and stage [5] of the disease. Revised Gleason grading system includes three grades: Grades 3, 4, and 5. Gleason grade 3 cancer is considered low grade and non-aggressive. Gleason grades 4 or 5 cancer is considered high grade, aggressive, and has potential for metastasis. Stage of the disease indicates the cancer's extent and how far it has spread from the prostate gland. Prostate biopsies are obtained under the guidance of transrectal ultrasound (TRUS) [3].

TRUS biopsies are recommended for men with a serum prostate-specific antigen (PSA) level above 4 ng/mL or with an abnormal digital rectal exam (DRE) [6]. PSA cutoff value 4ng/mL has limited sensitivity and specificity to indicate existence of aggressive tumors that are more likely to metastasize and lead to potentially lethal disease. Initial TRUS biopsies diagnose only 22–38% of prostate cancer and 30–40% of aggressive tumors that require curative treatment may remain undiagnosed [7, 8].

Some of these aggressive cancers remain undiagnosed because TRUS images show only the anatomical landmarks of the prostate gland, but not the individual cancer lesions. Therefore, TRUS biopsies are taken randomly without targeting any cancer lesion and hence prone to diagnostic errors. Diagnostic accuracy of TRUS biopsies can be improved by augmenting an imaging modality that can identify cancer lesions. The most promising strategy for imaging prostate cancer lesions is multiparametric magnetic resonance imaging (Mp-MRI) [9]. Mp-MRI includes anatomical sequences of conventional transverse relaxation time weighted (T2W) and longitudinal relaxation time weighted (T1W) imaging; functional sequences of dynamic contrast enhanced (DCE) and diffusion weighted (DW) imaging.

Anatomical sequence T2W imaging provides the highest soft tissue resolution for visualization of tumors, the zonal anatomy, and prostatic capsule [10]. Sensitivity for visualization depends on the tumor location within the prostate zonal anatomy [11]. On T2W images, peripheral zone (PZ) appears normally high in signal intensity whereas central gland (CG) including central zone (CZ) and transitional zone (TZ) has lower signal intensity. CG is separated from PZ by a pseudocapsule and PZ is surrounded with a hypointense true capsule. About 70% of all prostate cancers are located in the PZ [11]. On T2W, PZ cancers are seen as round or ill-defined, low signal intensity foci. However, this pattern is nonspecific and can be seen in atrophy, prostatitis, benign prostatic hyperplasia, and hemorrhage as well. Prostate cancer in the CG is more difficult to detect since signal characteristics of CG are heterogeneous and usually overlap with those of the tumor. Thus, T2W imaging has sensitivity and specificity for cancer detection in the range of 27–100% and 32–99%, respectively [10]. T1W imaging is of limited use since one cannot outline zonal anatomy or cancer lesions.

Functional sequence DCE imaging is obtained using low-molecular-weight gadolinium chelates as MRI contrast enhancement agent. On DCE imaging, tumors usually show early and rapid enhancement as well as early washout due to angiogenesis [10]. Higher wash-in and wash-out rates of DCE images enable detection of high Gleason grades and large tumors (≥ 1cc) whereas low volume (≥ 0.5 cc and <1 cc) and low Gleason grade tumors may remain undetected. Thus, DCE imaging has a wide range of sensitivity and specificity values for cancer detection: Sensitivity and specificity are 46–96% and 74–96%, respectively [10].

The other functional sequence DW imaging evaluates the Brownian motion of free water within tissues. DW imaging typically indicates tumors when there is a reduction in the diffusion of water. DW images are usually quantified by calculating the apparent diffusion coefficient (ADC). Tumors on ADC maps show decreased signal intensity relative to PZ. ADC values have been demonstrated to vary with histopathologic Gleason grade which is helpful in identifying aggressive prostate cancer [12]. Similar to other two sequences, DW imaging also has a wide range of sensitivity and specificity values for tumor detection: Sensitivity and specificity are 57–93% and 57–100%, respectively [10].

Mp-MRI with magnetic field strengths of 1.5 or 3.0 Tesla can be carried out using either a body surface coil or an endorectal coil for diagnosis and local staging of prostate tumors. However, 3T endorectal coil Mp-MRI appears to be more accurate [13]. Interpretation of Mp-MRI data is labor intensive, expensive, and highly operator dependent. Post-processing of these imaging sequences using various mathematical transformations can significantly reduce the cost and operator dependence while increasing the diagnostic utility [14].

Texture analysis and classification has many applications including medical image processing for diagnoses of tissues with abnormality such as cancer. In a recent study, we applied the recently introduced shearlet transformation [15] to whole-mounted prostate images for classification of benign versus malignant tissues and histopathologic Gleason grading of cancer [16]. Compared to histopathological evaluation, shearlet transform based analysis achieved 100% sensitivity for benign versus malignant tissue classification and 89% accuracy in Gleason grading. We also applied shearlet transform to images of breast biopsy tissues for successful classification of benign versus malignant breast tissue [17].

In this paper, we investigate shearlet transformation of T2W, DW, and DCE imaging sequences for features extraction and classification to significantly increase accuracy of prostate cancer detection on Mp-MRI. Compared with conventional wavelet filters such as Gabor filter, shearlet has inherent directional sensitivity, which makes it suitable for characterizing small contours of cancer cells.

In Section II we present our shearlet transform based method for Mp-MRI representation, feature extraction, and classification. In Section III, experimental results are provided including sensitivity and specificity for prostate cancer detection on various Mp-MRI sequences. Conclusions are presented in Section IV.

II. Methodology

We propose to use the shearlet transform for representing the local structure of image textures. Shearlet is a new transformation that is designed to effectively capture directional features such as orientations of curves, edges and points in images. To better understand the shearlet transformation, we first describe the new generation of mathematical transforms. When convolved with an image, wavelet transform has better resolution in both space and frequency domains and can extract important texture features [18]. However, wavelet transform does not provide directional information and is not effective in extracting different types of texture features as in cancer tissues. The curvelet transform was introduced by Candes and Donoho [19]. Curvelets are representation systems that depend on three parameters: Parameters are scale, location, and direction. Discrete version of this representation cannot be directly implemented. Since curvelets are rotation-based, a rotation destroys the discrete lattice structures. Therefore, a directional representation system is required which deals with anisotropic features in both the continuous and discrete domains. To overcome these shortcomings, the shearlet transform was developed. By taking advantage of the classical theory of affine systems, shearlets provide an effective approach for combining geometry and multi-scale analysis.

The continuous shearlet transform is defined as the mapping for f ε R²

$$S{H}_{\Psi }f(a,s,t)=<f,{\Psi }_{a,s,t}>,$$ (1)

Where the shearlets are given by

$${\Psi }_{a,s,t}(x)={\left|\mathit{\text{det}}{M}_{a,s}\right|}^{-\frac{1}{2}}\Psi ({M_{a,s}}^{-1}x-t)$$ (2)

In the above equation $M_{a,s}=\left(\begin{array}{cc}\hfill a\hfill & \hfill \sqrt{as}\hfill \\ \hfill 0\hfill & \hfill \sqrt{a}\hfill \end{array}\right)=B_s{A}_a$ for a > 0, sεR² tεR² where $A_a=\left(\begin{array}{cc}\hfill a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{a}\hfill \end{array}\right)$ and $B_s=\left(\begin{array}{cc}\hfill 1\hfill & \hfill -s\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$. Hence, there are two distinct actions associated to each matrix M_a,s: Two actions are anisotropic dilation produced by the matrix A_a and a shearing produced by the non-expansive matrix B_s. As a result, the shearlets form a collection of well-localized waveforms at various scales a, orientations s and locations t.

Discrete shearlet transform is obtained by sampling the continuous shearlet transform SH_Ψ f (a, s, t) on appropriate discretizations of the scaling, shear, and translation parameters a, s, t. The continuous translation variable tεR² is replaced by a point in the discrete lattice Z². Choosing a = 2^−j and s = −l with j, l ε Z one can acquire the collection of matrices M_2^−j,−l by observing that ${M_{2^{-j},-l}}^{-1}=M_{2^j,l}=\left(\begin{array}{cc}\hfill 2^j\hfill & \hfill l{2}_{j/2}^{j/2}\hfill \\ \hfill 0\hfill & \hfill 2^{j/2}\hfill \end{array}\right)={B_0}^l{A_0}^j$, Where $A_0=\left(\begin{array}{cc}\hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sqrt{2}\hfill \end{array}\right)$ and $B_0=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$. The discrete system of shearlets can be obtained as

$${\Psi }_{j,l,k}={|\mathit{det}{A}_0|}^{\frac{j}{2}}\Psi ({B_0}^l{A_0}^{j}x-k)$$ (3)

for j,lεZ, kεZ². The discrete shearlets share the special ability to deal with multidimensional functions with their continuous counterpart.

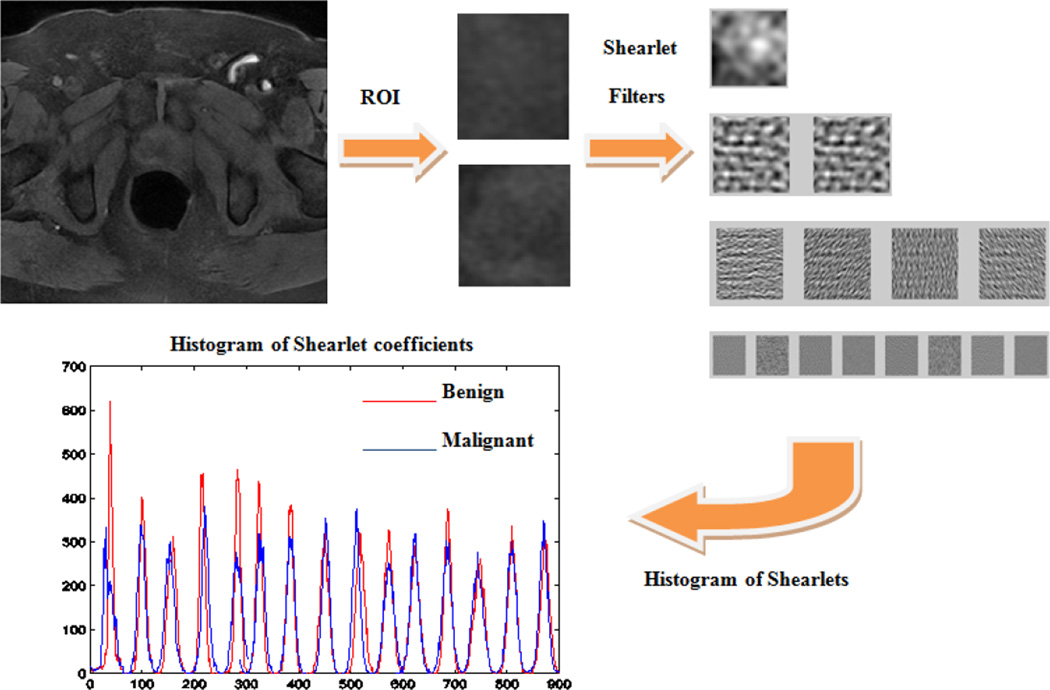
We use histogram of shearlet coefficients (HSC) [20] to have a compact representation of ROIs. However instead of choosing the number of orientations in shearlet transform as the number of bins for HSC, we choose a fixed number of bins. The shearlet coefficients of large magnitude come from edges [15]. Therefore the HSC method is based on the magnitude of shearlet coefficients at different scales and orientations. At each decomposition level, the HSC method estimates a histogram with a fixed number of bins and the entry at each bin is the shearlet coefficients within the certain range. Finally, the histograms computed for all levels are concatenated, resulting in a feature vector, which is used to describe the image. For this purpose we denote an image of size M × N as ${\mathit{I}}^{(\mathit{K})}=[I_{x,y}^{(K)}]$ where x = 1, …, M, y = 1, …,N are the pixel indices and k = 1, …, 20 is the image index. We denote the discrete shearlet coefficients by $s_{ij}^{(K,d)}={\sum }_{x,y}{I}_{x,y}^{(K)}{\mathrm{\psi }}_{i,j}^{(d)}(x,y)$ where i = 1, …, M and j = 1, …, N are the shearlet domain coordinates and d = 1, …, 4 is the decomposition level. The shearlet coefficient matrix is denoted using $S^{(K,d)}=[s_{ij}^{(K,d)}]$ for i = 1, …, M,, j = 1, …, N. Then we find the histogram of shearlet coefficients h^(K,d) = Hist{S^(K,d)} where Hist{․} means the normal histogram of data. This procedure is depicted in Fig. 1.

Fig. 1.

Our proposed Shearlet based method for feature representation.

III. Experiments and Results

A. Data

Four patients were included in this study. They had pre-surgery 3T endorectal coil Mp-MRI at the University of Colorado Hospital. T2W, DCE, and DW imaging sequences in DICOM file format were retrieved from our database. ADC maps were generated by fitting DW images. Our radiologist used Adobe Photoshop software to manually delineate prostate border and tumor boundaries on T2W, DCE and ADC maps. He used histopathological maps of prostates made by our pathologist to confirm and improve the accuracy of his interpretation. All image files were saved in TIFF format following classification by the radiologist. Original dimensions of T2W, DCE, and ADC maps in pixel counts were 512×512, 256×256, and 256×256, respectively. Following manual segmentation of the prostate border, dimensions of images were reduced to 180×140, 55×40, and 70×55 for T2W, DCE, and ADC, respectively. Since the size of these images was inadequate to run shearlet transform, we increased the overall size to 320×240 pixels by upsampling each image using bicubic interpolation technique. In the bicubic interpolation, the output pixel value is a weighted average of pixels in the nearest 4-by-4 neighborhood. Next, we selected malignant and benign rectangular ROIs for classification. Minimum ROI image size of 78×78 pixels is required to apply shearlet transform.

B. Classification

The inputs to our shearlet based method were the ROIs selected from ADC, DCE, and T2W images from four patients. For each patient, 10 benign ROIs and 10 malignant ROIs were selected from each one of ADC, DCE, and T2W images. We used the discrete shearlet transform toolbox to find the shearlet coefficients [15]. We used four decomposition levels and the shearlet coefficients at each decomposition level were determined. The histogram of shearlets with a fixed number of 60 bins returned the best classification rate. The histograms from each decomposition level were concatenated to form a single feature vector which was used for classification. Up to this point the, size of the feature vector was 1×885. The dimensionality of the features extracted from each ROI was large. Kernel principal component analysis (PCA) which is a nonlinear dimensionality reduction technique and an extension of PCA was used for feature reduction. Applying kernel PCA for feature reduction resulted in a feature size of 1×15 which contained 90% of total variance. Separate support vector machines (SVM) [21] with different kernels were trained based on the aforementioned features tested using half of the data for training and the other half for testing to classify ROIs as either containing malignant tumors or benign. Linear kernels returned the best classification results. SVM classification results are presented in the Table I. We pooled ROIs from all four patients to determine overall performance of shearlet based classification. Clearly, shearlet based classification can be used to accurately classify ROIs with prostate cancer.

TABLE I.

SVM classification results for mp-mri

Patient #	Parameter	Sensitivity	Specificity	Classification Rate
1	ADC	100%	100%	100%
	DCE	100%	100%	100%
	T2W	60%	100%	80%
2	ADC	100%	100%	100%
	DCE	100%	100%	100%
	T2W	80%	60%	70%
3	ADC	100%	100%	100%
	DCE	100%	100%	100%
	T2W	100%	60%	80%
4	ADC	80%	100%	90%
	DCE	100%	100%	100%
	T2W	100%	100%	100%
Overall	ADC	89%	100%	97%
	DCE	100%	100%	100%
	T2W	92%	83%	94%
HOG	ADC	90%	35%	63%
	DCE	70%	80%	75%
	T2W	80%	90%	85%
Gabor	ADC	70%	100%	85%
	DCE	60%	75%	68%
	T2W	65%	40%	53%

We have also extracted features from ROIs using Gabor filter [22] and Histogram of Oriented Gradients (HOG) [23] and compared the classification results with our proposed method. For Gabor filter we used 5 scales, 8 orientations, and a Gabor filter bank of size 10×10. Then we calculated the histogram of features extracted from Gabor filter using 60 bins and used it in classification. For HOG, we used 3 windows in each x and y direction and calculated the histogram of oriented gradients using 60 bins and used it for classification. The results are presented in Table I. Clearly, our proposed shearlet based method outperforms the other two methods.

IV. Conclusions

We have developed a method to correctly interpret and diagnose prostate cancer on Mp-MRI using the shearlet transform. Experimental data obtained from four patients show that our approach can identify malignant regions on T2W, DCE, and ADC imaging sequences with a high degree of accuracy. Our results are better than previously published results for these same imaging sequences [10]. Our experiments show that our proposed method outperforms state of the art methods [22, 23]. The proposed shearlet transform based method can be automated to assist radiologists to identify prostate cancer lesions. Then, TRUS augmented with Mp-MRI can be used for image guided prostate biopsies for early and accurate diagnosis of this disease. This has the potential to significantly improve patient quality of life and also could affect mortality outcomes for men with intermediate to high-risk disease with earlier diagnosis.