Contact efflorescence as a pathway for crystallization of atmospherically relevant particles

Significance

Atmospheric particles contain inorganic material that can effloresce to form a crystalline solid. The phase state of atmospheric particles influences the particle’s effect on climate and air quality. Despite the importance of particle phase, there is no comprehensive understanding of particle crystallization, and many climate models assume inorganic particles always remain liquid. Our study demonstrates that contact efflorescence, a previously unexplored pathway for crystallization, can lead to the formation of solid particulate at high relative humidity (RH, ∼80%) upon a single collision. Particles then remain crystalline at all relative humidities below their deliquescence point (<80% RH). Such a high efflorescence RH strongly suggests contact efflorescence may be an important atmospheric process to consider further.

Abstract

Inadequate knowledge of the phase state of atmospheric particles represents a source of uncertainty in global climate and air quality models. Hygroscopic aqueous inorganic particles are often assumed to remain liquid throughout their atmospheric lifetime or only (re)crystallize at low relative humidity (RH) due to the kinetic limitations of efflorescence (salt crystal nucleation and growth from an aqueous solution). Here we present experimental observations of a previously unexplored heterogeneous nucleation pathway that we have termed “contact efflorescence,” which describes efflorescence initiated by an externally located solid particle coming into contact with the surface of a metastable aqueous microdroplet. This study demonstrates that upon a single collision, contact efflorescence is a pathway for crystallization of atmospherically relevant aqueous particles at high ambient RH (≤80%). Soluble inorganic crystalline particles were used as contact nuclei to induce efflorescence of aqueous ammonium sulfate [(NH₄)₂SO₄], sodium chloride (NaCl), and ammonium nitrate (NH₄NO₃), with efflorescence being observed in several cases close to their deliquescence RH values (80%, 75%, and 62%, respectively). To our knowledge, these observations represent the highest reported efflorescence RH values for microdroplets of these salts. These results are particularly important for considering the phase state of NH₄NO₃, where the contact efflorescence RH (∼20–60%) is in stark contrast to the observation that NH₄NO₃ microdroplets do not homogeneously effloresce, even when exposed to extremely arid conditions (<1% RH). Considering the occurrence of particle collisions in the atmosphere (i.e., coagulation), these observations of contact efflorescence challenge many assumptions made about the phase state of inorganic aerosol.

Nucleation of the solid phase from a liquid solution (crystallization) is an important process in pharmaceuticals, manufacturing, and atmospheric science (1). In the atmosphere, the phase state and water content of particulate matter influences both heterogeneous chemistry and the aerosol direct and indirect effect on climate (2–6). Despite its importance, there is no comprehensive understanding of the phase state of atmospheric particulate, and the aerosol radiative forcing remains one of the largest uncertainties in climate predictions (6).

A significant fraction of aqueous atmospheric aerosol contains soluble inorganics such as chlorides, sulfates, and nitrates that can undergo efflorescence, i.e., the process of salt crystallization and water evaporation. Efflorescence often occurs at a significantly lower relative humidity (RH) than the reverse process of deliquescence (2, 7–12). A potent example of this hydration hysteresis is demonstrated with ammonium nitrate (NH₄NO₃), a hygroscopic component of atmospheric aerosol (9–11). NH₄NO_3(s) crystals will deliquesce to form an aqueous droplet at ∼62% RH (T = 295 K) (13). However, NH₄NO_3(aq) droplets do not homogeneously effloresce even at extremely low RH (∼0%) but instead remain in a metastable liquid state (i.e., supersaturated with respect to the aqueous solute) (2, 9, 10). Thus, many atmospheric chemistry and climate models assume that fully deliquesced inorganic particles such as NH₄NO₃ always remain in the aqueous state or only (re)crystallize at a very low ambient RH (<35%) (7, 14, 15).

Although the deliquescence RH (DRH) and efflorescence RH (ERH) for inorganic salts are well-characterized (2), heterogeneous efflorescence has been less extensively studied. Heterogeneous efflorescence occurs when a solid particle acts as a surface upon which nuclei can form, lowering the overall activation barrier for nucleation (2, 8–10). Analogous to heterogeneous ice formation, the solid particles can either be immersed inside the droplet (immersion mode of nucleation) or may come into contact with the exterior of the droplet (contact mode of nucleation) (16, 17). Past research has shown that immersion of solid particles such as mineral dust can raise the ERH of some salts relative to homogeneous efflorescence, causing the particles to be solid under a wider range of atmospherically relevant RH conditions (8–10). Similar experiments have not been performed to explore contact-mode efflorescence, and it has yet to be established whether contact would have a different effect on efflorescence than immersion.

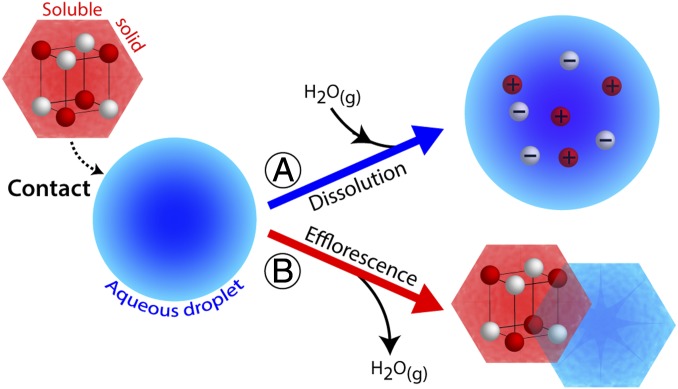
Although experimental studies of contact efflorescence have been lacking, a recent modeling study (11) considered phase changes of metastable liquid particles upon coagulation with dry solid particles (i.e., contact efflorescence). That study found an appreciable difference in the particle-phase concentrations of semivolatile inorganic species (e.g., NH₄NO₃) and total aerosol liquid water content when contact-induced phase changes were included in the simulation. Those simulation results point toward the potential real-world importance of contact efflorescence. Indeed, metastable liquid particles and crystalline particles of greatly different compositions can coexist simultaneously in the same air parcel (3, 7, 11, 18, 19). Although immersion efflorescence requires the heterogeneous nuclei to be insoluble or sparingly soluble, there is no such inherent limitation for contact efflorescence. Thus, even highly soluble solid particles can potentially serve as contact nuclei (CN). Alternatively, soluble particles may dissolve upon contact. The contrasting effects of dissolution upon contact compared with efflorescence are illustrated in Fig. 1. Although efflorescence is accompanied by crystallization and water loss, dissolution would be accompanied by droplet growth and water uptake to establish an equilibrium water activity. Reconciling which process preferentially occurs upon contact is thus necessary to predict the phase state and water content of atmospheric particles.

Fig. 1.

The potential outcomes of an externally located solid soluble inorganic aerosol coming into contact with a metastable aqueous inorganic microdroplet. In process A, dissolution of the solid particle accompanied by uptake of water. In process B, efflorescence accompanied by evaporation of water.

Here, we report on well-controlled experimental observations of contact efflorescence and a discussion of potential implications. To our knowledge, these experiments represent the first observations of contact efflorescence beyond our previous study (12) of aqueous ammonium sulfate [(NH₄)₂SO₄] microdroplets seeded with (NH₄)₂SO₄ microcrystals. In the present study, highly soluble inorganic salts of atmospheric relevance were used as CN. Due to their high solubility, these CN salts are not typically considered as effective heterogeneous nuclei. We probe the heterogeneous ability of these soluble CN by observing contact efflorescence of aqueous sodium chloride (NaCl), (NH₄)₂SO₄, and NH₄NO₃, three atmospherically abundant and important compounds (2–15). The highest single-collision contact efflorescence relative humidity (CERH) was measured for single optically levitated droplets exposed to single collisions with CN. We demonstrate that contact efflorescence is a pathway for crystallization of aqueous inorganic particles at the highest RH at which efflorescence is thermodynamically possible (near their respective DRH).

Materials and Methods

Droplet and CN Composition.

Contact efflorescence was studied for optically levitated microdroplets of (NH₄)₂SO_4(aq), NH₄NO_3(aq), and NaCl_(aq) (10 ± 3 µm average droplet diameter) at room temperature (295 ± 1 K). The crystalline compounds used as CN for all three aqueous compositions were potassium sulfate (K₂SO_4(CN)), sodium sulfate (Na₂SO_4(CN)), potassium chloride (KCl_(CN)), sodium bromide (NaBr_(CN)), (NH₄)₂SO_4(CN), and NaCl_(CN) (∼0.5–1.5 µm dry particle diameter). NH₄NO_3(aq) contact efflorescence was further probed using internally mixed CN composed of crystalline NH₄NO₃ and illite dust particles. Contact efflorescence using pure NH₄NO_3(CN) was not possible because CN were generated as aqueous droplets and then dried (see CN Preparation), but NH₄NO_3(aq) microdroplets do not homogeneously effloresce (2, 9, 10). Thus, illite particles were immersed before drying the CN to induce heterogeneous nucleation of the NH₄NO₃ component. NH₄NO₃+illite_(CN) was not used for (NH₄)₂SO_4(aq) and NaCl_(aq) contact efflorescence (see SI Materials and Methods for further details).

Droplet Levitation.

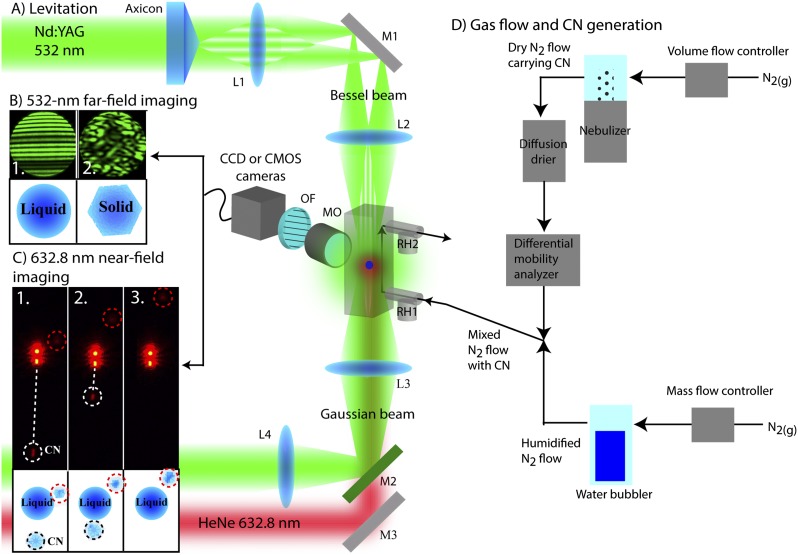
The entire experimental arrangement is shown in Fig. S1. The optical trap and trapping procedure have been described in detail elsewhere (12). In brief, the optical trap consisted of two vertical counter propagating beams generated using individual continuous-wave Nd:YAG lasers (λ = 532 nm). The levitation chamber was a black-anodized aluminum flow tube (12-mm inner diameter × 110-mm length) with four window ports at the trapping site (midpoint of the flow tube length). Levitated droplets were generated from a 5 wt% solution of NH₄NO₃, NaCl, or (NH₄)₂SO₄ using a piezo-driven device with a 15-µm-diameter orifice (Microfab MJ-APB-015).

Fig. S1.

Experimental arrangement for contact efflorescence experiments. (A) Aqueous droplets are optically levitated in a black-anodized aluminum flow tube (12-mm inner diameter × 110-mm length) with four window ports. A Bessel beam is generated from an axicon and focused onto the droplet from above with lenses L1 and L2. A Gaussian beam is focused from below with lenses L3 and L4. Beam steering mirrors M1 and M3 are used to align the lasers. (B) The elastically scattered 532-nm laser light was collected with a microscope objective (MO) and an optical polarization filter (OF) and imaged in the far field using a CCD camera. As shown in frame 1, linear interference fringes are present in the far-field image of a liquid droplet. Phase changes can be detected by changes in the far-field images, as shown in frame 2. An additional example is shown in Fig. 2. (C) Near-field imaging of a 632.8-nm HeNe probe laser scatter was used to track collisions with CN. The 632.8-nm HeNe probe laser passed through a dichroic mirror (M2). Near-field scattered laser light was collected with an MO and an optical band-pass filter (OF). An example is shown in which a CN makes contact but does not induce efflorescence. In frames 1 and 2, a CN (circled by white dashed line) is caught in the trapping laser and pushed toward the droplet. An additional particle (circled by red dashed line) has passed the droplet. In frame 3, the CN is no longer present as a result of contact and subsequent immersion in the droplet. The particle that did not make contact is still visible, demonstrating the disappearance of the CN could only be explained by contact with the droplet. See Fig. S2 for an example in which efflorescence occurs upon contact. Additional confirmation of contact with and without efflorescence can be seen in the 532-nm far-field images. (D) An N2 gas flow is used to control the RH and to deliver CN into the flow tube. CN are wet-generated with a medical nebulizer and dried in a diffusion drier. For experiments that used size-selected CN, the CN passed through a DMA. For all other experiments, the DMA was removed. The dry N2 gas flow carrying the CN was mixed with the N2 gas flow that was humidified with a water bubbler. The mixed gas flow with the CN entered the flow tube from the bottom. RH probes were placed before and after the flow tube (RH1 and RH2).

CN Preparation.

CN were generated as aqueous droplets and then crystallized. Aqueous particles were nebulized into a dry N₂ gas flow using a medical nebulizer (Omron NE-U22) and then directed through a diffusion dryer where the RH was <10% and the particles crystallized. Single-component CN were generated from a 10 wt% aqueous solution of KCl, K₂SO₄, NaCl, NaBr, (NH₄)₂SO₄, or Na₂SO₄. NH₄NO₃+illite CN were generated from a solution that was 10 wt% NH₄NO₃ and 5 wt% illite. The nebulizer contained a wire mesh with a pore size of 1 µm × 1 µm that limited the illite particle diameter to ≤ 1 µm.

CN Size.

To explore how the size of CN influenced the CERH, NaCl_(CN) were size-selected for several trials of NaCl_(CN)−(NH₄)₂SO_4(aq) contact efflorescence using a differential mobility analyzer (DMA). Separate trials were performed for 0.5 µm and 1 µm dry diameter NaCl_(CN). For all other CN−droplet combinations, CN were not size-selected, to increase the number concentration of CN and frequency of collisions. Using images of scattered laser light, the polydisperse size distribution of the dry CN was estimated to be ∼0.5–1.5 µm dry diameter (see SI Materials and Methods). Our previous study (12) of (NH₄)₂SO_4(CN)−(NH₄)₂SO_4(aq) used 1.5-µm seed crystals. Those experiments were repeated here using polydisperse (NH₄)₂SO_4(CN).

RH Control and Measurement.

The RH within the levitation chamber was controlled by mixing a dry N₂ gas flow with a humidified N₂ gas flow generated using a water bubbler. The flow carrying the dried crystalline particles was mixed with the humidified flow before entering the levitation chamber. The maximum RH achievable while flowing CN was ∼77–79%. Two RH probes [Vaisala HMP60, ±0.5 °C, ±3% RH uncalibrated, ±1% RH calibrated (12)] were placed before and after the levitation chamber. The RH at the trapping site was calculated as the average of the two RH measurements (±1 SD, 1–2% RH typical).

Detecting Efflorescence.

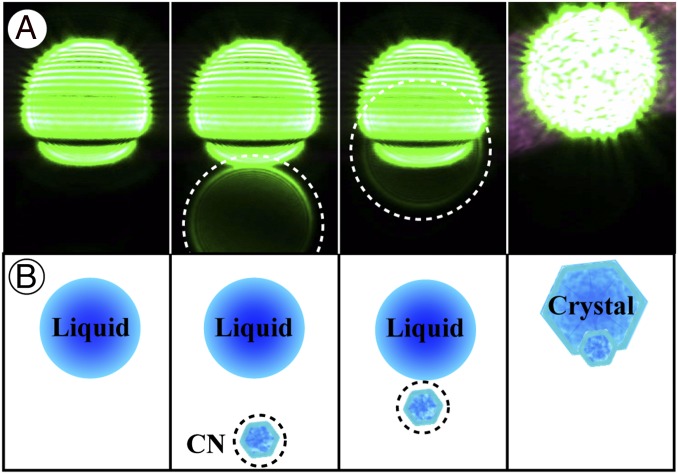
Efflorescence was detected using far-field imaging of elastically scattered laser light from the 532-nm trapping lasers (12). Light was imaged using a CCD camera. All images were recorded in LabVIEW for postprocessing. As demonstrated in Fig. 2, the far-field images of liquid droplets contained horizontal linear interference fringes (frames 1–3). Efflorescence is evident by the breakdown in the linear interference fringes and randomization of the laser light phase (frame 4). The number of fringes in an image scaled with droplet size. The diameter of droplets used (∼10 ± 3 µm) thus provided a sufficient number of fringes to make the occurrence of efflorescence unambiguous and distinct.

Fig. 2.

Observation of NaCl_(CN)−(NH₄)₂SO_4(aq) contact efflorescence at 38% RH (11 ± 2 µm droplet diameter, 0.5 µm CN diameter). (A) Far-field imaging of scattered laser light from the trapping lasers. In frame 1, the horizontal linear interference fringes are indicative of a liquid particle. In frame 2, the light scattered off of a CN (encircled by white dashed line) appears at the bottom of the image. In frame 3, the CN has moved closer to the droplet. In frame 4, efflorescence is evident by the breakdown in the linear interference fringes and the upward movement of the particle due to the loss of water mass. (B) Illustrated representation of what is shown in each frame of A.

Monitoring Collisions.

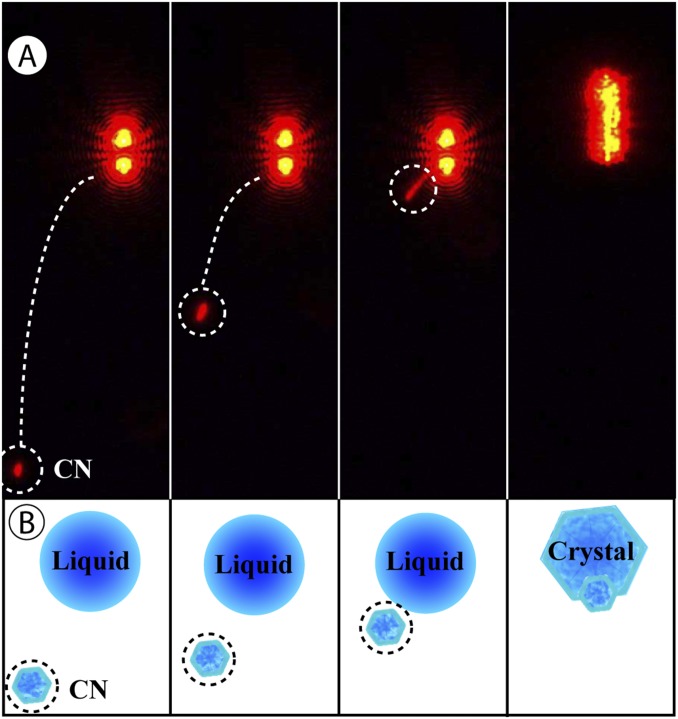
Collisions were monitored with the 532-nm far-field images (Fig. 2) as well as near-field images of scattered light from a 632.8-nm HeNe probe laser that illuminated the levitated droplet from below. Near-field images provided a clearer picture of CN trajectories, as demonstrated in Fig. S2. A custom LabVIEW image processing program assisted in identifying collisions by searching recorded images for the presence of CN. The velocity at which a CN particle collided with a levitated droplet was kept below ∼3 mm/s (total flow rate ≤ 25 sccm), which is an atmospherically realistic value (the mean thermal speed for a 1-µm-diameter particle is ∼4 mm/s) (20) and ensured a collision would be captured by the imaging cameras (the camera field-of-view was 200 µm, and ∼10 ms elapsed between captured image frames). Six or more images of a CN were typically captured using CN velocities of <3 mm/s.

Fig. S2.

Observation of NaCl_(CN)−(NH₄)₂SO_4(aq) contact efflorescence (single collision) at 38% RH. (A) Tracking the trajectory of a CN (encircled by white dashed line) until collision with the aqueous droplet using near-field imaging of scattered laser light from a 632.8-nm HeNe probe laser. In frames 1–3, the droplet is seen at the top of the image and displays the characteristic glare spots due to near-field scatter from a spherical droplet. The CN can be seen progressively approaching the droplet from below. The CN takes a curved trajectory, which is likely a result of the radial force of the trapping laser pulling the CN into the laser focus. In frame 4, efflorescence is evident by the upward movement of the particle due to loss of water mass and the randomization of the scattered laser light. (B) Illustrated representation of what is shown in each frame of A.

Determining CERH.

The highest single-collision CERH of an aqueous droplet was determined by monitoring collisions and systematically varying the ambient RH whenever efflorescence was not induced by a single collision. Efflorescence was considered to be contact-induced only if it occurred immediately upon contact (i.e., if efflorescence occurred between adjacent recorded images, ∼5–10 ms at 100–150 frames per second). If collisions were observed without efflorescence or multiple collisions occurred before efflorescence, a fresh droplet was trapped and a new experiment performed at a slightly lower RH (∼0.5–5% RH lower). Once single-collision contact efflorescence was observed, the RH was raised again by ∼2–5% RH, and the process was repeated. The average highest single-collision CERH was calculated from two to five trials (±1 SD with propagated error from the individual RH measurements).

SI Materials and Methods

Droplet Levitation.

The entire experimental arrangement is shown in Fig. S1. The optical trap and trapping procedure have been described in detail elsewhere (12). In brief, levitation is achieved with two vertical counterpropagating beams generated using the 532-nm second-harmonic output of individual continuous-wave diode-pumped Nd:YAG lasers. A Bessel beam is generated from an axicon and focused onto the droplet from above. A Gaussian beam is focused from below. Beam steering mirrors are used to align the lasers.

Imaging and Sizing.

The elastically scattered 532-nm laser light was collected with a microscope objective and a polarization filter. Light was imaged in the far field using a CCD camera. When imaged in the far field, the 532-nm elastically scattered laser light from a levitated droplet contains linear interference fringes. The angular distribution and intensity of these fringes describe a particle’s phase function, which is dependent on the size of the droplet (12). The droplet phase function was determined by measuring the intensity of light in recorded images and then plotting as a function of the angular range of light collected. The experimentally determined phase function was then compared with Mie theory calculations to determine the droplet size. Near-field 632.8-nm scattered laser light was also collected with a separate microscope objective and a complementary metal-oxide semiconductor (CMOS) camera. A band-pass filter transmitted the 632.8-nm light and removed the 532-nm light. An example of using the 632.8-nm near-field scatter to detect contact efflorescence is shown in Fig. S2.

NH₄NO₃−Illite Contact Nuclei.

For NH₄NO₃+illite_(CN)−NH₄NO_3(aq) contact efflorescence, the influence of the illite component of the CN must be separated from the influence of the crystalline NH₄NO₃ component of the CN. During preliminary NH₄NO_3(aq) contact efflorescence experiments using pure illite CN (nebulized from an illite slurry made with filtered and deionized water), NH₄NO_3(aq) contact efflorescence was never observed above ∼35% RH. In previous studies, efflorescence of NH₄NO₃ occurred at ∼10% RH with mineral dust in the immersion mode (9). For the isochemical NH₄NO₃ component of the CN, NH₄NO_3(aq) efflorescence is thermodynamically possible at any RH below the DRH (∼62%) and can occur via a crystal growth mechanism (12). It is thus unlikely that the presence of illite will significantly influence the NH₄NO₃+illite_(CN)−NH₄NO_3(aq) CERH.

CN Size Distribution.

CN were size-selected for several trials of NaCl_(CN)−(NH₄)₂SO_4(aq) contact efflorescence. Our previous study also size-selected 1.5-µm CN for (NH₄)₂SO_4(CN)−(NH₄)₂SO_4(aq) contact efflorescence (12). (NH₄)₂SO_4(CN)−(NH₄)₂SO_4(aq) experiments were repeated in the current study using polydisperse (NH₄)₂SO_4(CN). No resolvable size dependence was observed on the CERH when using size-selected CN in either NaCl_(CN)−(NH₄)₂SO_4(aq) or (NH₄)₂SO_4(CN)−(NH₄)₂SO_4(aq) contact efflorescence. Thus, for all other CN−droplet combinations, CN were not size-selected before entering the flow tube, to increase the number concentration of CN and frequency of collisions, and thereby decrease the time required for the experiment.

For experiments that did not use the size-selected CN, the size distribution of the dry CN was preestimated before performing contact efflorescence experiments. This was done by removing the diffusion drier, nebulizing the aqueous CN solution, and then flowing the aqueous nebulized particles into the levitation chamber at the experimental flow rate of <25 sccm. The wet particle diameter was then obtained by sizing the particles in situ using far-field images of scattered laser light (12). From the wet particle diameter, the dry particle diameter was estimated using the solute concentration of the wet particles and the density of the pure crystalline CN component. The solute concentration was calculated by correlating the ambient RH measured in the levitation chamber with the weight fraction of the solute as determined from the E-AIM model (13) [for NaCl, Na₂SO₄, NH₄NO₃, and (NH₄)₂SO₄] or the work of Cohen et al. (27) (for KCl and NaBr). The size range of the dry CN was estimated to be ∼0.5–1.5 µm when the initial nebulizer solution concentration was 10 wt%. The manufacturer-stated median diameter of a wet particle produced from the nebulizer is ∼4.2 µm, which would correspond to a dry particle diameter of ∼1.6 µm for 10 wt% (NH₄)₂SO₄, consistent with the estimate based on in situ sizing.

To further constrain the lower limit of the CN size distribution produced by the nebulizer, a scanning mobility particle sizer (SMPS) was used to measure the size distribution of dried particles. The gas flow rate used to deliver particles into the SMPS was 200 sccm, which is ∼20 times higher than the typical dry N₂ flow rate used during an experiment. (The lower flow rates used during an experiment lead to more coagulation of the wet particles upon being emitted from the nebulizer and thus larger CN sizes than indicated by the SMPS. Thus, the true experimental CN size distribution during an experiment could not be determined with the SMPS due to the higher required flow, but could be used to determine the lower limit.) At a flow rate of 200 sccm, the smallest particle diameter detected by the SMPS was 107 ± 3 nm. Particles as small as 100 nm can readily be detected using the 632.8-nm near-field imaging technique (12). Thus, it is unlikely that many CN−droplet collisions occurred where the CN was not detected.

Calculation of Lattice Mismatch (δ).

The standard expression for lattice mismatch (δ) is given by

$$\mathit{\delta }=\left(a_{CN}-a_{aq}\right)/a_{aq}$$ [S1]

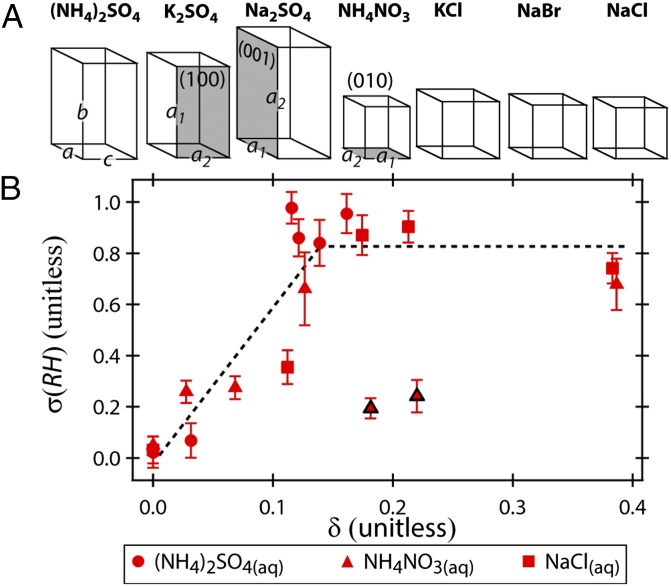
where a_aq is the lattice constant of the crystalline phase of the aqueous droplet component and a_CN is the lattice constant of the CN (given in Table S1) (22–24). When calculated with Eq. S1, δ is a 1D parameter that is only strictly valid for 2D crystal faces when the two lattice constants are equal (i.e., for the cubic structures where a = b = c and thus a₁=a₂) (38). Thus, Eq. S1 was only valid for calculating δ for KCl_(CN)−NaCl_(aq) and NaBr_(CN)−NaCl_(aq) contact efflorescence. However, as discussed in Heterochemical Contact Efflorescence and shown in Fig. 4A, the lattice constants are not equal for the orthorhombic crystals (a ≠ b ≠ c and thus a₁ ≠ a₂), and it is necessary to account for lattice mismatch in mutually perpendicular directions. Bryant et al. (22) noted that ice nucleation on simple inorganic structures can be correlated with the sum of the lattice mismatch in mutually perpendicular directions. A similar approach was taken here for salt crystal nucleation on the simple inorganic structures of the CN, where for CN−droplet pairs involving an orthorhombic crystal, δ was calculated as the average absolute mismatch of the lattice constants a₁ and a₂ of the crystal face (001), (010), or (100), as given in Eq. 2. The absolute value of each term was taken to avoid misleadingly low values of δ resulting from a positive term canceling a negative term. The crystal faces that yielded the smallest value of δ were used for the calculation. The crystal faces and resulting δ values are given in Table S2. For lattice mismatch between cubic structures, Eq. S1 and Eq. 2 are equivalent.

Table S1.

Unit cell constants for the crystalline compounds

Compound	Structure	a, Å	b, Å	c, Å
(NH4)2SO4	Ortho	7.73	10.56	5.95
K2SO4	Ortho	7.46	10.06	5.77
Na2SO4	Ortho	9.80	12.29	5.85
NH4NO3	Ortho	5.44	5.75	4.94
NaCl	Cubic	5.64	5.64	5.64
NaBr	Cubic	5.97	5.97	5.97
KCl	cubic	6.30	6.30	6.30

Fig. 4.

(A) Scaled representations of the unit cell structures for the crystalline compounds used in the present study. The orientation of the unit cell constants a, b, and c are depicted on (NH₄)₂SO₄. The orientation of the (100), (001), and (010) crystal faces are demonstrated on K₂SO₄, Na₂SO₄, and NH₄NO₃, respectively. The values for the lattice constants a₁ and a₂ correspond to the values of a, b, or c (e.g., for (100), a₁ = b and a₂ = c). (B) The σ(RH) plotted as a function of δ for all three aqueous compositions. In general, effective CN (i.e., σ(RH) < 0.4) had values of δ < 0.12, and less effective CN had values of >0.12. This trend is indicated by the dashed line. The two CN−droplet pairs that do not follow this trend are outlined in black.

Table S2.

The δ and crystal faces used to calculate δ

Droplet solute	CN	Solute crystal face	CN crystal face	δ
(NH4)2SO4	(NH4)2SO4	(001)	(001)	0
	K2SO4	(010)	(010)	0.03
	Na2SO4	(010)	(010)	0.14
	KCl	(010)	(100)	0.12
	NaCl	(010)	(100)	0.16
	NaBr	(010)	(100)	0.12
NH4NO3	NH4NO3-illite	(001)	(001)	0
	(NH4)2SO4	(001)	(010)	0.22
	K2SO4	(001)	(010)	0.18
	Na2SO4	(001)	(010)	0.39
	KCl	(001)	(100)	0.13
	NaCl	(001)	(100)	0.03
	NaBr	(001)	(100)	0.07
NaCl	NaCl	(001)	(001)	0
	(NH4)2SO4	(100)	(010)	0.21
	K2SO4	(100)	(010)	0.17
	Na2SO4	(100)	(010)	0.38
	KCl	(100)	(100)	0.11
	NaBr	(100)	(100)	0.06

When calculating δ for ice nucleation, it has been common to consider integer multiplication of the lattice constants (i.e., multiplication of a_CN and a_aq by nonzero integers) to minimize δ (22). If integer multiplication of a_CN and a_aq is considered here, the expression for lattice mismatch becomes

$${\delta }_i=\left[\left|(m{a}_{1,CN}-n{a}_{1,aq})/n{a}_{1,aq}\right|+\left|(x{a}_{2,CN}-y{a}_{2,aq})/y{a}_{2,aq}\right|\right]/2$$ [S2]

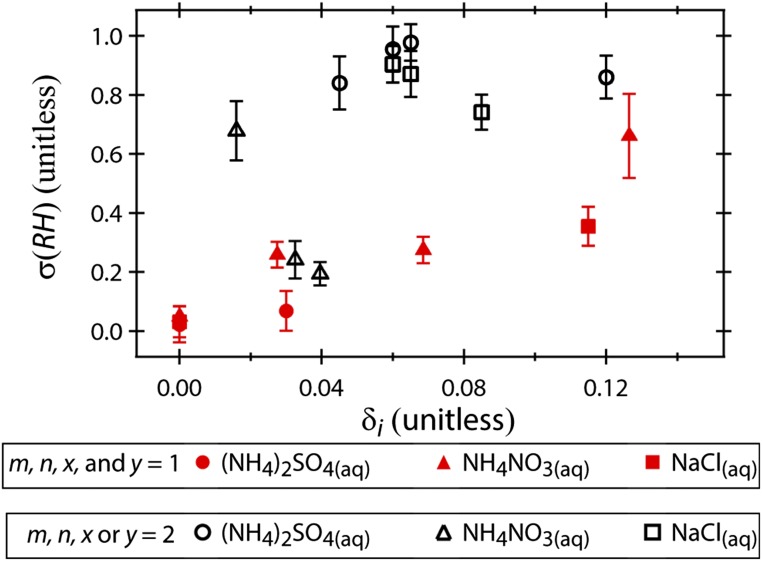
where m, n, x, and y are nonzero integers chosen such that δ_i is minimized (the i subscript specifies that δ_i was calculated with integer spacing of lattice constants and distinguishes it from δ as calculated with Eq. 2). Fig. S3 shows σ(RH) plotted as a function of δ_i. (For the calculation of δ_i given in Fig. S3, the maximum possible value of m, n, x, and y was set at 2.) As seen in Fig. S3, when integer multiplication is considered in the present study, there is no apparent correlation between σ(RH) and δ_i. Indeed, considering integer spacing is not a standard practice for the CN surfaces used in the present study (23, 38). Thus, further discussion of lattice mismatch is based on δ calculated without integer multiplication (i.e., Eq. 2).

Fig. S3.

A plot of σ(RH) as a function of δ_i. Note that when integer multiplication is used to minimize δ_i, it is possible to find a combination of crystal faces such that δ_i is less than ∼0.12 for all CN−droplet pairs and there is no apparent correlation between δ_i and σ(RH). Integer multiplication was used to minimize δ_i for the open black points (m, n, x, or y = 2 in Eq. S2). The solid red points are unmoved relative to Fig. 4B because δ_i is minimized when m, n, x, and y = 1 (and thus δ_i is equivalent to δ calculated with Eq. 2). As discussed in Heterochemical Contact Efflorescence, there is a general correlation between σ(RH) and δ calculated without integer multiplication.

Calculation of Coagulation Coefficients (K).

The coagulation coefficient (K) for collisions between two monodisperse populations of particles can be estimated from Eq. S3,

$$K=2\pi (D_{p1}+D_{p2})(D_1+D_2)$$ [S3]

where D_p1 and D_p2 are the diameters of the particles involved and D₁ and D₂ are the Brownian diffusion coefficients of the two particles (20). The values for K shown in Table 1 were calculated using Eq. S3 and the parameters shown in Table S3. Values for D were obtained or extrapolated from table 9.5 of Seinfeld and Pandis (20). Calculated values were crosschecked with tabulated and plotted values when available [e.g., table 13.3 and figure 13.5 of Seinfeld and Pandis (20)].

Table 1.

Parameters used to estimate the e-folding times (τ_col) for aqueous particles to undergo a collision with potential CN

Scenario	CN source	NCN, cm−3	Dp,CN, µm	Dp,aq, µm	K, cm3⋅s−1	τcol, s
Dp,aq >> Dp,CN	(NH4)2SO4 particle formation event (30)	1.5 × 105	0.01	1	3.4 × 10−7	20
	urban (36)*	5 × 104	0.04	1	2.4 × 10−8	850 [14 min]
	remote continental (36)	5 × 103	0.1	1	5.0 × 10−9	4 × 104 [11 h]
	wildfire BBA (34)*	4 × 104	0.15	1	3.5 × 10−9	7 × 103 [2 h]
	marine ultrafine SSA (31)*	100	0.05	1	2.0 × 10−8	5 × 105 [6 d]
Dp,aq << Dp,CN	urban (36)	900	0.6	0.04	1.5 × 10−8	7.5 × 104 [21 h]
	remote continental (36)/marine SSA (31)	10	1	0.04	2.4 × 10−8	4 × 106 [48 d]
Dp,liq ≈ Dp,sol	urban (36)†	2.5 × 104	0.04	0.05	3.8 × 10−9	1 × 104 [3 h]
	remote continental (36)†	2.5 × 103	0.1	0.1	1.5 × 10−9	2.3 × 105 [3 d]
	wildfire BBA (34)	4 × 104	0.15	0.1	1.8 × 10−9	1.4 × 104 [4 h]

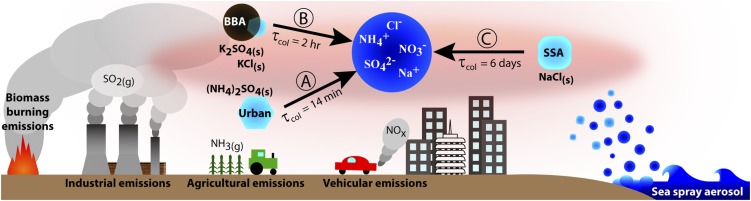
^*Urban, wildfire BBA, and ultrafine SSA are illustrated in Fig. 5 processes A, B, and C, respectively, for particle collision scenarios where D_p,aq >> D_p,CN.

^†Assuming half of particles are solid (i.e., potential CN).

Table S3.

Parameters used to calculate the coagulation coefficient K

Dp1, µm	Dp2, µm	D1 (20), cm2⋅s−1	D2 (20), cm2s−1	K, cm3⋅s−1
0.01	1	5.24 × 10−4	2.74 × 10−7	3.4 × 10−7
0.04	1	3.59 × 10−5	2.74 × 10−7	2.4 × 10−8
0.1	1	6.82 × 10−6	2.74 × 10−7	5.0 × 10−9
0.05	1	3.0 × 10−5	2.74 × 10−7	2.0 × 10−8
0.15	1	4.5 × 10−6	2.74 × 10−7	3.5 × 10−9
0.6	0.04	6.0 × 10−7	3.59 × 10−5	1.5 × 10−8
1	0.04	2.74 × 10−7	3.59 × 10−5	2.4 × 10−8
0.04	0.05	3.59 × 10−5	3.0 × 10−5	3.8 × 10−9
0.1	0.1	6.82 × 10−6	6.82 × 10−6	1.5 × 10−9
0.15	0.1	4.5 × 10−6	6.82 × 10−6	1.8 × 10−9

Results

The individual results for all CN−droplet contact efflorescence experiments are shown in Dataset S1. The NaCl_(CN)−(NH₄)₂SO_4(aq) contact efflorescence experiments using size-selected NaCl_(CN) (0.5 µm and 1 µm dry diameter) were compared with the results using polydisperse NaCl_(CN) (∼0.5–1.5 µm dry diameter). In each case, the highest single-collision CERH was ∼38% regardless of CN size, indicating that any potential CN size dependence is not resolvable over the range of sizes probed. Polydisperse CN were used for the experiments involving all of the other CN−droplet pairs.

The average highest single-collision CERH for all CN−droplet pairs is given in Fig. 3 and plotted on the characteristic hydration hysteresis diagram for each of the aqueous salts. (Hereafter, the use of CERH will refer to the average highest single-collision CERH.) It can be seen that some CN compositions dramatically increase the ERH, whereas others only modestly increase it. A phase transition is only thermodynamically possible below the droplet DRH. Thus, to place the CERH into the context of the range of possible and relevant RH values, a parameter σ(RH) is defined as

$$\sigma \left(RH\right)=(DRH-CERH)/(DRH-R{H}_{\min })$$ [1]

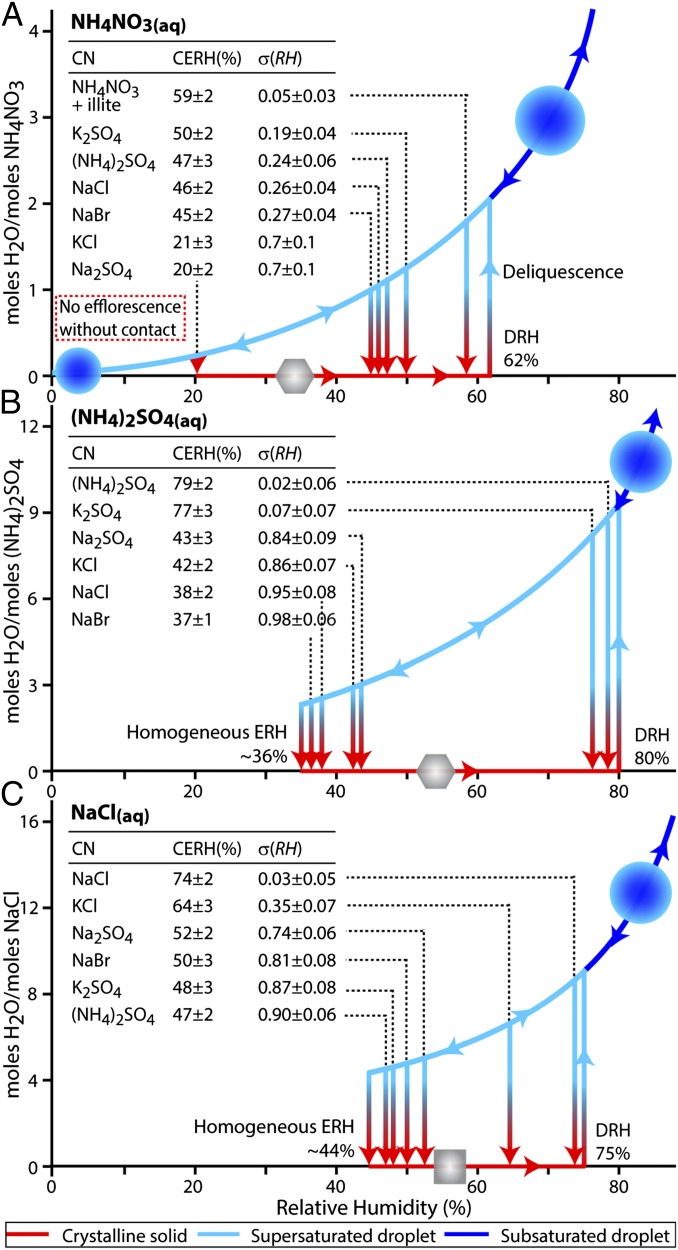
where DRH is 75%, 80%, and 62% RH for NaCl_(aq), (NH₄)₂SO_4(aq), and NH₄NO_3(aq), respectively, and RH_min is the lowest RH at which a droplet will retain water if no collisions occur. For (NH₄)₂SO_4(aq) and NaCl_(aq), RH_min is the homogeneous ERH (36 ± 2% and 44 ± 2% RH, respectively). NH₄NO_3(aq) did not homogeneously effloresce when exposed to extremely arid conditions (<1% RH) for 24 h, consistent with previous studies (9, 10), and always remained liquid if no collisions occurred. Thus, an RH_min of 0% was used for NH₄NO_3(aq). Average values for σ(RH) are included in Fig. 3, with values ranging from near zero to near unity. For instances in which σ(RH) ≈ 0, contact efflorescence occurred near the DRH of the droplet (i.e., CERH ≈ DRH, the maximum possible value), indicative of a highly effective CN. When σ(RH) ≈ 1, contact did not significantly influence efflorescence relative to the homogeneous case, indicative of a less effective CN. Note that for all instances, the CERH was greater than RH_min [σ(RH) < 1].

Fig. 3.

Contact efflorescence results depicted on characteristic hysteresis diagrams for (A) NH₄NO_3(aq), (B) (NH₄)₂SO_4(aq), and (C) NaCl_(aq). The CERH is indicated for each CN used. In all cases, contact raised the ERH relative to the homogeneous case. Note that, without contact, NH₄NO_3(aq) droplets do not homogeneously crystallize at low RH and remain on the hydrated (upper, blue) portion of the curve at all RH values. Aqueous droplets respond to changes in RH by increasing or decreasing in water content. If efflorescence occurs, crystalline particles remain on the dehydrated (lower, red) portion of the curve until the RH is raised to the DRH. Before deliquescence, crystalline particles do not substantially respond to changes in RH. Hydration values (y axes, moles H₂O per moles solute) were calculated using the Extended Aerosol Inorganic Model (E-AIM, www.aim.env.uea.ac.uk/aim/aim.php) (13).

Discussion

This study has experimentally demonstrated that a single solid−liquid collision can result in efflorescence of aqueous droplets at RH values significantly above RH_min of the pure aqueous component. Importantly, this study has also shown that even highly soluble crystalline particles can induce efflorescence of an aqueous droplet upon contact. Insolubility is frequently invoked as a requirement for an efficient heterogeneous nucleus (16), but all CN studied here were soluble and also capable of inducing efflorescence. For a given CN−droplet pair, the CERH did not vary more than ±1–2% RH in different trials. However, there was a wide variation in CERH when comparing CN of different compositions, likely due to differences in, e.g., CN crystal lattice structure, hygroscopic properties, solubility, and ionic interactions, as discussed in Isochemical Contact Efflorescence and Heterochemical Contact Efflorescence.

Isochemical Contact Efflorescence.

Crystal nucleation is the initial formation of the new crystalline phase. In the unique cases of isochemical contact efflorescence [i.e., NaCl_(CN)−NaCl_(aq), (NH₄)₂SO_4(CN)−(NH₄)₂SO_4(aq), and NH₄NO₃+illite_(CN)−NH₄NO_3(aq)], nucleation is not necessary because the seed crystal is of the same composition as the anticipated crystalline phase. In theory, crystal growth and subsequent loss of water (i.e., efflorescence) is therefore expected at all levels of supersaturation (any RH < DRH) if the seed crystal is larger than a critical cluster ($\mathrm{\lesssim }$ 10 nm) (21). As expected, the CERH was close to the DRH in all three isochemical cases. In each case, the CERH was slightly below the DRH due to experimental limitations and the uncertainty associated with the RH probes (±1%). It is likely that the true CERH values are closer to the DRH than reported here.

Heterochemical Contact Efflorescence.

Similarity in crystal lattice structure between the heterogeneous surface and the crystallizing compound has long been recognized as an important factor in heterogeneous nucleation (16, 22–24). Here, we explore the strength of this relationship by comparing crystal lattice structure and σ(RH). NH₄NO_3(s), (NH₄)₂SO_4(s), Na₂SO_4(s), and K₂SO_4(s) have orthorhombic lattice structures, whereas NaCl_(s), NaBr_(s), and KCl_(s) are cubic. A scaled representation of the unit cell structures for each salt is shown in Fig. 4A, with values for the unit cell constants a, b, and c given in Table S1. The standard expression for lattice mismatch (δ) between a substrate (i.e., the CN) and a crystalizing overlayer (i.e., the aqueous component) is given by δ = (a_CN – a_aq)/a_aq, where a_aq is the lattice constant of the crystalline phase of the droplet component and a_CN is the lattice constant of the CN (22–24). This equation was valid for cases where both species were cubic crystals. For the orthorhombic crystals, the lattice constants are not equal, and it is necessary to account for lattice mismatch in mutually perpendicular directions (22). Thus, δ was calculated as the average absolute mismatch of the lattice constants a₁ and a₂ of the (001), (010), and (100) crystal faces, as given by

$$\delta =\left[\left|(a_{1,CN}-a_{1,aq})/a_{1,aq}\right|+\left|(a_{2,CN}-a_{2,aq})/a_{2,aq}\right|\right]/2.$$ [2]

The orientation of these crystal faces is depicted in Fig. 4A. The crystal faces that yielded the lowest value of δ were used. (See SI Materials and Methods and Fig. S3 for further details and discussion of calculating δ with integer multiplication of a₁ and a₂.) Subscripts for δ of AS, AN, or SC specify the aqueous phase as (NH₄)₂SO_4(aq), NH₄NO_3(aq), or NaCl_(aq), respectively.

Fig. 4B shows σ(RH) plotted as a function of δ_AS, δ_AN, and δ_SC (see Table S2 for numerical values). For comparison, the isochemical points (δ = 0) are also included in Fig. 4B and all lie in an overlapping region near the origin. The point for NaBr_(CN)−NaCl_(aq) (CERH = 50%, σ(RH)=0.81, δ_SC = 0.03) is not shown because NaBr_(CN) particles are expected to be deliquesced above ∼45–48% RH (2, 12), thus negating the influence of the NaBr crystal lattice structure. In this instance, NaCl_(aq) efflorescence may have been induced by undissolved NaBr_(CN) particulate (12), ionic interactions (25), or the collision itself (17). (See SI Additional Discussion for more details). However, for the majority of CN−droplet pairs, δ is a good first-order approximation of σ(RH) (and thus CERH). Small lattice mismatches (δ < 0.12) generally indicate an effective heterogeneous nucleus [i.e., low σ(RH) and high CERH]. Notably, the high K₂SO_4(CN)−(NH₄)₂SO_4(aq) CERH of 77% (δ_AS = 0.03) clearly demonstrates that a low δ can lead to a profound effect and offers experimental support for simulations that suggest a small lattice mismatch may be more favorable than a perfect lattice match for nucleation on a heterochemical surface because the crystal nucleus does not necessarily have the same lattice constants as the bulk crystal (23). Larger lattice mismatches (δ $\mathrm{\gtrsim }$ 0.12) generally indicate a less effective heterogeneous nucleus. These observations are consistent with previous studies that suggest nucleation is no longer epitaxial (i.e., oriented by crystal lattice structure) at an absolute mismatch greater than ∼10–15% (23, 24). However, there were exceptions to these generalizations for NH₄NO_3(aq) contact efflorescence, where NaCl_(CN) had the lowest lattice mismatch (δ_AN = 0.03) but was not the most effective CN. K₂SO_4(CN) and (NH₄)₂SO_4(CN) were both slightly more effective than NaCl_(CN) despite larger lattice mismatches (δ_AN =0.18 and 0.22, respectively). In these instances, NH₄NO₃ nucleation may have been influenced by ionic interactions or a crystal face not considered here when calculating δ.

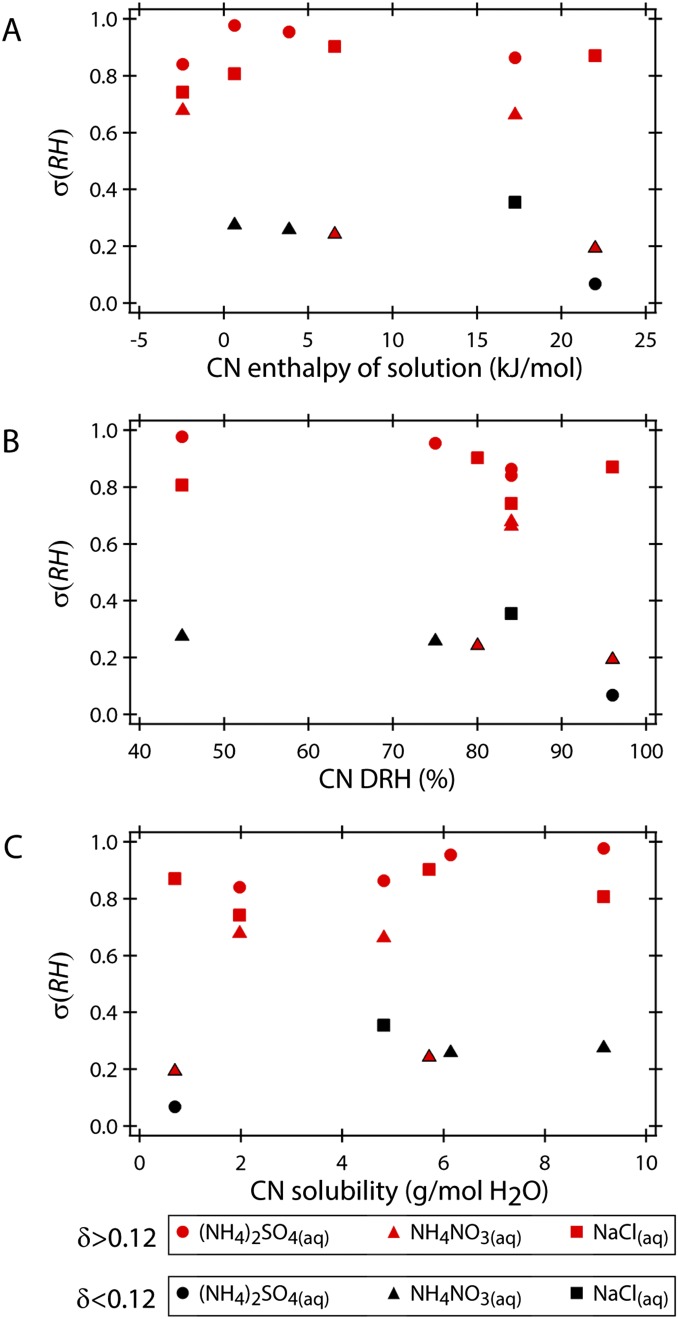
Although a small lattice mismatch appears to have the largest overall effect on CERH for the CN−droplet pairs used in the present study, other factors, such as the DRH of the CN, also influenced the CERH, as exemplified with NaBr_(CN)−NaCl_(aq) contact efflorescence. However, as shown in Fig. S4, there is no overall correlation between σ(RH) and the DRH, solubility, or heat of dissolution of the CN. Although there is no clear trend when considering the properties of the CN alone, ionic interactions between the droplet and CN solute may be an important factor on a case-by-case basis. The properties of a solute mixture differ from those of the individual components as a result of, e.g., the common-ion effect and short-range ionic interactions (2, 13, 25–27). For example, nucleation of NaCl can be induced during dissolution of KCl_(s) in bulk solutions (26). Thus, the KCl_(CN)−NaCl_(aq) CERH may have been influenced by KCl_(CN) dissolution as well as the small lattice mismatch (δ_SC = 0.11). Indeed, CN dissolution is possible to some extent before the onset of efflorescence because the droplets are unsaturated with respect to the CN solute. Another important consideration is the mechanical effect of the collision. Niehaus and Cantrell (17) have demonstrated that a solid surface is not necessary to induce ice nucleation upon contact, consistent with our observations of NaBr_(CN)−NaCl_(aq) contact efflorescence. A similar effect may be occurring here, particularly if salt crystal nucleation preferentially occurs at the surface of the droplet, as has been suggested (28). This points toward the possibility of efflorescence induced by amorphous (noncrystalline) aerosol.

Fig. S4.

Plots of σ(RH) as a function of CN thermodynamic properties for heterochemical contact efflorescence. (A) The σ(RH) plotted as a function of the enthalpy of solution of the CN. (B) The σ(RH) plotted as a function of the DRH of the CN. (C) The σ(RH) plotted as a function of the solubility of the CN.

Atmospheric Implications.

Atmospheric aerosol can contain significant fractions of the inorganic components used in the present study. In urban and remote regions, the dominant inorganic components are NH₄⁺, SO₄²⁻, and NO₃⁻, which are largely present as a result of secondary conversion of gaseous NH₃, SO₂, and NO_X emissions, respectively, and can exist as aqueous droplets or as solid particles, depending on ambient conditions and mechanism of formation (2, 11, 20, 29, 30). (NH₄)SO₄ has also been implicated in new particle formation events in some urban locations (30). In marine and coastal regions, Na⁺ and Cl⁻ can be found in high amounts due to sea spray aerosol (SSA), which can homogeneously effloresce at ∼44% RH (4, 20, 31, 32). SSA also contains SO₄²⁻, Br⁻, K⁺, NH₄⁺, and NO₃⁻. Additionally, biomass burning aerosol (BBA) can contain discrete KCl_(s) and K₂SO_4(s) crystal inclusions (33), compounds shown in the present study to be effective CN for efflorescence of NaCl_(aq), NH₄NO_3(aq), and (NH₄)₂SO_4(aq). (See SI Additional Discussion for further details of how the model aerosol used in the present study compares to ambient aerosol.) Many coastal regions such as the Los Angeles basin and surrounding areas of Southern California (United States) experience high levels of particulate matter with contributions from SSA (32), anthropogenic emissions (29), recurrent large-scale wildfires (34), and mineral dust (35). Such regions can also experience extreme variations in ambient RH during, e.g., Santa Ana wind events (meteorological events characterized by strong, arid winds originating from inland locations) (34, 35). The mixing of aerosol under changing RH conditions leaves open the possibility for contact efflorescence.

Ultimately, any potential relevance of contact efflorescence is dependent on the probability of a collision between particles at a suitable RH. Thus, contact efflorescence is most likely to be important where the particle number concentrations are high. In urban polluted areas, number concentrations typically exceed 10⁴ cm⁻³ and can reach even higher levels during, e.g., new particle formation (30) and biomass burning events (34), with the highest-number concentrations typically being for ultrafine particles (particles with diameters less than ∼100 nm) (3, 20, 29, 36). For a monodisperse population of aqueous particles with diameter D_p,aq externally mixed with a monodisperse population of solid CN with diameter D_p,CN, the e-folding time (τ_col) for the aqueous particles to undergo a solid−liquid collision is estimated as τ_col = (KN_CN)⁻¹, where N_CN is the number concentration of the CN and K is the coagulation coefficient (see SI Materials and Methods and Table S3) (20). The τ_col can be compared with the typical atmospheric lifetime of an aqueous particle to evaluate whether particle collisions can occur on a relevant timescale. [Note that τ_col for ambient aerosol will depend on the true size distribution. Furthermore, additional factors such as electroscavenging, diffusiophoresis, and thermophoresis can increase or decrease the number of particle collisions (37).] K varies strongly as a function of D_p,aq and D_p,CN (20). Thus, due to the wide range of particle sizes in the atmosphere, τ_col can vary greatly depending on location and particle sources, as shown in Table 1 and discussed for scenarios where D_p,aq >> D_p,CN, D_p,aq << D_p,CN, and D_p,aq ≈ D_p,CN.

D_p,aq >> D_p,CN.

Fig. 5 illustrates τ_col for large aqueous inorganic aerosol (∼1 µm diameter) from, e.g., SSA and fog droplet processing to undergo a collision with a potential CN (4, 20, 32, 36). If contact efflorescence occurs, the resulting water loss and change in morphology would influence the chemical reactivity, atmospheric lifetime, and optical properties of the large particle. If all potential CN are assumed to be solid or contain solid material, τ_col ranges from seconds at high number concentrations (N_CN = 10⁵ cm⁻³) to days at lower number concentrations (N_CN = 10² cm⁻³). The typical atmospheric lifetime for a 1-µm particle ranges from days to weeks (20). Thus, τ_col can be well within an atmospherically relevant timescale even if only a fraction of potential CN contain solid material.

Fig. 5.

A depiction of an urban coastal region to illustrate particle collision scenarios where D_p,aq >> D_p,CN. The aqueous phase (D_p,aq = 1 µm) is represented by processed SSA (primarily NaCl_(aq) when emitted) with accumulated SO₄²⁻, NO₃⁻, and NH₄⁺ via secondary aqueous-phase conversion of SO_2(g) (industrial emissions), NO_x (vehicular emissions) and NH_3(g) (agricultural emissions), respectively, during transport inland. In process A, urban ultrafine particles (D_p,CN = 0.04 µm) can contain (NH₄)₂SO_4(s) and coexist with the aqueous droplet as a result of secondary processes; τ_col is short compared with the lifetime of the aqueous particle. (Refer to Table 1 for parameters used to calculate τ_col.) In process B, wildfire BBA (D_p,CN = 0.15 µm) can contain discrete KCl_(s) and K₂SO_4(s) crystal inclusions; during wildfire events, τ_col can be well within the lifetime of the aqueous particle. In process C, effloresced ultrafine SSA (D_p,CN = 0.05 µm) can contain NaCl_(s) and coexist with the aqueous droplet as a result of the hydration hysteresis effect; τ_col can be comparable to the lifetime of the aqueous particle.

D_p,aq << D_p,CN.

A substantial number of liquid−solid collisions can also occur between a large solid particle and ultrafine aqueous particles (18, 19). Contact efflorescence could potentially occur in this scenario, as well. For example, urban ultrafine NH₄NO_3(aq) particles could effloresce upon contact with a solid SSA particle. In this scenario, τ_col is on the order of days to months, suggesting a substantial impact on total aerosol liquid water content only during high-number concentrations of large solid particles. However, even at low-number concentrations, contact efflorescence may still be important to consider for its influence on the surface properties of the large CN. As multiple collisions occur, the solid particle may develop a crystalline coating, which could influence the aging process and thus the particle shape, composition, and optical properties of the CN.

D_p,aq ≈ D_p,CN.

Diurnal variations in ambient RH and the hydration hysteresis effect can lead to the coexistence of solid and liquid particles with the same source and similar size distributions (11, 19). Coagulation coefficients become lowest when particle diameters are similar, but τ_col can still be within relevant timescales for ultrafine particles when number concentrations are ≥10³ cm⁻³.

SI Additional Discussion

NaBr_(CN)−NaCl_(aq) Contact Efflorescence.

For NaCl_(aq) contact efflorescence, NaBr_(CN) had the smallest lattice mismatch (δ_SC = 0.06) but was one of the least effective CN (CERH = 50%, σ(RH) = 0.81). This is because of the low DRH of NaBr (45–48% RH) (2, 12), which suggests the NaBr_(CN) were liquid droplets at the NaCl_(aq) CERH (50%). It thus remains intriguing how NaBr_(CN) were capable of inducing efflorescence of NaCl_(aq) above the NaBr DRH. Several laboratory studies have reported unusual postdeliquescence hygroscopic behavior for NaBr, including evidence for undissolved particulate in NaBr microparticles at an RH well above the DRH (12). Residual, undissolved particulate could explain how the NaBr_(CN)−NaCl_(aq) CERH was above the DRH of NaBr. Additionally, Niehaus and Cantrell (17) demonstrated that the mechanical effect of a collision may induce nucleation of ice during contact freezing. A similar phenomena may be occurring here, considering NaBr_(CN) are likely fully (or partially) deliquesced. Furthermore, regardless of the phase of NaBr_(CN) or the mechanical effect of the collision, ionic interactions during mixing of the CN solute could influence the solubility and relative solute supersaturation of NaCl_(aq) (25). Thus, contact could induce efflorescence via a salting-out of NaCl (see Ionic Interactions).

Ionic Interactions.

In the experiments reported here, the effects of CN dissolution were minimized by focusing on single collisions and only considering efflorescence to be contact-induced if it occurred between adjacently recorded images. However, ∼5–10 ms elapsed between recorded images, and, during this time, it is possible that some degree of CN dissolution and solute mixing occurred before the onset of efflorescence. The ionic activity of a solute is altered by the addition of another electrolyte (25). Thus, the solubility, deliquescence, and efflorescence behavior of an electrolyte mixture differs from that of the individual components (25–27). In some instances, the mixing of two solutes can induce precipitation of one or both of the solutes. This “salting-out” effect can be enhanced if the two solutes share a common ion (25, 26). In these instances, the solubility of both solutes will decrease, thus modifying the relative supersaturation of the solutes. For the case of NaBr_(CN)−NaCl_(aq) contact efflorescence, there is a common ion (Na⁺) in both the CN and aqueous composition. The common-ion effect, in addition to undissolved particulate in deliquesced NaBr, could explain how NaBr_(CN) was able to induce efflorescence of NaCl_(aq) at a CERH above the DRH of NaBr. Even if NaBr_(CN) is fully deliquesced at the moment of contact, the common-ion effect (or other ionic interactions) could potentially induce efflorescence of NaCl_(aq) during solute mixing due to, e.g., the different rates of diffusion of Na⁺ and Br⁻. The common-ion effect may have also influenced, e.g., (NH₄)₂SO_4(CN)−NH₄NO_3(aq), KCl_(CN)−NaCl_(aq), and K₂SO_4(CN)−(NH₄)₂SO_4(aq) contact efflorescence. In addition to the common-ion effect, any solute mixing can alter the ionic activity of the solution and thus the relative supersaturation of the droplet.

Thermodynamic Properties of the CN.

Fig. S4 shows σ(RH) plotted as a function of the thermodynamic properties of the CN for heterochemical contact efflorescence. There is no overall trend when considering enthalpy of solution, solubility, or DRH of the CN. However, for the (NH₄)₂SO4_(aq) contact efflorescence experiments in which lattice mismatch was high (δ > 0.12), there appears to be a slight correlation in which σ(RH) decreases (i.e., CERH increases) with increasing DRH and decreasing solubility of the CN. However, this correlation does not appear for NaCl_(aq) and NH₄NO_3(aq) contact efflorescence. Overall, the best of indicator of σ(RH) appears to be lattice mismatch.

Comparison of Model Aerosol to Ambient Tropospheric Aerosol.

Aqueous droplets used in the present study were ∼10 µm in diameter on average. This size is comparable to fog and cloud droplets, but larger than the typical supersaturated aqueous inorganic particle in the lower troposphere (36, 37). However, (NH₄)₂SO₄ nanoparticles of ∼0.03 µm (dry diameter) have been observed to effloresce homogeneously at an RH similar to that of 10-µm particles, and the homogeneous ERH can remain remarkably constant over a wide range of aqueous droplet sizes (39). Thus, it is likely that the concept of contact efflorescence can be extended to a wide range of droplet sizes. CN were ∼0.5–1.5 µm dry particle diameter. As discussed in Atmospheric Implications, ultrafine aerosol (<0.1 µm) typically represent the highest-number concentrations of ambient aerosol, and thus the highest-number concentration of potential CN (36). Immersion efflorescence of (NH₄)₂SO₄ has been observed with mineral dust particles of <0.1 µm in diameter (8), and it is thus likely that contact efflorescence can also occur with CN of <0.1 µm in diameter. Indeed, contact efflorescence may initiate efflorescence at a higher RH than immersion efflorescence for heterogeneous nuclei of the same composition and size, particularly if nucleation preferentially occurs at the surface of aqueous salt droplets [as has been suggested (28)]. Although the process of contact efflorescence is likely transformative to a wide range of particle sizes, the CERH may vary for droplet and/or CN sizes significantly different from those used in the present study. Another important consideration is that ambient aerosol particles are frequently mixed with organic compounds that could influence contact efflorescence. The presence of organic compounds typically inhibits the ERH of an inorganic compound (40). However, this has yet to be studied with respect to contact efflorescence.

Concluding Remarks

This study has established that contact efflorescence is a pathway for crystallization of microdroplets at high RH and that particle collisions can occur on atmospherically relevant timescales. Although contact efflorescence may be situational in some scenarios (e.g., during wildfire events and arid meteorological conditions), the effects would persist for a longer period because the effloresced particle will remain crystalline for as long as the ambient RH is below the DRH of the inorganic component. Considering these observations and the prevalence of soluble inorganic material in atmospheric particulate, contact efflorescence may be a potentially important process occurring in the atmosphere.