Significance
Successful sperm navigation is essential for sexual reproduction, yet we still understand relatively little about how sperm cells are able to adapt their swimming motion in response to chemical and physical cues. This lack of knowledge is owed to the fact that it has been difficult to observe directly the full 3D dynamics of the whip-like flagellum that propels the cell through the fluid. To overcome this deficiency, we apply a new algorithm to reconstruct the 3D beat patterns of human sperm cells in experiments under varying flow conditions. Our analysis reveals that the swimming strokes of human sperm are considerably more complex than previously thought, and that sperm may use their heads as rudders to turn right or left.
Keywords: sperm swimming, rheotaxis, fluid dynamics, microfluidics, simulations
Abstract
Rheotaxis, the directed response to fluid velocity gradients, has been shown to facilitate stable upstream swimming of mammalian sperm cells along solid surfaces, suggesting a robust physical mechanism for long-distance navigation during fertilization. However, the dynamics by which a human sperm orients itself relative to an ambient flow is poorly understood. Here, we combine microfluidic experiments with mathematical modeling and 3D flagellar beat reconstruction to quantify the response of individual sperm cells in time-varying flow fields. Single-cell tracking reveals two kinematically distinct swimming states that entail opposite turning behaviors under flow reversal. We constrain an effective 2D model for the turning dynamics through systematic large-scale parameter scans, and find good quantitative agreement with experiments at different shear rates and viscosities. Using a 3D reconstruction algorithm to identify the flagellar beat patterns causing left or right turning, we present comprehensive 3D data demonstrating the rolling dynamics of freely swimming sperm cells around their longitudinal axis. Contrary to current beliefs, this 3D analysis uncovers ambidextrous flagellar waveforms and shows that the cell’s turning direction is not defined by the rolling direction. Instead, the different rheotactic turning behaviors are linked to a broken mirror symmetry in the midpiece section, likely arising from a buckling instability. These results challenge current theoretical models of sperm locomotion.
Taxis, the directed kinematic response to external signals, is a defining feature of living things that affects their reproduction, foraging, migration, and survival strategies (1–4). Higher organisms rely on sophisticated networks of finely tuned sensory mechanisms to move efficiently in the presence of chemical or physical stimuli. However, various fundamental forms of taxis are already manifest at the unicellular level, ranging from chemotaxis in bacteria (5) and phototaxis in unicellular green algae (2) to the mechanical response (durotaxis) of fibroblasts (6) and rheotaxis (7, 8) in spermatozoa (3, 9–12). Over the last few decades, much progress has been made in deciphering chemotactic, phototactic, and durotactic pathways in prokaryotic and eukaryotic model systems. In contrast, comparatively little is known about the physical mechanisms that enable flow gradient sensing in sperm cells (3, 9–13). Recent studies (3, 12) suggest that mammalian sperm use rheotaxis for long-distance navigation, but it remains unclear how shear flows alter flagellar beat patterns in the vicinity of surfaces and, in particular, how such changes in the beat dynamics affect the steering process. Answering these questions will be essential for evaluating the importance of chemical (14) and physical (4) signals during mammalian fertilization (15–17).
A necessary requirement for any form of directed kinematic response is the ability to change the direction of locomotion. Multiflagellate bacteria achieve this feat by varying their motor activity, resulting in alternating phases of entangled and disentangled flagellar dynamics that give rise to run-and-tumble motion (5). A similar mechanism was recently discovered in the biflagellate eukaryote Chlamydomonas reinhardtii (18). This unicellular green alga actively redirects its swimming motion through occasional desynchronization of its two cilia (19), although it is still debated whether this effect is of mechanical (20) or hydrodynamic (21, 22) origin. Experiments (23) show that the alga’s reorientation dynamics can lead to localization in shear flow (24, 25), with potentially profound implications in marine ecology. In contrast to taxis in multiflagellate organisms (2, 5, 18, 26, 27), the navigation strategies of uniflagellate cells are less well understood. For instance, it was discovered only recently that uniflagellate marine bacteria, such as Vibrio alginolyticus and Pseudoalteromonas haloplanktis, use a buckling instability in their lone flagellum to change their swimming direction (28). However, as passive prokaryotic flagella differ fundamentally from their active eukaryotic counterparts, it is unclear to what extent such insights translate to spermatozoa.
Earlier studies of human sperm locomotion have identified several potential steering and transport mechanisms, including thermotaxis (4), uterine peristalsis (29, 30), and chemotaxis (14, 16, 31), but their relative importance has yet to be quantified. Recent experiments (3, 32, 33) demonstrate that rheotaxis, combined with steric surface alignment (12, 34), enables robust long-distance navigation by turning sperm cells preferentially against an externally imposed flow direction (9, 10), but how exactly this realignment process happens is unknown. It has been suggested (32, 35, 36) that the intrinsic curvature or chiral beat dynamics (37, 38) of the flagellum could play an essential role in rheotactic steering, but this remains to be confirmed in experiments. Similarly, an increasing number of theoretical models (36, 39–47) still await empirical validation, because 3D data for the beat pattern of sperm swimming close to surfaces has been lacking.
To examine the dynamics of human sperm rheotaxis quantitatively, we here combine microfluidic experiments with mathematical modeling and 3D flagellar beat reconstruction. Single-cell tracking reveals the existence of two kinematically distinct swimming states that result in opposite turning behaviors under flow reversal. We quantify this effect for a range of viscosities and shear rates, and use these comprehensive data to constrain an effective 2D model through a systematic large-scale scan (6,000 parameter combinations). To identify the details of the flagellar beat dynamics during rheotaxis, we developed an algorithm that translates 2D intensity profiles into 3D positional data. Our 3D analysis confirms that human sperm perform a rolling motion (48), characterized by weakly nonplanar beat patterns and a rotating beat plane. However, contrary to current beliefs, we find that neither the rolling direction nor beat helicity determine the turning direction after flow reversal. Instead, the rheotactic turning behavior correlates with a previously unrecognized asymmetry in the midpiece, likely caused by a buckling instability. These findings call for a revision and extension of current models (36, 39–44, 46).
Results
Reorientation Dynamics After Flow Reversal.
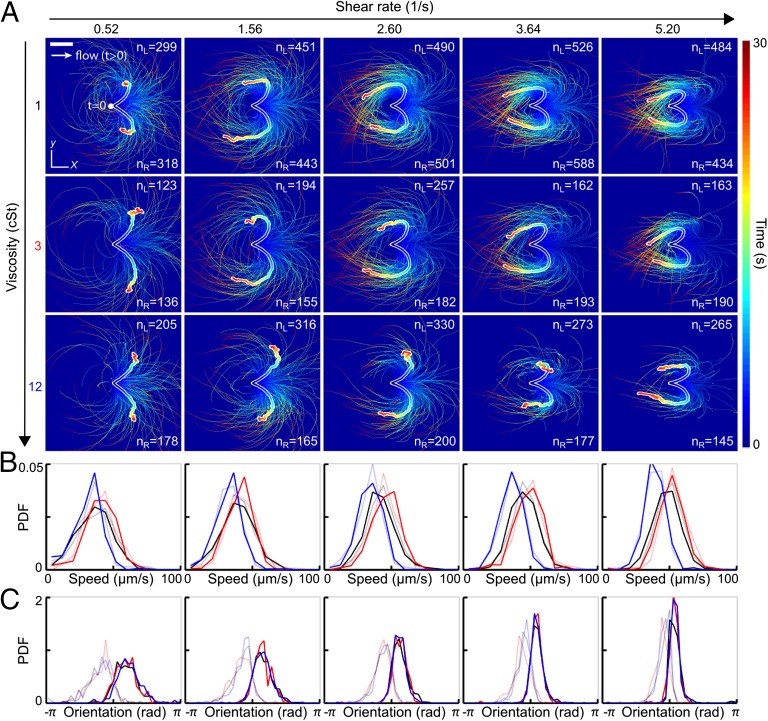
Understanding how efficiently a sperm cell can react to directional changes in ambient fluid flows is a first step toward evaluating the importance of uterine peristalsis on sperm transport during reproduction (29, 30). To examine the response of human sperm after a sudden flow reversal, we tracked individual cells in microfluidic channels (Experimental Details) at three different kinematic viscosities ν = 1 centi-Stokes (cSt), 3 cSt, and 12 cSt, and five different shear rates, = 0.52 s−1, 1.56 s−1, 2.60 s−1, 3.64 s−1, and 5.20 s−1 (Fig. 1). Hydrodynamic and steric forces cause sperm to accumulate near solid boundaries (12), where they remain trapped for several minutes while being exposed to a locally linear normal flow gradient. In our experiments, cells generally accumulated at distances of <10 μm from the wall. We therefore fixed the focal plane parallel to the upper wall of the microfluidic chamber, using a large depth of field to track all cells within distance 10 μm from the wall. The results presented below are thus integrated measurements over this accumulation layer. At time , a constant external flow field was applied in negative x direction, causing the cells to align preferentially in positive x direction (3, 32). At , the flow direction was rapidly reversed (switching time s), and the motions of 300 to randomly selected sperm cells were tracked for a period of >30 s for each parameter pair ().
Fig. 1.
Turning behavior of human sperm under flow reversal reveals two kinematically distinct swimming states. (A) Trajectories of individual sperm cells swimming close to the channel boundary in the plane, with initial positions superimposed at time (viewed from inside the channel). Equal-time trajectory averages for left- and right-turning cells are shown as thick white-shaded lines. Flow was reversed at , pointing in positive x direction for (white arrow). The shear velocity increases linearly in z direction. Color encodes time. (Scale bar, 200 μm.) (B) Normalized speed distributions before flow reversal at time . Faint lines indicate left-turning cells, and the other lines indicate right-turning cells. (C) Distribution of the orientation angles , measured relative to the x axis before flow reversal at time , signals two kinematically distinct cell populations. Colors in B and C indicate different viscosities (black, 1 cSt; red, 3 cSt; blue, 12 cSt).
Trajectory analysis shows that approximately half of the tracked cells respond to flow reversal by making a right turn whereas the other half pursue a left turn (Fig. 1A and Movies S1–S6). In both cases, the majority of cells perform a complete U-turn, provided the shear rate is sufficiently large . As the value of is increased, the characteristic curvature of the U-turns also increases, and the spread around the mean trajectories, obtained by averaging positions at equal time , is reduced (thick white-shaded lines in Fig. 1A).
The initial speed distributions, measured at the moment of the flow switch , show little variation between left-turning and right-turning cells (Fig. 1B). As expected, the maximum of the speed distribution is shifted to a lower value at high viscosity (blue curves in Fig. 1B). Strikingly, the initial offset angles of left-turning and right-turning individuals are bimodally distributed, suggesting that exposure to constant flow for separates two different alignment modes that become magnified during a flow reversal (Fig. 1C).
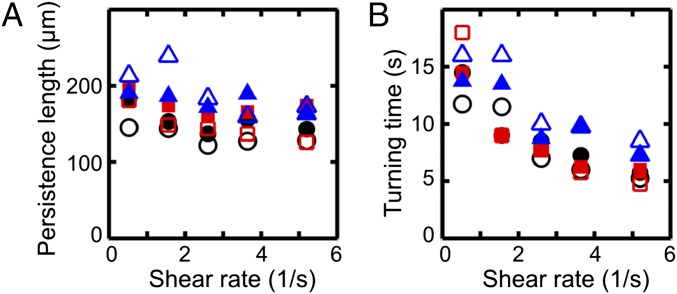
To characterize the typical distance scale associated with the turning process, we consider the downstream persistence length , defined as the maximum of the x component of a given mean trajectory in Fig. 1A. In our experiments, is found to increase slightly with viscosity ν while showing a weak systematic decrease with the shear rate (Fig. 2A). The downstream persistence length defines a characteristic turning time , corresponding to the time after which a given average trajectory in Fig. 1A begins to point against the flow. Assuming a passive response to the flow reversal, basic dimensional arguments suggest . This trend is confirmed in our experiments (Fig. 2B).
Fig. 2.
Characteristics of the turning process for the cell trajectories in Fig. 1, using the same color coding for viscosities, with filled (unfilled) symbols indicating right-turning (left-turning) trajectories. (A) The persistence length , defined as the maximum of the x component of each mean trajectory in Fig. 1A, shows weak variation with shear rate . (B) The mean turning time T, defined as the time after which the x component of a mean trajectory reaches its maximum, is approximately inversely proportional to the shear rate, .
Effective 2D Model Captures Turning Dynamics.
To capture the experimentally observed turning dynamics quantitatively in a mathematical model, we assume that the quasi-2D locomotion of a sperm cell near the boundary can be effectively described in terms of a position vector and a unit orientation vector . Considering flow along the x axis, the translation dynamics is governed by
| [1] |
where is the self-swimming speed, is the flow direction, and is the mean advective flow speed experienced by the cell. The reorientation dynamics is determined by an Adler-type equation
| [2] |
where is the rheotacic realignment time scale and is an intrinsic turning time, with accounting effectively for a preferential turning behavior. As in the experiments, we assume that the cells are viewed from inside the microchannel so that, in the absence of external flow (corresponding to ), the parameter choice corresponds to a left-turning cell. A microscopic physical mechanism underlying χ will be identified below. For the values of the shear-rate probed in our experiments, the rheotactic response is faster than the intrinsic circling period, . Instead of adding rotational noise (32) in Eq. 2, we sampled the turning times from Gaussian distributions (Parameter Scans), which seems more realistic because sperms cells experience only weak rotational diffusion due to their large size but may exhibit systematically different beat patterns across a range of individuals.
To determine how the model parameters () depend on the experimental control parameters , we simulated Eqs. 1 and 2 for >6,000 parameter combinations (Parameter Scans). Distribution parameters of the self-swimming speed V were directly estimated from experiments performed at (Fig. S1 and Parameter Scans). For each parameter pair , a best-fit model was determined by identifying the simulation run that most accurately reproduced the experimentally measured ensemble mean trajectories (Parameter Scans).
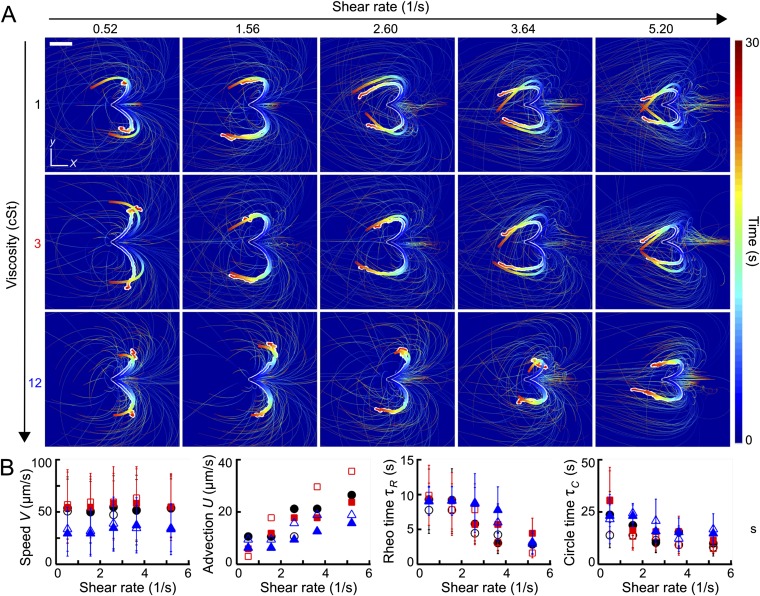
Fig. S1.
The effective 2D model defined by Eqs. 1 and 2 captures the ensemble turning dynamics. (A) Thin lines show individual simulated trajectories, and thick lines show the corresponding equal time averages. For comparison, the thick white-shaded lines are experimentally measured averages from Fig. 1A. Sample size . (Scale bar, 200 μm.) (B) Fit parameters used in A, obtained from systematic scans of parameter combinations (Parameter Scans). Distribution parameters of the self-swimming speed V were directly estimated from the experiments. The same color coding as in Fig. 1 is used. Filled (unfilled) symbols are mean values for right-turning (left-turning) cells. Error bars indicate SDs when model values were sampled from distributions (Parameter Scans).
The best-fit simulation runs and the experimentally measured mean trajectories are compared in Fig. S1. Although the underlying mathematical model is relatively basic, the numerically obtained mean trajectories generally agree well with their experimental counterparts (thick white-shaded lines in Fig. S1A). Note that the satisfactory quantitative agreement holds not only for the mean trajectory shape but also for the color-coded temporal progression. One can therefore conclude that the effective model defined by Eqs. 1 and 2 provides an adequate quantitative minimal representation of the rheotactic alignment process.
The dependencies between the best-fit model parameters and experimental control parameters are summarized in Fig. S1B: At high viscosity, the typical free-swimming speed V is significantly reduced. The mean advection speed U grows linearly with the shear rate . The rheotacic realignment time scale decays with , and so does the intrinsic circling time scale , consistent with the experimental results in Fig. 2B.
The model defined in Eqs. 1 and 2 postulates an intrinsic preference for left/right turning, encoded by the parameter and required to reproduce the experimentally observed turning dynamics. To understand how the flagellar beat dynamics determines the sign of χ, we next reconstructed the 3D flagellar pattern of individual sperm cells swimming freely near a surface in shear flow.
Three-Dimensional Beat Reconstruction.
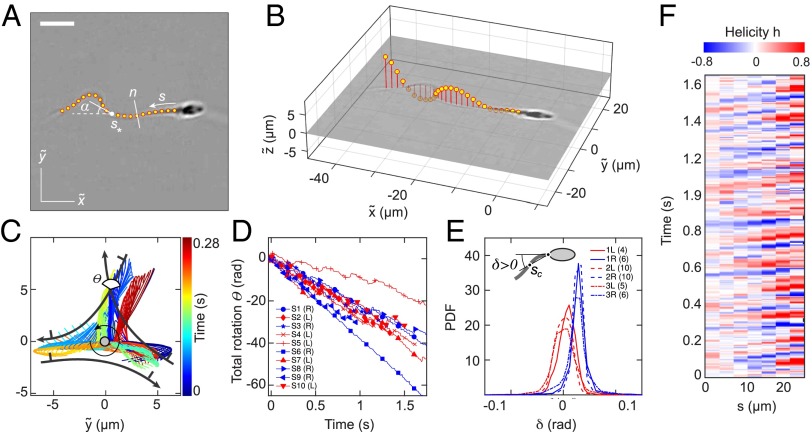
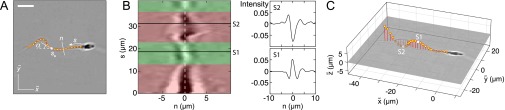
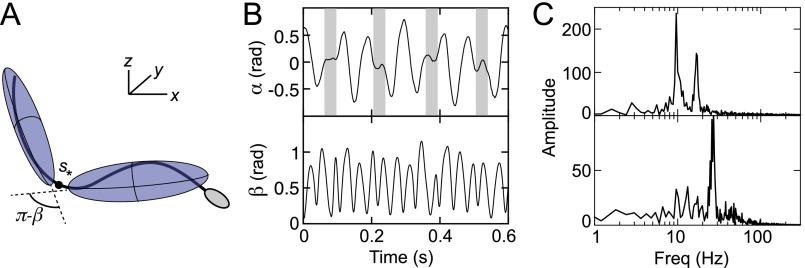
To identify the microscopic origin of the two distinct rheotactic responses, we developed a two-step algorithm that reconstructs the vertical beat component from 2D bright-field high-speed [450−600 frames per second (fps)] microscopy images (Fig. 3 A and B and Movie S7). The algorithm first identifies the projected 2D shape of the flagellum, based on the pixel intensity levels. Subsequently, the z coordinate is estimated by analyzing the intensity profile along cross sections normal to the flagellum (Beat Reconstruction and Fig. S2). As in Rayleigh−Sommerfeld back-propagation (49, 50), this reconstruction method exploits that an object located behind the focal plane appears bright with a dark halo, whereas a point source in front of the focal plane appears dark with a bright halo (51). The algorithm robustly recovers the 3D beat dynamics of the anterior ∼70% of the flagellum (Movie S7). The tail resolution is limited by the frame rate. The necessity of a full 3D analysis becomes evident when one compares the dynamics of the 2D projected (52) tangent angle at μm (Fig. 3) with the corresponding 3D angle (Fig. S3A). Although is periodic in time (Fig. S3B), it exhibits a spurious mode (36) that vanishes in the 3D signal (Fig. S3 B and C).
Fig. 3.
A 3D flagellar beat reconstruction reveals that a mirror symmetry breaking in the midpiece curvature separates left-turning from right-turning sperm. (A) A 2D bright-field image and tracked flagellum in the head-centered comoving frame, with arc-length s and normal line n. (Scale bar, 10 μm.) (B) A 3D beat reconstruction in the head-centered frame (Beat Reconstruction and Movie S7). (C) Typical 3D beat plane rotation for a single sperm, seen from head-on, with beat period of ∼0.08 s. The circular arrow indicates rolling direction of the flagellum. (D) The cumulative beat plane rotation θ, shown for 10 typical samples of left-turning (L) and right-turning (R) cells, implies that the rolling and turning direction are not correlated. (E) Midpiece curvature, quantified by the bend angle δ between the tangent at and the secant through μm, correlates strongly with the turning direction (three different donors, sample size in brackets). (F) A 3D reconstruction reveals ambidextrous helicity in the first ∼70% of the flagellum.
Fig. S2.
(A) Tracked 2D flagellum in the focal plane of the microscope in the head-centered comoving frame , in which the axis is aligned with the mean swimming direction; s denotes the arc length, and n denotes the line normal to the flagellum. (Scale bar, 10 μm.) (B) Intensity cross section along the flagellum. The dashed white line, , denotes the position of the flagellum centerline. Whenever the centerline passes through a dark (bright) region, the z coordinate is above (below) the focal plane, indicated in green (red) shaded regions. Two sample intensity profiles and are shown for illustration. (C) The width of the intensity maxima determines the z displacement, allowing for the 3D reconstruction of the flagellum (Movie S7).
Fig. S3.
(A) Schematic of coarse-grained double-ellipsoid approximation of 3D beat geometry. (B, Top) Direct analysis of the projected 2D beat patterns in terms of tangent angle results in spurious beat modes (highlighted in gray), reflected by a second peak in the power spectrum (C, Top). These spurious modes disappear when the 3D profile is analyzed in terms of the angle between two inertial ellipsoids (B, Bottom), leaving a single dominant frequency (C, Bottom).
Three-Dimensional Rolling Motion and Beat Planarity.
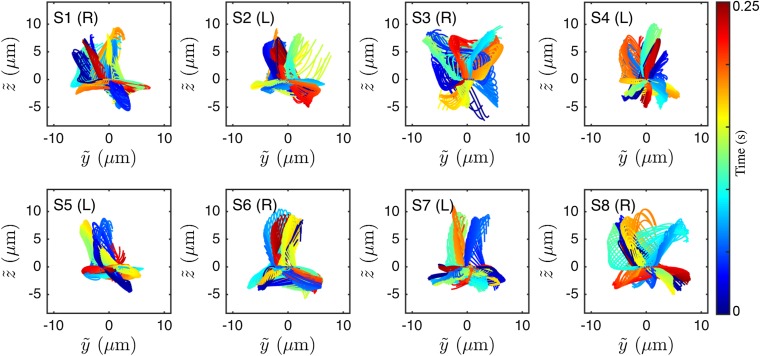
At low viscosities, human sperm cells swim in a rolling mode, characterized by a rotation of the flagellum around its longitudinal axis (35, 53). In our experiments, almost all cells perform rolling, as evident from the rotation of the sperm head (Movie S7). The 3D conical rolling beat pattern, thought to be linked to a calcium signaling pathway, leads to strong rheotactic alignment (3). Hydrodynamic models predict that the rolling motion and rheotaxis are caused by an out-of-plane component in the flagellar beat (40, 42, 46), but dynamics and geometry of this beat mode have yet to be confirmed through 3D measurements on freely swimming cells. To test the robustness of our reconstruction algorithm, we first analyzed the 3D rolling motion. When viewed from head on, we found that the flagellum beats almost always in a counterclockwise rolling motion as indicated in Fig. 3C, whereas the normal vector angle θ of the corresponding beat plane rotates in the opposite direction (Fig. 3 C and D; details and additional examples in Figs. S4 and S5). The rotation of the beat plane is synchronized with the beat dynamics such that the flagellum typically performs half a beat in a plane of fixed orientation, but then completes the second half in another plane. The beat envelope is not symmetric about the vertical axis, due to the presence of the wall, which is located below the cell in the body-centered frame (Fig. 3C). A large number of beats are performed parallel to the wall, reflecting inhibition of rolling by hydrodynamic and steric interactions between wall and flagellum, as also observed in previous experiments (48) and simulations (42).
Fig. S4.
The 3D beat reconstruction for eight representative samples of left-turning (L) and right-turning (R) sperm, viewed from the front in the comoving frame . Color encodes time.
Fig. S5.
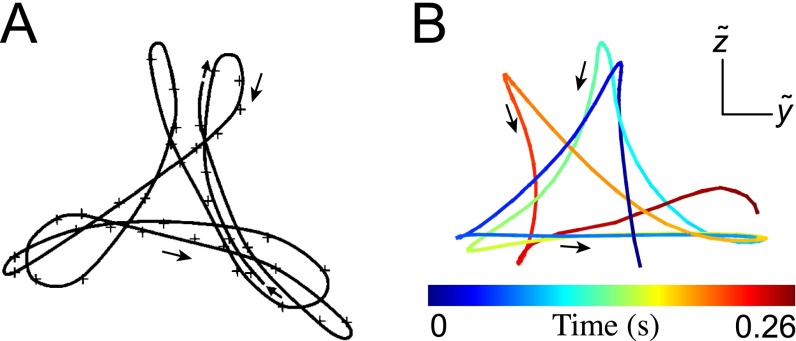
(A) Flagelloid curve for mouse sperm, reproduced from ref. 48. (B) Flagelloid curves for human sperm, obtained by observing the sperm head-on and tracking the motion of a single point located at μm.
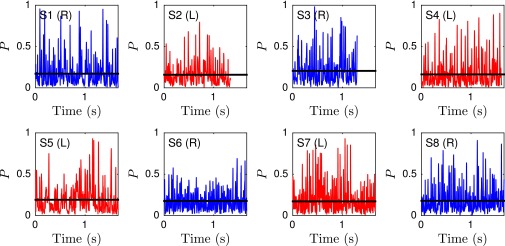
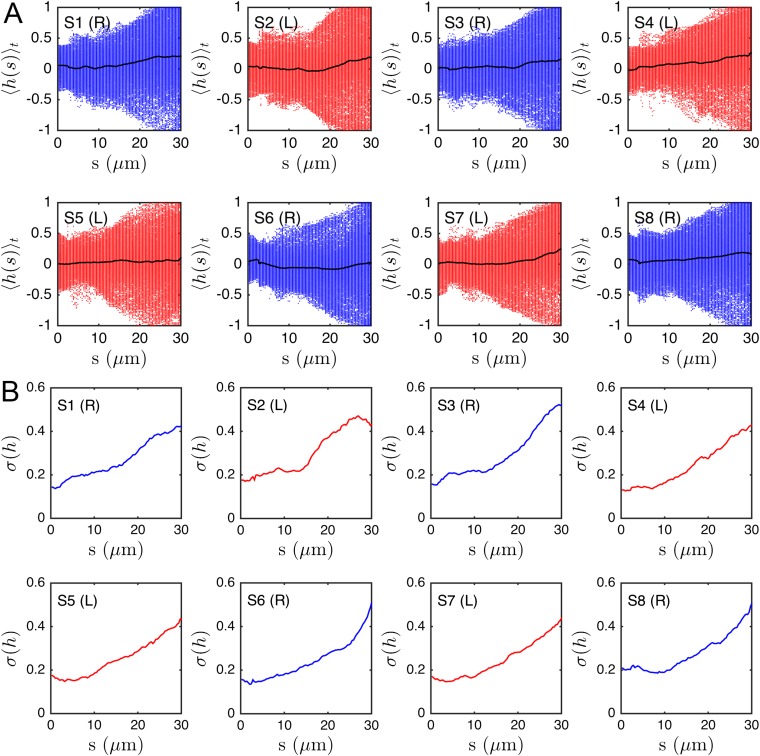
We quantify the beat planarity through the length ratio of the two minor axis vectors of the flagellar inertial ellipsoid (Fig. S6). The shortest axis is normal to the best-fit plane through the flagellum, and for planar curves. We find that the flagellum remains mostly planar (Fig. S7), with a sample mean of , in excellent agreement with estimates from previous 2D orthogonal measurements (35). Tracking a single point at arc length μm from the head, we obtain flagelloid curves similar to those observed in head-fixated mouse spermatozoa (Fig. S5) (48) and recent hydrodynamic simulations (40), corroborating the accuracy of the 3D reconstruction.
Fig. S6.
Illustration of the planarity measure by means of the inertia ellipsoid and its two minor axes and .
Fig. S7.
The time series of the planarity measure P reveals a mostly planar beat pattern. Shown are eight representative samples for left-turning (red) and right-turning (blue) sperm. Black lines denote the time-averaged planarity .
Turning Behavior Is Independent of Rolling.
To test if the rolling motion causes different turning directions, we track the normal vector of the best-fit plane through the flagellum in the head-centered frame (Fig. 3C). The projected orientation angle is found to undergo persistent clockwise rotation, interrupted by short periods of counterclockwise rotation (Fig. 3D). These results reconcile seemingly contradicting earlier reports of purely unidirectional (54) and bidirectional (35) rolling motion in human sperm. Importantly, however, our data show no correlation between rolling and rheotactic turning direction of the sperm cells (Fig. 3D).
Turning Behavior Is Independent of Beat Chirality.
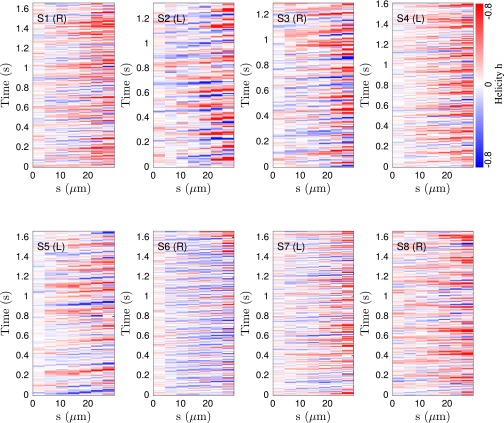
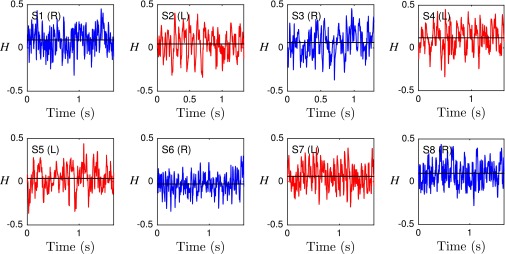
It has been suggested that the beat patterns of human sperm flagella resemble spirals of well-defined helicity (32, 35, 36). If true, then the different turning behaviors could be caused by a chiral mechanism. Even though helicoidal models of human sperm swimming are widely used in theoretical studies (32, 40, 46), the helicity of the beat patterns has never been measured directly in experiments. Using our 3D data, we can determine the local helicity of the flagellum shape at time t from the binormal vector . In the head-centered frame, a helicoidal flagellum winding in counterclockwise direction when viewed from the front has local helicity , whereas if the winding is clockwise. Plotting along the flagellum as a function of time, we find no persistent helicity (Fig. 3F). Instead, the flagellar dynamics is dominated by helicity waves of either handedness (Fig. 3F). The mean helicity fluctuates around zero, showing no discernible difference between left-turning and right-turning sperm (Figs. S8−S10).
Fig. S8.
Spatiotemporal plot of the local helicity h for eight representative samples for left- and right-turning sperm, illustrating the absence of a persistent helicity in the first ∼30 μm of the flagellum.
Fig. S10.
Averaged flagellar helicity H as function of time for eight representative samples. No distinct helicity discerning right-turning (blue) from left-turning (red) sperm cells is apparent. Black solid lines indicate the time averages of H.
Midpiece Asymmetry Determines Turning Direction.
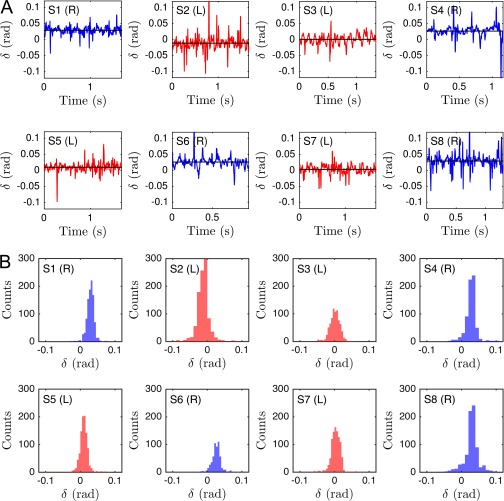
The midpiece connecting head and flagellar tail of a human sperm cell is ∼5 μm long, and its microstructure differs from that of the remaining flagellum (55). Our 3D data reveal that, unexpectedly, left-turning and right-turning sperm exhibit a notably different midpiece curvature. To quantify this effect, we measured the bend angle δ between the tangent at and the secant through μm, and found that the bend angle distributions of left-turning cells are centered near zero, whereas right-turning cells exhibit a mean bend angle of rad for cSt and (Fig. 3E and Fig. S11).
Fig. S11.
Average midpiece curvature, measured by the bend angle δ (see Fig. 3E), correlates with the turning behavior (eight typical samples shown): (A) Even though the individual δ-time series fluctuate considerably, (B) the distributions exhibit different mean angles for right-turning (blue) and left-turning (red) sperm cells.
Discussion
Structure of the 2D Model.
The 2D trajectory data reveal two kinetically distinct swimming states, corresponding to in Eqs. 1 and 2. More precisely, it is necessary to postulate an intrinsic preference for left turning (χ = +1) or right turning (χ = −1) in the effective 2D model because of the experimental observation that, after reversal of the flow direction, the majority of cells perform a complete U-turn (Fig. 1 and Movies S1–S6). To clarify this important detail, we may consider a hypothetical collection of cells without intrinsic turning preference, corresponding to . If the flow is along the negative x direction (), the only stable fixpoint of Eq. 2 is , corresponding to exact alignment against the flow direction. If we further assume that the cell orientations are approximately symmetrically distributed around this fixed point, then, after a flow reversal from to , about 50% of the cells would turn left and right, respectively. However, each of those subpopulations would stop turning once they reach the new stable orientation fixed point . Thus, the resulting trajectory ensemble would trace out an open W shape instead of the experimentally observed “closed heart” shape (Fig. 1A).
Ambidextrous Beat Helicity.
Our 3D analysis implies that neither rolling direction nor helicity controls the rheotactic turning behavior of sperm cells, challenging the current paradigm of human sperm rheotaxis. Although it is, in principle, possible that helicity becomes biased near the posterior tip, which could not be reliably tracked due to the experimental frame rate limitations, such a scenario seems rather implausible, as the chiral waves should propagate through the whole flagellum. Moreover, a recent 3D analysis of the malaria parasite Plasmodium berghei, which has a 9+2 axoneme structure similar to human sperm, also challenges the picture of persistent helicity in flagellar propulsion (50).
Intrinsic Midpiece Curvature vs. Buckling.
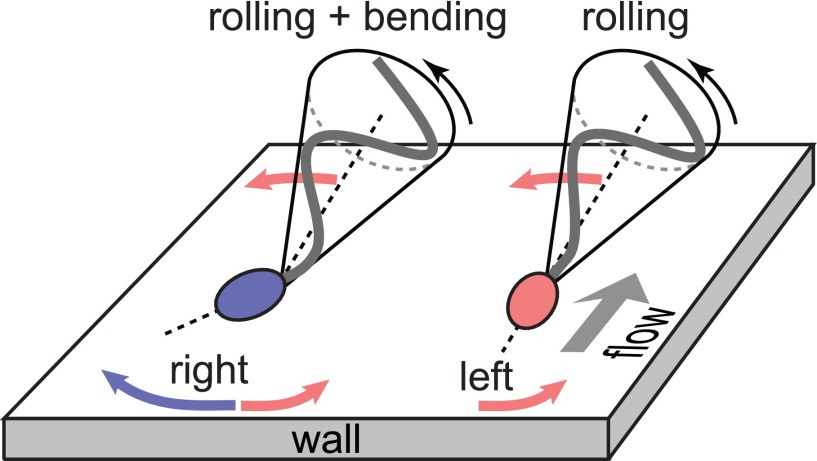
Our data demonstrate that the rheotactic turning behavior correlates with an asymmetry in the midpiece curvature distributions (Fig. 3E and Fig. S11). Recent hydrodynamic simulations show that midpiece curvature asymmetries strongly affect swimming trajectories, thus providing an effective long-range steering mechanism (42). Possible explanations for a curved midpiece are intrinsic curvature or symmetry breaking caused by a dynamic buckling instability. Intrinsic midpiece curvature is a known feature of rodent sperm (56) and has been linked to strongly asymmetric beat patterns (57). A less pronounced intrinsic curvature has been reported for human sperm, requiring artificial elevation of the intracellular calcium levels (58) absent in our experiments. An intrinsically curved midpiece per se does not explain the observed asymmetry in the distribution of the projected 2D bend angles (Fig. 3E), as the rolling motion would effectively symmetrize the distributions, and both left-turning and right-turning cells exhibit nearly identical rolling statistics (Fig. 3D). Therefore, a more plausible explanation is dynamic buckling, which is common in thin structures such as flagellar axonemes and cross-linked filament bundles (59). For sea urchin sperm, a buckling instability was suggested as an explanation for asymmetric compressed beat patterns at high viscosities (60). Nonlinear analysis and hydrodynamic simulations revealed that flagellar buckling arises generically from the interplay between elasticity and fluid forces (61), resulting in spontaneously broken symmetries of beat patterns and curved swimming trajectories. Although these buckling instabilities were predicted to affect the entire flagellum, localized buckling as observed in our experiments can be caused by inhomogeneities in the flagellar elastic stiffness. In human sperm cells, the midpiece carries the mitochondrial gyres and is therefore thicker than the tail of the flagellum (55); ergo, it is plausible that buckling occurs primarily at the transition point between midpiece and tail, triggered by perturbations that arise from the inhomogeneous material properties. In this picture, left-turning cells fluctuate symmetrically around the unbuckled state whereas right-turning cells predominately occupy a buckled configuration with positive bend angle δ (Fig. 3E). The two distinct turning behaviors can then be inferred from basic force balance considerations (32, 33, 62): Approximating the flagellar beat envelope by a cone rotating counterclockwise around its symmetry axis, hydrodynamic interactions with the wall effectively result in a left-turning torque (Fig. 4). This rheotactic turning mechanism depends only on the flagellar rolling motion but not on the head and its geometry, in agreement with recent experiments demonstrating rheotaxis for headless mouse sperm (3). For right-turning cells trapped in a buckled state, the head acts as a tilted hydrofoil (“front rudder”) that overcomes the rolling force. Thus, mirror symmetry is not just broken by the rolling motion but also by the midpiece bend.
Fig. 4.
Turning mechanisms implied by 3D data. Left-turning (red) and right-turning (blue) sperm cells roll their flagellum counterclockwise with a conical beat envelope, resulting in a left-turning torque. For right-turning sperm, this effect is counteracted by a larger opposing force due to the tilted head acting as a hydrofoil or “rudder.”
Conclusions
Our joint experimental and theoretical study focused on the dynamics of human sperm cells swimming under the influence of a time-dependent linear flow gradient near a solid surface, a situation that is common in a wide range of external and internal fertilization processes. We identified two kinematically distinct rheotactic turning behaviors and showed that an effective 2D mathematical model suffices to reproduce quantitatively the experimentally observed trajectory statistics. Building on, to our knowledge, the first systematic 3D beat reconstruction for freely swimming sperm cells, we found that human sperm flagella perform nearly planar beats in a stepwise-rotating plane. However, the rheotactic turning behaviors are independent of this rolling motion. Contrary to current opinion, the 3D beat patterns exhibit no persistent helicity but instead are composed of helical waves of either handedness. Interestingly, similar beating modes were reported recently for Trypanosoma brucei (63) and malaria parasites P. berghei (50). Taken together, these results suggest that ambidextrous beat patterns may be a common feature of eukaryotic uniflagellates that share the canonical 9+2 axoneme structure. Furthermore, our 3D beat pattern analysis reveals that rheotactic separation into left-turning and right-turning cells is related to a curved midpiece section. In the absence of evidence for intrinsic midpiece curvature in human sperm, a buckling instability combined with the wall-induced partial suppression of rolling can provide a plausible explanation for the observed bend angle asymmetry in right-turning cells. Recent experiments showed (28) that uniflagellate marine bacteria use buckling to change their swimming direction. Although passive prokaryotic and active eukaryotic flagella are built differently, buckling could provide a general physical mechanism for controlling reorientation in single-cell uniflagellates.
More generally, the above 3D observations call for a revision and extension of the currently prevailing helical models of flagellar propulsion. Future theoretical studies should focus on the interplay between rolling dynamics, wall interactions, and structural and elastic inhomogeneities in midpiece and flagellum. The basic ingredients for a bimodal rheotactic response—cell rolling and beat curvature asymmetry—are generic features of many sperm species (42, 48, 60, 61). It will thus be important to investigate experimentally if bimodal rheotactic response occurs in other species, in particular those featuring strong head asymmetries that may critically affect the proposed hydrofoil effect. Moreover, it will be interesting to study how calcium concentration (3), increased viscous load (36), and viscoelastic fluid environments affect the flagellar dynamics. The 3D beat reconstruction approach implemented here provides a promising starting point for such future studies.
Experimental Details
Sample Preparation.
Human sperm samples from healthy undisclosed normozoospermic donors were obtained from the Urology Clinic of the First Pavlov Medical University of St. Petersburg. Donors provided informed consent in accordance with the regulations of the Ethical Committee of St. Petersburg Academic University, which granted approval to this research under record number 04/14. The ejaculated samples were incubated at 37 °C for 30 mins, 1 h before injection into an intermediate microfluic channel. The motile cells fill the experimental channel within 10–20 mins by passing the one-way filtration channels and entering the media with a given viscosity. The medium was based on a standard Earle’s Balanced Salt Solution, containing 66.4 mM NaCl, 5.4 mM KCl, 1.6 mM CaCl2, 0.8 mM MgSO4, 1 mM N2H2PO4, 26 mM NaHCO3, 5.5 mM d-Glucose with pH 7.1–7.8 supplemented with 2.5 mM Na pyruvate and 0.1% wt/vol serum albumin. Viscosity of the medium was modified by adding methylcellulose (M0512; Sigma-Aldrich; approximate molecular weight 88,000) at concentrations 0%, 0.2%, and 0.4% wt/vol. At these low concentrations, the medium can be considered as a Newtonian fluid (64).
Microfluidics.
Microfluidic channels were manufactured using standard soft-lithography techniques. The multiple-layer mold was produced from SU8 2075 (MicroChem Corporation). The microfluidic chip containing the channels was cast from polydimethylsiloxane (Sylgard 184; Dow Corning) and bonded to covered glass. The channels were filled with the medium before the experiment. The inlets were sealed by metal stubs after the sample injection. The intermediate channel had 50 times smaller volume than the main channel of the flow application; therefore the sperm infusion step could not modify the viscosity in the main channel. The rectangular cross section of the main channel was 0.29 mm 3 mm. The flow was created by a microsyringe pump (Harvard Apparatus) at controlled flow rates of 1–10 μL/min. The shear rate at a given flow rate was determined from the flow velocity at distance 20 μm from the wall, assuming a linear shear profile (32). The concentration of the sperm cells in the experiments was kept far below 1% volume fraction.
Microscopy.
To identify the swimming characteristics of individual sperm cells, the trajectories were reconstructed by applying a custom-made particle tracking velocimetry algorithm to image data taken with a Nikon TE2000U inverted microscope using dark field illumination (4× objective, Pike F100 camera at 25 fps). The flagella dynamics was captured with an Edgertronics camera (450–600 fps, 40×/NA 1.3 objective). The calibration procedure of the velocity profile in the channel and calculation of the velocity gradients has been described previously (32). The field of view (normally 1,800 μm × 1,800 μm) was selected in the central part of the channel (with respect to the x direction), where the in-plane velocity gradient is negligible due to the high aspect ratio of the channel (32).
Parameter Scans
Eqs. 1 and 2 were solved numerically using an Euler scheme with time step s, for ensembles of particles with and particles with . We simulated trajectories over the interval s with flow reversal () at time s, and initial particle orientations sampled uniformly from a unit circle. At the beginning of each simulation, the self-swimming speed V of each particle was determined according to the rule , where Z is a standard Gaussian random number and the values are estimated directly from experiments at : Specifically, μm/s for viscosity cSt, μm/s for cSt, and μm/s for cSt. Similarly, we fixed, for each particle, the timescales and according to the rules and , where Z denotes independent standard Gaussian random numbers, s and , and with and . Thus, instead of adding rotational noise in Eq. 2, we sampled the turning times from distributions, which seems more realistic because sperms cells experience relatively small rotational diffusion due to their large size but may exhibit systematically different beat patterns across a range of individuals. The mean advective speed was varied according to where , resulting in 6,480 simulation runs in total. From these runs, we identified, for each parameter pair , the best fit to the experimentally measured equal time mean trajectories (thick lines in Fig. 1A) by minimizing the norm, weighted with experimental sample size, and accounting for physical monotonicity constraints. Note that this procedure does not identify the best possible fit to the data but merely yields the optimal physically consistent approximation on the 6D parameter grid explored in the simulations. The results of the fitting process are summarized in Fig. S1.
Beat Reconstruction
We reconstruct the 3D flagellar geometry from 2D bright-field microscopy images in two steps: First, we track the projected 2D shape of the flagellum based on the pixel intensity levels in the plane. Subsequently, the z position is estimated from the width of intensity maxima along cross sections normal to the flagellum.
Two-Dimensional Flagellar Tracking.
Grayscale microscopy images were imported into MATLAB and converted to pixel intensity values . After identifying the head centroid based on pixel intensity maxima, the coordinate system is centered at the sperm head. The starting point of the flagellum is searched for on a circle of radius around the head. The polar angle of the starting point is determined by the location of the intensity maximum, , along this circle. We chose μm, which is slightly larger than the average sperm head size 6.2 μm (65), to ensure a robust but equally distant starting position for all traced flagella.
Once the starting point is known, we assume that the next point on the flagellum lies on a circle of radius μm around with polar angle . Once was determined by the procedure described below, the coordinates of the new point are , and the next point is determined in the same way. Keeping r fixed, we thus iteratively obtain equally spaced points along the flagellum.
Given , we obtain the polar angle of the next point as follows: We first center a local coordinate system at the current point . We then compute squared intensity profiles along circles centered in with equally spaced radii
for . The width is chosen μm for all samples. An initial guess is then determined by the maximum of the average circular profile,
To ensure smooth tracking curves and enhanced robustness, the final angle is obtained from a moving average over the current guess and the angles , of the four preceding points. Knowing , the coordinates of the next point are found as . Note that we consider the squared intensity values, due to the fact that the flagellum can appear either brighter or darker than the background depending on its z coordinate. The radial averaging of profiles is performed to increase robustness of the algorithm and to overcome passages where the flagellum is hardly visible, occurring, for instance, if the vertical z displacement is very large.
Tracking stops if (corresponding to a projected flagellum length of ∼40 μm) or if
| [S1] |
where denotes the mean of the squared intensity over the entire 2D image, and its SD. The criterium (Eq. S1) ensures that tracking stops when the posterior part of the flagellum becomes undetectable.
The final set of N points is smoothened with a Savitzky−Golay filter with window size 9 and order 2. An illustration of a 2D traced flagellum is shown in Fig. S2A.
Three-Dimensional Reconstruction.
The 3D flagellum position is determined by reconstructing the z coordinate based on the principle of Rayleigh−Sommerfeld back-scattering (49–51). This reconstruction method uses the fact that an object located away from the focal plane will cast a blurred image. Specifically, if the object is behind the focal plane (upstream), the center of the source will appear bright with a dark halo, whereas a source in front (downstream) of the focal plane appears dark with a bright halo. The amount of displacement determines the width of the halo.
We assume that the flagellum consists of a superposition of point sources located at some distance z from the focal plane. We first identify for each 2D flagellar point whether it is located below or above the focal plane. To this end, we compute intensity cross sections of width μm through the flagellum by interpolating the intensity field along the normal vectors at each flagellar point (Fig. S2B). Precisely, is defined as the vector normal to the edge vector from to . Two typical cross section profiles for locations and are also shown Fig. S2B. Based on the relative size of the extrema, we determine if the flagellum is behind it (, bright center) or in front of it (, dark center). The value of vertical displacement can be reconstructed by solving an inverse optimization problem (50, 51). Given the large amount of high-speed data to analyze, we choose here a much faster but less accurate first-order approximation, by assuming that the z displacement for point is given by
| [S2] |
The sign is determined by the criterium above, i.e., positive (negative) sign for scatterers upstream (downstream) of the focal plane. As before, is the intensity average over the entire image; denotes the maximum of the quantity in brackets over all values . The above choice is motived by considering a rectangular intensity profile of width and height h,
The corresponding z value is , i.e., proportional to the width of the signal. Note that, to determine the value of k, one needs to know the point spread function of the microscope and optical imaging equipment, which is typically not readily available. We therefore choose a constant value of such that out-of-plane amplitudes are comparable in size to those of planar beats. We find, however, that the analysis described below is largely insensitive to this particular choice for k.
To remove noise in the obtained z values , we fit a fifth- and sixth-order polynomial through the points, where each point is weighted by the factor
i.e. z values with large intensity profile deviations from the mean are weighted more than weak intensity signals. The better of the two fits determines the z values for each point . Due to the displacement in z direction, we fit an arc-length parametrized spline through the 3D point and resample equally spaced 3D points from it.
The previous steps are performed for each frame separately. In a last step, we filter for temporal outliers by computing the time series of mean square displacements between flagella of succeeding frames. We detect outliers by an iterative Grubbs test (66), and replace these flagella with time-interpolated values from the previous and next frames. The cleaned 3D data points are smoothed in time using a temporal Savitzky−Golay filter with window size 11 and order 2, resulting in flagellar points for each frame. A cubic spline is fit through to obtain the smooth flagellar curve . For later analysis, the 3D flagella coordinates are transformed into the comoving frame , which is centered in the sperm head such that the x axis is aligned with the average swimming direction.
Beat Analysis
The 2D vs. 3D Flagellar Dynamics.
We first evaluate whether the beat pattern is planar and constrained to the focal plane, as observed and studied in previous high-viscosity experiments (38, 52, 67, 68). To this end, we compare dynamics of the 2D projected tangent angle at arc length μm, corresponding to about half of the 3D-reconstructed flagellum length (Fig. S2A) (52), with the 3D angle β between the major axes of two inertia ellipsoids, of which the first is constructed for and the second is reconstructed from the remaining flagellum, (Fig. S3A). Note that, by construction, attains positive and negative values, whereas is always positive. For the same periodic signal, will thus oscillate at twice the frequency of . As expected, both and are periodic (Fig. S3B). However, the α-time series exhibits a spurious mode (highlighted gray in Fig. S3B) that disappears in the power spectrum of the 3D β-signal (Fig. S3C). This qualitative difference demonstrates that 3D beat reconstruction is essential for understanding human sperm locomotion.
Rolling.
Sperm cells in our experiments almost always roll around their longitudinal axis during swimming. The rolling is readily observed by the visible rotation of the sperm head (the direction of rolling, however, cannot be inferred from the head rotation). Although rolling is characterized by 3D beat dynamics, we find that, most of the time, the flagellar beat remains nearly planar, with a plane of changing rotation as explained in Three-Dimensional Rolling Motion and Beat Planarity. The 3D flagellum dynamics for eight representative samples of left- and right-turning sperm cells is shown in Fig. S4 (head-on view from the front).
Woolley (48) reports characteristic flagelloid curves for mouse sperm in the rolling beat mode. These curves were found for head-fixated sperm pointing toward and being oriented perpendicular toward the coverslip. By focusing at a focal plane μm behind the sperm head, Woolley could directly observe the out-of-plane motion of a single point along the flagellum (Fig. S5A). Tracking the position of a point located at μm, we obtain flagelloid curves that are very similar to those obtained by Woolley (48) (Fig. S5B). In particular, we find that, in analogy with mouse spermatozoa, the human flagelloid curves are traced out in the counterclockwise direction. This is in agreement with earlier reports (54) of counterclockwise rolling of the human sperm flagellum. Note that, in order for the sperm cell to be torque-free, the head must rotate in the opposite direction (clockwise), which was confirmed for mouse spermatozoa by direct observation of the head (48).
Rolling Beat Patterns Are Mostly Planar.
To quantify beat planarity, we first construct the flagellar inertia ellipsoid for each time frame. The orientation and axes of the ellipsoid are given by the eigenvectors and eigenvalues of the inertia tensor
| [S3] |
Assuming unit mass density, the components of I are
where is the center of mass of the flagellum and are the Cartesian coordinates of the flagellar point . The ratio of the two minor axes and of the inertia ellipsoid thus expresses the planarity of the flagellum (Fig. S6), with for a completely planar curve.
Fig. S7 shows eight representative samples demonstrating that the flagellar beat is nearly planar most of the time, with a mean planarity (black line). This value is in excellent agreement with previous experiments that estimated the planarity by observing head-fixated sperm cells from different sides (35).
Helicity of Human Sperm Cells.
We define the local measure of helicity by means of the binormal vector
| [S4] |
In the comoving frame (), sperm cells swim in positive direction. For a right-handed helix (rotating CW when viewed from head to tail), the local measure of helicity
| [S5] |
is therefore negative for all s along the helix, whereas a left-handed helix (CCW) will have positive helicity . To calculate the binormal vector for the 3D reconstructed flagella, we use a discrete form of the binormal (69), calculated for each point according to
| [S6] |
Here, is the edge vector connecting to . The advantage of using the discrete binormal vector is that it is well defined even for collinear edges, in contrast to Eq. S4.
We surprisingly observe no persistent helicity in the μm of 3D tracked flagella. Instead, the flagellum appears to be ambidextrous, with waves of differing helicity traveling from the head to the tail, as demonstrated in most samples of Fig. S8. Plotting the time-averaged local helicity as a function of the arc length s, we find , with a tendency toward positive helicity values near the posterior parts of the flagellum, at least for some sperm cells (Fig. S9). The turning behavior, however, is not correlated to this effect, as evident from the time-averaged helicity (Fig. S9, black lines).
Fig. S9.
(A) Black lines show time-averaged local helicity, , along the flagellum for eight representative samples. Individual data points from each frame are shown to illustrate the spread over time (red, left-turning; blue, right-turning), indicating no persistent helicity. Although a slight tendency toward positive average helicity values is observed near the posterior parts of the flagellum, this bias does not correlate with the turning direction. (B) Helicity SD along the flagellum.
By integrating along the flagellum, we obtain the average flagellar helicity at a given time,
where L is the flagellum length. In the discrete setup outlined above, we replace the integral by a sum over the discrete helicity values of each point . We find that H fluctuates strongly as function of time, with a mean close to 0, suggesting there is no persistent net helicity in the flagellum (Fig. S10).
Midpiece Curvature Asymmetry.
For completeness, individual time series of the midpiece bend angle δ, as defined in Midpiece Asymmetry Determines Turning Direction, are provided in Fig. S11, along with their individual angle distributions. The individual time series exhibit strong fluctuations, but have distributions with distinct means separating right-turning sperm cells from left-turning ones.
Supplementary Material
Acknowledgments
The authors thank Jeff Guasto, Andreas Hilfinger, and Ingmar Riedel-Kruse for helpful discussions and the Bourn Hall Clinic and Martyn Blayney for fruitful collaboration. This work was supported by the Skolkovo Foundation (Grant agreement for Russian educational and scientific organization no. 4dd.25.12.2014 to A.B.), the Swiss National Science Foundation Grant 148743 (to N.S.), an MIT Solomon Buchsbaum Fund Award (to J.D.), and an Alfred P. Sloan Research Fellowship (to J.D.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1515159112/-/DCSupplemental.
References
- 1.Häder D-P. Polarotaxis, gravitaxis and vertical phototaxis in the green flagellate, Euglena gracilis. Arch Microbiol. 1987;147(2):179–183. doi: 10.1007/BF00415281. [DOI] [PubMed] [Google Scholar]
- 2.Witman GB. Chlamydomonas phototaxis. Trends Cell Biol. 1993;3(11):403–408. doi: 10.1016/0962-8924(93)90091-e. [DOI] [PubMed] [Google Scholar]
- 3.Miki K, Clapham DE. Rheotaxis guides mammalian sperm. Curr Biol. 2013;23(6):443–452. doi: 10.1016/j.cub.2013.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bahat A, et al. Thermotaxis of mammalian sperm cells: A potential navigation mechanism in the female genital tract. Nat Med. 2003;9(2):149–150. doi: 10.1038/nm0203-149. [DOI] [PubMed] [Google Scholar]
- 5.Berg HC, Brown DA. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972;239(5374):500–504. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- 6.Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophys J. 2000;79(1):144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pedley TJ, Kessler JO. Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu Rev Fluid Mech. 1992;24:313–358. [Google Scholar]
- 8.Marcos F, Fu HC, Powers TR, Stocker R. Bacterial rheotaxis. Proc Natl Acad Sci USA. 2012;109(13):4780–4785. doi: 10.1073/pnas.1120955109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Adolphi H. Die Spermatozoen der Säugetiere schwimmen gegen den Strom. Anat Anz. 1905;26(20-21):549–559. [Google Scholar]
- 10.Rothschild L. Non-random distribution of bull spermatozoa in a drop of sperm suspension. Nature. 1963;198(4886):1221–1222. doi: 10.1038/200381a0. [DOI] [PubMed] [Google Scholar]
- 11.Zimmer RK, Riffell JA. Sperm chemotaxis, fluid shear, and the evolution of sexual reproduction. Proc Natl Acad Sci USA. 2011;108(32):13200–13205. doi: 10.1073/pnas.1018666108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kantsler V, Dunkel J, Polin M, Goldstein RE. Ciliary contact interactions dominate surface scattering of swimming eukaryotes. Proc Natl Acad Sci USA. 2013;110(4):1187–1192. doi: 10.1073/pnas.1210548110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Elgeti J, Winkler RG, Gompper G. Physics of microswimmers—Single particle motion and collective behavior: A review. Rep Prog Phys. 2015;78(5):056601. doi: 10.1088/0034-4885/78/5/056601. [DOI] [PubMed] [Google Scholar]
- 14.Brenker C, et al. The CatSper channel: A polymodal chemosensor in human sperm. EMBO J. 2012;31(7):1654–1665. doi: 10.1038/emboj.2012.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eisenbach M, Giojalas LC. Sperm guidance in mammals—An unpaved road to the egg. Nat Rev Mol Cell Biol. 2006;7(4):276–285. doi: 10.1038/nrm1893. [DOI] [PubMed] [Google Scholar]
- 16.Kaupp UB, Kashikar ND, Weyand I. Mechanisms of sperm chemotaxis. Annu Rev Physiol. 2008;70:93–117. doi: 10.1146/annurev.physiol.70.113006.100654. [DOI] [PubMed] [Google Scholar]
- 17.Alvarez L, Friedrich BM, Gompper G, Kaupp UB. The computational sperm cell. Trends Cell Biol. 2014;24(3):198–207. doi: 10.1016/j.tcb.2013.10.004. [DOI] [PubMed] [Google Scholar]
- 18.Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. Chlamydomonas swims with two “gears” in a eukaryotic version of run-and-tumble locomotion. Science. 2009;325(5939):487–490. doi: 10.1126/science.1172667. [DOI] [PubMed] [Google Scholar]
- 19.Goldstein RE. Green algae as model organisms for biological fluid dynamics. Annu Rev Fluid Mech. 2015;47:343–375. doi: 10.1146/annurev-fluid-010313-141426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Friedrich BM, Jülicher F. Flagellar synchronization independent of hydrodynamic interactions. Phys Rev Lett. 2012;109(13):138102. doi: 10.1103/PhysRevLett.109.138102. [DOI] [PubMed] [Google Scholar]
- 21.Goldstein RE, Polin M, Tuval I. Emergence of synchronized beating during the regrowth of eukaryotic flagella. Phys Rev Lett. 2011;107(14):148103. doi: 10.1103/PhysRevLett.107.148103. [DOI] [PubMed] [Google Scholar]
- 22.Brumley DR, Wan KY, Polin M, Goldstein RE. Flagellar synchronization through direct hydrodynamic interactions. eLife. 2014;3:e02750. doi: 10.7554/eLife.02750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Durham WM, Kessler JO, Roman S. Disruption of vertical motility by phytoplankton layers. Science. 2009;323:1067–1070. doi: 10.1126/science.1167334. [DOI] [PubMed] [Google Scholar]
- 24.Zöttl A, Stark H. Periodic and quasiperiodic motion of an elongated microswimmer in Poiseuille flow. Eur Phys J E Soft Matter. 2013;36(1):4. doi: 10.1140/epje/i2013-13004-5. [DOI] [PubMed] [Google Scholar]
- 25.Rusconi R, Guasto JS, Stocker R. Bacterial transport suppressed by fluid shear. Nat Phys. 2014;10:212–217. [Google Scholar]
- 26.Leptos KC, et al. Antiphase synchronization in a flagellar-dominance mutant of Chlamydomonas. Phys Rev Lett. 2013;111(15):158101. doi: 10.1103/PhysRevLett.111.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bennett RR, Golestanian R. A steering mechanism for phototaxis in Chlamydomonas. J R Soc Interface. 2015;12(104):20141164. doi: 10.1098/rsif.2014.1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Son K, Guasto JS, Stocker R. Bacteria can exploit a flagellar buckling instability to change direction. Nat Phys. 2013;9:1–5. [Google Scholar]
- 29.Kunz G, Beil D, Deininger H, Wildt L, Leyendecker G. The dynamics of rapid sperm transport through the female genital tract: Evidence from vaginal sonography of uterine peristalsis and hysterosalpingoscintigraphy. Hum Reprod. 1996;11(3):627–632. doi: 10.1093/humrep/11.3.627. [DOI] [PubMed] [Google Scholar]
- 30.Fauci LJ, Dillon R. Biofluidmechanics of reproduction. Annu Rev Fluid Mech. 2006;38:371–394. [Google Scholar]
- 31.Spehr M, et al. Identification of a testicular odorant receptor mediating human sperm chemotaxis. Science. 2003;299(5615):2054–2058. doi: 10.1126/science.1080376. [DOI] [PubMed] [Google Scholar]
- 32.Kantsler V, Dunkel J, Blayney M, Goldstein RE. Rheotaxis facilitates upstream navigation of mammalian sperm cells. eLife. 2014;3:02403. doi: 10.7554/eLife.02403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tung CK, et al. Emergence of upstream swimming via a hydrodynamic transition. Phys Rev Lett. 2015;114(10):108102. doi: 10.1103/PhysRevLett.114.108102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Denissenko P, Kantsler V, Smith DJ, Kirkman-Brown J. Human spermatozoa migration in microchannels reveals boundary-following navigation. Proc Natl Acad Sci USA. 2012;109(21):8007–8010. doi: 10.1073/pnas.1202934109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ishijima S, Hamaguchi MS, Naruse M, Ishijima SA, Hamaguchi Y. Rotational movement of a spermatozoon around its long axis. J Exp Biol. 1992;163:15–31. doi: 10.1242/jeb.163.1.15. [DOI] [PubMed] [Google Scholar]
- 36.Smith DJ, Gaffney EA, Gadêlha H, Kapur N, Kirkman-Brown JC. Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity. Cell Motil Cytoskeleton. 2009;66(4):220–236. doi: 10.1002/cm.20345. [DOI] [PubMed] [Google Scholar]
- 37.Hilfinger A, Jülicher F. The chirality of ciliary beats. Phys Biol. 2008;5(1):016003. doi: 10.1088/1478-3975/5/1/016003. [DOI] [PubMed] [Google Scholar]
- 38.Friedrich BM, Riedel-Kruse IH, Howard J, Jülicher F. High-precision tracking of sperm swimming fine structure provides strong test of resistive force theory. J Exp Biol. 2010;213(Pt 8):1226–1234. doi: 10.1242/jeb.039800. [DOI] [PubMed] [Google Scholar]
- 39.Fauci LJ, McDonald A. Sperm motility in the presence of boundaries. Bull Math Biol. 1995;57(5):679–699. doi: 10.1007/BF02461846. [DOI] [PubMed] [Google Scholar]
- 40.Smith DJ, Gaffney EA, Blake JR, Kirkman-Brown JC. Human sperm accumulation near surfaces: A numerical study. J Fluid Mech. 2009;621:289–320. [Google Scholar]
- 41.Evans AA, Lauga E. Propulsion by passive filaments and active flagella near boundaries. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(4 Pt 1):041915. doi: 10.1103/PhysRevE.82.041915. [DOI] [PubMed] [Google Scholar]
- 42.Elgeti J, Kaupp UB, Gompper G. Hydrodynamics of sperm cells near surfaces. Biophys J. 2010;99(4):1018–1026. doi: 10.1016/j.bpj.2010.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gaffney EA, Gadelha H, Smith DJ, Blake JR, Kirkman-Brown JC. Mammalian sperm motility: Observation and theory. Annu Rev Fluid Mech. 2011;43:501–528. [Google Scholar]
- 44.Montenegro-Johnson TD, Smith AA, Smith DJ, Loghin D, Blake JR. Modelling the fluid mechanics of cilia and flagella in reproduction and development. Eur Phys J E Soft Matter. 2012;35(10):111. doi: 10.1140/epje/i2012-12111-1. [DOI] [PubMed] [Google Scholar]
- 45.Lauga E, Eloy C. Shape of optimal active flagella. J Fluid Mech. 2013;730:R1. [Google Scholar]
- 46.Ishimoto K, Gaffney EA. Fluid flow and sperm guidance: A simulation study of hydrodynamic sperm rheotaxis. J R Soc Interface. 2015;12(106):20150172. doi: 10.1098/rsif.2015.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lauga E, Powers TR. The hydrodynamics of swimming microorganisms. Rep Prog Phys. 2009;72:096601. [Google Scholar]
- 48.Woolley DM. Motility of spermatozoa at surfaces. Reproduction. 2003;126(2):259–270. doi: 10.1530/rep.0.1260259. [DOI] [PubMed] [Google Scholar]
- 49.Lee S-H, Grier DG. Holographic microscopy of holographically trapped three-dimensional structures. Opt Express. 2007;15(4):1505–1512. doi: 10.1364/oe.15.001505. [DOI] [PubMed] [Google Scholar]
- 50.Wilson LG, Carter LM, Reece SE. High-speed holographic microscopy of malaria parasites reveals ambidextrous flagellar waveforms. Proc Natl Acad Sci USA. 2013;110(47):18769–18774. doi: 10.1073/pnas.1309934110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wilson L, Zhang R. 3D localization of weak scatterers in digital holographic microscopy using Rayleigh-Sommerfeld back-propagation. Opt Express. 2012;20(15):16735–16744. [Google Scholar]
- 52.Riedel-Kruse IH, Hilfinger A, Howard J, Jülicher F. How molecular motors shape the flagellar beat. HFSP J. 2007;1(3):192–208. doi: 10.2976/1.2773861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Phillips DM. Comparative analysis of mammalian sperm motility. J Cell Biol. 1972;53(2):561–573. doi: 10.1083/jcb.53.2.561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Linnet L. Human spermatozoa: Unidirectional rotation of the tail as indicated by head-to-head agglutinates. Arch Androl. 1979;2(2):157–161. doi: 10.3109/01485017908987307. [DOI] [PubMed] [Google Scholar]
- 55.Mundy AJ, Ryder TA, Edmonds DK. Asthenozoospermia and the human sperm mid-piece. Hum Reprod. 1995;10(1):116–119. doi: 10.1093/humrep/10.1.116. [DOI] [PubMed] [Google Scholar]
- 56.Lindemann CB, Goltz JS. Calcium regulation of flagellar curvature and swimming pattern in triton X-100−extracted rat sperm. Cell Motil Cytoskeleton. 1988;10(3):420–431. doi: 10.1002/cm.970100309. [DOI] [PubMed] [Google Scholar]
- 57.Chang H, Suarez SS. Two distinct Ca2+ signaling pathways modulate sperm flagellar beating patterns in mice. Biol Reprod. 2011;85(2):296–305. doi: 10.1095/biolreprod.110.089789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bedu-Addo K, et al. Mobilisation of stored calcium in the neck region of human sperm—A mechanism for regulation of flagellar activity. Int J Dev Biol. 2008;52(5-6):615–626. doi: 10.1387/ijdb.072535kb. [DOI] [PubMed] [Google Scholar]
- 59.Gadêlha H, Gaffney EA, Goriely A. The counterbend phenomenon in flagellar axonemes and cross-linked filament bundles. Proc Natl Acad Sci USA. 2013;110(30):12180–12185. doi: 10.1073/pnas.1302113110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Woolley DM, Vernon GG. A study of helical and planar waves on sea urchin sperm flagella, with a theory of how they are generated. J Exp Biol. 2001;204(Pt 7):1333–1345. doi: 10.1242/jeb.204.7.1333. [DOI] [PubMed] [Google Scholar]
- 61.Gadêlha H, Gaffney EA, Smith DJ, Kirkman-Brown JC. Nonlinear instability in flagellar dynamics: A novel modulation mechanism in sperm migration? J R Soc Interface. 2010;7(53):1689–1697. doi: 10.1098/rsif.2010.0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lauga E, DiLuzio WR, Whitesides GM, Stone HA. Swimming in circles: Motion of bacteria near solid boundaries. Biophys J. 2006;90(2):400–412. doi: 10.1529/biophysj.105.069401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rodríguez JA, et al. Propulsion of African trypanosomes is driven by bihelical waves with alternating chirality separated by kinks. Proc Natl Acad Sci USA. 2009;106(46):19322–19327. doi: 10.1073/pnas.0907001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Herráez-Domínguez JV, Gil Garcia de León F, Diez-Sales O, Herraez-Dominguez M Rheological characterization of two viscosity grades of methylcellulose: An approach to the modeling of the thixotropic behaviour. Colloid Polym Sci. 2005;284(1):86–91. [Google Scholar]
- 65.Aziz N, Fear S, Taylor C, Kingsland CR, Lewis-Jones DI. Human sperm head morphometric distribution and its influence on human fertility. Fertil Steril. 1998;70(5):883–891. doi: 10.1016/s0015-0282(98)00317-3. [DOI] [PubMed] [Google Scholar]
- 66.Grubbs FE. Procedures for detecting outlying observations in samples. Technometrics. 1969;11(1):1–21. [Google Scholar]
- 67.Carlson AE, et al. CatSper1 required for evoked Ca2+ entry and control of flagellar function in sperm. Proc Natl Acad Sci USA. 2003;100(25):14864–14868. doi: 10.1073/pnas.2536658100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Werner S, Rink JC, Riedel-Kruse IH, Friedrich BM. Shape mode analysis exposes movement patterns in biology: Flagella and flatworms as case studies. PLoS One. 2014;9(11):e113083. doi: 10.1371/journal.pone.0113083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bergou M, Wardetzky M, Robinson S, Audoly B, Grinspun E. Discrete elastic rods. ACM Trans Graph. 2008;27(3):63. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.