Equilibrium Fluctuation Relations for Voltage Coupling in Membrane Proteins

Abstract

A general theoretical framework is developed to account for the effects of an external potential on the energetics of membrane proteins. The framework is based on the free energy relation between two (forward/backward) probability densities, which was recently generalized to non-equilibrium processes, culminating in the work-fluctuation theorem. Starting from the probability densities of the conformational states along the reaction coordinate of “voltage coupling”, we investigate several interconnected free energy relations between these two conformational states, considering voltage activation of ion channels. The free energy difference at zero membrane potential (i.e., between the two “non-equilibrium” conformational states) is shown to be equivalent to the free energy difference between the two “equilibrium” conformational states along the one-dimensional reaction coordinate of voltage coupling. Furthermore, the requirement that the application of linear response approximation to the free energy functions (free energies) of voltage coupling should satisfy the general free energy relations, yields a novel expression for the gating charge in terms of other experimentally measurable quantities. This connection is familiar in statistical mechanics, known as the equilibrium fluctuation-response relation. The theory is illustrated by considering the movement of a unit charge within the membrane under the influence of an external potential, using a coarse-graining (CG) model of membrane proteins, which includes the membrane, the electrolytes and the electrodes. The CG model yields Marcus–type voltage dependent free energy parabolas for the two conformational states, which allow for quantitative estimations of an equilibrium free energy difference, a free energy of barrier, and the voltage dependency of channel activation (Q-V curve) for the unit charge movement. In addition, our analysis offers a quantitative rationale for the correlation between the free energy landscapes (parabolas) and the Q-V curve, upon site-directed mutagenesis or drug binding. Taken together, by introducing the voltage coupling as a reaction coordinate of energy gab, the present theory offers a firm physical foundation from the equilibrium theory of statistical mechanics for the thermodynamic models of voltage activation in voltage-sensitive membrane proteins. This formulation also provides a powerful bridge between the CG model and the conventional macroscopic treatments, offering an intuitive and quantitative framework for a better understating of the structure-function correlations of voltage gating in ion channels as well as electrogenic phenomena in ion pumps and transporters.

1. Introduction

The advances in structural elucidation of voltage activated ion channels as well as in biophysical studies (e.g. Refs. [1–7]) have provided major clues about the relationship between the membrane voltage and the gating process. However, despite these great progress we still do not have a clear understanding of the corresponding structure-function correlation. Apparently, although there have been a significant progress in the computational/theoretical modeling of the energetics of ion channels (e.g. Refs. [8–22]) and the control of ion selectivity (e.g. Refs. [23–30]), the quantitative understanding of the voltage activation process is still somewhat limited. In addition to the obvious need for more structural information, the ability to obtain a microscopic description of the energetics of the conformational transition and the coupling to the external voltage is far from satisfactory. Similar problems occur with regards to the molecular understanding of the nature of the gating charge, where despite the enormous insight provided by macroscopic approaches [13, 14, 31], it is hard to be fully comfortable with the corresponding physical picture, which does not include the electrolytes and the electrodes explicitly (see discussion in Refs. [20, 32]).

A promising way for advancing our understanding of ion channels and related systems has been offered by the recent development of our coarse-grained (CG) model of voltage coupling [20, 21, 32, 33], which considers the entire membrane–protein, electrolytes and electrodes explicitly. The power and insight of this model have been illustrated in several works, but it seems that these advances have not been widely recognized, due in part to the use of descriptions that are very different than the familiar macroscopic formulation and the fact that the model does not use the straightforward fully microscopic treatment (that unfortunately does not offers yet converging free energy results [17, 34] nor a clear description of the nature of gating charge [35]). Thus we try to explore in the present work the relationship between our CG model of voltage coupling and the corresponding macroscopic continuum results.

Furthermore, more importantly, we introduce the general theoretical description of voltage coupling in membrane proteins, extending and generalizing the previous thermodynamic models of voltage activation in ion channels [1,19, 36–41]. This is done in the framework of equilibrium fluctuation relations, where linear response approximation to the free energy function of voltage coupling is introduced, resulting in the Marcus-Warshel (MW) type parabola, with the energy gap of voltage coupling as a reaction coordinate. A novel closed expression for the gating charge is then derived in the framework of the equilibrium fluctuation relations and linear response approximation and explored by using the CG model of voltage coupling. The corresponding results are validated against the macroscopic continuum results and applied to determining voltage dependent MW parabola for the movement of a unit charge within the membrane. We then use the MW type free energy parabolas in the framework of equilibrium fluctuation relations to formulate the quantitative relationship between the free energy landscapes and the Q-V curves, thus providing a new insight on the molecular information content of these curves.

2. Theory and methods

2.1. Free energy relations

We will start by defining formal free energy relationships that will result in free energy functions of the energy gap reaction coordinate, introduced by Warshel [36] and used extensively in studies of reactions in condensed phase (e.g. [37–41]). This will be done while exploring several variants of free energy relations in the general framework of equilibrium fluctuation relation.

The equilibrium probability densities for the initial (0) and the final (1) states (p_λ(u){λ = 0,1}) are related to each other [42], given by:

$$\frac{p_0(u)}{p_1(u)}=exp(u-\mathrm{\Delta }{G}_{\mathit{conf}}),$$ (1)

where k_BT=1 and ΔG_conf is the free energy difference between, for example, two conformational states in the present study. This relationship is referred to “the equilibrium fluctuation relation”, in an analogy with its generalization to non-equilibrium processes, known as the work-fluctuation theorem [43, 44]).

The equilibrium fluctuation relation is easily derived (see SI for a detailed derivation) by considering the system as being perturbed from its initial to final states by ΔU, with the Hamiltonian of the form H₁ = H₀ +ΔU:

$$\begin{array}{l}{p}_0(u)\equiv <\delta (u-\mathrm{\Delta }U(x)){>}_0\\ =\frac{\int \mathit{dx}exp(-H_0(x))\delta (u-\mathrm{\Delta }U(x))}{Z_0}\\ =\frac{Z_1}{Z_0}exp(u)\frac{\int \mathit{dx}exp(-H_1(x))\delta (u-\mathrm{\Delta }U(x))}{Z_1}\\ =exp(u-\mathrm{\Delta }{G}_{\mathit{conf}})p_1(u)\end{array}$$ (2)

where p_λ(u){λ = 0,1} are the probability densities of finding a particular value of u along a reaction coordinate ΔU(x), where x is a point in the 6N – dimensional phase space. In fact, this relation has been known to the community for some time ago as the theory of Bennett overlapping histogram (BOH) [41, 45], which is also here referred to the free energy relation of the first kind. In the following, the free energy difference between the two conformational states (ΔG_conf,) is defined by two different ways, eventually leading to an equivalent relation.

Notice that ΔG_conf, is identified as the value (u*) of reaction coordinate ΔU where the two probability densities intersect [41, 46]:

$$\frac{p_0(u\ast )}{p_1(u\ast )}=1=exp(u\ast -\mathrm{\Delta }{G}_{\mathit{conf}}),$$

leading to

$$\mathrm{\Delta }{G}_{\mathit{conf}}=u\ast =\mathrm{\Delta }U(x\ast )\equiv \mathrm{\Delta }U\ast$$ (3)

Rearranging Eq. (1) yields the free energy relation of the second kind:

$$\mathrm{\Delta }{f}_1(u)-\mathrm{\Delta }{f}_0(u)=u+ln\frac{p_{1,max}}{p_{0,max}}$$ (4)

or

$$\mathrm{\Delta }{g}_1(u)-\mathrm{\Delta }{g}_0(u)=u-\mathrm{\Delta }{G}_{\mathit{conf}}+ln\frac{p_{1,max}}{p_{0,max}},$$ (5)

where Δg_λ(u) and Δf_λ(u){λ = 0,1} are free energy functions or potentials of mean force (PMF) along the reaction coordinate of energy gap [36, 37, 41], which are related to each other by:

$$\mathrm{\Delta }{f}_1(u)\equiv \mathrm{\Delta }{g}_1(u)+\mathrm{\Delta }{G}_{\mathit{conf}}\equiv -ln\frac{p_1(u)}{p_{1,max}}+\mathrm{\Delta }{G}_{\mathit{conf}}$$ (6)

$$\mathrm{\Delta }{f}_0(u)\equiv \mathrm{\Delta }{g}_0(u)=-ln\frac{p_0(u)}{p_{0,max}}$$ (7)

Here, $p_{\lambda }^{max}\{\lambda =0,1\}$ are defined as the maximum values of the probability densities, such that Δg_λ{λ = 0,1} have their respective global minimum set to zero [41], i.e., Δg_λ(u_λ,min) = −ln[p_λ(u_λ,min)/p_λ,max] = 0, which results in the free energy relation of third kind:

$$\mathrm{\Delta }{f}_1(u_{1,min})-\mathrm{\Delta }{f}_0(u_{0,min})=\mathrm{\Delta }{G}_{\mathit{conf}}$$ (8)

This expression states that the free energy difference between the two equilibrium conformational states along a one-dimensional reaction coordinate of energy gap, (Δf₁(u_1,min)−Δf₀(u_0,min), defined from the second free energy relation, is equal to the free energy difference, ΔG_conf(= ΔU*)), determined using the equilibrium fluctuation relation or the first free energy relation. In other words, the free energy difference, ΔG_conf (= ΔU*), defined in two different ways from Eqs. (3) and (4) or (5), leads to an equivalent relation of Eq. (8), which is thus termed as the conformational free energy along the one-dimensional reaction coordinate of energy gap. A closely related derivation to Eq. (8) along “positional” reaction coordinates is found in Ref. [41] and applied to the thermodynamics of ion binding in a K⁺ channel [28], supporting the earlier proposal of the multi-ion mechanism of ion selectivity in K⁺ channels [27].

The additive constant on the right hand side in Eq. (4) or (5) vanishes in the case where Δg_λ{λ = 0,1} are functions with equal maximum values (curvatures) of the probability densities at their respective minimum (i.e., $p_1^{max}=p_0^{max}$). In the present study, the constant will be dropped out without a loss of generality [38, 41] and the approximation introduced here will be discussed in conjunction with the linear response expression for free energy functions (see Section 2.3). The second free energy relation of Eq. (4) was first recognized by Warshel and others [37–39] in formulating microscopic treatment of electron transfer in condensed phases and relating it to the framework of the macroscopic Marcus theory [47, 48]

Note that the free energy functions (Δf_λ(u){λ = 0,1}), whose final state (λ=1) is shifted by the free energy (ΔG_conf) from the reference free energy function (Δg₁(u)), intersect at u=0 along the energy gap coordinate [37–39], leading to:

$$\mathrm{\Delta }{f}_1(0)=\mathrm{\Delta }{f}_0(0)$$ (9)

or

$$\mathrm{\Delta }{g}_1(0)-\mathrm{\Delta }{g}_0(0)=-\mathrm{\Delta }{G}_{\mathit{conf}}$$ (10)

The free energy relations examined so far is illustrated in Fig. 1 with ΔU= Q_g.V, where Q_g and V are, respectively, the gating charge and the externally applied potential. This will be further investigated in the following section, with the energy gap of “voltage coupling” in ion channels to derive the fundamental free energy relations (see e.g. Ref.[1]) used to describe the voltage dependency of channel activation in ion channels.

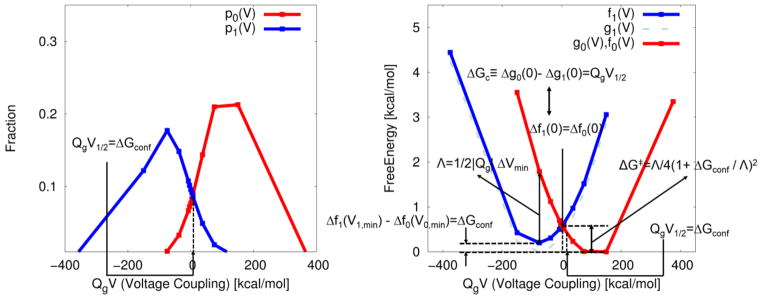
Figure 1.

Illustration of fundamental free energy relations found in the present study with the CG model system of Fig. 2. The calculations were done by moving the positive charge in a straight line between the left and right points (say from the activated to the resting) thus changing both f₀ and f₁. (A) The probability densities (p_λ(V){λ = 0,1) of finding the conformational states λ at an external potential of V (≡V_ext is assumed to be equal to the membrane potential of V_m), for the movement of a unit charge displaced by the external potential, where the subscripts 0 and 1 represent initial (activated) and final (resting) states. These probability densities are obtained from the voltage dependent CG free energy functions (parabolas) Δf_λ(V){λ = 0,1} with p_λ(V) ∝ exp(−Δf_λ(V)) (see Fig. 4A). ΔG_conf, is identified as the value (Q_gV*) of the reaction coordinate of voltage coupling (Q_gV) where two probability densities intersect (i.e., have equal probability), leading to Q_gV_1/2=ΔG_conf.. A reference free energy function (g₁(V)), whose minimum is zero, is shifted by the conformational free energy of Q_gV_1/2=ΔG_conf,, resulting in f₁(V). (B) The corresponding Marcus free energy parabolas along the reaction coordinate of voltage coupling. The parabolas are reconstructed from (A) using the Eqs. (6) and (7) with u=Q_gV. Λ represents reorganization energy, given by the form of Λ=−1/2Q_gΔV_min in voltage gated ion channel, leading to the free energy of barrier, given by the form of ΔG^╪ = Λ/4(1+ ΔG_conf/Λ)² (see Eq. (40) for details). The chemical component of free energy (g₀(0)−g₁(0)), the free energy difference between two non-equilibrium conformational states (i.e., at zero membrane potential), is shown to be equal to the free energy difference between two “equilibrium” conformational states along the reaction coordinate of voltage coupling (f₁(V_1.min)−f₀(V_0,min)), via the conformational free energy (Q_gV_1/2=ΔG_conf), determined using the equilibrium fluctuation relation of Eq. (15). Free energy function f₁(V) is shifted by the reference free energy from g₁(V) (, whose global minimum set to zero) (dashed line), resulting in the intersection with f₀(V) at V=0, i.e., f₀(0)=f₁(0), leading to g₀(0)−g₁(0)= Q_gV_1/2. Free energy functions (for 0 and 1 states) are related to each other by the second free energy relation f₀(V)−f₁(V)=−Q_gV or g₀(V)−g₁(V)= Q_gV_1/2 − Q_gV, which is equivalent to the equilibrium fluctuation relation for voltage activation (i.e., the equilibrium fluctuation relation or the first free energy relation of p₀(V)/p₁(V)= exp(Q_gV−Q_gV_1/2).

2.2 Free energy relations for voltage activation in ion channels

The general free energy relations investigated in the previous section can be applied to account for the kinetics/thermodynamics of voltage activation of ion channels by using the voltage dependent free energy functions. As a background for such considerations, we start by noting that the effect of an external potential on the activation of the voltage sensor domain (VSD) in ion channels is described by the voltage coupling to the gating charge Q_g. This coupling reflects the response of the system to the application of an external potential but before the ions are allowed to pass through the channel [1]. The gating charge, Q_g, is defined by determining the fraction of activated (up) and resting (down) channels as a function of the applied potential and asking what is the Boltzmann probability for the voltage induced structural change [1]. This assumption leads to the expression [1]:

$$Q_g\mathrm{\Delta }{V}_{\mathit{ext}}=\mathrm{\Delta }{G}^{\mathit{down}\to up},$$ (11)

where ΔG^down→up is the phenomenological free energy associated with conformational change between two “equilibrium” states (i.e., the conformational free energy of Eq. 8), which can be measured experimentally in Q-V measurements [1]. Basically this is equivalent to the assumption that the free energy needed to move the gating charge, Q_g, in the membrane electric field is equal to the work of moving the protein charges between the two conformations (activated and resting), under the membrane electric field. Now, Eq. (11) is basically a reasonable formal definition of the gating charge that does not tell us what is the relationship of this parameter to physical measured observables such as the integral of the current that flows to the electrodes, Q_ext, although many accept the identity of Q_ext with Q_g. The structure-based evaluation of Q_g is almost always done using reasonable but not necessarily microscopic assumptions. It is also not certain that in all cases that the actual electrode potential V_ext is equal to the membrane potential, V_m. These issues will be addressed below but at this point we just note that one of the problem is that the assumption that leads to Eq. (11) implies that the potential is linear across the membrane. This is likely to be a reasonable approximation and it has been used in previous macroscopic studies [13, 49]. Obviously, such a picture would be justified if the potential across the protein/membrane system was obtained by converging microscopic simulations. However, in such cases, it is unlikely that we will have the same potential in different sites with the same z value that is normal to the membrane surface. Thus such a treatment does not really provide a microscopic description even if a few of the relevant quantities (e.g. the average displacements) are evaluated microscopically [17]. Other related problems are discusses in our previous work [32].

In view of the above discussion we can write

$$\begin{array}{l}{\mathrm{Q}}_{\text{ext}}={\mathrm{c}}_1{Q}_{g.m}\\ {\mathrm{V}}_{\text{ext}}={\mathrm{c}}_2{\mathrm{V}}_{\mathrm{m}},\end{array}$$ (12)

where Q_g,m is the charge movement within the membrane and V_m is the change in the potential across the membrane. However, for simplicity we will assume below that c2 and c1 are approximately equal to one, while exploring this assumption by examining the correspondence between the energetics and charge movement, considering both only the membrane-protein system and the entire electrolyte/membrane-protein system. We start by considering only the membrane-protein system, whose Hamiltonian is given by [19]:

$$H_{1,m}=H_{0,m}+\mathrm{\Delta }U\equiv H_{0,m}+Q_{g,m}{V}_m,$$ (13)

where the subscripts 0 and 1 represent initial (activated) and final (resting) states, respectively, of, for example, VSD. The gating charge (Q_g,m) arises from the displacement of charged residues within membrane associated with conformational changes of VSD by V_m.

By taking an energy gap reaction coordinate of (ΔU= Q_g.m V_m) (referred to as the “voltage coupling “), we obtain from Eq. (3):

$$\mathrm{\Delta }{G}_{\mathit{conf}}=Q_{g,m}{V}_m\ast =Q_{g,m}{V}_{m,1/2},$$ (14)

where V_m,1/2 is a half voltage at which two conformational states have equal population. This relation along with Eqs. (19) and (20) is basically the same as the phenomenological free energy of conformational change of Eq. (11).

The equilibrium fluctuation relation or the first free energy relation of Eq. (1) for voltage activation is therefore expressed as:

$$\frac{p_0(V)}{p_1(V)}=exp(Q_{g,m}{V}_m-Q_{g,m}{V}_{m,1/2})$$ (15)

In fact, this fundamental relation has been known to the ion channel community to describe the kinetics/thermodynamics of voltage activation, e.g., as empirically derived in Hille’s book [1], which goes back to Hodgkin and Huxley for their formulation to quantify membrane currents and thus action potentials (spikes) in a nerve cell [50].

Using Eqs. (14) and (15), the second free energy relation of Eq. (4) or (5) leads to:

$$\mathrm{\Delta }{f}_0(V_m)-\mathrm{\Delta }{f}_1(V_m)=-Q_{g,m}{V}_m$$ (16)

or

$$\mathrm{\Delta }{g}_0(V_m)-\mathrm{\Delta }{g}_1(V_m)=Q_{m,g}{V}_{m,1/2}-Q_{m,g}{V}_{m,}$$ (17)

In addition, the free energy functions (Δf_λ(V){λ = 0,1}) of Eq. (16) intersect at V=0 along the reaction coordinate of voltage coupling, leading to the expression:

$$\mathrm{\Delta }{f}_0(0)=\mathrm{\Delta }{f}_1(0)$$ (18)

or from Eq. (17)

$$\mathrm{\Delta }{g}_0(0)-\mathrm{\Delta }{g}_1(0)=Q_{g,m}{V}_{m,1/2}$$ (19)

The expression (Eq. (16) or Eqs. (17)) are the fundamental free energy relation (equivalent to Eq. (15)), used to describe the voltage dependency of channel activation (Q-V curve) in voltage gated ion channels [19, 51]. The free energy difference between the two conformational states at zero membrane potential, (Δg₀(0)−Δg₁(0)), (i.e., between the two non-equilibrium states) is commonly known as the “chemical” component of the total free energy in ion channels under the external potential [19], which is represented by ΔG_c below. Combining Eq. (19) and Eq. (14) yields

$$\mathrm{\Delta }{G}_c(\equiv \mathrm{\Delta }{g}_0(0)-\mathrm{\Delta }{g}_1(0))=Q_{g,m}{V}_{m,1/2}=\mathrm{\Delta }{G}_{\mathit{conf}}$$ (20)

Thus we showed here the chemical component of the voltage dependent total free energy, ΔG_c(≡ Δg₀(0)−Δg₁(0)), is equal to the conformational free energy of ΔG_conf along a one-dimensional reaction coordinate of voltage coupling.

Finally, Eq. (20) combined with the third free energy relation of Eq. (8) implies that

$$\mathrm{\Delta }{G}_c=(\mathrm{\Delta }{G}_{\mathit{conf}}=Q_g{V}_{1/2})=\mathrm{\Delta }{f}_1(V_{1,min})-\mathrm{\Delta }{f}_0(V_{0,min}),$$ (21)

which is an explicit expression of the free energy difference between the two conformational states at zero membrane potential, ΔG_c ≡ Δg₀(0)−Δg₁(0), (i.e., between the two non-equilibrium states) in terms of the free energy difference between the two “equilibrium” conformational states (Δf₁(V_1,min)−Δf₀(V_0,min)) along the one-dimensional reaction coordinate of voltage coupling, via the conformational free energy of ΔG_conf, determined using the equilibrium fluctuation relation or the first free energy relation.

The free energy relations, investigated so far, are illustrated in Fig. 1, using the actual simulation data for the model system in section 3.

2.3 Linear response approximation satisfies the free energy relations (or the equilibrium fluctuation relation)

If we consider the effect of the overall electrode potential, i.e., an externally applied voltage, V_ext, on the energetics of the entire electrolyte/membrane-protein system, instead of just the membrane potential on the energetics of the membrane-protein system, the Hamiltonian in Eq. 12 may be rewritten formally as:

$$H_1=H_0-Q_{\mathit{ext}}{V}_{\mathit{ext}}$$ (22)

where Q_ext is the charge that flows through the electrodes and assumed to be equal to gating charge (see Eq. 12 and Fig. 2), which will be reviewed shortly below.

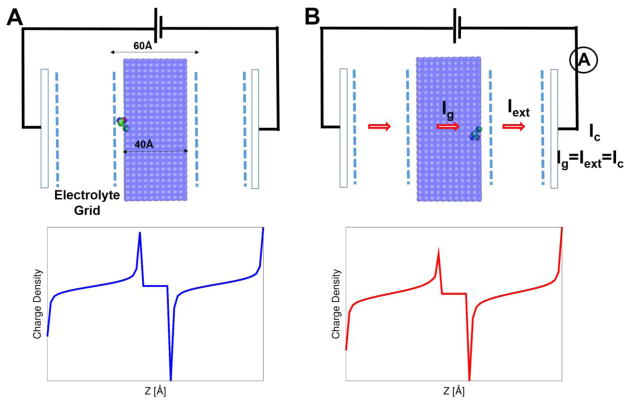
Figure 2.

Description of the model system (i.e., a unit charge embedded in the membrane between electrolytes that incorporates electrodes), used to illustrate the theoretical framework and the CG model of voltage coupling. The electrode potential (as in the Gouy-Chapman model), provided by a virtual battery, is determined by Eqs. (47), (48) and (49) with the appropriate boundary condition (i.e., the denominator in Eq. 47). I_g (defined as the gating current in the macroscopic continuum approach, of which time integration yields Q_g (see Eqs. (13), (23), and (27)) is shown to be equal to the current that flows through the electrode (defined as I_ext, of which time integration yields Q_ext; see Eqs. (22), (26), and (36)). The actual gating current measured in experiment corresponds to I_c in the external circuit. The area (A) and width (L) of membrane is 80×80Ų and 40Å width, respectively, and an electrolyte concentration of 250mM was used. (Top) The unit positive charge is initially positioned near the membrane surface on the left (i.e., state 0). An application of a positive external potential drives the unit charge to the right side (i.e., state 1) of the membrane. (Bottom) Net electrolyte charge distributions [e/ų] before (left) and after (right) the unit charge movement at 100mV; the integration of charge distribution along the axis normal to the membrane surface (multiplied by membrane area) yields state dependent gating charge shown in Fig. 3.

The state-dependent free energy of the voltage activation can be expressed by modifying the treatment of [52–54] and writing:

$$\mathrm{\Delta }{f}_{\lambda }(V_{\mathit{ext}})=\mathrm{\Delta }{f}_{\lambda }(0)-\left[\sum _j{q}_j{\varphi }_{mp,\lambda }(x_j)\right]V_{\mathit{ext}}+\frac{1}{2}{C}_{\lambda }^{\prime }{V}_{\mathit{ext}}^2$$ (23)

where Δf_λ(0) is related to the chemical component of free energy of Eq. (18) or (19).

Here the second term is the continuum expression for Q_λ,g,mV_ext (assuming that V_ext =V_m) and the last term is the interaction of the external potential with electrolytes, where C_λ′ is the capacitance of the electrolyte/membrane-protein system.

The function ϕ_λ,mp(x_j), which represents a fraction of membrane potential that falls on the j the charged amino acid [52, 53, 55], can be obtained by solving a modified Poisson-Boltzmann equation (PB-V) [54]. For a linearized membrane potential, it leads to the simple expression

$$\mathrm{\Delta }{\varphi }_{mp}(x_j)=\frac{{\epsilon }_L{z}_j}{{\epsilon }_{j}L},$$ (24)

which is often termed as the dielectric distance (see [33] and references therein). The expression is a generalization of a simple geometric distance (z_j/L) along the axis normal to the membrane surface, where ε_L and ε_j are, respectively, the dielectric constant of the membrane and the (frequently ill defined ) local dielectric constant in the region of the _jth charged amino acid. Here L is the width of membrane and z_j is a coordinate normal to the membrane.

Using Eqs. 23 and 24, in the case of linear change of the potential across the membrane, the state dependent gating charge becomes

$$Q_{g,\lambda }=\sum _l{(z_l{q}_l^p{\epsilon }_L/{\epsilon }_l)}_{\lambda }/L,$$ (25)

Finally, using the Hamiltonian of Eq. 22 and differentiating Δf_λ(V) with respect to the external potential gives (see the SI):

$$\begin{array}{l}{\frac{\partial \mathrm{\Delta }{f}_{\lambda }}{\partial V_{\mathit{ext}}}|}_{V_{\mathit{ext}}=0}={-\frac{\partial }{\partial V_{\mathit{ext}}}ln{Z}_{\lambda }|}_{V_{\mathit{ext}}=0}\\ =-<Q_{\mathit{ext}}{>}_{\lambda ,V_{\mathit{ext}}=0}\end{array}$$ (26)

We also have from Eq. 23

$${\frac{\partial \mathrm{\Delta }{f}_{\lambda }}{\partial V_{\mathit{ext}}}|}_{V_{\mathit{ext}}=0}={\left[\left(-\sum _j{q}_j{\varphi }_{\lambda ,mp}(x_j)\right)+C^{\prime }{V}_{\mathit{ext}}\right]|}_{V_{\mathit{ext}}=0}=-Q_{\lambda ,g,m}$$ (27)

This proves that Q_λ,g,m=<Q_ext>_λ,Vext=0 but it should be noticed that the equality reflects the assumption that Q_g,m is equal to Q_ext, each of which corresponds to charge coupling to the membrane potential and the external potential in their respective Hamiltonians (see Eqs. (13) and (22)).

In fact, the quadratic free energy expression in Eq. (23), which is familiar in the Marcus theory of electron transfer [37], is thought of as a realization of linear response approximation (LRA) [56–58] that is likely to be satisfied by many dimensional systems in their response to charging processes (e.g. by the responses to an external potential in the present study). Here, the LRA expression for the free energy functions (Δf_λ(V){λ=0,1}) is shown to satisfy the second free energy relation (Eq. 16), or equivalently, the equilibrium fluctuation relation (Eq. 15), leading to a novel expression for gating charge in terms of other experimentally measurable quantities.

The Hamiltonian used in the present study may also be expresses as follows:

$$H_{\mathit{1}}=H_{\mathit{0}}-Q_{\mathit{ext}}(V-V_{\mathit{0},\mathit{min}}),$$ (28)

where the subscript of V (“ext”) was dropped. The free energy functions of voltage activation (Δf_λ(V){λ=0,1}) can be expanded around their respective minima up-to a second order (i.e., using the equilibrium fluctuation-response relation) and expressed as (see SI for a detailed derivation):

$$\begin{array}{l}\mathrm{\Delta }{f}_0(V)=\mathrm{\Delta }{f}_0(V_{0,min})-\frac{1}{2}{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{(V-V_{0,min})}^2\\ =\mathrm{\Delta }{f}_0(V_{0,min})-\frac{1}{2}{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{V}_{0,min}^2+{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{V}_{0,min}V-\frac{1}{2}{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{V}^2,\\ =\mathrm{\Delta }{f}_0(0)+{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{V}_{0,min}V-\frac{1}{2}{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{0,min}}{V}^2\end{array}$$ (29)

where δQ_ext = Q_ext −〈Q_ext〉 Similarly, for the up state (state (1)) we have,

$$\mathrm{\Delta }{f}_1(V)=\mathrm{\Delta }{f}_1(0)+{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{1,min}}{V}_{1,min}V-\frac{1}{2}{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V_{1,min}}{V}^2,$$ (30)

Notice that these two expressions could be obtained by a direct application of linear response approximation, i.e., differentiation of the free energy function with respect to the external potential gives:

$${\frac{\partial \mathrm{\Delta }{f}_0}{\partial V}|}_V=-<Q_{\mathit{ext}}{>}_V=-<Q_{\mathit{ext}}{>}_{V_{0,min}}-<\delta Q_{\mathit{ext}}{>}_V=-<\delta Q_{\mathit{ext}}{>}_V$$ (31)

An explicit application of linear response approximation [58] yields:

$$\begin{array}{l}{\frac{\partial \mathrm{\Delta }{f}_0}{\partial V}|}_V=-<\delta Q_{\mathit{ext}}{>}_V\\ \simeq -<\delta Q_{\mathit{ext}}^2{>}_{V_{0,min}}(V-V_{0,min})\end{array}$$ (32)

Integration gives the same result as Eq. (29).

Subtracting Eq. (30) from Eq. (29) yields

$$\begin{array}{l}\mathrm{\Delta }{f}_0(V)-\mathrm{\Delta }{f}_1(V)=f_0(0)-f_1(0)+\left[{\langle \delta Q_{ex}^2\rangle }_{V=V_{0,min}}{V}_{0,min}-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}{V}_{1,min}\right]V\\ -\frac{1}{2}\left[{\langle \delta Q_{ex}^2\rangle }_{V=V_{0,min}}-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}\right]V^2\\ =\left[{\langle \delta Q_{ex}^2\rangle }_{V=V_{0,min}}{V}_{0,min}-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}{V}_{1,min}\right]V-\frac{1}{2}\left[{\langle \delta Q_{ex}^2\rangle }_{V=V_{0,min}}-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}\right]V^2\\ =C^{\prime }\mathrm{\Delta }{V}_{min}V,\end{array}$$ (33)

where $C^{\prime }\equiv -{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}=-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{0,min}}$ is the capacitance of the channel-membrane system and ΔV_min = V_1,min −V_0,min. The equality in the first line comes directly from Eq. (18) that the free energy functions intersect at V=0. The approximation of equal curvature for the quadratic free energy functions was used in the second line, leading to $C^{\prime }\equiv -{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{1,min}}=-{\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{0,min}}$ In fact, this approximation is the same level of approximation ( $p_1^{max}=p_0^{max}$) used to drop a constant for the second free energy relation of Eq. (16), when it moves from Eq. (5).

A comparison of Eq. (33) with Eq. (16) (i.e., the requirement that the LRA expression for free energy functions satisfy the second free energy relation) yields a novel expression for gating charge of the form:

$$Q_g=-C^{\prime }\mathrm{\Delta }{V}_{min},$$ (34)

This gating charge expression is the key relation of our paper, where a measure of voltage sensitivity (gating charge) is expressed in terms of the basic properties of channels, as probably conceived by Hodgkins and Huxley [50]. This relation may offer a simple rationale for the differences in gating charges among members of the voltage gated ion channels [59]. In addition, the LRA expressions of Eqs. (29) and (30) should satisfy the equilibrium fluctuation relation of Eq. (15) with the probability densities of finding the λ state at V, i.e., $p_{\lambda }(V)=\raisebox{1ex}{$exp(-f_{\lambda }(V))$}\!\left/ \!\raisebox{-1ex}{$Z_{\lambda }$}\right.$:

$$\begin{array}{l}\frac{p_0(V)}{p_1(V)}=\frac{Z_1}{Z_0}exp(\mathrm{\Delta }{f}_1(V)-\mathrm{\Delta }{f}_0(V))\\ \simeq \frac{Z_1}{Z_0}exp(-C^{\prime }\mathrm{\Delta }{V}_{min}V)\\ =exp(-C^{\prime }\mathrm{\Delta }{V}_{min}V-\mathrm{\Delta }{G}_{\mathit{conf}})\end{array}$$ (35)

The approximation in the second line comes directly from Eq. (33). A comparison with the equilibrium fluctuation relation of Eq. (15) yields the same gating charge expression as Eq. (34).

Last, the state dependent gating charge (Q_g,λ) can be defined from Eqs. (33) and (34) as:

$$Q_{g,\lambda }={\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{\lambda ,min}}{V}_{\lambda ,min},$$ (36)

The above expression may be rewritten as

$${\frac{\partial Q_{g,\lambda }}{\partial V}|}_{V=V_{\lambda ,min}}={\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{\lambda ,min}},$$ (37)

This relation is nothing but the fluctuation-response relation in voltage gated ion channels, where the response of the gating charge to the external potential (Q_λ,g = 〈Q_ext〉_λ as in the equivalence of Eq. (26) with Eq. (27)) is related to its fluctuation, by noticing the equivalent relation:

$${\frac{\partial <Q_{\mathit{ext}}{>}_{\lambda }}{\partial V}|}_{V=V_{\lambda ,min}}={\langle \delta Q_{\mathit{ext}}^2\rangle }_{V=V_{\lambda ,min}},$$ (38)

as implicated in Eq. (29) or (30) (see SI for a detailed derivation).

Considering the observation that we have quadratic Marcus-type free energies of equal curvature (which is reflected in the capacitance), we find out that the reorganization energy (Λ) for voltage coupling in membrane proteins is given by [60]:

$$\mathrm{\Lambda }=\frac{1}{2}{C}^{\prime }{(\mathrm{\Delta }{V}_{min})}^2=-\frac{1}{2}{Q}_g\mathrm{\Delta }{V}_{min},$$ (39)

which yields the free energy of (deactivation) barrier (from λ=0 to λ=1), given by:

$$\mathrm{\Delta }{\mathrm{G}}^{\ne }=\frac{\mathrm{\Lambda }}{4}{\left(1+\frac{\mathrm{\Delta }{\mathrm{G}}_{\mathit{conf}}}{\mathrm{\Lambda }}\right)}^2=-\frac{1}{8}{Q}_g\mathrm{\Delta }{V}_{\mathit{min}}{\left(1-\frac{2V_{1/2}}{\mathrm{\Delta }{V}_{\mathit{min}}}\right)}^2$$ (40)

Notice that the gating charge has a negative sign as we have consider the conformational transition from the activated (λ=0) to resting (λ=1) states.

2.4 Key Features of the Coarse-Graining (CG) Model

The energetics of our CG model is different than most other models as it focuses on reliable treatment of the electrostatic energy (ΔG_elec), considering the self-energy of ionizable residues and the charge–charge interaction with a realistic dielectric as well as the electrostatic energetics of protein-membrane system [20, 32]. The model also considers the hydrophobic contribution (ΔG_hydro) to the CG model that has been constantly refined over past years. Most importantly, the influence of an applied voltage was recently incorporated into the CG model (ΔG_{lyte-voltage(}V _ext)) − CG (semi-microscopic) model of voltage coupling in membrane proteins, referred to as the Kim-Dryga-Warshel (KDW) model – as a part of electrostatic contribution (ΔG_elec) [61]. The KDW model was successfully applied to evaluating the CG energetics of voltage coupling, as well as the gating currents in ion channels (Kv1.2) [21], and gating charge and voltage changes in Bacterial Reaction Center [33].

The energetics of the CG model is given by:

$$\mathrm{\Delta }{\mathrm{G}}^{\mathit{tot}}=\mathrm{\Delta }{\mathrm{G}}^{\mathit{fold}}=\mathrm{\Delta }{\mathrm{G}}_{\mathit{main}}+\mathrm{\Delta }{\mathrm{G}}_{\mathit{side}}$$ (41)

where the total free energy is taken relative to the free energy of the unfolded system in water at zero applied potential. The main chain energy is given by backbone and hydrogen bonds contributions with weights (w) optimized to yield the observed absolute folding free energies:

$$\mathrm{\Delta }{\mathrm{G}}_{\mathit{main}}={\mathrm{w}}_{\mathit{back}}\mathrm{\Delta }{\mathrm{G}}_{\mathit{back}}+{\mathrm{w}}_{HB}\mathrm{\Delta }{\mathrm{G}}_{HB},$$

while the side chain contribution is decomposed into four terms:

$$\mathrm{\Delta }{\mathrm{G}}_{\mathit{side}}=\mathrm{\Delta }{\mathrm{G}}_{\mathit{elec}}^0+\mathrm{\Delta }{\mathrm{G}}_{\mathit{hydro}}+\mathrm{\Delta }{\mathrm{G}}_{\mathit{polar}}+\mathrm{\Delta }{\mathrm{G}}_{\mathit{vdw}}$$ (42)

Finally, in the case of the presence of electrodes and electrolytes, $\mathrm{\Delta }{G}_{\mathit{lyte}-\mathit{voltage}}^{\mathit{fold}}(V_{\mathit{ext}})$ is added to the total free energy (Eq. 41), resulting in

$$\mathrm{\Delta }{G}^{\mathit{tot}}(V_{\mathit{ext}})=\mathrm{\Delta }{\mathrm{G}}^{\mathit{fold}}+\mathrm{\Delta }{G}_{\mathit{lyte}-\mathit{voltage}}(V_{\mathit{ext}}),$$ (43)

where the $\mathrm{\Delta }{G}_{\mathit{lyte}-\mathit{voltage}}^{\mathit{fold}}(V_{\mathit{ext}})$ is the CG representation of the effect of the external potential (KDW model), and the nature of this term will be elaborated below.

In the following, we consider the electrostatic contributions to the folding energy as a state dependent function of the form, given by:

$$\mathrm{\Delta }{G}_{\mathit{elec},\lambda }(V_{\mathit{ext}})=\mathrm{\Delta }{G}_{\mathit{elec},\lambda }^0+\mathrm{\Delta }{G}_{\mathit{lyte}-\mathit{voltage},\lambda }(V_{\mathit{ext}})$$ (44)

The first term represents the (voltage independent) electrostatic free energy of the “ionizable” residues, which is the sum of two contributions: a local-environment and membrane-depth dependent Born-type self-energy and charge-charge interaction energy with a distant dependent dielectric that approaches ~ 40 in an infinite distance:

$$\mathrm{\Delta }{\mathrm{G}}_{\mathit{elec},\lambda }^0=\mathrm{\Delta }{\mathrm{G}}_{\mathit{self}}+332\sum _{l,m}\frac{q_l^p{q}_m^p}{{\epsilon }_{lm}^{\mathit{eff}}(r_{lm})r_{lm}},$$ (45)

where we use a distant dependent effective dielectric function, ${\epsilon }_{lm}^{\mathit{eff}}=1+60[1-exp(-0.5r_{lm})]$. The ΔG_{lyte–voltage,λ}(V_ext) term represents voltage-dependent energetics of membrane proteins coupled to the externally applied potential, which includes the effects of electrolytes on the electrostatic energetics [33]:

$$\mathrm{\Delta }{G}_{\mathit{lyte}-\mathit{voltage},\lambda }(V_{\mathit{ext}})=\frac{1}{2}\sum _j{V}_{\mathit{ext}}^j{q}_j^g+\frac{1}{2}332\sum _{k\ne j}\frac{q_j^h{q}_k^g}{{\epsilon }_{kj}^{\mathit{eff},\mathit{lyte}}(r_{jk})r_{jk}}+\sum _l{V}_{\mathit{ext}}^l{q}_l^p+\frac{1}{2}332\sum _{k,m}\frac{q_m^p{q}_k^g}{{\epsilon }_{km}^{\mathit{eff}}(r_{km})r_{km}},$$ (46)

where the units are kcal/mol rather than the esu units in the above macroscopic expression and distant dependent effective dielectric constants of 40 and 60 were used, respectively, for the electrolyte response to the charging of protein residues ( ${\epsilon }_{km}^{\mathit{eff}}$) and external potentials ( ${\epsilon }_{kj}^{\mathit{eff},\mathit{lyte}}$). The first and second terms represents the contribution that arises from the polarization of electrolyte effective charges (q^g) by the external potential and all the other charge of the system. The third term represents voltage coupling to protein charges (q^p) and the last term represents the interaction between protein charges and electrolytes that arises when protein ionizable residues are charged.

More specifically, the electrolyte charges in this expression ( $q_j^g$) are represented by a grid with a charge distribution of the form:

$$q_j^{\pm }=\frac{z^{\pm }{N}_{\mathit{box}}^{\pm }{e}^{\mp \beta {\varphi }_j}}{{\displaystyle \sum _{k\in \mathit{box}}}{e}^{\mp \beta {\varphi }_k}},$$ (47)

where ( $q_j^g=q_j^{+}+q_j^{-}$) is determined by solving iteratively with the interactions between all the charges in the system, considering the local potential on each grid point [20, 32]:

$${\phi }_j=332\sum _m\frac{q_m^P}{{\epsilon }_{jm}^{\mathit{eff}}(r_{jm})r_{jm}}+332\sum _{k\ne j}\frac{q_k^g}{{\epsilon }_{kj}^{\mathit{eff}}(r_{jk})r_{jk}}+V_j^{\mathit{ext}},$$ (48)

where $V_j^{\mathit{ext}}$, is evaluated using the macroscopic formula [20, 32]:

$$V_j^{\mathit{ext}}=\underset{Z_0}{\overset{Z_j}{\int }}{D}_z^0/\overline{\epsilon }(Z)dZ$$ (49)

where Z₀ is the Z coordinate at the left electrode. Alternatively we can consider the potential from the electrode charges and using periodic boundary conditions.

The KDW model evaluates the gating charge in a direct manner by computing the cumulative electrolyte charges near the electrode that arises in response to charge movements within the membrane, using an integration through the relation:

$$Q_g=\underset{Z_0}{\overset{Z^{\prime }}{\int }}dZ\left(\mathrm{\Delta }(\mathrm{\Delta }{q}^{\mathit{grid}}(Z,V)/\mathrm{\Delta }Z)\right)=\sum _{i=0}^{i=i^{\prime }}\sum _{j,k}{q}_{i,j,k}^{\mathit{grid}}$$ (50)

where ΔΔq_grid(Z,V) is the difference in the accumulated sum of Δq_grid of the initial and final state, and Z′ is the point to the left of the membrane where the electrolyte charge distribution changes sign. At this point, the integrated charge reaches a plateau and then starts to decrease. The formal integral in the second term of Eq. 50 corresponds to the explicit summation on the grid points (in the third term), where j and k run on all the grid [points in the X and Y directions, whereas i runs from points neat the electrode to Z′.

The KDW model was recently applied to estimating gating charge in voltage gated K⁺ ion channel (Kv1.2) [21] and voltage changes in response to proton/electron transfer in bacterial reaction center [33].

With the above formulation we can try to look for the analogy to the macroscopic continuum treatment. The most obvious analogy come with the capacitor model where we note that the first two terms in Eq. (46) correspond to the free energy of charging (the membrane) between two electrolytes by an electric field in the macroscopic continuum approach. Here we can try to look for correspondence between the CG and continuum models and note that in the absence of the protein charge we have:

$$\frac{1}{2}\sum _j{V}_j^{\mathit{ext}}{q}_j^g+\frac{1}{2}332\sum _{k\ne j}\frac{q_j^g{q}_k^g}{{\epsilon }_{jk}^{\mathit{eff}}(r_{jk})r_{jk}}\leftrightarrow \frac{1}{2}{CV}_{\mathit{ext}}^2$$ (51)

This correspondence states that the free energy stored in the membrane capacitor is equal to the free energy of polarizing electrolyte solutions. The validity of this relationship will be explored in Section 3.1 (see also Fig. 4B).

Figure 4.

The voltage dependent Marcus-Warshel parabolas, obtained using the CG model of voltage coupling (the KDW model). (A) The free energy of a unit charge movement as a function of external potentials using the CG energetics of voltage coupling, which is approximately quadratic, as predicted by linear response approximation applied to the voltage coupling of charge displacement. Notice that f_λ(V) {λ=0,1} interest at V=0 along the reaction coordinate of voltage coupling, which is a natural consequence of the equilibrium fluctuation relation of Eq. (15) that any system of two equilibrium states described by a reaction coordinate of energy gap (voltage coupling in the present study) should satisfy. g₁(V) (dashed light blue) is obtained by shifting f₁(V) (blue) by the conformational free energy of −ΔG_conf. (B) The free energy of charging the membrane between two electrolytes (i.e., the model system of (A) but in the absence of any charge within the membrane). The free energy parabola obtained by our KDW model shows an excellent agreement with the capacitor formula (Eq. (55)) obtained from the macroscopic continuum approach by solving a modified Poisson-Boltzmann equation (PB-V), yielding a capacitance of ~2.34e/V (in comparison with 2.33e/V from the capacitor formula of Eq. (55)).

Now we investigate the relationship between the gating charge obtained by the macroscopic continuum and the KDW model, by formally rewriting the state dependent total CG energy as the free energy function, introduced before:

$$\mathrm{\Delta }{G}_{\lambda }^{\mathit{total}}(V_{\mathit{ext}})=\mathrm{\Delta }{f}_{\lambda }(V_{\mathit{ext}})$$ (52)

While the CG model of voltage coupling was used to evaluate gating charge in a direct manner by computing the cumulative electrolyte charges on the electrode generated in response to charge movements within the membrane, we can look for the trend in a state dependent gating charge, Q_g,λ, using the differentiation of Eq. 52, in an analogy with Eq. 27, which can be expressed as:

$$Q_{g,\lambda }=\partial \mathrm{\Delta }{f}_{\lambda ,\mathit{fold}}/\partial V_{\mathit{ext}}{\mid }_{V_{\mathit{ext}}=0}$$ (53)

This expression can clearly be explored by numerical differentiation. Furthermore, an inspection of our CG energetics (i.e. the third term in Eq. 46) against Eq. (23) yields the gating charge, through:

$$Q_{g,\lambda }=\sum _l{(V_m^l{q}_l^p)}_{\lambda }/V_m$$ (54)

This expression should have the same trend as the (linearized) macroscopic expression as Eq. 25. Both Eqs. 53 and 54 will be applied in Section 3 to estimate the gating charge.

3. Results

3.1 Gating charge

We start by illustrating the application of the free energy relations derived above to the analysis of the thermodynamics of voltage activation in ion channels. This is done by using our CG model to determine the energetics of moving a unit charge between the two sides of a membrane, in the presence of an external (see Fig. 2). The area (A) and width (L) of membrane are 80x80Ų and 60Å respectively, where the electrolyte concentration is taken as 250mM. The unit charge is initially positioned near the membrane on the left side (i.e., state 0). An application of a positive external potential drives the unit charge to the right side (i.e., state 1) of the membrane. Such a “non-equilibrium” movement of the charge within the membrane leads to accumulation of electrolyte charges near the membrane, where opposite electrolyte charges are accumulated near the electrode (see bottom in Fig. 2). The difference in electrolyte charges near the electrode before and after the charge movement is the actual gating charge measured in experiments. The charge movement can also generates voltage change (unless we keep the voltage constant), and be expressed as a change in the electrode potential.

Such a direct evaluation of the gating charge has been possible through the development of our CG model of membrane proteins that include membrane, electrolytes, and electrodes [20, 32], which is now called the KDW model in the present study. This model focuses on the actual measured quantity, namely the displacement current (e.g. [35]), rather than on its interpretation. Thus, the gating charge is evaluated by considering the fact that the gating current is due to the motion and accumulation of the electrolyte charges.

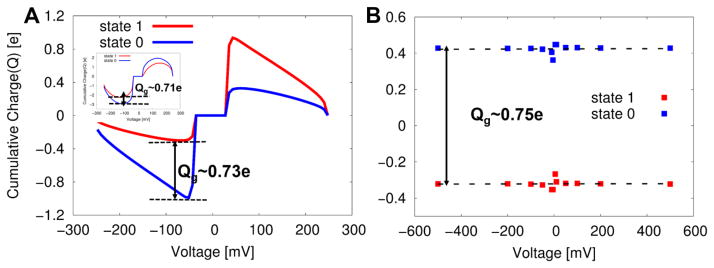
Figure 3A shows the gating charge determined by such a direct procedure, while using Eq. 50, yielding the gating charge of ~0.73e. It turns out that Δq_g(Z,V) is independent of the external potential [33], where the accumulated charge (gating charge) was produced at zero potential (also see inset of Fig 3A that shows the gating charge at an external potential of 100 mV).

Figure 3.

Evaluations of the gating charge by several different approaches: (A) The gating charge obtained using the direct CG approach of Eq. (50) at zero potential (and at 100mV in inset). The difference in cumulative electrolyte charges near the electrode that arises in response to charge movements within the membrane gives a gating charge of ~ 0.73e. (B) The gating charge obtained by the second indirect approach (i.e., using Eq. (54)). In this case a linear least square fits of data points from several different potentials gives approximately zero slope (zero dependence on the external potential) for both the 0 and 1 states, yielding a gating charge of ~0.76e estimated from the gap between the two parallel lines. This implies that the (total) gating charge is independent of external potentials without the consideration of voltage dependent population of each state.

The second approach, referred to here as the first “indirect method”, uses the free energy of voltage coupling to the protein charges, whose expression is obtained by treating the energetics of voltage activation from our KDW model (Eq. 53) in analogy to Eq. 27. The numerical differentiation of the CG free energies at zero membrane potential yields a gating charge of ~0.74e. In addition, we can use the second indirect approach (Eq. 54), which is an analogous expression to the corresponding macroscopic continuum expression (Eq. 25). This approach yields a gating charge of ~0. 75e, where the linear component of capacitance charge is subtracted, as shown in Fig. 3B.

The third approach uses a new expression of gating charge derived in the present study (Eq. 34, i.e., Q_g = −C′ ΔV_min), using a minimum voltage difference between two states and a capacitance of the system. The voltage difference, where the two states have their respective minimum, was obtained from the voltage dependent free energies using our CG model (Fig. 4A), yielding a value of 300mV (V_1,min−V_0,min). The capacitance of the model system, i.e., fluctuation of an external charge flowing through a complete circuit, can be estimated as a second derivative of the voltage dependent free energies with respect to an external potential, yielding the capacitance of ~ 2.52e/V, which is close to the membrane-only (between two electrolytes) capacitance of ~2.33e/V (0.58uF/cm²), determined by using the (linearized) macroscopic continuum approach [62]:

$$C=C_m\frac{1}{1+\frac{2{\epsilon }_m}{kL{\epsilon }_w}},$$ (55)

where 1/k Debye length, L(=60) is the width of membrane, ε_m (=4) and ε_w (=80) are dielectric constants of membrane and water respectively, and C_m is the capacitance of the pure membrane:

$$C_m=\frac{{\epsilon }_{m}A}{4\pi L}$$ (56)

Notice that our CG energetics of voltage coupling (the KDW model) also yields the free energy parabola that yields a membrane capacitance of ~2.34e/V, which is excellent agreement with the prediction of the macroscopic capacitor formula of ~2.33e/V (Fig. 4B), as predicted by the correspondence between our CG model of energetics of voltage coupling and the macroscopic continuum model (Eq. 51). At any rate, the newly developed expression for gating charge (Eq. 34, i.e., Q_g = −C′ ΔV_min) yields a similar gating charge (Q_g ~0.77e with C′=2.58 e/V and ΔV_min=300mV) to the charges obtained by the other approaches (0.73e from the direct approach and 0.74e/0.76e from the indirect approach). Last, for this particular simple system, assuming a linear membrane potential across the membrane, the simple dielectric distant formula with a uniform dielectric constant (Eq. 24 or 25) yields a value of 40/60e ~ 0.67e. The fact that we obtained similar results with different approaches is a comforting confirmation of the validity of our CG formulation that can be used in more challenging cases where the macroscopic approximation can be questionable.

3.2 Voltage dependent free energies and voltage dependency of activation (Q-V curve)

Figure 4A shows the voltage dependent CG (the KDW model) free energy functions (f_λ(V) {λ=0,1}) for moving the unit charge within the membrane as a result of the external potential. These type of free energy parabolas are familiar in the Marcus theory of electron transfer except that they are obtained here along the voltage coupling coordinate and evaluate microscopically. The parabolic dependence is a realization of linear response approximation, which should be satisfied approximately by any system that involves free energies of charging (by an external potential in the present study) along chosen reaction coordinates. The free energy difference between two equilibrium conformational states, i.e., f₁(V_1.min)−f₀(V_0,min), is about ~0.3 kcal/mol (Figs. 4A and 1B), yielding approximately the same result as the “chemical” component of free energy (~ 0.2 kcal/mol) obtained using the gating charge and half voltage (V_1/2) (see below and Eq. 20). Notice that f_λ(V) {λ=0,1} interest at V=0 along the reaction coordinate of voltage coupling, which is a natural consequence of equilibrium fluctuation relation (or the first free energy relation) that any system of two states described by the reaction coordinate of energy gap (voltage coupling in the present study) should satisfy. Last, the free energy of (deactivation) barrier (see Eq. (40)) yields of a value of ~ 0.7 kcal/mol (Figs. 4A and 1B).

The determination of voltage dependent free energies using our CG model of voltage coupling (the KDW model) allows for a direct evaluation of Q-V curve. That is, starting with the relation

$$p_{\lambda }(V)\propto exp(-\mathrm{\Delta }{f}_{\lambda }(V))$$ (57)

By normalization (or by an application of Bayes’ theorem with a uniform prior [63]), we obtain:

$$p_0(V)(\equiv Q_g(V)/Q_g^{max})=\frac{p_0(V)}{p_0(V)+p_1(V)}=\frac{1}{1+p_1(V)/p_0(V)},$$ (58)

where p_λ(V){λ = 0,1} are the probability densities of finding state λ of voltage sensor domain (VSD) at a given voltage V. Notice that the 0^th state is treated as the activated one (see Eq. (13)). Application of equilibrium fluctuation relation (Eq. 15) to Eq. 58 leads to the familiar Fermi-Dirac logistic function, given by

$$p_0(V)(\equiv Q_g(V)/Q_g^{max})=\frac{1}{1+exp(Q_g{V}_{1/2}-Q_{g}V)},$$ (59)

This analytic form of Q-V curve is commonly used in the field of ion channels to fit the observed open (activated) probability of voltage activation [19] to extract the thermodynamic information of voltage coupling such as a half voltage (where the initial (0) and final (1) states have equal probability), gating charge (notice, however, Q_g is equal to $Q_g^{\mathit{max}}$ only for the two state model) and thus chemical component of free energy of ΔG_c. Figure 5 shows the numerical Q-V curve for the unit charge movement using the voltage dependent CG free energies (Eqs. 57 and 58). The lease square fit [64] of the voltage dependent 0^th (activated) CG probability density (Eq. 58) to the analytic form of Q-V curve (Eq. 59) yields the half voltage (V_1/2) of ~−9.2mV and gating charge of ~−0.78e, thereby resulting in the chemical component of free energy of ~0.2 kcal/mol using ΔG_c≡g₀(0)−g₁(0))=Q_gV_1/2. As expected from Eq. 20, the chemical component of free energy (ΔG_c) is approximately equal to the conformational free energy (ΔG_conf) (~0.2 kcal/mol), obtained from the CG voltage dependent free energies using the equilibrium free energy difference (f₁(V_1.min)−f₀(V_0,min)) along the reaction coordinate of voltage coupling.

Figure 5.

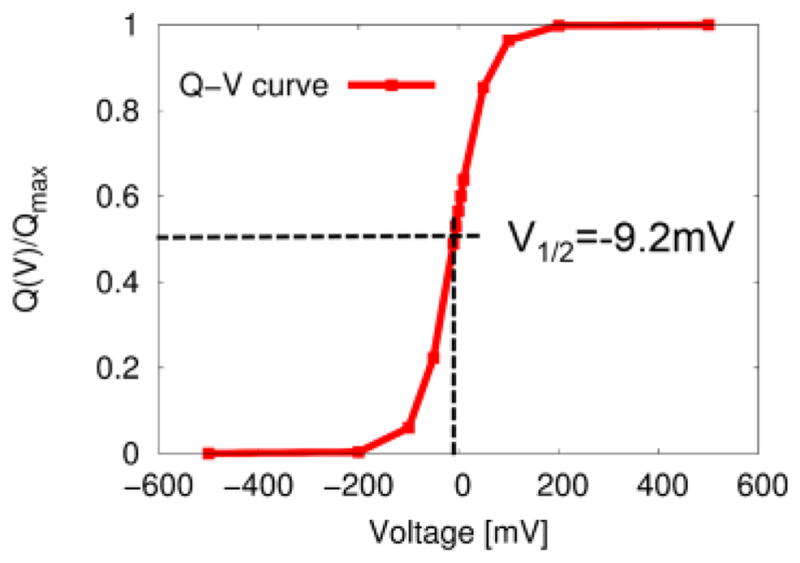
The voltage dependent open (activated) probability (Q-V curve) obtained using the CG model of voltage coupling (see Fig. 4A) with p_λ(V) ∝ exp(−Δf_λ(V)). The lease square fit of the voltage dependent open (final state) probability density of Eq. (58) to the analytic form of Q-V curve of Eq. (59) yields the half voltage (V_1/2) of ~ −9.2mV and gating charge of ~− 0.78e, resulting in the chemical component of free energy of ~0.2 kcal/mol using ΔG_c≡g₀(0)− g₁(0))=Q_gV_1/2. As expected from Eq. (21), ΔG_c is approximately equal to the free energy difference (~0.2 kcal/mol) between the two equilibrium conformational states along a reaction coordinate of voltage activation, i.e., Δf₁(V_1,min)−Δf₁(V_0,min).

3.3 Free energy functions (parabolas) along voltage coupling offers a new insight into the mechanisms of voltage activation in ion channels

Our understanding of voltage activation and gating processes benefits largely from the site-directed mutagenesis studies of selected residues that are critical for channel functions. The effects of such site-directed mutations on the functions of channels that contains voltage sensors modules have been commonly examined through electrophysiological measurements of macroscopic currents and gating currents. In particular, the resulting Q-V curve (and also shifts in the Q-V curve upon site-directed mutations) offers important thermodynamic information of voltage activation of ion channels. For example, specific mutations of key arginine or lysine residues of the S4 helix in the VSD of Shaker channel, which is due to the stabilization of the open-activated (up) state, causes a left shift in the Q-V curve (toward hyperpolarization) [65]. Also a specific set of mutations in the S3b helix of VSD in the same channel causes a right shift in the Q-V by destabilizing the open-activated (up) state of the channel [66]. However, quantitative interpretation of the Q-V curve in terms of the free energy landscapes of channel activation has been hampered due to several reasons; these include the lack of quantitative criteria exists about which conformational state is stabilized or destabilized to account for the observed shifts in the Q-V curve. It also reflects the lack of a quantitative relation between the free energy of stabilization or destabilization and the observed shifts in the Q-V curve exists (partly due to the absence of a reaction coordinate to describe thermodynamics of voltage activation).

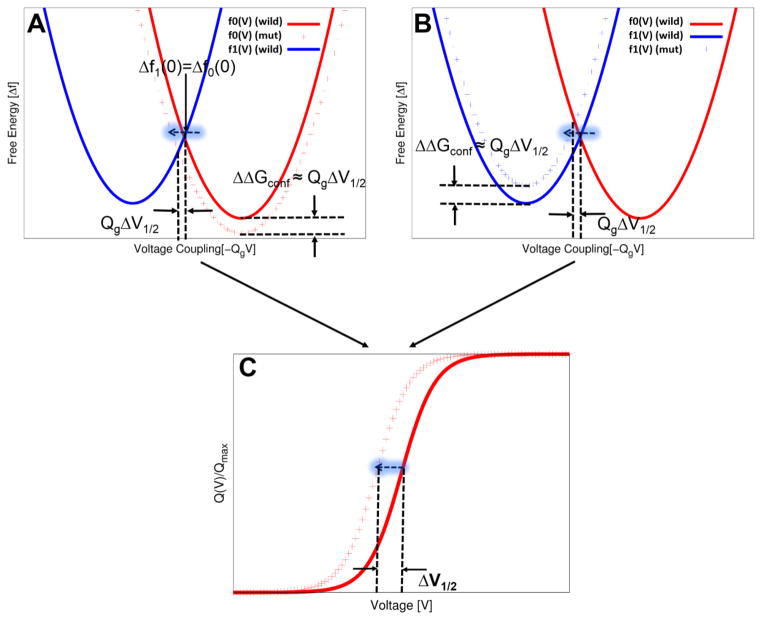
To progress in analyzing the above mutation effects we can exploit the findings of the previous subsection, where we show that the Marcus-type free energy parabolas along the reaction coordinate of voltage coupling allows one to obtain quantitative predictions of the Q-V curve. For example, Figure 6 show such a correlation between the free energies of voltage activation and the Q-V curve. Here, the “hypothetical” Marcus-type free energy parabolas of the 0 and 1 states are related each other by equilibrium fluctuation relation, intersecting each other at V=0 along the reaction coordinate of voltage coupling and yielding the conformational free energy of Q_gV_1/2. This figure shows that the hypothetical Q-V curve (Fig. 6C) could be shifted toward the left (toward hyperpolarization) in either way by the stabilization of the open activated (0) state (red dagger in Fig. 6A) or the destabilization of closed resting (1) state (red dagger in Fig. 6B). In addition, there exists a simple quantitative relation between the free energy of stabilization or destabilization and shift in the Q-V curve, given by Q_gΔV_1/2 ≈ ΔΔG_conf from Eq. (20), which can be explored by the CG model of voltage coupling. Thus, the proposed theory and the CG energetics of voltage coupling (the KDW model) offers a clear graphical and quantitative analysis on the correlation between the stabilization/destabilization in the free energies of voltage activation and shifts in Q-V curve by integrating equilibrium fluctuation relations and Marcus type parabolas using the reaction coordinate of voltage coupling. The accurate determination of equilibrium free energy changes of conformational states and corresponding shifts in activation free energy, upon site-directed mutations, have strong implications in designing pharmacophore in drug discovery targeting voltage sensing domains.

Figure 6.

Schematic illustrations of the quantitative correlation between free energy landscapes (parabolas) and a Q-V curve. (A) The stabilization of an open activated state, for example, upon mutations and dug binding, leads to a left shift (toward hyperpolarization) in the Q-V curve (C). (B) The destabilization of a closed resting state also results in the same shift in the Q-V curve. The shift in the Q-V curve in terms of V_1/2 is correlated with the stabilization or destabilization of the conformational states, with a quantitative relation of the form, Q_gΔV_1/2≈ΔΔG_conf (see Eq. 20).

4. Discussion

Starting from the equilibrium fluctuation relation that makes a connection between the conformational free energy between the two (forward/backward) probability densities, along the one-dimensional reaction of “voltage coupling”, we have offer a rigorous physical foundation for the fundamental free energy relations in the voltage gated ion channels, used to quantify kinetics/thermodynamics of voltage activation [1,19, 36–41]. We have shown that the chemical component of the voltage dependent free energy, namely, the free energy difference between two non-equilibrium conformational states at zero membrane potential (Q_gV_1/2), is equivalent to the free energy difference between two “equilibrium” conformational states in a one-dimensional space of voltage coupling.

Application of linear response approximation (LRA) to the free energies of voltage activation in the framework of equilibrium fluctuation relations yields a remarkable relation between gating charge and its fluctuation, i.e., in terms of the basic properties of channels. This relationship, which is known as the fluctuation-response relation in statistical mechanics, is reminiscent of the Nyquist relation for current fluctuation (as a realization of the fluctuation-dissipation theorem in an electric circuit) [67, 68], which was employed to estimate the number of channels and thus the gating charge per channel (see Ref. [69] and references therein). The gating charge expression developed in the present study could thus be considered a time independent version of Nyquist relation (as a realization of fluctuation-response relation in an analogous neuro-electric circuit). A recent realization of the non-equilibrium (and non-linear) extension of the relation in a quantum coherent conductor [70, 71] may further implicate the roles played by the Nyquist relation in ion channels in the framework of the non-equilibrium fluctuation theorem [72].

The accuracy of our CG model of the energetics of voltage coupling (the KDW model) in membrane proteins, simulated by using semi-”microscopic” grid-based electrolytes and implicit electrodes, was examined considering a well-defined test case (i.e., the membrane between two electrolytes) where we have clear results from macroscopic continuum model [62]. It was found that the free energy of charging (and also capacitance) obtained by using the KDW model, yields an excellent agreement with the macroscopic continuum prediction. Thus, our model offers a new explicit microscopic insight into the nature of the voltage coupling in membrane proteins.

The KDW model for a unit charge movement displaced by an external potential was also applied to simulate gating charge using three different approaches, including the new formula, yielding approximately equal result to each other. The KDW model was then used to illustrate the free energy relations for voltage activation in the simple model of the unit charge movement. The KDW model yields Marcus type parabolas along the reaction coordinate of voltage coupling, as predicted by linear response approximation, allowing for a direct prediction of voltage activation profiles, e.g., gating charge vs. voltage curve (Q-V curve). These free energy parabolas along the one-dimension reaction coordinate of voltage activation have allowed for a clear understanding of the correlation between the changes in the free energies of voltage activation and the shifts in Q-V curve, upon site-directed mutagenesis or drug binding.

Overall, the presented theory and the CG simulation of voltage couplings offers new quantitative tools for understanding the molecular basis of the action of mechanisms of voltage gating in voltage gated ion channels. This was be done in the framework of the equilibrium fluctuation relation and LRA, thus laying a firm quantitative foundation for a more unified understanding of voltage effects in ion channels, ion pumps, and transporters in general. Application of the framework developed in the present study to (real) membrane proteins is under way, considering the voltage sensor domain from a voltage sensitive phosphatase [73]. Note that, however, while we expect LRA to be very effective in approximating the energetics of the conformational changes, as it has been in our studies of processes in condensed phases and in proteins (e.g. [74]), the validity is not essential for the new derivation of the gating charge and for the CG treatment of the gating charge/current. That is, we emphasize the CG model of gating charge/charges follows LRA and gives very reasonable capacitor-like results because the electrolytes grid follows nicely LRA. This means that regardless of whether the protein free energy landscapes and conformational transitions follow LRA or not, we do have a reliable description of the gating charges when the structures of the open activated and closed resting state are known. This is indeed the case in our studies of Kv1.2, where we reproduced the observed gating charge/current [21].

In addition, the direct approach of the KDW model provides an effective way for determining the gating charge and the resulting changes in electrode potentials (voltage generation), that has been used to estimate electrogenicity in membrane proteins (e.g.[75]). This important feature has been illustrated in studies of the electrogenicity in the charge separation in bacterial RC [33], should offer a new insight into the mechanisms of proton/electron transfer in Cytochrome c Oxidase. The work in this direction is also in progress.