Abstract
Background
Selection of the first-dose-in-neonates is challenging. The objective of this proof-of-concept study was to evaluate a pharmacokinetic (PK) bridging approach to predict a neonatal dosing regimen.
Methods
We selected fluconazole as a paradigm compound. We used data from PK studies in juvenile mice and adults to develop population PK models using NONMEM. We also develop a physiologically-based PK model from in vitro–in silico data using Simcyp. These three models were then used to predict neonatal pharmacokinetics and dosing regimens for fluconazole.
Results
From juvenile mice to neonates, a correction factor of maximum lifespan potential should be used for extrapolation, while a “renal factor” taking into account renal maturation was required for successful bridging based on adult and in vitro-in silico data. Simulations results demonstrated that the predicted drug exposure based on bridging approach was comparable to the observed value in neonates. The prediction errors were -2.2%, +10.1% and -4.6% for juvenile mice, adults and in vitro-in silico data, respectively.
Conclusion
A model-based PK bridging approach provided consistent predictions of fluconazole PK parameters in neonates and demonstrated the feasibility of this approach to justify the first-dose-in-neonates, based on all data available from different sources (including physiological informations, preclinical studies and adult data), allowing evidence-based decisions of neonatal dose rather than empiricism.
Keywords: First dose in neonates, modeling, extrapolation, scaling, bridging, pharmacokinetics, dosage prediction, PBPK
Introduction
Pharmacological research in newborn infants is an important component of drug development programs [1].The overall goal is the determination of safe and effective regimens for neonates. The introduction of the Paediatric Regulation by the European Union, together with the renewal of the Pediatric Rule by the Food and Drug Administration on the requirements for pediatric labeling made it mandatory for sponsors to develop drugs for the pediatric population, focusing on a rational dosage selection in pediatric clinical trials [2, 3]. Neonatal drug evaluations present many challenges that are related to rapid physiological changes during early life as well as a myriad of ethical and practical obstacles to clinical research [4]. The selection of the first-dose to be given to neonates is a major challenge that should be based on the optimal use of all available data rather than a “trial and error method” that is associated with potential risks of inefficacy and/or toxicity.
Neonates cannot be included in dose escalation studies similar to those conducted in adults or older children. Therefore, in order to optimize dosage selection in neonatal clinical trials, extrapolation methodologies based on already available data should be promoted [5]. A valuable approach is pharmacokinetic (PK) bridging, which involves dose selection and adjustment in the target population based on known PK differences with a “reference” population [6].
We selected fluconazole as a model compound to conduct a proof-of-concept “bridging study”. Fluconazole has been used for many years to prevent or treat neonatal candidiasis in an off-label manner [7, 8]. According to regulatory guidelines from both the Food and Drug Administration (FDA) and the European Medical Agency (EMA) [9-11], fluconazole is a good candidate for PK bridging studies because 1) pharmacokinetic-pharmacodynamic (PK-PD) relationship can be assumed to be similar across all age groups including neonates, and 2) published data clearly show that PK parameters are highly dependent on age with major changes during the neonatal period [12, 13]. Our objective was to evaluate if selection of the first-dose-in-neonates using a PK model-based bridging approach was possible but also accurate, when based on available data from difference sources of studies (preclinical studies, adult PK data, and in vitro–in silico data), and knowledge of physiological changes and developmental PK.
Methods
Four sets of data were available to perform the bridging study (Table 1): juvenile animal PK data, adult and neonatal PK data and in vitro–in silico data (see appendix 1 for details). The different steps of the extrapolation approach are summarized in Figure 1.
Table 1. Study characteristics and patients' demographics.
| Juvenile mice | Neonates and young infants | Adult healthy volunteers | |
|---|---|---|---|
| Number of subjects | 230 | 13 | 12 |
| Gender (Male / Female) | - | 7 / 6 | 12 / 0 |
| Race (Caucasian / African American) | - | 5 / 8 | |
| Dosing regimen | 6 mg/kg/day or 60 mg/kg/day | LD of 25 mg/kg followed by MD of 12 mg/kg once daily | 100 mg |
| Treatment duration | 1 – 11 days | - | Single dose |
| Administration | Subcutaneous | Intravenous | Oral |
| Current weight | 6.52 (1.80 – 10.01) g | 3.0 (1.0 – 8.0) kg | 72 kg |
| Birth weight | - | 2.7 (0.8 - 3.5) kg | - |
| Gestational age at birth | 19 days | 37 (24 - 39) weeks | - |
| Postnatal age | 9 (2 - 12) days | 19 (5 – 262) days | 24 years |
| Postmenstrual age | - | 40.9 (28.7 - 75.7) weeks | - |
| Serum creatinin concentration | - | 0.5 (0.2 - 1.3) mg/dL | - |
| Total number of samples | 60 | 94 | - |
| Number of blood samples per subject | - | 8 (4 - 8) | 15 |
Values are expressed as median (range)
LD: Loading dose; MD: maintenance dose
Figure 1. The different modeling and extrapolation approaches available to predict the first dose in neonates.
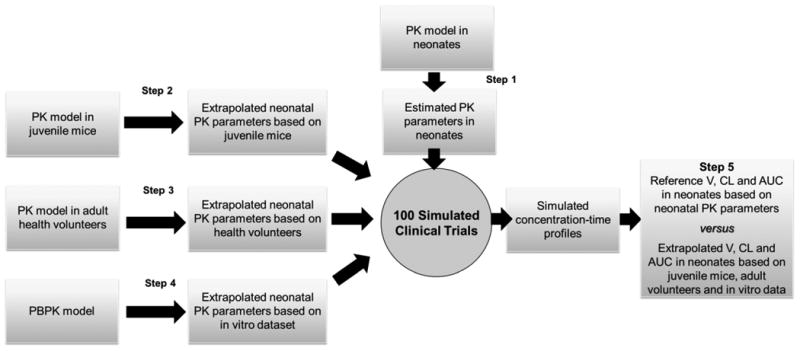
In the first step (step 1, population PK parameters in neonates, appendix 1), we developed and validated a population PK model, based on available data in neonates (94 fluconazole concentrations in 13 neonates). This model refers to “the reference model” for all comparisons performed in step 5 (see below).
In a second step (step 2, from juvenile mice to neonates, appendix 1), we developed a population PK model based on juvenile animal PK data (60 fluconazole concentrations obtained by pooling of blood of 230 animals) and performed an extrapolation from juvenile mice to neonates.
In a third step (step 3, from adult health volunteers to neonates, appendix 1), we identified a population PK model based on adult PK data (180 concentrations in 12 adult volunteers) and performed extrapolation from adults to neonates.
In a fourth step (step 4, from in vitro - in silico data to neonates, appendix 1), we developed a physiologically based pharmacokinetic (PBPK) model of fluconazole and performed prediction to neonates.
During step 5 (predictive performance in dosage prediction, appendix 1), we used the models developed during steps 2 to 4 and extrapolation methods to predict fluconazole exposure (AUC) obtained at steady-steady with a standard loading-dose schedule in neonates. The predicted AUC was compared with reference AUC obtained in step 1.
The predictive performance was evaluated by calculating the prediction error (PE) using equation 1:
| (Eq. 1) |
The PE was expressed as a percentage.
Results
Step 1. Reference PK parameters in neonates
A one-compartment model with first order elimination was fitted to the neonatal PK data. An exponential model best described inter-individual variability of CL and V. A proportional model best described residual variability. An analysis of covariates suggested that weight and gestational age had a significant impact on CL and only weight had a significant impact on V. Model diagnostics showed an acceptable fit of the model to the data. As shown in figure 2 A1-2, predictions were unbiased. In the diagnostic plots of conditional weighted residuals (CWRES) versus time and population predictions (PRED), no trends were observed (Figure 2 A3-4). In addition, the mean parameter estimates resulting from a bootstrap procedure (500 iterations) closely agreed with the respective values from the final population model, indicating that the estimates of the population pharmacokinetic parameters in the final model were accurate and that the model was stable (Table 2). Figure 2 A5-6 presents the results of normalized prediction distribution error (NPDE). NPDE distribution and histogram met the required theoretical N (0, 1) distribution and density, indicating a good fit of the model to the individual data. The mean and variance of NPDE were -0.02 (Wilcoxon signed rank test p=0.7) and 0.88 (Fisher variance test 0.4), respectively. The median values of estimated CL and V were 0.016 L/h/kg and 1.03 L/kg, respectively. These values were the “reference neonatal PK values” used for the last step of comparison.
Figure 2. Model evaluation in neonates and juvenile mice.
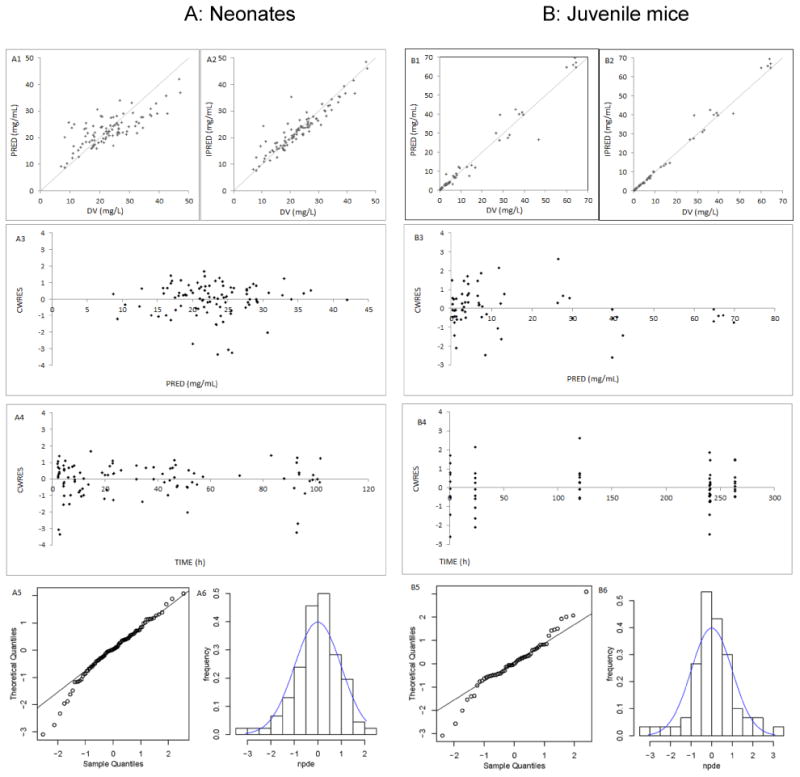
A: Neonates B: Juvenile mice (1, 2) Routine diagnostic goodness-of-fit plots: population predicted (PRED) versus observed concentrations (DV). Individual predicted (IPRED) versus observed concentrations (DV). (3, 4) Conditional weighted residuals (CWRES) versus time. Conditional weighted residuals (CWRES) versus population predicted concentrations (PRED). (5, 6) Normalized Prediction Distribution Errors (NPDE): QQ-plot of the distribution of the NPDE versus the theoretical N (0,1) distribution. Histogram of the distribution of the NPDE, with the density of the standard Gaussian distribution overlaid
Table 2. Population pharmacokinetic parameters of fluconazole determined in juvenile mice, neonates and adults.
| PK parameters | Juvenile mice | Neonates | Adults | ||
|---|---|---|---|---|---|
|
| |||||
| Final estimate (RSE) | Bootstrap median(2.5th – 97.5th) | Final estimate (RSE) | Bootstrap median(2.5th – 97.5th) | Final estimate | |
| Absorption rate constant Ka (h-1) | 16.2 (FIX) | 3.38 | |||
| Lag-time (h) | 0.23 | ||||
| Volume of distribution V (L) | 55.7 | ||||
| V= θ1 × (weight /median) θ2 | |||||
| θ1 | 0.006 (2.4) | 0.006 (0.003-0.006) | 3.0 (6.5) | 3.0 (2.6-3.4) | |
| θ2 | 0.628 (5.6) | 0.627 (0.542-0.7) | 0.907 (8.8) | 0.920 (0.699-1.179) | |
| Clearance CL (L/h) | 1.18 | ||||
| CL/F= θ3 × (weight /median) θ4× Fage | |||||
| θ3 | 0.00017 (15.7) | 0.00016 (0.00009-0.00022) | 0.0521(14.4) | 0.0519 (0.0370-0.0673) | |
| θ4 | 0.362 (38.4) | 0.372 (0.116-0.758) | 0.922 (25.6) | 0.897 (0.361-1.520) | |
| Fage (mice) = θ6 + EXP (θ5*PNA-9) | |||||
| θ5 | 0.468 (8.4) | 0.469 (0.394-0.588) | |||
| θ6 | 1.21 (23.5) | 1.26 (0.78-2.41) | |||
| Fage (neonates) = (GA/median) θ7 | 2.88 (25.3) | 2.89 (0.59-7.28) | |||
| Interindividual variability (%) | |||||
| Ka | 177.8 | ||||
| V | 19.1 (42.1) | 17.3 (8.1-24.2) | 17.4 | ||
| CL | 14.0 (35.4) | 13.0 (5.9-17.6) | 35.1 (30.6) | 30.1 (12.7-43.8) | 22.2 |
| Residual variability | |||||
| Proportional (%) | 11.0 (40.5) | 10.2 (5.8-15.6) | 15.0 (31.5) | 14.6 (10.7-20.0) | 14.7 |
| Additive (mg/L) | 0.08 | ||||
The median weight of juvenile mice and neonates are 6.52g and 3kg, respectively
Step 2. PK model juvenile mice and extrapolation to neonates
A one-compartment model with first order elimination was fitted to the PK data from juvenile mice. An exponential model best described inter-individual variability of apparent CL. A proportional model best described residual variability. The covariates analysis identified that current weight and postnatal age had a significant impact on CL and only weight had a significant impact on V. Table 2 presents the PK parameters of juvenile mice. The model was also validated by goodness-of-fit plots, bootstrap and NPDE (Figure 2 B1-6). The mean and variance of NPDE were 0.05 (Wilcoxon signed rank test p=0.7) and 1.13 (Fisher variance test 0.5), respectively.
Three methods of extrapolations were evaluated and compared
1. Weight normalized CL and V
The median individual Bayesian estimates for CL and V, which were calculated by population PK model in juvenile mice, were 0.076 L/h/kg and 0.91 L/kg, respectively.
2. Simple allometry for CL and V
After plotting individual Bayesian estimated CL and V as a function of bodyweight, the estimated coefficients and exponents using allometric equations (equations 3 and 7 in appendix 1) were 0.00005 and 1.2932 for CL, and 0.0018 and 0.6282 for V, respectively. After 100 simulations with these estimated parameters, the median predicted neonatal CL and V were 0.528 L/h/kg and 0.09 L/kg, respectively.
3. Simple allometry with a corrected factor of maximum lifespan potential (MLP) for CL
After plotting individual Bayesian estimated CL multiplied by the mean MLP value as a function of bodyweight on a log-log scale. The estimated coefficient and exponent using allometric equation (equation 4) were 1.2133 and 1.2932, respectively, After 100 simulations with these estimated parameters and a corrected factor of MLP, the median predicted neonatal CL was 0.016 L/h/kg,
The extrapolation approach using 0.91 L/Kg for V (weight normalized value of extrapolation method 1) and 0.016 L/h/kg for CL (allometry with corrected factor of MLP extrapolation method 3) gave the most consistent prediction of observed values (0.016 L/h/kg and 1.03 L/kg) in neonates (Table 3).
Table 3. Input variables / parameters for PBPK model of fluconazole (using Simcyp® ).
| Molecular weight (g/mol) | 306.3 |
| Log P | 0.5 |
| pKa (monoprotic base) | 1.76 |
| B/P ratio | 1 |
| Fu | 0.89 |
| CLR (L/h) | 1.1 |
Log P: octanol-water partition coefficient, B/P ratio: blood to plasma concentration ratio
Fu: unbound fraction, CLR: renal clearance
Step 3. From adults to neonates
Roos JF et al. developed a one-compartment model with lag-time and first-order elimination in adults [14]. We performed simulations based on the reported PK parameters and extrapolation using fix-exponent allometry with a corrected factor for postmenstrual age using NONMEM. The median predicted CL and V were 0.014 L/h/kg and 0.80 L/kg respectively (Table 3).
Step 4. From in vitro - in silico data to neonates
Table 4 shows input drug parameters for fluconazole. Its physicochemical properties including molecular weight, pKa and logarithm of the octanol-water partition coefficient (logP) were obtained from the product monograph and published information [15, 16]. Parameters of the PBPK model were included as follows:
Table 4. Predicted and reference PK parameters of fluconazole in neonates.
| CL (L/h/kg) | V (L/kg) | |
|---|---|---|
| Reference PK parameters in neonates | 0.016 (0.005-0.029) | 1.03 (0.76- 1.37) |
| Extrapolation from juvenile animal | ||
| CL | ||
| Weight normalized CL | 0.076 | |
| Simple allometry | 0.528 | |
| Simple allometry with corrected factor of MLP | 0.016 | |
| V | ||
| Weight normalized V | 0.91 | |
| Simple allometry | 0.09 | |
| Extrapolation from adult | 0.014 | 0.80 |
| Extrapolation from PBPK model | 0.016 | 0.96 |
Values are expressed as median (range)
The blood and plasma concentrations of fluconazole being equivalents, the blood to plasma partition ratio (B/P) was set to 1 [15]. Fraction unbound in plasma (Fu) has been reported as 0.89 [17]. In order to describe tissue distribution, a full PBPK distribution model was used with a fixed tissue/plasma partition coefficient of 10 in skin [15]. Data to define elimination was obtained from the PK study of intravenous fluconazole in adult healthy volunteers, where the total CL at steady state was 1.38 ± 0.24 L/h [18]. As the renal excretion is the major route of fluconazole elimination and the mean urinary recovery of unchanged fluconazole was 80% [15], fluconazole renal clearance (CLR) was fixed to 1.1 L/h to account for 80% of total systemic CL.
These parameters were entered in the Simcyp program (Table 3). The median predicted CL and V values for the 100 simulated clinical trials were 0.016 L/h/kg and 0.96 L/kg, respectively.
Step 5. Prediction of fluconazole AUC with different models (Steps 2, 3 and 4) and extrapolation methods. Comparison with the reference value obtained by the neonatal model (Step 1)
Using a “loading dose regimen” of 25 mg/kg followed by 12 mg/kg fluconazole daily over 2 hours, the median predicted AUCs obtained at steady state, determined with the three models (step 2 juvenile mice, step 3 adults, and step 4 PBPK), were 766, 862 and 747 mg•h/L, respectively (Table 4). These values were in close agreement with the AUC of 783 mg•h/L, calculated from neonatal population PK model (step 1). The PEs were -2.2%, +10.1% and -4.6% for juvenile mice, adults and in vitro-in silico data, respectively.
Discussion
The dosage regimen used in the very first studies in neonates is often based on empirical scaling methods. The commonly used method for initial dosing selection in children is to normalize the adult dose by body weight or body surface area (i.e. mg/kg or mg/m2), assuming a linear relationship between weight and/or surface area and dose [19]. Evaluation of these empirical methods has already shown that scaling based on body weight tended to under-predict drug CL in children and those based on body surface area frequently over-predict drug CL in young children. The prediction bias is even more pronounced in neonates [20]. Therefore, there is an urgent need to improve selection of the first dose by developing and evaluating bridging studies based on the optimal use of already available information when time for neonatal studies has come. To try to reach this goal, we evaluated how PK bridging studies could be used to support dose selection to conduct drug evaluation for a neonatal indication. Our results highlight the important methodological aspects of applying the PK bridging approach in neonates, namely, the correction for inter-species differences, developmental physiological aspects (i.e. renal maturation) and the need to include prior PK informations available in preclinical and adult studies. Taking these prerequisites into account, our results strongly support the use of all available sources of pharmacokinetic information to predict neonatal pharmacokinetics and initial dosage to be proposed for neonatal studies and/or recommended for therapeutic use.
It is currently stated that data from juvenile animals are better than data from adult animals to predict pediatric PK [21]. As this statement has never been validated, comparing juvenile and mature animals to predict the neonatal dose remains necessary. Previous research has shown that the inter-species PK extrapolation between mature i.e. mature animals and adults using the simple allometry without correction factor overestimated CL in humans [22]. In the present study, we have also shown that a bias exists in the extrapolation process from juvenile mice to neonates. The MLP factor (defined as the maximum observed life span of one species), was required to correct this bias. By including the correction MLP factor for CL and weight normalized V, we demonstrate for the first time that population PK based extrapolation from juvenile mice to neonates, using allometry is possible. Indeed, with an identical dosage regimen, fluconazole exposure calculated with the juvenile animal model was close to neonatal “real” exposure obtained with a model derived from “real neonatal data”. These data demonstrate good predictive performances of the juvenile animal model.
Adult pharmacokinetic data are frequently, but not always available prior to any administration of a drug to neonates. In order to extrapolate PK from adults to pediatrics the fixed-exponents allometric model (with exponents of 0.75 for CL and 1 for V), has been proposed, considering size as a major determinant reflecting maturation [23]. Although used for extrapolation from adults to adolescents and children with “acceptable” results, systematic biases were found in neonates and infants [20, 24]. This might reflects the continuous and rapid changes in PK that occur during the neonatal period as consequences of developmental changes affecting body composition, organ function and maturation of drug metabolic and excretion pathways. For fluconazole, it is known that renal maturation has an impact upon dose prediction in neonates [12] and this factor must be considered. We used the glomerular filtration rate (GRF) maturation model developed by Rhodin MM et al [25], based on a population meta-analysis of GFR (measured in 923 patients from very premature neonates to adulthood). The sigmoid hyperbolic model precisely describes the nonlinear relationship between GFR maturation and postmenstrual age after standardizing size effect using allometric scaling [25]. Extrapolation based on adult population PK model incorporating the renal maturation model gave satisfactory drug exposure in neonates.
In vitro-in silico extrapolation to neonates was based on a PBPK model, that offers a mechanistic approach to assess neonatal drug exposure. The PBPK approach establishes virtual populations by building up a mechanistic and physiological model, which incorporates known variabilities in demographic and biological parameters linked to drug-specific physico-chemical properties and data on drug ADME (absorption, distribution, metabolism and elimination) [26, 27]. The age-dependent changes in enzyme activities, blood flow, tissue size and composition (phospholipid, water and neutral lipid content) and their correlation with demographic factors (including weight, height and/or body surface area) were included in the Simcyp pediatric simulator [28]. A full PBPK distribution model to predict V is based on parameters describing 14 key organs using a PBPK tissue / plasma partition coefficient model. For drugs that are extensively eliminated by the kidneys, maturation of clearance reflects maturation of the glomerular filtration rate (GFR) and tubular function [29-31]. The renal maturation model in Simcyp was developed based on the changes of inulin, mannitol and 51Cr-EDTA clearance with age. This renal maturation model has predicted vancomycin CL successfully in neonates [28] and similarly showed good prediction of fluconazole CL in neonates.
In order to confirm that the dosage prediction was possible by using at least one of the proposed strategies, a loading dose treatment schedule was tested in the three models and compared to the “real neonatal model” developed from data obtained in neonates receiving fluconazole. The PEs varied from -4.6% to 10.1%, indicating a good predictive performance of model-based extrapolations from juvenile mice, adults and in vitro-in silico data.
Some limitations should be underlined. As a proof-of-concept study, our positive results are obtained with a kidney eliminated drug, for which the developmental changes have been extensively studied in neonates. This approach has been proposed for other drugs, including highly metabolized drugs, although modeling developmental metabolic processes will likely be much more complex than modeling renal maturation changes, as data of ontogeny of drug metabolism and transport are still limited. The present study gave consistent predations of neonatal PK from different sources. We cannot arbitrarily decide which approach is better than others. Given the complex in the prediction of first dose in neonate, we suggest an optimal use of all available sources. The final decision should also consider the safety of evaluated drugs and prior knowledge of developmental PK-PD in neonates.
Conclusion
We successfully used model-based PK bridging approaches to predict the pharmacokinetics of fluconazole in neonates from juvenile mice, adults and in vitro-in silico data. Our results firstly support the feasibility of PK bridging approach in neonates. Whichever the difficulties, such bridging approaches should be further tested and validated, as it looks being the only way to select the first dose in neonates using a scientific “evidence based” approach.
Table 5. Predicted and reference AUC0-24h values at steady-state in neonates with the loading dose regimen [Piper L et al., 2011].
| AUC at steady state (mg•h/L) | PE (%) | |
|---|---|---|
| Prediction | Median (5th-95th) | |
| Juvenile mice | 766 (541, 1098) | -2.2 |
| Adults | 862 (442, 1596) | 10.1% |
| PBPK | 747 (406, 1595) | -4.6% |
| Observation | ||
| Neonates | 783 (403, 2300) | |
| Target value | 800 |
Acknowledgments
This work is part of the TINN (Treat Infections in NeoNates) network supported by the European Commission under the Health Cooperation Work Programme of the 7th Framework Programme (Grant agreement n°223614) and the GRIP network (Global Research in Paediatrics – Network of Excellence) supported by the European Commission under the Health Cooperation Work Programme of the 7th Framework Programme (Grant Agreement number 261060).
Appendix 1
Methods
We derived the population PK models from juvenile mice and adult healthy volunteers, and PBPK model from in vitro – in silico data to predict fluconazole dose in neonates.
Population pharmacokinetic parameters in neonates
The data used to develop the population pharmacokinetic model was obtained from a prospective, single-center, open-label pharmacokinetic trial at Duke University Medical Center in Durham, NC. Thirteen neonates and young infants were given an intravenous loading dose (25 mg/kg administered over 2 hours via a syringe pump) followed by maintenance therapy (12 mg/kg/day over 1 hour every 24 hours). Blood samples were taken at the following time points after the end of the infusion: 0 to 30 minutes, 2 to 4 hours, 6 to 12 hours, and 18 to 24 hours after the first dose and peak and trough samples at doses 3 and 5 [32]. A summary of study characteristics and the demographic variables is provided in Table 1.
A total of 94 fluconazole concentrations ranging from 6.9 to 47.2 μg/mL were available. The population PK analysis was carried out using the nonlinear mixed effects modeling program NONMEM V 7.2 (Icon Development Solutions, USA). We used first order conditional estimation (FOCE) method with interaction option to estimate pharmacokinetic parameters and their variability. We estimated inter-individual variability of the pharmacokinetic parameters using an exponential model, which was expressed as follows:
where θ i represents the parameter value of the ith subject, θmean the typical value of the parameter in the population and ηi the variability between subjects which is assumed to follow a normal distribution with a mean of zero and variance ω2.
Covariate analysis followed a forward and backward selection process. We used stepwise covariate modelling [33] and likelihood ratio test to evaluate the effect of each variable. During the first step of covariate model building, a covariate was included if a significant (p<0.05, χ2 distribution with one degree of freedom) decrease (reduction>3.84) in the objective function value (OFV) from the basic model was obtained. All the significant covariates were then added simultaneously into a ‘full’ model. Subsequently each covariate was independently removed from the full model. If the increase in the OFV was lower than 6.635 (p<0.01, χ2 distribution), the covariate was considered significantly correlated to the pharmacokinetic parameter and was therefore included in the final model.
Model validation was based on graphical and statistical criteria. Goodness-of-fit plots, including observed (DV) versus individual prediction (IPRED), DV versus population prediction (PRED), conditional weighted residuals (CWRES) versus time and CWRES versus PRED were used initially for diagnostic purposes [34]. The stability and performance of the final model were also assessed by means of a nonparametric bootstrap with re-sampling and replacement. Re-sampling was repeated 500 times and the values of estimated parameters from the bootstrap procedure were compared with those estimated from the original data set. The entire procedure was performed in an automated fashion, using PsN (v2.30) [35]. The final model was also evaluated graphically and statistically by normalized prediction distribution errors (NPDE) [36]. 1000 datasets were simulated using the final population model parameters. NPDE results were summarised graphically by default as provided by the NPDE R package (v1.2) [37]: (i) QQ-plot of the NPDE; (ii) histogram of the NPDE. The NPDE is expected to follow the N (0, 1) distribution.
From juvenile mice to neonates
The PK data in juvenile mice (Swiss strain) was obtained from an open-label, repeated-doses PK study within the FP7 TINN project (Treatment Infection in NeoNates). The mice were born at 19 days gestation age. Two dosing regimens 6 mg/kg or 60 mg/kg once daily were given subcutaneously since postnatal day 2 (Table 1). PK samplings were obtained at times of T0.5h or T23h on day 1, T23h on day 5, T23h on day 10, or T0.5h or T23h on day 11.
Population PK analysis was carried out using NONMEM. Modeling and validation processes were similar to neonates, as described above.
We used the following extrapolation approaches to predict PK parameters in neonates from juvenile mice [22, 38-40]:
Clearance (CL)
Method 1: Weight normalized CL
| (Eq. 2) |
where CLNN is the predicted CL in neonates, WTNN is the bodyweight in neonates; a is the estimated weight normalized CL in juvenile mice.
Method 2: Simple allometry
| (Eq. 3) |
where CLNN is the predicted CL in neonates, WTNN is the bodyweight in neonates; b and c are the estimated coefficient and exponent obtained from the population PK model derived from juvenile mice.
Method 3: Simple allometry with corrected factor of maximum lifespan potential
| (Eq. 4) |
| (Eq. 5) |
In this approach, the individual Bayesian estimated CL in mice was multiplied by its maximum lifespan potential (MLP) value and were plotted as a function of bodyweight on a log-log scale. The coefficient and exponent (d and e in the equation) were estimated from the allometric equation. The MLP was calculated by the equation as described by Sacher [41]. Brain weight values are 120 mg on day 1, 248 mg on day 5 and 314 mg on day 11 [42], whereas 818000 hours is the MLP in humans.
Volume of distribution (V)
Method 1: Weight normalized V
| (Eq. 6) |
where VNN is the predicted V in neonates, WTNN is the bodyweight in neonates; f is the estimated weight normalized V in juvenile mice.
Method 2: Simple allometry
| (Eq. 7) |
where VNN is the predicted V in neonates; WTNN is the bodyweight in neonates; g and h are the estimated coefficient and exponent obtained from the population PK model of juvenile mice.
Although the bioavailability (F) of fluconazole is unknown in juvenile mice whatever the route of administration, “reference values” do exist showing that fluconazole is almost completely absorbed both in animals and humans: F was 108% in sea turtles after subcutaneous administration, >90% in human and 109% in cats after oral administration [43, 44]. Thus, we assumed a value of 100% for F after sub-cutaneous administration in juvenile mice and oral administration in human.
From adult health volunteers to neonates
The PK data in adult healthy volunteers was identified from literature [14]. In a phase 1 study, 12 healthy male volunteers received a single oral dose of fluconazole 100 mg. An average of 15 blood samples per patient was taken between 5 min and 168 h postdose. A one-compartment population PK model model was developed by Roos et al [14]. which was used in the present study.
We used the following extrapolation approach to predict PK in neonates from adult healthy volunteers [23, 25]:
Method: Fix- exponent allometry with corrected factor of postmenstrual age
| (Eq. 8) |
| (Eq. 9) |
| (Eq. 10) |
Where CLNN and VNN are the predicted CL and V in neonates; CLadult and Vadult are the observed CL and V in adults, respectively; WTNN is the bodyweight in neonates; MF is maturation function, PMA is postmenstrual age in weeks, PMA50 is PMA at which CL reaches half its maximal value and S is sigmoidicity coefficient. To describe renal maturation, PMA50 and S were set to 47.7 weeks and 3.4, as previously reported [25].
From in vitro - in silico data to neonates
The PBPK model was carried out using the software Simcyp version 12 release 1 (Simcyp Limited, Sheffield, UK). Drug data (e.g., drug molecular weight, physico-chemical characteristics such as log P (octanol-water partition coefficient) and pKa, drug elimination etc.) was obtained from the literature. The Systems data in children (e.g. physiology, anatomy, biology, and biochemistry defined based on pediatric population demographics) was set to default values, as described by Johnson TN et al [28].
Extrapolation approach
The default kidney maturation model in Simcyp was used for extrapolation [28]:
Evaluation of model-based extrapolations
Given our interest in dosage prediction using model-based approaches, we tested the performance of the proposed approaches via simulation. We extensively evaluated whether the two population PK models derived from juvenile mice and adults, and the PBPK model derived from in vitro-in silico data with associated extrapolation approaches could be used to accurately predict observed PK parameters in neonates. We elected CL and V as endpoints for the purpose of this evaluation and performed 100 simulations using NONMEM and Simcyp, respectively.
Predictive performance in dosage prediction
Fluconazole PK-PF relationship was best described by using AUC/MIC. The selection of pediatric dose is based on the target exposure (AUC0–24) of 800 mg•h/L, reported in adult intensive care patients or immunocompromised patients treated with fluconazole at 800 mg/day. This AUC target ensures that exposure exceeds the AUC/MIC PD target of 50 h for Candida species with a MIC of 8 mg/L [12, 45, 46].
In the next step, we tested different simulation scenarios to evaluate whether model-based extrapolation could be used to accurately predict drug exposure and support the dosage prediction in neonates. The loading dose regimen previously recommended for neonates [32], consisting of a loading dose of 25 mg/kg (intravenous infusion over 2 hours) followed by maintenance doses of 12 mg/kg (intravenous infusion over 1 hour) was used to perform 100 simulations using our models previously developed: population PK models in mice and adults, PBPK model and population PK model in neonates to calculate predicted and reference AUCs, respectively.
Footnotes
Conflict of Interest: The authors declare no conflict of interest related to this work.
Author contributions: Zhao W and Jacqz-Aigrain E designed the research
Benjamin DK Jr and Watt KM provided PK data in neonates
Matrot B and Bourgeois T provided PK data in juvenile mice
Le Guellec C, Hope WW, van den Anker JN, Benjamin DK Jr, Manzoni P and Jacqz-Aigrain E contributed to the discussion and interpretation of the results
Zhao W performed data analysis and wrote the manuscript, which was critically reviewed by the other authors.
References
- 1.Purohit VS. Biopharmaceutic planning in pediatric drug development. AAPS J. 2012;14(3):519–22. doi: 10.1208/s12248-012-9364-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Strougo A, Eissing T, Yassen A, Willmann S, Danhof M, Freijer J. First dose in children: physiological insights into pharmacokinetic scaling approaches and their implications inpaediatric drug development. J Pharmacokinet Pharmacodyn. 2012;39(2):195–203. doi: 10.1007/s10928-012-9241-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Manolis E, Osman TE, Herold R, Koenig F, Tomasi P, Vamvakas S, et al. Role of modelling and simulation in pediatric investigation plans. Paediatr Anaesth. 2011;21(3):214–21. doi: 10.1111/j.1460-9592.2011.03523.x. [DOI] [PubMed] [Google Scholar]
- 4.Kearns GL, Abdel-Rahman SM, Alander SW, Blowey DL, Leeder JS, Kauffman RE. Developmental pharmacology--drug disposition, action, and therapy in infants and children. N Engl J Med. 2003;349(12):1157–67. doi: 10.1056/NEJMra035092. [DOI] [PubMed] [Google Scholar]
- 5.Johnson TN. Modelling approaches to dose estimation in children. Br J Clin Pharmacol. 2005;59(6):663–9. doi: 10.1111/j.1365-2125.2005.02429.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cella M, Gorter de Vries F, Burger D, Danhof M, Della Pasqua O. A model-based approach to dose selection in early pediatric development. Clin Pharmacol Ther. 2010;87(3):294–302. doi: 10.1038/clpt.2009.234. [DOI] [PubMed] [Google Scholar]
- 7.Manzoni P, Stolfi I, Pugni L, Decembrino L, Magnani C, Vetrano G, et al. A multicenter, randomized trial of prophylactic fluconazole in preterm neonates. N Engl J Med. 2007;356(24):2483–95. doi: 10.1056/NEJMoa065733. [DOI] [PubMed] [Google Scholar]
- 8.Kaufman D, Boyle R, Hazen KC, Patrie JT, Robinson M, Donowitz LG. Fluconazole prophylaxis against fungal colonization and infection in preterm infants. N Engl J Med. 2001;345(23):1660–6. doi: 10.1056/NEJMoa010494. [DOI] [PubMed] [Google Scholar]
- 9. [March 2014];FDA Guidance for Industry: Exposure-Response Relationships — Study Design, Data Analysis, and Regulatory Applications. http://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm072109.pdf.
- 10. [March 2014];Points to consider on Pharmacokinetics and Pharmacodynamics in the development of antibacterial medicinal products (Doc Ref CPMP/EWP/2655/99) http://www.tga.gov.au/pdf/euguide/ewp265599en.pdf.
- 11. [March 2014];Guidance on Evaluation of Medicinal Products Indicated for Treatment of Bacterial Infections (CPMP/EWP/558/95 rev2) http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003417.pdf.
- 12.Wade KC, Wu D, Kaufman DA, Ward RM, Benjamin DK, Jr, Sullivan JE, et al. Population pharmacokinetics of fluconazole in young infants. Antimicrob Agents Chemother. 2008;52(11):4043–9. doi: 10.1128/AAC.00569-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Watt K, Benjamin DK, Jr, Cohen-Wolkowiez M. Pharmacokinetics of antifungal agents in children. Early Hum Dev. 2011;87(Suppl 1):S61–5. doi: 10.1016/j.earlhumdev.2011.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roos JF, Kirkpatrick CM, Tett SE, McLachlan AJ, Duffull SB. Development of a sufficient design for estimation of fluconazole pharmacokinetics in people with HIV infection. Br J Clin Pharmacol. 2008;66(4):455–66. doi: 10.1111/j.1365-2125.2008.03247.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fluconazole product monograph. Omega Laboratories; Montreal, Canada: [Google Scholar]
- 16.Dash AK, Elmquist WF. Fluconazole. Analytical Profiles of Drug Substances and Excipients. 2001;27:67–113. [Google Scholar]
- 17.Debruyne D, Ryckelynck JP. Clinical pharmacokinetics of fluconazole. Clin Pharmacokinet. 1993;24(1):10–27. doi: 10.2165/00003088-199324010-00002. [DOI] [PubMed] [Google Scholar]
- 18.Yeates RA, Ruhnke M, Pfaff G, Hartmann A, Trautmann M, Sarnow E. The pharmacokinetics of fluconazole after a single intravenous dose in AIDS patients. Br J Clin Pharmacol. 1994;38(1):77–9. doi: 10.1111/j.1365-2125.1994.tb04325.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cella M, Knibbe C, Danhof M, Della Pasqua O. What is the right dose for children? Br J Clin Pharmacol. 2010;70(4):597–603. doi: 10.1111/j.1365-2125.2009.03591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Johnson TN. The problems in scaling adult drug doses to children. Arch Dis Child. 2008;93(3):207–11. doi: 10.1136/adc.2006.114835. [DOI] [PubMed] [Google Scholar]
- 21.Guideline on the Need for Non-Clinical Testing in Juvenile Animals on human pharmaceuticals for paediatric indication. [March 2014];Committee for human medicinal products. http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003306.pdf.
- 22.Mahmood I. Interspecies scaling for the prediction of drug clearance in children: application of maximum lifespan potential and an empirical correction factor. Clin Pharmacokinet. 2010;49(7):479–92. doi: 10.2165/11531830-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 23.Anderson BJ, Holford NH. Mechanism-based concepts of size and maturity in pharmacokinetics. Annu Rev Pharmacol Toxicol. 2008;48:303–32. doi: 10.1146/annurev.pharmtox.48.113006.094708. [DOI] [PubMed] [Google Scholar]
- 24.Peeters MY, Allegaert K, Blussé van Oud-Alblas HJ, Cella M, Tibboel D, Danhof M, et al. Prediction of propofol clearance in children from an allometric model developed in rats, children and adults versus a 0.75 fixed-exponent allometric model. Clin Pharmacokinet. 2010;49(4):269–75. doi: 10.2165/11319350-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 25.Rhodin MM, Anderson BJ, Peters AM, Coulthard MG, Wilkins B, Cole M, et al. Human renal function maturation: a quantitative description using weight and postmenstrual age. Pediatr Nephrol. 2009;24(1):67–76. doi: 10.1007/s00467-008-0997-5. [DOI] [PubMed] [Google Scholar]
- 26.Rostami-Hodjegan A, Tucker GT. Simulation and prediction of in vivo drug metabolism in human populations from in vitro data. Nat Rev Drug Discov. 2007;6(2):140–8. doi: 10.1038/nrd2173. [DOI] [PubMed] [Google Scholar]
- 27.Barrett JS, Della Casa Alberighi O, Läer S, Meibohm B. Physiologically based pharmacokinetic (PBPK) modeling in children. Clin Pharmacol Ther. 2012;92(1):40–9. doi: 10.1038/clpt.2012.64. [DOI] [PubMed] [Google Scholar]
- 28.Johnson TN, Rostami-Hodjegan A, Tucker GT. Prediction of the clearance of eleven drugs and associated variability in neonates, infants and children. Clin Pharmacokinet. 2006;45(9):931–56. doi: 10.2165/00003088-200645090-00005. [DOI] [PubMed] [Google Scholar]
- 29.Zhao W, Lopez E, Biran V, Durrmeyer X, Fakhoury M, Jacqz-Aigrain E. Vancomycin continuous infusion in neonates: dosing optimisation and therapeutic drug monitoring. Arch Dis Child. 2013;98(6):449–53. doi: 10.1136/archdischild-2012-302765. [DOI] [PubMed] [Google Scholar]
- 30.van den Anker JN, Schwab M, Kearns GL. Developmental pharmacokinetics. Handb Exp Pharmacol. 2011;205:51–75. doi: 10.1007/978-3-642-20195-0_2. [DOI] [PubMed] [Google Scholar]
- 31.Chen N, Aleksa K, Woodland C, Rieder M, Koren G. Ontogeny of drug elimination by the human kidney. Pediatr Nephrol. 2006;21(2):160–8. doi: 10.1007/s00467-005-2105-4. [DOI] [PubMed] [Google Scholar]
- 32.Piper L, Smith PB, Hornik CP, Cheifetz IM, Barrett JS, Moorthy G, et al. Fluconazole loading dose pharmacokinetics and safety in infants. Pediatr Infect Dis J. 2011;30(5):375–8. doi: 10.1097/INF.0b013e318202cbb3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.De Cock RF, Piana C, Krekels EH, Danhof M, Allegaert K, Knibbe CA. The role of population PK-PD modelling in paediatric clinical research. Eur J Clin Pharmacol. 2011;67(Suppl 1):5–16. doi: 10.1007/s00228-009-0782-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hooker AC, Staatz CE, Karlsson MO. Conditional weighted residuals (CWRES): a model diagnostic for the FOCE method. Pharm Res. 2007;24(12):2187–97. doi: 10.1007/s11095-007-9361-x. [DOI] [PubMed] [Google Scholar]
- 35.Lindbom L, Ribbing J, Jonsson EN. Perl-speaks-NONMEM (PsN)—a Perl module for NONMEM related programming. Comput Methods Programs Biomed. 2004;75(2):85–94. doi: 10.1016/j.cmpb.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 36.Brendel K, Comets E, Laffont C, Laveille C, Mentré F. Metrics for external model evaluation with an application to the population pharmacokinetics of gliclazide. Pharm Res. 2006;23(9):2036–49. doi: 10.1007/s11095-006-9067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Comets E, Brendel K, Mentré F. Computing normalised prediction distribution errors to evaluate nonlinear mixed-effect models: the npde add-on package for R. Comput Methods Programs Biomed. 2008;90(2):154–66. doi: 10.1016/j.cmpb.2007.12.002. [DOI] [PubMed] [Google Scholar]
- 38.Mahmood I, Balian JD. Interspecies scaling: predicting clearance of drugs in humans. Three different approaches. Xenobiotica. 1996;26(9):887–95. doi: 10.3109/00498259609052491. [DOI] [PubMed] [Google Scholar]
- 39.Sinha VK, De Buck SS, Fenu LA, Smit JW, Nijsen M, Gilissen RA, et al. Predicting oral clearance in humans: how close can we get with allometry? Clin Pharmacokinet. 2008;47(1):35–45. doi: 10.2165/00003088-200847010-00004. [DOI] [PubMed] [Google Scholar]
- 40.Sinha VK, Vaarties K, De Buck SS, Fenu LA, Nijsen M, Gilissen RA, et al. Towards a better prediction of peak concentration, volume of distribution and half-life after oral drug administration in man, using allometry. Clin Pharmacokinet. 2011;50(5):307–18. doi: 10.2165/11539250-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 41.Sacher GA. Relation of lifespan to brain weight and body weight in mammals. In: wolstenholme GEW, O'Connor M, editors. Ciba Foundation Symposium - The Lifespan of Animals (Colloquia on Ageing) 1959. pp. 115–141. [Google Scholar]
- 42.Ullner PM, Di Nardo A, Goldman JE, Schobel S, Yang H, Engelstad K, et al. Murine Glut-1 transporter haploinsufficiency: postnatal deceleration of brain weight and reactive astrocytosis. Neurobiol Dis. 2009;36(1):60–9. doi: 10.1016/j.nbd.2009.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Craig AJ, Ramzan I, Malik R. Pharmacokinetics of fluconazole in cats after intravenous and oral administration. Res Vet Sci. 1994;57(3):372–6. doi: 10.1016/0034-5288(94)90133-3. [DOI] [PubMed] [Google Scholar]
- 44.Mallo KM, Harms CA, Lewbart GA, Papich MG. Pharmacokinetics of fluconazole in loggerhead sea turtles (Caretta caretta) after single intravenous and subcutaneous injections, and multiple subcutaneous injections. J Zoo Wildl Med. 2002;33(1):29–35. doi: 10.1638/1042-7260(2002)033[0029:POFILS]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 45.Clancy CJ, Staley B, Nguyen MH. In vitro susceptibility of breakthrough Candida bloodstream isolates correlates with daily and cumulative doses of fluconazole. Antimicrob Agents Chemother. 2006;50(10):3496–8. doi: 10.1128/AAC.00741-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Clancy CJ, Yu VL, Morris AJ, Snydman DR, Nguyen MH. Fluconazole MIC and the fluconazole dose/MIC ratio correlate with therapeutic response among patients with candidemia. Antimicrob Agents Chemother. 2005;49(8):3171–7. doi: 10.1128/AAC.49.8.3171-3177.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]


