Each‐step activation of oxidative phosphorylation is necessary to explain muscle metabolic kinetic responses to exercise and recovery in humans

Key points

• The basic control mechanisms of oxidative phosphorylation (OXPHOS) and glycolysis during work transitions in human skeletal muscle are still a matter of debate.

• We used simulations of skeletal muscle bioenergetics to identify key system features that contribute to this debate, by comparing kinetic model outputs with experimental human data, including phosphocreatine, pH, pulmonary oxygen uptake and fluxes of ATP production by OXPHOS (vOX), anaerobic glycolysis and creatine kinase in moderate and severe intensity exercise transitions.

• We found that each‐step activation of particular OXPHOS complexes, NADH supply and glycolysis, and strong (third‐order) glycolytic inhibition by protons was required to reproduce observed phosphocreatine, pH and vOX kinetics during exercise.

• A slow decay of each‐step activation during recovery, which was slowed further following severe exercise, was necessary to reproduce the experimental findings.

• Well‐tested computer models offer new insight in the control of the human skeletal muscle bioenergetic system during physical exercise.

Abstract

To better understand muscle bioenergetic regulation, a previously‐developed model of the skeletal muscle cell bioenergetic system was used to simulate the influence of: (1) each‐step activation (ESA) of NADH supply (including glycolysis) and oxidative phosphorylation (OXPHOS) complexes and (2) glycolytic inhibition by protons on the kinetics of ATP synthesis from OXPHOS, anaerobic glycolysis and creatine kinase. Simulations were fitted to previously published experimental data of ATP production fluxes and metabolite concentrations during moderate and severe intensity exercise transitions in bilateral knee extension in humans. Overall, the computer simulations agreed well with experimental results. Specifically, a large (>5‐fold) direct activation of all OXPHOS complexes was required to simulate measured phosphocreatine and OXPHOS responses to both moderate and severe intensity exercise. In addition, slow decay of ESA was required to fit phosphocreatine recovery kinetics, and the time constant of ESA decay was slower following severe (180 s) than moderate (90 s) exercise. Additionally, a strong inhibition of (anaerobic) glycolysis by protons (glycolytic rate inversely proportional to the cube of proton concentration) provided the best fit to the experimental pH kinetics, and may contribute to the progressive increase in oxidative ATP supply during acidifying contractions. During severe‐intensity exercise, an ‘additional’ ATP usage (a 27% increase at 8 min, above the initial ATP supply) was necessary to explain the observed ${\dot{V}}_{{\mathrm{O}}_2}$ slow component. Thus, parallel activation of ATP usage and ATP supply (ESA), and a strong inhibition of ATP supply by anaerobic glycolysis, were necessary to simulate the kinetics of muscle bioenergetics observed in humans.

Key points

• The basic control mechanisms of oxidative phosphorylation (OXPHOS) and glycolysis during work transitions in human skeletal muscle are still a matter of debate.

• We used simulations of skeletal muscle bioenergetics to identify key system features that contribute to this debate, by comparing kinetic model outputs with experimental human data, including phosphocreatine, pH, pulmonary oxygen uptake and fluxes of ATP production by OXPHOS (vOX), anaerobic glycolysis and creatine kinase in moderate and severe intensity exercise transitions.

• We found that each‐step activation of particular OXPHOS complexes, NADH supply and glycolysis, and strong (third‐order) glycolytic inhibition by protons was required to reproduce observed phosphocreatine, pH and vOX kinetics during exercise.

• A slow decay of each‐step activation during recovery, which was slowed further following severe exercise, was necessary to reproduce the experimental findings.

• Well‐tested computer models offer new insight in the control of the human skeletal muscle bioenergetic system during physical exercise.

Abbreviations

A_GL

relative activation of glycolysis

A_OX

relative activation of oxidative phosphorylation

A_UT

relative activation of ATP utilization

CK

creatine kinase

ESA

each‐step activation

KE

bilateral knee extension exercise

MAS

malate/aspartate shuttle

OXPHOS

oxidative phosphorylation

PCr

phosphocreatine

P_i

inorganic phosphate

S_CK

stoichiometry of proton production/consumption by CK

TCA

tricarboxylic acid cycle

vCK

muscle ATP production by creatine kinase

vGL

muscle ATP production by anaerobic glycolysis

vOX

muscle ATP production by oxidative phosphorylation

vUT

muscle ATP utilization (ATP hydrolysis)

${\dot{V}}_{{\mathrm{O}}_2}$

oxygen uptake (muscle or pulmonary)

Introduction

The basic mechanisms of the control of the skeletal muscle cell bioenergetic system, especially oxidative phosphorylation (OXPHOS), during work transitions are still a matter of debate. According to the original proposition by Chance & Williams (1955), based on studies on isolated mitochondria, only ATP usage (actomyosin‐ATPase and Ca²⁺‐ATPase) is directly activated by Ca²⁺ during rest‐to‐work transition in skeletal muscle, whereas the ATP‐supply system, including O₂‐consuming OXPHOS (${\dot{V}}_{{\mathrm{O}}_2}$), is activated indirectly through negative feedback via increased sarcoplasmic concentration of the products of ATP hydrolysis: ADP and P_i. Several theoretical models assume this mechanism, either explicitly or implicitly (Wilson et al. 1979; Wu et al. 2007; Wilson, 2015).

Jeneson et al. (1996) postulated that the mechanistic ${\dot{V}}_{{\mathrm{O}}_2}$‐[ADP] dependence is at least second‐order. The discovery that three tricarboxylic acid (TCA) cycle dehydrogenases (pyruvate dehydrogenase, isocitrate dehydrogenase, 2‐oxoglutarate dehydrogenase) are activated by Ca²⁺ ions (Hansford, 1980; Denton & McCormack, 1990) led to the postulate that the NADH‐supply system is directly activated together with ATP usage. This possibility was supported by the discovery of a large stimulation of ${\dot{V}}_{{\mathrm{O}}_2}$ in isolated brain mitochondria by Ca²⁺ ions acting through activation of the malate/aspartate shuttle (MAS) (Gellerich et al. 2012).

A general model of parallel activation of ATP usage and ATP supply during muscle contractions was postulated by Hochachka (1994), although this did not specify which particular enzymes/metabolic blocks in the ATP supply system were activated. It was subsequently proposed that not only ATP usage and NADH supply (including glycolysis), but also all OXPHOS complexes (complex I, complex III, complex IV, ATP synthase, ATP/ADP carrier, P_i carrier) are directly activated by some cytosolic mechanism predominantly involving cytosolic Ca²⁺ ions, calmodulin‐like protein and protein phosphorylation during the rest‐to‐work transition in skeletal and heart muscle cells (Korzeniewski, 1998; Korzeniewski, 2003; Korzeniewski, 2007; Korzeniewski, 2014; Korzeniewski, 2015). This process is termed each‐step activation (ESA) (Korzeniewski, 2014). In skeletal muscle, a mixed mechanism is probably manifest, in which all OXPHOS complexes are directly activated, but to a smaller extent than ATP usage, and therefore a moderate increase in [ADP] and [P_i] co‐operates with ESA to bring about OXPHOS activation (Korzeniewski, 2014). In intact heart muscle in vivo, there is no (or an extremely small) change in metabolite concentrations during work transitions (Katz et al. 1989). Therefore, although high expression of OXPHOS components may explain, in part, the a high sensitivity of ATP supply to very small changes in muscle metabolites, a ‘perfect’ ESA, directly activating both ATP usage and OXPHOS to the same extent, has been suggested to operate in intact heart in vivo (Korzeniewski, 2014). The possibility of the parallel activation of ATP demand and ATP supply during the rest‐to‐work transition in skeletal muscle was supported by Wüst et al. (2011) on the basis of experimental measurement of changes of muscle ${\dot{V}}_{{\mathrm{O}}_2}$ and [PCr] after the onset of electrically‐stimulated contractions in the canine hind limb. Nevertheless, evidence supporting or refuting ESA has proven technically challenging in human muscle as a result of the complexity involved in determining, at the necessary high temporal resolution, instantaneous intramuscular metabolite concentrations, fluxes and relative activities of the various components of the bioenergetics systems during exercise.

Additionally, it has been demonstrated both in vitro (Connet & Sahlin, 1996) and in intact human skeletal muscle (Sutton et al. 1981) that cytosolic acidification inhibits (anaerobic) glycolysis. Thus, during high‐intensity exercise characterized by a progressive metabolic acidosis, glycolytic inhibition may contribute to increasing the demands of ATP provision from OXPHOS.

The ESA mechanism was proposed mainly on the basis of theoretical studies carried out using a computer model of the skeletal muscle bioenergetic system developed previously (Korzeniewski, 1998; Korzeniewski & Zoladz, 2001; Korzeniewski & Liguzinski, 2004). This model includes a simple, semi‐quantitative inhibition of glycolysis by protons, in which the rate of glycolysis is inversely proportional to the instantaneous H⁺ concentration (the simplest possible description) (Korzeniewski & Liguzinski, 2004). Recent investigation led to the proposal that the inhibition of ATP supply from anaerobic glycolysis by progressive H⁺ ion accumulation, together with a slow decrease of ATP supply by creatine kinase (CK) and an additional progressive increase in ATP demand, may contribute importantly to the progressive increase in ${\dot{V}}_{{\mathrm{O}}_2}$ seen during high‐intensity constant power exercise: the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ slow component (Korzeniewski & Zoladz, 2015). The pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ slow component is generated principally within the exercising skeletal muscles (Poole et al. 1991).

Although this computational model was extensively verified by comparison with various experimentally measured parameter and variable values and system properties (Korzeniewski, 2007; Korzeniewski, 2014), rarely has a direct comparison with biological data been made that would provide a satisfying, strictly quantitative, verification of the model and its postulates. This is mainly because the necessary in vivo measurements of several different variables during rest‐to‐work and work‐to‐rest transitions below the lactate threshold (moderate intensity) and above critical power (severe intensity) were not previously available. Recently, several different system variables, including time courses of pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$, PCr and pH during transitions to and from moderate and severe intensity exercise, as well as the rate of ATP supply by OXPHOS (vOX), CK (vCK) and anaerobic glycolysis (vGL) after 3 and 8 min of exercise during bilateral knee extension (KE) in humans, were measured (Cannon et al. 2014). These data constitute an excellent reference point for computer model validation.

In the present study, we tested the previously‐developed computer model of the skeletal muscle bioenergetic system (Korzeniewski, 1998; Korzeniewski & Zoladz, 2001; Korzeniewski & Liguzinski, 2004) by direct comparison of computer simulations with published experimental data for transitions to and from moderate and severe intensity KE exercise in humans (Cannon et al. 2014). We hypothesized that a high intensity of ESA is necessary to account for the measured changes in fluxes and metabolite concentrations, as well as for the shape of time courses of these variables during transitions from rest to moderate or severe exercise and back to rest. We expected that ESA decays slowly during muscle recovery after exercise and that the characteristic decay time is longer after severe exercise than after moderate exercise. Finally, we tested the hypothesis that a progressive increase in ATP usage during exercise and a strong glycolytic inhibition by protons in severe intensity exercise could account for the relative magnitude of the ${\dot{V}}_{{\mathrm{O}}_2}$ and vOX slow component measured in vivo.

Methods

Ethical approval

The human data used in the present study for comparison with computational simulations were published previously (Cannon et al. 2014). All procedures were approved by The Biological Sciences Faculty Research Ethics Committee, University of Leeds, and the University of Liverpool Committee on Research Ethics, and complied with the latest revision of the Declaration of Helsinki. Written informed consent was obtained from all volunteers prior to their participation in the study. Further details on the experimental human data are available in Cannon et al. (2014).

Computer model

The theoretical model of the skeletal muscle cell bioenergetics including anaerobic glycolysis developed by Korzeniewski and Liguzinski (2004), based on earlier models by Korzeniewski and Zoladz (2001) and Korzeniewski (1998), was used in the present study. This model comprises particular OXPHOS complexes (complex I, complex III, complex IV, ATP synthase, ATP/ADP carrier, P_i carrier), anaerobic glycolysis, CK, ATP usage, NADH supply, and proton efflux and influx.

The model has been broadly validated by comparison of its predictions with the experimental data and was used in numerous theoretical studies (Korzeniewski, 2007; Korzeniewski, 2011; Korzeniewski 2014). The complete model description of the skeletal muscle bioenergetic system including anaerobic glycolysis is available online (http://awe.mol.uj.edu.pl/∼benio).

Simulation procedures

We aimed to model the on‐ (rest‐to‐work) and off‐ (work‐to‐rest) transition during exercise in human skeletal muscle during bilateral KE (Cannon et al. 2014). These published data used magnetic resonance spectroscopy of the quadriceps and pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ to measure the kinetics of muscle and whole‐body bioenergetics during and after 3 and 8 min of moderate and severe intensity KE exercise in healthy young humans (n = 13, one female; mean ± SD: age, 27 ± 8 years; height, 177 ± 8 cm; mass, 75 ± 12 kg).

Simulations were made for two exercise intensities: moderate‐intensity exercise below the lactate threshold and severe‐intensity exercise above critical power. It should be noted that critical power was not measured in the original study by Cannon et al. (2014). However, based on the non‐steady‐state behaviour of pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ and intramuscular metabolism, the exercise intensity in (Cannon et al. 2014) is assumed to be above critical power (Poole et al. 1988; Jones et al. 2008): variably termed very‐heavy or severe intensity exercise (Rossiter, 2011). Based on the experimental data, we adjusted the activity (rate constant) of ATP usage (hydrolysis, A _UT) to be elevated by 22‐fold during transition from rest to moderate‐intensity exercise, and by 47‐fold during transition from rest to severe‐intensity exercise. This gave the value of muscle ${\dot{V}}_{{\mathrm{O}}_2}$ equal to ∼2.6 mm min⁻¹ (58 ml kg⁻¹min⁻¹) after 8 min of moderate‐intensity exercise and ∼6.7 mm min⁻¹ (150 ml kg⁻¹min⁻¹) after 8 min of severe‐intensity exercise. Subsequently, model parameter values were adjusted independently for moderate and severe exercise, aiming to best fit the experimental data for the kinetics of muscle PCr, pH, vOX, vCK and vGL.

The activation of oxidative phosphorylation (A _OX; the relative increase of rate constants of complex I, complex III, complex IV, ATP synthase, ATP/ADP carrier, P_i carrier and NADH supply) (Korzeniewski, 1998; Korzeniewski, 2003; Korzeniewski, 2007; Korzeniewski, 2014) was adjusted following an exponential time course at exercise onset:

$$m_{\mathrm{ox}}=A_{\mathrm{OX}}-\left(A_{\mathrm{OX}}-1\right)·e^{-\mathrm{t}/\tau \left({\mathit{ON}}_{\mathrm{OX}}\right)}$$ (1)

where m _OX is the current activation (ratio of the current rate constant to the resting rate constant) of OXPHOS, A _OX is the relative activation of OXPHOS during moderate and severe‐intensity exercise, τ(ON_OX) = 3 s is the characteristic time of the activation of oxidative phosphorylation (Korzeniewski, 2003) and t is time after the onset of exercise. τ(ON_OX) was sufficiently small so as not to disturb the on‐transient.

It was assumed that glycolysis was directly activated (A _GL) during rest to moderate and severe intensity exercise transitions, and the magnitude of A _GL was adjusted to best fit the experimental data. The need for this strong direct parallel activation of glycolysis was demonstrated previously (Korzeniewski & Liguzinski, 2004). The increase in the rate constant of glycolysis was not instantaneous but occurred exponentially:

$$m_{\mathrm{GL}}=A_{\mathrm{GL}}-\left(A_{\mathrm{GL}}-1\right)·e^{-\mathrm{t}/\tau \left({\mathit{ON}}_{\mathrm{GL}}\right)}$$ (2)

where m _GL is the current activation (ratio of the current rate constant to the resting rate constant of glycolysis), A _GL is the relative activation of glycolysis during exercise, τ(ON_GL) = 6 s is the characteristic time for the activation of glycolysis and t is time after the onset of exercise. τ(ON_GL) was sufficiently small so as not to disturb the on‐transient.

After termination of exercise, the rate constants of ATP usage and glycolysis were decreased instantly to the initial (rest) values. The rate constants of oxidative phosphorylation complexes decreased exponentially according to the equation (Korzeniewski, 2003):

$$m_{\mathrm{OX}}=1+\left(A_{\mathrm{OX}}-1\right)·e^{-\mathrm{t}/\tau \left({\mathit{OFF}}_{\mathrm{OX}}\right)}$$ (3)

where m _OX is the current activation (ratio of the current rate constant to the resting rate constant) of OXPHOS, A _OX is the relative direct activation of OXPHOS during exercise, τ(OFF_OX) = 90 s and 180 s are the characteristic decay times of the activation of oxidative phosphorylation for moderate and severe exercise, respectively, and t is time after the onset of exercise.

There was no additional progressive component for ATP usage during moderate exercise. During severe exercise, to fit the experimental data, a linear increase in ATP usage was included, beginning at 100% of the ‘fundamental’ ATP usage rate (the rate at the immediate onset of exercise) and continuing until the end of exercise at 8 min (Paterson & Whipp, 1991; Barstow & Molé, 1991). This mechanism underlying the system behaviour of A _UT should not be confused with the behaviour of vOX itself (which is commonly approximated by a bi‐exponential).

The influence of glycolytic inhibition by protons was interrogated using two different inhibitory states: moderate and strong. The rate of glycolysis for moderate glycolytic inhibition by protons was described by a simple, semi‐quantitative equation (Korzeniewski & Liguzinski, 2004):

$$v_{\mathrm{GLYC}}=k_{\mathrm{GLYC}}·AD{P}_{\mathrm{te}}·(H_{\mathrm{rest}}^{+}/H^{+})$$ (4)

where k _GLYC is the rate constant of glycolysis, ADP_te is the cytosolic total (magnesium‐bound and magnesium‐free) free ADP concentration, H⁺ _rest = 10⁻⁷ m (pH 7.0) is the resting proton concentration and H⁺ is the current proton concentration.

The rate of glycolysis for strong glycolytic inhibition by protons was described by the simple equation:

$$v_{\mathrm{GLYC}}=k_{\mathrm{GLYC}}·AD{P}_{\mathrm{te}}·{(H_{\mathrm{rest}}^{+}/H^{+})}^3$$ (5)

Therefore, it was assumed that the rate of glycolysis was inversely proportional to the cube of the current proton concentration.

Three computer simulations were carried out to identify the best‐fit parameter values and conditions [A _OX, A _GL, τ(OFF_OX), magnitude of ‘additional’ ATP usage, and moderate or strong inhibition of glycolysis by protons] during moderate and severe intensity exercise.

• Simulation 1: Severe exercise with moderate glycolytic inhibition by protons

• Simulation 2: Severe exercise with strong glycolytic inhibition by protons

• Simulation 3: Moderate exercise with strong glycolytic inhibition by protons

Simulations 1 and 2 first established the set of system characteristics that best fit the experimental data under conditions where fluxes, metabolite concentrations and, in particular, pH were most disturbed (severe exercise). Subsequently, simulation 3 was conducted using moderate exercise with the parameters of glycolytic inhibition established by the best fit from simulations 1 and 2.

Results

The computer simulations performed in the present study were compared with the experimental data for transitions to and from moderate and severe intensity KE exercise in humans as published previously (Cannon et al. 2014).

Figure 1 shows the results of Simulation 1. The best‐fit model values with moderate glycolytic inhibition by protons (eqn 4) were: A _UT = 47, A _OX = 47^0.43 (5.24‐fold), A _GL = 47^0.65 (12.21‐fold), τ(OFF_OX) = 180 s, ‘additional’ ATP usage = 27%. The simulated kinetics of PCr (% of resting value) and pH, as well as the values of ATP supply by OXPHOS (vOX), CK (vCK) and anaerobic glycolysis (vGL) at 3 and 8 min of severe exercise with moderate glycolytic inhibition by protons (eqn 4), agreed well with the experimental data. Muscle ${\dot{V}}_{{\mathrm{O}}_2}$, PCr, pH, ADP, vOX, vCK, vGL and ATP usage (vUT) did not reach a steady state, but progressively changed during exercise (${\dot{V}}_{{\mathrm{O}}_2}$, ADP, vUT and vOX increased, whereas PCr, pH, vCK and vGL decreased). The main small differences between the simulation and the experimental data were a slower decrease in pH and a smaller magnitude of the initial transient alkalosis in the simulation. The former is most probably the result of insufficient glycolytic inhibition by protons (see Simulation 2). The latter is probably a result of the stoichiometry of proton consumption and production by the CK in the Lohmann reaction. The dependence of this stoichiometry on pH was extracted from Kushmerick (1997) and is S _CK = 0.63 – (pH – 6.0) × 0.43; which gives ∼0.2 for pH ∼7.0. For a higher value of S _CK, a more pronounced initial transient alkalosis was obtained in computer simulations (not shown).

Figure 1. Comparison of simulated (lines) and experimental (points) time course of PCr (percentage of resting values), pH (A) and ATP supply flux (B) during severe intensity rest‐to‐exercise‐to‐recovery transitions with moderate glycolytic inhibition by protons (Simulation 1) .

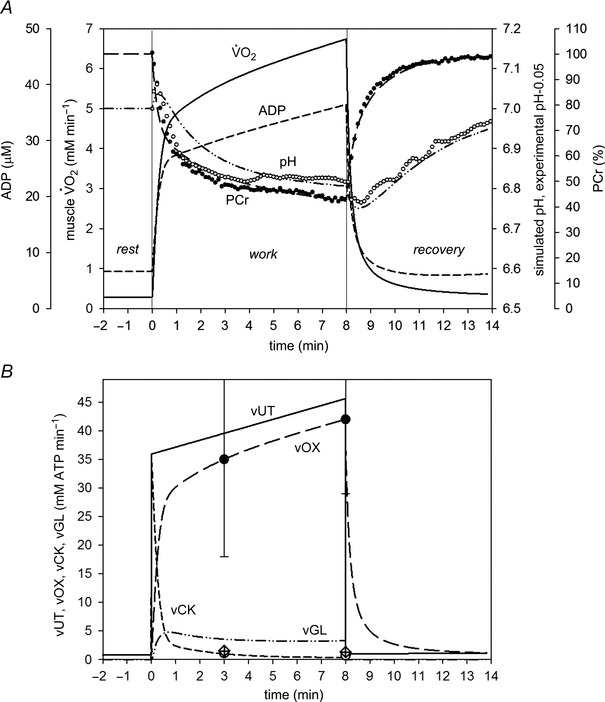
Time course of simulated muscle ${\dot{V}}_{{\mathrm{O}}_2}$ and ADP is also shown. Experimental points for bilateral KE exercise in humans were taken from Cannon et al. (2014). Vertical lines indicate the onset and cessation of exercise. vOX, ATP supply rate by OXPHOS; vCK, ATP supply rate by CK; vGL, ATP supply rate by anaerobic glycolysis; vUT, muscle ATP utilization (ATP hydrolysis). 0.05 was subtracted from experimental pH values to scale experimental pH at rest to the value of 7.0, used in computer simulations.

Additionally, a large slow component of the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ on kinetics appeared in this simulation (Simulation 1). This was caused not only mostly by an increase in ATP utilization during exercise (from 100% to 127% of the ‘fundamental’ rate of ATP turnover), but also, to a small extent, by a moderate inhibition of ATP supply by anaerobic glycolysis (vGL) by accumulating protons as exercise progressed, necessitating a supplementary increase in the ATP supply from OXPHOS (vOX) (Korzeniewski & Zoladz, 2015).

The introduction of a strong glycolytic inhibition by protons (eqn 5; glycolytic flux inversely proportional to the cube of the current proton concentration) for severe exercise, together with a stronger direct glycolytic activation at the onset of exercise (Simulation 2), significantly speeded the kinetics of the early intracellular pH response but did not affect the pH value after 8 min of exercise. This can be seen in Fig. 2. In Simulation 2, with strong glycolytic inhibition by protons (eqn 5), the model values were: A _UT = 47, A _OX = 47^0.43 (5.24‐fold), A _GL = 47^0.87 (28.49‐fold), τ(OFF_OX) = 180 s, ‘additional’ ATP usage = 27%. This simulation gave a much better fit to the experimentally‐measured time course of pH without influencing significantly the time course of PCr relative to the good fit observed in Simulation 1 (Fig. 2). The high direct activation of (anaerobic) glycolysis led to a rapid decrease in pH after the onset of exercise, whereas the strong (anaerobic) glycolytic inhibition by protons that took place afterwards (slowing vGL) prevented excessive cytosolic acidification. Generally, an excellent agreement of theoretical predictions with the experimental data was observed in this simulation. Not only time courses of PCr and pH, but also the values of ATP production by OXPHOS (vOX), CK (vCK) and anaerobic glycolysis (vGL) agreed well with the experimental data. The relative increase of the slow component of the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ on‐kinetics measured between 3 and 8 min of exercise in this simulation (20%) was similar to that of the measured pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ (22 ± 8%) (Cannon et al. 2014). Anaerobic glycolysis was strongly directly activated after the onset of exercise, which significantly elevated the initial ATP synthesis by this process. However, as exercise progressed, glycolysis was strongly (third‐order dependence) inhibited by accumulating protons, meaning that a significant additional fraction of ATP supply was provided by oxidative phosphorylation. The additional requirement for vOX can be observed in the reduction of vGL in Fig. 2, between the peak at ∼0.75 min and end‐exercise (8 min). In Simulation 2, both the strong (anaerobic) glycolytic inhibition by protons and the ‘additional’ ATP usage increasing during exercise from 0% of the ‘fundamental’ ATP usage at the onset of exercise to 27% after 8 min of exercise contributed to the slow component of the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ on‐kinetics.

Figure 2. Comparison of simulated (lines) and experimental (points) time course of PCr (percentage of resting values), pH (A) and ATP supply flux (B) during severe intensity rest‐to‐exercise‐to‐recovery transitions with strong glycolytic inhibition by protons (Simulation 2) .

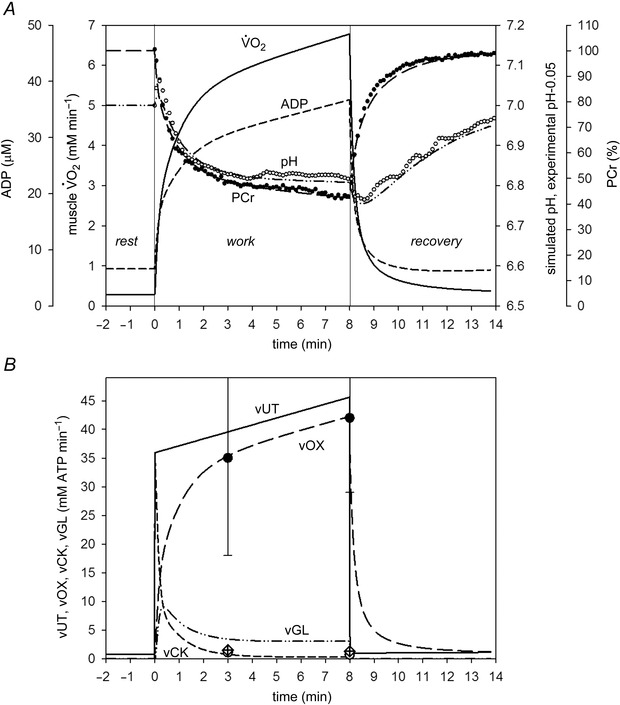
Time course of simulated muscle ${\dot{V}}_{{\mathrm{O}}_2}$ and ADP is also shown. Experimental points for bilateral KE exercise in humans were taken from Cannon et al. (2014). Vertical lines indicate the onset and cessation of exercise. vOX, ATP supply rate by OXPHOS; vCK, ATP supply rate by CK; vGL, ATP supply rate by anaerobic glycolysis; vUT, muscle ATP utilization (ATP hydrolysis). 0.05 was subtracted from experimental pH values to scale experimental pH at rest to the value of 7.0, used in computer simulations.

Simulation 3 (for moderate exercise and strong glycolysis inhibition by protons) also generally agreed very well with the experimental data reported by Cannon et al. (2014). This is shown in Fig. 3. The model values for moderate exercise with strong glycolytic inhibition by protons (eqn 5) were: A _UT = 22, A _OX = 22^0.56 (5.64‐fold), A _GL = 22^0.85 (13.84‐fold), τ(OFF_OX) = 90 s, ‘additional’ ATP usage = 0%. As expected, both experimental and simulated fluxes and metabolite concentrations during moderate exercise rest‐to‐work and work‐to‐rest transitions changed much less than during severe exercise. Additionally, unlike during severe exercise, a steady‐state was achieved after ∼3 min of exercise. The only exception appears to be that the mean experimental measurement of vOX after 3 min of exercise is greater than the simulation. vOX is 35% greater at 3 min than after 8 min of moderate exercise. However, although this difference is apparently large, as shown in the original study (Cannon et al. 2014), it was not statistically significant (Fig. 3). Of course, a difference in vOX between 3 and 8 min of exercise could not be reconciled with the presence of the steady‐state in the time course of the pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$, PCr and pH observed in this experiment for moderate exercise (Cannon et al. 2014), and is probably the result of variability in the measurement of this variable within subjects (see Discussion). However, it is not possible to know whether the variability influences to a greater extent the values at 3 or 8 min. In the present study, as in Cannon et al. (2014), we assumed that the 3 min pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ value ‘overshoots’ the expected steady state, albeit, non‐significantly. Nevertheless, adjusting the simulations to give vUT (and vOX) that was intermediate between 3 and 8 min of moderate exercise (i.e. 20 mm min⁻¹) did not substantially change the relative agreement between the experimental and simulated fluxes and metabolite concentrations (simulation not shown).

Figure 3. Comparison of simulated (lines) and experimental (points) time course of PCr (percentage of resting values), pH (A) and ATP supply flux (B) during moderate intensity rest‐to‐exercise‐to‐recovery transitions with strong glycolytic inhibition by protons (Simulation 3) .

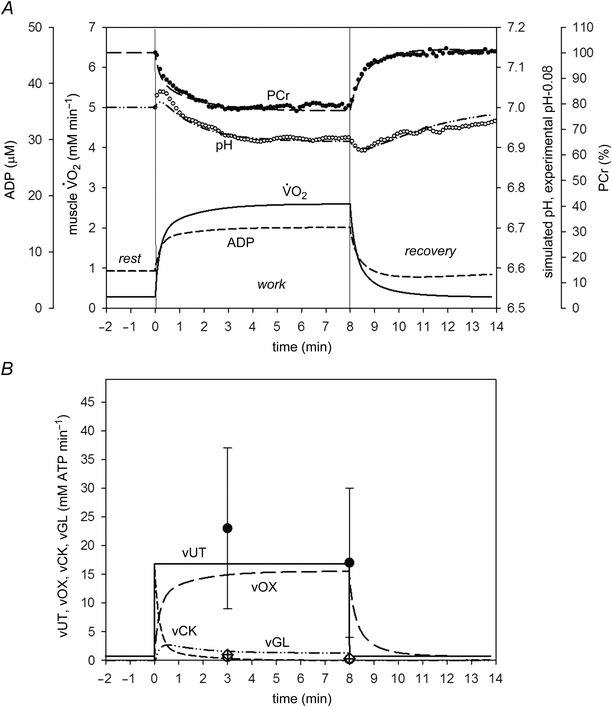
Time course of simulated muscle ${\dot{V}}_{{\mathrm{O}}_2}$ and ADP is also shown. Experimental points for bilateral KE exercise in humans were taken from Cannon et al. (2014). Vertical lines indicate the onset and cessation of exercise. vOX, ATP supply rate by OXPHOS; vCK, ATP supply rate by CK; vGL, ATP supply rate by anaerobic glycolysis; vUT, muscle ATP utilization (ATP hydrolysis). 0.08 was subtracted from experimental pH values to scale experimental pH at rest to the value of 7.0, used in computer simulations.

Discussion

The first objective of the present theoretical study was to determine whether a computer model of the skeletal muscle bioenergetic system (Korzeniewski, 1998; Korzeniewski & Zoladz, 2001; Korzeniewski & Liguzinski, 2004) was able to reproduce, strictly quantitatively, a particular concrete set of experimental data. Using the data from the experiment conducted by Cannon et al. (2014) as the frame of reference (because it involved simultaneous measurements of the time courses of PCr and pH for rest‐to‐work‐to‐rest transitions during moderate and severe exercise as well as vOX, vCK and vGL after 3 and 8 min of exercise), we found that, overall, the computer simulations produced a very good agreement with the experimental data (Figs 1, 2, 3). This confirmed that the model was able to reproduce correctly the complex set of the modelled system properties, and allowed us to test four specific hypotheses about the relative intensity of ESA and glycolytic inhibition by protons with respect to contributing to the observed metabolite concentrations and fluxes during moderate and severe intensity exercise.

Specifically, the important new findings of the present study were that: (1) high‐intensity ESA accounted for the system behaviour (changes in fluxes and metabolite concentrations during rest‐to‐work‐to‐recovery transitions) in human skeletal muscle during severe and moderate exercise (Figs 2 and 3, respectively); (2) the decay of ESA after exercise was slow, and slowed further by severe‐intensity, compared to moderate‐intensity, exercise (Figs 2 and 3); (3) strong (third‐order dependence) glycolytic inhibition by protons better simulated the time course of pH during severe exercise (Fig. 2) than moderate glycolytic inhibition (Fig. 1); and (4) the relative magnitude of the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component in vivo was better modelled by a large additional ATP usage increasing progressively during exercise together with a strong proton inhibition of (anaerobic) glycolytic flux.

ESA is obligatory for intramuscular bioenergetic flux control during exercise and recovery

The present study emphasizes that an intensive ESA during exercise and slow decay of ESA after termination of exercise are obligatory to reproduce quantitatively the muscle metabolite concentrations and fluxes of experimental data. The direct activation of all OXPHOS complexes and NADH supply (A _OX in computer simulations) is >5‐fold, namely 5.64‐fold and 5.24‐fold during transition from rest to moderate and severe work, respectively. The A _OX is even slightly greater for moderate work, although the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ is much greater for severe work, because the stability of PCr and pH is much better in the former case. ${\dot{V}}_{{\mathrm{O}}_2}$ is determined mostly by the ATP utilization rate (A _UT; as long as the OXPHOS capacity for ATP synthesis is not saturated in the absence of ESA; see below), whereas ESA intensity affects predominantly the stability of metabolite concentrations and their kinetics (Korzeniewski & Zoladz, 2004). The high predicted ESA intensity is not surprising because the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ increases 9.04‐fold during the moderate rest‐to‐exercise transition and 23.45‐fold during the severe rest‐to‐exercise transition, whereas [ADP] increases only 2.17‐fold and 5.49‐fold, respectively. Therefore, the phenomenological ${\dot{V}}_{{\mathrm{O}}_2}$–[ADP] relationship is very steep, much steeper than possible from first‐ or even second‐order rate reactions. An even steeper phenomenological ${\dot{V}}_{{\mathrm{O}}_2}$–[ADP] relationship is observed in some experiments (Wüst et al. 2011; Korzeniewski, 2014). For example, a 40‐fold increase in electrically‐stimulated dog muscle ${\dot{V}}_{{\mathrm{O}}_2}$ is accompanied by only 2.5‐fold increase in [ADP] (Zoladz et al. 2008).

The fact that A _OX was smaller than A _UT implies that OXPHOS is directly activated in parallel with ATP usage during rest‐to‐work transition, whereas OXPHOS activation is less than that of ATP usage. This corresponds to the mixed mechanism of bioenergetics control, where direct activation co‐operates with negative‐feedback activation (through an increase in [ADP] and [P_i]) in the control of OXPHOS (Korzeniewski, 2014).

Without ESA (A _OX = 1), the system collapses during severe exercise (A _UT = 47): [PCr] and [ATP] fall to zero (the latter is converted to ADP, and further by adenylate kinase to AMP), [P_i] and [Cr] increase to maximal values, and a huge cytosolic acidification occurs, whereas maximal muscle ${\dot{V}}_{{\mathrm{O}}_2}$ becomes limited to ∼3.5 mm min⁻¹. Of course, this is only a virtual prediction: in reality, in the absence of ESA, exercise would be slowed or terminated shortly after onset. Without ESA (A _OX = 1) during moderate exercise (A _UT = 22) and for lower ESA (e.g. for A _OX = 3) during moderate (A _UT = 22) and severe (A _UT = 47) exercise, the changes in metabolite concentrations predicted by the model are much greater than for high ESA, and therefore do not well fit the experimental data. Additionally, characteristic transition times (τ) for ${\dot{V}}_{{\mathrm{O}}_2}$ and metabolite concentrations during rest‐to‐work transitions are lengthened under conditions where lower ESA activities are used (Korzeniewski & Zoladz, 2004). Therefore, a decrease in ESA intensity in computer simulations results in wide disagreements with the experimental results.

In the bioenergetic system of the skeletal muscle cell, without ESA, huge changes in metabolite (ADP, PCr, P_i) concentrations take place when the relative ATP demand increases, and the system collapses when the energy demand (rate constant of ATP usage) exceeds the relative value of about A _UT = 30‐fold above resting ATP demand. Under these conditions, ATP and PCr concentrations fall to zero, Cr and P_i concentrations rise to the maximal values, [ADP] first rises to ∼1500 μm and then decreases toward zero as it is converted to AMP (by adenylate kinase) and there is no further increase in muscle ${\dot{V}}_{{\mathrm{O}}_2}$ together with an increase of ATP demand (Liguzinski & Korzeniewski, 2006). In the present study, the relative ATP demand (A _UT) for severe exercise was 47‐fold greater than resting, and is therefore far beyond this ‘collapse threshold’. For this reason, in the absence of ESA, system collapse is observed in simulations of severe intensity exercise conditions. Strong ESA allows moderate changes in muscle metabolite concentrations and pH to take place, whereas ${\dot{V}}_{{\mathrm{O}}_2}$ can reach values far above this threshold (Liguzinski & Korzeniewski, 2006).

Our comparison of computer simulations with the experimental data predicts that a slow decay of ESA takes place during muscle recovery after exercise. The simulated time course of [PCr] during recovery can be fitted to the experimental data only when a slow decay of ESA is assumed; otherwise, the PCr recovery would be much slower (Korzeniewski & Zoladz, 2013). The adjusted values of the characteristic ESA decay time τ(OFF_OX) were 90 s and 180 s for moderate and severe exercise, respectively. This is consistent with previous proposals suggesting that a greater muscle metabolic strain during exercise lengthens τ(OFF_OX), sometimes leading to a transient overshoot in PCr recovery (Korzeniewski & Zoladz, 2005). It appears to be logical that more intensive exercise causes greater muscle metabolic stress and strain. Therefore, in our simulations, ESA was necessary not only to account for the increase in muscle ${\dot{V}}_{{\mathrm{O}}_2}$ and vOX, and changes in metabolites during the on‐transient, but also to explain the system behaviour during the off‐transient.

The molecular mechanism of ESA remains in question. Glancy et al. (2013) showed that the activity of essentially all OXPHOS complexes was sensitive to Ca²⁺: isolated skeletal muscle mitochondria incubated with glutamate/malate and exposed to increased Ca²⁺ were found to increase overall OXPHOS activity by ∼2‐fold. In electrically‐stimulated canine muscle, direct measurement of the ${\dot{V}}_{{\mathrm{O}}_2}$–[ADP] relationship suggested an A _OX of ∼3–4‐fold with a τ(ON_OX) of ∼10 s (Wüst et al. 2011). The present study strongly suggests that OXPHOS complexes are activated directly >5‐fold during rest‐to‐work transitions in humans. In other muscles or under experimental conditions, this direct activation of OXPHOS can be even higher (Korzeniewski, 2014). Cytosolic Ca²⁺ was proposed to act in vivo via some protein analogous to calmodulin that causes protein (e.g. OXPHOS complexes) phosphorylation and that is also absent in the isolated mitochondrial system (Korzeniewski, 1998; Korzeniewski, 2007; Korzeniewski, 2014).

Generally, the consequence of ESA is that the regulation of OXPHOS in intact skeletal muscle is completely different from that in isolated mitochondria (at least in the absence of Ca²⁺). In other words, the resting state in muscles is different from state 4 in isolated mitochondria: there is some ATP usage for ‘basal’ ATP usage by reactions that keep the cell alive (RNA/protein synthesis, ion circulation) that is responsible for ∼40% of muscle ${\dot{V}}_{{\mathrm{O}}_2}$ in rat skeletal muscle, with the remaining ${\dot{V}}_{{\mathrm{O}}_2}$ being a result of proton leak (Rolfe & Brand, 1996). Additionally, moderate and severe exercise states in intact muscle are different from state 3 in isolated mitochondria: ${\dot{V}}_{{\mathrm{O}}_2}$, Δp (protonmotive force) and NADH are much greater, whereas [ADP] and [P_i] are much less in intact muscle (Korzeniewski, 2015). Therefore, experimental data from isolated mitochondria (at least in the absence of Ca²⁺) concerning the regulation of OXPHOS during increase in energy (ATP) demand cannot be simply extrapolated to intact skeletal muscle.

During rest‐to‐work transitions in skeletal muscle, some moderate increase in [ADP] and [P_i] takes place and therefore the negative‐feedback activation by these metabolites co‐operates with ESA in the regulation of OXPHOS (the mixed mechanism; Korzeniewski, 2014). During work transitions in the intact heart in vivo, metabolite (PCr, P_i, ADP, ATP, NADH) concentrations are essentially constant (Katz et al. 1989); in the nomenclature used in the present study, this reflects a ‘pure’ ESA‐controlled system. This is related to the fact that ATP supply is directly activated during low‐to‐high work transition to the same extent as ATP usage (Korzeniewski et al. 2005; Korzeniewski, 2006; Korzeniewski, 2007).

Although the ESA mechanism was proposed previously, the present study constitutes a very significant advance. Previous studies mostly used a semi‐quantitative indirect validation of ESA in relation to steady‐state changes in ${\dot{V}}_{{\mathrm{O}}_2}$ and [ADP] or [PCr] during rest‐to‐work transitions. The present study, however, offers a strictly quantitative direct validation, using: (1) several different variables (${\dot{V}}_{{\mathrm{O}}_2}$, PCr, pH, vOX, vCK, vGL); (2) whole time courses during rest‐to‐work‐to‐recovery transitions; and (3) both moderate and severe intensity exercise. The excellent agreement of computer simulations with the experimental data for such a broad range of system properties greatly supports the ESA mechanism and increases the reliability of the computer model.

In principle, it is possible that a mechanism other than ESA could account for the discussed experimental data. On the other hand, we do not know any probable candidate for such a mechanism. Alternative proposals also would have to explain the great number of different system properties, as well as time and intensity dependence, as explained by the ESA model with strong inhibition of glycolysis by protons, and it is doubtful that two completely different mechanisms would be able to achieve this. We mean not only the system properties simulated in the present study, but also numerous other properties; for example, the uniform distribution of metabolic control among OXPHOS complexes or PCr recovery overshoot, as discussed previously (Korzeniewski, 2007; Korzeniewski, 2011; Korzeniewski, 2014).

Recently Wilson (Wilson, 2015) presented a modified dynamic version of his previous static model (Wilson et al. 1979), involving, for example, the CK system. It was successful in reproducing semi‐quantitatively some system properties; for example, the time course of PCr after the onset of exercise. Although the kinetic description of cytochrome oxidase in this model is very complex, the suggestion that cytochrome oxidase determines the rate of oxygen consumption is not well supported by metabolic control analysis of isolated skeletal muscle mitochondria showing that flux control is more or less evenly distributed among OXPHOS complexes (Rossignol et al. 2000). Although this model proposes to explain the ‘lag phase’ in pulmonary or muscle ${\dot{V}}_{{\mathrm{O}}_2}$ observed in several studies, the extent to which this lag reflects the mitochondria–lung or mitochondria–muscle vein delay in oxygen transport, rather than an actual lag in mitochondrial ${\dot{V}}_{{\mathrm{O}}_2}$ on‐kinetics, remains uncertain. The interpretation of thermodynamic models is complicated because they do not distinguish differing effects of different metabolites (e.g. ADP and P_i). Therefore, in computer modelling, it is crucial to validate a model for the broadest set of variable values and system properties possible, as we have done in the present study and as reported previously (Korzeniewski, 2007; Korzeniewski, 2011; Korzeniewski, 2014).

Mechanisms of the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component in severe intensity exercise

Our original model of the skeletal muscle bioenergetic system with ATP and H⁺ production by anaerobic glycolysis (Korzeniewski & Liguzinski, 2004) included a simple kinetic description of glycolytic inhibition by protons. This description consists of an inverse linear dependence of the glycolytic flux on [H⁺] (Eqn 4) and was used in Simulation 1 (Fig. 1). However, Simulation 2 demonstrated that the time course of pH during on‐transient measured by Cannon et al. (2014) was reproduced better when a stronger glycolytic inhibition by [H⁺] is assumed (Fig. 2): specifically, an inverse dependence of the glycolytic flux on the cube of proton concentration (Eqn 5) (as well as a much stronger direct glycolysis activation after the onset of exercise). This assumption also worked well for moderate exercise (Simulation 3) (Fig. 3). Therefore, the present study provides an improved understanding of the kinetics of control and regulation of glycolytic flux by protons.

It should be emphasized that the kinetic description of the glycolytic inhibition by H⁺ in the model is only phenomenological, and may involve many variables, including buffers whose relative contribution to glycolytic inhibition is intensity‐ and/or pH‐dependent over the physiological ranges investigated, such as ammonia or inorganic phosphate. The phenomenological proton buffering capacity is taken into account within the model. We found that the current phenomenological model of strong glycolytic inhibition explained well both moderate and severe intensity exercise system kinetics.

Korzeniewski & Zoladz (2015) proposed that the two main mechanisms underlying the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component in skeletal muscle (Poole et al. 1994), at least during cycling exercise, are the gradual inhibition of ATP supply by anaerobic glycolysis by protons accumulating during exercise (together with a slow decay of ATP supply by CK) and a progressive increase in ATP utilization during constant power exercise. Although the latter has been frequently supported by experimental studies (Rossiter et al. 2002; Rossiter, 2011; Poole & Jones, 2012; Cannon et al. 2014), the former proposition, specifically linking progressive inhibition of glycolysis to the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component magnitude (Korzeniewski & Zoladz, 2015), remains untested outside of computer simulations.

In the present study, we found that the magnitude of the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ slow component in Simulations 1 and 2 was similar to the magnitude of the pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ slow component measured by Cannon et al. (2014) for bilateral KE exercise in humans. Specifically, the relative increase in muscle ${\dot{V}}_{{\mathrm{O}}_2}$ (and vOX) between 3 and 8 min of exercise was 20% in both simulations, and the relative increase in pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ was 22% in the measured data. This suggests that either moderate or strong glycolytic inhibition by protons contributes to the dynamics of in vivo muscle energetics in general, and to the dynamics of the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component in particular (with strong glycolytic inhibition better reproducing the dynamics of pH), by necessitating a greater vOX as vGL becomes increasingly inhibited by proton accumulation in severe‐intensity exercise in humans.

On the basis of the lack of correlation between the magnitude of the pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ slow component and the ‘slow component’ of the oxidative ATP supply (vOX), it has been proposed that a decrease in the P/O ratio may contribute to the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ on‐kinetics (Cannon et al. 2014). However, the interpretation of this finding is equivocal.

First, as discussed above, because the average relative increases in pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ and in vOX between 3 and 8 min of exercise are very similar, varying P/O ratio among subjects would imply that, in some subjects, P/O decreases over the course of exercise, whereas, in other subjects, it increases. The latter is doubtful. An alternative explanation could be a relatively large variability of vOX values (Figs 1, 2, 3) measured using the method based on the PCr recovery kinetics (see below).

Second, as discussed by Cannon et al. (2014), there are complexities associated with inferring muscle ${\dot{V}}_{{\mathrm{O}}_2}$ kinetics from pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ measurements. In the present study, the experimental pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ (including whole‐body O₂ uptake) is naturally much greater than the simulated muscle ${\dot{V}}_{{\mathrm{O}}_2}$ (isolated to the active muscle in silico) estimated from the oxidative ATP supply (vOX). Using pulmonary gas exchange measurements to infer kinetic changes across the skeletal muscle requires a number of assumptions, including the metabolic contribution of ‘resting tissues’ (basal metabolism in all bodily tissues) and ‘auxiliary tissues’ (activity of respiratory muscles, stabilizing muscles, cardiac muscle etc.) being constant during constant power exercise. With cycling exercise or seated single leg KE exercise, this assumption appears to be reasonable (Grassi et al. 1996; Krustrup et al. 2009) and, thus, the ${\dot{V}}_{{\mathrm{O}}_2}$ slow component can be inferred to be predominantly attributed to isolated active locomotor muscles (Poole et al. 1991). The study by Cannon et al. (2014) used bilateral KE exercise inside a superconducting magnet to measure phosphate metabolism by ³¹P magnetic resonance spectroscopy at the same time as maximizing the muscle mass engaged in the task and simulating conditions such as in walking or cycling. In this model, the contribution of ‘axillary tissues’ appears to be as much as approximately 35–45% of the pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ (assuming 6 or 5 kg of the mass of two active quadriceps, respectively). Importantly, it is not known whether oxygen consumption by these tissues changes substantially during exercise; any increase would contribute to the magnitude of the pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ slow component but not vOX or ${\dot{V}}_{{\mathrm{O}}_2}$in the muscles of interest.

During severe cycling exercise, working muscles are responsible for ∼85% of pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ (Poole et al. 1992), whereas ATP supply by ‘auxiliary tissues’ is ∼8%, as estimated by Liguzinski & Korzeniewski (2007), with the remainder being a result of metabolism in ‘resting tissues’. It appears that this relative contribution is much smaller in severe KE exercise, where the muscle mass activated for the external KE power production is smaller than in running or cycling. Additionally, the only known process that could decrease P/O, namely proton leak through the inner mitochondrial membrane, is estimated to be responsible for only ∼1% of muscle ${\dot{V}}_{{\mathrm{O}}_2}$ during severe exercise (Korzeniewski & Zoladz, 2015), reducing the likelihood that mitochondrial uncoupling contributes substantially to the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ slow component magnitude. Finally, a significant (∼20% at rest) fraction of O₂ is consumed in the skeletal muscle cell by non‐mitochondrial processes (residual oxygen consumption by, for example, NAPDH oxidase, nitric oxide synthase or xanthine oxidase), and not by OXPHOS in mitochondria (Rolfe et al. 1999). However, the possibility that a decrease in P/O contributes to some extent to the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ slow component on transition to KE exercise cannot be excluded.

We did not model the experimentally‐measured pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ (Cannon et al. 2014) because, as discussed above, the ratio of ‘active’ to ‘axillary’ and ‘resting’ tissues ${\dot{V}}_{{\mathrm{O}}_2}$ is unknown and may vary during exercise, and the outcome of the simulation rests entirely on the ratio selected. Additionally, a slow decay of ${\dot{V}}_{{\mathrm{O}}_2}$ by ‘auxiliary tissues’ and the contribution of circulatory dynamics to O₂ transport may dissociate pulmonary ${\dot{V}}_{{\mathrm{O}}_2}$ kinetics from the muscle (Barstow et al. 1990; Benson et al. 2013; Korzeniewski & Zoladz, 2013), especially during recovery (Krustrup et al. 2009). Instead, for comparison with simulated data, we relied on the on‐transition vOX measured from ³¹P magnetic resonance spectroscopy in Cannon et al. (2014), although we have no independent estimation of vOX in recovery other than that inferred from [PCr] recovery kinetics.

Data variability

We adjusted our model by parameter fitting to averaged data presented in Cannon et al. (2014). However, naturally, there is some variability in the original data, which may derive either from real differences between individuals (‘individual variability’) or from variability inherent in the measurement methods (‘method variability’). The variability of most variables in Cannon et al. (2014) is moderate, reflecting mostly ‘individual variability’. The only exception is vOX, which was especially variable during moderate intensity exercise. vOX is determined from the initial rate of change of PCr recovery kinetics, and therefore is influenced by the magnitude of the exercise‐induced PCr depletion (Rossiter et al. 2000). In this case, the ‘method variability’ is probably the major contributor to the overall variability in moderate intensity vOX, and is within the variability expected for this method (Rossiter et al. 2000).

We investigated the potential role of ‘individual variability’, using slight modifications of relevant parameter values in the computational model; for example: A _OX, A _GL, A _UT and/or OXPHOS activity (there is no reason for these values to be identical among different individuals). The ‘individual variability’ can be a result of, for example, genetic differences or physical training. It has been proposed that training may lead not only to an increase in OXPHOS activity related to mitochondrial biogenesis, but also to elevation of ESA intensity (increase of A _OX) (Korzeniewski & Zoladz, 2003; Korzeniewski & Zoladz, 2004). Both effects lead to acceleration of the ${\dot{V}}_{{\mathrm{O}}_2}$ on‐kinetics and to improvement of metabolite stability during rest‐to‐work transitions (Korzeniewski & Zoladz, 2003; Korzeniewski & Zoladz, 2004). Overall, we found that small modifications of relevant parameter values in the computational model could account for the ‘individual variability’ observed in several parameter values in moderate and severe intensity exercise. We also consider that the apparent (although not statistically significant) overshoot in vOX in moderate exercise is predominately a result of ‘method variability’; however, a direct identification of the source of this variability remains to be determined.

Conclusions

The computer model of the skeletal muscle cell bioenergetic system developed previously (Korzeniewski, 1998; Korzeniewski & Zoladz, 2001; Korzeniewski & Liguzinski, 2004) reproduces very well the experimental data of the time courses of [PCr] and pH during rest‐to‐work‐to‐rest transitions, as well as the ATP synthesis rate by OXPHOS (vOX), creatine kinase (vCK) and anaerobic glycolysis (vGL) after 3 and 8 min of moderate and severe bilateral KE exercise in humans (Cannon et al. 2014). An intensive ESA (over 5‐fold direct activation of all OXPHOS complexes and NADH supply in parallel with the activation of ATP usage) was necessary to account for the changes in ATP synthesis fluxes, PCr and pH encountered in human muscles in vivo. Also, a slow decay of ESA during recovery was necessary to fit the experimental data. A strong inhibition of glycolysis by protons improves the agreement between the simulated and measured kinetics of pH after the onset of exercise compared to a moderate glycolytic inhibition. It is suggested that strong inhibition by accumulating protons of ATP supply by anaerobic glycolysis (together with a slow decay of ATP supply by CK) and ‘additional’ ATP usage increasing gradually during severe exercise can explain the relative magnitude of the muscle ${\dot{V}}_{{\mathrm{O}}_2}$ slow component, although some contribution of a decrease in P/O cannot be explicitly excluded. Overall, this well‐tested computer model provides a useful tool for studying the dynamic behaviour of muscle metabolism during exercise and recovery.

Additional information

Competing interests

The authors declare that they have no competing interests.

Author contribution

BK and HBR designed the computer simulations. HBR prepared the experimental data for presentation. BK performed the computer simulations and prepared artwork. BK and HBR discussed the theoretical results and wrote the manuscript. Both authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

The experimental data collection was supported by Biotechnology and Biological Sciences Research Council (BBSRC) UK BB/I001174/1 and BB/I00162X/1.