Period-doubling and period-tripling in growing bilayered systems

Abstract

Growing layers on elastic substrates are capable of creating a wide variety of surface morphologies. Moderate growth generates a regular pattern of sinusoidal wrinkles with a homogeneous energy distribution. While the critical conditions for periodic wrinkling have been extensively studied, the rich pattern formation beyond this first instability point remains poorly understood. Here we show that upon continuing growth, the energy progressively localizes and new complex morphologies emerge. Previous studies have often overlooked these secondary bifurcations; they have focused on large stiffness ratios between layer and substrate, where primary instabilities occur early, long before secondary instabilities emerge. We demonstrate that secondary bifurcations are particularly critical in the low stiffness ratio regime, where the critical conditions for primary and secondary instabilities move closer together. Amongst all possible secondary bifurcations, the mode of period-doubling plays a central role - it is energetically favorable over all other modes. Yet, we can numerically suppress period-doubling, by choosing boundary conditions, which favor alternative higher order modes. Our results suggest that in the low stiffness regime, pattern formation is highly sensitive to small imperfections: surface morphologies emerge rapidly, change spontaneously, and quickly become immensely complex. This is a common paradigm in developmental biology. Our results have significantly applications in the morphogenesis of living systems where growth is progressive and stiffness ratios are low.

1. Motivation

Growth-induced wrinkling instabilities are an important mechanism in the evolution and morphogenesis of living systems [26]. Typical examples range from undesired folding in asthmatic airways [28], via wrinkling in skin [9], to desired cortical folding in mammalian brains [8, 31]. A growing layer, confined by a non-growing substrate with dissimilar material properties, eventually buckles into sinusoidal wrinkles with a well-defined wavelength [27]. Continued growth beyond the onset of primary wrinkling induces secondary bifurcations associated with advanced wrinkling modes of increasing complexity [2, 6]. This coordinated self-organizing mechanism creates a wide variety of surface patterns [20] and is an essential feature of life [14]. Understanding the critical conditions for these instabilities could allow us to control of surface pattern formation during organogenesis and manipulate congenital abnormalities.

Continuum approaches toward the formation of growth-induced instabilities in living systems typically adopt the concept of finite growth [32]. They couple growth and deformations at the kinematic level using the multiplicative decomposition of the deformation gradient into an elastic and a grown part [35]. In this description, confined growth induces residual stresses and triggers mechanical instabilities [17]. The resulting wrinkled state is permanent without any external impact [30]. Soft living materials are especially susceptible to surface buckling due to low elastic moduli and high stimulus-sensitivity [26]. However, studying instabilities in living systems is challenging from a conceptual point of view: it requires nonlinear constitutive equations and low moduli ratios between layer and substrate.

Several mechanical models have contributed to understanding the critical conditions of instabilities and the corresponding wrinkling patterns. While early analytical investigations were restricted to linear elastic materials and primary wrinkling modes [1, 3], more recent studies consider nonlinear elastic material behavior [13, 29] and explain secondary bifurcations in weakly nonlinear confined systems [5, 36]. However, those studies do not consider growing materials and fail to provide profound insight into the wrinkle-to-fold transition and multiple bifurcations in highly nonlinear confined layers [30]. Growth induces a non-conventional buckling problem, in which the critical load is not applied directly, but arises from the interplay between growth and geometric constraints. This mechanism is conceptually similar to manufacturing processes including cooling or consolidation, in which the critical load results from secondary effects [15]. Understanding the highly nonlinear postbuckling behaviour and advanced wrinkling modes requires the application of nonlinear elasticity [10, 33]. Finite element modeling proves practical to further explore growth-induced folding instabilities [22]. Motivated by the clinical problem of mucosal folding during chronic airway wall remodeling [16], researchers have observed secondary folding phenomena in double-layered hollow cylindrical tubes [25]. Those numerical studies investigate stiffness ratios of layer to substrate greater than one hundred. In soft materials such as living tissue, elastomers, and gels, however, the stiffness ratio between the different layers is typically only moderate. The objective of this manuscript is to analyze the critical conditions of growth-induced primary and secondary instabilities for small stiffness ratios between layer and substrate. We illustrate the corresponding failure modes using combined analytical bifurcation analyses and computational modeling.

In Section 2, we establish an exact finite strain bifurcation analysis to establish the critical wrinkling condition for a bilayered system with a growing Neo-Hookean layer bonded to a non-growing infinitely deep Neo-Hookean substrate. In Section 3, we illustrate the corresponding continuum model based on the theory of finite growth. In Section 4, we perform computational simulations to study the critical conditions for primary and secondary instabilities. We explore advanced post-bifurcation modes including period-doubling and period-tripling. We illustrate how appropriate boundary conditions can drive the solution into different bifurcation modes and demonstrate that period-doubling is energetically favorable over period-tripling. Although our study focuses exclusively on growth-induced instabilities, we expect our results to be generally applicable to any compressed bilayered system with moderate stiffness ratios between layer and substrate.

2. Analytical Model

In this section, we discuss the general condition for the onset of wrinkling in a constrained bilayered system in which uniform growth occurs in the layer and no growth occurs in the infinitely deep substrate. We will later see that our results easily generalize to growing substrates. Both layer and substrate are Neo-Hookean elastic with ground state shear moduli μ_l and μ_s. We assume a Cartesian coordinate system {x₁, x₂, x₃}, where x₁ is the direction parallel to the layer-substrate interface, x₂ is the thickness direction perpendicular to the interface, and x₃ is the out-of-plane direction in which no variation occurs under plane strain conditions.

Initially, the layer grows under homogeneous conditions and introduces stretches λ_I in all I = 1, 2, 3 directions. We assume a multiplicative decomposition of these total stretches λ_I into elastic contributions ${\lambda }_{\mathrm{I}}^{\mathrm{e}}$ and grown contributions ${\lambda }_{\mathrm{I}}^{\mathrm{g}}$,

$${\lambda }_1={\lambda }_1^{\mathrm{e}}{\lambda }_1^{\mathrm{g}}\doteq 1{\lambda }_2={\lambda }_2^{\mathrm{e}}{\lambda }_2^{\mathrm{g}}{\lambda }_3={\lambda }_3^{\mathrm{e}}{\lambda }_3^{\mathrm{g}}\doteq 1\text{with}J={\lambda }_1{\lambda }_2{\lambda }_3\doteq {\lambda }_2,$$ (1)

where the Jacobian J denotes the total volume change. Here, we have used the lateral boundary condition λ₁ ≐ 1 and the plain strain condition λ₃ ≐ 1, such that the total volume change is entirely attributed to changes in layer thickness J ≐ λ₂. Figure 1 suggests that we can picture the growth stretches ${\lambda }_{\mathrm{I}}^{\mathrm{g}}$ as the stretches, which would occur if the growing layer was not attached to the elastic substrate. For example, we could consider two-dimensional in-plane growth in line with the plane strain condition,

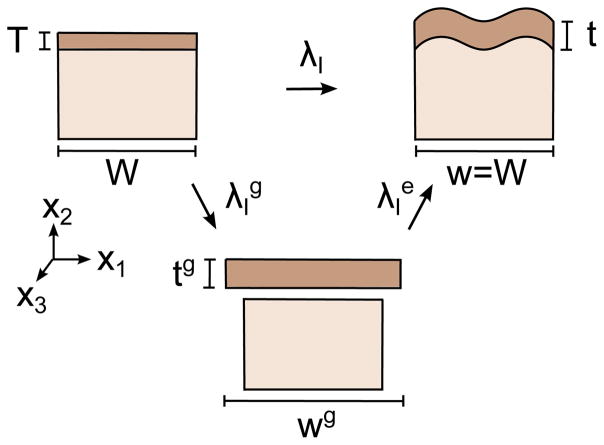
Figure 1.

Analytical model for growing layer on elastic substrate. In the initial, ungrown configuration, the layer has a width W and a thickness T. If the layer were unattached, it would undergo unconstrained growth towards a new width $w^{\mathrm{g}}={\lambda }_1^{\mathrm{g}}W$ and thickness $t^{\mathrm{g}}={\lambda }_2^{\mathrm{g}}T$. Reattaching the layer to the ungrown elastic substrate requires elastic stretches to bring the layer to its final width $w={\lambda }_1^{\mathrm{e}}{w}^{\mathrm{g}}={\lambda }_{1}W$ and thickness $t={\lambda }_2^{\mathrm{e}}{t}^{\mathrm{g}}={\lambda }_{2}T$. Here w ≐ W, such that λ₁ ≐ 1. Positive growth ${\lambda }_1^{\mathrm{g}}>1$ thus induces compression ${\lambda }_1^{\mathrm{e}}=1/{\lambda }_1^{\mathrm{g}}<1$. Beyond a critical amount of growth, the compressive energy in the layer exceeds a critical value and the layer buckles.

$${\lambda }_1^{\mathrm{g}}=\vartheta {\lambda }_2^{\mathrm{g}}=\vartheta {\lambda }_3^{\mathrm{g}}=1\text{with}{J}^{\mathrm{g}}={\lambda }_1^{\mathrm{g}}{\lambda }_2^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}={\vartheta }^2,$$ (2)

or three-dimensional isotropic growth,

$${\lambda }_1^{\mathrm{g}}=\vartheta {\lambda }_2^{\mathrm{g}}=\vartheta {\lambda }_3^{\mathrm{g}}=\vartheta \text{with}{J}^{\mathrm{g}}={\lambda }_1^{\mathrm{g}}{\lambda }_2^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}={\vartheta }^3.$$ (3)

For now, we will consider general, arbitrary growth with the only constraint that ${\lambda }_1^{\mathrm{g}}\ge {\lambda }_3^{\mathrm{g}}$ to ensure that the onset of wrinkling does not occur in the out-of-plane direction. We assume that the elastic deformation is incompressible, J^e ≐ 1, and derive the elastic stretches ${\lambda }_{\mathrm{I}}^{\mathrm{e}}$, which give rise to the stresses in the growing layer,

$${\lambda }_1^{\mathrm{e}}=1/{\lambda }_1^{\mathrm{g}}{\lambda }_2^{\mathrm{e}}={\lambda }_1^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}{\lambda }_3^{\mathrm{e}}=1/{\lambda }_3^{\mathrm{g}}\text{with}{J}^{\mathrm{e}}={\lambda }_1^{\mathrm{e}}{\lambda }_2^{\mathrm{e}}{\lambda }_3^{\mathrm{e}}\doteq 1.$$ (4)

This implies that the total volume change is entirely caused by growth, J ≐ J^g = λ₂. We denote the thickness of the layer prior to growth by T. If the layer were detached from substrate, its thickness would be $t^{\mathrm{g}}={\lambda }_2^{\mathrm{g}}T$. According to Figure 1, in the attached state, the grown layer thickness is

$$t={\lambda }_{2}T={\lambda }_2^{\mathrm{e}}{\lambda }_2^{\mathrm{g}}T={\lambda }_2^{\mathrm{e}}{t}^{\mathrm{g}}\text{with}{t}^{\mathrm{g}}={\lambda }_2^{\mathrm{g}}T.$$ (5)

The analysis in the Appendix reveals that, for any combination of growth stretches, the critical growth condition for the onset wrinkling depends on only two characteristics: the elastic stretch ratio between thickness and wrinkle direction, $r={\lambda }_2^{\mathrm{e}}/{\lambda }_1^{\mathrm{e}}={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}$, and the stiffness ratio between layer and substrate, μ_l/μ_s.

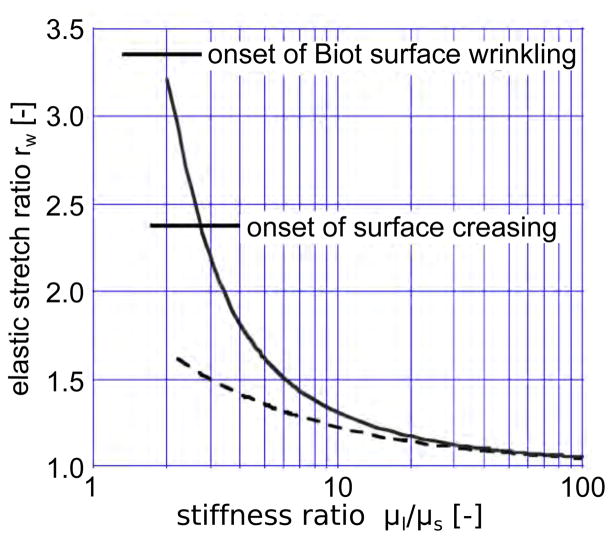
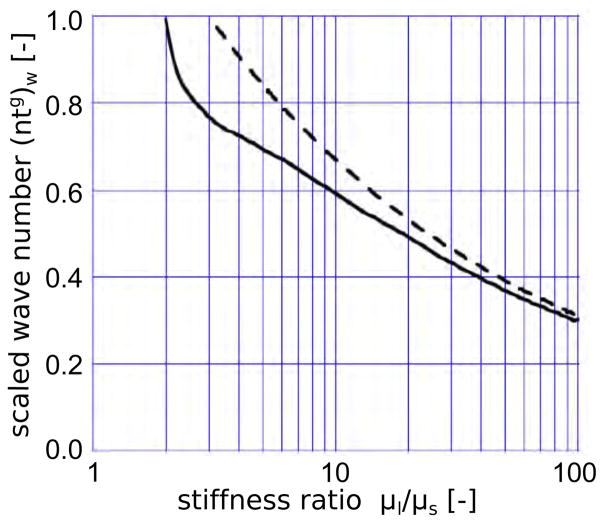
Figure 2 illustrates the critical elastic stretch ratios r_w at the onset of wrinkling for varying stiffness ratios μ_l/μ_s. Associated with this critical growth condition is the wavelength of the critical sinusoidal mode. Figure 3 illustrates the critical condition (nt^g)_w, which defines the wavelength,λ/t = 2π/[r_w(nt^g)_w], scaled by the current layer thickness t at the onset of wrinkling.

Figure 2.

Condition for the onset of wrinkling of a growing layer on an elastic substrate with varying stiffness ratio μ_l/μ_s. Uniform growth in the layer drives periodic wrinkling, where r_w is the critical value of the single growth parameter, $r={\lambda }_2^{\mathrm{e}}/{\lambda }_1^{\mathrm{e}}={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}$. The solid curve is based on the exact analysis and the dashed curve is the asymptotic result from equation (6.1) for large values of μ_l/μ_s.

Figure 3.

Dimensionless critical wave number of the sinusoidal mode associated with the condition for the onset of period wrinkling in Figure 2. The solid curve is based on the exact analysis outlined in the Appendix and the dashed curve is the asymptotic result from equation (6.2) for large values of μ_l/μ_s.

Included in Figures 2 and 3, as dashed curves, are the asymptotic results for layers satisfying μ_l/μ_s ≫ 1. The critical conditions for wrinkling of a growing, relatively stiff layer are

$$r_{\mathrm{w}}=1+\frac{1}{2}{[3{\mu }_{\mathrm{s}}/{\mu }_1]}^{2/3}\text{and}{({nt}^{\mathrm{g}})}_{\mathrm{w}}={[3{\mu }_{\mathrm{s}}/{\mu }_1]}^{2/3}.$$ (6)

The comparison between solid curves of the exact solution and the dashed curves of the asymptotic solution suggests that the asymptotic solution generates significant errors in the low stiffness ratio regime for μ_l/μ_s < 10.

In Figures 2 and 3, we have not analyzed stiffness ratios below μ_l/μ_s = 2 since wrinkling of the type analyzed here may not be the dominant mode in that regime. The wrinkles analyzed here have long wavelengths, which are significantly larger than the layer thickness. Included in Figure 2 are markers showing the condition for the onset of arbitrarily short-wavelength Biot surface wrinkles and arbitrarily small surface creases. The conditions for the onset of these modes can also be expressed as a critical conditions in terms of the elastic stretch ratio r. The Biot surface wrinkling condition is $r_{\text{biot}}={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}=3.383$ [4], and the surface creasing condition is $r_{\text{crease}}={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}=2.37$ [18, 19, 23].

Figure 2 confirms that the Biot condition is not met within the range of stiffness ratios considered here. However, the surface creasing condition is met prior to the condition for long-wavelength wrinkling for stiffness ratios μ_l/μ_s < 2.7. This implies that in this regime, small, finite strain creases are likely to form prior to wrinkling. Another possibility, however, is that long-wavelength folds may be unstable and imperfection-sensitive in this regime, and thereby likely to appear at lower growth strains than predicted by the bifurcation analysis.

For growing layers, the stability and imperfection-sensitivity of the long-wavelength mode has not been analyzed, but such an analysis has been carried out for the closely related Neo-Hookean bilayer problem where wrinkling is driven by the simultaneous compression of layer and substrate [21]. In that case, the long-wavelength mode becomes unstable and imperfection-sensitive in the range of μ_l/μ_s < 2.7. The above discussion suggests that modest stiffness contrasts in the range of μ_l/μ_s < 3, which are relevant for surface pattern formation due to differential growth in living systems [31], are likely to be complex and rich in phenomena.

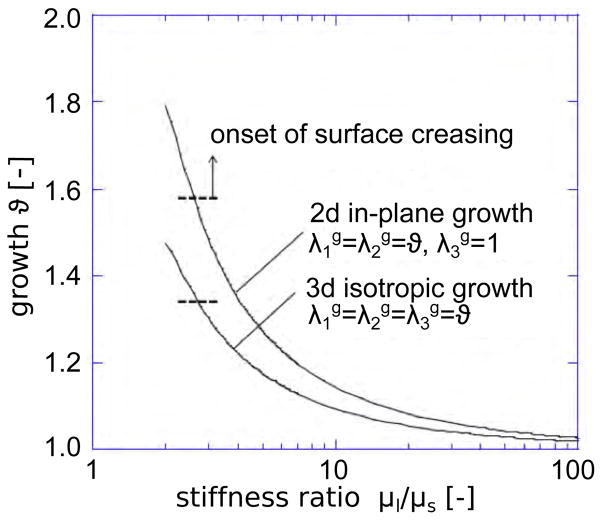
Figure 4 illustrates two special cases of growth: two-dimensional in-plane growth with r = ϑ² according to equations (2) and three-dimensional isotropic growth with r = ϑ³ according to equations (3). We can infer the corresponding wavelengths from Figure 3 using λ/t = 2π/[r_w(nt^g)_w]. Cases with ${\lambda }_1^{\mathrm{g}}={\lambda }_3^{\mathrm{g}}>1$ generate equibiaxial compression in the layer. Sinusoidal modes with the same critical wave-length exist at r_w with wrinkle variations in any direction parallel to the interface. Any superposition of these modes is also a bifurcation mode.

Figure 4.

Critical conditions for onset of wrinkling for two-dimensional in-plane growth and three-dimensional isotropic growth for varying stiffness ratio μ_l/μ_s. The critical growth to induce periodic surface wrinkling decreases with increasing stiffness ratio.

The results in Figures 2 and 3 for a uniformly growing layer on a Neo-Hookean elastic substrate also apply for growing substrates as long as growth in the layer is greater. Specifically, with ${\lambda }_{11}^{\mathrm{g}},{\lambda }_{21}^{\mathrm{g}},{\lambda }_{31}^{\mathrm{g}}$ now denoting uniform growth stretches in the layer and ${\lambda }_{1\mathrm{s}}^{\mathrm{g}},{\lambda }_{2\mathrm{s}}^{\mathrm{g}},{\lambda }_{3\mathrm{s}}^{\mathrm{g}}$ denoting growth stretches in the substrate, let ${\lambda }_1^{\mathrm{e}}={\lambda }_{1\mathrm{s}}^{\mathrm{g}}/{\lambda }_{11}^{\mathrm{g}}$, and ${\lambda }_3^{\mathrm{e}}={\lambda }_{3\mathrm{s}}^{\mathrm{g}}/{\lambda }_{31}^{\mathrm{g}}$, such that $r=[{({\lambda }_{11}^{\mathrm{g}})}^2{\lambda }_{31}^{\mathrm{g}}]/[{({\lambda }_{1\mathrm{s}}^{\mathrm{g}})}^2{\lambda }_{3\mathrm{s}}^{\mathrm{g}}]$. Figure 2 provides the critical value of r assuming ${\lambda }_{11}^{\mathrm{g}}/{\lambda }_{1\mathrm{s}}^{\mathrm{g}}>{\lambda }_{31}^{\mathrm{g}}/{\lambda }_{3\mathrm{s}}^{\mathrm{g}}$. The critical wavelength is λ/t = 2π/[r_w(nt^g)_w] where now $t=[{\lambda }_{11}^{\mathrm{g}}{\lambda }_{21}^{\mathrm{g}}{\lambda }_{31}^{\mathrm{g}}]/[{\lambda }_{1\mathrm{s}}^{\mathrm{g}}{\lambda }_{2\mathrm{s}}^{\mathrm{g}}{\lambda }_{3\mathrm{s}}^{\mathrm{g}}]T$ and (nt^g)_w follows from Figure 3. The current study is limited to wrinkling phenomena on flat substrates; on curved substrates, the analysis is conceptually similar but includes higher order correction terms. We have recently shown that curvature delays the onset of wrinkling and that flat regions tend to fold earlier than curved regions [16].

3. Continuum Model

To explore pattern evolution beyond the onset of folding, we model growth using the nonlinear field theories of mechanics supplemented by the theory of finite growth. This results in a set of five equations, which are the three-dimensional, finite deformation generalizations of the kinematic equation, the constitutive equation, the mechanical equilibrium equation, and the growth kinematics, and the growth kinetics, which define the evolution of growth. To characterize the kinematics of finite deformation, we introduce the deformation map φ, which maps points X from the ungrown configuration to their new positions x = φ (X, t) in the grown configuration. As the three-dimensional generalization of equations (1), we introduce the deformation gradient F = ∇_Xφ, which we multiplicatively decompose into an elastic part F^e and a growth part F^g,

$$\mathit{F}={\nabla }_{\mathit{X}}\mathit{\phi }={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}}\text{with}J=det(\mathit{F})=J^{\mathrm{e}}{J}^{\mathrm{g}}.$$ (7)

A similar multiplicative decomposition holds for the Jacobian J = det (F), which we decompose into an elastic part J^e and a growth part J^g. In analogy to equation (3), to define the growth kinematics, we assume that growth is purely isotropic, parameterized in terms of a single scalar-valued growth multiplier ϑ,

$${\mathit{F}}^{\mathrm{g}}=\vartheta \mathit{I}\text{with}{J}^{\mathrm{g}}=det({\mathit{F}}^{\mathrm{g}})={(\vartheta )}^{n_{dim}}.$$ (8)

This implies that the grown volume J^g is identical to the growth multiplier to the power of the number of spatial dimensions n_dim with n_dim= 2 in the case of two-dimensional in-plane growth according to equations (2) and n_dim= 3 in the case of three-dimensional isotropic growth according to equations (3). In analogy to equations (4), the elastic tensor F^e and its Jacobian J^e simply follow by scaling the total deformation gradient F and its Jacobian J by the amount of growth ϑ,

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}/\vartheta \text{with}{J}^{\mathrm{e}}=det({\mathit{F}}^{\mathrm{e}})=J/{(\vartheta )}^{n_{dim}}.$$ (9)

We introduce a Neo-Hookean free energy function parameterized exclusively in terms of the elastic tensor F^e and its Jacobian J^e,

$$\psi =\frac{1}{2}\lambda {ln}^2(J^{\mathrm{e}})+\frac{1}{2}\mu [{\mathit{F}}^{\mathrm{e}}:{\mathit{F}}^{\mathrm{e}}-n_{dim}-2ln(J^{\mathrm{e}})],$$ (10)

where λ and μ are the Lamé constants. This implies that only the elastic part of the deformation generates stress. Following standard arguments of thermodynamics, the Piola stress P follows as energetically conjugate to the deformation gradient F,

$$\mathit{P}=\frac{\partial \psi }{\partial \mathit{F}}=\frac{\partial \psi }{\partial {\mathit{F}}^{\mathrm{e}}}:\frac{\partial {\mathit{F}}^{\mathrm{e}}}{\partial \mathit{F}}=\mu \left[\frac{1}{{\vartheta }^2}\mathit{F}-{\mathit{F}}^{-\mathrm{t}}\right]+\lambda ln(J^{\mathrm{e}}){\mathit{F}}^{-\mathrm{t}}.$$ (11)

The Piola stress enters the standard balance of linear momentum, the equation of mechanical equilibrium. In the absence of inertia terms and volume forces, the balance of linear momentum reduces to the vanishing divergence of the Piola stress,

$$\text{Div}(\mathit{P})\doteq \mathbf{0}.$$ (12)

In contrast to the analytical model, now we are not only interested in the critical condition at which growth occurs. Rather, we want to explore the evolution of surface patterns beyond the onset of folding for ϑ > ϑ^crit. It thus remains to define the kinetics of growth, the equation that characterizes the evolution of growth in time. For simplicity, we assume that growth is purely morphogenetic, independent of mechanical stress or strain, characterized exclusively by the linear growth rate g,

$$\stackrel{.}{\vartheta }=g.$$ (13)

In the following examples, we consider a growing layer, g_l > 0, on a Neo-Hookean elastic substrate, g_s = 0. We solve the nonlinear set of equations within a finite element framework implemented in Matlab [29], and represent growth as a scalar-valued internal variable ϑ at the integration point level [7].

4. Computational Model

For the following examples, we consider a periodic, two-dimensional plane strain domain, which consists of a growing layer on a Neo-Hookean elastic substrate. The domain width W is constant; the domain height H and layer thickness T evolve as growth progresses. For the growing layer, we assume Lamé constants of λ_l = 34.2 kPa and μ_l = 3.3 kPa [8] and allow it to grow linearly in time. For the elastic substrate, we assume Lamé constants of λ_s = μ_s/μ_l λ_l and μ_s where μ_l/μ_s denotes the stiffness contrast between layer and substrate. Here we focus on the range of stiffness contrasts between 2 ≤ μ_l/μ_s ≤ 12 to mimic instability phenomena in living matter.

We adopt plain strain conditions and apply periodic boundary conditions on the left and right boundaries. We constrain the bottom nodes orthogonal to the boundary, but allow them to slide freely along the edge. To mimic an infinitely thick substrate, we select a specimen height that is significantly larger than the expected wavelength, H ≫ λ. We estimate the wavelength λ numerically in a preliminary simulation with a large domain width, W ≫ λ. For all following simulations, we explore two different domain widths, W = 2 λ and W = 3 λ. We discretize the growing layer with 4 and the Neo-Hookean elastic substrate with 48 bi-linear quadrilateral elements along the height H and with 64 to 128 elements along the width W depending on the estimated wavelength λ. To trigger instabilities in this homogeneous setup, we apply a small kinematic imperfection inside a vertical band in the center of the substrate and confirm numerically that both the wavelength λ and the amplitude A are insensitive to this imperfection. To accurately capture the onset of the bifurcation, we adopt an adaptive time stepping scheme, in which we adjust the time step size based on convergence of the global Newton Raphson iteration [24].

4.1. Emerging instability patterns of primary and secondary bifurcations

To explore the morphogenesis of primary and secondary bifurcations, we analyze the instability pattern of a progressively growing layer on a Neo-Hookean elastic substrate. We compare two different widths, W = 2 λ and W = 3 λ, of the periodic simulation domain to drive the solution into two distinct instability patterns: period-doubling and period-tripling.

Figure 5 illustrates the instability patterns of primary and secondary bifurcations, which emerge for domain widths of W = 2 λ and W = 3 λ at a stiffness contrast of μ_l/μ_s = 3. The color code reflects the normal compressive stress in the growing layer, with blue indicating low and red indicating high levels of compression. Once the compressive stress reaches a critical primary bifurcation point, the layer wrinkles into a periodic sinusoidal pattern to release the growth-induced residual stress, first row. Further growth triggers symmetry breaking into a non-symmetric wrinkling mode with sharper valleys and smoother ridges, second row. With continuing growth, the stresses in the growing layer reach a critical secondary bifurcation point and advanced wrinkling modes emerge, third row. These secondary instability patterns are sensitive to the domain width: A width of W = 2 λ favors period-doubling, left column; a width of W = 3 λ favors period-tripling, occurring slightly later, right column. Secondary instability patterns alternate between growing and decaying valleys with progressively increasing and decreasing amplitudes. As growth continues, contact zones emerge along the neighboring edges of a growing valley, while decaying valleys have almost entirely flattened out, fourth row. As the left and right close-ups of growing and decaying valleys indicate, amplitude growth increases the stress in the layer, while amplitude decay decreases the stress. In summary, this example suggests that instabilities emerge according to a distinct time line with a primary bifurcation point of periodic wrinkling followed by a secondary bifurcation point of period-doubling. With the choice of appropriate boundary conditions, we can suppress the mode of period-doubling and drive the solution into a later secondary bifurcation of period-tripling [34].

Figure 5.

Emerging instability patterns of primary and secondary bifurcations: Moderate growth beyond the first instability point creates symmetric, sinusoidal wrinkling patterns, which are similar for period-doubling and -tripling (first row). Further growth triggers symmetry breaking into non-symmetric wrinkling patterns with sharper valleys and smoother ridges (second row). Continuing growth beyond a second instability point initiates period-doubling and period-tripling with alternating increasing and decreasing amplitudes (third row). As growth continues, contact zones emerge along two neighboring edges of a growing valley, while decaying valleys have almost entirely flattened out (fourth row). The close-ups of each snapshot highlight increasing (left) and decreasing (right) amplitudes.

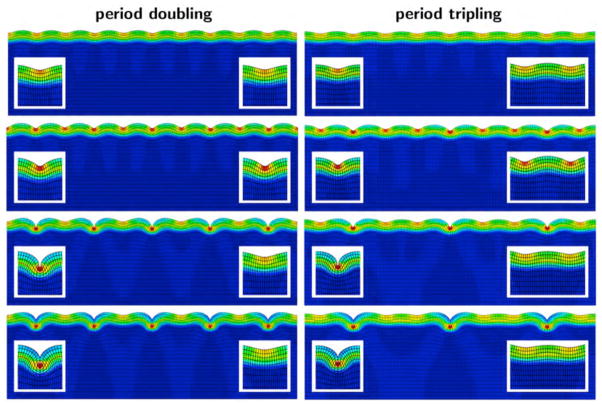
Figure 6 summarizes the final configurations at the formation of contact between two neighboring edges of a growing valley for period-doubling, period-tripling, period-quadrupling, period-quintrupling. Increasing the width of the simulation domain by multiples of the wavelength, W = 2λ, 3λ, 4λ, 5λ drives the numerical solution into different secondary bifurcation modes, from row 3 to row 6. While the modes of period-doubling in row 3 and period-tripling in row 4 display two distinct amplitudes, one increasing and one decreasing, the modes of period-quadrupling in row 5 and period-quintupling in row 6 display three distinct amplitudes, one increasing, one decreasing, and one in between.

Figure 6.

Emerging instability patterns of primary and secondary bifurcations: Symmetric sinusoidal wrinkling, non-symmetric periodic wrinkling, period-doubling, period-tripling, period-quadrupling, period-quintrupling (from top to bottom).

4.2. Pitchfork bifurcations of period-doubling and period-tripling

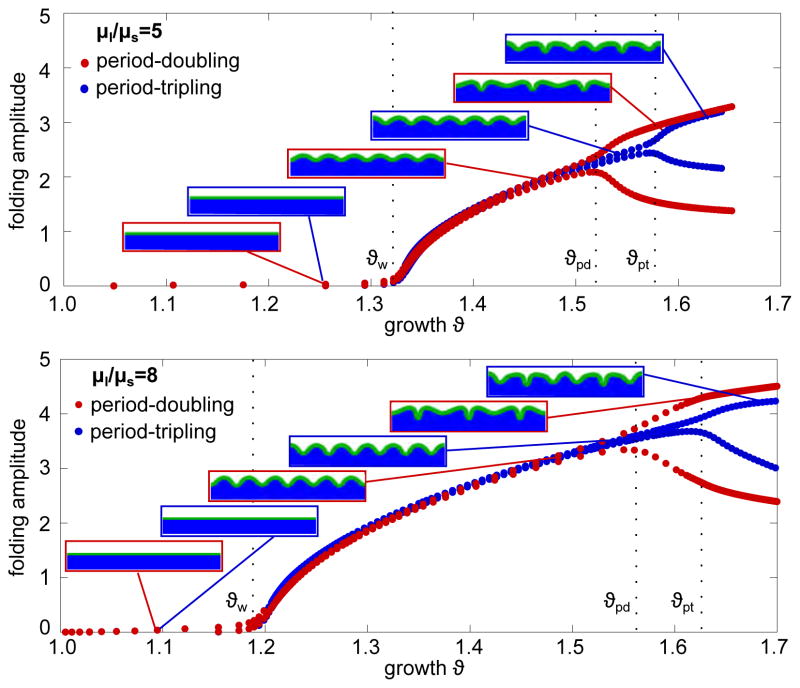
The previous analysis suggests a characteristic time line for emerging instabilities of primary and secondary bifurcations. To investigate this time line more closely, we monitor the temporal evolution of the folding amplitude for two different stiffness contrasts, μ_l/μ_s = 5 and μ_l/μ_s = 8.

Figure 7 illustrates the emerging folding amplitudes for progressive growth. At the first instability point ϑ_w, the initially flat growing layer wrinkles into a sinusoidal pattern to partially release residual stresses and the amplitudes begin to grow uniformly. Once growth reaches the second instability point ϑ_pd, a second instability mode of period-doubling occurs. Every second amplitude accelerates to grow, while those in between decay. Choosing the domain width to W = 3 λ instead of W = 2 λ suppresses the period-doubling mode and triggers a different secondary instability pattern, period-tripling. The solution passes the point of period-doubling ϑ_pd without undergoing a bifurcation. Further growth triggers the advanced mode of period-tripling at a later secondary bifurcation point ϑ_pt. This indicates that period-doubling is energetically favorable over period-tripling. Yet, we can suppress the period-doubling mode numerically by choosing the domain size such that periodicity favors the mode of period-tripling. The direct comparison of the pitchfork bifurcations for two different stiffness contrasts, μ₁/μ_s = 5 and μ₁/μ_s = 8, suggests that the distance between primary and secondary bifurcations increases with increasing stiffness contrast.

Figure 7.

Pitchfork bifurcations of period-doubling and period-tripling for stiffness contrasts of μ_l/μ_s = 5 and μ_l/μ_s = 8. Initially, the growing layer is flat and the amplitudes are zero. At first instability point ϑ_w, all amplitudes begin to grow simultaneously. For the case of period-doubling (red curves), at the second instability point ϑ_pd, a pitchfork bifurcation occurs: every second amplitude grows and those in between decay. For the case of period-tripling (blue curves), ϑ_pd is passed without bifurcation. Further growth initiates period-tripling at the secondary bifurcation point ϑ_pt: every third amplitudes grows and those in between decay. The time between primary and secondary bifurcation increases with increasing stiffness contrast μ_l/μ_s.

4.3. Stiffness sensitivity of primary and secondary bifurcations

The previous example suggests that the evolution of primary and secondary bifurcations is highly sensitive to the stiffness contrast between layer and substrate. To explore this sensitivity further, we systematically vary the stiffness contrast between 3 ≤ μ₁/μ_s ≤12. For each stiffness contrast, we numerically identify the critical growth multiplier at the onset of periodic wrinkling ϑ_w, at the onset of period-doubling ϑ_pd, and the onset of period-tripling ϑ_pt using an accompanying eigenvalue analysis: The smallest eigenvalue of the system decreases progressively until it reaches a first minimum close to zero, which we define as the primary instability point; then, the smallest eigenvalue increases, but soon decreases again towards a second minimum, which we define as second instability point.

Figure 8 illustrates the critical growth of periodic wrinkling ϑ_w, period-doubling ϑ_pd, and period-tripling ϑ_pt for varying stiffness contrasts μ₁/μ_s. In analogy to the analytical estimates in Figure 4, the primary critical condition for periodic wrinkling ϑ_w decreases asymptotically as the stiffness contrast μ₁/μ_s increases. The secondary critical condition for both period-doubling ϑ_pd and period-tripling ϑ_pt seems only marginally sensitive to the stiffness contrast. This implies that for increasing stiffness contrasts, the secondary bifurcation points ϑ_pd and ϑ_pt move further away from the primary bifurcation point ϑ_w. Critical growth for period-doubling ϑ_pd, with a mean of 1.56 ± 0.03, is consistently lower than critical growth for for period-tripling ϑ_pt, with a mean of 1.64 ± 0.03. This supports the findings from our previous example that period-doubling occurs earlier than period-tripling and seems to be the energetically favorable mode.

Figure 8.

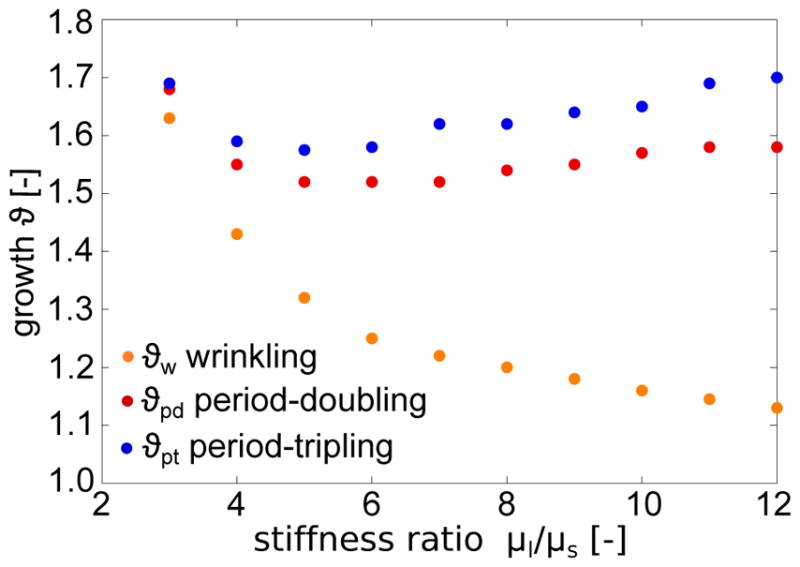
Stiffness sensitivity of primary and secondary bifurcations. The primary critical condition for periodic wrinkling ϑ_w (orange) decreases asymptotically with increasing stiffness contrast μ₁/μ_s. The secondary critical condition for period-doubling ϑ_pd (red) and period-tripling ϑ_pt (blue) is only marginally sensitive to the stiffness contrast. The critical growth for period-doubling ϑ_pd is lower than the critical growth for period-tripling ϑ_pt, which suggests that period-doubling is energetically favorable over period-tripling. For increasing stiffness contrasts, the primary and secondary bifurcation point move further apart.

4.4. Stiffness sensitivity of folding amplitude during period-doubling

Our previous examples suggest that the growing and decaying amplitudes during secondary bifurcation are highly sensitive to the stiffness contrast between layer and substrate. To explore this sensitivity further, we systematically vary the stiffness contrast between 4 ≤ μ₁/μ_s ≤ 12 in increments of Δμ₁/μ_s = 2. For each stiffness contrast, we illustrate the emerging secondary instability mode and analyze the evolution of the amplitude ratio, the relation between growing and decaying amplitudes A₁/A₂, beyond the secondary bifurcation point Δϑ = ϑ − ϑ_pd.

Figure 9 illustrates the stiffness sensitivity of the folding amplitude for period-doubling. With increasing stiffness contrast of μ₁/μ_s = 4, 6, 8, 10, 12, the amplitude ratio of growing and decaying amplitudes decreases, from top to bottom. For μ₁/μ_s = 4, the decaying amplitude has almost entirely flattened out while for μ₁/μ_s = 12, it is still markedly present. With increasing stiffness contrast, both the maximum amplitude and the wavelength increase.

Figure 9.

Stiffness sensitivity of folding amplitude for period-doubling. With increasing stiffness contrast of μ₁/μ_s = 4, 6, 8, 10, 12 (from top to bottom), the amplitude ratio of growing and decaying amplitudes decreases. For μ₁/μ_s = 4 (top), the decaying amplitude has almost entirely flattened out while for μ₁/μ_s = 12 (bottom), it is still markedly present. With increasing stiffness contrast, both the maximum amplitude and the wavelength increase (from top to bottom).

Figure 10 shows the evolution of the amplitude ratio A₁/A₂ for progressive growth after the onset of period-doubling for the range of stiffness contrasts 4 ≤ μ₁/μ_s ≤ 12. With increasing stiffness contrast, the slope of the curves decreases. This implies that the amplitudes grow and decay slower and the pitchfork narrows.

Figure 10.

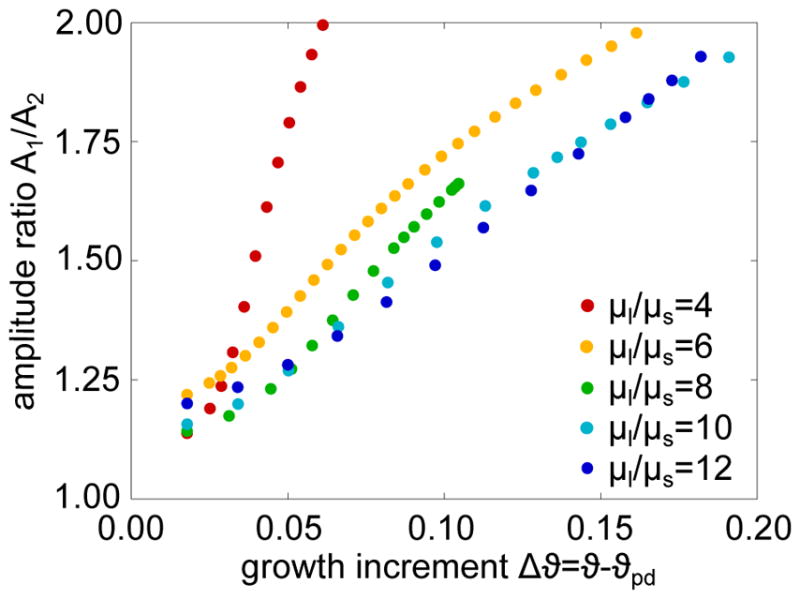
Stiffness sensitivity of folding amplitude for period-doubling. At the onset of period-doubling ϑ_pd, every second amplitude A₁ grows while every other amplitude A₂ decays. This implies that the amplitude ratio A₁/A₂ increases progressively with Δϑ beyond the secondary bifurcation point. For increasing stiffness contrasts μ₁/μ_s, the amplitude ratio A₁/A₂ decreases (see Figure 9).

5. Concluding Remarks

Growing layers on elastic substrates can create a rich set of surface morphologies beyond the commonly studied primary instability: moderate growth creates symmetric, sinusoidal wrinkling patterns; further growth triggers symmetry breaking into non-symmetric patterns with sharp valleys and smooth ridges; and continuing growth initiates secondary bifurcations with alternating increasing and decreasing amplitudes. Here we have studied the emergence of surface morphologies upon progressive growth for low stiffness ratios between layer and substrate. Our simulations reveal that the critical amount of growth required for primary surface wrinkling increases exponentially as the stiffness ratio decreases, while the critical growth for secondary instabilities remains almost constant. This suggests that in the low stiffness ratio regime, the conditions for primary and secondary bifurcations move closer together and secondary folding becomes progressively more common. Most existing studies focus on large stiffness ratios and naturally overlook these secondary phenomena because they occur significantly later than classical periodic wrinkling. Yet, in living systems, in particular during organogenesis when new systems form, stiffness contrasts are low and these phenomena are critical. Our results suggest that for low stiffness ratios, emergent morphologies are highly sensitive to small imperfections: surface morphologies emerge rapidly, change spontaneously, and quickly become immensely complex. This is a common paradigm in developmental biology. Understanding emerging higher order bifurcations in layered structures could have significantly applications in the morphogenesis of living systems where growth is progressive and stiffness ratios are low.

A. Appendix: Analytical Model

In what follows, we summarize the bifurcation analysis of a Neo-Hookean bilayer with uniform growth in the layer and no growth in the infinitely deep substrate. We construct the governing equations of the bifurcation problem from exact solutions for increments of displacements and stresses in a uniformly stretched layer [11]. Imagine the two layers are detached from one another. The Cartesian coordinates {x₁, x₂, x₃} label material points in the unstressed layer at the current state of growth with x₁ parallel to the interface in the direction of the wrinkle variation, x₂ perpendicular to the interface, and x₃ in the out-of-plane direction, for which we assume a plane strain state. The displacement increments associated with the bifurcation mode are u₁ and u₂, while u₃ ≐ 0. The layer grows uniformly denoted by the growth stretches ${\lambda }_1^{\mathrm{g}},{\lambda }_2^{\mathrm{g}}$, and ${\lambda }_3^{\mathrm{g}}$. There is no growth in the infinitely deep substrate. In the unattached state the layer is grown but stress free. Reattaching the grown layer to the ungrown substrate requires stress-generating elastic stretches in the layer,

$${\lambda }_1^{\mathrm{e}}=1/{\lambda }_1^{\mathrm{g}}{\lambda }_2^{\mathrm{e}}={\lambda }_1^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}{\lambda }_3^{\mathrm{e}}=1/{\lambda }_3^{\mathrm{g}},$$ (A.1)

where ${\lambda }_2^{\mathrm{e}}=1/({\lambda }_1^{\mathrm{e}}{\lambda }_3^{\mathrm{e}})={\lambda }_1^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}$ follows from the elastic incompressibility condition, $J^{\mathrm{e}}={\lambda }_1^{\mathrm{e}}{\lambda }_2^{\mathrm{e}}{\lambda }_3^{\mathrm{e}}\doteq 1$. The thickness of the growing layer in the fictitious, unattached state is $t^{\mathrm{g}}={\lambda }_2^{\mathrm{g}}T$ and the current thickness in the grown, attached state is t^g = λ₂ T, where T is the initial thickness prior to growth. In the Neo-Hookean layer with ground state shear modulus μ_l, separated solutions to the field equations for the incremental problem exist with displacement increments,

$$\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]=\left[\begin{array}{l}{U}_{1}sin({nx}_1)\\ U_{2}cos({nx}_1)\end{array}\right],$$ (A.2)

with coefficients

$$\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\left[\begin{array}{rrr}\hfill -c_1{e}^{{\mathit{rnx}}_2}-c_2& \hfill r^{-1}{e}^{{nx}_2}+c_3{e}^{-{\mathit{rnx}}_2}+c_4& \hfill r^{-1}{e}^{-{nx}_2}\\ \hfill c_1{e}^{{\mathit{rnx}}_2}+c_2& \hfill e^{{nx}_2}+c_3{e}^{-{\mathit{rnx}}_2}+c_4& \hfill e^{-{nx}_2}\end{array}\right].$$ (A.3)

Here, $r={\lambda }_2^{\mathrm{e}}/{\lambda }_1^{\mathrm{e}}={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}$, denotes the ratio between the elastic stretches in thickness and wrinkle direction under the assumption that r ≠ 1. The current stretch state enters (A.3) only through this ratio r. The solution holds for any wave number n. We can express the associated nominal stress increments,

$$\left[\begin{array}{c}{n}_{21}\\ n_{22}\end{array}\right]=\left[\begin{array}{l}{N}_{21}sin({nx}_1)\\ N_{22}cos({nx}_1)\end{array}\right],$$ (A.4)

with the following coefficients, defined as force per undeformed area,

$$\begin{array}{l}{N}_{21}=-{\mu }_{1}n[c_{1}2r{e}^{{\mathit{rnx}}_2}+c_2{r}^{-1}(r^2+1)e^{{nx}_2}+c_{3}2r{e}^{-{\mathit{rnx}}_2}+c_4{r}^{-1}(r^2+1)e^{-{nx}_2}]\\ N_{22}=-{\mu }_{1}n[-c_1{r}^{-1}(r^2+1)e^{{\mathit{rnx}}_2}-c_{2}2e^{{nx}_2}+c_3{r}^{-1}(r^2+1)e^{-{\mathit{rnx}}_2}+c_{4}2e^{-{nx}_2}].\end{array}$$ (A.5)

This Lagrangian formulation, which employs the components of the second Piola-Kirchhoff stress, is similar to the stability analysis of wrinkling of a homogeneous half-space [4, 11, 12]. To express the coefficients [c₃, c₄] in terms of [ c₁, c₂ ] we enforce the traction free condition, [N₂₁, N₂₂] = [0,0] on x₂ = t^g, in the layer with 0 ≤ x₂ ≤ t^g, in the unstressed state at the current state of growth,

$$\left[\begin{array}{c}{c}_3\\ c_4\end{array}\right]=\mathbf{A}\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right],$$ (A.6)

with

$$\mathbf{A}={\left[\begin{array}{ll}2r{e}^{-{\mathit{rnt}}^{\mathrm{g}}}\hfill & \hfill r^{-1}(r^2+1)e^{-{nt}^{\mathrm{g}}}\\ r^{-1}(r^2+1)e^{-{\mathit{rnt}}^{\mathrm{g}}}\hfill & \hfill 2e^{-{nt}^{\mathrm{g}}}\end{array}\right]}^{-1}\left[\begin{array}{ll}-2r{e}^{{\mathit{rnt}}^{\mathrm{g}}}\hfill & \hfill -r^{-1}(r^2+1)e^{{nt}^{\mathrm{g}}}\\ r^{-1}(r^2+1)e^{{\mathit{rnt}}^{\mathrm{g}}}\hfill & \hfill 2e^{{nt}^{\mathrm{g}}}\end{array}\right].$$ (A.7)

We can then solve for the interface tractions [N₂₁, N₂₂] on x₂ = 0⁺ in terms of the coefficients [c₁, c₂],

$$\left[\begin{array}{c}{N}_{21}\\ N_{22}\end{array}\right]={\mu }_{1}n\mathbf{B}\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right],$$ (A.8)

with

$$\mathbf{B}=\left[\begin{array}{cc}-2r(1+A_{11})-r^{-1}(r^2+1)A_{21}& -r^{-1}(r^2+1)(1+A_{22})-2r{A}_{12}\\ r^{-1}(r^2+1)(1-A_{11})-2A_{21}& 2(1-A_{22})-r^{-1}(r^2+1)A_{12}\end{array}\right].$$ (A.9)

Next, solve for the interface displacements [U₁, U₂] on x₂ = 0⁺ in terms of the coefficients [c₁, c₂] using equations (A.3) and (A.6) with (A.7),

$$\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\mathbf{C}\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right],$$ (A.10)

with

$$\mathbf{C}=\left[\begin{array}{cc}-1+A_{11}+r^{-1}{A}_{21}& -r^{-1}+A_{12}+r^{-1}{A}_{22}\\ 1+A_{11}+A_{21}& 1+A_{12}+A_{22}\end{array}\right].$$ (A.11)

By equations (A.8) to (A.11), the increments of nominal tractions and displacements on the bottom of the layer, x₂ = 0⁺, which has a traction-free top surface, are related by

$$\left[\begin{array}{c}{N}_{21}\\ N_{22}\end{array}\right]={\mu }_{1}n\mathbf{B}{\mathbf{C}}^{-1}\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right].$$ (A.12)

Now we consider the semi-infinite substrate which is unstressed in the reference state with no growth. We denote all substrate quantities by an overbar and introduce its Cartesian coordinates as {x̄₁, x̄₂, x̄₃}. In analogy to equations (A.2) and (A.4), substrate displacements and nominal tractions associated with the bifurcation solution have the form,

$$\left[\begin{array}{c}{\overline{u}}_1\\ {\overline{u}}_2\end{array}\right]=\left[\begin{array}{l}{\overline{U}}_{1}sin(\overline{n}{\overline{x}}_1)\\ {\overline{U}}_{2}cos(\overline{n}{\overline{x}}_1)\end{array}\right]$$ (A.13)

and

$$\left[\begin{array}{c}{\overline{n}}_{21}\\ {\overline{n}}_{22}\end{array}\right]=\left[\begin{array}{l}{\overline{N}}_{21}sin(\overline{n}{\overline{x}}_1)\\ {\overline{N}}_{22}cos(\overline{n}{\overline{x}}_1)\end{array}\right].$$ (A.14)

The solution for the unstressed infinitely deep substrate provides the following connection between its variables on its top surface,

$$\left[\begin{array}{c}{\overline{N}}_{21}\\ {\overline{N}}_{22}\end{array}\right]={\mu }_{\mathrm{s}}\overline{n}\left[\begin{array}{c}{\overline{U}}_1\\ {\overline{U}}_2\end{array}\right],$$ (A.15)

where μ_s denotes the ground state shear modulus of the substrate. Continuity of displacement increments and nominal tractions across the layer-substrate interface requires that

$$\left[\begin{array}{l}{\overline{U}}_{1}sin(\overline{n}{\overline{x}}_1)\\ {\overline{U}}_{2}cos(\overline{n}{\overline{x}}_1)\end{array}\right]=\left[\begin{array}{l}{U}_{1}sin({nx}_1)\\ U_{2}cos({nx}_1)\end{array}\right]$$ (A.16)

and

$$\left[\begin{array}{l}{\overline{N}}_{21}sin(\overline{n}{\overline{x}}_1)\\ {\overline{N}}_{22}cos(\overline{n}{\overline{x}}_1)\end{array}\right]=\frac{1}{{\lambda }_1^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}}\left[\begin{array}{l}{N}_{21}sin({nx}_1)\\ N_{22}cos({nx}_1)\end{array}\right].$$ (A.17)

The factor $1/{\lambda }_1^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}$ in equation (A.17) accounts for the fact that the nominal stress increments in the two layers are defined relative to different interface areas. Displacement continuity (A.16) across the interface requires that

$$\left[\begin{array}{c}{\overline{U}}_1\\ {\overline{U}}_2\end{array}\right]=\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]\text{with}\overline{n}{\overline{x}}_1={nx}_1,$$ (A.18)

such that $x_1={\lambda }_1^{\mathrm{g}}{\overline{x}}_1$ and $n=\overline{n}/{\lambda }_1^{\mathrm{g}}$. Traction continuity (A.17) across the interface together with equations (A.12) and (A.15) requires that

$$\mathbf{M}\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right]=\mathbf{0}\text{with}\mathbf{M}={\mathbf{BC}}^{-1}-2r\frac{{\mu }_{\mathrm{s}}}{{\mu }_1}\mathbf{I},$$ (A.19)

where I is the identity matrix. The eigenvalue problem, which governs the bifurcation is |M | ≐ 0. Significantly, M depends only on the stretch ratio $r={({\lambda }_1^{\mathrm{g}})}^2{\lambda }_3^{\mathrm{g}}$, the stiffness ratio μ₁/μ_s, and the thickness-scaled wave number nt^g.

We interpret r as the eigenvalue associated with growth, and denote the critical eigenvalue, i.e., the smallest value associated with the onset of wrinkling, by r_w. This critical value follows from minimizing r over all values of nt^g. Consequently, r_w, and with it the associated minimizing value of (nt^g)_w, depend only on the stiffness ratio between layer and substrate μ₁/μ_s. This implies that the curves in Figures 2 and 3 apply to all uniform growth conditions in the layer governed by ${\lambda }_1^{\mathrm{g}},{\lambda }_2^{\mathrm{g}}$, and ${\lambda }_3^{\mathrm{g}}$, as long as ${\lambda }_1^{\mathrm{g}}\ge {\lambda }_3^{\mathrm{g}}$. To generate the solid curves in Figures 2 and 3, we solved the eigenvalue problem (A.19) numerically. The critical wavelength with respect to the current state is

$$\lambda =\frac{2\pi }{{\overline{n}}_{\mathrm{w}}}\frac{\lambda }{t^{\mathrm{g}}}=\frac{2\pi }{{\lambda }_1^{\mathrm{g}}{({nt}^{\mathrm{g}})}_{\mathrm{w}}}\frac{\lambda }{t}=\frac{2\pi }{r_{\mathrm{w}}{({nt}^{\mathrm{g}})}_{\mathrm{w}}},$$ (A.20)

where λ/t^g denotes the dimensionless wavelength normalized by the thickness of the fictitious unattached grown layer, $t^{\mathrm{g}}={\lambda }_2^{\mathrm{g}}T$, and λ/t denotes the dimensionless wavelength normalized by the current thickness of the grown layer at the onset of the bifurcation, $t={\lambda }_{2}T={\lambda }_1^{\mathrm{g}}{\lambda }_2^{\mathrm{g}}{\lambda }_3^{\mathrm{g}}T$.