Development of common neural representations for distinct numerical problems

Abstract

How the brain develops representations for abstract cognitive problems is a major unaddressed question in neuroscience. Here we tackle this fundamental question using arithmetic problem solving, a cognitive domain important for the development of mathematical reasoning. We first examined whether adults demonstrate common neural representations for addition and subtraction problems, two complementary arithmetic operations that manipulate the same quantities. We then examined how the common neural representations for the two problem types change with development. Whole-brain multivoxel representational similarity (MRS) analysis was conducted to examine common coding of addition and subtraction problems in children and adults. We found that adults exhibited significant levels of MRS between the two problem types, not only in the intra-parietal sulcus (IPS) region of the posterior parietal cortex (PPC), but also in ventral temporal-occipital, anterior temporal and dorsolateral prefrontal cortices. Relative to adults, children showed significantly reduced levels of MRS in these same regions. In contrast, no brain areas showed significantly greater MRS between problem types in children. Our findings provide novel evidence that the emergence of arithmetic problem solving skills from childhood to adulthood is characterized by maturation of common neural representations between distinct numerical operations, and involve distributed brain regions important for representing and manipulating numerical quantity. More broadly, our findings demonstrate that representational analysis provides a powerful approach for uncovering fundamental mechanisms by which children develop proficiencies that are a hallmark of human cognition.

How are abstract problems represented in the brain? How do experience and development shape neural representations for abstract problems? The answers to these questions are crucial for understanding the neural basis of skill acquisition and cognitive development. The internalized representation of problem solutions has long been debated with arguments for decontextualized abstracted solution representations, non-abstract context-dependent processes or even hybrid views, as best exemplified by models in the domain of numerical problem solving (Campbell, 1994; Dehaene, Molko, Cohen, & Wilson, 2004; McCloskey, 1992). Characterizing the developmental profile of neural representations associated with efficiently processing strings of abstract symbols can provide new insights into the nature of the underlying code for these processes. While localization of brain activation has provided useful knowledge about the relative engagement of task-specific brain areas during problem solving, they offer limited insights into the cognitive and neural representations of distinct numerical problems in the brain. Here we use novel multivoxel representational similarity (MRS) analyses to investigate how neural representations for abstract problems are formed and mature after more than a decade of experience with problem solving.

We tackle this fundamental question using numerical problem solving, a cognitive domain crucial for academic skill development. Foundational math problem solving skills contribute to proficiency in a wide range of contexts from advanced scientific and engineering reasoning, to more simple quantitative operations important for daily life (Butterworth, Varma, & Laurillard, 2011; Geary, 2013; Geary, Hoard, Nugent, & Bailey, 2013). Converging evidence from infants, children and adults as well as non-human primates suggests that representation of quantity is a foundational ability for numerical problem solving tasks ranging from simple number comparisons to complex arithmetic (Ansari & Dhital, 2006; Cantlon & Brannon, 2006; Cohen Kadosh, Lammertyn, & Izard, 2008; Dehaene, Piazza, Pinel, & Cohen, 2003; Izard, Sann, Spelke, & Streri, 2009; Simon, 1997, 1999; Soltesz, Szucs, & Szucs, 2010; Xu & Spelke, 2000). This ability is supported by multiple brain areas including the intraparietal sulcus (IPS) in the dorsal posterior parietal cortex (PPC), the fusiform gyrus (FG) in the ventral temporal-occipital cortex (VTOC), and prefrontal cortex (PFC; Ansari & Dhital, 2006; Arsalidou & Taylor, 2011; Cantlon & Brannon, 2006; Cohen Kadosh et al., 2008; Houde, Rossi, Lubin, & Joliot, 2010; Menon, Rivera, White, Glover, & Reiss, 2000; Wu et al., 2009). Normative developmental neuroimaging studies in children and adults have shown that there is decreased dependence on the PFC and greater reliance on the IPS and other subdivisions of the PPC with experience and learning (Ansari & Dhital, 2006; Cantlon, Brannon, Carter, & Pelphrey, 2006; Cantlon et al., 2009; Kawashima et al., 2004; Rivera, Reiss, Eckert, & Menon, 2005). Similar to the IPS, activity levels in VTOC, including the FG, also increase with age during numerical problem solving (Rivera et al., 2005). Beyond this frontal to posterior shift in the locus of activation, little is understood about how the brain builds representations for numerical problems during development.

Among the functional circuits implicated in numerical problems, current cognitive models have suggested different representations in posterior brain areas, with perceptual representations supported by visual number form processing within the VTOC, whereas the parietal cortex is thought to support semantic representations and manipulation of quantity along a mental number line (Ansari, 2008; Arsalidou & Taylor, 2011; Cantlon et al., 2009; Cohen Kadosh et al., 2008; Dehaene et al., 2003; Holloway, Battista, Vogel, & Ansari, 2013). Consistent with this view, one cross-linguistic fMRI study found that perceptual processing of digits and ideographs was associated with activation in the FG whereas semantic processing of both symbol types was associated with modulation of IPS activation (Holloway et al., 2013). Critically, these models of information processing are mainly based on studies in adults, and thus, their relevance to the understanding of maturing representations in the developing brain remains unclear. An important unresolved question is whether children and adults have similar representations in the IPS and FG, two brain areas important for different aspects of abstract numerical problem solving (Cantlon et al., 2009; Holloway et al., 2013; Rivera et al., 2005).

To investigate the maturation of brain representations for abstract numerical problems we focused on addition and subtraction, two complementary arithmetic operations that manipulate the same quantity in opposite directions. In elementary school curriculum, addition is learned as the primary operation whereas subtraction builds upon prior knowledge of addition and its inverse relationship with addition (Campbell, 2008). Behavioral studies have characterized distinctive strategies used to solve these arithmetic operations at different developmental stages. School-age children, particularly 3^rd graders, apply retrieval strategies to solve addition problems 65% of the time, while only 19% of subtraction problems are solved using this strategy (Barrouillet, Mignon, & Thevenot, 2008). In contrast, adults solve 76% of addition problems by retrieval and still use this strategy during subtraction 58% of the time (Campbell & Xue, 2001). These differences in retrieval rates suggest that with development, there is a shift from effortful counting to automatic fact retrieval, leading to a convergence of problem solving strategies across the two operations.

Voxel-based univariate analyses have provided evidence for both distinct and overlapping brain responses across arithmetic operations (De Smedt, Holloway, & Ansari, 2011; Fehr, Code, & Herrmann, 2007; Kawashima et al., 2004; Rosenberg-Lee, Chang, Young, Wu, & Menon, 2011). However, no consensus has yet emerged for how addition and subtraction are represented in the brain. Critically, nothing is known about the similarities in neural representations for the two types of distinct numerical problems and how they mature with development. Common representations are a powerful approach for examining abstract coding of perceptual objects and semantic categories independent of low-level features (Edelman, 1998). In the perceptual domain, common, invariant, representations play a fundamental role in object recognition and categorization (Biederman, 1987). While some progress has been made in identifying brain areas that support object invariance in perceptual domains (Drucker & Aguirre, 2009), little is known about the nature of common representations for abstract numerical problems.

Multivariate pattern analysis is uniquely suited to addressing important unaddressed questions related to neural representations for distinct numerical problems. MRS analysis probes the spatial correlation in activity patterns associated with distinct stimuli and can provide novel insights into information processing that are often missed by conventional methods which emphasize localization of brain responses (Kriegeskorte, Mur, & Bandettini, 2008; Mur, Meys, Bodurka, Bandettini, & Kriegeskorte, 2009). Although MRS has been primarily used in studies of low-level visual perception (Connolly et al., 2012; Kriegeskorte et al., 2008; Mur et al., 2009; Said, Moore, Engell, Todorov, & Haxby, 2010), an emerging literature is beginning to suggest that it is also a promising tool for probing higher cognitive functions (Ashkenazi, Rosenberg-Lee, Tenison, & Menon, 2012; Blair, Rosenberg-Lee, Tsang, Schwartz, & Menon, 2012; Ezzyat & Davachi, 2014; Gagnepain, Henson, & Anderson, 2014; LaRocque et al., 2013; Prado et al., 2011; Qin et al., 2014; Xue et al., 2013; Xue et al., 2010). For example, Xue and colleagues reported that greater MRS across repetitions of an item was associated with higher rates of subsequent memory recall in adults (Xue et al., 2010). In this study, we use a whole-brain MRS approach to probe the common neural representations for distinct numerical problems in young children and adults.

We acquired fMRI data from 28 adults (ages 19–22) and 28 children (ages 7–10) while they solved single-digit addition and subtraction problems. We implemented a novel whole-brain analysis to first investigate MRS across the two operations in each group and then examined age-related differences by contrasting MRS between adults and children. MRS has been primarily implemented using a region of interest (ROI) approach to probe cognitive function in predefined regions (Ashkenazi et al., 2012; Blair et al., 2012; Kriegeskorte et al., 2008; Prado et al., 2011; Said et al., 2010; Xue et al., 2010). Limitations of this approach include the restricted brain areas examined and biases inherent in selection of regions-of-interest (ROIs; Fox, 1991; Kriegeskorte, Simmons, Bellgowan, & Baker, 2009; Vul, Harris, Winkielman, & Pashler, 2009). Searchlight methods, which span the entire brain, can overcome these limitations (Connolly et al., 2012; Devereux, Clarke, Marouchos, & Tyler, 2013; Qin et al., 2014; Rothlein & Rapp, 2014; Xue et al., 2013) and offer a powerful technique to investigate how learning and development shape neural representations across multiple brain areas. To contrast age-related differences in VTOC areas associated with visual number form versus dorsal parietal areas associated with semantic representation of quantity (Ansari, 2008; Arsalidou & Taylor, 2011; Cohen Kadosh et al., 2008; Dehaene et al., 2003), here we also examine MRS in cytoarchitectonically-defined subdivisions of the PPC and VTOC.

Based on the behavioral studies reviewed above, which have pointed to convergence of problem solving strategies for addition and subtraction with development (Barrouillet et al., 2008; Campbell & Xue, 2001), we predicted that adults would show more similar neural representations across addition and subtraction problems in core brain areas implicated in arithmetic problem solving. Statistically significant levels of MRS during addition and subtraction problem solving would provide evidence for common representations across the two inverse operations. Conversely, non-significant levels of MRS would indicate dissimilar or weak common representations across the two operations. In particular, we hypothesized that adults would show significant levels of MRS between the two operations in PPC regions involved in semantic representations and manipulation of quantity but not in VTOC regions involved in perceptual representation of problems (Holloway et al., 2013). We further hypothesized that, compared to adults, children would show significantly lower levels of MRS in the PPC but not in VTOC regions linked to visual symbol-form perception. Together, these results would provide novel insights into the development of common and distinct neural representations for abstract mathematical problems. Critically, linking multivariate measures of brain activity to abstract problem representations has the potential to inform functional models of information processing in adults and children.

Methods

Participants

Children were recruited from a wide range of schools in the San Francisco Bay area using mailings to schools, postings at libraries and community groups. Adults were recruited from local colleges in the San Francisco Bay Area. All of the participants were right-handed with no history of psychiatric or neurological disorders. Participants’ intelligence was assessed using the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999), with the inclusion criteria of full scale IQ above 90. The sample consisted of twenty-eight adults (11 males, 17 females) and twenty-eight children (13 males, 15 females). The age of the adults ranged from 19.0 to 22.6 (M = 20.4 years, SD = 1.0), whereas the age of children ranged from 7.7 to 10.7 (M = 8.9 years, SD = .7). Children and adults did not differ in standardized (age-normed) measures of IQ or mathematical or reading abilities (Table 1).

Table 1.

Standardized IQ, mathematical, and reading ability scores for adults and children.

Measure	Group
	Adults (N=28)		Children (N=28)
	M	SD	M	SD	p-value
Males/Females	11/17		13/15
Age	8.85	0.67	20.42	1.05	< 0.001
WASI
Verbal	116.07	12.65	113.29	14.31	0.444
Performance	112.25	11.21	109.68	12.39	0.419
Full Scale	115.96	11.18	113.28	10.52	0.360
WIAT-II
Numerical Operation	113.32	7.59	110.25	10.79	0.224
Mathematical Reasoning	111.21	9.73	113.39	11.87	0.456
Reading Comprehension	111.57	15.65	110.82	9.69	0.830

WASI = Wechsler Abbreviated Scales of Intelligence; WIAT-II = Wechsler Individual Achievement Test – Second Edition.

Standard Assessments of Math and Reading Abilities

Participant’s mathematical and reading abilities were assessed using the Wechsler Individual Achievement Test Second Edition (WIAT-II; Wechsler, 2001). This achievement battery includes nationally standardized measures of academic skills and problem-solving abilities for Grades preK to 16, which are normed by grade and time of the academic year (separate Fall, Spring, or Summer for Grades preK-8 and yearly-based after Grade 8). The Numerical Operations subtest is a paper-and-pencil test that measures number writing and identification, rote counting, number production, and simple addition, subtraction, multiplication, and division calculations. For example, 37+54 is presented vertically on the answer sheet and the participant is required to write down the solution. The Mathematical Reasoning subtest is a verbal problem-solving test that measures counting, geometric shape identification, and single- and multi-step word problem-solving involving time, money, and measurement with both verbal and visual prompts. The participant is required to solve problems with whole numbers, fractions or decimals, interpret graphs, identify mathematical patterns, and solve problems of statistics and probability. For example, a dime is presented and the participant is asked: “How many pennies does it take to equal the value of one dime?” A probability problem asks: “If you flipped a coin ten times, how many times would the coin be most likely to land on heads?” The WIAT-II was also used to assess reading abilities. The Reading Comprehension subtest requires participants to match words to pictures and answer questions about sentences and passages they have read. The reading ability assessment was used to match children and adults on reading abilities.

Experimental Procedures

The fMRI experiment consisted of one run of addition and one run of subtraction. Within each run there were four task conditions: (1) Complex arithmetic, (2) Simple arithmetic, (3) Number identification and (4) Passive fixation. In the Complex addition task, participants were presented with an equation involving two addends and asked to indicate, via a button box, whether the answer shown was correct or incorrect (e.g. “3 + 4= 8”). The first operand ranged from 2 to 9, the second from 2 to 5 (tie problems, such as “5 + 5 =10”, were excluded), and answers were correct in 50% of the trials. Incorrect answers deviated by ± 1 or ± 2 from the correct sum. The Simple addition task was identical except that one of the operands was ‘1’ (e.g. “3 + 1 = 4”). In the Complex subtraction task, the first operand ranged from 3 to 14 and the second operand from 2 to 5. In the Simple subtraction task, the first operand ranged from 2 to 14 and the second operand was always ‘1’. As in the Addition task, incorrect answers for Subtraction deviated by ± 1 or ± 2 from the actual difference, with the additional constraint that the first operand was always greater than the second operand (i.e. problems such as “5 – 6 = −1” were excluded), and presented answers were always greater than zero. In the Number identification task, arithmetic symbols were replaced by alternative keyboard symbols (e.g. “4 o 5 @ 7”) and participants were asked to assess if “5” was among the presented digits. This task was intended to control for basic visual number processing and motor response. Finally, in the Passive fixation task, the symbol “*” appeared at the center of the screen and participants were asked to focus their attention on it.

Stimuli were presented in a block fMRI design in order to optimize signal detection and statistical power (Buxton, Wong, & Frank, 1998; Friston, Zarahn, Josephs, Henson, & Dale, 1999). In each task, stimuli were displayed for 5 seconds with an inter-trial interval of 500 milliseconds. There were 18 trials of each task condition broken up into 4 blocks of 4 or 5 trials, thus, each block lasted either 22 or 27.5 seconds. The order of the blocks was randomized across participants with the following constraints: in every set of 4 blocks, all of the conditions were presented and the Complex and Simple arithmetic task blocks were always separated by either a Number identification or a Passive fixation block. All orders of arithmetic and non-arithmetic task conditions were equally likely. The total length of each experimental run was 6 minutes and 36 seconds.

Data for this study were drawn from a large longitudinal study which prioritized acquisition of high-quality data in the addition task from a maximum number of children (Qin et al., 2014), as well as children with dyscalculia (not included here; Rosenberg-Lee et al., 2015). Accordingly, all participants performed the addition task first followed by subtraction. This manipulation did not cause fatigue: even in children, average accuracy reached 84% for subtraction problems, consistent with previously published results in this age range (Barrouillet et al., 2008).

fMRI data acquisition

Images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil at the Stanford University Lucas Imaging Center. Head movement was minimized during the scan by cushions placed around the participant’s head. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged using a T2* weighted gradient echo spiral in-out pulse sequence (Glover & Lai, 1998) with the following parameters: TR = 2 s, TE = 30 ms, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim, Adalsteinsson, Glover, & Spielman, 2002).

fMRI data preprocessing

Functional MRI data were pre-processed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm). The first 5 volumes were not analyzed to allow for signal equilibration effects. Images were reconstructed, by inverse Fourier transform, for each of the time points into 64 × 64 × 28 image matrices (voxel size 3.125 × 3.125 × 4.5 mm). A linear shim correction was applied separately for each slice during reconstruction using a magnetic field map acquired automatically by the pulse sequence at the beginning of the scan (Glover & Lai, 1998). All participants had movement less than 5 mm in all of the x, y, and z directions. We used a procedure similar to those used in AFNI 3d Despike to correct for transient excesses in participant movement. Deviant volumes were identified as having either total displacement from the initial volume greater than half of a voxel size (1.67 mm in this study) or change in global signal greater than 5%. The total displacement is computed as the square root of the sum of both translational and rotational displacement by first converting rotational displacement from degree to millimeters, assuming a brain radius of 65 mm. No participant had more than 10% deviant volumes. Deviant volumes were then interpolated using the two adjacent scans. Importantly, there were no significant group differences between the percentage of deviant volumes between children (addition: M = .84%, SD = .84; subtraction: M = 1.29%, SD = 1.48) and adults (addition: M = .63%, SD = .42; subtraction: M = .77%, SD = .69; p = .23 and .10 for addition and subtraction, respectively). Images were realigned to correct for head motion and corrected for errors in slice-timing. To allow a direct comparison between groups, all participants’ imageswere spatially transformed to the same standard stereotaxic space (based on the Montreal Neurologic Institute coordinate system), resampled every 2 mm using sinc interpolation, resulting in 2 × 2 × 2 mm voxels. Finally, images were smoothed with a 6mm full-width half-maximum Gaussian kernel to decrease spatial noise prior to statistical analysis.

fMRI data analysis

Individual and group-level analysis

Univariate statistical analysis was performed on both individual and group-level data using the GLM implemented in SPM8. Individual subject analyses were first performed by modeling task-related regressors as boxcar functions corresponding to the epochs during which each condition was presented, and convolved with a hemodynamic response function. Task-unrelated regressors were also included using the 6 motion parameters generated in SPM8’s realignment procedure. For the first-level analysis on each individual, the contrast between Complex and Simple problems for each arithmetic operation were generated and used for all subsequent univariate GLM and multivariate representational similarity analyses. Our analyses focused on arithmetic complexity-related brain responses because stimuli in the Simple task have the same format as the Complex task, providing a high-level control for sensory and number processing, as well as decision-making and response selection within each fMRI run. Between-operation comparison was also generated for each individual subject by contrasting Complex addition – Simple addition with Complex subtraction – Simple subtraction and entered into the second level group analysis. These contrast images were then analyzed in a between-group two-sample t-test to find brain regions with different activation levels between adults and children. Finally, significant clusters of activation were determined using the voxel-wise height threshold of p < .01, with multiple comparison corrections at p < .05, resulting in a cluster extent of 100 voxels, based on Monte Carlo simulations (Cho et al., 2012).

Multivoxel Representational Similarity (MRS) analysis – whole brain

MRS was used to assess the similarity of spatial activity patterns associated with two experimental conditions (Kriegeskorte et al., 2008). We implemented MRS using a newly developed whole-brain searchlight algorithm. A 6 mm radius sphere (containing 113 voxels) surrounding each voxel across the whole brain was first used to define a searchlight region. The Pearson correlation coefficient between t-scores for the contrasts of Complex addition – Simple addition and Complex subtraction – Simple subtraction was then computed for each sphere. Correlation coefficients were normalized using Fisher’s r-to-Z transform: Z = 0.5 * ln((1+r)/(1−r)), which were then entered into a one-sample t-test for group level analysis followed by a two-sample t-test to directly compare MRS between adults and children. Finally, significant MRS clusters were determined using a voxel-wise height threshold of p < .01, with multiple comparison corrections at p < .05, resulting in a cluster extent of 100 interpolated voxels, based on Monte Carlo simulations (Cho et al., 2012). Previous studies have suggested that a set of brain regions, most notably the angular gyrus (AG) region of the PPC, consistently shows reductions in activation during effortful cognitive tasks (Greicius, Krasnow, Reiss, & Menon, 2003; Raichle et al., 2001; Shulman et al., 1997). To exclude deactivation-related effects, we applied an exclusive mask generated from omnibus deactivations. The mask was created by conducting a one-sample t-test on the contrast of Rest minus (Complex addition + Simple addition + Complex subtraction + Simple subtraction) on the data from pooled adults and children together, with a voxel-wise height threshold of p < .01.

Multivoxel Representational Similarity (MRS) analysis – cytoarchitectonic probabilistic maps of the IPS and FG

Additional analyses using MRS values within unbiased anatomical ROIs were conducted using cytoarchitectonically distinct subdivisions of the IPS in PPC and FG in the VTOC (J. Caspers et al., 2012; S. Caspers et al., 2006; Choi et al., 2006; Scheperjans et al., 2008). The three distinct subdivisions of the IPS included hIP2 on the anterior lateral bank of the IPS, hIP1 which is posterior to hIP2 (Choi et al., 2006), and hIP3 which is posterior and medial to both regions (Scheperjans et al., 2008). These maps are based on observer-independent analyses of cytoarchitechtonic organization and they provide an anatomically precise and consistent basis for examining the differential profile of MRS as well as univariate fMRI responses as demonstrated in several prior studies (Ashkenazi et al., 2012; Rosenberg-Lee et al., 2011; Wu et al., 2009). In the VTOC, ROIs included FG1 and FG2, two distinct cytoarchitectonic areas recently identified in the FG (J. Caspers et al., 2012). FG1 is located on the medial aspects of the posterior FG, extending rostrally to the lateral bank of the collateral sulcus. FG2 is located lateral to FG1 on the lateral aspects of the FG extending into the lateral occipitotemporal sulcus. Finally, based on the prominent role ascribed to the AG in arithmetic fact retrieval (Dehaene et al., 2003; Grabner et al., 2007; Rosenberg-Lee et al., 2011; Wu et al., 2009), we conducted additional analysis using observer independent cytoartchitectonically-defined ROIs encompassing the PGa and PGp, the two anterior and posterior subdivisions of the AG (S. Caspers et al., 2006; Wu et al., 2009).

Results

Behavior

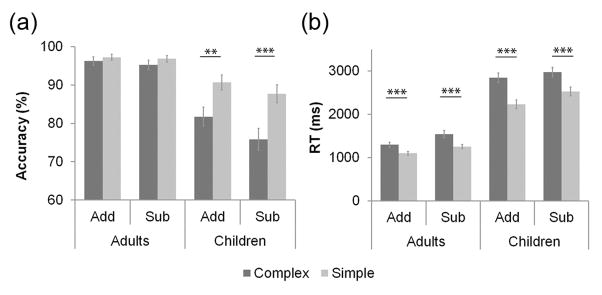
All participants had accuracy greater than 60% for both addition and subtraction problems. Mean accuracy of each participant was entered into a three-way ANOVA with Operation (Addition, Subtraction) and Complexity (Complex, Simple) as within-subjects factors and Group (Adults, Children) as a between-subjects factor. All three main effects were statistically significant, with participants responding less accurately to Subtraction than Addition problems (89% vs. 92%, F (1, 54) = 4.847, p =.032, η_p² = .082), Complex than Simple problems (87% vs. 93%, F (1, 54) = 23.797, p < .001, η_p² = .306), and Children with less accuracy than Adults (84% vs. 96%, F (1, 54) = 43.811, p < .001, η_p² = .448). There was also a Complexity by Group interaction (F (1, 54) = 14.466, p < .001, η_p² = .211), wherein Children were less accurate in answering Complex, than Simple, problems (79% vs. 89%, F (1, 27) = 23.250, p < .001, η_p² = .463) but Adults were equally accurate for both problem types (96% vs. 97%, F (1, 27) = 1.524, p = .228, η_p² = .053). No other interactions were significant (all ps > .11, all η_p² < .046; Figure 1a).

Figure 1. Performance during Addition and Subtraction problems in Adults and Children.

(a) Both Adults and Children were less accurate on Subtraction, compared to Addition, problems (p = .032). Adults were more accurate than Children (p < .001). While Adults were equally accurate in solving Complex and Simple problems (p = .228), Children were less accurate in solving Complex compared to Simple problems (p < .001). (b) Both Adults and Children were slower on Subtraction, compared to Addition, problems (p < .001). Adults were significantly faster than Children (p < .001). Both groups responded more slowly to Complex than Simple problems. The pattern was more pronounced in children than adults (p < .001). Add, addition. Sub, subtraction. *** p < .001. ** p < .01.

A parallel analysis was conducted on median reaction times of each participant. Similar to accuracy, all three main effects were statistically significant. Participants responded more slowly to Subtraction than Addition problems (2064 vs. 1859 ms, F (1, 54) = 60.027, p < .001, η_p² = .526), Complex over Simple problems (2155 vs. 1768 ms, F (1, 54) = 172.707, p < .001, η_p² = .762), and Children more slowly than Adults (2641 vs. 1281 ms, F (1, 54) = 144.885, p < .001, η_p² = .728). The Complexity by Group interaction was also significant, such that the task complexity cost (Complex – Simple) was higher in Children (532 ms) than Adults (241 ms, F (1, 54) = 24.382, p < .001, η_p² = .311). There was a weak Complexity by Group by Operation interaction (F (1, 54) = 4.694, p = .035, η_p² = .080). In Adults, the reaction time difference between Complex and Simple problems was in the expected direction: smaller for Addition (197 ms) than for Subtraction (286 ms) and marginally significant (F (1, 27) = 3.374, p = .077, η_p² = .111); whereas in Children, the interaction was in the opposite direction and again not significant (Addition, 613 ms; Subtraction, 451 ms, F (1, 27) = 2.378, p = .135, η_p² = .081). There were no other significant interactions (all ps > .52, all η_p² < .007) (Figure 1b).

Taken together, these results provide evidence for immature numerical problem solving skills in 7–10 year old children, when compared to adults, both in terms of accuracy and reaction time.

Multivoxel Representational Similarity – whole-brain analysis

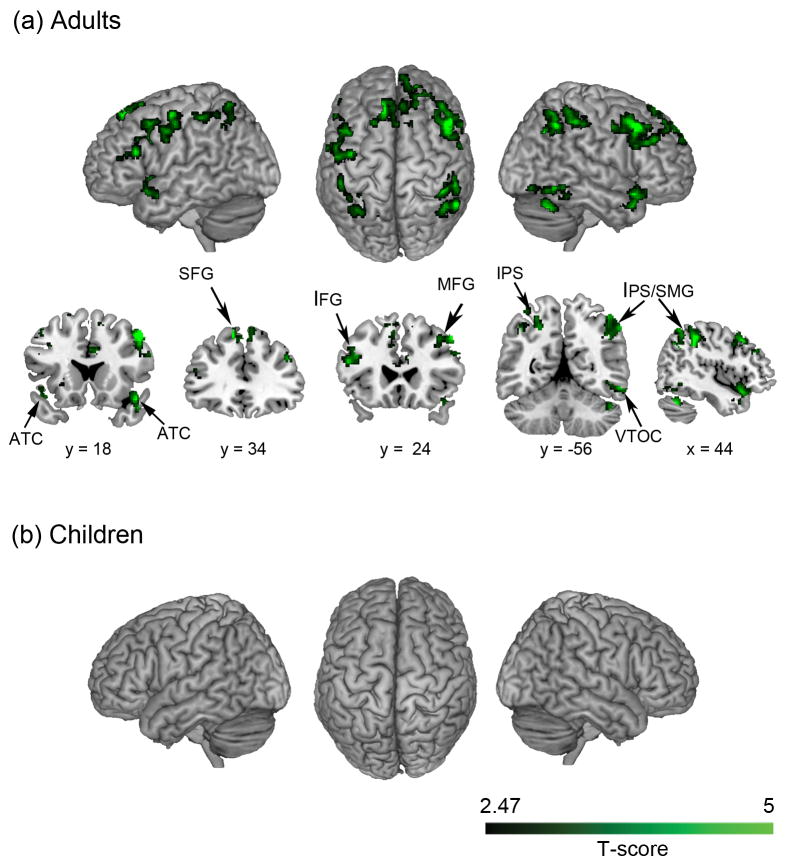
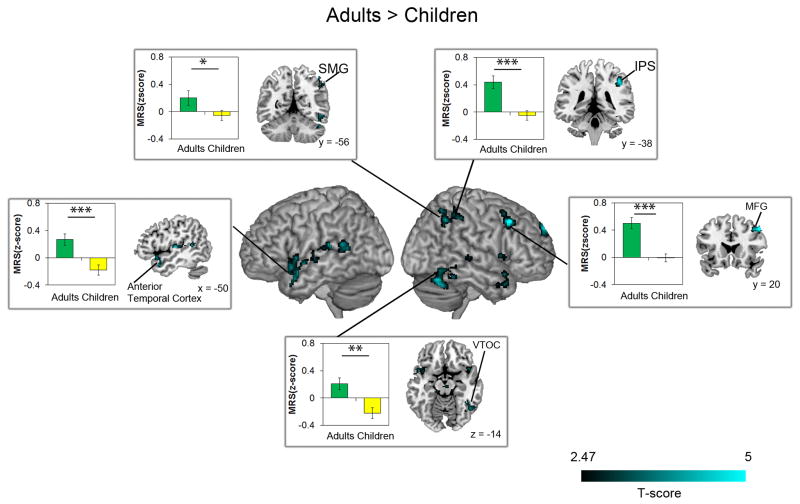
To avoid biases associated with a priori selection of ROIs, we first implemented a whole-brain searchlight algorithm for MRS analysis. Adults showed highly significant MRS between addition and subtraction problems in multiple brain areas, including bilateral IPS and right supramarginal gyrus (SMG) in the PPC; bilateral superior frontal gyrus, left inferior and right middle frontal gyri in the PFC; left parahippocampal gyrus (PHG) in the medial temporal lobe; left and right lateral occipital cortex with adjoining FG in VTOC; bilateral temporal pole in the anterior temporal cortex; and bilateral thalamus and right cerebellum (Figure 2a, Table 2). In sharp contrast, no brain areas showed significant MRS between Addition and Subtraction problems in Children (Figure 2b, Table 2). We then directly contrasted MRS in adults and children at each voxel in the brain. This analysis revealed significantly higher MRS in adults, compared to children, in multiple cortical regions, including right IPS (F (1, 54) = 17.552, p < .001, η_p² = .245) and SMG (F (1, 54) = 3.891, p = .054, η_p² = .067) in PPC, right lateral occipital cortex and FG in VTOC (F (1, 54) = 13.444, p = .001, η_p² = .199), right middle (F (1, 54) = 25.011, p < .001, η_p² = .317) and superior frontal (F (1, 54) = 15.260, p < .001, η_p² = .220) gyri in the PFC, left (F (1, 54) = 15.659, p < .001, η_p² = .225) and right (F (1, 54) = 1.524, p = .222, η_p² = .027) temporal pole in the anterior temporal cortex, as well as the cerebellum and left thalamus in subcortical regions (Figure 3, Table 3). Additional analyses revealed that these age-related differences in MRS were specifically associated with arithmetic problem complexity (Supplementary Results 1, Supplementary Figures S1 and S2).

Figure 2. Brain regions that showed significant multivoxel representational similarity (MRS) between addition and subtraction problems.

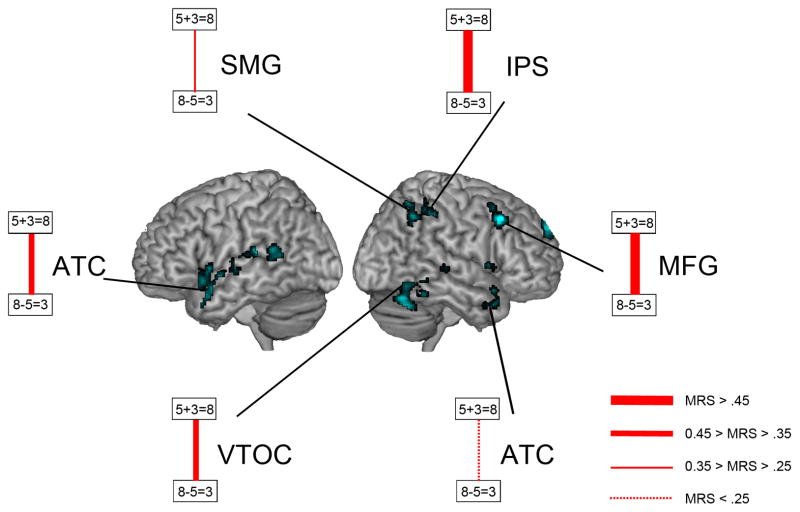
(a) Adults showed significant MRS in multiple brain regions, including bilateral intraparietal sulcus (IPS) and supramarginal gyrus (SMG) in posterior parietal cortex, inferior and middle frontal gyri (IFG, MFG) in prefrontal cortex, anterior temporal cortex (ATC), and right ventral temporal-occipital cortex (VTOC). (b) Children, in contrast, did not show significant MRS in any brain region. Color intensity indicates the MRS levels (T-score) in each group.

Table 2.

Brain regions that adults and children show greater similarity across addition and subtraction problems.

Region	BA	# of Voxels	Peak Z-Score	Peak MNI Coordinates (mm)
				X	Y	Z
Adults
R MFG/SFG	9	1038	5.99	50	20	44
R SMG/IPS	39/40	970	4.60	42	−64	38
L/R SFG	8	471	4.41	−10	34	52
L Precentral Gyrus/IFG	44/6/48	1074	4.34	−40	−6	54
R Anterior Temporal Cortex	38	259	4.23	46	18	−18
R Cerebellum		106	4.22	44	−62	−30
L IPS	40/7	477	4.09	−42	−54	44
L Anterior Temporal Cortex	48	362	4.04	−26	14	2
L Cingulate Gyrus	24	161	4.02	−4	28	16
R VTOC	37	379	3.70	54	−54	−12
L Thalamus		175	3.67	−14	−12	18
L Insula	48	110	3.66	−40	−16	6
L Occipital Gyri	17	159	3.65	−10	−66	6
R Thalamus		139	3.57	2	−18	−8
L PHG	30	129	3.33	−12	−26	−10
Children
None

Note: Each cluster was determined using the voxel-wise height threshold of p < .01, multiple comparison correction at p < .05 using a Monte Carlo determined cluster extent of 100 voxels after gray matter masking. BA, Brodmann area. L, left. R, right. MFG, middle frontal gyrus. SFG, superior frontal gyrus. IPS, intraparietal sulcus. SMG, supramarginal gyrus. IFG, inferior frontal gyrus. VTOC, ventral temporal-occipital cortex. PHG, parahippocampal gyrus.

Figure 3. Brain regions that showed developmental changes in multivoxel representational similarity (MRS).

Compared to adults, children showed significantly lower MRS for addition and subtraction problems in distributed brain regions, including the right intra-parietal sulcus (IPS) and supramarginal gyrus (SMG) in posterior parietal cortex, fusiform gyrus (FG) in ventral temporo-occipital cortex (VTOC), and middle and superior frontal gyri (MFG, SFG) in the prefrontal cortex. *** p < .001, ** p < .01, * p ≤ .05.

Table 3.

Brain regions that adults show greater similarity across addition and subtraction than children.

Region	BA	# of Voxels	Peak Z-Score	Peak MNI Coordinates (mm)
				X	Y	Z
R MFG	9	198	5.51	52	20	44
R IPS	40	217	4.42	44	−38	44
R SFG	9	111	4.05	6	60	34
L STG	48	452	4.04	−36	−8	−4
R Cerebellum/VTOC	19/20	459	4.03	40	−64	−24
L Thalamus		517	3.84	−6	−24	0
R SMG	40	132	3.72	56	−54	46
R Insula/IFG		105	3.72	46	8	6
L Anterior Temporal Cortex		389	3.71	−38	14	−10
L MTG	21	173	3.61	−60	−46	16
R MTG	21/20	100	3.50	50	−26	−2
R Anterior Temporal Cortex		143	3.37	46	14	−28
Cingulate Gyrus		160	3.32	2	8	40

Note: Each cluster was determined using the voxel-wise height threshold of p < .01, multiple comparison correction at p < .05 using a Monte Carlo determined cluster extent of 100 voxels after gray matter masking. BA, Brodmann area. L, left. R, right. MFG, middle frontal gyrus. IPS, intraparietal sulcus. SFG, superior frontal gyrus. STG, superior temporal gyrus. VTOC, ventral temporal-occipital cortex. SMG, supramarginal gyrus. IFG, inferior frontal gyrus. MTG, middle temporal gyrus.

To validate that differential MRS in children and adults was not caused by age-related performance or head movement differences, we conducted additional analyses including behavioral task performance and mean scan-to-scan displacement as covariates in the MRS clusters that showed significant group differences. In order to (i) control for differences in behavior between Children and Adults, (ii) account for potential differences in speed and accuracy tradeoffs present in the performance profiles among the two groups, and (iii) obtain a general performance index of Addition and Subtraction tasks, we computed a composite measure of performance efficiency by averaging z-scores for accuracy and negative z-scores for reaction time for both of Addition and Subtraction tasks (Salthouse & Hedden, 2002; Supekar et al., 2013). The mean scan-to-scan displacement for each subject was computed as the average of the displacements between successive volume acquisitions (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). We conducted an ANCOVA with Group as a between participants factor while covarying out the task performance and movement. Except for the cingulate gyrus cluster, the main effect of Group remained significant in all other MRS clusters, with higher MRS in Adults compared to Children (all ps < .016, all η_p² > .106).

Next, to examine whether age-related differences in MRS were due to greater task-related activity levels between addition and subtraction in adults, we investigated age-related group differences in brain activation between the two operations across the whole brain. Three brain areas showed significant complexity related Group by Operation interactions: one in the right posterior IPS with adjoining AG, another in the middle occipital gyrus, and the third one in the cerebellum (Figure S3, Table S1). Notably, none of these regions overlapped with the clusters that showed differences in MRS between adults and children. ROI analysis of the MRS clusters also did not reveal any effect of Group differences in either the Addition (all ps > .124) or the Subtraction (all ps > .051) tasks and there was no significant interaction between Group and Operation (all ps > .097). These results suggest that age-related differences in MRS reported here do not arise from overall differences in signal level.

Taken together, these results demonstrate that children show weak MRS between related addition and subtraction problems, and further suggest that common neural representations of these problems undergo significant maturation from childhood to adulthood.

Multivoxel Representational Similarity – cytoarchitectonically defined IPS and FG ROIs

To further investigate the anatomical localization of neural representations between addition and subtraction in the PPC and VTOC, we conducted ROI analyses using MRS values within unbiased cytoarchitectonically defined subdivisions of the IPS and FG. We examined MRS between addition and subtraction within the three cytoarchitectonically distinct subdivisions of the IPS regions, hIP2, hIP1, and hIP3 that span its anterior to posterior axis (Figure S4a). MRS measures were entered into a three-way ANOVA, with Subdivision (hIP2, hIP1, hIP3) and Hemisphere (Left, Right) as within-subjects factors and Group (Adults, Children) as a between-subjects factor. Group was the only significant main effect, with Adults showing greater MRS than Children (F (1, 54) = 6.832, p = .012, η_p² = .112). There was a strong Group by Hemisphere by Subdivision interaction (F (2, 108) = 5.402, p = .006, η_p²= .091). Pair-wise comparisons showed the interaction was driven by greater MRS in Adults than Children in right hIP2 (F (1, 54) = 24.388, p < .001, η_p²= .311), but not in any other cytoarchitectonically defined IPS regions (all p > .09, all η_p² < .052, Figure S4a).

To further validate that differences in MRS between children and adults in the right hIP2 were not biased by spurious systematic variations between the two groups, we computed the partial correlation coefficient between addition and subtraction problems while controlling for the Number identification task using the approach described in Supplementary Results 2. We found MRS in right hIP2 remained significantly greater in adults than children (F (1, 54) = 14.064, p < .001, η_p² = .207). To validate that differential MRS in children and adults in the right hIP2 was not caused by age-related performance and head movement differences, we conducted an ANCOVA with Group as a between participants factor while covarying out task performance and movement using the approach described above. We found the main effect of Group remained highly significant in right hIP2 (F (1, 52) = 19.787, p < .001, η_p² = .276), with higher MRS in adults compared to children.

We then examined MRS within FG2 and FG1 subdivisions that span the posterior to anterior gradient of the FG (Figure S4b). MRS measures were entered into a three-way ANOVA, with FG Subdivision (FG2, FG1) and Hemisphere (Left, Right) as within-subjects factors and Group (Adults, Children) as a between-subjects factor. There was a significant Group by Hemisphere interaction (F (1, 54) = 4.399, p = .041, η_p² = .075). Posthoc analysis showed that the interaction resulted from greater MRS in adults than children in right (F (1, 54) = 5.228, p = .026, η_p²= .088) but not in left FG (F (1, 54) = .252, p = .618, η_p² = .005, Figure S4b). No other main effects or interactions were significant (all ps > .806, all η_p² < .001).

To further validate that differential MRS in children and adults in the right FG was not biased by spurious systematic variations between the two groups, we again computed the partial correlation coefficient between addition and subtraction problems while controlling for the Number identification task using the approach described above. We found MRS in right FG was still significantly greater in adults than children (F (1, 54) = 8.080, p = .006, η_p² = .130). To validate that differential MRS in children and adults in the right FG2 was not caused by age-related performance and head movement differences, we conducted an ANCOVA with Group as a between participants’ factor while covarying out task performance and movement using the approach described above. We found main effect of Group remained significant in right FG2 (F (1, 52) = 8.068, p = .006, η_p² = .134), with higher MRS in Adults compared to Children.

Multivoxel Representational Similarity in deactivated AG ROIs

Based on the prominent roles ascribed to the AG in some models of arithmetic fact retrieval (Dehaene et al., 2003; Grabner et al., 2007; Rosenberg-Lee et al., 2011; Wu et al., 2009), we investigated whether, despite its deactivation, developmental changes in MRS can also be detected in the AG. MRS measures were entered into a three-way ANOVA, with Subdivision (PGa, PGp) and Hemisphere (Left, Right) as within-subjects factors and Group (Adults, Children) as a between-participants factor. We found a significant Group effect: Adults showed greater MRS than Children (F (1, 54) = 9.509, p = .003, η_p² = .150). No other main effects or interactions were significant (all ps > .113, all η_p² < .046). These results suggest that the maturation of neural representation is characterized by more similar patterns of disengagement during addition and subtraction problem solving.

Relation between MRS and task performance – whole-brain analysis

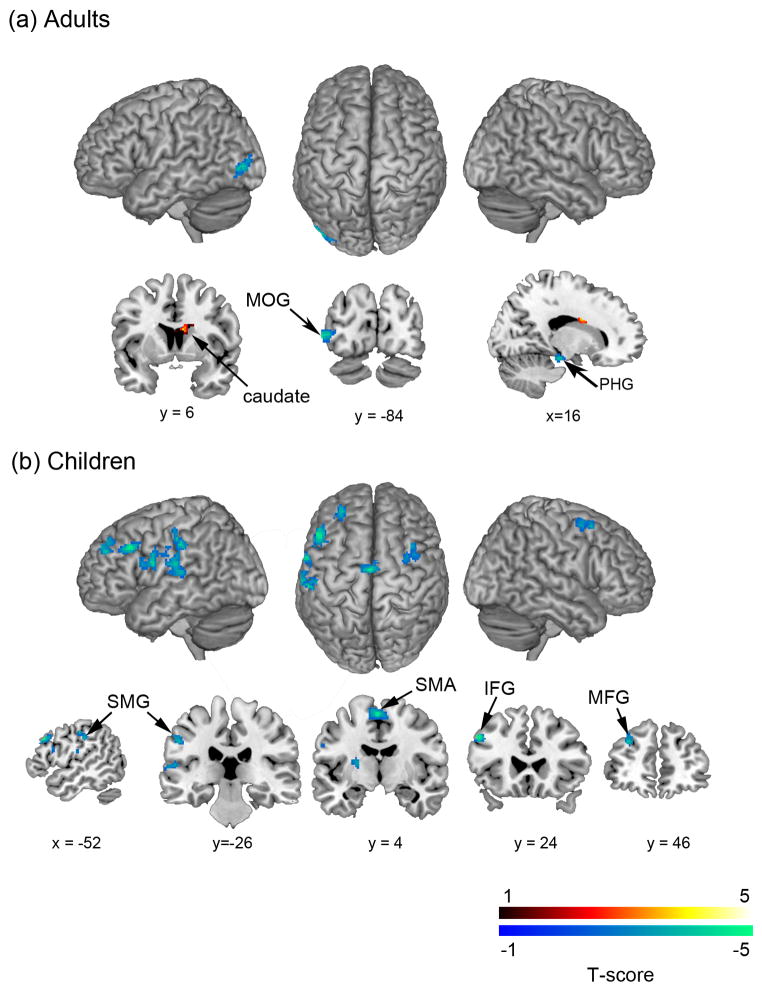
Next, we conducted a whole-brain regression analysis to investigate the relation between MRS and arithmetic task performance in each group. Behavioral performance was computed as a composite efficiency score by combining the standardized accuracy and reaction time of Addition and Subtraction using the method mentioned in the previous section. We found that adults showed a positive correlation between MRS in right caudate and a negative correlation in middle occipital gyrus (MOG) and PHG (Figure 4a, Table 4). In contrast, children showed significant negative correlations with MRS in multiple brain regions, including left SMG and postcentral gyrus in PPC, inferior and middle frontal gyri (IFG, MFG) in PFC, and supplementary motor area (SMA). No positive correlations were found in children (Figure 4b, Table 4).

Figure 4. Brain regions in which adults and children showed correlation between multivoxel representational similarity (MRS) and arithmetic task performance.

(a) Adults’ task performance was positively correlated with MRS in right caudate and negatively correlated with MRS in middle occipital gyrus (MOG) and parahippocampal gyrus (PHG). (b) Children’s task performance, in contrast, was negatively correlated with MRS in multiple brain regions, including left supramarginal gyrus (SMG) and postcentral gyrus in posterior parietal cortex, inferior and middle frontal gyri (IFG, MFG) in prefrontal cortex, and supplementary motor area (SMA). Red and blue color intensity indicate positive and negative correlation between task performance and MRS levels (T-score), respectively, in each group.

Table 4.

Brain regions that adults and children show correlation between MRS and arithmetic task performance.

Condition	Region	BA	# of Voxels	Peak Z-Score	Peak MNI Coordinates (mm)
					X	Y	Z
Adult
Positive
	R Caudate		118	3.69	8	6	20
Negative
	L MOG	19	151	3.92	−48	−84	0
	R PHG	30	115	3.76	14	−24	−16
Children
Positive
	None
Negative
	L MFG	44	126	4.03	−52	24	36
	SMA	6	201	3.98	−2	−8	60
	L SMG/Postcentral	2/3/48	415	3.81	−60	−24	38
	Gyrus
	L Postcentral Gyrus/IFG	44	167	3.74	−62	4	42
	L MFG	46	105	3.58	−28	46	32
	R Thalamus		123	3.44	20	−20	8
	L Thalamus		190	3.42	−22	2	12
	R Insula	48	109	3.41	32	0	12
	R MFG	9	140	3.33	36	14	56

Note: Each cluster was determined using the voxel-wise height threshold of p < .01, multiple comparison correction at p < .05 using a Monte Carlo determined cluster extent of 100 voxels after gray matter masking. BA, Brodmann area. MOG, middle occipital gyrus. PHG, parahippocampal gyrus. MFG, middle frontal gyrus. SMA, supplementary motor area. IFG, inferior frontal gyrus.

Age-related differences in the relation between MRS and task performance – cytoarchitectonically defined IPS and FG ROIs

Finally, we examined the relation between task performance and MRS within the three cytoarchitectonically distinct subdivisions of the IPS and FG regions. Only the right hIP2 subdivision showed a negative correlation between the task performance and MRS. Furthermore, as shown in Figure S5, this relation was observed only in children (R = −.497, p = .007) but not in adults (R = −.031, p = .877). Performance was not correlated with any other IPS or FG subdivisions.

Discussion

In the present study, we investigated how the brain represents distinct numerical problems and how these representations mature in the developing brain after more than a decade of experience with problem solving. We first examined whether adults and children show common neural representations for addition and subtraction problems, two complementary arithmetic operations with cognitive solution architectures thought to converge over development. We then examined how the common representations for the two problem types change with development. To accomplish this we used MRS analysis at the whole-brain level to assess the similarity of neural representations for addition and subtraction problems during numerical problem solving. Compared to children, adults showed significant MRS between addition and subtraction problems in the PPC, VTOC, PFC and anterior temporal cortex. Notably, no brain areas showed significant MRS between the two operations in children. Furthermore, because our analysis focused on arithmetic complexity effects, these results are independent of basic number, sensory, and decision making processes associated with each operation. Our study demonstrates that the maturation of arithmetic problem solving skills is characterized by significant developmental changes in common neural representations across the two operations and provide novel evidence for convergence in cognitive and brain mechanisms for two distinct, but related, problem types. Our findings point to the development of problem representations that are independent of overall differences in signal level and provide insights into distributed neural representations that support mature problem-solving abilities.

Developmental differences in representational similarity and emergence of common neural representations

To our knowledge, this is the first study to examine the similarity of neural representations between related abstract problems and the first to examine how common representations emerge with development. Our results demonstrate that adults, but not children, display similar neural representation across operations in multiple regions, including key parietal, inferior temporal and prefrontal cortex regions consistently associated with arithmetic problem solving. Importantly, no brain regions showed significant MRS in 7- to 10-year old children. Because MRS examines correlations between spatial activity patterns, our findings are independent of the activation level elicited by each arithmetic operation.

One potential cause for this developmental profile may be the variability of strategies used at different ages. Children in the 2^nd and 3^rd grades solve addition and subtraction problems using a range of strategies including finger counting, verbal counting, decomposition, and retrieval (Barrouillet et al., 2008; Siegler, 1987; Siegler & Shrager, 1984). With age, the general arc of strategy development shifts from effortful counting to more automatic fact retrieval (Geary, Brown, & Samaranayake, 1991; Jordan, Hanich, & Kaplan, 2003; Ostad, 1999). In the end state, adults predominantly apply direct retrieval strategies to solve single-digit arithmetic problems, not only for addition but also subtraction (Campbell & Xue, 2001), suggesting greater similarities in cognitive processing. Consistent with this view, behavioral studies have demonstrated that adults do not benefit from presenting subtraction problems in addition format for arithmetic problem solutions (e.g., 13 = 6 + _) when the minuend is less than 10, indicating that adults solve small subtraction problems by directly retrieving arithmetic facts (Campbell, 2008). Children, in contrast, reported only 31% direct fact retrieval, 33% reference to addition and 37% procedural calculation even for small subtraction problems with minuends less than 10 (Barrouillet et al., 2008). Taken together, these findings suggest that the maturation of arithmetic skills is characterized by a progression from variable to stable strategy use across operations, leading to common representations for these distinct arithmetic problems at the neural level. The arithmetic complexity-dependent MRS effects further confirm the specificity of age-related progression of neural representations independent of basic number, sensory, and decision making processes.

Common neural representations in posterior parietal cortex

The PPC, and primarily the IPS, has been a focus of research into arithmetic problem solving in both children and adults (Arsalidou & Taylor, 2011; De Smedt et al., 2011; Houde et al., 2010; Rosenberg-Lee et al., 2011; Xue et al., 2013). We found significant increases in MRS between the two operations in the IPS from childhood to adulthood. The IPS is thought to play an essential role in manipulation of quantity along a mental number line (Cohen Kadosh et al., 2008; Dehaene et al., 2003). Consistent with this view, the IPS shows strong MRS between responses to number comparison and subtraction problems (Prado et al., 2011). The high levels of MRS between addition and subtraction problems observed in our study may therefore be related to overlapping representation of quantity across the two operations. Additional analysis of the three major cytoarchitectonically-defined subdivisions of the IPS revealed that its anterior-most subdivision, right hIP2, showed the most significant differences in MRS between children and adults. Furthermore, adjacent regions of the inferior parietal lobule encompassing cytoarchitectonically distinct subdivisions of the right SMG also showed significantly greater MRS between the two problem types in adults compared to children. Our results suggest that common problem representations emerge in two keys areas of the PPC associated with quantity representation and manipulation (Cohen Kadosh et al., 2008; Dehaene et al., 2003).

Our findings also help to clarify and expand on previous studies that have used traditional univariate methods to assess developmental changes between childhood and adulthood. Previous developmental investigations have reported increased engagement of the IPS and the supramarginal gyrus with age. Rivera and colleagues examined brain activations in response to arithmetic problems that involved a combination of addition and subtraction operations, in children, adolescents, and adults ranging in age from 8 to 22. They found that IPS responses increased linearly with age (Rivera et al., 2005). Similarly, Kucian and colleagues also observed greater IPS activity in adults than children during approximate addition (Kucian et al., 2006). Such patterns of developmental change have also been reported in symbolic and nonsymbolic number comparison tasks (Ansari & Dhital, 2006; Cantlon et al., 2009; Holloway & Ansari, 2010). In the present study we found no significant age-related activation decreases or increases in IPS regions that showed increased MRS. Our findings suggest, for the first time, that irrespective of changes in IPS activation levels with age, greater MRS between the two operations in adults reflects use of more similar, and efficient, strategies.

In contrast to developmental studies, short-term arithmetic training studies in adults have generally reported decreases in IPS activation and increased activation, more likely decreased deactivation, in the AG following one or two weeks of training (Delazer et al., 2005; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007; Ischebeck et al., 2006). These results were interpreted as reflecting a shift in strategy from procedural calculation to automated retrieval of trained problems. In the present study, we did not find overall changes in IPS activation levels with age, nor any evidence for decreases in AG deactivation in adults, relative to children. Remarkably, despite being deactivated, adults showed greater arithmetic complexity-related MRS in the AG, when compared to children. This finding suggests that complexity dependent maturation of neural representations in adults is further characterized by more similar processing of addition and subtraction problems even in AG regions that are deactivated during arithmetic problem solving. Although previous findings of increased AG response with training in adults has been interpreted as reflecting greater retrieval of facts, deactivation of this region leaves the precise contribution of this region to retrieval unclear. What is clear, however, is that neural representations associated with more complex addition and subtraction become more stable with age, in both the IPS and AG. This process likely reflects more efficient coding in adults that is independent of both the level and the direction of activation.

Common neural representations in ventral temporal-occipital cortex

We had hypothesized that, unlike posterior PPC regions involved in semantic representations and manipulation of quantity, VTOC regions involved in perceptual representation of number strings would not show age-related differences in MRS. Our hypothesis was based on differences in perceptual characteristics of the two problem types. Although addition and subtraction problems share some perceptual characteristics, there are important differences as well. Crucially, in our stimulus set, subtraction problems could have double-digit numbers in the first operand, while addition problems did not. Conversely, addition problems could have double-digit numbers in the answer position, while subtraction problems did not. Our hypothesis regarding the VTOC was based on such differences. However, contrary to our hypothesis, we found that adults also showed high MRS in the VTOC, similar to the PPC.

In contrast to the IPS, the VTOC is thought to support perceptual representations and visual number form processing. For example, a recent cross-linguistic fMRI study found that perceptual aspects of processing digits and ideographs was associated with activation in the FG whereas semantic processing of both symbol types was associated with modulation of IPS response (Holloway et al., 2013). In the present study, within the VTOC, adults exhibited significant MRS in the FG and adjacent lateral occipital gyrus, a finding confirmed by cytoarchitectonic mapping. These visual association cortical regions have been linked with functional specialization of category-specific information such as words and numbers (Cohen et al., 2000; Holloway et al., 2013), objects (Gauthier, Tarr, Anderson, Skudlarski, & Gore, 1999), faces (Kanwisher, 2000; Weiner & Grill-Spector, 2012), as well as visual object shape (Drucker & Aguirre, 2009). Additional analysis of the two major cytoarchitectonically-defined subdivisions of the FG (J. Caspers et al., 2012) revealed that its lateral subdivision, FG2, showed the most significant differences in MRS between children and adults. Although Caspers and colleagues have suggested that right FG2 is the likely subdivision of the fusiform face area (J. Caspers et al., 2012), our findings suggest that this area is broadly tuned to also represent visual number form. Taken together, these results suggest that common neural representations for abstract arithmetic problems are coded not only in IPS regions involved in semantic aspects of quantity processing but also in VTOC regions involved in visual symbol decoding.

Common neural representations beyond the PPC and VTOC

A novel and unexpected finding from the whole-brain MRS analysis is that common representations emerged with age in the PFC and anterior temporal cortex. Adults, but not children, also demonstrated common neural representations in the PFC, despite decreases in age-related activation (Cantlon et al., 2006; Rivera et al., 2005). Notably, the PFC regions which showed high levels of MRS between addition and subtraction problems were localized to bilateral dorsolateral PFC regions that have been implicated in arithmetic problem solving (De Smedt et al., 2011; Metcalfe, Ashkenazi, Rosenberg-Lee, & Menon, 2013; Rivera et al., 2005; Rosenberg-Lee et al., 2011; Wu et al., 2009). This link was substantiated by additional quantitative analysis using Neurosynth (Yarkoni, Poldrack, Nichols, Van Essen, & Wager, 2011), as depicted in Figure 5. Furthermore, intrinsic functional connectivity and white matter tractography have provided converging evidence that the right IPS region hIP2 has strong connections with the dorsolateral PFC (Uddin et al., 2010). The dorsolateral PFC and SMG form a core fronto-parietal circuit important for maintaining and manipulating information in working memory (Klingberg, 2006; Klingberg, Forssberg, & Westerberg, 2002; Rottschy et al., 2012). As summarized in Figure 6, the strongest age-related differences in MRS were also observed in the right PFC and the right PPC, pointing to a crucial role for a right hemisphere fronto-parietal circuit in the neural representation maturation. Unlike adults, children did not show significant MRS in this frontal-parietal circuit, possibly due to greater variability in how they engage the circuit and manipulate arithmetic related codes within working memory. These results suggest that fronto-parietal circuits associated with the IPS and SMG play an important role in the development of common representations for arithmetic problems.

Figure 5. Overlap between multivoxel representational similarity (MRS) maps and brain regions involved in arithmetic problem solving.

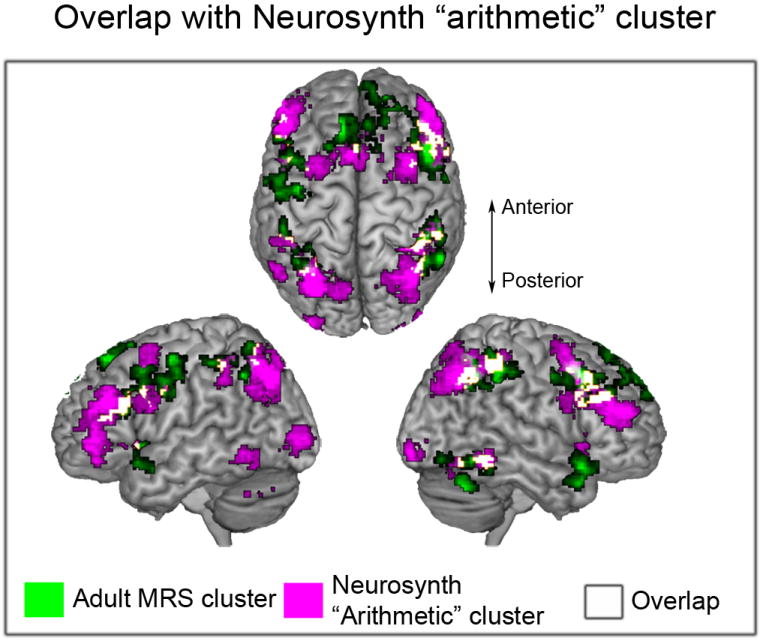
Brain regions that showed significant MRS in adults (shown in green), and brain regions involved in arithmetic processing (shown in purple), as identified by Neurosynth using Bayesian meta-analysis of 48 studies (search term “arithmetic” in www.neurosynth.org). Overlapping voxels are shown in white.

Figure 6. Summary of developmental changes in multivoxel representational similarity (MRS) between addition and subtraction problems.

The intra-parietal sulcus (IPS) and middle frontal gyrus (MFG) showed the strongest developmental changes, followed by anterior temporal cortex (ATC), ventral-occipital temporal cortex (VTOC) and supramarginal gyrus (SMG). The width of the red lines represents the strength of MRS differences between adults and children.

Another unexpected finding of our study was the emergence of common neural representations for abstract problems in bilateral anterior temporal cortex. The only brain imaging study to investigate anterior temporal cortex activity in arithmetic processing found that children who primarily used retrieval strategies showed significantly different multivariate activity patterns in this region when compared to children who primarily used counting strategies (Cho, Ryali, Geary, & Menon, 2011), suggesting that more mature and less variable strategies may underlie the increase in MRS between addition and subtraction problems observed in adults. More broadly, converging functional imaging studies have suggested the anterior temporal cortex plays an integrative role in semantic (Binder et al., 2011) and conceptual knowledge (Kriegeskorte et al., 2009).

Functional imaging studies, mainly using linguistic tasks, have demonstrated that anterior temporal cortex activation increases when perceiving semantically congruent sentences compared to single words and semantically random sentences (Humphries, Binder, Medler, & Liebenthal, 2006). Transcranial magnetic stimulation administered to bilateral anterior temporal cortex has also been found to impair semantic decision making (Lambon Ralph, Pobric, & Jefferies, 2009). Beyond these cognitive domains, the role of the anterior temporal cortex in arithmetic has been investigated only in patients with semantic dementia. These studies have suggested that arithmetic performance in semantic dementia is aberrant and have further suggested a close link between semantic memory and arithmetic knowledge (Julien, Thompson, Neary, & Snowden, 2008). Together, these findings suggest that the anterior temporal cortex plays an important, and heretofore unrecognized, role in the maturation of common semantic representations for related arithmetic problems. Further studies are needed to clarify the role of this region in the development of problem representations and semantic knowledge of mathematical facts.

Developmental differences in PPC and PFC MRS-behavior relations

Despite weaker overall MRS, children displayed a strong and distinct profile of MRS-behavior relations in both the PPC and the PFC. Surprisingly, lower MRS in multiple PPC regions, most notably the left SMG, the hIP2 subdivision of the IPS, the PFC, and most notably the IFG and MFG, were predictive of better performance in children. On the one hand, this result seems paradoxical given that adults showed higher levels of performance as well as MRS than children in multiple PPC and PFC regions, suggesting that better performance should be related to higher MRS. On the other hand, our findings point to a non-linear profile of developmental differences in MRS associated with maturation and differentiation of problem solving strategies across the two operations. Behavioral research has demonstrated that in the early stages of arithmetic skill development children use different cognitive processes to solve addition and subtraction problems (Barrouillet et al., 2008; De Smedt et al., 2011). Specifically, elementary school children show lower levels of retrieval strategy use and greater strategy variability for subtraction when compared to addition problems (Barrouillet et al., 2008). Individual children are at different stages of developing proficiency for addition and subtraction, and as indexed by our MRS measures, the most proficient among them show increased differentiation between the two operations. We hypothesize that with development, problem solving strategies converge across the two operations, leading to better overall performance and increased MRS by adulthood. Further longitudinal research is needed to test this hypothesis and capture the full developmental trajectory of abstract problem representations.

Conclusions

Our findings provide new insights into the maturation of neural representations for abstract numerical problems. We show, for the first time, that the maturation of arithmetic problem solving skills is characterized by the emergence of common neural representations across operations, not only in the IPS but also in multiple, distributed, foci in ventral occipito-temporal cortex, prefrontal cortex and anterior temporal cortex. Together, these foci encompass multiple stages of the information processing hierarchy, spanning brain regions specialized for symbol decoding and semantic representations of quantity. Critically, unlike adults, children failed to show common neural representations in any of these brain regions and processing stages. Our findings provide novel evidence that even in brain areas where the level of functional engagement is mature by age 10, the underlying neural representations continue to be refined. Furthermore, our study highlights the role of distributed neural activity patterns in shaping and developing brain representations for abstract problems. Our findings demonstrate that multivoxel representational similarity analysis provides a powerful framework for relating cognition, brain activity and development. More broadly, this approach has the potential to significantly enhance our understanding of the fundamental mechanisms by which children develop proficiencies that are the hallmark of human cognition.

Highlights.

• Neural representations for distinct numerical problems change with development.

• Only adults show representational similarity between distinct numerical problems.

• Common neural representations emerge with maturation of problem solving skills.

• Representational analysis links higher-order cognition, brain activity & development.