Hybrid bilayer plasmonic metasurface efficiently manipulates visible light

Two highly coupled plasmonic metasurfaces exhibit much higher conversion efficiency and extinction ratio than individual ones.

Abstract

Metasurfaces operating in the cross-polarization scheme have shown an interesting degree of control over the wavefront of transmitted light. Nevertheless, their inherently low efficiency in visible light raises certain concerns for practical applications. Without sacrificing the ultrathin flat design, we propose a bilayer plasmonic metasurface operating at visible frequencies, obtained by coupling a nanoantenna-based metasurface with its complementary Babinet-inverted copy. By breaking the radiation symmetry because of the finite, yet small, thickness of the proposed structure and benefitting from properly tailored intra- and interlayer couplings, such coupled bilayer metasurface experimentally yields a conversion efficiency of 17%, significantly larger than that of earlier single-layer designs, as well as an extinction ratio larger than 0 dB, meaning that anomalous refraction dominates the transmission response. Our finding shows that metallic metasurface can counterintuitively manipulate the visible light as efficiently as dielectric metasurface (~20% in conversion efficiency in Lin et al.’s study), although the metal’s ohmic loss is much higher than dielectrics. Our hybrid bilayer design, still being ultrathin (~λ/6), is found to obey generalized Snell’s law even in the presence of strong couplings. It is capable of efficiently manipulating visible light over a broad bandwidth and can be realized with a facile one-step nanofabrication process.

INTRODUCTION

The ability of bending and molding propagating light beams is of great importance in science and technology. Conventionally, light deflection relies on the gradual phase accumulation along the light path by using, for example, lenses and prisms. However, the limited range of permittivity and permeability values of natural materials imposes significant limitations in the design of these conventional optical components, for example, in terms of their thickness, which is generally comparable to the operating wavelength, hence hindering their integration with nanophotonic circuits. Metamaterials, composed of artificial nanostructures, have been shown to allow extreme control of electromagnetic fields, much beyond what is attainable with naturally occurring materials. In particular, metamaterials can be tailored to exhibit exotic and intriguing effects, such as negative refraction, perfect lensing, and cloaking (1–3). However, the fabrication of three-dimensional (3D) large-scale metamaterials remains a big technological challenge. Another major problem in plasmonic metamaterials is represented by the strong energy dissipation in metals, especially at visible frequencies.

Recently, planarized 2D metamaterials, or “metasurfaces,” have gained increasing attention, because they may allow realization of anomalous effects, while relaxing the limitations and challenges of bulk metamaterials (4–6). Notably, ultrathin metasurfaces have been suitably designed to deflect an impinging beam into anomalous refraction channels, obeying “generalized Snell’s laws,” by imparting a controlled gradient of phase discontinuities along the metasurface (7–12). The thickness of these structures is far smaller than the operational wavelength, allowing, in principle, the miniaturization and integration of several optical components and systems. Many different metasurfaces, including plasmonic and dielectric designs, as well as ultrathin and finite-thickness configurations, have been reported (13–26). Metasurfaces operating in reflection mode have been shown to exhibit relatively higher efficiencies. However, reflective metasurfaces involve more complicated optical setups and may introduce certain inconvenience in many applications. Particular interest has been devoted to ultrathin metasurfaces working in transmission mode, based on arrays of metallic nanoantennas, or Babinet-inverted designs, namely, arrays of apertures in a metallic sheet (4, 5, 9, 11, 14, 15). However, Monticone et al. (13) theoretically demonstrated in their study (and Supplementary Materials therein) that any passive metasurface with infinitesimal thickness can fully manipulate the phase of cross-polarized transmitted light at only 25% of the total impinging energy. Realistic implementations have shown even lower efficiency in the order of a few percent (13–15). Although high diffraction efficiency (~80%) was reported using Si metasurfaces (23), it follows the similar definition of extinction ratio, which describes the ratio of the power of anomalous components over the transmitted power. It is worth noting that it is still challenging to achieve high conversion efficiency of the overall system, corresponding to the power of converted anomalous components versus the total incident power, that is, transmission coefficient multiplied with diffraction efficiency. In the study of Lin et al. (23), on the basis of the presented data, the best two cases (at 550 and 650 nm) yield ~20% in conversion efficiency because the highest transmission coefficient and highest diffraction efficiency arise at the different wavelengths.

It has been reported that, by using isotropic metamaterial Huygens surfaces, consisting of cascaded metasurface layers, it is possible to achieve high efficiency in anomalous deflection of the incident light at telecommunication wavelength around 1.5 μm, thanks to the interference of the fields radiated by effective electric and magnetic surface currents (7, 10, 27). These designs generally require sophisticated fabrication processes and unit cells, which result in great challenges to apply this conception in the visible range. These works primarily focused on the manipulation of the copolarized component of the transmitted field, and it is imperative to find an accessible recipe to achieve a highly efficient manner to manipulate cross-polarization directly in visible regime using ultrathin metasurfaces. The resultant recipe should be easily and readily scaled into longer wavelengths.

Here, we propose and experimentally demonstrate an efficient bilayer plasmonic metasurface working in transmission mode at visible frequencies. Owing to the properly tailored intra- and interlayer couplings, significantly larger cross-polarization conversion efficiency of up to 36.5% has been achieved in simulations and 17% in experiments. Notice that the 25% theoretical limit for cross-polarized conversion efficiency does not apply to our metasurface design because of its finite, yet small, thickness, which allows breaking the radiation symmetries of ultrathin metasurfaces. The results reported in this paper represent a significant improvement in the manipulation of visible light by metasurfaces in terms of conversion efficiency and extinction ratio. The structure proposed here has a total thickness of only 130 nm (~λ/6) and has been realized by using a facile one-step fabrication process, as described in the following.

RESULTS AND DISCUSSION

The basic structure proposed here consists of two physically separated plasmonic layers: the top layer is a 2D array of gold V-shaped nanoantennas, whereas the bottom layer is a 2D array of V-shaped Babinet-inverted apertures in a gold film, as shown in the inset of Fig. 1A. The two layers are separated by conformal pillars made of hydrogen silsesquioxane (HSQ) negative E-beam resist. Similar complementary configurations with different shapes have been investigated previously for different applications, such as biosensing (28–30), high extinction ratio polarizers (31–33), high-resolution printing of color images (34, 35), and dark plasmonic resonance excitation (36). To design a metasurface for cross-polarization conversion and beam deflection, we define a supercell consisting of six basic elements, which provide similar cross-polarization transmission amplitude and incremental transmission phase with π/3 steps. Subunits 1 to 3 are constructed by properly changing the length and the angle between the two arms of nanoantennas, similar to the design in studies of Yu et al. (4) and Ni et al. (5) (the symmetry axis of the V-shaped antennas is along 45° relative to the x axis). Subunits 4 to 6, instead, are constructed by simply rotating the symmetry axis of subunits 1 to 3 90° clockwise. This provides a full coverage of the transmission phase range. The subunit cell period is 150 nm; therefore, the overall dimension of the supercell is 900 × 150 nm. The height H of the HSQ pillars and the thickness T of the gold layers (inset of Fig. 1A) are 100 and 30 nm, respectively. The separation between the two plasmonic layers D is therefore 70 nm, much smaller than the working wavelength in the visible range, implying a strong coupling between top and bottom metasurfaces, similar to gap-surface plasmon effects discussed by Pors et al. (12). The total thickness of the proposed device is only 130 nm (~λ/6).

Fig. 1. High-efficiency beam bending of visible light with a complementary bilayer metasurface.

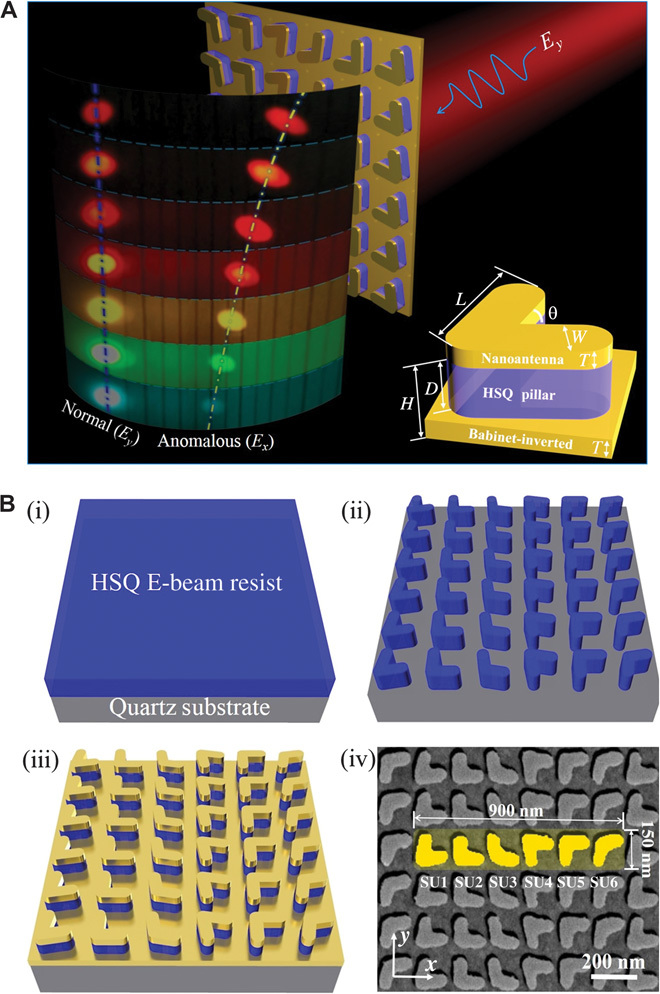
(A) Working principle of the designed structure. The light spots on the screen in the foreground are the combined real photo images of anomalous light deflection for different wavelengths. Inset: Sketch of the subunit cell, which consists of one layer of gold nanoantennas on the top and its Babinet-inverted pattern at the bottom, separated by conformal HSQ pillars. L and W are the length and width of the nanoantenna arms, respectively; θ is the angle between two arms; T is the thickness of the gold film; H is the height of the HSQ pillar; and D is the nominal space between the top and bottom layers. (B) Schematic representation of the fabrication procedure. (i) A 100-nm-thick layer of HSQ is spin-coated onto a SiO₂ substrate. (ii) Patterning using EBL. (iii) A 30-nm-gold film is deposited on the sample by electron beam evaporator. (iv) Top view of SEM image of the bilayer metasurface. The supercell (yellow) comprises six V-shaped nanoantennas. The supercell repeats with a periodicity of 900 nm along x axis and 150 nm along y axis. SU, subunit.

A key feature of our bilayer metasurface is its ease of fabrication, as shown in Fig. 1B (i to iii). By using electron beam lithography (EBL), we patterned the structure on a SiO₂ substrate with a layer of HSQ 100 nm thick, followed by a gold deposition with an E-beam evaporator. Lift-off process is avoided (further details are discussed in Materials and Methods). The fabrication process of our bilayer metasurface is arguably easier than the fabrication of single-layer metasurfaces composed of nanoantenna arrays, which requires to carefully lift off the metal on the unexposed photoresist. The fabrication of the bilayer metasurface with such one-step process is therefore more viable and cost-effective, largely beneficial for practical applications. A top-view scanning electron microscopy (SEM) image of our bilayer metasurface sample with Γ_x = 900 nm and Γ_y = 150 nm is shown in Fig. 1B (iv), where Γ_x and Γ_y are the periodicities of the supercell along the x and y axes, respectively. A 3D surface profile measured by an atomic force microscope (AFM) showed that the thickness of the fabricated structure is around 100 nm, as shown in fig. S1.

Two important figures of merit for any spatial modulators are the peak conversion efficiency and the extinction ratio. Here, the conversion efficiency is defined by normalizing the transmitted power of the anomalous refracted beam to the power transmitted through a bare SiO₂ substrate. The extinction ratio, in turn, is expressed as ER = 10 log(P_Ex/P_Ey)dB, where P_Ex and P_Ey indicate the transmitted power that undergoes anomalous refraction with cross-polarization and normal refraction with copolarization, respectively. Therefore, extinction ratio larger than 0 dB means that the anomalous transmission dominates. Figure 2A shows the measured figures of merit of the fabricated bilayer metasurface. Despite the discretization and other imperfections, experimental data show that the conversion efficiency from E_y to E_x components reach a peak value of 17%, which is significantly larger than that of previous experiments based on single-layer metasurfaces (4, 11). It inevitably has some deviation between experiments and simulations because of the fabrication and characterization challenges (for further details, see figs. S2 and S3). Despite that, the experimental extinction ratio still exceeds 0 dB in the wavelength range from 680 to 720 nm, with a peak value of 0.73 dB at 700 nm, which is much larger than any previous transmitting metasurface design to the best of our knowledge, demonstrating the potential of the proposed bilayer metasurface.

Fig. 2. Performance of the bilayer plasmonic metasurface.

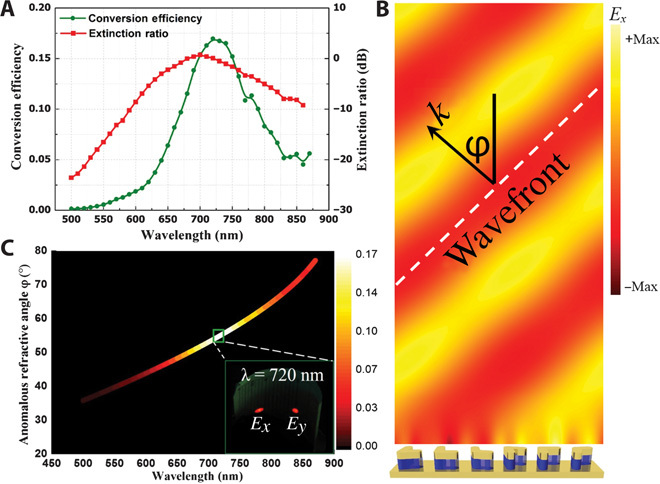
(A) Experimental results of the conversion efficiency and extinction ratio. (B) Simulated cross-polarized E_x component of the transmitted field of a bilayer metasurface at 770 nm, which is the peak value position of the conversion efficiency in simulation. The geometrical parameters used in the simulations are obtained by measuring the fabricated sample with SEM and AFM techniques. The lengths of each antenna and the angles between the two arms for unit cells 1 to 3 are as follows: L_i = 130, 125, and 120 nm, and θ_i = 70°, 90°, and 110°, respectively; width of the nanoantennas W = 55 nm, thickness of the gold film T = 30 nm, and height of the HSQ pillar H = 100 nm. Unit cells 4 to 6 are constructed by rotating the symmetry axis of unit cells 1 to 3 90° clockwise. A sketch of the supercell consisting of six subunits is shown at the bottom of the field pattern, where the actual sample would be placed. (C) Relationship of transmittance of anomalous light on the wavelength and the anomalous refraction angle. False-color map indicates the experimentally measured intensity of the anomalous refracted beam. Inset: Optical image of the transmission spots at a wavelength of 720 nm.

With the geometrical parameters directly measured from the fabricated samples, as shown in Fig. 2B, the transmitted electric field distribution for the cross-polarized component E_x was calculated at 770 nm, corresponding to the peak value position of the conversion efficiency in simulation, which clearly demonstrates an anomalously deflected planar wavefront. Because the period of the supercell in the x direction is larger than the working wavelength, multiple diffraction orders may be allowed to propagate. However, if the metasurface is properly designed, only the diffraction order responsible for the anomalous refraction will be efficiently excited, and other residual diffraction orders will not seriously affect the conversion efficiency or the planarity of the wavefront (see fig. S4).

Recently, dielectric metasurfaces with high efficiency have been demonstrated (23, 37, 38). Notice that the diffraction efficiency for circularly polarized light at 75% in a visible region, reported by Lin et al. (23), is defined as the ratio of the power converted into anomalous component over the power of the overall transmittance, similar to the extinction ratio used in our work. Apart from the extinction ratio, the conversion efficiency would be another important consideration, which marks the capability of converting total incident power into the transmitted anomalous component. Plasmonic metasurfaces with high conversion efficiency and positive extinction ratio have not been reported for visible light. However, the poly-Si metasurface, when thin enough as used in the study of Lin et al. (23), can be decently transparent and achieve quite high conversion efficiency in visible light. This may further consolidate the widely accepted perception that dielectric metasurfaces outperform the plasmonic ones thanks to the lower ohmic loss. Counterintuitively, our work demonstrated that our coupled bilayer plasmonic metasurface, still being ultrathin, could behave almost equivalently to (in experiment) or even slightly better than (in simulation) the dielectric counterpart, which will be elaborated with details in Conclusions.

The measured cross-polarization conversion efficiency against wavelength and angle is plotted in Fig. 2C. The relationship between wavelength and refraction angle is in good agreement with the theoretical predictions calculated by the generalized Snell’s law ${\mathit{n}}_{\mathit{t}} \text{sin} {\mathrm{\theta }}_{\mathit{t}}-{\mathit{n}}_{\mathit{i}} \text{sin} {\mathrm{\theta }}_{\mathit{i}}=\frac{\mathrm{\lambda }}{2\mathrm{\pi }}\frac{\mathit{d}\mathrm{\phi }}{\mathit{d}\mathit{x}}$ (4), as the dash-dotted line shown in Fig. 1A. To better visualize the deflection effect, we also projected the transmitted light onto a sheet of white paper behind the sample in our experiments. As seen in Figs. 1A and 2C, there are two light spots on the screen at each wavelength, corresponding to the normal and anomalous refracted beams. From these optical images, we can clearly see that the relative intensity of the anomalous spots grows with increasing wavelength. When the wavelength of the linearly polarized light reaches 700 nm, the anomalous refracted spot is even brighter than the normal one, which can be appreciated by the naked eye as shown in Fig. 1A.

In all previous realizations of single-layer metasurfaces based on nanoantenna arrays, it was generally assumed that the coupling between adjacent unit cells was negligible at the design stage (4, 8, 11). Instead, for our bilayer metasurface, the intralayer coupling effect not only cannot be overlooked but also plays an important role in the spatial modulation process. In our structure, the subunits are arranged close to each other, leading to a well-confined electric field at the gap between adjacent nanoantennas (see fig. S5). As the subperiodicity Λ decreases from 180 to 150 nm, the conversion efficiency markedly increases from 9 to 29% (Fig. 3A), although the filling fraction (structural area versus the total surface area) only increases from 21 to 30.3%. It indicates that the intralayer coupling plays an important role in enhancing the manipulation performance of the proposed metasurface, a significant difference with respect to earlier metasurface designs, which did not exhibit such sensitivity to the distance between neighboring elements. This feature is evident in Fig. 3 (B and C), which considers only one of the two layers at a time. Further decreasing the subperiodicity will indeed support even higher conversion efficiency. However, it would also make the fabrication process very difficult; therefore, subperiodicity is chosen to be 150 nm in the experiment. Conversely, the extinction ratio of all three types of metasurfaces is almost insensitive to the variation in subperiodicities, as seen in Fig. 3 (D to F). However, the extinction ratio of the bilayer metasurface can reach a peak value of 12 dB and is larger than 0 dB over a broad wavelength range (see Fig. 3D), which is favorable for practical applications. In contrast, either single-layer nanoantenna metasurface or the Babinet-inverted type metasurface only exhibits peak value around 0 dB.

Fig. 3. Comparison of three different types of metasurfaces, showing different sensitivities to the subperiodicity (that is, the distance between neighboring cells).

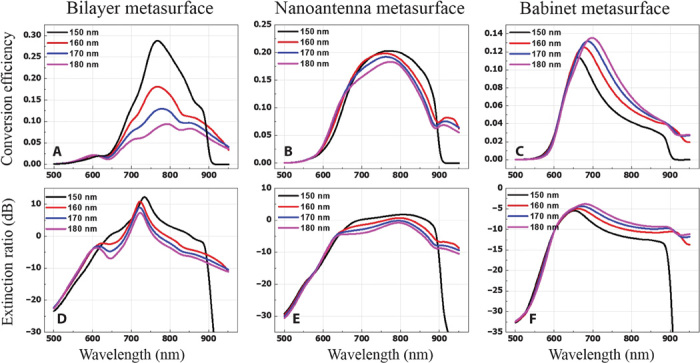
For ease of comparison, in these simulations, the same parameters were used for all the three types of metasurfaces. (A to C) Dependence of the conversion efficiency on the subperiodicities for three types of metasurfaces as the subperiodicities increase from 150 to 180 nm. (D to F) Dependence of the extinction ratio on the subperiodicities for three types of metasurfaces as the subperiodicities increase from 150 to 180 nm.

As discussed above, the conversion efficiency of the proposed bilayer metasurface can reach a value of 29%, which even exceeds the theoretical limit for single-layer metasurfaces (13). This is possible because the designed metasurface interacts with the impinging light over a finite thickness, breaking the radiation symmetries that fundamentally limit the performance of infinitesimally thin structures (13). In particular, for the structure considered here, the radiation symmetry is broken because of the structural asymmetry of the two metasurface layers. For a single-layer ultrathin nanoantenna metasurface, only transverse electrical currents ${\mathit{J}}_{\mathit{s}}=\widehat{\mathit{n}}\times {\mathit{H}}_{\mathit{a}}$ are induced (H_a is the magnetic field on the surface, and $\widehat{\mathit{n}}$ indicates the unit vector normal to the metallic screen, pointing toward the half-space of interest) and are bound to symmetrically radiate on both sides of the metasurface, fundamentally limiting the ratio of transmitted energy. In this sense, a single ultrathin metasurface is equivalent to a shunt (parallel) reactance, which can only introduce a discontinuity on the transverse magnetic field, whereas the transverse electric field remains continuous.

As a result, a single ultrathin metasurface supporting purely electric currents cannot fully manipulate the transmitted waves. To determine a discontinuity of the transverse electric field, it is necessary to introduce an impedance element in series, which necessarily implies a structure with finite thickness. A metasurface structure that includes both parallel and series impedance elements (for example, in the form of a Π network, or T network) can therefore determine an arbitrary discontinuity in the propagating electromagnetic field, hence allowing full control of the transmission coefficient. In the bilayer structure proposed in this paper, the nanoantenna metasurface and the nanoaperture metasurface represent shunt impedances of capacitive and inductive type, respectively (if the nanoantennas and nanoapertures are smaller than their resonance length). In addition, the metasurfaces are separated by a small gap that introduces an equivalent series capacitance. Thanks to this combination of parallel and series elements, the proposed metasurface structure is therefore able to manipulate the transmitted beam to a large extent, breaking the 25% efficiency barrier of single ultrathin metasurfaces. It should also be stressed that, although dual-layer metasurfaces exhibiting strong chiral effects and efficient polarization conversion have been reported before (39–42), our goal is not only to achieve high conversion efficiency but also to locally control the phase of the cross-polarized transmission over the entire 2π phase range, which is challenging with conventional design principles. In particular, the complementary nature of the two metasurfaces, one capacitive and the other inductive, is beneficial to achieve large coverage of the transmission phase, consistent with the results of Monticone et al. (13). In this context, our results clearly demonstrate that “two highly coupled plasmonic metasurfaces can do much better than one,” in analogy with the recent investigation of bilayer 2D materials (43).

The geometrical parameters used in the simulations of Fig. 3 are extracted from the fabricated sample by using AFM and SEM techniques. The conversion efficiency may be further increased to 36.5% with a proper optimization of the structure, as shown in Fig. 4. We also performed numerical simulations to investigate the near-field distributions of our metasurface structure and its resonance properties. In Fig. 5A, the z components of electric and magnetic fields and the displacement current density are plotted for the second subunit of the designed supercell at wavelength 815 nm under antisymmetric excitation (the polarization of incident light is perpendicular to the symmetry axis of the V-shaped antenna). A unit cell in a uniform periodic structure has been considered here (simulated by imposing periodical boundary conditions on the sides of the cell). According to the Babinet principle, if the direct structure has an E-field resonance mode, the complementary structure will exhibit a corresponding H-field resonance mode at the same frequency (44–46), assuming that the structures are made of infinitely thin perfectly conducting sheets, and the wave propagates perpendicularly toward the sheets. Although real metals can no longer be considered perfectly conducting at optical frequencies, the field distributions of the V-shaped nanoantennas on the top and their complementary on the bottom are indeed in agreement with the Babinet principle, as seen in Fig. 5A. The E-field distribution on the top layer shows an antisymmetric resonance, whereas the H-field shows a symmetric resonance at the bottom Babinet structure. We also show the displacement current density at the resonant frequency on both arms of the HSQ pillar, where the green (orange) arrows indicate that J_z is toward the −z (+z) direction. The resonant displacement current determines strong interlayer coupling, which contributes to the high efficiency exhibited by the proposed metasurface design.

Fig. 4. Simulated transmittance with the optimized structure.

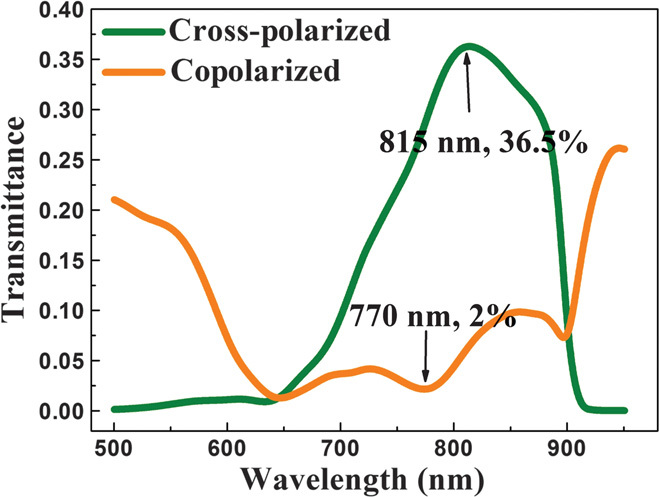
The parameters were defined as follows: For the length of each antenna and the angle between the two arms for units 1 to 3, L_i = 140, 130, and 125 nm, and θ_i = 70°, 90°, and 110°, respectively; W = 50 nm, T = 30 nm, and H = 100 nm. Unit cells 4 to 6 are constructed by rotating the symmetry axis of unit cells 1 to 3 90° clockwise.

Fig. 5. Field and current distributions for one selected subunit (that is, SU2 in Fig. 1B, iv) under antisymmetric excitation.

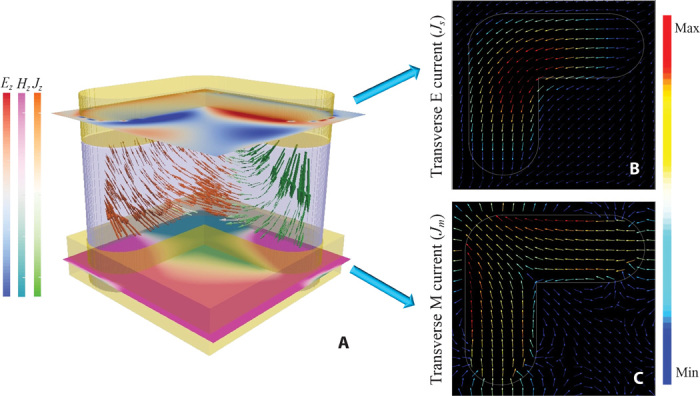
(A) z components of electric and magnetic field distributions on the top and bottom layers of the bilayer metasurface, respectively. The displacement current density J at resonance on both arms of the HSQ pillar is represented by vector arrows, where green and orange indicate whether the z component of the displacement current (J_Z) is toward −z and +z directions, respectively. (B and C) Transverse electrical current (J_s) and equivalent transverse magnetic current (J_m) of the bilayer metasurface. The position of the V-shaped nanoantenna on the top and the Babinet-inverted aperture on the bottom are indicated by the white outlines. The amplitudes are represented by the color of the arrows with the same relative scale for J_s and J_m, respectively.

According to the surface equivalence theorem (47), small apertures in a metallic screen, as in the case of Babinet-inverted metasurfaces, can be treated as arrays of magnetic current elements. In particular, if E_a is the electric field on an aperture in a perfectly conducting screen, the aperture is equivalent to a transverse magnetic current ${\mathit{J}}_{\mathit{m}}=-\widehat{\mathit{n}}\times {\mathit{E}}_{\mathit{a}}$ on the aperture plane (47). Although this equivalence is exactly valid only for perfectly conducting screens, it also approximately holds for metallic sheets at optical frequencies, provided that the screen is sufficiently opaque, for example, the thickness of the metallic screen is larger than the skin depth in the wavelength range of interest (48). To show the complementary response of the two metasurfaces, we numerically investigated the transverse electric current J_s and the effective transverse magnetic current J_m induced on the subunit cell under antisymmetric excitation. In particular, Fig. 5 (B and C) shows the J_s distribution on the nanoantenna at the top layer and the J_m distribution on its complementary Babinet-inverted structure at the bottom. The transverse electric current J_s flows, with high intensity along the V-shaped nanoantenna (Fig. 5B), whereas the transverse magnetic current J_m is very weak in the same region (not plotted), as expected. Meanwhile, at the bottom complementary structure, the effective transverse magnetic current J_m is concentrated in the aperture region and flows from the two tips toward the apex of the V shape, as shown in Fig. 5C. The induced currents for symmetric excitation also exhibit similar behavior (see fig. S6). Because the incident plane wave impinges from the side of the nanoapertures, the problem of electromagnetic transmission through the bilayer metasurface can be equivalently studied as a radiation problem from the magnetic currents induced on the apertures. The radiation from these current elements is affected by the presence of the nanoantennas. If their distance is properly tailored, a high radiation efficiency can be realized, which in turn corresponds to a high transmission efficiency. These considerations provide a different perspective on how the radiation symmetries are broken by the presence of the two metasurfaces.

From a ray optics perspective, there is no direct light path from the input surface to the output surface because of the complement of two layers. Moreover, according to Bethe’s predictions (49), for a subwavelength aperture in an ultrathin metallic sheet, transmission is inversely proportional to the wavelength’s fourth power, which would imply a very small transmission. However, simulation results showed that the total transmission of our bilayer metasurface (copolarized and cross-polarized) has a peak of 38%, around 780 nm. This value is even larger than the ratio of the slot area to the total area of the gold film, which is about 30.3%. This large transmittance may result from the phenomenon of extraordinary transmission of light through small apertures, which involves the excitation of leaky plasmon modes on periodic metallic screens, and has been extensively studied in recent years (50–53).

It should be noted that our design mechanism is different from previous metasurfaces, which relies on the creation of a library correlating phase and amplitude information of the scattered light with the corresponding geometrical parameters of one subunit cell. Then, a supercell could be formed to cover the required phase range in a discretized fashion. The prerequisite of such a procedure is based on the assumption that the mutual coupling among adjacent subunits is negligible. On the contrary, our design principle exploits not only the intralayer coupling but also the interlayer coupling to enhance the overall transmission and the conversion efficiency. Therefore, to design the geometry at a given wavelength, we need to tailor the parameters of all subunit cells as a whole by considering the coupling of all neighboring elements. Our findings show that the generalized Snell’s law is still operational in the presence of strong mutual coupling. The working wavelength can be adjusted by changing the width and length of the antennas (see figs. S7 and S8). This mechanism may be extended to even higher frequencies by using silver or aluminum bilayer metasurfaces.

CONCLUSIONS

In summary, we numerically and experimentally demonstrated a bilayer metasurface design composed of a nanoantenna-based metasurface paired with its Babinet-inverted counterpart, connected via conformal HSQ pillars. Thanks to the combination of parallel and series impedance elements (namely, the two metasurfaces, one capacitive, the other inductive, and the gap between them), which allows for suitable breaking of the radiation symmetries of the structure, our hybrid design can achieve high conversion efficiency and high extinction ratio simultaneously, with a 36.5% conversion efficiency achieved in simulation and 17% in experiment. It is noted that the dielectric metasurface (23) operating in visible light provides about 20% conversion efficiency (transmission multiplied by diffraction efficiency) in both simulation and experiment, on the basis of the best two cases captured at 550- and 650-nm wavelengths in Fig. 3D and fig. S5C of the study by Lin et al. (23). At the same time, our extinction ratio can be as high as 0.73 dB experimentally, also significantly larger than that of previous works. Although there are strong mutual couplings (in contrast to those previously reported metasurface without mutual coupling) between neighboring elements, the generalized Snell’s law is still applicable. Our metasurface design can work over a broadband range through visible and near-infrared frequencies. The overall thickness of the bilayer structure is only 130 nm (λ/6), and its fabrication process is significantly more viable. It is expected that the overall efficiency of our hybrid plasmonic metasurface can be markedly improved further with better optimization and more precise nanofabrication, which potentially exceed the performance of all previously demonstrated metasurfaces in the transmission at visible range.

MATERIALS AND METHODS

Sample preparation

The bilayer metasurface was fabricated using EBL, followed by the deposition of one layer of gold by E-beam evaporator, as shown in Fig. 1B. The structure was fabricated on a 1-mm-thick quartz substrate. After thoroughly cleaning the substrate by acetone, isopropyl alcohol, and deionized (DI) water, the negative-tone electron beam resist HSQ (formulated as product no. XR-1541-006, Dow Corning) was spin-coated onto quartz substrates with a thickness of 100 nm, followed by spin-coating 10 to 20 nm of water-soluble conducting polymer (Espacer) as the charge-dissipating agent during EBL process. To avoid thermally induced cross-linking of the resist, which would weaken the developing contrast and lead to the worse resolution, no prebaking process was used. The designed structure was created by AutoCAD in dxf format. Then, the HSQ patterns were lithographically defined by EBL using an Elionix ELS-7000 system with an accelerating voltage of 100 kV and dose of 5200 μC/cm². The pattern was arranged in 100 × 100 μm, and no proximity effect correction was performed for the exposure. After patterning, we washed out the Espacer by DI water first, and then a high-contrast develop process was used by developing samples in a formulation of aqueous 1% NaOH and 4% NaCl in DI water at room temperature for 1 min, followed by rinsing with DI water for 2 min, and drying the sample by N₂ blowing. After EBL patterning, a layer of 30-nm gold was deposited on the sample by electron beam evaporator (Explorer Coating System, Denton Vacuum). Lift-off process is not needed. The fabricated structures were imaged using Elionus ESM-900 scanning electron microscope with an accelerating voltage of 10 kV. The surface profile of the sample was measured by an AFM (ICON-PKG, Bruker), as shown in fig. S1.

The bilayer metasurface is constructed by lifting the V-shaped gold nanoantennas above their Babinet-complementary structures with conformal HSQ pillars. The shape and size of the nanoantennas on the top layer are the same as the Babinet-inverted apertures on the bottom gold film. The distance between the two layers is only 70 nm, implying that, from a ray-optic perspective, there is no direct light path from the input to the output windows. Additionally, the width of the slots is 55 nm, and their length is around 130 nm, which are much smaller than the working wavelength in the visible range.

Numerical simulation

All simulation results were performed using the commercially available finite-difference time-domain software Lumerical. In simulations, a single supercell with six subunits on a quartz substrate was modeled, and we applied periodic boundary conditions along x and y axes and perfectly matched layer along z axis. The incidence wave in all cases was assumed to be an E_y–linearly polarized plane wave normally illuminating the surface from the SiO₂ substrate. The dielectric function of the gold film was described by fitting the gold-Palik database in Lumerical’s material library. We also measured the real and imaginary parts of the refractive index (n, k) of the actual gold film used in our experiment, and the measured values were found to fit well with the gold-Palik database. The refractive index of the quartz substrate was taken as n_SiO2 = 1.46, and for HSQ pillar, we assumed n_HSQ = 1.41 according to the product description from the factory. The medium above the metasurface was chosen to be air. To avoid sharp edges that could give rise to numerical artifacts, we introduced round ends for each antenna arm, with the curved radius being half of the nanoantenna width in all simulations. The polarized transmittance was calculated by integrating the Poynting vector with different polarized components on the monitor plane, normalizing them by the source power

$${\mathit{T}}_{{\mathit{E}}_{\mathit{x}}}=\frac{\frac{1}{2}{\displaystyle \int }\text{real}({\mathit{E}}_{\mathit{x}}\times \text{conj}({\mathit{H}}_{\mathit{y}}))\mathit{d}\mathit{S}}{\text{Source power}}$$ (1)

$${\mathit{T}}_{{\mathit{E}}_{\mathit{y}}}=\frac{\frac{1}{2}{\displaystyle \int }\text{real} (-{\mathit{E}}_{\mathit{y}}\times \text{conj}({\mathit{H}}_{\mathit{x}}))\mathit{d}\mathit{S}}{\text{Source power}}$$ (2)

Optical characterization

Experimental characterization of the fabricated structures was performed by a home-built microregion spectrum testing system. A schematic of the setup is shown in fig. S9. A low-power supercontinuum laser (SC450-6, Fianium), tunable from 300 to 2000 nm, was weakly focused on the sample using a plano-convex lens with focal length F = 60 mm. A polarized beam splitter prism was used before the focusing lens to obtain E_y–linearly polarized incidence light, and a polarizer was used after the sample to detect the polarization property of the anomalous and normal transmission beams. Scanning the wavelength of a supercontinuum laser, the transmitted power at each refracted angle for each wavelength was measured by optical power meter (model 1830-c, Newport) with low-power calibrated photodiode sensors (model 818-UV, Newport) within the wavelength range from 500 to 880 nm. To visualize the relationship between wavelength and deflection angle, we also projected the transmitted light onto a white paper and recorded it using a commercial digital camera, as shown in Fig. 1A.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/1/e1501168/DC1

Deviation between experiment and simulation

Effect of higher-order diffraction mode

Dependence of resonant wavelength on geometric parameters

Fig. S1. Surface profile measured by AFM.

Fig. S2. Tilted SEM image of the fabricated bilayer metasurface, showing nonuniform grains of gold at the sidewall of HSQ pillars.

Fig. S3. Dependence of the extinction ratio on the thickness of cladding layer and the thickness of deposited gold film.

Fig. S4. Refraction efficiency of the cross-polarized component in each diffraction orders.

Fig. S5. Electric field distribution on the top layer of the bilayer metasurface at 770 nm.

Fig. S6. Transverse currents distribution under symmetric excitation.

Fig. S7. Dependence of the conversion efficiency on the width of nanoantennas.

Fig. S8. Dependence of the conversion efficiency on the length of nanoantennas.

Fig. S9. Schematic representation of the optical measurement setup.

Fig. S10. Dependence of the conversion efficiency on the height of the HSQ pillars.