Measuring Ability, Speed, or Both? Challenges, Psychometric Solutions, and What Can Be Gained From Experimental Control

Abstract

The main challenge of ability tests relates to the difficulty of items, whereas speed tests demand that test takers complete very easy items quickly. This article proposes a conceptual framework to represent how performance depends on both between-person differences in speed and ability and the speed-ability compromise within persons. Related measurement challenges and psychometric models that have been proposed to deal with the challenges are discussed. It is argued that addressing individual differences in the speed-ability trade-off requires the control of item response times. In this way, response behavior can be captured exclusively with the response variable remedying problems in traditional measurement approaches.

In their book on the measurement of intelligence, Thorndike, Bregman, Cobb, and Woodyard (1926) present a theorem, which says that “other things being equal, if intellect A can do at each level the same number of tasks as intellect B, but in a less time, intellect A is better.” (p. 33). This statement illustrates that in any performance measure, both the result of interacting with an item and how long it took to reach the result need to be considered and that comparing individuals in one respect requires keeping the other aspect constant. Along these lines, Thorndike et al. (1926) proposed the concepts of level (i.e., ability) and speed, which are empirically defined by the produced products (item responses) and the time required to produce them (response times). In measurement literature, various concepts such as ability, level, and power have been used to refer to a disposition explaining individual differences in response accuracy (Gulliksen, 1950; Thorndike et al., 1926; Thurstone, 1937); for consistency reasons, only the term ability will be used in this paper. A wide range of approaches have been suggested to conceptualize and model the latent structure underlying observed responses and response times, not only in the field of psychometrics (e.g., van der Linden, 2009a), but also in mathematical psychology and cognitive process modeling (e.g., Ratcliff & Smith, 2004). From a measurement perspective, however, it seems to be a reasonable starting point to assume that the latent variables ability and speed exist and that they account for item response and response-time variations between persons.

The following questions arise from the fact that ability and speed jointly affect response behavior in assessment instruments (e.g., Lohman, 1989; Partchev, De Boeck, & Steyer, 2013; van der Linden, 2009a): How can the difference between a test taker giving slow correct responses and one giving faster but more incorrect responses be measured? How should incorrect responses be treated in tests in which speed is supposed to be the primary source of individual differences (“speed test”)? In the same vein, how should response-time differences be dealt with in tests in which ability is expected to determine performance differences (“power test”)? How does the joint influence of ability and speed affect the validity of test-score interpretation? How can speed be controlled for if ability is measured, and how can ability be controlled for if speed is measured?

The general goal of this article is to address the traditional and common distinction between ability and speed measures and to provide a joint perspective on how to conceptualize and assess individual differences in ability and speed. The first section discusses ability and speed as sources of difference in responses and response times and the implications of the speed-ability trade-off for measurement. On the basis of this, the second section derives a conceptual measurement framework for ability and speed, distinguishing between a between-person level and a nested within-person level. This provides the conceptual background for the third section, which describes and discusses practical issues and challenges in measuring ability and speed. The fourth section revisits important measurement models and other models taking both responses and response times into account to address some of the measurement problems discussed before and to address substantive research questions (e.g., on the response process). In the final section, I argue that experimental control of item response times is required to resolve the problem of individual differences in the speed-ability compromise. Using item-level time limits allows researchers to capture response behavior solely by means of the response variable, even for speed tests, and thereby remedies problems of measurement approaches that accept differences in the speed-ability compromise. Hence, in this article the intricate and at the same time intriguing relation between responses and response time as indicators of ability and speed are discussed and consequences and new perspectives for the measurement of ability and speed are delineated.

ABILITY AND SPEED AS SOURCES OF INDIVIDUAL DIFFERENCES IN ITEM RESPONSES AND RESPONSE TIMES

The constructs of ability and speed have a long tradition in the psychology of individual differences as well as in educational and psychological testing (e.g., Carroll, 1993; Gulliksen, 1950; Kelley, 1927; Thorndike et al., 1926). In general, speed can be conceived as the rate at which something happens or changes across a unit of time. In testing, “something” refers to the amount of labor to be done to complete an item (Partchev et al., 2013; van der Linden, 2009a). Thus, speed represents the rate of getting the labor done, whereas ability reflects the capacity to get the labor done successfully. Constructs of ability and speed can be found primarily in cognitive domains. However, response times are also considered in the field of noncognitive domains—for instance, with regard to attitudes or personality variables (Bassili, 1995, 1996; Bassili & Fletcher, 1991; Eisenberg & Wesman, 1941; Ferrando & Lorenzo-Seva, 2007; Ranger & Kuhn, 2012).

Differences in responses and response times to an item are the result of not only between-person differences in ability and speed but also within-person differences that need to be taken into account. From the perspective of ability measurement, Thurstone (1937) described for a fixed person how the probability of obtaining a correct response to an item depends on the time taken to respond and the difficulty of the item. The probability of a correct response decreases with difficulty and increases with response time and vice versa. Hence, his conception suggests the existence of a within-person trade-off between speed and accuracy.

Speed-accuracy and speed-ability trade-off

The speed-accuracy trade-off has traditionally been investigated in experimental reaction-time research to get insights into information processing dynamics (Luce, 1986; Schouten & Bekker, 1967; Wickelgren, 1977). It is conceptualized as a within-person phenomenon and suggests that the more time a person takes, the more and better information is available for making a decision—that is, the greater the person’s response accuracy (Luce, 1986; Roskam, 1997). Speed-accuracy trade-off functions (SATF) are investigated experimentally across time-limit conditions and relate the mean response time under a condition to the proportion of correct responses. The SAFT is also called the macro trade-off. The conditional accuracy function (CAF) represents the probability of a correct response as a function of time within a time-limit condition and is called the micro trade-off. In experimental research, this is obtained as a proportion-correct conditioning on observed response time for each time-limit condition. For both SATF and CAF, a certain person ability and item difficulty are assumed to be given (i.e., these parameters are kept constant; Roskam, 1997; van Breukelen, 2005). Experimental research typically computes group means to investigate SATF and CAF. From a measurement perspective, however, SATF and CAF need to be tapped as the within-person relation between (expected) response time and response accuracy, which may differ between individuals. The SATF is supposed to increase monotonically; whereas, for the CAF other forms may also be observed depending on the difference between mean correct response time and mean incorrect response time (Heitz, 2014; Luce, 1986). For instance, an erroneous process associated with both a long response time and an incorrect response would produce a decreasing CAF (van Breukelen, 2005).

The (experimental) speed-accuracy trade-off refers to observed performance. In the context of measurement, it becomes a speed-ability trade-off referring to latent person parameters (van der Linden, 2009a). The trade-off suggests that in any measure, the test taker operates at a certain (effective or exhibited) level of speed and ability. Hence, in one situation, or condition, the test taker may work accurately and slowly, whereas in another, he or she works quickly but with many errors, with both conditions resulting in the same individual efficiency in information processing.

Implications for measurement

From a measurement perspective, the speed-ability trade-off represents a problem, as it may jeopardize the comparability of performance measures if there is between-person variation in adopted speed-ability compromise (e.g., Dennis & Evans, 1996; Lohman, 1989; Sorensen & Woltz, 2015). As pointed out by Lohman (1989), there are two reasons why individuals differ in response accuracy. They might differ in ability and/or they might differ in the speed-ability compromise. Thus, the ability 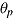of test taker 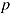cannot be conceived as a single measurement but has to be viewed as a monotonic decreasing function that defines the within-person relation between ability 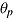and speed 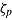; that is, 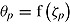(cf. van der Linden, 2009a). From this, it can be assumed that when test takers operate at different speeds, ability estimates 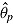indicate individual ability differences that are confounded with the test takers’ decisions on speed. Figure 1 (upper part) illustrates how this confounding could even reverse the expected rank order of two persons (Person 1 vs. Person 2). If test takers keep their speed constant when proceeding through a test (“stationarity assumption” (van der Linden, 2007), the problem of comparing ability estimates still exists as long as test takers select different levels of speed as indicated by the variance of speed, .

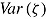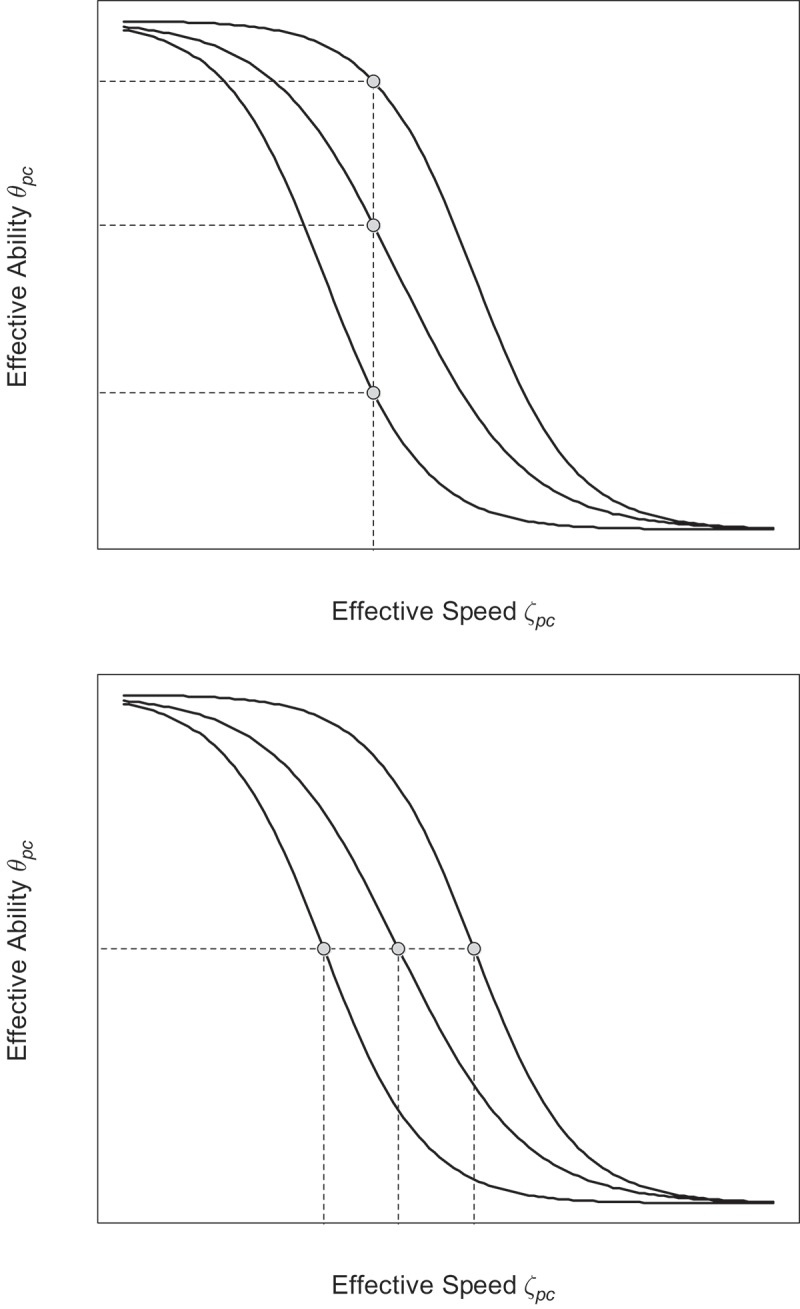
FIGURE 1 .

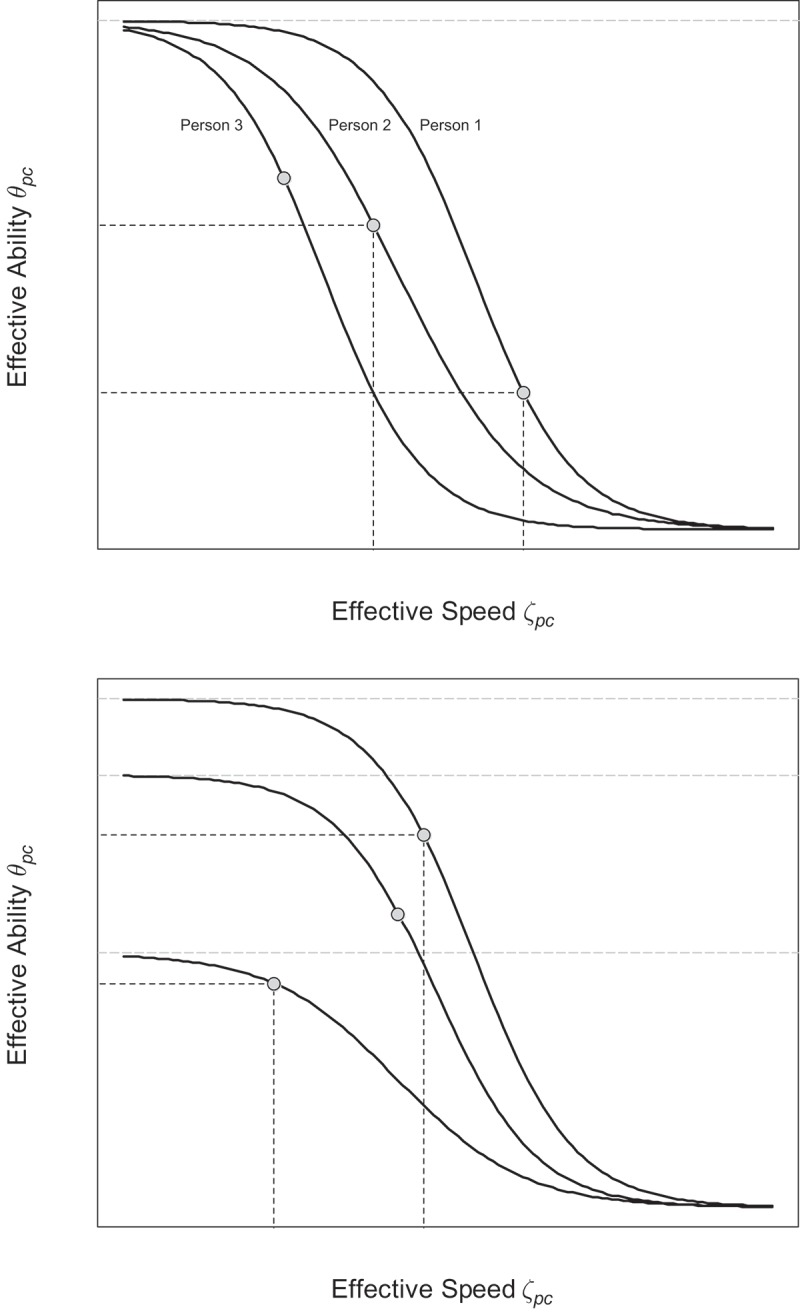
Speed-ability trade-off with effective ability 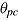as a monotonically decreasing function of effective speed 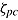. Upper part: speed-ability curves of three persons completing a speed test (indicated by the same ability asymptote). Lower part: speed-ability curves of three persons completing an ability test (indicated by vertically displaced ability asymptotes).

Figure 1 also illustrates that when switching from the within-person level to a population (between-person level), the relation between speed and ability may show very different patterns, for instance, a positive relation (Figure 1, lower part) or a negative relation (Figure 1, upper part), although within each person the speed-ability trade-off remains a negative relation between speed and ability. Consequently, at the population-level findings on the relation between speed and ability may be very heterogeneous (cf. Goldhammer et al., 2014). Finally, Figure 1 depicts the difference between speed tests and ability tests. In the condition of very low speed, almost all test takers can solve the easy items from a speed test successfully, resulting in high-ability estimates for all test takers (Figure 1, upper part). In an ability test, however, lower speed does not pay off for all as the level of ability that can be exhibited by a test taker is constrained by his or her maximum ability level (Figure 1, lower part).

Speed-ability functions

The shape of the individual speed-ability function chosen in Figure 1 is hypothetical. Following Wickelgren (1977) on how to parameterize the (experimental) SATF, persons can be assumed to differ in a speed intercept, 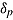; rate parameter, 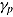; and ability asymptote, 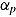. The speed intercept determines when ability elevates from the minimum to a higher ability level indicated by nonrandom responses (i.e., it defines the location of the curve on the speed axis). The rate parameter represents the slope of the function indicating how strong ability changes per unit of speed. The ability asymptote reflects the maximum ability level that can be achieved. For speed tests, only two parameters—intercept and rate—may be sufficient as all test takers are expected to reach the same maximum ability 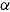. For ability tests in which the asymptotic ability level is supposed to differ substantially between test takers, all parameters are needed. To assess ability, the differences in the vertical displacement of ability asymptotes are of interest; whereas for speed it is the horizontal displacement reflected by the speed intercept (cf. Lohman, 1989). The degree to which a particular (hybrid) test is more of an ability test or more of a speed test can be determined by the variance in asymptotic ability. Little variance indicates a speed test whereas large variance points to an ability test.

Following Wickelgren (1977), an exponential function can be used to represent the speed-ability trade-off. To incorporate an asymptote for the minimal ability level when responding at chance as well (cf. the sigmoid function found empirically, for instance, by Schouten & Bekker, 1967), the function proposed by Wickelgren (1977) can be modified slightly and turned into a logistic function,

(1)

This function was used to create the curves in Figure 1. The relations among the three parameters governing the speed-ability trade-off need to be discovered empirically. Depending on the correlation structure, the individual SATFs could be well ordered or disordered with crossing curves. However, it seems reasonable to assume that a more able test taker shows higher ability levels at any speed level—that is, the curves do not intersect, suggesting a positive correlation between maximum ability and speed intercept and/or rate.

For instance, in a study by Lohman (1986), mental rotation tasks were presented under various exposure-time conditions. Individual-differences analysis revealed a strong positive correlation between rate and asymptotic ability. Furthermore, group differences in the speed-accuracy trade-off by item type demonstrated that the SATFs for high- and low-performing groups do not intersect. The main distinguishing factor was asymptotic ability, while differences in rate were only small (the intercept was assumed to be the same for all persons).

A CONCEPTUAL MEASUREMENT FRAMEWORK FOR ABILITY AND SPEED

Individual differences in test performance depend on both between-person differences in speed and ability (i.e., the location of individual speed-ability curves) and the adopted speed-ability compromise within persons (i.e., the location within a speed-ability curve). The proposed conceptual measurement framework nests these two sources of (observed) individual differences in responses and response times (see Figure 2).

FIGURE 2 .

Conceptual framework on the measurement of ability and speed. Individual differences in item responses and response times depend on both between-person differences in speed-ability functions (represented by speed intercept 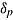, rate 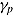, and maximum ability 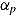) and the speed-ability trade-off within the person (represented by effective speed 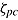and ability ).

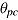The upper (between-person) level includes the population of individuals differing in their speed-ability functions. These functions can be described by the person parameters of speed intercept 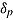, rate 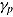, and maximum ability 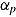. A joint distribution of these parameters is assumed in the population from which a person is sampled.

The medium (within-person) level of the framework includes a within-person distribution of speed 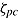and ability 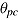, as suggested by the individual speed-ability function. The joint distribution of speed and ability for a particular person can be conceived as a population of conditions 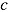under which the person may operate with regard to speed and ability. The trade-off suggests a negative correlation between the two person parameters for any person. From this population, the condition of test completion is assumed to be sampled. Condition 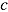determines the location of the person on the individual speed-ability function and, in turn, the effective level of speed 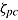and ability 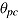. Conditions can be implemented externally by means of an experimental manipulation of the time available (e.g., Goldhammer & Kroehne, 2014; Semmes, Davison, & Close, 2011; Walczyk, Kelly, Meche, & Braud, 1999; Wright & Dennis, 1999) or by emphasizing either speed or accuracy in the test instructions (e.g., Jentzsch & Leuthold, 2006; Zhang & Rowe, 2014). However, the condition can also be set within each person due to differences in individual understandings of the instructions or response style that favor speed over accuracy or vice versa. Thus, the within-person level allows person parameters to change across conditions.

The lower level represents the empirical test-taking behavior—that is, item responses 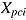and item response times 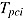. Subscript 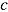was added to the observations and person parameters to indicate that the observed variables depend on the person’s speed-ability trade-off realized in condition 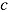. As discussed in the following section, various measurement models have been developed to link these observed variables to latent variables representing the constructs of ability and speed (e.g., Loeys, Rosseel, & Baten, 2011; van Breukelen, 2005; van der Linden, 2007). Figure 2 also allows for residual correlations between errors in the item response and the response-time model (e.g., Ranger & Ortner, 2012; van Breukelen, 2005), which means that the structure of (item-specific) correlations between response and response time may be more complex than is represented by measurement models assuming a simple structure and a latent correlation between speed and ability. This is also suggested by random response time effects on task success varying considerably across items (Goldhammer, Naumann, & Greiff, 2015; Goldhammer et al., 2014).

As for person parameters, properties of the multivariate distribution for item parameters can be estimated (Klein Entink, Fox, & van der Linden, 2009; Klein Entink, Kuhn, Hornke, & Fox, 2009; van der Linden, 2007). For instance, in many instances item difficulty 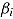and time intensity 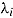may be correlated positively, since more difficult items presumably require a greater time investment.

Both observed variables, item response 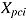and item response time 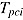, are considered to be random variables which vary randomly within a person even if they are observed under identical conditions. A third random variable 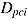, indicating whether an item has been reached or not, is required to fully represent response behavior (van der Linden, 2009a). This variable takes into account the fact that tests are usually administered with an overall time limit. Given a certain test-level time constraint, the cumulation of the test taker’s speed and the time intensities of a series of items determines whether an item is expected to be reached or missed.

The framework outlined here follows the hierarchical model presented by van der Linden (2007), but explicitly incorporates the speed-ability trade-off. In doing so, it provides a more comprehensive understanding of how latent speed and ability variables determine observed variables and, inversely, how responses and response times can serve as indicators when making inferences on differences in speed and ability.

MEASURING INDIVIDUAL DIFFERENCES IN SPEED AND ABILITY

Speed and ability tests

The question of whether a test is a speed test or an ability test depends on whether completing the test is challenging due to limited time or item difficulty. Following Gulliksen (1950), a pure speed test is “a test composed of items so easy that the subjects never give the wrong answer to any of them” (p. 230). Individual differences in speed are then reflected either by the number of items completed before a certain amount of time has passed or by the time that is needed to complete a fixed amount of items. Strictly speaking, the number of correct responses (given within a fixed time limit) and the total time (spent to complete a fixed number of items) can be used interchangeably as speed measure only if the probability of obtaining a correct response is one (van der Linden, 2009a). In a pure ability test, “all the items are attempted so that the score on the test depends entirely upon the number that are answered, and answered correctly” (Gulliksen, 1950, p. 231)—that is, individual differences in ability are represented by the number of items solved correctly without time limit.

The assumptions of infinite item easiness and infinite time can never be met in real-world testing. Rather, tests are always a mixture of speed and ability tests in that they typically include items of varying difficulty that are administrated with a time limit (Roskam, 1997). Thurstone (1937) suggested the hybrid nature of test items, that is, that any item has both an ability and a speed aspect. Even for a very easy item in a speed test, the probability of success is not one—that is, not all items will be completed correctly by all test takers. Also, even in an ability test there is usually some time limit, either defined by the test developer or due to practical constraints, which means that not all test takers will be able to attempt all items, or they will have to spend less time on each item in order to attempt them all (see also Rindler, 1979). As shown in Figure 2, the hybrid nature of test items is fully captured by the three random variables, response 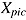, response time 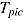, and item reached .

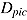Test designs inducing speededness

Speededness describes a central property of a test reflecting the degree to which performance is affected by a time limit. For a speed test, speededness is a necessary requirement that is fulfilled by presenting too many (easy) items relative to the given time limit. For an ability test, a time limit is often used for practical administration purposes. The resulting speededness could affect performance above and beyond individual knowledge and skill; for instance, it may prevent the completion of all items or require the completion of items with increased speed and the feeling of time pressure.

The degree to which ability and speed are required can be changed arbitrarily by changing the range of item difficulty and/or available time. Apart from the extremes representing (more or less) perfect speed and ability tests, test results are a composite measure of ability and speed (see e.g., Preckel, Wermer, & Spinath, 2011; Wilhelm & Schulze, 2002). This suggests that imposing time limits to an ability test introduces a confounding with speed that may threaten the unidimensionality of the test (see e.g., de Ayala, 2009) and its validity (e.g., Lu & Sireci, 2007). An instructive example is given by Chuderski (2013), who could show that when participants are given only half of the recommended time, a test of fluid intelligence functions as a test of working memory capacity. To avoid construct-irrelevant variance, test developers usually control the overall level of test speededness by defining an appropriate time limit. Trialing a new test version serves to determine speededness empirically by assessing the proportion of test takers that do not reach all items or guess randomly at the end to finish the test (cf. Rindler, 1979; Schnipke & Scrams, 1997). Several procedures have been proposed to determine the extent to which a measure assesses speed and ability (cf. Cronbach & Warrington, 1951; Lienert & Ebel, 1960; Lu & Sireci, 2007; Partchev et al., 2013; Rindler, 1979; Stafford, 1971; Wilhelm & Schulze, 2002). They provide measures of test speededness describing condition c under which test takers adopt a speed-ability compromise.

Test takers may experience differential speededness if they receive different item sets and the items vary in time intensity. This is an issue in test designs using different booklets (e.g., in large scale assessments) or adaptive item selection (cf. van der Linden, 2005). Especially in adaptive testing, there may be large differences in speededness as more difficult items assembled for the more-able test takers often require more time. Assuming a fixed number of items and the same time limit for all test takers, differential speededness induced by items’ differences in time intensity increases time pressure for some test takers. As a consequence, those test takers may increase their speed at the expense of their effective ability to complete all items in time, or they do not adapt their speed level in a timely manner but make rapid guesses on the items at the end of the test. In both cases, the obtained test score will be lower than if the items had taken less time (cf. van der Linden, 2009b). Therefore, special procedures have been proposed for controlling differential speededness in adaptive testing. They further optimize item selection by taking into account the time intensity of already-presented items and still-to-be-selected items (van der Linden, 2009b; van der Linden, Scrams, & Schnipke, 1999).

Test-taking strategies affecting effective speed and ability

The test design determines the overall degree of test speededness and, thereby, the degree to which test performance depends on ability and speed. However, for a given test, persons showing the same speed-ability function (cf. Figure 1) may choose different levels of effective speed. This decision affects how items are completed once they are reached, whether all items can be reached and whether time pressure is experienced when proceeding through the test items. Individual differences in the chosen speed-ability compromise may depend on the time management strategies selected given a certain time limit, response styles favoring accuracy or speed, and also the importance of the test outcome for the test taker.

Assuming that there is almost always a time limit even in an ability test, test takers can apply various strategies to deal with the time constraint at the test level (cf. Semmes et al., 2011). The time management strategy means that the test taker tries to continuously monitor the remaining time and the number of remaining items and adopts a level of speed to ensure that all items can be reached. Therefore, effective ability also reflects the test’s speededness as induced by the time limit. Some test takers may fail to attempt all items in time, although they tried; others may decide from the very beginning to work on the items as if there were no time limit. If the available testing time is about to expire, there are basically two strategies for finalizing the test. One strategy is to change the response mode from solution behavior to rapid guessing behavior (cf. Schnipke & Scrams, 1997). Solution behavior means that the test taker is engaged in obtaining a correct response for the task, whereas in the mode of rapid-guessing behavior, the test taker makes responses quickly when he or she is running out of time (see also Yamamoto & Everson, 1997). Alternatively, the test taker does not change the response mode by increasing speed but rather accepts that remaining items will not be reached. Unlike in the time-management strategy, strategies ignoring the overall time limit imply that performance in items completed in the solution behavior mode is not affected by speededness due to the time limit.

Regardless of whether a test has a time limit or is self-paced, test takers can differ in effective speed because of differences in personality dispositions. Research on cognitive response styles (e.g., impulsivity vs. reflectivity; Messick, 1994) has shown that there are habitual strategies that can be generalized across tasks. For instance, in a study by Nietfeld and Bosma (2003), subjects completed academic tasks under control, fast, and accurate conditions. Impulsivity and reflectivity scores were derived using speed-accuracy trade-off scores. Results revealed that in the control condition, there were considerable individual differences in balancing speed and accuracy, which could be observed quite consistently across various cognitive tasks. An experimental study of spatial synthesis and rotation by Lohman (1979) demonstrated that individual differences in the speed-accuracy trade-off were nine times greater than the variation in the speed-accuracy trade-off across experimental conditions. Furthermore, previous research work has shown that cognitive response style may be related to personality variables and that it can be manipulated to some extent by instructions that emphasize working either more quickly or more accurately (e.g., Drechsler, Rizzo, & Steinhausen, 2010; Nietfeld & Bosma, 2003; Sorensen & Woltz, 2015).

The importance of expected test outcomes for the test taker also influences effective speed. In high-stakes testing (e.g., admission tests for a university), test takers probably actively try to follow the instructions and to put in their best effort. However, the same test takers may show aberrant test-taking behavior in low-stakes testing, where a lack of test-taking engagement is common and may threaten the validity of the measure (Lee & Jia, 2014; Wise & Kong, 2005). Considering Figure 1, lower effort could be indicated by a higher level of speed (up to rapid guessing) and an acceptance of lower effective ability.

ITEM RESPONSE AND RESPONSE-TIME MODELS

A manifold of psychometric models including not only item responses but also response times have been proposed to address measurement issues such as differential speededness or differences in the speed-ability compromise, and to investigate substantive research questions such as describing speed differences, the latent structure of fast and slow responses, or the relation between response time and the probability of success (for an overview, see Lee & Chen, 2011; Schnipke & Scrams, 1997; van der Linden, 2007, 2009a).

In the following section, different types of psychometric models are reviewed. Basically, they differ in the role the response-time variable plays: Response-time information may be considered when scoring item performance (e.g., Maris & Van Der Maas, 2012; Partchev & De Boeck, 2012), used as indicator of a latent speed construct (e.g., Klein Entink, Fox, et al., 2009; Loeys et al., 2011; van Breukelen, 2005; van der Linden, 2007), or as a predictor in an explanatory item response model accounting for differences in the probability of obtaining a correct response (e.g., Goldhammer et al., 2014; Roskam, 1987, 1997). Although the selected models differ in how responses and response times are modeled, quite a few can be accommodated into the generalized linear modeling framework proposed by Molenaar, Tuerlinckx, and van der Maas (2015). This framework represents modeling differences in different forms of cross-relations linking separate measurement models for item responses and response times.

From a different line of research, cognitive process models from mathematical psychology are considered inasmuch as they target (random) person effects (i.e., latent variables), accounting for individual differences in responses and response times (e.g., Ranger, Kuhn, & Gaviria, 2015; van der Maas, Molenaar, Maris, Kievit, & Borsboom, 2011).

Measurement models for ability with response time-based scoring

Partchev and De Boeck (2012) proposed a two-level branching model to investigate potential differences in processes underlying fast and slow responses (see also De Boeck & Partchev, 2012). They categorized responses as fast or slow by using categorical definitions of speed (i.e., a within-person definition with an intraindividual median split of item response times and a within-item definition with an interindividual median split by item). The first level of the branching model distinguishes between fast and slow responses; and the second level, between correct and incorrect responses for the respective speed branch. Thus, the model includes three nodes (speed with branches to fast ability and slow ability) and four response categories (fast correct, fast incorrect, slow correct, slow incorrect). The probability of selecting one of the two branches 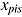(e.g., 1 for left, 0 for right) of the same node s is assumed to depend on item i and person p:

(2)

where 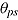denotes the person’s propensity to select the left branch at node s, the item’s difficulty in terms of selecting the left branch at node s, and 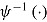the inverse logit function. Thus, for each node item and person, parameters are estimated with a multivariate normal (MVN) distribution of person parameters, 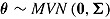, where 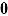represents the vector of means (constrained to be zero), and 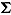represents the covariance matrix of parameters. In the study by Partchev and De Boeck (2012), there was a person parameter representing the propensity to give a fast response, one representing the propensity to give a slow correct response, and another one representing the propensity to give a fast correct response. Node-specific responses are assumed to be independent conditioned on the person parameters. Then, the probability for each of the four response categories can be obtained by multiplying the probabilities of the involved branches, for instance, for a fast incorrect response, 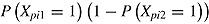. The model can provide interesting insights into how latent traits and item properties differ depending on whether items are completed more quickly or more slowly. As stated by the authors, an interesting expansion of the model would be to allow for a continuous change between fast and slow responses.

Maris and van der Maas (2012) proposed an ability model for time limit tasks based on a scoring rule taking both item response and item response time into account. The model is suitable for tasks that have an explicit time limit. Their starting point was the Signed Residual Time (SRT) scoring rule. Applying the rule means that for a correct response the item score is the residual time to the time limit (score gain), whereas for an incorrect response the item score is the negative value of the remaining time (score loss). Thus, persons need to be both fast and accurate to get a high score and, thereby, a high ability estimate, while fast incorrect responses are penalized. The total test score is calculated as the sum of the item scores and considered to be the sufficient statistic for person ability. Based on the SRT rule, Maris and van der Maas (2012) derived an item response model that was found to be a two-parameter logistic (2 PL) model with time limit d as discrimination parameter:

(3)

where 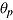represents person ability and 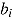item difficulty. A decrease in time limit d decreases discrimination, whereas time limit does not influence item difficulty. The model allows for predictions of the SATF—that is, the relation between expected response time and expected item response, depending on person parameter 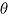and time limit d, respectively (see Maris & van der Maas, 2012). For the CAF—that is, the expected item response conditional on response time—the model predicts that a person whose ability exceeds item difficulty shows a negative CAF—that is, fast responses tend to be correct and slow ones to be incorrect. Similarly, a person whose ability is below item difficulty is supposed to show a positive CAF. In the SRT rule, rewards for correct responses and punishments for incorrect ones are equal, although alternative weights are possible. Interestingly, the weights used in the scoring rule can be used to influence how test takers balance accuracy and response time. As emphasized by the authors, for this, test takers need to be aware of the scoring rule and get feedback about their item scores.

Joint measurement models for ability and speed

Univariate and Bivariate Mixed Regression Approach

Van Breukelen (2005) developed a mixed and conditional regression approach for modeling item response times and item responses. The focus is on speeded measures including tasks that can be solved in an unlimited time. Within this modeling framework, separate measurement models for response and response time are proposed with intercepts and slopes varying randomly across persons. Fixed effects can be included as well—for instance, the effect of item variables. The (univariate) mixed logistic regression model for response correctness defines the probability of success as a function of the weighted sum of K predictors:

(4)

where 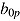is the random person intercept (i.e., ability) and 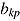is the random person slope of observed covariate 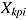, with 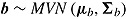, where 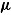represents the vector of mean weights, and 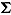represents the covariance matrix of weights. Common IRT models represent special instances of the response model; for example, the Rasch model is obtained by including a random person intercept 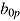(ability parameter) and dummy item indicators with fixed effects.

Similarly, the (univariate) mixed regression model for response time regresses the log-transformed response time 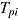on K predictors:

(5)

where 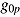is the random person intercept (i.e., speed) and 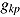is the random person slope of covariate 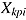, with 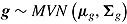. To investigate the strength and direction of the CAF, van Breukelen (2005) suggested including response time as covariate in the response model and response accuracy as covariate in the response-time model, respectively. However, as pointed out by Klein Entink, Kuhn, et al. (2009), understanding response time as a person-level predictor (speed) might be problematic, as this would require the same time intensity across items, which does not seem plausible in many cases. Finally, the joint (bivariate) analysis integrates both models (4) and (5) and allows for an investigation of the correlation between residuals in (4) and (5), which is assumed to be related to the CAF. Furthermore, the correlation between the person parameters, 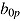(ability) and 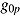(speed), can be determined.

A related (mixed) modeling approach for jointly analyzing item responses and response times was suggested by Loeys et al. (2011). It assumes not only random person intercepts but also random item intercepts for both the item response and the response-time models. This allows for estimates of the correlation between item characteristics (i.e., time intensity and difficulty) in addition to the correlation of person parameters. The model may include both person- and item-level covariates with fixed effects and can be extended to include random effects as well (Loeys et al., 2011).

Hierarchical Modeling Approach

Van der Linden (2007, 2009a) proposed a very flexible hierarchical modeling approach with separate measurement models for test takers’ ability and speed (for a further development, see Klein Entink, Fox, et al., 2009, Klein Entink, Kuhn, et al., 2009). At the lower level, van der Linden (2009a) suggested a 3 PL item response model and a lognormal response-time model, although other models can be assumed. The 3 PL model defines the probability that test taker p answers item i correctly as a function of the test taker’s ability θ_p and the item’s difficulty b_i, discrimination a_i, and guessing parameter c_i:

(6)

Similarly, the log normal model for response times models the log-transformed response time 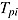as a function of the test taker’s speed 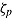and the item’s time intensity 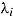(cf. van der Linden’s, 2009a, fundamental equation of RT modeling):

(7)

where 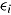denotes the residual, which is distributed 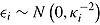. The item parameter 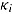represents the reciprocal of the standard deviation of the response times on item 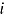and can therefore be regarded as a discrimination parameter (van der Linden, 2009a). The parameterization of the log normal model allows for the disentangling of person effects (i.e., speed) and item effects (i.e., time intensity and discrimination) on response time, similarly to the item response model. At the higher level, the joint multivariate normal (MVN) distributions of person parameters, 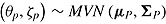, and item parameters, 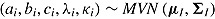, are defined, where 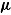represents the mean vector and 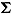the covariance matrix of parameters (cf. van der Linden, 2009a). Person-level covariates can be introduced into the model to explain individual differences in ability and speed (Klein Entink, Fox, et al., 2009) and item design factors to explain item characteristics (Klein Entink, Kuhn, et al., 2009).

A major assumption of the model is the conditional independence of observations—that is, responses and response times, respectively, are expected to be independent across items conditional on the respective person parameter. Based on this, responses and response times are supposed to be conditionally independent also within an item—that is, the levels of speed and ability presumably completely capture the covariance between responses and response times to an item (cf. van der Linden, 2007; van der Linden & Glas, 2010).

The correlation between speed and ability has a clear interpretation. The same does not apply to the correlation between item responses and item response times across test takers (or items) since spurious correlations may occur, driven by the correlation of person parameters (or item parameters) serving as hidden covariates. Accordingly, the correlation between number-correct score and total time may be unpredictable and, therefore, hard to interpret, as it depends on both the correlation between underlying person-level parameters and on the correlation between underlying item-level parameters (van der Linden, 2007, 2009a). The model is supposed to hold for tests with generous time limits. Hence, test takers are expected to be able to complete items at a fixed level of speed and ability, respectively, and do not change effective speed and ability due to strict time limits. Therefore, the speed-ability trade-off was purposefully not incorporated into the model.

Controlling Differential Speededness

Information about the speed 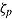of test takers and the time intensity 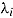of items can be used to optimize test design and, in particular, to control the speededness of different test forms in adaptive testing (van der Linden, 2005). Item selection is done as usual with the objective of maximizing information on the test taker’s ability, but at the same time the selection algorithm considers how much testing time is left, how time intensive possible items are and, depending on the measurement goal, also the test taker’s speed.

If the measurement goal is to measure a combination of ability and speed, the test taker’s ability estimate will also reflect his or her decision on speed as suggested by the individual speed-ability trade-off. In this kind of hybrid testing, the time limit at the test-level needs to have an equal effect on all test takers—that is, test speededness and induced time pressure need to be the same although items differ between test takers. Therefore, in adaptive testing the time intensity of selected items has to be controlled (van der Linden, 2005). A test assembly constraint is applied in order to ensure that the sum of the time intensities of already administered items and those of (maximally informative) items that may be selected from the item pool for the remaining portion of the test do not exceed the total time available (see van der Linden, 2005).

If the measurement goal is to measure only ability and speed is considered to be a nuisance factor, the time limit at test level should not have an effect and put test takers under time pressure. To create an adaptive test that is comparably unspeeded, item selection needs to be controlled for both with regard to the items’ time intensity and the test taker’s speed to avoid a situation in which the test taker is starting to run out of time. As proposed by van der Linden (2005), a constraint is required that controls the test taker’s expected total time, regardless of the selected speed level (see also van der Linden, 2009b). This requires a continuous estimation of the test taker’s speed based on response times to previous items. From a selection of items that fit the test taker’s current ability estimate, test takers showing high speed can get more-time-intensive items while slower test takers can receive items that take less time in order to avoid speededness. Optimizing test design by means of shadow tests (van der Linden, 2005) is a powerful approach to counter differential speededness in adaptive time-limit tests. However, it cannot prevent individual differences in the speed-ability compromise selected by each person. Even if (differential) test speededness can be removed by taking into account the individual decision on speed, this decision still affects effective ability.

Explanatory item response models

Fixed Response-Time Effect

Roskam (1987, 1997) proposed an item response model incorporating the log-transformed item response time as predictor. The main motivation of the model was to account for the trade-off between response accuracy and invested time in time-limit tests with a mixture of speed and ability components (for an application see van Breukelen & Roskam, 1991). Therefore, he incorporated the CAF representing the probability of obtaining a correct response conditional upon the response time into the 1 PL item response model. In Roskam’s (1997) model, the traditional ability parameter of the 1 PL model was replaced by “effective ability” as the product of time and mental speed. Roskam (1997) assumed that on the person level, the probability of success depends on effective ability, which increases as more time, 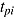, is spent on an item. The rate of this increase is the person parameter referred to as mental speed, 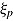, and reflects the fact that test takers differ in how strong the probability of giving a correct response changes with increasing response time. Using an exponential scale, the effective ability becomes the sum of 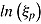and 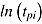. This results in the following model:

(8)

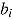where and are the logarithms of mental speed, 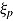, and item difficulty, 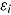, respectively. In (8) the effect of response time can be conceived as fixed to one.

Verhelst, Verstralen, and Jansen (1997) developed an item response model for time-limit tests very similar to the one proposed by Roskam (1987). Instead of the time spent on each item, they introduced an individual speed parameter as the regressor.

Roskam’s (1987) model (and also the one by Verhelst et al., 1997) suggests that a person completing an item obtains a higher probability of success if he or she takes more time to solve the item and vice versa. However, van der Linden (2007) concluded that Roskam’s model holds only for a person with fixed levels of ability and speed—that is, it does not capture the within-person level. The trade-off is a within-person phenomenon, and within-person differences in the speed-ability compromise occur, for instance, when completing an item or its replica across different experimental time-limit conditions 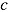(cf. medium level in Figure 2). For a given item, however, Roskam’s model only captures between-person differences in response time.

Wang and Hanson (2005) explained that Roskam’s (1987) model is most suitable for tests with a strong speed component as the probability of a correct response approaches one if the response time is increased regardless of the item’s difficulty. For ability tests with a time limit, they proposed a 3 PL model including in the exponent the term 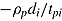(instead of 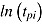as in Roskam’s model), where 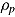reflects the slowness of the test taker (i.e., the pace of test taking) and 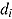the slowness of the item (i.e., the time intensity). If the response time is relatively short compared to the product of the slowness parameters reflecting the need to spend time on an item, the probability of a correct response is decreased substantially; whereas, for infinite response time the probability approaches the one predicted by the regular 3 PL model. Applying the model requires the assumption that a person’s response time is independent of his or her ability and the slowness parameters. This assumption is met if the response time is controlled externally by the test administrator but hardly met in typical conditions of test administration (cf. Wang & Hanson, 2005).

Random Response Time Effects

Goldhammer et al. (2014) proposed a response-time modeling approach within the generalized linear mixed models (GLMM) framework (e.g., Baayen, Davidson, & Bates, 2008; De Boeck et al., 2011; Doran, Bates, Bliese, & Dowling, 2007). Their goal was to investigate the heterogeneity of the association of response times with responses across items and persons; unlike Roskam’s (1987) model, the within-person (trade-off) level was not targeted. The item response model with fixed and random response-time effects was specified as follows (cf. Goldhammer et al., 2014):

(9)

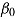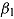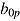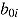where and represent the general intercept and the fixed effect of response time, respectively, whereas and are the random intercepts across persons (i.e., ability) and items (i.e., easiness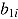) and and 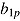denote the random response-time effects across items and persons. The distribution of the random effects across items and persons, respectively, is modeled as a multivariate normal distribution, 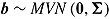, with 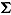as the covariance matrix of the respective random effects. The random effects 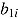and 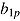indicate how the fixed response-time effect 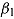is adjusted by item and by person. As the by-item adjustment 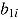(by-person adjustment 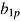) and item easiness 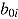(ability 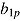) are tied to the same observational unit—that is, item (person)—their correlation can be estimated as well.

As suggested by (7), the effect of a response-time predictor reflects the effect of both the person’s speed 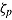and the item’s time intensity 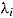. The fixed effect 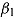represents only the overall association between response time and the log odds of the probability of a correct response. This association cannot be interpreted clearly and used to describe properties of persons and/or items, as it depends both on the correlation between underlying person parameters and on the correlation of corresponding item parameters (cf. van der Linden, 2007, 2009a). This problem is resolved by modeling the effect of response time as a random effect across items and/or persons. Thereby, influences from the item and person levels can be disentangled. More specifically, by introducing the by-item adjustment 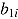—that is 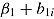—response time is turned into a person-level covariate varying between items. This allows for the interpretation of response time as an item-specific speed parameter predicting task success above and beyond individual ability. In a similar vein, by adding the person-specific adjustment 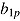—that is, 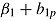—response time is turned into an item-level covariate varying between persons. This means that response time can be conceived as an item-level covariate that is specific to persons and predicts task success above and beyond item easiness. Model (9) can be easily extended with person-level and item-level covariates, which may interact with response time. This can further clarify which item and person characteristics drive the variability in the response time effect (Goldhammer et al., 2015; Naumann & Goldhammer, 2015).

In some of the presented models, response time 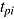is understood as a fixed value (Goldhammer et al., 2014; Roskam, 1987; but see also Roskam, 1997; Wang & Hanson, 2005). However, comparable to the item response, the response time can also be assumed to be a random variable. Thus, fixed values of 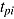in a response model that does not include a probability model for 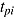should be regarded as specifications of the conditional distribution of 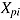given 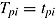(van der Linden, 2009a).

Cognitive Process Models

In the first place, measurement models such as the ones presented above serve to explain differences in observed responses and response times by latent (trait) variables. They can be regarded as statistical models in that they do not target cognitive processes and mental representations underlying responses and response times (e.g., Ranger et al., 2015). As discussed by Rouder, Province, Morey, Gomez, and Heathcote (2015), psychometric modeling may not fit the data in all details as required for investigating real cognitive structures; however, they are useful for measurement purposes in that they are statistically tractable, provide information on individual differences in latent variables, and allow for the inclusion of covariates to explain such differences. Although process models from cognitive psychology stem from a different tradition than psychometric models, their parameters may lend themselves to assessing individual differences. In the diffusion model (Ratcliff & Smith, 2004), for instance, the drift-rate parameter seems to be related to person ability since it describes the amount of evidence accumulated over time—and, thus, individual differences in the efficiency of information processing. Several models for responses and response times have been proposed, with claims that they focus on cognitive solution processes without sacrificing statistical tractability by limiting model complexity. Unlike typical cognitive process models for simple discrimination tasks with many repetitions of the same task, these new models are supposed to be suitable for the measurement context including a range of test items of varying complexity and relatively small item samples.

A first example is the Q-diffusion model proposed by van der Maas et al. (2011). It extends previous work by Tuerlinckx and De Boeck (2005) and represents an adaptation of the diffusion model to make it suitable for psychometric ability tests. Major parameters of the diffusion model are drift rate (i.e., amount of evidence accumulated over time) and boundary separation (i.e., response caution), which together provide an account of the speed-accuracy trade-off in decision making. In the Q-diffusion model, drift rate and boundary separation are decomposed into a person and item part—that is, ability and difficulty, as well as response caution and time pressure. Thus, the model provides information about individual differences in ability and response caution for a testing situation with response processes governed by a diffusion model. The model is limited to the assessment of simple abilities, that is, test items that can be completed by any individual possessing this ability if sufficient time is available (van der Maas et al., 2011).

The lognormal race model proposed by Rouder et al. (2015) represents another model addressing simpler and more-tractable cognitive processes to meet psychometric needs. It assumes an accumulator for each response option accumulating evidence for this option. The first accumulator exceeding its bound determines the response option and response time. Person and item effects can be incorporated into the structural part of the model to explain finishing times (response time less nondecision time). For educational and psychological testing, these parameters are of key interest as they allow for the description of individual differences that determine performance via a set of items. Ranger et al. (2015) also presented a race model for response and response time in test items. Two processes are assumed, reflecting the accumulation of knowledge with respect to the correct and an incorrect response. The accumulator’s threshold indicates the level of knowledge required to give the corresponding response. Individual differences in the amount of information and misinformation gained can be incorporated into the race model by assuming latent traits. Other parameters of the race model can be assumed to depend on the item. Note also that the model proposed by Partchev and De Boeck (2012) has its basis in cognitive psychology in that it represents a binomial tree process model (Batchelder & Riefer, 1999) taking individual differences into account.

CONTROLLING THE SPEED-ABILITY TRADE-OFF EXPERIMENTALLY

Some of the presented models (cf. Roskam, 1987, 1997; van Breukelen, 2005) have been proposed to address the trade-off between response accuracy and response time in traditional assessment settings in which a test taker completes a range of items at his or her own pace and usually within a given time limit at the test level. Although such test designs allow for estimates of effective speed and ability (Klein Entink, Fox, et al., 2009; Loeys et al., 2011; van der Linden, 2007), they cannot provide any information about the trade-off within a person. To assess the speed-ability compromise, a test design is required that varies the speed of completing a set of tasks within a person. Van Der Linden (2007, 2009a) argued that there is no need to incorporate the speed-ability trade-off into his model as test takers are expected to keep constant their effective speed and their effective ability when proceeding through a test (“stationarity assumption”). However, even if test takers work at a fixed level of speed, the problem of the confounding of effective ability with the decision on speed still exists if test takers select very different levels of speed.

Thurstone (1937) proposed “that mental ability as power can be experimentally determined so as to be independent of the speed of the performance” (p. 249). More specifically, ability can be assessed as the degree of difficulty, which is associated with a probability of success of .50 given infinite time. As infinite time cannot be implemented experimentally, a selected number of different values of available time and different values of difficulty are considered and ability is estimated as the interpolated asymptote. Hence, Thurstone’s approach was to prevent individual differences in the probability of a correct response due to speed differences, ideally by providing infinite time and practically by fixing the amount of time to certain values.

I argue that, in a similar fashion, the interdependence of speed and ability can be resolved by fixing speed in completing an item between test takers to obtain comparable estimates of individual ability. By implementing conditions under which test takers operate at the same levels of speed, estimated ability levels are no longer confounded (cf. Goldhammer & Kroehne, 2014; Lohman, 1989). Thus, a separate analysis of accuracy data is no longer deceiving, and individual differences in observed response behavior can be translated into more valid conclusions on ability differences.

Manipulating effective speed by item-level time limits

The upper part of Figure 3 displays the speed-ability functions of three test takers. Constraining them to work at the same speed level within a particular time-limit condition provides ability estimates that perfectly reflect the rank-order of the functions as opposed to the untimed administration illustrated in Figure 1 (upper part).

FIGURE 3 .

Resolving between-person differences in the speed-ability compromise. Upper part: Constraining effective speed provides ability estimates unconfounded by the decision on speed. Lower part: Constraining effective ability provides speed estimates unconfounded by the decision on ability (only suitable for speed tests).

Imposing an item-level time limit can be understood as constraining speed between test takers by item (Goldhammer & Kroehne, 2014). As shown in (5), the log-transformed response time 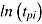can be broken down into the speed 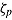of person 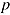and the time intensity 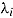of item i. Speed 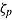while completing an item i can be standardized by constraining the time available for task 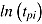—that is, the time that can be spent on processing the stimulus and responding. Thus, those test takers able to meet the time constraint at the item level have adapted their effective speed 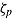to the level required by the time-limit condition 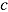—that is, .

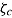If time intensity is equal across items, which may be the case for homogenous elementary cognitive tasks as used in experimental reaction-time research, speed is constant across items given the same time constraint (i.e., 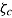). Cognitive items typically used to measure abilities, skills, or learning outcomes are much more heterogeneous. As such, items differ in the amount of required labor; time intensity is also supposed to vary substantially. Thus, if the same time limit is imposed, speed differs across items in that more time-intensive items require higher speed and vice versa. However, as desired, among test takers responding to a particular item, the speed level is still fixed to the same level (i.e., 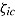). If time limits are defined item by item depending on the item’s time intensity (e.g., by selecting a certain percentile of the item response time distribution obtained from untimed administration), speed can be fixed to be equal between items.

Implementing item-level time limits means handing over speed control from the test taker to the test developer (cf. Wainer et al., 1990). There are various (experimental) methods available to control time spent on tasks, which prevent either too-fast responses, too-slow responses, or both in each speed-accuracy trade-off condition (e.g., Davison, Semmes, Huang, & Close, 2012; Lien, Ruthruff, Remington, & Johnston, 2005; Reed, 1973; Semmes et al., 2011; Wickelgren, 1977; Wright & Dennis, 1999). For instance, the response deadline method requires persons to provide a response within a time deadline and, thus, imposes an upper time limit. The time-bands method defines a time window by imposing both an upper and a lower time limit. The response-signal method requires participants to give a response at the same time as the offset of the stimulus or the onset of a response signal, such as an auditory one (for an overview, see Wickelgren, 1977). The response-signal paradigm is considered to be the more efficient method of controlling the trade-off since the deadline method and the time-bands method accept greater between-person differences in the time taken to complete an item. Alternative approaches try to manipulate the balance of speed and accuracy through instruction or rewards. However, they seem to be less efficient in reducing individual differences (Lohman, 1989; Nietfeld & Bosma, 2003).

Choosing item-level time limits

Full information on the individual speed-ability trade-off—that is, speed intercept, rate, and asymptotic ability—can be obtained if test takers complete linked sets of test items under various time-limit conditions (cf. speed-accuracy study proposed by Lohman, 1989). However, to control speed for ability measurement, in principle, only one time-limit condition in the range from chance to asymptotic ability is needed. How to implement experimental control by means of item-level time limits heavily depends on whether the test is considered a speed test, an ability test with speed as a nuisance factor, or an ability test with the speed component that should be included into the measure.

Speed Items

In a pure speed test, the challenge for the test taker is limited time. Typically, there are too many (easy) items, only some of which can be completed given the time limit at the test level. Hence, imposing strict time limits at the item level instead of at the test level lends itself to the measurement of speed constructs. The demand is somewhat changed in that the test taker is now required to complete individual items correctly and on time. Traditionally, when a fixed number of items are administered, response times are used as a measure of speed differences. However, when applying item-level time limits, differences in speed are solely captured by observed item responses. A correct response indicates that the test taker gave the right answer and, most importantly, that he or she was able to give it in time. Thus, the difficulty of an item is not only determined by its content (which is easy) but also by the time available to complete the item. To put it differently, by using item-level time limits, speed-test items are turned into ability-test-like items. Thereby, the conceptual differences between measuring speed and ability constructs vanish. It follows that speed can be reframed as the ability to continue giving correct responses in time under increasing time constraints at the item level.

Figure 3 (upper part) suggests how to select a suitable speed condition. Obviously, for tests showing a strong speed component, a medium-speed level seems most appropriate to observe large response variability. In contrast, high levels of speed imply random guessing; whereas at very low levels many test takers approach the same asymptotic ability and individual differences are minimized. The time limit needs to be determined empirically by trialing the items under an untimed condition. Time limits are then selected based on percentile values of the observed response-time distribution such that a certain portion of test takers—for instance, 50%—would be able to solve a particular item correctly and in time (cf. Davison et al., 2012; Goldhammer & Kroehne, 2014).

Following (1), Figure 3 assumes that ability is a function of speed, 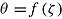, suggesting that speed can be controlled by the test taker or test developer and ability depends on chosen speed. For speed tests, the speed-ability trade-off appears to represent a symmetrical relation—that is, it is possible to control speed and assess ability (Figure 3, upper part) or to control ability and assess speed (Figure 3, lower part). Holding effective ability to a particular level among test takers can be achieved by adapting the time allowed to be spent on individual items (cf. Goldhammer, Moosbrugger, & Krawietz, 2009; Moosbrugger & Goldhammer, 2007), which in turn affects the accuracy of responses (for experimental paradigms manipulating the signal level adaptively, see Kaernbach, 1991). Thereby, individual differences in time allowed to complete items under the condition in which the same target ability is seen across test takers indicate individual differences in the speed construct. Thus, speed can be defined as the rate of work associated with a fixed level of effective ability. For ability tests, however, such an approach would not be feasible, as the effective ability level is not fully under the control of the testing procedure but also depends on the individual’s maximum ability level.

Ability Items

Ability constructs are measured by tests in which the main challenge relates to the difficulty of items rather than time constraints. However, the idea of using experimental control to avoid individual differences in the speed-ability trade-off may be applied to ability-test items as well (cf., for instance, the approach by Wright & Dennis, 1999). Figure 1 (lower part) suggests how to select a suitable speed condition in the range from chance performance to asymptotic ability. Obviously, by forcing test takers to adopt a low level of speed, effective ability estimates reflect differences in asymptotic ability (cf. Thurstone’s 1937 proposal of assessing power given infinite time). Thus, if only ability is to be measured and speed considered a nuisance factor, test takers should not experience time pressure and effective ability should approach asymptotic ability. Further research needs to investigate how to realize such testing conditions. For instance, setting both upper and lower item-level time limits may be too restrictive since test takers presumably differ in the effective speed that enables asymptotic ability (see Figure 1, lower part). Instead a response window could be used to prevent the test taker from proceeding too quickly or unusually slowly. An even-less-strict testing procedure could display the remaining recommended time at the item level (e.g., the 90th percentile of the correct-response-time distribution from untimed administration) and provide feedback if test takers proceed relatively quickly to the next item (e.g., compared to the median correct-response time), without forcing them to work further on the current item (cf. Hacker, Goldhammer, & Kroehne, 2015). The implementation should be sufficiently effective to reduce individual differences in time-management strategies and the speed-ability compromise. Ideally, time limits, time feedback, and/or displayed time information are perceived as supportive time-management tools that do not introduce construct-irrelevant variance.

If the ability measure is allowed to include a speed component, item-level time limits can be used to make sure that the level of speededness is kept constant between test takers as they proceed through the test. An item-level time limit can be defined as a certain percentile of the item response time distribution obtained from untimed administration; the smaller the selected percentile, the stronger the speed component. As opposed to a time limit at the test level, item-level time limits prevent potential individual differences in time-management strategies. Increasing speed in an ability test does not necessarily change the rank order of effective ability, but very high speed implies chance performance and individual differences in effective ability diminish (see Figure 1, lower part). As discussed by Ranger et al. (2015), emphasizing speed may have general effects on the response process in an ability test such as increasing motivation and test-taking effort. However, relatively high speed levels in ability tests probably do not just imply a need to adapt decision criteria as can be expected for simple cognitive tasks solved by continuous information accumulation (as described, e.g., by a diffusion model). Instead, the response process could be changed qualitatively by requiring responses based on partial knowledge or intelligent guessing (Ranger et al., 2015). Thus, when increasing speed in an ability test, not only a decrease in effective ability can be expected (cf. Figure 1, lower part), but also a change of the construct represented by effective ability may be manifested. There is empirical evidence that administering ability tests under time constraints at the test level increases shared variance with mental speed (e.g., Preckel et al., 2011; Wilhelm & Schulze, 2002). Semmes et al. (2011) introduced speededness in numerical reasoning at the item level by setting a one-tailed upper time limit (response-deadline method) at the median item response time obtained from untimed administration (see also Davison et al., 2012). Their findings showed the existence of a speed dimension explaining individual differences in timed item performance. Although time constraints can be considered a confounding factor, the correlations between timed and untimed ability measures were still found to be high. At the latent level, correlations of greater than .90 have been reported (Preckel et al., 2011; Wilhelm & Schulze, 2002) and at the manifest level correlations of about .80 have been reported (Davison et al., 2012; Vernon, Nador, & Kantor, 1985). Interestingly, Kendall (1964) investigated the predictive validity of an intelligence test and showed that for test-level time limits ranging from 15 to 30 minutes, not the most liberal time limit of 30 minutes but the medium limit of 22 minutes yielded the highest correlation with the criterion (see also Baxter, 1941). If test speededness (which should be standardized among test takers by item-level time limits) actually improves the desired predictive validity of a measure, it no longer represents a nuisance factor.

So far, research on item-level time limits in ability tests is limited. To judge the fruitfulness and feasibility of item-level time limits in ability tests, future research needs to address how item-level time limits can be implemented efficiently and how the variation of item-level time limits from generous to very limited affects reliability, ability correlations between untimed and timed conditions (cf. Davison et al., 2012; for speeded measures, see Goldhammer & Kroehne, 2014; for a posterior time-limit approach, see Partchev et al., 2013) and the validity of test-score interpretations, such as predictive validity with external criteria (Kendall, 1964).

Potential benefits from item-level time limits

Comparable Test-Taking Behavior

The major expected benefit from using item-level time limits is that ability estimates can be obtained that are not confounded with individual decisions regarding speed and individual differences in the speed-ability compromise. Furthermore, item-level time limits prevent test takers from running out of time at the end of the test, which means that all items can be attempted by all test takers. Thus, the speededness of items does not depend on their position in the test but only on the imposed item-level time limit. From this, it also follows that individual strategies, such as rapid guessing at the end of a test due to time pressure, will no longer play a role and that individual differences in time-management strategies among test takers will be reduced.

Interestingly, time constraints may also remedy the problem of low test-taking effort, for which rapid-guessing response behavior is a common indication (Wise & DeMars, 2006; Wise & Kong, 2005). For instance, Walczyk et al. (1999) allowed adults to read texts under various time-pressure conditions. Most importantly, their findings revealed that under mild time pressure, reading comprehension improved. Walczyk et al. (1999) assumed that mild time constraints increase test takers’ “mindfulness” (Salomon & Globerson, 1987), meaning that they invest more effort and have higher motivation. Thus, a moderate challenge causing slight anxiety may facilitate mindful monitoring and effortful test taking (cf. Walczyk & Griffith-Ross, 2006). Under severe time pressure, however, participants displayed reduced performance and increased stress levels.

A study by Lohman (1986) also sheds some light on the motivational effect of item-level time limits. Participants completed an experimenter-paced, mental rotation task in high- and low-incentive conditions. In the high-incentive condition, there were monetary rewards for correct responses. Results revealed that the incentive condition had no effect at the group level, suggesting that motivation is no longer dependent on incentives when trials are experimenter-paced rather than self-paced.

Another line of research supports the hypothesis that performance benefits from mild time pressure. As shown by Breznitz (1987), when a text was presented to children at their maximal normal reading rates, they achieved higher reading accuracy and higher comprehension scores (“acceleration phenomenon,” Breznitz & Berman, 2003). These findings seem to contradict the prediction of the speed-ability function. However, such results may simply suggest that under typical testing conditions, especially in low-stakes testing, test takers perform below their maximum effective ability.

Increased Reliability and Validity

Goldhammer and Kroehne (2014) demonstrated that item-level time limits in speeded measures imposed by the response signal method have a substantial influence on the reliability as assessed by Cronbach’s α and the ICC(k) coefficient. They found very low reliability for the untimed condition; whereas, reliability was much higher in the timed conditions as long as the time limit was not too short. Low reliability in the untimed condition could not be explained by the low level of item difficulty and the potentially associated variance restriction (ceiling effect). In the very slow timed conditions, average effective ability was comparably high (word recognition) or even higher (figural discrimination) than in the untimed condition, but the reliabilities of these timed conditions substantially exceeded the ones of the untimed condition. This suggests that differences in response times and in balancing the speed-ability trade-off heavily impair reliability in the untimed condition. Goldhammer and Kroehne (2014) discuss that the reliability seems to be threatened by inconsistent within-subject variation in response time, which is associated with changes in how individuals’ response times differ. If a test taker’s response time relative to that of others’ varies from item to item, their relative success rate may also vary, reducing the association between item response variables.

Partchev et al. (2013) applied (one-tailed) posterior time limits to reasoning data to disentangle power and speed. Their analysis of recoded data—that is, time data and time-accuracy data—showed that decreasing the posterior time limit did not have a negative effect on reliability as assessed by the test-information function and Cronbach’s α. Moreover, they demonstrated that item discrimination and reliability can actually increase as the time limit becomes stricter. Further research is needed to show whether results obtained by means of posterior time limits can be replicated for experimentally imposed item-level time limits. Goldhammer and Kroehne (2014) found for two speeded measures that applying (two-tailed) posterior time limits to untimed response data increased reliability substantially as well as the correlation between ability dimensions in the untimed and timed conditions.

In the study by Davison et al. (2012), participants completed timed numerical reasoning items. The (upper) time limit was determined to be the median correct-response time from an untimed condition. The results suggested that the speed dimension captured by timed item administration can improve the prediction of accuracy in math tasks performed under time constraints and, thereby, predictive validity.

Goldhammer, Kroehne, and Hahnel (2014) compared the convergent validity of untimed and timed measures of word recognition and sentence verification with reading comprehension. Items were completed both in an untimed condition, allowing individual response-time differences, and in a timed condition in which the time available for item completion was limited by means of a response signal. In addition, participants completed reading comprehension items (without item-level time limits). Results revealed that the correlation between the untimed measures of word recognition and sentence verification was only of medium size. However, the correlation between the timed measures was significantly higher. In terms of the association with reading comprehension, the untimed measures of word recognition and sentence verification were moderately correlated with reading. Most importantly, the corresponding correlations of timed measures with reading were significantly higher. This results pattern suggests that item-level time limits in speeded measures improve construct validity by removing individual differences in how speed and ability are balanced.

Data Structure

Using item-level time limits changes the set of random variables that are needed to capture the response behavior (cf. Figure 2). The missing data indicator 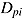no longer represents individual differences in items reached as each test taker is supposed to attempt all items. If the response-time variable 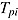is controlled by the test developer, it becomes a fixed variable (however, there may be some response-time variation within a certain time-limit condition). Thus, the item response variable 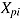is the only random person-level variable left with regard to response behavior. This is an interesting aspect of item-level time limits, as it simplifies the data structure and allows for a focusing on item responses only. For instance, if not-reached items, representing presumably non-ignorable missing data, were to be observed, this would require extra statistical effort to prevent biased estimations of item and person characteristics (cf. Glas & Pimentel, 2008).

As regards speed tests, item-level time limits determine the items’ speededness and in turn their difficulty. Scoring the right answer given in time as correct and the other ones as incorrect provides an opportunity to apply common IRT methods, as is the case for data from ability tests. This is an attractive feature since it opens the door to well-developed testing technology being available for categorical response data.

In addition, some specific models and applications of models have been proposed to analyze time-limit data. For instance, the model by Maris and van der Maas (2012) explicitly assumes an upper time limit at the item level. Their model, see (3), based on the SRT rule was shown to be a 2 PL model with time limit as the discrimination parameter. Van Breukelen and Roskam (1991) presented mental rotation tasks with various stimulus presentation times to participants. They used the extended Rasch model by Roskam (1987), see (8), to test the trade-off hypothesis that the probability of a correct response on a given test item completed by a given subject increases monotonically with the amount of time invested (as manipulated by stimulus exposure time).

CONCLUSIONS AND FINAL REMARKS

The initial question, “Measuring ability, speed, or both?” needs to be answered cautiously. First, what is to be measured depends on the kind of inferences that will be made on the basis of the test score—that is, the kind of test score interpretation (Kane, 2013). For instance, extrapolating the test score to a criterion from a different performance domain (e.g., job performance on the assembly line) may require the measurement of a composite of ability and speed. Second, in this article I argued that regardless of whether it is speed or ability—or (more realistically) a composite of ability and speed—that is to be measured purely, the balance of effective speed and effective ability within a person should be controlled at the between-person level. Even if the intention is to measure a combination of ability and speed (i.e., ability given a certain level of test speededness), test takers may select different levels of speed, thus confounding the ability measure. My literature review revealed that several joint-measurement models have been developed to represent individual differences in effective speed and effective ability. However, the proposed conceptual framework (see Figure 2) suggests that estimates of effective ability and speed originate at the within-person level, described by individual speed-ability functions (whereas between-person differences relate to the parameters specifying these functions). Therefore, single estimates of effective speed and ability can hardly be used to compare individuals.

As described, stipulating the individual speed-ability compromise in the assessment of speed or ability requires the implementation of a suitable item-level–time-limit condition. An obvious extension would be to implement multiple time-limit conditions in order to probe the whole range from chance ability to asymptotic ability (cf. speed-accuracy study proposed by Lohman, 1989). Such an assessment would probably require five or six times the amount of data needed to obtain a single estimate of effective ability. However, it would provide information about individual differences in the SAFT parameters, in particular the rate parameter, and provide insights into how trade-offs between effective speed and ability function within persons. The added value of the SATF parameters—for instance, with regard to predictive validity—was indicated in Lohman’s (1986, 1989) findings.

The speed-ability curve represents a plausible way to capture possible combinations of speed and ability (cf. Figure 1). However, it is not certain that given a particular level of speed the (maximum) effective ability is actually achieved. There may be further factors that bring about a lower effective ability, such as a lack of test-taking effort; that is, even if the person does not increase test-taking speed he or she may not care about solving the items correctly. Related to that, a lack of persistence or continuance (cf. Furneaux, 1961; White, 1973) reflects test takers’ tendency to abandon an item after it has already been considered (e.g., because of perceived difficulty) even though it might be solvable with greater perseverance.

A general prerequisite of item-level time limits is that test takers are equally able to adapt their timing and response behavior to the introduced time constraints. Basically, this assumption needs to hold for both speed and ability tests. Thus, confounding of item-level time limits with other construct-irrelevant dimensions, such as test anxiety due to severe time constraints (e.g., Onwuegbuzie & Seaman, 1995; Veenman & Beishuizen, 2004), should be avoided. A general negative effect of strict item-level time limits on performance is expected. However, the validity of interpreting test scores would be threatened if some test takers continue to perform at their ability limits under such time constraints whereas others showing the same speed-ability curve are affected more and operate below their ability limits because, for instance, text anxiety interferes with their ability to complete the primary task. Note that if the measure is supposed to tap speed or ability under an experimental speed condition, the impact of test takers’ ability to deal with the time pressure or their flexibility to operate at different speed-ability compromises on the measure would actually be a desired outcome. This would not be the case for ability measures that are not supposed to include a speed component.

An interesting measurement perspective is given by the dependency of item difficulty on the time available to complete the item. Especially for speed tests, it is obvious that item difficulty can be manipulated by limiting the time available for completion. This would be beneficial for automatic item generation and adaptive testing, since items of arbitrary difficulty can be created by increasing or decreasing item presentation time (cf. Goldhammer et al., 2009; Moosbrugger & Goldhammer, 2007; Wainer et al., 1990). To create an item-generation model, a calibration study is required, revealing how items become more difficult as available time decreases. A crucial point is that overly strict time limits give rise to rapid random guessing (similar to speededness at the test level), compromising item discrimination. Wright and Dennis (1999) discussed the possibility of manipulating item difficulty through item-level time limits for adaptive ability tests. This requires that time limits primarily change item difficulty, but not the nature of the assessed construct, by varying speededness. Partchev et al. (2013) conducted posterior time-limit analyses of reasoning data and concluded that it is not possible to increase the range of item difficulty by adding timed to untimed items, since timed items always measure a composite of speed and ability. However, if the inclusion of the speed component is acceptable from the perspective of validity, the difficulty of a test can be changed by introducing item-level time limits.

Item-level time limits, displaying time information, and giving time feedback have clearly not been a great focus of measurement research and practice. One reason may be that traditional paper-and-pencil testing does not allow for that. However, with the increasing deployment of computer-based assessments, defining item-level time limits and providing information on available time to the individual test taker has become straightforward, even in the context of large-scale assessments. This provides a promising new direction for future research to improve the measurement of ability and speed.