Pharmacokinetics of Morphine and Its Metabolites in Infants and Young Children After Congenital Heart Surgery

Abstract

The objective of this study was to characterize morphine glucuronidation in infants and children following cardiac surgery for possible treatment individualization in this population. Twenty children aged 3 days to 6 years, admitted to the cardiovascular intensive care unit after congenital heart surgery, received an intravenous (IV) loading dose of morphine (0.15 mg/kg) followed by subsequent intermittent IV bolus doses based on a validated pain scale. Plasma samples were collected over 6 h after the loading dose and randomly after follow-up doses to measure morphine and its major metabolite concentrations. A population pharmacokinetic model was developed with the non-linear mixed effects software NONMEM. Parent disposition was adequately described by a linear two-compartment model. Effect of growth (size and maturation) on morphine parameters was accounted for by allometric body weight-based models. An intermediate compartment with Emax model best characterized glucuronide concentrations. Glomerular filtration rate was identified as a significant predictor of glucuronide formation time delay and maximum concentrations. Clearance of morphine in children with congenital heart disease is comparable to that reported in children without cardiac abnormalities of similar age. Children 1–6 months of age need higher morphine doses per kilogram to achieve an area under concentration–time curve comparable to that in older children. Pediatric patients with renal failure receiving morphine therapy are at increased risk of developing opioid toxicity due to accumulation of morphine metabolites.

INTRODUCTION

Morphine sulfate is one of the most frequently used opioids for management of post-operative pain in children and adults. Morphine is mainly eliminated by hepatic metabolism via glucuronidation to morphine-3-glucuronide (M3G) and morphine-6-glucuronide (M6G) (1). The glucuronidation pathway is present, but immature, at birth (2,3) and reaches maturity sometime between the second week and sixth month of life (4–6). Morphine clearance is reduced and its effect is prolonged in neonates compared with older children and adults (7). In addition to these developmental changes, morphine metabolism may be influenced by surgery (4) and cardiac status (8). Cardiac surgery-induced alterations in hepatic blood flow may affect the disposition of drugs metabolized by the liver.

The disposition of the metabolites of morphine is also important to consider. Morphine glucuronides are excreted by the kidneys, and impaired renal function leads to accumulation of M3G and M6G with repeated administration of morphine (9,10). While M3G has antagonistic effects (11,12), M6G has greater analgesic potency than morphine (13,14). Therefore, patients with kidney disease are at risk of developing opioid resistance or toxicity when treated with morphine. Patients with renal failure receiving morphine have been reported to exhibit severe and prolonged respiratory depression that has been attributed to inability to clear M6G (15,16).

Despite the documented large inter-individual variability of morphine disposition (7,17), only a few individual studies have addressed the effect of heart disease on morphine pharmacokinetics (PK) in the pediatric population (8,18). The objective of this study is to develop a population PK model for morphine glucuronidation in infants and young children following congenital heart surgery that accounts for the effects of development, cardiac condition, and renal function for possible treatment individualization in this population.

MATERIAL AND METHODS

Patients, Morphine Dosing, and Monitoring

Following Institutional Review Board (IRB) approval, we enrolled 20 patients, aged 0–6 years, admitted to the cardiovascular intensive care unit (CVICU) after congenital heart surgery. Exclusion criteria were (1) single-ventricle physiology, (2) weight <3 kg, (3) significant renal, hepatic, or neurologic impairment, (4) anticipated mechanical ventilation <24 h, (5) administration of morphine during the 12-h period prior to the study, and (6) chronic opioid therapy for 30 days prior to study enrollment.

Intraoperative anesthetic management was guided by standard anesthetic practice at Lucile Packard Children’s Hospital (Palo Alto, CA) and Children’s Hospital Colorado (Aurora, CO). Morphine was not administered during surgery. After the patient had been transferred to the CVICU post-operatively and demonstrated a need for analgesia, the patient received a loading intravenous morphine sulfate dose of 0.15 mg/kg (range. 0.14–0.17 mg/kg). Subsequent doses of morphine sulfate were delivered by nurse-controlled analgesia (NCA) via a PCA pump as needed according to changes in vital signs with stimulation (e.g., tachycardia, increase in systemic, pulmonary artery, and/or left atrial pressure) and Face, Legs, Activity, Cry, Consolability (FLACC) scores ≥4 (19,20). The NCA dose was initially 0.02 mg/kg and was increased in increments of 0.01 mg/kg or 10% at the discretion of the treating CVICU physicians. The average NCA delivered dose was 0.06 mg/kg (range, 0.02–0.21 mg/kg). Persistent pain despite morphine administration was treated with fentanyl 1–2 mcg/kg IV. Lorazepam 0.025 mg/kg IV was administered for sedation. Excessive movement was treated with additional sedative medications (e.g., lorazepam, propofol, dexmedetomidine, ketamine, and midazolam), and neuromuscular blocking agents were administered if the movement was excessive according to the standard of care in the CVICU.

Safety monitoring included continuous recording of vital signs, electrocardiogram, invasive hemodynamic parameters (systemic +/− pulmonary artery and atrial pressures), and monitoring of laboratory values. Documentation of adverse events included clinically significant changes in hemodynamics, deviations from expected clinical post-operative recovery, and respiratory depression.

Venous blood samples for PK analysis were obtained after admission to the CVICU (baseline). Following administration of the morphine sulfate loading dose, venous blood samples were drawn at 5, 15, and 30 min, then at 1, 2, 4, and 6 h. Subsequent to the NCA delivered doses, blood samples were collected at random time points. The blood samples were drawn into EDTA tubes that were gently mixed and put on ice. Samples were centrifuged following collection at 1,500×g for 10 min at 4°C; plasma was then placed in propylene tubes that were frozen for subsequent determination of morphine, M3G, and M6G concentrations.

Analytical Methods

Morphine, M3G, and M6G were simultaneously measured in plasma using a validated liquid chromatography tandem mass spectrometry assay previously developed by our group (21). The assay had the following performance characteristics: range of reliable response of 0.25–1,000 ng/mL (r ² > 0.99) for morphine, 1–1,000 ng/mL (r ² > 0.99) for M3G, and 2.5–1,000 ng/mL (r ² > 0.99) for M6G. Extrapolation below the lower limit of quantification was allowed, as long as the signal-to-noise ratio was better than 3:1 as recommended by applicable regulatory guidance (22,23). Inter-day accuracy and precision for morphine and its metabolites were within 15% of the nominal values. There was no carryover, ion suppression, or matrix interferences with the quantification of the analytes.

Pharmacokinetic Model

The PK model used for analysis of morphine and metabolite data is shown in Fig. 1. Morphine plasma concentration–time data were represented as a two-compartment linear disposition model parameterized in terms of total clearance (CL), inter-compartmental clearance (CL _D), central (VC), and peripheral (VP) volume of distribution. An intermediate compartment was linked to the morphine central compartment to account for metabolite formation time delays. Concentration of morphine–metabolite intermediate, C _int, is described by the following equation:

$$\frac{d{C}_{\mathrm{i}\mathrm{n}\mathrm{t}}}{dt}=K_{\mathrm{i}\mathrm{n}\mathrm{t}}\cdot \left(C-C_{\mathrm{i}\mathrm{n}\mathrm{t}}\right)$$ 1

where C is morphine concentration at the central compartment, and K _int is the rate constant for the intermediate compartment. Morphine glucuronidation process is modeled with an empirical Emax transduction function that relates morphine–metabolite intermediate concentration (C _int) to metabolite plasma concentration (M):

$$M=\frac{M_{\text{max}}\cdot C_{\mathrm{i}\mathrm{n}\mathrm{t}}}{C_{\mathrm{i}\mathrm{n}\mathrm{t},50}+C_{\mathrm{i}\mathrm{n}\mathrm{t}}}$$ 2

where M _max is maximum metabolite concentration, and C _int,50 is intermediate concentration producing half-maximal metabolite concentration.

Fig. 1.

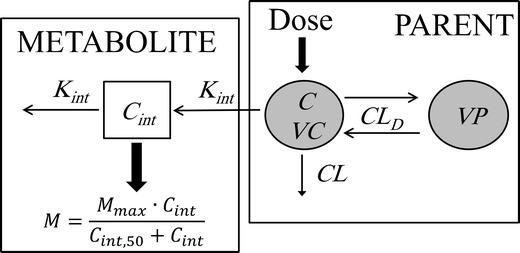
Schematic representation of the pharmacokinetic model for morphine and its metabolites. CL and CL _D denote morphine total and inter-compartmental clearances, respectively; VC and VP denote morphine central and peripheral distribution volumes, respectively; C _int denotes morphine–metabolite intermediate concentrations; K _int is the rate constant for intermediate compartment; M denotes metabolite (M3G or M6G) concentrations; M _max is the maximum metabolite concentration; and C _int,50 is intermediate concentration producing half-maximal metabolite concentration

Population Pharmacokinetic Analysis

Morphine and metabolite plasma concentration–time data were analyzed using the non-linear mixed effects modeling software program NONMEM (version VII; Icon Development Solutions, Ellicott City, MD). The first-order conditional estimation (FOCE) with η–ε interaction was used for the estimation of the model parameters. The convergence criterion was three significant digits. The model was specified using NONMEM general differential equation solver ADVAN6 TOL5. To reduce run time, a sequential approach was used in the analysis. Using morphine plasma concentrations, a two-compartment model was initially fitted and morphine post hoc PK parameter estimates were obtained for each subject. In the second stage, Eqs. 1 and 2 were fit to metabolite data conditional on morphine individual predictions in each subject.

Doses and concentrations were converted to molar units using molecular weights of 758.83, 285.34, and 461.46 g/mol for morphine sulfate, morphine, and the metabolites, respectively. Since the morphine sulfate molecule comprises two morphine molecules, the equivalent morphine dose was obtained by multiplying morphine sulfate moles by two. The concentrations were logarithmically transformed, and an additive residual error model was used. Inter-individual variability in the PK parameters was represented by an exponential model under the assumption that the PK parameters are log-normally distributed.

For morphine, one- and two-compartment models were tested as structural models. Besides the intermediate compartment with Emax model used in this work, structural models by Bouwmeester et al. (24) and Knibbe et al. (25) were evaluated as possible candidates for metabolite data. Models of Bouwmeester and Knibbe represent each metabolite as a compartment in first-order connection with the parent central compartment. The metabolite compartment is parameterized in terms of formation clearance, elimination clearance, and metabolite volume of distribution. For the metabolite parameters to be identifiable, the distribution volume is either fixed to literature adult values scaled by body weight (24) or expressed as fraction of morphine central volume of distribution (25). Choice of morphine and metabolite structural models was based on the Akaike information criterion (AIC) (26).

Following principles of pediatric clinical pharmacology and previous population PK models in infants (27), an allometric body weight-based model scaled to a 6-kg child (median body weight in this study) was first implemented to account for the influence of body size on morphine clearance and volume parameters. Considering the allometric weight model as the base model, we then investigated the effect of postnatal age, gestational age, gender, kidney function (evaluated by estimated glomerular filtration rate), hepatic function (evaluated by serum alanine transaminase (ALT) and aspartate transaminase (AST)), and congenital heart defects (tetralogy of Fallot (TOF), atrioventricular septal defects (AVSD), ventricular septal defect (VSD), or other) on morphine CL, CL _D, VC, and VP. Estimated glomerular filtration rate (GFR) was calculated using Schwartz formula (28) to account for the effect of age on renal function. Linear, exponential, or power functions were used to model the relationship between a continuous covariate and a PK parameter. The covariate was centered or normalized using the corresponding median value in the population investigated. Relationship between a categorical covariate and a PK parameter was developed to get a particular parameter estimate for every cluster. For metabolite PK parameters, body weight, postnatal age, gestational age, gender, GFR, ALT, AST, and cardiac status were investigated as potential covariates on K _int, M _max, and C _int,50 using linear, exponential, or power and categorical models.

The covariate model was built using a standard forward addition and backward deletion procedure. Using the basic PK model, each potential covariate was separately included and the model was tested. A covariate was considered to significantly improve the model if the decline in NONMEM objective function value (OFV) was ≥3.84 (corresponding to a likelihood ratio test at significance level α = 0.05 and 1 degree of freedom). If more than one significant covariate was found, the covariate with the greatest reduction in the OFV was added to the base model, and the entire procedure was repeated until no further improvement could be achieved (stepwise forward addition). In the subsequent step down approach, each covariate was eliminated separately from the model, until an OFV increase of more than 10.83, corresponding to a p < 0.001.

The final model was evaluated by visual inspection of observed versus predicted concentrations and normalized prediction distribution errors (NPDE) versus time and population predictions. NPDEs were automatically generated using NONMEM from 1,000 simulations. NPDEs for an efficient model should follow a standard normal distribution (29). Frequency distribution of the NPDEs was examined, and deviation of the mean and variance of the NPDEs from 0 and 1, respectively, was tested using t test for mean and Fisher test for variance. Precision of the final model parameter estimates was assessed by the relative standard error (%SE) calculated as the percentage of the standard error provided by NONMEM $COVARIANCE step to the parameter estimate. Additionally, model robustness was investigated using non-parametric bootstrapping as implemented in Perl-speaks-NONMEM (30). A total of 1,000 bootstrap datasets were generated from the original data set by repeated sampling with replacement, and the final pharmacokinetic model was used to estimate model parameters for each data set, then confidence intervals were constructed.

Simulation

A simulation study was performed to investigate the influence of developmental changes on morphine exposure as well as the effect of renal function on glucuronide exposure. The fixed effects and inter-subject variability parameter estimates of the final population model were used to predict morphine area under concentration–time curve for 24 h (AUC_0–24 h) in three age groups: group I, 1-month-old, 4.5 kg; group II, 6-month-old, 6 kg; and group III, 2-year-old, 12 kg. Additionally, M3G and M6G AUC_0–24 h in a 6-month-old child (typical body weight of 6 kg) were predicted in four GFR groups: 20, 50, 70, and 100 mL/min/1.73 m².

A total of 100 subjects were simulated per group using NONMEM. The assumed morphine dose was 0.1 mg/kg every 3 h. Log-transformed AUC values were compared between various groups by univariate analysis of variance (ANOVA) and Bonferroni post hoc analysis. P values <0.05 were regarded as statistically significant.

RESULTS

The analysis used 1,080 concentration observations from 20 subjects. Demographic data, cardiac diagnosis, and dosing characteristics are depicted in Table I, and plasma concentration–time profiles for morphine, M3G, and M6G are shown in Fig. 2.

Table I.

Summary of Patient Demographic Data, Cardiac Diagnosis, and Dosing Characteristics

Characteristic	Mean (SD)	Range
No. of subjects	20	–
Age (years)	1.4 (1.6)	3 days–5.4 years
Weight (kg)	7.8 (4.3)	3.1–18.5
Body surface area (m2)	0.36 (0.14)	0.20–0.60
Gestational age (weeks)	38 (1.3)	35–40
Gender (n)
Male	10
Female	10
Serum creatinine (mg/dL)	0.5 (0.2)	0.3–1.2
Glomerular filtration rate (mL/min/1.73 m2)a	79 (38)	19–158
Serum ALT (U/L)	49 (25)	25–108
Serum AST (U/L)	228 (150)	78-659
Diagnosis (n)
TOF	12
AVSD	3
VSD	1
Other	4
No. of drug administrations per subject	18 (7.4)	7–35
Loading dose (mg/kg)	0.15 (0.01)	0.14–0.17
Follow-up dose (mg/kg)	0.06 (0.04)	0.02–0.21
Morphine concentration (μg/L)	29 (47)	0.20–348
M3G concentration (μg/L)	220 (303)	0.39–2,630
M6G concentration (μg/L)	29 (45)	0.86–383

^aEstimated using Schwartz formula Schwartz et al. (28)

Fig. 2.

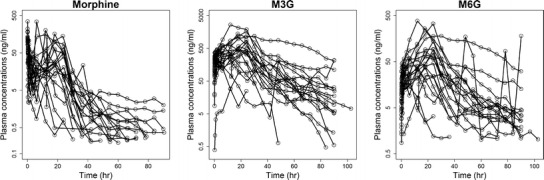
Morphine, M3G, and M6G plasma logarithmic concentration–time profiles obtained in 20 post-cardiac surgery pediatric patients. Lines connect observations obtained in the same individual

A two-compartment model was better than one-compartment for morphine data (ΔOFV = −388, AIC = 133 versus 513). Our metabolite model (the intermediate compartment with Emax model) better described the data compared to Bouwmeester et al. (24) and Knibbe et al. (25) models as indicated by lower AIC value (228 versus 444 and 312 for both models, respectively).

Using exponential, weight-based allometric models to account for size differences reduced the OFV of the morphine model from 115 to 96 (p < 0.001). Additionally, adjusting for body weight in our base model decreased the random effects variability on CL, CL _D, and VP by 56%, 25%, and 15%, respectively. Estimating the exponents of the weight-based allometric models rather than fixing it to 0.75 or 1 for each of the clearance and volume parameters, respectively, failed to reduce the OFV by 3.85 (i.e., p value >0.05 on χ ² likelihood ratio test with 1 degrees of freedom). Therefore, using the variable power model would have resulted in an over-parameterized model.

Our covariate analysis indicated that, after adjusting for body weight, age-based maturation of morphine clearance and volume of distribution cannot be detected. Moreover, none of the other covariates (including cardiac condition) had a significant effect on any of morphine PK parameters. For metabolite parameters, renal function was the most important covariate affecting M3G and M6G formation time delay and maximum concentrations. This statistically based finding was further asserted by the strong correlation between post hoc K _int and M _max against GFR (Fig. 3). GFR power model exponents of the two metabolites were very close to unity; therefore, we decided to fix the exponents to 1 for K _int and −1 for M _max with only 2 point increase in NONMEM OFV. The final covariate model is shown in Table II. Between-subject random effects of M3G and M6G were very close. Therefore, inter-subject variability parameters were shared between M3G and M6G. As a result of this sharing, the OFV was reduced by 34 points.

Fig. 3.

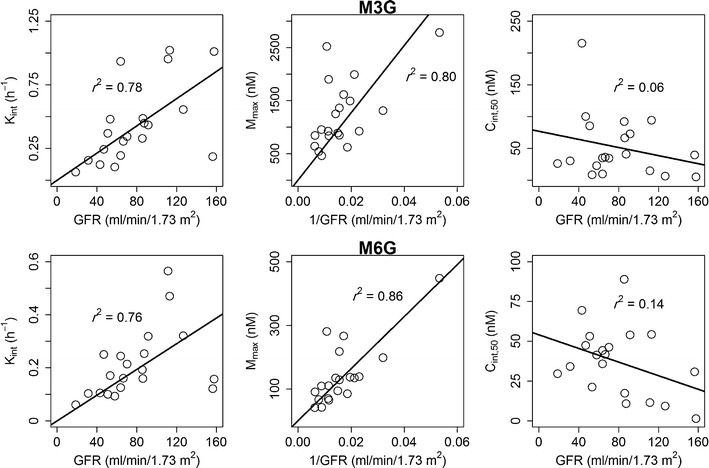
Effect of glomerular filtration rate on individual (post hoc) predicted PK parameters of M3G and M6G. Linear regression lines are shown

Table II.

Morphine and Its Metabolites Population Pharmacokinetic Parameter Estimates and Bootstrap Statistics Using the Final Pharmacokinetic Model

Parameter (unit)	Model	Estimate	Bootstrap median [95% C.I.]	Inter-individual variability (%CV)
Fixed effects (%SE)
CL (L/h)	θ CL × (WT/6)0.75			0.20 (45)
θ CL		8.7 (12)	8.6 [7.0, 11.2]
VC (L)	θ VC × (WT/6)1.0			0.67 (82)
θ VC		18.7 (21)	18.7 [13.1, 29.0]
CL D (L/h)	θ CLD × (WT/6)0.75			0.17 (41)
θ CLD		0.88 (15)	0.91 [0.60, 1.4]
VP (L)	θ VP × (WT/6)1.0			0.42 (65)
θ VP		25.2 (32)	25.2 [15.0, 61.1]
K int (h−1)	θ K int × GFR/70			0.27 (52)
θ K int, M3G		0.30 (14)	0.30 [0.21, 0.43]
θ K int, M6G		0.24 (13)	0.24 [0.18, 0.32]
M max (nM)	θ Mmax × 70/GFR			0.23 (48)
θ Mmax, M3G		1,257 (14)	1,254 [950, 1,744]
θ Mmax, M6G		109 (15)	109 [81.3, 153]
C int,50 (nM)	–			1.26 (112)
C int,50, M3G		40.4 (32)	40.9 [21.6, 81.4]
C int,50, M6G		21.9 (27)	22.8 [11.9, 43.6]
Residual variability (%CV)
σ 2 (morphine)		0.32 (57)	0.32 [0.21, 0.50]
σ 2 (M3G)		0.32 (57)	0.32 [0.19, 0.49]
σ 2 (M6G)		0.39 (62)	0.38 [0.18, 0.72]

%SE relative standard error, %CV coefficient of variation (square root of the value multiplied by 100%), C.I. confidence interval, σ ² intra-individual variance, θ fixed effect parameter, CL and CL _D morphine elimination and distribution clearances, respectively, VC and VP morphine central and peripheral distribution volumes, K _int rate constant for intermediate compartment, M _max maximum metabolite concentration, C _int,50 intermediate concentration producing half-maximal metabolite concentration

Table II lists the final population PK model parameter estimates calculated for morphine, M3G, and M6G, along with their %SE, between-subject variability, and bootstrap statistics. The model fixed effects were estimated with reasonable precision, as indicated by %SE < 32%. All parameters exhibited relatively narrow bootstrap 95% confidence intervals. Distribution of parameter estimates around the bootstrap median was not always symmetric, suggesting non-Gaussian, asymptotic distribution of the estimated parameters. However, the match between the point estimates from the original dataset and the bootstrap median values indicates stability and robustness of the population PK model. Table II shows that inter-individual variability of morphine and metabolite PK parameters are very large with %CV reaching more than 80% for some parameters.

Basic goodness-of-fit plots of the final population PK model are depicted in Fig. 4. The figure shows that the model reasonably fit the data, at the population and subject levels, as suggested by the symmetric distribution around the identity line and the good agreement between observed concentrations and both population and individual predictions. Performance of the metabolite model was further investigated by plotting observed M3G and M6G concentrations against predicted concentrations at the intermediate compartment (Fig. 5). The clear Emax relationship and the close agreement between observed and individual predicted metabolite concentrations in four representative subjects confirm the adequacy of this model.

Fig. 4.

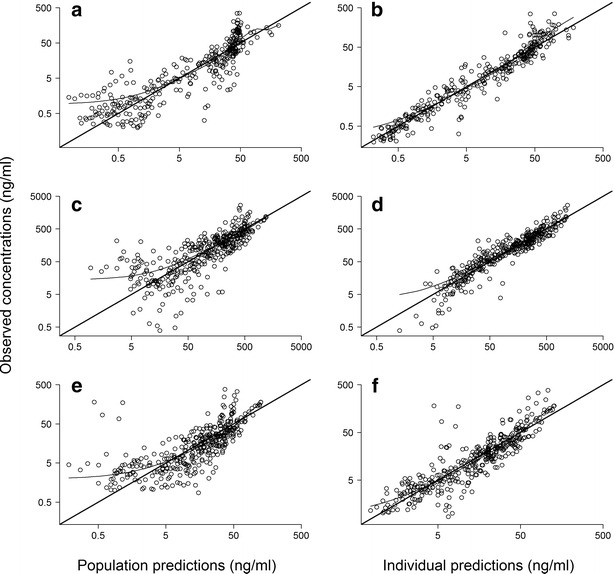
Goodness-of-fit plots for the final population pharmacokinetic model of morphine and its metabolites showing observed versus population (left column) and individual predicted concentrations (right column) for morphine (a and b), M3G (c and d), and M6G (e and f). Concentrations are shown on logarithmic scales

Fig. 5.

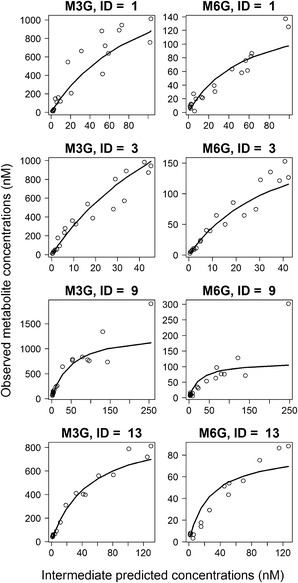
Plot of M3G (left column) and M6G (right column) observed plasma concentrations against predicted concentrations at the intermediate compartment in four representative subjects showing Emax relationship. The solid lines are metabolite individual predictions

NPDE diagnostics are shown in Fig. 6. Distributions of morphine, M3G, and M6G NPDEs were almost symmetrical (Fig. 6, left column), suggesting that the features of the observed data can be adequately replicated using the model and confirming good estimation of the variability parameters. This finding is confirmed by average NPDE that is not significantly different from zero and variance that is not significantly different from one. Variability of M6G concentrations was slightly underestimated by our model, as indicated by variance smaller than one. Morphine, M3G, and M6G NPDEs were randomly distributed around the zero line when plotted against time (Fig. 6, middle column) and population predictions (Fig. 6, right column), indicating lack of any patterns in the model fit across the plasma concentration or time ranges in this study.

Fig. 6.

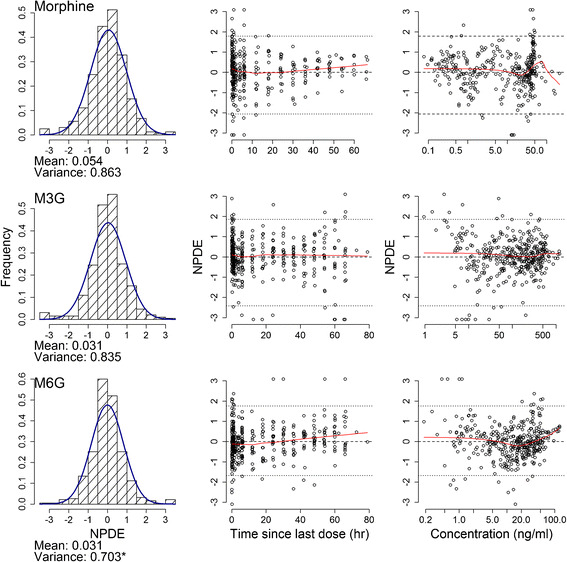
The final population pharmacokinetic model normalized prediction distribution error (NPDE) results for morphine (upper row), M3G (middle row), and M6G (lower row). The histograms show the NPDE distribution, and the solid lines represent the normal distribution. The mean and variance of the NPDE are shown below each histogram. Asterisk indicates significant difference of the mean from 0 and the variance from 1 at the p < 0.05 level, using Student’s t test for mean and Fisher test for variance. The scatter plots show the distribution of NPDE versus time since last dose and population predicted concentrations (on logarithmic scale). The dotted lines represent the NPDE 5th and 95th percentiles. Zero line (dashed) and LOWESS smoother (solid) are shown

The effect of developmental changes (i.e., weight increase by aging) on morphine exposure as well as the effect of renal function (i.e., estimated glomerular filtration rate) on glucuronide exposure is shown in Fig. 7. Morphine median AUC_0–24 h increases from 331 ng h/mL in a 1-month-old child to 353 ng h/mL in a 6-month-old child and to 408 ng h/mL in a 2-year-old child. The pairwise comparison failed to detect a significant difference (p > 0.05) between the 1- and the 6-month groups but revealed a significant difference (p < 0.05) upon comparing with the 2-year-old group. Compared with a 6-month-old child having a normal kidney function (GFR of 70 mL/min/1.73 m²), the median metabolite AUC_0–24 h of a patient suffering severe kidney failure (GFR of 20 mL/min/m²) was ∼2.7-fold higher. The pairwise comparison detected significant differences between the different GFR groups.

Fig. 7.

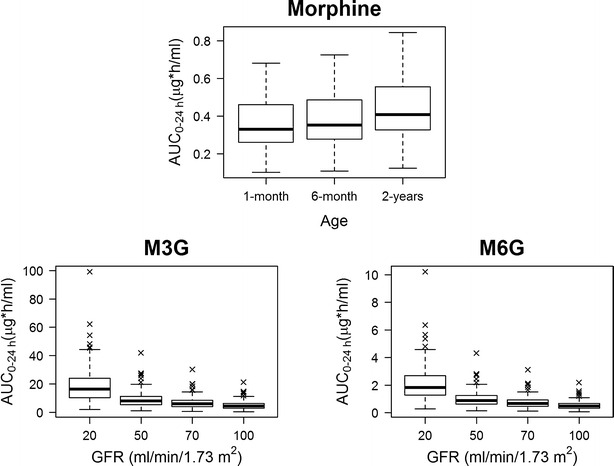
Box plot of the simulation results following the administration of 0.1 mg/kg morphine every 3 h showing morphine AUC_0–24 h in 1-month-, 6-month-, and 2-year-old children, M3G, and M6G AUC_0–24 h in patients, with glomerular filtration rates of 20, 50, 70, and 100 mL/min/1.73 m², respectively

DISCUSSION

In this study, we developed a model that efficiently characterized morphine disposition and glucuronidation in pediatric patients with heart disease. The model appeared adequate (goodness-of-fit plots in Fig. 4), robust (bootstrap statistics in Table II), reproduced the observed variability in morphine, M3G, and M6G concentrations (NPDEs frequency distribution in Fig. 6), and was unbiased over the entire time or population predictions ranges (NPDEs versus time and concentration in Fig. 6).

Consistent with previous pediatric studies (25,31), a two-compartment model corresponding to plasma and tissue distribution was adequate to describe morphine PK. The large between-subject variability in morphine PK parameters (Table II) supports a previous suggestion that morphine disposition is extremely variable, especially in children with complex pathophysiology (7). The relatively high residual variability of morphine and its metabolite concentrations (Table II) has been previously documented (24).

Morphine clearance ontogeny in children involves maturation of the glucuronidation enzymes within 6 months of birth (4–6). In this study, age was not identified as a covariate on clearance. This may be attributed to the strong co-linearity between postnatal age and body weight (r ² = 0.93). Consequently, a single function based on body weight was adequate for describing the combined effects of size and maturation of hepatic enzymes on morphine glucuronidation. This finding is in accordance with a previous study (25).

Our estimated clearance on per kilogram basis (37.8 mL/min/kg) was in agreement with the values reported by Olkkola et al. (32) in >1-month-old infants (25.8–75.6 mL/min/kg), Lynn et al. (33) in 1-month- to 1-year-old infants (25.3–48.9 mL/min/kg), and Choonara et al. (5) in >1-year-old children (25 mL/min/kg). However, the model over-predicts morphine clearance in neonates (5–9 mL/min/kg (5,32,33)), which is understandable since our study involved only one neonate younger than 1-week-old and two neonates younger than 1-month-old. Divergence of neonatal clearance values from older children was previously reported (5,32,33).

It has been suggested that clearance rates of opioids are affected by hepatic blood flow which follows changes in cardiac output (34). Therefore, we hypothesized that cardiac anomalies associated with reduced systemic flow (and, therefore, a reduction in hepatic blood flow) after surgery would reduce morphine clearance in this study. The finding that our estimated clearance was in the range of values reported in children without heart problems (5,32,33) suggests that morphine clearance may be determined by hepatic intrinsic clearance rather than by hepatic blood flow. However, this conclusion should be interpreted with caution since direct measurement of cardiac output was not available, and liver enzyme levels failed to predict morphine clearance in this study.

Dagan and colleagues (8) reported significantly lower clearance in children undergoing the Fontan procedure compared to those undergoing procedures for correction of TOF (0.86 versus 1.39 L/h/kg). Additionally, children who needed inotropic support at high doses had significantly lower clearance rates (0.73 versus 1.5 L/h/kg). Accordingly, it was concluded that morphine clearance correlates with cardiovascular status and the need for inotropic support. In this study, none of our children underwent single-ventricle (e.g. Fontan) repair or required high doses of inotropic support, which may explain failure to identify cardiovascular status as a predictor of morphine clearance and the dissimilarity between our estimated clearance value (2.3 L/h/kg) with that reported by Dagan et al. in post-cardiac surgery pediatric patients (1.5 L/h/kg).

The morphine steady-state volume of distribution that we observed in this study, 7.3 L/kg, is closer to values reported in cancer patients (35) and patients receiving mechanical ventilation (6,18), 5 L/kg, than to the value reported in post-cardiac surgery patients (8), 13 L/kg. Similar to clearance, distribution volume is not influenced by cardiovascular status. The lack of volume dependence on age is consistent with the finding by a previous meta-analysis of morphine PK in children (7).

It is well established from literature data that clearance of M3G and M6G is influenced by renal function in diverse populations (36–38). In this study, we were able to detect a correlation between GFR and both metabolite formation time delay and maximum concentrations (Fig. 7).

Effective pain relief depends on factors that affect subjects’ perception of pain, with its two components, the sensory and emotional experiences (39). Subjects’ perceptions of pain likely vary according to age, physical status, type of surgery, duration of surgery, and behavioral, emotional, and cultural factors. Therefore, it is not surprising to see wide ranges of morphine minimum effective concentrations reported in the literature (40–42). From a pharmacokinetic perspective, it seems that 1–6-month-old children need higher doses per kilogram to achieve a morphine exposure comparable to that in older children (Fig. 7, upper row). This finding is in agreement with clinical observations that morphine dosing requirement correlated negatively with age in post-operative infants older than 1 month (43). Due to immaturity of the glucuronidation enzymes in newborns (2,3), the influence of age on morphine exposure as predicted by our model may not be valid for this age group.

Since M6G, like morphine, binds with high affinity to μ-opioid receptors (13,14), resulting in analgesic effects, and M3G, although still controversial, is thought to antagonize morphine analgesic effects (11,12), adjusting the morphine treatment period to avoid potential morphine/metabolite interactions in children with renal problems is necessary. Our simulation results (Fig. 7, lower row) indicate that in patients with renal insufficiency, it will be beneficial to switch to a structurally dissimilar opioid such as fentanyl or hydromorphone.

CONCLUSIONS

In conclusion, we developed a population PK model for morphine and its metabolites, M3G and M6G, in pediatric patients following cardiac surgery. Clearance of morphine in children with congenital heart disease is comparable to that reported in children without cardiac abnormalities of similar age. One- to 6-month-old children need higher doses of morphine per kilogram of body weight to achieve a morphine area under concentration–time curve comparable to that in older children. Pediatric patients with renal dysfunction receiving morphine therapy are at increased risk of developing opioid toxicity due to accumulation of morphine metabolites.