Josephin Domain Structural Conformations Explored by Metadynamics in Essential Coordinates

Abstract

The Josephin Domain (JD), i.e. the N-terminal domain of Ataxin 3 (At3) protein, is an interesting example of competition between physiological function and aggregation risk. In fact, the fibrillogenesis of Ataxin 3, responsible for the spinocerebbellar ataxia 3, is strictly related to the JD thermodynamic stability. Whereas recent NMR studies have demonstrated that different JD conformations exist, the likelihood of JD achievable conformational states in solution is still an open issue. Marked differences in the available NMR models are located in the hairpin region, supporting the idea that JD has a flexible hairpin in dynamic equilibrium between open and closed states. In this work we have carried out an investigation on the JD conformational arrangement by means of both classical molecular dynamics (MD) and Metadynamics employing essential coordinates as collective variables. We provide a representation of the free energy landscape characterizing the transition pathway from a JD open-like structure to a closed-like conformation. Findings of our in silico study strongly point to the closed-like conformation as the most likely for a Josephin Domain in water.

Author Summary

Proteins are fascinating molecular machines capable of organizing themselves into well-defined hierarchical structures through a huge number of conformational changes to accomplish a wide range of cellular functions. Protein conformational changes may be characterized by transitions from a low-energy conformation to another. Computer simulations and in particular molecular modelling may be able to predict protein transition dynamics and kinetics, thus playing a key role in describing protein tendencies towards specific conformational rearrangements. Approaching this problem from an energetic point of view is of great importance especially in case of amyloidogenic proteins, given the intimate interconnection between the functional energy landscape and aggregation risk. In this work we have employed molecular modelling techniques to shed light into conformational dynamics and kinetics of the Josephin Domain, part of the protein Ataxin 3, which is responsible for the spinocerebbellar ataxia 3, also called Machado Joseph Disease. In greater detail, we have employed enhanced sampling approaches to provide an estimation of the free energy landscape characterizing the transition pathway among several known molecular arrangements of the Josephin Domain.

Introduction

Proteins are fascinating molecular machines capable of organizing themselves into well-defined hierarchical structures through a huge number of conformational changes, in order to accomplish a wide range of cellular physiological functions. From an energy landscape point of view, protein conformational changes may be characterized by transitions from a low-energy conformation to another. In this connection, computational approaches have widely demonstrated their utility by providing important insights into the protein conformational features [1–5]. Molecular Dynamics simulations, and in particular enhanced sampling techniques, are able not only to predict protein transition pathways, but also to quantify the free-energy landscape along selected reaction coordinates, thus playing a key role in describing protein tendencies towards specific conformational rearrangements. Approaching this problem from an energetic point of view is of great importance especially in case of amyloidogenic proteins, given the intimate interconnection between the functional energy landscape and aggregation risk [6].

The Josephin Domain (JD), i.e. the N-terminal domain of Ataxin 3 (At3) protein, is an interesting example of competition between physiological function and aggregation risk [6,7]. In fact, the fibrillogenesis of Ataxin 3 is responsible for the spinocerebbellar ataxia 3, also called Machado Joseph Disease (MJD). Structurally, At3 is composed of a structured globular N-terminal region (i.e. the JD, residues Met1-Arg182 in the human protein), combined with a more flexible C-terminal tail that contains the polyQ tract and the Ubiquitin Interacting Motifs (UIM) [8,9].

The expansion of polyglutamine (polyQ) tract in Ataxin 3 (so-called expanded At3) is considered a cause for protein misfolding and aggregation, but the underlying mechanism remains to be elucidated.

Although it is known that the polyQ tract is necessary for kinetic instigation of an aggregation mechanism [10–14], several experimental studies support the hypothesis that JD structural stability could play a major role in determining the aggregation features and toxicity of polyQ proteins [7,15–21].

In this regard, experimental evidences have suggested a two-stage pathway for At3 fibrillogenesis: the first, JD-mediated and the second, polyQ-dependent [19,22,23]. Fibrillar aggregates of both not-expanded At3 and isolated JD have shown markedly similar morphological and mechanical properties, suggesting a leading role for the JD in the mechanism of fiber formation [17]. Moreover, inhibition of JD self-association by a small heat-shock protein significantly slows down expanded At3 aggregation [24]. For these reasons, the role of JD has been the subject of a robust debate in the past [6,7,18–21,25,26].

To date, several JD models solved by NMR are available in the literature (PDB entry 2JRI [27], 1YZB [28], 2AGA [29] and 2DOS [30]—UNIPROTID: P54252). Differences in the available models are located in the hairpin region (region α2-α3, residues Val31-Leu62). In particular, the 1YZB and 2JRI models are characterized by a “half-open” and “open” L-shape hairpin conformation, respectively. On the other hand, the “closed” 2AGA and “half-closed” 2DOS models exhibit the hairpin region packed against the rest of the globular structure [30]. Whereas all the above-mentioned NMR data have demonstrated the existence of several different available conformations for the JD, issues concerning i) the likelihood of JD achievable conformational states in solution, and ii) the role played by environmental conditions (such as the solution’s pH) and interacting physiological partners (such as ubiquitin) in JD conformational arrangement are still unresolved. Specifically, results from a recent characterization of the JD free energy landscape using MD simulations suggested the open-like model as the most representative of the JD structure in solution [31]. Nevertheless, other previous experimental and computational studies strongly support the idea that JD has a highly flexible extended hairpin in dynamic equilibrium between open and closed states [1,30]. In a very recent in silico study, the early stage of the JD-JD dimerization mechanism [1] has been investigated by MD and indicates that the JD-JD binding might play a role in determining the kinetics of hairpin opening/closure. However, the previous computational investigation is limited to a classical MD approach with a relatively short simulation timescale [1].

In principle, to prove the JD open-like or the JD closed-like configuration as favored, it would be necessary to show not only that i) there is more sampling in one state during a classical MD, but also that ii) several transitions between states are sampled during the simulation. Hence, an accurate evaluation of the JD conformational changes requires a longer simulation time-scale and robust sampling methods. In this regard, enhanced sampling methods represent a powerful tool to improve the sampling efficiency of classical MD [32–40], including those that artificially add an external driving force to guide the protein from one structure to another [38,41]. Moreover, reducing the dimensionality of the trajectory obtained from MD simulations can help identify the dominant modes in the motion of the molecule [38,41].

Motivated by the still open debate regarding the most representative JD structural arrangement [1,30,31,42,43], we have carried out an investigation on JD conformational changes using both unbiased MD and Metadynamics guided by essential coordinates. In this work, we provide an estimation of the free energy landscape characterizing the transition pathway from a JD open-like to a closed-like structure (which is henceforth called the folding pathway). The findings of our in silico study strongly suggest the closed conformation as the most likely for a Josephin Domain in water.

Materials and Methods

Classical Molecular Dynamics and Principal Component Analysis

The 1YZB model [28,42] of JD was selected as the starting point for the present work. The rationale for this choice is in the experimental work of Nicastro et al. [42] indicating a satisfactory validation of the 1YZB model through the application of an arsenal of tools for checking the quality, accuracy and mutual consistency of the structures available.

The 1YZB model was solvated in a dodecahedron box where the minimum distance between the protein and the edge of the box was 1 nm, resulting in a molecular system of about 50,000 interacting particles. The net charge of the system was neutralized by the addition of Cl⁻ and Na⁺ ions. AMBER99-ILDN force-field [44–46] and water TIP3P model [47] were chosen to describe the system’s topology. Particle-Mesh Ewald method with a short-range cut off of 1.2 nm was applied to treat electrostatics. A cut-off of 1.2 nm was also applied to Lennard-Jones interactions.

The system was minimized by the steepest descent energy minimization algorithm (1000 steps). Then, in order to increase the statistics of MD data, five replicas, differing in initial atom velocities, were created from the minimized system. In particular, for each replica, a random velocity taken from a Maxwell-Boltzmann distribution at 310 K was assigned to every atom of the system (i.e. JD, water and ions). A position-restrained and production MD simulations were carried out as described in the following. Two subsequent MD simulations (500 ps, and 100 ps, respectively) were run in the NPT ensemble, applying position restraints of 1000, and 100 kJ/mol/nm², respectively, to the JD Cα atoms. System temperature was set at 310 K by using the v-rescale [48] thermostat with a coupling time step of 0.1 ps. Moreover, in NPT simulations a Berendsen barostat [49] was also employed with a reference pressure of 1 atm and a coupling time step of 1.0 ps. A third position restrained dynamics simulation (100 ps) was carried out by applying a force constant of 10 kJ/mol/nm²in the NVT ensemble at 310 K. Finally, an unrestrained production MD of 500 ns was run in the NVT ensemble at 310 K, as done in several previous Molecular Dynamics studies [50–52]. GROMACS 4.6 package was employed for all MD simulations and data analysis [53]. Ensemble data taken from all production MD trajectories of the above-mentioned five replicas (each simulated for 500 ns) were used for JD conformational analysis. The Visual Molecular Dynamics (VMD) package [54] provided the visual inspection of the simulated systems. Dedicated GROMACS tools were used for quantitative analyses in terms of Root-Mean-Square Deviation (RMSD) and Root-Mean-Square Fluctuation (RMSF). The secondary structure of the protein has been calculated by the STRIDE software [55] on several snapshots along the simulation time.

The identification of JD conformational transitions from open to closed JD conformations has been carried out by employing quantities which have already been demonstrated to be meaningful in describing the JD transition pathway: the radius of gyration (RG) and the hairpin angle [1,31].

Given that the NMR models (1YZB, 2JRI, 2DOS, and 2AGA) considered in this work present a different number of residues, the RG has been calculated by considering all the residues in common among the above mentioned PDB models. In detail, the residue range 1Met-171Asp (according to 1YZB numbering) has been chosen.

The hairpin angle was calculated from the centers of mass of the Cα atoms from three distinct JD regions: globular subdomain (residues 111–113, 122–125 and 162–165), hinge (residues 32–35) and loop (residues 45–48 and 58–61) [31] (Section 3 in S1 Text).

Principal Component Analysis (PCA) was applied to classical MD trajectories. PCA is an established method which allows to elucidate large-scale and low-frequency modes, respectively, yielding collective motions directly related to a specific molecular event [56]. In detail, after the alignment of the JD Cα Cartesian coordinates, the covariance matrix was calculated and diagonalized (Section 2 in S1 Text).

Metadynamics

The free energy landscape representing the JD folding pathway was investigated by means of Metadynamics [58,59], a powerful technique for enhancing the sampling in MD simulations and reconstructing the free-energy surface as a function of few selected collective variables (CVs). The first eigenvector derived from the PCA was used as CV for a well-tempered Metadynamics simulation of 500 ns starting from the open-like 1YZB model [16]. The JD model was prepared for Metadynamics by applying system minimization and position restraint dynamics, as described above for the classical MD.

To perform Metadynamics simulations, a Gaussian width of 0.1 was used. Along the simulation, the initially prescribed Gaussian deposition rate value of 0.2 kJ/mol·ps was used and it gradually decreased on the basis of an adaptive scheme, with a bias factor of 20. The setting of Gaussian width and deposition rate was done on the basis of a well-established scheme [37,40]. In particular, the Gaussian width value was of the same order of magnitude as the standard deviation of the collective variable, calculated during unbiased simulations (production MD). The authors have also verified that the maximum force introduced by a single Gaussian distribution is smaller than the typical derivative of the free energy.

The estimation of the free energy profile was performed by employing the reweighted-histogram procedure [60,61], taking into account for the following collective variables: the projection along the first PCA eigenvector, the JD’s RG, the hairpin angle and the alphaRMSD variable. More specific information about the definition of the CVs, the convergence of the Metadynamics simulations and the free energy reconstruction is reported in Section 3 in S1 Text. GROMACS 4.6 package patched with PLUMED was employed for metadynamics simulations and data analysis [57].

Results

Classical Molecular Dynamics and Mode Analysis

As stated above, five independent replicas of a single JD in explicitly modeled water and ions were simulated for 500 ns. Structural conformational properties and stability were initially checked by monitoring the time evolution of the RMSD and secondary structure (Section 1 in S1 Text). The data generated indicated that a reasonable stability of the above-mentioned quantities has been reached in all cases in the last 100 ns of the production run of the MD simulations. Moreover, the JD secondary structure showed to be highly conserved throughout the whole simulation time (Section 1 in S1 Text).

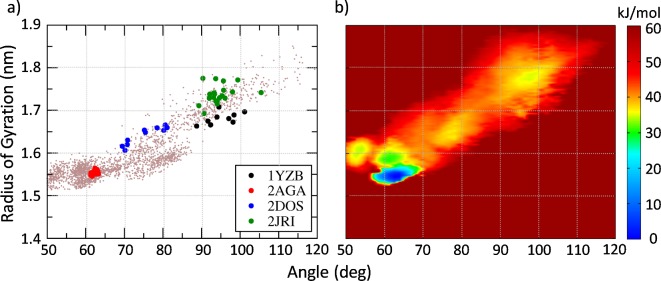
The time evolution of the RG calculated over the classical MD trajectories (Fig 1A) reveals the JD transition for all replicas, from a half-open (starting configuration 1YZB) to a closed or half-closed conformation, characterized by RG lower than 1.6 nm (Fig 1A) and a hairpin angle lower than 80° (Fig 1B). Several intermediate half-open and half-closed conformations are explored during the MD simulation (Fig 1C). Moreover, no transition from the reached JD closed-like to the open-like structure has been detected during the simulated time.

Fig 1. Time evolution of the JD radius of gyration (a) and hairpin angle (b) throughout the MD trajectory of each replica.

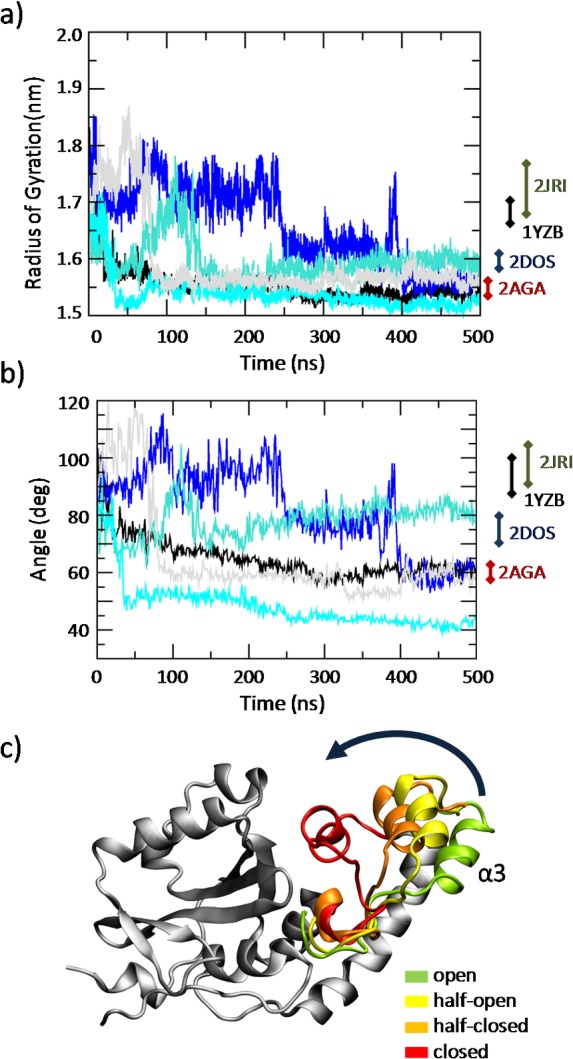
(c) Visual inspection of the JD conformations taken from the classical MD simulations. The MD trajectories reveal a JD transition from an open state to a closed state, through an half-open and half-closed state. For each snapshot the α3 region (Asp57-Leu62) is highlighted with a different color: green (open), yellow (half-open), orange (half-closed) and red (closed).

By analyzing the same data in the form of a distribution plot (Fig 2), it is possible to observe that sampled structures in the stability region of the simulation (400–500 ns) are far from open like JD arrangement.

Fig 2. Distribution of JD radius of gyration (a) and hairpin angle (b) calculated for the entire MD trajectories (black dashed curve) and at the stability (from 400 to 500 ns, red line).

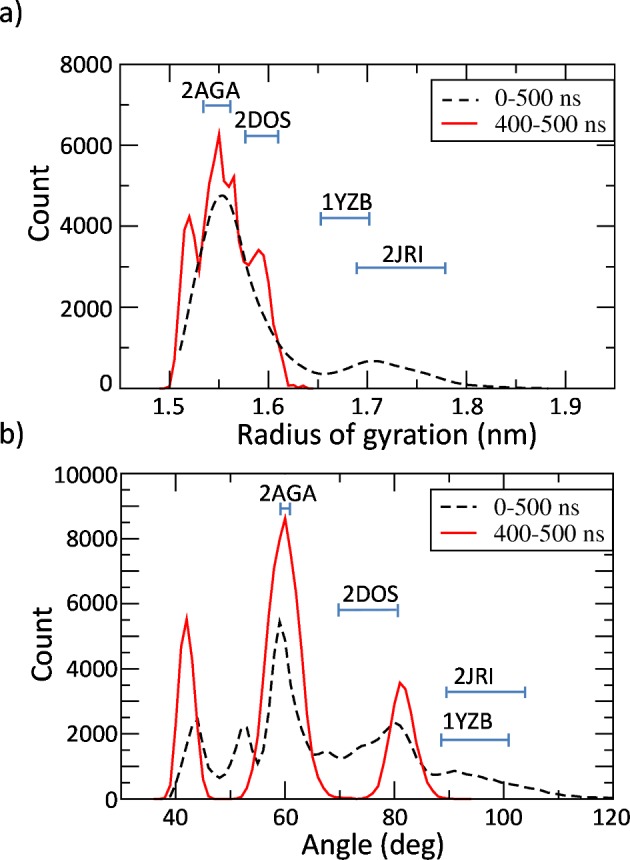
MD trajectories of the five replicas are used as ensemble data. Cyan bars indicate the value range of RG (a) and hairpin angle (b) calculated by NMR available data of 2JRI, 1YZB, 2DOS, and 2AGA.

Secondly, it is worth mentioning the different distribution shape when considering the whole trajectory (0–500 ns, black dashed line in Fig 2) and the trajectory in the stability region (400–500 ns, red line in Fig 2). Specifically, a curve comparison of both the RG and hairpin angle distribution indicates how intermediate states have a tendency to converge toward closed like arrangements. The importance of using both the RG and hairpin angle to analyze the JD arrangement is demonstrated by looking at the NMR range values labeled in Fig 2. Namely, whereas the RG helps in discerning between half-open (1YZB) and open (2JRI) JD arrangement (Fig 2A) the hairpin angle perfectly distinguish between closed (2AGA) and half-closed (2DOS) JD (Fig 2B).

To reduce the high-dimensionality of the MD trajectory and to identify the dominant molecular phenomena related to the hairpin closure, PCA was applied. After the alignment of the JD Cα atoms, the MD trajectory was filtered to show only the motion along the first eigenvector, calculated by covariance matrix diagonalization. More information on PCA and the eigenvector values is reported in Section 2 in S1 Text. The JD Root Mean Square Fluctuation (RMSF) calculated over the filtered trajectory (Fig 3) shows that, as expected, the first PCA eigenvector effectively captures the hairpin motion (RMSF_hairpin>0.5 nm).

Fig 3. Root Mean Square Fluctuation plot.

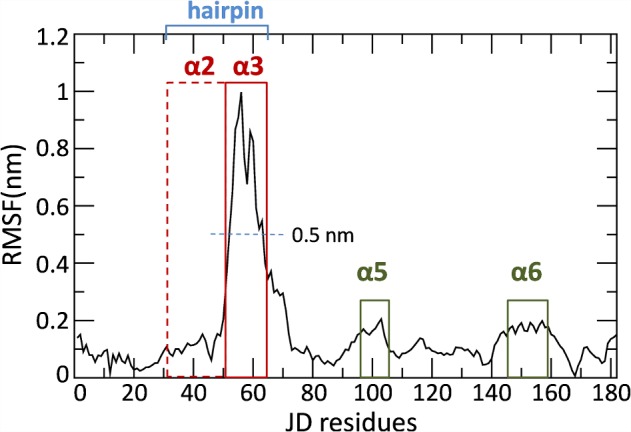
Each point represents the mean fluctuation for each JD residue calculated over the whole MD trajectory (500 ns and five replicas taken together) filtered on the first PCA eigenvector. The hairpin region (Val31-Leu62), composed by helix α2 (dashed red line) and α3 (continuous red line) is highlighted in blue. Secondary structure α6 (Asp145-Glu158) is highlighted in dark green.

Metadynamics

The first eigenvector derived from the PCA was used as collective variable (CV) for a well-tempered Metadynamics simulation. Analyzing the free energy profiles reported in Fig 4A as a function of the RG, two energy wells of 36 kJ/mol and 4 kJ/mol, located at RG values of 1.55 nm and 1.78 nm, respectively, can be identified. This result is also confirmed by reweighting the free energy profile as function of the hairpin angle (Fig 4B). In this case, the deepest free energy minimum (36 kJ/mol) is found to be located at a value of the hairpin angle equal to 63°. A second minimum (5 kJ/mol) is found to be located at a value of the hairpin angle equal to 100°.

Fig 4. Free energy profiles of the JD transition pathway as function of the (a) radius of gyration (RG) and (b) hairpin angle.

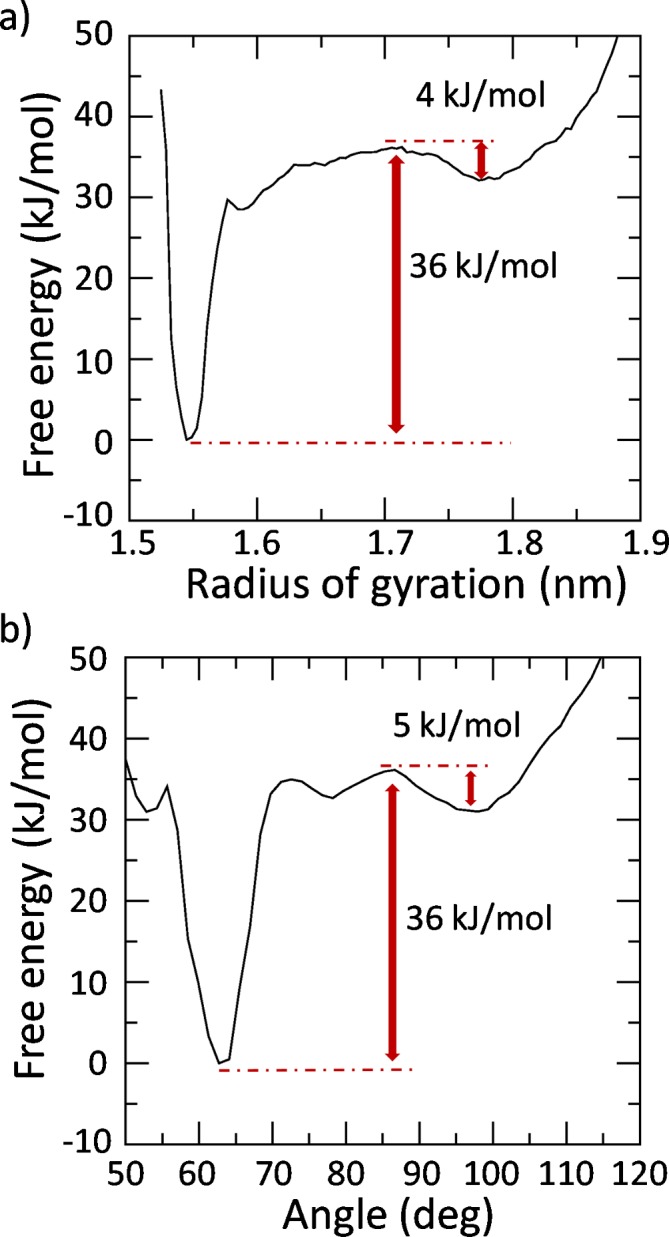
The depth of the energy well corresponding to the absolute free energy minimum is highlighted in red. The absolute free energy well is set as zero.

As expected, the RG and hairpin angle values corresponding to the free energy wells (Fig 4A) are in agreement with the distribution peaks obtained from the unbiased MD simulations in the stability region (400–500 ns) shown in Fig 2. This finding confirms the reliability of our Metadynamics results given that the free energy minima are expected to identify the most energetically favorable configuration.

An overall picture of the JD free energy landscape is provided in Fig 5B, showing the 2D color map of the free energy profile as a function of the RG and hairpin angle. Again, the free energy minima are expected to match the most energetically favorable JD configurations. Hence, it is interesting to compare the free energy map with the JD configurations sampled by classical MD (Fig 5A). Fig 5A also provides the snapshots derived from the JD models available in the literature. Interestingly, 2AGA, 2DOS and 2JRI models lie in regions regularly sampled by classical MD, and characterized by absolute or relative free energy minima. The most sampled configurations by classical MD, corresponding in term of RG and hairpin angle to the 2AGA model, is also the deepest energy minimum in the free energy landscape. Similar characteristics between metadynamics lowest energy state and the 2AGA model are also highlighted by contact maps reported in Section 2 in S1 Text. On the contrary, values of the RG and hairpin angle corresponding to the 1YZB, i.e., starting structure of our simulations, are merely sampled by classical MD and far from the absolute energy minimum in Metadynamics.

Fig 5. (a) Each point (colored in pink) represents a snapshot identified by the radius of gyration (y axis) and the hairpin angle (x axis) for the entire MD conformational ensemble sampled by classical MD (5 replicas of 500 ns). The hairpin angle and radius of gyration of all NMR snapshots derived from the JD models available in literature are colored in red (2AGA), blue (2DOS), black (1YZB) and green (2JRI). (b) 2D color map of the JD free energy landscape, calculated by the reweighting histogram approach on the Metadynamics outcome.

The free energy values are represented as function hairpin angle and JD radius of gyration. The absolute free energy well is set as zero.

Discussion

The characterization of the free energy landscape in a protein folding pathway represents a significant contribution to both experimental and theoretical approaches, given the intimate interconnection between the functional energy landscape and aggregation risk [6].

The JD folding pathway is an issue still debated in the literature [30,31,42] since a decisive proof of the most likely JD conformation has not been provided yet. Several JD models, solved by NMR, are available in the literature: open (2JRI) [27], half-open (1YZB [28], closed (2AGA) [29] and half-closed (2DOS) [30]. The above mentioned models have been questioned and debated in the recent literature on both computational and experimental studies. In agreement with previous research in this area [30] we have recently observed the metastable behavior of the JD, which is dynamically able to switch between an open-like and closed-like structure during the dimerization [1]. However, in order to predict the JD free energy landscape, the conformational ensemble provided by the classical MD simulation is not adequate. In particular, data from MD with a timescale of hundreds of ns show that the JD closed-like state is achievable starting from an open-like state whereas a transition from a completely closed-like to an open-like state has never be detected (Fig 1 and Section 1 in S1 Text). The classical MD simulation sampling is in this case insufficient, because when the system is trapped in the energy minimum characterized by the closed-like structure, thermal fluctuations are not enough to overcome the energy barrier (around 36 kJ/mol) needed to switch to an open-like configuration. A classical MD simulation might never be able to get out of such a deep energy minimum. To overcome this limitation, inherent to the classic MD, Metadynamics can be used to sample large-scale protein transitions as demonstrated by some relevant and pioneering papers in the field [62–64].

Our work brings together the efficient sampling of Metadynamics with a MD-PCA-based dimensionality reduction method. In particular, PCA was used to elucidate the transition pathway between the JD open-like and closed-like models, and Metadynamics was performed to estimate the corresponding free-energy landscape. Nevertheless, this computational approach was already successfully applied earlier [38,65–69], thus confirming its promise as a successful strategy for investigating conformational changes in complex biomacromolecules.

A limitation of the presented approach is, in fact, that preliminary information regarding the molecular transition is needed in order to calculate the essential coordinates: the transition from a JD open-like to a closed-like conformation allowed us to obtain the CV to guide the Metadynamics method.

Our findings confirm that the JD hairpin region, which protrudes out into the solvent, can be responsible for an extensive conformational change, switching between the open-like conformation and the closed-like one. As suggested in previous works [1,30], the hairpin mode of motion mainly consists of movement of region α3 (Asp57-Leu62) toward α6 (Asp145-Glu158) (Figs 1C and 3).

Interestingly, in our simulations, when the JD is alone in water environment the most stable configuration is characterized by the hairpin packed against the globular core, in agreement with models 2AGA [29] (Figs 4 and 5). However, an energy well of about -5 kJ/mol has been also detected corresponding to the open conformation, in agreement with the 2JRI [27] model. In general, such free energy minima should predict the most favorable conformational state. In fact, the RG values corresponding to the free energy minima are consistent with the peaks of the RG distribution of the unbiased simulation at equilibrium (Figs 1, 4 and 5), indicating the reliability of the presented approach in describing the JD free energy landscape. Surprisingly the JD half-open structure, with the RG and hairpin angle mainly corresponding to the 1YZB is the less sampled structure even during classical MD simulations.

In this connection, it is important to clarify that our work is not oriented to evaluate the “quality” of produced NMR which has already been checked with proper methodologies [42]. Instead, a first novel aspect of our work is that the employed approach has demonstrated to explore the state space by granting several transitions among closed and open JD conformations.

Data reported in recent literature [31] indicated the JD open structure (particularly referring to the 1YZB model) as the most likely JD conformation in water. Moreover, it has been emphasized how the 2AGA ensemble data were far away from the calculated free energy minima [31]. However, it is worth mentioning that, all the previous computational works [1,31,43] did not show transitions between open and closed JD and viceversa. In our opinion, such transitions are required to claim that a specific protein conformational state is characterized by lower free energy minima than another one. In fact, in the partial section of the free energy profile corresponding to the JD open-like structure, our results are in agreement with the above mentioned recent work [31]. However, the representation of the whole free energy profile describing both open and closed structures demonstrates the closed arrangement as the most likely for a Josephin Domain in water environment.

Nonetheless, there may be conditions under which the open-like state is stabilized (e.g. in the context of the full-length protein or in the presence of a physiological partner). For example, we have recently shown how the JD conformational state might be affected by the presence of another interacting JD [1] as well as by an inorganic surface [43]. In addition, as already suggested [30], the JD free energy landscape could be influenced by other environmental conditions, such as temperature and pH.

Further investigations are planned and will help in clarifying the influence of JD functional partners and environmental factors affecting the JD conformational arrangement. This information may be relevant not only to better understand the physiological function of the Josephin Domain, but also to provide insight into molecular phenomena characterizing the pathological nature of spinocerebellar ataxia 3.

Supporting Information

S1 Text. The file contains: data analysis on Classical Molecular Dynamics trajectories and Metadynamics Lowest Energy States (Section 1); details on Principal Component Analysis (Section 2); procedures and validation checks on Metadynamics simulations (Section 3).

(PDF)

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work was supported by a grant from the Swiss National Supercomputing Centre (CSCS) under project ID S530.The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.