Separating Fractal and Oscillatory Components in the Power Spectrum of Neurophysiological Signal

Abstract

Neurophysiological field-potential signals consist of both arrhythmic and rhythmic patterns indicative of the fractal and oscillatory dynamics arising from likely distinct mechanisms. Here, we present a new method, namely the Irregular-Resampling Auto-Spectral Analysis (IRASA), to separate fractal and oscillatory components in the power spectrum of neurophysiological signal according to their distinct temporal and spectral characteristics. In this method, we irregularly resampled the neural signal by a set of non-integer factors, and statistically summarized the auto-power spectra of the resampled signals to separate the fractal component from the oscillatory component in the frequency domain. We tested this method on simulated data and demonstrated that IRASA could robustly separate the fractal component from the oscillatory component. In addition, applications of IRASA to macaque electrocorticography (ECoG) and human magnetoencephalography (MEG) data revealed a greater power-law exponent of fractal dynamics during sleep compared to wakefulness. The temporal fluctuation in the broadband power of the fractal component revealed characteristic dynamics within and across the eyes-closed, eyes-open and sleep states. These results demonstrate the efficacy and potential applications of this method in analyzing electrophysiological signatures of large-scale neural circuit activity. We expect that the proposed method or its future variations would potentially allow for more specific characterization of the differential contributions of oscillatory and fractal dynamics to distributed neural processes underlying various brain functions.

1. INTRODUCTION

RICH temporal dynamics of neural activity is commonly captured by electrophysiological recordings, e.g. local field potential (LFP), electrocorticogram (ECoG), electroencephalography (EEG) and magnetoencephalography (MEG) (Nunez and Srinivasan, 2006). Such neural signals exhibit a variable mixture of rhythmic and arrhythmic patterns (Buzsáki et al., 2012). The former arises from oscillatory network activity with a characteristic time scale (Buzsáki and Draguhn, 2004), whereas the latter is not confined to any specific scale and reflects the so-called fractal (or scale-free) dynamics (He et al., 2010). When these signals are transformed to corresponding power spectra, the oscillatory component results in multiple discrete peaks at specific frequencies, and the fractal component manifests itself as a descending straight line on the log-log plot suggesting a power-law relationship (Miller et al., 2009).

Oscillatory and fractal activities are likely generated through different mechanisms (Buzsáki and Draguhn, 2004; He et al. 2010) and report on distinct features of large-scale neural networks (Bullmore and Sporns, 2009; Engel et al., 2013; Siegel et al., 2012). In particular, neuronal oscillations have been of long-standing interest to neurophysiologists, and in practice are extracted by applying band-pass filtering to neural signals. However, the resulting band-limited signals, although appearing oscillatory, can result from filtering even in the absence of any biological oscillator, and thus may sometimes reflect artificially extracted fractions of the brain’s arrhythmic activity (He, 2014).

Analysis of fractal dynamics has also attracted growing interest with the current emphasis directed upon its frequency scaling property (Ciuciu et al., 2012; El Boustani et al., 2009; Fransson et al., 2013; Freeman, 2007; He et al., 2010; Manning et al. 2009). To characterize this property, power spectral density (PSD) of neural signals is often fitted by a power-law function, or equivalently a linear function in double-logarithmic coordinates, where the slope provides an estimate of the underlying power-law (or frequency-scaling) exponent (Manning et al., 2009; Miller et al., 2009). The precision of such estimation, however, is compromised in the presence of prominent oscillations that deviate the PSD from a power-law distribution (He et al., 2010; Miller et al., 2009).

Therefore, it is desirable to separate fractal and oscillatory components in order to analyze their individual characteristics without being concerned about their mutual interference. Toward this end, a method known as the coarse graining spectral analysis (CGSA) has been developed to extract and analyze the fractal dynamics (Yamamoto and Hughson, 1991, 1993) of human ECoG signals (He et al., 2010). Central to CGSA is the so-called self-affinity property of any fractal time series: the statistical distribution remains unchanged when resampled at different time scales (Mandelbrot and Van, 1968). It follows that after resampling a time-series signal (e.g. by a factor of 2 or ½), the cross power spectrum of the original and resampled signals is expected to follow a power-law distribution if the signal is self-affine or fractal, but close to zero if the signal is simply periodic or oscillatory (Yamamoto and Hughson, 1991, 1993). For this reason, CGSA has been presumed to be able to extract the fractal component from the power spectrum of a time series that mixes both fractal and oscillatory processes (González et al., 1999; He et al., 2010; Pereda et al., 1998; Yamamoto and Hughson, 1991, 1993). Although it sounds intuitively reasonable, this presumption is questionable in theory. When a signal is composed of both fractal and oscillatory time series, the cross power spectrum of this signal and its resampled version includes non-negligible contributions from the interactions of the original (or resampled) fractal time series and the resampled (or original) oscillatory time series. Such interactions are difficult to remove based on the cross-spectral analysis, bringing into question the practical efficacy of CGSA for separating the spectral components attributed to the fractal and oscillatory dynamics.

Here we propose a new method, referred to as the Irregular-Resampling Auto-Spectral Analysis (IRASA), to separate fractal and oscillatory components in the power spectrum of neurophysiological signals. In IRASA, we resample a neural signal by multiple non-integer pairwise factors (positive numbers and their reciprocals), and then compute the geometric mean of the auto-power spectra of every pair of the resampled signals. In the resulting spectrum, the power associated with the oscillatory component is redistributed away from its original (fundamental and harmonic) frequencies by a frequency offset that varies with the resampling factor, whereas the power solely attributed to the fractal component remains the same power-law statistical distribution independent of the resampling factor. It follows that taking the median of the mean auto-power spectra of the variously resampled signals can extract the power spectrum of the fractal component, and the difference between the original power spectrum and the extracted fractal spectrum offers an approximate estimate of the power spectrum of the oscillatory component.

In what follows, we will show that IRASA is robust against the presence of the complex interaction between fractal and oscillatory components, being useful to extract the broadband activity that conforms to the scale-free dynamics. To demonstrate this point, we have evaluated IRASA with both simulation and experimental (MEG and ECoG) data. We have noted that the fractal dynamics in different behavioral states gives rise to distinct broadband features, suggesting that IRASA can be used to potentially reveal and differentiate the varying fractal signatures across brain states. Other implications and future applications are also discussed. In the online supplementary materials, we will further compare IRASA with CGSA in theory and with simulation data.

Methods and Materials

The problem addressed here is to separate the power spectra of the unknown fractal activity, f(t), and the unknown oscillatory activity, x(t), given the measured neural signal, y(t), which is assumed to consist of both f(t) and x(t) through a simple additive model without noise.

$$y(t)=f(t)+x(t)$$ (1)

To solve this problem, we have developed the IRASA method that utilizes the self-affine property of fractal time series and the frequency-specific nature of oscillatory time series (Fig. 1). For IRASA, the spectral component due to the fractal activity was first extracted from the spectrum of the mixed neural signal, and then taking the difference between the mixed spectrum and the extracted fractal spectrum served to approximate the spectral component due to the oscillatory activity. In the following, we will first introduce the temporal and spectral characteristics of fractal and oscillatory signals; then we will elaborate the theory and algorithm for IRASA; lastly we will describe the simulation and experimental data used for performance evaluation. The theoretical basis and limitations of CGSA are elaborated in the online supplementary materials in addition to (Yamamoto et al. 1991, 1993).

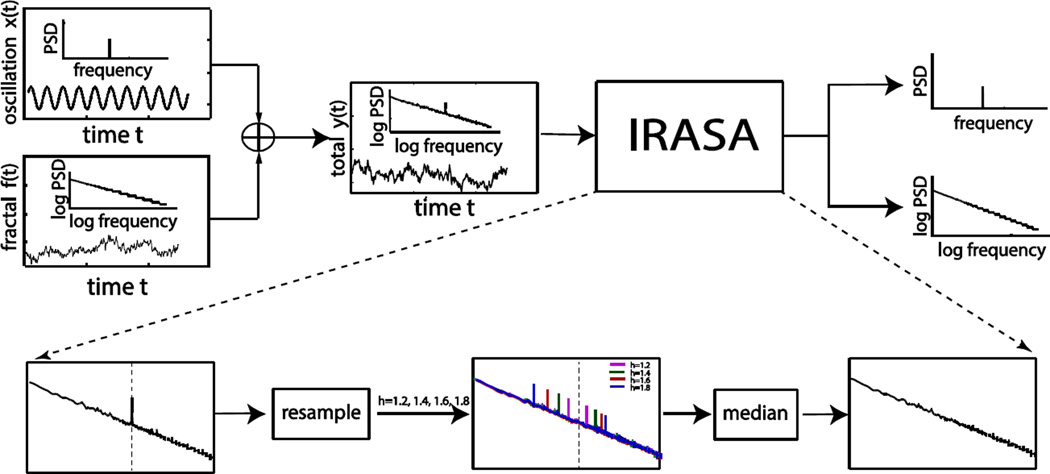
Fig. 1.

Overall schematic illustration of IRASA. The input for IRASA is a mixed time series composed of both fractal and oscillatory signals and the output is the separated power spectra of these two components.

2.1 Self-Affinity of Fractal Time Series

A fractal time series, f(t), satisfies a self-affine relationship expressed as (2).

$$f_h(t)\triangleq h^{H}f(t)$$ (2)

It indicates that when the fractal time series is resampled by a factor of h (h>0), the resampled time series, denoted as f_h(t), has the same statistical distribution as the original one scaled by a factor of h^H, where H is called the Hurst exponent (Mandelbrot and Van, 1968). Applying the Fourier transform to f(t) and f_h(t) yields F(ω)e^jα(ω) and F_h(ω)e^jα_h(ω) respectively, where F(ω) and α(ω) are the amplitude and phase at specific angular frequencies ω for f(t), and F_h(ω) and α_h(ω) are the counterparts for f_h(t). This self-affine relationship is equivalent to the frequency scaling property expressed as (3).

$$F_h(\omega )=h^{H}F(\omega )$$ (3)

It means that the amplitude spectrum of the resampled fractal time series is the same as that of the original time series scaled by a factor of h^H. Note that Eq. 3 holds true only if F(ω) follows a power-law distribution shown as a line in log-log coordinates.

2.2 Narrow-Band Nature of Oscillations

Let x(t) stand for an oscillatory time series and x_h(t) be the time series obtained by resampling x(t) by a factor of h. Let X(ω)e^jβ(ω) and X_h(ω)e^jβ_h(ω) be the Fourier representations of x(t) and x_h(t), respectively. By definition x(t) is a periodic and narrow-banded signal. The power spectra of both x(t) and its resampled version x_h(t) are non-zero only at specific frequencies and close to zero elsewhere. The “sparse” spectral distribution is the characteristic of oscillations in contrast to the fractal dynamics, which has a “continuous” broadband distribution.

2.3 Irregular-Resampling Auto-Spectral Analysis (IRASA)

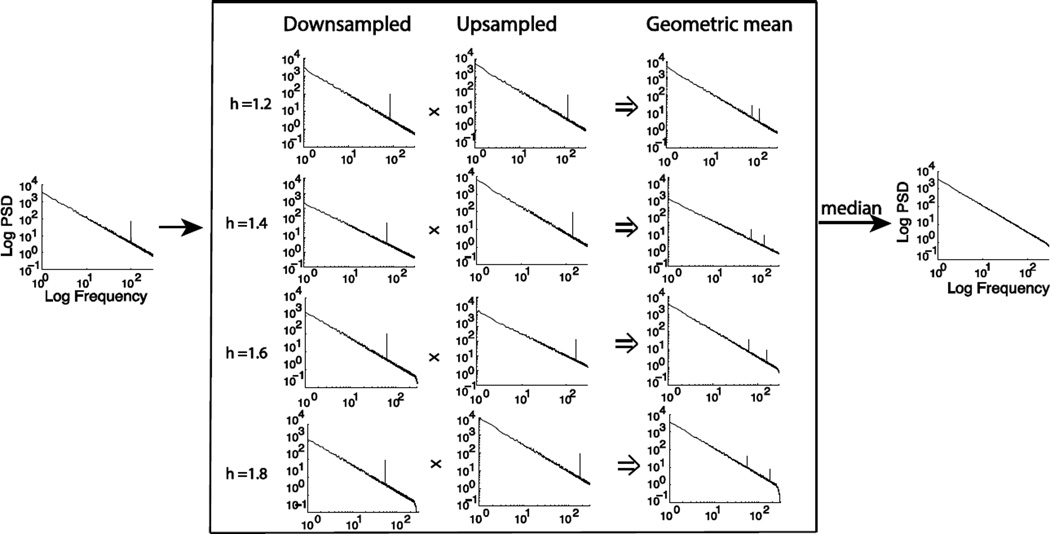
In IRASA, we extract the fractal power spectrum through computing the auto-power spectra of the resampled signals that result from downsampling and upsampling the measured signal by a set of non-integer factors. As such, the resulting time series signals are “irregularly” resampled from the original signal.

The auto-power spectra of y_h(t) and y_1/h(t) are as (4) and (5), respectively.

$$S_{y_h{y}_h}(\omega )=[F_h(\omega )e^{j{\alpha }_h(\omega )}+X_h(\omega )e^{j{\beta }_h(\omega )}][F_h(\omega )e^{-j{\alpha }_h(\omega )}+X_h(\omega )e^{-j{\beta }_h(\omega )}]=h^{2H}{F}^2(\omega ){\Vert 1+{\mathrm{\Psi }}_h(\omega )e^{j{\theta }_h(\omega )}\Vert }^2$$ (4)

$$S_{y_{1/h}{y}_{1/h}}(\omega )=[F_{1/h}(\omega )e^{j{\alpha }_{1/h}(\omega )}+X_{1/h}(\omega )e^{j{\beta }_{1/h}(\omega )}][F_{1/h}(\omega )e^{-j{\alpha }_{1/h}(\omega )}+X_{1/h}(\omega )e^{-j{\beta }_{1/h}(\omega )}]=h^{-2H}{F}^2(\omega ){\Vert 1+{\mathrm{\Psi }}_{1/h}(\omega )e^{j{\theta }_{1/h}(\omega )}\Vert }^2$$ (5)

where Ψ_h(ω) = X_h(ω)/F_h(ω), θ_h(ω) = α_h(ω) − β_h(ω), Ψ_1/h(ω) = X_1/h(ω)/F_1/h(ω), θ_1/h(ω) = α_1/h(ω) − β_1/h(ω). Note that Ψ and θ indicate the relationship between the oscillatory and fractal components in terms of their ratio in magnitude and their difference in phase, respectively.

By computing the geometric mean of these two auto-power spectra, we can obtain an initial estimate of the fractal power spectrum, which is denoted as S̄_h(ω) and expressed as (6).

$${\overline{S}}_h(\omega )=\sqrt{S_{y_h{y}_h}(\omega )S_{y_{1/h}{y}_{1/h}}(\omega )}=F^2(\omega )\Vert 1+{\mathrm{\Psi }}_h(\omega )e^{j{\theta }_h(\omega )}\Vert \Vert 1+{\mathrm{\Psi }}_{1/h}(\omega )e^{j{\theta }_{1/h}(\omega )}\Vert$$ (6)

If y(t) only contains the fractal component, Ψ_h(ω) and Ψ_1/h(ω) are equal to zero for any ω, and S̄_h(ω) is then independent of h and always equals to the fractal power spectrum. If y(t) only contains the oscillatory component with a single harmonic frequency ω₀, S̄_h(ω) is equal to zero for any frequency.

If both fractal and oscillatory components are present in y(t), S̄_h(ω) is as (7).

$${\overline{S}}_h(\omega )=\{\begin{array}{cc}{F}^2(\omega ),\hspace{1em}\omega \ne {\omega }_{0}h\text{and}\hfill & \omega \ne {\omega }_0/h\hfill \\ F^2(\omega )\Vert 1+{\mathrm{\Psi }}_h(\omega )e^{j{\theta }_h(\omega )}\Vert ,\hfill & \omega ={\omega }_{0}h\hfill \\ F^2(\omega )\Vert 1+{\mathrm{\Psi }}_{\frac{1}{h}}(\omega )e^{j{\theta }_{\frac{1}{h}}(\omega )}\Vert ,\hfill & \omega ={\omega }_0/h\hfill \end{array}$$ (7)

It suggests that S̄_h(ω) is an unbiased estimate of the fractal power spectrum at the oscillatory frequency as well as other frequencies except ω₀h and ω₀/h. Importantly, since the estimation errors are expected to occur only at frequencies that are dependent on the resampling factor h, setting different non-integer values (e.g. between 1.1 and 1.9) to h relocates the oscillation-associated power and yields a set of estimates for the fractal power spectrum {S̄_h(ω)}. In every one of these estimates, the oscillatory power is relocated to different frequencies (as illustrated in Fig. 2). In other words, these h-dependent spectral estimates, viewed at every individual frequency, are expected to mostly center about the true power of the underlying fractal component with typically one deviation due to the interference from the underlying oscillatory component. This deviation is an “outlier” within a set of otherwise unbiased fractal power estimates at each frequency (as illustrated in Fig. S2). We can eliminate the bias from the outlier by taking the median of these fractal power estimates at every frequency.

$$F^2(\omega )={\text{median}}_h\{{\overline{S}}_h(\omega )\},\text{for each}\omega$$ (8)

Fig. 2.

Procedures to estimate the power spectrum of the fractal component by statistically summarizing the geometric means of the auto-power spectra of the signals un-sampled and down-sampled by a set of non-integer factors

Since the median is a very robust sampling statistic against the presence of outliers with a breakdown point of 50% (Bassett, 1991), Eq. 8 is expected to yield an unbiased estimate of the power of the fractal component at any specific frequency as long as the number of outliers is less than half at this frequency. See Fig. 2 and Fig. S3 for more detailed illustrations and explanations.

To further estimate the PSD of the oscillatory component, we derive Eq. (9) from Eq. (1).

$$Y^2(\omega )=F^2(\omega )+X^2(\omega )+2F(\omega )X(\omega )\text{cos}(\alpha (\omega )-\beta (\omega ))$$ (9)

It shows that the PSD of the oscillatory component is related not only to the difference between the PSD of the mixed signal and the PSD of the fractal component, but also to another confounding term that depends on the relative phase difference between the fractal and oscillatory components. Assuming no phase-phase coupling between the fractal and oscillatory components, the expectation of this confounding term is close to zero. To approximate the expectation, we can select multiple time segments within the given period during which the signal is assumed to be stationary. After averaging the PSD of the segmented signal across segments, the confounding term reduces to zero. Therefore, the difference of the averaged PSD of the raw signal and the estimated PSD of the fractal component can serve as an unbiased estimate for the expectation of the PSD of the oscillatory component.

2.4 Algorithm

1. From a given period of the time series signal, we chose ten time segments. Every time segment was 90% of the total length. These segments were evenly distributed within the total period and were partially overlapping.

2. For each segment defined in (a), the auto-power spectrum was estimated from the original signal by using fast Fourier transform (FFT) tapered with a Hanning window. The number of frequency points (NFFT) was chosen to be two times the smallest power of two that was greater than the number of time points in each segment. Given h<2 as used in (c), NFFT is guaranteed to be greater than the number of time points in the original signal or its down-sampled or up-sampled version, ensuring equal sampling in the angular frequency without losing any overall spectral energy.

3. For each segment defined in (a), we resampled the signal by h and 1/h, where h ranged from 1.1 to 1.9 with the increment of 0.05. In order to irregularly upsample the signal by h, we interpolated the signal by using a cubic spline method. To irregularly downsample the signal, we first applied an anti-aliasing low-pass filter and then used the cubic spline interpolation. Then we estimated the auto-power spectra of the resampled signals using the same FFT-based method and the same number of frequency points as in (b).

4. For each segment defined in (a), the geometric mean of the auto-power spectra of the up-sampled and down-sampled signals was calculated for each h value. The median of the results with all h-values was obtained to estimate the power spectrum of the fractal component.

5. The estimated PSD of the fractal component and the calculated PSD of the signal were both averaged across all time segments defined in (a).

6. The average power spectrum of the fractal component was subtracted from the average power spectrum of the original signal to yield the estimated power spectrum of the oscillatory component.

The above algorithm was implemented in Matlab and will soon be made publicly available with example datasets on our website (http://engineering.purdue.edu/libi/lab/Resource.html).

The estimated power spectrum of the fractal component was transformed to the log-log scale only for the display and quantification of the power-law distribution. In the log scale, there are increasingly more spectral sampling points for higher frequencies. Therefore, we resampled the frequencies to be evenly spaced in the log scale, in order to prevent the higher frequency range from dominating the estimation of the power-law properties. Then we used the least squares estimation to obtain a linear function that best fitted the estimated fractal power spectrum. The slope of the linear function was the estimated power-law exponent, β, and the intercept of the linear function was referred to as the log-power intercept. The mean power in the log scale was the estimated broadband power (Miller et al., 2009).

Note that a sliding window can be used to progressively select shorter periods out of a relatively longer period, as commonly used in short-time Fourier transform. Within each sliding window, the above algorithm and quantification can be used to separate the power spectra of the fractal and oscillatory components of the signal, resulting in time frequency representations of the fractal and oscillatory components.

2.5 Computer Simulation

For the initial tests of the proposed IRASA method, we simulated fractal and oscillatory time series without considering noise. The fractal time series was generated by inverse FFT applied to a power-law Fourier spectrum as described in (Yamamoto and Hughson, 1993). Briefly, the power distribution followed a 1/f trend with a preset power-law exponent β. The phase distribution was random and followed a uniform distribution between 0 and θ_max, where θ_max ≤ 2π.

The oscillatory component was simulated as a single sinusoidal signal or the sum of a varying number of sinusoidal signals, and then added to the simulated fractal component. The amplitudes of the additive sinusoidal signals were systematically varied from 10 to 400% of those of the fractal component at the same frequencies. All of the simulated time series signals included 8500 time points with a 1000-Hz sampling rate. With these noise-free simulation data, we evaluated the performance of separating and characterizing the power spectrum of the fractal component as a function of the number of oscillations, the phase distribution of the fractal time series, and the relative amplitude of the oscillatory component to the fractal component. In addition, we also applied the IRASA to estimate the PSD of the simulated multifractal time-series component that exhibited power-law distributions in multiple separate frequency ranges with different power-law exponents.

Although the aforementioned theoretical derivation is based on a noise-free model, we also simulated data with additive white noises. For an initial testing purpose, we first mixed one 10Hz oscillatory signal with the simulated scale-free signal as aforementioned; then we added randomly generated noise to the mixed signal such that the signal to noise ratio, defined as the ratio of the variance of the mixed signal to the variance of the additive noise, varied at 1, 10, and 100. With these data, we evaluated the robustness of IRASA against noise contamination.

2.6 Experiment Data and Analyses

We also used the proposed IRASA method to analyze in vivo ECoG and MEG data. The ECoG data were downloaded from the website of the Project Tycho (http://neurotycho.org). The ECoG data were originally collected with a sampling rate of 1kHz from macaque brain in the eye-closed wakeful resting state and the sleep state by using 128 sensors covering the entire lateral surface of the left macaque cortex. In this study, we analyzed data from two macaques, 4 sessions for each macaque, and each session included two segments of 5-min time series with one in wakefulness and the other in sleep. The MEG data were obtained from a previously published study (Liu et al., 2010). It was recorded in three different behavioral states, the eyes-closed, eyes-open and sleep states for a total of 40 minutes. We analyzed the MEG data from 5 subjects.

For both ECoG and MEG data, we applied IRASA to a sliding time-window to obtain a time-varying fractal and oscillatory spectra (i.e. time-frequency representation or spectrogram). The sliding window was set to be 3s with 1s increments. We fitted a power-law function to the estimated fractal spectrum (1–30Hz) at every sliding time window, and obtained the time courses of the power-law exponent, the intercept of the power-law function in log-log coordinates, and the broadband power. We further averaged the time-resolved spectral components within distinct behavioral states and compared the results across states. The purpose was to characterize and differentiate different behavioral states based on their broadband scale-free signatures as opposed to narrowband oscillations.

RESULT

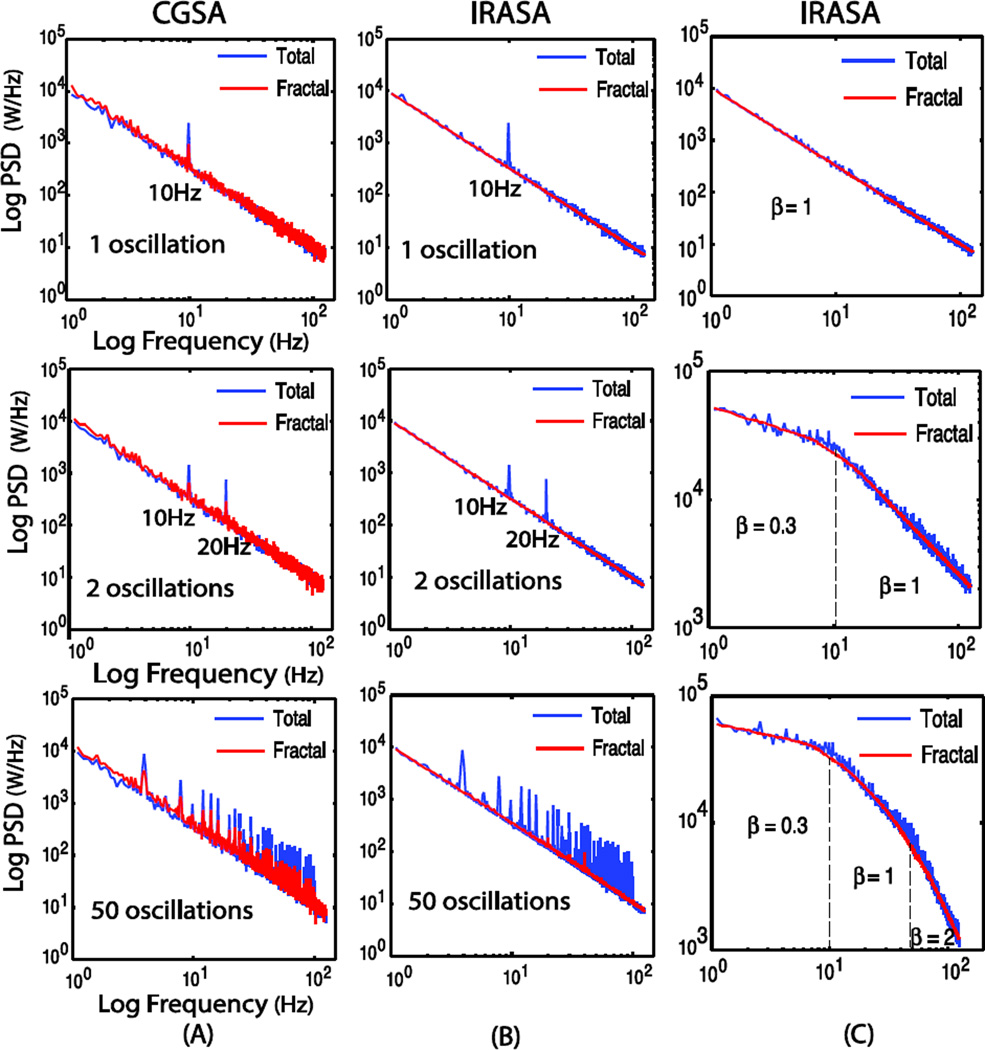
We initially evaluated the efficacy of IRASA in comparison with CGSA by using simulated time-series signals with various mixtures of fractal and oscillatory components. Fig. 3.A and 3.B show the PSD of the simulated signals and the PSD of the fractal components estimated by using CGSA and IRASA. For CGSA, the extracted fractal PSD generally followed a power-law (1/f) trend with “noisy” deviations especially at the oscillation frequencies where the spectral peaks remained obvious despite the reduced power. Note that CGSA could not lead to the complete separation of the fractal and oscillatory components even if the oscillation only had a single frequency (as predicted by its theoretical limitations elaborated in the online supplementary material), and its performance became worse when an increasing number of oscillations were included. In contrast, IRASA could be used to successfully remove oscillations and obtain an accurate fractal PSD that strictly obeyed the power-law distribution. The residual oscillation-related spectral peaks were negligible when the signal included a small number of oscillations. Even if as many as 50 oscillations were included, IRASA was still able to exclude most oscillations and resulted in a clean power-law PSD that well characterized the underlying fractal component with minor interference from the oscillatory component. In addition, IRASA could also be used to estimate the PSD of a multifractal time-series component, albeit blurred breakpoints between these frequency ranges (Fig. 3.C).

Fig. 3.

Comparison between the estimated power spectra of the fractal component based on CGSA (A) and IRASA (B), given different numbers (1, 2, 50) of oscillation frequencies, and the result of IRASA in multiple fractal components (C). Fractal time series has random phase uniformly distributed between 0 and 2π and power-law exponent is set to 1.5 in (A) and (B)

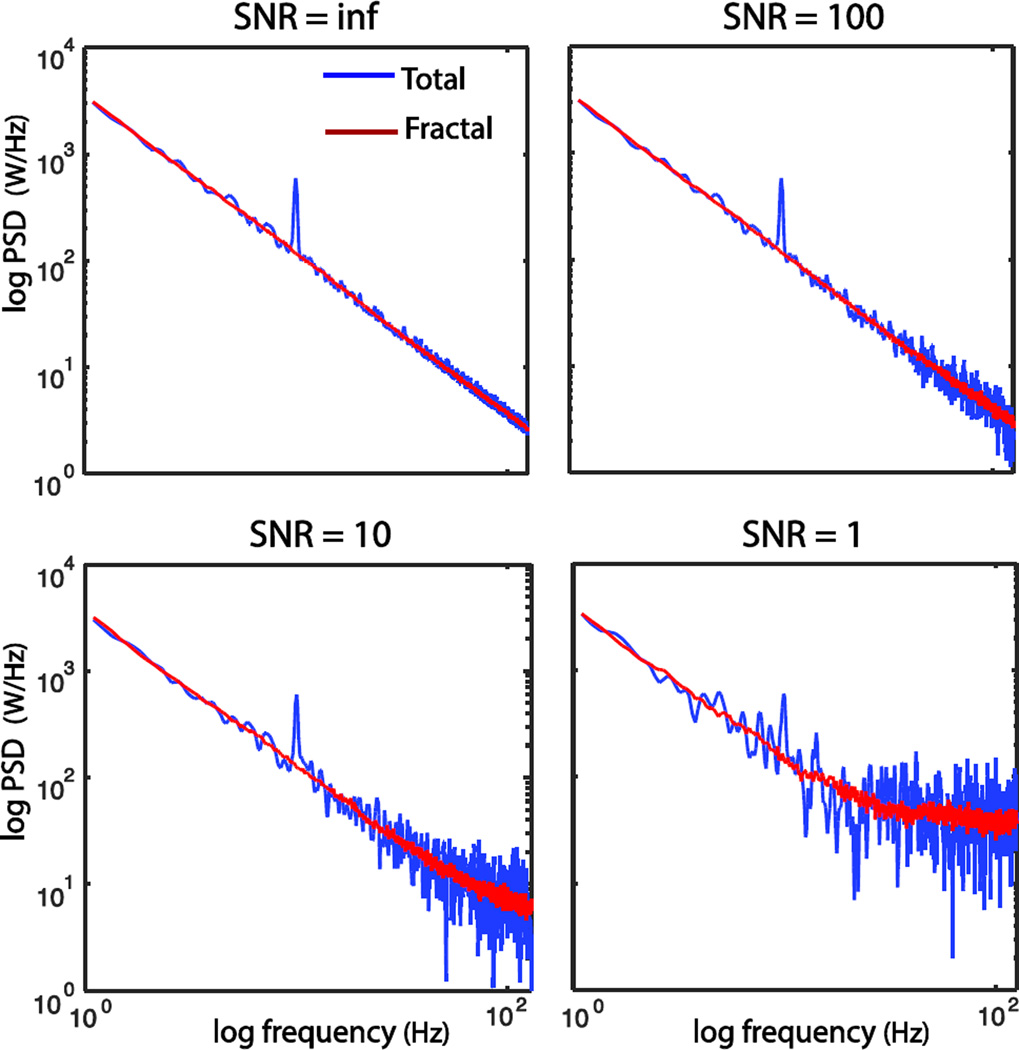
With various levels of additive white noises, we evaluated the robustness of IRASA against noise contamination. Fig. 4 shows that the performance of IRASA in extracting the fractal PSD deteriorated with decreasing SNR. When the overall SNR was as low as 1, the noise affected the high frequency range in which the measured signal was dominated by the noise; however, the extracted fractal component still followed a clear power-law distribution in the low frequency range. In general, IRASA performed well with modest to high SNR in a simulation setting.

Fig. 4.

Robustness evaluation of IRASA on extracting the PSD of fractal component under different levels of additive white noise contamination.

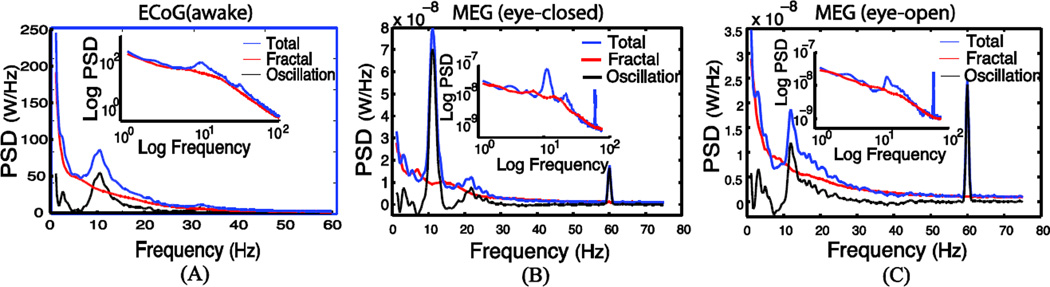
To further test the practical utility of IRASA, we used IRASA to differentiate fractal and oscillatory neuroelectrical activities observed with ECoG and MEG data. Fig. 5.A shows the IRASA-extracted fractal and oscillatory PSD of the example ECoG signals recorded from one sensor located in the frontal lobe of a macaque brain. The fractal PSD depicted the broadband activity of the ECoG spectrum. This broadband activity was approximately an exponential function in the regular coordinate or equivalently a linear function in the double-logarithmic coordinate. The PSD of the oscillatory component, obtained by subtracting the extracted fractal PSD from the raw ECoG PSD, provided a clear depiction of alpha (8–13Hz) rhythm. Similarly, Fig. 5.B and 5.C show the separated fractal and oscillatory components of one MEG sensor over the occipital lobe under the eyes-closed and eyes-open conditions, respectively. The IRASA-extracted oscillatory component included peaks at the alpha and beta bands, as well as the 60Hz power-line noise. The eyes-open condition had much reduced alpha power and diminished beta power relative to the eyes-closed condition. Figures 6 and 7 show the results of the separated fractal dynamics in different brain regions as observed with macaque ECoG and human MEG data, respectively. These results demonstrate the efficacy of the proposed method to extract the fractal component from measured electrophysiological signals.

Fig. 5.

Separated power spectra of the fractal and oscillatory components underlying the eyes-closed awake state macaque ECoG (A), as well as human MEG signals in the eyes-closed (B) and eyes-open (C) conditions

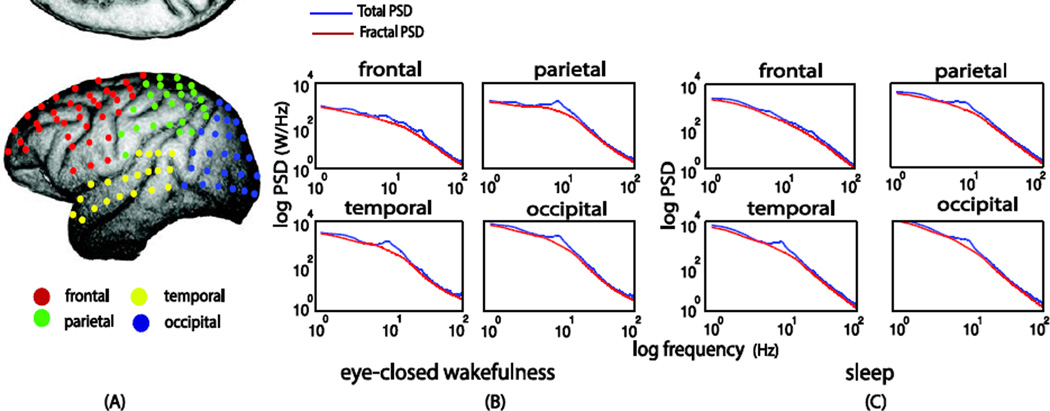
Fig. 6.

Extracted PSD of fractal dynamics from macaque ECoG data of 128 sensors. (A) the colored dots are the 128 sensor in different brain regions. (B) Averaged fractal power spectra in different brain regions in the eyes-closed awake condition. (C) Averaged fractal power spectra in the sleep condition

Fig. 7.

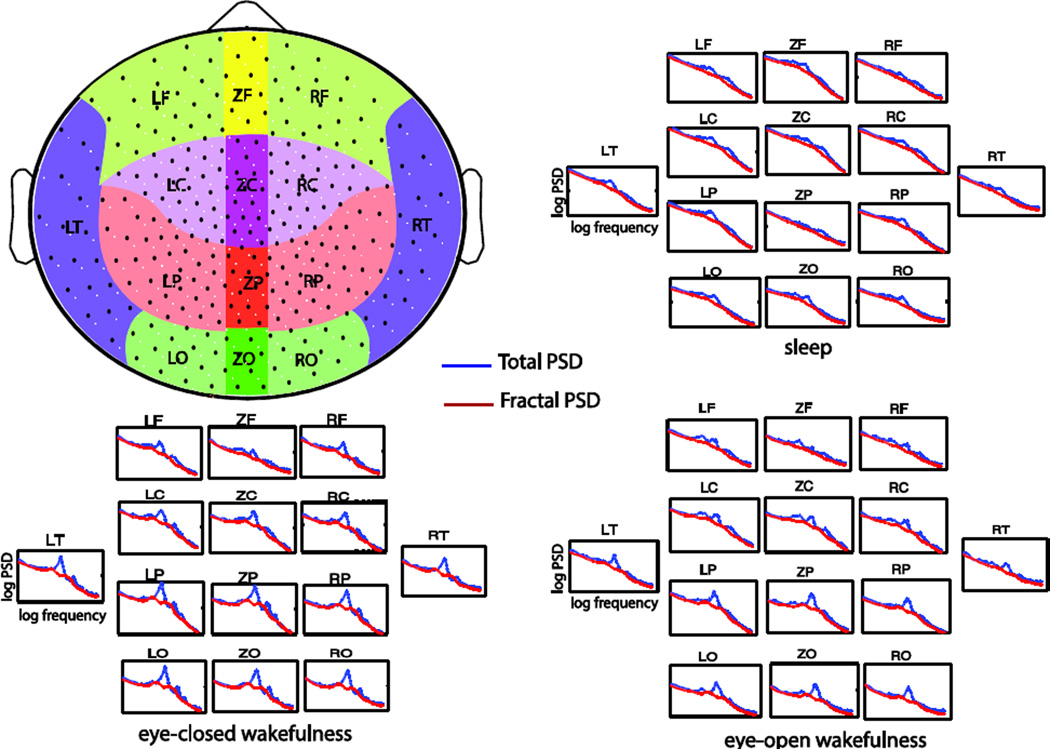
Extracted PSD of fractal dynamics in human MEG data of 274 sensors. The black dots in the upper left figure are the MEG sensor locations. The fractal power spectra averaged within different brain regions are separately shown for the eyes-closed, eyes-open and sleep conditions

Moreover, one can also use IRASA to obtain the spectrograms showing the temporal dynamics of the fractal and oscillatory spectra by using short sliding time windows. To demonstrate this point, we separately extracted the fractal and oscillatory spectrograms and obtained the time courses of the alpha power (i.e. the average power in 8–13 Hz), the power-law exponent, the log-power intercept, as well as the broadband power from the macaque ECoG and the human MEG signals.

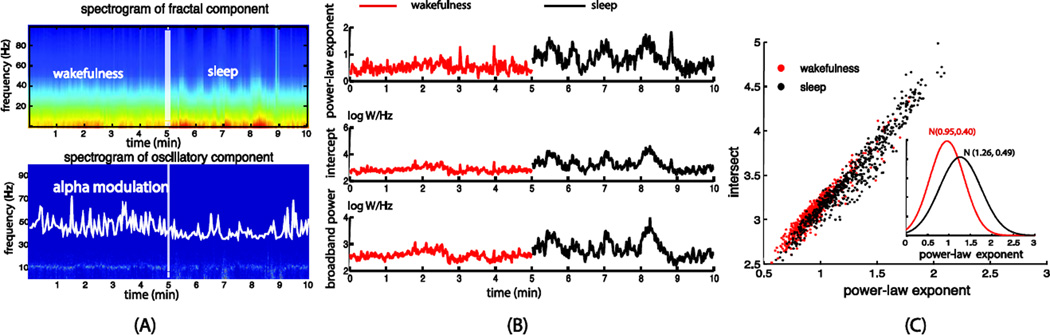
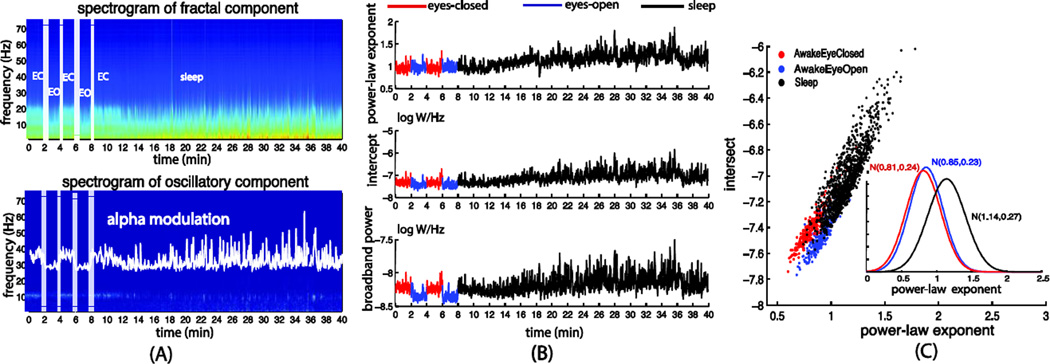
Similar to previous studies (Olbrich et al., 2009), the distinct behavioral states exhibited different patterns of oscillations, especially in the alpha frequency range (Fig. 8.A and Fig 9.A). We observed much stronger alpha oscillations during eyes-closed wakefulness relative to the eyes-open and sleep states (Fig. 9.A). Interestingly, we also found that the fractal component differed considerably across these behavioral and arousal states. In the macaque ECoG data (Fig. 8), we found that the power-law exponent was larger in the sleep state, with a mean and the standard deviation of 1.26±0.49, than the eyes-closed wakeful state (0.95±0.40) (Fig. 8.B and 8.C). For the human MEG data (Fig. 9), the power-law exponents increased from 0.81±0.24 to 1.14±0.27 as the subjects fell into sleep from eyes-closed wakefulness. We also observed greater variance in the power-law exponent during the sleep state than the wakeful states. Moreover, the broadband power also differed across these behavioral and arousal states, being lower when the eyes were open than that in the eyes-closed condition and being higher as the subjects fell asleep. These results suggest that distinct behavioral states may be characterized not only by frequency-specific oscillations but also by broadband fractal activities.

Fig. 8.

(A) Separated spectrograms of the fractal and oscillatory components averaged across all sensors underlying the macaque ECoG signals in the eyes-closed awake (from 0 to 5 min) and sleep (from 5 to 10 min) conditions. (B) Time courses of the power-law exponent, intercept and broadband powers derived from the power-law fitting of the fractal spectrogram. (C) Scatter plots and histograms of the power-law exponent and the log-power intercept in wakefulness and sleep

Fig. 9.

(A) Separated spectrograms of the fractal and oscillatory components averaged across all sensors underlying the human MEG signals in the eyes-closed (from 0 to 2 and 4 to 6 min periods), eyes-open (from 2 to 4 and 6 to 8 min periods) and sleep (from around 12min to the end) conditions. (B) Time courses of the power-law exponent, the log-power intercept and the broadband power derived from the power-law fitting of the fractal spectrogram. (C) Scatter plots and histograms the power-law exponent and log-power intercept in the three different states

Discussions

The signal processing technique (IRASA) presented here allows the separation of fractal and oscillatory components of neurophysiological signals in the spectral domain, with the assumption that neural recordings are formed by the sum of scale-free and frequency-specific components. Arguably, such separated oscillatory and scale-free dynamics may report useful information about rhythmic and arrhythmic dynamics emerging from interacting neural circuits. When applied to various electrophysiological signals, the values and dynamics of the power-law exponent and broadband power may provide complementary perspectives to those that report on neuronal oscillations. However, it awaits future studies to investigate whether the scale-free broadband component indeed originates from neuronal population activities with fractal dynamics, as well as the specific functional role of such activities.

In the following, we discuss multiple methodological considerations as well as speculative implications and applications to neuroscience research.

Comparison with CGSA

This work is inspired by the earlier CGSA methods (Yamamoto and Hughson, 1991, 1993). However, the cross-spectral analysis in CGSA suffers from theoretical limitations (see the online supplementary material). The difference between IRASA and CGSA has the following aspects.

Firstly, IRASA is based on the auto spectra of the up-sampled and down-sampled signals, whereas CGSA is based on the magnitudes of the cross spectra between the original signal and its up-sampled and down-sampled versions. This difference is critical in that it enables IRASA to relocate the spectral energy associated with oscillations away from their occurring frequencies, while part of such energy always remains at the original oscillation frequencies for CGSA.

Secondly, IRASA uses non-integer (irregular) resampling, whereas CGSA, as in (Yamamoto et al., 1991, 1993; He et al., 2010), uses integer (regular) resampling. Although it requires time-series interpolation with slightly higher computation demand, the irregular resampling is more advantageous than regular resampling in that the spectra of the resampled oscillations do not overlap with the original spectrum when the oscillatory component occurs at multiple harmonic frequencies, which is often the case in realistic neural signals. Although it has not been used with CGSA in published studies (to the best of our knowledge), the irregular resampling is expected to also benefit CGSA in addressing issues related to harmonic frequencies.

Thirdly, IRASA uses a number of non-integer resampling factors, whereas CGSA uses only one, at least as described in (Yamamoto et al., 1991, 1993; He et al., 2010). Combined with the two features mentioned above, this feature utilizes the fact that changing the resampling factor in IRASA leads to relocation of the oscillation-related energy to different frequencies. It follows that taking the median of the results obtained with different resampling factors enables IRASA to almost completely exclude the contribution and interference from the oscillatory component in estimating the spectrum of the fractal component. However, this similar ‘trick’ does not benefit CGSA in the same way (Fig. 3 and Fig. S2).

Choosing the resampling factors

We choose the resampling factor (h and 1/h) as non-integer numbers for irregular resampling of the original time series. For any h>0, either h or 1/h is greater or equal to 1. Without loss of generality, we choose h>1. A large h value would lead to greater dispersion of the spectra of the resampled oscillatory component (Fig. 2). However, it would limit the bandwidth of the final estimate of the fractal spectrum, because the bandwidth is reduced by a factor of h following the resampling. For example, for a typical EEG sampling frequency of 1000 Hz, the bandwidth is 500 Hz. A resampling factor of 2 would reduce the bandwidth to 250 Hz but still covers the frequency range of interest. If the original sampling rate is overly high, it is more preferable to use a wider range for h. Within any range of choice, one may further choose more h values such that taking the median would likely yield a more accurate and robust estimate of the fractal PSD yet at the cost of increasing computational time. Balancing the above considerations, we choose the value of h between 1.1 and 1.9 with a 0.05 increment. Although such a choice is pragmatic and not entirely principle-driven, it has given rise to robust results in extracting the scale-free broadband activity in both simulation and experimental data included in this study.

For any choice of the h values, one can zero-pad all resampled time series to the same length equal to the power of 2. This will permit FFT with the same number of frequency points for all resampled signals and allow for subsequent computation in the frequency domain.

Multi-scale fractal dynamics

One assumption for both IRASA and CGSA is that the fractal dynamics obeys a power law. It should be noted that this assumption does not always hold true in practice when a very wide frequency range is of interest. Some neuronal signals have different frequency scaling properties for different frequency ranges (Hwa and Ferree, 2002; Miller et al., 2009; Robinson, 2003). We found that IRASA performed well even for such multi-scale fractal signals, although it blurred the ‘breakpoints’ where the frequency ranges of distinct fractal components intersected (Fig. 3.C). The practical utility of IRASA for multifractal time series awaits further investigation and should be taken with caution as of now.

Fractal vs. scale-free

The terms of fractal and scale-free have often been used or discussed interchangeably. Although these two concepts are closely related, there are some conceptual distinctions perhaps worth noting. For an extreme example, a deterministic signal (e.g. a linear drift) has the scale-free property and obeys a 1/f power law. But it is obviously of little interest for brain research and may likely be mistaken as the spectral characteristic of the brain’s arrhythmic activity. Therefore, another important feature of the scale-free activity has to lie in its phase distribution. A random fractal process should possess a random phase distribution within [0, 2π] (Yamamoto and Hughson, 1993), whereas fractal processes are not all characterized by random phase distribution. The IRASA method serves to extract the PSD of the signal components that comply with the scale-free property, as expressed by Eq. (2) and (3). Such extracted spectral components contain no phase information, and may or may not reflect a fractal process of biological significance.

Magnitude vs. phase

Of note, IRASA, as well as CGSA, can only separate the power spectra of the fractal and oscillatory components of neurophysiological signals. It is currently difficult, if possible at all, to separate these components in the time domain or uncover their phase differences or relationship. This imposes a technical barrier for investigating phase-phase and phase-amplitude couplings of fractal dynamics between different frequency points or between different spatial locations. Future technical development is highly desirable to resolve this barrier.

Other alternative solutions

In addition, it is also of future interest to compare the spectral analysis method with other alternative time-series analysis methods, e.g. DFA (Peng et al., 1995) or its recent variations such as adaptive fractal analysis (AFA) (Gao et al., 2011). Note that although IRASA is based on the Fourier transform, similar concepts might be useful for other time-frequency analysis methods, such as those based on wavelet transform.

Implication to neuronal oscillations

One motivation of this study is to better extract neural oscillations from electrophysiological signals. Here we assume that oscillations co-occur with the broadband activity that approximately follows a power-law distribution. As such, the temporal modulation in power or amplitude of oscillatory activity is mixed with the modulation of the underlying broadband activity. Both modulations contribute to the amplitude or power envelops of band-limited signals, or the power fluctuation observed with the time-frequency analysis. Without separating oscillatory and fractal activities, the fluctuation of band-limited signals may not be entirely specific to the frequency band of interest, but contains a variable fraction owing to the frequency non-specific broadband modulation. Arguably, separating the fractal component may provide more accurate estimation of the modulation of neuronal oscillations. This is beneficial when one is interested in the amplitude (not phase) relationship between distinct frequency bands, or in the contributions of various frequency bands to other brain signals, such as neuronal spikes or hemodynamic signals.

Unlike the ideal oscillations assumed in our model Eq. (1), realistic oscillatory activity is not always localized in frequency, but manifests itself in a frequency band. In such cases, the nominal fractal and oscillatory spectra, extracted by using IRASA (and likewise CGSA), may still contain residuals that comprise their corresponding spectral behaviors from being strictly scale-free or frequency specific. To partly overcome this, one could choose a larger range of resampling values as permitted by the original sampling frequency and the desired overall frequency range of interest, as aforementioned for the practical choice of the resampling factors.

Implication to neuronal fractal activity

The fractal dynamics, as the broadband activity underneath neural oscillations, fluctuates over time in a way that seems functionally relevant. For example, it varies by voluntary eyes opening and closing in terms of the broadband power and the power-law exponent (Fig. 9). As such, the broadband fractal activity is at least not pure noise, and likely bears some functional significance. However, where the fractal dynamics comes from and how it serves brain functioning remain poorly understood and await future research (He et al., 2010; He 2014). For example, it is of potential interest to investigate inter-regional correlations in the temporal fluctuation of fractal dynamics, and to compare the resulting correlational patterns against those based on oscillatory dynamics or the structural networks observed with diffusion MRI. This would help address the network origin of fractal vs. oscillatory dynamics. It is also of potential interest to investigate the spatiotemporal characteristics of fractal dynamics during not only simple behavioral tasks but also complex cognitive tasks in a rich and naturalistic behavioral context. This would help address the functional significance of fractal dynamics.

However, the proposed IRASA method is not intended to address the generative mechanism of the scale-free broadband signal or the frequency-specific narrowband signal observed in neural recordings. As a signal processing method, the IRASA method by itself offers little information about the theoretical basis and functional role of the apparent scale-free or oscillatory activity in the context of neural synchrony, coupling or computation.

Differentiate functional states with fractal characteristics

A large amount of literature has reported on neural oscillations in a variety of brain states (Başar, 2001; Buzsáki and Draguhn, 2004; Gray 1994; Hanslmayr et. al., 2011; Lakatos, at el., 2008; Rinzel and Ermentrout, 1998; Schabus et al., 2011). For example, the brain’s vigilance and attention level has been measured mainly by the oscillation power of a single frequency band, e.g. the alpha band (8–13Hz), or the relative amplitudes of several frequency bands, especially the alpha, theta and delta bands (Olbrich et al., 2009; Wong et al. 2013). Combined with other event-like signatures, e.g. k-complex, spindles, oscillatory patterns have been serving as the main clues for sleep staging.

However, how the broadband fractal dynamics varies across behavioral states remains poorly understood. Following IRASA, one can quantify the broadband fractal characteristics by using the power-law exponent (He et al., 2010; He 2014), the intercept of the power-law function at zero log-frequency, and the broadband power (Miller, et. al. 2009) as a linear function of the exponent and the intercept. These quantities collectively define the feature space for potential classification of various functional states based merely on the fractal characteristics. As an initial proof of concepts, the broadband power of fractal dynamics differed notably across behavioral and arousal states: higher in sleep than wakefulness, and higher in eyes-closed condition than the eyes-open condition.