The neural encoding of formant frequencies contributing to vowel identification in normal-hearing listeners

Abstract

Even though speech signals trigger coding in the cochlea to convey speech information to the central auditory structures, little is known about the neural mechanisms involved in such processes. The purpose of this study was to understand the encoding of formant cues and how it relates to vowel recognition in listeners. Neural representations of formants may differ across listeners; however, it was hypothesized that neural patterns could still predict vowel recognition. To test the hypothesis, the frequency-following response (FFR) and vowel recognition were obtained from 38 normal-hearing listeners using four different vowels, allowing direct comparisons between behavioral and neural data in the same individuals. FFR was employed because it provides an objective and physiological measure of neural activity that can reflect formant encoding. A mathematical model was used to describe vowel confusion patterns based on the neural responses to vowel formant cues. The major findings were (1) there were large variations in the accuracy of vowel formant encoding across listeners as indexed by the FFR, (2) these variations were systematically related to vowel recognition performance, and (3) the mathematical model of vowel identification was successful in predicting good vs poor vowel identification performers based exclusively on physiological data.

I. INTRODUCTION

Vowels convey critical information for speech understanding. Among a wide range of models that attempted to explain vowel recognition in normal-hearing (NH) listeners, the majority of the previous models proposed that NH listeners identify vowels on the basis of either (i) the formant frequency pattern (i.e., formant model) or (ii) the gross shape of spectral envelope, or some combination thereof (for reviews, see Klatt, 1982; Nearey, 1989; Hillenbrand and Nearey, 1999). The formant model is based upon the assumption that vowels are identified primarily by the distribution of formant frequencies (primarily the first two formants). This model is supported by the findings of the relationship between measures of formant frequencies and vowel recognition (e.g., Peterson and Barney, 1952; Bladon and Lindblom, 1981) and the high intelligibility of signals synthesized using formant information alone (e.g., Remez et al., 1981; Klatt, 1982).

In most cases, the formant model has been tested using acoustic manipulations of signals (e.g., Strange et al., 1983; Jenkins et al., 1983; Kewley-Port and Zheng, 1998; Liu and Kewley-Port, 2004) or by examining the relationship between discrimination thresholds for formants and vowel recognition performance (e.g., Sagi et al., 2010a; Sagi et al., 2010b, for cochlear implant users). Such an approach is useful to understand the importance of acoustic formants to vowel recognition; however, little is known about how these formants are encoded in the auditory neural system and subsequently contribute to vowel perception. The purpose of this study was to examine how the auditory system encodes vowel formants and how such neural encoding of formants relates to vowel recognition performance across individual listeners. The primary hypothesis was that individual differences in neural encoding of vowel formants may account for a portion of the underlying uncertainty that explains vowel confusions across subjects.

To test this hypothesis, we compared frequency-following responses (FFRs) to vowel identification in adults with NH. The FFR was chosen because it provides an objective and physiological measure of neural activity that can reflect vowel formant encoding (e.g., Smith et al., 1975; Krishnan, 2002; Aiken and Picton, 2008; Zhu et al., 2013). Previous studies showed that neural representations of formant information are different across individual listeners (e.g., Anderson et al., 2012; Bidelman et al., 2014; Sadeghian et al., 2015; Ruggles et al., 2011, 2012; Clinard et al., 2010; Clinard and Tremblay, 2013). In the current study, individual differences in neural encoding of vowel formant information were examined across 38 NH listeners. To this end, formant information was extracted from FFR waveforms elicited by four different synthesized vowels. These synthesized vowel stimuli were used for both vowel recognition and FFR recording in the same group of NH subjects. Finally, a mathematical model, called “multidimensional phoneme identification” (MPI) (Svirsky, 2000) was used to understand the effects of neural formant representation on vowel recognition performance. Previous studies have used mathematical models to evaluate the effects of specific acoustic features [e.g., fundamental frequency (F0), vowel formant frequencies, spectral representation of loudness density, etc.] on vowel perception and quality (e.g., Bladon and Lindblom, 1981; Kewley-Port and Zheng, 1998), but the question of how the central auditory system utilizes such acoustic vowel information is largely unknown.

The MPI model was originally proposed by Svirsky (2000) to predict phoneme confusion matrices based on a listener's discrimination ability for a set of postulated acoustic cues. In the current study, the MPI model was used to predict vowel confusion patterns based on FFR-derived estimates of first (F1) and second (F2) formant frequencies extracted from individual listeners. These predictions, obtained exclusively from physiological (FFR) data, were then compared to vowel confusion patterns observed from the same human listeners. Comparing speech-evoked FFRs to the recognition of the same synthesized speech tokens makes it possible to examine perceptual and physiological aspects using the same vowel stimuli. With this theoretical framework, the effect of individual differences in encoding of vowel formants (inferred from FFRs) on behavioral vowel recognition was evaluated.

II. MATERIALS AND METHODS

A. Subjects

Thirty-eight native speakers of American English (age range = 22–67 yrs; mean age = 36 yrs; one standard deviation = 16 yrs; 28 females and 10 males), who were residents in the Pacific Northwest, and who had NH participated in this study (thresholds ≤ 20 dB hearing level at octave frequencies between 250 and 8000 Hz). NH subjects with a wide range of age were enrolled in the current study to have variability in vowel identification performance. This study was approved by the University of Washington Institutional Review Board.

B. Stimuli

Four synthesized vowels (/u, ʊ, ʌ, ɑ/), as in the words “who'd, hood, hud, and hod,” were synthesized using the SynthWorks software (Scicon R & D Inc., Beverly Hills, CA), which implements the Klatt synthesizer (Klatt and Klatt, 1990). These synthetic vowels were used for the vowel identification test and FFR recording. Table I shows the formant frequencies and formant bandwidth information for the four vowel stimuli employed in this study. The top row of Fig. 1 shows spectrograms for the four synthetic vowel stimuli. From the left to the rightmost columns, spectrograms of the synthetic vowel /u/, /ʊ/, /ʌ/, and /ɑ/ are shown. The stimuli were set to be 70 ms long in duration to eliminate duration cues and to increase the difficulty of the vowel identification task. F0 for the four vowels was fixed at 100 Hz. First and second formant frequencies (F1 and F2) were set to the average midpoint frequencies for male speakers from the Pacific Northwest region (Wright and Souza, 2012). F1 and F2 for these four vowels are typically below 1500 Hz, which makes them ideal for FFR study; FFRs generally show spectral magnitude greater than the noise floor below 1500 Hz (e.g., Plyler and Ananthanarayan, 2001; Krishnan, 2002; Zhu et al., 2013). The third formant frequency (F3) for each vowel was estimated using regression formulas proposed by Nearey (1989), and the fourth formant frequency (F4) was fixed at 3500 Hz. Formant bandwidths were calculated from the algorithm described in Johnson et al. (1993). Finally, the vowels were low-pass filtered at 2000 Hz (second order Butterworth filter). Because of the stimulus characteristics, we expected that F1 and F2 frequencies would be the primary acoustic cues for listeners to identify vowels. As a result, F1 and F2 were the two dimensions that we used in the mathematical model (see Sec. II E).

TABLE I.

Formant frequency (F) and associated bandwidth (B) information for the synthesized vowels (in Hz).

IPA	/hVd/	F1	F2	F3	F4	B1	B2	B3	B4
u	Who'd	324	1223	2149	3500	65	110	140	200
ʊ	Hood	465	1444	2180	3500	80	100	80	200
ʌ	Hud	575	1200	2355	3500	80	50	140	200
ɑ	Hod	700	1110	2486	3500	130	70	160	200

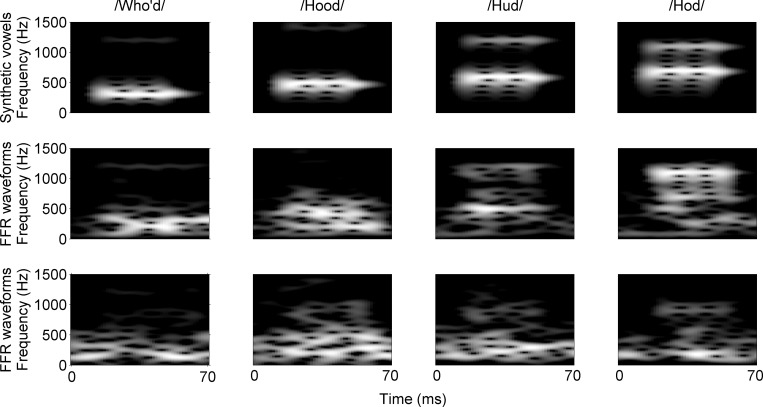
FIG. 1.

Spectrograms of the synthetic vowels (upper row) and the corresponding FFRs recorded from two different subjects (middle and bottom rows). From the left to the rightmost columns, spectrograms for the vowel /u/, /ʊ/, /ʌ/, and /ɑ/ are shown. In the middle row, spectrograms of FFRs for the subject who showed the smallest difference in formant frequencies between the original (i.e., from the synthetic vowels) and estimated values from the FFRs are shown. In the bottom row, spectrograms of FFRs for the subject who showed the greatest difference in formant frequencies are shown. In these spectrograms, different amplitudes of the synthetic vowels or FFRs are depicted as a gray scale over a dynamic range of 20 dB. For these spectrograms, the number of a fast-Fourier transform was set to 10 000 points, and Hanning window and overlap were set to 20 and 19 ms, respectively.

C. FFR recording

FFRs were recorded at a 20 kHz analog-to-digital sampling rate using a NeuroScan RT acquisition system (Compumedics USA, Charlotte, NC). An active electrode was placed at Cz, a ground electrode was placed at forehead, and two linked on-line reference electrodes were placed on each earlobe (one at each mastoid) with all impedances below 5 kΩ. Stimuli were presented binaurally through magnetically-shielded ER-3 insert earphones in a sound-attenuating booth. Stimuli were equated in the same root-mean-square (rms) value and presented at 80 dB sound pressure level (SPL) in alternating polarities with a repetition rate of 8.33 per second. Previous studies showed that robust FFR neural responses can be obtained at this level of stimulation (e.g., Krishnan, 2002; Skoe and Kraus, 2010). Two thousand individual artifact-free sweeps were collected for each stimulus polarity. Artifact rejection was performed online, rejecting any sweeps with voltage exceeding ±30 μV. During FFR recordings, subjects were comfortably seated in a reclined chair in a sound-attenuating booth and they were instructed to relax quietly. For offline processing, FFRs were bandpass filtered from 70 to 2000 Hz (12 dB/octave, zero phase-shift) using NeuroScan Edit 4.3. FFRs were additionally low-pass filtered at 1500 Hz in Matlab (third order Butterworth filter) to remove energy beyond the phase-locking limits of the FFR (Palmer and Russell, 1986; Zhu et al., 2013). These filtering processes did not have a significant effect on F1 and F2 information in the FFR waveforms because F1 and F2 were located below 1500 Hz in the acoustic signals. FFR waveforms were averaged for each stimulus polarity and then subtracted. This method preserves the information of the spectral frequency of the input stimulus in FFR waveforms (Aiken and Picton, 2008).

In order to evaluate the variability in neural representations of formants across listeners and for further model simulations, formant frequencies were extracted from the FFR waveforms using PRAAT software (Boersma and Weenink, 2009). A PRAAT batch processing was run on 152 raw FFR data files, implementing the following parameters: time step = 0.01 s, maximum number of formants = 2, maximum formant = 1500 Hz, window length = 0.04 s, and pre-emphasis filter cutoff = 50 Hz. Out of the 152 raw data files (i.e., 4 vowels × 38 subjects), undefined formant values (i.e., formant estimation failure) were shown for 1.9% of the FFR waveforms. Such FFR waveforms were not included in further data analyses, thus results (i.e., FFR-derived formant values) are reported for 35 subjects. In the middle and bottom rows of Fig. 1, spectrograms of FFR waveforms for two different individual subjects are shown. The middle row shows spectrograms of FFRs recorded from the subject who had the best match between formant frequencies of the original acoustic stimuli and those of the FFR response. In contrast, the bottom row shows spectrograms of FFRs recorded from the subject who showed the greatest difference between formant frequencies of the acoustic stimuli and those of the FFR response, showing a poor representation of formant frequency in FFRs.

D. Vowel identification

A Matlab graphical user interface running on a personal computer was used to present acoustic vowel stimuli to listeners. Stimuli were equated in the same rms value and presented at 80 dB SPL binaurally through magnetically-shielded ER-3 insert earphones, just like it was done for FFR recording. Before testing, subjects listened to each vowel three times by selecting the virtual buttons on the computer screen labeled with each vowel to ensure that they were familiar with the task using these synthesized vowel stimuli. During testing, two random sequences of 40 presentations were created for each subject (4 different vowels × 10 presentations per vowel). Subjects responded by clicking on virtual buttons labeled with each vowel in the /hVd/ context on a computer screen. Thus, percent correct scores for each subject were based on 80 responses, 20 per vowel. Feedback was not provided. The order of vowel identification vs FFR recording was counterbalanced across subjects.

E. MPI model

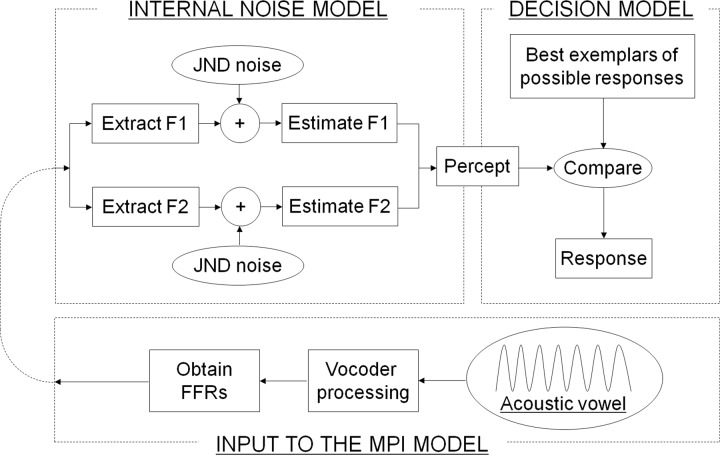
To assess if vowel identification could be predicted by an individual subject's neural representation of the same vowel, the MPI model was implemented. Three steps were used to implement the model. Step 1: dimensions relevant to vowel recognition were postulated, providing a framework for the model. Step 2: the mean location of each vowel along each postulated perceptual dimension was measured. Step 3: Monte Carlo simulation was performed to produce simulated confusion matrices that best fit with each subject's vowel confusion matrices. A detailed description of each step is described below as well as in Sagi et al. (2010b). Figure 2 shows the summary of the MPI model implementation.

FIG. 2.

Implementation of the MPI model. See text for details.

1. Step 1: Define perceptual dimensions

Frequencies of the first two formants (as measured either from the FFRs or from the acoustic waveforms) were defined as the relevant perceptual dimensions for vowel identification by human listeners. Only the first two formants were proposed because FFR is most sensitive below 1500 Hz as indicated above.

2. Step 2: Stimulus measurement

For each individual subject, the formant frequencies (in Hz) were converted to units of distance along the cochlea (millimeters from the most basal turn) using Greenwood's function (Greenwood, 1990), because Greenwood's function captures the relationship between the anatomical positions of the cochlea and their corresponding resonance frequencies in response to sound.

3. Step 3: Monte Carlo simulation

Figure 2 shows two sub-components of the MPI model: an internal noise model and a decision model. The internal noise model postulates imperfect representation of a given stimulus due to sensory and memory noise (Durlach and Braida, 1969), so listeners would have a slightly different perception from successive presentation of the same vowel token. The distribution of the locations of vowel percepts relative to the vowel token locations is modeled with a two-dimensional Gaussian distribution. The center of this Gaussian distribution along each dimension is equal to the value of the mean formant frequency locations (in mm), and the standard deviation is a model parameter proportional to the listener's just-noticeable difference (JND) for the vowel formants. The decision model takes the percept generated by the internal noise model and selects the vowel that has the response center closest to the percept. The “response center” represents the listener's internal exemplar about how a given vowel should sound. Response centers are assumed to be equal to the average locations of vowels in the perceptual space (i.e., stimulus centers). This way, the present study treats listeners as ideal experienced listeners without a bias between the response and stimulus centers. A total of 500 iterations were used to construct a simulated confusion matrix.

F. Model analysis I: Model predictions and comparisons of the formant JND parameters for acoustic and neural conditions

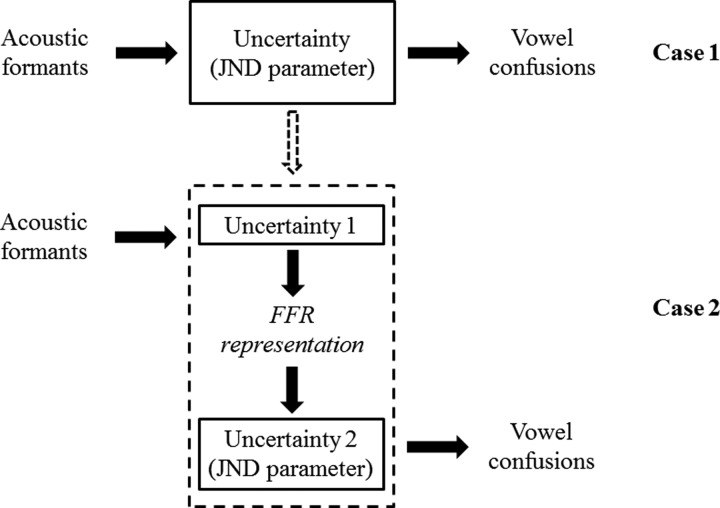
As described above, vowel confusions are related to uncertainty in vowel formant values in the MPI model. This uncertainty can be treated as a black box that includes sensory and memory components (i.e., from peripheral to cognitive processing). The upper row of Fig. 3 (i.e., case 1) illustrates the input and output relationship for vowel confusions when listeners are presented with the acoustic vowel formants. Here, the uncertainty is captured in the JND parameter for the acoustic vowel formants and larger JND parameters are related to more confusion in the behavioral vowel identification performance. Presumably, the uncertainty in the FFR-derived formant values contributes to this chain. With this assumption, the uncertainty in the upper row of Fig. 3 could be broken down into two separate levels: (1) from the acoustic formants to the FFR representations (i.e., “uncertainty 1”), and (2) from the FFR representations to the vowel confusion output (i.e., “uncertainty 2”). In the lower row of Fig. 3, the JND parameter is now only a measure of uncertainty 2, because the uncertainty related to the sensory component is reflected in the FFRs. Based on these theoretical assumptions described above, the first model analysis was designed to test the primary hypothesis of the current study that individual differences in neural encoding of vowel formants may account for a portion of the underlying uncertainty that explains vowel confusions across subjects. If differences in the FFR-derived formant values contribute to the overall uncertainty, then the overall JND parameter in case 1 (i.e., upper row of Fig. 3) should be reduced when the FFR-derived formant values are included in the MPI model (i.e., case 2 in the lower row of Fig. 3) without worsening the fit to the behavioral data. The hypothesis would be supported if this model prediction holds true.

FIG. 3.

Theoretical framework for Model analysis I. See text for details.

To this end, two sets of simulations were performed. For the first set of model simulations, vowel confusion matrices across 35 subjects were pooled together to construct a grand confusion matrix. Then the MPI model was run with acoustic measures of F1 and F2 values (shown in Table I) to find the JND parameter that provides a best fit to the grand confusion matrix by minimizing the rms difference between the model and observed matrices. For each model simulation, the JND parameter was varied independently for F1 and F2 from 0.01 to 3.91 mm in steps of 0.1 mm. The lower bound of 0.01 mm was selected as it represents a reasonable estimate of the frequency discrimination in NH listeners (Moore, 1973). A Monte Carlo algorithm was used to construct 1600 simulated confusion matrices (i.e., 40 JNDs for F1 × 40 JNDs for F2) and compute rms differences between the simulated and observed grand matrices. The rms difference is computed by taking the square-root of the sum of the difference between each element of the simulated and observed matrices divided by the total number of elements in the difference matrix. When calculating rms difference, rows of simulated and observed matrices were expressed in percent, and rms difference is in units of percent. The model-predicted matrix that shows the lowest rms (i.e., min-rms) was defined as the best-fit to the observed matrix, and a percent correct for this best-fit matrix was obtained as a model-predicted score. A total of 1000 model simulations were performed to compute the distributions of rms values and JNDs for F1 and F2 (hereafter referred to as the acoustic MPI condition). For the second set of model simulations, the MPI model was run using mean FFR-derived F1 and F2 values averaged across 35 subjects to find the JND that provides a best fit to the grand confusion matrix by minimizing the rms difference between the model and observed matrices (hereafter referred to as the neural MPI condition). Another 1000 model simulations were carried out to compute the distributions of rms values and JNDs for F1 and F2 for the neural MPI condition. Finally, the distributions of the rms values, and JNDs for F1 and F2 for the acoustic and neural MPI conditions were compared.

G. Model analysis II: Predicting good vs poor performers in the vowel identification task

This analysis was designed to examine predicted vs observed vowel identification scores at several fixed values of vowel formant JND. The goal was not to obtain optimal fits to the data, as previous studies have shown that good fits require assuming that there are individual differences across listeners in JND (Sagi et al., 2010a; 2010b; Svirsky et al., 2011). Instead, the goal of this analysis was to see whether the individual differences indexed by the FFR-derived formant values would have any explanatory power. For each value of JND, the neural MPI model was run to predict the confusion matrix and the corresponding vowel identification score assuming that JND was constant across listeners. Again, because the goal was not to obtain optimal fits but rather to assess the predictive power of a very simple model we also assumed that JND was constant across the two formants (F1 and F2). This analysis was conducted separately for each subject using their own confusion matrix for 6 different values of JND: 0.05, 0.1, 0.2, 0.4, 0.6, and 0.8 mm.

III. RESULTS

A. Vowel identification performance

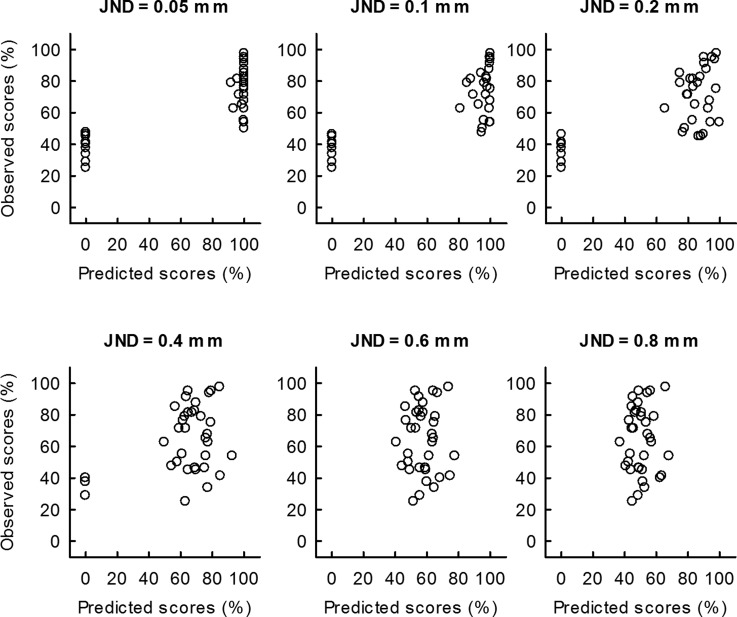
Mean vowel identification performance averaged across 35 subjects was 64.2%. Identification scores for individual subjects are displayed in Fig. 4 along the vertical axis. For the purpose of this initial discussion please disregard scores along the horizontal axis, which represent the model predictions and are discussed later. Note that chance performance for the 4-alternative forced-choice vowel identification test was 25%, which was significantly lower than the observed mean score [t(34) = 11.0, p < 0.001]. More importantly, a wide range of performance was observed in vowel identification, represented by one-standard deviation of 21.0%. Despite the use of only four vowel stimuli, such a wide range of vowel identification performance was observed partly due to the design of the vowel stimuli with which subjects were forced to use partial speech cues (i.e., formant information only) to identify vowels. There was no significant correlation between the subjects' ages and vowel identification scores.

FIG. 4.

Vowel identification scores measured from human subjects vs scores predicted by the MPI model for fixed JND values of 0.05, 0.1, 0.2, 0.4, 0.6, and 0.8 mm are shown. Despite the coarseness of the implementation, the model accurately predicts good and bad performers for a wide range of JND values (0.05 to 0.2, inclusive). Predictions become weaker for higher values of JND.

B. Neural representations of formant frequencies

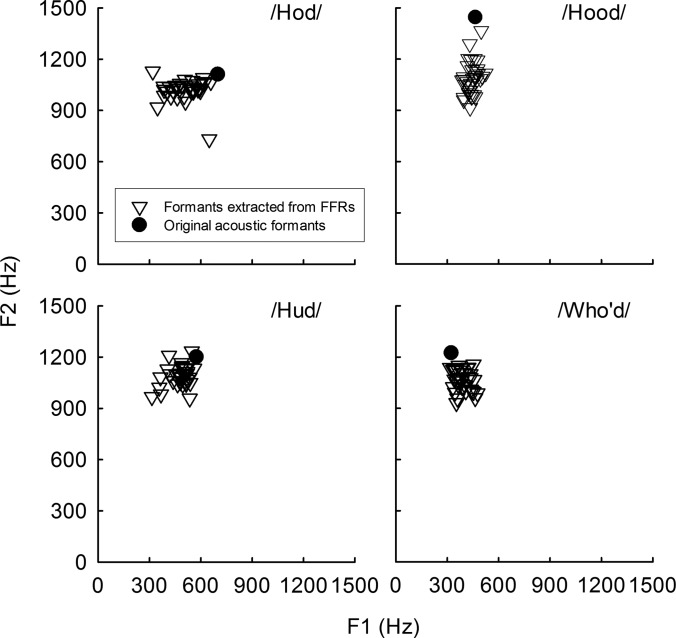
Figure 5 shows scatterplots of F1 and F2 that were estimated from individual subjects' FFR waveforms in response to the synthetic vowel stimuli. Some subjects showed F1 and F2 extracted from FFRs that were fairly close to the original acoustic F1 and F2 values for the synthetic vowels. Most importantly, for each synthetic vowel, there was substantial variability in F1 and F2 extracted from FFRs across subjects. Visual inspections on Fig. 5 show that for the vowel /ɑ/ (i.e., /Hod/), the variation in F1 extracted from FFRs was more variable than the variation in F2, but for the vowels /u, ʊ/ (i.e., who'd and hood) the variation in F2 was more variable than the variation in F1. To test whether F1 and F2 values extracted from FFRs significantly differed across subjects, two separate one-way repeated measures analysis of variance (RM ANOVA), one for F1 and another one for F2, were conducted with subject as a factor. The Shapiro-Wilks test for normality indicated that the distribution of F1 values extracted from FFRs was normally distributed. However, the distribution of F2 values was not normally distributed; thus for F2 values, we report results for RM ANOVA on ranks. These RM ANOVA analyses indicated that the effect of subject on F1 values extracted from FFRs was significant [F(34, 102) = 2.43, p < 0.001]. The effect of subject on F2 values extracted from FFRs was also significant [df = 34, Chi-square = 59.4, p = 0.004]. Therefore, these results are consistent with the previous studies (e.g., Bidelman et al., 2014; Sadeghian et al., 2015; Anderson et al., 2012; Ruggles et al., 2011, 2012) that neural representations of formants differ across individual listeners.

FIG. 5.

Scatterplots of first (F1) and second (F2) formant frequencies estimated from FFR waveforms (shown as triangles) for individual listeners. Original F1 and F2 frequencies for the synthetic vowel stimuli that were used to evoke FFRs are shown as filled circles.

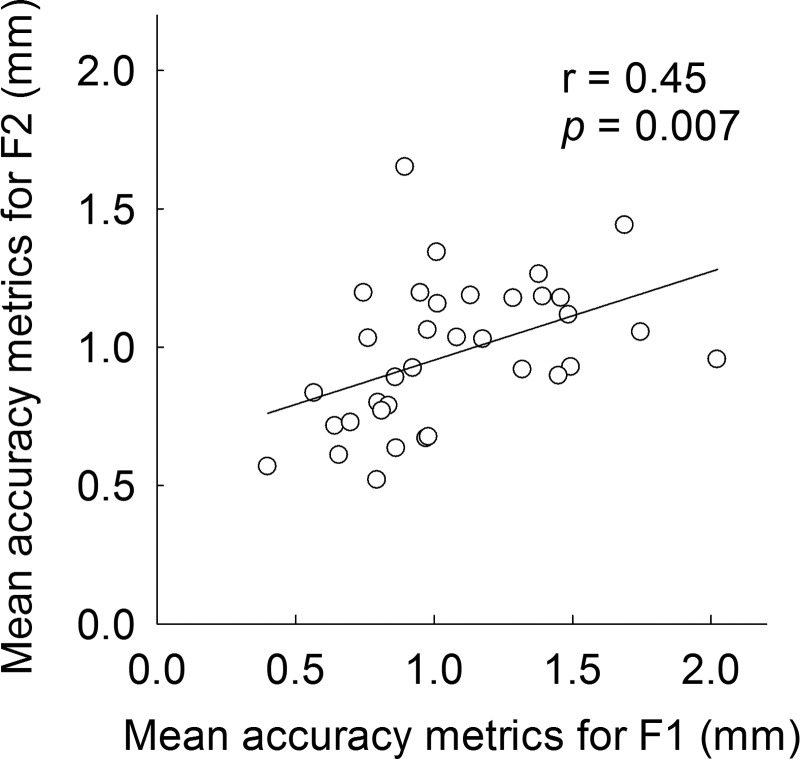
The accuracy of neural encoding of vowel formant was quantified with an assumption that subjects showing a smaller difference between the original and FFR-derived formant frequencies may have more accurate neural encoding of vowel formants. For this analysis, the original formant frequencies shown in Table I and FFR-derived formant frequencies (in Hz) for each subject were converted to units of distance along the cochlea (mm from the most basal turn) using Greenwood's function (Greenwood, 1990). Then differences (in mm) between the original and FFR-derived formant were computed for F1 and F2 for the four vowels. Finally, mean differences averaged across the four vowels were computed for each individual subject. Hereafter, these mean differences are referred to as the “accuracy metric.” Figure 6 shows that there was a significant correlation (r = 0.45, p = 0.007) between the accuracy metrics for F1 and F2, suggesting that listeners with a better F1 representation also showed a better F2 representation in the FFR waveforms. However, there were no significant correlations between the accuracy metrics (both for F1 and F2) and vowel identification scores, highlighting the importance of mathematical models to link physiologic data to behavioral performance. Furthermore, there were no significant correlations between the accuracy metrics and subjects' age.

FIG. 6.

Relationship between the “accuracy metrics” for F1 and F2. See text for details. A linear regression is represented by the solid line.

C. Model analysis I

For model analysis I, two different sets of model simulations were done. For both simulations, the MPI model used a grand confusion matrix that was pooled together across 35 subjects. For the first condition (referred to as the “acoustic” MPI condition), the model was run with acoustic measures of F1 and F2 values that are shown in Table I. For the second condition (referred to as the “neural” MPI condition), the FFR-derived formant frequencies were provided to the model.

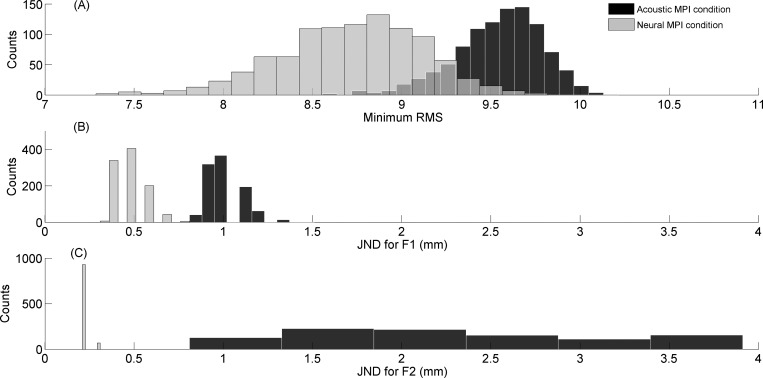
Figure 7(A) shows histograms of minimum rms (min-rms) values for the acoustic (black bars) and neural (gray bars) MPI conditions out of 1000 model simulations. Mean min-rms values for all considered JND combinations averaged across 1000 simulations were 9.54% for the acoustic MPI condition and 8.72% for the neural MPI condition. An independent samples t-test indicated that min-rms values for the neural MPI condition were significantly smaller than for the acoustic MPI condition (p < 0.001). Similar patterns were observed for model JNDs for both F1 [Fig. 7(B)] and F2 [Fig. 7(C)], showing that JND parameters for F1 and F2 were significantly smaller for the neural than for the acoustic MPI conditions. These model simulations demonstrate that the JND parameters were significantly reduced in the neural MPI condition without worsening the fit to the observed vowel confusion matrix from human subjects.

FIG. 7.

Histograms of minimized rms values (A) and associated input JNDs for F1 (B) and F2 (C) that provided a best fit to the observed grand confusion matrix. Each histogram represents multiple iterations of the following procedure. Model-predicted confusion matrices were generated for different JND values (i.e., 40 JNDs for F1 × 40 JNDs for F2). The model-predicted matrix that showed the minimum rms difference from the observed grand confusion matrix was chosen as the best-fit. This procedure was repeated 1000 times and resulting minimized rms values and associated JND inputs were compiled to produce the histograms. Black and gray bars indicate the acoustic and neural MPI conditions, respectively.

D. Model analysis II

Two different types of approaches were used to assess the ability of the MPI model to predict vowel identification scores for each simulated JND value: (1) simple comparison of the observed and predicted vowel identification scores, and (2) examining the potential relationship between the observed vowel scores and the JND values that produced the best-fit. The first approach compared observed and predicted scores across subjects, which are shown in Fig. 4 for each fixed value of JND. The top left panel shows results for a JND of 0.05 mm. Clearly, the prediction is not 100% accurate. Most predicted percent correct values are either very poor (essentially zero) or very good (100% correct or at least close to that). What is remarkable here is that all 11 subjects who were predicted to show poor performance indeed scored below 50% correct and all 24 subjects who were predicted to show good performance had scores of 50% or higher. In other words, a prediction obtained with zero degrees of freedom and based only on physiological data was perfectly accurate in terms of predicting good vs poor performers, as shown in the top left panel of Table II. Predictions obtained with JND values of 0.1 or 0.2 also resulted in very accurate predictions of good vs poor performers (see two rightmost top panels of Table II). Higher values of JND resulted in weaker predictions, as can be observed in the bottom panels of Fig. 4 and Table II.

TABLE II.

Summary of MPI predictions for the model analysis II. Two-by-two contingency tables are shown for each modeled JND; comparing observed and predicted vowel identification performance. A cutoff value of 50% was used to separate 34 subjects into “good” and “poor” performers on the vowel identification test.

	JND = 0.05 mm		JND = 0.1 mm		JND = 0.2 mm
	Observed ≥ 50%	Observed < 50%	Observed ≥ 50%	Observed < 50%	Observed ≥ 50%	Observed < 50%
Predicted ≥ 50%	24	0	24	1	24	4
Predicted < 50%	0	11	0	10	0	7
	JND = 0.4 mm		JND = 0.6 mm		JND = 0.8 mm
	Observed ≥ 50%	Observed < 50%	Observed ≥ 50%	Observed < 50%	Observed ≥ 50%	Observed < 50%
Predicted ≥ 50%	23	8	19	9	12	5
Predicted < 50%	1	3	5	2	12	6

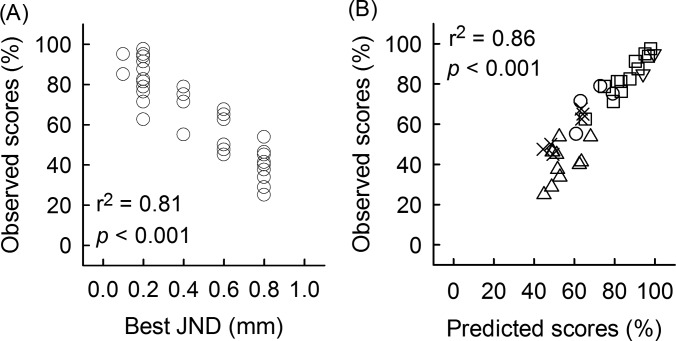
With regard to the second approach, data shown in Fig. 4 and Table II illustrate a trend for individuals with higher (i.e., better) observed vowel identification scores to have more accurately predicted vowel identification scores with JND values less than 0.4 mm (i.e., better formant discrimination). Given these patterns, the second type of measure utilized a more global comparison between model predictions and observed vowel identification performance. For this analysis, of the six possible JND parameter values, the one that best estimated each subject's observed vowel identification score was determined. Then each subject's observed vowel identification score is plotted as a function of these best JND values. Figure 8(A) shows that there was a significant correlation between best-predicted JNDs and observed vowel identification scores, supporting the prediction that subjects with better vowel identification performance show more accurately predicted vowel identification scores with smaller JND values. To examine if subjects' ages affected this analysis, a correlation was computed between subjects' ages and best JND values; however, there was no significant correlation.

FIG. 8.

(A) Relationship between the best JND values that showed most accurate predictions and observed vowel identification scores. (B) The predicted vowel identification scores that were most accurate are plotted against the observed scores for each subject. Different JNDs are represented by the following symbols: 0.1 mm (down triangles), 0.2 mm (squares), 0.4 mm (circles), 0.6 mm (×), 0.8 mm (up triangles).

Next, predicted scores obtained with these JND values that showed the best fits were used for an additional linear regression analysis. This analysis was done with the expectation that allowing the JND value to be variable across subjects may result in a more accurate prediction by allowing for individual variability. Figure 8(B) illustrates that observed vowel identification scores were accurately predicted when an individual's best predicted score was used (r²= 0.86, p < 0.001). In Fig. 8(B), different symbol types represent predicted scores from different JND parameter values. Higher observed scores were best associated with smaller JNDs (i.e., better formant discrimination), while poorer observed scores were best associated with larger JNDs (i.e., poorer formant discrimination).

IV. DISCUSSION

A. Variability in neural encoding of F1 and F2 across individual subjects

In the current study, a multidisciplinary approach was used employing psychoacoustics, electrophysiology, and a computational model to understand the effects of neural encoding of formants on behavioral vowel recognition. Formant locations were estimated from far-field recordings of the FFR from human subjects. Within individual listeners, different neural activities associated with F1 and F2 were observed across the four different vowel stimuli. Substantial across-subject variability was also observed in the F1 and F2 values extracted from the FFR waveforms.

Previous studies have demonstrated that JNDs for vowel formant discrimination for NH subjects depend on the formant frequency being tested and measurement methods as well (e.g., Liu and Kewley-Port, 2004; Oglesbee and Kewley-Port, 2009). For example, Oglesbee and Kewley-Port (2009) tested 11 NH subjects on vowel formant discrimination using a 2-alternative forced-choice paradigm for the first two formant frequencies of the vowels /ɪ/ and /ʌ/. Oglesbee and Kewley-Port's JND values for F1 and F2 for the vowels /ɪ/ and /ʌ/ corresponded to 0.31–0.48 mm with respect to the cochlear locations for F1 and F2. More importantly, Oglesbee and Kewley-Port (2009) observed a wide range of across-subject variability in formant frequency discrimination thresholds, which is largely consistent with the across-subject variability in the neural encoding accuracy of formant frequencies found in the current study (Fig. 4). Furthermore, the effects of subject on F1 and F2 values extracted from FFRs reached were significant, suggesting that neural representations of vowel formants would differ across individual listeners.

B. Contribution of variability in neural encoding of formants to vowel confusion patterns

The variability observed in vowel identification scores and FFR-derived formant values raised the possibility of predicting vowel identification performance based on physiological responses. To explore this possibility, the current study used the MPI model to link the neural encoding of formant frequencies to behavioral vowel identification performance. Two sets of model analyses were performed. Model analysis I compared the distributions of rms values and JNDs for F1 and F2 that provides a best fit to the observed grand confusion matrix when acoustic formant values were provided to the model vs when FFR-derived formant values were provided to the model. These model simulations demonstrated that the minimum rms values and JND parameters were significantly smaller for the neural MPI condition.

In the MPI model, vowel confusions were related to uncertainty in formant values. This uncertainty was treated as a “black box” that included sensory and memory components (i.e., early and late stages of auditory processing) (see case 1 in Fig. 3). Therefore, this uncertainty could be further divided by two separate levels: one is from the acoustic formants to the FFR representations (i.e., reflecting early auditory processing) and another is from the FFR representations to the vowel confusion output (i.e., reflecting late stage of auditory processing) (see case 2 in Fig. 3). In the acoustic MPI condition, the model outputs (e.g., minimum rms, JNDs for F1 and F2) were expected to capture the uncertainty of the entire peripheral and central processing. In contrast, for the neural MPI condition, the uncertainty of the neural processing up to the generator of FFRs (i.e., inferior colliculus; Smith et al., 1975) was already inferred by F1 and F2 values extracted from FFRs; therefore, the model outputs might be more restricted to the uncertainty of higher levels of central processing beyond the inferior colliculus.

With this theoretical framework of the model implementation shown in Fig. 3, we predicted that the overall minimum rms values and JNDs for F1 and F2 would be reduced in the neural MPI condition without worsening the fit to the observed grand confusion matrix. Note that for the neural MPI condition for model analysis I, mean FFR-derived F1 and F2 values for the four vowels averaged across 35 subjects were used as an input to the MPI model. For the acoustic MPI condition, four sets of the acoustic F1–F2 locations of the vowels were provided as an input to the MPI model. The results for model analysis I showed that the neural MPI condition provided a slightly better fit to the group vowel matrix with lower values of the JND parameters in comparison to the acoustic MPI condition (Fig. 6). This observation supports the hypothesis of the current study that neural representations of formant values (inferred by FFR-derived formant values) may account for a portion of the underlying uncertainty that explains vowel confusion patterns in NH subjects. Furthermore, this finding suggests the intriguing possibility that a better account of the group vowel confusion pattern may be obtained with neurally-derived formant values than with acoustic formant values.

C. Model predictions of vowel identification using physiological responses

Model analysis II provided interesting information in support of the hypothesis of the current study that individual differences in neural encoding of vowel formants may account for a portion of the underlying uncertainty that explains vowel confusions across subjects. Recall that the predicted scores in each panel in Fig. 4 were obtained based only on physiological data, with zero degrees of freedom. The predictions were not perfect and we should not expect them to be perfect because different listeners are likely to have different JNDs. Nonetheless, the predictions of good vs poor listeners (defined as those whose scores were above or below 50% correct) were remarkably accurate for a wide range of possible JND values, from 0.05 to 0.2 mm as shown in Table II. This suggests that the FFR captures important information about early stages of speech processing in the auditory system, given that FFRs reflect brainstem level activity (e.g., inferior colliculus; Smith et al., 1975). Neural activity related to FFRs can be modulated by listening experience and may contribute to individual differences (Krishnan et al., 2012; Chandrasekaran and Kraus, 2010). Further studies are needed to better understand how the early and late (i.e., central) auditory processing explain listeners' vowel identification performance.

D. Implications of the use of mathematical model to link perceptual and neural data

The approach shown in the current study is particularly useful for understanding the encoding of speech cues in the central auditory system. It advances our current state of knowledge that has been limited mostly to animal models of auditory-nerve responses. For example, Swaminathan and Heinz (2012) related consonant identification measured from human listeners to the temporal processing quantified from a phenomenological model of the cat's auditory-nerve (Zilany and Bruce, 2006, 2007). Furthermore, Svirsky et al. (2011) showed that many aspects of consonant identification from a degraded signal (such as the one provided by a cochlear implant) may be based on identification of the relevant formant frequency values. Here, we measured vowel identification and vowel-elicited FFRs from the same group of human subjects using the same set of stimuli, allowing us to develop a more direct comparison between the perceptual and neural domains. This is an important aspect of the design of the current experiment in light of the mounds of evidence documenting the role of central auditory processing in speech perception (for reviews, see Molfese et al., 2005). Previous FFR studies also demonstrated such evidence (Galbraith et al., 1995; Parbery-Clark et al., 2009; Song et al., 2011; Marmel et al., 2013); however, these studies recorded electrophysiological responses using one stimulus (e.g., a synthesized speech syllable) and compared them to behavioral measures that are cognitively and linguistically loaded using completely different sets of speech stimuli (e.g., sentence recognition in noise). Such an approach is useful when evaluating normal and disordered neural coding in different subject populations with different ages (Anderson et al., 2012), neurological diseases (Hornickel and Kraus, 2013), and different degrees of musical training (Parbery-Clark et al., 2009; Skoe and Kraus, 2012), but less sensitive when investigating the specific relationship between acoustic cues and speech perception.

The present study demonstrates how the MPI model can be used to study vowel perception and encoding for NH listeners, making it possible to analyze the relationship between behavioral and physiological data. This may be partly due to the design of the vowel stimuli with which subjects were forced to use partial speech cues to identify vowels (i.e., formant information only). In the current experiment, the implementation of the MPI model was specific to static formant coding. Given the numerous cues for vowel identification, this implementation is rather simple; however, the framework can easily be used to assess other acoustic cues, e.g., F0 and formant transitions, spectral envelope shape, or vowel duration. Moreover, the experimental and modeling design here will be readily applicable to understand the neural coding of speech cues when the original speech signals are degraded either by the presence of background noise or by the signal processing for hearing prostheses.

Furthermore, one can combine physiologically plausible auditory-nerve models (e.g., Patterson et al., 1995; Zilany and Bruce, 2006, 2007; Zilany et al., 2014; Ronne et al., 2012) with the general framework of the present study to take into account the contribution of peripheral auditory processing. The MPI model did not take into account the effect of a temporal coding deficit in the current study. However, one can process vowel waveforms using the vocoder processing proposed by Lopez-Poveda and Barrios (2013), which provides researchers with a useful tool to manipulate signals to test specific hypotheses. Then, the vocoded vowels could be presented to listeners for vowel identification, FFR recordings, and the MPI model analysis. This point is particularly important for hearing prostheses given that there is an increasing awareness of the importance of central processing for performance when using hearing aids or cochlear implants (Friesen et al., 2009; Billings et al., 2011; Tremblay and Miller, 2014). In addition, previous work has shown abnormal brainstem encoding to occur for both simple and complex signals in middle-aged and older people; the population most often affected by decreased speech understanding related to peripheral and central aspects of presbycusis (Clinard et al., 2010; Clinard and Tremblay, 2013). Such information may guide efforts to develop hearing prostheses to enhance neural coding of important speech cues.