Droplet-based microfluidics platform for measurement of rapid erythrocyte water transport

Abstract

Cell membrane water permeability is an important determinant of epithelial fluid secretion, tissue swelling, angiogenesis, tumor spread and other biological processes. Cellular water channels, the aquaporins, are important drug targets. Water permeability is generally measured from the kinetics of cell volume change in response to an osmotic gradient. Here, we developed a microfluidics platform in which cells expressing a cytoplasmic, volume-sensing fluorescent dye are rapidly subjected to an osmotic gradient by solution mixing inside a ~ 0.1 nL droplet surrounded by oil. Solution mixing time was < 10 ms. Osmotic water permeability was deduced from a single, time-integrated fluorescence image of an observation area in which time after mixing is determined by spatial position. Water permeability was accurately measured in aquaporin-expressing erythrocytes with half-times for osmotic equilibration down to < 50 ms. Compared with conventional water permeability measurements using costly stopped-flow instrumentation, the microfluidics platform here utilizes sub-microliter blood sample volume, does not suffer from mixing artifact, and replaces challenging kinetic measurements by a single image capture using a standard laboratory fluorescence microscope.

Introduction

The water permeability of cell membranes is a subject of great interest. Many cell membranes are highly water permeable because of expression of membrane water channels, called aquaporins (AQPs).¹ High cell membrane water permeability facilitates a number of fundamental biological processes, including epithelial fluid secretion, cell migration, neuroexcitation and brain swelling.^2–4 The aquaporin water channels are considered important drug targets for development of small molecule modulators, whose broad clinical indications are predicted to include edema, cancer, epilepsy, wound healing and others.⁵

Measurement of cell membrane water permeability is crucial in elucidating the roles of aquaporins in various organ and cellular function, in studying disease pathogenesis mechanisms, and in drug discovery. For example, loss-of-function mutations in the AQP2 water channels cause the inherited disease nephrogenic diabetes insipidus in which low water permeability in kidney collecting duct epithelial cells impairs urinary concentrating function.⁶ Determination of water permeability across cell plasma membranes generally involves measurement of the kinetics of cell volume change in response to an osmotic challenge.^7,8 A variety of experimental approaches have been developed to subject cells to an osmotic gradient and record the resultant kinetics of cell volume from which water permeability is deduced.⁹ However, the available methods to measure osmotic water permeability are technically challenging, require many cells, are subject to various mixing/flow-related artifacts, and are not easily applied to highly water-permeable cells. The poor progress in identification of aquaporin-targeted therapeutics has been considered to be due, in part, to challenges and artifacts in measurement of cell membrane water permeability.⁵

Here, we developed a droplet-based microfluidics approach to measure cell membrane osmotic water permeability using ultra-small volumes of cell suspensions, without the need for specialized instrumentation such as stopped-flow mixing devices. Following the original descriptions of Thorsen et al.¹⁰ and Anna et al.¹¹ in which monodisperse droplets of nanoliter or picoliter volume were generated, droplet-based microfluidics has been applied to a variety of fluid- and cell-based assays¹² based on the efficient mixing inside the droplet by chaotic advection.¹³ However, the challenge in existing channel designs is in accomplishing fast mixing (< 10 ms) and long-time measurement ( > 1 s), largely because fast mixing requires a high flow rate and long-time observation requires a long channel, which produces a high pressure drop.

Here, we used a droplet microfluidics device in which a mixing channel was combined with ‘delta’ geometry, as in a river delta, in which equal fluid exit pressure was produced by a symmetrically repeated microstructure. As diagrammed in Fig. 1A, an aqueous stream containing fluorescently labeled cells is mixed with a second solution, of different osmolarity, and encapsulated inside ~ 0.1 nL droplets surrounded by mineral oil. A central stream of aqueous, isosmolar solution prevents pre-mixing prior to droplet formation. Passage of the fused droplet through a mixing region exposes cells to an osmotic gradient with mixing time of a few milliseconds. The droplet then passes into a wide observation area in which time (after mixing) is deduced from droplet velocity. A single, time-integrated fluorescence image gives the kinetics of cell volume in response to an osmotic challenge from which osmotic water permeability is computed. The microfluidics method was validated and applied to measure and characterize aquaporin-facilitated osmotic water permeability in erythrocytes, as well as the permeability of small, polar non-electrolytes such as urea.

Figure 1.

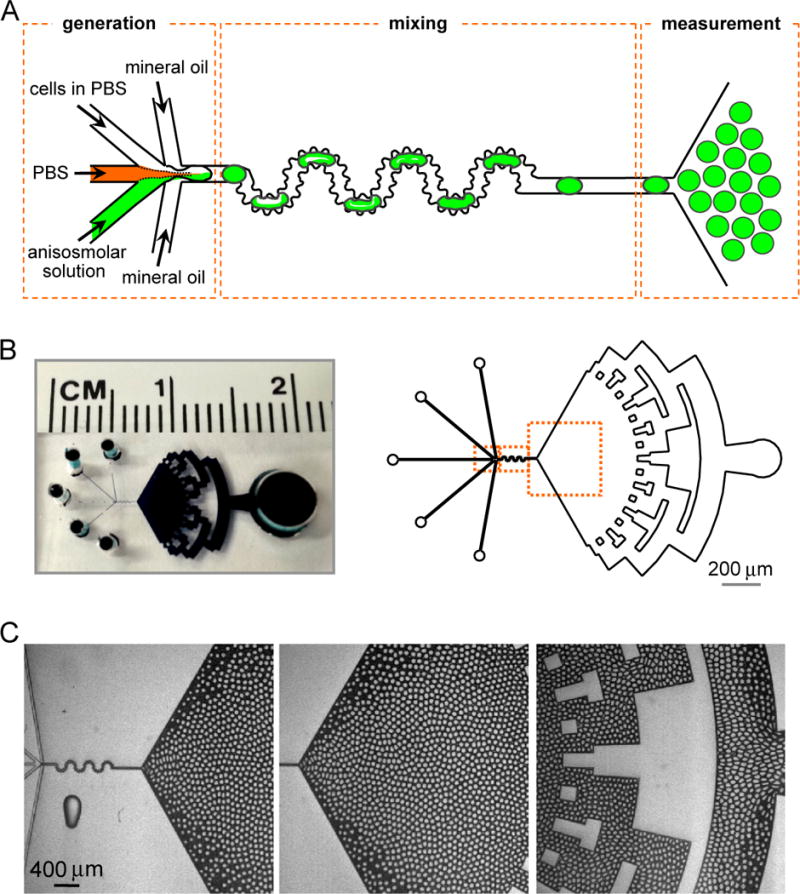
Microfluidic channel for water permeability measurement. A. Channel design, showing generation of droplets, mixing area and triangular measurement area. B. Photograph of dye-filled channel (left) and diagram of entire channel (right) showing injection ports and a symmetrically repeated microstructure for fluid exit. C. Light micrographs showing generation of monodisperse droplets (left), stable droplet pattern in the observation area (center), and symmetrical pattern formation during fluid exit (right) (see related Supplementary Videos SV1 and SV2).

Methods

Microfluidic channel fabrication

The microfluidic channel was fabricated on a 4-inch silicon wafer (Addison Engineering Inc., USA) using standard soft lithography procedures.^14,15 Replica PDMS channels were molded on the silicon wafer by pouring a 5:1 mixture of PDMS base and curing agent (DA-184A and DA-184B, Dow Corning, USA), followed by 14-min incubation at 80 °C in a natural convection oven (model 107800, Boekel Scientific, USA). The PDMS plate was made by pouring a 20:1 mixture of PDMS base and curing agent on a cover glass and incubating for 10 min at 80 °C. The PDMS replica was fabricated using an excess of the base (DA-184A), whereas the PDMS plate contained an excess of the curing agent (DA-184B). The PDMS replica was peeled off of the wafer, adhered to the PDMS plate, and incubated for 2 hours at 80 °C. This plasma-free channel fabrication method makes a tight bind with hydrophobic surface channels for droplet microfluidics.^16,17

Microfluidics platform setup

The microfluidics chamber and three syringe pumps (Gemini 88 dual syringe pump, KDS 200, KD Scientific, USA) with 250-μl Luer-lock glass syringes (Hamilton, 1700 series, USA) were connected using Teflon tubing and connectors (P-659 and F-331Nx, Upchurch, USA), and mounted on the stage of an inverted epifluorescence microscope (ECLIPSE TE2000-U, Nikon, USA). As diagrammed in Fig. 1A, a total of five syringes were used to inject mineral oil containing 1% oil surfactant (Span 80, Sigma-Aldrich, USA), PBS, a cell suspension in PBS, and an anisosmolar solution.

An EMCCD camera (Digital camera C9100, Hamamatsu, Japan) was used for fluorescence image recording. In some studies a high-speed camera (NAC, Memrecam GX-3, Japan) with intensifier (UVi 1850-10, Invisible Vision Ltd., UK) was used to capture droplet generation images. Imaging was done using a 4× or 10× magnification lens (Plan Fluor, Nikon, Japan) for short-time measurement (~ 1 s) and 2× (Plan UW, Nikon, Japan) for long-time measurement (~ 5 s).

Determination of mixing time

Solution mixing time was determined from the quenching of fluorescein-dextran (70 kDa, Sigma-Aldrich, USA) by iodide using KI (Sigma-Aldrich, USA).¹⁸ Channels were perfused with a 1 μM fluorescein-dextran in PBS and 500 mM KI in PBS at a total flow-rate of 1300 μl/h, which produces ~40% fluorescence quenching. Because of the non-uniformity of the bumpy mixing channel, fluorescence intensity was area-integrated along the mixing portion of the channel. The time at the each location was calculated by dividing volume by flow velocity; ‘dead time’, t_dead, defined as the time between solution mixing and observation, was computed from total length of the mixing channel.

Deduction of time from spatial position

Time after solution mixing at each position in the triangular observation area was deduced by velocity field measurement. Fluorescent particles (7-μm diameter, Bangs Lab, USA) were injected and encapsulated inside droplets, which moved in a radial direction in the observation area, generating streak-lines from which velocities were calculated by dividing streak-line length by exposure time. Streak-lines were measured in the entire velocity field using 4× magnification lens and 100 ms exposure time for 500 μl/h flow rate, which was combined images taken with a 10× magnification lens and 20 ms exposure time was used for better resolution in the early part of the observation area. For the higher flow rate (1200 μl/h), 20 ms, 5 ms and 2 ms exposure times were used for 4×, 10× and 20× lenses, respectively. The analysis was restricted to the central 60-degree area (of the full 120-degree triangular area) because small satellite droplets detaching from the primary droplets move along the near-boundary region. The time after mixing, t, was deduced by integrating the radial velocity, V(r): t = ∫ 1/V(r) dr.

Water permeability measurement

Calcein-labeled erythrocytes, anisosmolar solution, PBS, and mineral oil were injected for ~ 1 min to generate a stable droplet pattern in the observation area. Total flow rates was 1200 μl/h. After confirmation of a stable droplet pattern, the white light source was turned off. Calcein fluorescence was excited at 500 nm using an excitation filter (ET500/20x, Chroma Technology Corp., USA) and detected at 535 nm through emission filter (ET535/30m (EM), Chroma Technology Corp.). Compounds 1 and 3 (reported as AQP1 inhibitors¹⁹) were purchased from ChemBridge (San Diego CA); AqB013²⁰ was synthesized from furosemide in two steps, and AqF026 was synthesized by the reported procedure.^{21 1}H-NMR and LC-MS (ESI) of AqB013 and AqF026 matched reported data.

The fluorescent cell-containing droplets travel in a radial direction in the triangular observation area (Fig. 2A, left), which generates fluorescent streak-lines for a short exposure time (Fig. 2A, right). The fluorescence signal, F(r,θ), decreases with radial expansion and increases with decreased velocity: F(r,θ) ~ 1/r×1/V(r) ~ 1/r×r ~ constant, where V(r) is velocity as deduced from streak-line analysis as described above. A uniform fluorescence field is thus predicted in the observation area with perfusion of an isosmolar solution (Fig. 2B, left). However, in practice, the field was slightly non-uniform at the near-boundary because of small satellite droplets movement, and in the central observation area because of non-uniform droplet density as the inter-droplet space increases with radial expansion, with the droplets are more compacted in the beginning part of the triangular observation area. The slight non-uniformity was corrected by normalizing F(r,θ) measured in the presence of an osmotic gradient to that measured in the absence of an osmotic graidient. Iso-timelines were deduced as described in the ‘Deduction of time from spatial position’ section above.

Figure 2.

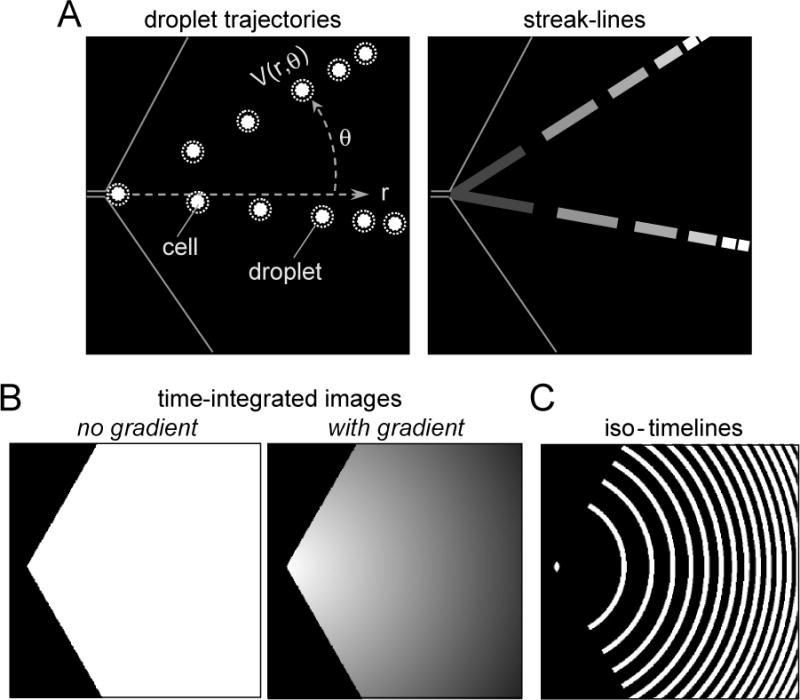
Velocity field determination by streak-line analysis and water permeability measurement. A. Schematic showing radial droplet trajectories (left) and fluorescent streak-lines measured using short exposure time (right). B. Time-integrated fluorescence fields in the absence (left) and presence (right) of an osmotic gradient. C. Iso-timelines deduced as described in the ‘Deduction of time from spatial position’ section.

The fluorescence signal changes were analyzed using Matlab (The Mathworks, version 7.1). The triangular measurement area was divided into multiple iso-timeline masks with equal spacing in radius (50 or 100 μm) using the central 60-degree area of the observation region, and the fluorescence signal was summed and averaged in each iso-timeline mask. The standard deviation was determined from three 10-s time-integrated fluorescence images. The mean background signal was subtracted from the fluorescence signal. The approximate water permeability coeffient (P_f) was computed as: dV/dt = P_fv_wS/V(ΔOsm), where v_w is the molar volume ratio, S/V the surface-to-volume ratio and ΔOsm the osmotic gradient.

Erythrocyte labeling

Whole blood was collected from ~12 wk-old wild-type, AQP1-null²² and UT-B-null²³ mice in a CD1 genetic background. Human blood was obtained from a single donor. The collection of mouse blood was done in compliance with UCSF guidelines and approved by the UCSF committee on animal research. Human blood from a single donor was obtained with proper explanation and consent. Erythrocytes were washed 3 times with PBS (3000 × g, 15 min) and then fluorescently labeled by incubation with 15 μM calcein-AM (Invitrogen, USA) at 37 °C for 1.5 h. Erythrocytes were then washed twice with PBS (3000 × g, 10 min) to remove extracellular calcein-AM and diluted 15-fold in PBS. For AQP1 inhibition studies, erythrocytes were incubated with 4-chloromercuribenzenesulfonic acid (pCMBS) (Carbosynth LLC, UK) at 37 °C for 30 min before assay. For testing of other putative AQP1 modulators, erythrocytes were incubated with compounds in DMSO (0.5 % final DMSO concentration) for 10 min at a concentration of 50 μM.

For microfluidics, erythrocytes (equivalent to 15 μl whole blood) were mixed with 200 μl PBS, which allowed for multiple measurements, with less than 10 μl needed for one measurement (15 μl × 10 μl/(200 μl) ~ 0.75 μl whole blood).

Stopped-flow measurements

The permeability of erythrocytes to water and urea analogs was measured by stopped-flow light scattering using a Hi-Tech Sf-51 instrument (Wiltshire, UK) as described.²⁴ Briefly, dilutions of whole blood in PBS (hematocrit ~0.5%) were subjected to inwardly directed gradient of NaCl, urea, methylurea and acetamide. The resultant kinetics of cell volume were measured from the time course of 90° scattered light intensity at 530 nm, with decreasing cell volume resulting in increased scattered light intensity. For testing of putative AQP1 modulators, compounds were incubated with the erythrocyte suspension for >10 min at 50 μM prior to stopped-flow measurement.

Computation of osmotic water permeability (P_f)

P_f (in cm/s) was calculated from the initial slope of the calcein fluorescence quenching curve induced by osmotic challenge,

$$\mathrm{dV}/\mathrm{dt}={\mathrm{P}}_{\mathrm{f}}{\mathrm{v}}_{\mathrm{w}}({\mathrm{S}}_{\mathrm{o}}/{\mathrm{V}}_{\mathrm{o}})\left({\mathrm{C}}_{\mathrm{i}}\right(\mathrm{t}=0)-{\mathrm{C}}_{\mathrm{o}})$$ (1)

where V is cell volume normalized at t = 0, v_w is the partial molar volume of water (18 cm³/mol), S_o/V_o is initial cell surface-to-volume ratio, C_i the initial cell osmolarity and C_o the outside osmolarity.²⁵ Erythrocyte S_o/V_o was taken to be ~1.5 μm⁻¹, as reported.²⁶

Results

Microfluidic channel design

The design specifications for the microfluidic channel included rapid mixing of a cell suspension with a solution of different composition, and optical measurement of cell fluorescence for many seconds following mixing. Fig. 1A shows the microfluidic channel design, which consists of generation, mixing and measurement regions. The generation region contains inlets to inject the cell suspension and a solution of different composition to impose an osmotic or solute concentration gradient; in addition, a third, central inlet is used to inject an aqueous fluid stream of the same composition as the cell-containing solution to prevent pre-mixing of the cell-containing and second aqueous solutions prior to droplet formation. Two injection port are used to infuse oil. Droplets are formed by two immiscible fluids, such as water and oil, by a pressure build-up mechanism at low flow rates, or by a shear-induced mechanism in high flow rates.²⁷

The serpentine and bumpy channel design facilitates efficient mixing within the newly formed droplets.^{13, 28} The bumpy channel was designed with average size of 40 μm with 20 μm roughness. A triangular observation area allowed observation of droplets during their radial movement, with their velocity inversely proportional to radial distance, which allowed long-time measurement. In order to generate a symmetric radial velocity field, with angle-independent ‘iso-time lines’, the outer boundary of the observation area was designed to have equal pressures using a symmetrically repeated microstructure.

A photograph of the channel, with overall dimensions 40-μm width, 40-μm thickness and 20-mm length, is shown in Fig. 1B. Fig. 1C shows the aqueous droplets, surrounded by oil, in the channel generation, mixing and observation regions (Supplementary Video SV1). After their formation and passage through the mixing region, the droplets travel in a radial direction. Fig. 1C (center) shows a stable pattern of monodisperse droplets in the observation region. Fig. 1C (right) shows symmetrical pattern formation by the repeated microstructure. Stable droplet patterns are were seen within 1 min after start of perfusion (Supplementary Video SV2).

Microfluidic channel characterization

Droplet volume in the experiments reported here is typically ~0.1 nL, which could be varied by changing flow rates or channel width. T-junction channels¹⁰ or focusing channels¹¹ have been used to generate droplets. We used a focusing channel with unequal oil flow rates in order to enhance mixing efficiency, as diagrammed in Fig. 3A. Rapid video imaging (1000 Hz) in Fig. 3B and in Supplemental Video SV3 shows droplet images in the generation and mixing regions. The unequal oil flow rates generate a horse-shoe-shaped solution composition profile, which enhances mixing efficiency.

Figure 3.

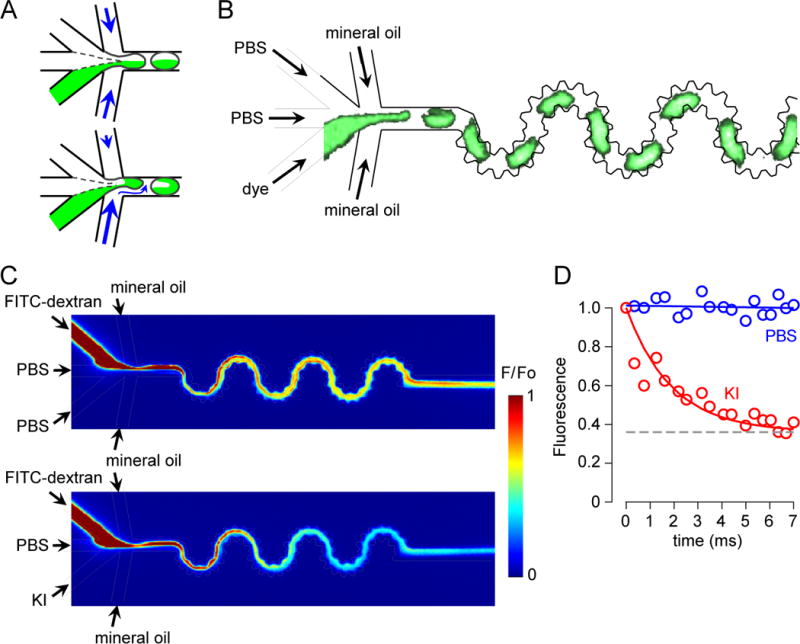
Mixing time determination from the kinetics of FITC-dextran quenching by iodide. A. Schematic showing mixing of solutions within droplets formed using equal (top) and unequal (bottom) flow rates. The unequal flow rate condition enhances mixing efficiency. B. Fluorescence micrograph of droplet generation and mixing. Calcein (1 μM), PBS (upper), PBS (center channel), mineral oil (top) and mineral oil (bottom) were injected at flow rates of 200, 100, 100, 300 and 600 μl/h, respectively. Droplet images were captured at 1000 Hz (see related Supplementary Video SV3). C. Perfusates were FITC-dextran (1 μM) (upper), PBS or 500 mM KI (lower), PBS (center channel), mineral oil (top) and mineral oil (bottom) at flow rates of 200, 200, 100, 250 and 450 μl/h, respectively. Pseudocolor images of the droplet generation and mixing regions with side channel perfused with PBS (control, no fluorescence quenching) (top) or 500 mM KI (bottom). D. Area-integrated fluorescence with exponential regression (t_1/2 ~ 2 ms) for KI curve.

Solution mixing time was measured from the kinetics of FITC-dextran quenching by iodide, which occurs instantaneously upon mixing. As diagrammed in Fig. 3C, in a control study (top panel) inlet perfusates contained 1 μM FITC-dextran in PBS, PBS (in the central channel), and PBS. In the quenching study (bottom panel) the PBS was replaced with 500 mM KI, which gives a 200 mM final KI concentration that quenches FITC-dextran by ~40 %. Because of the non-uniform channel width of the bumpy channel, the fluorescence images were area-integrated, showing reduced fluorescence from left-to-right as KI contacts the FITC-dextran. Fig. 3D shows the deduced course of FITC-dextran fluorescence from micrographs as in B, in which time was determined from position and flow velocity, and area-integrated fluorescence inside the channel. At a flow rate of 1300 μl/h, t_1/2 for mixing was ~2 ms.

Determination of time after mixing at each location in the observation region required measurement of the velocity field, which was determined using fluorescent particles as described in the Methods section. Each droplet containing the fluorescent particles generates streak-lines (Fig. 4A, left) (Supplementary Video SV4), in which velocity is calculated by dividing streak-line length by exposure time (Fig. 4A, right). A total of 500 streak-lines images were used for the velocity field determination. The deduced velocity field fitted well to a 1/r curve (V(r)/Q = 2038/r) (Fig. 4B, left), so that time after mixing could be deduced from radial position by integrating the radial velocity (t = ∫ dt = ∫ 1/V(r) dr = r²/(2038×Q)) (Fig. 4B, right), where Q is total flow rate.

Figure 4.

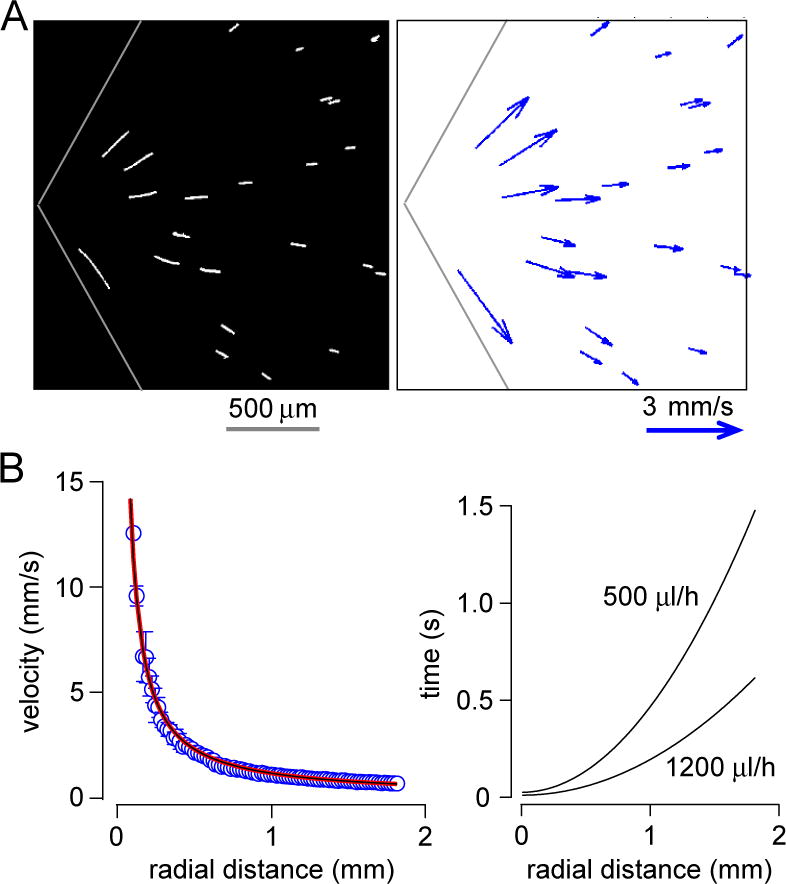
Velocity field determination by streak-line analysis. A. Streaks created by 100-ms exposure of 7-μm diameter fluorescent particles encapsulated inside droplets (left) and deduced velocity field (right). B. Velocity as a function of radial position, with fitted curve V(r)/Q = 2038/r, where Q is total flow rate (left), and deduced relationship between time and radial position shown for two total flow rates (right).

Erythrocyte water permeability measurements

The microfluidic channel was used to measure rapid transport of water across the erythrocyte plasma membrane, as well as transport of small polar non-electrolytes including urea. Erythrocyte volume measurement was based on calcein fluorescence quenching with reduced erythrocyte volume, which results from near-instantaneous protein (hemoglobin) quenching of calcein.²⁹ Calcein-loaded erythrocytes were generated by incubation of erythrocytes with cell-permeable calcein-AM, intracellular cleavage to membrane-impermeant fluorescent calcein, and washing of extracellular dye. The erythrocyte cytoplasm was stained green with the entrapped calcein (Fig. 5A, left). Fig. 5A (right) shows encapsulated erythrocytes in aqueous fluid droplets in the microfluidic channel. On average 20- 30 erythrocytes were encapsulated inside individual droplets for a 5 % hematocrit sample.

Figure 5.

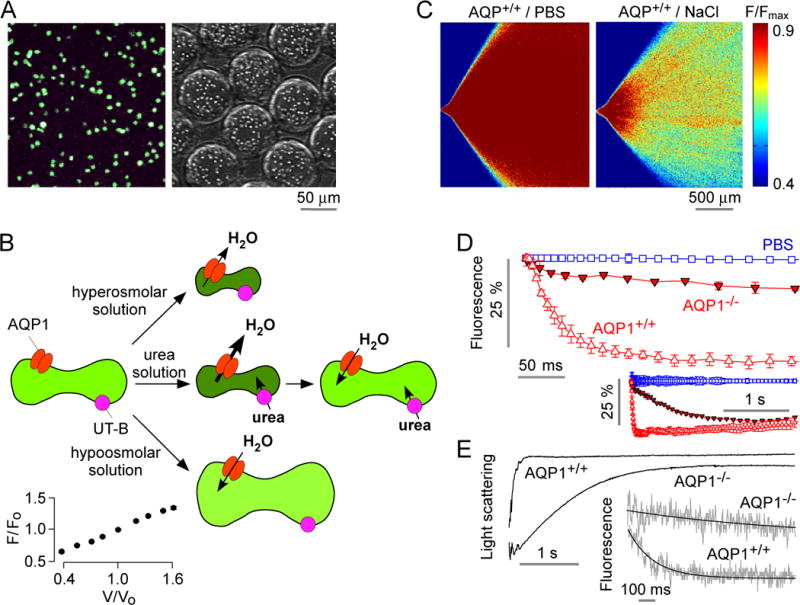
Osmotic water permeability measurement in mouse erythrocytes. A. Fluorescence micrographs of calcein-loaded erythrocytes on a coverglass (left) and in aqueous droplets generated in the microfluidic channel (right). B. Schematic of measurement method in which osmotic water permeability is measured from the kinetics of cell volume changes in response to mixing of erythrocytes with an anisomolar solution; urea transport is measured from the biphasic kinetics after mixing with a hyperosmolar, urea-containing solution. Inset (lower left), relationship between calcein fluorescence and relative erythrocyte volume, as deduced from static plate reader measurements. C. The microfluidic channel was perfused with an erythrocyte suspension (from wild-type mouse) in PBS, PBS (in central channel), and PBS containing 500 mM NaCl (bottom channel), to give a 200-mM NaCl gradient. Fluorescence micrographs of the measurement region for zero (control) gradient (left) or the 200-mM NaCl gradient (right). D. Deduced time course of erythrocyte calcein fluorescence (inset shows data on a longer time scale using 2× magnification lens). Data shown from erythrocytes from wild-type and AQP1-knockout mice for the 200-mM NaCl gradient, and (from wild-type mouse) for zero NaCl gradient. Error bars (S.E.M.) were calculated from 3 different time-integrated images. E. Osmotic water permeability in erythrocytes measured by stopped-flow light scattering. Erythrocytes from wild-type and AQP1 knockout mice were subjected to a 200-mM NaCl gradient. Inset shows stopped-flow fluorescence measurement with calcein-labeled human erythrocytes.

Fig. 5B diagrams the approach to measure erythrocyte water and solute transport. Water transport measurement involves rapid mixing of the calcein-loaded erythrocyte suspension with an anisomolar (hyperosmolar or hypoosmolar) solution to cause cell shrinking or swelling, which reduces or increases calcein fluorescence, respectively. Transport of a solute such as urea involves rapid mixing of the erythrocyte suspension with a hyperosmolar urea-containing solution, which results in rapid water efflux and cell shrinking, following by coupled water and urea influx with reswelling to the initial volume. Fig. 5B (inset) shows an approximately linear relationship between calcein fluorescence and relative erythrocyte volume, as deduced from static plate reader measurements.

Fig. 5C shows time-integrated fluorescence micrographs in which the microfluidic channel was perfused with calcein-labeled erythrocytes (from wild-type mice) in PBS, PBS (in the central channel) and PBS or PBS containing 200 mM NaCl. Little change in fluorescence was seen in the absence of an osmotic gradient (left). Fluorescence decreased with radial distance as a result of cell shrinking and calcein fluorescence quenching (right). Fig. 5D shows the deduced kinetics of calcein fluorescence, with a rapid reduction in fluorescence with t_1/2 of 23 ± 1 ms in erythrocytes from wild-type mice, corresponding to an osmotic water permeability, P_f, ~0.02–0.04 cm/s, in agreement with published data.³⁰ P_f was reduced ~ 14-fold in erythrocytes from mice lacking water channel AQP1 (t_1/2 ~ 311 ms), in agreement with prior results.³⁰ Fig. 5E shows stopped-flow light scattering measurements of erythrocyte water permeability, done using the same osmotic gradient as used in the microfluidic measurement. A rapid increase in scattered light intensity was seen, which was ~13-fold slowed in AQP1-deficient erythrocytes. Fig. 5E (inset) shows similarly slowed erythrocyte water permeability as measured by stopped-flow fluorescence with calcein-labeled erythrocytes.

The extent and rate of erythrocyte volume change depends on the size and direction of the osmotic gradient. Fig. 6A shows the kinetics of calcein fluorescence following mixing with solutions of different composition to give indicated inwardly or outwardly directed osmotic gradients. There was a decrease in calcein fluorescence, corresponding to osmotic water efflux, with hyperosmolar solutions (PBS containing 50, 100 or 200 mM NaCl) and an increase in calcein fluorescence, corresponding to osmotic water influx, with a hyposmolar solution (PBS containing 20 % water).

Figure 6.

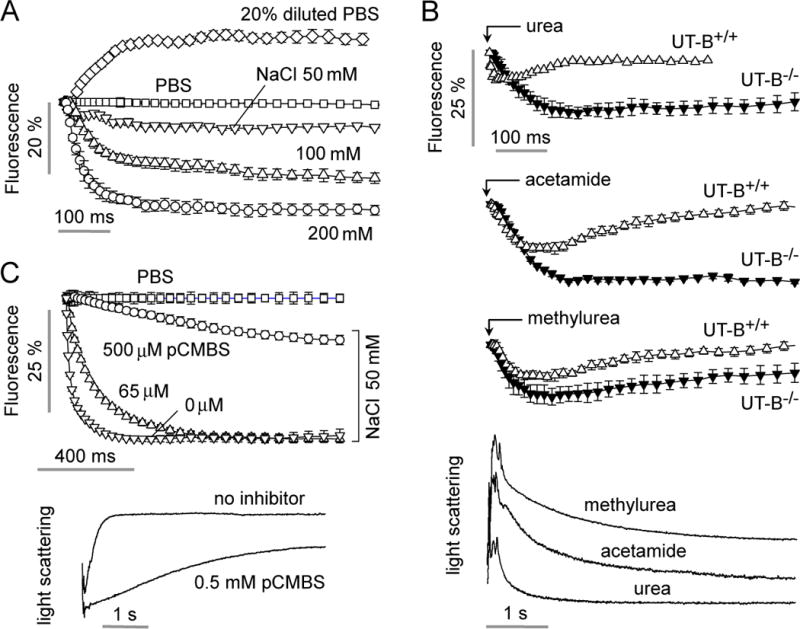
Characterization of water and urea permeability in murine erythrocytes. A. Water permeability measured as in Fig. 5D in erythrocytes from wild-type mice as a function of osmotic gradient size and direction. B. Permeability measurement of urea, acetamide and methylurea in erythrocytes from wild-type mice and mice lacking urea transporter UT-B. Flow rates were 200, 200, 100, 250, 450 μl/h, respectively, for the urea analog (500 mM in PBS) solution, erythrocyte suspension, PBS (center channel), mineral oil (top) and mineral oil (bottom). (bottom) Stopped-flow light scattering measurement of urea, methylurea and acetamide transport in mouse erythrocytes. Solute gradient was 250 mM.

Fig. 6B shows an application of the microfluidic method to measure erythrocyte transport of urea and the urea analogs acetamide and methylurea. The channel was perfused with erythrocytes in PBS, PBS (central port) and urea analogs. In each case there was an initial decrease in calcein fluorescence, corresponding to osmotic water efflux and cell shrinking, followed by return of calcein fluorescence to the original level. The return of fluorescence was remarkably slowed in erythrocytes from mice lacking the urea transport protein, UT-B. For comparison, Fig. 6C provides stopped-flow light scattering data, with time course results in agreement with those measured using the microfluidic channel.

Water permeability in human erythrocytes and testing of putative AQP1 modulators

Fig. 7A shows water transport in human erythrocytes using 250 mM Na gluconate gradient. Each measurement required 500 nL of human blood. The measured t_1/2 was 49 ± 10 ms (P_f ~ 0.018 cm/s), which increased ~2-fold with the mercurial AQP1 inhibitor pCMBS (150 μM). The results are in agreement with data obtained using the stopped-flow light scattering method (Fig. 7B), which showed ~2-fold slowed osmotic water permeability with 150 μM pCMBS. The microfluidics method was then used to test putative inhibitors of human AQP1, AqB013,²⁰ and compounds 1 and 3,¹⁹ and the putative activator AqF026.²¹ No significant effect on erythrocyte water permeability was found using high concentrations (50 μM) of each compound, both using the microfluidics method (Fig. 7C) and by conventional stopped-flow light scattering (Fig. 7D). Possible reasons for lack of inhibition are discussed below.

Figure 7.

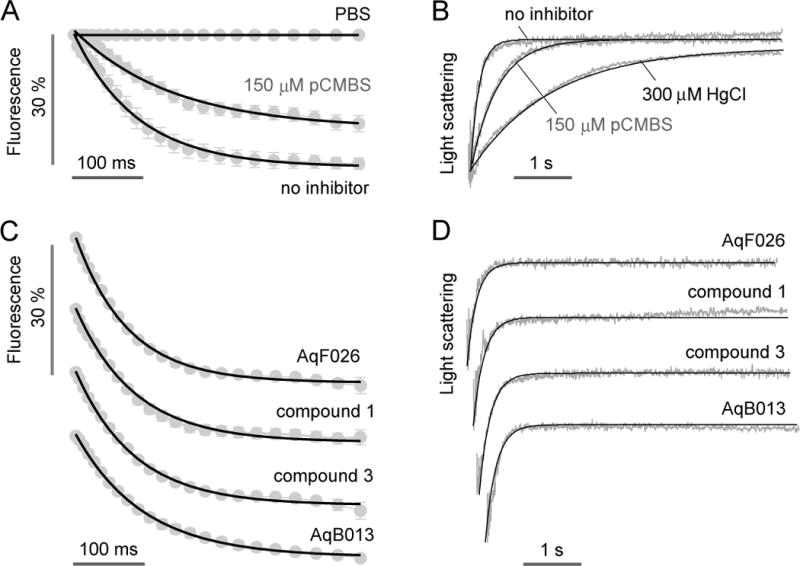
Water permeability and inhibitor testing in human erythrocytes. A. Microfluidics measurement of osmotic water permeability in untreated and 150 μM pCMBS-treated human erythrocytes. Flow rates were 400, 400, 200, 500, 500 μl/h, respectively, for the Na gluconate solution, erythrocyte suspension, PBS (center channel), mineral oil (top) and mineral oil (bottom). The Na gluconate gradient was 250 mM. B. Stopped-flow light scattering measurement of osmotic water permeability in human erythrocytes (250 mM Na gluconate gradient), with indicated inhibitors. C. Microfluidics measurement of osmotic water permeability in the presence of putative AQP1 modulators (at 50 μM). D. Stopped-flow light scattering measurement of osmotic water permeability for the same compounds (at 50 μM).

Discussion

The droplet microfluidics approach developed here is technically simple and suitable for measurement of rapid volume changes using very small quantities of suspended cells, vesicles or liposomes. For more than 50 years the gold standard for measurements of osmotic water permeability in erythrocytes has been the stopped-flow method in which a cell suspension is subjected to an osmotic gradient by rapid propulsion of syringe-loaded solutions into a mixing chamber followed by sudden succession of flow, after which the kinetics of cell volume change is deduced from the time course of an optical signal such as scattered light intensity.^7,31,32 The stopped-flow method requires specialized, costly instrumentation, large (generally >0.5 ml) volumes of solution, and is associated with significant dead time and mixing artifact that arises from turbulent solution mixing and sudden succession of flow. The droplet-based microfluidics approach here simplifies the measurement of water permeability to the acquisition of a single, time-integrated fluorescence image using a conventional fluorescence microscope-camera set-up. As demonstrated here, the analysis of a single time-integrated image produces accurate kinetic data with high signal-to-noise ratio utilizing nanoliter-size sample volumes.

Important design criteria for the microfluidics approach developed here included rapid mixing and relatively long observation times following mixing. A novel feature of the microfluidic channel was the triangular observation channel in which droplets travel in a radial direction away from an inlet, allowing time after mixing to be deduced from particle position. Unlike prior designs involving long, folded continuous channels,¹³ the open triangular observation channel allows for long-time measurement at high flow-rates and without high pressure differential. For the same channel size and flow rate conditions, a folded channel design requires an ~ 50 cm long channel for ~ 3 s measurement time (L= V×t = Q/(WH) ×t = 1200 μl/h/(50 μm×40 μm) × 3 s ~ 50 cm, where L is channel length, V velocity, t measurement time, Q flow rate, W channel width, H channel height). The pressure drop in the microfluidic channel is approximately proportional to channel length and inversely proportional to channel width:^33,34 ΔP₁/ΔP₂ ~ (L₁/w₁)/(L₂/w₂), where ΔP₁, L₁ and w₁ are the pressure drop, channel length and channel width in a long folded channel; in the microfluidic channel used here L₁ = 50 cm, w₁ = 50 μm, L₂ = 2 mm, w₂ = L₂ sin 60°, where w₂ is the average channel width of the triangular observation area, which gives ΔP₁/ΔP₂ ~ 3000. Therefore, a long, folded channel design requires ~3000-fold greater pressure differential than the present design for the same observation time. In addition, it is challenging to position many folded channels in the field view, which also limits measurement resolution.

Rapid mixing of a cell-containing solution with a second solution of different composition was achieved by formation of small droplets, as adapted from prior designs. Typical values of convective to diffusional time-scales in microfluidic channels, as described by the Peclet number, Uh/D (U is the velocity, h characteristic length, D diffusion coefficient), are between 10¹ and 10⁵, so that convection is much faster than diffusion.³⁵ Chaotic advection accelerates mixing inside droplets moving in a channel by using non-steady-fluid flow to stretch and fold a volume of fluid through a serpentine channel.¹³ A bumpy serpentine channel further enhances mixing by thinning the lubrication oil film thickness to increase shear stress.²⁸ The rapid aqueous diffusion of solution contents, which was facilitated by the convolved channel design, produced efficient mixing with 50 % mixing in < 1 ms. The small droplet size also enhances mixing efficiency, as does the different oil phase flow rates. An additional design feature was the inclusion of a central aqueous fluid stream of the same composition as the cell-containing solution to prevent mixing of the cell-containing and isosmolar solutions prior to droplet generation.

Some other technical issues deserve mention. The number of cells per droplet (and the fraction of the empty droplets) affects signal-to-noise ratio (S/N). A large fraction of empty droplets reduces S/N, whereas too many cells per droplet ultimately interferes with the stable monodisperse droplet pattern. In the present study, we have found empirically that ~10~30 erythrocytes per droplet was suitable. Droplet size has two possible effects in the present study: (i) mixing inside droplets is more efficient for small than for large droplets,³⁶ and (ii) the cell streaklines could be curved (helical) in droplets that are much larger than the channel height due to the rotational flow pattern inside droplets by continuous phase shear stress and wall shear stress.³⁷ However, within the flow rate range in the present study, the droplet sizes are not much larger than the channel height, giving straight streaklines and uniform iso-timelines. Cells might be affected by shear stress during focusing droplet generation and by rotational movement inside droplets. In the present study, cell water permeability responses were similar to those determined by the conventional measurement method, so the stress level is probably minimal.

The water permeability measurements done in murine and human erythrocytes using the microfluidic channel were in agreement with measurements done using the conventional stopped-flow light scattering method and with data reported in the literature. Inhibition of water permeability by the non-selective mercurial sulfhydryl-reactive compound pCMBS was demonstrated and in agreement with stopped-flow results. Testing of putative modulators, including the reported inhibitors AqB013,²⁰ and compounds 1 and 3,¹⁹ and the activator AqF026,²¹ showed no significant inhibition of erythrocyte water permeability, which is mediated by AQP1 water channels. This conclusion was supported by stopped-flow light scattering results. The prior data showed activity of these compounds in Xenopus laevis oocytes expressing AQP1.^19–21 We cannot determine the reason(s) why the prior studies showed AQP1 modulation in oocytes; however, as reviewed,⁵ there are a number of possible artifacts in oocyte studies that can confound data interpretation, including off-target actions or the dependence of oocyte swelling on multiple factors, such as oocyte geometry and plasma membrane physical properties. Further, it is a priori unlikely that a small molecule could activate AQP1, which is thought to be constitutively fully active.

There are many applications for the droplet-based microfluidics approach developed here such as in the measurement of water or urea permeability in drug discovery and cell physiology studies. The small sample size requirement allows measurements to be made on precious or limited materials, such as reconstituted proteoliposomes or diagnostic human biopsy material. In general, any transport or other biological process, such as ligand-receptor binding or protein conformational dynamics, can be measured provided the kinetics are on a appropriate time-scale and the availability of a suitable optical read-out.

Alternative methods for rapid mixing of a cell-containing and cell-free solutions have been considered. One approach is the droplet merging technique in which two different nL-volume droplets are fused by pillar geometry,³⁸ size or viscosity differences,³⁹ or other mechanisms.⁴⁰ In the pillar-induced droplet merging technique, one droplet is trapped in a micropillar structure until another droplet arrives and fuses with the immobilized droplet. Mixing times down to ~7 ms were reported with this method.³⁸ However, pillar-induced droplet merging is not suitable for water permeability measurements here because it is necessary but difficult to synchronize two different droplet streams for exact 1:1 merging with highly precision, and surfactant cannot be used, which was necessary here to prevent droplet merging in the observation area. Another method involves active or passive mixing in microchannels using continuous flows,⁴¹ though the mixing time is relatively long and high flow rates are required for efficient mixing.⁴² Lastly, dynamic trapping methods for single cell trapping⁴³ can be combined with fast solution exchange to accomplish the fast mixing and long time measurement, though not applicable here because of the small size and flexibility of erythrocytes.

With regard to cell volume and water permeability measurement, a few other microfluidics approaches have been reported. Kumar et al.⁴⁴ measured single cell water permeability by labeling cells (plant protoplasts) with magnetic particles, immobilizing them on the chip by magnetic forces, and merging cell-containing droplets with droplets containing anisosmotic osmotic solutions. Cell volume changes were inferred from the size of ellipses fitted to individual cells. A limitation of this method is the relatively slow mixing time (> 1 s) by electromechanically induced droplet merging.⁴⁵ Ateya et al.⁴⁶ developed a non-invasive microfluidic/electrical sensor that provides real-time measurement of changes in cell volume, where cells were cultured on glass coverslips and cell volume inferred by electrical impedance; however, the fluid exchange was relatively slow (90% exchange in 4–7 s). Hua et al.⁴⁷ immobilized single MDCK cells in microstructures and deduced cell volume changes by electrical impedance; however, only one cell can be studied at a time. Because of the small size and flexibility of erythrocytes, and the rapid kinetics of osmotic equilibration, these prior methods are not suitable for the osmotic water permeability studies reported here.

Finally, limitations of the approach here are noted. The volume measurement method requires fluorescent labeling of cells with suitable volume-sensing indicators, such as with the exogenously added label calcein used here, because label-free measurement of cell volume by confocal microscopy would be impractical because of the rapid changes in cell volume, non-spherical cell shape and cell movement within the moving aqueous droplets. As time-integrated image capture is used, heterogeneity in individual droplets is averaged out and so that it is not possible to resolve water permeability in different cell populations, though video-rate image capture would address this limitation. The determination of time after mixing from position in the measurement area requires correction for spatial variations in illumination and small differences in droplet density, both of which can be corrected by normalization to images acquired in the absence of an osmotic gradient; an alternative approach involving ratio imaging using a non-volume-sensing aqueous phase dye (such as rhodamine dextran) would obviate the need for a second measurement. Finally, as is the case for other microfluidic channels, application to primary high-throughput screening requires challenging compound delivery and incubation steps.

Conclusion

We developed a steady-state microfluidics approach to measure rapid water and solute permeability using small solution volumes and readily available laboratory instrumentation. The complexities and artifacts from forced mixing of macroscopic solution volumes and sudden stopping of flow are obviated by continuous solution mixing and a single image acquisition in which position encodes time after mixing. Many applications in cell research, drug discovery and diagnostics are anticipated.

Supplementary Material

Movie 1

Supplemental Video SV1. Generation of monodisperse droplets, a stable droplet pattern in the observation area, and symmetrical pattern formation during fluid exit. Images were captured using 4x magnification lens for the 600 μl/h total flow rate.

Movie 2

Supplemental Video SV2. Initial formation of the stable droplet pattern within 1 min after start of perfusion. Initial flow rates for solution injections were 300 μl/h for PBS (top), PBS (bottom), PBS (center), mineral oil (top) and mineral oil (bottom), and then flow rates were changed into 100, 100, 50, 150, 200 μl/h, respectively. Imaging was captured using 4× magnification lens with 10 ms exposure time.

Movie 3

Supplemental Video SV3. Rapid video imaging (1000 Hz) of droplet generation and mixing. Calcein (1 μM), PBS (upper), PBS (center), mineral oil (top) and mineral oil (bottom) were injected through each inlet with flow rates of 200, 100, 100, 300, 600 μl/h, respectively. Droplet images were captured at 1000 Hz using a high-speed camera and 10× magnification lens.

Movie 4

Supplemental Video SV4. Radial movement of fluorescent particles (7-μm diameter) encapsulated inside droplets. Streak-lines were measured using 4× magnification lens and 100 ms exposure time at 500 μl/h flow rate.