Learning interactions via hierarchical group-lasso regularization

Abstract

We introduce a method for learning pairwise interactions in a linear regression or logistic regression model in a manner that satisfies strong hierarchy: whenever an interaction is estimated to be nonzero, both its associated main effects are also included in the model. We motivate our approach by modeling pairwise interactions for categorical variables with arbitrary numbers of levels, and then show how we can accommodate continuous variables as well. Our approach allows us to dispense with explicitly applying constraints on the main effects and interactions for identifiability, which results in interpretable interaction models. We compare our method with existing approaches on both simulated and real data, including a genome-wide association study, all using our R package glinternet.

1 Introduction

Given an observed response and explanatory variables, we expect interactions to be present if the response cannot be explained by additive functions of the variables. The following definition makes this more precise.

Definition 1

When a function f(x, y) cannot be expressed as g(x) + h(y) for some functions g and h, we say that there is an interaction in f between x and y.

Interactions of single nucleotide polymorphisms (SNPs) are thought to play a role in cancer [Schwender and Ickstadt, 2008] and other diseases. Modeling interactions has also served the recommender systems community well: latent factor models (matrix factorization) aim to capture user-item interactions that measure a user’s affinity for a particular item, and are the state of the art in predictive power [Koren, 2009]. In look-alike-selection, a problem that is of interest in computational advertising, one looks for features that most separates a group of observations from its complement, and it is conceivable that interactions among the features can play an important role.

Linear models scale gracefully as datasets grow wider — i.e. as the number of variables increase. Problems with 10,000 or more variables are routinely handled by standard software. Scalability is a challenge when we model interactions. Even with 10,000 variables, we are already looking at a 50 × 10⁶-dimensional space of possible interaction pairs. Complicating the matter are spurious correlations amongst the variables, which makes learning even harder.

Finding interactions often falls into the “p ≫ n” regime where there are more variables than observations. A popular approach in supervised learning problems of this type is to use regularization, such as imposing an ℓ₂ bound of the form ${\Vert \beta \Vert }_2^2\le s$ (ridge) or an ℓ₁ bound ||β||₁ ≤ s (lasso) on the coefficients. The latter type of penalty has been the focus of much research since its introduction in [Tibshirani, 1996], and is called the lasso. One of the reasons for the lasso’s popularity is that it does variable selection: it sets some coefficients exactly to zero. There is a group analogue to the lasso, called the group-lasso [Yuan and Lin, 2006], that sets groups of variables to zero. The idea behind our method is to set up main effects and interactions (to be defined later) via groups of variables, and then we perform parameter selection via the group-lasso.

Discovering interactions is an area of active research; [Bien et al., 2013] give a good and recent review. Other recent approaches include [Chen et al., 2011], [Bach, 2008], [Rosasco et al., 2010] and [Radchenko and James, 2010]. In this paper, we introduce glinternet (group-lasso interaction network), a method for learning first-order interactions that can be applied to categorical variables with arbitrary numbers of levels, continuous variables, and combinations of the two. Our approach uses a version of the group lasso to select interactions and enforce hierarchy.

For very large problems, we precede this with a screening step that gives a candidate set of main effects and interactions. Our preferred screening rule is an adaptive procedure that is based on the strong rules [Tibshirani et al, 2012] for discarding predictors in lasso-type problems. Strong rules also lead to efficient algorithms for solving our group-lasso problems, with our without screening.

While screening potentially misses some candidate interactions, we note that our approach can handle very large problems without any screening. In Section 7.3 we fit our model with 27K Snps (three-level factors), 3,500 observations, and 360M candidate interactions, without any screening.

1.1 A simulated example

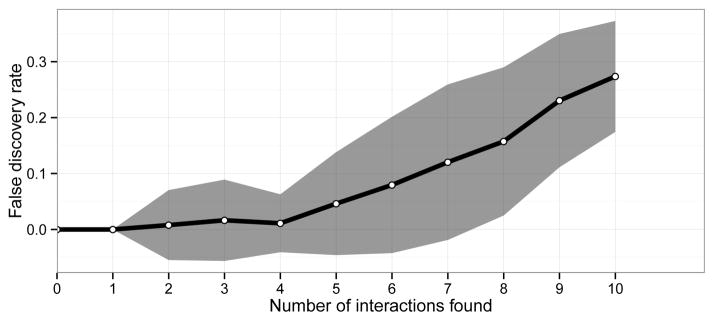
As a first example and a forward peek at the results, we perform 100 simulations with 500 3-level categorical variables and 800 observations (squared error loss with quantitative response). There are 10 main effects and 10 interactions in the ground truth, and the noise level is chosen to give a signal to noise ratio of one. We run glinternet without any screening, and stop after ten interactions have been found. The average false discovery rate and standard errors are plotted as a function of the number of interactions found in Figure 1. As we can see in the figure, the first 10 interactions found (among a candidate set of 125,000) include 7 of the 10 real interactions, on average.

Figure 1.

False discovery rate vs number of discovered interactions, averaged over 100 simulations with 500 3-level factors. The ground truth has 10 main effects and 10 interactions.

1.2 Organization of the paper

The rest of the paper is organized as follows. Section 2 introduces the problem and notation. In Section 3, we introduce the group-lasso and how it fits into our framework for finding interactions. We also show how glinternet is equivalent to an overlapped group lasso. We discuss screening in Section 4, and give several examples with both synthetic and real datasets in Section 7. We relegate the specific details of our algorithmic implementation of the group lasso to Appendix A.3. We conclude with a discussion in Section 8.

2 Background and notation

We use the random variables Y to denote the response, F to denote a categorical feature, and Z to denote a continuous feature. We use L to denote the number of levels that F can take. For simplicity of notation we will use the first L positive integers to represent these L levels, so that F takes values in the set {i ∈ ℤ : 1 ≤ i ≤ L}. Each categorical F has an associated random dummy vector variable X ∈ ℝ^L with a 1 that indicates which level F takes, and 0 everywhere else.

When there are p categorical (or continuous) features, we will use subscripts to index them, i.e. F₁, …, F_p. Boldface font will always be reserved for vectors or matrices that comprise of realizations of these random variables. For example, Y is the n-vector of observations of the random variable Y, likewise for F and Z. Similarly, X is a n × L indicator matrix whose i-th row consists of a 1 in the F_i-th column and 0 everywhere else. We use a n × (L_i · L_j) indicator matrix X_i:j to represent the interaction F_i : F_j. We will write

$${\mathbf{X}}_{i:j}={\mathbf{X}}_i\ast {\mathbf{X}}_j$$

for the matrix consisting of all pairwise products of columns of X_i and X_j. For example,

$$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\ast \left(\begin{array}{cc}e& f\\ g& h\end{array}\right)=\left(\begin{array}{cccc}ae& af& be& bf\\ cg& ch& dg& dh\end{array}\right).$$

2.1 Definition of interaction for categorical variables

To see how Definition 1 applies to this setting, let 𝔼(Y|F₁ = i, F₂ = j) = μ_ij, the conditional mean of Y given that F₁ takes level i, and F₂ takes level j. There are 4 possible cases:

1. μ_ij = μ (no main effects, no interactions)

2. ${\mu }_{ij}=\mu +{\theta }_1^i$ (one main effect F₁)

3. ${\mu }_{ij}=\mu +{\theta }_1^i+{\theta }_2^i$ (two main effects)

4. ${\mu }_{ij}=\mu +{\theta }_1^i+{\theta }_2^i+{\theta }_{1:2}^{ij}$ (main effects and interaction)

Note that all but the first case is overparametrized, and a common remedy is to impose sum constraints on the main effects and interactions:

$$\sum _{i=1}^{L_1}{\theta }_1^i=0,\sum _{j=1}^{L_2}{\theta }_2^j=0$$ (1)

and

$$\sum _{i=1}^{L_1}{\theta }_{1:2}^{ij}=0\text{for}\text{fixed}j,\sum _{j=1}^{L_2}{\theta }_{1:2}^{ij}=0\text{for}\text{fixed}i.$$ (2)

In what follows, θ_i, i = 1, ···, p, will represent the main effect coefficients, and θ_i:j will denote the interaction coefficients. We will use the terms “main effect coefficients” and “main effects” interchangeably, and likewise for interactions.

2.2 Weak and strong hierarchy

An interaction model is said to obey strong hierarchy if an interaction can be present only if both of its main effects are present. Weak hierarchy is obeyed as long as either of its main effects are present. Since main effects as defined above can be viewed as deviations from the global mean, and interactions are deviations from the main effects, it rarely make sense to have interactions without main effects. This leads us to prefer interaction models that are hierarchical. We see in Section 3 that glinternet produces estimates that obey strong hierarchy.

2.3 First order interaction model

Our model for a quantitative response Y is given by

$$E(Y\mid X)=\mu +\sum _{i=1}^p{X}_i{\theta }_i+\sum _{i<j}{X}_{i:j}{\theta }_{i:j},$$ (3)

and for a binary response, we have

$$\text{logit}(\mathbb{P}(Y=1\mid X))=\mu +\sum _{i=1}^p{X}_i{\theta }_i+\sum _{i<j}{X}_{i:j}{\theta }_{i:j}.$$ (4)

We fit these models by minimizing an appropriate loss function ℒ, subject to many constraints. Even if p is not too large, we will need to impose the identifiability constraints (1) and (2) for the coefficients θ. But we will also want to limit ourselves to the important interactions and main effects, while maintaining the hierarchy mentioned above. We achieve all these constraints by adding an appropriate penalty to the loss function. We give the loss functions here, and then develop the group-lasso penalties that achieve the desired constraints.

For a quantitative response, we typically use squared-error loss:

$$\mathcal{L}(\mathbf{Y};\mu ,\theta )=\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\sum _{i=1}^p{\mathbf{X}}_i{\theta }_i+\sum _{i<j}{\mathbf{X}}_{i:j}{\theta }_{i:j}\Vert }_2^2,$$ (5)

and for a binary response the “logistic loss” (negative Bernoulli log-likelihood):

$$\mathcal{L}(\mathbf{Y};\mu ,\theta )=-\left[{\mathbf{Y}}^T(\mu ·\mathbf{1}+\sum _{i=1}^p{\mathbf{X}}_i{\theta }_i+\sum _{i<j}{\mathbf{X}}_{i:j}{\theta }_{i:j})-{\mathbf{1}}^{T}log\left(1+exp(\mu ·\mathbf{1}+\sum _{i=1}^p{\mathbf{X}}_i{\theta }_i+\sum _{i<j}{\mathbf{X}}_{i:j}{\theta }_{i:j})\right)\right],$$ (6)

where the log and exp are taken component-wise.

2.4 Group-lasso and overlapped group-lasso

Since glinternet’s workhorse is the group-lasso, we briey introduce it here. We refer the reader to [Yuan and Lin, 2006] for more technical details.

The group-lasso can be thought of as a more general version of the well-known lasso. Suppose there are p groups of variables (possibly of different sizes), and let the feature matrix for group j be denoted by X_j. Let Y denote the vector of responses. For squared-error loss, the group-lasso estimates ${\{{\widehat{\beta }}_j\}}_1^p$ by solving

$${\text{argmin}}_{\mu ,\beta }\frac{1}{2}\Vert \mathbf{Y}-\mu ·\mathbf{1}-\sum _{j=1}^p{\mathbf{X}}_j{\beta }_j{\Vert }_2^2+\lambda \sum _{j=1}^p{\gamma }_j{\Vert {\beta }_j\Vert }_2.$$ (7)

Note that if each group consists of only one variable, this reduces to the lasso criterion. In our application, each indicator matrix X_j will represent a group. Like the lasso, the penalty will force some β̂_j to be zero, and if an estimate β̂_j is nonzero, then all its components are typically nonzero. Hence the group-lasso applied to the X_j’s intuitively selects those variables that have a strong overall contribution from all their levels toward explaining the response.

The parameter λ controls the amount of regularization, with larger values implying more regularization. The γ’s allow each group to be penalized to different extents, and should depend on the scale of the matrices X_j. The nature of our matrices allows us to set them all equal to 1 (see online Appendix A.2 for details). To solve (7), we start with λ just large enough that all estimates are zero. Decreasing λ along a grid of values results in a path of solutions, from which an optimal λ can be chosen by cross validation or some other model selection procedure.

The Karush-Kuhn-Tucker (KKT) optimality conditions for the group-lasso are simple to compute and check. For group j, they are

$${\Vert {\mathbf{X}}_j^T(\mathbf{Y}-\widehat{\mathbf{Y}})\Vert }_2\le {\gamma }_j\lambda \text{if}{\widehat{\beta }}_j=0$$ (8)

$${\Vert {\mathbf{X}}_j^T(\mathbf{Y}-\widehat{\mathbf{Y}})\Vert }_2={\gamma }_j\lambda \text{if}{\widehat{\beta }}_j\ne 0.$$ (9)

The group-lasso is commonly fit by iterative methods — either block coordinate descent, or some form of gradient descent, and convergence can be confirmed by checking the KKT conditions. Details of the algorithm we use can be found in Appendix A.3.

The overlap group-lasso [Jacob et al., 2009] is a variant of the group-lasso where the groups of variables are allowed to have overlaps, i.e. some variables can show up in more than one group. However, each time a variable shows up in a group, it gets a new coefficient. For example, if a variable is included in three groups, then it has three coefficients that need to be estimated, and its ultimate coefficient is the sum of the three. This turns out to be critical for enforcing hierarchy.

3 Methodology and results

We want to fit the first order interaction model in a way that obeys strong hierarchy. We show in Section 3.1 how this can be achieved by adding an overlapped group-lasso penalty to the loss ℒ(Y; μ, θ), in addition to the sum-to-zero constraints on the θs. We then show how this optimization problem can be conveniently and efficiently solved via a group-lasso without overlaps, and without the sum-to-zero constraints.

3.1 Strong hierarchy through overlapped group-lasso

Adding an overlapped group-lasso penalty to ℒ(Y; μ, θ) is one way of obtaining solutions that satisfy the strong hierarchy property. The results that follow hold for both squared error and logistic loss, but we focus on the former for clarity.

Consider the case where there are two categorical variables F₁ and F₂ with L₁ and L₂ levels respectively. Their indicator matrices are given by X₁ and X₂. (These results generalize trivially to the case of pairwise interactions among more than 2 variables). We solve

$$\begin{array}{l}{\text{argmin}}_{\mu ,\alpha ,\stackrel{\sim }{\alpha }}\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{X}}_1{\alpha }_1-{\mathbf{X}}_2{\alpha }_2-[\begin{array}{ccc}{\mathbf{X}}_1& {\mathbf{X}}_2& {\mathbf{X}}_{1:2}\end{array}]\left[\begin{array}{c}{\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\Vert }_2^2\\ +\lambda \left({\Vert {\alpha }_1\Vert }_2+{\Vert {\alpha }_2\Vert }_2+\sqrt{L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}\right)\end{array}$$ (10)

subject to

$$\sum _{i=1}^{L_1}{\alpha }_1^i=0,\sum _{j=1}^{L_2}{\alpha }_2^j=0,\sum _{i=1}^{L_1}{\stackrel{\sim }{\alpha }}_1^i=0,\sum _{j=1}^{L_2}{\stackrel{\sim }{\alpha }}_2^j=0$$ (11)

and

$$\sum _{i=1}^{L_1}{\alpha }_{1:2}^{ij}=0\text{for}\text{fixed}j,\sum _{j=1}^{L_2}{\alpha }_{1:2}^{ij}=0\text{for}\text{fixed}i.$$ (12)

Notice that the main effect matrices X_j, j = 1, 2, each have two different coefficient vectors α_j and α̃_j, creating an overlap in the penalties, and their ultimate coefficient is the sum θ_j = α_j + α̃_j. The $\sqrt{L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}$ term results in estimates that satisfy strong hierarchy, because either ${\widehat{\stackrel{\sim }{\alpha }}}_1={\widehat{\stackrel{\sim }{\alpha }}}_2={\widehat{\alpha }}_{1:2}=0$ or all are nonzero, i.e. interactions are always present with both main effects.

The constants L₁ and L₂ are chosen to put α̃₁, α̃₂, and α_1:2 on the same scale. To motivate this, note that we can write

$$X_1{\stackrel{\sim }{\alpha }}_1=X_{1:2}{[\underset{L_2\text{copies}}{\underbrace{{\stackrel{\sim }{\alpha }}_1,\dots ,{\stackrel{\sim }{\alpha }}_1}}]}^T,$$

and similarly for X₂α̃₂. We now have a representation for α̃₁ and α̃₂ with respect to the space defined by X_1:2, so that they are “comparable” to α_1:2. We then have

$$\Vert [\underset{L_2\text{copies}}{\underbrace{{\stackrel{\sim }{\alpha }}_1,\dots ,{\stackrel{\sim }{\alpha }}_1}}]{\Vert }_2^2=L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2$$

and likewise for α̃₂. More details are given in Section 3.2 below.

The estimates for the actual main effects and interactions as in (3) are

$$\begin{array}{r}{\widehat{\theta }}_1={\widehat{\alpha }}_1+{\widehat{\stackrel{\sim }{\alpha }}}_1\\ {\widehat{\theta }}_2={\widehat{\alpha }}_2+{\widehat{\stackrel{\sim }{\alpha }}}_2\\ {\widehat{\theta }}_{1:2}={\widehat{\alpha }}_{1:2}.\end{array}$$

Because of the strong hierarchy property mentioned above, we also have

$${\widehat{\theta }}_{1:2}\ne 0\Rightarrow {\widehat{\theta }}_1\ne 0\text{and}{\widehat{\theta }}_2\ne 0.$$

In standard ANOVA, there are a number of ways of dealing with the overparametrization for factors, other than the sum-to-zero constraints we use here; for example, setting the coefficient for the first or last level to zero, or other chosen contrasts. These also lead to a reduced parametrization. While this choice does not alter the fit in the standard case, with parameter regularization it does. Our choice (all levels in with sum-to-zero constraint) is symmetric and appears to be natural with penalization, in that it treats all the levels as equals. It also turns out to be very convenient, as we show in the next section.

3.2 Equivalence with unconstrained group-lasso

We now show how to solve the constrained overlapped group-lasso problem by solving an equivalent unconstrained group-lasso problem — a simplification with considerable computational advantages.

We need two lemmas. The first shows that because we fit an intercept in the model, the estimated coefficients β̂ for any categorical variables in the model will have mean zero.

Lemma 1

Let X be an indicator matrix with L columns, corresponding to an L-level factor. Then the solution β̂ to

$${\text{argmin}}_{\mu ,\beta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\mathbf{X}\beta \Vert }_2^2+\lambda {\Vert \beta \Vert }_2$$

satisfies

$$\sum _{\ell =1}^L{\widehat{\beta }}_{\ell }=0.$$

The same is true for logistic loss.

Proof

Because X is an indicator matrix, each row consists of exactly a single 1 (all other entries 0), so that

$$\mathbf{X}·c\mathbf{1}=c\mathbf{1}$$

for any constant c. It follows that if μ̂ and β̂ are solutions, then so are μ̂ + c and β̂ − c1. But the norm ||β̂ − c1||₂ is minimized for $c=\frac{1}{L}{\sum }_{\ell =1}^L{\widehat{\beta }}_{\ell }$.

Note that this would be true for each of any number of X_j and β_j in the model, as long as there is an unpenalized intercept.

The next lemma states that if we include two intercepts in the model, one penalized and the other unpenalized, then the penalized intercept will be estimated to be zero.

Lemma 2

The optimization problem

$${\text{argmin}}_{\mu ,\stackrel{\sim }{\mu },\beta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\stackrel{\sim }{\mu }·\mathbf{1}-\mathbf{X}\beta \Vert }_2^2+\lambda \sqrt{{\stackrel{\sim }{\mu }}^2+{\Vert \beta \Vert }_2^2}$$

has solution μ̃ = 0 for all λ > 0. The same result holds for logistic loss.

The proof is straightforward: we can achieve the same fit with a lower penalty by taking μ ← μ + μ̃.

The next theorem shows how the overlapped group-lasso in Section 3.1 reduces to a group-lasso. The main idea boils down to the fact that quadratic penalties on coefficient vectors are rotation invariant. This allows us to rotate from the “main-effects + interactions” representation to the equivalent “cell-means” representation without changing the penalty.

Theorem 1

Solving the constrained optimization problem (10) – (12) in Section 3.1 is equivalent to solving the unconstrained problem

$${\text{argmin}}_{\mu ,\beta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{X}}_1{\beta }_1-{\mathbf{X}}_2{\beta }_2-{\mathbf{X}}_{1:2}{\beta }_{1:2}\Vert }_2^2+\lambda ({\Vert {\beta }_1\Vert }_2+{\Vert {\beta }_2\Vert }_2+{\Vert {\beta }_{1:2}\Vert }_2).$$ (13)

Proof

We need to show that the group-lasso objective can be equivalently written as an overlapped group-lasso with the appropriate constraints on the parameters. We begin by rewriting (10) as

$$\begin{array}{l}{\text{argmin}}_{\mu ,\stackrel{\sim }{\mu },\alpha ,\stackrel{\sim }{\alpha }}\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{X}}_1{\alpha }_1-{\mathbf{X}}_2{\alpha }_2-[\begin{array}{cccc}\mathbf{1}& {\mathbf{X}}_1& {\mathbf{X}}_2& {\mathbf{X}}_{1:2}\end{array}]\left[\begin{array}{c}\stackrel{\sim }{\mu }\\ {\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\Vert }_2^2\\ +\lambda \left({\Vert {\alpha }_1\Vert }_2+{\Vert {\alpha }_2\Vert }_2+\sqrt{L_1{L}_2{\stackrel{\sim }{\mu }}^2+L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}\right).\end{array}$$ (14)

By Lemma 2, we will estimate μ̃ = 0. Therefore we have not changed the solutions in any way.

Lemma 1 shows that the first two constraints in (11) are satisfied by the estimated main effects β̂₁ and β̂₂. We now show that

$${\Vert {\beta }_{1:2}\Vert }_2=\sqrt{L_1{L}_2{\stackrel{\sim }{\mu }}^2+L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}$$

where the α̃₁, α̃₂, and α_1:2 satisfy the constraints in (11) and (12), and along with μ̃ represent an equivalent reparametrization of β_1:2.

For fixed levels i and j, we can decompose β_1:2 (see [Scheffe, 1959]) as

$$\begin{array}{l}{\beta }_{1:2}^{ij}={\beta }_{1:2}^{··}+({\beta }_{1:2}^{i·}-{\beta }_{1:2}^{··})+({\beta }_{1:2}^{·j}-{\beta }_{1:2}^{··})+({\beta }_{1:2}^{ij}-{\beta }_{1:2}^{i·}-{\beta }_{1:2}^{·j}-{\beta }_{1:2}^{··})\\ \equiv \stackrel{\sim }{\mu }+{\stackrel{\sim }{\alpha }}_1^i+{\stackrel{\sim }{\alpha }}_2^j+{\alpha }_{1:2}^{ij}.\end{array}$$

It follows that the whole (L₁L₂)-vector β_1:2 can be written as

$${\beta }_{1:2}=\mathbf{1}\stackrel{\sim }{\mu }+{\mathbf{Z}}_1{\stackrel{\sim }{\alpha }}_1+{\mathbf{Z}}_2{\stackrel{\sim }{\alpha }}_2+{\alpha }_{1:2},$$ (15)

where Z₁ is a L₁L₂ × L₁ indicator matrix of the form

$$\underset{L_1\text{columns}}{\underbrace{\left(\begin{array}{cccc}{\mathbf{1}}_{L_2\times 1}& 0& \cdots & 0\\ 0& {\mathbf{1}}_{L_2\times 1}& \cdots & 0\\ 0& 0& \ddots & 0\\ 0& 0& 0& {\mathbf{1}}_{L_2\times 1}\end{array}\right)}}$$

and Z₂ is a L₁L₂ × L₂ indicator matrix of the form

$$L_1\text{copies}\{\left(\begin{array}{c}{I}_{L_2\times L_2}\\ ⋮\\ I_{L_2\times L_2}\end{array}\right)$$

It follows that

$${\mathbf{Z}}_1{\stackrel{\sim }{\alpha }}_1={(\underset{L_2\text{copies}}{\underbrace{{\stackrel{\sim }{\alpha }}_1^1,\dots ,{\stackrel{\sim }{\alpha }}_1^1}},\underset{L_2\text{copies}}{\underbrace{{\stackrel{\sim }{\alpha }}_1^2,\dots ,{\stackrel{\sim }{\alpha }}_1^2}},\dots ,\underset{L_2\text{copies}}{\underbrace{{\stackrel{\sim }{\alpha }}_1^{L_1},\dots ,{\stackrel{\sim }{\alpha }}_1^{L_1}}})}^T$$

and

$${\mathbf{Z}}_2{\stackrel{\sim }{\alpha }}_2={({\stackrel{\sim }{\alpha }}_2^1,\dots ,{\stackrel{\sim }{\alpha }}_2^{L_2},{\stackrel{\sim }{\alpha }}_2^1,\dots ,{\stackrel{\sim }{\alpha }}_2^{L_2},\dots ,{\stackrel{\sim }{\alpha }}_2^1,\dots ,{\stackrel{\sim }{\alpha }}_2^{L_2})}^T.$$

Note that α̃₁, α̃₂, and α_1:2, by definition, satisfy the constraints (11) and (12). This can be used to show, by direct calculation, that the four additive components in (15) are mutually orthogonal, so that we can write

$$\begin{array}{l}{\Vert {\beta }_{1:2}\Vert }_2^2={\Vert \mathbf{1}\stackrel{\sim }{\mu }\Vert }_2^2+{\Vert {\mathbf{Z}}_1{\stackrel{\sim }{\alpha }}_1\Vert }_2^2+{\Vert {\mathbf{Z}}_2{\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2\\ =L_1{L}_2{\stackrel{\sim }{\mu }}^2+L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2.\end{array}$$

We have shown that the penalty in the group-lasso problem is equivalent to the penalty in the constrained overlapped group-lasso. It remains to show that the loss functions in both problems are also the same. Since X_1:2Z₁ = X₁ and X_1:2Z₂ = X₂, this can be seen by a direct computation:

$$\begin{array}{l}{\mathbf{X}}_{1:2}{\beta }_{1:2}={\mathbf{X}}_{1:2}(\mathbf{1}\stackrel{\sim }{\mu }+{\mathbf{Z}}_1{\stackrel{\sim }{\alpha }}_1+{\mathbf{Z}}_2{\stackrel{\sim }{\alpha }}_2+{\alpha }_{1:2})\\ =\mathbf{1}\stackrel{\sim }{\mu }+{\mathbf{X}}_1{\stackrel{\sim }{\alpha }}_1+{\mathbf{X}}_2{\stackrel{\sim }{\alpha }}_2+{\mathbf{X}}_{1:2}{\alpha }_{1:2}\\ =[\begin{array}{cccc}\mathbf{1}& {\mathbf{X}}_1& {\mathbf{X}}_2& {\mathbf{X}}_{1:2}\end{array}]\left[\begin{array}{c}\stackrel{\sim }{\mu }\\ {\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\end{array}$$

Theorem 1 shows that we can use the group-lasso to obtain estimates that satisfy strong hierarchy, without solving the overlapped group-lasso with constraints. The theorem also shows that the main effects and interactions can be extracted with

$$\begin{array}{l}{\widehat{\theta }}_1={\widehat{\beta }}_1+{\widehat{\stackrel{\sim }{\alpha }}}_1\\ {\widehat{\theta }}_2={\widehat{\beta }}_2+{\widehat{\stackrel{\sim }{\alpha }}}_2\\ {\widehat{\theta }}_{1:2}={\widehat{\alpha }}_{1:2}.\end{array}$$

Although this theorem is stated and proved with just two categorical variables F₁ and F₂, the same results extends in a trivial way to all pairs of interactions with p variables. The only small modification is that a main effect will potentially get contributions from more than one interaction pair.

This equivalence has considerable impact on the computations. A primary operation in computing a group-lasso solution is a matrix multiply as in (8), which is also used in the strong rules screening (Section 4). For these operations we do not need to compute all the matrices in advance, but compute the multiplies on the fly using the stored factor variables. Furthermore, these operations can be run in parallel on many processors.

We discuss the properties of the glinternet estimates in the next section.

3.3 Properties of the glinternet penalty

While glinternet treats the problem as a group-lasso, examining the equivalent overlapped group-lasso version makes it easier to draw insights about the behaviour of the method under various scenarios. Recall that the overlapped penalty for two variables is given by

$${\Vert {\alpha }_1\Vert }_2+{\Vert {\alpha }_2\Vert }_2+\sqrt{L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}.$$

We consider a noiseless scenario. If the ground truth is additive, i.e. α_1:2 = 0, then α̃₁ and α̃₂ will be estimated to be zero. This is because for L₁, L₂ ≥ 2 and a, b ≥ 0, we have

$$\sqrt{L_2{a}^2+L_1{b}^2}\ge a+b.$$

Thus it is advantageous to place all the main effects in α₁ and α₂, because doing so results in a smaller penalty. Therefore, if the truth has no interactions, then glinternet picks out only main effects.

If an interaction was present (α_1:2 > 0), the derivative of the penalty term with respect to α_1:2 is

$$\frac{{\alpha }_{1:2}}{\sqrt{L_2{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L_1{\Vert {\stackrel{\sim }{\alpha }}_2\Vert }_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}}.$$

The presence of main effects allows this derivative to be smaller, thus allowing the algorithm to pay a smaller penalty (as compared to no main effects present) for making α̂_1:2 nonzero. This shows interactions whose main effects are also present are discovered before pure interactions.

3.4 Interaction between a categorical variable and a continuous variable

We describe how to extend Theorem 1 to interaction between a continuous variable and a categorical variable.

Consider the case where we have a categorical variable F with L levels, and a continuous variable Z. Let μ_i = 𝔼[Y|F = i, Z = z]. There are four cases:

• μ_i = μ (no main effects, no interactions)

• ${\mu }_i=\mu +{\theta }_1^i$ (main effect F)

• ${\mu }_i=\mu +{\theta }_1^i+{\theta }_{2}z$ (two main effects)

• ${\mu }_i=\mu +{\theta }_1^i+{\theta }_{2}z+{\theta }_{1:2}^{i}z$ (main effects and interaction)

As before, we impose the constraints ${\sum }_{i=1}^L{\theta }_1^i=0$ and ${\sum }_{i=1}^L{\theta }_{1:2}^i=0$. We will also assume that the observed values z_i are standardized to have mean zero and variance one; see also Appendix A.2. An overlapped group-lasso of the form

$$\begin{array}{l}{\text{argmin}}_{\mu ,\alpha ,\stackrel{\sim }{\alpha }}\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\mathbf{X}{\alpha }_1-\mathbf{Z}{\alpha }_2-[\begin{array}{ccc}\mathbf{X}& \mathbf{Z}& (\mathbf{X}\ast \mathbf{Z})\end{array}]\left[\begin{array}{c}{\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\Vert }_2^2\\ +\lambda \left({\Vert {\alpha }_1\Vert }_2+\mid {\alpha }_2\mid +\sqrt{{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L{\stackrel{\sim }{\alpha }}_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}\right)\end{array}$$ (16)

subject to

$$\sum _{i=1}^L{\alpha }_1^i=0,\sum _{i=1}^L{\stackrel{\sim }{\alpha }}_1^i=0,\sum _{i=1}^L{\alpha }_{1:2}^i=0$$

allows us to obtain estimates of the interaction term that satisfy strong hierarchy. This is again due to the nature of the square root term in the penalty. The actual main effects and interactions can be recovered as

$$\begin{array}{r}{\widehat{\theta }}_1={\widehat{\alpha }}_1+{\widehat{\stackrel{\sim }{\alpha }}}_1\\ {\widehat{\theta }}_2={\widehat{\alpha }}_2+{\widehat{\stackrel{\sim }{\alpha }}}_2\\ {\widehat{\theta }}_{1:2}={\widehat{\alpha }}_{1:2}.\end{array}$$

We have the following extension of Theorem 1:

Theorem 2

Solving the constrained overlapped group-lasso above is equivalent to solving

$${\text{argmin}}_{\mu ,\beta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\mathbf{X}{\beta }_1-\mathbf{Z}{\beta }_2-(\mathbf{X}\ast [\begin{array}{cc}\mathbf{1}& \mathbf{Z}\end{array}]){\beta }_{1:2}\Vert }_2^2+\lambda ({\Vert {\beta }_1\Vert }_2+\mid {\beta }_2\mid +{\Vert {\beta }_{1:2}\Vert }_2).$$ (17)

Proof

We proceed as in the proof of Theorem 1 and introduce an additional parameter μ̃ into the overlapped objective:

$$\begin{array}{l}{\text{argmin}}_{\mu ,\stackrel{\sim }{\mu },\alpha ,\stackrel{\sim }{\alpha }}\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-\mathbf{X}{\alpha }_1-\mathbf{Z}{\alpha }_2-[\begin{array}{cccc}\mathbf{1}& \mathbf{X}& \mathbf{Z}& (\mathbf{X}\ast \mathbf{Z})\end{array}]\left[\begin{array}{c}\stackrel{\sim }{\mu }\\ {\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\Vert }_2^2\\ +\lambda \left({\Vert {\alpha }_1\Vert }_2+\mid {\alpha }_2\mid +\sqrt{L{\stackrel{\sim }{\mu }}^2+{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L{\stackrel{\sim }{\alpha }}_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2}\right)\end{array}$$ (18)

As before, this does not change the solutions because we will have $\widehat{\stackrel{\sim }{\mu }}=0$ (see Lemma 2).

Decompose the 2L-vector β_1:2 into

$$\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\end{array}\right],$$

where η₁ and η₂ both have dimension L × 1. Apply the ANOVA decomposition to both to obtain

$$\begin{array}{l}{\eta }_1^i={\eta }_1^{·}+({\eta }_1^i-{\eta }_1^{·})\\ \equiv \stackrel{\sim }{\mu }+{\stackrel{\sim }{\alpha }}_1^i\end{array}$$

and

$$\begin{array}{l}{\eta }_2^i={\eta }_2^{·}+({\eta }_2^i-{\eta }_2^{·})\\ \equiv {\stackrel{\sim }{\alpha }}_2+{\alpha }_{1:2}^i.\end{array}$$

Note that α̃₁ is a (L × 1)-vector that satisfies ${\sum }_{i=1}^L{\stackrel{\sim }{\alpha }}_2^i=0$, and likewise for α_1:2. This allows us to write

$${\beta }_{1:2}=\left[\begin{array}{c}\stackrel{\sim }{\mu }·{\mathbf{1}}_{L\times 1}\\ {\stackrel{\sim }{\alpha }}_2·{\mathbf{1}}_{L\times 1}\end{array}\right]+\left[\begin{array}{c}{\stackrel{\sim }{\alpha }}_1\\ {\alpha }_{1:2}\end{array}\right]$$

It follows that

$${\Vert {\beta }_{1:2}\Vert }_2^2=L{\stackrel{\sim }{\mu }}^2+{\Vert {\stackrel{\sim }{\alpha }}_1\Vert }_2^2+L{\stackrel{\sim }{\alpha }}_2^2+{\Vert {\alpha }_{1:2}\Vert }_2^2,$$

which shows that the penalties in both problems are equivalent. A direct computation shows that the loss functions are also equivalent:

$$\begin{array}{l}(\mathbf{X}\ast [\begin{array}{cc}\mathbf{1}& \mathbf{Z}\end{array}]){\beta }_{1:2}=[\begin{array}{cc}\mathbf{X}& (\mathbf{X}\ast \mathbf{Z})\end{array}]{\beta }_{1:2}\\ =[\begin{array}{cc}\mathbf{X}& (\mathbf{X}\ast \mathbf{Z})\end{array}]\left(\left[\begin{array}{c}\stackrel{\sim }{\mu }·{\mathbf{1}}_{L\times 1}\\ {\stackrel{\sim }{\alpha }}_2·{\mathbf{1}}_{L\times 1}\end{array}\right]+\left[\begin{array}{c}{\stackrel{\sim }{\alpha }}_1\\ {\alpha }_{1:2}\end{array}\right]\right)\\ =\stackrel{\sim }{\mu }·\mathbf{1}+\mathbf{X}{\stackrel{\sim }{\alpha }}_1+\mathbf{Z}{\stackrel{\sim }{\alpha }}_2+(\mathbf{X}\ast \mathbf{Z}){\alpha }_{1:2}.\end{array}$$

Theorem 2 allows us to accommodate interactions between continuous and categorical variables by simply parametrizing the interaction term as X * [1 Z], where X is the indicator matrix representation for categorical variables that we have been using all along. We then proceed as before with a group-lasso.

3.5 Interaction between two continuous variables

We have seen that the appropriate representations for the interaction terms are

• X₁ * X₂ = X_1:2 for categorical variables

• X * [1 Z] = [X (X * Z)] for one categorical variable and one continuous variable.

How should we represent the interaction between two continuous variables? We follow the traditional approach, and use the bilinear interaction term Z₁ · Z₂. We can use exactly the same framework as before:

$$\begin{array}{l}{\mathbf{Z}}_{1:2}=[\begin{array}{cc}\mathbf{1}& {\mathbf{Z}}_1\end{array}]\ast [\begin{array}{cc}\mathbf{1}& {\mathbf{Z}}_2\end{array}]\\ =[\begin{array}{cccc}\mathbf{1}& {\mathbf{Z}}_1& {\mathbf{Z}}_2& ({\mathbf{Z}}_1\ast {\mathbf{Z}}_2)\end{array}].\end{array}$$

This is indeed the case. A linear interaction model for Z₁ and Z₂ is given by

$$\mathbb{E}[Y\mid Z_1=z_1,Z_2=z_2]=\mu +{\theta }_1{z}_1+{\theta }_2{z}_2+{\theta }_{1:2}{z}_1{z}_2.$$

Unlike the previous cases where there were categorical variables, there are no constraints on any of the coefficients, and so no simplifications arise. It follows that the overlapped group-lasso

$$\begin{array}{l}{\text{argmin}}_{\mu ,\stackrel{\sim }{\mu },\alpha ,\stackrel{\sim }{\alpha }}\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{Z}}_1{\alpha }_1-{\mathbf{Z}}_2{\alpha }_2-[\begin{array}{cccc}\mathbf{1}& {\mathbf{Z}}_1& {\mathbf{Z}}_2& ({\mathbf{Z}}_1\ast {\mathbf{Z}}_2)\end{array}]\left[\begin{array}{c}\stackrel{\sim }{\mu }\\ {\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\\ {\alpha }_{1:2}\end{array}\right]\Vert }_2^2\\ +\lambda \left(\mid {\alpha }_1\mid +\mid {\alpha }_2\mid +\sqrt{{\stackrel{\sim }{\mu }}^2+{\stackrel{\sim }{\alpha }}_1^2+{\stackrel{\sim }{\alpha }}_2^2+{\alpha }_{1:2}^2}\right)\end{array}$$ (19)

is trivially equivalent to

$${\text{argmin}}_{\mu ,\beta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{Z}}_1{\beta }_1-{\mathbf{Z}}_2{\beta }_2-([\begin{array}{cc}\mathbf{1}& {\mathbf{Z}}_1\end{array}]\ast [\begin{array}{cc}\mathbf{1}& {\mathbf{Z}}_2\end{array}]){\beta }_{1:2}\Vert }_2^2+\lambda (\mid {\beta }_1\mid +\mid {\beta }_2\mid +{\Vert {\beta }_{1:2}\Vert }_2),$$ (20)

with the β’s taking the place of the α’s. Note that we will have $\widehat{\stackrel{\sim }{\mu }}=0$, as will be the first element of $\widehat{{\beta }_{1:2}}$. Since its coefficient is zero, we can omit the column of 1s in the interaction matrix.

4 Strong rules and variable screening

glinternet works by solving a group-lasso with $p+\left(\begin{array}{c}p\\ 2\end{array}\right)$ groups of variables. Our algorithms scale well; we give an example in Section 7.3 where p = 27, 000, leading to a search space of 360 million possible interactions. This is partly attributable to our use of strong rules [Tibshirani et al, 2012], a computational hedge that we describe below.

However, for larger p (e.g. ~ 10⁵), we require some form of screening to reduce the dimension of the interaction search space. We have argued that models satisfying hierarchy make sense, so it is natural to consider screening devices that hedge on the presence of main effects. Again we use the strong rules, but this time in adaptive fashion. In our simulation experiments we compare this to an approach based on gradient boosting, which in the interest of space we describe in the online Appendix A.1.

4.1 Strong rules

The strong rules [Tibshirani et al, 2012] for lasso-type problems are effective heuristics for (temporarily) discarding large numbers of variables that are likely to be redundant. As a result, the strong rules can dramatically speed up the convergence of algorithms because they can concentrate on a smaller strong set of variables that are more likely to be nonzero. After our algorithm has converged on the strong set, we have to check the KKT conditions on the discarded set. Any violators are then added to the active set, and the model is refit. This is repeated till no violators are found. In our experience, violations rarely occur, which means we rarely have to do multiple rounds of fitting for any given value of the regularization parameter λ.

In detail, suppose we have a solution Ŷ_ℓ at λ_ℓ, and wish to compute the solution at λ_ℓ+1 < λ_ℓ. The strong rule for the group-lasso involves computing $s_i={\Vert {\mathbf{X}}_i^T(\mathbf{Y}-{\widehat{\mathbf{Y}}}_{\ell })\Vert }_2$ for every group of variables X_i. We know from the KKT optimality conditions (see Section 2.4) that

$$\begin{array}{ccc}{s}_i\le {\lambda }_{\ell }& \text{if}& {\widehat{\beta }}_i=0\\ s_i={\lambda }_{\ell }& \text{if}& {\widehat{\beta }}_i\ne 0,\end{array}$$ (21)

(assuming the γ_i in (8) are all 1; if not, γ_i multiplies λ_ℓ in (21)). When we decrease λ to λ_ℓ+1, we expect to enlarge the active set. The strong rule discards a group i if s_i < λ_ℓ+1 − (λ_ℓ − λ_ℓ+1).

We do not store all the matrices X_i in advance, particularly for those based on factor variables, but rather compute the inner-products directly using the underlying variables. Note also that these operations are easily run in parallel when p is large.

4.2 Adaptive screening

If $p+\left(\begin{array}{c}p\\ 2\end{array}\right)$ is too large, then we cannot accommodate all possible interactions, and instead use a hedge (also based on the strong rules). The idea is use the strong rules to screen main-effect variables only, and then consider all possible interactions with the chosen variables.

An example will illustrate. Suppose we have 10,000 variables (~ 50×10⁶ possible interactions), but we are computationally limited to a group-lasso with 10⁶ groups. Assume we have the fit for λ = λ_ℓ, and want to move on to λ_ℓ+1. Let r_λℓ = Y − Ŷ_λℓ denote the current residual. At this point, the variable scores $s_i={\Vert {\mathbf{X}}_i^T{r}_{{\lambda }_{\ell }}\Vert }_2$ have already been computed from checking the KKT conditions at the solutions for λ_ℓ. We restrict ourselves to the 10,000 (main-effect) variables, and take the 100 with the highest scores. Denote this set by ${\mathcal{T}}_{100}^{{\lambda }_{\ell +1}}$. The candidate set of variables for the group-lasso is then given by ${\mathcal{T}}_{100}^{{\lambda }_{\ell +1}}$ together with the pairwise interactions between all 10,000 variables and ${\mathcal{T}}_{100}^{{\lambda }_{\ell +1}}$. Because this gives a candidate set with about 100 × 10, 000 = 10⁶ terms, the computation is now feasible. We then compute the group-lasso on this candidate set, and repeat the procedure with the new residual r_λℓ+1.

5 Related work and approaches

Here we describe two related approaches to discovering interactions. An earlier third approach, logic regression [Ruczinski I, 2003] is based on Boolean combinations of variables. Since it is restricted to binary variables, we did not include it in our comparisons.

5.1 hierNet [Bien et al., 2013]

This is a method for finding interactions, and like glinternet, imposes hierarchy via regularization. HierNet solves the optimization problem

$${\text{argmin}}_{\mu ,\beta ,\theta }\frac{1}{2}\sum _{i=1}^n{(y_i-\mu -x_i^T\beta -\frac{1}{2}{x}_i^T\mathrm{\Theta }{x}_i)}^2+\lambda {\mathbf{1}}^T({\beta }^{+}+{\beta }^{-})+\frac{\lambda }{2}{\Vert \mathrm{\Theta }\Vert }_1$$ (22)

subject to

$$\mathrm{\Theta }={\mathrm{\Theta }}^T,{\Vert {\mathrm{\Theta }}_{j·}\Vert }_1\le ({\beta }_j^{+}+{\beta }_j^{-}),{\beta }_j^{+}\ge 0,{\beta }_j^{-}\ge 0,$$

where Θ_j is the jth row of Θ. The main effects are represented by β, and interactions are given by the matrix Θ. The first constraint enforces symmetry in the interaction coefficients. ${\beta }_j^{+}$ and ${\beta }_j^{-}$ are the positive and negative parts of β_j, and are given by ${\beta }_j^{+}=max(0,{\beta }_j)$ and ${\beta }_j^{-}=-min(0,{\beta }_j)$ respectively. The constraint ${\Vert {\mathrm{\Theta }}_{j·}\Vert }_1\le ({\beta }_j^{+}+{\beta }_j^{-})$ implies that if some components of the j-th row of Θ are estimated to be nonzero, then the main effect β_j will also be estimated to be nonzero. Since nonzero Θ_ij corresponds to an interaction between variables i and j, by symmetry we will have both ||Θ_i·||₁ > 0 and ||Θ_j·||₁ > 0. This implies that the solutions to the hierNet objective satisfy strong hierarchy. One can think of $min[({\beta }_i^{+}+{\beta }_i^{-}),({\beta }_j^{+}+{\beta }_j^{-})]$ as a budget for the amount of interactions that are allowed to be nonzero. Alternatively, a strong interaction will force the main effects to be large, a somewhat surprising side effect.

The hierNet objective can be modified to obtain solutions that satisfy weak hierarchy (by removing the symmetry constraint); we use both in our simulations, giving hierNet a potential advantage. Currently, hierNet is only able to accommodate binary and continuous variables, and is practically limited to fitting models with fewer than 1000 variables.

5.2 Composite absolute penalties [Zhao et al., 2009]

Like glinternet, this is also a penalty-based approach. CAP employs penalties of the form

$${\Vert ({\beta }_i,{\beta }_j)\Vert }_{{\gamma }_1}+{\Vert {\beta }_j\Vert }_{{\gamma }_2}$$

where γ₁ > 1. Such a penalty ensures that β̂_i ≠ 0 whenever β̂_j ≠ 0. It is possible that β̂_i ≠ 0 but β̂_j = 0. In other words, the penalty makes β̂_j hierarchically dependent on β̂_i: it can only be nonzero after β̂_i becomes nonzero. It is thus possible to use CAP penalties to build interaction models that satisfy hierarchy. For example, a penalty of the form ||(θ₁, θ₂, θ_1:2)||₂+||θ_1:2||₂ will result in estimates that satisfy θ̂_1:2 ≠ 0 ⇒ θ̂₁ ≠ 0 and θ̂₂ ≠ 0. We can thus build a linear interaction model for two categorical variables by solving

$${\text{argmin}}_{\mu ,\theta }\frac{1}{2}{\Vert \mathbf{Y}-\mu ·\mathbf{1}-{\mathbf{X}}_1{\theta }_1-{\mathbf{X}}_2{\theta }_2-{\mathbf{X}}_{1:2}{\theta }_{1:2}\Vert }_2^2+\lambda ({\Vert {\theta }_1,{\theta }_2,{\theta }_{1:2})\Vert }_2+{\Vert {\theta }_{1:2}\Vert }_2)$$ (23)

subject to (1) and (2). We see that the CAP approach differs from glinternet in that we have to solve a constrained optimization problem which is considerably more complicated, thus making it unclear if CAP will be computationally feasible for larger problems. The form of the penalties are also different: the interaction coefficient in CAP is penalized twice, whereas glinternet penalizes it once. It is not obvious what the relationship between the two algorithms’ solutions would be.

6 Simulation study

We perform simulations to see if glinternet is competitive with existing methods. hierNet is a natural benchmark because it also tries to find interactions subject to hierarchical constraints. Because hierNet only works with continuous variables and 2-level categorical variables, we include gradient boosting (see Appendix A.1) as a competitor for the scenarios where hierNet cannot be used.

6.1 False discovery rates

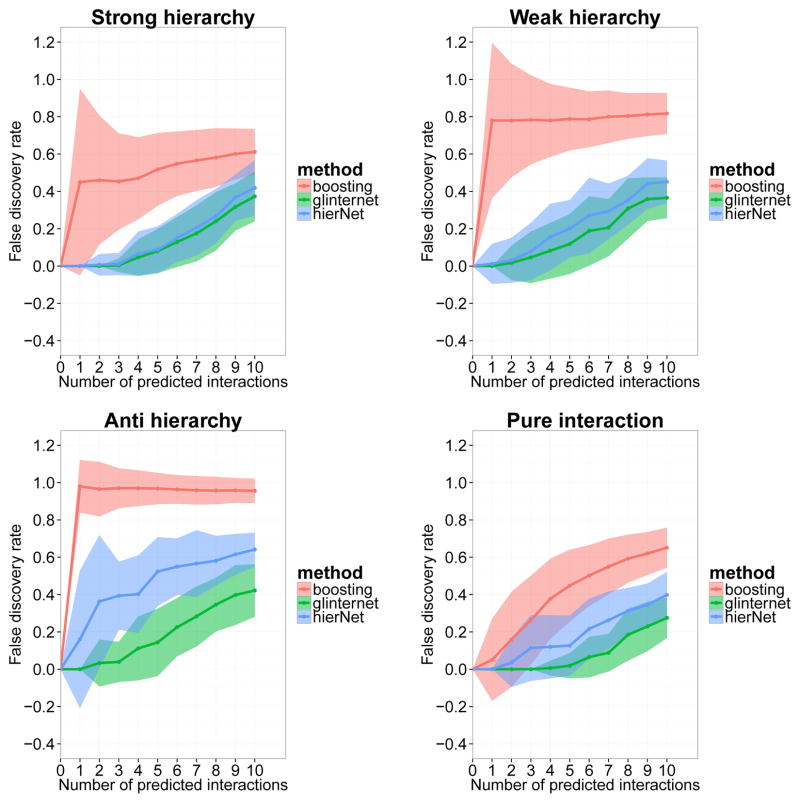
We simulate 4 different setups:

1. Truth obeys strong hierarchy. The interactions are only among pairs of nonzero main effects.

2. Truth obeys weak hierarchy. Each interaction has only one of its main effects present.

3. Truth is anti-hierarchical. The interactions are only among pairs of main effects that are not present.

4. Truth is pure interaction. There are no main effects present, only interactions.

Each case is generated with n = 500 observations and p = 30 continuous variables, with a signal to noise ratio of 1. Where applicable, there are 10 main effects and/or 10 interactions in the ground truth. The interaction and main effect coefficients are sampled from N(0, 1), so that the variance in the observations should be split equally between main effects and interactions.

Boosting is done with 5000 depth-2 trees and a learning rate of 0.001. Each tree represents a candidate interaction, and we can compute the improvement to fit due to this candidate pair. Summing up the improvement over the 5000 trees gives a score for each interaction pair, which can then be used to order the pairs. We then compute the false discovery rate as a function of the number of ordered interactions included. For glinternet and hierNet, we obtain a path of solutions and compute the false discovery rate as a function of the number of interactions discovered. The default setting for hierNet is to impose weak hierarchy, and we use this except in the cases where the ground truth has strong hierarchy. In these cases, we set hierNet to impose strong hierarchy. We also set “diagonal=FALSE” to disable quadratic terms.

We plot the average false discovery rate with standard error bars as a function of the number of predicted interactions in Figure 2. The results are from 100 simulation runs. We see that glinternet is competitive with hierNet when the truth obeys strong or weak hierarchy, and does better when the truth is anti-hierarchical. This is expected because hierNet requires the presence of main effects as a budget for interactions, whereas glinternet can still esimate an interaction to be nonzero even though none of its main effects are present. Boosting is not competitive, especially in the anti-hierarchical case. This is because the first split in a tree is effectively looking for a main effect.

Figure 2.

Simulation results for continuous variables: Average false discovery rate and standard errors from 100 simulation runs.

Both glinternet and hierNet perform comparably in these simulations. If all the variables are continuous, there do not seem to be compelling reasons to choose one over the other, apart from the computational advantages of glinternet discussed in the next section.

6.2 Feasibility

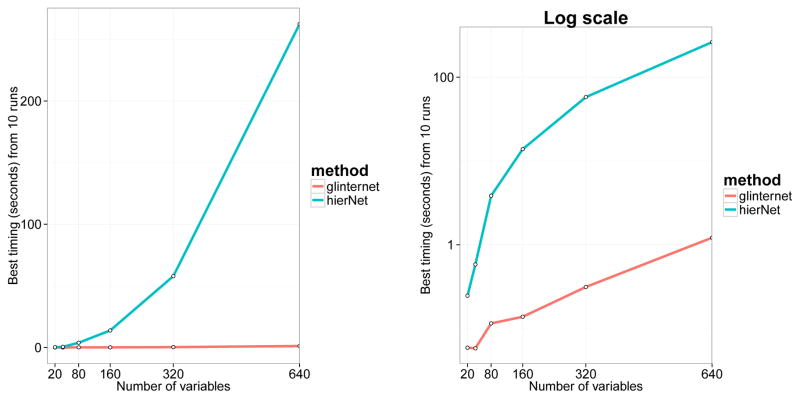
To the best of our knowledge, hierNet is the only readily available package for learning interactions among continuous variables in a hierarchical manner. Therefore it is natural to use hierNet as a speed benchmark. We generate data in which the ground truth has strong hierarchy as in Section 6.1, but with n = 1000 quantitative responses and p = 20, 40, 80, 160, 320, 640 continuous predictor variables. We set each method to find 10 interactions. While hierNet does not allow the user to specify the number of interactions to discover, we get around this by fitting a path of values, then selecting the regularization parameter that corresponds to 10 nonzero estimated interactions. We then refit hierNet along a path that terminates with this choice of parameter, and time this run. Both software packages are compiled with the same options. Figure 3 shows the best time recorded for each method over 10 runs. These simulations were timed on a Intel Core-i7 3930K processor. We see that glinternet is faster than hierNet by a factor of about 100 on these smaller problems, and is not feasible for problems larger than about 1000.

Figure 3.

Left: Best wall-clock time over 10 runs for discovering 10 interactions. Right: Same as left, but on the log scale. Both packages consist of R interfaces to C code, compiled with the same options.

7 Real data examples

We compare the performance of glinternet on several prediction problems. The competitor methods used are gradient boosting, lasso, ridge regression, and hierNet where feasible. In all situations, we determine the number of trees in boosting by first building a model with a large number of trees, typically 5000 or 10000, and then selecting the number that gives the lowest cross-validated error. We use a learning rate of 0.001, and we do not sub-sample the data since the sample sizes are small in all the cases.

The methods are evaluated on three measures:

1. misclassification error, or 0–1 loss

2. area under the receiver operating characteristic (ROC) curve, or AUC

3. cross entropy, given by $-\frac{1}{n}{\sum }_{i=1}^n[y_{i}log({\widehat{y}}_i)+(1-y_i)log(1-{\widehat{y}}_i)]$.

7.1 Spambase

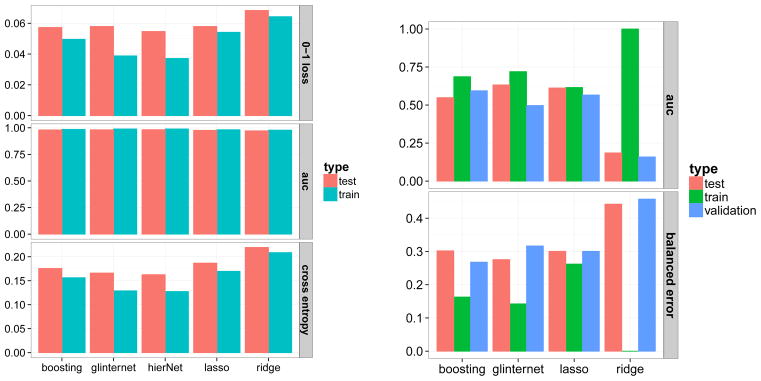
This is the Spambase data taken from the UCI Machine Learning Repository. There are 4601 binary observations indicating whether an email is spam or non-spam, and 57 integer-valued variables. All the features are log-transformed by log(1 + x) before applying the methods, since they all tend to be very skew, with point masses at zero. We split the data into a training set consisting of 3065 observations and a test set consisting of 1536 observations. The methods are tuned on the training set using 10-fold cross validation before predicting on the test set. The results are shown in the left panel in Figure 4.

Figure 4.

Left panel: Performance on Spambase. Right panel: Performance on Dorothea.

7.2 Dorothea

Dorothea is one of the 5 datasets from the NIPS 2003 Feature Learning Challenge, where the goal is to predict if a chemical molecule will bind to a receptor target. There are 100000 binary features that describe three-dimensional properties of the molecules, half of which are probes that have nothing to do with the response. The training, validation, and test sets consist of 800, 350, and 800 observations respectively. More details about how the data were prepared can be found at http://archive.ics.uci.edu/ml/datasets/Dorothea.

We ran glinternet with screening on 1000 main effects, which resulted in about 100 million candidate interaction pairs. The validation set was used to tune all the methods. We then predict on the test set with the chosen models and submitted the results online for scoring. The best model chosen by glinternet made use of 93 features, compared with the 9 features chosen by ℓ₁-penalized logistic regression (lasso). The right panel of Figure 4 summarizes the performance for each method. (Balanced error is the simple average of the fractions of false positives and false negatives, and is produced automatically by the challenge website.) We see that glinternet has a slight advantage over the lasso, indicating that interactions might be important for this problem. However, the differences are small, and boosting, glinternet and lasso all show similar performance.

7.3 Genome-wide association study

We use the simulated rheumatoid arthritis data (replicate 1) from Problem 3 in Genetic Analysis Workshop 15. Affliction status was determined by a genetic/environmental model to mimic the familial pattern of arthritis; full details can be found in [Miller et al., 2007]. These authors simulated a large population of nuclear families consisting of two parents and two offspring. We are then provided with 1500 randomly chosen families with an affected sibling pair (ASP), and 2,000 unaffected families as a control group. For the control families, we only have data from one randomly chosen sibling. Therefore we also sample one sibling from each of the 1,500 ASPs to obtain 1,500 cases.

There are 9,187 single nucleotide polymorphism (SNP) markers on chromosomes 1 through 22 that are designed to mimic a 10K SNP chip set, and a dense set of 17,820 SNPs on chromosome 6 that approximate the density of a 300K SNP set. Since 210 of the SNPs on chromosome 6 are found in both the dense and non-dense sets, we made sure to include them only once in our analysis. This gives us a total of 9187 − 210 + 17820 = 26797 SNPs, all of which are 3-level categorical variables.

We are also provided with phenotype data, and we include sex, age, smoking history, and the DR alleles from father and mother in our analysis.¹ Sex and smoking history are 2-level categorical variables, while age is continuous. Each DR allele is a 3-level categorical variable, and we combine the father and mother alleles in an unordered way to obtain a 6-level DR variable. In total, we have 26,801 variables and 3,500 training examples.

We run glinternet (without screening) on a grid of values for λ that starts with the empty model. The first two variables found are main effects:

• SNP6_305

• denseSNP6_6873

Following that, an interaction denseSNP6_6881:denseSNP6_6882 gets picked up. We now proceed to analyze this result.

Two of the interactions listed in the answer sheet provided with the data are: locus A with DR, and locus C with DR. There is also a main effect from DR. The closest SNP to the given position of locus A is SNP16_31 on chromosome 16, so we take this SNP to represent locus A. The given position for locus C corresponds to denseSNP6_3437, and we use this SNP for locus C. While it looks like none of the true variables are to be found in the list above, these discovered variables have very strong association with the true variables.

If we fit a linear logistic regression model with our first discovered pair denseSNP6_6881:denseSNP6_6882, the main effect denseSNP6_6882 and the interaction terms are both significant:

A χ² test for independence between denseSNP6_6882 and DR gives a p-value of less than 1e-15, so that glinternet has effectively selected an interaction with DR. However, denseSNP6_6881 has little association with loci A and C. The question then arises as to why we did not find the true interactions with DR. To investigate, we fit a linear logistic regression model separately to each of the two true interaction pairs. In both cases, the main effect DR is significant (p-value < 1e – 15), but the interaction term is not:

Therefore it is somewhat unsurprising that glinternet did not pick these interactions.

This example also illustrates how the the group-lasso penalty in glinternet helps in discovering interactions (see Section 3.3). We mentioned above that denseSNP6_6881:denseSNP6_6882 is significant if fit by itself in a linear logistic model (Table 1). But if we now fit this interaction in the presence of the two main effects SNP6_305 and denseSNP6_6873, it is not significant:

Table 1.

Analysis of deviance table for linear logistic model fitted to first interaction term that was discovered. The Df for interaction is 1 (and not 2) because of one empty cell in the interaction table.

	Df	Dev	Resid. Dev	ℙ(> χ2)
NULL			4780.4
denseSNP6_6881	1	1.61	4778.7	0.20386
denseSNP6_6882	2	1255.68	3523.1	<2e-16
denseSNP6_6881:denseSNP6_6882	1	5.02	3518.0	0.02508

	Df	Dev	Resid. Dev	ℙ(> χ2)
NULL			4780.4
SNP6_305	2	2140.18	2640.2	<2e-16
denseSNP6_6873	2	382.61	2257.6	<2e-16
denseSNP6_6881:denseSNP6_6882	4	3.06	2254.5	0.5473

This suggests that fitting the two main effects fully has explained away most of the effect from the interaction. But because glinternet regularizes the coefficients of these main effects, they are not fully fit, and this allows glinternet to discover the interaction.

The ANOVA analyses above suggest that the true interactions are difficult to find in this GWAS dataset. Despite having to search through a space of about 360 million interaction pairs, glinternet was able to find variables that are strongly associated with the truth. This illustrates the difficulty of the interaction-learning problem: even if the computational challenges are met, the statistical issues are perhaps the dominant factor.

8 Discussion

In this paper we introduce glinternet, a method for learning linear interaction models that satisfy strong hierarchy. We demonstrate that the performance of our method is comparable with past approaches, but has the added advantage of being able to accommodate both categorical and continuous variables, and on a much larger scale. We illustrate the method with several examples using real and simulated data, and also show that glinternet can be applied to genome-wide association studies.

There are many approaches for fitting a group lasso. We describe the specific algorithm used in our implementation in Appendix A.3. glinternet is available on CRAN as a package for the statistical software R. The functions in this package interface to our efficient C code for solving the group lasso.

Our paper is mostly about computations, and how to finesse the big search space when dealing with interactions. But there is an equally big statistical bottleneck: when the space of searched interactions is very large, it is much easier to find false positives. This is not addressed in this paper, and is an important area for further research.

Table 2.

Analysis of deviance table for linear logistic regression done separately on each of the two true interaction terms. In the second table, the Df for interaction is 8 (and not 10) because of empty cells in the interaction table.

	Df	Dev	Resid. Dev	ℙ(>χ2)
NULL			4780.4
SNP16_31	2	3.08	4777.3	0.2147
DR	5	2383.39	2393.9	<2e-16
SNP16_31:DR	10	9.56	2384.3	0.4797
NULL			4780.4
denseSNP6_3437	2	1.30	4779.1	0.5223
DR	5	2384.18	2394.9	<2e-16
denseSNP6_3437:DR	8	5.88	2389.0	0.6604

A Appendix

A.1 Screening with boosted trees

AdaBoost [Freund and Schapire, 1995] and gradient boosting [Friedman, 2001] are effective approaches for building ensembles of weak learners such as decision trees. One of the advantages of trees is that they are able to model nonlinear effects and high-order interactions. For example, a depth-2 tree essentially represents an interaction between the variables involved in the two splits, which suggests that boosting with depth-2 trees is a way of building a first-order interaction model. Note that the interactions are hierarchical, because in finding the optimal first split, the boosting algorithm is looking for the best main effect. The subsequent split is then made, conditioned on the first split.

If we boost with T trees, then we end up with a model that has at most T interaction pairs. The following diagram gives a schematic of the boosting iterations with categorical variables.

(24)

In the first tree, levels 2 and 3 of F₁ are not involved in the interaction with F₂. Therefore each tree in the boosted model does not represent an interaction among all the levels of the two variables, but only among a subset of the levels. To enforce the full interaction structure, one could use fully-split trees, but we do not develop this approach for two reasons. First, boosting is a sequential procedure and is quite slow even for moderately sized problems. Using fully split trees will further degrade its runtime. Second, in variables with many levels, it is reasonable to expect that the interactions only occur among a few of the levels. If this were true, then a complete interaction that is weak for every combination of levels might be selected over a strong partial interaction. But it is the strong partial interaction that we are interested in.

Boosting is feasible because it is a greedy algorithm. If p is the number of variables, an exhaustive search involves 𝒪(p²) variables, whereas boosting operates with 𝒪(p). To use the boosted model as a screening device for interaction candidates, we take the set of all unique interactions from the collection of trees. For example, in our schematic above, we would add F_1:2 and F_5:7 to our candidate set of interactions.

In our experiments, using boosting as a screen did not perform as well as we hoped. There is the issue of selecting tuning parameters such as the amount of shrinkage and the number of trees to use. Lowering the shrinkage and increasing the number of trees improves false discovery rates, but at a significant cost to speed.

A.2 Defining the group penalties γ

Recall that the group-lasso solves the optimization problem

$${\text{argmin}}_{\beta }\mathcal{L}(\mathbf{Y},\mathbf{X};\beta )+\lambda \sum _{i=1}^p{\gamma }_i{\Vert {\beta }_i\Vert }_2,$$

where ℒ(Y, X; β) is the negative log-likelihood function. This is given by

$$\mathcal{L}(\mathbf{Y},\mathbf{X};\beta )=\frac{1}{2n}{\Vert \mathbf{Y}-\mathbf{X}\beta \Vert }_2^2$$

for squared error loss, and

$$\mathcal{L}(\mathbf{Y},\mathbf{X},\beta )=-\frac{1}{n}[{\mathbf{Y}}^T(\mathbf{X}\beta )-{\mathbf{1}}^{T}log(\mathbf{1}+exp(\mathbf{X}\beta ))]$$

for logistic loss (log and exp are taken component-wise). Each β_i is a vector of coefficients for group i. When each group consists of only one variable, this reduces to the lasso.

The γ_i allow us to penalize some groups more (or less) than others. We want to choose the γ_i so that if the signal were pure noise, then all the groups are equally likely to be nonzero. Because the quantity ${\Vert {\mathbf{X}}_i^T(\mathbf{Y}-\widehat{\mathbf{Y}})\Vert }_2$ determines whether the group X_i is zero or not (see the KKT conditions (8)), we define γ_i via a null model as follows. Let ε ~ (0, I). Then we have

$$\begin{array}{l}{\gamma }_i^2=\mathbb{E}{\Vert {\mathbf{X}}_i^T\epsilon \Vert }_2^2\\ =\text{tr}{\mathbf{X}}_i^T{\mathbf{X}}_i\\ ={\Vert {\mathbf{X}}_i\Vert }_F^2.\end{array}$$

Therefore we take γ_i = ||X_i||_F, the Frobenius norm of the matrix X_i. In the case where the X_i are orthonormal matrices with p_i columns, we recover ${\gamma }_i=\sqrt{p_i}$, which is the value proposed in [Yuan and Lin, 2006]. In our case, the indicator matrices for categorical variables all have Frobenius norm equal to $\sqrt{n}$, so we can simply take γ_i = 1 for all i. The case where continuous variables are present is not as straightforward, but we can normalize all the groups to have Frobenius norm one, which then allows us to take γ_i = 1 for i = 1, …, p.

A.3 Algorithmic details

We describe the algorithm used in glinternet for solving the group-lasso optimization problem. Since the algorithm applies to the group-lasso in general and not specifically for learning interactions, we will use Y as before to denote the n-vector of observed responses, but X = [X₁ X₂ … X_p] will now denote a generic feature matrix whose columns fall into p groups.

Fast iterative soft thresholding (FISTA) [Beck and Teboulle, 2009] is a popular approach for computing the lasso estimates. This is essentially a first order method with Nesterov style acceleration through the use of a momentum factor. Because the group-lasso can be viewed as a more general version of the lasso, it is unsurprising that FISTA can be adapted for the group-lasso with minimal changes. This gives us important advantages:

1. FISTA is a generalized gradient method, so that there is no Hessian involved

2. virtually no change to the algorithm when going from squared error loss to logistic loss

3. gradient computation and parameter updates can be parallelized

4. can take advantage of adaptive momentum-restart heuristics.

Adaptive momentum restart was introduced in [O’Donoghue and Candes, 2012] as a scheme to counter the “rippling” behaviour often observed with accelerated gradient methods. They demonstrated that adaptively restarting the momentum factor based on a gradient condition can dramatically speed up the convergence rate of FISTA. The intuition is that we should reset the momentum to zero whenever the gradient at the current step and the momentum point in different directions. Because the restart condition only requires a vector multiplication with the gradient (which has already been computed), the added computational cost is negligible. The FISTA algorithm with adaptive restart is given below.

At each iteration, we take a step in the direction of the gradient with step size s. We can get an idea of what s should be by looking at the majorized objective function about a fixed point β₀:

$$M(\beta )=\mathcal{L}(\mathbf{Y},\mathbf{X};{\beta }_0)+{(\beta -{\beta }_0)}^{T}g({\beta }_0)+\frac{1}{2s}{\Vert \beta -{\beta }_0\Vert }_2^2+\lambda \sum _{i=1}^p{\Vert {\beta }_i\Vert }_2.$$ (25)

Here, g(β₀) is the gradient of the negative log-likelihood ℒ(Y, X; β) evaluated at β₀. Majorization-minimization schemes for convex optimization choose s sufficiently small so that the LHS of (25) is upper bounded by the RHS. One strategy is to start with a large step size, then backtrack until this condition is satisfied. We use an approach that is mentioned in [Becker et al., 2011] that adaptively initializes the step size with

$$s=\frac{{\Vert {\beta }^{(k)}-{\beta }^{(k-1)}\Vert }_2}{{\Vert g_k-g_{k-1}\Vert }_2}.$$ (26)

We then backtrack from this initialized value if necessary by multiplying s with some 0 < α < 1. The interested reader may refer to [Simon et al., 2013] for more details about majorization-minimization schemes for the group-lasso.

Algorithm 1.

FISTA with adaptive restart

glinternet is available on CRAN as a package for the statistical software R. The functions in this package interface to our efficient C code for solving the group lasso. The user has the option of using multiple cores/CPUs, but this requires that the package be compiled with OpenMP enabled. The user may also benefit from compiling with a higher level of optimization (such as O3 for gcc). For example, all our results were obtained by compiling with the following command (same command used for hierNet):

icc -std=gnu99 -xhost -fp-model fast=2 -no-prec-div -no-prec-sqrt -ip -O3 -restrict