Conformational Selection in a Protein-Protein Interaction revealed by Dynamic Pathway Analysis

SUMMARY

Molecular recognition plays a central role in biology, and protein dynamics has been acknowledged to be important in this process. However, it is highly debated whether conformational changes happen before ligand binding to produce a binding-competent state (conformational selection) or are caused in response to ligand binding (induced fit). Proposals for both mechanisms in protein/protein recognition have been primarily based on structural arguments. However, the distinction between them is a question of the probabilities of going via these two opposing pathways. Here we present a direct demonstration of exclusive conformational selection in protein/protein recognition by measuring the flux for rhodopsin kinase binding to its regulator recoverin, an important molecular recognition in the vision system. Using NMR spectroscopy, stopped-flow kinetics and isothermal titration calorimetry we show that recoverin populates a minor conformation in solution that exposes a hydrophobic binding pocket responsible for binding rhodopsin kinase. Protein dynamics in free recoverin limits the overall rate of binding.

INTRODUCTION

Molecular recognition dynamics in protein/ligand or protein/protein interactions is a fundamental phenomenon that has been extensively discussed during the last 50 years in light of two opposing mechanisms: the induced fit (IF) (Koshland, 1958) and the conformational selection (CS) model (Changeux and Edelstein, 2011; Monod et al., 1965). The experimental detection of discrete conformational sub-states of individual proteins in solution and their structural characterization has brought renewed interest to the CS model in recent years (Boehr et al., 2006; Clore, 2014; Cornish-Bowden, 2014; Di Cera, 2014; Feixas et al., 2014; Hatzakis, 2014; James et al., 2003; James and Tawfik, 2005; Lange et al., 2008; Nussinov et al., 2014; Tzeng and Kalodimos, 2009; Vogt et al., 2014). However, even in cases where atomic resolution structures of different conformations of the free protein have been solved (James et al., 2003; Lange et al., 2008), it is not clear whether or not this conformational equilibrium is important for ligand binding. Sampling a “bound-like conformation” of the protein before the ligand is actually bound has been used as the strongest evidence for CS in a growing number of systems (Boehr et al., 2009; James and Tawfik, 2005; Lange et al., 2008; Tzeng and Kalodimos, 2009). However, pre-sampling the bound conformation is a necessary but not sufficient condition for a CS mechanism (Bouvignies et al., 2011; Tang et al., 2007; Weikl and Paul, 2014). The distinction between the two opposing binding models can only be made on the basis of flux measurements through the two pathways based on simple and long-known kinetic principles (Fersht, 1999; Foote and Milstein, 1994; James et al., 2003; Lancet and Pecht, 1976; Monod et al., 1965; Strickland et al., 1975). Fueled by an explosion of publications claiming to reveal a CS mechanism based only on pre-existing structures in the apo-proteins (Al-Hashimi, 2013; Boehr et al., 2006; James et al., 2003; Lange et al., 2008), several papers appeared reminding the community of the fundamental need to kinetically discriminate between the two models (Daniels et al., 2014; Greives and Zhou, 2014; Hammes et al., 2009; Weikl and Paul, 2014; Zhou, 2010).

Previous studies have focused solely on either a structural argument or a kinetic determination of flux (Foote and Milstein, 1994; Lancet and Pecht, 1976), but not on both as needed (Hammes et al., 2009; Palmer, 2014). Here we combine both structural identification of the pre-existing conformations and kinetic measurements of flux for binding of rhodopsin kinase to its regulator recoverin to unambiguously identify the pathway of protein complex formation.

Recoverin is a 23 kDa Ca²⁺-binding protein that belongs to the Neuronal Calcium Sensing (NCS) family (Burgoyne and Weiss, 2001; Weiss and Burgoyne, 2002). Recoverin inhibits rhodopsin kinase, a Serine/Threonine kinase responsible for termination of the photo-activated state of rhodopsin in rod photoreceptor cells (Chen et al., 1995; Klenchin et al., 1995). Under in vitro conditions, recoverin inhibits rhodopsin kinase in a Ca²⁺-dependent manner resulting in extended activation of rhodopsin. Ca²⁺-loaded recoverin binds the N-terminal helix of rhodopsin kinase (Ames et al., 2006; Higgins et al., 2006), an amphipathic helix recognized also by rhodopsin (Higgins et al., 2006; Palczewski et al., 1993), and thus prevents phosphorylation of activated rhodopsin. When Ca²⁺ concentrations are low, rhodopsin kinase is released by recoverin and is then able to phosphorylate rhodopsin in a reaction that helps terminate the photo-activated state.

Recoverin contains four EF-hands, only two of which are functional in binding Ca²⁺. When Ca²⁺ binds, recoverin undergoes a conformational change (Ames et al., 1995). The solution structure of Ca²⁺-loaded recoverin in complex with a peptide corresponding to the N-terminal 28 amino acids of rhodopsin kinase (RK^N) has been determined by NMR spectroscopy, showing RK^N bound as an amphipathic helix with its hydrophobic surface docked to a hydrophobic surface of recoverin (Ames et al., 2006). The fact that the structures of peptide-bound and peptide-free forms of recoverin are largely similar has given rise to a simple model for the recoverin/rhodopsin kinase interaction in which the binding of Ca²⁺ to recoverin induces a conformation that is complementary to the N-terminal helix of rhodopsin kinase, and binding results from docking of the two proteins (Ames et al., 2006). In contrast here we provide comprehensive evidence for CS in a protein/protein interaction. To our knowledge, rhodopsin kinase binding to recoverin is the first example of a direct demonstration of an exclusive CS mechanism for a protein/protein interaction.

RESULTS

Design of best rhodopsin kinase mimic for recoverin binding studies

While this simple model is appealing, it is to be noted that the conformation of recoverin in the complex is clearly distinct from the Ca²⁺-loaded form of peptide-free recoverin (Ames et al., 2006). There is a global conformational rearrangement of the backbone of recoverin in the RK^N-bound structure relative to free recoverin (Fig. 1A). The global conformational differences between free recoverin and recoverin bound to the rhodopsin kinase-peptide are further demonstrated by chemical shift differences throughout the protein, including residues not in close proximity to the bound peptide (Fig. 1B, C).

Figure 1. Recoverin binding to rhodopsin kinase – conformational pathways and structural rearrangements.

A. Overlay of the free (blue) and RK^N-bound (red, RK^N in orange) recoverin structures (1JSA (Ames et al., 1997) and 2I94 (Ames et al., 2006), respectively). The two calcium ions bound to the EF hands are shown as spheres. B. Overlay of ¹H-¹⁵N HSQC spectra of free (blue) and RK-GB1 bound (red) recoverin recorded at 30 °C. C. Residues with chemical-shift perturbations upon RK-GB1 binding plotted onto the solution structure of recoverin (PDB: 1JSA) using a color gradient. D. Two alternative kinetic pathways from free Rv (upper left) to the RK-GB1 bound Rv* structure (bottom right) are induced fit (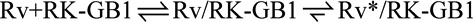) and conformational selection (). The experimentally known structures are circled. The rhodopsin kinase peptide is shown in orange. See also Fig. S1.

Consequently, the mechanism of protein/protein interaction seems to be more complex than a simple docking event; a conformational change must happen either before (i.e., conformational selection) or after (i.e., induced fit) binding (Fig. 1D). We therefore designed a set of experiments that allowed us to directly distinguish between these opposing binding mechanisms. Monitoring the binding process directly over a wide range of protein concentrations is essential for this distinction (Daniels et al., 2014; Greives and Zhou, 2014; Hammes et al., 2009; Weikl and Paul, 2014; Zhou, 2010). Due to solubility issues of the RK^N peptide used for the structure determination (Ames et al., 2006), we first had to identify a suitable rhodopsin kinase peptide that has sufficient aqueous solubility to permit examination of the binding kinetics at high peptide concentrations, while maintaining all binding determinants for recoverin. We found that a fusion of the B1 domain of immunoglobulin protein G to the N-terminal helix of rhodopsin kinase produced a peptide target (hereafter referred to as RK-GB1) with appropriate solubility for both NMR experiments (Fig. 1C and 2E) and determination of binding kinetics by stopped-flow fluorescence spectroscopy (Fig. 3A–F). Notably, identical HSQC spectra were obtained for Ca²⁺-loaded recoverin bound to either RK-GB1 or the full N-terminal rhodopsin kinase domain (RGS domain (Singh et al., 2008), Fig. S1A). In addition, ITC experiments confirmed that the affinity of recoverin for RK-GB1 is the same as for the entire RGS domain (Fig. S1B), assuring that RK-GB1 is a suitable construct to study the mechanism of rhodopsin kinase binding to recoverin.

Figure 2. Quantitative analysis of the conformational transition.

A. ¹⁵N CPMG relaxation dispersion profiles for representative recoverin residues (9-blue, 130-green and 201-red) recorded at 30 °C at 900 MHz (open squares) and 600 MHz (filled squares). Data at both field strengths were globally fit (lines in respective colors) and yield values of k_ex = 1085 ± 100 s⁻¹ and p_B = 3.2 ± 0.5%. B. ¹⁵N CPMG relaxation dispersion profiles of recoverin recorded at 10 °C (900 MHz) for the same representative residues fit to a similar rate of interconversion (1025 ± 200 s⁻¹) and population of the minor state (2.5 ± 0.5%) as at 30 °C. C. Forty-five residues (in blue) distributed throughout the protein show a dispersion profile that fit to a single, global exchange process. The residues for which no information is available (e.g., proline, unassigned, or overlapped) are shown in grey. These residues are mapped onto the free recoverin crystal structure (golden, PDB 1OMR (Weiergraber et al., 2003)) with rhodopsin kinase peptide shown in transparent orange to indicate the rhodopsin kinase binding pocket. D. Residues outside the peptide binding pocket show good correlation between the Δω_N,CPMG and Δω_N,HSQC. The sign of Δω_N,CPMG values were determined as described in Experimental Procedures. The red line is for visual guidance. E. ¹⁵N CPMG relaxation dispersion data for the recoverin/RK-GB1 complex at 30 °C and 900 MHz did not show exchange for any residue. Representative residues (9-blue, 130-green and 186-red) are shown. Uncertainties in the R₂^eff values in A, B and E were estimated from the standard deviation of R₂^eff of a set of non-exchanging peaks (n=10). Uncertainties in global fit parameter (D) were estimated by jackknifing method. See also supplemental dataset 1.

Figure 3. Global fit of RK-GB1 binding and dissociation kinetics to recoverin in the CS model.

A–E. Binding kinetics measured by stopped-flow fluorescence monitoring intrinsic Tryptophan fluorescence of 10 µM recoverin with increasing RK-GB1 concentrations at 30 °C (left) and 10 °C (right). F. Determination of k_off by stopped-flow fluorescence using a 25-fold dilution of a 50 µM recoverin/RK-GB1 complex at 30 °C and at 10 °C. G–I. Overall dissociation constants K_D^obs by isothermal titration calorimetry at 10 °C (G), 20 °C (H) and 30 °C (I). The fits with the optimal parameters (Fig. 5B) are shown as red lines in panels A to F. See also Fig. S2.

Recoverin pre-samples rhodopsin kinase-bound-like structure

Since the key difference between CS and IF is whether the conformational change happens in the apo protein or in the complex (Fig. 1D), we first measured protein dynamics of Ca²⁺-loaded recoverin, both free and when bound to RK-GB1 using ¹⁵N Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion NMR (Palmer, 2004; Palmer et al., 2001). CPMG relaxation experiments, that exploit suppression of transverse magnetization loss due to conformational exchange by applying 180 degree pulses, is a powerful method to characterize millisecond conformational exchange between states with atomic resolution. This method provides information about the relative populations, the rate constant of interconversion, and structural information on the hidden state in the form of chemical shifts. A total of 45 amides were observed to undergo exchange in the CPMG experiments in recoverin (Fig. 2A–C). The exchanging residues were distributed throughout the protein (Fig. 2C) and the dynamics could be fit globally to a single exchange process (Davis et al., 1994; Palmer et al., 2001). Relaxation dispersion data were collected at two different field strengths, 600 and 900 MHz, and simultaneous fitting of the data allowed us to determine the rate constant of interconversion, relative populations and the chemical shifts of the exchanging species. The global fitting provided a population of 3.2 ± 0.5% for the minor species at 30 °C and a rate constant for going from the major to minor state (k_for for Rv→Rv*) of 35 ± 5 s⁻¹ (Fig. 2A, C, and supplemental dataset 1A). As will become a crucial fact in delivering direct evidence for a CS mechanism presented later, the rate of exchange has a shallow temperature dependence as measured by repeating the relaxation dispersion experiments at 10 °C, which yielded a global k_for of 25 ± 5 s⁻¹ and 2.5 ± 0.5% minor population (Fig. 2B).

The CPMG experiments clearly indicate that Ca²⁺-loaded recoverin exists in two different states: a major form, Rv, corresponding to the known structure from NMR solution studies in the presence of Ca²⁺, and a minor form, Rv*, of unknown structure. Even though all NMR experiments were performed under Ca²⁺-saturating conditions, we still confirmed that the measured relaxation dispersion curves were not a result of calcium binding and dissociation (supplemental dataset 1B).

The obvious next question to ask was whether or not the minor form corresponded to a conformation similar to recoverin when bound to the rhodopsin kinase-peptide. Structural information about the minor state is obtained on a per-residue basis from the relaxation dispersion data in the form of chemical shift differences (Δω_N,CPMG) between the two exchanging conformers. If the hidden state, Rv*, corresponds to the conformation attained by recoverin when bound to RK-GB1, then, for all residues outside of the peptide binding pocket, the ¹⁵N chemical shifts of Rv*, which are invisible to direct measurement, will be the same as those of recoverin bound to RK-GB1. Whereas the chemical shift changes between Rv and Rv* are invisible to direct measurement, they can be extracted from the CPMG experiments (Δω_N,CPMG). A comparison of those values measured in apo-recoverin with the chemical shift differences for spectra of recoverin and RK-GB1-bound recoverin (Δω_N,HSQC; Fig. 2D) for 25 residues outside the rhodopsin kinase-binding pocket indicates that the minor form Rv* indeed resembles the peptide-bound conformation. We note that this correlation is seen only for residues that are distant from the rhodopsin kinase-binding site, as residues within the binding pocket display additional chemical shift perturbations as a result of proximity to RK-GB1 (supplemental dataset 1C, D).

While the ability of a ligand-free protein to sample a bound-like conformation has been used extensively in recent years as proof for the CS binding mechanism (Boehr et al., 2006; James et al., 2003; James and Tawfik, 2005; Lange et al., 2008; Tzeng and Kalodimos, 2009), it does not establish such a mechanism (Bouvignies et al., 2011; Hammes et al., 2009). In fact, as is well known from simple kinetics, the major flux for binding would occur via the IF mechanism unless the minor conformation has much higher affinity for the ligand, simply because of the higher concentration of the major conformation (Hammes et al., 2009) (Fig. 1D). Thus, the only way to establish which mechanism (i.e., IF or CS) predominates is to measure directly the flux through the two pathways at varying RK-GB1 concentrations (described below).

Rv/RK-GB1 complex does not show millisecond motions in NMR experiments

Importantly, a flux through the IF pathway strictly requires a conformational change of the complex (Fig. 1D). CPMG relaxation dispersion experiments of Ca²⁺-loaded recoverin in the presence of saturating concentrations of RK-GB1 showed no exchange at 30 °C, even at the highest available field-strength of 900 MHz (Fig. 2E). The inability to observe exchange in the complex cannot be interpreted as direct evidence against the IF mechanism, as it is possible that the conformer populations and exchange kinetics were outside the limits of detection in the CPMG experiments. However, our results impose constraints on the amount of flux via the Rv/RK-GB1 → Rv*/RK-GB1 isomerization step in the IF mechanism: In the limit of slow exchange on the NMR time scale (k_ex ≤ Δω), the minor state must be less than 5% of the total, as we do not see a second set of minor peaks in the ¹⁵N HSQC spectra of RK-GB1-bound recoverin (Fig. 1B). In the limit of fast exchange (k_ex ≥ Δω, faster than 100 s⁻¹ for typical chemical-shift differences), the minor state must be present at less than 1% in order to have a flat CPMG relaxation dispersion profile (Fig. 2E).

In summary, the CPMG dispersion data gave us a first clue that binding of rhodopsin kinase to recoverin might be rooted in a CS mechanism.

Role of the hidden state Rv* in binding RK-GB1

Next, we investigated the flux via the CS and IF pathways for RK-GB1 binding to recoverin (Fig. 1D) using stopped-flow fluorescence spectroscopy. Kinetics of the binding reaction was quantified by monitoring quenching of intrinsic tryptophan fluorescence in recoverin upon binding to various concentrations of RK-GB1 (Fig. 3A–E). Since the IF and CS pathways (Fig. 1D) both consist of two steps, one would expect to observe a double-exponential fluorescence time course. The pseudo-first-order physical binding event is linearly dependent on ligand concentration, whereas the kinetics for the conformational transition will display non-linear behavior in a manner that depends on the model. However, the binding kinetics in our experiments appear to be single exponential at both temperatures and all ligand concentrations (Fig. 3A–E and supplemental dataset 2A–E). The observed rate constant (k_obs) changes non-linearly with ligand concentration indicating that we are monitoring the conformational transition, which is fortunately the crucial step to distinguish between both models. The actual binding step is either completed within the dead-time of the instrument (~3 ms) and/or too low in amplitude to be detected.

The observed rate constant (k_obs) is higher at low RK-GB1 concentrations and approaches a constant value of 32 ± 4 s⁻¹ (at 30°C) at high ligand concentrations (Fig. 3A–E, Fig. 4A). Such concentration dependence of the observed rate constant is a unique signature of the CS model (Fig. 4 red line). Importantly, the IF model has the opposite behavior of k_obs as a function of ligand concentration, an increase in apparent rate constant with increasing ligand concentrations (Fig. 4, black dotted line) (Weikl and Paul, 2014) (Copeland, 2011).

Figure 4. Unambiguous experimental determination of CS mechanism from binding kinetics.

Dependence of the observed rate constant (k_obs) from the RK-GB1 concentration at 30 °C (A) and 10 °C (B). The k_obs values were determined by exponential fitting of the binding data in Fig. 3A–E. The predicted dependence of k_obs on the ligand concentration for the CS model (red line) and IF model (black dashed line) are shown (see Methods). Uncertainties of k_obs values reflect mean ± s.e.m.; n=5 experiments. More detailed analysis is shown in supplemental dataset 2.

We note a technical yet important consideration. Only at ligand concentrations exceeding the recoverin concentrations the pseudo-first order approximation is met while at sub-stoichiometric to stoichiometric ligand concentrations the ligand is depleted during the kinetics experiment. As a result, kinetics curves under the latter conditions (Fig. 3A–C) are not strictly single-exponential. Using numerical simulations with the kinetic parameters of our system we could show however that the single-exponential fits are sufficient approximations for all ligand concentrations (supplemental dataset 2A–E). This ligand depletion during the kinetic traces at the substoichiometric/stoichiometric boundary leads to an apparent “dip” in the observed rate constants as shown in the simulation (Fig. 4, red line). We indeed experimentally observe such minimum of k_obs at equimolar concentration of Rv and RK-GB1.

The most striking observation is the fact that the observed rate constant at high ligand concentrations (32 ± 4 s⁻¹ at 30 °C) is within experimental error of the rate constant measured for formation of Rv* (Rv → Rv*) in the NMR experiments of peptide-free, Ca²⁺-loaded recoverin (35 ± 5 s⁻¹ at 30 °C). This is exactly as predicted for a clean CS mechanism at all ligand concentrations: at high RK-GB1 concentrations, the rate constant of forming the complex is identical to the production of the binding-competent form of free recoverin (Rv → Rv*). To buttress this key conclusion, we repeated the stopped-flow binding experiments at 10 °C (Fig. 3A–E, 4B), and compared the results to our NMR data where we had previously observed a shallow temperature dependence for the interconversion (Fig. 2B and supplemental dataset 1A). Indeed, at this second temperature (10 °C), the limiting observed rate constant from the stopped-flow binding experiments at high RK-GB1 concentrations (Fig. 4B, 24 ± 3 s⁻¹) was again within experimental error of the rate constant for formation of Rv* (Rv → Rv*) in the NMR relaxation dispersion experiments at 10 °C (25 ± 5 s⁻¹).

Global fit of flux binding data over a large RK-GB1 concentration range

The observed ligand-concentration dependence of k_obs and the fact that the observed rate constant of RK-GB1 binding at high RK-GB1 concentrations is identical to the rate of formation of free Rv* are two strong pieces of evidence supporting a model in which the flux goes through the CS pathway. However, we felt that it was important to rigorously determine the pathway for kinetic flux over a wide range of RK-GB1 concentrations and to globally fit all data to CS and IF. In particular, we investigated the kinetics of binding at low RK-GB1 concentrations, where the difference between CS and IF mechanisms is most prominent (Copeland, 2011; Fersht, 1999).

The binding kinetics were globally fit by numerical simulations to the CS and the IF models (Fig. 3 and supplemental dataset 2F–K). We would like to point out that this approach offers a more rigorous treatment of the system and does not contain approximations described above. In addition to the kinetic data for the association reaction, we included the measured dissociation kinetics of the Rv*/RK-GB1 complex (Fig. 3F), the forward and reverse rate constants from NMR relaxation dispersion experiments (Fig. 2A) and the observed overall dissociation constant (K_D^obs) from ITC experiments (Fig. 3G–I) in the fitting. This strategy reduces the solution space of the numerical fit, and the fit indeed converges to a unique solution. From the global fit, all microscopic rate constants for the binding scheme were determined (Fig. 5). The data fit cleanly to a CS model, which is evident from the agreement of the numerical fit with the binding and dissociation data at both 30 °C and 10 °C (Fig. 3).

Figure 5. Conformational selection pathway of recoverin binding to RK-GB1.

A. Conformational selection (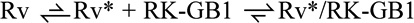) cleanly fits all data, even at high RK-GB1 concentrations. The CS pathway is shown with the corresponding microscopic rate constants at 30 °C (see B). B. Values of microscopic rate constants for RK-GB1 binding to recoverin determined by numerical global fitting of kinetics in the conformational selection path and the thermodynamic dissociation constants. C. Schematic visualization of the free energy landscape of Rv binding RK-GB1. The rate determining step in the ms timescale (33 s⁻¹) is marked with the dashed grey arrow. The faster timescale dynamics (ps-µs) define the conformational ensemble within each kinetically distinct state, but do not affect the reaction kinetics (see text for details).

Similarly, to test for compatibility with the IF mechanism, all binding kinetics (Supplemental dataset 2F–J, dissociation kinetics (supplemental dataset 2K) and K_D^obs (Fig. 3G–I) were included with no restrictions on the conformational exchange in the complex.. The fit to the IF model fails, especially at the low ligand concentrations (supplemental dataset 2F–K) since the experimentally observed rates decrease with higher ligand concentrations, that is the opposite to the behavior for an IF mechanism (Fig. 4). Theoretically, from simple kinetic laws the contribution from IF to the overall flux of complex formation would increase at high ligand concentrations (Daniels et al., 2014). However our kinetics data impose a narrow restriction on the required rates for the conformational exchange within the recoverin/RK-GB1 complex (Fig. 1): The reverse induced fit step k´_rev is defined by the observed dissociation rate (5.5 s⁻¹, Fig. 3 F) and the sum of the forward and reverse induced fit (k´_for +k´_rev) would equal the measured plateau of k_obs (33 s⁻¹, Fig. 4A). Both kinetic parameters are incompatible with our NMR experiments on the complex. Thus, at all concentrations tested (up to 160 µM of ligand), the binding of RK-GB1 to Ca²⁺-loaded recoverin proceeds by the CS mechanism. Theoretically we cannot rule out a small contribution of the IF pathway to the overall flux at even higher ligand concentration which seems to far exceed physiological concentrations.

We note that the observed dissociation constant of the complex (K_D^obs) is an important constraint in the distinction between the mechanisms as the relationship between K_D^obs and the microscopic equilibrium constants (K_disso, K_iso) is different in CS and IF mechanisms (Lancet and Pecht, 1976; Strickland et al., 1975). For CS, the overall affinity is decreased by the fraction of protein in the binding-incompetent state, while in IF, it is increased by shifting the equilibrium of the protein/protein complex towards the final conformation (see methods for details). To provide this essential experimental value K_D^obs, we determined the thermodynamic binding constants in the 10 °C to 30 °C temperature range by isothermal titration calorimetry enabling global fitting of the kinetics data at these different temperatures (Fig. 3G–I). The data reveal that the observed affinity is indeed decreased by ~30-fold as a consequence of conformational selection (Fig. 5).

Inspection of peptide-bound structure and the conformation of the binding-competent apo protein (Rv*) makes another powerful prediction: Binding of rhodopsin kinase to recoverin is driven by the burial of a large water-accessible hydrophobic surface which would result in a large negative change in heat capacity of binding (ΔC_P). Based on thermodynamic principles, a large negative ΔC_P could potentially result in a change from an endothermic to an exothermic binding reaction with increasing temperatures. Despite the fact that we could only measure binding in a relatively narrow temperature range, we indeed observe this phenomenon (Fig. 3G–I) (Baker and Murphy, 1997; Datta and LiCata, 2003; Takeda et al., 1992). From the hydrophobic surface area that gets buried upon binding one can do a rough back-of the envelope calculation of the expected ΔC_P to be around −0.5 kcal/(mol*K)(Gill and Wadso, 1976; Matulis, 2001), in good agreement with our experimentally determined ΔC_P of −0.45 ± 0.05 kcal/(mol*K) and values seen in other systems (Baker and Murphy, 1997). A binding process that is primarily driven by burial of hydrophobic surfaces and hence by removal of ordered water molecules also explains the finding that binding is strongly entropically driven (Fig. 3G–I).

DISCUSSION

Understanding the fundamental principles of a protein binding to its protein-binding partner has received considerable attention due to the central role of protein/protein interactions in biology, and the increasing demand for designing such specific interactions. From first principles two opposite mechanisms have been discussed in the last 50 years, the IF and CS mechanisms. While recent reports have emphasized the simple underlying rate equations differentiating the two mechanisms (Daniels et al., 2014; Greives and Zhou, 2014; Hammes et al., 2009; Weikl and Paul, 2014; Zhou, 2010), significant confusion and controversy remain because of a focus on structural descriptions instead of a clear determination of the flux through the two alternate pathways. We illustrate here with recoverin and its binding partner rhodopsin kinase the necessity to actually measure the kinetics of binding and then to relate these data to structural transitions measured in the NMR relaxation experiments. Ensemble descriptions of protein structures without a description of the corresponding energy landscape have further contributed to confusion about the linkage between protein dynamics and the biologically relevant process of binding. Here we have determined the essential role of excursion to the minor Rv* state since this dynamic process (i) produces the binding-competent state, and (ii) represents the overall rate limiting step for binding to rhodopsin kinase (Fig. 5C). Of course each of the states Rv, Rv* and Rv*/RK-GB1 are composed of multiple conformations, which are separated by much smaller energy barriers (interconversion on the ps-µs timescale (Fig. 5C)). However these faster transitions do not contribute to the binding kinetics since those substates re-equilibrate much faster than the major to minor transition and the physical binding step.

Several recent theoretical papers (Daniels et al., 2014; Greives and Zhou, 2014; Hammes et al., 2009; Zhou, 2010) have noted that increased partitioning of flux through the IF pathway relative to CS is favored at high ligand concentration. However, we show for recoverin, that even at very high ligand (RK-GB1) concentrations, the observed rate constant of binding is identical to the rate of formation of Rv*. Thus, we can’t detect significant partitioning of recoverin through the IF pathway. RK-GB1 can only bind via a CS mechanism, demonstrating that recoverin’s major conformation is incapable of binding. Our data demonstrate the power of an unequivocal signature of the CS mechanism: that is, when the rate-determining step of binding is equal to the rate of formation of a binding-competent minor conformation from a major conformation that cannot bind ligand (Hammes et al., 2009; Palmer, 2014).

While early studies inferred CS mechanisms from binding kinetics (Foote and Milstein, 1994; Lancet and Pecht, 1976), recent literature has focused more on structural evidence, identifying bound-like structures in the absence of ligand (Al-Hashimi, 2013; Boehr et al., 2006; Henzler-Wildman and Kern, 2007; Lange et al., 2008; Tzeng and Kalodimos, 2009). We combined these two approaches to show that rare excursions to the higher-energy conformation Rv* are essential for binding due to an obligate CS mechanism with recoverin and rhodopsin kinase. The formation of Rv* is energetically unfavorable because it is accompanied by exposure of the hydrophobic rhodopsin kinase-binding pocket, and the binding-competent state is present as a small fraction of the total population. Consequently, Rv* is hidden from conventional methods of structural characterization. Functionally, the apparent affinity of recoverin for RK-GB1 is decreased by the large fraction of the population in the binding-incompetent state, Rv. However, this higher energy state provides the specific hydrophobic binding pocket for rhodopsin kinase, as verified by a large observed negative change in heat capacity upon binding and the strong positive entropy contribution to binding. To reinforce the major findings, recoverin could not shut down signaling in the vision system via inhibition of rhodopsin kinase without the rare and slow excursion to a binding-competent state (Fig. 5C).

In recent years, the binding of ubiquitin to its various protein binding partners has become a key model system for investigations of conformational selection versus induced fit in protein/protein interactions (Bezsonova et al., 2008; Fenwick et al., 2011; Korzhnev et al., 2009; Lange et al., 2008; Michielssens et al., 2014; Phillips et al., 2013). While both mechanisms have been reported, some of the studies have been controversial and uncertainty persists in the field (Lange et al., 2008; Michielssens et al., 2014; Phillips et al., 2013). We briefly discuss below results with ubiquitin to highlight similarities and differences with the experimental approach presented here for recoverin.

Using residual dipolar couplings (RDCs) from NMR studies it has been reported that ubiquitin pre-samples all bound conformations in the ligand-free state (Lange et al., 2008). These results were used to argue in favor of a CS model for interaction with protein-binding partners. However, as discussed above, this conclusion must also be based upon kinetic data demonstrating flux through the CS pathway, but kinetic data were not provided as part of the study. Follow-up papers have shown that the conformational ensemble calculated from NMR RDCs overestimated the amplitude of motions (Fenwick et al., 2011; Grishaev et al., 2010; Maltsev et al., 2014), calling the interpretation of the results into question. Subsequent studies employed computationally designed mutant proteins, changing the population of the binding-competent state of ubiquitin for its partner dsk2 and measuring differences in overall K_D values (Michielssens et al., 2014). This is an interesting approach, and experimental measurements of population and flux showing actual differences between wild-type and mutant proteins could indeed address directly the question of CS versus IF for ubiquitin in the future.

An IF mechanism was put forward for various ubiquitin mutants based on NMR relaxation of free ubiquitin and measurements of binding kinetics for interaction with a deubiquitinase (DUB) target (Phillips et al., 2013). While at first glance this study seems to address the question of flux in a similar manner as we have performed for recoverin binding to RK-GB1, there are several concerns. First, the slowing of conformational exchange in the ubiquitin mutants to the millisecond time regime (and therefore increasing the energy barrier to make the binding-competent state) without effect on the overall rate of binding was used as argument for an IF binding pathway (Fig. 7 in (Phillips et al., 2013)). However, the binding reaction takes place over about 20 minutes, indicating that there is a much larger energy barrier in the overall reaction than the conformational sampling in free ubiquitin. Simply put, conformational exchange is not the rate-limiting step in the overall process. Consequently, there is a disconnect in time scale of motion in ubiquitin versus the binding kinetics. In contrast, we have demonstrated an absolute correspondence between the conformational exchange rates of free recoverin and the binding kinetics (Fig. 5C). An additional point of concern in the ubiquitin study (Phillips et al., 2013) is the large excess of ubiquitin used in determination of rates for the binding reaction. At those ubiquitin concentrations the minor, competent-binding form of the protein was present in excess over the DUB partner under all conditions tested, rendering it impossible that the conformational exchange step could limit overall kinetics for the binding reaction. In our experiments, recoverin was kept constant and at limiting concentrations, whereas RK-GB1 (the “ligand”) was varied as mandated by the kinetic equations (Copeland, 2011; Fersht, 1999; Hammes et al., 2009).

In summary, the data published to date on ubiquitin cannot unambiguously distinguish between the CS and IF models for binding, highlighting the difficulty associated with experimental discrimination between these two fundamentally different mechanisms (Weikl and Paul, 2014). Nature certainly uses both mechanisms in binding processes, as shown recently for binding of the anti-cancer drug Gleevec to protein kinases (Agafonov et al., 2014). We hope that the combination of conformational and kinetics studies, as described here for the inhibition of rhodopsin kinase by recoverin in the vertebrate vision system, will provide a foundation for the study of other systems to enhance our mechanistic understanding of protein/protein interactions in biology.

EXPERIMENTAL PROCEDURES

Expression and purification of recoverin

Unlabeled recoverin was over-expressed in E. coli BL21(DE3) cells following standard protocols (Ames et al., 1994; Ranaghan et al., 2013). Uniformly labeled recoverin (¹⁵N; ¹⁵N,¹³C; and ¹⁵N,¹³C,²H) was harvested from appropriate M9 growth media (1 g/L ¹⁵NH₄Cl and 2 g/L glucose – ¹²C/¹³C/¹³C₆²H₆) in H₂O or D₂O (Cambridge Isotopes Laboratories, Andover, MA) supplemented with 10% E. coli OD2 (Silantes GmbH, München, Germany) for protonated and deuterated samples, respectively. The cells were grown at 37 °C from overnight culture (0.5% inoculums) and induced by adding 1 mM IPTG when OD₆₀₀ reached 0.6–0.8. The induced culture was harvested by centrifugation 4 hours after induction, and the re-suspended cell pellet was lysed using a sonicator (Misonix Sonicator 3000) with 20 s pulses of ~40 Watts separated by 40 s temperature re-equilibration time for 4 cycles. Recoverin, in 20 mM Tris, pH 8.0, 10 mM TCEP, and 20 mM CaCl₂ buffer (buffer A), was purified using Q-Sepharose (QFastFlow, GE Healthcare) by elution with 500 mM KCl dissolved in buffer A. The buffer was exchanged for 10 mM Tris, pH 7.0, containing 100 mM KCl, 10 mM CaCl₂, 5 mM TCEP, 0.01% NaN₃, and the protein applied to a S-100 column for gel filtration (GE Healthcare). All columns were run at 4 °C.

Expression and purification of rhodopsin kinase

Two constructs containing the target N-terminal helix from rhodopsin kinase were used in these studies. The first, RK-GB1 [HHHHHH-GB1(W43F)-RK(1–32)], consists of the first 32 amino acids of rhodopsin kinase fused to the GB1 solubility tag. Trp43 in GB1 was mutated to Phe using QuickChange (Agilent Technologies) to facilitate stopped-flow fluorescence experiments. The second, RGS, is a previously described truncated form of rhodopsin kinase comprised only of the RGS homology domain; the catalytic domain was replaced with a short GSGS linker (Ranaghan et al., 2013; Singh et al., 2008). Both constructs contain an N-terminal hexa-His tag and were purified from induced E. coli cultures by affinity chromatography on Ni²⁺-Sepharose (HisTrap FastFlow, GE Healthcare). The proteins were in 20 mM Tris, pH 8.0, 20 mM CaCl₂, 0.01% NaN₃ buffer (buffer B) and were eluted with 500 mM imidazole dissolved in buffer B. Chromatography was performed at 4 °C.

Sequence specific resonance assignment of recoverin and chemical shift mapping

All NMR experiments were performed with the proteins in 10 mM Tris buffer, pH 7.0, containing 100 mM KCl, 10 mM CaCl₂, 5 mM TCEP, 0.01% NaN₃ and 10% D₂O. Backbone and Cβ assignments for Ca²⁺-bound recoverin (protonated sample, ¹³C/¹⁵N-labeled) were performed at 30 °C with a standard suite of triple-resonance experiments: TROSY versions (Loria et al., 1999a) of HNCA, HN(CO)CA, HNCACB, C(CCO)NH, CBCA(CO)NH, HNCO and HSQC using a Varian Inova 600 MHz spectrometer. Data were processed using NMRPipe (Delaglio et al., 1995), and assignments were made in CARA (http://wiki.cara.nmr.ch). NMRViewJ (Johnson, 2004) was used for visualization of spectra. Assignments of HSQC cross peaks at other temperatures were transferred via a series of HSQCs acquired at temperatures in 5 °C intervals. In experiments with the recoverin/RK-GB1 complex, 0.7 mM of ¹⁵N-labeled recoverin was saturated with 2 mM unlabeled RK-GB1 or 2 mM unlabeled RGS. The chemical shift perturbations were calculated according to (Cavanagh et al., 1995) as CSP = ((Δδ_H^N)² + (0.1Δδ_N)²)^1/2.

Relaxation dispersion NMR experiments

TROSY ¹⁵N CPMG relaxation dispersion experiments (Loria et al., 1999b; Mulder et al., 2001) were performed on Varian Inova 600 MHz spectrometer (room temperature HCN probe) and Varian Inova 900 MHz spectrometer equipped with cryoprobe (Rocky Mountain Regional 900 MHz NMR facility, University of Colorado) at both 10 °C and 30 °C. Recoverin was 0.7 mM in 10 mM Tris buffer, pH 7.0, containing 100 mM KCl, 10 mM CaCl₂, 5 mM TCEP, 0.01% NaN₃ and 10% D₂O. In experiments with the recoverin/RK-GB1 complex, 0.7 mM of ¹⁵N-labeled recoverin was saturated with 2 mM unlabeled RK-GB1. The constant-time T_CP delay in all experiments was chosen such that the residual signal intensity was ~55% of maximum intensity, between 24 and (10 °C) 40 ms (30 °C). The experiments were performed with 2 s recycle delay between increments using 11 different refocusing field strengths between 83.3–1000 Hz (10 °C) and 50–1000 Hz (30 °C) collected interleaved with 512 (¹H) and 128 (¹⁵N) complex points, respectively. CPMG experiments took approximately 3 days to complete, and standard ¹H-¹⁵N TROSY-HSQC spectra were collected before and after each experiment to monitor sample stability. Data on the Inova 900 MHz spectrometer were recorded as downfield and upfield pairs to minimize off-resonance effects for the larger sweep width required at this magnetic field strength.

NMR data was processed using the NMRPipe software suite (Delaglio et al., 1995). Peak intensities were extracted and spectra were visualized with NMRViewJ (Johnson, 2004). Relaxation dispersion data were fit with the general Carver-Richards equation for two-site exchange (Carver and Richards, 1972; Davis et al., 1994; Jen, 1978).

$$R_2^{\mathit{\text{eff}}}=\frac{1}{2}(R_{2A}^0+R_{2B}^0+k_{\mathit{\text{ex}}}-\frac{1}{{\tau }_{CP}}\text{cos}{\mathrm{h}}^{-1}[D_{+}\text{cos}\mathrm{h}({\eta }_{+})-D_{-}\text{cos}({\eta }_{-})])$$

where $D_{\pm }=\frac{1}{2}[\pm 1+\frac{\psi +2\mathrm{\Delta }{\omega }_N^2}{{({\psi }^2+{\zeta }^2)}^{1/2}}],{\eta }_{\pm }=\frac{{\tau }_{CP}}{\sqrt{2}}{[\pm \psi +{({\psi }^2+{\zeta }^2)}^{1/2}]}^{1/2}$,

$$\psi ={(R_{2A}^0-R_{2B}^0-p_A{k}_{\mathit{\text{ex}}}+p_B{k}_{\mathit{\text{ex}}})}^2-\mathrm{\Delta }{\omega }_N^2+4p_A{p}_B{k}_{\mathit{\text{ex}}}^2,$$

$$\zeta =2\mathrm{\Delta }{\omega }_N(R_{2A}^0-R_{2B}^0-p_A{k}_{\mathit{\text{ex}}}+p_B{k}_{\mathit{\text{ex}}})$$

and k_ex is the rate of exchange between states A and B, $R_{2A}^0$ and $R_{2B}^0$ are the inherent transverse relaxation rates in state A and B, respectively (assumed to be the same), p_A and p_B are the populations of state A and B, respectively, Δω_N is the ¹⁵N chemical shift difference between the two exchanging sites, and τ_CP is the time between 180° pulses in the CPMG pulse train.

Fitting of CPMG relaxation dispersion data to this analytical equation was performed using software developed by Dimitry Korzhnev (Korzhnev et al., 2004), that implemented the Levenberg-Marquardt algorithm for non-linear least squares minimization. Uncertainties in R₂^eff were estimated from the standard deviation in R₂^eff values of residues not experiencing exchange (n=10). Uncertainties in global fits were estimated by a jackknife method.

Measurement of the sign of Δω_N

The sign of each Δω_N,CPMG for conformational exchange in recoverin was determined from a comparison of HSQC and HMQC experiments (Skrynnikov et al., 2002) recorded on a 800 MHz Bruker Avance spectrometer with cryoprobe using a ²H, ¹⁵N labeled sample (Supplemental dataset 1E). A total of 1024 and 440 complex points were collected in the direct and indirect dimensions, respectively, with 48 scans for each increment and 2 s inter-scan delay. Only peaks that showed more than 0.3 Hz separation in the ¹⁵N dimension were considered for analysis (39 out of 45 residues).

Isothermal titration calorimetry

The isothermal titration calorimetry experiments were performed using a VP-ITC MicroCalorimeter from MicroCal, LLC (Northampton, MA, USA). Recoverin from a 660 µM stock solution was titrated into a 1.4 mL solution of RK-GB1 (60 µM) in 10 µL aliquots over 20 s. Each injection was separated by 600 s. For RGS, a 325 µM solution of recoverin was titrated into a 1.4 mL solution containing 30 µM RGS. In both cases the proteins were in a 10 mM Tris buffer, pH 7.0, containing 10 mM CaCl₂, 100 mM KCl, and 5 mM TCEP. The protein solutions were degassed prior to titration. The data were fit with the Origin (OriginLab Corp, Northampton, MA, USA) data-fitting template provided with the instrument.

Stopped-flow fluorescence

The kinetics for binding of RK-GB1 to recoverin was monitored by following intrinsic tryptophan fluorescence using an Applied Photophysics (Surrey, UK) SX-20 stopped-flow spectrometer. Samples were excited at 288 nm (9 nm bandwidth), and emission was detected with a long-pass 320 nm cut-off filter. The binding reaction was monitored in the symmetric mixing mode. The dissociation reaction to determine k_off was accomplished by diluting 50 µM of the recoverin/RK-GB1 complex 25 times using the non-symmetric mixing mode. Reactions were in 10 mM Tris, pH 7.0, 10 mM CaCl₂, 100 mM KCl, and 5 mM TCEP at both 10 °C and 30 °C. The fast binding kinetics of Rv* (~3% of population at 30 °C) in the dead-time of the instrument (3 ms) is beyond detection. The configuration of the optical cell was chosen such that the inner filter effect was minimum. Each of the binding and dissociation data sets is an average of at least 5 independent runs and has been corrected for photo-bleaching (Fig. S2A,B) (Lakowicz, 2007). Data were analyzed with Origin (OriginLab Corp, Northampton, MA, USA).

Calculation of observed dissociation constants from kinetic rate constants for IF and CS

For the induced fit scheme, the overall dissociation constant,

$$K_D^{\mathit{\text{obs}}}=K_{\mathit{\text{disso}}}\frac{K_{\mathit{\text{iso}}}}{(1+K_{\mathit{\text{iso}}})}$$

where $K_{\mathit{\text{disso}}}=\frac{k{\text{'}}_{\mathit{\text{off}}}}{k{\text{'}}_{\mathit{\text{on}}}}$ and $K_{\mathit{\text{iso}}}=\frac{k{\text{'}}_{\mathit{\text{rev}}}}{k{\text{'}}_{\mathit{\text{for}}}}$, k’_on, k’_off, k’_for and k’_rev are as defined in Fig. 1D; for the conformational selection scheme, the overall dissociation constant,

$$K_D^{\mathit{\text{obs}}}=K_{\mathit{\text{disso}}}(1+K_{\mathit{\text{iso}}})$$

where $K_{\mathit{\text{disso}}}=\frac{k_{\mathit{\text{off}}}}{k_{\mathit{\text{on}}}}$ and $K_{\mathit{\text{iso}}}=\frac{k_{\mathit{\text{rev}}}}{k_{\mathit{\text{for}}}}$, k_on, k_off, k_for and k_rev are as defined in Fig. 1D.

Global fitting and numerical simulation of kinetic data

The full kinetic data-set obtained using stopped-low fluorescence (binding and dissociation) together with the overall dissociation constants were fit simultaneously to the CS model based on numerical integration of the full rate equations using Kintek Global Explorer software (Johnson, 2009; Johnson et al., 2009). The k_for and k_rev were constrained within the range determined using NMR ¹⁵N backbone amide CPMG relaxation experiments (Palmer, 2004; Palmer et al., 2001). From this global fit all microscopic constant were determined (Fig. 5B).

As a second approach, we determined the individual k_obs at different RK-GB1 concentrations by fitting each of the kinetic traces to single exponential functions (Fig. 4, see also Fig. 3A–E). These experimental k_obs (blue data points in Fig. 4) were compared to a theoretically expected cures for CS and IF models (red line and dashed black line in Fig. 4). To obtain the theoretical curves, theoretically binding kinetics were simulated for a range of ligand concentrations in Kintek using the parameters from our global fit. Those curves were then fit with single exponents to produce theoretical k_obs versus ligand concentration. Comparison of the simulated curves with the experimental data unambiguously shows that only CS model reproduces the observed behavior (Fig. 4). The error bars for the individual k_obs values reflect mean ± s.e.m ; n=5 experiments.

This entire process (global fit and individual fits) was repeated to fit the data to an IF model. However, the IF model has no constraints for k’_for and k’_rev (the only constraint was that the microscopic rate constants will satisfy the experimental K_D according to IF model).