Mandarin Chinese Tone Identification in Cochlear Implants: Predictions from Acoustic Models

Abstract

It has been established that current cochlear implants do not supply adequate spectral information for perception of tonal languages. Comprehension of a tonal language, such as Mandarin Chinese, requires recognition of lexical tones. New strategies of cochlear stimulation such as variable stimulation rate and current steering may provide the means of delivering more spectral information and thus may provide the auditory fine structure required for tone recognition. Several cochlear implant signal processing strategies are examined in this study, the continuous interleaved sampling (CIS) algorithm, the frequency amplitude modulation encoding (FAME) algorithm, and the multiple carrier frequency algorithm (MCFA). These strategies provide different types and amounts of spectral information. Pattern recognition techniques can be applied to data from Mandarin Chinese tone recognition tasks using acoustic models as a means of testing the abilities of these algorithms to transmit the changes in fundamental frequency indicative of the four lexical tones. The ability of processed Mandarin Chinese tones to be correctly classified may predict trends in the effectiveness of different signal processing algorithms in cochlear implants. The proposed techniques can predict trends in performance of the signal processing techniques in quiet conditions but fail to do so in noise.

1 Introduction

Since their development in the early 1970s, auditory prostheses, most notably cochlear implants, have enabled an estimated 100,000 profoundly deaf individuals to experience sound (Zeng 2004). Cochlear implants restore a sense of hearing through electrical stimulation of the auditory nerve, the primary organ of the inner ear. Most cochlear implant recipients are speakers of western languages. Western languages, such as English, German, and French, require less spectral resolution properties for speech recognition than eastern or tonal languages, such as Mandarin Chinese, Cantonese and Vietnamese.

In tonal languages the pitch or range of pitches of a vowel sound defines the meaning of the word in which it occurs. In Mandarin Chinese the fundamental frequency (F0) contour of a vowel sound can have four different variations, called tones, all of which reflect different lexical meanings. The four tones are flat, rising, falling-rising, and falling. This naming convention refers to the changes in F0 over time. A single consonant-vowel combination can take on four lexical meanings depending on the tone with which it was spoken. The different tones must be classified by listeners for accurate speech perception.

The signal processing strategies used in current cochlear implants are relatively effective at restoring speech perception to speakers of western languages. However, the limited spectral information presented by modern cochlear implant speech processing strategies is insufficient for reliable tone recognition (Zeng et al. 2005; Fu et al. 1998; Luo and Fu 2004a,b; Wei et al. 2004; Lan et al. 2004). Delivering more spectral information to cochlear implant recipients may offer more accurate tonal language speech perception and improve the quality of life of a large population of deaf people around the world.

It has been found that the rate of pulsatile stimulation can change the perceived pitch (e.g. (Tong and Clark 1985; Zeng 2002)). These so called “variable stimulation rates” can be used with pulsatile stimulation to include more spectral information (Fearn 2001; Lan et al. 2004; Throckmorton et al. 2006; Zeng et al. 2005). It has also been shown that through simultaneous stimulation of neighboring electrodes intermediary locations of the cochlea can be stimulated. This can cause pitch perceptions which are not possible through single electrode stimulation (Townshend et al. 1987; Koch et al. 2005). Varying the amount of current delivered by the two electrodes can vary the location of maximum stimulation along the cochlea and thus vary the perceived pitch. These techniques may enable cochlear implants to transmit the additional spectral information required for accurate perception of tonal languages.

Several signal processing strategies which make use of the possible additional spectral information have been proposed to improve the perception derived from cochlear implants in noisy conditions and aid in Mandarin Chinese tone recognition. The frequency amplitude modulation encoding (FAME) algorithm (Nie et al. 2005), and the multiple carrier frequency algorithm (MCFA) (Throckmorton et al. 2006) are considered in this study. As a baseline, the continuous interleaved sampling (CIS) strategy (Wilson et al. 1991), which does not include varying frequency information, will also be studied for comparison purposes. These strategies, save CIS, have not been implemented in cochlear implant recipients but rather have been studied using acoustic models and normal hearing subjects.

Cochlear implant acoustic models have been used for more than 20 years to gauge the possible performance of cochlear implants through the use of normal hearing individuals. Remus and Collins (2003) showed that English vowel and consonant confusions can be predicted by analyzing the acoustic model outputs of different cochlear implant strategies. These predictions can then be used to evaluate the effectiveness of different strategies for transmitting the necessary information for the specific task.

This research analyzes the output of cochlear implant acoustic models to predict trends in Mandarin Chinese tone perception performance provided by several different speech processing strategies. Automated evaluation of different cochlear implant strategies using acoustic models could potentially provide a relative performance measure without the use of human subjects, which drastically reduces experimentation times. In order to determine the validity of predictions, predictions are compared to data obtained in a listening experiment using normal hearing subjects and acoustic models. Accurate performance predictions can help to focus future studies on the more promising signal processing strategies.

The remainder of this paper is structured as follows. Section 2 provides a description of the speech processing strategies compared in this study. Section 3 outlines the listening experiment that was used to assess the performance of the different speech processing strategies using acoustic models. The methodology used to automatically classify the processed Mandarin Chinese tones is described in section 4. The results and accuracy of the predictions are given in section 4.5 with a discussion and conclusion following in sections 5 and 6.

2 Speech Processing Algorithms

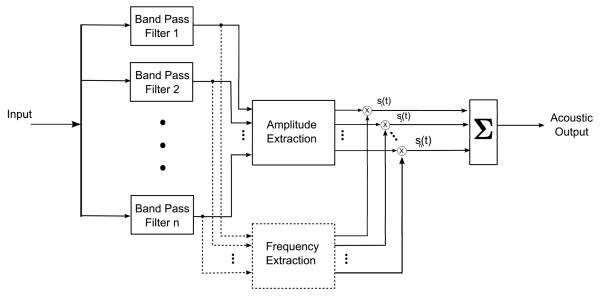
Through the use of cochlear implant acoustic models, normal hearing people can be used to evaluate trends in performance that may be possible through the use of new signal processing strategies. The goal of an acoustic model is to create an acoustic signal that contains the maximum amount of information provided by the speech processor. Since their introduction in 1984, (Blamey et al. 1984a,b) acoustic models have been used and are now accepted for the study of possible cochlear implant performance (Dorman et al. 1997; Shannon et al. 1995). Acoustic models significantly reduce the time required to test new signal processing algorithms through the use of normal hearing subjects. They also serve as a means of testing a signal processing algorithm without the psychophysical and perceptual effects inherent in cochlear implant recipients. The block diagram of a typical cochlear implant acoustic model is shown in Fig. 1. The model works in much the same way that a cochlear implant works. A window of data is captured from the microphone and is bandpass filtered for each electrode. From each bandpass filtered signal, amplitude and frequency information (if utilized) are extracted. In currently used signal processing strategies only amplitude information is extracted and used with a fixed frequency carrier. The acoustic model uses the amplitude and frequency information for each electrode to drive a bank of sources, s_i (t), ∀ i = 1, …, n, which are then summed to generate the output signal. Acoustic models use either sinusoids or band limited noise as the sources. The frequency of each sinusoidal source is obtained using the Greenwood map (Greenwood 1990, 1961) and the nominal location of the electrode. The spectral bands assigned to each channel in this research are: 150-240, 240-384, 384-615, 615-984, 984-1574, 1574-2519, 2519-4031, and 4031-6450 Hz. The window length was set to 32 ms with 50% overlap when applicable. Therefore, amplitude and frequency information is updated every 16 ms.

Fig. 1.

The block diagram for a cochlear implant acoustic model. The method of frequency extraction is different for each of the speech processing strategies considered. The CIS strategy does not perform frequency extraction.

The method used to extract the amplitude information from each bandpass filtered signal is consistent across the speech processing techniques examined in this paper and is consistent with that performed by the CIS strategy. Amplitude information is extracted in each case through full wave rectification and low pass filtering (250 Hz). The strategies other than CIS also extract frequency information from the signals. The CIS strategy uses a single frequency for each source to represent each electrode. The other strategies considered here use different methods to extract frequency information. The differences in the frequency extraction methods are described below.

The FAME strategy extracts band-limited instantaneous frequency from each bandpass filtered signal for use as the carrier frequency for each signal source (Nie et al. 2005). The instantaneous frequency is estimated through use of the Flanagan phase vocoder (Flanagan and Golden 1966). The Flanagan phase vocoder extracts instantaneous frequency information for each sample by estimation of the derivative of the phase of the Fourier transform of the speech waveform. The estimates of instantaneous frequency provided by the Flanagan phase vocoder are continuous in nature. This makes the FAME strategy independent of window length as the amplitude and frequency information for each signal source can be updated every sample.

The MCFA finds an estimate of instantaneous frequency and maps this frequency to one of several predetermined frequencies. The use of a discrete number of predetermined frequencies instead of a continuum was based on the hypothesis that a continuum of rates would not necessarily be discriminable as suggested by the pulse rate discrimination literature (Fearn and Wolfe 2001; Zeng 2002; Townshend et al. 1987; McDermott and McKay 1997). Throckmorton et al. (2006) hypothesize that using known psychophysical parameters to tune the algorithm may improve speech recognition performance in cochlear implant recipients. In acoustic model studies, however, FAME performance is always an upper bound of MCFA performance. The frequency in each spectral band with greatest energy (mean square value) for each window is determined through use of the fast Fourier transform (FFT). Each of these frequencies is then mapped to one of the N predetermined frequencies for its given band. N is a chosen design parameter. Results of the MCFA strategy will be examined for values of N equal to 2 and 8. The predetermined frequencies for the acoustic model were selected by evenly dividing each spectral band using the Greenwood map.

3 Listening Experiment

3.1 Experiment

The performance of each of the algorithms discussed in section 2 was evaluated using a listening experiment. This experiment was performed under the approval of the Duke University institutional review board. The tests were administered in a sound proof booth and stimuli were presented to the subjects using headphones at a comfortable volume. Each subject was administered an audiogram to ensure normal hearing prior to beginning the experiment. A four alternative forced choice test was administered to ten native Mandarin Chinese speakers from the Duke University graduate student population. For each presented stimulus the subjects were to select the perceived tone, from the set of four possible tones, using a graphical user interface on a computer. All code was developed in MATLAB. Each strategy (CIS, MCFA 2, MCFA 8, FAME) was tested at four signal to noise ratios (SNRs): Quiet, 5 dB, 0 dB, and −5 dB. The level of the signal with additive noise was constant at a fixed comfortable level for each subject. The additive noise was speech shaped noise from the HINT (Nilsson et al. 1994). A sequence of 20 tones from both a male and female speaker were presented to each subject in a random order for each SNR. The strategies were presented in a different order for each subject to remove bias and the SNRs were presented in decreasing order for each model. Prior to the testing portion of the experiment a training session, in which feedback was provided, was administered to establish familiarity with the task.

The speech corpus was previously used to test Mandarin Chinese tone perception in cochlear implants, (Wei et al. 2004), and was obtained from The Hearing Speech Lab at the University of California, Irvine. The data set contains 25 consonant vowel combinations spoken by both a male and a female. Each of these consonant vowel combinations is spoken using each of the four lexical tones. This yields 100 samples for each speaker, male and female. For each experimental condition the set of 20 tones were selected randomly from the speech corpus such that 10 were from a male speaker and 10 were from a female speaker. They were also selected, such that 5 samples of each of the four tones were selected and that each consonant vowel combination was selected only once. All of the samples are in .wav PCM 16 bit format with a sampling frequency of 16 kHz. Duration can be the primary cue for single syllable tone recognition but is not useful for tone recognition in natural human interaction (Whalen and Xu 1992; Xu et al. 2002). To remove duration as a possible cue, the samples were modified so that each had the same duration (the duration of the longest sample). This was accomplished through interpolation of the outputs of a vocoder with a high number of channels (Laroche and Dolson 1999).

3.2 Results

The proportion of Mandarin Chinese tones correctly identified in the listening experiment for each of the speech processing strategies is shown in Fig. 2. The horizontal axis indicates the signal processing strategy and the SNR is indicated through shading. These results have been pooled across all subjects as no outliers were observed. They have also been pooled across all tones and both speakers as no biases were found in either of these parameters. The pooled results are thus composed of 200 total samples for each speech processing strategy and SNR. The 95% confidence intervals are also shown. The confidence intervals were calculated using the Clopper-Pearson method of binomial confidence interval estimation (Clopper and Pearson 1934).

Fig. 2.

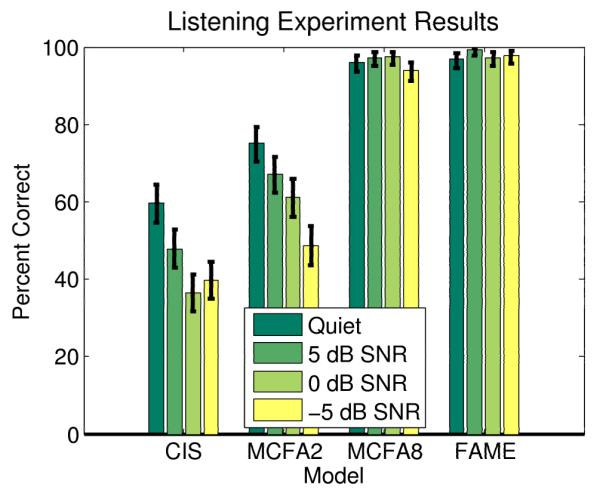
The proportion of Mandarin Chinese tones correctly identified in the listening experiment using each of the speech processing strategies. The strategies are listed along the horizontal axis. Shading indicates SNR, and error bars indicate 95% confidence intervals.

3.3 Discussion

In general, the results of the listening experiment are consistent with expectations. Those models which present more spectral information yield better tone classification performance. An important observation associated with these results is that tone recognition performance associated with those strategies that provide greater amounts of spectral information does not degrade as significantly in noise. This phenomenon has been observed in the past with regards to English vowels and consonants (Nie et al. 2005; Throckmorton et al. 2006). With strategies containing less spectral information (CIS and MCFA 2), performance degrades rapidly as a function of SNR. Those strategies that provide greater spectral information (MCFA 8 and FAME), on the other hand, yield robust performance in noisy scenarios. Although differences between, for example, the MCFA 8 and FAME strategies at some SNRs may become more statistically significant if more test samples were collected, the overall trend of their resilience in noisy conditions compared to the CIS and MCFA2 strategies would remain. This broader trend is of greater interest to this research.

Previous studies have conducted similar listening experiments using some of the signal processing strategies examined in this study in quiet conditions. These studies may differ in their individual implementations of the models being tested. Parameters such as the window length and the cut-off frequency of the envelope extraction filter are often different across studies. The window length changes the lowest frequency which can be estimated in the signal as well as the rate at which frequency information is updated. The cut-off frequency of the envelope extraction filter has been shown to affect tone classification (Kong and Zeng 2006; Fu et al. 1998; Xu et al. 2002). For these reasons, the comparisons between the listening experiments conducted in this research and those in other studies should be taken with caution.

Several studies have examined the CIS strategy in quiet conditions using acoustic models to process Mandarin Chinese tones (Kong and Zeng 2006; Zeng et al. 2005; Fu et al. 1998; Xu et al. 2002). Although these studies observed performances ranging from 70-80% correct using an 8 channel acoustic model, Lan et al. (2004) observed approximately 40% correct using a similar 8 channel CIS model. This is a much lower estimate than the other studies. The results of this study are in between these two ranges (60%). The performance of an eight channel model using the FAME strategy was examined by Zeng et al. (2005) and 100% classification was observed. This is consistent with the results of this study.

Kong and Zeng (2006) analyzed both the CIS and FAME strategies in noisy conditions. Similar to the trends shown in the listening experiment conducted in the present research, the FAME strategy provided more robust performance in noisy conditions. While the performance provided by the CIS is drastically affected by the presence of noise. These comparisons show that the results found here are similar to previously conducted listening experiments.

4 Prediction Techniques

Automated analysis of the performance of each of the speech processing strategies is performed through analysis of the output of the acoustic models. The goal of this analysis is to predict the relative performance seen in the results of the listening experiment. These predictions are done using automated techniques akin to those used for Mandarin Chinese automated speech recognition (ASR). Tone recognition for Mandarin Chinese ASR is usually accomplished through extraction of the F0 contour followed by pattern classification techniques applied to features extracted from the F0 contour (eg. (Tian et al. 2004; Li et al. 1999)). Extraction of the F0 contour from speech passed through cochlear implant acoustic models is not clearly defined and, as a result, different techniques are utilized to mimic this task. Two different techniques were used to derive features from Mandarin Chinese speech passed through cochlear implant acoustic models which are indicative of the tone of the speech.

4.1 F0 Contour Approximation

The first method for characterization of the spectral changes over time is based on the transmission of the F0 contour through the cochlear implant acoustic models. The F0 contour is extracted from the original speech by using the simple inverse filtering technique (SIFT) (Markel 1972). The SIFT estimates the F0 in each window of data by applying an inverse filter followed by autocorrelation analysis. The first step of the SIFT is to perform linear prediction analysis to derive the inverse filter. This implementation uses 12th order linear prediction. The signal is then filtered through the inverse filter and the autocorrelation of the resultant signal is found. The first peak in the autocorrelation in a specified range of time is selected as the estimate of the period of F0. A maximum and minimum value for this period is selected to limit the estimated F0 to the range of human F0 as well as limit changes in F0 from the previous window. Since F0 is undefined for unvoiced speech, such as most consonants, the SIFT must differentiate voiced and unvoiced speech. This is accomplished by comparing the normalized value of the chosen peak to a threshold. This threshold was set to 0.2 as specified by Luo and Fu (2004a) for normalized ([−1, 1]) data. The voice/unvoiced decision is also altered based on the voicing of the previous two windows as specified by Markel (1972). A spectral range of 35 Hz above and below the previous F0 is observed if the previous window was found to be voiced. If the previous window was not voiced, all of the values in the human F0 range are possible. The length of the observed window limits the lowest possible F0 which can be estimated. Using the specified 32 ms analysis window yields a lowest possible frequency estimate of 31.25 Hz. This is below the range of human F0 and is thus suitable.

Due to the nature of acoustic models, the frequency content of the output of an acoustic model is already known. This information is obtained by retaining the frequencies used on each channel as a function of time. This information is shown in Fig. 3 in what is termed a freqtrodogram. Finding appropriate values for the threshold parameters associated with the SIFT to reliably extract the F0 contours from processed speech proved difficult; therefore, the approximate F0 contour is found by comparing the F0 contour found from the unprocessed signal to the freqtrodogram resulting from the modeled speech. For each analysis window, the entry in the freqtrodogram which most closely matches the F0 extracted from the unprocessed signal is chosen as the F0 extracted from the processed signal.

Fig. 3.

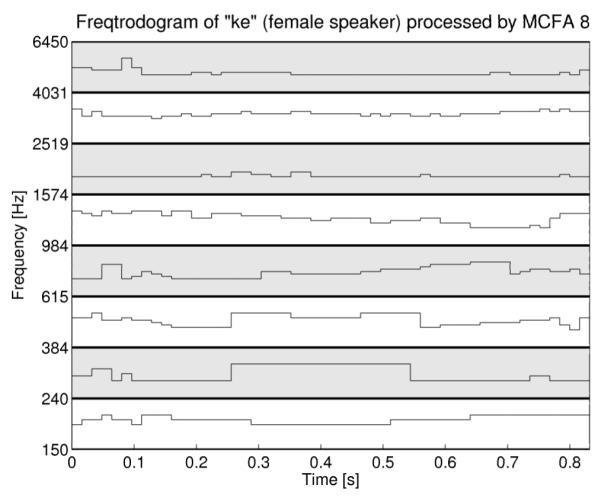
Freqtrodogram of the falling-rising tone of “ke” said by a female speaker. The presented frequencies for each spectral band are plotted as functions of time. Each spectral band is represented with shading. Note that the vertical axis is logarithmically spaced.

Fig. 4 shows an example of the F0 curves attained for the word “xi” spoken by a female. The subplots show how the differing frequency resolutions of each of the models affects the preservation of the F0 contour. In the background of each subplot a portion of the spectrogram of the original signal is shown. The F0 contour extracted from the original signal is shown as a solid line. The CIS algorithm has only one frequency possible for each electrode and therefore a broad range of frequencies are mapped to each possible frequency. The resulting approximate F0 contour is a poor representation of the original. The MCFA strategy using 2 frequencies shows slight visual improvement over the CIS strategy but shows much better preservation when using 8 frequencies in each spectral band. Each results in a quantized version of the F0 contour. The FAME algorithm yields an F0 contour which is very similar to the original, differing only slightly due to a small amount of error in the instantaneous frequency calculation.

Fig. 4.

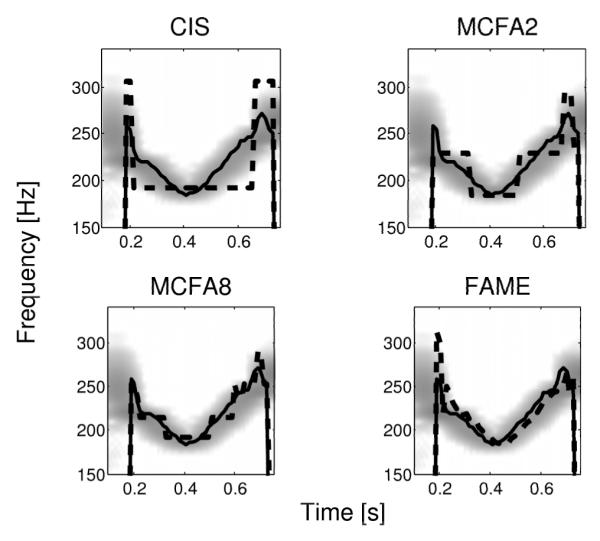
Approximation of F0 contours for the falling-rising tone of “xi” spoken by a female. The F0 contour extracted from the unprocessed speech token is shown in solid while the approximated F0 contour is shown in dashed. A portion of the spectrogram of the unprocessed speech token is shown in the background of each plot.

4.2 Spectral Intensity Contour Tracking

The parameters which were used for the acoustic model limit the lowest frequency to 150 Hz. As stated previously the range of human F0 is 50-450 Hz. This implies that the F0 of certain words, particularly for male speech, is not transmitted to cochlear implants. Despite this fact, Mandarin Chinese tone classification in cochlear implants is above chance, which implies that there are other cues beside the F0 contour which are used by the human perceptual system for Mandarin Chinese tone classification. To investigate this, it was hypothesized that classification could occur if other spectral intensity contours which change over time, such as other formants (F1-F4) and harmonics of F0, were tracked, modeled and parameterized.

The estimation of the formants of speech has been explored using a variety of techniques. These techniques are primarily concerned with estimation of only formants and not their harmonics. Of interest in this work is the tracking of all spectral intensity contours, including the harmonics of formants. Particle filters for formant tracking have been successfully employed in previous studies (Shi and Chang 2003; Zheng and Hasegawa-Johnson 2003, 2004), however, each of these previous studies only tracked formants, not all spectral intensity contours, and only in quiet conditions. This study extends the use of particle filters to the tracking of all spectral intensity contours in quiet as well as in noise.

Particle filters provide a means of estimating and tracking the probability density function of a non-stationary state vector, x (Arulampalam et al. 2002). The state vector contains all relevant information regarding the system. For example, the implementation of the particle filter used for spectral intensity contour tracking has a state vector which models the frequency and shape of the spectral intensity peak at a fixed point in time. The probability density function of this state vector is tracked over the duration of the speech token and the spectral intensity contour can be estimated through a maximum a posteriori estimate at each point in time.

Each iteration of the particle filter uses 32 ms of data (512 samples at 16 kHz with 50% overlap). This is the same observation window as in the cochlear implant acoustic models. The three lowest spectral bands of the acoustic models are used to initialize each of the three spectral intensity tracking particle filters. One hundred particles are initialized uniformly in each spectral band and then recursively updated.

The observations in each window are the magnitude of the discrete Fourier transform. The implementation of the particle filter requires a parameterized function which models a spectral intensity contour in a particular window. A spectral intensity contour as observed in the magnitude of the discrete Fourier transform in a particular window is positive and unimodal, therefore it can be appropriately modeled by a parametric function of similar form, such as a radial basis function or the Kaiser window function. The chosen form for this implementation is the Kaiser window function parameterized by β.

$$w\left(k\right)=\{\begin{array}{cc}\hfill \frac{I_0\left(\beta \sqrt{1-{\left(\frac{2k}{N}-1\right)}^2}\right)}{I_0\left(\beta \right)}\hfill & \hfill \text{if}0\le k\le N\hfill \\ \hfill \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \text{otherwise}\hfill \end{array}\phantom{\}}$$ (1)

In Eq. 1, I₀ (·) is the zeroth-order modified Bessel function of the first kind, and β is a free parameter which determines shape. A value of β = 0 corresponds to a rectangular window and as β increases the window becomes narrower.

The joint probability density function of the frequency of the spectral intensity contour and the β parameter of a Kaiser window is tracked by the two dimensional particle filter. The particles are initialized uniformly in the β space from 0 to 32. This range for β provides an adequate range of spectral shapes ranging from a rectangular template to a template with a sharp peak.

The mapping of a state, x_k, to an observation, z_k, is known as the observation function. In this implementation the observation function is assumed to be an additive function of a template, t_k, and white Gaussian noise, n_k. The template, t_k, is an adaptive Kaiser window where the β parameter is tracked as part of the state vector and is thus a function of the current state, x_k.

$$z_k=t_k\left(x_k\right)+n_k$$ (2)

The likelihood of a particle, $x_k^i$, is then given by the following equation.

$$\begin{array}{cc}\hfill p\left(z_k\mid x_k^i\right)& =\int \delta \left(z_k-t_k\left(x_k^i\right)-n_k\right)p_{n_k}\left(n_k\right){\mathit{dn}}_k\hfill \\ \hfill & =p_{n_k}\left(z_k-t_k\left(x_k^i\right)\right)\hfill \end{array}$$ (3)

In Eq. 3, δ (·) is the Dirac delta function. The assumption that the observation noise is white and Gaussian with zero mean and variance, ${\sigma }_n^2$, leads to the formulation that the likelihood is given by the following equation.

$$p\left(z_k\mid x_k^i\right)=N\left(z_k-t_k\left(x_k^i\right),{\sigma }_n^2\right)$$ (4)

If we assume that the template, $t_k\left(x_k^i\right)$, consists of m samples, the likelihood of the particle over these samples assuming independence is given by the following equation.

$$p\left(z_k^{\overrightarrow{m}}\mid x_k^i\right)=\prod _{j=1}^{m}N\left(z_k^j-t_k^j\left(x_k^i\right),{\sigma }_n^2\right)$$ (5)

The observation for each particle is normalized before it is subtracted from the template since the shape of the intensity contour is of primary interest rather than the particle nominal amplitude value. In theory a third dimension could be added to the particle filter to also track amplitude, however tracking amplitude would provide little advantage and would greatly increase the complexity as the number of particles that would need to be used would increase.

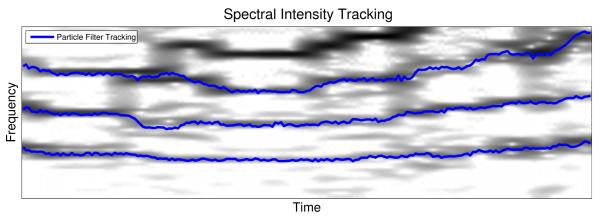
The observation noise variance, ${\sigma }_n^2$, was set to 0.01 while the template length was set to a length of 11 samples. These values were found to suit the data well through empirical analysis. With the observation window set to 512 samples at 16 kHz, the template covers a spectral range of 343 Hz centered around the particles proposed location of the intensity contour. To guard against the propagation of degenerate particles the sequential importance resampling algorithm was utilized (Gordon et al. 1993). The threshold for degeneracy, N_T, was set to 300. An example of the spectral intensity tracking performed by the particle filter is shown in Fig. 5.

Fig. 5.

The narrowband spectrogram of the falling-rising tone of “ke” spoken by a female and processed through the MCF8 acoustic model with the spectral intensity contour tracking overlaid in dark lines.

4.3 Features

To classify the Mandarin Chinese tones from F0 contours or spectral intensity tracks it is necessary to parameterize the curves so as to limit the number of features used for pattern classification. The features extracted from the F0 contours used in this research are based on a set of features proposed in (Tian et al. 2004) for tone recognition for the speech-to-text application. To find the features, the F0 contour is partitioned into four equal length segments. In each segment the mean and mean of the approximate derivative of each segment are used as the features. These features were found to yield better classification results than linear regression coefficients and quadratic regression coefficients. The number of segments used for subdivision (4) was also suggested in (Tian et al. 2004) as providing the best classification results.

The same segmented mean and mean derivative features are extracted from the approximated F0 contour as well as each of the extracted spectral intensity contours. Therefore, the feature set for the spectral intensity contours contains 3 times as many features as the feature set derived from the approximated F0 contour.

4.4 Pattern Classification Techniques

The procedure utilized here for automated tone classification in cochlear implants is similar to that of automated tone classification for other applications such as automated speech recognition (ASR) of Mandarin Chinese (eg. (Tian et al. 2004; Li et al. 1999)). ASR of Mandarin Chinese requires not only recognition of consonants and vowels but also tone recognition. Automated tone classification is typically accomplished by finding the F0 contour and extracting features from this contour. The features extracted from the F0 contour are chosen such that the curve is well parameterized. Following this, pattern classification techniques are applied to classify the data relative to a set of training data. In this study two types of pattern classification techniques were utilized. A generalized likelihood ratio test (GLRT) (Duda et al. 2004) serves as a parametric classifier whereas the K nearest neighbor (KNN) technique (Cover and Hart 1967) serves as a non-parametric classifier.

The GLRT derives from the framework of Bayesian decision making (Whalen 1971). Any Bayesian method for pattern classification requires that the probability density functions of the data under each of the hypotheses are known or can be accurately estimated. The GLRT used in this study assumes that each dimension of the feature vector is normally distributed, i.e. that the feature vector is a multidimensional Gaussian random variable. The probability density function for each class can then be found by estimating the mean vector and the covariance matrix, which are estimated from the training data. To ensure reasonable estimates of the parameters given the limited amount of training data, it is necessary to assume that the features are independent. This eliminates estimation of the covariance between features and makes the covariance matrix of the multi-dimensional Gaussian random variable diagonal. While this assumption is a simplification since the features are in general not independent, the negative effects that result from making the assumption of feature independence are far less severe than the negative effects associated with poor parameter estimation resulting from limited training data (Duda et al. 2004). Once the mean vector and covariance matrix for each class have been estimated using the training data, the GLRT can be used to discriminate between the classes. The Mandarin Chinese tone identification task is a four-hypothesis classification problem and, as such, the GLRT must be slightly adapted. The assumption is that each null hypothesis, H₀, is uniformly distributed and that the likelihood ratio will reduce to the likelihood function for each class. If it is assumed that each class is equally probable, the discriminant function for class i can be written as

$$g_i\left(\overrightarrow{x}\right)=-{(\overrightarrow{x}-{\overrightarrow{\mu }}_i)}^t{\Sigma }_i^{-1}(\overrightarrow{x}-{\overrightarrow{\mu }}_i).$$ (6)

Here ${\overrightarrow{\mu }}_i$ is the mean vector for class i and ${\Sigma }_i^{-1}$ is the inverse of the covariance matrix for class i. Each test vector, $\overrightarrow{x}$, is used to calculate the discriminant function for each of the classes. The class which yields the largest discriminant function is assigned to the test vector. Eq. 6 is derived by taking the natural log of the likelihood of each Gaussian random variable. This yields identical classification because the natural log is a monotonically increasing function.

The KNN approach to pattern classification is different from the GLRT in that it does not require that the probability density functions be explicitly estimated, although the technique does stem from density estimation. The training samples are viewed in D dimensional space where D is the number of dimensions in the feature vector. Each test vector is also viewed in this D dimensional space, and the closest k samples are found. The class to which the majority of these k samples belong is the assigned class for the test vector. In this work the distance measure used to find the “closest” samples is the L₂ norm or the Euclidean distance. Several values of k were used for this procedure but the best results were found when k was chosen to be one. That is, only the nearest neighbor is used.

The same data set as was used in the listening experiment is employed for the automated classification. Given the small amount of data, the testing and training strategies must be such that testing and training are not performed on the same data but an accurate measure of performance is nevertheless achieved. Leave-one-out cross-validation is therefore utilized. In leave-one-out cross-validation the entire data set, save one sample, is used for training data and the final sample is used for testing (Duda et al. 2004). This process is repeated so that each sample is used as a testing sample. The aggregate results of each of these trials are used to calculate the performance metric, in this case percent correct.

4.5 Results

Using each of the feature sets derived from the spectral contour estimation methods with each of the pattern classification methods, automated predictions of Mandarin Chinese tone classification in cochlear implant acoustic models can be made. Fig. 6 shows the results of the automated classification using the F0 contour approximation method along with the results of the listening experiment for each SNR. Similar to the listening experiment results the plots are once again shown as percent correct but they are now divided into four subplots; one for each SNR. The results of the listening experiment are shown in the background in black bars while the automated classification results using both classifiers are shown in the foreground. Fig. 7 shows the results of automated classification using data acquired by parameterizing the spectral intensity contours extracted using particle filters. Fig. 7 is an analogous plot to Fig. 6. These figures also show error bars indicating the 95% confidence interval of each percent correct estimate (Clopper and Pearson 1934).

Fig. 6.

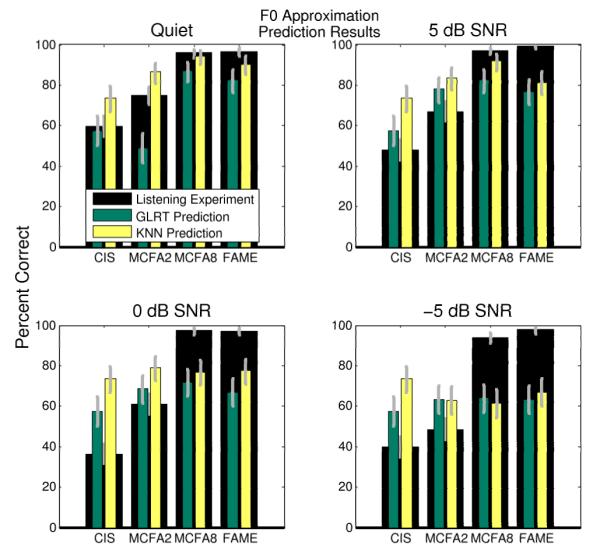
Predicted results using the F0 contour approximation method. The results are shown with the listening experiment results. The predicted results are shown in the foreground with the analogous listening experiment results shown in the background. The error bars indicate the 95% confidence interval.

Fig. 7.

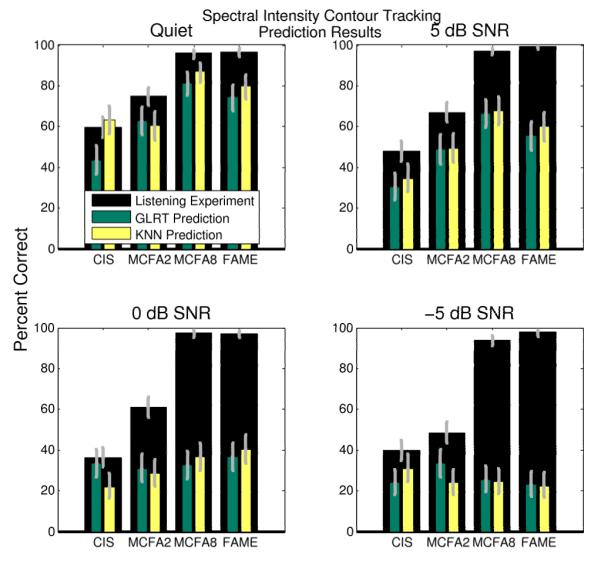
Predicted results using the spectral intensity contour tracking method. The results are shown with the listening experiment results. The predicted results are shown in the foreground with the analogous listening experiment results shown in the background. The error bars indicate the 95% confidence interval.

The predictions provided by the two methods vary in accuracy as they are based on different assumptions and use different amounts of a priori knowledge. It is important to note that listening experiment results from acoustic models and normal hearing listeners are meant to represent trends in performance rather than exact predictions. It follows, therefore, that the differences in percent correct between the listening experiment and the automated classification are not of primary interest. What is of importance is the relative performance predicted by each method. It is for this reason the error of the predictions is difficult to quantify.

The proposed metric for the evaluation of the prediction methods is based on the Kullback-Leibler divergence (KLD) between a normalized form of the listening experiment results and the predicted results. The KLD is a measure of difference between two probability density functions. For discrete random variables P and Q over n events with probabilities, p₁, p₂, …, p_n, and q₁, q₂, …, q_n, respectively the KLD from P to Q is given by

$$D(P\Vert Q)=\sum _i^m{p}_i\log \frac{p_i}{q_i}.$$ (7)

The KLD is in units of bits when the logarithm is taken with base 2. If two probability density functions are identical the KLD between them is zero. Larger values indicate that the probability density functions are more different.

For a given SNR and a given prediction method, the KLD can be used to measure the accuracy of a prediction of the listening experiment. First however, both quantities must be expressed as probability density functions. This can be done by normalizing the collection of percent correct values for the signal processing techniques to sum to one. Following this, Eq.7 can be applied. The KLD metric for each of the prediction methods is shown in Fig. 8.

Fig. 8.

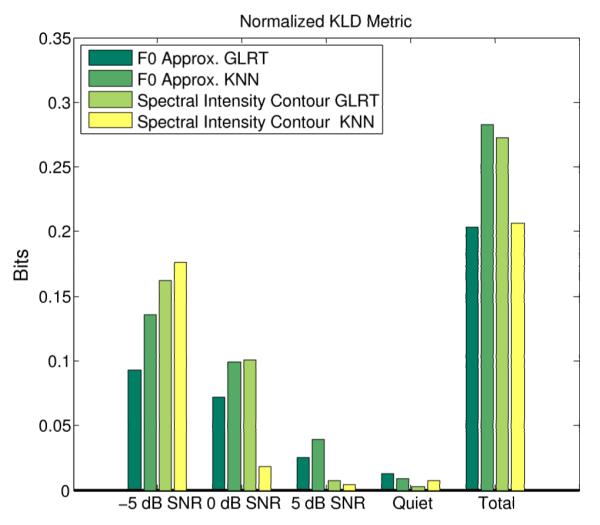
The normalized Kullback-Leibler divergence between each of the prediction techniques and the results of the listening experiment. Lower values indicate a better prediction.

4.6 Prediction Discussion

The predicted results in quiet using both of the prediction methods with each of the pattern classification techniques are similar to those seen in quiet for the listening experiment. The models are rank ordered in their classification performance as they would be if they were ranked by the amount of spectral information they present. Therefore, the results of the automated classification show the relative performance of the models.

The other SNRs (5 dB, 0 dB, and −5 dB) yield prediction results which are inconsistent with those found from the listening experiment when using the automated techniques. The primary theory behind the strategies, FAME and MCFA, is that they will aid in speech recognition in noise. As mentioned previously, this has been shown to be true for both strategies with English vowels and consonants (Throckmorton et al. 2006). The listening experiment shows that performance of these strategies does not degrade in noise, however, the prediction techniques fail to predict this result.

The KLD metric shown in Fig. 8 provides a method of quantifying the quality of each of the prediction methods. Recalling that lower values correspond to a better prediction, it can be seen that the best overall predictors are the KNN classifier applied to the spectral intensity contour features and the GLRT classifier applied to the F0 approximation features. These two prediction methods have similar total performance but have different strengths. The KNN classifier applied to the spectral intensity contour features provides the best prediction at higher SNRs (quiet, 5 dB and 0 dB) but the worst performance at −5 dB SNR. The GLRT classifier applied to the F0 approximation features has below average performance at the higher SNRs (quiet and 5 dB) but provides the best predictions at −5 dB SNR. This plot also shows that the predictions at higher SNRs (quiet and 5 dB) are both more accurate and more consistent across prediction methods.

Both of the sets of features used for prediction fail to quantify the necessary information required to predict the results of the listening experiment in noisy conditions. The approximate F0 contour method does not predict the results of the listening experiment well due to the differing effect that noise has on each of the processing strategies. For example, the approximate F0 contour determined for the CIS strategies will remain the same independent of the level of noise. Although the presence of the noise will negatively affect temporal amplitude information, the frequency information remains constant and thus the approximate F0 contour does not change. In a similar manner the MCFA 2 strategy is effected by the noise differently than the MCFA8 or FAME strategies. The presence of the noise will negatively impact the estimation of the frequency with maximum energy within window. When fewer frequencies are able to be selected, such as in the MFCA2 strategy, the changes in the approximate F0 contour are not as drastic. The differing effect of noise on the extraction of the F0 contour across the different strategies limits the ability of the approximate F0 contour features to correctly predict the results of the listening experiment.

The presence of noise also negatively impacts the estimation of the spectral intensity contours, however, the same effects are observed in each of the strategies. The STFT based algorithm for estimating the spectral intensity contours is not robust under noisy conditions. Thus, the accuracy of the estimated spectral intensity contours is not sufficient enough to correctly model the underlying spectral intensity contours. This limits the ability of the spectral intensity contour features to correctly predict the results of the listening experiment.

5 Discussion

The listening experiment conducted in this research suggests that cochlear implant signal processing strategies that present more spectral information enable more accurate Mandarin Chinese tone classification. This result is congruent with the results of the experiments presented by Kong and Zeng (2006). The listening experiment conducted in this research provides a comparison of the continuous range of frequency information provided by the FAME strategy to that of the discrete frequency information provided by the MCFA strategy within the task of Mandarin Chinese tone classification in noisy conditions. Similar to results seen in English vowel and consonant recognition (Nie et al. 2005; Throckmorton et al. 2006), both the MCFA and FAME strategies show a greater robustness to performance degredation in noisy conditions.

Although cochlear implant acoustic models do not provide a direct measurement of the performance of speech processing algorithms in cochlear implant subjects, they provide a means of predicting trends likely to be seen (Dorman et al. 1997; Shannon et al. 1995). Although cochlear implant acoustic models do not adequately model all of the factors which affect performance, they do provide a basis for investigation of expected trends. Similar to the work done by Remus and Collins (2003) for predicting English vowel and consonant confusions, this research analyzes the output of cochlear implant acoustic models as an alternative means for predicting trends likely to be seen in cochlear implant subjects. The listening experiment that was conducted serves as a baseline and by predicting trends in the results of the listening experiment using acoustic models, information regarding the trends likely to be seen in cochlear implant subjects is gained.

This research has shown that trends in performance of Mandarin Chinese tone classification in cochlear implant acoustic models can be adequately predicted in quiet by using a priori knowledge of the underlying F0 contour or without a priori knowledge by tracking spectral intensity contours. The predicted trends verify the appropriateness of automated classification in quiet conditions by comparison to the theoretical spectral content of each algorithm but also by comparison to the results with experimental data. Direct comparisons with cochlear implant Mandarin Chinese tone recognition scores are not possible since MCFA, and FAME have not yet been implemented in speech processors. However, if it is assumed that trends in studies of normal hearing individuals and cochlear implant acoustic models can be used to predict trends in cochlear implant subjects, the prediction techniques presented here could be used to predict trends in cochlear implants in quiet conditions. However, the results of the listening experiment in noisy conditions are not accurately predicted using the proposed techniques. Although the features used in this research were derived from understanding of the spectral characteristics of Mandarin Chinese tones, the effects of noise on feature extraction were too detrimental to enable accurate prediction. Further understanding of the cues used by the human perceptual system may aid in the development of new features.

The necessary cues for Mandarin Chinese tone classification has been analyzed in previous studies. Through the use of auditory chimeras (Smith et al. 2002), Xu and Pfingst (2003) were able to analyze the effects of envelope and fine-structure (defined using the Hilbert transform) on Mandarin Chinese tone classification performance in quiet conditions. Xu and Pfingst determined that when only limited frequency information is presented fine-structure information is more important for Mandarin Chinese tone classification than envelope information. The effects of noise on Mandarin Chinese tone classification with varying amounts of amplitude and spectral information were first analyzed by Kong and Zeng (2006). Kong and Zeng further distinguished the types of temporal and spectral information into four categories, temporal envelope, temporal fine-structure, spectral envelope, and spectral fine-structure. The results of the listening experiments conducted by Kong and Zeng suggest that either temporal or spectral fine-structure information is necessary for reliable Mandarin Chinese tone recognition in noisy conditions. They also suggest that the varying frequency information provided by the FAME algorithm, and thus the MCFA, is temporal fine-structure information which can be used as a cue for Mandarin Chinese tone classification in noisy conditions. This conclusion is consistent with the results of the listening experiments presented by Kong and Zeng and this research.

Despite the fact that both the approximate F0 and spectral intensity contour features used in this research quantify fine-structure information, neither feature set was capable of predicting the results of the listening experiment in noisy conditions. The calculation of both sets of features was highly susceptible to the presence of noise. To enable the prediction of Mandarin Chinese tone classification results in noisy conditions, a set of features capable of quantifying the necessary fine-structure information in the presence of noise must be found.

One possible source of features that may be able to quantify fine-structure information in the presence of noise may be neural models of the auditory system. Neural models of the auditory system, such as the one presented by Sene (1988) have been used as a means for speech recognition (e.g. (Strope and Alwan 1997; Tchorz and Kollmeier 1999; Nogueira et al. 2007)) and may help to mitigate the effects of noise. Features which quantize the necessary cues for Mandarin Chinese tone recognition may be able to be extracted from the output of neural models even in the presence of noise. Another possibility for noise resilient features could lie in more robust F0 estimation techniques such as the one proposed by Zakis et al. (2007). Noise robust F0 estimation techniques may not only enable better prediction methods but also may aid in the development of new cochlear implant signal processing strategies which can choose to present more beneficial frequency information on a given electrode in the presence of noise.

Pitch perception, and thus Mandarin Chinese tone recognition, in cochlear implant recipients may be improved by the inclusion of additional fine-structure information. A number of algorithms have been proposed to include additional fine-structure information through various stimulation paradigms (van Hoesel and Tyler 2003; Vandali et al. 2005; Nogueira et al. 2005; Grayden et al. 2006; Arnoldner et al. 2007) but most have had only limited testing and have not been evaluated on the task of Mandarin Chinese tone recognition. Evaluation of these processing strategies as well as the FAME and MCFA strategies in cochlear implant recipients on the task of Mandarin Chinese tone recognition would allow for the validation of the predicted trends using the automated techniques presented in this research. An automated algorithm capable of accurately predicting trends in algorithm performance could then be used to evaluate newly derived signal processing algorithms without the need for testing in human subjects.

6 Conclusion

This paper has shown that automated Mandarin Chinese tone classification may provide a means of predicting trends in performance of cochlear implant speech processing strategies on the task of Mandarin Chinese tone identification in quiet conditions. Accurate prediction of Mandarin Chinese tone classification in noisy conditions requires a feature extraction technique that is not only capable of distinguishing between Mandarin Chinese tones but is also robust to the presence of noise. Creating a new set of features may allow accurate prediction of Mandarin tone identification in noisy conditions without the use of human subjects.