Imputation approaches for potential outcomes in causal inference

Abstract

Background: The fundamental problem of causal inference is one of missing data, and specifically of missing potential outcomes: if potential outcomes were fully observed, then causal inference could be made trivially. Though often not discussed explicitly in the epidemiological literature, the connections between causal inference and missing data can provide additional intuition.

Methods: We demonstrate how we can approach causal inference in ways similar to how we address all problems of missing data, using multiple imputation and the parametric g-formula.

Results: We explain and demonstrate the use of these methods in example data, and discuss implications for more traditional approaches to causal inference.

Conclusions: Though there are advantages and disadvantages to both multiple imputation and g-formula approaches, epidemiologists can benefit from thinking about their causal inference problems as problems of missing data, as such perspectives may lend new and clarifying insights to their analyses.

Key Messages

• Causal inference can be regarded as a missing data problem; therefore, missing data approaches can be taken to causal inference.

• The exchangeability assumption central to causal inference is closely related to the way in which potential outcomes are missing.

• Multiple imputation and the parametric g-formula can each be used to impute missing potential outcomes.

Introduction

When we state that an exposure (or treatment) X causes an outcome Y, we usually mean that if X is present, then Y is more likely to occur; and also that if X is absent, then Y is less likely to occur (or will occur at a later time than it would have otherwise, as with inevitable outcomes such as death). To estimate the causal effect of X on Y, we would like to compare values of Y had a participant been exposed and had that same participant been unexposed. We refer to these two potential values for Y as potential outcomes. However, we never observe the outcome Y simultaneously for both X present (X = 1) and X absent (X = 0) for a single study participant i; this can be regarded as a problem of identifiability. Instead, under the counterfactual consistency theorem,^1–3 we observe exposed participants’ outcomes when they are exposed, but we do not observe what exposed participants outcomes would have been had they been unexposed. For unexposed participants, the reverse is true. As a result, the true causal effect of X is not identifiable at the individual level. The fundamental problem of causal inference, and thus of analytical epidemiology, is therefore one of missing data, or the inability to observe all but one potential outcome.^4,5

Yet, when epidemiologists analyse data for the purposes of causal inference, in the absence of explicitly missing data they typically do not consider missing-data approaches to analysis. Most often epidemiologists approach causal inference using some form of regression analysis. Less often, they use methods that explicitly model marginal (population-level) potential outcomes, such as the g-computation algorithm formula,⁶ also known as the g-formula,^7–9 or inverse probability weights.¹⁰ In fact, inverse probability weights, as commonly used to fit marginal structural models, were originally developed as a tool for data missing by design in survey sampling,¹¹ and later adapted for general missing data settings, and then causal inference.¹² Other techniques developed for missing data such as multiple imputation,^13,14 are typically used only when some measured variables are partially missing (e.g. when the epidemiologist wishes to control for age but some study participants are missing a birthdate). Rubin¹⁵ described the link between causal inference and missing data and proposed a Bayesian framework for inference based on multiple imputation, and Rubin and others later specifically suggested using multiple imputation to address the problem of missing potential outcomes.^16–18 The g-formula⁹ is another approach to imputing missing potential outcomes.

However, these missing-data methods have not been used frequently in the epidemiological literature, and the connections between causal inference and missing data are often not made explicit, especially in use of traditional regression approaches to data analysis. Here we describe missing-data approaches to causal inference as an alternative way to think about causal inference and missing data,¹⁹ and to assist in understanding identification conditions²⁰ necessary for causal inference. We include an algorithmic approach as well as a simulation study to help build intuition.

In the remainder of this paper, we review both potential outcomes and selected approaches to missing data, and demonstrate how missing data methods can be used to obtain causal contrasts in a simple example. We discuss advantages and disadvantages of various approaches to causal inference that take a missing data perspective. Throughout, we focus equally on multiple imputation and the g-formula as possible approaches to handling missing potential outcomes.

Potential Outcomes

Neyman proposed the potential outcomes model of causality⁴ which was subsequently popularized in settings with time-fixed exposures by Rubin⁵ and later generalized to settings with time-varying exposures by Robins.⁶ Suppose we have a dichotomous outcome Y_i and a dichotomous exposure X_i, for participant i (hereafter we assume data are independently and identically distributed and suppress participant-specific indices i). The potential outcome Y^X=x (hereafter, Y^x) is the outcome that we would observe if we intervened to set the exposure X equal to x. For dichotomous X (0 or 1), each participant has two potential outcomes Y^x, namely Y⁰ and Y¹.

The potential outcomes are always hidden.²¹ We can link potential outcomes to the observed data using the counterfactual consistency theorem^{1–3,22–24} to assign $Y^x=Y$ for individuals with $X=x$ (here we do not enter into discussions of treatment variation irrelevance, see;^1,2 or interference, see²⁵). The fundamental problem of causal inference is that Y⁰ remains missing for individuals with $X=1$ and Y¹ remains missing for individuals with $X=0$; for this reason, we cannot in general estimate individual contrasts in potential outcomes. We can estimate a marginal contrast in potential outcomes, $\text{E}\left(Y^1-Y^0\right)=\text{E}\left(Y^1\right)-\text{E}(Y^0)$, if we can recover $\text{E}\left(Y^x\right)$ for patients with $X\ne x$ by assuming that the expected values of the potential outcomes are independent of the actual exposure received, or exchangeability: $\text{E(}{Y}^x\text{)=E(}{Y}^x\text{|}X\text{)}$.^21,22,26

In a randomized setting, we intervene to set the exposure X on each participant based on a random process. Because treatment is assigned randomly, those assigned to X = 0 and those assigned to X = 1 are exchangeable: specifically, the potential outcomes are independent of treatment assignment for all individuals and thus E(Y¹|X=1) = E(Y¹|X=0) and similarly E(Y⁰|X=1) = E(Y⁰|X=0). Thus, randomization allows an unbiased comparison of marginal potential outcomes. In contrast, in an observational setting, we can relax the unconditional exchangeability assumption by assuming exchangeability conditional on a set of observed confounders, chosen based on background knowledge of the investigative team.²⁷ The conditional exchangeability condition can be stated explicitly in terms of potential outcomes: conditional on observed covariate set Z, exchangeability is $Y^x{{\displaystyle \coprod }}^{}X|Z$ for all values x.²⁶ Under conditional exchangeability, we also require positivity, or a nonzero probability of all levels of the exposure for all covariate combinations,^22,28 although we can relax positivity (e.g. if we allow model extrapolation).

As noted above, the fundamental problem of causal inference is that, for a dichotomous exposure under the counterfactual consistency theorem, each participant is missing at least one potential outcome: that corresponding to the exposure or treatment not received. For a continuous exposure, each participant has one observed potential outcome and infinitely many missing potential outcomes. To make causal inference using a counterfactual framework, we must now find a way to impute the missing potential outcomes either implicitly or explicitly, both of which require the counterfactual consistency theorem, and either an assumption of unconditional exchangeability or of conditional exchangeability with positivity, as detailed above.

We recognize that epidemiological analyses (for example regression adjustment, or a Mantel-Haenszel estimator) that are estimating a causal effect typically impute the missing potential outcomes implicitly. As well, inverse probability weighting or standardization can be used to generate a pseudo-sample in which confounding is absent. All of these methods estimate unbiased causal effects subject to the counterfactual consistency theorem and (conditional) exchangeability (and positivity) assumptions.

From the above, it is evident that we may view causal inference as a missing data problem—specifically, of missing potential outcomes. Thus, we will examine some assumptions required to handle missing data in the following section. Then, we describe two approaches that explicitly impute the potential outcomes.

Missing Data

Discussions of missing data frequently concentrate on three types of missing data: missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR; sometimes NMAR¹³). We have an exposure X, an outcome Y and a vector Z comprising covariates of interest (e.g. a set of confounders sufficient to ensure conditional exchangeability between the treated and untreated); let U be a vector of additional covariates (not part of Z). We define outcome missingness R such that R = 0 denotes a record which is missing Y, and R = 1 denotes a record which is not missing Y; we assume that X and Z are fully observed. Here, data are said to be MCAR if the missingness of Y is independent of all variables of interest, specifically P(R=0|U, Y, X, Z) = P(R=0|U).^13,14,29,30 Informally, MCAR data are those in which the observed data constitute a simple random sample from the full data, and thus the only effect of missing data is to reduce sample size but introduce no bias. Of course, missingness of Y may depend on some external factors U, but the fact that U is not of interest in this analysis is paramount.

MAR data are those in which the missingness of Y depends only on fully observed ^13,14,29,30 but not partially observed or unobserved variables; formally for these data P(R=0|U, Y, X, Z) = P(R=0|U, X, Z).¹³ Finally, MNAR data are those in which missingness is related to partially observed or unobserved variables of interest; in this case, where the missingness of Y depends on the unobserved values of Y. We denote MNAR formally for these data as P(R=0|U, Y, X, Z) ≠ P(R=0|U, X, Z).¹³ In passing, we note that a complete case analysis is unbiased under MCAR, but may be biased under either MAR or MNAR, depending on which variables are incomplete and how these variables are related to the outcome.^31,32

There is a one-to-one relationship between the missingness of the potential outcomes and the exchangeability assumption.²² This relationship is explicit in the formal statement of exchangeability (again, $Y^x{{\displaystyle \coprod }}^{}X$; similarly for conditional exchangeability), but may not be immediately apparent. The relationship becomes more clear if we imagine two datasets, one containing only Y⁰ and covariates Z and a second containing only Y¹ and Z, both omitting observed outcomes Y and exposures X. In the first dataset Y⁰ is partially observed; similarly in the second dataset Y¹ is partially observed. In each dataset, we can consider whether missingness in the potential outcomes is: completely at random; at random given Z; or not at random. If missingness of the potential outcomes is completely at random in both datasets, this is equivalent to no confounding; if it is not at random in either dataset, then this is equivalent to having unmeasured confounding. Otherwise, missing potential outcomes are a combination of missing completely at random and missing at random given Z; this is equivalent to no unmeasured confounding.

A main assumption of common missing data methods, MAR, is therefore closely related to the conditional exchangeability condition which (framed as ‘no uncontrolled confounding’) underlies the typical analytical approaches taken to observational data.Therefore, we should have the exact same level of confidence that potential outcomes are missing at random as we have regarding the ‘no uncontrolled confounding’ assumption in a typical regression analysis. With this in mind, we now briefly describe two analytical approaches to impute potential outcomes, multiple imputation and the g-formula, reminding the reader that other approaches are possible and are discussed later.

Multiple Imputation

Multiple imputation was developed by Rubin^13,14,30 as a general method for missing data (specifically, for non-response in surveys) which yields asymptotically consistent estimates of parameters when data are MAR and the imputation model is correctly specified. When data are MAR, the observed data may be thought of as a simple random sample from the full data conditional on levels of observed values of variables, but not conditional on unobserved variables or missing values of observed variables. Multiple imputation may be used to account for data missing by chance or by design;³³ in the former case, as in this problem, a model for the mechanism by which the data became missing must be assumed. We use one imputation approach (monotone logistic) in the simulation example below.

Briefly, imputation works by generating a copy of the full dataset in which the missing values are predicted using an imputation model. There are a variety of methods used to generate these predictions. Stuart et al.³⁴ and Schafer³⁵ provide reviews of these methods. Multiple imputation repeats this process; we draw m (say 50) sets of complete data, allowing for variation in the previously missing data. Then we fit m analysis models and combine the results of the m models by using standard approaches which account for both within- and between-imputation variance with correction for the fact that m is finite. Some implementations of multiple imputation rely on assumptions of normality or multivariate normality among variables affected by missingness.

Here we suggest an algorithm for programming multiple imputation of potential outcomes¹⁹ in a setting of a dichotomous point treatment X, an outcome Y and a vector of covariates Z = z to estimate a causal risk difference. The algorithm is shown in Table 1 (left column).

Table 1.

Proposed algorithms for imputation of potential outcomes using multiple imputation and the g-formula

	Multiple imputation	The parametric g-formula
1a	For each of N observations, defined by {Y=y, X=x, Z=z}, create two additional
	Variables Y0 and Y1 which are initially set to missing.
	The observation is now defined by {Y=y, X=x, Z=z, Y0=., Y1=}
1b	Assuming counterfactual consistency, set Yx = Y. That is, if X = 0, then set Y 0= Y
2		Fit a model (e.g. logistic regression) for the association of X, Z on Y, resulting in estimated model parameters β
3a	Perform m imputations (e.g. in SAS procedure MI) for the missing values of Y1 based on observed values of Z.	For each observation, use the model (fit in step 1) to predict expected value of Y1 setting X = 1, and of Y0 setting X = 0
	This will result in m complete datasets
3b	Impute the missing values of Y0 based on observed values of Z in each of the m datasets. This keeps total number of datasets at m	Note that if Y is dichotomous, the expected value is the same as probability P(Yx=1)
4a	Within each of m complete datasets, do:
4b	Calculate the mean of Y0 and Y1 and take the difference (ratio) of the two means for the estimated causal risk difference (ratio)
4c	… and then combine across imputations by taking a simple mean (on the log scale for a risk ratio)
5	Bootstrap the process b times to obtain standard errors

In the algorithm, note that one must impute Y¹ and Y⁰ separately (steps 3a and 3b) because the original data contain no information about the joint distribution of Y¹ and Y⁰; thus the data structure precludes the imputation of both potential outcomes simultaneously. Step 3a also requires assuming a model for the process by which the data became missing. In addition, note that in these steps, we impute only based on Z, because the exchangeability means exactly that the potential outcome is independent of the observed exposure given covariates. In Step 4c, note that we are only estimating a mean, so accounting for between-imputation variance is unnecessary; and related in step 5, Rubin’s formula for the variance¹¹ cannot be used because every observation contributes to both exposed and unexposed calculations, and therefore we bootstrap. A closed-form variance estimator is likely possible though not explored here.

The G-Formula

The nonparametric g-formula is a generalization of direct standardization to allow for time-varying as well as time-fixed covariates.⁶ The parametric g-formula (hereafter, the g-formula) is a finite-dimension model-based version of the g-formula which allows for handling higher-dimension problems, for example continuous data or multiple covariates.^7–9 With a time-fixed exposure, the g-formula is straightforward to describe, again with a dichotomous point treatment X, an outcome Y and a vector of covariates Z=z.

The algorithm for imputation of potential outcomes with the g-formula is shown in Table 1 (right column). Comparing the left and right columns of Table 1, it is immediately clear that the g-formula algorithm is similar to the multiple imputation (MI) algorithm in the left column, differing only at steps 1b, 2, 4a and 4c. Like multiple imputation, the g-formula is asymptotically consistent if potential outcomes are MAR conditional on covariates included in the model fit in step 2 of the algorithm, and if parametric model specifications are correct. The large-sample behaviour of both MI and the g-formula should be similar in the sense that both are consistent, asymptotically normal and parametrically efficient.

There are three key differences between the approaches: first, MI does the imputation m times, rather than once; this can be seen as increasing the Monte Carlo sample, and could be done equivalently in the g-formula (by resampling with replacement from the original data at a larger sample size). Second, our implementation of MI incorporates sampling of parameter values prior to imputing missing data, which is termed ‘proper’ by Rubin;¹³ see also;³⁶ and ensures the propagation of uncertainty into estimates of variance when using Rubin’s formula. The g-formula does not incorporate sampling of parameter values. In this example, however, variance estimates for both MI and the g-formula are obtained by non-parametric bootstrap, and so this distinction is less critical. One final difference is that in the MI case, we use the counterfactual consistency theorem to set Y^x = Y for observed X=x, and thus only impute one of (Y¹, Y⁰), whereas in the g-formula we impute both Y¹ and Y⁰. We could take a similar approach in the g-formula, but this would break from the method of the g-formula and can be seen as a hybridization of MI and the g-formula.

Example

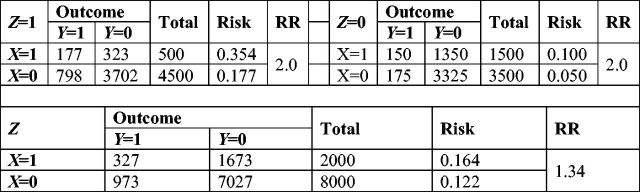
Here we present an example to illustrate the use of missing data methods in a causal inference framework, and compare these methods with more traditional approaches. We illustrate these methods with a simple simulated dataset. We simulated a dichotomous exposure X, a dichotomous outcome Y and one dichotomous confounder Z. Marginal prevalence of X, Y and Z were fixed at 0.20, 0.13 and 0.50, respectively. The relationship between X and Y was defined using a log-binomial model with an intercept of 5% incidence, a risk ratio of 2 for X and a risk ratio of 3.5 for Z; the association of Z on X was also defined using a log-binomial model with an intercept of 30% and a risk ratio of 1/3. One realization of such a dataset including 10 000 participants is shown in Figure 1.

Figure 1.

Expected realization for 10 000 participants from example data, by stratum of Z and overall.(Color online).

We performed four analyses on these data: (i) a crude analysis; (ii) an adjusted analysis using a correctly specified log-binomial regression model; (iii) a multiple imputation analysis using default SAS procedures (see algorithm above; here we used a ‘logistic monotone’ imputation approach, to reflect dichotomous outcomes); and (iv) a parametric g-formula analysis using a log-binomial model (see algorithm above). For each analysis, we simulated 5000 datasets of size 1000 individuals each; we report mean coefficient and standard error for each method in Table 2.

Table 2.

Estimated beta coefficients, exponentiated beta coefficients and standard errors derived from 5000 samples of 1000 individuals sampled from a population with the same characteristics as the sample population shown in Figure 1 and described in the text

Approach	Parametric assumption	Average beta	Exp (average beta)	Average standard error
Crude regression	Log-binomial	0.290	1.336	0.1889
Adjusted regression	Log-binomial	0.686	1.986	0.1882
Multiple imputation	Logistic monotone	0.684	1.982	0.1967
Parametric g-formula	Log-binomial	0.686	1.986	0.1882

As expected, the crude estimate of effect is biased (due to confounding by Z), whereas the adjusted log-binomial model is unbiased. Multiple imputation (with a monotone logistic imputation approach) and the parametric g-formula (using the correct parametric model) both yielded unbiased results. The standard errors of all methods were similar. Overall, we demonstrate that imputation of potential outcomes by MI or the g-formula can estimate the same quantity as a standard approach using regression analysis.

Discussion

All approaches to causal inference implicitly account for the missing potential outcomes. This accounting is hidden from casual users of regression analysis but, as we have demonstrated, the conditional exchangeability assumption necessary to identify causal effects, also known as the assumption of no uncontrolled confounding, is equivalent to the assumption that the missing potential outcomes are MAR given the measured confounders. Here we have demonstrated valid results from regression analyses and also from two different methods for imputation of potential outcomes in a simple setting.

As noted above, our chief goal in this work is to propose an alternative way to think about causal inference and missing data; that said, the g-formula is of late enjoying wider use for the purposes of causal inference in observational data (e.g.³⁷). In either context, it is worth recalling the point made above that conditional exchangeability is the condition in which missing potential outcomes are MAR, rather than MNAR. Reiterating our statement from above: whatever our level of confidence about a ‘no uncontrolled confounding’ assumption in a regression analysis (for example), we should have the same level of confidence that the potential outcomes are missing at random.

In both the multiple imputation and g-formula analyses above, we estimated standard errors using the bootstrap; as noted, a closed form approach to variance estimation accounting for inflated sample size may be possible here. An alternative approach to imputation in time-fixed data which may have implications for precision is a hybrid approach of the two methods: in the g-formula step 3, if X = 1 then assume Y¹ = Y, and only predict the value of Y⁰—and vice versa. Related, readers may have noted that our g-formula approach did not impute potential outcomes per se, but rather estimated probabilities (expected values) of these potential outcomes. An additional step could resolve these probabilities into outcomes (0s and 1s), but doing so is unnecessary. Both approaches may have benefits depending on the setting:^8,9 for example, imputation of outcomes rather than probabilities is necessary for the estimation of relative hazards.⁹

Alternative missing data approaches, such as direct maximum likelihood,³⁸ may also be viable approaches to handle missing potential outcomes. In addition, multiple imputation and the parametric g-formula can be refined to increase their utility. For example, multiple imputation can be performed by chained equations,³⁹ and the g-formula can be made more robust to model misspecification through machine-learning techniques.⁴⁰ The parametric g-formula can be used to impute potential outcomes in longitudinal data,⁹ even in the presence of time-varying confounding, though other methods may also work well⁴¹ in this setting.

Here we have explained and illustrated how missing data methods can be used in much the same way as traditional approaches to data analysis, as well as how causal inference can be viewed as inference under missing (potential outcome) data. The use of such techniques—though more technically complex than regression approaches even in point-exposure settings—often results in the concentration on a single causal model for a single causal effect of interest, and thus may help avoid problems such as the misinterpretation of the regression coefficients for covariates as causal effects when such interpretations are not justified.⁴² In all cases, however, we believe that epidemiologists can benefit from thinking about their causal inference problems as problems of missing data, as such perspectives may lend new and clarifying insights to their analyses.

Funding

This work was supported in part by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health.

Conflict of interest: None declared.