Graphene-Based Liquid-Gated Field Effect Transistor for Biosensing: Theory and Experiments

Abstract

We present an experimental and theoretical characterization for reduced Graphene-Oxide (rGO) based FETs used for biosensing applications. The presented approach shows a complete result analysis and theoretically predictable electrical properties. The formulation was tested for the analysis of the device performance in the liquid gate mode of operation with variation of the ionic strength and pH-values of the electrolytes in contact with the FET. The dependence on the Debye length was confirmed experimentally and theoretically, utilizing the Debye length as a working parameter and thus defining the limits of applicability for the presented rGO-FETs. Furthermore, the FETs were tested for the sensing of biomolecules (bovine serum albumin (BSA) as reference) binding to gate-immobilized anti-BSA antibodies and analyzed using the Langmuir binding theory for the description of the equilibrium surface coverage as a function of the bulk (analyte) concentration. The obtained binding coefficients for BSA are found to be same as in results from literature, hence confirming the applicability of the devices. The FETs used in the experiments were fabricated using wet-chemically synthesized graphene, displaying high electron and hole mobility (μ) and provide the strong sensitivity also for low potential changes (by change of pH, ion concentration, or molecule adsorption). The binding coefficient for BSA-anti-BSA interaction shows a behavior corresponding to the Langmuir adsorption theory with a Limit of Detection (LOD) in the picomolar concentration range. The presented approach shows high reproducibility and sensitivity and a good agreement of the experimental results with the calculated data.

1. Introduction

Graphene is a material of growing interest owing to its unique properties (Geim and MacDonald, 2007; Prasher, 2010), and a wide range of applications (Yang et al., 2010; He et al., 2012; Wei et al., 2012; Kang et al., 2010). It also has been shown that graphene is an excellent substrate for biosensing (Brownson and Banks, 2010; Pumera, 2011). Although a lot of research on graphene was reported in the last years, only little work tried to combine theory with experimental results, especially in the field of graphene field effect transistor devices used as biosensors. Lacking a theoretical formulation for quantitative data analysis of the experimental results and a missing transformation of the established transistor theories to graphene FETs in the literature triggered our interest in presenting a mathematical approach in this work. Previous studies reported chemical vapor deposition (CVD) graphene transistors being insensitive to pH changes (Fu et al., 2011), yet other studies reported otherwise (Ohno et al., 2009). Despite the fact that a wide variety of biosensor devices based on graphene have been developed and optimized, the basic requirements for the construction of an applicable biosensor (reproducibility, a routine for signal prognosis, and easy handling) have not been studied so far. The advantage of the presented platform is the fabrication of reproducible and therefore theoretically predictable devices without use of complex equipment or fragile production steps. Other studies have shown great reproducibility (He et al., 2012) but most fabricated devices take great effort for the exact graphene distribution and electrode positioning. While graphene synthesis methods like CVD (Liu et al., 2010) allow for the exact material positioning, the advantage of using liquid-dispensed graphene flakes from wet chemical synthesis is their easy application but comes with the disadvantage of a partially random and uncontrollable distribution of the flakes, resulting in a random localization during the adsorption from the liquid onto the gate surface. This problem can be solved by the choice of a relatively long conducting channel (4mm), contrary to very short channels being used if the graphene is positioned exactly. In this work statistical balancing of total graphene-covered surface area over all separate graphene connections is ensured by the choice of a long conducting channel. While this can ensure reproducibility of the devices, other methods with similar reproducibility use bulky equipment for exact graphene positioning and have high production costs. The development of portable devices is a long-term aim of this work, implying miniaturization and the availability of commercial micro-electronics. Portable devices rely even more on defined and reproducible measurement, which is depending on many criteria, e.g. setup geometry, liquid properties or shock resistance. These criteria make the use of defined setup like the presented flow cell for experiments crucial for reproducibility in a wider field. The purpose of this paper is to present a theory and mathematical formulation for the comprehensive description of graphene field effect transistors fabricated by a simple protocol at low fabrication cost. The study should help in understanding of graphene biosensor device features, e.g. the rGO’s intrinsic properties, the influence of cell & device geometry changes on parameters like carrier mobility and the derivation of a mathematical routine for result interpretation.

2. Material and methods

All materials were purchased from Sigma Aldrich, unless stated otherwise.

2.1. Preparation of field effect transistor devices

Silicon substrate with 300nm oxide layer was chosen as basal layer for the FETs. The SiO₂ substrates were cleaned with a standard RCA cleaning procedure. The substrates were then submerged in a 1-2% APTES solution in Ethanol for 1h, APTES forming a self-assembled monolayer to increase the adsorption of graphene. After rinsing with ethanol, the substrates were heated to 120°C for two hours and afterwards cooled to room temperature. Graphene oxide sheets were prepared using a variation of the Hummers method derived for the application on FETs (Larisika et al., 2012). The obtained graphene oxide was applied on Si-Wafer via Spin coating or drop casting of the top portion of the graphene-oxide solution. The devices were then treated in hermetically sealed glass petri dishes with Hydrazine at 70°C overnight to accomplish graphene-oxide reduction, forming the graphene structure consisting of sp2-hybridized bonds. Graphene oxide reduction success was checked in previous studies using XPS. Flake distribution was preliminary checked with an optical microscope and chosen devices then characterized using SEM. Electrical properties of the FET devices were tested analogously to (Larisika et al., 2012) shown in Fig. S1 of the supporting information. For the attachment of the antibody to the sensing area, the graphene surface was chemically modified by a bi-functional linker, 1-pyrenebutanoic acid succinimidyl ester (PBSE). On one end the linker firmly attaches to the graphene surface through π-π interactions with a pyrene group and on the other hand covalently reacts with the amino group of the protein to form an amide bond. Therefore, 20 μL of a 2.5 μM PBSE solution in Tetrahydrofuran was placed onto the rGO-FET channel.

2.2. Electrical preparation

Electrodes were applied consisting of gold (60-100nm) with an adhesive layer of chrome (2-3nm) using a standard evaporation process with a shadow mask. A chip-holder was designed for this process, ensuring the central positioning of the electrodes as well as reducing electrode geometry glazing because of unwanted shadow offset during the evaporation process. Success of the used reduction technique via hydrazine was probed before (Larisika et al., 2012), so resistance of the fabricated devices was measured for check-up of graphene-oxide reduction quality using a Fluke Multimeter ”87 V True RMS Multimeter”. To assure conductivity of the used electrolyte not being higher than the conductivity of used graphene layers, all devices displaying higher conductivity than ~800 ohm were dismissed, equivalent to the resistance of 170mM PBS buffer at room temperature. A silver-silver chloride reference electrode (Flex ref, World Precision Instruments) was used to operate the FET device in liquid gate configuration with a constant gate bias (V_g) of −0.3 V and a constant source-drain bias (I_DS) of 0.2 V. The general procedure of the whole titration experiment started with continuously flushing the detection area with pure buffer (1 mM PBS, pH = 8.0), until a stable baseline of drain current was established.

2.3. Preparation of solutions

Phosphate buffered saline with total ionic strength of 17mM were used for all experiments, pH-values were adjusted using NaOH and KOH solutions. 1-pyrenebutanoic acid succinimidyl ester (PBSE) was used as linker, purchased from ”Sigma Aldrich” and diluted to a 2.5μM solution in tetrahydrofuran (THF) and applied on prepared FET device shortly before antibody incubation for 5 minutes until the THF is vaporized. Anti-BSA stock solution was diluted in PBS at 1μM concentration and incubated after linker immobilization for two hours on the devices. Bovine serum albumin used for experiments was also solved in 17mM PBS buffer with pH 7.4 and further diluted to the desired concentration.

2.4. Characterization techniques & measurement setup

Scanning electron microscopy (SEM) images were recorded using a Zeiss ”SUPRA^™ 40 Field Emission Scanning Electron Microscope” instrument. Optical microscopy images were taken with an ”Olympus BX51M” microscope.

Electrical measurements (I_D vs. t and I_DV_G) were conducted using a probe station “Keithley 4200”. All measurements were performed using a custom made flow cell made of PMMA with fixed flow channel geometry (16μL), ensuring a defined flow rate of 300μL/min to minimize mass transfer limitations of the analyte to the sensor surface in all experiments. Furthermore electrode drillings for constant gate-electrode distance (2mm) and a hollow with FET geometry for fixed positioning of the devices were incorporated to the flow cell. As observed in almost all biosensor devices, a slight drift in source-drain current was observed with time. For this reason, the drain current response curves were normalized by subtraction to the baseline current (supporting information).

3. Results and discussion

3.1. Setup

For the derivation of a mathematical formulation a specially designed flow cell (Figure 1a) with defined dimensions and properties is crucial. The material of the cell was chosen to be PMMA, because of its reported biocompatibility (Wegmüller et al., 1986). For the generation of a defined flow speed, fixed flow channel geometry, exact electrode-contacts and FET positioning, and a defined sample volume are necessary. The construction also provides shock resistance and ensures the setup being largely unaffected by lateral movement or axial orientation. The interplay of the analyte liquid solution, the charged interface, and the graphene in the semiconductor-channel determines the devices conductivity, represent simultaneously the carrier medium and the contact layer, and enables a real-time read out for different applications.

Figure 1.

a) Image of the flow cell used for all experiments; b) optical image of the split geometry with channel width 40μm and length 4mm; c) SEM image of the rGO distribution in the FET channel; d) Measured channel resistance in ambient conditions vs. measured channel current (I_D) in liquid gate configuration. FETs were chosen with the maximal avalaible variation in resistance for demonstration of the dry device resistance on the resistance in liquid phase. I_D remains constant at a minimum of around 100μA with increasing channel resistance due to electrolyte conductivity.

3.2. Device selection

The fabricated FET devices were checked for graphene distribution by SEM images first, showing a uniform graphene distribution repeatedly (figure 1c). After this initial study resistance measurements across the semiconductor channel of 40μm (figure 1b) at ambient conditions was used as reference for graphene contact evaluation (selection of 750 devices, data not shown). The channel width was characterized by optical imaging and verified to be constant at 40 ± 4 μm. Only devices displaying a resistance of less than R = 800Ω were used, ensuring that the channel conductivity of these devices is higher than the conductivity of the dielectric isolator/medium layer (figure 1d). This approach creates a low variation in the fabricated FET’s graphene distribution, resistance and channel size. As experimentally verified, the FET baseline stability of I_D in a liquid gate configuration stabilizes over time (after ~60min), so a washing step is required prior to any measurement.

3.3. Electrical output characteristics

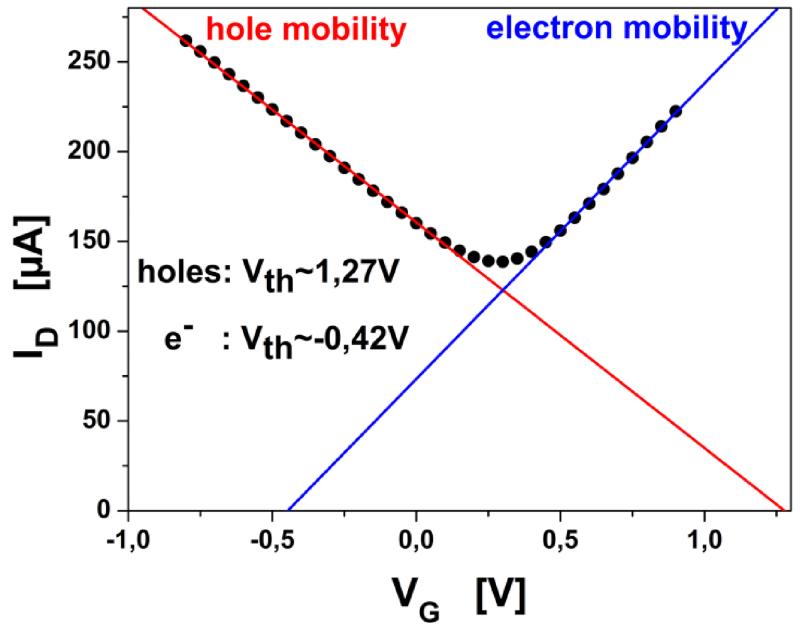
Gate-Source Voltage vs. Drain Current (I_DV_G) relations were investigated first. The examined devices showed ambipolar nature, with a linear regime for both charge carrier types below ±1V_G (figure 2). For the mathematical routine of determining the Drain-Source current, the charge carrier mobility (μ) had to be determined from the linear regime in the I_DV_G graph according to (Tanaka et al., 2010):

$$\mu =\frac{1}{\alpha e}\frac{\mathrm{d}\sigma }{\mathrm{dV}}$$ Eq. 1

where α is the induced carrier density by the gate voltage (V_G) change of 1V and e the electron charge. From the expression for the linear regimes in the I_DV_G diagram (Eq. 1) using a similar approach as (Tanaka et al., 2010) the electron/hole mobility is obtained after adaptation considering the devices properties:

$${\mu }_{\mathrm{eff}}=m_{\mathrm{lin}}\frac{\mathrm{L}}{W{V}_{\mathrm{D}}{C}_i}$$ Eq. 2

where m_lin is the obtained slope from the linear fits in the I_DV_G diagram, W is the channel width, L the channel length, V_D the applied Source-Drain voltage and C_i the gate insulator capacitance per unit area. The charge carrier mobility was found in the range of 30000 to 40000 Vs/cm² for electrons, and the hole mobility from 20000 to 30000 Vs/cm². These results are consistent with average data of high mobility FETs in other work on rGO-graphene (Castro et al., 2010). The knowledge of the charge mobility can lead to equations for channel current and electron density for both charge carrier types.

Figure 2.

I_DV_G graph measured from −0.8V to 0.7V. Colored lines indicate fits for the linear regimes of holes and electrons respectively with intercepts defining the threshold voltage (V_th). Dirac Voltage is found around 0.3V.

3.4. Calculation of the transistor channel current

For the ambipolar devices a threshold voltage (V_th) had to be defined for the branches in the I_DV_G diagram by choosing the intercept of the linear fit with the Voltage axis (figure 2). The same principle is applied for the calculation of expected current in the linear model for MOSFETs (Zeghbroeck, 2007), but there it is derived on the basis of the Source-Drain Voltage vs. Current diagram (I_DV_D). Applying the same calculation routine transformed for the approach in the I_DV_G curve instead of I_DV_D of the presented graphene FETs, yields experimentally confirmed a priori calculations of channel resistance, replacing the oxide layer capacitance with the electrolyte capacitance which is considered variable depending on liquid gate isolator properties. Due to the ambipolar nature of the graphene FET devices the routine has to be divided into two regimes - left and right of the Dirac minimum - depending on the Gate Voltage, taking into account the corresponding regime for either hole or electron charge carrier use. Specific threshold voltages were defined for each charge carrier type. Therefore the developed theory will not be sufficient for results measured with V_G at the Dirac-Point. For the calculation of the oxide layer capacitance the relative permittivity of the electrolyte has to be taken into account. Concerning the aims of this study the detection of low molecular concentrations (no viscosity change) and the change in pH or ionic strength shall be considered. Studies for these factors have shown that the relative permittivity of an electrolyte can vary by a factor of 70 or 80, depending on ionic strength and measurement’s frequency (Gadani et al., 2012). Implying these considerations for the derivation of the equation for the presented liquid-gate FET and modifying the equation taken from the MOSFET theory (in the linear model), we obtain an equation for the channel current (I_D):

$$I_D=\mu C_{\mathrm{ox}}\frac{W}{L}(V_G-V_{\mathrm{th}})V_D$$ Eq. 3

The precision of this equation was checked on devices measured at different V_G, gaining threshold voltages first from the I_DV_G diagram (intercept in Fig. 2), then making a routine measurement at constant electrolyte properties. For oxide layer capacitance (C_ox) the capacitance of the ionic liquid-graphene interface has to be used, corresponding to 3μF/cm², as shown in different studies (Randin and Yeager, 1972). The observed capacitance (C_obs) can be expressed as 1/C_obs = 1/C_H + 1/C_diff, with C_H the Helmholtz layer capacitance and C_diff the diffuse double layer capacitance (Pope, 2013). At low electrolyte concentrations C_diff is lowered and C_obs becomes approximately equal to C_diff (C_obs~C_diff). For high ionic concentration C_obs is defined by C_H because of increasing C_diff. Since phosphate buffered saline were used as electrolyte medium in our experiments, the low viscosity and the small solvated ionic radius remain constant throughout the experiments and the dissociated ion concentration remains the only variable in this study with influence on the electric double layer capacitance because of the associated dielectric constant variation. For all tested FETs the channel current baseline level agreed with the results from equation 3 for the corresponding devices with an error of 2% for the linear regime and an increased error if V_G is closer to the Dirac Voltage than 0.3V due to the nonlinearity of this curve region.

3.5. pH analysis

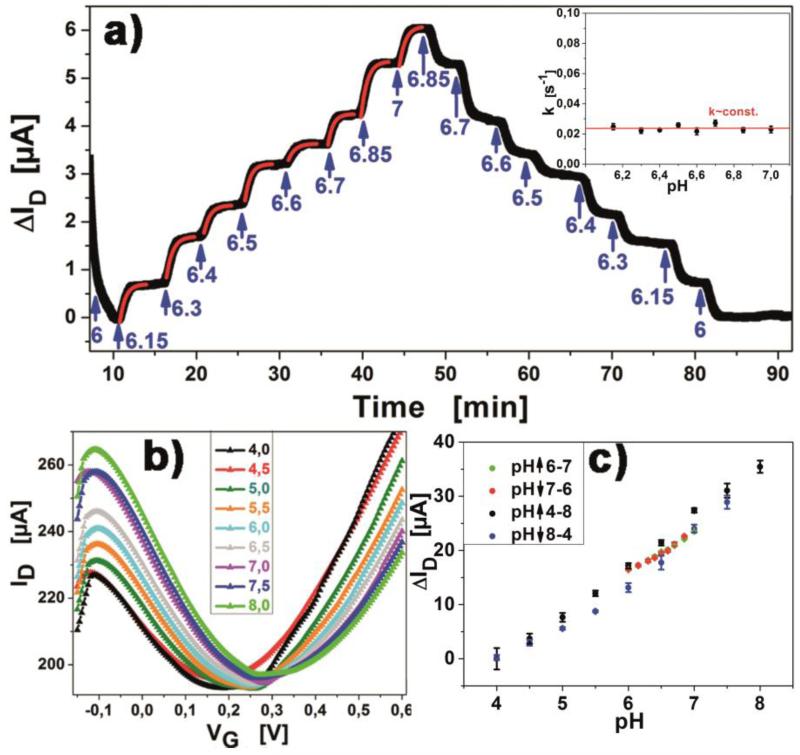
The dependency of electron and hole mobility, respectively, on pH change of the used buffer solution was investigated. Titration curves and I_DV_G relations were measured with the use of liquids with constant ionic strength and a pH varying from 6 to 7 (figure 3a) in steps of ΔpH = 0.1, as well as from pH4 to pH8 in steps of ΔpH = 0.5 (figure 3b). From these I_DV_G curves the electron and hole mobility of graphene in liquids with varying pH can be calculated from m_lin of the linear fits in the branches aside of the current minimum. This in turn gives information about the graphene-liquid interface as well the graphene itself. The study was conducted with a detailed analysis of values from pH6 to pH7, obtaining a titration curve (figure 3a) for this region. From the obtained curve, exponential fits were applied for the kinetic parameters of each pH step, showing consistent behavior with constant exponential factor in the fits for all concentrations (see insert figure 3a). This behavior can be understood assuming a Gouy-Chapman diffuse electrical double layer is being established across the channel length with a reaction rate constant k depending on the length of the channel and the liquid flow speed, i.e., the liquid exchange speed across the FET channel. The linear relation of conductance and pH change (30μS per pH unit change, figure 3c) is indicating that the relative surface potential has a linear relation to surface charge changes which is essential for the quantitative detection of biomolecules with the device. This result is in accordance with experimental results and theoretical considerations described in the literature (Tain et al., 2011). The shift of the minimum in the I_DV_G diagram, also reported in other work (Pope, 2013) was confirmed with an offset from 0.175V for pH4 to 0.31V for pH8 (0.034V/pH) (figure 3b).

Figure 3.

a) Titration of the pH of the buffer from pH6 to pH7 in steps of ΔpH=0.1, showing reversibility of the measurements. Exponential fits (red lines) have been applied for each pH transition. Insert shows that transition rates are constant for varying pH. b) I_DV_G curves for pH values in the range pH 4-8, in steps of ΔpH=0.5. c) Regression of change in channel current with pH value. Arrows indicate if data was obtained from ascending or descending pH value titration.

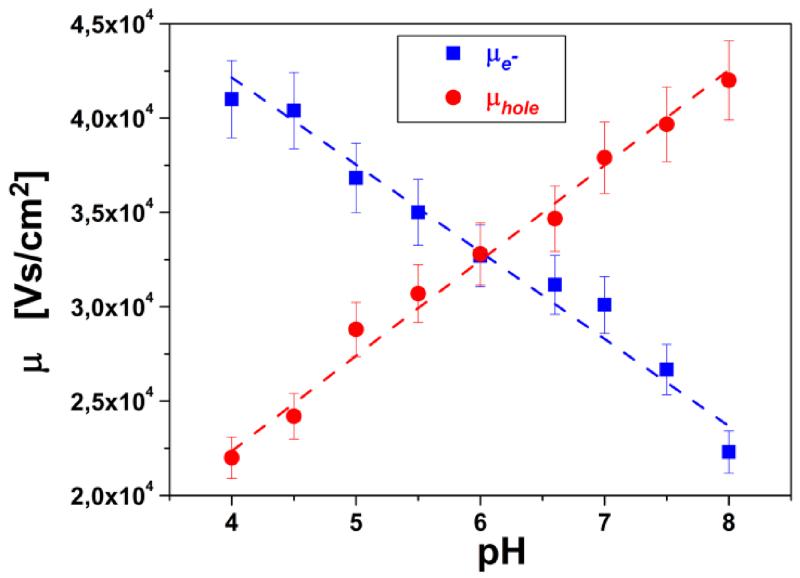
The electron and hole mobility, respectively, derived from fits of the I_DV_G relations and their dependence on the pH value (figure 4) show a transition of majority charge carrier type from electrons to holes at around pH6. This means that below pH6 electrons are the most prominent charge carriers and above pH6 holes become more prominent. This indicates an intrinsic property of rGO, similar to the isoelectric point, which in analogy could be called “isomobility point” of rGO. For the analysis of the system with regard to the ionic strength of the electrolyte used as insulator gate medium titration curves and I_DV_G diagrams were measured (see supplemental information). The Dirac point voltage was confirmed to be constant and independent of the ionic strength; furthermore, the total conductivity of the FET devices increased only slightly with increasing total ionic strength.

Figure 4.

charge carrier mobility for electrons and holes in dependence on pH of electrolyte. (Obtained from fits of I_DV_G measurement in figure 3b)

The ionic strength of the liquid is also a key factor for the Debye-length, defining the interactive radius of molecules in the medium and the thickness of the electrical double layer. As stated by the Debye theory an increase in ion concentration reduces the Debye-length (Debye, 1942). At the same time, the electrical double layer at the graphene-liquid interface is influenced by a more pronounced charge separation due to the increased ion concentration resulting in a higher potential and exhibits a stronger force on charge carriers in graphene. Thus, an increase in the ionic strength results in an increase in charge carrier mobility.

3.6. Detection of proteins

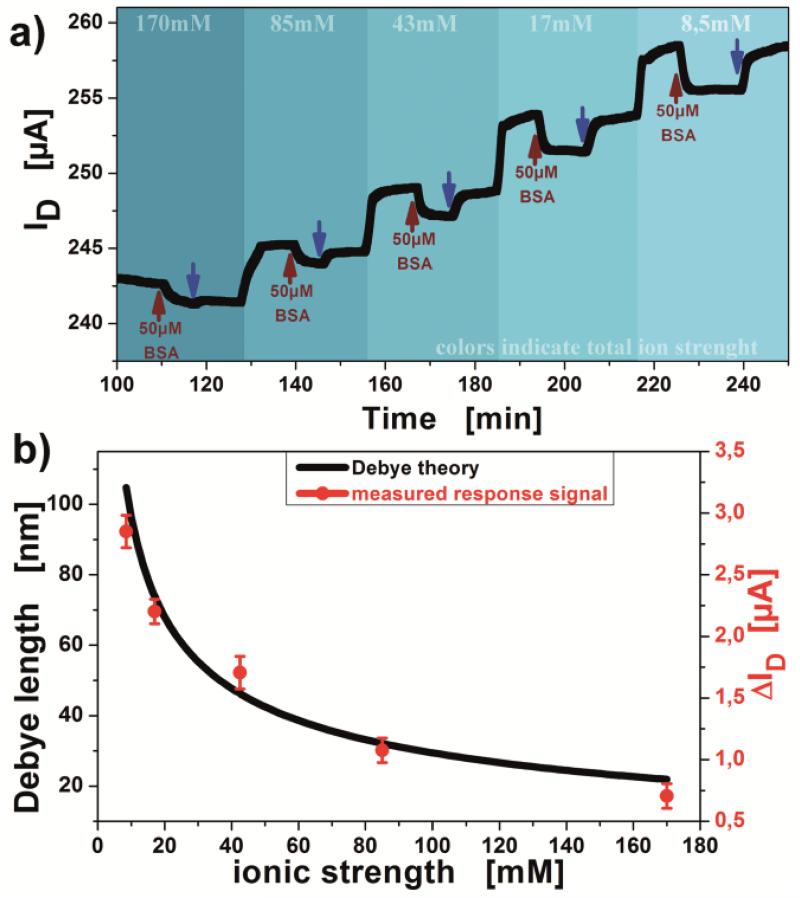
The detection of proteins depends on various parameters, e.g., the variation in Debye length or a charge carrier mobility change induced by the electrolyte’s ionic strength. Since for low ion concentrations of the used electrolyte the Debye lengths increases but at the same time the double layer capacitance and electron mobility decrease, in sum a stronger response of the system for the detection of bovine serum albumin was observed. Experimental data conducted in this study indicates a good agreement with the Debye-theory for ion concentration variation (figure 5b). For the Debye-length calculation a variable capacitance and ionic strength have been considered. The measured electrical response of the system for 50μM bovine serum albumin detection are linked with a factor of (28.6±2.9) nm/μA by the surface potential to the calculated Debye length values (figure 5b). Showing the Debye-length influence on the detection signal, protein detection measurements were conducted in a buffer of pH 7.4, clearly above the isoelectric point (iP) of bovine serum albumin (pH 5.4) (Khan et al., 2010). At this pH the molecules are negatively charged, so detection signals are predicted to be of negative response. The signal response in PBS buffers, with various ionic strengths was tested aiming at a quantitative evaluation of sensitivity change in correspondence to the Debye-length variation. The increase of total drain current with decreasing ionic strength (figure 5a) can be associated with the change of the capacitance in the electrical double layer interface and the charge carrier density in the graphene, respectively. With lower ion concentrations, the charge mobility slightly decreases, but increasing the capacitance of the gate insulator plane generates a higher total current flow for voltages close to the Dirac Minimum in the I_DV_G diagrams (V_i). For higher voltage, V_G-V_i (further away from the Dirac voltage), the effect of charge mobility outweighs the decrease in capacitance change and the total current increases with ionic strength of the electrolyte. The results from figure 5a have been superimposed with the calculated curve for the Debye length dependence on ionic strength from the Debye theory (figure 5b). For the Debye-length calculation a variable capacitance and ionic strength have been considered. This procedure yields a good agreement of the Debye curve characteristics with the measured experimental data for 50μM BSA injections, linked by a factor of (28.6±2.9) nm/μA. The response signal (current readout) can be transcribed to the surface potential via conversion to the conductivity. As stated by the Grahame equation the surface potential is connected to the surface charge via the Debye length. The relation can be simplified for low potentials to σ=εε₀ψ/λ_D, where σ is the surface charge, ε the dielectric constants, ψ the surface potential and λ_D the Debye length.

Figure 5.

a) Measurement of detection signal behavior for 50μM BSA, gradually decreasing the ionic strength (indicated by background color change) from 170mM to 8.5mM at V_G= −0.2V. Blue arrows indicate wash-off with same buffer solution used for associated BSA injection. b) Overlap of responses from figure a) and the Debye-theory calculation.

3.7. Protein adsorption/desorption kinetics

With the assumption of the responsive current change being linearly dependent on surface coverage of bovine serum albumin on the (layer of) binding sites on the FET, the Langmuir formulation (Langmuir, 1917) can be transformed to ΔI_D, ideally yielding a mathematical expression for the system when binding constants are known (de Mol and Fischer, 2008). This procedure theoretically enables the determination of unknown target molecule concentrations in the electrolyte. The equation for the channel current thus derived reads as followed:

$$I_{\mathrm{DS}}=\mu C_{\mathrm{OX}}\frac{W}{L}(V_{\mathrm{GS}}-V_{\mathrm{th}})V_{\mathrm{DS}}+\theta \left(\mathrm{pH}\right)\cdot \left[\frac{k_{\mathit{\text{on}}}\left[c\right]R_{\max }}{k_{\mathit{\text{on}}}\left[c\right]+k_{\mathit{\text{off}}}}\right]\cdot \left(1-e^{-\left(k_{\mathit{\text{on}}}\right[c]+k_{\mathit{\text{off}}})t}\right)$$ Eq 4

with R_max being the maximum response signal, [c] the observed analyte concentration and Θ(pH) the Heaviside-function determining the prefix defining if positive or negative detection signals are expected (Θ(pH) being sign(pI-pH) for proteins, and (−1) for uncharged molecules). t defines the equilibrium setting time of the observed concentration, starting with 0 at injection. k_on and k_off for the equation are obtained from the linear fit in the Langmuir model (figure 6b). The formulation shows good agreement with experiments conducted on multiple FET devices, exhibiting a maximum error of 10%, but being dependent on the device’s baseline stability.

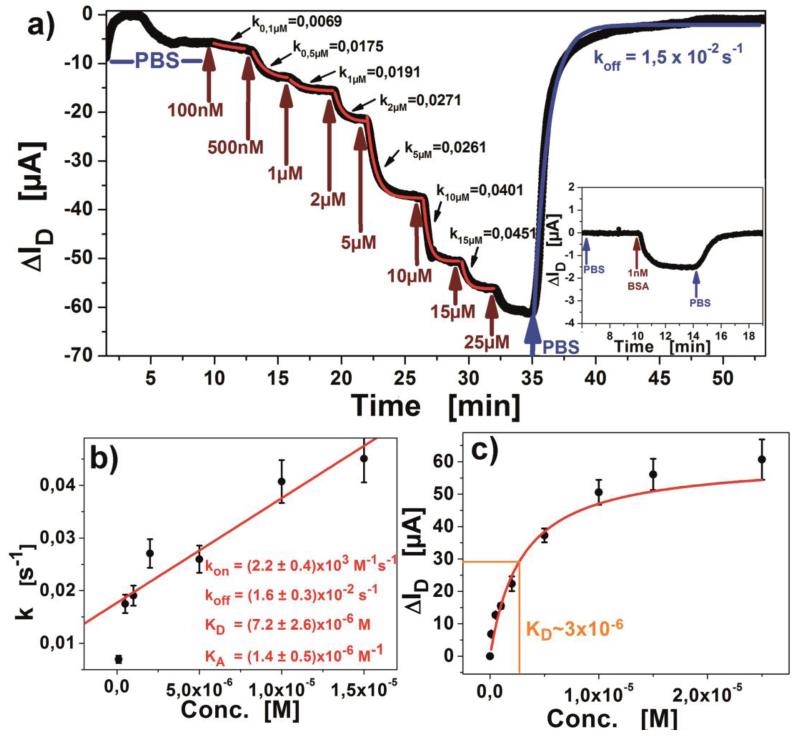
Figure 6.

a) Titration of BSA from 100nM until saturation is observed at 25μM. The first few minutes show a drift due to the graphene charging behavior, stabilizing after 7 minutes; insert shows the low concentration detection, indicating the limit of detection below 1nM; b) kinetic analysis of the obtained association constants; c) Equilibrium titration with binding isotherm.

As for proof, a well-studied target molecule, bovine serum albumin (BSA) was chosen for detection. Titrations of BSA (figure 6a) were experimentally conducted and analyzed according to the Langmuir theory (Langmuir, 1917). The obtained dissociation constant of K_D=(7.2±2.6) × 10⁻⁶ M compares well to values estimated by other groups with a comparable setup (Ohno et al., 2009), measured on different semiconducting materials (Khan et al., 2010, 2011) or reported in the literature as average results (Talmage, 1957).

The binding constants k_on (supplemental information) were calculated separately for each concentration’s observed kinetic constant and found to be independent of target concentration which points to a true Langmuir behavior. The desorption constant k_off was obtained directly from the kinetic measurements as well as from the linear fit in figure 6b. Binding site saturation was observed above a BSA concentration of 25μM (figure 6c). The limit of detection was found to be better than 1nM (66ng/mL, see inset in figure 6a), but still having a Signal-to-Noise Ratio of well above 10, so even lower concentrations could be detected. This result corresponds to the average limits of detection by other methods (Prasad et al., 2013).

4. Conclusion

This evaluation of the presented rGO-FETs demonstrates that the ion strength and pH dependence of the response signals is linear, characterizes the shift of charge carrier type with pH and shows that the experimental results are in agreement with the developed mathematical formulation. It is shown that the downside of random flake distribution using wet-chemically synthesized graphene is statistically balanced by the use of long Source-Drain channel, and yields good reproducibility of the FETs. The response dependence to Debye length is investigated and renders the Debye length as a working parameter rather than a limiting factor. Comparable detection of BSA yield similar binding constants like detection methods from literature (K_D=7.2×10⁻⁶ M). The aim for future measurements is the detection of toxins from real-life food samples, using a passivation layer and array measurements of several comparable rGO-FETs.