Contribution of inhibitory mechanisms to direction selectivity and response normalization in macaque middle temporal area

Abstract

Inhibitory mechanisms contribute to directional tuning in primary visual cortex, and it has been suggested that, in the primate brain, the middle temporal area (MT) inherits most of its directional information from primary visual cortex (V1). To test the validity of this hierarchical scheme, we investigated whether directional tuning in MT was present upon blockade of local γ-aminobutyratergic (GABAergic) inhibitory mechanisms. Direction selectivity during the initial 50 ms after response onset was abolished in many MT cells when the local inhibitory network was inactivated whereas direction selectivity in later response periods was largely unaffected. Thus, direction selectivity during early response periods is often generated autonomously within MT whereas direction selectivity during later response periods is either inherited from other visual areas or locally mediated by mechanisms other than γ-aminobutyric acid type A receptor (GABA_A) inhibition. GABAergic inhibition may also mediate contrast normalization. Our data suggest that GABA_A inhibition implements a local direction-selective static nonlinearity, rather than a full normalization in MT. These findings put constraints on strict hierarchical models according to which MT performs more complex computations based on local motion measurements provided by earlier areas, arguing for more distributed and independent information processing.

Visual motion processing has been the subject of intense research over the past decades (1-10). In primates, directional motion selectivity in the geniculo-cortical system occurs first in primary visual cortex (V1) (e.g., see ref. 11). Direction selectivity is just one of the various specific operations performed by V1. Due to these “simple” but specific operations, it has been suggested “to think of V1 as a vast clearing house that dispatches specific preliminary analyses of the visual scene to the various extrastriate areas” (12, 13). Motion information should thus be dispatched to the middle temporal area (MT), the main hub for the analysis of direction of motion (14-16). Although MT is not entirely dependent on input from V1, overall responsiveness and direction selectivity are greatly reduced after inactivation of V1 (10, 17). Moreover, anatomical (18) and electrophysiological data (13) support the idea that MT depends heavily upon directional information from V1, V2, and V3. MT is thought to perform more complex computations based on local motion primitives supplied by earlier areas, rather than generating directional information de novo, in line with the idea of a hierarchical motion processing system. Although it is beyond doubt that many MT cells perform more complex operations on motion signals than V1 neurons (e.g., see refs. 19-21), the possibility remains that a subset of MT neurons perform very basic motion operations in parallel and in collaboration with V1 and other areas neurons. We tested this possibility by reducing local inhibition within MT. Inhibition substantially contributes to the generation of direction selectivity in V1 (3, 4, 6-9). We hypothesized that MT direction selectivity should be largely unaffected by removal/reduction of inhibition, if inherited from earlier areas, whereas direction selectivity should be substantially reduced if generated de novo within MT.

Methods

General. All experiments were approved by the local ethics committee and carried out in accordance with the European Communities Council Directive 1986 (86/609/EEC) and the National Institutes of Health guidelines for care and use of animals for experimental procedures. A total of 66 direction-selective neurons were recorded from MT in three anesthetized and paralyzed macaque monkeys (for details, see ref. 22).

Visual Stimulation. Initially, the receptive field (RF) of each neuron was mapped. Thereafter, direction selectivity was determined by presenting sine wave gratings (4 Hz, 0.5 cycles per degree, on a cathode ray tube at 800 × 600 pixels at 75 Hz) moving along eight different directions within a square (cell set 1) or circular aperture (cell set 2). RFs were mapped by moving a bar across the screen and determining the borders beyond which no response could be elicited. The size of the aperture was then adjusted to these RFs. For cell set 2, we additionally presented annuli of various sizes to determine the size of the annular RF, a measure of the spatial area within which a neuron pools excitatory inputs (23). For all our cells from set 2, the aperture was smaller than the annular RF, i.e., the stimulus did not encroach into the RF surround. For the first 300 ms of each trial, the screen was homogenously gray (20 cd/m²); thereafter, the moving stimulus was presented with a sudden stimulus onset. Stimulus presentation and data acquisition were under the control of REC2 (written by A.T.) or CORTEX 5.95 (www.cortex.salk.edu).

Recordings and Application of Bicuculline-Methiodide (BMI). Recordings were performed with tungsten in glass microelectrodes centered in a micropipette with a filament. The electrode tip protruded from the micropipette by ≈20 μm. Micropipette opening area was ≈7-10 μm² (impedance of 10-30 MΩ). Micropipettes were filled with BMI (5 mM BMI in 165 mM NaCl adjusted to pH 3.0 with HCl) (Sigma). BMI was iontophoretically applied with ejection currents of +40 nA (NeuroPhore BH-2, Digitimer, Welwyn Garden City, Hertfordshire, England). Retention currents during control and recovery were -100 nA. We did not apply compensation currents but routinely checked for current effects on firing rates by carefully monitoring the onset and offset of firing rate changes after switching between retention and ejection currents. We never observed instant activity changes; in all cases, the effects evolved slowly (>30 s) over time, arguing against the possibility that current application were responsible for the observed effects. We initially recorded the neuronal activity in the absence of BMI, followed by one to three recordings in the presence of BMI, followed by one to two recordings after a 3- to 10-min recovery period.

Data Analysis. We determined the preferred direction (PD) of motion for each neuron within a time period of 50-700 ms after stimulus onset, and the activity for motion in the antipreferred direction (the direction of motion opposite to the PD), and calculated the direction index [DI = 1 - (activity in antipreferred direction)/(activity in preferred direction), baseline activity subtracted]. We included only neurons with a DI ≥ 0.5 for further analysis. We then determined neuronal latency at a resolution of 5 ms for motion in PD in the presence and absence of BMI (for details, see ref. 24). The latencies were well correlated (r = 0.795), but there was a significant trend for latencies in the presence of BMI to be shorter (median without BMI, 50 ms; median with BMI, 45 ms, P = 0.023, signed rank test). The time-resolved DI was calculated in windows of 0-50 ms, 50-200 ms, and 200-700 ms after response onset (latency) in the absence of BMI. As a control we also calculated the time-resolved DI from the response onset for the responses in the absence of BMI and from the response onset for the responses in the presence of BMI, which did not affect any of the results reported here.

For those cells for which we recorded the directional tuning at different contrast level, we fitted each response associated with a certain direction of motion (PD, 45° off PD, etc.) with the following Naka-Rushton formula:

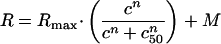1

where R is the response as a function of contrast, R_max is the response at 100% contrast, c₅₀ is the contrast at which the half maximal response is reached, n corresponds to the slope of the contrast response function, and M corresponds to the maintained activity.

Histology. At the end of the experiments, the animals were killed with an overdose of pentobarbital and perfused through the heart, and the tissue was prepared for standard histological procedures (22). In short, 50 μm of parasagittal sections were cut on a microtome and stained for Nissl, Klüver-Barrera, neutral red, or myelin, respectively. Penetration tracks and recording sites were reconstructed from serial sections in relation to microlesions made during the experiments at certain positions and the penetration scheme. All neurons reported in this study were within MT.

Results and Discussion

We recorded MT responses to sine-wave gratings moving in eight different directions under control conditions and when BMI was iontophoretically applied near the recorded neuron. BMI blocks the γ-aminobutyric acid type A receptor (GABA_A), thereby reducing intraarea inhibition. We recorded a total of 49 direction-selective neurons in MT of two anesthetized and paralyzed monkeys at high luminance contrast (100% Michelson contrast), and a further 17 direction-selective cells at a variety of luminance contrasts in a third animal (see Methods for details). For all 66 cells, we found a significant effect of BMI application on spontaneous and/or stimulus-induced firing rate (P < 0.05, t test corrected for multiple comparisons), which returned to baseline after recovery.

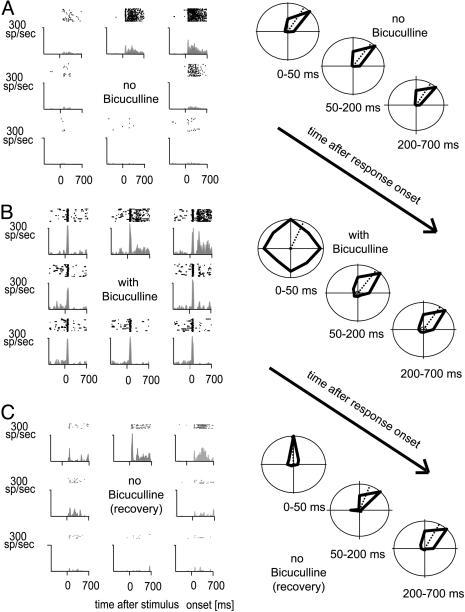
Application of BMI resulted in increased stimulus-driven activity, often associated with increased spontaneous activity. Fig. 1 shows an example of increased activity during BMI application. Fig. 1A shows the activity during initial determination of direction selectivity. The neuron preferred motion to the upper right. A time-resolved analysis of its motion preference is shown in Fig. 1A Right. It shows the mean activity as a function of direction of motion, calculated over the periods of 0-50, 50-200, and 200-700 ms after response onset (response onset for each neuron corresponds to the latency associated with motion in PD; see Methods). During all time periods, the neuron was highly direction selective. When BMI (Fig. 1B) was applied, a transient initial response occurred for all directions of motion, rendering the early response period unselective. Later parts of the response, however, remained tuned for motion direction, similar to tuning in the absence of BMI (Fig. 1B Right). Fig. 1C shows the neuronal activity of the neuron after recovery from BMI application. The neuron fully recovered its direction selectivity during the early transient response.

Fig. 1.

Single-cell raster plots and histograms as a function of direction of motion and presence or absence of BMI. (A) Neuronal activity before application of BMI. (B) Neuronal activity during application of BMI. (C) Neuronal activity after 3 min of recovery. (Right) Mean activity (thick black lines) for three time periods after response onset. Dashed lines indicate the preferred direction calculated from the mean activities. Directional tuning in the presence of BMI was substantially decreased during the early-response period.

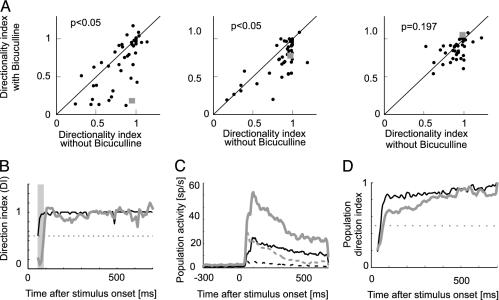
To quantify the effect of BMI application across the population of cells, we calculated the DI (see Methods) as a function of time in the absence and presence of BMI. The DI values are plotted in Fig. 2A. As a reference, the DI for the neuron from Fig. 1 is indicated by a square symbol. Many neurons were substantially less well tuned for direction of motion during the early response phases in the presence of BMI (0-50 ms and 50-200 ms, P < 0.01, signed rank test) whereas this difference was not significant during late response periods (200-700 ms, P = 0.119). To get a more detailed impression of the evolution of DI over time, Fig. 2B shows the DI for the neuron from Fig. 1 at a resolution of 10 ms for the control and BMI condition. DIs are dependent on the preferred direction of motion rate, the antipreferred direction of motion rate, and the maintained activity. Fig. 2C shows these population activities (n = 49 neurons measured at 100% contrast) in the absence and presence of BMI. Maintained, preferred, and antipreferred activities were increased in the presence of BMI compared with baseline level, with the largest increase occurring for the antipreferred direction, thereby reducing the neurons' direction selectivity. This reduction is evident from Fig. 2D, which plots a time-resolved DI for the population response in the presence and absence of BMI. These findings imply that, in a subset of neurons, directional tuning during the early response period is substantially shaped by inhibition mediated through GABA_A from within MT whereas, during late-response periods, either afferent inputs supply the directional information or inhibitory mechanisms other than GABA_A participate in its generation (25). This finding contradicts a strictly hierarchical view in which directional tuning is simply inherited from earlier stages (13) and where MT neurons perform more complex and global computations about object and/or ego-motion (13, 26).

Fig. 2.

DI as a function of time. (A) DI for neurons recorded at 100% luminance contrast (n = 49) during three response periods [0-50 ms (Left), 50-200 ms (Center), and 200-700 ms (Right)] in the presence and absence of BMI. For a large fraction of neurons, the early responses were nondirectional (or only slightly directional) in the presence of BMI. Late-response periods were substantially less affected. P values show the significance of the effects of BMI application (signed rank test). ▪, DI as a function of time and BMI for the neuron shown in Fig. 1. (B) Time-resolved directional tuning for Fig. 1 neuron represented by the square in A. DI was calculated over 10-ms bins from response onset (60 ms after stimulus onset) when BMI was absent (black line) and when BMI was present (gray line). Gray bar, time period for which responses were direction selective when BMI was absent, but non-direction-selective when BMI was applied (30 ms). The horizontal line indicates DI values of 0.5, generally taken as the cutoff to classify neurons as direction selective. (C) Population activity in the presence (gray curves) and absence (black curves) of BMI for motion in preferred (solid lines) and antipreferred (dashed lines) direction of motion. (D) Time-resolved population DI in the presence (gray line) and absence (black line) of BMI, calculated from the data in C.

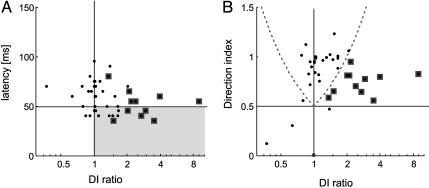
We were interested to determine which neurons exhibited the lack of directional tuning during the early-response period when inhibition was reduced due to BMI application. These might be neurons with a short latency, i.e., neurons relatively upstream in the hierarchy, or neurons further downstream exhibiting a longer latency. If the former were true, MT might generate directional tuning initially on its own, potentially feeding this information back to earlier areas for amplification or refinement (27, 28), in addition to fast basic feature processing to be dispatched to higher areas. Fig. 3A shows the GABA_A-mediated directionality (DI_noBMI/DI_BMI; for brevity called DI ratio) as a function of neuronal latency. The large majority of neurons with latencies ≤ 50 ms (81.8%) showed evidence of GABA_A-mediated directionality, i.e., DI ratios were >1. However, this behavior was not restricted to neurons with short latencies. In most neurons (79.1%) with longer latencies (>50 ms), GABA_A inhibition also strongly shaped directional tuning during the early response period, which means either that even delayed input to MT is nondirectional or that MT cells pool activity from neurons with a range of preferred directions. DI ratios >1 could occur if the early-response period was only weakly biased for direction of motion in the absence of BMI whereas it was almost completely nondirectional with BMI present. Then, inhibition in MT would play only a minor role in mediating directional tuning. If, however, directional tuning in MT in the absence of BMI during the early response period was strong, the role of inhibition in the generation of directional tuning is more substantial. We therefore plotted the DI of the early-response period in the absence of BMI vs. the GABA_A-mediated directionality (DI ratio) in Fig. 3B. It shows that most neurons with moderate and large DI ratios (>1.0) exhibit substantial directional tuning from response onset on, i.e., a substantial proportion of MT neurons initially receive nondirectional (or only weakly directionally biased) input, with fast acting inhibition within area MT rendering the early responses direction selective. Alternatively, MT neurons might pool direction-selective inputs from a wide range of PDs (rather than from nondirectional inputs), and internal inhibitory mechanisms within MT regenerate direction selectivity from the full range of direction-selective inputs.

Fig. 3.

Change of directionality as a function of neuronal latency. (A) Ratio of direction index (DI_noBMI/DI_BMI) for the early-response period as a function of neuronal latency. Data points within the gray box correspond to short latency neurons with reduced directionality during the early response in the presence of BMI. (B) Ratio of direction index for the early-response period as a function of DI in the absence of BMI. Data points within the borders of the curved dashed lines correspond to neurons that were direction selective in the absence and presence of BMI. Data points outside these dashed lines indicate that neurons were either direction selective (DI > 0.5) in the absence, but not in the presence of BMI (right hand dashed curve, n = 11, symbols surrounded by squares), or neurons whose initial responses were direction selective only in the presence of BMI (left hand dashed curve, n = 1). Data points falling below the dotted horizontal line represent neurons that were not direction selective during the early response period.

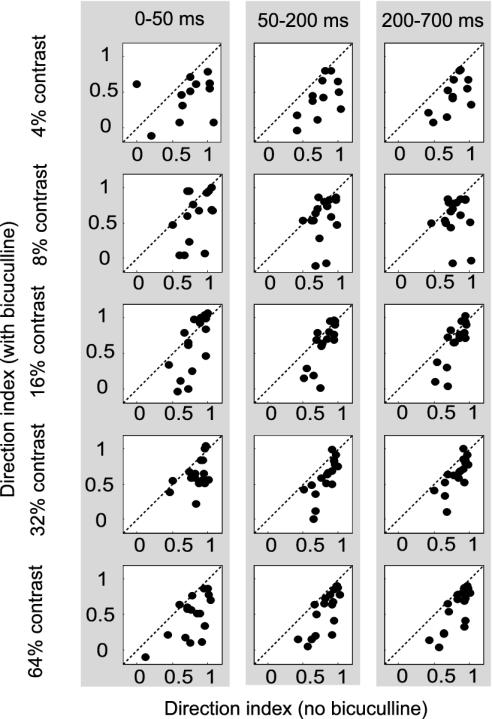
A less interesting explanation for the lack of direction selectivity during the early response is response saturation with motion in PDs due to disinhibition. Disinhibition would increase responses to all directions of motion. Due to limitations of a neurons' maximum firing rate, responses in PD would seem to be less increased than responses in an antipreferred direction. If true, early responses 45° off the PD should also saturate upon BMI application (because these stimuli elicit high firing rates in the absence of BMI), i.e., reach the same level as responses in PD. Almost all our neurons exhibited a stronger response to motion in PD than to motion 45° off PD after BMI application, arguing against an explanation based on response saturation. We calculated the ratio of the response with motion in PD and the motion 45° off the PD (the average between the two directions that were 45° off the PD) for the first 50 ms of the response. A ratio of 1 indicates that both responses were identical, which, in the presence of BMI, might signal response saturation. In the absence of BMI, the average ratio was 0.42 ± 0.28. In the presence of BMI, this ratio slightly increased (0.57 ± 0.44), but it was still significantly different from 1 (P < 0.001, t test). To further validate that the reduced DIs were not due to response saturation, we recorded an additional 17 direction-selective cells in one monkey at five luminance contrasts (4%, 8%, 16%, 32%, and 64%). Responses at low and medium luminance contrast were smaller than at high luminance contrast during all response periods even in the presence of BMI for all cells investigated, ensuring that BMI-induced changes to DI at low and medium luminance contrast were not due to response saturation. DIs as a function of contrast and BMI application are plotted in Fig. 4. The three columns show DIs for the three time periods (0-50, 50-200, and 200-700 ms after response onset). DIs were significantly reduced in the presence of BMI at all contrast levels and during all, even the late, response periods (P < 0.05, signed rank test), which differs from the sample presented above (Fig. 2A). The difference is likely due to different cell samples and the fact that our initial sample was measured at 100% luminance contrast whereas the maximum contrast presented to cell set 2 was 64%. More importantly, DIs increased from early- to late-response periods at all luminance contrasts, which replicates the findings from our first cell sample measured at 100% contrast. Details about the average DI as a function of luminance contrast and response period in the presence and absence of BMI are given in table 1. These additional data also demonstrate that our finding of reduced DIs in the presence of BMI cannot be explained by response saturation.

Fig. 4.

DI for neurons measured at 4%, 8%, 16%, 32%, and 64% luminance contrast (top to bottom) during three response periods. Application of BMI had a significant influence on DI at all luminance contrasts and in all response periods (P < 0.05, signed rank test); however, average DIs slightly increased for later response periods when BMI was externally applied.

Table 1. DI as a function of BMI application, stimulus contrast, and time after stimulus onset.

	DI no BMI			DI BMI
Contrast, %	0-50 ms	50-200 ms	200-700 ms	0-50 ms	50-200 ms	200-700 ms
4	0.71 ± 0.33	0.76 ± 0.21	0.78 ± 0.19	0.44 ± 0.28	0.48 ± 0.27	0.47 ± 0.25
8	0.85 ± 0.17	0.79 ± 0.15	0.79 ± 0.15	0.49 ± 0.45	0.51 ± 0.36	0.59 ± 0.28
16	0.79 ± 0.16	0.79 ± 0.14	0.79 ± 0.15	0.54 ± 0.62	0.57 ± 0.38	0.60 ± 0.37
32	0.84 ± 0.16	0.89 ± 0.14	0.89 ± 0.14	0.57 ± 0.31	0.59 ± 0.27	0.64 ± 0.22
64	0.78 ± 0.23	0.81 ± 0.17	0.82 ± 0.17	0.46 ± 0.30	0.54 ± 0.29	0.57 ± 0.29

DI were largely independent of stimulus contrast and time after stimulus onset in the absence of BMI. BMI had significant effects on DI during all response periods.

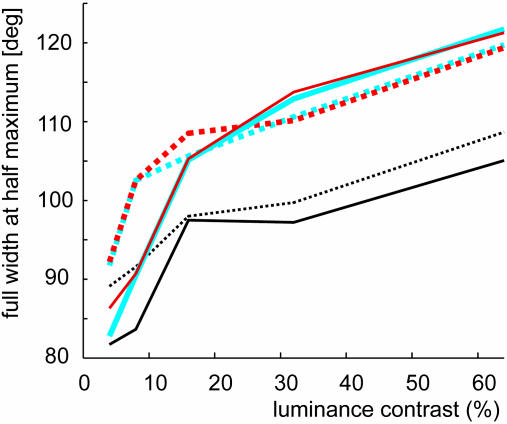
The DI is a parameter that takes into account only the responses in preferred and antipreferred directions and that is additionally influenced by the ongoing activity. A parameter that is uninfluenced by ongoing activity and takes responses to all directions of motion into account is the tuning width when assessed by fitting a Gaussian to the population response. We determined the tuning width by measuring full width at half maximum (FWHM). FWHM was analyzed for both sets of cells as a function of response time and as a function of luminance contrast (the latter for cell set 2 only). For cell set 1 (100% luminance contrast), FWHM was wider in the presence of BMI application during the early response period (FWHM no BMI, 72.87°; FWHM BMI, 85.65°), as well as during the late-response periods, although the difference was reduced (FWHM_noBMI, 84.18°; FWHM_BMI, 85.84°). For cell set 2 (various luminance contrasts), the tuning width during the early responses was always wider in the presence of BMI (Fig. 5, solid vs. dashed lines). Interestingly, tuning width increased with increasing luminance contrast in the absence and presence of BMI, which is contrary to predictions made by recent psychophysical findings (29). During the later response periods, tuning width also increased with increasing contrast (Fig. 5, blue and red curves). For these response periods, BMI affected tuning width mostly at low luminance contrast whereas tuning width was in effect slightly reduced at high contrast in the presence of BMI. Increase in tuning width could be due to response saturation at high contrast. However, because BMI increased a neurons' firing at all luminance contrasts, responses in the absence of BMI were not saturated but were suppressed by inhibition. Release of this inhibition might now cause response saturation and increase the tuning width differences between low and high-contrast stimulation, particularly during the initial transient of a neuron's response. Although tuning width of the initial response period was increased by reduction of local inhibition, the tuning width difference between low and high contrast did not increase upon BMI application (Fig. 5). This finding argues against response saturation in MT as an explanation for increasing tuning width with increasing contrast.

Fig. 5.

Tuning width as a function of BMI application, luminance contrast, and time after response onset. Solid lines show the tuning width (FWHM) of the population responses (fitted with a Gaussian) for the first 50 ms after response onset (black lines), for the response period from 50-150 ms after response onset (red lines), and the response period from 150-700 ms after response onset (blue lines). The corresponding dotted lines show the tuning width when BMI was applied.

Our interference with inhibition may also have affected cortical gain control mechanisms, namely response normalization. Contrast normalization may mediate tuning invariance under changing illumination conditions (30-32), possibly through γ-aminobutyratergic (GABAergic) mechanisms (33) or synaptic depression (34). To investigate the effect of BMI on contrast normalization, we fitted a Naka-Rushton equation (χ² fitting, all data yielded acceptable fits, P > 0.2, see Methods and ref. 35) to each cell's contrast-response function for each direction of motion. These fits yielded for each cell and direction of motion an estimate of the maximal response (R_max), an estimate of the contrast that yields half-maximum responses (c₅₀), and the slope of the contrast-response function (n). Contrast normalization predicts that R_max changes with direction of motion whereas half-maximal response (c₅₀) remains constant. Reducing contrast normalization (by reduction of inhibition through BMI application) should increase the response gain (R_max) and decrease the slope of the contrast-response function (n), while leaving the contrast gain (c₅₀) unaffected if a normalization stage was implemented in MT. We found, indeed, that R_max significantly increased during the three response periods for all directions of motion with BMI applied [P < 0.001, two-factor repeated measurement (RM) ANOVA on ranks; factor A, BMI treatment; factor B, motion direction] and that the slope of the contrast response function (n) became significantly shallower in the presence of BMI (P < 0.05, two-factor RM ANOVA on ranks), whereas c₅₀ did not differ significantly with BMI absent or present (P = 0.28, two-factor RM ANOVA on ranks). This finding shows that contrast normalization is locally mediated by GABAergic mechanisms also in MT, not just in early visual areas (33, 36). However, we found that R_max, c₅₀, and n also changed significantly with direction of motion. Standard normalization models (30-32) predict that c₅₀ should be identical for all directions of motion whereas we found c₅₀s to be largest for the direction 135° and 90° off the PD (P < 0.001, two-factor RM ANOVA on ranks). This finding was the case for all response periods and was independent of BMI application. A similar result was found for the slope of the response function, but here the steepest slopes occurred for the antipreferred direction, with slopes decreasing as direction of motion approached the PD (P < 0.001, two-factor RM ANOVA on ranks). Could these variations in c₅₀ be described by changes in the slope n or by a combination of changes? We fitted each neuron's contrast-response functions such that c₅₀ could vary for each direction of motion whereas the fits for all directions were constrained to have the same slope (the slope could be different for BMI present and absent). With these constraints, c₅₀ still changed significantly with direction of motion (P < 0.01, two-factor RM ANOVA on ranks) for all three response periods. The slope was significantly affected by BMI application, but c₅₀ was affected by BMI application only in the late-response period (200-700 ms). Thus, changes in c₅₀ with direction of motion cannot be accounted for by changes in the slope. Constraining the fits such that c₅₀ was forced to be identical for all directions of motions, however, affected the slope. With these fitting constraints, slopes were no longer affected by direction of motion (P = 0.128, response period 0-50 ms; P = 0.874, response period 50-200 ms; P = 0.510, late-response period) whereas a trend for shallower slopes in the presence of BMI remained although it did not reach significance (P < 0.1, all three response periods). The latter suggests that changes in slope can somewhat be accounted for by changes in c₅₀ whereas the opposite was not found. The high values for c₅₀ we found for off-directions might reflect the V1 input whereas extensive pooling performed by MT neurons may increase contrast sensitivity. This result would imply an additional local normalization stage in MT restricted to a direction column, i.e., representing a local static nonlinearity rather than a full normalization, a finding somewhat contrary to previous reports arguing against such a local mechanism (37).

Intracellular studies investigating the contribution of off-preferred axis inhibition to orientation and directional tuning in V1 have remained somewhat controversial (3, 38). Jagadeesh et al. (38) argue that direction selectivity in V1 simple cells is entirely determined by feed-forward input from nondirectional lateral geniculate nucleus cells, with a threshold nonlinearity generating the directionally selective spike outputs. BMI could disrupt the threshold nonlinearity by decreasing the membrane potential (and changing membrane conductance) such that previously subthreshold inputs generate spiking outputs. However, such a scenario cannot easily account for our finding of direction-selective responses after the initial transient or the reduction of direction selectivity at low-luminance contrast. Moreover, a recent comprehensive intracellular study (39) found evidence for contributions of off-axis inhibition to tuning properties of V1 cells. It is interesting to note that BMI mostly affected the early-response period whereas later periods show stronger directionality, even in the presence of BMI. A study on the contribution of GABA_A vs. GABA_B in shaping tuning functions has demonstrated that GABA_A mostly influence the early-response component whereas the sustained response is mostly affected by GABA_B (25). Based on these findings, it is tempting to speculate that neurons that are nondirectional during their early-response period in the presence of BMI (a GABA_A antagonist) might not regain their directionality during later response periods if baclofen (a GABA_B antagonist) was also applied. This scenario would imply that a proportion of MT neurons receive afferent directional input (those that show no changes in directionality when BMI was applied) whereas other MT neurons generate direction selectivity de novo by means of two inhibitory mechanisms. Alternatively, a subset of MT neurons might increase the selectivity of the afferent input through inhibition during the early-response period and feed that signal back to early areas, in a reiterative feedback loop to enhance stimulus selectivity by enhancing selectivity of afferent input.

Our data confirm previous results demonstrating that inhibition is an important contributor to directional tuning (3, 7, 9). It has previously been thought that most of MT's input is highly direction selective (12, 13, 26). We demonstrate that MT neurons also receive nondirectional input (or pool from a variety of cells with different PD), and subsets of MT cells generate direction selectivity de novo. These cells might possibly receive their input by means of a fast collicular-thalamic route (10, 17, 40, 41), or through nondirectional input from V1 and V2. This result allows for the possibility that feedback from area MT aids in the generation of direction selectivity in early areas through back projections (27, 28) and would put important constraints on a strictly hierarchical scheme of cortical processing.