A modified classification tree method for personalized medicine decisions

Abstract

The tree-based methodology has been widely applied to identify predictors of health outcomes in medical studies. However, the classical tree-based approaches do not pay particular attention to treatment assignment and thus do not consider prediction in the context of treatment received. In recent years, attention has been shifting from average treatment effects to identifying moderators of treatment response, and tree-based approaches to identify subgroups of subjects with enhanced treatment responses are emerging. In this study, we extend and present modifications to one of these approaches (Zhang et al., 2010 [29]) to efficiently identify subgroups of subjects who respond more favorably to one treatment than another based on their baseline characteristics. We extend the algorithm by incorporating an automatic pruning step and propose a measure for assessment of the predictive performance of the constructed tree. We evaluate the proposed method through a simulation study and illustrate the approach using a data set from a clinical trial of treatments for alcohol dependence. This simple and efficient statistical tool can be used for developing algorithms for clinical decision making and personalized treatment for patients based on their characteristics.

1. INTRODUCTION

The ultimate goal of personalized medicine is selecting and tailoring treatments for specific patients so that the best possible outcome can be achieved. With an ever increasing number of possible predictors of good response including genetic and other biomarkers, and many treatment options, the task of identifying an optimum treatment is daunting. This process is further complicated because most clinical trials focus on average treatment effects and investigate potential moderators one at a time [16]. For example, the primary analysis of the COMBINE Study (the largest clinical trial of treatments for alcohol dependence in the USA [1]) found a significant main effect of one of the considered pharmacological treatments (naltrexone) but not of the other (acamprosate). To date, however, only individual moderators of treatment effects have been considered in COMBINE (e.g. [2]) and “unsupervised” learning methods have been applied [3]. As an alternative to this approach, a systematic search of the large number of collected data on baseline predictors in order to identify subgroups with differential treatment effects would be valuable.

Methods based on recursive partitioning such as Classification and Regression Trees [4, 28] provide a tool of simultaneous consideration of a large number of potential predictors and identification of combinations of patient characteristics associated with good outcome. Classical CART methods focus on predictors of good outcome. We previously used classical tree-based approaches to identify predictors of good outcome regardless of treatment in COMBINE [12]. For the purposes of personalized medicine, however, identifying for whom a particular treatment may be more effective than another treatment is of particular interest. This is the goal of recent developments both in tree methods (e.g. [29, 9]) and in approaches for individualized treatment rules [25, 30, 14]. The motivation for the current study was to develop and apply a modified tree-based approach that would allow us to guide selection of the best treatment for a particular individual based on baseline characteristics.

Tree-based methods originated with the development of automatic interaction detection (AID) algorithms by Morgan and Sonquist [22], Morgan and Messenger [21] and Kass [15]. CART methods were formalized by Breiman and colleagues [4]. Modern developments include deterministic and random forests [5, 28] and take full advantage of the computational power available today.

Using classical recursive partitioning methods, tree based methods divide the study sample recursively into subgroups that are most homogeneous with respect to the outcome and most distinct from one another. All predictors and all possible cutoffs for splitting on each predictor are considered. Different versions of the algorithm incorporate different statistical criteria for splitting the sample and determining the optimal size of the tree.

Tree-based methods are appealing alternatives to standard linear model techniques when assumptions of additivity of the effects of explanatory variables, normality and linearity are untenable. Tree-based and forest-based methods are nonparametric, computationally intensive algorithms that can be applied to large data sets and are resistant to outliers. They allow consideration of a large pool of predictor variables and can discover predictors that even experienced investigators may have overlooked. These methods are most useful for identification of variable interactions and may be easier to use in clinical settings because they require evaluation of simple decision rules rather than mathematical equations [28].

Modifications of decision trees proposed in recent years allow identification of subgroups of subjects for whom there are significant differences in effectiveness of treatments and vary in the type of outcomes they can be used to predict. The approaches proposed by Zhang et al. [29] and Foster et al. [9] focus on binary outcomes, Su et al. [26], Dusseldorp et al. [6] and Dusseldorp and Van Mechelen [7] develop interaction tree methods for continuous outcomes, and the approaches of Negassa et al. [23] and Loh et al. [19] are appropriate for censored continuous outcomes. The SIDES and SIDESscreen approaches [17, 18] can be used with either binary or continuous outcomes.

Approaches also vary by whether they focus on identification of treatment-covariate interactions or on identification of subgroups of patients with enhanced treatment effect (i.e. subgroups for which one treatment is significantly better than a control treatment). Treatment-covariate interactions can be restricted to be qualitative (i.e. in different subgroups different treatments are more beneficial or there may be subgroups where the two treatments are approximately equivalent, [7]) or unrestricted (i.e. both quantitative and qualitative interactions can be identified, e.g. [27]). Approaches that identify subgroups with enhanced treatment effect can build complete trees (e.g. [9]) and thus completely partition the sample space, or can focus on identification of subgroups for whom the treatment effect is most significant (e.g. [17, 18]) and hence provide only a partial partition of the sample space.

Most of the proposed approaches rely on modifying the splitting criterion to build trees for identification of moderator effects, however some (e.g. the Virtual Twin method of Foster et al. [9]) use a modified outcome variable. The Virtual Twin method relies on classical tree-building and pruning methods but uses the estimated causal treatment effect (i.e. the estimated difference between the outcome on the actual and counterfactual treatment for each subject) as the dependent variable.

In this manuscript, we chose to focus on the approach of Zhang et al. [29] because it provides clear tree structures on the original outcome, can handle different types of predictors (binary, nominal, ordered categorical, continuous) and can be easily automated. This method uses a modified splitting criterion based on comparing the difference in treatment effectiveness for subjects in a particular node of the tree to the corresponding differences in the potential daughter nodes. The original publication of this method [29] was not targeted to a statistical audience so herein we explain the method in more detail. Also, in the originally proposed method, pruning is done manually so that daughter nodes that favor the same treatment are combined. Herein, we extend the approach to incorporate an automatic pruning step and propose a measure of the algorithm’s predictive performance. We evaluate the algorithm and the performance measure via a simulation study and apply the methods to the data from the COMBINE Study. We also compare our method to the Virtual Twin approach of Foster et al. [9] in terms of final trees produced, classification accuracy and expected reward. R code for fitting the models is available from the authors.

2. METHODS

2.1 Notation

Consider a study with the following data design: (Y_i, T_i, X_i), i = 1, …, N, where i denotes the subject, Y_i denotes a binary outcome of interest for subject i, T_i denotes treatment assignment for subject i (either treatment A or B), and X_i = (X_i1, …, X_ip) denotes a vector of potential categorical or continuous predictors for subject i.

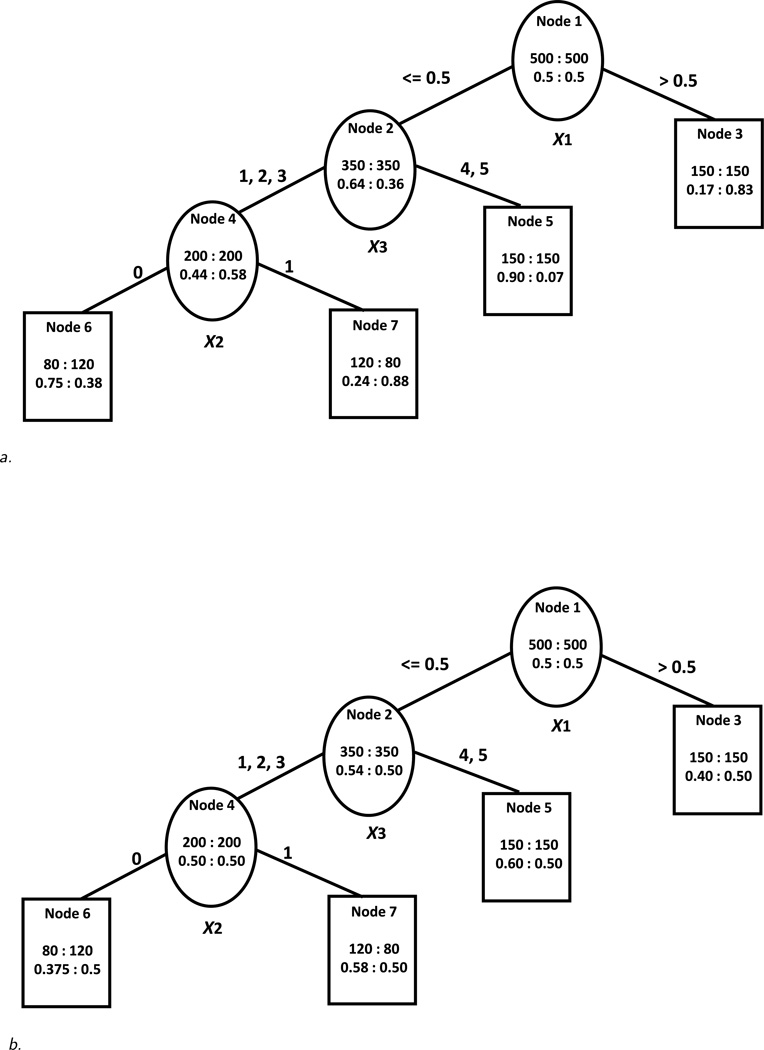
A binary tree structure is shown in Figure 1a and will be used for illustration. The tree is composed of a root node (Node 1), internal nodes denoted by ovals, and terminal nodes denoted by rectangles. The root node contains all the observations in the sample. Each internal node has two offspring (daughter) nodes. Terminal nodes do not have offspring nodes. For a tree with k layers, there are at most 2^k−1 terminal nodes.

Figure 1.

a. Tree structure for the scenario with sizeable treatment-covariate interactions. Within each node, the top number represents a total number of subjects in treatment group A:B and the bottom number stands for a percentage of subjects in A:B who have a response. The splitting variable is shown underneath each internal node. The splitting value or category is shown above the solid line connecting the parent node to the left or right daughter node.

b. Tree structure for the scenario with small treatment-covariate interactions. Within each node, the top number represents a total number of subjects in treatment group A:B and the bottom number stands for a percentage of subjects in A:B who have a response. The splitting variable is shown underneath each internal node. The splitting value or category is shown above the solid line connecting the parent node to the left or right daughter node.

Tree building proceeds in two steps: tree growing and tree pruning. An initial large tree is built recursively starting with the root node. For each internal node of the tree, the best splitting variable and cutoff on this variable is selected according to a statistical criterion based on differential treatment effectiveness as described below. The initial large tree is built by making all possible splits according to the splitting criterion within the limits imposed by the stopping criterion. Tree pruning is then performed from the bottom-up so that sibling nodes with similar treatment effects are combined.

2.2 Building an initial large tree

To build an initial large tree, we start with the root node of the tree containing the entire sample of subjects. The number of subjects and the response rates on each treatment (A on the left, B on the right) are shown in the top and bottom part of the root node respectively. In the root node in Figure 1a there are 500 subjects on treatment A and 500 on treatment B and the proportions of subjects with good outcome on both treatments are 0.5. We seek to split the sample in two parts with most differing treatment effects. To do this we calculate the squared difference in the response rates on the two treatments in the node (t) that we are seeking to split:

$$\mathit{\text{DIFF}}(t)={(\mathit{\text{Pr}}(Y=1|T=A,t)-\mathit{\text{Pr}}(Y=1|T=B,t))}^2$$

and compare it to the weighted sum of the corresponding difference measure of the two potential daughter nodes t_s, s = L, R, respectively:

$$\mathit{\text{DIFF}}(t_L,t_R)={(n_L+n_R)}^{-1}.$$

$$\sum _{s=\{L,R\}}\left[n_s{(\mathit{\text{Pr}}(Y=1|T=A,t_s)-\mathit{\text{Pr}}(Y=1|T=B,t_s))}^2\right].$$

Here t_L and t_R denote left and right daughter nodes, while n_L and n_R are the number of subjects in the left and right daughter nodes, respectively.

We split only when the offspring nodes provide a larger difference between the effects of the two treatments compared to their parent node, that is, when

$$\mathit{\text{DIFF}}(t_L,t_R)>\mathit{\text{DIFF}}(t).$$ (1)

To decide which variable to split on and what cutoff to select, we consider all predictor variables and all possible splits on these variables. For continuous predictor variables with k distinct levels or ordinal predictor variables with k levels, there are k − 1 possible cutoffs that need to be considered for splitting. For binary predictors, there is only one possible split. Nominal categorical variables with k levels require consideration of all 2^k−1 − 1 possible splits so that any grouping of categories per daughter node can be considered. We select the variable and the cutoff with the largest DIFF(t_L, t_R) value and split the sample on this variable and cutoff.

In Figure 1a, X₁ is selected as the best splitting variable of the root node and 0.5 is selected as the best splitting point so that subjects with values less than or equal to the cutoff (350 on each treatment) are placed in the left daughter node and the rest of the subjects (150 on each treatment) are placed in the right daughter node of the root node. While in classical trees the splitting criterion is focused on separating the sample so that subjects in the two daughter nodes differ the most in the proportions with good outcome, in the modified approach, we focus on treatment assignments to identify subgroups of patients who respond more favorably to one treatment than to another. In Figure 1a, a larger proportion of subjects in the left daughter node who receive treatment A have a good outcome compared to subjects who receive treatment B (64% vs. 36%) while the opposite is true in the right daughter node (17% vs. 83%).

After dividing the root node, we proceed recursively by trying to divide each daughter node according to the criterion in (1) until no further splits are possible or a stopping criterion is satisfied. The stopping criterion involves limiting the total number of subjects in each node or the minimum number of subjects per treatment within a node. For example, one might set the minimum number of subjects in the node to be 50, or to have at least 25 subjects in a node on each treatment. The criterion and number of subjects need to be pre-set before growing the tree. We recommend at least 30 subjects per treatment within each node so that the results are more likely to validate internally and/or externally. It is also possible to limit the number of layers in the tree so that overly complicated combinations of variables can be avoided.

2.3 Pruning the tree

Zhang et al. [29] proposed a manual pruning approach so that any pair of terminal offspring nodes is merged if the same treatment is identified as more beneficial in both nodes. In this manuscript, we propose a new automatic pruning approach based on comparing the odds ratios for the association between treatments and outcome in sibling nodes. Let OR_s, s = L, R, denote the odds ratio obtained from the left or right daughter node and let $n_{k1}^s,n_{k2}^s$ be the number of subjects assigned to each treatment (k = 1 for treatment A, and k = 2 for B) in a daughter node s, who don’t have and have the desired outcome (Y_i = 1), respectively. For each set of paired nodes (t_L, t_R), one can compute the odds ratios for the association between treatment and outcome based on the two by two contingency tables as shown in Table 1. A constant (e.g. 0.5) can be added to the cell counts in order to avoid problems with zero counts and to improve performance for small counts as necessary.

Table 1.

Contingency tables and odds ratios obtained from the paired daughter nodes (t_L, t_R)

	Paired daughter nodes
	Left daughter node (tL)		Right daughter node (tR)
	Outcome (Y)		Outcome (Y)
Trt	0	1	0	1
A	$n_{11}^L$	$n_{12}^L$	$n_{11}^R$	$n_{12}^R$
B	$n_{21}^L$	$n_{22}^L$	$n_{21}^R$	$n_{22}^R$
	$O{R}_L=(n_{11}^L{n}_{22}^L)/(n_{21}^L{n}_{12}^L)$		$O{R}_R=(n_{11}^R{n}_{22}^R)/(n_{21}^R{n}_{12}^R)$

Let δ_s = e^θ_s − 1, where θ_s = log OR_s, s = L, R. We consider the following scenarios:

1. The odds ratios of the considered sibling nodes are significantly different from 1 and in the same direction. That is, OR_L and OR_R are either both larger than 1 or both smaller than 1, which implies that δ_Lδ_R > 0.

2. The odds ratios of the considered sibling nodes are significantly different from 1 and in different directions. In this case, either OR_L > 1 and OR_R < 1, or OR_L < 1 and OR_R > 1, so that δ_Lδ_R < 0.

3. The odds ratios of the considered sibling nodes are both not significantly different from 1 and are either in different directions or in the same direction, or at least one of the odds ratios is not significantly different from 1. In this case, δ_Lδ_R ≈ 0.

To decide whether the set of terminal nodes should be pruned, we formulate the following hypothesis test:

$$H_0:{\delta }_L{\delta }_R\ge 0\text{vs}.{\delta }_L{\delta }_R<0.$$

Then by the delta method, the test statistic has the form of

$$Z=\frac{(e^{\widehat{{\theta }_L}}-1)(e^{\widehat{{\theta }_R}}-1)}{\sqrt{\hat{V}(\widehat{{\theta }_L},\widehat{{\theta }_R})}},$$

where $\widehat{{\theta }_s}=\text{log}{n}_{11}^s+\text{log}{n}_{22}^s-\text{log}{n}_{12}^s-\text{log}{n}_{21}^s$, s = L, R, and

$$\hat{V}(\widehat{{\theta }_L},\widehat{{\theta }_R})=e^{2\widehat{{\theta }_L}}{(e^{\widehat{{\theta }_R}}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^L}+e^{2\widehat{{\theta }_R}}{(e^{\widehat{{\theta }_L}}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^R}.$$

The proof provided in Appendix A shows that the test statistic Z asymptotically follows a standard normal distribution. Thus, the decision rule developed for pruning is to prune if Z ≥ −Z_α, where Z_α is the 100 × (1 − α)% percentile of a standard normal distribution. That is, the sibling terminal nodes are pruned if we do not reject the null hypothesis: Z ≥ −Z_α and are not pruned if we reject the null hypothesis in favor of the alternative. By choosing a lower α level (e.g. ≤ 0.05) more parsimonious trees that are more likely to be replicated will be favored. A higher α level (e.g. > 0.05) will favor larger trees with more splits.

2.4 Tree performance evaluation

In order to use a constructed tree as a tool for guiding treatment decisions, the performance of the tree should be validated on an independent sample if available, and if not, it should be validated on the existing sample. Herein, we propose a measure of predictive performance of a particular tree based on weighted differences in the proportions of subjects with good outcome on the two treatments in the terminal nodes of the tree. We first estimate the magnitude of the discrimination between treatments on the sample on which the final tree was built by computing the measure U described below. This measure can be interpreted as the estimated difference in probabilities of good outcome on the better treatment in each terminal node compared to the worse treatment in each terminal node. Thus, it is somewhat similar to the expected value/reward measure of an individualized treatment rule E(A) [25, 30], which in our context is the empirical average of the proportions of subjects with good outcome among those who were assigned to the better treatment in each terminal node. In this special case, the expected value/reward is simply a measure of how good the outcome could be if everybody got the treatment that the built tree predicts to be their better treatment. In contrast, our proposed measure shows how much better the outcome could be if we chose the better treatment compared to the worse treatment for each subject based on the built tree. However, calculating either measure on the sample used to build the tree is of limited value as we are ultimately interested in how the tree will perform on an independent sample. Thus using a similar formula based on the better and worse treatments in the original sample, we propose a new corresponding measure (U^*) to be used with the independent validation sample. When an external independent sample is not available, we can use counterfactual datasets (as in Foster et al. [9]) based on the original sample as described below and calculate U^* for these datasets. The proposed procedure is as follows:

1. Calculate the U measure based on the final tree applied to the original sample.

   Let the tree have m terminal nodes with n_k subjects in terminal node k, and let p_k,Tk, k = 1, …, m, denote the response rate for individuals in terminal node k on treatment T_k, where T_k = A or B. If N is the total sample size, U is defined as follows:

   $$0\le U=\frac{{\sum }_{k=1}^m{n}_k|p_{k,A}-p_{k,B}|}{N}\le 1.$$
   The larger the differences in proportions of subjects with good outcome between the two treatments in the terminal nodes in either direction, the higher the value of this measure. The value of 1 can be achieved only when there is complete separation of outcomes in the terminal node (that is, all subjects on A have one outcome and all subjects on B have the other outcome in all of the terminal nodes). The value of 0 can be achieved only with a degenerate tree consisting only of a root node where the proportion of subjects with good outcome on A and B is exactly the same. Note that U simply shows how much separation there is between the outcomes of the subjects on the two alternative treatments in the terminal nodes of the tree. Larger values are achieved when there are large treatment-by-covariate interactions and the algorithm successfully identifies these interactions. An equivalent way of expressing U is as follows:

   $$U=\frac{{\sum }_{k=1}^m{n}_k[(p_{k,A}-p_{k,B})I_k+(p_{k,B}-p_{k,A})(1-I_k)]}{N}$$

   where

   $$I_k=\{\begin{array}{cc}1,\hfill & \text{if}{p}_{k,A}>p_{k,B}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$
   The relationship between the proposed measure U and the expected value/reward measure E(A) of our algorithm is clearer when we write E(A) in the following way:

   $$E(A)=\frac{{\sum }_{k=1}^m[n_{k,A}{p}_{k,A}{I}_k+n_{k,B}{p}_{k,B}(1-I_k)]}{{\sum }_{k=1}^m[n_{k,A}{I}_k+n_{k,B}(1-I_k)]},$$

   where all the notation is as above except that n_k,A and n_k,B are the corresponding sample sizes on treatments A and B in the kth terminal node respectively. E(A) is an empirical average of the outcome for subjects who are on the better treatment in each terminal node and thus tells us how well we can do in terms of outcome if subjects are assigned to the better treatment.

   We now proceed to calculating the corresponding measures on the validation sample.

2. Calculate the U^* measure based on the same tree as in (i) but on another sample. The other sample can be an independent external validation sample, if available, or a generated sample with estimated counterfactual outcomes based on the original dataset.

   The formula for calculation of U^* is as follows:

   $$U^{*}=\frac{{\sum }_{k=1}^m{n}_k^{*}[(p_{k,A}^{*}-p_{k,B}^{*})I_k+(p_{k,B}^{*}-p_{k,A}^{*})(1-I_k)]}{N^{*}},$$

   where $n_k^{*}$ is the sample size in terminal node k in the new sample (external or counterfactual), N^* is the total sample size in the new sample and $p_{k,T_k^{*}}^{*}$, k = 1, …, m are the response rates for individuals in terminal node k on treatment $T_k^{*}$ in the new sample. I_k is based on the original sample. This introduces a penalty when in a terminal node the better treatment in the original sample happens to be worse in the validation sample. Thus the measure U^* is not restricted to be between 0 and 1. It can be less than 0 if in the new sample the terminal nodes favor different treatments than in the original sample. For example, if in the original sample p_k,A > p_k,B, but in the new sample $p_{k,A}^{*}<p_{k,B}^{*}$, then the corresponding term for this terminal node in the sum for U^* is going to be negative. If this happens for a sufficient number of terminal nodes in the new sample, then the entire U^* may be negative. Intuitively, U^* is a weighted average across terminal nodes of differences in proportions of subjects with good outcome on the better treatment and with good outcome on the worse treatment, where better and worse treatments are defined based on the original sample.
   The expected value/reward can also be calculated on the new sample (we will denote this as E(A)^* to distinguish from E(A)), but as for U^* we will base this calculation on the better treatment in the original sample and not in the validation sample. The formula for E(A)^* is then:

   $$E{(A)}^{*}=\frac{{\sum }_{k=1}^m[n_{k,A}^{*}{p}_{k,A}^{*}{I}_k+n_{k,B}^{*}{p}_{k,B}^{*}(1-I_k)]}{{\sum }_{k=1}^m[n_{k,A}^{*}{I}_k+n_{k,B}^{*}(1-I_k)]}.$$

   In contrast to U^*, E(A)^* is an empirical average of the outcome for subjects who are on the better treatment (according to the original sample) in each terminal node and thus tells us how well we can do in terms of outcome if subjects are assigned to the better treatment. E(A)^* does not tell us how much better the better outcome is compared to the worse outcome and thus is more a measure of absolute rather than comparative effect. The magnitude of U^* can be evaluated in the context of difference in probabilities, while E(A)^* can be evaluated as an absolute probability.

   When the new sample on which we desire to calculate U^* or E(A)^* is an independent external data set (or a left-over sample of the original data set), the calculations are straightforward. However, when no such data set is available, we can generate a sample of counterfactual outcomes for the subjects in the original data set following the idea of Foster et al. [9] based on random forests and then calculate U^* and E(A)^* as follows:

   • Step 1: We fit a general random forest algorithm for prediction of outcome with all possible covariates and treatment to the original data set. We follow the recommendation of Foster et al. [9] to include interactions between the treatment and all covariates, and between the alternative treatment and all covariates as potential predictors for all subjects. This has been empirically shown to improve prediction slightly.
   • Step 2: We generate a counterfactual treatment assignment for each subject i by changing the treatment assignment for this subject from the one received to the alternative (counterfactual) treatment. That is, we switch the treatment assignment to B if subject i actually received A, and vice versa.
   • Step 3: We obtain the predicted probabilities for the counterfactual treatment $T_i^{*}$ using the result from the random forest algorithm from Step 1, simulate a new set of binary outcomes from Bernoulli distributions $Y_{i,T_i^{*}}^{*}$, and combine them with the predictor variables to generate a new independent sample, i.e., ($Y_{i,T_i^{*}}^{*},T_i^{*}$, X_i), i = 1, …, n.

   The U^* and E(A)^* measures are calculated for the sample of counterfactual outcomes as one would for an external data set. Higher values for U^* indicate that subjects have substantially better outcome on the better treatment identified in the original sample for them than on the worse treatment. Higher values of E(A)^* indicate how good the outcome would be if subjects were placed on their predicted better treatment identified from the tree built on the original sample. The magnitude of these measures depends strongly on the signal-to-noise ratio in the data. We study the performance of the measures via simulations. To improve the robustness of U^* and E(A)^*, multiple counterfactual data sets are generated and the average and standard deviation for each of these two measures are calculated. Since U^* is a weighted average of differences in proportions, we can interpret its magnitude as an effect size for a difference in proportions. Value of U^* that are .5 or higher correspond to very large separation of treatments, values between .2 and .5 correspond to more modest separation of treatments in terms of outcome, lower values that are still positive may be considered of interest in scenarios where even a small improvement in probability of outcome is of interest while negative values show poor predictive ability of the tree on the external validation sample or the counterfactual outcomes sample.

3. SIMULATION STUDY

In this section, we examine how the proposed algorithm performs depending on the strength of treatment-covariate interactions and the level of noise in a data set. We consider two scenarios: one tree structure with sizeable treatment-covariate interactions (e.g. sizeable treatment effects in different directions in different subgroups of the sample) and the same tree structure but with small treatment-covariate interactions. Figures 1a and 1b present these two scenarios. The trees in these figures are what we call the “true” tree designs. For each of the two scenarios, a sample of 1,000 subjects is generated according to the tree structure in the two figures. That is, there is a binary outcome variable, a binary treatment indicator variable, and three different covariates related to treatment effects, including one continuous variable (denoted by X₁), one binary variable (denoted by X₂), and one variable with five categories (denoted by X₃). The rates of the outcomes on the different treatments for the subgroups identified by combinations of predictor levels are as indicated in the nodes of the trees.

We then consider 3 settings for each of these two scenarios called Design 1, 2 and 3 that vary in the proportion of noise variables included among the predictors, where a noise variable is one that does not associate with differential treatment response (see Online Supplement (http://www.intlpress.com/SII/p/2016/9-2/SII-9-2-TSAI-supplement.pdf) for a detailed description of the data generation method). In Design 1 there are no noise variables in the data set, that is, we construct and evaluate a tree based only on the variables that moderate treatment effects according to the tree structures in the figures. Design 2 has 21 noise variables, including 10 continuous variables, 10 binary variables, and one nominal variable with 3 levels. We call this setting the design with some noise variables. The noise variables are generated randomly so that they are not associated with the outcome, and are added to the Design 1 data set. A tree is then constructed and evaluated when both the “true” splitting variables and the noise variables are in the data set. Design 3 has 100 noise variables among which there are 75 continuous variables, 15 binary variables, and 10 nominal variables (4 nominal variables are with 3 levels, 3 are with 4 levels, and 3 are with 5 levels). This is called the design with many noise variables. As in Design 2, the noise variables are generated randomly so that they are not associated with the outcome and are added to the Design 1 data set. A tree is then constructed and evaluated when both the “true” variables and the noise variables are in the data set. The word “true” is in quotes because especially in scenarios with many noise variables, it is possible that a different set of variables might produce similar or even better classification of individuals in terminal nodes in terms of differential treatment effects. The evaluation of each constructed tree is based on 1,000 samples with counterfactual outcomes.

We also considered a scenario that did not have a tree structure. Data in this case were generated according to the following logistic regression model with main effects only (see Online Supplement for details): logit P(Y_i = 1) = −1 + 0.3I(T_i = B) + 0.5X_1i + 0.5I(X_3i ≥ 3) + 0.5X_2i, where I denotes the indicator function.

Table 2 shows the means and the standard deviations of U^* based on the samples with counterfactual outcomes. Since the U^* measure is specific to our approach while the E(A) measure can be calculated for any algorithm we compare the performance of our approach to the performance of the Virtual Twin approach of Foster et al. [9] in terms of E(A) on the original sample and mean (standard deviation) of the E(A)^* measures on the samples with counterfactual outcomes. We also compare methods based on classification error since in the simulation study we do know what the true best treatment for each individual is and we can see whether the recommended treatment by each algorithm corresponds to the best treatment. We consider different alpha levels (0.05 and 0.20) for pruning.

Table 2.

Simulation study results: U measures of constructed trees, means (SD) of the U^* measure, expected value/reward and classification error for each combination of scenario (sizeable treatment-covariate interaction, small treatment-covariate interaction, and no interaction effects) and level of noise in the data (design 1 = no noise variables; design 2 = some noise variables; design 3 = many noise variables)

	Proposed method					Foster’s Virtual Twin method
Design	Ua	E(A)b	Classification error	U*c Mean(SD)	E(A)*d Mean(SD)	E(A)	Classification error	Mean(SD) E(A)*
Sizable treatment by covariate interactions
Design 1	0.65	0.85	< 1%	0.54 (0.03)	0.79 (0.02)	0.85	< 1%	0.79 (0.02)
Design 2	0.65	0.85	< 1%	0.36 (0.05)	0.68 (0.02)	0.85	< 1%	0.68 (0.02)
Design 3	0.65	0.85	< 1%	0.32 (0.07)	0.67 (0.03)	0.85	< 1%	0.67 (0.03)
Small treatment by covariate interactionse
Design 1	0.13	0.56	24%	0.16 (0.03)	0.59 (0.02)	0.54	22%	0.60 (0.02)
Design 2	0.24	0.62	51%	0.00 (0.03)	0.50 (0.02)	0.55	39%	0.52 (0.02)
Design 3	0.30	0.65	49%	−0.02 (0.03)	0.49 (0.02)	0.52	50%	0.50 (0.02)
No treatment by covariate interactions (main effects model)
Design 1	0.05	0.55	0%	0.11 (0.03)	0.62 (0.03)	0.60	29%	0.64 (0.02)
Design 2	0.14	0.60	31%	0.03 (0.03)	0.55 (0.02)	0.56	19%	0.55 (0.02)
Design 3	0.11	0.59	19%	0.02 (0.03)	0.54 (0.02)	0.55	0%	0.55 (0.02)

^aU - weighted difference in proportions of subjects with good outcome on the better treatment compared to the worse treatment based on the constructed tree on the original sample.

^bE(A) - expected value/reward based on the original sample.

^cU^* - weighted difference in proportions of subjects with good outcome on the better treatment compared to the worse treatment based on the constructed tree on the original sample, evaluated on the counterfactual samples.

^dE(A)^* - expected value/reward calculated on the counterfactual samples.

^eAlpha level of 0.20 was used for pruning. In the remaining scenarios alpha level of 0.05 was used for pruning. For sizeable treatment by covariate interactions, the results were the same regardless whether alpha level was 0.05 or 0.20.

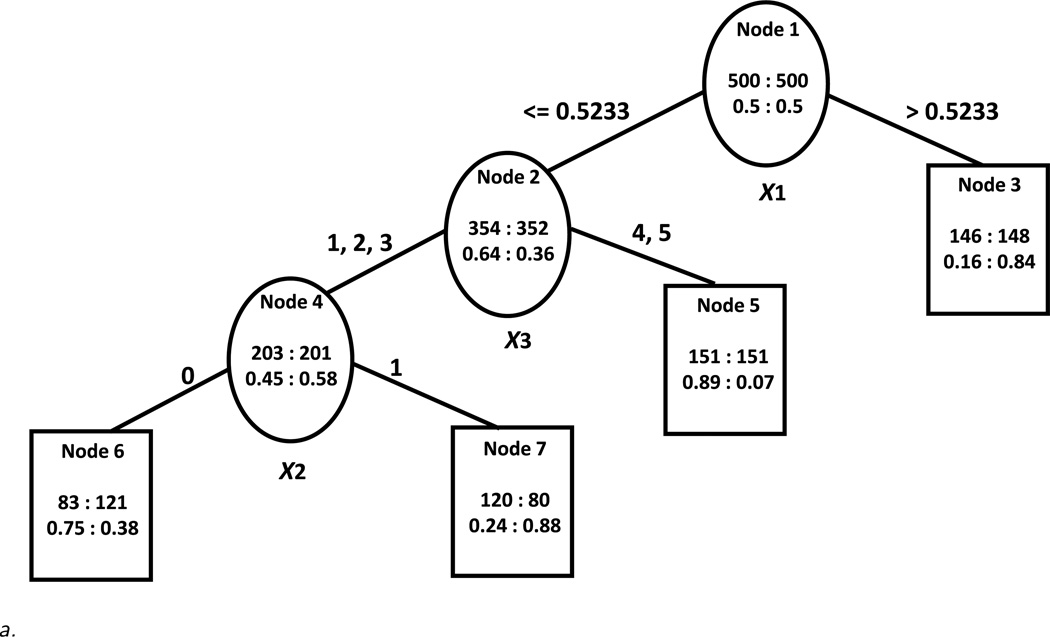
In the scenario with sizeable treatment effects (Figure 1a), the trees constructed based on the proposed algorithm under the restriction of no fewer than 30 subjects per treatment per node are almost identical under all noise scenarios to the original “true” tree and do not depend on the chosen alpha level (0.05 or 0.20). In particular, the tree constructed under Design 3 (with many noise variables) is shown in Figure 2a. The only difference between this tree and the “true” tree is a slight difference in the exact cutoff for the continuous variable. This demonstrates that the algorithm is able to identify the correct tree structure under different levels of noise in the data set accurately when there are sizeable treatment-covariate interactions. The U measure for the constructed trees is fairly large (U = 0.65) which can be interpreted as an absolute difference in probabilities on the better and worse treatment of 0.65. This indicates that the sample is separated into subgroups with decidedly different treatment effects. Also, the expected value/reward of all trees is high (E(A) = 0.85) which suggests that the good outcome can be achieved about 85% of the time if subjects are placed on the better treatment as indicated by the terminal node to which they belong. The approach of Foster gives very similar results although for Design 3 the tree (not shown) is a little larger than the true tree. Almost no subjects are misclassified in terms of their best treatment in both approaches in this scenario (classification error < 1% in all cases). However since both U and E(A) are calculated on the same sample on which the trees are developed, they are potentially optimistic. When the measures are calculated on the 1,000 samples of counterfactual outcomes unsurprisingly the U^* measures decrease on average for the constructed trees as the level of noise in the data set increases (i.e. Mean(U^*) is the highest for Design 1 and the lowest for Design 3). Also, the variability of the U^* measures increases as the level of noise increases as evidenced by the change in SD(U^*). The expected value/reward measures E(A)^* are also high in this scenario (from 0.79 to 0.67) for both approaches and decrease as the noise in the data increases.

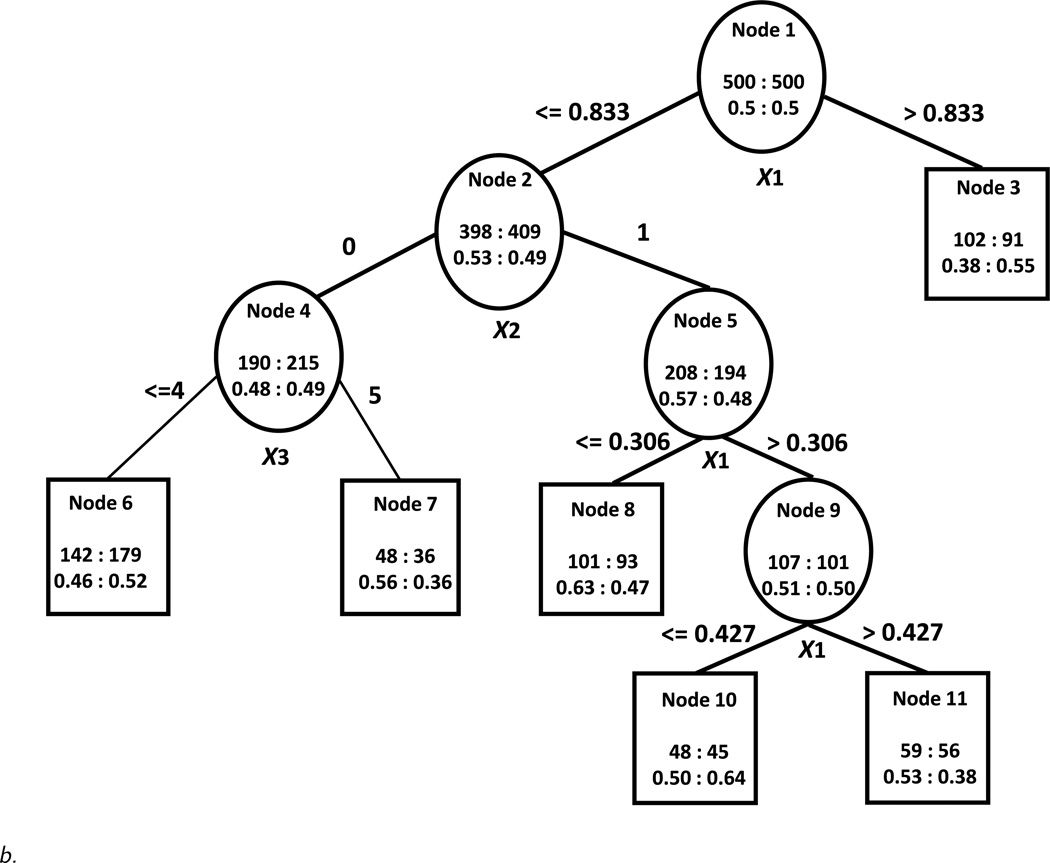
Figure 2.

a. Constructed tree using the proposed algorithm in the scenario with sizeable treatment-covariate interactions and many noise variables.

b. Constructed tree using the proposed algorithm based on the scenario with small treatment-covariate interactions and no noise variables.

In contrast to the scenario with sizeable treatment-covariate interactions, in the scenario with small treatment-covariate interactions (Figure 1b), the trees constructed based on the proposed algorithm under the node size restriction as above (i.e. no fewer than 30 subjects per treatment per node) are different from the “true” tree. If an α level of 0.05 is used, all branches of the trees are pruned. Using an alpha of 0.20 results in trees with several splits. We show the constructed tree under the design with no noise variables (Design 1) in Figure 2b. We notice that even in this simple case, the constructed tree is larger and more difficult to interpret, the selected cutoffs for the continuous and ordinal variables are different, more than one split occurs on the continuous variable and the order of splitting in the constructed tree is different from the order in the “true” tree. However, the samples of subjects in the terminal nodes favoring one treatment overlap significantly with the corresponding samples of subjects in the terminal nodes favoring the same treatment of the “true” tree. In the designs with noise variables the constructed trees are even larger and very different from the “true” tree (not shown). All trees constructed using Foster’s approach are also with a different structure than the “true” tree. In both approaches, when noise variables are present, the true splitting variables are not generally picked as splitting variables but rather other continuous predictors are chosen as splitters.

Interestingly, the U measures increase as the level of noise in the data set increases (U = 0.13 in Design 1, U = 0.24 in Design 2 and U = 0.30 in Design 3). This is because when the effect sizes are small, combinations of noise variables may be associated with better prediction than the variables in the “true” tree by chance in the sample on which the tree is built. The expected value/reward values show a similar trend but classification error rates also increase. However, in these cases the U^* measures are quite small (i.e. for the constructed trees in Designs 2 and 3, the average U^* values are 0 and −0.02 respectively with standard deviations of 0.03) and suggest that outcomes do not vary significantly if subjects are assigned to the better treatment compared to the worse treatment for the terminal node to which they belong. The expected value/reward measures E(A)^* in the counterfactual samples of both approaches are lower than in the sizeable treatment-covariate interactions scenario and decrease with increasing noise as expected.

In the scenario with no underlying tree structure, with α = 0.05, our approach correctly pruned all branches of the tree when there were no noise variables but split several times when there were noise variables. In contrast, Foster’s approach resulted in the root-only tree when there were many noise variables (Design 3) but not in the other two designs. Expected value/reward measures and classification errors were similar in the two approaches.

The simulations suggest that when there are sizeable treatment-covariate interactions, the “true” tree structure can be recovered and U^* measures are reasonably large. In contrast, when there are only small or no treatment-covariate interactions, the constructed trees reflect the noise in the data and values of U^* hover around 0. Classification errors are quite sizeable in all scenarios except when there are sizeable treatment-covariate interactions. Expected value/reward measures do not provide much information regarding how well treatment effects are distinguished by the trees. They simply show how good the outcome is on the better treatment identified by the trees. For data sets with underlying tree structures, our approach has comparable performance to Foster’s Virtual Twin approach.

4. THE COMBINE STUDY: A CLINICAL TRIAL IN ALCOHOL DEPENDENCE

In this section, we use the proposed approach to identify subgroups with differential treatment effects to naltrexone and acamprosate on abstinence from heavy drinking during the last eight weeks of treatment in the COMBINE Study [1]. The study sample consisted of 1,383 abstinent alcohol dependent patients across 11 sites and the primary goal was to assess the main and interactive effects of the two pharmacological treatments (naltrexone and acamprosate) and behavioral therapy (the Combined Behavioral Intervention – CBI) on drinking measures assessed during the 16-week double-blind phase of the study. The primary analyses revealed a significant effect of naltrexone but not of acamprosate. However, acamprosate is an approved treatment for alcohol dependence and has been previously found to be especially effective among those who are committed to abstinence [20]. Hence, it is likely that there are subgroups of subjects for whom one treatment is more effective than the other and vice versa.

The design of the COMBINE Study was a 2 × 2 × 2 factorial. However, in the current manuscript we compare the two active treatment conditions of acamprosate and naltrexone. To do so, we focus only on subjects who received naltrexone but not acamprosate and those who received acamprosate but not naltrexone. Both medication groups include those who did and did not receive CBI. We also selected the outcome measure of no heavy drinking during the last 8 weeks of double-blind treatment because measures of heavy drinking after a grace period have been recommended as the best outcome in clinical trials of alcohol dependence [8]. The purpose of our study was to identify subgroups of patients with alcohol dependence who benefit more from acamprosate than from naltrexone and those who benefit more from naltrexone than from acamprosate. There were 611 subjects in our data set.We randomly divided this sample in 2:1 ratio into a training sample and a validation sample. The training sample consisted of 408 alcohol dependent patients while the validation sample consisted of 203 individuals. We considered 77 continuous, 11 binary, and 8 categorical predictors with more than 2 levels, including demographics and measures of baseline alcohol consumption, alcohol severity, prior alcohol treatment, drinking goal, family history, craving, smoking, alcohol abstinence self-efficacy, quality of life, general health, mood, perceived stress, legal problems and laboratory biomarkers. A description of these measures is provided in [12].

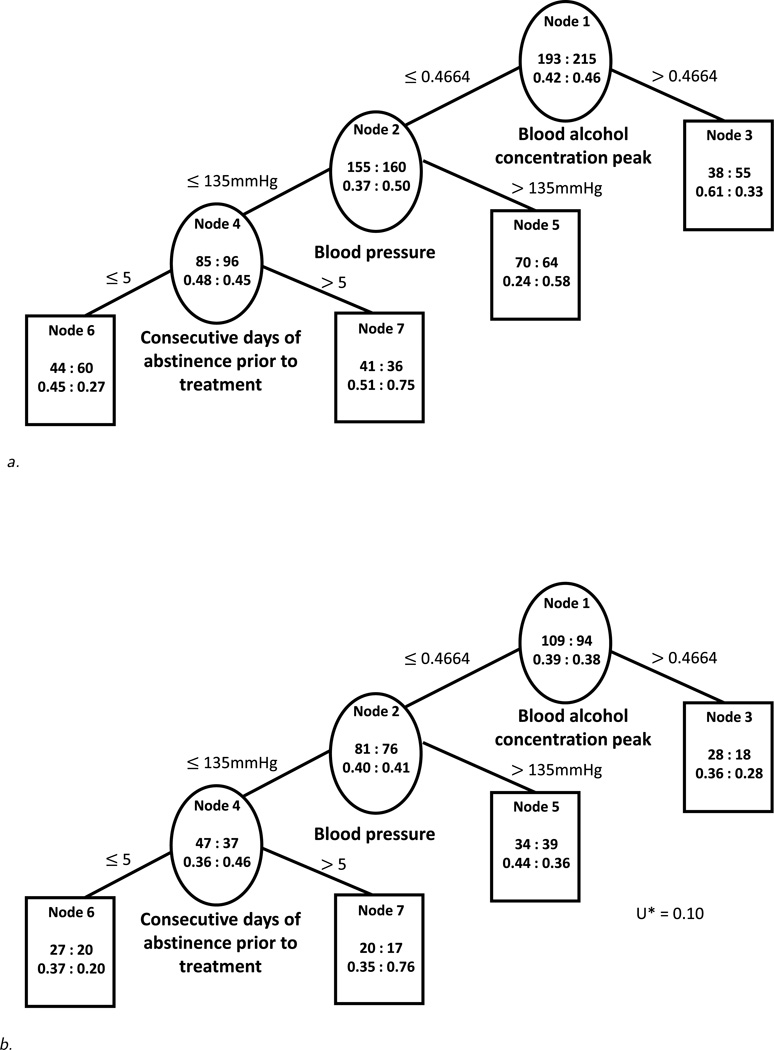
We used the proposed tree construction approach, limited the number of subjects in each node on each treatment to 30 or more and used an alpha level of 0.20 for pruning. The constructed tree is displayed in Figure 3a. There are two subgroups of subjects who seem to benefit more from acamprosate than from naltrexone: those with high Blood Alcohol Concentration (BAC) peak {BAC peak > 0.4664} and among those with lower BAC peak, those with lower systolic blood pressure (BP) and who have 5 or fewer Consecutive Days of Abstinence (CDA) prior to treatment {BAC peak ≤ 0.4664, BP ≤ 135, CDA ≤ 5}. On the other hand, we find two subgroups of subjects who appear to benefit more from naltrexone: subjects with higher systolic blood pressure and low BAC peak {BAC peak ≤ 0.4664, BP > 135} and subjects with longer pre-treatment abstinence who have lower BAC peak and lower systolic blood pressure {BAC peak ≤ 0.4664, BP ≤ 135, CDA > 5}. The U measure of the constructed tree in Figure 3a is 0.27 suggesting that treatment-covariate interactions effect sizes are small. The U^* measure in the validation data set is 0.10 which indicates a small difference in outcome between the two treatments. Figure 3b shows that in the validation data set all but one of the terminal nodes (node 5, patients with lower BAC and higher BP) favor the same treatments as the corresponding terminal nodes in the training sample (Figure 3a). However, the mean value and the standard deviation of U^* based on 1,000 counterfactual datasets are −0.02 and 0.05, respectively, suggesting that the level of noise in the data is high and that we are in small treatment by covariate interactions scenario with many noise variables. Hence, the constructed tree may not be picking up the most important combinations of moderator variables. This also explains why Foster’s approach results in a very different regression tree (not shown). The expected value/reward of our approach on the training and validation samples is 0.59 and 0.42, respectively, while the expected value/reward of Foster’s approach is 0.41 and 0.38, respectively. Thus on this particular example our approach performs better on this measure on the independent validation data set than Foster’s approach.

Figure 3.

a. Constructed tree using the proposed algorithm based on the training sample from the COMBINE study. Within each node, the top number on the left: right side represents the total number of patients in the acamprosate: naltrexone group, and the bottom number stands for a percentage of subjects with no heavy drinking in the acamprosate: naltrexone group.

b. Constructed tree from training sample (Figure 3a) evaluated on the validation sample from the COMBINE study. Within each node, the top number on the left: right side represents the total number of patients in the acamprosate: naltrexone group, and the bottom number stands for a percentage of subjects with no heavy drinking in the acamprosate: naltrexone group.

Of the splits in our tree, the split on systolic blood pressure fails to validate in the left-out sample and is difficult to explain from a subject-matter perspective. On the other hand, blood alcohol concentration peak is a moderator of naltrexone effect as indicated using both tree and logistic regression models in the same data set (manuscript under preparation). Also, consecutive days of abstinence prior to treatment has been identified as a moderator of acamprosate effect compared to placebo in the same data set using trajectory and logistic regression approaches [11]. Both BAC and consecutive days of abstinence are meaningful clinical variables that can be used in order to inform treatment assignment. However, due to the high signal-to-noise ratio in this data set, the findings are unlikely to be robust and further external validation of these results is necessary.

5. DISCUSSION

In summary, in this work we extended the recursive partitioning algorithm of Zhang et al. [29] for identification of subgroups with differential treatment effects by incorporating an automatic pruning step and proposed a method to evaluate the constructed trees on simulated counter-factual or independent validation samples. Our simulation study shows that tree structure can be successfully recovered when the signal-to-noise ratio in the data set is high but that noise variables are often chosen as node-splitters when the signal-to-noise ratio is small. The proposed U and U^* measures indicate how discriminating the tree is with respect to the outcome on different treatments in the terminal nodes and how well the tree validates within the same sample or on an external validation sample. When values of U and U^* are small, results must be interpreted with caution. While establishing cutoffs for acceptable values of U and U^* is desirable, such cutoffs are likely to be data-dependent and to vary widely based on the subject-matter area.

The proposed method can deal with predictor variables of different types: continuous, ordinal, binary, and nominal. However, the simulation study and the data example show that continuous variables are picked as splitters much more frequently because of the many possible cutoffs that can be considered for each variable. A penalty in the algorithm could be incorporated into the program so that continuous and ordinal measures with many levels are chosen less frequently. An approach to that effect has been considered by Lipkovich et al. [17] and can be adapted in our algorithm. Alternatively, continuous and ordinal variables can be a priori categorized based on practical or clinical considerations into a similar number of categories. This reduces the chance of over-selecting continuous covariates as splitters and can make results more interpretable [13]. For example, laboratory measures and other clinical measures such as blood pressure can be categorized as below the lower limit of the normal range (if applicable), one or more categories covering values within the normal range (e.g. lower third, middle third and upper third of the normal range), one or more categories above the upper limit of the normal range (if applicable). Such categorizations assure that results can be communicated more easily to clinicians and may be more likely to validate externally.

Our algorithm can be extended in several possible ways. We can modify the splitting criterion to consider a different type of outcome (e.g. continuous, survival) or to focus on identification of subgroups with enhanced treatment effect rather than subgroups with differential treatment effects (e.g. like the approach of Lipkovich and Dmitrienko [18]). An interactive version of the algorithm can also be programmed so that the investigator can override automatic choices of splitting variables and/or cutoffs based on substantive considerations. As we have previously shown [12], selecting variables and cutoffs based on practical and clinical considerations in addition to statistical considerations may validate externally better than trees based on purely statistical considerations. A useful extension of the approach will be to construct deterministic or random forests and develop variable importance measures so the best potential moderator effects in a data set can be identified for further testing.

While tree-based methods can accommodate a large number of potential splitting variables, our simulations suggest that adding variables that are known a priori not to influence the relationship between treatment and response increases the signal-to-noise ratio and potentially lowers the probability of identifying the “true” moderators. Therefore, predictor variables should be chosen carefully based on assessment of their potential for identifying subgroups with differential treatment effect and their practical utility. However, when there is no prior knowledge of the moderator effect of a potential variable, it is better to include this variable in the tree-building procedure rather than run the risk of missing a potentially important effect.

In conclusion, the proposed simple and efficient statistical tool can be used to inform clinical decision making and personalized treatment for patients based on their characteristics. Extensions of the algorithm to construction of forests, incorporation of clinical and practical considerations in variable and cutoff selection, and development of variable importance measures can further increase its utility.

APPENDIX A. DERIVATION OF THE PROPOSED PRUNING APPROACH

Let OR_L and OR_R denote the odds ratio obtained from a left (right) daughter node. Also, let δ_L = OR_L − 1 and δ_R = OR_R − 1. We consider the following hypothesis:

$$H_0:{\delta }_L{\delta }_R\ge 0\text{vs}.{\delta }_L{\delta }_R<0.$$

Let θ_L = log OR_L and θ_R = log OR_R. Then

$${\delta }_L{\delta }_R=(e^{{\theta }_L}-1)(e^{{\theta }_R}-1),$$

and the asymptotic distribution of $\widehat{{\delta }_L{\delta }_R}=(e^{\widehat{{\theta }_L}}-1)(e^{\widehat{{\theta }_R}}-1)$ is given by

$$g(\hat{\mathit{\theta }})=\widehat{{\delta }_L{\delta }_R}~𝒩((e^{\text{log}O{R}_L}-1)(e^{\text{log}O{R}_R}-1),\mathit{\text{Var}}(g(\hat{\mathit{\theta }}))),$$

where

$$\hat{\mathit{\theta }}=(\widehat{{\theta }_L}\widehat{{\theta }_R})\prime =\left(\text{log}\frac{n_{11}^L{n}_{22}^L}{n_{12}^L{n}_{21}^L}\text{log}\frac{n_{11}^R{n}_{22}^R}{n_{12}^R{n}_{21}^R}\right)\prime \stackrel{d}{\to }{𝒩}_2(\mathit{\theta },\mathit{\text{Cov}}(\hat{\mathit{\theta }})),$$

and

$$\mathit{\text{Cov}}(\hat{\mathit{\theta }})=\left(\begin{array}{cc}\hfill {\sum }_{i=1}^2{\sum }_{j=1}^2\frac{1}{n_{ij}^L}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\sum }_{i=1}^2{\sum }_{j=1}^2\frac{1}{n_{ij}^R}\hfill \end{array}\right).$$

Let g(t) be a differentiable function and let ϕ_i = ∂g/∂θ_i, i = L, R, denote ∂g/∂t_i evaluated at t = θ. By the delta method,

$$g(\hat{\mathit{\theta }})\stackrel{d}{\to }{𝒩}_2(g(\mathit{\theta }),\mathit{\varphi }\prime \mathit{\text{Cov}}(\hat{\mathit{\theta }})\mathit{\varphi }),$$

where ϕ′ = (ϕ_L ϕ_R), g(θ) = (e^θ_L − 1) (e^θ_R − 1) and the asymptotic variance is

$$\mathit{\varphi }\prime \mathit{\text{Cov}}(\hat{\mathit{\theta }})\mathit{\varphi }={\varphi }_L^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^L}+{\varphi }_R^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^R}.$$

Since ϕ_L = ∂g(θ)/∂θ_L = e^θ_L (e^θ_R − 1) and ϕ_R = ∂g(θ)/∂θ_R = e^θ_R (e^θ_L − 1), the asymptotic variance is given by

$$e^{2{\theta }_L}{(e^{{\theta }_R}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^L}+e^{2{\theta }_R}{(e^{{\theta }_L}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^R}.$$

Thus we obtain

$$g(\hat{\mathit{\theta }})~𝒩((e^{\text{log}O{R}_L}-1)(e^{\text{log}O{R}_R}-1),\mathit{\text{Var}}(g(\hat{\mathit{\theta }}))),$$

where

$$\mathit{\text{Var}}(g(\hat{\mathit{\theta }}))=e^{2\text{log}O{R}_L}{(e^{\text{log}O{R}_R}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^L}+e^{2\text{log}O{R}_R}{(e^{\text{log}O{R}_L}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^R},$$

and

$$\hat{\mathit{\theta }}=(\widehat{{\theta }_L}\widehat{{\theta }_R})\prime =\left(\text{log}\frac{n_{11}^L{n}_{22}^L}{n_{12}^L{n}_{21}^L}\text{log}\frac{n_{11}^R{n}_{22}^R}{n_{12}^R{n}_{21}^R}\right)\prime .$$

Hence, the test statistic is given by

$$Z=\frac{\widehat{{\delta }_L{\delta }_R}}{\sqrt{\widehat{\mathit{\text{Var}}}(g(\hat{\mathit{\theta }}))}}$$

where

$$\widehat{\mathit{\text{Var}}}(g(\hat{\mathit{\theta }}))=e^{2\widehat{{\theta }_L}}{(e^{\widehat{{\theta }_R}}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^L}+e^{2\widehat{{\theta }_R}}{(e^{\widehat{{\theta }_L}}-1)}^2\sum _{i=1}^2\sum _{j=1}^2\frac{1}{n_{ij}^R},$$

$$\widehat{{\theta }_L}=\text{log}\frac{n_{11}^L{n}_{22}^L}{n_{12}^L{n}_{21}^L}\text{and}\widehat{{\theta }_R}=\text{log}\frac{n_{11}^R{n}_{22}^R}{n_{12}^R{n}_{21}^R}.$$

Since $\widehat{{\theta }_L}$ or $\widehat{{\theta }_R}$ can equal zero or ∞ if one of the cells in Table 1 is zero, following [10] and [24], we modify the estimators of θ_L and θ_R by adding 0.5 to each cell:

$$\widehat{{\theta }_L}=\text{log}\frac{(n_{11}^L+0.5)}{(n_{12}^L+0.5)}\frac{(n_{22}^L+0.5)}{(n_{21}^L+0.5)}\text{and}$$

$$\widehat{{\theta }_R}=\text{log}\frac{(n_{11}^R+0.5)}{(n_{12}^R+0.5)}\frac{(n_{22}^R+0.5)}{(n_{21}^R+0.5)}.$$