Beyond the continuum: a multi-dimensional phase space for neutral–niche community assembly

Abstract

Neutral and niche processes are generally considered to interact in natural communities along a continuum, exhibiting community patterns bounded by pure neutral and pure niche processes. The continuum concept uses niche separation, an attribute of the community, to test the hypothesis that communities are bounded by pure niche or pure neutral conditions. It does not accommodate interactions via feedback between processes and the environment. By contrast, we introduce the Community Assembly Phase Space (CAPS), a multi-dimensional space that uses community processes (such as dispersal and niche selection) to define the limiting neutral and niche conditions and to test the continuum hypothesis. We compare the outputs of modelled communities in a heterogeneous landscape, assembled by pure neutral, pure niche and composite processes. Differences in patterns under different combinations of processes in CAPS reveal hidden complexity in neutral–niche community dynamics. The neutral–niche continuum only holds for strong dispersal limitation and niche separation. For weaker dispersal limitation and niche separation, neutral and niche processes amplify each other via feedback with the environment. This generates patterns that lie well beyond those predicted by a continuum. Inferences drawn from patterns about community assembly processes can therefore be misguided when based on the continuum perspective. CAPS also demonstrates the complementary information value of different patterns for inferring community processes and captures the complexity of community assembly. It provides a general tool for studying the processes structuring communities and can be applied to address a range of questions in community and metacommunity ecology.

1. Background

The two dominant theories on the development and structure of communities are niche and neutral theory. Niche theory explains the structure of communities using the relationship between species traits and habitat characteristics. Meanwhile, neutral theory assumes a fixed species pool in the absence of speciation and invasion, and considers all species to be ecologically equivalent, with stochastic dispersal and ecological drift being the only processes determining community structure. Despite contrasting opinions on the value of neutral theory [1,2], it is now generally accepted that neutral and niche processes interact in natural communities and both contribute towards the structure of species assemblages [3]. The relative roles of neutral and niche processes have been shown to differ across spatio-temporal scales [4,5] and modelling these processes in combination (composite models) better represents biological patterns than neutral or niche models alone [6,7].

Two composite-model approaches have been used to jointly examine niche and neutral processes in communities. A phenomenological approach involves directly modelling the abundance of species using differential equations and probability distributions, taking interactions between species into account (e.g. [6,8–10]). By contrast, a mechanistic approach is based on a ‘filter paradigm’ [11,12], where propagules pass through a succession of filters that structure the community (figure 1a). These filters are defined by interactions between the propagules and their surrounding environment, favouring some individuals and species over others during the colonization of empty sites. The number of filters can vary depending on the conceptual model [5,7,13], but there are two general successive filters: a neutral dispersal filter representing the probability of propagules reaching a given location, and a niche filter, representing their probability of survival in the location based on biotic and abiotic conditions, i.e. based on niche selection [13]. Although these composite models are increasingly used to describe community dynamics, the way in which neutral and niche processes interact and their relative importance in structuring communities is still unclear [3].

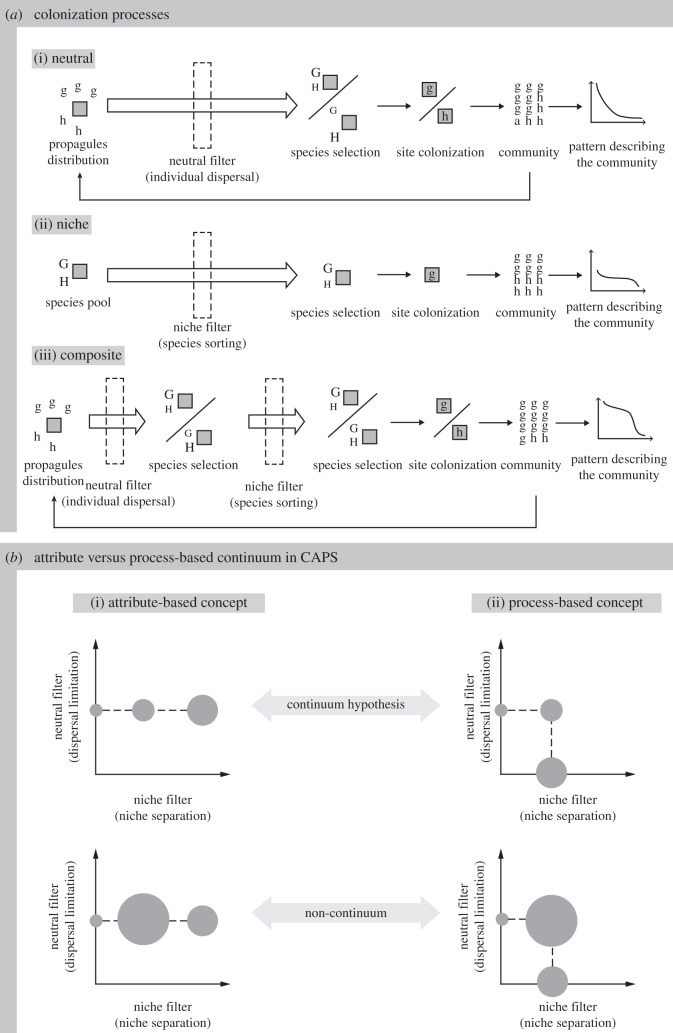
Figure 1.

The Community Assembly Phase Space (CAPS) for neutral–niche community dynamics in which (a) independent neutral and niche filters may operate separately or in combination, resulting in neutral, niche or composite processes. (a(i)) Given some propagules (lowercase g and h) in the vicinity of an empty location, the neutral filter can select for different species (uppercase G and H; the size of the capital letters represents the probability of the species colonizing the site) depending on the number and distance between the propagules and the site, which varies with time through feedback with the community. (a(ii)) With a niche filter, a location will always tend to select the same species with the selection strength depending on the relative niche of the species. (a(iii)) When niche and neutral filters operate in combination, the niche process is included in the feedback, resulting in a different community to one produced by either process independently. (b) In a multi-dimensional phase space, a process-based concept (that compares a composite process to a neutral process with no niche separation and a niche process with no dispersal limitation) is more appropriate than a community attribute-based concept (that compares a composite process to processes with no and strict niche separation but the same dispersal limitation) for understanding the process–pattern relationship. In CAPS, patterns from a composite process do not necessarily (but can) lie within the range of patterns produced by pure neutral and niche processes, refuting the continuum hypothesis (circle size in (b(i)(ii)) represents the relative value of a community pattern).

The neutral–niche continuum proposes that natural communities lie along a continuum based on the relative importance of these processes, with pure neutral- (no or equal niche selection amongst species) and pure niche- (strict niche separation; each species survives under a single, unique set of environmental conditions) driven communities at either extreme [3,10,13]. For example, Mutshinda & O'Hara [10] locate a community along the continuum using a neutrality index (bounded between 0 and 1), computed as the degree of average niche overlap, i.e. the strength of interspecific competition (see also [7,9]). This index is therefore mechanistic and the niche characteristics of the species are an intrinsic attribute of the community. However, it ignores the role of dispersal and, as a result, the neutrality index only encompasses a subset of processes that may play a role in a neutral community.

A different way of defining neutrality along the continuum has also been proposed to account for both distance-limited dispersal and niche separation [3,13]. It is based on the variability in the outputs of independent simulation model replicates in a spatially explicit, composite model of plant communities. With this definition, Gravel et al. [13] compute a neutrality index using the variability in species abundance, whereas Bar-Massada et al. [3] use the variability in the species identity occupying a cell. In these models, strict niche separation leads to a deterministic output with no variability because one habitat can only be occupied by one particular species. At the other end of the continuum, neutral models with complete niche overlap should produce the highest variability in species identity. These indices therefore measure an emergent property of a community rather than niche overlap per se and are thus phenomenological rather than mechanistic. Using these indices, changes in species attributes (dispersal distance, niche width) have been shown to interact with several extraneous variables (species richness in [13], environmental heterogeneity in [3]) to alter the location of communities along the neutral–niche continuum.

Here, we show that there are two main problems with the neutral–niche continuum regardless of the neutrality index used, making it conceptually inadequate for assessing the relative importance of the neutral and niche processes in the assembly of communities. First, both kinds of indices equate the niche process with the community attribute of strict niche separation between species. This is inconsistent with the filter paradigm, in which the niche filter can accommodate different degrees of niche separation, independently of the neutral filter. To assess the relative importance of neutral and niche processes, both processes must first be modelled independently, and then compared to a composite model that combines both niche and neutral process. Second, considering a community to lie along a continuum implies that all patterns that result from neutral and niche processes in combination should fall within the range of values generated by neutral and niche processes (figure 1b; electronic supplementary material, figure C1), which has not yet been demonstrated.

In place of the neutral–niche continuum, we introduce the Community Assembly Phase Space (CAPS), using a filter-based approach as well as mechanistic definitions for both niche and neutral processes. CAPS uses community processes (such as dispersal and niche selection), rather than the single community attribute of niche separation, to define the neutral and niche limiting conditions and to test the continuum hypothesis. This is therefore a process-based, neutral–niche space, in contrast to the original attribute-based continuum. CAPS enables a more comprehensive assessment of the relationship between patterns and processes in the dynamics of community assembly (figure 1). We demonstrate CAPS and its application using an individual-based model (IBM) of a plant community. We show that patterns arising from the composite model can have values outside of the range of neutral and niche model outputs, i.e. can lie beyond expectations of the neutral–niche continuum. The patterns also vary non-monotonically with increasing niche separation, thereby refuting the original attribute-based, neutral–niche continuum. This reveals previously unsuspected feedback in the interactions between the neutral and niche processes and the environment.

2. The Community Assembly Phase Space for neutral and niche processes

(a). Neutral–niche filters and processes in community assembly and their relationship with metacommunity theory

The CAPS (figure 1) is constructed with the intention to better describe, model and analyse community processes and the patterns they produce. CAPS is a tool that enables robust construction and identification of the different processes structuring communities. It is applicable to a range of hypotheses and theories in community ecology, including both the neutral–niche dichotomy and metacommunity theory. In this paper, we are particularly interested in applying CAPS to assessing the validity of the neutral–niche continuum hypothesis—a hypothesis still current in the literature (e.g. [3])—and we developed CAPS to do so.

Given an empty location available to be colonized, the neutral filter is a mechanism that favours a species independently of niche selection and differences among species. Excluding speciation, it is therefore only based on propagule pressure and the dispersal limitation of individuals (all individuals are considered to have the same dispersal limitations) (figure 1a(i)). With no interspecific variation in dispersal limitation, dispersal limitation therefore acts as a neutral filter in our model. These two terms are therefore equivalent in this context. In contrast, the niche filter favours a species based on the match between its niche preferences and available habitat characteristics (i.e. niche selection), ignoring dispersal limitation and propagule pressure (figure 1a(ii)). Both filters are based on different community attributes, and each can be modelled with a completely different set of parameters. They are therefore independent of each other.

Neutral and niche processes can then, respectively, be defined as the dynamic realization of neutral and niche filters in a temporally and spatially changing context (figure 1a). Neutral processes can be characterized by different dispersal limitations as long as the role of the niche is precluded. Because neutral processes depend on the dynamic spatial distribution of the species, there is feedback between the community and the filter (figure 1a(i)). By contrast, niche processes can consider different niche distributions and different degrees of niche separation, as long as the roles of dispersal limitation and propagule pressure are precluded (figure 1a(ii)). This model therefore relies on the same assumptions underlying the metacommunity species-sorting paradigm [14,15], i.e. that community structure can be explained by niche differences and spatial heterogeneity only, and there is no feedback with the community (electronic supplementary material, figure C2). A composite process then considers both the role of dispersal-limited propagule pressure and niche difference among species. As in the pure neutral process, there is feedback between the community and the neutral filter (figure 1a(iii)). By allowing individuals to disperse in a heterogeneous environment, both processes may interact in a similar way to the metacommunity mass-effect paradigm, in which dispersal maintains source–sink relations among populations in different patches [14,15]. For example, aggregated groups of individuals from the same species may act as a source of propagules and allow for a rescue effect in nearby low-quality habitat.

(b). Attribute-based versus process-based neutral–niche continuum within the Community Assembly Phase Space

For simplification, let us consider that the strength of the neutral and niche filters can each be represented by a single attribute of the community, such as dispersal limitation and niche separation, and that each filter can therefore be modelled using a single parameter. A two-dimensional space in which each parameter varies independently on its respective axis, the CAPS, is then needed to depict the interactions of the two processes (figure 1b; see electronic supplementary material, appendix A, for extending the concept to more than two parameters or community attributes). The composite process is located within the space referenced by the neutral and niche axes, and coordinates in CAPS represent values for the dispersal limitation and niche separation parameters, i.e. the strengths of the neutral and niche filters (figures 1b; electronic supplementary material, figure C1).

Using the filter paradigm (figure 1a), the composite process therefore converges on the niche axis, i.e. on a niche process, when dispersal limitation declines (dispersal increases) and the neutral filter becomes weaker. It converges on the neutral axis, i.e. becomes more neutral, when the niche separation between species decreases and the niche filter becomes weaker. A neutral process with no dispersal limitation (infinite dispersal) and a niche process with no niche separation (complete niche overlap) are both equivalent to a spatially random distribution of individuals, located at the origin of both axes (figure 1b; electronic supplementary material, figure C1). The Cartesian coordinates in CAPS therefore provide a full description of the two processes involved in community assembly in this case. CAPS is related to the three-dimensional space used by Logue et al. [15] to represent metacommunity paradigms [15] (electronic supplementary material, figure C2). However, in CAPS, the axes are each analytically defined, using different, independent filters.

In CAPS, for a given dispersal limitation, the original neutral–niche continuum [13] compares the community produced by a given niche separation with communities produced by complete niche overlap and strict separation as limiting cases (figure 1b(i)). This concept of a neutral–niche continuum is therefore based on an attribute of the community (the degree of niche separation between species) and is one-dimensional. Using CAPS, it becomes obvious that considering communities to be bounded by the CAPS axes (i.e. a process-based instead of an attribute-based continuum) is more appropriate for assessing the relative strength of the neutral and niche filters, and the role of the neutral and niche processes in community assembly (figure 1b(ii)).

Importantly, we argue that contrary to the neutral–niche continuum hypothesis, community patterns produced by composite processes in CAPS should not be assumed to be a linear combination of patterns from pure neutral and niche processes (figure 1b; electronic supplementary material, figure C1b,d). Rather, patterns emerge from interactions between a full range of niche and neutral processes, through feedback with the environment (figure 1a). This may lead to nonlinear behaviours [16] and to patterns with values that lie beyond those expected between pure niche and pure neutral processes. The phase space therefore allows the differences between the values of different community patterns to be visualized, with respect to their positions along the niche and neutral axes. By explicitly relating the values of the process parameters on each axis with the emergent patterns, it will also be possible to understand how the processes interact and to quantify the conditions required for different metacommunity paradigms to be relevant, such as neutral model, species sorting and the mass effect (electronic supplementary material, figure C2).

3. Material and methods

(a). Model implementation

To demonstrate CAPS, we implemented an IBM representing a plant community in a heterogeneous landscape using the filter paradigm (figure 1a) in NetLogo v. 5.0.4 [17] (code available in the electronic supplementary material; see electronic supplementary material, appendix B, for simulation parameters). The environment was represented by a lattice of 101 × 101 cells, with each cell occupied by only one individual. Each cell was characterized by an environmental variable E with no unit, ranging between 0 and 100. Following Hubbell's zero-sum assumption, a given number of individuals are randomly removed at each iteration, representing ecological drift, and the empty cells are immediately colonized by new individuals based on the neutral, niche or composite processes defined below.

(i). Neutral process

The probability of species i colonizing an empty cell in a system governed by the neutral process is the relative probability of arrival with respect to other species 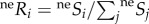, where 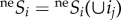represents the probability of at least one individual i_j of species i reaching the focal cell (figure 1a(i); see electronic supplementary material, appendix B, for formulation), with ^neS_i = 1 for all species under infinite dispersal. The probability of an individual i_j of species i dispersing across distance r and reaching a focal cell is assumed to be species-insensitive [13], 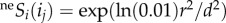, where d is the inverse of dispersal limitation and represents the distance for which ^neS_i(i_j) = 0.01 (i.e. the dispersal ability). Due to computational limitations, ^neS_i was approximated by applying electronic supplementary material, equation B3, only to individuals closer than d (or five cells for d = 2), and the influence of the total community was considered as:

3.1

where parameter m (=0.1 in the simulation) represents the proportion of long-range dispersal in propagules and n_i is the abundance of species i (see electronic supplementary material, appendix B, for details).

(ii). Niche process

Each species i is characterized by a Gaussian fundamental niche λ_i, representing its performance in an environment of value E [16,18], 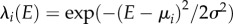, where μ_i is the niche optimum of species i, and σ its niche width (equal for all species). For infinite niche width, we have λ_i = 1 for all E values, i.e. complete overlap. As σ decreases, niche separation increases. Following Gravel et al. [13], we fixed niches optima and only varied the niche width in the model. The niche process filters species based on the relative performance of species i compared to the other species in the focal cell, 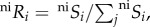where 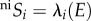(figure 1a(ii)), in a process equivalent to the species-sorting paradigm [14,15].

(iii). Composite process

Since ^neS_i and ⁿⁱS_i are independent, the composite process filters species based on the probability ^mS_i = ^neS_i × ⁿⁱS_i of a species both reaching a cell and surviving in it (figure 1a(iii)). The probability of species i colonizing an empty cell in a system governed by the composite process can then be given by 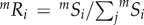. This formulation allows ^mR_i to vary continuously from a pure neutral (^neR_i) to a pure niche (ⁿⁱR_i) process as dispersal limitation (1/d) decreases and niche separation (1/σ) increases (figure 1b(ii)) (see electronic supplementary material, appendix B, for details).

(b). From process to pattern

To test the neutral–niche continuum hypothesis, we examined four different, complementary community patterns. Aggregate community patterns (such as species abundance distributions) have been extensively used to describe natural communities and to investigate the processes that generate them [19,20]. Empirical data are not readily available for succession dynamics [5], and well-replicated empirical community assembly data [3,13] are also scarce. Although observing differences between community patterns necessarily indicates a difference in the nature of the processes involved, similarity of a single pattern is usually considered to be inconclusive, because different processes can produce similar patterns [8]. Using several patterns simultaneously is therefore necessary to better discriminate between the processes generating them [21]. Understanding how particular patterns vary with changes in the neutral and niche processes is nonetheless important because the information value of multiple patterns may be redundant or complementary. Different patterns may contain similar information on processes, and therefore be redundant [22], or may be differently sensitive to changes in processes [23], and behave nonlinearly [16]. We therefore examined how the four following community patterns varied with changes in the parameters of the three models (neutral, niche and composite).

(i). Pattern 1. Rank abundance distribution

Rank abundance distributions (RAD) were used to depict the patterns of commonness and rarity in the community [9,18,24]. As we are only interested in the RAD shape, species were sorted according to their abundance for each simulation, regardless of their identity. The number of species for the 25% and 75% percentiles of abundance was computed over all simulations for model comparison. The area under the curve (AUC) of the normalized RADs is reported (i.e. abundance rescaled between 0 and 1), with an AUC closer to 0 for larger differences between abundant and rare species.

(ii). Pattern 2. Species–area relationship

Species–area relationships (SAR) were used as a proxy for spatial aggregation to assess the relative positions of conspecifics, with aggregated species having low probabilities of being present in samples [25]. Consequently, evenly distributed species produce steep SARs for small areas, and aggregated species produce a more shallow slope [26]. Nested SARs were calculated by plotting the number of species present in plots of increasing grain [27], dividing the environment into a lattice of square plots, with each plot containing 4 × 4 to 101 × 101 cells. The 25% and 75% percentiles of the number of species for each grain were computed over all simulations for model comparison. The AUC of the SARs was used to summarize the results, with a steeper SAR producing a higher AUC.

(iii). Pattern 3. Diversity signature

Compositional diversity was assessed using diversity signatures, produced by plotting β-diversity against α-diversity [19], with β-diversity computed using Jaccard dissimilarity [28]. To vary α- and β-diversity, we computed indices for square plots of increasing grain, from 4 × 4 to 20 × 20 point cells. The α- and β-diversity for each pair of cells produced a diversity signature point on an α–β plot, and the surface densities of these points over all replicates was used for model comparison.

(iv). Pattern 4. Fundamental versus realized niche

Realized and fundamental niches were compared to assess species distributions relative to the spatial distribution of the environmental variable [29]. For each simulation, the species were ordered by their fundamental niches (μ_i). The means of their realized niches were computed using a weighted linear regression to account for greater stochasticity among rare species (species were weighted according to their abundance). The slope of the fundamental niches is 1, since there are 100 species whose niches are regularly spaced over the range of environmental values, which varies between 0 and 100. The slope of the realized niche should be 1 for strict niche separation, and tend towards 0 as the separation between the fundamental niches decreases. The same analysis was also performed by sorting species according to their realized, rather than fundamental niche, for each simulation, since fundamental niches are meaningless in the neutral model.

According to the process-based neutral–niche continuum in CAPS, patterns from the composite model should be similar to those from the neutral model if the niche separation is small (large niche width σ), similar to those from the niche model for weak dispersal limitation (large dispersal ability d), or otherwise lie in between the neutral and niche model outputs. The three models should produce similar, spatially random distributions of individuals when species have no dispersal limitation or niche separation (very large d and σ). Analyses were performed with R v. 3.0.2 [30].

4. Results

The relative values of the four community patterns for the neutral, niche and composite models differed under various combinations of dispersal limitation and niche separation. For very weak dispersal limitation and niche separation (long-range dispersal and large niches), the three models converged to spatially random distributions, resulting in indistinguishable patterns.

(a). Neutral and niche models

Neutral and niche models generated distinct community patterns. The aggregation resulting from the dispersal limitation in the neutral model produced steep RADs and shallow SARs (low AUCs) for short-range dispersal, and tended towards uniform RADs and steep SARs (high AUC) as dispersal increased (dispersal limitation decreased) (figure 2; electronic supplementary material, figures C4 and C5). The niche model produced approximately uniform RADs and steep SARs (high AUC) regardless of the niche separation, due to the almost uniform distribution of the environmental variable (electronic supplementary material, figure C3). The diversity signatures for all models decreased linearly as the grain increased, from near-zero α-diversity and maximum β-diversity, towards the opposite (electronic supplementary material, figures C6 and C7). However, the neutral model produced lower α-diversity and higher β-diversity than the niche model, and its diversity signature did not reach maximum α-diversity and zero β-diversity at the coarsest grain used (electronic supplementary material, figures C6 and C7).

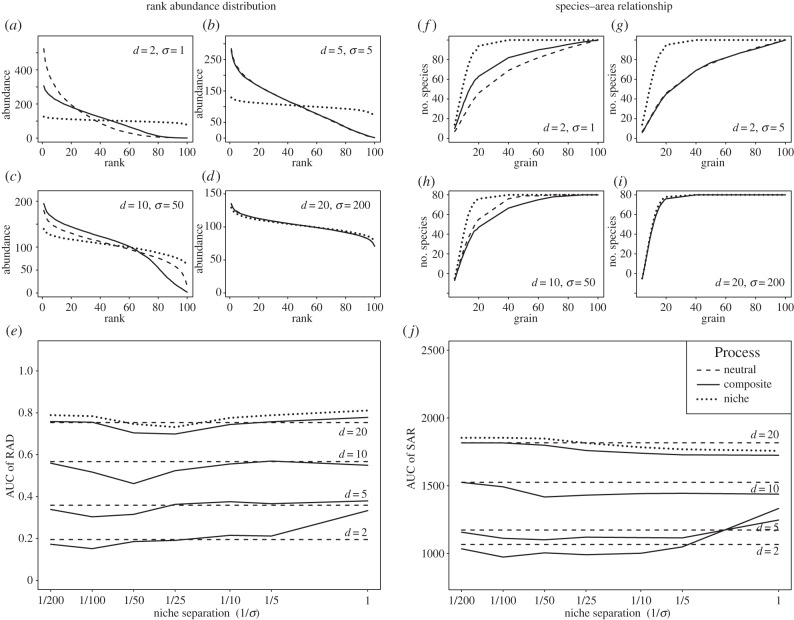
Figure 2.

Rank abundance distributions (RADs) and species-area relationships (SARs) produced by neutral, niche and composite processes for different combinations of dispersal limitation 1/d and niche separation 1/σ (log scale). Four specific, different positions of the composite outputs with respect to the neutral and niche processes are first shown for both the RADs (a–d) and the SARs (f–i). For concise presentation of the results of all parameter combinations, the AUC of (e) the RADs (rescaled between 0 and 1) and of (j) the SARs are shown. A low AUC indicates a steep RAD or a shallow SAR. (a,f) For strong dispersal limitation and niche separation, the composite outputs lie between the neutral (lowest AUCs) and niche (highest AUCs) model outputs; (b,g) for weaker dispersal limitation and niche separation, the composite model outputs are equivalent to the neutral model outputs, and their AUCs are lower than for the niche model; (c,h) as dispersal limitation and niche separation decrease further, the composite model outputs lie outside of the neutral and niche model outputs, and the AUCs are lower than for both the neutral and niche models; (d,i) with very weak dispersal limitation and niche separation the three processes approach spatially random distributions and are indistinguishable, and they have similar AUCs. Note that scales differ between (a) and (d). (e,j) The AUCs generated by the composite model are lower than both the AUCs generated by the neutral and niche models, i.e. lie outside of the neutral–niche continuum for a wide range of parameter values.

The slope of the means of unsorted realized niches was 0 for all values of dispersal d in the neutral model, indicating no association between species distribution and the environmental variable E (figure 3a; electronic supplementary material, figure C8). Once the species were sorted by their realized niches, strong dispersal limitation (low d) led to a slope of 0.3 in the neutral model, due to a non-causal correlation between the spatial aggregation of the species and the environment (figure 3b; electronic supplementary material, figure C9). The slope declined (to 0.22, 0.14 and 0.1) as dispersal limitation decreased and the spatial aggregation of the species no longer matched the spatial distribution of the environment. For the niche model, the slope was approximately 1 for narrow niches (σ = 1) and decreased to almost 0 for wide niches (σ = 200), as the model becomes similar to a spatially random distribution.

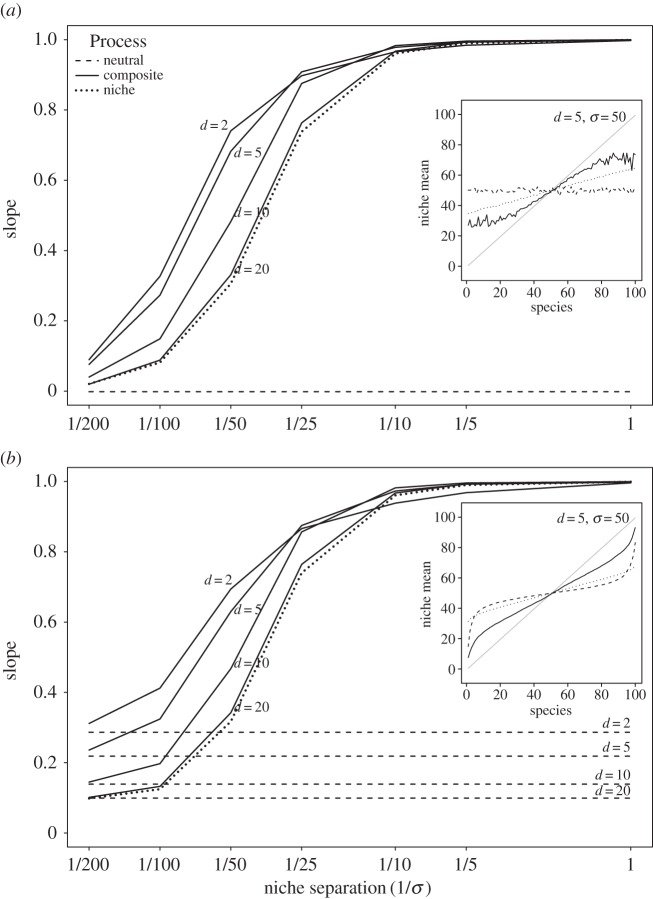
Figure 3.

Effect of neutral, niche and composite processes on the realized niche. Slopes of the realized niches for different combinations of dispersal limitation 1/d and niche separation 1/σ (log scale): (a) species are not sorted according to their realized niche; (b) species are sorted according to their realized niche. The insets provide examples of the realized niches for all species (from which the slopes were computed) for the three models, compared to the fundamental niches represented as a grey line and with a slope of 1. A slope of 1 therefore means that the realized and fundamental niches are equivalent (the realized niches would coincide with the fundamental niches in the insets), whereas a slope of 0 means that all species have the same realized niche (the realized niches in the insets would show a horizontal line). For weak dispersal limitation and strong niche separation, the composite model generates similar slopes to the niche model. As niche separation decreases and dispersal limitation increases (lower d), the composite model generates steeper slopes than the niche model, and the realized niches are more similar to the fundamental ones.

(b). Composite models

The SAR, RAD and diversity signature patterns generated by the composite model occupied three positions with respect to the patterns generated by the neutral and niche models, depending on the model parameters. First, for strong dispersal limitation and niche separation (short-range dispersal and narrow niches), the composite model produced RADs, SARs and diversity signatures lying between those produced by the neutral and niche models (intermediate AUCs, figure 2a,f; electronic supplementary material, figures C4–C7). Then, as dispersal limitation and niche separation decreased (d and σ increased), the composite model produced patterns similar to the neutral model (figure 2b,g; electronic supplementary material, figures C4–C7). Finally, as dispersal limitation and niche separation decrease further, the composite outputs lay beyond the patterns produced by neutral and niche models, with steeper RADS and SARs (lower AUCs, figure 2c,h; electronic supplementary material, figures C4 and C5), and lower α-diversity but intermediate or higher β-diversity values (electronic supplementary material, figures C6 and C7c,d; see tables S1 and S2, for numerical values). The exact dispersal and niche parameter values for which the composite model lay beyond the neutral model varied depending on the community pattern.

Contrary to the SAR, RAD and diversity signature, the realized niches generated by the composite model were more similar to those generated by the niche than by the neutral model (figure 3; electronic supplementary material, figures C8 and C9). The slopes of the realized niches generated by the composite and the niche models were both higher than the slopes generated by the neutral model. However, the slopes generated by the composite models were higher by more than 5% than those generated by the niche models for strong dispersal limitation (low d) and intermediate niche separation (figure 3; electronic supplementary material, figures C8 and C9). This means that the realized niche was closer to the fundamental niche for the composite model, lying outside of the range of the neutral and niche model outputs.

5. Discussion

Using CAPS, we have shown that patterns emerging from the interactions between neutral and niche filters do not consistently lie within the range of corresponding neutral and niche model outputs (figure 4), even when considering the original attribute-based continuum (electronic supplementary material, appendix E), except for communities of species with strong dispersal limitation and niche separation (low d and σ). This finding is not consistent with the concept of a neutral–niche continuum that assumes a simple trade-off between pure neutral and pure niche processes. The neutral–niche continuum therefore has limited value for describing how neutral–niche interactions generate emergent community patterns (electronic supplementary material, appendix A, discusses the inclusion of more complex processes in CAPS and conditions under which the continuum hypothesis holds).

Figure 4.

(a–d) Summary of the position of the four community patterns generated by the composite model with respect to those generated by the neutral and niche models, across the range of dispersal limitation and niche separation parameters. Symbols represent six different outcomes for each pattern, as described in the legend. Black-filled shapes mean that the composite pattern lies outside the range of the neutral and niche patterns. The results are shown within the space defined by the CAPS (figure 1b). For the realized niche, we present the results for species sorted according to their fundamental niches. Slope differences less than 0.05 were considered similar.

By comparison, the more complex multi-dimensional CAPS revealed previously under-appreciated interactions between neutral and niche filters that result from feedback between individuals and the biotic and abiotic context. In the neutral model, strong dispersal limitation implies that species will only be able to colonize nearby cells. There will therefore be differences in species abundance due to species aggregation, which increases the propagule pressure (figure 2); a well-known feature of neutral dynamics [18]. In the niche model, narrow niches confine species to specific environments, and species abundance thus depends on environmental heterogeneity (equivalent to species-sorting) [14,15]. In the composite model, community patterns result from dispersal and environmental heterogeneity [31]. As a result of aggregation and strong dispersal limitation, some species colonize cells that are non-optimal through a mass-effect. Species are therefore more aggregated in the composite than niche model. However, strong niche separation will limit aggregation due to environmental constraints and prevents individuals in the composite model from being as aggregated as in the neutral model. This negative feedback that neutral and niche processes can have on each other explains why the composite model outputs lie between the neutral and niche model outputs for short-range dispersal and narrow niches for RADs, SARs and diversity signatures (figure 4a–c).

As dispersal limitation decreases (d increases), species become able to overcome environmental barriers and locate specific niche conditions [32]. Alternatively, as niche separation decreases (σ increases), the environment becomes more suitable and does not represent efficient barriers to establishment [33]. In these two situations, species can aggregate in larger clusters, with dispersal limitation preventing species sorting, and the composite model outputs for RADs, SARs and diversity signatures become similar to the neutral model outputs (figure 4a–c). As the dispersal limitation and the niche separation decrease further, habitat selection and dispersal-limited aggregation amplify each other through positive feedback. This reveals a new kind of interaction between neutral and niche processes, unaccounted for by metacommunity theory. Specifically, in a spatially autocorrelated environment, two individuals from the same species have a higher chance of being located close to each other simply because of niche selection [34]. Nearby locations will in turn be more likely to be colonized by individuals from the same species due to the dispersal process. As a result, species relative abundance, aggregation and community composition resulting from the composite model lie outside of the range of neutral and niche model outputs, refuting the neutral–niche continuum hypothesis (figure 4a–c).

This positive feedback between the neutral and niche processes also explains why the composite model produces more similar realized and fundamental niches than the niche model, for strong and medium dispersal limitation, and weak and medium niche separation (figure 4d). As niche separation decreases, niche selection becomes weaker, increasing stochasticity during colonization. In the niche model, ecological drift then reduces the correlation between the mean of the environmental variable of the occupied cells and the niche optimum. However, in the composite model, dispersal limitation reduces the impact of ecological drift, because only species within a given distance of the focal cell can colonize it, therefore reducing local stochasticity. Since the environment is spatially autocorrelated, there is a greater chance that species with a matching niche optimum will be present in the vicinity of the focal cell, leading to a stronger correlation between realized and fundamental niches in the composite model.

The application of CAPS has revealed two novel aspects of community dynamics. First, the reciprocal amplification of neutral and niche processes produced by composite models has different impacts on different community patterns, separating them into two groups: (i) the RAD, SAR and diversity signature patterns are most similar to neutral model outputs, and (ii) the patterns of realized niches are most similar to niche model outputs (figure 4). It has previously been shown that both neutral and non-neutral models produce similar RADs [8] and such community patterns have been considered uninformative [3]. Here, we argue instead that the two processes generate multiple patterns differently. This provides an interesting way to reconcile neutral and niche theories: the niche filter determines where different species are found with respect to the environmental variables, whereas the neutral filter determines the relative positions of individuals and species. This explains why neutral models have sometimes successfully reproduced patterns such as RADs and SARs in natural systems [18,35], while failing to explain invasion processes [36] or species co-occurrence [37].

Second, our analyses based on CAPS question the veracity of previous process-based interpretations of community patterns. In similar environments, observing communities with a turnover lower than expected under neutrality is usually attributed to species-specific ‘deterministic’ niche separation [19]. By contrast, communities with a higher turnover are assumed to be structured by external ‘stochastic’ processes. For example, Australasian coral communities were less similar (higher β-diversity) than neutral model predictions [38]. Dornelas et al. [38] suggest that the direction of this departure is explained by asynchrony in fluctuations in environmental conditions [39]. However, using CAPS, for some combinations of neutral and niche filters, our composite model produces β-diversity values higher than neutral model outputs (electronic supplementary material, figures C6 and C7, and table D2). This is because the niche process can no longer be considered deterministic in the composite model. Rather the niche process amplifies the stochastic aspect of the neutral process through feedback with the environment. Although we do not rule out the potential effect of external stochastic processes for explaining the observed turnover of coral communities, we show that a more parsimonious explanation is possible for some combinations of neutral and niche filters alone. Therefore, without comparing all three models in CAPS to assess if the composite model outputs lie between the neutral and niche model outputs, processes other than neutral and niche processes cannot be supported.

6. Conclusion

The CAPS for neutral–niche community dynamics provides a conceptual and methodological advance for understanding and modelling community assembly. It is based on clear, multi-dimensional, mechanistic definitions of neutrality and its niche alternative, rather than on a single community attribute such as niche overlap. It encompasses more of the complexity of the interactions between neutral and niche processes than the widely adopted neutral–niche continuum, which only holds for a limited set of conditions. CAPS enhances the value of community patterns for inferring the roles played by neutral and niche processes and questions previous process-based interpretations of pattern in natural communities.

Data accessibility

The NetLogo code for running the model and the synthetic data for initializing simulations are available in the electronic supplementary material.

Authors' contribution

G.L., C.H. and M.A.M. jointly conceived the research. G.L. developed the model, performed the analyses and drafted the manuscript. C.H. and M.A.M. contributed to the design of the experiments, the interpretation of the results, and to the manuscript preparation. All authors gave final approval for publication.

Competing interests

The authors declare that this research was conducted in the absence of any competing interest.

Funding

This work was supported by Monash University and Australian Research Council grant no. DP150103017. C.H. received support from the National Research Foundation of South Africa (76912 and 81825).