Unexpected complexity in the haplotypes of commonly used inbred strains of laboratory mice

Abstract

Investigation of sequence variation in common inbred mouse strains has revealed a segmented pattern in which regions of high and low variant density are intermixed. Furthermore, it has been suggested that allelic strain distribution patterns also occur in well defined blocks and consequently could be used to map quantitative trait loci (QTL) in comparisons between inbred strains. We report a detailed analysis of polymorphism distribution in multiple inbred mouse strains over a 4.8-megabase region containing a QTL influencing anxiety. Our analysis indicates that it is only partly true that the genomes of inbred strains exist as a patchwork of segments of sequence identity and difference. We show that the definition of haplotype blocks is not robust and that methods for QTL mapping may fail if they assume a simple block-like structure.

Studies of sequence variation between inbred strains of laboratory mice suggest that the distribution of polymorphisms has a mosaic structure of alternating segments of high and low frequency (1-3), consistent with descent of the most commonly used strains from a few subspecies, such as Mus musculus musculus (4). Understanding the structure of sequence variation is important because correlations between genetic and phenotypic variation could help identify the molecular variants underlying quantitative trait loci (QTL) (1, 5), which have proved so refractory to positional cloning (6).

The apparent mosaic structure of the mouse genome can be exploited for QTL mapping in two ways. First, it focuses the search for functional variants into regions of sequence variation. Most QTL are mapped in F2 or back-crosses between inbred strains, a method with great power to detect small effects but with poor resolution: The 95% confidence interval often encompasses half a chromosome (7). The advantage of the mosaic model is that long regions of sequence identity can be excluded as locations for the QTL. Second, QTL mapping can be carried out by associating phenotypic variation in inbred strains with their strain distribution pattern (SDP) [in silico mapping (8)], where an SDP is the pattern of allelic similarities and differences among strains at a locus. If single-nucleotide polymorphisms (SNPs) are randomly distributed across the genomes of inbred strains, mapping QTL by SDP association with phenotype will require a very dense set of markers, but if the distribution is segmented, then a few markers will be sufficient to identify common haplotypes. The approach is identical to the exploitation of haplotype blocks (regions of complete or almost complete linkage disequilibrium) in the human genome for association mapping (9) but requires a different analysis to take advantage of the small number of founder animals from which laboratory strains are descended.

Our understanding of the distribution of polymorphisms is largely based on studies that compare whole-genome shotgun sequence reads, a method that gives a relatively coarse picture. Despite the high overall density of coverage, not all variants are assayed in all strains. If the genome is sequenced so that each nucleotide position is covered with good-quality sequence x times on average, then the probability that a polymorphism is not covered in one strain will be e^-x, assuming a Poisson distribution. Hence, the probability that a site is covered in each of N strains will be (1 - e^-x)^N. For example, analyzing shotgun reads covering chromosome 16 in four strains (3, 10), enough sequence was generated to cover the chromosome 1.3 times for each strain, assuming every strain made an equal contribution. Although 71,000 SNPs were analyzed, just 7.8% of the genome was covered in all strains (x = 1.3 and n = 8 gives 0.727⁸). An alternative strategy is to use primer-directed sequencing, a more efficient strategy when many strains are compared. However, sampling has so far been carried out at a low density: Wiltshire and colleagues (3) sequenced 2,600 evenly distributed loci at intervals of ≈1.1 megabases (Mb) in eight inbred strains.

We do not yet know whether claims for the utility of the mosaic structure of inbred strain sequences for QTL mapping will be supported by higher resolution data on polymorphism distribution. Here, we report an analysis of primer-directed sequencing that sampled, at intervals of <10 kb, a 4.8-Mb region on mouse chromosome one in eight inbred strains (C57BL/6J, C3H/HeJ, DBA/2J, A/J, BALB/cJ, AKR/J, RIII/DmMobJ, and I/LnJ; hereafter referred to as C57BL/6, C3H, DBA/2, A/J, BALB/c, AKR, RIII, and I). These strains are the progenitors of a genetically heterogeneous stock used to map a QTL influencing anxiety to this locus. We were thus able to investigate in more detail the haplotype structure in a well characterized region of the genome containing at least one QTL.

Methods

Contig Construction. We identified mouse bacterial artificial chromosomes (BACs) from RPCI-23 and RPCI-24 libraries (derived from strain C57BL/6) for sequencing (11, 12) by using already published markers (13). We purified BAC clones by using a Qiagen (Valencia, CA) large construction kit and used them for end sequencing with T7 and SP6 primers. fiberfish was used to confirm the BAC order and establish the extent of overlap of clones (14).

Genomic DNA Sequencing. BACs were shotgun sequenced and assembled as described in ref. 15. DNA from eight strains (C57BL/6, C3H, DBA/2, A/J, BALB/c, AKR, RIII, and I), was resequenced by amplification of genomic DNA (note that we included the reference C57BL/6 for resequencing). DNA from inbred lines was obtained from The Jackson Laboratory. Oligonucleotide primers were designed to amplify genomic DNA in a 50-μl PCR with 10 pmol of oligonucleotides (synthesized at MWG Biotech, Ebersberg, Germany), 100 ng of DNA, 0.2 units of Taq Gold, 8 mM dNTP, 8 mM 1× PCR buffer, and 25 mM MgCl_2. PCR conditions were 1 cycle at 95°C for 15 min, 95°C for 30 s, and 62°C for 30 s at 0.5°C per cycle; 13 cycles at 72°C for 60 s, 95°C for 30 s, and 58°C for 30 s; 29 cycles at 72°C for 55 s; and 1 cycle at 72°C for 7 min. PCR products were purified in a 96-well Millipore purification plate and resuspended in 30 μl of H₂O. Two sequencing reactions were prepared for each DNA sample, one with the forward primer and one with the reverse primer. The PCR reagents were removed from solution by an ethanol precipitation in the presence of sodium acetate. All sequencing reactions were run out on an ABI3700 sequencer and assembled by using phred/phrap (16).

Sequence Analysis and Gene Identification. The sequenced region was split into 40-kb consecutive regions and compared against the National Center for Biotechnology Information nonredundant protein database by using blastx (17). The most significant nonoverlapping hits (E < 10^-4) were superimposed on the mouse sequence by using artemis (www.sanger.ac.uk/Software/Artemis). Predicted mouse protein sequences were then searched against the nonredundant protein database, and top matches were used to predict gene structures with genewise (www.ebi.ac.uk/Wise2). Pseudogenes were identified as those that contained no introns and those with no evidence of expression or those that included frameshifts and stop codons. Protein sequences that were only found in rodents and no other species were presumed to be spurious gene predictions (e.g., translated transposable elements or endogenous retroviruses). The complete sequence was also searched against a nonredundant set of mouse cDNAs (18).

Analysis of Strain Distribution Patterns. The spatial structure of SDPs across the sequence was determined by using a dynamic programming algorithm that identifies blocks of contiguous diallelic variants, each block labeled by its most frequent SDP. The optimal block partitioning has a score that maximizes the total number of variants whose SDP matches the corresponding block SDP minus a factor C times the number of block transitions. The positive parameter C is the cost of a block transition. Let N be the total number of diallelic variants. Define Y(i, s) to be the score of the optimal block partitioning for variants 1... i, subject to variant i being in a block with SDP s. Let X(i, s) = 1 if variant i has SDP s, and be 0 otherwise. Y is computed by the recurrence relation

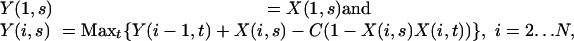where the maximization is performed over all SDPs t. The optimal choice of t is denoted by T(i, s). The blocks are found by backtracking; the sequence σ₁, σ₂,..., σ_N of optimal SDPs at each variant position is computed backwards from N, with

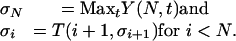A block boundary occurs whenever σ_i differs from σ_{i+ 1}

Results

Sequence Analysis and Gene Identification. We constructed a complete BAC contig of 4,785,409 bp located on chromosome 1 between megabases 142.8 and 147.6 of assembly 30 of the mouse genome. We constructed our own contig to be certain of its accuracy, because earlier drafts of the mouse genome were too unreliable and unstable; however, our contig and assembly 30 are very similar. The contig contains four gaps with an estimated total length of <20 kb. This region corresponds to the 95% confidence interval of a behavioral QTL (13, 19). By using a combination of gene prediction programs and EST databases we identified nine genes and 17 pseudogenes. There are two genes of unknown function: BC027756, a cdc73 homologue, and B830045N13Rik, a homologue of BMP/retinoic acid-inducible neural-specific protein 3 (brinp3). There are three housekeeping genes, glutaredoxin 2 (glrx2), ubiquitin carboxyl-terminal hydrolase isozyme L5 (uchl5) and Sjögren's syndrome antigen A2 (ssa2). There are also four regulators of G protein signaling (rgs1, rgs2, rgs13, and rgs18). The annotated genes were in broad agreement with those in the University of California, Santa Cruz, (http://genome.ucsc.edu) and ensembl (http://mouse.ensembl.org) genome browsers.

To determine additional regions of potential functional significance, we compared the mouse contig with other eukaryotic sequences. We searched the Fugu rubripes genome with tblastx and retrieved 59 regions of significant homology, all of which were components of the nine genes previously identified. To identify conserved noncoding sequences (CNS), we made a comparison with the syntenic region on human chromosome 1 and identified 567 regions with a sequence similarity of >70% that extended ≥100 bp and that did not match any expressed sequences.

Frequency and Distribution of Sequence Variants. We obtained sequence data for all genes in each of the eight strains that constitute the heterogeneous stock. First, we resequenced all exons, including at least 1 kb of flanking sequence. Next, we resequenced all CNS and finally a random selection of 1- to 2-kb segments of nonconserved sequence at intervals of ≈10 kb over the 4.8-Mb region. In total, we obtained 582,503 bp of finished sequence in each of the eight strains (12.17% of the region of interest). On average, the distance between sample sequences was 8.2 kb.

We identified 1,720 sequence variants consisting of 258 microsatellite variants, 137 insertion deletion polymorphisms, and 1,325 SNPs (see www.well.ox.ac.uk/rmott/MOUSE for full details). Table 1 describes the overall sequence coverage within functional (exons and introns, 5′ and 3′ UTRs, and CNS) and nonfunctional regions (all remaining sequences obtained). The estimates are commensurate with those reported for sparser analyses of the whole genome, and they suggest that the region is not unusual in the type and distribution of sequence variants. Extrapolating from observed rates, the unsequenced 4.2 Mb of DNA would be expected to yield a further 1,811 microsatellites, 1,025 indels, and 12,230 SNPs. There were no significant differences in the densities of variants for the different types of sequence except in the coding sequences.

Table 1. Classification of variants by type and context.

		Insertion/deletion			Microsatellite			SNP
Context	bp	No. of variants	Rate/kb	SE	No. of variants	Rate/kb	SE	No. of variants	Rate/kb	SE
3′ UTR	6,767	2	0.296	0.209	1	0.148	0.148	10	1.478	0.467
5′ UTR	783	0	0	0	0	0	0	4	5.109	2.548
CNS	42,795	4	0.093	0.047	7	0.164	0.062	91	2.126	0.223
Coding	9,291	0	0	0	0	0	0	9	0.969	0.323
Intron	144,046	40	0.278	0.044	78	0.541	0.061	337	2.34	0.127
Promoter	5,618	0	0	0	12	2.136	0.616	19	3.382	0.775
Nonconserved	373,203	91	0.244	0.026	160	0.429	0.034	855	2.291	0.078
Unsequenced prediction	4,202,906	1,025	0.244		1,811	0.431		12,230	2.291

Shown is the length of high-quality sequence in each strain, the number of variants per kilobase, and the SE of the rate. The bottom row gives the predicted variants in the remaining sequence.

We investigated how many additional variants are present in two other inbred strains (LP/J and CBA/J) by resequencing 19 contigs (17,087 bp, containing 87 variants) uniformly spaced across the region. No new variants were found, and LP/J was identical to DBA/2 and CBA/J to C3H and A/J at all sampled sites.

We also resequenced a different set of 28 contigs (22,863 bp) in three wild-derived inbred strains [CAST/EiJ, PERC/EiJ, and SPRET/EiJ, which are known to be more genetically divergent from the commonly used inbreds (4)] and one other unrelated inbred strain (SENCARC/PtJ). As expected, a further 310 variants were identified. Table 2 gives the pairwise percentage dissimilarities between all strains and shows that CAST and SPRET are distinct from the others.

Table 2. Dissimilarities among 12 strains based on sequence data from 28 contigs (349 variant sites).

	A/J	AKR	BALB/c	C3H	C57BL/6	DBA	I	RIII	CAST	PERC	SENCARC	SPRET
A/J	0	5	9	0	9	9	9	9	37	11	13	76
AKR	5	0	7	5	7	7	7	7	34	8	11	74
BALB/c	9	7	0	9	0	0	0	1	34	8	5	74
C3H	0	5	9	0	9	9	9	9	37	11	13	76
C57BL/6	9	7	0	9	0	0	0	1	34	8	5	74
DBA	9	7	0	9	0	0	0	1	34	8	5	75
I	9	7	0	9	0	0	0	1	34	8	5	74
RIII	9	7	1	9	1	1	1	0	34	8	4	74
CAST	37	34	34	37	34	34	34	34	0	36	32	73
PERC	11	8	8	11	8	8	8	8	36	0	12	75
SENCARC	13	11	5	13	5	5	5	4	32	12	0	74
SPRET	76	74	74	76	74	75	74	74	73	75	74	0

Dissimilarities are expressed as the percentage of the variant sites for cases in which a pair of strains differ.

Spatial Distribution of Variants. We examined how the density of sequence variants changes across the region and compared the density to a random (Poisson) distribution. Our data are from 1,149 sequenced contigs. Each contig was classified as Coding (66 contigs), Intron (60), Promoter (9), 3′ UTR (8), 5′ UTR (12), CNS (567), or Nonconserved (639). Any case in which a contig contained a mixture of types was divided and treated as two abutting contigs. For each class of contig c, we calculated the average density of SNPs, μ_c (see Table 1). Then for a contig i of class c(i) and length l(i), the number of SNPs in the contig should follow a Poisson distribution with expected number of variants r(i) = l(i)μ_c(i). By summing over all contigs, the expected number of contigs with exactly n SNPs is

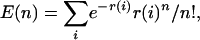with standard deviation E(n)^0.5. Table 3 compares the observed and expected numbers of contigs containing varying numbers of SNPs. There is a significant excess of contigs with no SNPs and a corresponding deficiency of contigs with them, indicating that polymorphism density is clustered. Moreover, contigs with no SNPs are approximately uniformly distributed throughout the region, and SNP density varies in an unstructured manner across the region with alternating SNP-dense contigs and microdeserts (Fig. 2, which is published as supporting information on the PNAS web site). Although it is generally true that the rates of SNP density in each pairwise comparison fluctuate between two extremes of high and low, there are also intermediate rates. For example, in an 800-kb interval (between 3.8 and 4.6 Mb), three strain comparisons (C3H versus C57BL/6, I versus C57BL/6, and C3H versus I) show an average of 0.8 variants per 10 kb, compared to a rate of <0.5 variants per Mb for the A/J versus C3H comparison. Fluctuating frequency makes it difficult to determine whether smaller deserts exist within regions of high SNP density. For example, there are regions of 25 kb that contain just one or two SNPs within the high-density regions in comparisons between I and RIII or between C3H and C57BL/6.

Table 3. Expected and observed number of variants per sequenced contig.

No. of variants per contig	Observed frequency	Expected frequency	SD*
0	734	412.27	20.30
1	191	260.41	16.14
2	99	188.91	13.74
3	38	128.12	11.32
4	25	73.23	8.56
5	19	36.39	6.03
6	9	16.87	4.11
7	9	8.07	2.84
8	5	4.43	2.10
9	2	2.91	1.71
>9	19	18.38	4.29

^*SD of the values given for expected frequency.

Strain Distribution Patterns. We next analyzed the SDP at each sequence variant. Because there are eight strains, there are 127 possible SDPs; yet we identified just 19 SDPs among the SNPs and indels (microsatellites were omitted from this analysis).

In Table 4, the SDPs are represented as a series of 0s and 1s (where the first element is always 0) in the order A/J, AKR, BALB, C3H, C57BL/6, DBA, I, and RIII. Two variants can have the same SDP but have different alleles. The top three SDPs account for 58% of all variants, and the top 13 for almost 99%.

Table 4. Frequencies of SDP.

SDP	Count (%)	Cumulative percentage
Common variants
01000101	349 (23.82)	23.82
01101111	320 (21.84)	45.67
01101100	183 (12.49)	58.16
00101111	120 (8.19)	66.35
00000001	105 (7.17)	73.52
00101000	88 (6.01)	79.52
01000000	72 (4.92)	84.44
01000111	56 (3.82)	88.26
01101110	43 (2.94)	91.20
00000011	40 (2.73)	93.93
00000010	29 (1.98)	95.90
01000100	25 (1.71)	97.61
00101110	20 (1.37)	98.98
Rare variants
00101010	6 (0.41)	99.39
00101011	4 (0.27)	99.66
00010000	2 (0.14)	99.80
00100000	1 (0.07)	99.86
00001000	1 (0.07)	99.93
00000100	1 (0.07)	100.00

Each SDP is represented as a string of 0s and 1s, with the first element constrained to be 0. Shown is the frequency at which the SDP was observed and the cumulative percentage of variants for a given SDP.

We estimated how many additional SDPs would have been detected had we sequenced the entire region by sampling from our data the same percentage of information that we extracted from the whole region. We performed 1,000 simulations in which 12% of the sequenced contigs were subsampled (i.e., 1.44% of the region). The mean number of SDPs found in the sampled data was 13.21 ± 0.045, or 69.5% of all observed SDP. However, the missing SDPs were rare, accounting for <2% of all variants. If we had sequenced the entire region, we expect unobserved SDPs to have accounted also for <2% of the total. Consequently, we expect to have encountered all but the rarest SDPs.

We next examined the spatial distribution of SDPs to investigate whether we can infer the presence of regions of sequence similarity (or haplotype blocks) from adjacent markers with the same SDP. In Fig.1a we show the distribution of the 13 most common SDPs (from Table 4) occurring in 1,450 diallelic variants. The figure shows that variants with the same SDP tend to occur nearby but, significantly, are often intermixed with other SDPs.

Fig. 1.

Haplotype structure of 1,450 diallelic variants with SDP frequency >1% between eight inbred strains across a 4.8-Mb region of mouse chromosome 1. The region is represented along the horizontal axis and scaled such that the nth coordinate from the left edge corresponds to the nth variant, broken into two parts for clarity with the top section showing the first 725 variants and the bottom showing the remainder. (a) The alternating gray and white tracks show the spatial arrangement of the 13 most common SDP arranged from top to bottom in the same order as in Table 4 (so that the top SDP is 01000101 and the bottom SDP is 00101110). Each track represents one SDP, with a bar on the track at points where the corresponding variant has that SDP. (b) The gray and orange bands show the block partitioning produced by a dynamic programming algorithm that identifies an optimal partition that minimizes the SDP heterogeneity within each block, subject to a block transition cost C = 8 (see Methods). The strains are (top to bottom) A/J, AKR, BALB/c, C3H, C57BL/6, DBA/2, I, and RIII. Block boundaries are white vertical lines. Within each block, the major SDP is indicated by the black and orange horizontal bands. Strains with the same color have the same allele. (c) The optimal block partitioning for C = 0, i.e., perfect SDP fidelity within each block. Boundaries are not shown because many blocks have a length of 1 bp and would therefore be invisible.

To investigate the importance of SDP mixing, we devised a dynamic programming algorithm to construct an optimal block partition of the region. The algorithm maximizes the number of variants that constitute the most common SDP within a single block. The likelihood of a block transition is controlled by a positive cost C, with low values encouraging transitions. Zhang and coworkers (20) describe a dynamic programming algorithm to find the block structure that minimizes the numbers of SNPs needed to determine haplotypes. Here, our aim is different: to make the pattern of haplotype sharing between the inbred strains nearly constant within each block.

We show the block structure found by using C = 8 in Fig. 1b and C = 0 in Fig. 1c. When C = 8, although the smallest number of blocks is found, the resulting block structure fails to capture much of the variation among the SDPs. Within each of the 13 blocks in Fig. 1b, the fidelity, defined as the percentage of variants with the most common SDP of the block, varied from 56% to 94%, with an average of 78%. Overall, 80% of the variants shared the major SDP for their block. Physical block length varied from 40 kb to 1.51 Mb. The number of blocks can be increased by reducing C but at the cost of losing much of the larger scale structure. Moreover, the average fidelity does not exceed 80% until C = 3 with 22 blocks. Perfect fidelity occurs when C = 0, with 374 blocks (Fig. 1c, Table 5, and Fig. 3, which is published as supporting information on the PNAS web site).

This analysis shows the difficulty of defining a simple block structure when many strains are considered simultaneously. However, the block structure in Fig. 1b can be explained in terms of a mosaic of phylogenetic trees connecting the strains; the great majority of variants within a block are consistent with the same tree, indicating that Fig. 1b has biological validity. Some blocks share the same tree, with five distinct trees occurring across the region (Fig. 4, which is published as supporting information on the PNAS web site). Gene conversion events might explain some of the alternating tree patterns observed.

Discussion

We report here the most detailed study to date of local polymorphism distribution in multiple inbred mouse strains. We analyzed a 4.8-Mb region on chromosome 1, selected because it contains a QTL influencing anxiety in mice, but we see no reason why the conclusions we draw should not be applicable to other genomic regions. Some of our findings are reminiscent of observations on the distribution of haplotype blocks in the human genome, where a number of mechanisms could explain the observation of long tracts of linkage disequilibrium (21-23). Our data confirm that the distribution of sequence variants in the genomes of common inbred mouse strains is not random, but the data also indicate that there are important limitations to exploiting the haplotype structure for QTL mapping.

First, SNP deserts (regions that have very few SNPs in a comparison between two strains) vary considerably in the frequency of variants, complicating their use to exclude regions from containing QTL. In some cases the strategy may work: We found only 2 SNPs that distinguish A/J and C3H in the entire 4.8 Mb, so a QTL mapped in a cross between A/J and C3H could be excluded from this region. By contrast, there are 38 SNPs that differentiate C3H and C57BL/6 in a 1.3-Mb region (3.3-4.6 Mb); a similar density was found in comparisons between I and C57BL/6. Although it is reasonable to describe SNP distribution as bimodal with some regions of high density and some of low density, there is considerable variation within the high-density regions, with an excess of microdeserts.

To what extent is the current picture of the distribution of SNP deserts based on how densely the genome has been sampled? Our data are for a SNP-dense region, but 64% of the contigs we sequenced contained no variants. Consequently, if M 1-kb segments were sampled at random across a SNP-dense region in the genome, the probability that none contained a SNP in all eight strains, would be 0.64^M. If SNPs were 200 kb apart and M = 5, then 10% of the time, a 1-Mb desert would be reported incorrectly. Very long deserts are more likely to be genuine, as the A/J versus C3H comparison shows.

A second concern is the difficulty of defining an accurate haplotype block structure. Our analysis indicates it is unsafe to assume that a high-fidelity haplotype block exists between markers that share the same SDP. Although variants with the same SDP tend to be clustered together, they do not generally occur in simple blocks. This point is critical for in silico mapping strategies that attempt to correlate phenotypic variation to haplotypes: The presence of a QTL is indicated by finding an SDP block (or haplotype) common to diverse inbred strains that also share a phenotype. If we insist on perfect agreement of SDPs to define a block, then the 5-Mb region contains 374 distinct blocks (Table 5); if the region were fully resequenced, the blocks would likely be further fragmented. Consequently in silico haplotype mapping based on a sparse marker density will have an unacceptably high false-negative rate for QTL detection.

Table 5. SDP block structure.

C	No. of blocks	Block fidelity, %	Variant fidelity, %
0	374	100.0	100.0
1	71	86.6	87.6
2	31	81.4	84.1
3	22	80.3	82.6
4	17	78.2	81.4
5	15	76.7	80.7
6	15	76.7	80.7
7	14	75.7	80.3
8	13	77.6	79.8
9	11	76.6	78.6
10	11	76.6	78.6
11	11	76.6	78.6
12	11	76.6	78.6
13	11	76.6	78.6
14	11	76.6	78.6

Data were obtained from 1,450 common diallelic variants by varying the block transition cost C. Shown are the number of SDP blocks, the percentage average fidelity per block and the percentage of variants whose SDP matched the major SDP of their block.

Furthermore, our results indicate that haplotype analysis may not provide as high a resolution for mapping as some have predicted. Wade and colleagues (1) estimate in a comparison between C57BL/6 and 129 that >90% of the genome can be classified as either high (45 per 10 kb) or low (1.0 per 10 kb) SNP content occurring in segments with an average size of 1.2 Mb. Consequently, a QTL could be mapped into a region of about 2 Mb by using sequence variant information, and combining mapping information from additional strains could further reduce the interval (3, 5).

However, our data argue that increasing the number of strains for QTL mapping would not increase resolution to the expected extent. Assuming that block boundaries occur randomly with a mean block length of L bp and that each strain is independent, the SDP pattern among N strains would be expected to change every L/(N - 1) bp on average. Consequently if L = 1.2 Mb, mapping resolution with eight strains should be 1.2/(8-1) = 0.17 Mb. In fact, all of our 13 blocks are much larger, with a mean length of 4.8/12 = 0.4 Mb, over twice that of Wade and colleagues (1) (the 13 blocks in Fig. 1b were treated as 12 because the first and last blocks were unbounded).

Our observations do not invalidate attempts to map QTL by using the mosaic structure of sequence variation in inbred mouse strains, but they do impose some restrictions on the methods. We argue that successful QTL mapping requires complete sequence information, so that we can avoid using blocks altogether by characterizing any region by the distribution of its SDP frequencies and mapping QTL by trait-SDP association. A QTL would correspond to any region dense in SDPs associated with the trait. Alternatively, by interpreting the block structure as a phylogenetic mosaic, it might be possible to map QTL by using a block-based strategy, constraining any functional variant within a block to be consistent with the block's phylogenetic tree (24).

It might be thought that using complete sequence information from multiple strains would impose an intolerably high significance threshold for detecting QTL, but this is not the case. Statistical power to detect QTL will be affected by the number of independent tests to be performed, which depends on the number of SDPs or trees across the genome rather than the number of variants. Our analysis suggests that only a limited number of SDPs will occur. Although theoretically the number of SDPs is 2^{N - 1}, it is more likely that there will be far fewer, perhaps of the order N, if the strains can be fitted on to a small number of phylogenetic trees. However we do not yet know how the number of SDPs across the genome depends on the number of strains. Should many SDPs occur, higher mapping resolution would be possible, but at the cost of lower power or more false positives.

The picture of the laboratory mouse genome as a mosaic of internally consistent haplotype blocks might not be the best view from the standpoint of QTL mapping experiments. If a QTL is caused by a single diallelic variant, then all nearby variants with the same SDP will appear to be functional candidates as well. It will be more fruitful for QTL mapping to treat the SDP distribution across the genome in a probabilistic manner, in which regions are characterized by their SDP profiles. The consequences of the haplotype structure presented here for mapping the behavioral QTL in the region are discussed elsewhere. We require a method that can assign the probability that any variant is the QTL and then test that likelihood against others, thereby providing a ranking of QTL sequences for functional investigation.