Abstract
Despite the well-known design principles of vascular systems, it is unclear whether the vascular arterial tree obeys some scaling constraints during normal growth and ageing in a given species. Based on the micro-computed tomography measurements of coronary arterial trees in mice at different ages (one week to more than eight months), we show a constant exponent of 3/4, but age-dependent scaling coefficients in a length–volume scaling law (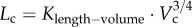
Lc is the crown length, Vc is the crown volume, Klength–volume is the age-dependent scaling coefficient) during normal growth and ageing. The constant 3/4 exponent represents the self-similar fractal-like branching pattern (i.e. basic mechanism to regulate the development of vascular trees within a species), whereas the age-dependent scaling coefficients characterize the structural growth or resorption of vascular trees during normal growth or ageing, respectively. This study enhances the understanding of age-associated changes in vascular structure and function.
Keywords: arterial tree, scaling law, growth and ageing
1. Introduction
The vascular system undergoes substantial changes during normal growth and ageing [1]. The relationship between a biologic variable and body weight (BW) has been characterized by a scaling power-law (i.e. interspecific scaling law), which is considered a universal principle that dictates allometry. The fourth-dimension allometric scaling law was found to relate BW to the shape, anatomy or physiological parameters among species [2,3]. Seiler et al. reported a power-law structure (i.e. intraspecific scaling law) of epicardial coronary arterial trees in the early 1990s [4,5]. In 1997, West et al., proposed a mathematical model referred to as the West, Brown and Enquist (WBE) model to explain the allometric 3/4 scaling law of metabolism [6]. This motivated a series of studies on the fourth-dimension of biological allometry between species (interspecific) [7–14]. Moreover, we deduced mathematical scaling models that dictate the design of coronary arterial trees within a given species (intraspecific) [15,16]. We also investigated intraspecific scaling laws in arterial/venous trees down to the capillaries within various organs of different species [17–20]. It is unknown, however, whether intraspecific laws hold during growth and ageing in the coronary arterial trees (table 1).
Table 1.
Nomenclature.
| interspecific scaling law | a scaling power-law to show the allometric relationship between a biologic variable and body weight. A general format of the interspecific law is written as: A = K · Ba, where A refers to the shape, anatomy, or physiological parameters among species, B body weight, K the scaling coefficient and a the scaling exponent. |
| Y = Kmetabolism · B3/4 | the allometric 3/4 scaling law of metabolism (i.e. an interspecific scaling law), where ‘Y’ is the metabolic rate and ‘Kmetabolism’ is the corresponding scaling coefficient. |
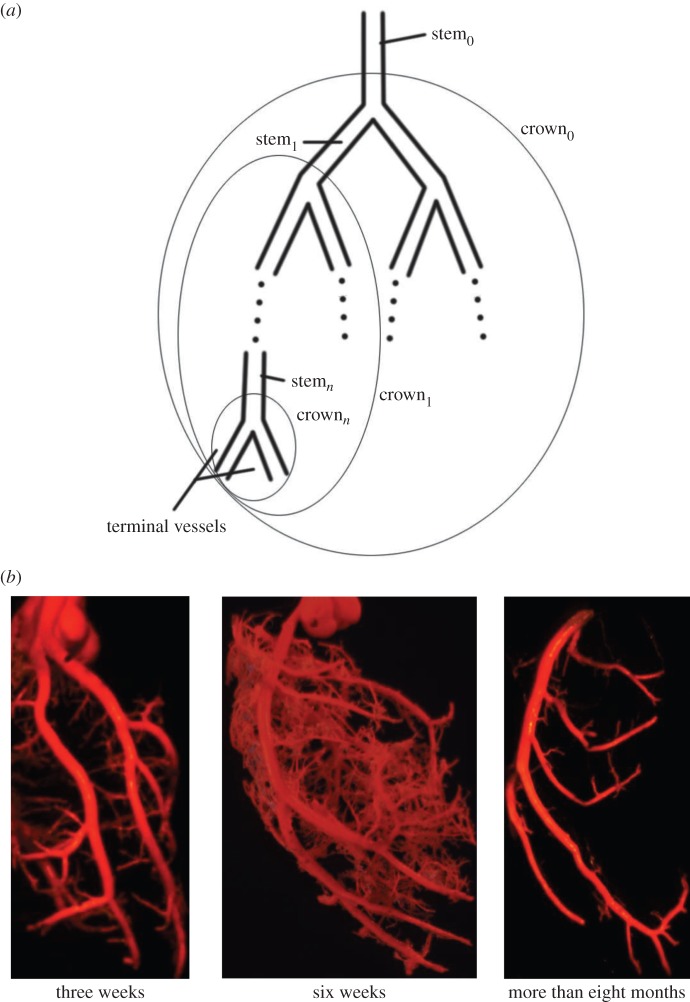
| the stem–crown units | a vessel in a tree is selected as a stem and the subtree distal to the stem down to the terminal vessels is defined as a crown. A tree structure consists of many stem–crown units, as shown in figure 1a. In a stem–crown unit, the crown volume, Vc, is the sum of the intravascular volume of each vessel from the stem to the terminal vessels and the crown length, Lc, is the sum of the length of each vessel from the stem to the terminal vessels. |
| intraspecific scaling law | a scaling power-law to dictate the design of cardiovascular trees within a given species. A general format of the intraspecific law is written as: A = K · Ba, where A and B refer to morphometric or physiological parameters in an integrated system of stem–crown units, K the scaling coefficient and a the scaling exponent. |
 |
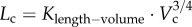the length–volume scaling law (i.e. an intraspecific law), where ‘Klength–volume’ is the scaling coefficient of the length–volume scaling law. |
Here, the objective is to understand the scaling laws that dictate the age-related structural and functional changes in the coronary arterial trees. Based on the micro-computed tomography (µCT) measurements of coronary arterial trees in normal mice at different ages (one week to more than eight months), we show an age-independent 3/4 exponent in the length–volume scaling law. The scaling coefficient, Klength–volume, characterizes the structural adaptation (growth or resorption) of the coronary arterial tree during normal growth or ageing, respectively. The scaling constraint of the exponent represents the self-similar fractal-like branching pattern under physical and biological constraints relevant to diffusion-limited aggregation [21–23]. Hence, although the scaling of morphology or pattern of the vascular tree is maintained throughout normal growth and ageing, the absolute size changes.
2. Material and methods
2.1. Theory
The stem–crown units are defined in figure 1a. A tree structure consists of many stem–crown units. Similar to a previous study [19], the branching ratio, diameter ratio and length ratio in a fractal-like idealized symmetric tree are defined as: 
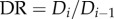and 
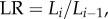where ni, Di and Li are the number, diameter and length of vessels in level i, 
where the inlet of the tree is level 0, and the terminal vessels refer to level Ni. Based on the assumptions of 
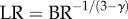and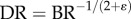 
(parameters γ and ɛ are constants that vary among organs and species), we derive the intraspecific length–volume scaling law, i.e. 
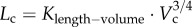(see the mathematical derivation in appendix A).
Figure 1.
(a) A schematic illustration of the definition of stem–crown units; (b) the casts of coronary arterial trees of mice at ages of three weeks, six weeks and more than eight months. (Online version in colour.)
2.2. Experiments
2.2.1. Study design
To investigate the effects of growth and ageing on the scaling coefficient and exponent of the scaling law, coronary arterial trees of Institute of Cancer Research (ICR) mice were reconstructed from µCT images. The ICR mice were divided into six groups as: one-week group (six mice and 17 coronary arterial trees), three-weeks group (nine mice and 26 coronary arterial trees), six-weeks group (10 mice and 28 coronary arterial trees), 12-weeks group (six mice and 18 coronary arterial trees), five- to six-months group (nine mice and 27 coronary arterial trees) and more than eight-months group (10 mice and 28 coronary arterial trees).
2.2.2. Specimen preparation
The animal was anaesthetized with pentobarbital sodium (60 mg kg−1) and heparinized with undiluted heparin (1 ml, 1000 USPU ml−1). After midline incision for laparotomy, the animal was terminated by injecting an overdose of pentobarbital sodium through the inferior vena cava. Heparinized PBS (1 unit heparin ml−1) at 37°C was injected into the thoracic aorta and drained from the sectioned inferior vena cava for 10 min. The heart was exposed, and heparinized PBS was used to maintain epicardial moisture. The thoracic aorta was then filled with acetone solution at a constant pressure of 100 mmHg. After 3 min, the thoracic aorta was perfused with the casting solution (7 g acrylonitrile butadiene styrene and 10 g lead tetroxide microspheres in 100 ml acetone solution) at a constant pressure of 100 mmHg. The flow of orange cast solution was observed to pass by the epicardial coronary arteries down to the intramyocardial vessels, but it was not found in the veins, because the lead tetroxide microspheres with diameter of 8–15 µm blocked the distal small arteries. The flow of cast solution was zero during the 90 min prior to hardening of the cast at a constant pressure of 100 mmHg. The animal was stored in 10% formalin in the refrigerator for 24 h. Reperfusion was then performed to prevent possible cast shrinkage at a constant pressure of 100 mmHg. The heart was dissected and stored in 10% formalin in the refrigerator until µCT scans.
After µCT scans, three hearts (i.e. a heart at three weeks, a heart at six weeks and a heart at more than eight months) were corroded with a 30% KOH for a week similar to previous studies [24,25]. After the tissue was washed away with soap and water, a solid cast of the vasculature was obtained from each heart. The trunks of coronary arterial trees were easily identified in a cast, as shown in figure 1b.
2.2.3. Micro-computed tomography imaging acquisition and three-dimensional reconstruction of coronary arterial trees
µCT scanning was performed using the ZKKS-MCT-Sharp µCT scanner (Guangzhou, China). Images were collected in a 360° scan with 0.72° increments (500 rotation steps). The X-ray energy power and voltage were 35 W and 60 kV, respectively. Data matrices were 400 × 400 × 400 with an isotropic voxel size of 20 µm. Total scan time for each heart was 30–50 min. The morphometric data of coronary arterial trees were extracted from µCT images using a grey-scale threshold method in the MIMICS software (Materialise, NV, Belgium). Briefly, a low CT-threshold of 100 was selected to include the small vessel segments. A centreline was formed by a series of centre points which were located in the centre on the cross-sectional views of the contour of the three-dimensional vessel. Subsequently, the best-fit diameter, Dfit, was calculated as twice the average radius between the point on the centreline and the contour forming the three-dimensional vessel. Similar to previous studies [26–28], the blurring of small vessel edges was corrected to yield Dcorrect by fitting a Gaussian distribution function (i.e. the modulation transfer function of the µCT scanner) to the line profiles followed by computation of the input square wave. To reduce the sampling error of the finite discrete grid, the coronary arterial trees with vessel diameter greater than or equal to 40 µm (twice the voxel size) were used for testing the validity of the intraspecific length–volume scaling law.
2.2.4. Measurements of the cast of coronary arterial trees
The arterial casts were dissected and viewed under a stereo-dissecting microscope (80 × magnification, 3.6 µm optical resolution) similar to previous studies [24,25]. The cast images were taken from different angles by the stereo-dissecting microscope. The trunk of each coronary artery was sketched, and the centreline and the best-fit diameters of its vessels were measured by the SigmaScan Pro v. 5 software for comparison with the µCT measurements. The subtrees arising from the trunk were labelled, pruned, placed in separate jars, further pruned, sketched and measured. This process was continued until the cast of the entire tree was sketched and its morphometric measurements were made. The coronary arterial trees were made of vessels with diameters greater than or equal to 40 µm in correspondence with the µCT measurements.
2.2.5. Generation of stem–crown units
Because a vessel (a segment between two nodes of bifurcation) included 10–80 centre points, the length and intravascular volume of a vessel were defined as: vessel length = ∑ the length between consecutive centre points and intravascular volume of a vessel = ∑ the length between consecutive centre points ·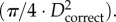 
The cross-sectional area (CSA) of a vessel equalled the intravascular volume divided by the length. Similar to previous studies [18,19,29,30], the stem–crown units were defined for the coronary arterial trees of mice. The crown length and crown volume were determined for each stem–crown unit. The sum of vessel length and intravascular volume of an entire coronary arterial tree down to the terminal vessels (vessel diameter greater than or equal to 40 µm) were defined as 
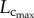and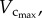 
respectively. The CSA averaged over all vessels of an entire coronary arterial tree was defined as 
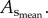The relative errors for 
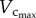and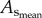 
between µCT and cast measurements were defined as: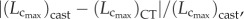 
and 
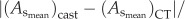
respectively. A comparison of µCT and cast measurements showed less than 3% relative error for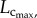 
less than 8% relative error for 
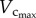and less than 10% relative error for 
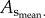This validated the three-dimensional reconstruction from µCT images.
Through the Hagen–Poiseuille law, the resistance of the steady laminar flow in a vessel can be written as: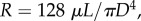 
where μ (4 cp) is the fluid viscosity [20]. The blood flow in a coronary arterial tree follows the conservation of mass at each junction, Qmother
=
∑Qdaughters, and the continuous pressure at each junction, P(L)mother = P(0)daughters, where P(0) and P(L) are the pressures at the entrance and exit of vessels, respectively. Similar to previous studies [31,32], the resistance of a coronary arterial tree, Rtotal, is calculated backward from the terminal vessels to the inlet, based on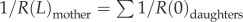 
and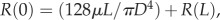 
where R(0) and R(L) are the resistance at the entrance and exit of a vessel, respectively.
2.3. Statistical analysis
Similar to a previous study [29], we determined the following parameters: (i) both scaling coefficient K0 and exponent a in a power-law relation: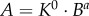 
(defined as the two-parameter model) and (ii) scaling coefficient K with exponent a equal to the theoretical value (i.e. 3/4 in the length–volume scaling law) in a power-law relation: 
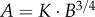(defined by the one-parameter model) by a least-square fit of all stem–crown units in a coronary arterial tree to the length–volume scaling law. The mean and standard deviation (mean ± s.d.) were computed by averaging over all coronary arterial trees (or mice) in each group. Repeated-measures ANOVA was used to compare parameters among those groups, where a p-value less than 0.05 represented a statistically significant difference.
3. Results
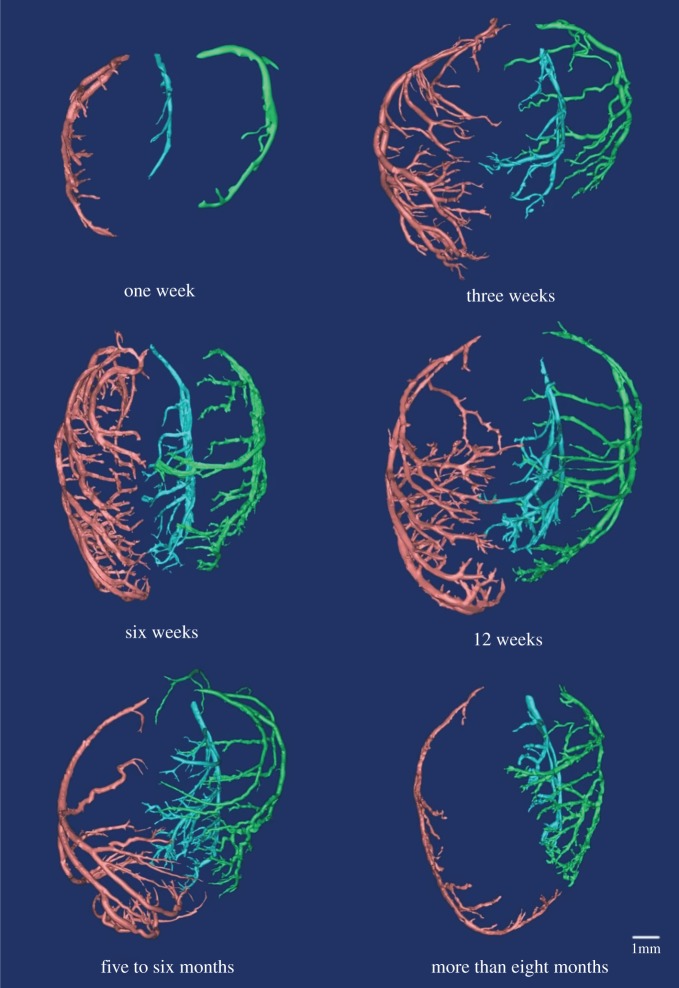
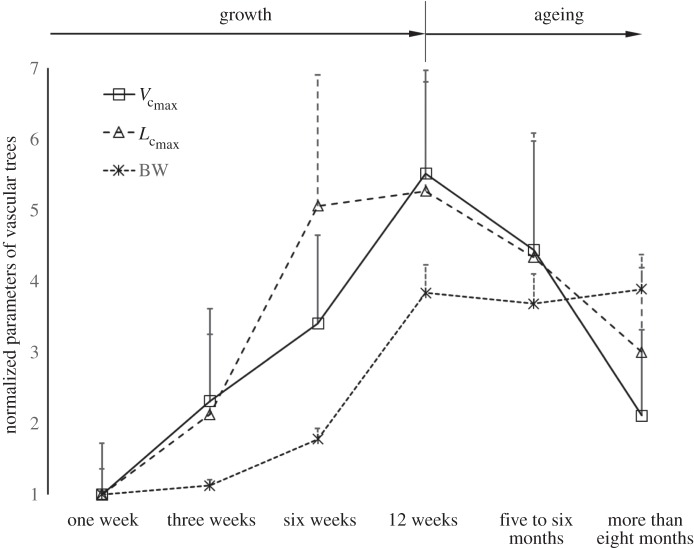
Figure 2 shows coronary arterial trees of mice at different ages (50 mice from one week to more than eight months) reconstructed from µCT images. The three-dimensional µCT reconstruction revealed three major coronary arterial trees in the majority of mice. The corresponding morphometric data of these mice are listed in table 2, where the mean ± s.d. are computed by averaging over all coronary arterial trees (or mice) in each group. The body weight (BW) showed a classical sigmoidal curve during growth (from one to 12 weeks) and ageing (from 12 weeks to more than eight months) in figure 3. The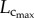 
and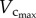 
showed a parabolic curve, which increased during growth, but decreased with ageing. During the period of growth, a significant increase of 
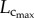occurred from three to six weeks while 
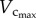had a slight increase. A significant increase of 
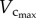also occurred from six to 12 weeks while 
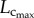remained relatively unchanged. Hence, the length of the coronary arterial tree increases with the enlarged heart size as does the intravascular volume to meet metabolic demand. There was a faster decrease of 
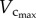than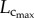 
with ageing, because the former consists of the diameter and length of vessels, both of which are affected by ageing (table 2).
Figure 2.
Coronary arterial trees (from dorsal view) of mice at ages of one week, three weeks, six weeks, 12 weeks, five to six months and more than eight months reconstructed from µCT images. (Online version in colour.)
Table 2.
Morphometric data (mean ± s.d.) reconstructed from µCT images. 
sum of vessel length of the entire coronary arterial trees (down to the terminal vessels reconstructed from µCT images) in a mouse;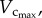 
sum of intravascular volume of the entire coronary arterial trees in a mouse; 
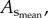CSA averaged over all vessels of an entire coronary arterial tree; BW, body weight; stem–crown number, the total number of stem–crown units in an entire coronary arterial tree; mean ± s.d., the 
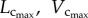and BW were averaged over mice in each age group; the 
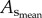and stem–crown number were averaged over all coronary arterial trees in each age group.
| morphometry of coronary arteries |  |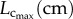
 |
 |
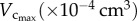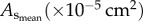BW (g) | stem–crown number |
|---|---|---|---|---|---|
| one week | 3.32 ± 1.20 | 5.31 ± 3.08 | 7.35 ± 1.56 | 9.8 ± 0.4 | 9 ± 5 |
| three weeks | 7.06 ± 3.74 | 12.3 ± 5.57 | 8.02 ± 1.78 | 11.0 ± 0.8 | 23 ± 18 |
| six weeks | 16.8 ± 6.13 | 18.1 ± 5.31 | 6.05 ± 1.02 | 17.4 ± 1.5 | 69 ± 50 |
| 12 weeks | 17.5 ± 5.12 | 29.3 ± 6.24 | 7.81 ± 1.24 | 37.6 ± 3.9 | 61 ± 48 |
| five to six months | 14.4 ± 5.80 | 23.6 ± 6.55 | 7.19 ± 1.59 | 36.1 ± 4.1 | 44 ± 26 |
| more than eight months | 9.96 ± 3.96 | 11.2 ± 5.19 | 6.22 ± 1.11 | 38.1 ± 4.8 | 36 ± 27 |
| statistical difference (p < 0.05) | 1 w versus 6 w 1 w versus 12 w 1 w versus 5–6 m 1 w versus >8 m 3 w versus 6 w 3 w versus 12 w 3 w versus 5–6 m 6 w versus >8 m 12 w versus >8 m |
1 w versus 6 w 1 w versus 12 w 1 w versus 5–6 m 3 w versus 12 w 3 w versus 5–6 m 6 w versus 12 w 6 w versus >8 m 12 w versus >8 m 5–6 m versus >8 m |
1 w versus 6 w 3 w versus 6 w 3 w versus >8 m 6 w versus 12 w 6 w versus 5–6 m 12 w versus >8 m |
1 w versus 6 w 1 w versus 12 w 1 w versus 5–6 m 1 w versus >8 m 3 w versus 6 w 3 w versus 12 w 3 w versus 5–6 m 3 w versus >8 m 6 w versus 12 w 6 w versus 5–6 m 6 w versus >8 m |
1 w versus 6 w 1 w versus 12 w 1 w versus 5–6 m 3 w versus 6 w 3 w versus 12 w 6 w versus >8 m |
Figure 3.
The mean ± s.d. of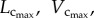 
and BW of vascular trees of mice at ages of one week, three weeks, six weeks, 12 weeks, five to six months and more than eight months, where the error bar refers to the s.d. in each age group. The mean ± s.d. values were normalized by the mean values at the age of one week.
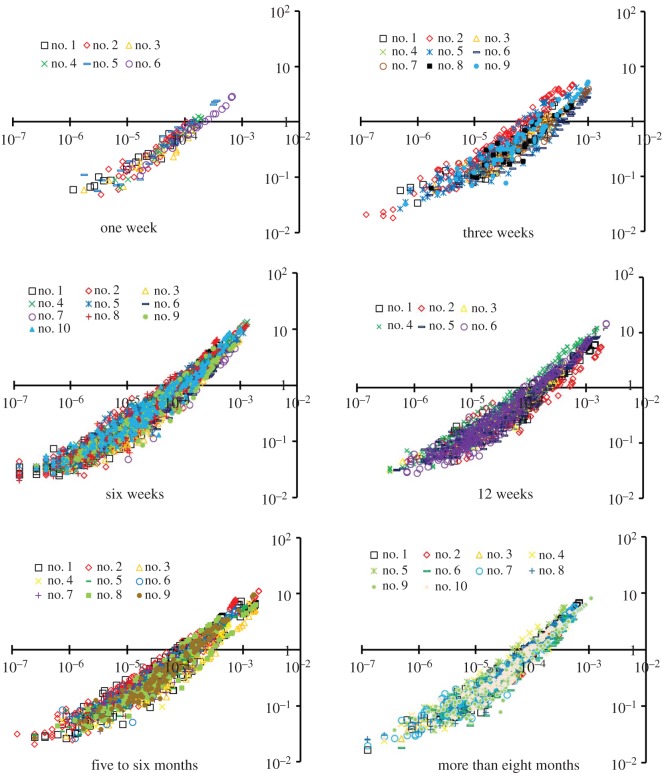
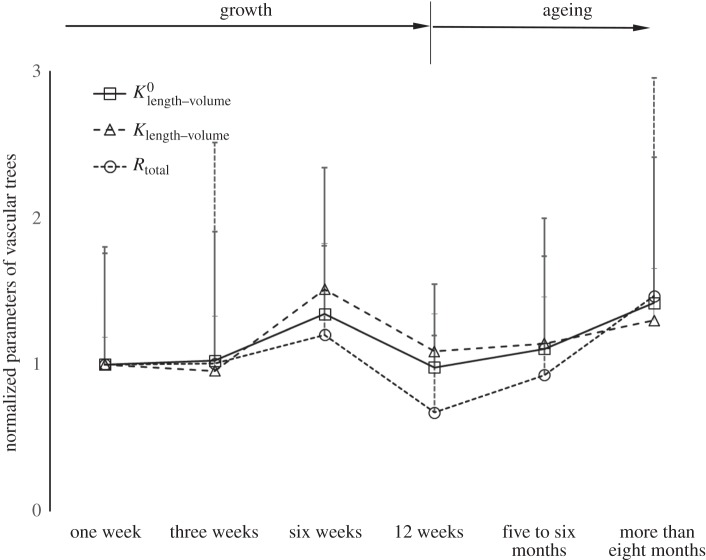
Figure 4 shows the log–log plots of crown length versus crown volume (Lc versus Vc) for all mice at different ages. Accordingly, the scaling coefficients and exponents (averaged over each coronary arterial tree within an age group) of the intraspecific length–volume scaling law are listed in table 3. The least-square fit of the intraspecific length–volume scaling law showed a high correlation coefficient (R2 ≥ 0.93 for all groups), which can be attributed to the integrated nature of both crown volume and crown length (i.e. the sum of the intravascular volume or the length of each vessel in each stem–crown unit). There was an age-independent 3/4 exponent in the scaling law. Figure 5 shows the mean ± s.d. of normalized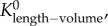 
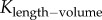and Rtotal of vascular trees of mice. During the period of growth, the scaling coefficients (
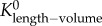and 
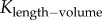) and the vascular resistance (Rtotal) remained relatively unchanged from one to three weeks, increased from three weeks to six weeks, but decreased from six weeks to 12 weeks. These parameters increased with ageing (five to six months and more than eight months).
Figure 4.
A log–log plot of crown length versus crown volume (Lc versus Vc) for all mice at ages of one week, three weeks, six weeks, 12 weeks, five to six months and more than eight months. The abscissa is the crown volume (unit: ml) and the ordinate is the crown length (unit: cm). (Online version in colour.)
Table 3.
Scaling coefficients and exponents (mean ± s.d.) of the length–volume scaling law in coronary arterial trees of mice at different ages. mean ± s.d.,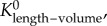 
a and Klength–volume were averaged over all coronary arterial trees in each age group.
least-squares fit of both 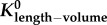 and a (two-parameter model) | |||
|---|---|---|---|
length–volume scaling law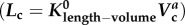 
|
 |
a | R2 |
| one week | 797 ± 603 | 0.73 ± 0.09 | 0.96 ± 0.04 |
| three weeks | 818 ± 701 | 0.75 ± 0.08 | 0.93 ± 0.04 |
| six weeks | 1071 ± 795 | 0.73 ± 0.06 | 0.94 ± 0.03 |
| 12 weeks | 782 ± 451 | 0.74 ± 0.05 | 0.94 ± 0.02 |
| five to six months | 883 ± 708 | 0.74 ± 0.06 | 0.96 ± 0.02 |
| more than eight months | 1131 ± 792 | 0.76 ± 0.08 | 0.94 ± 0.03 |
least-squares fit of 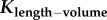 with a = 3/4 (one-parameter model) | |||
|---|---|---|---|
length–volume scaling law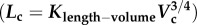 
|
 |
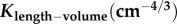R2 | statistical difference (p < 0.05) |
| one week | 712 ± 133 | 0.96 ± 0.04 | 1 w versus 6 w 1 w versus >8 m 3 w versus 6 w 3 w versus >8 m 6 w versus 12 w 6 w versus 5–6 m 12 w versus >8 m |
| three weeks | 681 ± 265 | 0.93 ± 0.04 | |
| six weeks | 1070 ± 215 | 0.94 ± 0.03 | |
| 12 weeks | 776 ± 180 | 0.94 ± 0.02 | |
| five to six months | 814 ± 224 | 0.96 ± 0.02 | |
| more than eight months | 925 ± 256 | 0.94 ± 0.03 | |
Figure 5.
The mean ± s.d. of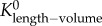 
(scaling coefficients determined by the two-parameter model), Klength–volume (scaling coefficients determined by the one-parameter model) and Rtotal of vascular trees of mice at ages of one week, three weeks, six weeks, 12 weeks, five to six months and more than 8 months, where the error bar refers to the s.d. in each age group. The mean ± s.d. values were normalized by the mean values at the age of one week.
4. Discussion
The key finding is that the exponent in the intraspecific length–volume scaling law of coronary arterial trees (with terminal diameter ≥ 40 µm) has a constant value approximately equal to 3/4 = 0.75 throughout the ages considered, whereas the scaling coefficient is significantly affected by growth and ageing. The measurements support the 3/4 intraspecific scaling law derived in appendix A. In the derivation of scaling law, we used only the assumption of the self-similar fractal-like branching pattern [33] given cardiovascular trees have fractal-like features [34–38]. The self-similar fractal-like branching pattern owing to diffusion-limited aggregation [21–23] obeys the 3/4 intraspecific length–volume scaling law, which appears to be the basic mechanism that guides the growth and ageing of coronary arterial trees. We also resolved the controversial space-filling assumption [39,40] using the fractal axiom that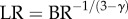 
(BR and LR are the branching ratio and length ratio, respectively, as shown in appendix A).
Another key finding is that the age-dependent changes of the scaling coefficient in the 3/4 intraspecific length–volume scaling law have a similar trend to those of the vascular resistance (Rtotal) for coronary arterial trees. Based on the assumption of the self-similar fractal-like branching pattern, we showed that Rtotal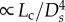
[20] and 
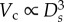[19], which deduced that Rtotal
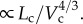The scaling coefficient, Klength–volume, equals to 
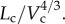Hence, Klength–volume and Rtotal have similar variation during normal growth and ageing, as shown in figure 5.
Because Rtotal is determined by multiple parallel and series resistances of blood vessels, the approximately 2.6% decrease of mean CSA as well as the approximately 2.4-fold increase of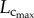 
does not ensure a reduction of Rtotal at 12 weeks compared with three weeks given the approximately threefold increase in total vessel number, as shown in table 2 and figures 3 and 5. Based on the self-similar nature of the coronary arterial tree, 
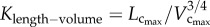and Rtotal
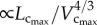. Hence, the scaling coefficient and vascular resistance are determined by the interplay of 
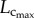and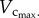 
The changes of the scaling coefficient and vascular resistance during growth seem different from those during ageing. During the period of growth, as shown in figures 3 and 5, an increase in 
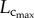and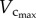 
results in the relatively unchanged Klength–volume and Rtotal from one to three weeks. A faster increase of 
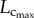than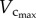 
owing to the enlarged heart size leads to an increased Klength–volume and Rtotal from three to six weeks. A greater increase of 
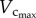than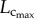 
causes a decreased Klength–volume and Rtotal from six to 12 weeks to satisfy the increased metabolic demand given that 
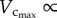metabolic rate3/4 [6]. Conversely, a greater decrease of 
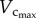than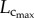 
explains the gradual increase of Klength–volume and Rtotal with ageing. The crown volume is determined by three key factors, i.e. vessel length, vessel diameter and vessel number. The faster increase of 
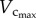than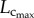 
from six to 12 weeks is caused by the increased CSA of vessels while the faster decrease of 
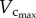than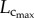 
with ageing is attributed to the decreased CSA of vessels as well as the reduction in vessel number, as shown in table 2.
Based on the minimum energy hypothesis, West et al. [6] derived that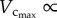 
BW. In this study, 
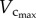was not proportional to BW during initial period of growth (from one to three weeks) and with ageing (from 12 weeks to more than eight months), whereas 
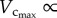BW from postnatal to maturity (from three to 12 weeks), as shown in figure 3. Although this is consistent with the conclusion of West et al. [6], because the interspecific 3/4 allometric metabolic scaling law underlies a large range of body size over 21 orders of magnitude among species (whereas the age-related changes in BW within a species are negligible in comparison), the result does not extend to the intraspecific scaling law relevant to normal growth and ageing of the whole life.
4.1. Significance of the study
The intraspecific scaling laws have been proposed to investigate the structure–function relationship within a given species [4,5,15–20]. The least-square fit of µCT data to the length–volume scaling law showed a high correlation coefficient and low coefficient of variation given the integrated properties of both crown volume and length [29,30]. This is the first study, to the best of our knowledge, to find an age-independent 3/4 exponent, but age-dependent scaling coefficients in the length–volume scaling law. The self-similar fractal-like branching pattern [33] owing to diffusion-limited aggregation [21–23] is found to be the basic mechanism for the constant 3/4 exponent. The changes of scaling coefficient have a similar trend to those of vascular resistance, both of which are attributed to the inconsistent growth/ageing rate of crown length and volume. In addition to understanding the nature of growth and ageing, these findings can provide methods to quantify vascular patterns in healthy individuals in reference to diagnosis of diseases.
4.2. Study limitations
Optimal casting may require various conditions (e.g. pressures, flow rates, etc.) for different animals. Here, we performed the casting at a constant pressure of 100 mmHg with zero flow during casting. Because the passive diameter of coronary arteries showed less than 3% relative error in the pressure range of 80–120 mmHg [41], a sensitivity analysis was carried out to investigate the effects of cast perfusion on the length–volume scaling law. The 3–5% changes in vessel diameter resulted in an error bound of 2.6 ± 0.3%–4.5 ± 0.3% for the age-dependent coefficients with a negligible effect on the age-independent exponent. The effect of casting did not alter the conclusions in table 3.
Based on the volume–diameter scaling law and the minimum energy hypothesis, we previously derived a 7/9 exponent of the length–volume scaling law [19]. The design of coronary arterial trees, however, obeys the minimum energy hypothesis from postnatal to maturity (from three to 12 weeks), but not with ageing (from 12 weeks to more than eight months), because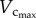 
is not proportional to BW, as shown in figure 3. In contrast, this study deduced that 
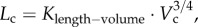from the fractal nature of vascular trees only. The least-square fit of µCT data to the 7/9 and 3/4 length–volume scaling laws showed the exponent to be closer to 3/4 albeit the difference between the two exponents was not statistically significant.
The 3/4 length–volume scaling law was derived based on the fractal assumptions of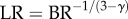 
and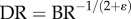 
(see appendix A). The µCT measurements showed constant parameters, γ and ɛ, during normal growth and ageing in the coronary arterial trees of mice. Further measurements in various organs of different species during normal growth and ageing are needed to validate the exponent of the length–volume scaling.
5. Conclusion
An intraspecific scaling law describes the development of coronary arterial trees during normal growth and ageing. The exponent of length–volume scaling law has a constant value of 3/4, whereas the scaling coefficient changes during growth and ageing. Moreover, the changes of the scaling coefficient over time show a similar trend to those of vascular resistance.
Acknowledgements
We thank all participants of the study in Peking University and Hebei University.
Appendix A
Similar to a previous study [19], a proximal vessel is defined as a stem and the subtree distal to the stem (down to the terminal vessels reconstructed from µCT images) is defined as a crown, as shown in figure 1a. A tree consists of many stem–crown units. The vessel is assumed to be a cylindrical tube. In a tree, ni, Di and Li refer to the number, diameter and length of vessels in level i, i = 0, … , Ni, where the inlet of the tree is level 0, and the terminal vessels refer to level Ni. In an integrated system of stem–crown units, the crown volume (Vc; unit: ml) is defined as the sum of the intravascular volume of each vessel in a stem–crown unit from the stem to the most distal vessels; the crown length (Lc; unit: cm) is defined as the sum of the length of each vessel in a stem–crown unit from the stem to the most distal vessels.
A.1. Branching ratio
The branching ratios (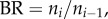
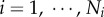) are relatively constant in each level from the inlet (level 0) to the terminal vessels (level Ni), such that 
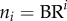in a crown.
A.2. Diameter ratio
The diameter ratio is defined as: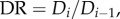 
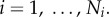It can be shown that 
(
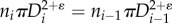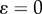represents area-preservation from one level to the next and 
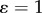represents Murray's law). This provides the relation: 
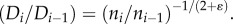Therefore, the diameter ratio relates to the branching ratio as 
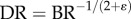or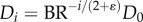 
in a crown.
A.3. Length ratio
The length ratio is defined as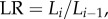 
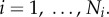West et al. [6] proposed that the perfused volume from one level to the next was constant, such that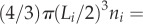 
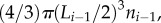which has been highly disputed [39,40] and for which there are no supporting experimental data. Here, we assume a more general relation that has an experimental basis, namely: 
(
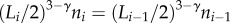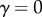represents space filling, 
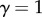represents area filling, and 
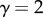represents length preservation). This leads to 
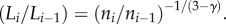The length ratio relates to the branching ratio as: 
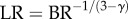or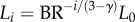 
in a crown.
A.4. Crown length
The crown length, Lc, can be written as
 |
A 1 |
From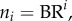 
, 
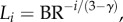and equation (A 1), we obtain the following equation
 |
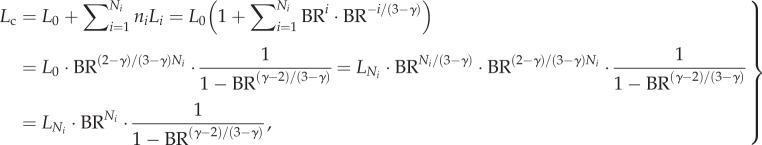A 2 |
where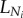 
is the length of terminal vessels and is a constant. Hence,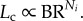 
A.5. Crown volume
The crown volume, Vc, can be written as
 |
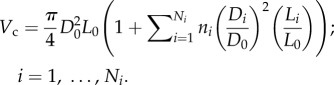A 3 |
From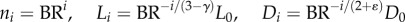 
and equation (A 3), we obtain the following equation
 |
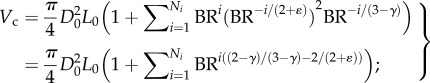A 4 |
Because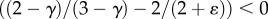 
for most vascular trees, equation (A 4) is written as
 |
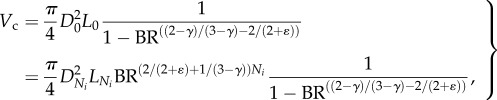A 5 |
where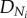 
is the diameter of terminal vessels and is a constant. Equation (A 5) exits even if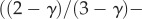 
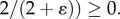
A.6. The length–volume scaling law
From equation (A 5),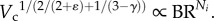
Moreover, 
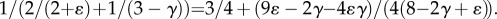Based on morphometric data of γ and ɛ in reference [19] as well as the present measurements,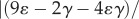 
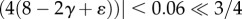such that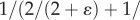 
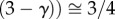for coronary arterial trees. From Lc
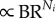and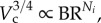 
we obtain the length–volume scaling law as
 |
A 6 |
where Klength–volume is the scaling coefficient.
Ethics
All animal experiments were performed in accordance with Chinese National and Hebei University ethical guidelines regarding the use of animals in research.
Authors' contributions
Y.L.H. designed this research project. G.S.K. and Y.L.H. performed the theoretical analysis. P.N., X.N., W.S., F.D., L.D. and X.W. performed the animal experiments. Y.G. and Y.H. performed the µCT scanning. X.C. performed the µCT reconstruction and measurement. X.C., W.T. and Y.L.H. performed the data and statistical analysis. G.S.K., W.T. and Y.L.H. conceived the concept and prepared this manuscript.
Competing interests
We declare we have no competing interests.
Funding
This research is supported in part by the Natural Science Foundation of China grant no. 11372010 (Y.L.H.) and the China MOST grant no. 2014DFG32740 (Y.L.H.).
References
- 1.Wei JY. 1992. Age and the cardiovascular system. N. Engl. J. Med. 327, 1735–1739. ( 10.1056/NEJM199212103272408) [DOI] [PubMed] [Google Scholar]
- 2.Kleiber M, Cole HH. 1939. Body size and energy metabolism in growth hormone rats. Am. J. Physiol. 125, 747–760. [Google Scholar]
- 3.Kleiber M. 1941. Body size and metabolism of liver slices in vitro. Proc. Soc. Exp. Biol. Med. 48, 419–423. ( 10.3181/00379727-48-13340) [DOI] [Google Scholar]
- 4.Seiler C, Kirkeeide RL, Gould KL. 1992. Basic structure–function relations of the epicardial coronary vascular tree. Basis of quantitative coronary arteriography for diffuse coronary artery disease. Circulation 85, 1987–2003. ( 10.1161/01.CIR.85.6.1987) [DOI] [PubMed] [Google Scholar]
- 5.Seiler C, Kirkeeide RL, Gould KL. 1993. Measurement from arteriograms of regional myocardial bed size distal to any point in the coronary vascular tree for assessing anatomic area at risk. J. Am. College Cardiol. 21, 783–797. ( 10.1016/0735-1097(93)90113-F) [DOI] [PubMed] [Google Scholar]
- 6.West GB, Brown JH, Enquist BJ. 1997. A general model for the origin of allometric scaling laws in biology. Science 276, 122–126. ( 10.1126/science.276.5309.122) [DOI] [PubMed] [Google Scholar]
- 7.West GB, Brown JH, Enquist BJ. 1999. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science 284, 1677–1679. ( 10.1126/science.284.5420.1677) [DOI] [PubMed] [Google Scholar]
- 8.Banavar JR, Maritan A, Rinaldo A. 1999. Size and form in efficient transportation networks. Nature 399, 130–132. ( 10.1038/20144) [DOI] [PubMed] [Google Scholar]
- 9.Gillooly JF, et al. 2001. Effects of size and temperature on metabolic rate. Science 293, 2248–2251. ( 10.1126/science.1061967) [DOI] [PubMed] [Google Scholar]
- 10.Reich PB, Tjoelker MG, Machado J-L, Oleksyn J, 2006. Universal scaling of respiratory metabolism, size and nitrogen in plants. Nature 439, 457–461. ( 10.1038/nature04282) [DOI] [PubMed] [Google Scholar]
- 11.Savage VM, Bentley LP, Enquist BJ, Sperry JS, Smith DD, Reich PB, Von Allmen EI, 2010. Hydraulic trade-offs and space filling enable better predictions of vascular structure and function in plants. Proc. Natl Acad. Sci. USA 107, 22 722–22 727. ( 10.1073/pnas.1012194108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Banavar JR, Moses ME, Brown JH, Damuth J, Rinaldo A, Sibly RM, Maritan A, 2010. A general basis for quarter-power scaling in animals. Proc. Natl Acad. Sci. USA 107, 15 816–15 820. ( 10.1073/pnas.1009974107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kolokotrones T, Van Savage ME, Deeds EJ, Fontana W, 2010. Curvature in metabolic scaling. Nature 464, 753–756. ( 10.1038/nature08920) [DOI] [PubMed] [Google Scholar]
- 14.Gillooly JF, Charnov EL, West GB, Savage VM, Brown JH, 2002. Effects of size and temperature on developmental time. Nature 417, 70–73. ( 10.1038/417070a) [DOI] [PubMed] [Google Scholar]
- 15.Zhou YF, Kassab GS, Molloi S. 1999. On the design of the coronary arterial tree: a generalization of Murray's law. Phys. Med. Biol. 44, 2929–2945. ( 10.1088/0031-9155/44/12/306) [DOI] [PubMed] [Google Scholar]
- 16.Choy JS, Kassab GS. 2008. Scaling of myocardial mass to flow and morphometry of coronary arteries. J. Appl. Physiol. (1985) 104, 1281–1286. ( 10.1152/japplphysiol.01261.2007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kassab GS. 2006. Scaling laws of vascular trees: of form and function. Am. J. Physiol. Heart Circ. Physiol. 290, H894–H903. ( 10.1152/ajpheart.00579.2005) [DOI] [PubMed] [Google Scholar]
- 18.Huo Y, Kassab GS. 2009. A scaling law of vascular volume. Biophys. J. 96, 347–353. ( 10.1016/j.bpj.2008.09.039) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huo Y, Kassab GS. 2012. Intraspecific scaling laws of vascular trees. J. R. Soc. Interface 9, 190–200. ( 10.1098/rsif.2011.0270) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huo Y, Kassab GS. 2009. The scaling of blood flow resistance: from a single vessel to the entire distal tree. Biophys. J. 96, 339–346. ( 10.1016/j.bpj.2008.09.038) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gazit Y, Berk DA, Leunig M, Baxter LT, Jain RK, 1995. Scale-invariant behavior and vascular network formation in normal and tumor tissue. Phys. Rev. Lett. 75, 2428–2431. ( 10.1103/PhysRevLett.75.2428) [DOI] [PubMed] [Google Scholar]
- 22.Masters BR. 2004. Fractal analysis of the vascular tree in the human retina. Annu. Rev. Biomed. Eng. 6, 427–452. ( 10.1146/annurev.bioeng.6.040803.140100) [DOI] [PubMed] [Google Scholar]
- 23.Iber D, Menshykau D. 2013. The control of branching morphogenesis. Open Biol. 3, 130088 ( 10.1098/rsob.130088) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kassab GS, Rider CAA, Tang NJ, Fung Y-CB. 1993. Morphometry of pig coronary arterial trees. Am. J. Physiol. 265, H350–H365. [DOI] [PubMed] [Google Scholar]
- 25.Huo Y, Guo X, Kassab GS. 2008. The flow field along the entire length of mouse aorta and primary branches. Ann. Biomed. Eng. 36, 685–699. ( 10.1007/s10439-008-9473-4) [DOI] [PubMed] [Google Scholar]
- 26.Jorgensen SM, Demirkaya O, Ritman EL. 1998. Three-dimensional imaging of vasculature and parenchyma in intact rodent organs with X-ray micro-CT. Am. J. Physiol. 275, H1103–H1114. [DOI] [PubMed] [Google Scholar]
- 27.Kline TL, Zamir M, Ritman EL. 2010. Accuracy of microvascular measurements obtained from micro-CT images. Ann. Biomed. Eng. 38, 2851–2864. ( 10.1007/s10439-010-0058-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marxen M, Thornton MM, Chiarot CB, Klement G, Koprivnikar J, Sled JG, Henkelman RM, 2004. µCT scanner performance and considerations for vascular specimen imaging. Med. Phys. 31, 305–313. ( 10.1118/1.1637971) [DOI] [PubMed] [Google Scholar]
- 29.Huo Y, Wischgoll T, Choy JS, Sola S, Navia JL, Teague SD, Bhatt DL, Kassab GS, 2013. CT-based diagnosis of diffuse coronary artery disease on the basis of scaling power laws. Radiology 268, 694–701. ( 10.1148/radiol.13122181) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huo Y, Choy JS, Wischgoll T, Luo T, Teague SD, Bhatt DL, Kassab GS, 2013. Computed tomography-based diagnosis of diffuse compensatory enlargement of coronary arteries using scaling power laws. J. R. Soc. Interface 10, 20121015 ( 10.1098/rsif.2012.1015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huo Y, Kassab GS. 2015. Remodeling of left circumflex coronary arterial tree in pacing-induced heart failure. J. Appl. Physiol. (1985) 119, 404–411. ( 10.1152/japplphysiol.00262.2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huo Y, Kassab GS. 2006. Pulsatile blood flow in the entire coronary arterial tree: theory and experiment. Am. J. Physiol. Heart Circ. Physiol. 291, H1 074–H1 087. ( 10.1152/ajpheart.00200.2006) [DOI] [PubMed] [Google Scholar]
- 33.Mandelbrot BB. 1977. Fractals: form, chance, and dimension. San Francisco, CA: Freeman. [Google Scholar]
- 34.Bassingthwaighte JB, Malone MA, Moffett TC, King RB, Chan IS, Link JM, Krohn KA, 1990. Molecular and particulate depositions for regional myocardial flows in sheep. Circ. Res. 66, 1328–1344. ( 10.1161/01.RES.66.5.1328) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sernetz M, Wubbeke J, Wlczek P. 1992. Three-dimensional image-analysis and fractal characterization of kidney arterial vessels. Physica A 191, 13–16. ( 10.1016/0378-4371(92)90498-F) [DOI] [Google Scholar]
- 36.Ellsworth ML, Liu A, Dawant B, Popel AS, Pittman RN, 1987. Analysis of vascular pattern and dimensions in arteriolar networks of the retractor muscle in young hamsters. Microvasc. Res. 34, 168–183. ( 10.1016/0026-2862(87)90051-3) [DOI] [PubMed] [Google Scholar]
- 37.Ley K, Pries AR, Gaehtgens P. 1986. Topological structure of rat mesenteric microvessel networks. Microvasc. Res. 32, 315–332. ( 10.1016/0026-2862(86)90068-3) [DOI] [PubMed] [Google Scholar]
- 38.Huang W, Mclaurine M, Yen RT. 1993. Morphometry of the human pulmonary arterial tree. FASEB J. 7, A790. [DOI] [PubMed] [Google Scholar]
- 39.Dodds PS, Rothman DH, Weitz JS. 2001. Re-examination of the ‘3/4-law’ of metabolism. J. Theor. Biol. 209, 9–27. ( 10.1006/jtbi.2000.2238) [DOI] [PubMed] [Google Scholar]
- 40.Kozlowski J, Konarzewski M. 2004. Is West, Brown and Enquist's model of allometric scaling mathematically correct and biologically relevant? Funct. Ecol. 18, 283–289. ( 10.1111/j.0269-8463.2004.00830.x) [DOI] [Google Scholar]
- 41.Huo Y, Cheng Y, Zhao X, Lu X, Kassab GS, 2012. Biaxial vasoactivity of porcine coronary artery. Am. J. Physiol. Heart Circ. Physiol. 302, H2058–H2063. ( 10.1152/ajpheart.00758.2011) [DOI] [PMC free article] [PubMed] [Google Scholar]