Abstract
Motivation: Rapid advances in genotyping and genome-wide association studies have enabled the discovery of many new genotype–phenotype associations at the resolution of individual markers. However, these associations explain only a small proportion of theoretically estimated heritability of most diseases. In this work, we propose an integrative mixture model called JBASE: joint Bayesian analysis of subphenotypes and epistasis. JBASE explores two major reasons of missing heritability: interactions between genetic variants, a phenomenon known as epistasis and phenotypic heterogeneity, addressed via subphenotyping.
Results: Our extensive simulations in a wide range of scenarios repeatedly demonstrate that JBASE can identify true underlying subphenotypes, including their associated variants and their interactions, with high precision. In the presence of phenotypic heterogeneity, JBASE has higher Power and lower Type 1 Error than five state-of-the-art approaches. We applied our method to a sample of individuals from Mexico with Type 2 diabetes and discovered two novel epistatic modules, including two loci each, that define two subphenotypes characterized by differences in body mass index and waist-to-hip ratio. We successfully replicated these subphenotypes and epistatic modules in an independent dataset from Mexico genotyped with a different platform.
Availability and implementation: JBASE is implemented in C++, supported on Linux and is available at http://www.cs.toronto.edu/∼goldenberg/JBASE/jbase.tar.gz. The genotype data underlying this study are available upon approval by the ethics review board of the Medical Centre Siglo XXI. Please contact Dr Miguel Cruz at mcruzl@yahoo.com for assistance with the application.
Contact: anna.goldenberg@utoronto.ca
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Genome-wide association studies (GWAS) have been successful in identifying thousands of novel disease markers. However, the discovered associations explain only a small proportion of theoretically estimated heritability of most diseases (Manolio et al., 2009). This is referred to as the missing heritability problem. Among the main hypotheses attempting to explain the missing heritability (Manolio et al., 2009), four of them can be addressed with more detailed genetic data and more advanced methods: (i) rare variants and structural variants (SVs), which are not covered by the common single-nucleotide polymorphism (SNP) arrays used in GWAS; (ii) spurious associations caused by population stratification; (iii) interactions between variants, i.e. epistasis and (iv) phenotypic heterogeneity. Solutions to each problem have been sought with varying degrees of success. For example, full assessment of the impact of rare variants and SVs on phenotypic variation requires larger cohorts, which is becoming feasible with affordable sequencing technologies and meta-studies. It is now possible to detect and remove spurious associations using efficient linear mixed models (Listgarten et al., 2012). In this article, we focus on epistasis and phenotype heterogeneity—two major computational problems potentially contributing to missing heritability.
Recent large-scale genomic studies on model organisms (Huang et al., 2012), as well as theoretical findings (Zuk et al., 2012) revealed that epistasis may hinder identification of genetic associations. It is possible to categorize epistasis detection algorithms into three types: (i) pre-GWAS algorithms that were mostly developed for small-scale datasets, e.g. multi-factor dimensionality reduction (Ritchie et al., 2001); (ii) exhaustive search algorithms, such as TEAM (Zhang et al., 2010b), SIXPAC (Prabhu and Pe’er, 2012) and GWIS (Goudey et al., 2013), which scale to GWAS datasets but only detect pairwise and often limited types of interactions and (iii) stochastic search methods such as BEAM (Zhang and Liu, 2007), a generative latent variable framework that models marginal (independently acting) and epistatic effects allowing for any number of interactions. Its successors include BEAM2 (Zhang et al., 2011) and BEAM3 (Zhang, 2012). Most of these methods rely on Markov chain Monte Carlo for inference.
Many complex human diseases, such as autism, diabetes and cancer, are very heterogeneous. For example, it has been observed that risk variants associated with Type 2 diabetes (T2D) differ in patients with high and low body mass indices (BMIs) (Perry et al., 2012). Similarly, in medulloblastoma, analysis of 1000 genomes revealed extensive subgroup specific variants that give rise to subgroup specific phenotypes, i.e. subphenotypes (Northcott et al., 2012). There is now increasing evidence from breast cancer, hearing loss, cholesterol-related disorders, mental illnesses and T2D studies that many complex diseases may be better characterized as a collection of distinct and less common subdiseases (Bergen, 2014; McClellan and King, 2010; Stessman et al., 2014). Disease heterogeneity, if not taken into account, can have profound consequences on the success of association studies. It reduces statistical power to detect causal variants (Fig. 1A) and confounds replication studies such that true associations fail to replicate and become classified as false positives (Fig. 1B and also a detailed discussion in Supplementary Material Section S1). Subphenotyping attempts to solve these problems by (automatically) stratifying the global population to identify homogeneous patient subgroups.
Fig. 1.
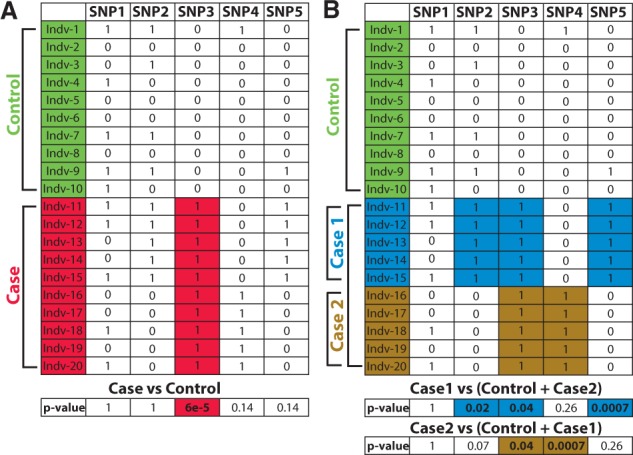
Effects of hidden subphenotypes on GWAS. (A) Classical CC GWAS wherein heterogeneity in the case population is hidden or is not accounted for; can recover only shared causal markers (SNP3) (B) Subphenotyping approach to the same data recovers both shared (SNP3) and subphenotype causal-specific markers (SNP2, SNP4 and SNP5)
Several approaches have recently been developed to address disease heterogeneity in the context of the missing heritability problem. These approaches can be grouped into two categories: (i) those with prior knowledge of subphenotypes (Manning et al., 2012; Perry et al., 2012; Timpson et al., 2009) and (ii) those that simultaneously infer both subphenotypes and associated markers (Warde-Farley et al., 2012). In the first case, the grouping information might come from prior medical knowledge, e.g. in T2D, the cases were stratified according to patients’ BMI using canonical BMI categories of obese versus non-obese. However, relying only on prior knowledge limits the space of accessible discoveries. Moreover, it is also undesirable as subphenotypes often give rise to overlapping multivariate phenotype distributions, which cannot be studied with hard threshold-based approaches. Simultaneous identification of subgroups and group-specific markers removes the bias of potentially arbitrary thresholds while enabling the study of overlapping subphenotypes. The SNPMix approach (Warde-Farley et al., 2012) addresses this problem by modeling the population as a mixture of subphenotypes, with individual-to-subgroup assignment being unknown and trying to simultaneously identify marginally affecting markers and subgroup assignments. This is a promising first step but it focuses solely on marginal associations.
Joint models for partitioning genotype and phenotype simultaneously have been proposed in the expression quantitative trait loci (eQTL) framework. Methods described in Kim and Xing (2009) and Chen et al. (2012) identify modules of genes and corresponding variants. The partitioning in these models is in the gene space rather than in the patient space, thus these models are not directly applicable to our problem. A notable exception is Zhang et al. (2010a), which proposes a Bayesian partitioning method in the eQTL context that not only models marginal and epistatic effects of variants (explaining gene expression modules) but also encodes potential partitioning of the cohort. Unfortunately, there are several key properties of this model that make it inapplicable to subphenotyping. For example, the variable corresponding to the partitioning of individuals is integrated out, i.e. it is not actually inferred. Additionally, the groupings of individuals are independent between eQTL modules. Thus, as is shown in the real case scenario in Zhang et al. (2010a), each module has its own subgroup of individuals without any way to reconcile them. To summarize, Zhang et al. (2010a) does not infer subphenotypes with respect to the disease but uses the idea of subgroups of individuals to identify more meaningful eQTL modules. The only way to coerce Zhang et al. (2010a) model to our setting would be to set the number of modules to 1. However, this would mean that there would have to be only one genotypic module that has to explain the full heterogeneity of the data, an assumption that is not supported by the current line of evidence on the genetics of subphenotypes (Bergen, 2014; Northcott et al., 2012; Perry et al., 2012; Stessman et al., 2014).
Motivated by the fact that epistasis and phenotype heterogeneity represent two of the main challenges for the missing heritability problem and the fact that none of the existing methods address both issues simultaneously, we introduce the JBASE model, which accounts for epistasis and subphenotyping while providing an easily interpretable probabilistic framework.
2 Methods
Suppose that N individuals are genotyped at M markers and are measured on F phenotype features. This data is represented in an matrix, where each individual i (ith row) consists of gi (genotype profile) and zi (phenotype profile) vectors. We further assume that each individual belongs to a phenotypic subpopulation whose phenotype variation is associated with the genotypic variation at the underlying causal/associated markers. Since subpopulation membership is not known a priori, we introduce a latent discrete variable , parameterized by the mixing coefficient vector π, which defines the assignment of individual i to one of the K subpopulations, which needs to be supplied as input.
When modeling the genotype, JBASE extends the probabilistic model implemented in BEAM (Zhang and Liu, 2007), a probabilistic framework that finds causal variants acting on binary phenotypes independently (marginally) or jointly, i.e. epistatically. Hence, we model each subphenotype’s genotype submatrix as a collection of three genotype components: is the null component that contains markers not associated with the phenotype; is the marginal component consisting of markers that independently affect the phenotype and is the epistatic component containing markers that contribute to the phenotype via non-linear interactions.
As these components are not known a priori, they must be inferred as well. For this reason, we also introduce the latent variable , which denotes the assignment of a marker m to one of the three marker components of population k. Hence, denotes the marker-to-genotype component assignment vector for subphenotype k. As such, the major difference in our model compared with BEAM (Zhang and Liu, 2007) is the addition of the multivariate phenotype component and the corresponding breaking down of the parameters into the K phenotypic groups. We present the likelihood function here. Supplementary Material Section S2 contains more details, including the derivation of the posterior distribution, hyper-parameter choices, sampling efficiency and post-processing methodology.
We start with the marginal component. For k and m such that , let , be the genotype frequencies of each biallelic marker—a marker that has only 3 states (AA, Aa, aa) based on the number of minor alleles it has—in the marginal component of population k. Then, due to independent effects of markers in this group, we can write the likelihood of the marginal component of the subpopulation k as follows:
| (1) |
where is the number of individuals in subpopulation k that has jth genotype for marker m.
Markers in the epistatic component are assumed to be generated by a single multinomial distribution. As each marker can have three states, this multinomial distribution can have states, i.e. interactions, whose frequencies are governed by the parameter . Thus, we get:
| (2) |
where denotes the number of individuals in subpopulation k with the genotype combination j over the epistatic markers. Note that, ek, and hence the dimensionality of vary depending on the state of (see Supplementary Material Section S2.2 for details).
The last genotype component to model is the null component. The parameters of the null component are shared across all components, i.e. a marker that is not related to the phenotype should have the same allelic distribution as other subpopulations in which it is assigned to the null component. Let be the genotype frequencies of a marker m in the general population. Then, we have:
| (3) |
where is the number of the occurrence of state j for marker m across all individuals where it is classified as a null marker.
The final component of the likelihood is the phenotype. In this work, we have focused on categorical phenotypes only. We model the phenotype likelihood as a multinomial distribution:
| (4) |
parameterized with , where T is the number of all possible combinations of values of the different phenotypic variables, which is fixed based on cardinality of the multinomial distribution, and is the number of individuals in subpopulation k with a phenotype value t. Putting these together, we get the following form for likelihood :
| (5) |
where we used to denote the collection of null components across all subphenotypes
Using conjugate Dirichlet priors for ψ, θ, and ω, as well as for the mixing coefficient parameter vectors π and α, allows us to integrate out all of the model parameters except latent variables and (see Supplementary Material Section S2.1 for details). The final form of the posterior is presented in Equation (6). As such, the posterior distribution depends only on the hyper-parameters , which are given as input, and the latent variables and , which are inferred. We perform inference via sampling from the posterior using the metropolis hastings algorithm (see Supplementary Material Sections S2.2 and S2.3 for details). It is also worth mentioning that JBASE can control for linkage disequilibrium (LD), which can introduce false-positive epistatis, and for population stratification. For LD, JBASE accepts an optional input file that lists the markers known to be in LD with associated lists of linked markers. JBASE, via its proposal distribution on , ensures that linked marker pairs are never assigned to marginal and/or epistatic components simultaneously. In addition, one can also specify an optional genomic distance threshold such that markers closer than the given distance are not allowed to be simultaneously assigned to the marginal and/or epistatic component of a subpopulation. As for population stratification, JBASE leverages the information obtained from the principal component analysis (PCA) of individuals by ensuring that the subpopulation means of the most important PCA dimension(s) do not significantly differ between subpopulations (see Supplementary Material Section S2.2). This is achieved by rejecting proposals on variable if it causes the means between subphenotypes to diverge beyond a threshold. Other biological constraints can easily be integrated into the proposal distribution of the metropolis hastings algorithm by eliminating the undesirable assignments from the state space of the posterior distribution.
| (6) |
3 Experiments
In this section, we elaborate on our results obtained with JBASE in extensive simulation studies of established disease models and also in real GWAS from T2D studies.
3.1 Simulation experiments
There exists a limited number of traits, such as coat color in mice and comb shape in chickens, where interacting loci and the specific alleles are well characterized. In this work, we follow the simulation approach and the disease models described in Zhang and Liu (2007) with some modifications and improvements. The framework of Zhang and Liu (2007) was designed for case–control (CC) studies. We extended their simulations to account for continuous phenotypes and two case subpopulations. In what follows, we include brief descriptions of the disease models used by Zhang and Liu (2007) and give details of the modifications we introduced. We used five disease models; their risk structures are shown in Supplementary Figure S4.
Model 1: Two disease loci with independent effects.
Model 2: Two loci model, where disease occurs only when at least one disease-associated allele exists in both loci.
Model 3: Two loci threshold model such that a single disease associated allele is sufficient to confer disease risk and additional ones do not increase the risk.
Model 4: Three loci model in which increased disease risk is associated with certain genotype combinations. Disease alleles at each locus also contribute a small (possibly zero) additive effect to the risk.
Model 5: Three loci model with a mixture of two two-way epistatic interactions, wherein each two-way interaction increases the risk. Risk does not increase further when both of the two-way epistatic interactions are present.
Using a generative mixture model scheme (see Supplementary Material Section S3.1), we simulated 2000 datasets with K = 2 (i.e. two case subpopulations and one control subpopulation), N = 1000 individuals and M = 1000 markers. We generated datasets such that we have at least 20 datasets for each of the 25 possible disease model pair combinations for the two disease subpopulations. We varied the size of the larger case subpopulation to be 250, 300, 400 or 500. Note that when one of the case subpopulations is of size 500, we have just cases and controls, i.e. without any case subphenotypes, where the true and the specified . We intentionally included this extreme scenario to measure performance of JBASE when the number of subpopulations is misspecified and the disease does not have subphenotypes.
We compare JBASE with a variety of approaches including both traditional GWAS, i.e. variants of χ2 tests, and more recent methods, i.e. BEAM (Zhang and Liu, 2007), ordered subset analysis for CC (OSACC, Qin et al., 2010) and Multinom (Morris et al., 2010), that are designed to handle epistasis or subphenotyping. A summary of the algorithms compared across a set of seven desired properties is presented in Table 1. Below is a brief description of each of the competing methods:
The χ2 CC algorithm corresponds to the traditional CC study, in which the phenotype is set to 0 for controls and 1 for all cases. Each marker is tested for association independently from the others. We use χ2 CC as the baseline approach.
In χ2 multiway, each marker is tested for association with a K-way χ2 test where K is the number of distinct categories of the phenotype obtained by categorization using an equal-bin discretization scheme. This method is a natural extension of χ2 CC and represents a naive baseline approach for subphenotyping.
Multinom (Morris et al., 2010) improves on the χ2 multiway by addressing disease heterogeneity in a multinomial regression framework, wherein phenotype is assumed to be sampled from a mixture of K subphenotypes. These K subphenotypes are derived from the case population using prior biomedical knowledge. A multinomial regression model is fitted for each marker, followed by a log-likelihood ratio test-based P-value calculation to assess the significance of association. A substantial shortcoming of this approach is that it requires the phenotype group assignment as input, which are often not readily available. In our simulations, we use the true subphenotype labels as input to the algorithm, which is the best possible scenario for this model.
OSACC algorithm (Qin et al., 2010) is a non-parametric method that works on continuous phenotypes. It first sorts the cases by phenotype. Starting with the small subpopulation of 50 cases with the most extreme phenotype values, it iteratively adds cases to the subpopulation. At each iteration, contingency tables are formed, and the threshold with the maximum association across iterations is identified. Significance is estimated by permutation tests.
BEAM algorithm (Zhang and Liu, 2007) shares the same underlying probabilistic marker partition model as the JBASE. The BEAM model, however, is designed for CC studies. It does not utilize any additional phenotype information and hence does not account for phenotypic heterogeneity.
Table 1.
Summary of the six algorithms used for comparison
| Algorithm | Epis | Subphe | Case versus | Univariate | Multivariate |
|---|---|---|---|---|---|
| tasis | notyping | control | phenotype | phenotype | |
| BEAM | + | − | + | + | − |
| OSACC | − | + | − | + | − |
| χ2 CC | − | − | + | + | − |
| χ2 multiway | − | + | + | + | − |
| Multinom | − | + | + | + | − |
| JBASE | + | + | + | + | + |
For fairness, we simulated univariate continuous phenotypes, as JBASE is the only method that can handle multivariate phenotypes. For algorithms that work with continuous phenotypes, such as OSACC, we used continuous phenotype and discretized it for the other methods. To demonstrate JBASE’s robustness across parameter choices, we report its performance with two highly different parameter settings: one with true hyper-parameters used in the simulations, which are not known in real applications, and one with default parameters we suggest to use when no prior information is available, which is often the case in exploratory data analysis (see Supplementary Material Section S2.4).
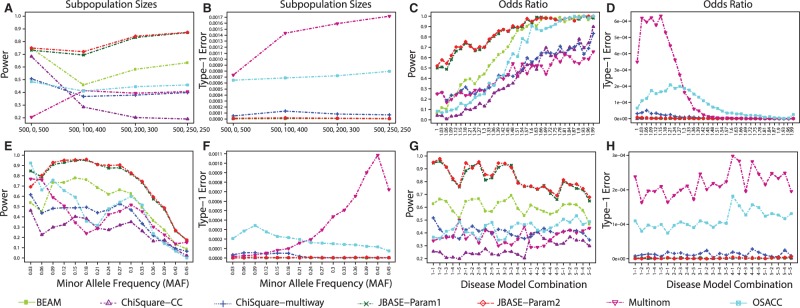
We analyzed the performance of all algorithms (including JBASE with two parameter settings) in terms of power (= true-positive rate) and Type 1 Error (= false-positive rate) for detecting the embedded causal markers. Both metrics were computed based on whether a given method can recover a causal marker regardless of its embedded classification (marginal versus epistatic). We analyzed the performances across various settings of minor allele frequency (MAF), odds ratio, disease models and subpopulation size.
3.1.1 Subpopulation size analysis
The effect of subpopulation size on the power and Type 1 Error of the methods is captured in Figure 2A and B. The first population is always the control group and is always of size 500. The remaining 500 individuals are assigned to two disease subphenotypes of varying sizes, with size of the larger one listed in the third position. For example, (500, 200, 300) means that the cohort consists of a control group with size 500 and two disease subphenotypes of sizes 200 and 300.
Fig. 2.
Disease model results: performance of all algorithms across four dimensions: subpopulation size (A, B), odds ratios (C, D), MAF (E, F) and disease model combinations (G, H). For each plot, the performance is averaged over dimensions other than the dimension in focus. For example, for (A) all MAF, odds ratios and disease model combinations are averaged over and broken into subpopulation size combinations (see also Supplementary Figs. S6 and S7 for additional results under various call confidence thresholds)
Despite performing the best, along with BEAM, the (500, 0, 500) setting appears to be the most difficult one for JBASE. In this setting, the specified number of subphenotypes is 2, whereas the true number of case subpopulations is 1 and hence K is misspecified. Yet JBASE’s power is virtually the same as BEAM’s and is better than all of the compared methods. This is in spite of the fact that BEAM deals with the more facile task of finding the causal markers given the subpopulation labels, while JBASE has to infer the subpopulation assignments, in addition to the causal markers, with an incorrect value set for K. Similarly, we also see that (500, 100, 400) presents the most difficult setting for BEAM, where only the markers of the larger subphenotype (of size 400) were discovered while markers causal to the smaller subpopulation were missed. This is why BEAM’s statistical power is only in the setting of highly skewed subpopulation sizes. JBASE clearly stands out from its competitors, including other subphenotyping methods. As the smaller subpopulation becomes larger, BEAM’s power increases, though it is always significantly lower than JBASE’s. JBASE’s performance consistently increases as skew in subphenotype proportions diminishes. Both OSACC and ChiSquare-multiway have relatively constant power at around 40%, while the Multinom model shows high variance and has extremely low power when K = 2. This shows that the algorithm is very unstable if the number of subpopulations is misspecified. Moreover, both Multinom and OSACC have very high Type 1 Error rates, which is also the case in other evaluation criteria (see below). Overall, we see that JBASE delivers superior performance across all subpopulation size settings.
3.1.2 Odds ratio analysis
Odds ratio is a classical metric used in GWAS for measuring association strength and is defined as the odds of having a specific allele in cases compared with that in controls. All algorithms perform as expected across the odds ratio spectrum, i.e. the higher the odds ratio, the higher the power and the lower the Type 1 Error rate (Fig. 2C and D). However, JBASE outperforms all algorithms by a large margin even at very low odds ratios and consistently achieves a power of starting at around 1.5. BEAM catches up with JBASE in power only after the odds ratio exceeds 1.6, a value rarely observed in real GWAS datasets. Similarly, OSACC, despite having high Type 1 Error, catches up with JBASE and BEAM after the odds ratio increases to , which is even less common in real datasets. It should be noted that other algorithms do not reach 90% power even in the case of extremely high odds ratios, i.e. . This implies that, contrary to common perception, small population size is not the only performance bottleneck, since JBASE, and to an extent BEAM, perform reasonably well in those conditions.
3.1.3 MAF analysis
For a given SNP, MAF refers to the frequency of the less common allele in a given population. Since some algorithms have performance biases across the MAF spectrum, we demonstrate the performance of each algorithm across the full MAF spectrum. Note that the MAF ranges are not simulated directly as the disease simulation models depend only on risk parameters α and Δ. However, as these parameters vary, MAFs of the underlying embedded variants also vary. As with the odds ratio analysis, all algorithms behave as expected across the MAF spectrum (Fig. 2E and F). At the ends of the spectrum (i.e. and ), power of all algorithms degrades. Best performance is achieved at moderate MAF ranges: . Note that the relatively high variance of algorithms at small MAF values might be simply due to smaller sample size, since much fewer () markers with were generated in our simulation experiments. This is because we aimed to match our experimental MAF spectrum to that of loci discovered in GWAS (see Supplementary Material Section S3.2.2 for additional analysis of MAF effects). Typically, GWAS are designed to exclude SNPs with an , as very strong statistical power is required to detect associations of such rare markers. Although not shown in the plots, there seems to be a negative correlation () between MAF and odds ratio. This explains the decrease in power towards higher MAF.
3.1.4 Disease model analysis
Finally, we analyzed the algorithms’ behavior for all disease model combinations (Fig. 2G and H). On average, as we move from left to right, the complexity increases due to an increase in combinations that include model 4 and model 5, which are more complex than model 1, model 2 and model 3. For all algorithms, we see a steady degradation of power from left to right, correlating with the underlying increase in complexity. JBASE maintains best performance across all combinations by a large margin, followed by BEAM with the second highest power. All other algorithms suffer from low power across the majority of disease model combinations. OSACC and Multinom also exhibit high Type 1 Error rates, while providing inferior power.
In summary, our extensive simulations show that JBASE and BEAM have substantially higher power in most of the scenarios we explored. Even though BEAM also accounts for epistasis, its performance significantly degrades in the presence of phenotype heterogeneity—precisely the shortcoming JBASE aims to address. OSACC and Multinom, on the other hand, perform poorly across the board, implying that subphenotype modeling without accounting for epistasis not only fails to provide power but also results in higher false-positive rates. We performed additional comparisons under various thresholds for Type 1 Error (see Supplementary Material Section S3.2.2), which show results to the same effect. Our simulations show that in the presence of heterogeneity our model is able to capture the subpopulations while other methods are not. JBASE also achieves the performance of BEAM in case control scenario.
3.2 T2D experiments
T2D is a common and complex metabolic disease affecting millions of individuals worldwide (Imamura and Maeda, 2011). Long-term complications of T2D include cardiovascular disease, stroke, diabetic retinopathy, kidney problems and neuropathy, among others. These factors jointly decrease the life expectancy of a T2D patient by up to 15 years (Davies et al., 2004). T2D is one of the classic examples of missing heritability: while family heritability has been estimated to be between 26% and 64%, only around 10% has been accounted for by loci identified in T2D GWAS (Stahl et al., 2012).
We studied a Mexican T2D dataset, which has rich phenotypic data (Parra et al., 2011). As for phenotypes, we studied BMI and waist-to-hip ratio (WHR) traits. For a detailed description of the experimental setup, data pre-processing and the schematic overview of the full analysis pipeline, see Supplementary Material Section S4.1.
We applied JBASE to each pair of chromosomes independently to generate an initial set of candidate markers. We ran JBASE with 10 random restarts lasting 200 000 sampling iterations for each chromosome pair. Although it would be preferable to run all chromosomes jointly, the computational burden necessitates heuristic screening and prioritization steps. Markers that were classified as marginal or epistatic in at least 10 of the runs were selected as candidate markers. We obtained 64 candidate SNPs (see Supplementary Table S5). Since the candidate markers were discovered from runs conducted on pairs of chromosomes independently, we ran JBASE again after pooling them together. Note that the regions containing candidate sets of markers were highly enriched for associations with T2D-related GWAS (see Supplementary Material Section S4.2). In 70 of the 100 pooled runs, JBASE converged to a solution with two epistatic modules and one weak marginal association distinguishing two subgroups differentiated based on both BMI and WHR.
The larger subphenotype contains 631 patients with a median BMI of 30.4 and median WHR of 0.98 (Table 2). The smaller one contains leaner patients () with median BMI of 27.3 and median WHR of 0.94. Two epistatic sets consisting of two markers each are associated with these subphenotypes: (i) (rs1159752, rs4885712) with a joint marginal P value of (according to the test) and (rs8103847, rs12461255) with a joint marginal P value of -25 ( test) (Table 3). rs1159752 is located at the 5′-end of an uncharacterized gene (LOC101927224). There are several reported cholesterol and triglyceride associations in its immediate vicinity. We used HaploReg (Ward and Kellis, 2012) to check for regulatory signals in the nearby markers (). Within kb upstream is the SNP rs1929051 (), which modifies a binding motif of the myocyte enhancer factor 2A (MEF2A) gene, a transcription factor that regulates many muscle-specific, growth factor-induced and stress-induced genes. It has been associated with several T2D-related disorders such as cardiovascular disorders, insulin resistance and hypertension. Its epistatic pair rs4885712 is an intergenic SNP and is centrally located in a cluster of associations related to adiposity, cholesterol, blood pressure and T2D. HaploReg analysis suggests that it lies within an enhancer. It is located 71 kb upstream of the sprouty homolog 2 (SPRY2) gene recently associated with obesity (Kilpeläinen et al., 2011). Recent studies have identified SPRY1, a homolog of SPRY2, as a critical regulator of adipose tissue differentiation (Urs et al., 2010).
Table 2.
Summary of the discovered subphenotypes
| Mexico-1 |
Mexico-2 |
|||||
|---|---|---|---|---|---|---|
| Obese | Lean | P | Obese | Lean | P | |
| BMI | 30.4 | 27.3 | 8.98e-16 | 30.7 | 28.23 | 0.032 |
| WHR | 0.98 | 0.94 | 0.0016 | 0.94 | 0.91 | 9.1e-08 |
P values are calculated with Wilcoxon rank-sum test.
Table 3.
Summary of the discovered association markers
| Mexico-1 |
Mexico-2 |
|||||
|---|---|---|---|---|---|---|
| Module | Type | P | Module | Proxy(r2) | Type | P |
| rs8103847 | Epis. | 1.71e-25 | rs4805561 | 1.0 | Epis. | 2e-10 |
| rs12461255 | rs4932867 | 1.0 | Epis. | |||
| rs1159752 | Epis. | 3.45e-22 | rs1929045 | 0.84 | Epis. | 1e-2 |
| rs4885712 | rs4885712 | 1 | Epis. | |||
The Proxy column is the LD (as measured by r2) between the Mexico-1 marker and its paired proxy in Mexico-2 dataset. Joint marginal P-values are calculated with χ2 test.
The second epistatic module contains two SNPs: rs8103847 and rs12461255. rs8103847 is located within an intron region of zinc finger protein 536 (ZNF536), which is involved in transcriptional regulation of neuron differentiation. The immediate region 100 kb upstream of the ZNF536 gene contains a cluster of associations in BMI, C-reactive protein, cholesterol and hip size. Strikingly, this region was previously identified as a significant risk factor associated with T2D in lean European-American individuals (Tudor, 2011). Moreover, HaploReg suggests that it modifies a binding motif of the paired box 4 (PAX4) gene as well as the E1A binding protein p300 (EP300) transcription factors. PAX4 is involved in pancreatic islet development and differentiation of insulin-producing beta cells, while EP300 is mostly involved in cell differentiation and proliferation. The EP300 protein physically interacts with the homeobox A protein (HNF1), which is a key gene associated with several metabolic disorders. The other marker of the epistatic pair, rs12461255, is an intergenic SNP located within a region with many zinc finger genes. Its haplotype neighborhood contains several binding regions for transcription factors and several other modified motifs, suggesting that it sits in a hotspot of regulatory activity.
Finally, JBASE also identified a weak marginal marker rs1948122 with a posterior probability of and marginal association P value of less than of being associated with the obese subphenotype in the Mexico-1 experiments. Because of the low posterior marginal probability JBASE reported, we did not expect this weak association to replicate.
Before advancing to replication studies, we performed rigorous genotyping quality, LD and population stratification analysis-based tests. This was to ensure that these newly discovered subphenotypes are not artifacts of data quality, LD and/or population stratification (see Supplementary Material Section S4.3 for details).
3.2.1 Replication experiments
We analyzed a second dataset from Mexico City (Mexico-2) with JBASE. Mexico-2 is also an admixed dataset consisting of N = 864 samples genotyped on the Affymetrix Axiom Genome-Wide LAT-1 Array. It includes 817810 SNPs particularly chosen to maximize the coverage of common genome variation present in Hispanic populations (Hoffmann et al., 2011). For markers without an exact match in the two datasets, we selected the closest tag SNPs within their haplotype mates with . After quality filtering, as applied to the Mexico-1 dataset, we obtained rs1929045 as a proxy for rs1159752 (), rs4805561 for rs8103847 () and rs4932867 for rs12461255 (). All of these SNPs have high-quality genotyping in the Mexico-2 set (Supplementary Fig. S16).
JBASE recovered two subphenotypes (Tables 2 and 3), which are very similar to the original subphenotypes, along with the respective epistatic modules rs1929045–rs4885712 () and rs4805561–rs4932867 (). The BMI and WHR medians are 30.07 and 0.94, respectively, for the first subphenotype (obese) and 28.23 and 0.91 for the second (lean). The relative sizes of the obese (0.70 versus 0.65) and lean (0.30 versus 0.35) subphenotypes as well as the median values of the subphenotypes are close to that of the Mexico-1 dataset. The exception is WHR, which has a higher overall mean in the Mexico-2 dataset. BMI phenotype is highly overlapping in the Mexico-2 dataset, hence the higher P value. rs8103847, which we chose as proxy for rs4805561, shows a very significant marginal association, while none of the other three markers have significant marginal associations. Similar to the Mexico-1 dataset, analysis of PCA coordinates indicates that the obtained subphenotypes are not due to population stratification (Supplementary Fig. S11).
We included two proxies for the marginal marker rs1948122 in the replication experiments: rs1386751 () and rs2279789 (). As expected, the weak marginal association did not replicate in the Mexico-2 dataset, indicating a false positive, which JBASE correctly classified as a null marker.
4 Discussion
Existing association discovery methods for complex phenotypes do not account for phenotype heterogeneity and epistasis simultaneously. Here, we have demonstrated that ignoring either of these factors leads to a loss of power in discovery of associations with subphenotype specific effects, especially in the presence of non-additive variant effects.
Our method, JBASE, is a unified statistical algorithm for inference of subphenotypes and their associated variants that takes epistasis into account. Instead of tackling the two seemingly unrelated challenges of missing heritability separately, our probabilistic model JBASE performs joint inference. JBASE achieves this by modeling the phenotype as a mixture of subpopulations with distinct (yet possibly overlapping) distributions. Each of these distributions has its own mixture of null, marginal and epistatic genotype components. We chose to extend the original BEAM framework, rather than extending its successors (BEAM2 (Zhang et al., 2011), BEAM3 (Zhang, 2012), to reduce the complexity and increase the computational efficiency. We provide an efficient Markov chain Monte Carlo-based inference algorithm along with improvements in handling LD and population stratification with a lower computational burden than previous extensions. JBASE is particularly well suited as a meta-analysis tool for combining candidate regions and markers across a variety of cohorts as it increases power for the detection of marginal and epistatic associations by identifying more homogeneous subpopulations within these very large cohorts.
Through our detailed experiments, we showed that JBASE outperforms all existing methods across various disease models and settings of heterogeneity levels, MAF and odds ratios. Applying JBASE to a real T2D dataset, we were able to discover—and independently replicate—novel associations that were not discovered in previous analyses of these datasets.
There are several potential extensions for JBASE. One extension could be to model subphenotypes as an infinite mixture model, introducing the capability of automatically detecting the number of subphenotypes. One must be mindful that such models also come with additional computational requirements. In such a model, downstream analysis and validation of a higher number of subphenotypes will most likely be a tedious task. As such, a trade-off should be made between model complexity and feasibility of downstream analysis on a case-by-case basis.
To summarize, JBASE is the first algorithm to tackle modeling of epistasis and subphenotyping simultaneously. We show that taking both of these causes of missing heritability into account increases the power and reduces the Type 1 Error in detecting associations.
Supplementary Material
Acknowledgement
We thank Daniel Hidru, Shankar Vembu and Andrew Paterson for useful feedback on the manuscript.
Funding
This work was supported by the SickKids Research Institute (A.G.), by NSERC 386671-1 and CIHR MOP-123526 (to P.M.K.) and by an NSERC CGS-D3 Scholarship (to R.C.). In Mexico, this work was supported by SSA/IMMS/ISSSTE-CONACYT 2010-2, clave 150352, Apoyo Financiero Fundacion IMSS and Fundacion Gonzalo Rio Arronte I, IMSS Scholarship.
Conflict of Interest: none declared.
References
- Bergen S.E. (2014) Genetic modifiers and subtypes in schizophrenia. Curr. Behav. Neurosci. Rep., 1, 197–205. [Google Scholar]
- Chen X., et al. (2012) A two-graph guided multi-task Lasso approach for eQTL mapping. J. Machine Learn. Res., 22, 208–217. [Google Scholar]
- Davies M.J., et al. (2004) Prevention of type 2 diabetes mellitus. A review of the evidence and its application in a UK setting. Diabet. Med., 21, 403–414. [DOI] [PubMed] [Google Scholar]
- Goudey B., et al. (2013) GWIS—model-free, fast and exhaustive search for epistatic interactions in case-control GWAS. BMC Genomics, 14(Suppl 3), S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann T.J., et al. (2011) Design and coverage of high throughput genotyping arrays optimized for individuals of east Asian, African American, and Latino race/ethnicity using imputation and a novel hybrid SNP selection algorithm. Genomics, 98, 422–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W., et al. (2012) Epistasis dominates the genetic architecture of Drosophila quantitative traits. Proc. Natl. Acad. Sci. USA, 109, 15553–15559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imamura M., Maeda S. (2011) Genetics of type 2 diabetes: the GWAS era and future perspectives. Endocr. J., 58, 723–739. [DOI] [PubMed] [Google Scholar]
- Kilpeläinen T.O., et al. (2011) Genetic variation near IRS1 associates with reduced adiposity and an impaired metabolic profile. Nat. Genet., 43, 753–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S., Xing E.P. (2009) Statistical estimation of correlated genome associations to a quantitative trait network. PLoS Genet., 5, e1000587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J., et al. (2012) Improved linear mixed models for genome-wide association studies. Nat. Methods, 9, 525–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning A.K., et al. (2012) A genome-wide approach accounting for body mass index identifies genetic variants influencing fasting glycemic traits and insulin resistance. Nat. Genet., 44, 659–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T.A., et al. (2009) Finding the missing heritability of complex diseases. Nature, 461, 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClellan J., King M.-C. (2010) Genetic heterogeneity in human disease. Cell, 141, 210–217. [DOI] [PubMed] [Google Scholar]
- Morris A.P., et al. (2010) A powerful approach to sub-phenotype analysis in population-based genetic association studies. Genet. Epidemiol., 34, 335–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northcott P.A., et al. (2012) Subgroup-specific structural variation across 1 000 medulloblastoma genomes. Nature, 488, 49–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parra E., et al. (2011) Genome-wide association study of type 2 diabetes in a sample from Mexico City and a meta-analysis of a Mexican-American sample from Starr County, Texas. Diabetologia, 54, 2038–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perry J.R.B., et al. (2012) Stratifying type 2 diabetes cases by BMI identifies genetic risk variants in LAMA1 and enrichment for risk variants in lean compared to obese cases. PLoS Genet., 8, e1002741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prabhu S., Pe’er I. (2012) Ultrafast genome-wide scan for SNP–SNP interactions in common complex disease. Genome Res., 22, 2230–2240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin X., et al. (2010) Ordered subset analysis for case-control studies. Genet. Epidemiol., 34, 407–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritchie M.D., et al. (2001) Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet., 69, 138–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahl E.A., et al. (2012) Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet., 44, 483–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stessman H.A., et al. (2014) A genotype-first approach to defining the subtypes of a complex disease. Cell, 156, 872–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timpson N.J., et al. (2009) Adiposity-related heterogeneity in patterns of type 2 diabetes susceptibility observed in genome-wide association data. Diabetes, 58, 505–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tudor S. (2011) Gene by BMI interactions influencing C-reactive protein levels in European-Americans. MSc Thesis, The University of Texas Graduate School of Biomedical Sciences at Houston. [Google Scholar]
- Urs S., et al. (2010) Sprouty1 is a critical regulatory switch of mesenchymal stem cell lineage allocation. NFASEB J., 24, 3264–3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward L.D., Kellis M. (2012) HaploReg: a resource for exploring chromatin states, conservation, and regulatory motif alterations within sets of genetically linked variants. Nucleic Acids Res., 40(Database Issue), 930–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warde-Farley D., et al. (2012) Mixture model for sub-phenotyping in GWAS. In: Altman R.B., et al. (eds) Proceedings of the Pacific Symposium Biocomputing, Hawaii, World Scientific Publishing Co., Inc., Printed by Curran Associates, Inc., pp. 363–74. [PubMed] [Google Scholar]
- Zhang B.Y., et al. (2011) Block-based Bayesian epistasis association mapping with application to wTCCC type-1 diabetes data. Ann. Appl. Stat., 5, 2052–2077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W., et al. (2010a) A Bayesian partition method for detecting pleiotropic and epistatic eQTL modules. PLoS Comput. Biol., 6, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., et al. (2010b) TEAM: efficient two-locus epistasis tests in human genome-wide association study. Bioinformatics, 26, 217–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. (2012) A novel Bayesian graphical model for genome-wide multi-SNP association mapping. Genet. Epidemiol., 36, 36–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Liu J.S. (2007) Bayesian inference of epistatic interactions in case-control studies. Nat. Genet., 39, 1167–1173. [DOI] [PubMed] [Google Scholar]
- Zuk O., et al. (2012) The mystery of missing heritability: genetic interactions create phantom heritability. Proc. Natl. Acad. Sci. USA, 109, 1193–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.