Sliding Contact Fatigue Damage in Layered Ceramic Structures

Abstract

Porcelain veneered restorations often chip and fracture from repeated occlusal loading, making fatigue studies relevant. Most fatigue studies are limited to uniaxial loading without sliding motion. We hypothesize that biaxial loading (contact-load-slide-liftoff, simulating a masticatory cycle) as compared to uniaxial loading accelerates the fatigue of layered ceramics. Monolithic glass plates were epoxy joined to polycarbonate substrates as a transparent model for an all-ceramic crown on dentin. Uniaxial and biaxial cyclic contact was applied through a hard sphere in water with a mouth-motion machine. The uniaxial (contact-load-hold-liftoff) and traditional R-ratio fatigue (indenter never leaves the specimen surface) produced a similar lifespan, while biaxial fatigue was more severe. The accelerated crack growth rate in biaxial fatigue is attributed to enhanced tensile stresses at the trailing edges of a moving indenter. Fracture mechanics descriptions for damage evolution in brittle materials loaded repeatedly with a sliding sphere are provided. Clinical relevance is addressed.

INTRODUCTION

One of the emerging causes of fracture of all-ceramic dental restorations is the generation of microcracks due to occlusal contact and wear. In order to improve the contact damage resistance of dental ceramics, it is important to understand the damage mechanisms involved.

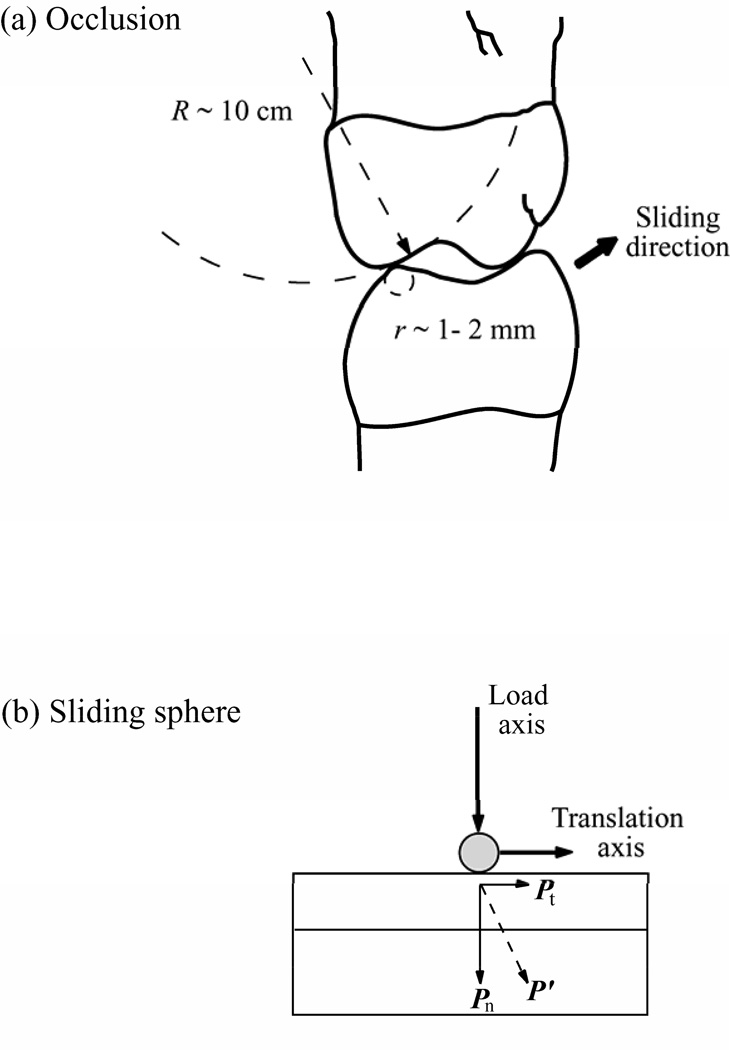
A three-phase model of a chewing cycle has been put forward by DeLong and Douglas (1983). A preparatory phase, during which the mandible is positioned; a crushing phase, which starts from tooth contacts with the food bolus until it contacts with the opposing tooth; and a final grinding or sliding phase, where the two opposing teeth slide against each other under the masticatory force. The sliding phase for the molar teeth begins with an eccentric contact of the mandibular buccal cusps with the inner inclines of the maxillary buccal cusps, followed by a sliding movement through centric occlusion, and then lifting off [Fig. 1(a)]. The average length of the sliding path of a first molar is ~0.5 mm (DeLong and Douglas, 1983). The actual sliding path is in a form of an arc due to the occlusal anatomy. However a straight-line motion gives a good approximation because sliding movement is much smaller than the radius of the cusps, typically R ~10 cm (DeLong and Douglas, 1983). The magnitude of the masticatory forces is 9–180 N (Kelly, 1999). The duration of the forces is 0.25–0.33 s (Jemt et al., 1979).

FIGURE 1.

Schematic of contact with load-slide action. (a) Tooth eccentric occlusal position of right side first molar. Arrow indicates direction of sliding as teeth move to centric occlusion. Relative tooth radii at buccal cusp contacts are shown. (b) Experimental arrangement for indentation of brittle layer on compliant substrate with superposed tangential force component.

The above contact-slide action is most pertinent to porcelain occlusal damage and wear. Yet most contact fatigue studies use uniaxial loading without the critical sliding action. This study sought to address this by employing mouth-motion like fatigue loading (contact-load-slide-liftoff) on crack evolution in ceramics with uniaxial and R-ratio controls.

MATERIALS & METHODS

Material systems

Soda-lime glass was used as a model material owing to its similar physical properties to dental porcelains and its transparency which allows in-situ observation of the entire evolution of fracture. Glass plates (25×25×1 mm, Daigger, Wheeling, IL) were polished on side surfaces for in-situ viewing during testing. The top surfaces of the glass plates were lightly abraded with 600-grit SiC to provide an adequate density of flaws for cone crack initiation, so as to introduce flaws comparable in scale (~10–20 µm in size) to those associated with crystallites in the porcelain and glass-ceramic interior. The bottom surfaces of the plates were etched with 9.5% hydrofluoric acid for 5 min to remove surface flaws and to avoid flexure-induced bulk fracture from the cementation interface. Plates were then joined to the polycarbonate substrates (12.5 mm thick, AlN Plastics, Norfolk, VA) with a thin layer (~10–20 µm) of epoxy adhesive, which was allowed to cure for 48 hrs. Since the elastic modulus of epoxy (3.5 GPa) is similar to polycarbonate (2.3 GPa), the structure is effectively a glass/polycarbonate bilayer. For reference, porcelain (LAVA Ceram, 3M/ESPE, St. Paul, MN) (ϕ20 × 1 mm) veneered fully sintered CAD/CAM zirconia plates (ϕ20 × 0.5 mm) (LAVA Frame, 3M/ESPE) were cemented (Rely X, ARC, 3M/ESPE) to composite blocks (Z100, 3M/ESPE) (Kim et al., 2007).

Fatigue tests

To facilitate direct comparison of damage response of brittle materials under R-ratio, uniaxial, and biaxial loading, Hertzian indentation fatigue tests were carried out on glass/polycarbonate bilayers at P_m = 120 N (peak load) with tungsten carbide (WC) spheres of radius r =1.5 mm in room temperature water. For comparison, biaxial tests were conducted on the porcelain veneered zirconia system. The R-ratio fatigue tests were carried out on a servo-hydraulic universal testing machine (Model 8502, Instron Corp., Canton, MA) with an oscillating load between a maximum load P_m = 120 N and a minimum load 2 N (indenter never leaves surface), at a constant frequency f = 1 Hz. The uniaxial and biaxial fatigue tests were carried out on a mouth-motion simulator (Elf 3300, EnduraTEC Division of Bose, Minnetonka, MN) with a controlled profile: P_m = 120 N, loading and unloading rates 1000 N/s, and a chewing frequency ~1 Hz. For the uniaxial fatigue tests, each load cycle consisted of the indenter contacting the specimen, loading to a maximum, holding for 0.35 s, unloading, and lifting off (0.5 mm) from the specimen surface and restricted to a vertical motion. For the biaxial tests, specimens were fixed onto a lateral motion drive table. A load profile identical to the uniaxial loading was employed, except while the indenter was holding the maximum load for 0.35 s, the table moved laterally at a constant velocity v = 2 mm/s for 0.7 mm, and then during the indenter lifting off phase, the specimen table returned to its original position [Fig. 1(b)]. The friction coefficient for sliding in water was µ ≈ 0.58. It was estimated using equation (A4) with a measured value of α’, the inclination angle for distorted cone cracks in sliding contact, while assuming α = 22°, the inclination angle for classical Hertzian cone cracks in uniaxial loading (Appendix). A minimum of 3 tests were conducted for each condition. All tests were recorded using a video camcorder (Canon XL1, Canon, Lake Success, NY) equipped with a custom designed microscope zoom system (Zhang et al., 2005a). Crack depth and angle were measured from video frames to ± 5 µm and ± 0.5°, respectively.

RESULTS

Crack morphology

In all instances, cone cracks were the dominant mode of fracture but differed in evolution with R-ratio and uniaxial fatigue most similar [see sequence in Fig. 2(a), P_m = 120 N]. In both R-ratio and uniaxial fatigue, outer cone initiated first and propagated downward and outward at a slow but steady pace. The angle of the cone crack, α, in respect to the free surface was typically 22 ± 5°. Subsequently, an inner cone formed within the contact region from the occlusal surface and extended downward at a relatively high rate and steep angle (55 ± 15°). Intrusion of water into the inner cone crack was evident, especially during the loading cycle. When inner cones propagated approximately halfway through the glass thickness, they began to experience the plate flexure-induced tensile stresses and surged abruptly to the glass polycarbonate interface. In all tests, failure of the glass layer resulted from the deep penetrating inner cones.

FIGURE 2.

Side view video sequence of cone cracks evolving in glass plate on polycarbonate bilayer with (a) uniaxial and (b) biaxial loading following various numbers of cycle n. Indentation with tungsten carbide (WC) sphere of radius r = 1.5 mm, in water. Only the glass plate of thickness d = 1 mm is shown here. Note in (a) outer cone (O) forms first but inner cones (I) propagate to glass/polycarbonate interface, while in (b) partial cones (P) penetrate through the glass layer. Also shown here are the top view optical micrographs of a (c) glass/polycarbonate bilayer and (d) LAVA porcelain veneered zirconia subjected to single cycle biaxial loading at P_m = 120 N with a WC sphere of r = 1.5 mm, in water. Note: the damage patterns are similar in glass and porcelain. Arrows in (b), (c) and (d) indicate the sliding direction for the biaxial test.

In biaxial fatigue at the same load [P_m = 120 N, Fig. 2(b)], a comparable sequence of observations reveals a series of partial cone cracks forming in the first sliding cycle (distorted outer cones of uniaxial loading, see Appendix). The trailing edges of the partial cones having an inclination angle α’ = 52 ± 10°, which was much steeper than for classical Hertzian outer cones in uniaxial loading (α = 22 ± 5°). Water intrusion was observed from the second sliding cycle onward. These partial cones became increasingly unstable as they approaching the mid thickness of the glass plate and ultimately jumped to the glass polycarbonate interface. The final crack configuration had a tilted aspect, somewhat like the schematic in Appendix [Fig. A1(b)]. The main difference between the biaxial fatigue and uniaxial or R-ratio fatigue was propagation of the partial cones to the glass polycarbonate interface rather than the inner cones in the latter.

Similar sliding damage features, a series of partial cones, were observed in surface view optical micrographs of glass/polycarbonate and porcelain/zirconia/composite structures subjected to single-cycle biaxial loading (P_m = 120 N, WC indenter, r = 1.5 mm) in water [Figs. 2(c) and (d)].

Crack evolution

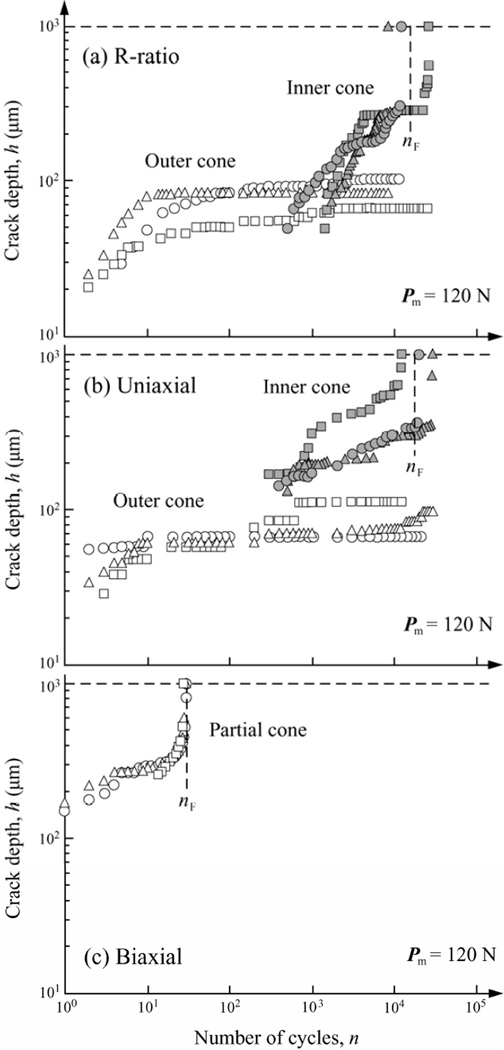
Crack depth h was measured at the point of maximum penetration for prescribe number of cycles in the video footages. Plots of crack evolution for glass/polycarbonate structures under fatigue loading in R-ratio, uniaxial, and biaxial profiles were constructed [Figs. 3(a)–(c) respectively]. Data points are individual measurements for each fracture type. The data for outer (unfilled symbols) and inner cones (filled symbols) showed similar trends in R-ratio and uniaxial fatigue [Figs. 3(a) and (b)]. The outer cone cracks formed within 10 cycles and propagated rapidly to a depth ~100 µm before leveling out over the remaining cycles. The inner cones became visible at ~500 cycles, which was considerably late compared to outer cones, but quickly outgrew the outer cones and propagated substantially deeper, becoming more unstable as they began to experience flexural tensile stresses, ultimately penetrating abruptly to the glass polycarbonate interface. Whereas the well-developed outer cones followed a classical slow crack growth (SCG) dependence, the inner cones followed a much steeper depth-cycle curve, indicating a sustained driving force throughout the entire crack evolution (Zhang et al., 2005b). The number of cycles to failure was similar in R-ratio and uniaxial fatigue [vertical dashed lines in Figs. 3(a) and (b)].

FIGURE 3.

Plot of crack depth h as a function of number of cycles n in glass/polycarbonate bilayer, for (a) R-ratio fatigue; (b) uniaxial fatigue; and (c) biaxial fatigue. Indentation with WC sphere of radius r = 1.5 mm, maximum load P_m = 120 N, in water. Failure occurs when crack depth h reaches glass/polycarbonate interface (top of the vertical axis, glass thickness d = 1000 µm) at critical number of cycles n_F (vertical dashed lines). Note: crack growth substantially enhanced in biaxial loading.

During the first sliding cycle of biaxial fatigue [Fig. 3(c)] a series of partial cone cracks formed, at a much greater depth (~200 µm) and a steeper angle to the classical outer cone cracks of uniaxial loading. Under the subsequent sliding contacts, one of the partial cone cracks, usually the second or the third one from the initial contact point, began to dominate. This dominate crack extended downward dramatically to the half thickness of the glass plate, followed by a rapid jump to the glass polycarbonate interface. The number of cycles required for cracks to penetrate the entire glass layer was over two orders of magnitude less for partial cones as compared to inner cones in both uniaxial and R-ratio fatigue (vertical dashed lines in Figs. 3). A 1-sample t-test showed this difference to be significant (p < 0.001).

DISCUSSION

This paper has considered the influence of biaxial fatigue on crack modes in brittle layer structures using a hard sphere in water, with data on model glass/polycarbonate bilayers as a case study. For the glass thickness of 1 mm used here, the dominant stresses are the near-contact Hertzian stresses. The corresponding mode of fracture is occlusal surface cone cracking. Definitive experiments have been conducted to identify the effect of the initial quasi-impact contact and sliding action (analogous to tooth contact during mastication) on the damage modes and fatigue life of brittle layers on compliant substrates. Our findings show that an initial quasi-impact contact has little influence on either damage modes or fatigue life of glass/polycarbonate bilayers. However, sliding motion under masticatory force is highly deleterious to the lifetime. Therefore, sliding action must be considered in any laboratory simulation of the clinical environment intended to establish the longevity of all-ceramic crowns.

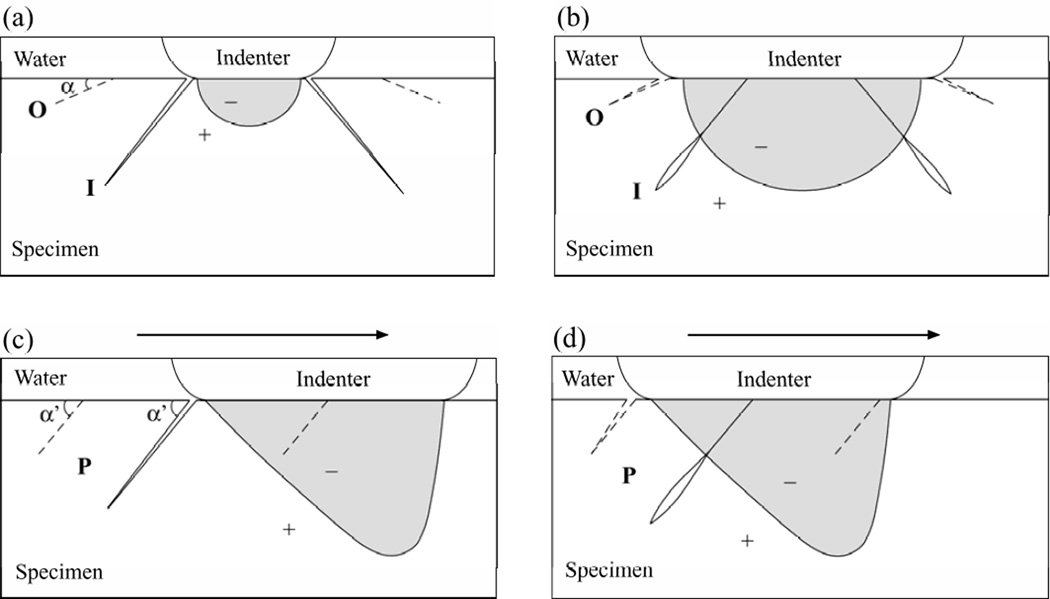
Friction associated with sliding action intensifies the tensile stresses at the trailing edges of the contact, generating a series of partial cone cracks. Both theory (Appendix) and experiments indicate, for a given load, partial cone cracks penetrate deeper into the material relative to uniaxial outer cone cracks. The uniaxial outer cones experience tensile stresses throughout the entire load-unload cycle [Figs. 4(a) and (b)], while partial cones experience both compressive (shaded grey) and tensile stresses as the indenter slides across the surface [Figs. 4(c) and (d)]. Therefore, partial cones undergo hydraulic pumping, as the inner cones in uniaxial loading. Fracture mechanics descriptions for hydraulic pumping of inner cones in uniaxial fatigue loading in water have been developed (Bhowmick et al., 2005; Chai and Lawn, 2005; Zhang et al., 2005b). Briefly, inner cones initiate within the contact region. As the load increases, the inner cone crack initially experiences small tensile stresses which open the crack, allowing water to enter. Upon increasing load, the indenter engulfs the crack, sealing the crack mouth and subjecting the water-filled crack to a Hertzian compression zone. Once the inner cones grow sufficiently large to extend beyond the compression zone, the extremities of the inner cones enter a tensile field [Figs. 4(a) and (b)]. Compressive crack mouth pinching forces water downward, driving the inner cones deeper [Fig. 4(b)]. By a similar mechanism, partial cones penetrate through the ceramic layer more rapidly than inner cones. This is because (1) partial cones can form in a large size within a few sliding cycles and their extremities immediately experience the tensile stresses as the indenter slides across the surface [Figs. 4(c) and (d)]. Inner cones must undergo an incubation stage during which they are completely trapped in the Hertzian compression zone; and (2) partial cones experience an enhanced compressive stress at the full engulfment of the indenter, plus an intensified tensile stress at the trailing edge of the moving indenter. Inner cones only experience smaller tensile stresses [Fig. 4(a)].

FIGURE 4.

Schematic demonstrating water entrapment model for fatigue loading with (a) and (b) uniaxial, and (c) and (d) biaxial configurations. Shaded area beneath contact designates approximate compression zone. The inclination angles for partial and outer cones in uniaxial and biaxial loading are α’ and α, respectively. (a) Water enters inner cone crack (I) prior to contact engulfment. (b) As the indenter contact expands, the water is trapped and is squeezed toward the crack tip, causing downward penetration. Note: in (a) and (b) outer cone crack (O) always lies in the Hertzian tensile field outside the contact and water is never trapped in this crack. (c) Water enters partial cone crack (P) at the trailing edge of the contact at the n cycle. (d) As the indenter slides across the surface in the n + 1 cycle, compressive crack mouth pinching squeezes the water toward crack tip. Cyclic contact repeats the process, forcing more water into crack in successive cycles. Arrows in (c) and (d) represent the sliding direction for the biaxial test. +: tension; −: compression.

We have not considered internal radial cracks, originating from the cementation surfaces. These far-field flexural stress induced cracks are not sensitive to loading conditions: uniaxial or biaxial (Lee et al., 2001). Radial cracks can become dangerous in thin ceramic crowns as they propagate rapidly and the load for initiation falls off rapidly with diminishing thickness. Radial fracture will not be an immediate threat for ceramic thickness >1 mm. For dental crowns, the norm is a thickness of 1.5 mm, but geometrical constraints imposed by tooth position and the opposing dentition may limit thickness.

Our studies find that cone cracks cease at the glass/polycarbonate interface—neither propagating into the polycarbonate base nor extending along the interface. Although the incidence of occlusal cone cracks may not result in catastrophic failure of the ceramic crowns as may cementation radial fractures (i.e. bulk fracture), they may nevertheless provide pathways for external elements to the interior of the layer system. In the case of weak interfaces, cone cracks can promote interlayer delamination.

We acknowledge that occlusion involves enamel-porcelain or porcelain-porcelain antagonistic contacts with various cuspal radii. The question arises: how the choices of indenter material and radius influence the mechanics? A recent study has shown that the critical loads and number of cycles to penetrate an occlusal surface cone crack through a glass layer is insensitive to either the indenter material (WC or glass) or indenter radius (r = 1.6–12.5 mm) (Bhowmick et al., in press). The choice of a hard WC indenter is simply to enable multiple testing without the need for test-by-test replacement of the indenter. Our results might be modified in saliva which is known to reduce the friction coefficient between the slider and the ceramic surface (Koran et al., 1972). Further investigation into the effect of saliva is warranted.

In summary, occlusal-like biaxial loading of brittle crown-like structures can trigger a series of partial cone cracks, capable of causing failure by propagation to the intervening interface. Fracture mechanics descriptions (Appendix) have been developed for the evolution of partial cones in brittle materials loaded repeatedly with a sliding sphere. In aqueous environments the friction-activated partial cone cracks are much more deleterious than the outer and inner cone cracks associated with uniaxial fatigue loading.