Correlated Parameter Fit of Arrhenius Model for Thermal Denaturation of Proteins and Cells

Abstract

Thermal denaturation of proteins is critical to cell injury, food science and other biomaterial processing. For example protein denaturation correlates strongly with cell death by heating, and is increasingly of interest in focal thermal therapies of cancer and other diseases at temperatures which often exceed 50 °C. The Arrhenius model is a simple yet widely used model for both protein denaturation and cell injury. To establish the utility of the Arrhenius model for protein denaturation at 50 °C and above its sensitivities to the kinetic parameters (activation energy E_a and frequency factor A) were carefully examined. We propose a simplified correlated parameter fit to the Arrhenius model by treating E_a, as an independent fitting parameter and allowing A to follow dependently. The utility of the correlated parameter fit is demonstrated on thermal denaturation of proteins and cells from the literature as a validation, and new experimental measurements in our lab using FTIR spectroscopy to demonstrate broad applicability of this method. Finally, we demonstrate that the end-temperature within which the denaturation is measured is important and changes the kinetics. Specifically, higher E_a and A parameters were found at low end-temperature (50°C) and reduce as end-temperatures increase to 70 °C. This trend is consistent with Arrhenius parameters for cell injury in the literature that are significantly higher for clonogenics (45 – 50 °C) vs. membrane dye assays (60 –70 °C). Future opportunities to monitor cell injury by spectroscopic measurement of protein denaturation are discussed.

1. INTRODUCTION

Proteins are large biological molecules that consist of one or more chains of amino acids, and possess complicated three-dimensional folded structures and unique functionality.^[1] Protein denaturation refers to a conformational change resulting in partial or total unfolding of a protein from its native state, and/or structural damage to the molecule.^[2] Specifically, the unfolding includes changes in secondary structures such as α-helices and β-sheets, and leads to change or inactivation of protein function. This process is important for a number of biotechnologies^{[2, 3]}, disease conditions and treatments.^{[4, 5]} Thermally induced protein denaturation, in particular, has found important applications in food processing,^[3] burn injury, and thermal ablation of diseased or cancerous tissue,^{[6, 7]} and has been proposed to correlate with cell injury.^{[4, 8]}

The dynamic measurement of protein denaturation is most readily achieved by optical and calorimetric approaches. Typical measurement techniques for protein denaturation, especially protein thermal denaturation, are listed in Table 1. Among all the methods, X-ray crystallography and NMR spectroscopy are known to determine the three dimensional structure of proteins,^[1] but X-ray crystallography is limited to static measurements since it requires proteins in a crystalline state. Optical approaches such as birefringence, vibrational spectroscopy (i.e. Fourier transform infrared spectroscopy (FTIR) and 2D correlation infrared spectroscopy (IR)) and circular dichroism (CD) are more suited to measure the dynamic change in the secondary structure of proteins during denaturation, in particular α-helix and β-sheet structures (IR band changes^[8]) or loss of structure (order to disorder in birefringence^[9]). On the other hand, differential scanning calorimetry (DSC) measures the enthalpic change during protein denaturation and unfolding. In this study, FTIR is used to monitor protein denaturation during thermal treatment.

Table 1.

Measurement techniques for protein denaturation

Technique	Measurement	Sample requirement	Static/Dynamic	Ref.
X-ray crystallography	3D structure	Protein in crystal state	Static	[1]
NMR+ spectroscopy	3D structure	Small proteins or protein domains (≤20kD)	Dynamic	[1, 48]
FTIR	Secondary structure	Surface or thin sample (<100µm)	Dynamic	[8]
2D IR	Secondary structure and hydration	Surface or thin sample (<100µm)	Dynamic	[49]
Circular dichroism (CD)	Secondary structure	Minimal preparation. Minimize absorption of other species in UV range.	Dynamic	[50]
DSC	Calorimetric effect associated with protein structure change.	Sample volume range from ng (Nano DSC) to mg (traditional DSC) depending on the instrument	Dynamic	[4, 8]
Birefringence	Anisotropy in tissue	Optically accessible	Static	[9]
Dilatometry	Density change	Liquid sample	Dynamic	[51]
Rheometry	Viscosity change	Liquid sample	Dynamic	[52]

⁺NMR stands for Nuclear magnetic resonsance. Heat induced protein aggregation can be challenging to study with NMR.^[48]

Different models have been used to describe the kinetics of protein denaturation. For example, protein denaturation can be described as an absolute rate process between a native state, the final denatured state and one or several macrostates in between. One of the best-known models is the Lumry-Eyring model (or three state model) ^[10–12] which assumes that protein denaturation occurs in two steps: (1) reversible unfolding of native protein (N); and (2) irreversible change of unfolded protein (U) to the final denatured state (D).

$$N\rightleftharpoons U\to D$$ (1)

Furthermore, the two-step Lumry-Eyring model can be simplified to a one-step, two-state irreversible denaturation model when the irreversible step is significantly faster than reversible unfolding step. ^{[11, 13]}

$$N\stackrel{k}{\to }D$$ (2)

This first-order irreversible reaction kinetic model has been widely used for the analysis of protein denaturation and thermal injury of cells and tissues.^{[7, 14, 15]} The reaction rate of this irreversible process is described by a temperature dependent rate constant (Arrhenius equation)

$$\mathrm{k}=\mathrm{A}\text{exp}(-\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{R}\mathrm{T}})$$ (3)

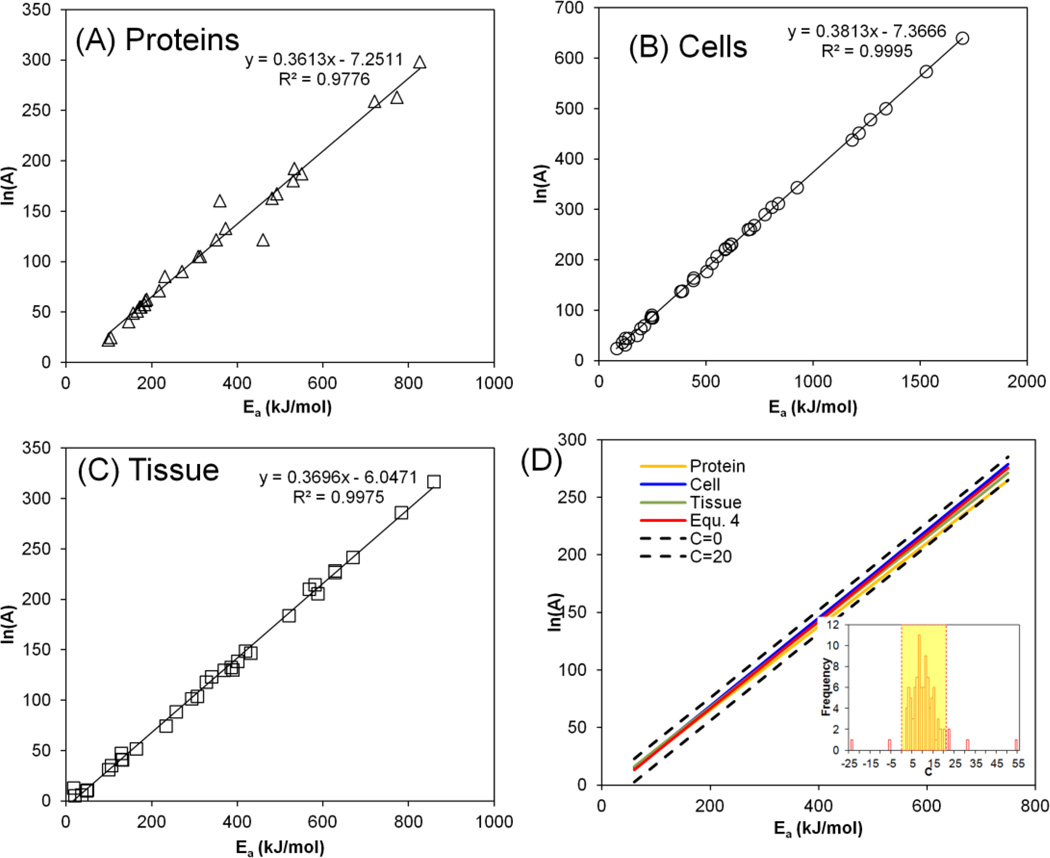
where A is the frequency factor (s⁻¹), and E_a is the activation energy (kJ mol⁻¹). Two parameters (E_a and A) are used to describe the kinetics of thermally induced protein denaturation where E_a is related to the reaction activation enthalpy and A depends on the reaction entropy according to the Eyring-Polyani equation.^[16]. The activation energy in various protein systems varies between 100 and 800 kJ mol⁻¹ and the frequency factor varies between 10⁹ to 10¹²⁹ s⁻¹ (i.e. 20~300 for ln{A}) as shown in Figure 1.

Figure 1.

Empirical correlation between the activation energy (E_a, kJ mol⁻¹) and natural logarithm of frequency factor (ln{A}, s⁻¹) values for (A) proteins, (B) cells, and (C) tissues. (D) shows that the range of C chosen encompasses the linear fits for proteins, cell and tissues shown in (A–C). The kinetic parameters are plotted from tables in He et al.^[7] and updated with recently reported data.^{[25, 53, 54]} Inset histogram shows the distribution of C values and the highlighted region represents the range of C for the fit (0<C<20).

Despite the wide variation of the activation energy and frequency factor, it has been suggested that there is a relationship between the parameters (enthalpy-entropy compensation or alternatively Meyer-Neldel rule).^{[17, 18]} The compensation law states that the kinetic rate varies exponentially with temperature, and a linear relationship exists between the thermal activation energy and logarithm of the prefactor, or frequency factor. This has been demonstrated for a variety of thermally activated processes including semiconductor conductivity, annealing phenomena, aging of insulating polymers, chemical reactions and biological death rates.^{[18, 19]} Rosenberg was among the first to report the compensation behavior for thermal inactivation of different protein systems (pure protein, virus, yeasts, and bacteria).^[17] The linear relation between the activation energy and ln{A} has also recently been demonstrated in more complex protein systems such as cells and tissues. Here, He et al. reported a linear correlation between E_a and ln{A} which likely represents the compensation law:^[7]

$$\text{ln}\{\mathrm{A}\}=0.38{\mathrm{E}}_{\mathrm{a}}-9.36$$ (4)

Around the same time, Wright et al. also reported similar correlation (ln{A} = 0.3832*E_a - 10.042).^[20] The correlations reported by He et al. and Wright et al. are similar to the one reported by Rosenberg (ln{A} = (0.366~0.370)*E_a −14.5).^[17] Figure 1 shows E_a versus ln{A} plots of thermally induced denaturation of pure proteins (A), cells (B) and tissues (C) demonstrating a linear correlation in each case. It has also been suggested that random and systematic errors can lead to apparent compensation behavior which necessitates more careful considerations.^{[21, 22]} In addition, modification of the Arrhenius model has also been reported to reduce the difficulty to fit the correlated kinetics parameters by introducing an optimum reference temperature.^[23]

In this report, we first performed a detailed analysis on the characteristics of the Arrhenius model by examining its sensitivities to the kinetic parameters (E_a and A). We propose a correlated parameter fit that leverages the empirical correlation between the two kinetic parameters for protein denaturation in biological systems, and demonstrated the utility of this correlated parameter fit with several protein and cell systems measured by FTIR spectroscopy. We envision that the correlated parameter fit will simplify the measurement and analysis of protein thermal denaturation, and project towards future opportunities to monitor cell injury by spectroscopic measurement of protein denaturation.

2. MATERIALS AND METHODS

Cell culture

Several different cell types were used in the study including human dermal fibroblasts (HDF) and LNCaP Pro 5 tumor cells. HDF cells were obtained from cryopreserved stock (Cambrex, East Rutherford, NJ) and cultured in Dulbecco’s modified Eagle medium (DMEM) containing 10% fetal bovine serum (FBS) and 1% penicillin/streptomycin (p/s) in saline (Invitrogen, Carlsbad, CA). LNCaP cells were obtained from cryopreserved stock (MD Anderson Cancer center, Houston, TX) and cultured in DMEM F-12 media (Gibco, Grand Island, NY) and supplemented with 10% FBS and 1% p/s in saline. All cells were trypsinized using 0.05% Trypsin and 0.53mM EDTA (Gibco, Gaithersburg, MD). The trypsin was inactivated using serum filled media. Cells were then centrifuged at 400g for 10min, the media removed, and 12µL of the cell pellet was sandwiched between CaF₂ windows for FTIR analysis. Historical data on dunning AT-1 prostate cancer cell (ref #8) and HuH-7 liver cancer cell (ref #8) were performed with the same protocol.

Measurement of Protein Denaturation with FTIR

FTIR spectra were obtained using a Nicolet Magna 750 spectrometer (Thermo-Nicolet, Madison, WI) equipped with a TGS detector similar to that used by Wolkers et al.^[24] Spectra were acquired at 4cm⁻¹ resolution using 32 co-added interferograms between 4000-900 cm⁻¹ wave number ranges. Strong vibration bands from water are observed at ~3200–3600 cm⁻¹, ~2200 cm⁻¹ and ~1650 cm⁻¹ corresponding to the –OH stretching vibration, the libration and bending combination vibration, and the scissoring vibration, respectively. The symmetric and asymmetric –CH₂ stretching bands of lipid acyl chains are visible between 3000-2800 cm⁻¹. Characteristic protein bands are visible at ~1650 cm⁻¹, ~ 1550 cm⁻¹ and ~1250 cm⁻¹ corresponding to the amide-I, amide-II and amide-III bands respectively.

The samples were mounted into a specialized temperature cell whose temperature was regulated using a temperature controller (Minco products Inc., Minneapolis, MN). Sample temperature, also monitored separately using a thermocouple, was increased from room temperature to 90°C at 1°C min⁻¹. Spectral analysis was carried out using Omnic software (Thermo-Nicolet, Madison, WI). Protein denaturation was determined by monitoring area changes of the raw spectra in the α helical (~1315cm⁻¹) and the β sheet (~1235cm⁻¹) regimes in the amide III region as a function of temperature as previously described.^[24] The fractional denaturation (FD) of protein was calculated by the change in the β sheet. Protein denaturation is then normalized within the temperature range of interest (onset to end–temperature 50, 60, 70 or 80 °C). The onset temperature of protein denaturation is defined as the temperature where the fractional denaturation displays an abrupt increase above 37°C (Supplemental 1).^[8]

Kinetic model and correlated parameter fitting method

A rate constant can be derived from the one step irreversible Arrhenius denaturation model using Equation (3). The fractional denaturation (FD) is then calculated by integrating the rate (k) and considering constant rate heating from low to high temperatures

$$\mathrm{F}\mathrm{D}=1-\text{exp}(-\frac{1}{\mathrm{B}}{\int }_{{\mathrm{T}}_0}^{{\mathrm{T}}_{\text{end}}}\mathrm{k}\mathrm{d}\mathrm{T})$$ (5)

where B is the rate of temperature change (or heating rate, K s⁻¹).

For the traditional fit, the entire E_a-ln{A} parameter space is scanned and every combination of E_a and ln{A} is evaluated. This procedure consists of two steps. First, a grid search was performed on a selected 2D matrix so that all the possible combinations of Ea and ln{A} can be tested. The goodness of the fit (R²) was evaluated as follows

$$R^2=1-\frac{{\mathrm{\Sigma }}_{i=1}^N{(Y_i-F_i)}^2}{{\mathrm{\Sigma }}_{i=1}^N{(Y_i-Ȳ)}^2}$$ (6)

where Y_i and F_i are the ith experimental data point and model fit respectively, and Ȳ represent the average of all experimental data. This grid search procedure yields a Ea-ln{A} combination with the maximum R². Next gradient descent procedure was performed to further find a local optimal R². In brief, the gradient at current point is calculated and steps are taken to calculate the R² at the new point. If the R² is higher than the current point, then the optimization step is accepted and it proceeds to the next optimization. On the other hand, if the R² is lower than the current point, this optimization step is rejected and then a smaller step is taken.

The characteristics of the Arrhenius model were studied by testing the sensitivities of the fit to the variations by changing E_a & ln{A} separately, and by changing them at the same time according to Equation 4.

For the correlated parameter fit, E_a is chosen and then only E_a and ln{A} values close to the E_a-ln{A} correlation (Equation 4) are evaluated (Figure 1D between the dashed lines), followed by the gradient descent procedure as described above. The fitting procedure was performed with programs written in MATLAB. It is likely that the best E_a-ln{A} fit will not always appear on the E_a-ln{A} line. As a result, the intercept (9.36, in Equation 4) is allowed to vary within a small range by introducing a floating constant (C) that varies within 0 to 20. The kinetic rate can be thus expressed as

$$\mathrm{k}=\text{exp}[(0.38-\frac{1}{\mathrm{R}\mathrm{T}}){\mathrm{E}}_{\mathrm{a}}-\mathrm{C}]$$ (7)

Although a smaller range of C could be selected, this current selection is a conservative choice. The frequency factor - or more frequently the natural logarithm of frequency factor, if needed - can be calculated by

$$\text{ln}\{A\}=0.38E_a-C$$ (8)

3. RESULTS

First, we performed detailed analysis of the characteristics of the Arrhenius model using protein denaturation data from the literature. Then we validated our correlated parameter fit approach with literature data including denaturation of a pure protein (collagen peptides)^[25] and a cell line (AT-1)^[8], and demonstrated the close agreement of our proposed protocol with the literature data. Finally, we demonstrated the utility of the correlated parameter fit on thermally induced denaturation of a pure protein (bovine serum albumin) and several cell lines (new data on HDF and LNCaP; historial data on AT-1 (ref# 8 and HuH-7 (ref# 5)) as measured by FTIR spectroscopy.

Characteristics of Arrhenius Model

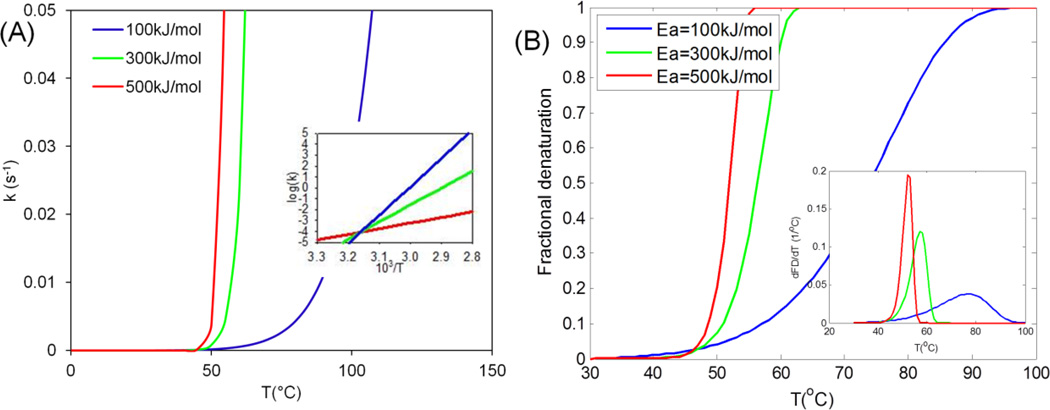
First we plotted the denaturation kinetics for low, medium and high activation energies (100, 300 and 500 kJ mol⁻¹) as shown in Figure 2. The frequency factor is obtained using Equation (4), i.e. C=9.36. The reaction rate increases faster with temperature for higher activation energy (Figure 2A), and changes exponentially with the inverse of temperature, as would be expected experimentally during isothermal protocols (Figure 3A inset and Table 2). Figure 3B shows the expected denaturation rate (i.e. excess C_p for DSC) and fractional denaturation that can be measured by DSC or FTIR.

Figure 2.

Representative Arrhenius kinetic plots for low, medium and high activation energies. (A) Reaction rate vs. temperature. Inset shows the logarithm of k is linearly proportional to 10³/T. (B) Fractional denaturation (FD) vs. temperature at 2°C min⁻¹ heating rate. Inset shows rate of denaturation (dFD/dT) with temperature. Mathematically, it is the first derivative of fractional denaturation (FD) with temperature.

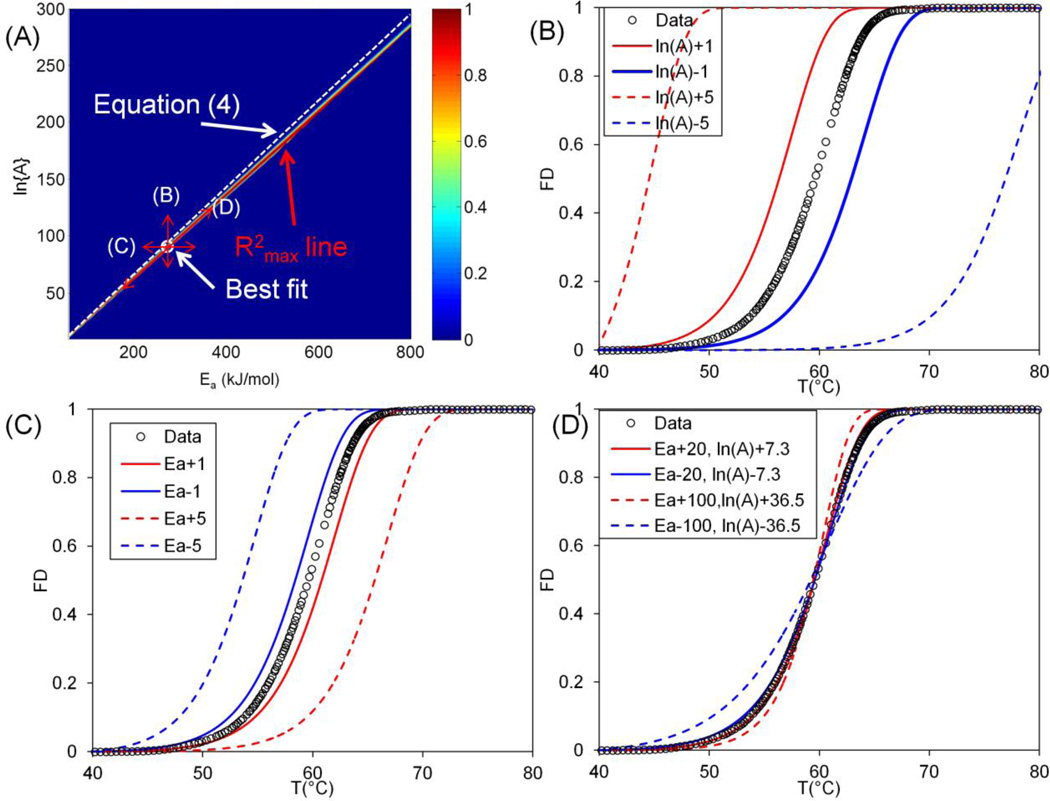
Figure 3.

Sensitivity analysis of the fitting results. (A) shows the distribution of R² for E_a-ln{A} space for Miles et al. 0.1°C min⁻¹. There exists a high R² region and a line can be plotted along the highest R² (R²_max line). The R²_max line is close to Equation 4. The white circle corresponds to the best fit. The arrows show the method of varying E_a and ln{A} with corresponding plots (B–D). (B) and (C) show the theoretical prediction when changing ln{A} and E_a by ±1s⁻¹and ±1kJ mol⁻¹ respectively. (D) shows the theoretical prediction when shifting the E_a value around the optimal E_a by ±20 and ±100kJ mol⁻¹ along the R²_max line. FD: Fractional Denaturation.

Table 2.

Protocols of measuring protein thermal denaturation and methods of interpreting protein denaturation data

Heating method	Experiments	Result interpretation methods	Ref.
Isothermal (Temperature jump)	≥ 5 temperatures, n=3	(1) Plot ln{k} vs. 1/T (2) Linear fit to obtain Ea and ln{A}	[27, 30, 32]
Controlled heating rate	N=3	Scanning method	[25]
		Integral transform	[25]
		DSC thermogram shape analysis	[25, 26]
		Flexible tolerance	[8]
		Correlated parameter fit, Eqn. 7	This work
Transient heating, T(t) with a single endpoint measurement.	N=3	Paired Ea and ln{A} values that minimize the error in injury parameter yield an equivalent isothermal experiment.	[47]

Next we examined the sensitivity and characteristics of the curve fit. The goodness of fit (R²) for the entire space was plotted in Figure 3A for the case of 0.1°C min⁻¹ from Miles et al.^[25] It shows a clear region where the R² value is the highest, namely the R²_max line. The linear correlation (Equation 4) was plotted as the white dashed line and is close to the R²_max line. The best fit value (E_a=273.5 kJ mol⁻¹, ln{A} = 90.9) is close to the line given by Equation (4) as well. Further, we analyzed the distribution of R² along the R²_max line (the line fitted from the value that gives the highest R² at different E_a values) as shown in Supplemental 2. The peak value on the plot shows the optimal fit. Carefully examining the region close to the optimal fit shows that a range of Ea values give a good fit (E_a = 260 ~ 290 kJ mol⁻¹, R²>0.9995). Note that this is based on the condition that corresponding ln{A} values were defined by the R²_max line shown in Figure 3A. If plotting the R² value by keeping either the ln{A} or E_a constant as shown in Figure S2–C and D respectively, the distribution is much sharper (ΔE_a < 4kJ mol⁻¹, and Δln{A} < 2 for R²>0.9). Further, we examined the result of theoretical prediction when shifting away from the best fit (Figure 3A). Specifically, changing only ln{A} by 1 ~ 5 while keeping E_a constant or changing only the E_a value by 1 ~ 5kJ mol⁻¹ with ln{A} constant causes the theoretical prediction to shift away from the experimental data significantly (Figure 3B and C). However, changing the E_a value by 20 kJ mol⁻¹ along the R²_max line only slightly changes the slope of the fitted curve, as shown in Figure 3D.

Historical Data Fits

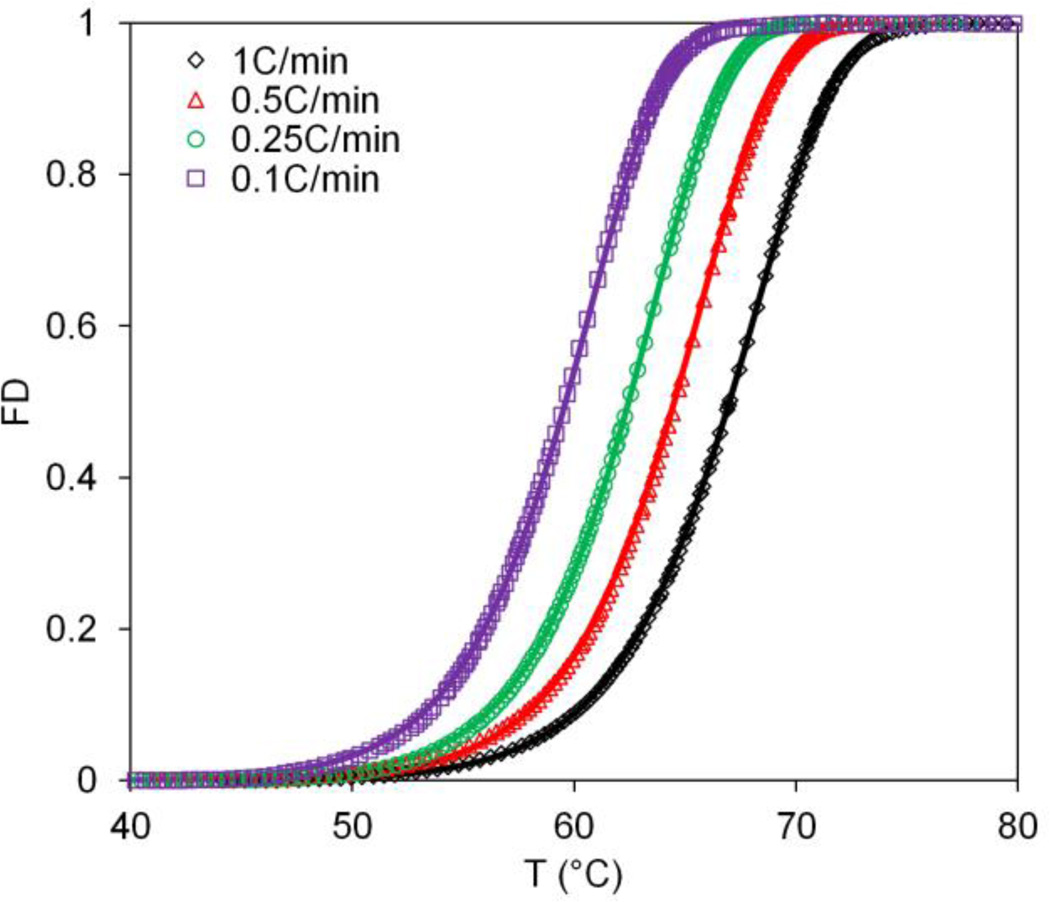
Miles et al. have performed seminal work on the thermal denaturation of collagen, an important ECM protein, using DSC.^[25–27] Taking one of his recent publications on the thermal denaturation of a collagen-like peptide (Pro-Hyp-Gly)₁₀^[25] we show close agreement between our correlated parameter fit values with the previous fitting approach^[25], as shown in Figure 4 and Table 3. Specifically, Miles reported the curve fit activation energy to be within 270 – 283kJ mol⁻¹, and our approach matches reasonably for all of the cases (Table 3). Furthermore, previous data from our lab, where we had fit the thermal denaturation of proteins in AT-1 cells by both DSC and FTIR, were also re-analyzed. Here we are also able to show good agreement between the more complicated flexible-tolerance two-parameter method used by He et al.^[8] and the more easily implemented correlated parameter fit shown here (E_a = 127.8 v.s. 141.5 kJ mol⁻¹). It is worth noting here that the activation energy does not depend on heating rate (Table 3), indicating that activation energy is an intrinsic property of the protein. Higher heating rate, however, delays the denaturation events to higher temperatures (Figure 4) since protein experiences less time at each temperature.

Figure 4.

Correlated parameter fit for the thermal denaturation of collagen like peptide (Pro-Hyp-Gly)₁₀. Four different heating rates (1, 0.5, 0.25, 0.1 °C min⁻¹) were analyzed. Data from Miles et al. ^[25] 2007. FD: Fractional Denaturation.

Table 3.

Validation of correlated parameter fit (CP) with literature. Results and methods from Miles et al. ^[25] and He et al. ^[8] were compared and shown in bold.

Range	Ea (kJ mol−1)	ln{A}	R2
Pure protein
Miles et al.[25]	270~283	89~95	NA
CP fit of Miles et al. 1C min−1	264.4	87.8	1.0000
CP fit of Miles et al. 0.5C min−1	273.4	91.0	1.0000
CP fit of Miles et al. 0.25C min−1	282.6	94.3	1.0000
CP fit of Miles et al. 0.1C min−1	273.5	90.9	0.9999
Cell proteins
He et al.[8] AT-1 FTIR	141.5	45.7	0.996
CP fit of He et al. AT-1 FTIR	127.8	40.7	0.9977
He et al. AT-1 DSC	159.7	52.2	0.997
CP fit of He et al. AT-1 DSC	147.1	47.6	0.999

Protein Denaturation Fit

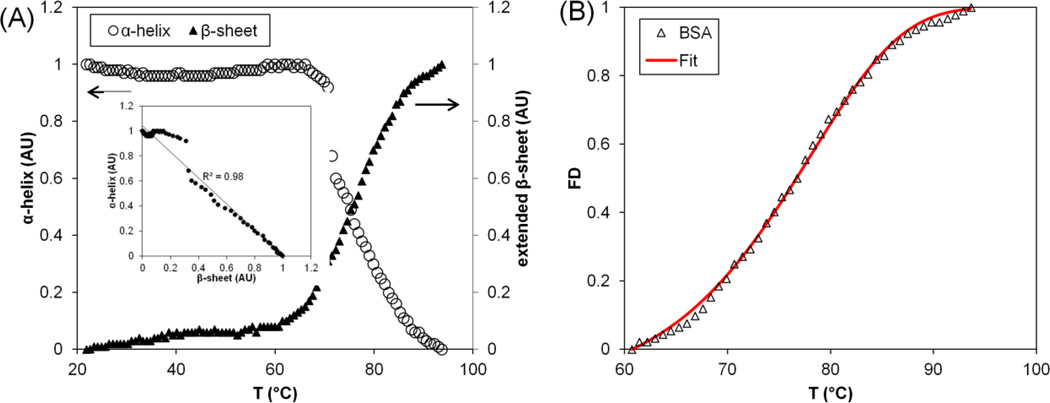
Thermal denaturation of a model pure protein, Bovine Serum Albumin (BSA), was studied by monitoring the infrared spectrum changes with FTIR. Figure 5 depicts the increase in extended β-sheet structures and the concomitant decrease in α-helical structures during thermal denaturation of BSA. An inverse linear correlation (R²=0.98) is obtained between the decrease in α-helical structure and increase in β-sheet structures (Figure 5A – inset). The onset temperature (T_onset) of BSA is 60.7°C, which is determined at zero first derivative of the fractional denaturation before fractional denaturation displays an abrupt change above 37 °C.^[8] The correlated parameter fit was then applied to BSA (Figure 5B) and the activation energy determined to be 115.4 kJ mol⁻¹.

Figure 5.

Protein denaturation of Bovine Serum Albumin (BSA). (A) BSA thermal denaturation characterized by monitoring changes to the α-helical and extended β-sheet structures as a function of temperature increases from 20°C to 95°C. The inset depicts the correlation between the decrease in α-helical and the increase in extended β-sheet content during thermal denaturation. (B) Fitting of BSA thermal denaturation by the correlated parameter model. FD: Fractional Denaturation.

Cell Denaturation Fit

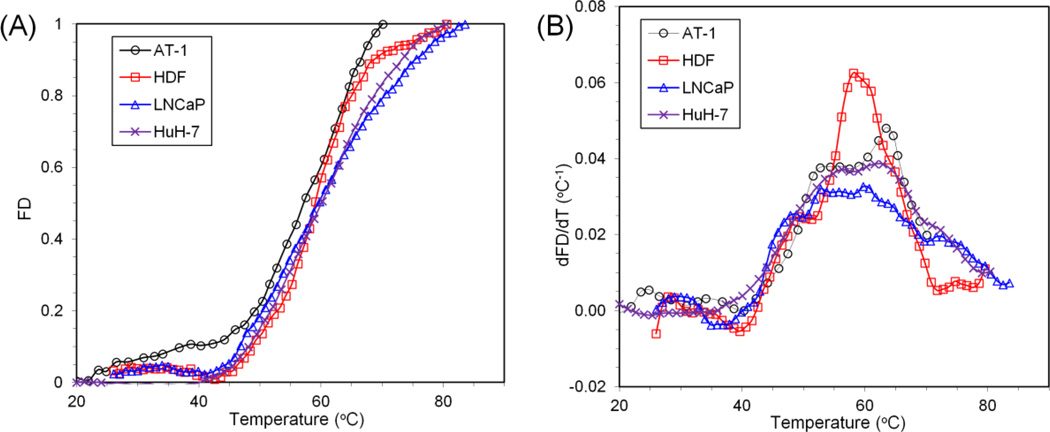
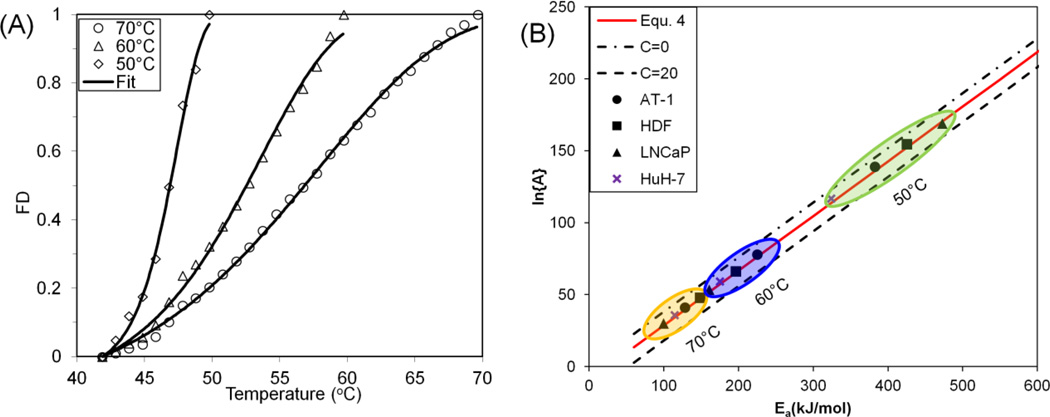
The fractional denaturation of two different cell types (HDF & LNCaP) was quantified during heating from room temperature to 90°C at a rate of 1°C min⁻¹. In addition, AT-1 and HuH-7 cell denaturation data were obtained from He et al. (heating rate: 2°C min⁻¹)^[8] and Avaralli et al. (heating rate: 2°C min⁻¹).^[5] Figure 6A shows the increase in the β sheet structures for these cell types as a function of temperature. First derivative plots (Figure 6B) are included to identify peaks and patterns in the denaturation profiles. Specifically, it has been suggested that 5 to 8 specific protein groups can be identified to reside within different thermal regimes from higher order derivatives of protein denaturation plots, and that one or more group may be rate limiting to cell injury.^{[4, 8]} This further highlights the cell-specific nature of protein denaturation (or “thermal fingerprinting”^[28]) with profiles differing in the onset temperature of protein denaturation (T_onset), the slope of the curve, and the distribution of transition regions. The onset denaturation temperatures (T_onset) for AT-1, HDF, LNCaP and HuH-7 are 40.27°C, 42.53°C, 40.88°C and 40.03 °C respectively (Table 4). The activation energy of protein denaturation for the cells was assessed using the correlated parameter fit, and the results are listed in Table 4. The protein denaturation data is further analyzed at different end temperatures after renormalization. At lower end temperatures (50 °C) corresponding to the first transition regions, the activation energy is highest, as shown in Table 4 and Figure 7. Several other end-temperatures (60 and 70 °C) were used to encompass more of these transition regions. The effect of including more or fewer protein transitions is shown by varying the end temperature in Figure 7.

Figure 6.

Protein denaturation signature of four different cell types (AT-1, HDF, LNCaP, and HuH-7). (A) Comparison of the protein denaturation of four different cell types – Dunning AT-1 prostate cancer cells, human dermal fibroblasts (HDF), LNCaP prostate tumor cell, and HuH-7 liver cancer cell – characterized by monitoring changes to the extended β-sheet structures as a function of temperature increase from 20°C to 90°C. The error bars were omitted for easier data visualization. (B) First derivative of the average denaturation curves are plotted as a function of temperature. Note that AT-1 data is from He et al.^[8] and HuH-7 data is from Avaralli et al.^[5] FD: Fractional Denaturation.

Table 4.

Kinetic parameter fittings for four cell lines (AT-1, HDF, LNCaP, and HuH-7) with different end temperatures.

Cell line	Tonset	Tend	Ea (kJ mol−1)	ln{A}	R2
AT-1	40.27	70	128.6	41.0	0.9979
		60	225.3	78.0	0.9976
		50	382.4	139.0	0.9889
HDF	42.53	80.54	119.8	37.0	0.9950
		70	148.7	47.8	0.9990
		60	196.4	66.1	0.9851
		50	425.1	154.5	0.9908
LNCaP	40.88	83.52	61.4	15.3	0.9983
		70	99.7	29.9	0.9984
		60	160.9	53.5	0.9960
		50	472.7	169.0	0.9956
HuH-7	40.03	80.4	84.1	24.3	0.9985
		70	114.5	35.9	0.9985
		60	175.1	59.3	0.9975
		50	323.8	116.8	0.9900

Figure 7.

Summary of correlated parameter fit. (A) Fitting of protein denaturation for LNCaP cells at different end temperatures (70, 60, and 50°C); (B) Summary of correlated parameter fit at different end temperatures. FD: Fractional Denaturation.

4. DISCUSSION

Characteristics of Arrhenius Model and Debate on Compensation Behavior

While the correlation of the activation energy and frequency factor in Arrhenius kinetics has been recognized for years, the possible existence of the compensation law has stirred intensive debate.^{[17, 29]} One possible explanation is that the parameters are correlated, but that complications from experimental errors and the form of the Arrhenius equation itself lead to the proposed compensation law behavior in multiple systems.^{[21, 22, 30]} There are several ways that the linear relationship (i.e. compensation law behavior) between activation energy and logarithm of frequency factor can be derived, including from the transition state theory^[7] and statistical mechanics. Yelon et al. ^[31] suggested that the compensation law holds as long as the activation energy is large compared with the typical excitations (i.e. infrared vibrations or phonons^[19]) and with the thermal energy (k’T, k' = Boltzmann constant). Recently it has been suggested that random errors in experimental measurement can lead to an apparent compensation effect, and that a confidence ellipse should be calculated in order to eliminate this effect.^[30] We have performed this calculation and demonstrate that there is correlation between the parameters even with random experimental errors (Figure S3).

A further simple exercise demonstrates the correlation between the Arrhenius parameters by rewriting Equation (3), to obtain

$$\mathrm{k}=\text{exp}[\text{ln}\{\mathrm{A}\}-\frac{\mathrm{E}\mathrm{a}}{\mathrm{R}\mathrm{T}}]$$

Now considering the relatively small temperature range (1/RT ~ constant), ln{A} and E_a have to be inter-related to obtain a rate constant (k).¹ For instance, as shown in Figure 3, changing E_a and ln{A} separately by a small magnitude (1 kJ mol⁻¹and 1 s⁻¹ respectively) leads to significant shift in the predicted curve, while changing E_a and ln{A} proportionally by a large magnitude (20 kJ mol⁻¹and 7.3 s⁻¹) along the R²_max line changes the prediction curve only marginally.

Advantages of the Correlated Parameter Fit

Regardless of the existence of a compensation law, the proposed correlated parameter fit has several advantages over other approaches. One advantage is that it can significantly simplify the way kinetic parameters are obtained from experimental data. Traditionally, the kinetic parameters are fitted to isothermal temperature jump (T-jump) experiments as routinely performed for chemical kinetic experiments.^[13] Specifically, the sample is held at various temperatures (usually ≥ 5 points) for extended amount of time. A linear fit (Arrhenius plot) can be correlated between ln{k} and 1/T. The activation energy and frequency factor can be determined from the slope and intercept of the linear fit, respectively.^{[7, 15, 32]} This procedure involves tedious experiments under many different conditions over several orders of magnitude in heating time. With the controlled heating rate method proposed, it is possible to obtain the kinetic parameters from fewer experiments (3 runs, instead of 5 × 3 runs). For instance, it is possible to scan the samples with constant heating rates to certain temperatures. Then similar to the procedure described in this report, the kinetic parameters can be extracted with our proposed correlated parameter fit approach. This avoids the more difficult approach of fitting two parameters (2P, E_a and A) simultaneously, which necessitates time-consuming experimental repeats at different isothermal temperatures or complicated fitting routines in dynamically heated data (Table 2).

In both the calorimetric and FTIR spectroscopic measurement, the constant heating rate scan is a commonly-used and simpler method to measure protein denaturation, as discussed above. The heating rate or scanning rate is thus an important parameter and higher heating rate delays the denaturation events to higher temperatures (Figure 4) since protein experiences less time at each temperature. Since the scanning rate is incorporated in the fitting (Equation 6, parameter B), it does not affect the resulting kinetic parameters (Table 3).

Due to experimental errors, a tolerance range (C) has been used. The proposed tolerance range (0 < C < 20) can well encompass the experimental variation observed within the data tested in this report and beyond. The C values obtained from this report range maximally from 7 to 13, well within the proposed range (0–20). For the protein systems shown in Figure 1, the C values are within the proposed range, except for only 6 out of the 99 samples from the literature (Figure 1D inset). One of the 5 discordant samples has a very low activation energy (16.7 kJ mol⁻¹), which may fall outside of the range where compensation behavior is typically observed. It may be possible to further refine this range in the future. However, a conservative choice was made for purposes of this study.

Relevance of Protein Denaturation to Cell Injury

The denaturation of pure proteins can be modeled by the Arrhenius model, as shown for the collagen like peptide and BSA in this study. The denaturation of protein mixtures and cells are more involved and may present multiple peaks from denaturation of different proteins that may partially overlap. For instance, the denaturation of egg white (60–65% ovalbumin, among other proteins^[33]) displays two distinct peaks (at 65.7°C and 77.5°C as seen in Supplemental 4). In cells, the denaturation of proteins is believed to involve up to four to seven major protein transitions or groups^{[4, 8]}. Each protein group can often be modeled as a separate first-order irreversible kinetic process (Arrhenius model). As a result, four to seven pairs of kinetic parameters can be calculated.^[8] Further, deconvolution of protein denaturation in such complex systems may help uncover critical targets, and hence the rate limiting events for cell thermal injury. However, further work is needed to understand the function and location of these protein groups (i.e. membrane, cytoplasmic or cytoskeletal), and to directly observe them during denaturation. This may be possible in the near future by using advanced optical imaging techniques such as confocal Raman microspectroscopy, as has been demonstrated for chemical denaturation in cells.^[5]

The proposed correlated parameter fit approach can be used to assess denaturation of additional protein groups by increasing the end-temperature limit. This has relevance to both the amount and type of protein denatured and the kinetics of cell death measured thereafter by various assays. As shown in this study, the activation energy increases with decreasing end temperature (Table 4 and Figures 7). This agrees with fits on deconvolved protein groups in previous work, where the initial protein group has the highest activation energy, and all protein groups together have lower activation energy.^[8] Further, cell protein denaturation can be correlated with different cell injury assays, such as clonogenics and membrane integrity assays, after thermal treatment. For instance, the activation energies obtained from the clonogenic proliferation assay (E_a > 400 kJ mol⁻¹) are usually much larger than the membrane integrity assay (e.g. Propidium Iodide – E_a < 300 kJ mol⁻¹).^{[7, 34]} A narrower temperature range for protein denaturation correlates well with clonogenic assays (close to 50°C) while a larger range of protein denaturation (up to roughly 60°C) correlates well with PI/Hoechst cell membrane integrity.^[8]

Protein denaturation may be used as spectroscopic signature to assess cell injury in vivo. Currently, thermal therapies rely on predetermined protocols or advanced treatment planning to treat localized tumors.^[35–37] Although there have been some efforts using imaging guidance,^[38] employing real-time MR thermography and computation to adjust for patient-specific variations of the thermal responses,^[39] very limited efforts have been focused on assessing cancer cell injury in vivo during thermal therapy. This work suggests new opportunities to use spectroscopic signatures from protein denaturation as a guide to assess cell injury in vivo. An earlier study suggested that only 5 – 10% of the total cellular protein denaturation, i.e. only the most thermally sensitive protein group(s), leads to 80 ~ 90% loss in viability by clonogenics.^[4] This approach may become increasingly feasible as advanced imaging techniques become available.

Limitation of the Current Work

There are several limitations in this simplified correlated parameter model. Firstly, the complex process of protein folding and unfolding and its pathways are active areas of research themselves ^[40] and are not considered in the simple two-state irreversible kinetic model. For instance, typical protein unfolding involves several intermediate steps, each with different characteristics, as reviewed by Daggett et al.^[41] Instead, here the protein denaturation is assumed to be a one-step first-order irreversible kinetic process in a lumped parameter sense. Many important protein interaction processes involve reversible steps,^{[42, 43]} which were not included in this analysis. The impact of heat shock (and other chaperone) proteins in preventing thermal protein denaturation was also not considered (i.e. the development of thermo-tolerance), although it should be noted that heat shock proteins are expected to be most active in the range of 40 – 45 °C not above 50 °C. Secondly, only thermal denaturation has been considered. There are many other denaturants, such as chemical agents (e.g. urea), pressure, and pH, that can also affect the denaturation kinetics, and are not considered in this report. Thirdly, protein denaturation under higher temperatures and on short time scales appears to deviate from simple first order kinetics and compensation law behavior. It can be estimated that at 90 to 100°C or higher temperatures, proteins will denature on time scales of micro to nano seconds, ^{[44, 45]} and molecular dynamic (MD) simulations suggests very low activation energies (33 ~ 56 kJ mol⁻¹, Supplemental 5).^[44] Further work is needed to probe the protein denaturation kinetics in this temperature range, such as might occur for proteins attached or in close proximity to nanoparticles being heated by lasers^[46] or at the edge of cavitation bubbles during high intensity focused ultrasound.

While protein denaturation is linked to cell injury, the precise correlation between the amount and timing of protein denaturation to cell death remains a central question in this field.^{[4, 8, 47]} For instance, some work suggests that immediate cell injury or death by protein denaturation can occur with as little as 5 to 10% of the cellular proteins being destroyed.^[4] In this case, the Arrhenius approach suggested here may be useful in predicting the temperature and time necessary to achieve this. However, there are more subtle forms of delayed cell injury that can occur post heating, such as thermotolerance, receptor-induced and/or intrinsic apoptosis and necroptosis.^{[42, 43]} These cell death processes are not immediate and can involve dynamic cascades and reversibility in systems of proteins that are outside the treatment of this paper and not amenable to the Arrehnius model. To model these complicated processes, more intricate mathematical constructs and parameters are required than Arrhenius kinetics provides, and are beyond the scope of this work.^{[42, 43]}

5. CONCLUSIONS

This work brings together an improved framework for experimental and theoretical work on thermal protein denaturation. Specifically, we examined the characteristics of the Arrhenius model and further explore the correlation of activation energy to frequency factor, thereby allowing a more intuitive correlated parameter fit of the Arrhenius model. This simultaneously supports simpler experimentation (i.e. dynamic heating vs. isothermal heating) and easier fitting of protein denaturation data. Furthermore, we demonstrated that by selecting appropriate end temperatures the protein denaturation kinetics is different and can be potentially used to explain the cell injury kinetics measured by different cell viability assays after thermal treatment. Future opportunities to monitor cell injury by spectroscopic measurement of protein denaturation were discussed.