Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jan 12;6:19244. doi: 10.1038/srep19244

Evaluation of the 2b-RAD method for genomic selection in scallop breeding

Jinzhuang Dou 1,2, Xue Li 1, Qiang Fu 1, Wenqian Jiao 1, Yangping Li 1, Tianqi Li 1, Yangfan Wang 1, Xiaoli Hu 1,3, Shi Wang 1,4,a, Zhenmin Bao 1,3,b
PMCID: PMC4709697  PMID: 26754638

Abstract

The recently developed 2b-restriction site-associated DNA (2b-RAD) sequencing method provides a cost-effective and flexible genotyping platform for aquaculture species lacking sufficient genomic resources. Here, we evaluated the performance of this method in the genomic selection (GS) of Yesso scallop (Patinopecten yessoensis) through simulation and real data analyses using six statistical models. Our simulation analysis revealed that the prediction accuracies obtained using the 2b-RAD markers were slightly lower than those obtained using all polymorphic loci in the genome. Furthermore, a small subset of markers obtained from a reduced tag representation (RTR) library presented comparable performance to that obtained using all markers, making RTR be an attractive approach for GS purpose. Six GS models exhibited variable performance in prediction accuracy depending on the scenarios (e.g., heritability, sample size, population structure), but Bayes-alphabet and BLUP-based models generally outperformed other models. Finally, we performed the evaluation using an empirical dataset composed of 349 Yesso scallops that were derived from five families. The prediction accuracy for this empirical dataset could reach 0.4 based on optimal GS models. In summary, the genotyping flexibility and cost-effectiveness make 2b-RAD be an ideal genotyping platform for genomic selection in aquaculture breeding programs.

Genomic selection (GS), which was initially proposed by Meuwissen et al.1, can greatly increase the genetic gain and reduce the generation interval through the selection of candidates based on the genomic estimated breeding values (GEBVs) calculated using genome-wide single-nucleotide polymorphisms (SNPs). After the successful implementation of GS in dairy cattle2, its applicability has also been investigated in maize, wheat and apple breeding programs3,4,5. In the field of aquaculture breeding, previous studies have focused on investigating the benefits of implementing this approach in family-based breeding schemes using simulations6,7,8, and demonstrate that higher-accuracy breeding values could be obtained by GS compared with the traditional breeding method. A recent empirical study conducted in Atlantic salmon using an admixed population also confirmed the advantage of GS in aquaculture breeding9.

Nonetheless, one major premise of the use of GS in practical breeding is the requirement of sufficient genetic markers. High-density markers ensure that the linkages between markers and quantitative trait loci (QTLs) are tight so that recombination does not cause them to decay rapidly1, and therefore QTLs can be determined by the neighboring markers. Traditionally, it is difficult for aquacultural breeders to obtain high-density markers at a low cost and this situation is even worse for species with little or no genomic resources. Recent development of genotyping-by-sequencing (GBS) methods that reduce genome complexity via restriction enzymes10,11, is revolutionizing the way of genetic marker discovery and genotyping. The most significant advantage of GBS methods for the implementation of GS in breeding programs is the low per-sample cost needed to generate tens of thousands of molecular markers. It is notable that 2b-restriction site-associated DNA (2b-RAD) represents one of efficient GBS methods, which features even and tunable genome coverage and provides a flexible genotyping platform to meet diverse research purposes12,13,14,15,16. The prediction accuracy achieved using GBS data is comparable to that obtained using the SNP array datasets in the recent maize breeding project17. Currently, it remains largely unknown whether the marker density provided by GBS methods is sufficient for accurately estimating breeding values for aquaculture breeding, although these methods have significant advantages in reducing the cost of high-density marker genotyping.

Yesso scallop (Patinopecten yessoensis), which is cultured mainly in Liaoning and Shandong provinces of China, has been among the most important commercial shellfish since its introduction from Japan in the early 1980 s18. Conventional breeding approaches, such as polyploidy breeding19, species hybridization20, and gynogenesis21 have been investigated for genetic improvement of Yesso scallop. Most recently, extensive transcriptomic resources have been generated for Yesso scallop22,23,24,25, and a number of growth- and immune-related genes have been characterized26,27,28,29,30. A whole-genome sequencing project for this species has been initiated by our group (NCBI BioProject no. PRJNA259405), making it an ideal subject for GS.

The objective of this study was to evaluate the potential applicability of the 2b-RAD method in the GS of Yesso scallop through simulation and empirical data analyses. Key factors affecting prediction accuracy of breeding values were assessed, such as marker density, heritability, and statistical models. Our study supports 2b-RAD to be a very powerful and promising tool for genomic selection in aquaculture breeding programs.

Results

Simulation data analysis

We first investigated whether the marker densities generated by the 2b-RAD method are sufficient to capture the QTL effects using GS models. We generated high-density marker panels (HD-SNPs) consisting of 250 k SNPs spaced evenly along the Yesso scallop genome, medium-density marker panels (MD-SNPs) consisting of 61 k SNPs located in BsaXI tags (i.e., 5′-N10ACN5CTCCN8-3′), and low-density marker panels (LD-SNPs) consisting of 5 k SNPs located in reduced tag representation (RTR)-BsaXI tags (i.e., 5′-AN9ACN5CTCCN7T-3′), which contain approximately 250, 50, and 5 markers per Mb, respectively. Among all SNPs, 5,000 loci were randomly chosen as candidate QTLs with the allelic effects sampled from a normal distribution with a mean of 0 and a variance of 1. The initial breeding population was simulated for 1,000 generations according to the Fisher-Wright population model with the genetic parameter values specified in Table 1 (see Simulation 1). The genomic prediction results in G1 for three panels with different statistical models are summarized in Table 2. Small difference was observed between HD-SNPs and MD/LD-SNPs for each statistical model under different heritabilities, suggesting that the marker densities generated by 2b-RAD exhibited comparable performance with that obtained using the array-based genotyping technology. Notably, at heritability values greater than 0.2, prediction accuracies obtained with LD-SNPs using G-BLUP, BayesA, and BayesB models are similar to those obtained with MD-SNPs. For example, the accuracy of BayesA can reach 0.92 with a heritability of 0.5 using only LD-SNPs. In terms of the statistical models, G-BLUP, RR-BLUP, BayesA, and BayesB exhibited the highest prediction accuracy for all cases with no significant differences among them. In addition, the advantage of these models over LASSO and BL was more pronounced at heritability values lower than 0.2. One possible explanation for the poorer performance of shrinkage and selection approaches (LASSO and BL) is that the genetic variance is largely uniformly distributed over all of the chromosomes specified in our simulation dataset. It is well known that minimizing the cost function by variable selection could result in an upward bias of the estimates of marker effects31. The over-generation prediction accuracies (G1 − > G2) are provided in Table 2, with no significant difference observed among the three marker-density panels, which is likely due to high LD within families.

Table 1. The parameters used for scallop population/family simulation.

Simulation Dataset type Sample size Marker density Genetic model
1 Population-based 2,000 HD-SNPs (250 k) MD-SNPs (61 k) LD-SNPs (5 k) Additive
2 Family-based 20 × 50a LD-SNPs (2,364) Additive
3 Family-based 5 × 50 LD-SNPs (2,364) Additive + Dominant
Open in a new tab

a20 × 50 denotes a population composed of 20 sub-families with each containing 50 samples.

Table 2. Accuracy of GEBVs estimated from the simulated population-based datasets (Simulation 1) under different heritabilities.

Case Marker density Method h2 = 0.1 h2 = 0.2 h2 = 0.3 h2 = 0.4 h2 = 0.5
G1   BLUP 0.29 0.47 0.53 0.68 0.70
  HD LASSO 0.50 0.54 0.65 0.79 0.78
    RR-BLUP 0.74 0.82 0.89 0.92 0.92
    BL 0.29 0.42 0.47 0.63 0.65
    G-BLUP 0.74 0.81 0.88 0.94 0.94
    BayesA 0.74 0.82 0.88 0.94 0.94
    BayesB 0.73 0.82 0.89 0.94 0.93
  MD LASSO 0.39 0.56 0.60 0.75 0.78
    RR-BLUP 0.69 0.86 0.87 0.92 0.92
    BL 0.23 0.39 0.54 0.63 0.65
    G-BLUP 0.70 0.86 0.87 0.92 0.92
    BayesA 0.70 0.86 0.87 0.92 0.92
    BayesB 0.70 0.86 0.87 0.92 0.92
  LD LASSO 0.44 0.50 0.64 0.77 0.83
    RR-BLUP 0.47 0.72 0.88 0.90 0.92
    BL 0.23 0.33 0.43 0.55 0.66
    G-BLUP 0.69 0.82 0.84 0.90 0.92
    BayesA 0.72 0.82 0.86 0.90 0.92
    BayesB 0.76 0.82 0.90 0.90 0.92
G1- > G2   BLUP 0.24 0.37 0.57 0.59 0.76
  HD LASSO 0.39 0.62 0.61 0.68 0.81
    RR-BLUP 0.77 0.90 0.91 0.91 0.94
    BL 0.59 0.76 0.79 0.82 0.89
    G-BLUP 0.74 0.87 0.92 0.93 0.94
    BayesA 0.73 0.86 0.91 0.93 0.93
    BayesB 0.73 0.87 0.91 0.93 0.95
  MD LASSO 0.31 0.48 0.63 0.77 0.78
    RR-BLUP 0.73 0.85 0.91 0.94 0.94
    BL 0.26 0.39 0.48 0.59 0.65
    G-BLUP 0.72 0.85 0.91 0.93 0.93
    BayesA 0.73 0.85 0.91 0.93 0.93
    BayesB 0.73 0.86 0.91 0.93 0.93
  LD LASSO 0.44 0.67 0.72 0.83 0.87
    RR-BLUP 0.27 0.89 0.89 0.92 0.93
    BL 0.31 0.38 0.51 0.56 0.65
    G-BLUP 0.76 0.88 0.88 0.92 0.94
    BayesA 0.80 0.85 0.89 0.92 0.94
    BayesB 0.81 0.89 0.89 0.92 0.93
Open in a new tab

Given the reliance of many aquaculture breeding schemes on sib testing6, we further investigated the impact of sample size on genomic prediction for a family-based breeding population under low marker density (Table 1, Simulation 2). The breeding population composed of 20 families with each containing 50 individuals. To create datasets with different sample sizes, 5, 10, 15 and 20 families were randomly chosen and combined, resulting in population sizes ranging from 250 to 1000. To enable a uniform comparison with the empirical data analysis in the following section, only a subset of 2b-RAD markers (2,364) randomly chosen from the LD-SNP panel were utilized. Principal coordinate analysis (PCA) and genetic kinship analysis suggested that most of the 20 families can be genetically separated (Supplementary Figs S1a,b). Table 3 shows the prediction accuracies for different levels of family combinations using six GS models. At a heritability greater than 0.2, the prediction accuracies using only 5 families can range from 0.83 to 0.92 for G-BLUP, BayesA and BayesB, and no significant improvement was obtained with the sample size increasing up to 1,000 (20 families). At a low level of heritability (i.e., h2 = 0.1), a substantial increase in accuracy was observed with the inclusion of more individuals in the training set. For example, the prediction accuracy for BayesB increased by 12% with a sample size of 500 (10 families), and by 14% with a sample size of 1,000 (20 families), indicating that sample size and phenotype heritability should be considered simultaneously in the implementation of GS. Overall, even for a dataset consisting of 250 individuals (5 families), acceptable prediction accuracies (over 0.8) could be obtained by selection of optimal statistical models (e.g. G-BLUP and Bayes-alphabet).

Table 3. Accuracy of GEBVs estimated from the simulated family-based datasets (Simulation 2) under the low marker density.

No. of families Model h2 = 0.1 h2 = 0.2 h2 = 0.3 h2 = 0.4 h2 = 0.5
5 BLUP 0.27 0.39 0.47 0.63 0.69
  LASSO 0.33 0.43 0.41 0.52 0.60
  RR-BLUP 0.27 0.28 0.32 0.32 0.42
  BL 0.16 0.24 0.39 0.56 0.58
  G-BLUP 0.63 0.84 0.89 0.91 0.92
  BayesA 0.67 0.83 0.89 0.90 0.92
  BayesB 0.66 0.83 0.90 0.90 0.92
10 BLUP 0.31 0.43 0.55 0.63 0.69
  LASSO 0.24 0.45 0.49 0.60 0.69
  RR-BLUP 0.24 0.28 0.70 0.61 0.66
  BL 0.14 0.39 0.41 0.53 0.65
  G-BLUP 0.74 0.82 0.84 0.90 0.93
  BayesA 0.79 0.81 0.84 0.90 0.93
  BayesB 0.82 0.84 0.87 0.90 0.92
15 BLUP 0.36 0.44 0.55 0.63 0.69
  LASSO 0.25 0.48 0.61 0.72 0.77
  RR-BLUP 0.25 0.28 0.88 0.88 0.92
  BL 0.13 0.37 0.43 0.54 0.68
  G-BLUP 0.66 0.83 0.89 0.88 0.93
  BayesA 0.68 0.83 0.89 0.89 0.93
  BayesB 0.68 0.84 0.89 0.90 0.93
20 BLUP 0.38 0.44 0.57 0.67 0.70
  LASSO 0.37 0.50 0.65 0.75 0.79
  RR-BLUP 0.31 0.84 0.87 0.90 0.92
  BL 0.25 0.35 0.50 0.57 0.61
  G-BLUP 0.70 0.75 0.86 0.90 0.92
  BayesA 0.75 0.80 0.86 0.90 0.92
  BayesB 0.80 0.84 0.87 0.91 0.92
Open in a new tab

Real data analysis

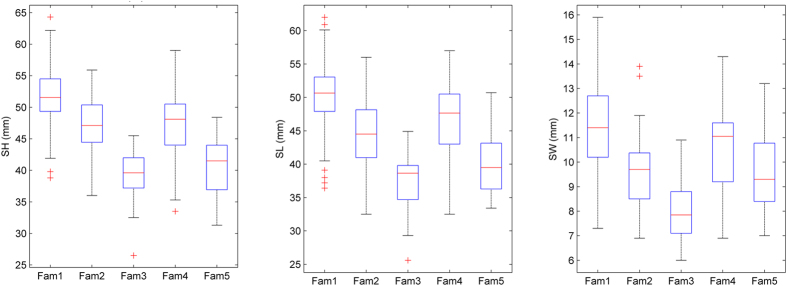
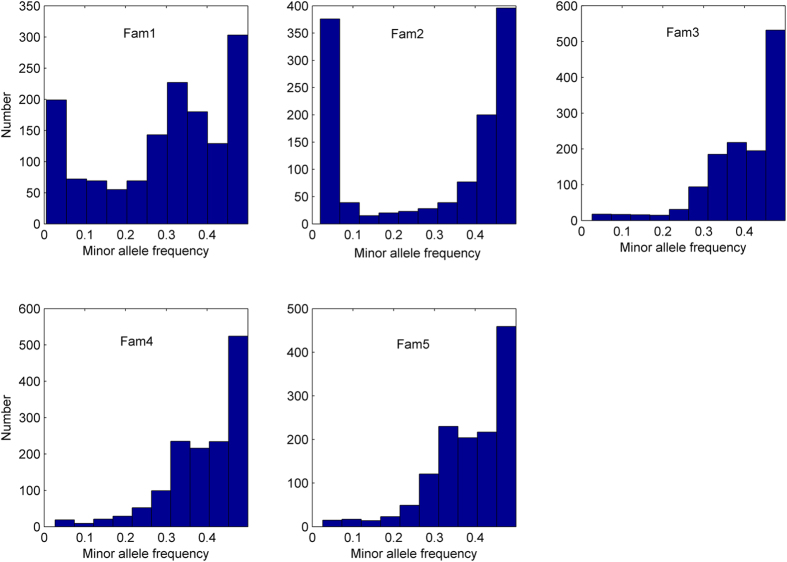
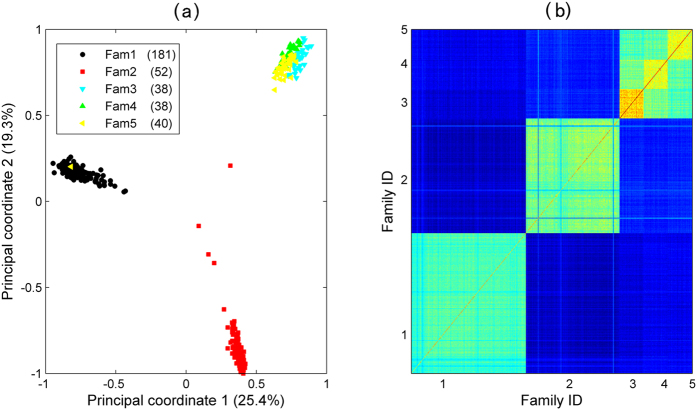
The real dataset was composed of 349 Yesso scallop individuals that were derived from two full-sib families and three bi-parental families. Box and whisker plots exhibited the first and third quartiles of shell length (SL), shell width (SW), and shell height (SH) among the five families (Fig. 1). According to the one-way ANOVA analysis, the p values among the five families for SL, SW, and SH were statistically significant, with values of 2e-6, 2e-6 and 3.6e-3, respectively. For all individuals, 2b-RAD reads and mapping rates were summarized in Supplementary Table S1. After screening for minor allele frequency (>5%) and SNP calling frequency (>70%), a high-quality set of SNPs (2,364) with an average calling rate of 84% was used in genomic selection models (Fig. 2). PCA and genetic kinship analysis suggested that the three bi-parental families were closer to each other but are genetically distinct from the other two full-sib families (Fig. 3a,b). Significant genotypic variance estimates had been observed among all these traits using the entire population, with medium heritabilities (0.36 ~ 0.48). Meanwhile, for single families, the heritability ranged from 0.28 to 0.61 for SH, from 0.26 to 0.60 for SL, and from 0.15 to 0.48 for SW (Table 4).

Figure 1. Box and whisker plots of three traits shown for five Yesso scallop families.

Figure 1

Open in a new tab

SH, shell height; SL, shell length; SW, shell width.

Figure 2. Distribution of the minor allele frequencies of 2,364 markers in five Yesso scallop families.

Figure 2

Open in a new tab

Figure 3. Principal component analysis (a) and genetic kinships (b) of the five empirical families based on 2,364 markers.

Figure 3

Open in a new tab

Table 4. Estimation of variance components and heritabilities for three traits including shell height (SH), shell length (SL) and shell width (SW).

  Across-family Fam1 Fam2 Fam3 Fam4 Fam5
SH
 σa2 14.58 (2.56a) 9.21 (2.49) 6.38 (2.13) 8.56 (1.10) 12.27 (4.21) 17.8 (2.75)
 σe2 15.84 (1.18) 14.88 (1.05) 16.31 (1.15) 7.01 (0.55) 19.09 (1.51) 14.2 (0.96)
 h2 0.48 (0.05) 0.38 (0.07) 0.28 (0.08) 0.41 (0.05) 0.39 (0.09) 0.54 (0.06)
SL
 σa2 16.30 (2.68) 9.93 (3.07) 7.24 (3.11) 1.79 (0.87) 7.74 (1.73) 5.92 (2.51)
 σe2 17.48 (1.16) 16.42 (1.32) 20.47 (1.39) 14.23 (0.98) 25.81 (2.14) 15.29 (1.34)
 h2 0.48 (0.05) 0.38 (0.08) 0.26 (0.06) 0.11 (0.05) 0.23 (0.05) 0.26 (0.09)
SW
 σa2 2.66 (0.29) 0.52 (0.37) 2.15 (0.35) 0.91 (0.04) 2.53 (0.14) 1.91 (0.16)
 σe2 4.68 (0.15) 3.07 (0.15) 2.37 (0.15) 1.24 (0.04) 1.32 (0.06) 2.43 (0.08)
 h2 0.36 (0.06) 0.15 (0.08) 0.48 (0.05) 0.67 (0.03) 0.65 (0.04) 0.71 (0.04)
Open in a new tab

The genetic variances (σa2), error variance (σe2), and narrow-sense heritabilities (h2) were calculated for the entire population and individual families.

aStandard error.

The prediction accuracies assessed using five-fold cross-validation for the entire population are shown in Table 5. The prediction accuracies varied from 0.15 to 0.40 across the three traits, which were substantially lower than those obtained from the family-based simulation analysis (Table 3). This difference can be partly attributed to the fact that the prediction accuracy for the real dataset was calculated based on the correlation between the observed phenotypes and GEBVs, as the true breeding values is unknown in practice. By dividing the square-root of the corresponding heritability, the adjusted accuracies could reach 0.6 across these methods, which is still lower than that obtained in the simulation case. The coefficient of regression (slope) of the observed phenotype on the estimated breeding values was calculated as a measurement of the bias of each method. For all situations, the slopes of these models were not significantly different from 1.0, with the largest deviation being less than 0.06, indicating the absence of significant bias in the prediction. G-BLUP, BayesA and BayesB outperformed the other methods due to their better performance across the three traits (Table 5). The genetic effects of all markers that were calculated based on five GS models were shown in Supplementary Table S2. The PCA analysis based on all marker effects demonstrated that LASSO is markedly different from the other methods (Fig. 4), as was also confirmed by pairwise comparisons among these methods with the pair of LASSO and BayesB having the largest derivation for the SL trait (Table 6).

Table 5. Accuracy of GEBVs assessed by five-fold cross-validation based on a combined dataset consisting of five scallop families.

  r(y, EBV)
 r(TBV, EBV)b
SH SL SW SH SL SW
LASSO 0.20 (0.09)a 0.27(0.13) 0.15 (0.10) 0.29 (0.13) 0.39 (0.19) 0.25 (0.17)
RR-BLUP 0.30 (0.16) 0.37 (0.09) 0.18 (0.08) 0.43 (0.23) 0.53 (0.13) 0.30 (0.13)
BL 0.31 (0.16) 0.36 (0.08) 0.15 (0.07) 0.44 (0.23) 0.51 (0.12) 0.25 (0.12)
G-BLUP 0.37 (0.08) 0.32 (0.09) 0.33 (0.09) 0.53 (0.12) 0.46 (0.13) 0.55 (0.15)
BayesA 0.40 (0.07) 0.33 (0.08) 0.35 (0.09) 0.57 (0.10) 0.47 (0.12) 0.58 (0.15)
BayesB 0.40 (0.07) 0.34 (0.07) 0.36 (0.08) 0.57 (0.10) 0.49 (0.10) 0.60 (0.13)
Open in a new tab

aStandard error.

bThe correlation between EBV and TBV is calculated as the r(y, EBV) divided by the square root of the heritability of a given trait.

Figure 4. Principal component analysis of five GS models based on the estimated genetic effects of 2,364 markers.

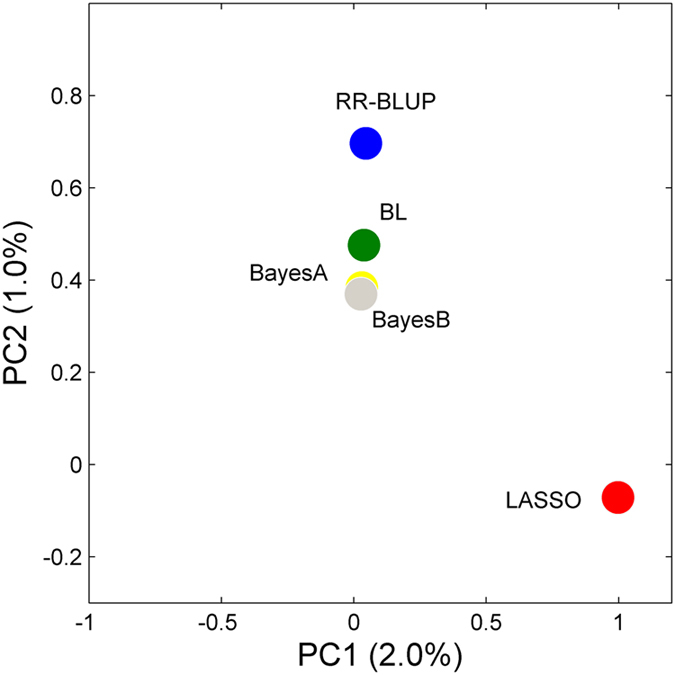
Figure 4

Open in a new tab

G-BLUP is not included in comparison because genetic effect is not estimated for individual markers in this model.

Table 6. The correlation of marker effects estimated using five GS models based on a combined family dataset for the trait of shell length.

  LASSO RR-BLUP BL BayesA BayesB
LASSO 1.00 0.32 0.30 0.26 0.23
RR-BLUP   1.00 0.82 0.72 0.72
BL     1.00 0.62 0.62
BayesA       1.00 0.87
BayesB         1.00
Open in a new tab

Discussion

2b-RAD: a cost-effective genotyping platform for genomic selection

The comprehensive set of restriction-site associated sequences generated by the 2b-RAD method provides an excellent fractional representation of the targeted genome12,13,14,15,16. The expected number of polymorphic markers can be readily predicted based on the total number of restriction sites and the polymorphism rate in a given genome. For Yesso scallop, approximately 242,044 BsaXI sites were identified from the reference genome dataset (~0.97G, unpublished), generating approximately 61,000 SNPs at a polymorphism rate of 2% (i.e., MD-SNPs). The prediction accuracies obtained by using MD-SNPs were comparable to those obtained by using HD-SNPs (Table 2), indicating the feasibility of determining an optimal sequencing plan that balances prediction accuracy and sequencing cost. This finding is also in agreement with the results of a recent empirical investigation in an Atlantic salmon breeding project which revealed that increasing the SNP density to over 22k had no substantial improvement on the genomic accuracy9. The generality of this observation, however, needs to be investigated in more aquaculture species, as marker density needed for GS implementation is also dependent on other factors, such as population structure, mating schemes, effective population size and mutation rate. For species with large genomes, sequencing all BsaXI sites at a depth of 20x for all individuals remains a substantial investment. For example, sequencing 1,000 Yesso scallop individuals would require approximately 5 billion reads, which are approximately equivalent to the number of reads produced from >30 sequencing lanes using the HiSeq2000 platform. Of course, high genome prediction (>90%) under this situation can be obtained (Table 2). A notable feature of the 2b-RAD method is the tunable genome representation from RTR libraries that are constructed using less degenerate adaptors12,14. For example, only 1/10th of total BsaXI sites in the Yesso scallop genome are targeted by using adaptors with 5′-NNA-3′ overhangs. Thus, the sequencing cost can dramatically decrease compared with that cost associated with the use of a standard BsaXI library, and the prediction abilities in this case remain acceptable (Tables 3 and 5). Our empirical data analysis suggests that integrating multiple families in a training set can be regarded as an effective approach to GS, not only because the effects of markers can be estimated from a relatively larger number of phenotypes but also low-density markers may be sufficient to pick up high linkage disequilibrium within full-sib families.

Comparison of the simulated and empirical cases

There is a decline of prediction accuracy from the simulation case to the empirical case even when both cases have a similar sample size and a similar marker density. Potential reasons for this decrease in accuracy include but are not limited to the following: (i) The genetic architecture. It is challenging to generate a simulated dataset that mostly resembles to a real case because genetic backgrounds of real breeding families/populations are usually unavailable in practice. Most of existing GS models do not consider non-additive effects and may partly misclassify the non-additive effects into the random error term, resulting in a decrease of the additive heritability. To explore this possibility, we performed an additional simulation analysis (Table 1, Simulation 3), considering the dominant effects, one source of non-additive genetic effects. When the dominant and additive variances relative to the total genetic variance are both 0.3, the prediction accuracies for Bayes-alphabet approaches will decrease by approximately 20% (Supplementary Fig. S2) in comparison with the additive-only simulation datasets (Table 3), but prediction difference between the new simulation and real datasets becomes smaller. Although a model that includes both additive and non-additive genetic effects could be beneficial for exploitation of specific combining ability32,33, the computational demand for these models is generally high and usually requires greater computing resources or more efficient algorithms. (ii) The sample size. Although our simulation analysis suggested that small family-based sample size could achieve reasonable prediction accuracies (Table 2), it does not necessarily apply to all types of real datasets which can be substantially different from simulation datasets. Hence, a careful examination should be performed before drawing inferences for situations in practical aquaculture breeding. (iii) The markers closest to a QTL may not be segregating in breeding families. For example, we observed a higher number of monogenic markers in the families 3, 4 and 5 in contrast to the other families (data not shown), which may cause some QTL regions to be undetected due to the lack of segregating markers. (iv) Multiple QTL alleles. SNP markers are usually biallelic and can thus only distinguish two alleles. If multiple alleles at a QTL are present and the QTL is adjacent to a SNP, it is quite possible that one SNP allele may be linked to more than one QTL allele. Therefore, the presence of identical SNP alleles in different samples does not necessarily imply identical QTL alleles.

Comparison of different GS models

In this study, we evaluated a wide range of GS models for their potential use in aquacultural GS projects. It is currently challenging to find a statistical model that is optimal for all breeding projects, as each model has its advantages and disadvantages depending on the scenarios (heritability, sample size, population structure, etc.)31. As expected, different performance was observed among these models under both simulation and empirical analyses. The Bayes-alphabet and BLUP-based models had relatively better performance in all cases than the other models because they can effectively capture the polygenic resemblance and genetic relationships31,34,35.

Conclusion

Our simulation and empirical analyses support 2b-RAD to be a powerful and cost-effective genotyping platform for GS implementation in aquaculture breeding programs. Comparison of six GS models revealed variable performance in prediction accuracy depending on the scenarios (e.g., heritability, sample size, population structure), but Bayes-alphabet and BLUP-based models generally outperformed other models though additional, larger studies are required to verify these suggestive findings.

Methods

Genetic resource simulation

The simulation dataset for in silico analysis was created from the draft genome sequence of Yesso scallop (~0.97G, unpublished). We first introduced SNPs at a rate of 2% by adding alleles to the diploidized genome. Hence, approximately 5,000 loci were randomly chosen as candidate QTLs and the allelic effects were sampled from a normal distribution with a mean of 0 and a variance of 1. The 2b-RAD method was then used for in silico marker genotyping. Two marker panels with different marker densities were generated by extracting all BsaXI tags (i.e., 5′-N10ACN5CTCCN8-3′) and RTR-BsaXI tags (i.e., 5′-AN9ACN5CTCCN7T-3′) generated using selective adaptors with the 5′-NNA-3′ overhangs. Only SNPs located in the BsaXI tags were considered for subsequent simulation analysis.

Breeding population simulation

A breeding population was simulated for 1000 generations according to the Fisher-Wright population model using the quantiNemo software36. The detailed parameters for the generation of simulated populations/families can be found in Table 1. The first simulation was generated as follows: 100 male and 100 female candidates from G1000 were selected as sires and dams and randomly mated in pairs with 20 offspring/pair to generate G1. This process was repeated to generate G2. For all of the samples in G1 and G2, the markers were genotyped and the traits were recorded. Phenotypic records were generated by adding the genetic values to a normally distributed error term and the variance was determined by heritability. The second simulation was composed of 20 full-sib families with each one containing 50 offspring by mating 10 males and 10 females from G1000 randomly. Different from the second experiment, the third simulation considered not only the additive genetic effects, but also dominant effects.

2b-RAD experiments and data analysis

A total of 349 Yesso scallop individuals that were derived from two full-sib families and three biparental families were included in 2b-RAD sequencing and genotyping. These families were established with assistance of the Dalian Zhangzidao Fishery Group Corporation. Growth-related traits including shell length (SL, mm), shell width (SW, mm), and shell height (SH, mm) were measured for all samples at the age of 15 months. The 2b-RAD libraries were prepared following the protocol developed by Wang et al.12 and were subject to single-end sequencing using an Illumina HiSeq2000 platform. 2b-RAD genotyping was performed using the RADtyping program v1.537 with default parameters. Segregating markers that could be genotyped in at least 70% of the individuals with minor allele frequency (>5%) were retained for subsequent analysis. Missing genotype values were estimated using the mean algorithm implemented in the R package rrBLUP38. In addition, associations among the genotypes were analyzed by principal component analysis (PCA) using the MATLAB software. Estimates of the narrow-sense heritability (h2) of each trait were obtained as the ratio of additive variance (σa2) to the total phenotypic variance (σa2 + σe2) using the REML algorithm38 with the genetic relationship matrix calculated using 2,364 genetic markers.

Cross-validation

To validate the accuracy of family/population-based prediction, we divided all of the samples into five subsets. Four of the subsets (80%) were used to estimate the marker effects, whereas the remaining subset (20%) was used as the validation set. For the over-generation prediction, all of the samples in G1 were considered as the training set, and the samples in G2 were used as the validation set. The prediction accuracy r was calculated using the correlation between the true breeding values (TBVs) and the estimated breeding values (EBVs) by sampling the training and validation sets for 100 times. For the empirical data analysis, the prediction accuracy r was adjusted according to the Equation (1) because the true breeding values are unknown in practice.

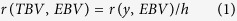graphic file with name srep19244-m1.jpg

where y is the observed phenotype and h is the square-root of heritability.

Statistical models

Six GS models including G-BLUP, BayesA, BayesB, Random Regression Best Linear Unbiased Prediction (RR-BLUP), Least Absolute Shrinkage And Selection Operator (LASSO), and Bayesian LASSO (BL) were used to estimate the marker effects. The basic model is as follows:

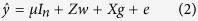graphic file with name srep19244-m2.jpg

where y is the vector of the phenotype for a given trait, μ is an intercept, Z is a design matrix assigning individuals to families, w is the vector of the family effect, and X is a design matrix allocating records to the SNP effects, in which element Xij = 0, 1, or 2 if the genotype of individual i at the jth SNP is AA, AB, or BB, respectively.

BLUP

For the traditional BLUP method, the genetic effect is defined as following:

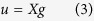graphic file with name srep19244-m3.jpg

It follows that

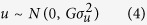graphic file with name srep19244-m4.jpg

Where G is the kinship coefficient matrix determined by the pedigree information.

G-BLUP

Different from the traditional BLUP method, G-BLUP estimates the kinship coefficient matrix based on the genome-wide genotyping information.

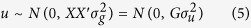graphic file with name srep19244-m5.jpg

where G = XX’k with a common choice of k as follows:

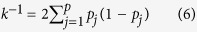graphic file with name srep19244-m6.jpg

where pj is an estimate of the frequency of the allele codes at the jth marker. Therefore, the representation of G-BLUP is given by the following model:

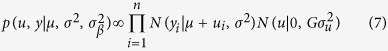graphic file with name srep19244-m7.jpg

The posterior mode of this approach can be rewritten as:

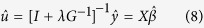graphic file with name srep19244-m8.jpg

In other words, the method can be understood easily by replacing the standard pedigree-based numerator relationship matrix used in the traditional BLUP approach with a marker-based estimate of additive relationships.

BayesA

For the BayesA approach, the following prior assumption regarding the distribution of SNP effects made:

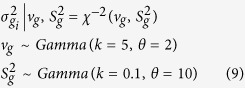graphic file with name srep19244-m9.jpg

BayesB

For BayesB, a priori SNP effect is assumed to be zero with probability πg, and normally distributed with a mean equal to 0 and a locus-specific variance with probability (1–πg). BayesA is a special case of BayesB in which πg = 0.

graphic file with name srep19244-m10.jpg

RR-BLUP

For RR-BLUP, a vector of SNP effects g is assumed to be normally distributed, and the direct solution of equation (2) would be obtained:

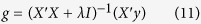graphic file with name srep19244-m11.jpg

where λ = σe2/(σg2/k), k = 2pi(1-pi) and pi is the allelic frequency of the ith marker.

BL

For the BL approach, g is assigned a prior double exponential (DE) distribution:

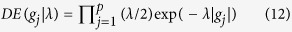graphic file with name srep19244-m12.jpg

And the residual variance σe2 is assigned a scaled inverse chi-square prior distribution.

LASSO

For the LASSO approach, the genetic effect g is a solution to an optimization problem of the following form

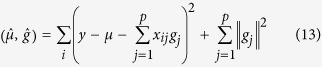graphic file with name srep19244-m13.jpg

The RR-BLUP method was implemented using the rrBLUP package38, whereas the LASSO approach was implemented using the glmnet package39, and the others were implemented using the BLR packages40. The breeding values for the validation population were estimated as:

graphic file with name srep19244-m14.jpg

Additional Information

How to cite this article: Dou, J. et al. Evaluation of the 2b-RAD method for genomic selection in scallop breeding. Sci. Rep. 6, 19244; doi: 10.1038/srep19244 (2016).

Supplementary Material

Supplementary Figures S1 and S2
srep19244-s1.pdf (822.7KB, pdf)
Supplementary Table S1
srep19244-s2.xls (64.5KB, xls)
Supplementary Table S2
srep19244-s3.xls (894KB, xls)

Acknowledgments

This work was supported by National High Technology Research and Development Program of China (2012AA10A405), National Natural Science Foundation of China (31322055 and 31302182), Natural Science Foundation for Distinguished Young Scholars of Shandong Province (JQ201308), and Fok Ying-Tong Education Foundation (141026).

Footnotes

Author Contributions Z.B., S.W. and J.D. conceived and designed the study. X.L., Q.F. and W.J. were involved in preparation of 2b-RAD libraries for sequencing. J.D., T.L. and Y.L. conducted the major part of the bioinformatics analysis. J.D., Y.W., X.H., S.W. and Z.B. drafted the manuscript. All authors read and approved the final manuscript.

References

  1. Meuwissen T. H., Hayes B. J. & Goddard M. E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Hayes B. J., Bowman P. J., Chamberlain A. J. & Goddard M. E. Invited review: Genomic selection in dairy cattle: progress and challenges. J. Dairy Sci. 92, 433–443 (2009). [DOI] [PubMed] [Google Scholar]
  3. Jannink J. L., Lorenz A. J. & Iwata H. Genomic selection in plant breeding: from theory to practice. Brief. Funct. Genomics 9, 166–177 (2010). [DOI] [PubMed] [Google Scholar]
  4. Poland J. et al. Genomic selection in wheat breeding using genotyping-by-sequencing. Plant Genome 5, 103–113 (2012). [Google Scholar]
  5. Kumar S. et al. Genomic selection for fruit quality traits in apple (Malus × domestica Borkh). PLoS One 7, e36674 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Sonesson A. K. & Meuwissen T. H. Testing strategies for genomic selection in aquaculture breeding programs. Genet. Sel. Evol. 41, 37 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Nielsen H. M., Sonesson A. K., Yazdi H. & Meuwissen T. H. Comparison of accuracy of genome-wide and BLUP breeding value estimates in sib based aquaculture breeding schemes. Aquaculture 289, 259–264 (2009). [Google Scholar]
  8. Nirea K. G., Sonesson A. K., Woolliams J. A. & Meuwissen T. H. Strategies for implementing genomic selection in family-based aquaculture breeding schemes: double haploid sib test populations. Genet. Sel. Evol. 44, 30 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Odegard J. et al. Genomic prediction in an admixed population of Atlantic salmon (Salmo salar). Front. Genet. 5, 402 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Davey J. W. et al. Genome-wide genetic marker discovery and genotyping using next-generation sequencing. Nat. Rev. Genet. 12, 499–510 (2011). [DOI] [PubMed] [Google Scholar]
  11. Poland J. A. & Rife T. W. Genotyping-by-Sequencing for plant breeding and genetics. Plant Genome 5, 92–102 (2012). [Google Scholar]
  12. Wang S., Meyer E., McKay J. K. & Matz M. V. 2b-RAD: a simple and flexible method for genome-wide genotyping. Nat. Methods 9, 808–810 (2012). [DOI] [PubMed] [Google Scholar]
  13. Seetharam A. S. & Stuart G. W. Whole genome phylogeny for 21 Drosophila species using predicted 2b-RAD fragments. PeerJ 1, e226 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Jiao W. et al. High-resolution linkage and quantitative trait locus mapping aided by genome survey sequencing: building up an integrative genomic framework for a bivalve mollusc. DNA Res. 21, 85–101 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cui Z. et al. High density linkage mapping aided by transcriptomics documents ZW sex determination system in the Chinese mitten crab Eriocheir sinensis. Heredity 115, 206–215 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Dixon G. B. et al. Genomic determinants of coral heat tolerance across latitudes. Science 348, 1460–1462 (2015). [DOI] [PubMed] [Google Scholar]
  17. Crossa J. et al. Genomic prediction in maize breeding populations with genotyping-by-sequencing. G3 3, 1903–1926 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Guo X. Use and exchange of genetic resources in molluscan aquaculture. Rev. Aquacult. 1, 251–259 (2009). [Google Scholar]
  19. Chang Y., Xiang J., Wang Z., Ding J. & Yang C. Tetraploid induction in Patinopecten yessoensis with chemicals. Oceanol. Limnol. Sin. 33, 105–112 (2002). [Google Scholar]
  20. Lu Z., Yang A., Wang Q., Liu Z. & Zhou L. Assortative fertilization in Chlamys farreri and Patinopecten yessoensis and its implication in scallop hybridization. J. Shellfish Res. 25, 509–514 (2006). [Google Scholar]
  21. Pan Y., Li Q., Yu R., Wang R. & Zheng Z. Studies on the induction of artificially genetic inactivation and effects of ultraviolet irradiation on the morphological structure of sperm in Japanese scallop, Patinopecten yessoensis. J. Ocean U. China 34, 949–954 (2004). [Google Scholar]
  22. Hou R. et al. Transcriptome sequencing and de novo analysis for Yesso scallop (Patinopecten yessoensis) using 454 GS FLX. PLoS One 6, e21560 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ding J. et al. Transcriptome sequencing and characterization of Japanese scallop Patinopecten yessoensis from different shell color lines. PLoS One 10, e0116406 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Sun X., Yang A., Wu B., Zhou L. & Liu Z. Characterization of the mantle transcriptome of Yesso scallop (Patinopecten yessoensis): identification of genes potentially involved in biomineralization and pigmentation. PLoS One 10, e0122967 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Meng X. et al. The transcriptomic response to copper exposure in the digestive gland of Japanese scallops (Mizuhopecten yessoensis). Fish Shellfish Immunol. 46, 161–167 (2015). [DOI] [PubMed] [Google Scholar]
  26. Feng L. et al. A scallop IGF binding protein gene: molecular characterization and association of variants with growth traits. PLoS One 9, e89039 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Sun Y. et al. Identification of two secreted ferritin subunits involved in immune defense of Yesso scallop Patinopecten yessoensis. Fish Shellfish Immunol. 37, 53–59 (2014). [DOI] [PubMed] [Google Scholar]
  28. Li R. et al. Characterizations and expression analyses of NF-κB and Rel genes in the Yesso scallop (Patinopecten yessoensis) suggest specific response patterns against Gram-negative infection in bivalves. Fish Shellfish Immunol. 44, 611–621 (2015). [DOI] [PubMed] [Google Scholar]
  29. Zou J. et al. The genome-wide identification of mitogen-activated protein kinase kinase (MKK) genes in Yesso scallop Patinopecten yessoensis and their expression responses to bacteria challenges. Fish Shellfish Immunol. 45, 901–911 (2015). [DOI] [PubMed] [Google Scholar]
  30. Ning X. et al. Genome-wide identification and characterization of five MyD88 duplication genes in Yesso scallop (Patinopecten yessoensis) and expression changes in response to bacterial challenge. Fish Shellfish Immunol. 46, 181–191 (2015). [DOI] [PubMed] [Google Scholar]
  31. Neves H. H., Carvalheiro R. & Queiroz S. A. A comparison of statistical methods for genomic selection in a mice population. BMC Genet. 13, 100 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Van Tassell C. P., Misztal I. & Varona L. Method R estimates of additive genetic, dominance genetic, and permanent environmental fraction of variance for yield and health traits of Holsteins. J. Dairy Sci. 83, 1873–1877 (2000). [DOI] [PubMed] [Google Scholar]
  33. Sun C., VanRaden P. M., Cole J. B. & O’Connell J. R. Improvement of prediction ability for genomic selection of dairy cattle by including dominance effects. PLoS One 9, e103934 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Resende M. F. et al. Accuracy of genomic selection methods in a standard data set of loblolly pine (Pinus taeda L.). Genetics 190, 1503–1510 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Moser G., Tier B., Crump R. E., Khatkar M. S. & Raadsma H. W. A comparison of five methods to predict genomic breeding values of dairy bulls from genome-wide SNP markers. Genet. Sel. Evol. 41, 56 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Neuenschwander S., Hospital F., Guillaume F. & Goudet J. QuantiNemo: an individual-based program to simulate quantitative traits with explicit genetic architecture in a dynamic metapopulation. Bioinformatics 24, 1552–1553 (2008). [DOI] [PubMed] [Google Scholar]
  37. Fu X. et al. RADtyping: an integrated package for accurate de novo codominant and dominant RAD genotyping in mapping populations. PLoS One 8, e79960 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Endelman J. B. Ridge regression and other kernels for genomic selection with R package rrBLUP. Plant Genome 4, 250–255 (2011). [Google Scholar]
  39. Friedman J., Hastie T., Simon N. & Tibshirani R. glmnet: Lasso and elastic-net regularized generalized linear models (2015) Available at: https://cran.r-project.org/web/packages/Glmnet/index.html. (Accessed: 20th August 2015).
  40. De los Campos G., Perez P., Vazquez A. I. & Crossa J. Genome-enabled prediction using the BLR (Bayesian Linear Regression) R-package. Methods Mol. Biol. 1019, 299–320 (2013). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figures S1 and S2
srep19244-s1.pdf (822.7KB, pdf)
Supplementary Table S1
srep19244-s2.xls (64.5KB, xls)
Supplementary Table S2
srep19244-s3.xls (894KB, xls)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES