The complexity of protein energy landscapes studied by solution NMR relaxation dispersion experiments

Abstract

The millisecond timescale motions in ribonuclease A (RNase A) were studied by solution NMR CPMG and off-resonance R_1ρ relaxation dispersion experiments over a wide pH and temperature range. These experiments identify three separate protein regions termed Cluster 1, Cluster 2, and R33 whose motions are governed by distinct thermodynamic parameters. Moreover each of these regions has motions with different pH dependencies. Cluster 1 shows an increase in activation enthalpy and activation entropy as the pH is lowered, whereas Cluster two exhibits the opposite behavior. In contrast the activation enthalpy and entropy of R33 show no pH dependence. Compounding the differences, Δω values for Cluster 2 are characteristic of two-site conformational exchange yet similar analysis for Cluster 1 indicates that this region of the enzyme exhibits conformational fluctuations between a major conformer and a pH-dependent average of protonated and de-protonated minor conformers.

1. INTRODUCTION

The existence of conformational dynamics across multiple timescales within biomolecules is ubiquitous and is necessary for their proper function. In enzymes, this flexibility is often involved in catalysis,^1–4 allostery,⁵ and ligand binding and product release.^{6, 7} These conformational changes are a result of thermal fluctuations in the enzyme as it traverses energy barriers that separate local energy minima on a rugged, multi-dimensional energy landscape,⁸ and the timescales of these motional processes are governed by the heights of the barriers between interconverting ensembles. The overall terrain of this free energy hyper-surface may be altered by modulation of the local environment.^{3, 9, 10} These changes may include the binding of ligand, alteration of solvent conditions, temperature changes, or mutagenesis. That enzymes have evolved the ability to utilize these conformational changes in adequately carrying out their biological roles implies a fine-tuning between the native free energy landscape and its response to the various thermodynamically stable states along the catalytic pathway. Although much work, both experimental and theoretical, has been done to date to characterize the relationship between biological function and conformational motions, the details underlying this coupling in many enzymes remains unclear. Due to the complexity and fine-structure of the topographical surface of a biomolecule’s energy landscape, conformational fluctuations spanning timescales from picoseconds (ps) to seconds (s) are inherently present. Solution nuclear magnetic resonance (NMR) spectroscopy is ideal for studying these varied dynamic processes, as it is a non-invasive biophysical technique that allows quantitative access to these various time-scales, with atomic resolution.

The focus of the study presented here is on motions on the timescale of catalytic turnover (µs -ms) in Ribonuclease A (RNase A). RNase A is a 13.7 kDa enzyme that binds to single stranded RNA and catalyzes its transphosphorylation into 2’,3’-cyclic monophosphate nucleotides.¹¹ In the apo enzyme, multiple protein isomerization events occurring on the ms timescale have previously been identified as catalytically relevant and have been partially characterized through temperature-jump experiments by the Hammes laboratory in the 1960s,^12–16 and later by 1D proton NMR by Markley.¹⁷ These global motional processes were later reinvestigated by biochemical and biophysical means in our laboratory. Characterization of these global dynamics via NMR relaxation dispersion experiments initially identified an enzyme-wide global backbone motion occurring on a similar timescale as catalysis, with the ground-state conformer having an equilibrium population of ~95%. Further investigation involving solvent kinetic isotope effects and mutagenesis studies revealed that this global motion was actually comprised of two independent conformational changes, each originating from a distinct cluster of flexible residues,⁷ as shown in Figure 1A. These dynamic clusters appear to be kinetically and thermodynamically identical at the pH corresponding to optimal enzymatic activity (pH = 6.4) at 25°C; here we show that these motions are different under all other conditions.

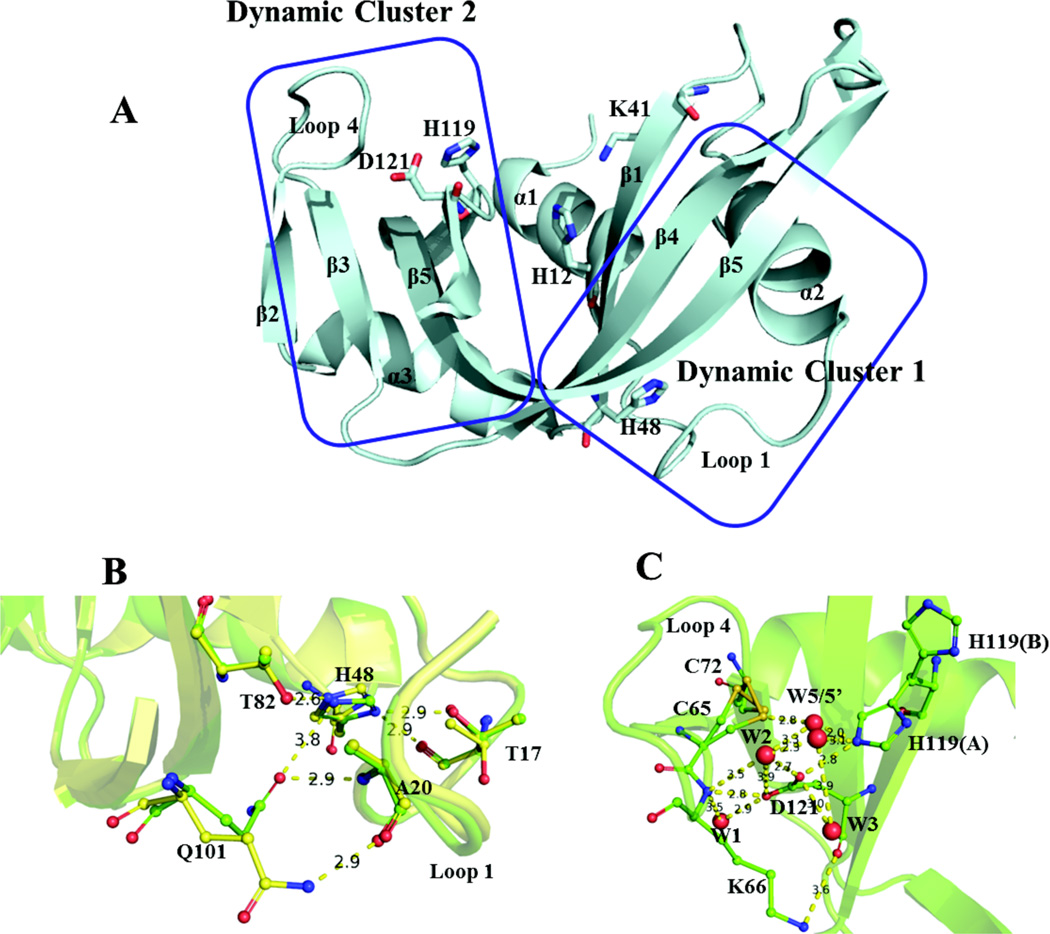
Figure 1.

(A) Crystal structure of apo WT RNase A (PDBID: 7RSA). Active site residues H12, K41, and H119, as well as dynamically important residues H48 and D121 are depicted as sticks and are labeled, along with the elements of secondary structure. (B, C) Important electrostatic interactions within dynamic clusters 1 and 2, with distances between heavy atoms reported in angstroms (Å). Crystal structures at pH 8.8 and 5.2 (PDBID 1KF8 and 1KF2, respectively) are aligned for cluster 1 to depict pH-dependent side-chain conformations (T17, H48, and Q101), while the latter structure is used to depict the interactions within cluster 2. The side-chains of residues such as T17, C65, C72, and H119 can adopt multiple conformations at a given pH value. Water oxygens are represented as red spheres. W1, W2, and W3 are conserved between pH 5.2 and 8.8, while W5 and W5’ are observed at pH 5.2 and are preceded by W4 at pH 5.9 (not shown).

Subsequently, dynamic cluster 1 was found to be involved in the rate-limiting product release step as first postulated by Hammes and co-workers.¹² The protonation state of H48, a residue that is situated in the heart of this dynamic cluster and ~20 Å from the active site, controls the rate of this motion and, therefore, the product release rate constant k_off and the rate of catalytic turnover, k_cat. Dynamic cluster 2 is situated on the opposite side of the enzyme and is involved in ligand binding and primarily involves loop 4, which imparts RNase A with binding specificity for purine nucleotides located on the 5’ side of bond cleavage,¹⁸ and the active site residue H119. The global dynamics of this cluster are linked to the active site via an interaction with D121, a residue that is conserved in the RNase A superfamily.

Interestingly, neither H48 nor D121 make contact with bound ligand; instead they provide the means to couple and regulate global dynamics within the enzyme and importantly, within the active site. This coupling appears to be crucial for the correct catalytic function of RNase A, as mutation of either H48 or D121 to alanine disrupts the global ms dynamics of only the residues in the dynamic cluster containing the mutation, with a concomitant reduction in k_cat by at least an order of magnitude. Such mutations perturb hydrogen-bonding networks that exist within the two clusters, yet the molecular mechanism of how the global motions of these two clusters are controlled and synchronized remains aloof.

H48 (Figure 1) is located on β-strand 1 and serves as a connection to loop 1 via a hydrogen bond between the imidazole NH^δ1 and the oxygen of T17, and as a connection to β-strand 4 via a hydrogen bond between the imidazole NH^ε2 and O^γ1 of T82. RNase A shows optimal catalytic activity between pH 5.5 and 6.5,²⁰ which is similar to the pK_a of H48.²¹ Previous studies have implicated the origin of this motion in RNase A to the flexible loop 1 (residues 14 – 25), the backbone of which samples a lowly populated conformation that resembles its conformation in the substrate-bound form²². Loop 1 motion occurs between the hinge residues S18 and N24. It has been suggested that the energy of this motion is propagated to the active site via dynamic residues in the β-sheets located in the region of cluster 1, which include F46, V47, T82, D83, T100, and Q101. The side-chains of some residues in this cluster, such as T17, H48, and Q101, display pH-dependent conformations (Figure 1B). The most significant occurs at pH < 7, where the Q101 side-chain amide breaks a hydrogen bond with the backbone carbonyl oxygen of A20 on loop 1 by moving ~5 Å towards H48, followed by a ~180° rotation about its C^δ-C^γ axis, which serves to establish interactions with the imidazole N^ε2 of H48 and the backbone nitrogen of A20. Previous work demonstrated the importance of H-bonds to H48 in modulating these interactions. Mutation of H48 or T82 to alanine,^{7, 23} or swapping the entire loop 1 for the, shorter 6-residue loop-1 from the homologous enzyme ECP²⁴ all have the similar effect of quenching ms motions in cluster 1, while mutation of T17 to alanine maintains coupling between the two regions of the cluster, at the expense of an elevated rate of interconversion.²³ These structural perturbations also had varying effects on the kinetics of ligand binding and dissociation, thus underscoring the importance of the coupling and tuning of these distal, motions with the RNase A active site.

Dynamic cluster 2, which includes the flexible loop 4 and the catalytic dyad comprised of H119 and D121, is connected to β-strand 3 via a disulfide bond between C65 and C72, which can isomerize between two side-chain conformations (Figure 1C), as evidenced by the crystal structures of apo and sulfate-bound RNase A in the pH range 5.2 – 8.8.²⁵ Similarly, the side-chain imidazole of active site residue H119 is seen to adopt two conformations: trans (conformation A) and gauche⁺ (conformation B). These two conformations show a pH dependence, with conformation A being favored at high pH, and both A and B showing occupancy at pH values below the pK_a of the H119 imidazole ring. The two states are related by a large rotation of the imidazole ring about the C^α-C^β bond (χ_1,A = 159° and χ_1,B = 60°)¹⁸, resulting in an effective flipping of the imidazole ring towards or away from D121 (conformers A and B, respectively). The carboxylate moiety of D121 is situated between loop 4 and H119, and forms interactions with N^ε2 of the A conformer of the imidazole ring of H119 and with the backbone nitrogen of K66. Thus, the sidechain of D121, which is conserved in mammalian ribonucleases²⁶, serves as a connecting residue between two catalytically important regions in RNase A. This idea was further bolstered by the observation that mutation of D121 to alanine (D121A) resulted in loss of ms dynamics in loop 4, and a 2–3 fold increase in the rate of interconversion of H119 between conformations A and B.¹⁸

To help better understand the molecular motions of these different regions in RNase A, we sought to characterize the apo enzyme’s energy landscape through temperature-dependent studies, as well as measure the effect of pH on these motions. In this study, we explore the native free energy landscape of RNase A using solution NMR relaxation dispersion methods.²⁷ Such a characterization of the molecular motions in RNase A offers further insight into the microscopic nature of these global conformational changes, including their transition states.

MATERIALS

The plasmid containing the protein sequence cloned into a pET22b(+) vector was transformed into C41(DE3) E. coli. All expression was performed in MJ media supplemented with MEM vitamins, MgSO₄, trace metals, thiamine, glucose, and carbenicillin.²⁸ For preparation of ¹⁵N-labeled RNase A, ¹⁵NH₄Cl provided the sole nitrogen source. Cells were grown at 37°C in a shaker operating at ~250 rpm. Typically, 3L of cell growth were sufficient for a single NMR sample. Protein expression was induced for 5 hrs after the addition of IPTG when the culture OD₆₀₀ ~ 0.7 – 0.8. Cell pellets were collected by centrifugation, with typical total cell pellet yields of 7 – 9g. ¹⁵N-labeled wild type (WT) RNase A was purified based on the previously published protocol of delCardayré et al.²⁹ The purified RNase A was dialyzed into NMR buffer (5mM MES, 7mM NaCl, 0.01% W/V NaN₃, 5% V/V D₂O, 1% W/V DSS, pH 6.4) overnight, followed by concentration to ~550µL in a Centricon concentrator (10 kDa molecular weight cutoff). Changes in pH were performed by direct addition of dilute HCl or NaOH to the NMR tube. A deuterated RNase A sample used in the rotating-frame relaxation studies was purified by a similar procedure, with H₂O replaced by D₂O during the expression phase of the protocol.

METHODS

All relaxation-compensated Carr-Purcell-Meiboom-Gill (rcCPMG) experiments were conducted on 500 µM RNase A at 11.7 and 14.1 T on four channel Varian spectrometers equipped with HCN room temperature probes. Proton (nitrogen) 90° pulse widths were typically calibrated to 6.5 – 7.5 µs (38 – 42 µs), with the ¹H carrier frequency set coincident with the water resonance and the ¹⁵N frequency set to 120 ppm. The water resonance of each set of CPMG spectra was measured relative to DSS (0 ppm), and all spectra were referenced accordingly. The experimental temperatures were calibrated with a 100% methanol sample.³¹ Spectral widths at 11.7 T (14.1 T) were set to 2,200 Hz (2,640 Hz) in t₁ and 8,500 Hz (10,250 Hz) in t₂, with 100 and 1088 points in each, respectively. The CPMG pulse sequence used in all experiments employed a train of heat-compensating 180° pulses on the nitrogen channel during the recycling delay, as well as a 3-9-19 water suppression block, centered on the amide proton region, prior to acquisition.³² The recycle delay was set to 2.7 s. 5 kHz ¹⁵N-decoupling during acquisition was performed using GARP modulation.³³ The total CPMG relaxation time was held fixed³⁴ at 40 ms and 1/τ_cp was set to 0, 100, 200, 300, 400 (×2), 500, 599, 800, 1000, 1400 (×2), and 1600 s⁻¹. Uncertainties in transverse relaxation rates were estimated from duplicate spectra. NMR peaks were selected for dispersion analysis based on the criterion that there was no significant overlap with other peaks. Transverse relaxation rates, R₂(1/τ_cp), from CPMG experiments were measured from peak intensities, I_υ, in spectra with v values for τ_cp and from intensities obtained from the τ_cp = 0 s⁻¹ reference spectrum (I₀) according to

$$R_2(1/{\tau }_{cp})=-T^{-1}ln\frac{I_{\nu }}{I_o},$$ (1)

where T is the constant relaxation time of 40 ms in these studies.

For CPMG data, plots of R₂(1/τ_cp) vs 1/τ_cp were analyzed for the presence or absence of dispersion, as follows. Residues initially selected for global analysis were ones previously identified as belonging to the solvent-isotope-sensitive dynamic cluster 1 or the solvent-isotope-insensitive dynamic cluster 2⁷ (Figure 1). Residue-specific dispersion profiles at a given pH and temperature were considered further if R_ex = Φ_ex/k_ex > 1.5 s⁻¹ at 500 MHz. At a given pH, only residues that showed significant dispersion and did not show peak overlap over the entire temperature range were chosen for global analysis. This was done to ensure that the data analyzed in all subsequent Arrhenius and Van’t Hoff treatments were not influenced by variations between datasets across the temperature range at a given pH.

All analyses of the global conformational changes associated with clusters 1 and 2 were carried out in Mathematica 8.0 (Wolfram, Inc.). All two-field temperature dependent datasets belonging to one of the two clusters at a given pH were simultaneously fit with equation (2), which encompasses all exchange regimes of ms dynamics:

$$R_2(1/{\tau }_{cp})=R_2^0+(k_{ex}-{\tau }_{cp}^{-1}{\text{cosh}}^{-1}[D_{+}\text{cosh}({\eta }_{+})-D_{-}\text{cos}({\eta }_{-})\left]\right),$$ (2)

where

$$D_{\pm }=\frac{1}{2}{[\pm 1+\frac{\mathrm{\Psi }+2\mathrm{\Delta }{\omega }^2}{\sqrt{{\mathrm{\Psi }}^2+{\zeta }^2}}]}^{1/2},$$

$${\eta }_{\pm }=\frac{{\tau }_{cp}}{\sqrt{2}}{[\pm \mathrm{\Psi }+\sqrt{{\mathrm{\Psi }}^2+{\zeta }^2}]}^{1/2},$$

$$\mathrm{\Psi }={\left(\frac{\zeta }{2\mathrm{\Delta }\omega }\right)}^2-\mathrm{\Delta }{\omega }^2+4p_A{p}_B{k}_{ex}^2,$$

and

$$\zeta =2\mathrm{\Delta }\omega (p_A{k}_{ex}+p_B{k}_{ex}).$$

At a given pH, global values of k_ex and p_A were allowed to vary over the temperature range but were shared amongst all residue datasets at a given temperature. The problem of assigning residue-specific motions to appropriate exchange regimes³⁵ for the purpose of fitting was overcome by providing additional constraints on Δω. These constraints exploit the facts that at a given pH a single residue’s Δω value scales linearly with the applied static field and that this value does not appreciably vary with temperature. Thus, this methodology was used to analyze the temperature dependence of the global conformational exchange of cluster 1 at pH 7.0 and 6.4 and cluster 2 at pH 7.0, 6.4, 5.5, and 4.5. Each set of best-fit parameters obtained from global fits of equation (2) was validated in Mathematica 8.0 by generating 500 synthetic datasets, each randomly noise-corrupted by a Gaussian distribution whose standard deviation (SD) is given by the average experimental uncertainty of all R²(1/τ_cp) points included in that dataset. These synthetic datasets were each re-fit with equation (2) and the resulting statistics of best-fit parameters were used to gauge the validity of the original fit.^36–40 These results are summarized in SI Figure 1 and validate the robustness of this fitting scheme. Residues whose conformational exchange motion was in the fast limit at pH 5.5 were analyzed with equation (3), where usable dispersion data was available (10 – 20°C):

$$R_2(1/{\tau }_{cp})=R_2^o+\frac{{\mathrm{\Phi }}_{ex}}{k_{ex}}[1-\frac{2}{k_{ex}{\tau }_{cp}}\text{tanh}(\frac{k_{ex}{\tau }_{cp}}{2}\left)\right]$$ (3)

In summary, the following residues were included in global analyses of CPMG data:

• pH 7.0; cluster 1: S16, T17, F46, V47, T82, D83, and Q101

  cluster 2: A64, K66, T70, and N71

• pH 6.4; cluster 1: S15, S16, T17, F46, T82, D83, and Q101

  cluster 2: A64, K66, T70, and N71

• pH 5.5; cluster 1: F46, D83 and T100

  cluster 2: A64, K66, T70, and N71

• pH 4.5; cluster 2: K66 and N71

Off-resonance TROSY-selected R_1ρ − R₁ experiments⁴¹ were performed on a 600µM ²H, ¹⁵N-labeled RNase A sample at a static magnetic field strength of 14.1 T at 25° C and pH 4.5. The magnitude of the spin-lock radio frequency pulse was calibrated prior to each experiment using off-resonance continuous wave decoupling.²⁷ R_eff = R_1ρ − R₁ at each value of the spin-lock field was measured by fitting the signal intensity at relaxation times of 2, 10, 25, 50, 75, 100, 130, 160, 200, and 225 ms to a single exponential decay function. Moreover, global analysis of off-resonance R_1ρ dispersion data at pH 4.5 and 25° C involved cluster 1 residues: S15, F46, V47, H48, T82, D83, and T100; and cluster 2 residues: A64, K66, T70, and N71. For R1_ρ data, residues within a dynamic cluster were assumed to be in fast exchange and were fit to equation (4).

$$R_{\mathit{\text{eff}}}=R_{\mathit{\text{eff}}}^o+\frac{p_A{p}_B\mathrm{\Delta }{\omega }^2{k}_{ex}}{{\omega }_e^2+k_{ex}^2}$$ (4)

In equation (4), ω_e is the effective field applied during the relaxation period and is equivalent to ${\omega }_e^2={\omega }_1^2+\mathrm{\Delta }{\mathrm{\Omega }}^2$ in which ω₁ is the amplitude of the applied field and ΔΩ is the offset frequency of the ω₁ field from the resonance of interest.

All NMR data were processed using NMRPipe,⁴² while visualization, resonance assignment, and measurement of chemical shifts and peak intensities were performed in SPARKY (http://www.cgl.ucsf.edu/home/sparky/). In this work we repeated CPMG experiments using ¹⁵N/¹H or ¹⁵N/²H labeled enzyme and observe no significant change in exchange kinetics.

The temperature dependence of the CPMG-derived motional parameters at each pH was analyzed. Rate constants were subjected to Arrhenius and Eyring analyses, yielding global activation parameter information (activation enthalpy ΔH^‡, activation entropy ΔS^‡, and activation Gibbs free energy ΔG^‡) for the forward and reverse processes, while a Van’t Hoff analysis of p_A yielded the global thermodynamics: the enthalpy ΔH, and the entropy ΔS. ΔG, the difference in Gibbs free energy between the lowly populated and ground state conformations, was calculated using

$$\mathrm{\Delta }G=-\mathit{\text{RTln}}\left(\raisebox{1ex}{$p_B$}\!\left/ \!\raisebox{-1ex}{$p_A$}\right.\right)$$ (5)

where R is the universal gas constant (in units of kcal mol⁻¹K⁻¹). When temperature dependent kinetic data was not available at all 4 temperatures at a given pH, such as is the case with residues in cluster 1 at pH values of 4.5 and 5.5, $\mathrm{\Delta }{G}_{\mathit{\text{rev}}}^{†}$ was estimated by using

$$\mathrm{\Delta }{G}_{\mathit{\text{rev}}}^{†}=\mathrm{\Delta }{G}_{\mathit{\text{ref}}}^{†}-RT\mathrm{l}\mathrm{n}\raisebox{1ex}{$k(T)$}\!\left/ \!\raisebox{-1ex}{$k_{\mathit{\text{ref}}}(T)$}\right.$$ (6)

where $\mathrm{\Delta }{G}_{\mathit{\text{ref}}}^{†}$ and k_ref(T) are the activation Gibbs free energy and rate constant at temperature T and some reference pH (pH 6.4 in this case), ΔG^‡ and k(T) are the activation Gibbs free energy and rate constant at temperature T at a different pH, and R is the universal gas constant. Here, k_ex was used as a proxy for k_rev, since k_ex ≈ k_rev for highly skewed populations. This assumption was made for convenience, as the true populations at pH 5.5 and 4.5 were not able to be determined. However, similar results are obtained when considering other ratios of the exchanging populations. In such cases, $\mathrm{\Delta }{S}_{\mathit{\text{rev}}}^{†}$ was estimated by exploiting the differences in the estimates of $\mathrm{\Delta }{G}_{\mathit{\text{rev}}}^{†}$ at two temperatures (if available).

RESULTS AND DISCUSSION

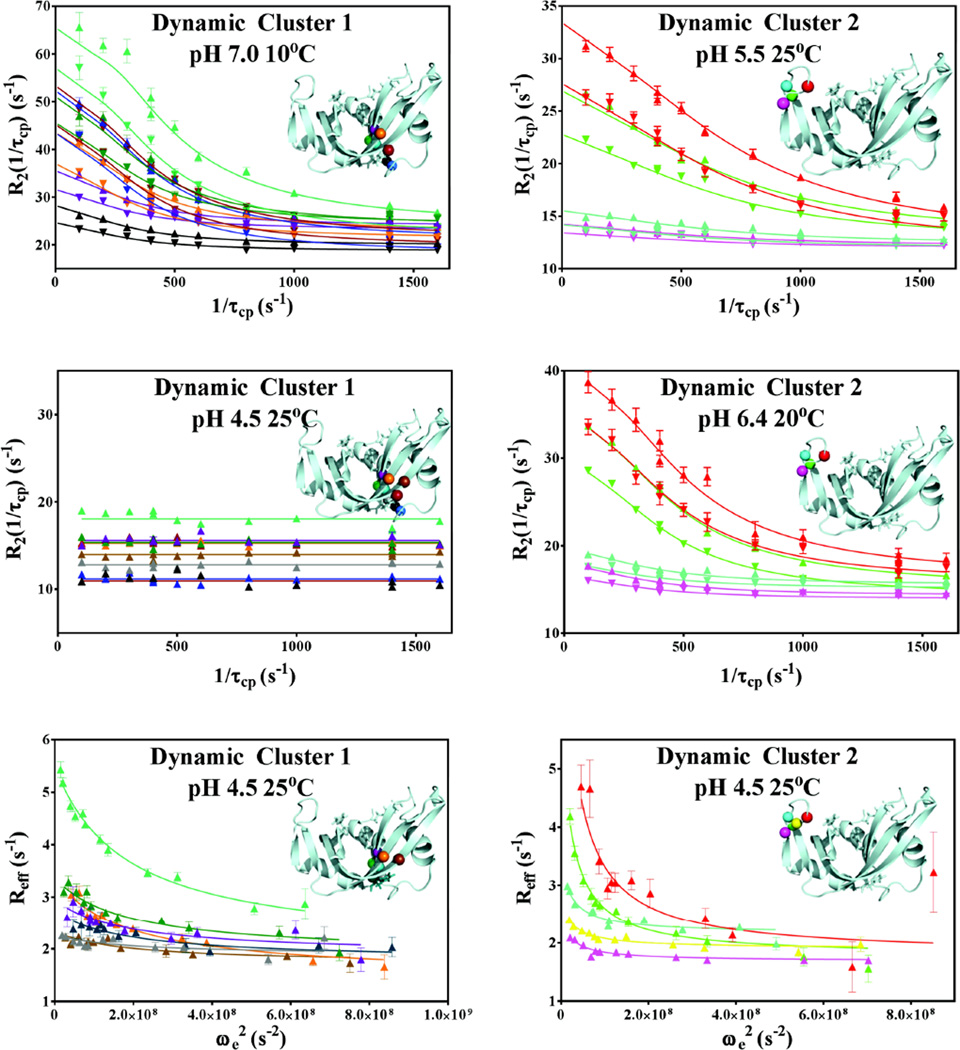
The pH dependence of the global dynamics in RNase A was investigated at two static fields (500 and 600 MHz) at pH values of 4.5, 5.5, 6.4 and 7.0, as shown in Figure 2. Moreover, at each pH the temperature dependence of these global dynamics was investigated at 10, 15, 20, and 25°C. Many residues displayed clear evidence of ms dynamics at all temperatures at pH values of 6.4 and 7.0, while many became too fast to accurately quantitate with CPMG experiments at pH ≤ 5.5. Two exceptions to this are the loop 4 residues K66 and N71, which displayed quantifiable CPMG dispersion under all conditions investigated. At pH = 4.5, no ms timescale dispersion for residues in cluster 1 was detected by CPMG experiments at any temperature but motions could be quantitated under these conditions by off-resonance R_1ρ experiments. Likewise, residues in cluster 2 did show appreciable CPMG and R_1ρ dispersion at this pH (Figure 2), and thus were amenable to global analysis. These faster motions that are observed at 25° C and pH 4.5 were investigated with TROSY R_1ρ − R₁ experiment⁴¹ and the resulting global fits are depicted in Figure 2. Representative Arrhenius, Van’t Hoff, and Eyring analyses of clusters 1 and 2 are presented in Figure 3, and all measured global kinetic and thermodynamic parameters are summarized in SI Tables 1 – 6. Monte Carlo validation of these kinetic and thermodynamic global fits is presented in SI Figure 1. All best-fit parameters clearly fall into tight, Gaussian-shaped clusters around the best-fit values, thereby providing confidence in the correctness of all derived parameters. In agreement with previous studies, it was found that there are two distinct and independent global conformational exchange processes within RNase A that occur on identical timescales at pH = 6.4 and T = 25°C but differ under all other conditions. These processes are localized to cluster 1, which exhibits a strong kinetic solvent isotope effect (KSIE), as well as a solvent isotope-insensitive region within cluster 2 that is localized to the vicinity of loop 4 (Figure 1).

Figure 2.

Representative global fits of relaxation dispersion data. Data collected at 500 and 600 MHz are represented with ▼ and ▲, respectively. Global 2-field CPMG fits of dynamic cluster 1 at 10°C, pH 7.0 and dynamic cluster 2 at 25°C, pH 5.5 and 20°C, pH 6.4 are shown, as well as lack of CPMG-detected dispersion for Cluster 1 at 600 MHz at 25°C, pH 4.5. 600 MHz R_1ρ data at 25°C and pH 4.5 of both clusters are shown in the bottom panels. The backbone nitrogen atoms of the residues involved in each global fit are mapped onto the structure in each panel and are color matched to the color of the respective dispersion data. Dynamic cluster 1 residues S15, S16, T17, F46, V47, H48, T82, D83, T100 and Q101 are shown in gray, black, blue, purple, green, dark teal, teal, orange, brown, and dark red, respectively. Dynamic cluster 2 residues A64, C65, K66, T70, and N71 at 25°C and pH 5.5 are shown in fuchsia, yellow, red, cyan, and green, respectively.

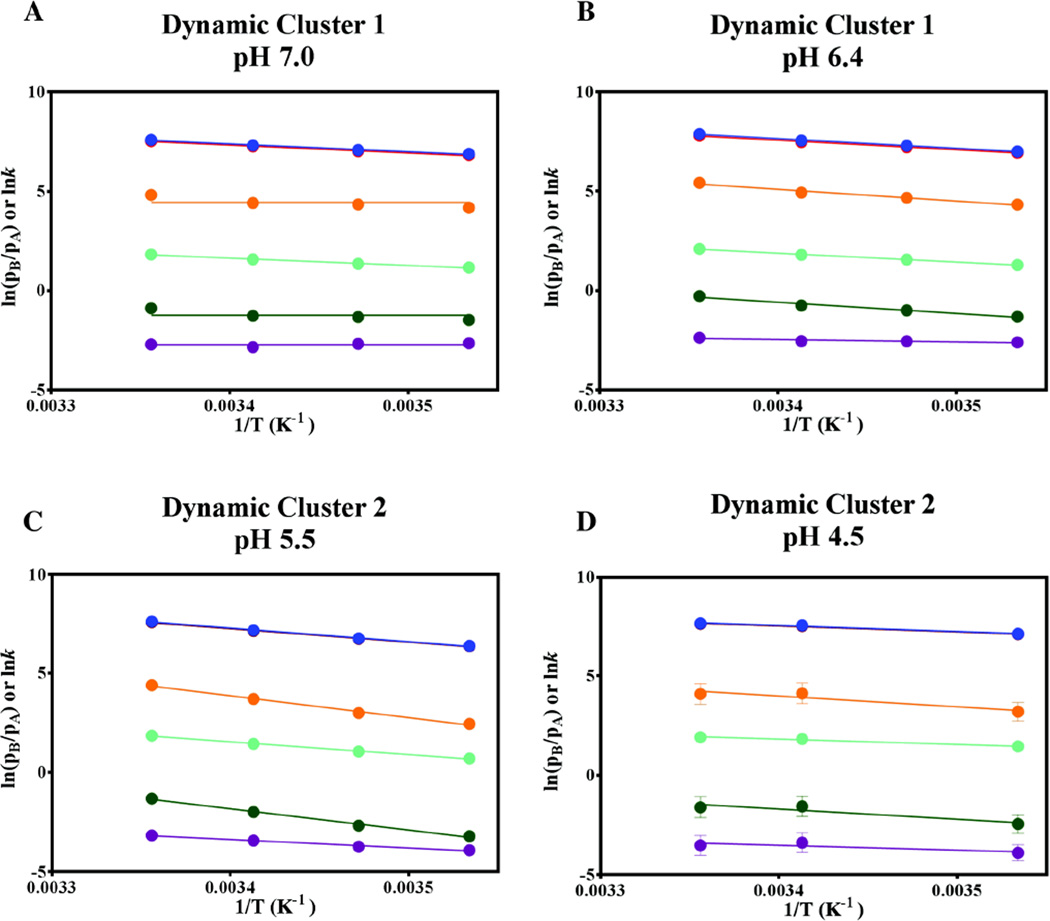
Figure 3.

Representative Arrhenius, Van’t Hoff, and Eyring analyses of global CPMG exchange parameters for dynamic clusters 1 and 2. The logarithms of k_ex (blue), k_fwd (orange), k_rev (red), p_A/p_B (burgundy), k_fwd/T (green) and k_rev/T (cyan) are plotted against 1/T, with the plots of lnk_exand ln k_rev appearing overlapped due to the skewed nature of the populations (0.93:0.07). The activation energies and thermodynamic parameters obtained from these analyses are summarized in SI Tables 5 and 6 and Figure 4.

Temperature and pH Dependence of Motional Kinetics and Populations

Cluster 1

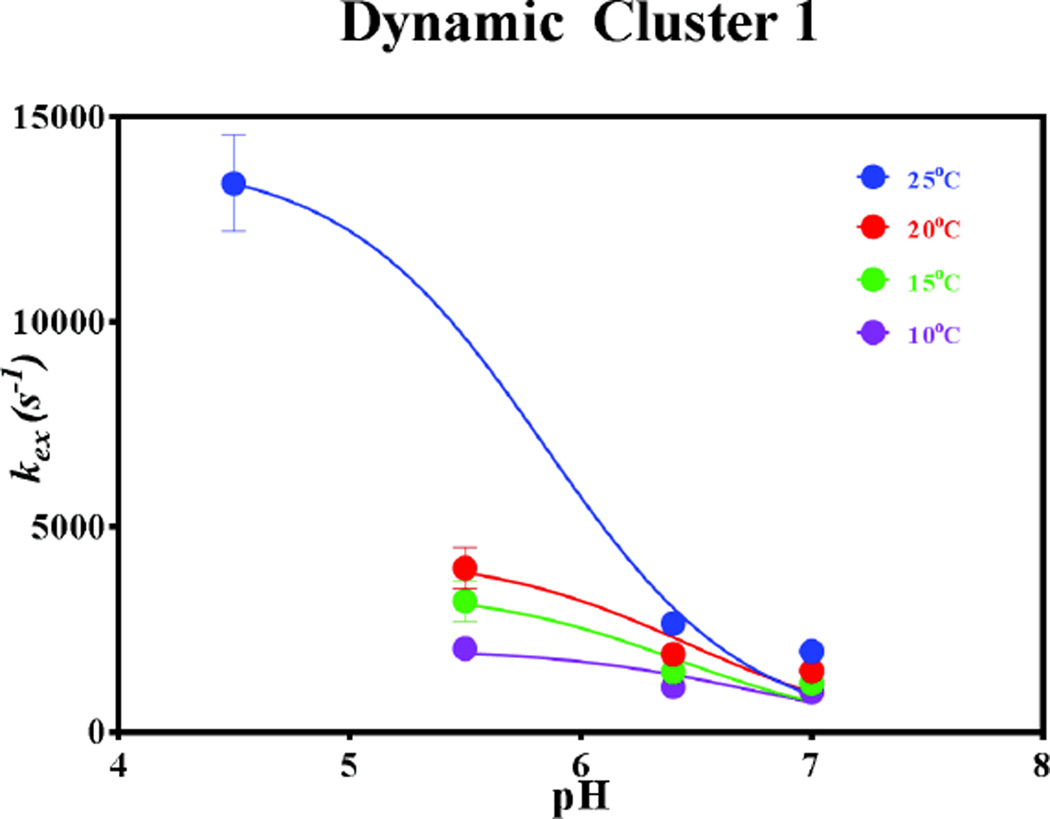
The global dynamics of cluster 1 were observed to be significantly more sensitive to changes in pH than those of cluster 2. Indeed, upon lowering the pH from 7.0 to 6.4, cluster 1 showed a modest yet reproducible increase in k_ex at all 4 temperatures, as well as changes in the activation parameters of the exchange process. At pH 7.0, k_ex was found to be 1,970, 1,500, 1,190, and 980 s⁻¹ at 25, 20, 15, and 10°C, respectively, while the corresponding values at pH 6.4 were found to be 2,650, 1,900, 1,470, and 1,100 s⁻¹. As the pH was decreased from 6.4 to 5.5, the observed temperature-dependent trend of elevated k_ex in cluster 1 was even more pronounced. Global fitting with equation (3) yielded k_ex = 2,040 s⁻¹ at 10°C, and k_ex ≥ 3,000 s⁻¹ at both 15 and 20°C. At 25°C and pH = 5.5, cluster 1 residues did not show any CPMG dispersion curves that were quantifiable, suggesting even faster motions beyond the CPMG detection window. Consistent with this, at pH 4.5, CPMG relaxation dispersion data at all 4 temperatures yielded flat lines for all residues in cluster 1 (Fig. 2), but the ¹⁵N R_1ρ experiment, which is capable of probing exchange processes up to k_ex ~ 50,000 s⁻¹ showed dispersion in measured rates with changes in the applied effective field. Analysis of R_1ρ relaxation dispersion with equation (4) at 25°C yielded k_ex = 13,400 s⁻¹ for cluster 1 (Fig. 2).

Cluster 2

In contrast, the global dynamics of cluster 2 are not sensitive to pH values between 5.5 and 7.0 (SI Table 1). As such, at pH values of 5.5, 6.4, and 7.0, the k_ex values were averaged with resulting overall averages from the CPMG dispersion analysis of 1,610, 1,074, 784, and 508 s⁻¹ at 25, 20, 15, and 10°C, respectively. Also unlike cluster 1, cluster 2 residues, K66 and N71 exhibited quantifiable CPMG dispersion data at pH = 4.5, with k_ex = 2080 ± 340 s⁻¹ at 25 °C. R_1ρ relaxation dispersion for the other cluster 2 residues at 25°C yielded k_ex = 5,000 ± 600 s⁻¹. The erroneously high k_ex value of cluster 2 obtained from R_1ρ measurements is a factor of two larger than the value obtained from CPMG measurements. This is due to the fact that the true k_ex of 2,080 s⁻¹, as measured by CPMG, is on the slower end of kinetics that may accurately be estimated by R_1ρ methodology while employing the form of R_ex given in equation (4) as previously described by Korzhnev et. al.⁴³ This was further corroborated by performing Monte Carlo simulations using the CPMG-obtained parameters as input and fitting with the R_1ρ equation (4), as shown in SI Figure 2. Unlike the erroneously low k_ex reported by R_1ρ experiments for cluster 2, the higher value of k_ex for cluster 1 (13,400 s⁻¹) is accurately measured by the R_1ρ experiment.

As shown in Figure 3, the equilibrium populations of cluster 1 exhibit no temperature dependence at pH 7.0 (burgundy data points), with the average population of the ground state conformer, p_A, being 93.8 ± 0.5%. At pH 6.4, a weak temperature dependence (R² = 0.80) was observed for cluster 1, with p_A showing a similar average value of 92.5 ± 0.7%. In contrast, the populations of cluster 2 showed dependence on temperature but not on pH. Thus, at each temperature the individual cluster 2 p_A values were averaged from CPMG dispersion datasets over the entire pH range. These average values and their standard deviations were found to be 95.9 ± 0.9% at 25°C, 96.4 ± 0.6% at 20°C, 97.2 ± 0.5% at 15°C, and 97.6 ± 0.4% at 10°C, and were used in all subsequent kinetic and thermodynamic analysis of CPMG data at the four pH conditions for cluster 2. These analyses reveal that the motional process of cluster 2 is pH-insensitive in the pH range 5.5 – 7, but that changes in the kinetics, not the thermodynamics, occur at pH 4.5. These results are summarized in Figure 3 and SI Table 6.

In contrast to the two dynamic clusters that show varying degrees of sensitivity to pH, a newly identified flexible residue, R33, was observed with motional properties distinct from those of cluster 1 and cluster 2. The conformational exchange dynamics of R33 do not respond to changes in pH in the range 4.5 – 7.0, at 10, 20, 15, and 25Δ°C Thus, all two-field spin relaxation data for this residue were globally fit with shared k_ex, p_A, and Δω values. The results of these global fits are depicted in SI Figure 3, along with their Monte Carlo validation in SI Figure 3. At 25° and 20°C k_ex was determined to be 1,215 and 630 s⁻¹, respectively, while at 15 and 10°C the dispersion profiles of R33 were best modeled by lines with slope = 0 (SI Figure 3B).

The amplitude of the dispersion profiles for R33 decreases as temperature is decreased, a hallmark of two-site exchange between two populations that become more skewed as the temperature is decreased.^{7, 27} At 25 and 20° C, the two-field relaxation data was best modeled with a global, pH-independent population, which was found to be 99.5%. Thus, since no CPMG dispersion is observed at 15 and 10°C at all four pH values, the population must remain skewed across the entire temperature range. This hypothesis is further supported by synthetic data modeling, as shown in SI Figure 3C.

Activation and Thermodynamic Parameters

Cluster 1

Upon lowering the pH from 7.0 to 6.4, E_a,fwd and E_a,rev of cluster 1 increased by 3.9 and 1.6 kcal/mol, respectively, with ΔH^‡_fwd and ΔH^‡ _rev showing similar behavior (Fig. 4 and SI Fig. 4). Although the system is in fast exchange at pH = 5.5, it was possible to estimate certain thermodynamic quantities. In making these estimations, it was assumed that the populations remain highly skewed (k_ex ≈ k_rev) at pH = 5.5. This approximation was employedbecause the populations of the two conformations are not known at these conditions, but it is unlikely that the populations become similar (i.e. p_a ≅ p_b) as the pH is lowered from 6.4 to 5.5.

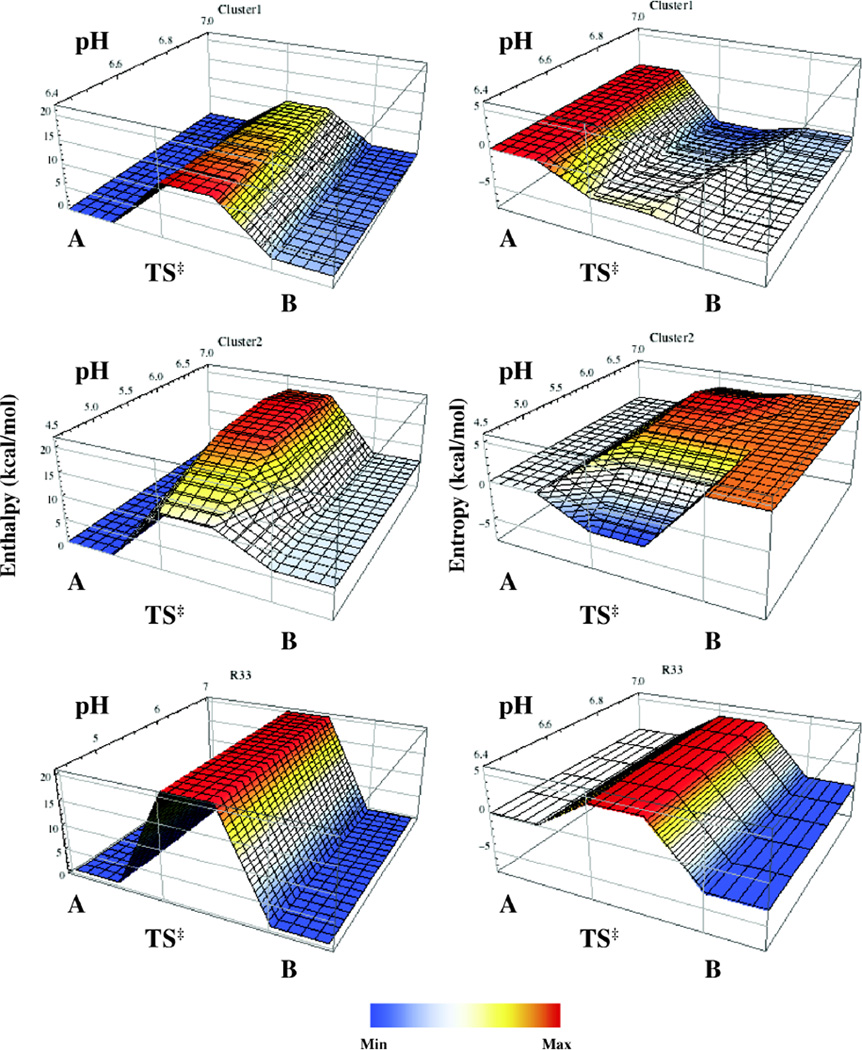
Figure 4.

Energy landscape surfaces for conformational changes (A ⇌ TS^† ⇌ B) in RNase A. pH-dependent changes in enthalpy (left) and entropy (right) are depicted for Cluster 1 (top), 2 (middle), and R33 (bottom). Data were obtained from temperature dependent NMR relaxation experiments. In all cases conformation A is set at a reference value of 0 kcal/mol.

For cluster 1, ΔH^‡_rev at pH 5.5 was found to be ~17 kcal/mol using ΔH^‡_rev = TΔS^‡_rev + ΔG^‡_rev. The reverse activation entropy term became less negative as the pH was decreased, (TΔΔS^‡_rev = 5 kcal/mol at 25°C), and thus, more favorable. Both ΔG^‡_fwd and ΔG^‡_rev show a slight decreasing trend with decreasing pH and are in agreement with the observed increasing trend in k_ex at a given temperature as the pH is decreased. These pH-dependent reductions in ΔG^‡ are accounted for by the over-compensation provided by an increase in the activation entropies in response to the elevated activation enthalpies.

For cluster 1, ΔG^‡ for both the forward and reverse motions is larger than 10 kcal/mol in the pH range 4.5–7.0, which is slightly larger than the typical energy needed for dissociation of product from RNase A (ΔG^‡_diss = ΔG_diss ≈ 6.5 kcal/mol).^{18, 23, 24, 44–46} This value is consistent with previous suggestions linking the motion of loop 1 with the product release step. The propagation of this energy to the active site necessarily requires the involvement of multiple residues with correlated dynamics over a region of the enzyme that spans the origin of the motion and the active site, a requirement RNase A has clearly evolved to satisfy.

Cluster 2

In cluster 2, the activation parameters remained relatively constant between pH 5.5 – 7.0, but changed appreciably at pH 4.5 (Fig. 4 and SI Fig. 4). E_a,fwd and E_a,rev (as well as the activation enthalpies) are each reduced by ~8 kcal/mol at pH 4.5 from their respective values of 20 and 13.5 kcal/mol. The activation entropy terms show a similar behavior, destabilizing the transition state by ~7.5 kcal/mol at pH 4.5 and 25°C. These changes in the activation enthalpies and entropies have the net favorable effect of stabilizing the conformational transition state by lowering ΔG^‡_fwd and ΔG^‡_rev by less than 1 kcal/mol (0.8 and 0.3 kcal/mol, respectively). This is in agreement with the observation that the global k_ex value of cluster 2 becomes elevated at pH 4.5 relative to its fairly constant value between pH 5.5 – 7.0.

As discussed above, the activation parameters of dynamic cluster 1 exhibit a higher degree of sensitivity to changes in pH than those of cluster 2, as shown in Figure 4, SI Figure 4, and SI Tables 5 and 6. Similarly, the equilibrium populations of the motional process of cluster 1 showed a dependence on pH, while those of cluster 2 did not. At pH 7.0, the difference between the two conformational states of cluster 1 is purely entropic (viz. ΔH = 0). As the pH was lowered from 7.0 to 6.4, the minor conformation of cluster 1 became slightly endothermic (ΔΔH = 2.3 kcal/mol), while being entropically stabilized (TΔΔS = 2.5 kcal/mol at 25°C). In contrast, the conformational enthalpy and entropy terms in cluster 2 were found to be constant at 6.3 and 4.4 kcal/mol, respectively, at 25°C throughout the pH range. ΔG did not vary from a value of ~2 kcal/mol at pH 7.0 and 6.4. However, since the transition to the minor conformer is associated with a protonation event, it is expected that ΔG would become less positive as the pH is lowered.

Unlike clusters 1 and 2, the activation parameters and equilibrium populations of R33 do not depend on pH in the range investigated. As the populations do not show a dependence on pH, ΔH = 0, TΔS = −3.1 kcal/mol (at 25°C), and ΔG = 3.1 kcal/mol. However, as only an estimate of the upper boundary on k_ex at 10°C is available from data modeling, only an estimate of the lower boundaries for the activation parameters of this motional process could be determined, as depicted in SI Figure 5. Thus, the lower boundaries of ΔH^‡_fwd, ΔH^‡_rev, ΔG^‡_fwd, ΔG^‡_rev, TΔS^‡_fwd and TΔS^‡_rev (at 25° C) are 20.5, 20.5, 16.5, 13.44, 4.1, and 7.2 kcal/mol.

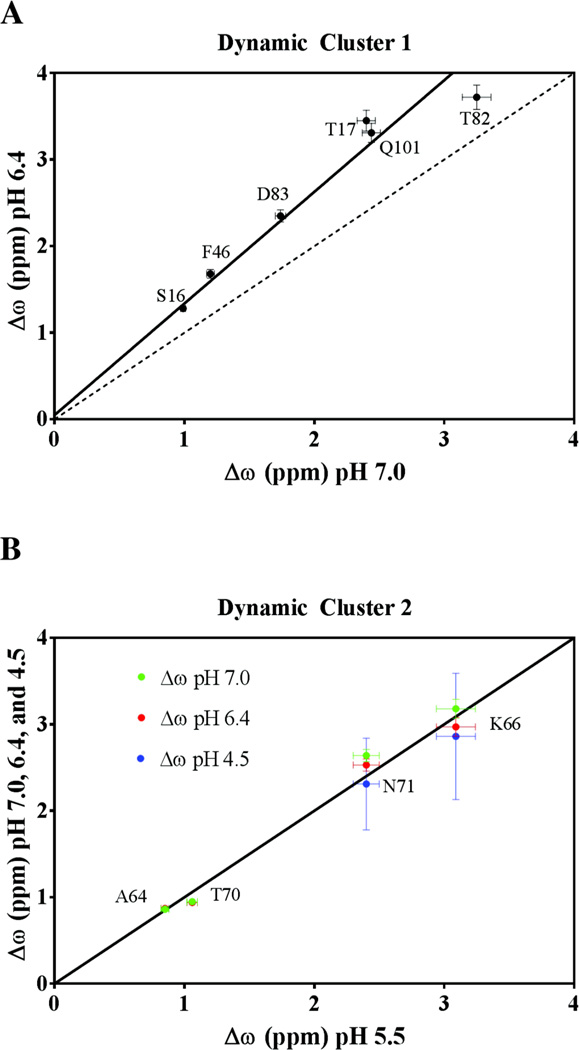
Global fitting of dynamic clusters 1 and 2 yielded information regarding the value of each flexibil residue’s individual Δω. Δω is the magnitude of the difference between the ¹⁵N chemical shifts of two exchanging conformational states of RNase A. The measured values of Δω obtained at various values of pH are reported in SI Table 7, and the pH dependence of Δω is summarized in Figure 5. All residues in cluster 1 display a pH-dependent difference (pH 6.4 vs. 7.0) in their Δω values, whereas residues in cluster 2 showed no such dependence between pH 4.5 – 7.0. Plots of Δω of cluster 2 residues at pH 5.5 vs. those at the other three pH values are best fit with a line of unit slope passing through the origin (R² ≥ 0.92), whereas cluster 1 residues, while having highly correlated Δω values, were better fit with a line of slope 1.3 (R² = 0.97). Both dynamic clusters showed a distribution of Δω values, with 0.99 ≥ Δω ≤ 3.25 ppm and 0.94 ≤ Δω ≤ 3.72 for cluster 1 at pH 7.0 and 6.4, respectively, and 0.86 ≤ Δω ≤ 3.08 ppm for cluster 2 from pH 5.5 to 7.0. Of the residues investigated in cluster 1, S15 at pH 6.4 showed the smallest Δω, which was found to be 0.94 ppm. In cluster 2, both A64 and T70 exhibited comparably low values of Δω, which were found to be 0.86 and 0.99 ppm, respectively. T82 and K66 have the highest value of Δω in clusters 1 and 2, respectively, at all pH values investigated.

Figure 5.

The dependence of Δω on pH. (Top) Correlation plot of Δω at pH 7.0 vs. Δω pH 6.4 of dynamic cluster 1 residues, S16, T17, F46, T82, D83, and Q101. The dashed line of unit slope shows a weak correlation (R² = 0.46) with the data at the two values of pH, and is depicted for reference. The data is best described by a line of slope 1.29 ± 0.16 (weighted R² = 0.97), with near-zero y-intercept, suggesting that the global motion may not be adequately described by a simple two-state model. (Bottom) Correlation plot of Δω at pH 5.5 vs. Δω at pH 7.0 (green), 6.4 (red) and 4.5 (blue) of loop 4 residues A64, K66, T70, and N71. Δω values determined at each of four pH values are well-described by a line of unit slope passing through the origin (R² > 0.98), suggesting that the two chemical environments being sampled by cluster 2 remain unchanged over the pH range.

No correlations were found between a residue’s location in the protein and the magnitude of its Δω. The consistently elevated Δω for each cluster 1 residue at pH 6.4 relative to pH 7.0 is unlikely to arise from a systematic error or a transition between more than two on-path conformational states. If this observed increase in Δω originated from a systematic error due to experimental issues, then these errors should also manifest in the cluster 2 data. However, no such offset was observed in cluster 2. In addition, all attempts to fit the CPMG dispersion data with multi-site exchange models⁴⁷ resulted in poor fits with ambiguous dynamics parameters; the data is better described by a two-state model in all cases. The offset of Δω for cluster 1 residues suggests that an additional conformation is being sampled by this group of residues. Thus, if the motion undergone by cluster 1 is to be described by multi-state exchange, this model must manifest itself as an effective two-site motional process.

Scheme 1-I illustrates the simplest kinetic model between the conformational and protonation states of cluster 1 that can adequately account for the observed dynamics data including prior work implicating the involvement of H48.^{12, 13, 17, 19, 23, 24, 48–50} Here, RNase A can undergo a conformational transition from the major A state with H48 deprotonated to the minor B state, which may or may not be accompanied by a concomitant protonation event at H48. The two ionization states of the B state exist in a rapid equilibrium with each other on the NMR timescale with respect to the interconversion of A and B (k_B→BH+ and k_BH+→B >> k_A→B and k_B→A) and A and BH⁺ (k_B→BH+ and k_BH+→B >> k_A→BH+ and k_BH+→A). Thus, this cyclical model reduces to an effective two-state exchange process with the A conformer exchanging with the ensemble average of the two ionization states of the B conformer (Scheme 1-II). Furthermore, the rates at which A interconverts with B and BH⁺ are not equal, with k_BH+→A >> k_B→A. Thus, as pH is lowered the k_BH+→A process contributes proportionately more to the measured k_ex, as well as increasing the measured effective two-state Δω values. The latter phenomenon is caused by a shift in the equilibrium between the two rapidly exchanging B and BH⁺ conformers, the relative populations of which determine the position of the minor resonance in the effective two-site exchange model. No such additional step is necessary to describe the motion of cluster 2, for which the data is adequately accounted by a two-site exchange model. Recent developments in experimental access to histidine pK_a values of higher-energy conformations have found them to differ from their ground state values.^{51, 52} These measurements were carried out on proteins that exist in equilibrium between a native, folded protein (ground state) and a folding intermediate (higher-energy state). While it does not describe a protein folding equilibria, our proposed scheme is consistent with this general observation, with the pK_a of H48 being modulated during loop 1 motion as it becomes more solvent-exposed and as the interactions between side chains change. We expect that the apparent pK_a of this global motion is lower than that of H48 (i.e. pK_a < 6.1²¹), as the populations (and ΔG) remained constant and skewed towards the major A conformation at pH 7.0 and 6.4. Our model is also in agreement with the observed trend in the activation parameters of the effective two-state model. This suggests that the protonated form of H48 facilitates the rate of interconversion of the enzyme between its two conformational states.

Scheme 1.

(I) The proposed cyclic three-state equilibrium to describe the global motion undergone by dynamic cluster 1. The two ionization states of minor conformation B are in rapid equilibrium with each other with respect to the chemical shift timescale, resulting in a pH-dependent effective two-state exchange process (II) between their ensemble average and the deprotonated major A conformer.

Lastly, Δω of R33 was found to be 5.41 +/− 0.30 ppm. This value is pH independent like its k_ex and p_A values. A Δω of 5.4 ppm is the highest backbone nitrogen Δω thus far observed in RNase A. Although clearly in slow chemical exchange, no minor peak could be detected for this residue, as the populations remain highly skewed under all conditions.

Modeling k_ex vs. pH

To further assess the viability of our proposed model of the global motion of cluster 1 (Scheme 1), we derived an expression for the apparent k_ex as a function of pH. The details of the derivation are presented in Supporting Information, with the final result taking the form

$$k_{ex}={(\frac{1}{k_{ex}^{(\mathit{\text{conf}})}}+\frac{{10}^{pH}}{k_{ex}^{(\mathit{\text{prot}})}})}^{-1}$$ (7)

Here, k_ex^(conf) is the effective exchange rate constant due to conformational change and k_ex^(prot) is the effective exchange constant resulting from the protonation of H48, with or without an accompanying global conformational change. Thus, k_ex^(conf) = f(k_AB,k_BA, k_BH+→A) and k_ex^(prot) = f(k_B→BH+, k_A→BH+).

Using this model the pH dependence of k_ex at 4 temperatures was investigated. The results of the fits of k_ex vs pH at the four temperatures are presented in Figure 6, the best-fit values of which are summarized in SI Table 8. No information regarding the apparent pK_a value could be reliably retrieved from the k_ex vs pH profiles. Although a visual inspection of Figure 6 reveals that the inflection point of each best-fit curve is not constant, it remains unclear whether this effective pK_a varies significantly with temperature. The inadequate fit is due, in part, to the small number of data points. However, the resulting best-fit parameters are reasonable within the context of Scheme 1, though probably overestimated. In particular, as the pH is lowered, resulting in B + H⁺ being negligible and BH⁺ favored, the observed k_ex at 25°C approximates k_ex^(conf). Similar conclusions seem reasonable at the other temperatures, though no k_ex information was obtained at pH 4.5 at any temperature other than 25°C. The magnitude of k_ex^(prot), ~10⁹ s⁻¹, remained relatively invariant with temperature, and is in-line with diffusion-limited protonation processes⁵³.

Figure 6.

k_ex vs pH profiles at 4 temperatures for dynamic cluster 1.

The response of the backbone dynamics of R33 to various alterations in the chemical environment of RNase A was investigated further. Unlike other residues, the dynamics of R33 are unperturbed by alterations in the surrounding buffer.⁵⁴ All dispersion profiles have similar slow-exchange characteristics (k_ex/Δω ~ 0.75 at 500 MHz), as shown in SI Figure 3, with <R₂°> = 15.6 ± 0.7 s⁻¹ at 600MHz. Indeed, the best-fit k_ex, Δω, and p_A under all conditions were found to be 1,210 s⁻¹, 5.22 ppm, and 99.6%. Thus it appears that the dynamics of R33 are pH-independent in the pH range 4.5 – 7.0 and resilient to alterations in buffer solute content. Moreover, the motions of R33 are robust with respect to mutation at other sites in RNase A. R33 motions in the D121N and D121A mutant are the same as WT with k_ex = 1,466 s⁻¹, Δω = 5.67 ppm, and p_A = 99.6%. Mutations within dynamic cluster 1, which are more proximal to R33, resulted in varying degrees of modulation of its ms motions. The T17A mutant resulted in small changes to R33 motions with Δω and k_ex slightly reduced to 4.66 ppm and 540 s⁻¹, respectively. However, in the T82A mutant and the Loop 1_ECP chimera, the backbone dynamics of R33 become undetectable in ¹⁵N CPMG experiments, with the values of $R_2^0$ showing no signs of elevation, indicating motion did not shift to a faster timescale. Thus, while R33 motions are independent of Cluster 2, under certain conditions its motions change when perturbations to Cluster 1 are made. The dynamics parameters obtained for R33 under all of these various conditions are summarized in SI Table 9.

Conclusions

The role of H48 in RNase A conformational exchange motions in cluster 1 have been well-documented^{7,19, 23, 50, 55} and the pH dependence of these motions have been described here and elsewhere.^{12, 17} In addition, these studies show that the dynamics of cluster 2 are not pH dependent until a value of 4.5 is reached, at which there is a slight elevation in k_ex at all 4 temperatures. This may suggest that the conserved residue D121^{18, 56} plays a role in these motions, given its pK_a ~ 3.0,²¹ and possibly its interaction with H119 and the local water network. Changes in local water networks in lysozyme and RNase A were previously found to affect motion^{57, 58}. Although if bound waters played a large role this might predict a solvent kinetic isotope effect on loop 4 motions, yet none was observed experimentally. ^{7, 19} The structure of this water network around D121 and the active site appears to be correlated to the electrostatic environment of cluster 2, screening the delocalized negative charge provided by D121, and expanding in size in response to protonation of H119 (Fig. 2C). The observed decrease in all of the activation parameters for cluster 2 at pH = 4.5, along with the lack of changes in thermodynamic parameters, suggests that only the transition state between the two exchanging loop 4 conformations is affected at these solution conditions. This is further evidenced by the constant values of Δω for the residues in loop 4 over the entire pH range. At pH = 4.5, the entropic transition state becomes more ordered relative to both conformations, as $\mathrm{\Delta }{S}_{\mathit{\text{fwd}}/\mathit{\text{rev}}}^{†}<0$. This decrease in activation entropy is accompanied by a favorable decrease in the activation enthalpies by a factor of 2, implying more favorable electrostatic interactions in the transition state. The net result is an increase in the conformational exchange rate.

The crystal structure of the D121A mutant shows the absence of this water network in the cavity between loop 4 and H119, with the backbone of the former and the side chain of the latter adopting different conformations relative to the WT enzyme. As noted previously, the consequences of such a mutation are an increase in the rate of H119 ring flip and a loss of ms dynamics in the entire backbone of loop 4, with the exception of C65. Thus, the water network found in cluster 2 is integral to the proper catalytic function of RNase A and along with D121 may be involved in coordinating the conformational exchange motions between loop 4 and the active site. This interaction, mediated by H-bonds is somewhat analogous to the role of the H-bond between T17 and H48 in cluster 1 that results in linking motions from loop 1 to β-sheet 1, which plays a role in the product release step.¹⁸ The current and previous findings highlight how complex and fine-tuned the catalytically important ms motions are in RNase A. At the pH of optimal catalytic activity (pH = 6.4), the rate constant for motions of cluster 1, cluster 2, H119, k_cat, and k_off are identical. A similar merging of distinct ms motions at a specific temperature and pH was also observed in Bile Acid Binding Protein.⁵⁹ At pH < 5.5, the motions of the two clusters and the active site are similar but begin to diverge as the pH is lowered. Under these conditions RNase A displays sub-optimal catalytic activity, yet the rates of the conformational motions increase. A similar phenomenon was observed in Triosephosphate isomerase (TIM) upon insertion of glycine residues at hinge positions in the active-site loop.⁶⁰ In the TIM mutant, active site loop motion was increased yet k_cat was significantly decreased. Those studies implied that the loop kinetics, in particular its closure, was required to occur on a timescale that was similar to the chemical reaction to prevent water from entering the active site. Perhaps a similar synchrony of events is necessary in RNase A. Alternatively, a decrease in pH could slow the chemical steps such that conformational motions become less important to the overall catalytic cycle.

It is not clear what happens to these global motions in RNase A at pH > 8, as backbone amide protons exchange rapidly with solvent, severely hampering NMR experiments under these conditions. X-ray structures reveal no major perturbations to the backbone structure up to pH = 8.8. Based on the current data we speculate that deprotonation of ionizable residues at basic pH values would additionally alter the ms motions in RNase A.

The present data indicate a complex energy landscape in which different regions of the enzyme exhibit distinct pH and temperature dependent alterations in their ms motions. These motions happen to occur with identical kinetics and populations at the pH of maximal catalytic activity. However, the thermodynamics governing their motion diverge under other conditions. The activation enthalpy for cluster 1 increases as pH is lowered whereas it decreases for cluster 2 when the pH is reduced. Likewise the activation entropies for both clusters exhibit opposite pH dependencies. Furthermore, analysis of the Δω values indicate that while cluster 2 undergoes a simple two-site exchange, the motion of cluster 1 is more complex. It is remarkable that the ms motions of two spatially close regions of RNase A are governed by such markedly different thermodynamics. Superimposed on these ms motions are varied ps - ns motions that exhibit diverse temperature dependent dynamics.⁴⁶ In some regions of RNase A, the temperature dependence of these ps - ns motions are quite varied and in others the temperature dependent ps - ns dynamics occur within a narrow range. The multifaceted nature of the motions in RNase A and almost certainly in other enzymes suggests that there remains much to discover about how molecular motions and biological function are coupled.

ABBREVIATIONS

NMR

Nuclear Magnetic Resonance

RNase A

ribonuclease A

MES

2-(N-morpholino)ethanesulfonic acid

DSS

4,4-demethyl-4-silapentane-1-sulfonic acid

CPMG

Carr-Purcell-Meiboom-Gill