Multi-Slice Magnetic Resonance Imaging with the Dynamic Multi-Coil Technique

Abstract

To date, spatial encoding for MRI is based on linear X, Y and Z field gradients generated by dedicated X, Y and Z wire patterns. We recently introduced the Dynamic Multi-Coil Technique (DYNAMITE) for the generation of magnetic field shapes for biomedical MR applications from a set of individually driven localized coils. The benefits for B0 magnetic field homogenization have been shown as well as proof-of-principle of radial and algebraic MRI. In this study the potential of DYNAMITE MRI is explored further and the first multi-slice MRI implementation is presented in which all gradient fields are purely DYNAMITE-based. The obtained image fidelity is shown to be virtually identical to a conventional MRI system with dedicated X, Y and Z gradient coils. Comparable image quality is a milestone towards the establishment of fully functional DYNAMITE MRI (and shim) systems.

INTRODUCTION

Spatial encoding for magnetic resonance imaging (MRI) is traditionally based on magnetic field gradients to induce a linear dependency between spatial position and field amplitude (i.e. Larmor frequency). The applied X, Y and Z gradient shapes are hereby generated by dedicated X, Y and Z wire patterns, respectively. The multi-coil (MC) technique enables the generation of a multitude of magnetic fields relevant to biomedical MR. Low-order spherical harmonic (SH) shapes, including linear field gradients, pose a subsection of the fields that can be realized (1; 2). As such, the MC approach and, moreover, the switched application of MC fields, also referred to as DYNAmic Multi-coIl TEchnique (DYNAMITE), naturally lends itself to spatial encoding and MRI. Proof-of-principle MRI with radial encoding (1; 3) and based on algebraic reconstruction through singular value decomposition (4) have been demonstrated recently. However, full MRI capability and high-level image fidelity have not been shown yet in a systematic fashion. The comparison to standard technology is a must for every new method and an important hurdle to take. The goal of this study was therefore to reproduce all gradient fields of a regular multi-slice MRI sequence with MC-generated fields and to demonstrate that equivalent image fidelity can be achieved with DYNAMITE MRI. The first multi-slice MRI implementation is presented in which all gradient fields throughout the sampled imaging volume are purely MC-based. More importantly, the obtained image fidelity comprising localization accuracy, signal strength and contrast behavior is shown to be virtually identical to conventional MRI relying on dedicated X, Y and Z gradient coils. Comparable image quality is a milestone towards establishing fully functional and purely MC-based MRI (and shim) systems. Integrated MRI and B₀ shim capability with DYNAMITE is expected to allow open MR scanner designs to reduce claustrophobia and anxiety in human subjects, or specific installations such as one-sided MRI of the spinal cord. The extension of low-amplitude gradient capabilities (e.g. from a body coil) with DYNAMITE furthermore has the potential to boost the gradient performance for demanding applications such as diffusion tensor imaging (DTI) or high-resolution anatomical MRI while, at the same time, providing excellent B₀ shim capabilities.

Preliminary results of this work have been published in abstract form (5).

METHODS

Multi-Slice Radial MRI

MRI sequences rely on the serial application of scaled X, Y and Z gradient shapes in combination with well-timed radio-frequency (RF) pulses and intermediate delays (Fig. 1A). In this study, a multi-slice radial MRI sequence was chosen in which axial slices were selected in a spin-echo scheme by frequency selective excitation and refocusing RF pulses in the presence of Z gradient shapes. In-plane radial encoding was based on X and Y gradients and scaled combinations thereof to rotate the resultant projection gradients around the magnet’s iso-center. The goal of this study was to demonstrate that high-level MRI can be achieved with the DYNAMITE approach and that the obtained images are equivalent to those obtained with conventional gradient coils. The established MRI sequence allowed to alternate between the MC technology and the scanner’s gradient system while the overall MRI method (including RF pulses and sequence timing) remained identical for both conditions. As such, MRI properties not related to the gradient performance, such as RF behavior or overall MRI contrast, remained unchanged and the gradient-induced aspects could be isolated for the assessment of the true potential of DYNAMITE MRI.

Fig. 1.

Spin-echo radial MRI with conventional and DYNAMITE gradient encoding. A: Conventional MRI employs a combination of X, Y and Z gradient fields that are generated by dedicated X, Y and Z wire patterns. B: Every effective field shape is optimized individually with DYNAMITE and played out based on a series of TTL trigger signals (gray).

With DYNAMITE, every effective gradient shape was optimized individually and played out in a serial fashion to establish the same MRI sequence (Fig. 1B). Individual field shapes from a matrix of localized coils were combined to produce a target field shape at hand (1; 2) such as Z-gradients for slice-selection or oblique gradients for radial in-plane encoding. Any MC field generation potentially involved all available channels of the MC array and, in principle, the number of field traces of the MR sequence equaled the number of coils (e.g. 48). Such MC visualization, however, would be neither helpful nor intuitive due to the large number of channels and, more importantly, as individual basis fields have limited meaning with the use of non-orthogonal basis field shapes (1; 2). Instead, X, Y and Z gradient directions were collapsed to a single MC trace for presentation purposes (Fig. 1B). Note that the gradient orientation is no longer immediately visible with that convention. In practice, the DYNAMITE field shapes were initiated and played out in a serial fashion based on properly spaced TTL trigger signals generated by the MR scanner’s sequence controller, thereby synchronizing the gradient waveforms with the RF pulse shapes and the acquisition system (gray trace).

The standard radial MRI sequence employed a series of rotating read-out gradients with one of the two gradient systems, i.e. conventional or DYNAMITE, in an equiangular fashion between 0 and 180°·(N-1)/N to encode the sample magnetization for the slice at hand with a set of N projections (Fig. 2A). The resultant raw data matrix therefore contained one k-space and one angular dimension (Fig. 2B). Data processing relied on one-dimensional Fourier transformation to convert the k-space in a spatial dimension (Fig. 2C). The resultant set of magnitude intensity profiles is referred to as a sinogram and provides an intuitive intermediate means of the radial image reconstruction (6). Finally, the full MRI consisting of two spatial dimensions was obtained by inverse Radon transform (7) of the sinogram’s angular dimension (Fig. 2D). Standard (low-pass) Shepp-Logan filtering and linear interpolation were employed with the backprojection.

Fig. 2.

Encoding and processing of radial MRI. A: A series of rotating gradient fields spanning an angle range between 0 and 180°·(N-1)/N are applied to encode the subject magnetization in N radial projections. B: The resultant raw data matrix contains one spatial (k-space) and one angular dimension. C: One-dimensional Fourier analysis along the spatial dimension leads to a set of intensity projections (sinograms). D: The 2-dimensional MRI is finally obtained by inverse Radon transform.

Global versus Local Generation of Gradient Fields

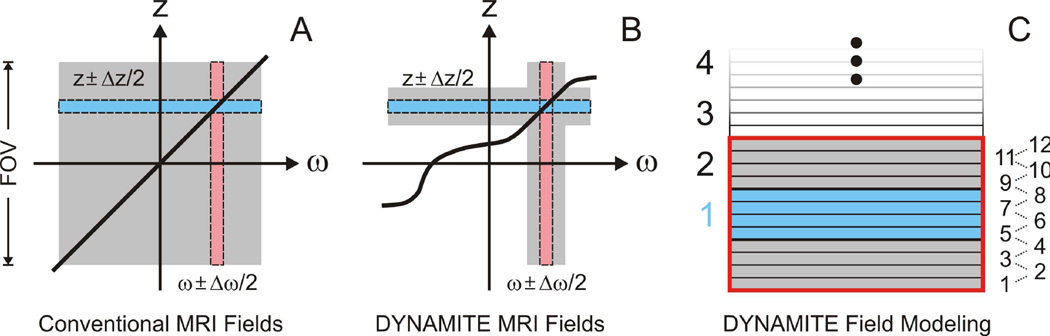
Conventional gradient coils are designed to provide accurate field shapes over a predefined spatial range that is chosen large enough to include the range of targeted subject dimensions and placement variations. Examples of this concept include a ‘diameter spherical volume’ (DSV) covering a third of the coil diameter (8) or a cylindrical volume that spans 54% of both the coil’s diameter and length (9). Once the gradient coil is built, the magnetic field amplitude is a simple linear function of the applied coil current and independent of the considered field-of-view (FOV) or regions-of-interest therein (Fig. 3A, gray). The excitation of a selected axial slice (blue) of a given thickness and position, for instance, is then achieved by a dedicated combination of a Z gradient (tilted black line) and an RF pulse of the appropriate frequency bandwidth and offset (pink). Different slice positions can be easily realized by shifting the carrier frequency of the RF pulse. As such, stacks of slices, e.g. for multi-slice MRI, typically rely on an array of otherwise identical RF pulses at equally spaced offsets.

Fig. 3.

Design and application of DYNAMITE gradient fields. A: Conventional gradient coils generate the desired field shape (black line) over large volumes including the FOV at hand (gray). The combination of a frequency-selective RF pulse with a bandwidth Δω and a center frequency ω (pink) and a Z gradient of given strength (i.e. slope) then selects a slice of thickness Δz at position z (blue). B: MC field modeling allows to optimize magnetic field shapes for individual parts of the FOV. For every slice (blue), regionally accurate field shapes were provided in slabs including the slice at hand (gray + blue). C: DYNAMITE fields for slice-selection and in-plane radial encoding were optimized over volumes covering three times the targeted slice (gray + blue = red box). This volume was subdivided into a grid of 12 virtual slices to assure the correct 3-dimensional behavior.

While convenient, gradient fields for multi-slice MRI do not need to be accurate over large parts of the scanner bore. In fact, the selective excitation of a specific slice volume only requires the accurate definition of singleton frequencies at its boundaries (Fig. 3B). As such, any regionally accurate magnetic that fulfills this condition over the transition zone of the slice at hand and its surrounding can be combined with a frequency-selective RF pulse to discriminate both volumes. Magnetic fields for spatial selection do not even have to be linear and, in principle, any shape can be used as long as the range of field values remains unique inside versus outside the selected slice to avoid back-folding. Note that the latter condition does not only comprise the immediate FOV of the MRI experiment, but includes the entire sensitive area of the RF coil. Similarly, while gradient fields for in-plane spatial encoding have to be as accurate as possible over the FOV, simple uniqueness is sufficient for the intersection of slice areas outside the (in-plane) FOV and the sensitive volume of the RF coil.

The MC approach allows the synthesis of magnetic field shapes in selected volumes and the flexible trade of field accuracy for gradient strength (1; 2). We employed these principles along with above considerations to establish multi-slice MRI based on magnetic gradient fields that were purely MC-generated. More specifically, regionally accurate copies of all gradient fields of a multi-slice MRI sequence were generated with DYNAMITE to establish equivalent imaging capabilities (Fig. 2B). While DYNAMITE fields resembled the gradient fields only locally, the same RF pulses selected the exact same physical slices. Note that such slice-specific approach is not possible with conventional gradient coils. In a recent paper, we discuss MC magnetic field shaping and possible optimization strategies in detail (2). Important for our study here is the finding that linear gradient fields can be generated by a basic MC array at small errors and efficiencies in the same order of magnitude of dedicated X, Y and Z gradient coils, thereby allowing MRI applications.

MR Scanner, Multi-Coil Setup and MRI Sequence

Experiments were performed on a 9.4 Tesla magnet (Magnex Scientific, Oxford, UK) that was equipped with a BFG-150/90–750-S gradient and shim system (Resonance Research Inc, Billerica, MA) interfaced to a Varian Direct Drive spectrometer and operated with VnmrJ 2.3A software (Varian Inc, Palo Alto, CA). A multi-slice radial MRI sequence was implemented that was capable of using the scanner’s gradient system (rise time 180 µs) or DYNAMITE hardware (rise time 10 µs) for the generation of gradient fields for spatial encoding. Background B₀ magnetic field inhomogeneity was corrected with static SH homogenization up to the third order with the scanner’s shim system for both conventional and DYNAMITE MRI. For DYNAMITE, a MC setup was used that had been designed for B₀ field shimming in the mouse brain (10) and applied for the first DYNAMITE MRI implementations (1; 3; 4). In essence, 48 individually-driven, localized coils were arranged in 6 rows of 8 coils (coil diameter 13 mm, 30 turns, OD 35 mm, ID 29 mm) inside a cylindrical former (Fig. 4A). A shielded custom-built Bolinger RF coil was placed inside the MC array for spin handling and signal reception (OD 26 mm, ID 17 mm, Fig. 4B). Note that this basic setup was enough to provide the DYNAMITE imaging capability described in this study.

Fig. 4.

Multi-coil setup for DYNAMITE MRI. A: All spatial encoding fields for MRI are generated by a matrix of 48 circular, individual coils arranged in 6 rows of 8 coils and placed inside a cylindrical acrylic former. B: Combination with a Bollinger RF coil and placement inside a 9.4 Tesla small animal scanner allowed to establish a fully functional DYNAMITE MRI system.

Design and Implementation of DYNAMITE Fields

Given the overall dimensions of the employed MC setup, an example radial MRI protocol was defined that employed 11 slices, 96 angle steps for radial in-plane encoding of a centered 12×12×11 mm³ FOV, along with 12-ms echo time and 2.5 s repetition time for T2*-weighted tissue contrast. In a next step, the average error of every DYNAMITE field was requested to remain below 1%. Field simulations were then performed with customized Matlab software (MathWorks, Natick/MA) in a slice-specific fashion for all gradient fields of the MRI sequence to be employed for slice selection and radial encoding. The computations were based on experimental calibration fields of the MC setup at hand and considered the ±1 A limit per coil to assure experimental feasibility. More specifically, the targeted field gradient for a given slice (Fig. 3C, blue, 1 mm) was optimized over a slab that was tripled in thickness (blue + gray = red box, 3 mm) at a four-fold refined spatial grid (0.25 mm vs. 1 mm), i.e. at a total of 12 virtual sub-slices per optimization volume. As such, intra-slice field components were considered and the larger scale field behavior was taken into account. The latter was particularly relevant for the slice-selection gradients to differentiate the volume of the slice itself from its surroundings and to synthesize true regional copies for all gradient fields at hand. A 30 kHz/cm (7 G/cm) amplitude was found to be within the technical limits throughout the stack of slices. For simplicity, this gradient amplitude was chosen for both slice selection and in-plane radial encoding in this study. Shinnar-Le Roux RF pulses (2 ms duration, band width 3 kHz) were applied to selectively excite and refocus the 1-mm slices. The 12-mm in-plane FOV resulted in a MRI acquisition bandwidth of 36 kHz.

Once the theoretical experiment design was completed, a set of 48 DYNAMITE currents was calculated ahead of time for the considered 1067 field scenarios corresponding to 11 slice selection gradients plus 96 slice-specific radial encoding steps (total computation time 5 hours). They were uploaded to the MC amplifier unit as described previously (1). For DYNAMITE MRI, ten TTL trigger events were used per sequence trace (i.e. repetition time, Fig. 1B, TTL) and a total of 96·10=960 TTL switches were necessary to fully select and spatially encode an individual MRI slice. Consequently, the complete multi-slice MRI sequence consisted of a total of 960·11=10560 events. The same processing was applied to the data acquired with both conventional gradient coils and DYNAMITE to assure comparability of the results.

RESULTS

Phantom Evaluation

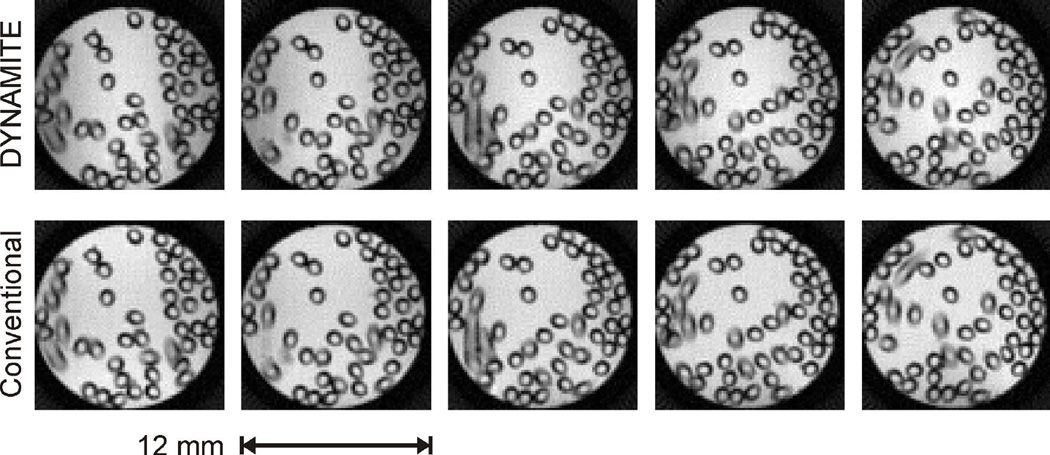
DYNAMITE MRI was first tested and evaluated in a resolution phantom. To this end, an infusion capillary (Becton Dickinson Inc, ID 0.58 mm, OD 0.97 mm) was filled with water, folded many times and placed inside a water-filled cylindrical tube (ID 12 mm). DYNAMITE field modeling was able to provide physical copies of all field gradients required for multi-slice MRI. The DYNAMITE-based slice profiles resemble those obtained with conventional gradients with high accuracy up to the maximum slice offset employed in this work (Appendix A). Note that the slice-specific synthesis of regionally accurate gradient fields with DYNAMITE (compare figure 3) is characterized by a complete lack of spurious signal outside the selected slice similar to conventional gradient fields that are applied globally. Radial encoding with DYNAMTE provided images that were virtually identical to those acquired with the scanner’s conventional gradient system (Figs. 5). More specifically, images had the correct FOV, orientation, homogeneous intra-slice spacing and were free of artifacts that could be attributed to the DYNAMITE encoding. The overall image quality, consisting of signal strength and contrast behavior, was also comparable to conventional MRI. Note that even the partial volume effects of capillaries penetrating individual slices in an oblique fashion were identical, confirming that both slice position and thickness accurately resembled the geometry of conventional MRI to a precision level well below 1 mm.

Appendix A (Fig. 9).

Comparison of slice selection provided by the scanner’s built-in gradient system (A) and the MC approach (B). The DYNAMITE-based slice profiles resemble those obtained with conventional gradients with high accuracy from the isocenter up to the maximum FOV employed for multi-slice MRI in this work. Note that the slice-specific synthesis of regionally accurate gradient fields with DYNAMITE (compare figure 3) is characterized by a complete lack of spurious signal outside the selected slice similar to conventional gradient fields that are applied globally.

Fig. 5.

Phantom evaluation of DYNAMITE MRI. The images obtained from a customized resolution phantom (water-filled tube and folded infusion line) by multi-slice DYNAMITE MRI (upper row) are virtually identical to those that employed the MR system’s conventional gradient system (lower row) and the otherwise identical MRI sequence.

Anatomical MRI

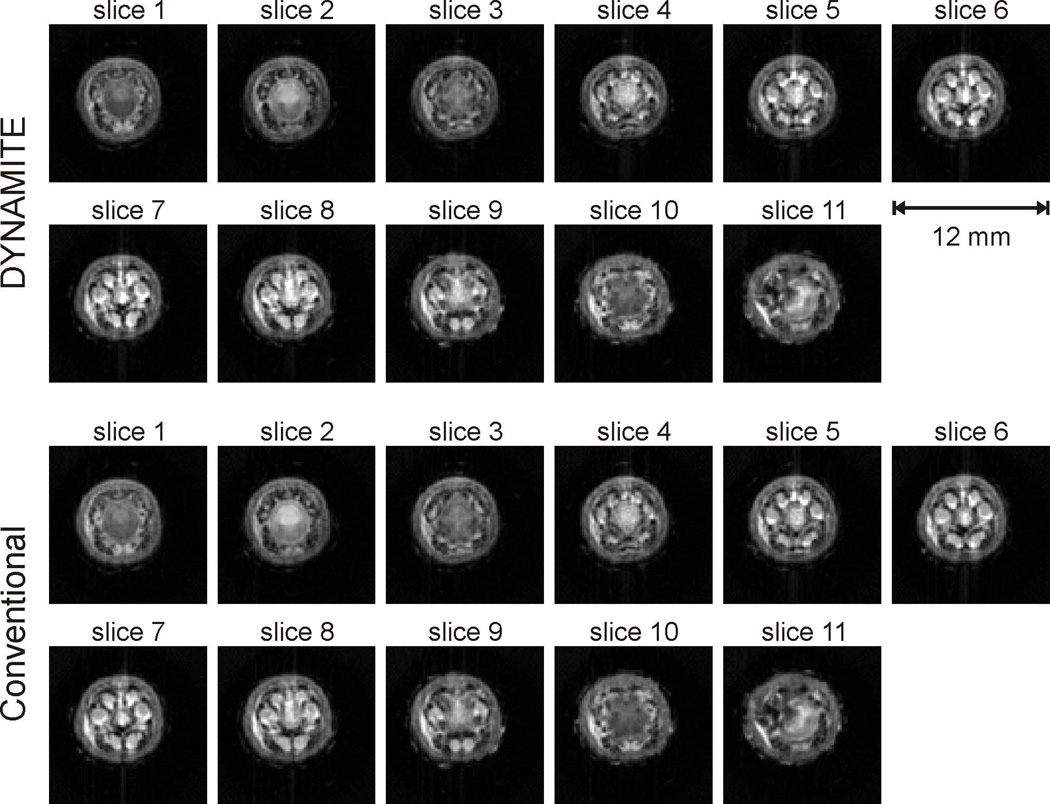
MRI of anatomical structures does not only require accurate spatial encoding, but also relies on meaningful tissue contrast. In order to test the contrast behavior of DYNAMITE MRI, we imaged a tail and a foot of a rat as both anatomical structures contain a diverse mixture of muscle, fat, skin, bone, cartilage, ligaments and blood vessels. DYNAMITE MRI obtained from an ex vivo foot of a rat appeared virtually identical to reference images that were acquired at identical parameter settings with the scanner’s built-in X, Y and Z gradient coils (Fig. 6, selected slices throughout the FOV, all slices in Appendix B). A high degree of spatial accuracy is achieved with DYNAMITE that manifests itself in both slice-selection and radial, i.e. in-plane, encoding. In line with the phantom evaluation (Fig. 5), even partial volume effects of small anatomical structures within individual slices share the identical appearance (e.g. white arrow) and thereby imply a spatial specificity of the DYNAMITE field generation that exceeds the employed 1-mm slice dimensions.

Fig. 6.

Multi-slice DYNAMITE MRI (upper row) provided virtually identical image fidelity for imaging a foot of a rat compared to conventional MRI (lower row) that was based on the scanner’s set of X, Y and Z gradient coils. (for all slices: compare Appendix B)

Appendix B (Fig. 10).

Complete comparison of the DYNAMITE and conventional gradient encoding for multi-slice MRI of an ex vivo rat foot. (compare figure 6)

We have shown high-quality MRI that indirectly indicates a high-accuracy of the employed gradient fields. Previous work has demonstrated directly and quantitatively that DYNAMITE fields can be generated in a very accurate and predictable fashion. In addition, straight-forward encoding and reconstruction has been applied in this study for a transparent comparison of DYNAMITE and conventional MRI. More importantly, the equivalence of the employed gradient fields can also be directly appreciated from the sinograms. They represent an intermediate step of the processing chain that allows an unobstructed and intuitive view on individual projections before they are combined by the inverse Radon transform (compare Fig. 2). The close resemblance of the sinograms obtained with DYNAMITE and conventional field gradients (Fig. 8, rat foot) demonstrates that the high-level MRI similarity is not due to specific properties of the radial encoding or processing, but a direct consequence of largely equivalent raw data due to accurate DYNAMITE gradient fields.

Fig. 8.

Multi-slice DYNAMITE images (upper row) of a rat tail are largely identical to conventional MRI (lower row) based on the scanner’s set of X, Y and Z gradient coils. (for all slices: compare Appendix C)

MR images of an ex vivo rat tail acquired at identical parameter settings with DYNAMITE and the scanner’s built-in X, Y and Z gradient coils are largely identical (Fig. 8, selected slices throughout the FOV, all slices in Appendix C, difference map in Appendix D). With DYNAMITE MRI, a high degree of spatial accuracy is achieved as well as identical contrast behavior. The distinct tissue contrast (along with the recurring vertebra structure and the symmetry of the rat tail) allow a clear identification of anatomical structures similar to (11).

Appendix C (Fig. 11).

Complete comparison of the DYNAMITE and conventional gradient encoding for multi-slice MRI of an ex vivo rat tail. (compare figure 6)

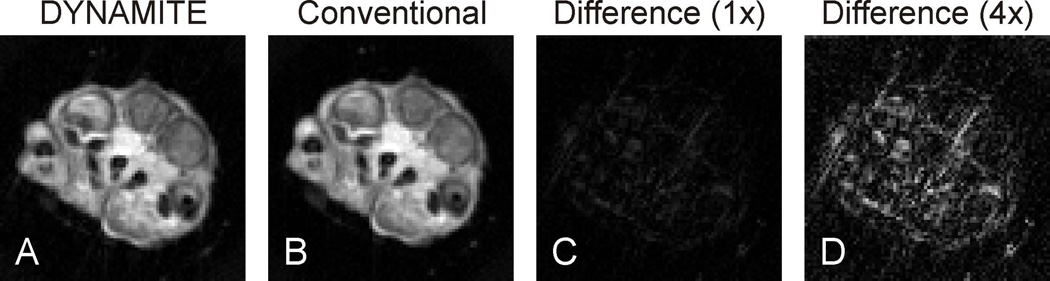
Appendix D (Fig. 12).

Example analysis of MRI of a rat foot acquired with DYNAMITE (A) and the scanner’s built-in gradient coils (B). The deviation between the two images is expressed as magnitude difference at the original MRI scaling (C) and with four-fold amplification (D).

DISCUSSION

This study aimed at realizing a physical copy of a conventional MRI sequence and to demonstrate identical MRI outcome. To this end, the decision was made to synthesize DYNAMITE fields that were regionally accurate for the specific application at hand, i.e. slice selection or in-plane radial encoding. The optimization of selection field shapes along with the corresponding RF pulses has not been intended here. While not applied in this study, the ability of DYNAMITE to tailor magnetic field shapes to a selected region at hand bears the potential to further improve individual characteristics of the slice selection fields, e.g. the generation efficiency. For instance, amplitude offsets at off-center positions are inherent to gradient fields generated by conventional coils and require a corresponding array of RF offsets for slice-selection. The gradient strength, however, solely relies on the change in field amplitude per unit length. A stack of slices can therefore also be selected with an array of offset-free DYNAMITE gradient fields at individual slice positions in combination with an (identical) on-resonance, frequency-selective RF pulse. Note that the generation of strong gradient fields required the MC channels to overlap in a largely constructive fashion, e.g. as opposed to certain B₀ shim applications (10). In practice, the uniqueness of field terms was therefore easily achieved in this study even far outside the immediate FOV for MRI without specific measures. Identical sequence timing was used for DYNAMITE and conventional gradient encoding to ensure comparable signal and contrast behavior. The problem of largely varying switching times of the gradient system (180 µs) and the current DYNAMITE installation (10 µs) was overcome by delaying the onset of DYNAMITE fields by 85 µs relative to the onset of gradient ramps generated by scanner’s gradient system (and vice versa for declining ramps) to maintain both the gradient’s moment as well as its effective timing within the MR sequence (compare Fig. 1B).

An acquisition bandwidth of 36 kHz was employed in this study and allowed MRI, but higher bandwidths might be desirable to minimize the effects of limited B₀ homogeneity. The bandwidth was limited by the maximum gradient strength that could be generated with the MC amplifier system (dynamic range ±1 A per channel) and MC setup at hand (10). The MC field modeling approach allows one to trade shape accuracy for gradient efficiency (2). Stronger peak gradient amplitudes and higher imaging bandwidths can therefore be realized if some shape imperfections are accepted. Once the field synthesis is truly amplitude-limited, the desired field amplitude is no longer reached which manifests itself as FOV increase or, alternatively, an apparent shrinkage of the object under investigation (3). As such, accurate FOV as demonstrated here provides compelling evidence that the correct absolute gradient strengths (in kHz/cm) were synthesized. MC field amplitudes can be significantly increased when stronger, readily available amplifiers are applied or coils with more turns are used. For instance, a 100 kHz bandwidth can be realized if the employed 1 A amplifiers are replaced by equivalent 3 A models. Together, these approaches should eliminate the problem of limited amplitude strength and imaging bandwidth in future implementations of DYNAMITE MRI in small animal setups.

We have shown in recent theoretical work (2) that DYNAMITE is capable of providing a repertoire of magnetic field gradients at generation efficiencies and gradient amplitudes suitable for MRI. In the same vein, Z and rotating X-Y gradient shapes have been generated in a series of slice-specific planar slabs in this study to assemble a 3-dimensional imaging volume. The concatenation of these fields allowed us to establish a full MRI sequence scheme and thereby the indirect experimental validation of above theoretical work. DYNAMITE describes a general field modeling approach for the generation of arbitrary field shapes in arbitrary regions-of-interest. In this study, a multi-slice MRI sequence with axial slice orientation was chosen, however, other slice orientations are expect to be equally possible (2). Radial MRI was applied in this study, but other MR sequences are expected to be equally possible. In fact, phase encoding gradients for Fourier reconstruction require only a subset of the field shapes employed here. The DYNAMITE approach is best suited for region-specific applications and therefore multi-slice MRI was chosen as opposed to 3-dimensional MRI that relies on multiple phase encoding dimensions and therefore impedes the dynamic gradient approach applied here (Fig. 3B/C). MC magnetic field modeling is capable of providing accurate magnetic field shapes in larger volumes, however, at a progressively reduced efficiency of the field generation (2).

All encoding fields were computed ahead of time and no further processing was necessary during the experimental sessions. The inhomogeneity of the background B₀ magnetic field was mitigated through static third order SH shimming for both conventional and DYNAMITE MRI. The benefits of the DYNAMITE for B₀ shimming have been shown in the mouse (10), the rat (12) and human (13; 14) brain. The establishment of an integrated DYNAMITE approach comprising combined MRI encoding and B₀ shim fields is the next logical step and currently being pursued in our laboratory. The consideration of the B₀ conditions for the study subject at hand is straightforward, but demands the tailored calculation of all MC fields for the superposition of individual gradient fields for MRI and required B₀ shim fields during the MR session. Note that the reservation of parts of the dynamic amplifier range to MRI only and B₀ shimming only allows one to compute the MRI gradient fields ahead of time and only the B₀ shim fields need to be processed (and added) during the session. While the latter approach reduces the computational burden during experimental sessions, it is not necessarily ideal as both the field shaping capability and the field generation efficiency might be compromised. These disadvantages are avoided, if the effective field shape to be generated, i.e. the sum of a gradient and a B₀ shim field, is modeled directly employing the full dynamic range of available amplifier currents.

The multi-coil field processing in this study was aimed at providing accurate fields for MRI. It was not optimized for speed and the resultant 5-hour processing time practically impedes changes of the MRI geometry during experimental sessions with this first implementation. However, all computations are truly independent and therefore natural candidates for parallel processing strategies. We also expect significant gains in processing speed by simplification of the computational problem including a reduction of the geometric grid size, the initialization of the regularization problems for a given radial gradient field with current settings from neighboring projections and maybe even the interpolation of intermediate projections from neighboring trajectories. Such optimization of the MC processing speed is necessary to provide larger flexibility during experimental and, more importantly, to pave the way for a fully integrated application of MRI, B₀ shimming and specialized applications (e.g. (15)) in the future. The established DYNAMITE MRI methods are furthermore expected to provide a powerful theoretical and experimental framework for the exploration of non-linear MRI applications (4; 16–20).

The demonstration of image fidelity comparable to standard technology is a necessity for any novel method and an important hurdle to take. In this study, a fully functional MRI system based on DYNAMITE rather than conventional gradient coils has been presented. To the best of our knowledge, this is the first high-level MR imaging system that does not rely on dedicated wire patterns for the generation of individual SH shapes, but employs as set of local coils. Linear field gradients, i.e. first order SH shapes, are synthesized individually with the MC approach for individual gradient shapes of the MRI sequence. The demonstration of DYNAMITE MRI is a milestone towards the establishment of flexible MRI solutions. With the gains for shimming in both performance and efficiency (2; 10; 12–14), the MC technology has the potential to complement or substitute SH coil systems for special applications. Dedicated DYNAMITE installations with MRI and B₀ shim capability are expected to facilitate open scanner designs and to thereby help to reduce claustrophobia and anxiety in human studies. The extension of low-amplitude gradient systems (e.g. body coils) with DYNAMITE technology furthermore promises a boost in gradient performance for demanding applications such as DTI of the brain or high-resolution anatomical MRI of the spinal cord while, at the same time, providing excellent B₀ shim capabilities.

Fig. 7.

Sinograms of a rat foot. Example intensity projections obtained with DYNAMITE and conventional gradient coils for the radial encoding of an ex vivo rat foot (compare Fig. 6) are largely identical, thereby demonstrating the physical equivalence of the underlying gradient fields.

Abbreviations

MC

multi-coil

DYNAMITE

dynamic multi-coil technique

SH

spherical harmonic

TTL

transistor-transistor logic