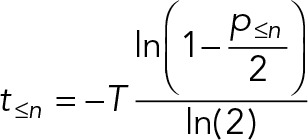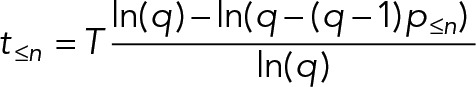Analyzing the dynamics of cell cycle processes from fixed samples through ergodic principles

Abstract

Tools to analyze cyclical cellular processes, particularly the cell cycle, are of broad value for cell biology. Cell cycle synchronization and live-cell time-lapse observation are widely used to analyze these processes but are not available for many systems. Simple mathematical methods built on the ergodic principle are a well-established, widely applicable, and powerful alternative analysis approach, although they are less widely used. These methods extract data about the dynamics of a cyclical process from a single time-point “snapshot” of a population of cells progressing through the cycle asynchronously. Here, I demonstrate application of these simple mathematical methods to analysis of basic cyclical processes—cycles including a division event, cell populations undergoing unicellular aging, and cell cycles with multiple fission (schizogony)—as well as recent advances that allow detailed mapping of the cell cycle from continuously changing properties of the cell such as size and DNA content. This includes examples using existing data from mammalian, yeast, and unicellular eukaryotic parasite cell biology. Through the ongoing advances in high-throughput cell analysis by light microscopy, electron microscopy, and flow cytometry, these mathematical methods are becoming ever more important and are a powerful complementary method to traditional synchronization and time-lapse cell cycle analysis methods.

INTRODUCTION

Cyclical cellular processes, particularly the cell cycle, are central to cell biology. Three major methods are used to analyze these processes: 1) analysis of individual cells over time (time-lapse analysis), 2) analysis of synchronized populations of cells over time, and, less commonly, 3) use of mathematical methods to extract dynamic data from a single time point of an asynchronous population (Mitchison, 1971). Each of these methods has particular advantages, and all three can be applied to any cyclical cellular process, not just the cell cycle.

There are many situations in which live-cell observation is impractical or impossible, as cells must remain confined and viable for a long period of time. Destructive analysis when tracking individual cells over time is not possible, preventing fixation for electron micro­scopy, immunofluorescence, flow cytometry, or techniques such as single-cell sequencing (Eberwine et al., 2014). Analysis of synchronized populations of cells comes with limitations, as environmental (Scherbaum and Zeuthen, 1954; Williamson and Scopes, 1961) or chemical (Xeros, 1962; Stubblefield and Klevecz, 1965; Chowdhury et al., 2008) synchronization treatments may have complex side-effects or simply not have been developed for that system. Synchronized populations achieved through purification of cells at a single cell cycle stage (Johnston and Johnson, 1997; Kabani et al., 2010; Archer et al., 2011) often rapidly loose synchrony.

An asynchronous population contains cells at all stages of a cycle, and so it contains all the data need to analyze that cycle. Mathematical analyses of cyclical processes from an asynchronous population are simple and well established (Mitchison, 1971) and provide a complementary set of tools for cell cycle analysis. This approach does not require exogenous synchronization treatments or tracking of individual cells over time, and destructive imaging/biochemical techniques can be used. Furthermore, the dynamics of an entire cyclical process can be determined from a single sample rather than a time series. However, some previous understanding of the cycle is required, as the order of events cannot always be determined ab initio from the single sample.

This type of mathematical analyses of asynchronous populations can collectively be termed ergodic analysis (Kafri et al., 2013). Although basic applications are well established, there have been recent powerful advances in this type of approach. This review focuses on providing an intuitive understanding of the concepts of ergodic analysis on an example-by-example basis, from basic concepts to practical experimental analysis, and the opportunities the latest developments confer.

OSCILLATIONS AND CYCLES

Oscillatory systems (a two-state cycle) concisely demonstrate the concept of ergodic analysis. For example, Escherichia coli oscillates between swimming and tumbling modes of movement (Berg, 2004), and from a short videomicrograph, the proportion of cells undergoing each form of motion can be determined. Intuitively, a larger proportion of cells undergoing a particular form of motility correspond to a larger time spent by cells in that state. This conclusion is valid only when the cells do not undergo the behaviors in synchrony; synchronization from the environment (as in the swimming response of Euglena gracillis to light; Diehn et al., 1975) or autosynchronization (as in cardiomyocyte contraction; Viatchenko-Karpinski et al., 1999) break this correspondence. If the process moving the cells between different states is cyclical, regular, and of a known length, then the proportion of cells in each successive cycle stage corresponds to the timings of the progression of cells through these stages.

These requirements can be formally stated as weak and strong ergodic assumptions (Box 1). If these assumptions are correct, then the time a cell spends in each cycle stage is simply the proportion in that state multiplied by the cycle length (Box 2, Eq. 1). In an experimental system, it is rare that the strong ergodic assumption can be completely met, due to cell-to-cell biological variability, with ergodic analysis giving the average cell behavior. However, the more closely the strong ergodic assumption can be met, then the more closely will the average behavior of the population of cells match the behavior of any single cell.

Box 1.

The weak ergodic assumption:

If the distribution of cells among different states does not change over time, then the proportion observed in any state is proportional to the time each cell spends, on average, in that state.

Strong ergodic assumption:

If all cells are going through an identical cycle of events, then the proportion of cells in any cycle stage observed in the population at a single time point is the same as the proportion of time spent in cycle stage as a single cell progresses through the cycle.

Box 2.

If the ergodic assumptions are met, the timings of a series of stage-to-stage transitions in a cyclical process can be calculated using the following equations (derivations shown in the Supplemental Appendix).

For cycles with no offspring (cycles not linked with division events), (1) where t≤n is the time spent in stages up to and including stage n of the cycle, T is the time taken for one complete cycle, and p≤n is the proportion of cells observed in stages up to and including stage n of the cycle.

For cycles with two offspring (binary fission), (2)

For cycles with an arbitrary number of proliferative offspring (multiple fission, or a chance of terminal differentiation), (3) where q is the number of proliferative offspring per division.

For ergodic analyses based on classification of cells based on discrete features, p≤n is the proportion of cells that match the required features for that stage or any earlier stage of the cycle.

For ergodic analyses based on continuously varying features of cells, p≤n = r/k, where r is the rank position of that cell through the cycle and k is the total number of cells measured. Any set of continuously varying features, selected based on previous knowledge of the cycle, can be used to determine the rank position of the cell through the cycle.

CELL CYCLES

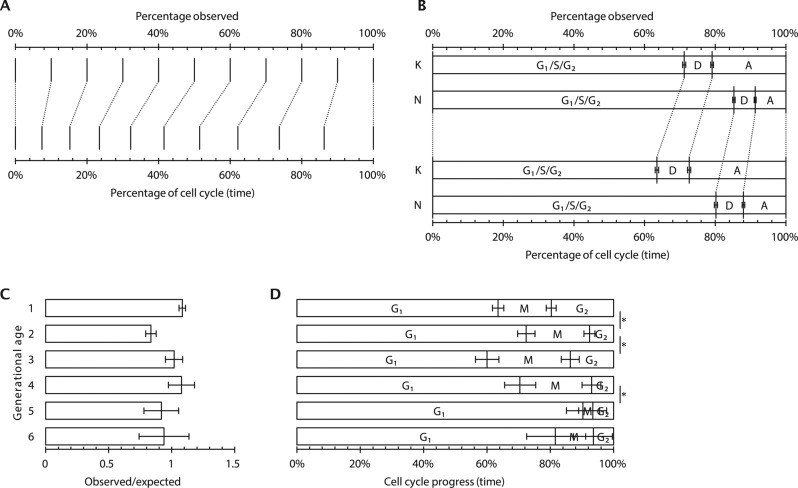
The most widely analyzed cyclical process is the proliferative cell cycle. Intuitively, it might be thought that (in an asynchronous population) the proportion of cells in a cell cycle stage is proportional to the time spent during that stage of the cell cycle. However, during division, a cell typically generates two proliferating daughters, leading to twice as many cells immediately after division as immediately before it. This bias leads to a higher occurrence of early cell cycle stages in a snapshot of an asynchronous culture. Overrepresentation of early cell cycle stages has well-established mathematical descriptions (Mitchison, 1971; Williams, 1971; Box 2, Eq. 2), which can be illustrated graphically (Figure 1A). To apply the equation, a measurement of the proportion of cells up to and including a cell cycle stage (based on some classification criteria, such as DNA content to identify G₁ and S phase) and the cell cycle length (the doubling time) are required. The time taken to reach that transition between them can then be calculated. The time taken to reach each of several cell cycle stages can be calculated for a more complete picture.

FIGURE 1:

Application of ergodic analysis to find cell cycle timings from discrete cell properties. (A) Graphical representation of the correspondence between the proportion of cells observed up to and including an arbitrary cell cycle stage and the corresponding time through the cell cycle. (B) Application of the relationship in A as used to analyze the T. brucei cell cycle. The proportions of cells with a single (G₁/S/G₂) dividing (D) or duplicated (A) kinetoplast (K) or nucleus (N) are shown (Gull et al., 1990; Woodward and Gull, 1990). (C) The proportion of S288C S. cerevisiae cells of different ages seen in exponential liquid-phase culture (Hagiwara et al., 2011) relative to the expected proportion assuming no cellular senescence. (D) Relative time spent in different stages of the cell cycle for the cells of different ages shown in C. Significant changes from the cell cycle timings of the previous generation (p < 0.05, chi-squared test) are indicated with an asterisk.

This simple and powerful technique was used for the earliest quantifications of timing and rate of DNA synthesis during S phase, derived from the proportion of cells in asynchronous exponential culture that had incorporated [³H]thymidine into DNA (Stanners and Till, 1960). More recently, it allowed the analysis of the cell cycle of the trypansomatids (Gull et al., 1990; Woodward and Gull, 1990; Elias et al., 2007; Ambit et al., 2011; Wheeler et al., 2011; Figure 1B), unicellular protist parasites for which techniques for cell cycle synchronization are not efficient and cells are highly motile, making time-lapse microscopy impossible.

Analysis of the cell cycle by this method is subject to the two requirements of an ergodic analysis: progression through the cell cycle analyzed must be completely asynchronous, and every cell must be progressing through the same cell cycle at the same rate. In practice, these requirements can be confirmed by showing that population growth is smoothly exponential, showing that the same result is obtained by analyzing a later time point/higher culture density, and ensuring that there is no quiescent population or cell death (Stanners and Till, 1960; Wheeler et al., 2011; Kafri et al., 2013).

This approach is applicable to the analysis of the cell cycle of any cell that generates two proliferative daughters. Any feature of cells that can be used to classify them into particular cell cycle stages, including DNA content, levels of particular cyclins, cell size, and so on, can be used as the basis for this type of analysis. It is also applicable to any other biological structure within a cell that undergoes replication by binary fission, parent organelle–templated formation, or ab initio assembly through standard intermediates.

Not all cell divisions generate two proliferative daughters. Generation of terminally differentiated cells in metazoans involves division of a stem cell to generate one nonproliferative daughter (often associated with the daughter centriole; Wilson, 2008; Nigg and Stearns, 2011; Pelletier and Yamashita, 2012). In some organisms, most famously Plasmodium parasites (Arnot and Gull, 1998; Bannister et al., 2000; Gerald et al., 2011; Francia and Striepen, 2014), multiple rounds of mitosis are followed by multiple fission (schizogony). In these situations, overrepresentation of early cell cycle stages requires a different correction (Box 2, Eq. 3), with a factor q that represents the number of proliferative offspring from the division. For example, for a proliferating stem cell with a 70% chance of generating one nonproliferative daughter, q = 2 − 0.7 = 1.3, whereas for schizogenous division in Plasmodium with 20 offspring, q = 20.

CELLULAR SENESCENCE

Some experimental systems allow the separate analysis of the two progeny of a division event; for example, in Saccharomyces cerevisiae, division leaves a bud scar on the cell wall of one daughter cell, these accumulate over multiple divisions, and this “older” daughter divides more slowly (Steinkraus et al., 2008). This deviation from uniform cell cycle behavior across the population breaks the strong ergodic assumption, meaning that any ergodic analysis will represent only an average cell cycle. The ability to test whether the population of cells is undergoing this form of unicellular aging is therefore important. The expected proportion of cells p_n that have been through n divisions is p_n = 2^–n when there is no difference in cell cycle length between the daughter cells.

Any deviation from this value indicates that the population does not have the uniform behavior required for the strong ergodic assumption. Data on the proportion of cells with different numbers of bud scars in liquid-phase culture of S. cerevisiae S288C cells illustrate this issue (Hagiwara et al., 2011; Figure 1C). Although deviation from uniform cell cycle length prevents the accurate analysis of the entire asynchronous population by ergodic principles, the behavior of a subpopulation of a single age still meets the strong ergodic assumption. The cell cycle and how it changes with cell age can therefore be analyzed, manifesting as changes in the duration, as a fraction of the cell cycle, of G₁, S, and G₂ for cells of different ages (Figure 1D).

Decreased capacity to divide during “aging” of unicellular organisms is conceptually similar to systems in multicellular organisms for homeostasis of a tissue with asymmetric division of stem cells to generate fully or partially differentiated daughter cells, an important and growing field (Anderson and Stearns, 2009; Arquint et al., 2014). This type of analysis is applicable to both.

FROM DISCRETE EVENTS TO CONTINUOUS VARIABLES

The foregoing examples concern discrete classification of cells—whether swimming or tumbling, in G₁ or S phase, and so on. This fails to capture many of the types of change a cell undergoes, which include continuously varying properties such as mass, volume, length, DNA content, and protein activity or quantity. Ergodic analysis in multiplying populations to analyze continuous variables is a well-established concept, particularly in the analysis of human populations (Inaba, 1989), but is a recent development for quantitative cell biology (Wheeler et al., 2011; Kafri et al., 2013).

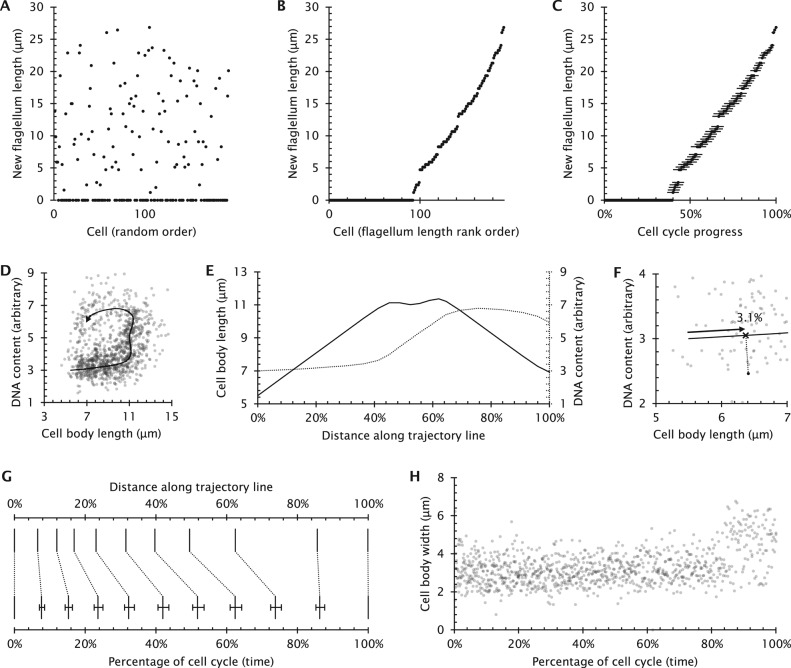
An example of a continuously varying property is the length of a flagellum. Flagella often undergo well-regulated growth linked with the cell cycle, seen in systems including the metazoan primary cilium (Seeley and Nachury, 2010), Trypanosoma flagella (Gull et al., 1990; Tyler et al., 2001), Leishmania flagella (Wheeler et al., 2011), and Chlamydomonas flagella (Cavalier-Smith, 1974; Tuxhorn et al., 1998). The flagellum of Trypanosoma brucei is particularly amenable to analysis, as the single flagellum, once formed, never disassembles. A single new flagellum grows each cell cycle, and the two flagella are partitioned to the two daughters (Gull et al., 1990). Using ergodic principles, the kinetics of growth of a new flagellum can be analyzed from the distribution of new flagellum length in an asynchronously growing population (Tyler et al., 2001; Figure 2A).

FIGURE 2:

Application of ergodic analysis to find cell cycle timings from continuously varying cell properties. (A) Previously published data (Tyler et al., 2001) concerning the growing new flagellum length in 192 cells from an asynchronous population of T. brucei. Each data point represents a single length measurement, arranged in a random order along the horizontal axis. (B) The same data as in A, but arranged in rank order of increasing flagellum length. As the new flagellum only elongates through the cell cycle, this can be used to determine the flagellum growth rate through the cell cycle from ergodic principles. (C) The transformed result, showing new flagellum length as a function of cell cycle progress. New flagellum length increases at a constant rate (R² = 0.992) Error bars indicate the SE of determination of time through the cell cycle for each data point. (D) The two gradually changing cell properties (cell body length and DNA content) used for the analysis of Leishmania division and the trajectory derived by fitting a line through regions of this plot with high point density (Wheeler et al., 2011). (E) The pattern of cell body and DNA content changes along the trajectory line. (F) Graphical representation of assignment of a data point to a distance along the trajectory line. The distance along the trajectory line from its start to the point closest to the data point corresponds to that data point’s distance along the trajectory line. (G) The correspondence between distance along the trajectory line and percentage of time spent in that state derived from the Leishmania cell cycle data (Wheeler et al., 2011). This provides a way to map any single cell to a particular cell cycle stage, allowing analysis of any of its secondary properties. (H) Mapping of Leishmania cell body width changes through the cell cycle (Wheeler et al., 2011) from the cell cycle stages derived from E–G.

To analyze T. brucei flagellum growth rate, the simplest ergodic analysis would use the proportion of cells in an asynchronous population that are at cell cycle stages before the start of new flagellum growth. Using Eq. 2 in Box 2 and the fully assembled flagellum length allows calculation of average growth rate but gives no information about how the flagellum growth rate depends on length. To extract this information, the cells could be further subcategorized into cells with no new flagellum or a new flagellum <3 μm in length, <6 μm in length, and so on. The timings of transitions between each of these classes can then be calculated, allowing comparison of growth rate at different lengths. More subcategories give more detail, and with extremely small subcategorization, all subcategories will contain either one or zero cells. In this situation, measurements of new flagellum length can simply be ordered by increasing length (Figure 2B). The position in this rank order, as a fraction of the total number of cells, can then be used to analyze the cell cycle progression of that particular cell on the basis of flagellar length using Eq. 2 of Box 2; Figure 2C), from which more detailed analysis of flagellum growth kinetics can be made.

This method derives the kinetics of flagellum growth directly from the data, but the inverse is also possible: using a model of flagellum growth to predict flagellum length distribution in the population, which can then be accepted or rejected based on its fit to the data. This has been applied to examine the elongation kinetics of the hook structure in Salmonella typhimurium flagella (Koroyasu et al., 1998) and uses the population balance method (Randolph and Larson, 1988).

The cell-by-cell calculation of cell cycle progression on the basis of one parameter (new flagellum length) is possible when that parameter gradually increases or decreases through the cell cycle and allows the analysis of how any second parameter (e.g., DNA content) changes through the cell cycle. However, in this example, the ordering cells into cell cycle stage on the basis of flagellum length does not provide any information concerning cell cycle stage for cells within the first 40% of the cell cycle in which the new flagellum has not yet started to form (Figure 2C).

MULTIPLE CONTINUOUS VARIABLES

Because many properties of cells undergo gradual changes through the cell cycle, two or more of these parameters can be selected that undergo changes at different cell cycle stages. These can provide complementary information, allowing unambiguous determination of how far any individual cell has progressed through the cell cycle (so long as the ergodic assumptions are met). This measure of cell cycle stage of each individual cell can then be used to determine quantitatively the correlation of any other cellular property through the cell cycle. This approach has recently been developed independently on three occasions: 1) in Leishmania mexicana, in which cell body length and total cellular DNA content measurements by light microscopy were used to derive cell cycle stage, from which the properties of mitochondrial and nuclear DNA S phase and cell body and flagellar morphogenesis were derived (Wheeler et al., 2011); 2) in the MOLT-4 lymphoblastic leukemia cell line, in which cyclins A2 and B1, phosphor-S10-histone H3, DNA content and light scatter measurements by flow cytometry were used illustrate that this concept was feasible (Jacobberger et al., 2012); and 3) in HeLa cells, in which DNA content and anaphase-promoting complex activity measurements by light micro­scopy were used to derive cell cycle stage, from which an analysis of the rate of growth of cell mass as a function of cell cycle and cell size and feedback mechanisms for cell size regulation were derived (Kafri et al., 2013).

When considering two or more gradually changing cellular properties, the strong ergodic assumption indicates there is a single path (a trajectory) through these data that describes how the properties of an individual cell change during progression through the cell cycle (Figure 2C). This trajectory might be known from time-lapse or synchronization experiments (Jacobberger et al., 2012) or be unknown and need to be derived from the data. Both previous applications derived the trajectory from the data, using path-walking algorithms from a known start point through regions of high point density in the data—from cell body length/DNA content (Wheeler et al., 2011) and geminin/DNA content (Kafri et al., 2013) data, respectively. Correct definition of this trajectory is critical for accurate analysis, and support from the trajectory from an alternative experimental method is important—for example, by time-lapse microscopy (Wheeler et al., 2011; Kafri et al., 2013).

Any gradually changing cell parameters may be suitable for defining a trajectory but must allow unambiguous mapping of data points to distances along the trajectory line. This means that only trajectories with no crossing points can be used. Using more data dimensions to define the line is advantageous, as it provides more dimensions across which the data are separated (Jacobberger et al., 2012).

Having defined the trajectory (Figure 2, D and E), a measure of progress of any individual cell through the cell cycle is given by its distance along the trajectory line. However, experimental error in measuring cell properties causes deviation in measured cell properties from the trajectory; distance along the trajectory must therefore be determined on a cell-by-cell basis by determining the closest point on the trajectory to each data point (Figure 2G), a process termed parameterization of cell cycle stage (Kafri et al., 2013). Having determined the distance along the trajectory, Eq. 2 of Box 2 can be used to convert ranked distances along the trajectory to time through the cell cycle for each individual cell (Figure 2H).

Any secondary properties of the cell can now be analyzed to determine how they vary over the course of the normal cell cycle. Both previous applications of this method focused on secondary variables relating to morphogenesis in the cell cycle—a descriptive analysis of cell body shape change and flagellum growth in the case of Leishmania (Wheeler et al., 2011) (Figure 2H), and a study of growth feedback related to cell mass in the case of the HeLa system (Kafri et al., 2013). This method has general applications, and is a new way to analyze core cell biology questions.

CONCLUSIONS

I have rehearsed a range of ergodic analyses, ranging from analysis of discrete measurements from simple oscillating and cyclical systems, up through the complexities of analyzing a population undergoing exponential growth, and reaching examples in which the ergodic analysis is used to assign a cell cycle stage to individual cells on the basis of measuring two continuously varying cellular properties. By illustrating the conceptual links between these examples of increasing complexity, supported by a rederivation of these related equations from first principles (Supplemental Appendix), I have built an intuitive explanation of these approaches.

Ergodic analysis is extremely flexible and can be used in any cyclical process in a cell, so long as the ergodic assumptions are met. Potential applications range from analysis of biochemical cycles such as p53 and Mdm2 oscillations (Geva-Zatorsky et al., 2006) to the cell cycle, including situations with cellular senescence and terminal differentiation. The potential for future analyses using these approaches is greatest when studying dynamic processes in cells that require destructive analysis methods for single cells using modern biochemical and imaging methods, where time-lapse or real-time analysis is impossible.