Orchestration of ErbB3 signaling through heterointeractions and homointeractions

ErbB receptors form homodimers and heterodimers between family members. To model ErbB2/ErbB3 signaling, single-particle tracking data are used to create a simulation space with overlapping receptor domains. Stochastic modeling of receptor dimerization and phosphorylation reveals the complexity of ErbB2-3 interactions.

Abstract

Members of the ErbB family of receptor tyrosine kinases are capable of both homointeractions and heterointeractions. Because each receptor has a unique set of binding sites for downstream signaling partners and differential catalytic activity, subtle shifts in their combinatorial interplay may have a large effect on signaling outcomes. The overexpression and mutation of ErbB family members are common in numerous human cancers and shift the balance of activation within the signaling network. Here we report the development of a spatial stochastic model that addresses the dynamics of ErbB3 homodimerization and heterodimerization with ErbB2. The model is based on experimental measures for diffusion, dimer off-rates, kinase activity, and dephosphorylation. We also report computational analysis of ErbB3 mutations, generating the prediction that activating mutations in the intracellular and extracellular domains may be subdivided into classes with distinct underlying mechanisms. We show experimental evidence for an ErbB3 gain-of-function point mutation located in the C-lobe asymmetric dimerization interface, which shows enhanced phosphorylation at low ligand dose associated with increased kinase activity.

INTRODUCTION

The ErbB family of receptor tyrosine kinases consists of four related receptors that form both homodimers and heterodimers (Lemmon and Schlessinger, 2010), as well as potentially higher-order oligomers (Kozer et al., 2013). This work focuses on an unusual property of ErbB3: dependence on engagement with a heterodimerizing partner for its transphosphorylation and up-regulation of its inherently weak catalytic activity (Shi et al., 2010; Steinkamp et al., 2014). Previous studies suggested that ErbB3 favors ErbB2 over other ErbB family members for heterodimerization (Zhang et al., 2009) and ErbB2/ErbB3 interactions are important in both normal developmental processes (Yarden and Sliwkowski, 2001), as well as in cancer initiation and progression (Liu et al., 2007; Vaught et al., 2012). Although ErbB3 and ErbB4 share heregulin/neuregulin 1 (HRG/NRG1) as a ligand and can form heterodimers (Monsey et al., 2010), it is the ErbB3/ErbB2 complex that is implicated in melanoma growth and survival (Zhang et al., 2013). ErbB3 expression has been linked to resistance of tumors to tyrosine kinase inhibitor therapies (Sergina et al., 2007; Huang et al., 2013; Sato et al., 2013; Lee et al., 2014), motivating more comprehensive analyses of ErbB3 dynamics and signaling capabilities.

Mathematical modeling has emerged as a powerful method to explore the complexity of ErbB family signaling (Andrews and Bray, 2004; Blinov et al., 2006; Zhang et al., 2009; Kholodenko et al., 2010; Radhakrishnan, 2010; Kleiman et al., 2011), particularly when supported by high-quality, quantitative measurements at different time and length scales (Pryor et al., 2013; Shankaran et al., 2013). Most prior computational studies neglected ErbB3 as a significant catalytic entity. A notable exception is the work of Telesco et al. (2011), who suggested that even the minimal level of basal ErbB3 autophosphorylation could alter the dynamics of ErbB signaling pathways and contribute to drug resistance. Recently we demonstrated that tyrosine kinase activity is significant in immunoisolated, intact ErbB3 after binding HRG, with the requirement that ErbB2 is coexpressed (Steinkamp et al., 2014). High- resolution imaging methods, such as single-particle tracking (SPT), captured ErbB3-ErbB3 and ErbB3-ErbB2 interactions in real time. Ligand-bound ErbB3 was found to engage in homointeractions that are three to four times more stable than heterointeractions with ErbB2 (Steinkamp et al., 2014). These observations raised intriguing questions. Under what conditions is ErbB3’s catalytic activity important? What is the potential effect of spatial organization and serial engagements of both homodimer and heterodimer configurations on signaling?

We approach these questions using a computational model of the system that reflects characteristics of the membrane landscape underlying the anomalous diffusion characteristics of ErbB receptors (Low-Nam et al., 2011; Steinkamp et al., 2014), as well as simulating the random nature of receptor encounters in the two-dimensional (2D) fluidic membrane. Recently applied to the study of ErbB1/epidermal growth factor receptor (EGFR) homodimerization (Pryor et al., 2013), our spatial stochastic simulation method incorporates a rule-based approach that explicitly considers important structural features that control ErbB signaling. The stable upright configuration of the extracellular domain of ErbB2 (Cho et al., 2003; Garrett et al., 2003) renders it competent to form heterodimers throughout the simulation; the lower affinity of ErbB2 self-association is represented by a low on-rate for ErbB2 homodimers. Ligand-bound ErbB3 (Dawson et al., 2007) is upright and dimerization competent in simulations, whereas the unliganded ErbB3 is assumed to transition from the tethered (self-inhibited) to a dimerization-capable state as for the EGFR (Ziomkiewicz et al., 2013). In the model, this flux is represented by a probability term; at each microsecond time step in the simulation, only 0.01% of resting ErbB3 receptors are upright and available to dimerize. The model also takes into account the asymmetric orientation of the kinase domains in a dimer (Zhang et al., 2006; Jura et al., 2009), assuming a random process by which each monomer in the pair is assigned as a receiver or an activator. This simulation strategy sets up a scenario in which individual receptor monomers swap their status as a receiver or activator only through a stochastic process of dissociation and rebinding. During these encounters, the model tracks the phosphorylation state of each receptor monomer. Phosphorylated receptors are assumed to exhibit increased catalytic activity. This increased activity is represented in the model by applying a receptor-specific multiplier. Our model is governed by experimentally defined rate constants for phosphorylation, dephosphorylation, and dimer dissociation. ErbB receptors cycle through many encounters during these simulations, revealing steady-state properties that drive signal propagation. Properties that influence phosphorylation state include the relative ratios of each receptor species, receptor density, and dwell times.

SPT data are used to estimate the size of membrane domains (“confinement zones”; Simson et al., 1995) that transiently trap ErbB2 and ErbB3, incorporating previously described overlap of these domains (Hsieh et al., 2008) with their respective dwell times. These factors translate in the model into probabilities for escape from confinement. We use the model to explore the potential effect of ErbB3 mutations on model parameters, including conformation, dimer stability, and receiver/activator function. These simulations suggest differing activation mechanisms across the full spectrum of recently described ErbB3 mutations, which are distributed across both the extracellular and kinase domains and may each have unique contributions to dimer stability or kinase activity. One such mutation is E933Q, which is located within the C-lobe of the ErbB3 kinase domain and was discovered by us as a heterozygous mutation in the SKBR3 breast cancer cell line. We show that ErbB3^E933Q expressed in CHO cells is more readily phosphorylated at low ligand dose than wild-type ErbB3 (ErbB3^WT), with accompanying higher catalytic activity. SPT data showed that the gain-of-function status was not linked to longer homodimer lifetimes for ErbB3^E933Q compared with ErbB3^WT. Because ligand binding was also unaltered, we speculate that the E933Q mutation renders it a better activator. This work sets the stage for mechanistic classification of the entire spectrum of ErbB3 oncogenic mutations (Jaiswal et al., 2013).

RESULTS

Modeling scheme

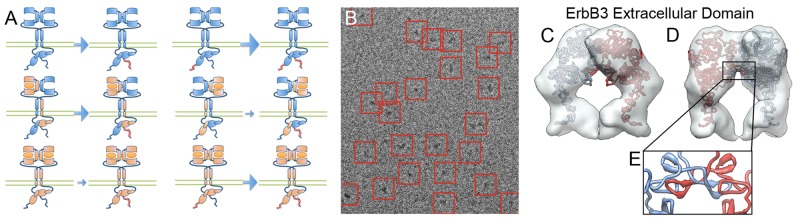
The ErbB3 homodimerization and heterodimerization model introduces layers of complexity not considered in our spatial stochastic EGFR homodimer models (Hsieh et al., 2008; Pryor et al., 2013). For instance, we previously established that ligand-dependent up-regulation of ErbB3 catalytic activity requires ErbB2, since it can be abrogated by pretreatment with the ErbB2-specific inhibitors pertuzumab and lapatinib (Steinkamp et al., 2014). We also established that the off-rate for ErbB2-ErbB3 heterodimers is approximately threefold faster than that for ErbB3 homodimers bound to HRG (Steinkamp et al., 2014). The general scheme for the dimerization model is provided in Figure 1A, where ErbB2 monomers are represented in blue and ErbB3 monomers are in orange. Dimers are formed by engaging the dimer arms of upright monomers only. During the simulation, there is a random assignment of the orientation of their cytoplasmic tails such that only one monomer is up-regulated through contact of its N-lobe with the C-lobe of the activator. This asymmetrical orientation renders one monomer as the “receiver” and the other monomer as the “activator.” Stochastic release and rebinding (or new pairings) is required to swap the activation state of individual monomers. For simplification, we make several assumptions for the rule-based model: 1) the receiver monomer transphosphorylates only the activator monomer tail while they are dimerized, 2) ErbB2 phosphorylation of ErbB3 up-regulates ErbB3 activity, and 3) ErbB2 is always upright and dimer competent, with a strong preference for heterodimerization with ErbB3. The weighted arrows for each reaction reflect the relative phosphorylation rate associated with the dimer state of the specific reaction.

FIGURE 1:

(A) Cartoon of dimer types and phosphorylation reactions represented in the simulation. The phosphorylation rate (or kinase activity), represented by blue arrows, changes, depending on the dimer type. Unphosphorylated ErbB3 homodimers (orange) have a negligible phosphorylation rate, whereas activated ErbB3 has an intermediate phosphorylation rate after productive encounters with the active kinase ErbB2 (blue). We use the asymmetric kinase domain shuffle mechanism used in Pryor et al. (2013) to permit phosphorylation of activator monomers by receiver monomers within a dimer. (B–E) Three-dimensional (3D) reconstruction of fully hydrated ErbB3 homodimers (extracellular domain only) based on cryo-EM of recombinant protein in the presence of HRG. (B) Electron micrograph displaying fully hydrated, well-separated particles (red boxes). Protein appears dark on light background. Width of the box is 22 nm. (C) Surface representation of the ErbB3-dimer 3D reconstruction. Homology models of ErbB3 monomers (red and blue ribbon representations) were fitted into the density. (D) View turned 45° clockwise from C around the vertical axis. (E) Detail showing potential intradimer interactions.

Homology model for ErbB3 homodimer orientation

Our prior work indicated that ErbB2-ErbB3 heterodimers occur through canonical engagement of their dimer arms, since signaling is blocked by binding of the therapeutic antibody pertuzumab to the ErbB2 dimer arm. However, there is some evidence that ErbB3 homointeractions might involve other interfaces (Kani et al., 2005). We therefore sought experimental evidence for an important additional assumption in the model: 4) ErbB3 homodimers also occur principally through their dimer arms. To do so, we isolated recombinant ErbB3 by methods similar to those described for EGFR preparation by Mi et al. (2011) and performed structural analysis by single-molecule cryo–electron microscopy (cryo-EM). Results for ligand-bound ErbB3 extracellular domains are reported in Figure 1, B–E, which provides a good fit to an ErbB3 homology model based on ligand-bound EGFR homodimers. Work is ongoing to extend the cryo-EM studies for new insight into ErbB3 homointeractions and heterointeractions. Of importance, these early results support the simulation rule that both ErbB3 homodimer and heterodimer interactions engage the dimerization arm and are therefore mutually exclusive. Because we have not yet observed higher oligomers through single-particle tracking, we did not include the interesting possibility of heterotetramers that has been proposed by others (Zhang et al., 2012).

Simulation landscape: single-particle tracking of ErbB3 and ErbB2 diffusion indicates that receptors transiently reside in partially overlapping confinement zones

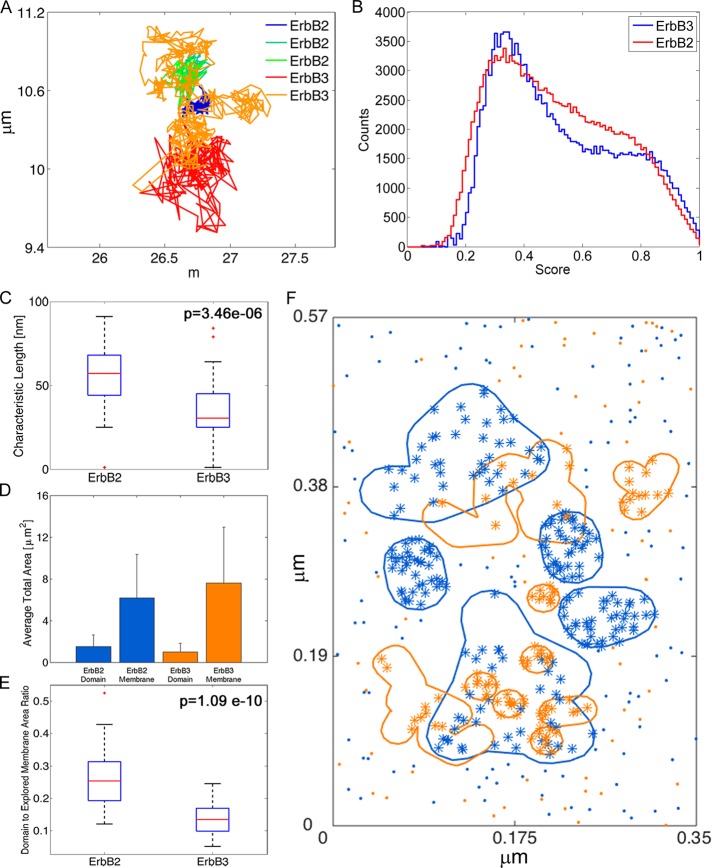
Our spatial stochastic model takes into consideration the potential effect of membrane topography on diffusion-limited reactions between receptors. Our previous models relied on “snap-shot” images of ErbB receptor distributions on fixed cell membranes, as observed by immuno–electron microscopy, to populate the 2D simulation landscape with domains that transiently confined receptors (Hsieh et al., 2008; Pryor et al., 2013). In this work, we expand on this concept by using SPT data to estimate the area and shapes of confinement zones, as well as to address the possibility that ErbB3 and ErbB2 receptors might exhibit individual characteristics such as domain dwell time and distribution. For this portion of the study, we used data sets acquired using two-color quantum dot (QD) tracking on CHO cells stably expressing hemagglutinin peptide tag (HA)-ErbB2 (^HAErbB2) and transiently expressing ErbB3. ^HAErbB2 was tracked with anti-HA-FAB-QD⁵⁸⁵, and ErbB3 was tracked with HRG-conjugated QD⁶⁵⁵. An example of trajectories from a single observation area is shown in Figure 2A, where three ErbB2 and two ErbB3 were tracked in a single movie (individual receptors are color coded in the legend to Figure 2A).

FIGURE 2:

Characterization of confinement zones using SPT data. (A) ErbB2 and ErbB3 trajectories from SPT data. (B) Compiled ranks of all points for ErbB2 and ErbB3. A bimodal distribution for both species distinguishes points where receptors are confined vs. freely diffusing. Compilation of the ranks for SPT experiments in which ErbB2 was tracked using QD⁵⁸⁵ and ErbB3 was tracked using QD⁶⁵⁵. (C) Box plots of characteristic lengths calculated for each SPT data file. The characteristic lengths for ErbB2 and ErbB3 are statistically different, p = 3.46 × 10⁻⁶ (one-way ANOVA test). (D) Average total areas of domains and explored membrane for ErbB2 (blue) and ErbB3 (orange). The explored membrane was calculated using the DRA and setting the characteristic length to the localization error of the SPT experiments. Whereas ErbB2 domains are larger, ErbB3 receptors explore more of the open membrane. (E) Box plots of the ratio of domain area to explored membrane area for ErbB2 and ErbB3. Ratios are statistically different, p = 1.09 × 10⁻¹⁰ (one-way ANOVA test). (F) Reconstructed simulation space for the 2D spatial stochastic model with overlapping ErbB3 domains (orange) and ErbB2 domains (blue) based on the DRA analysis. Domains derived from the SPT data were added to the simulation space until the ratio of domain area to explored membrane area was equal to the ratio calculated for all points in the SPT data file. Receptor densities for ErbB3 (orange stars and dots) and ErbB2 (blue stars and dots) were calculated based on the estimated number of receptors per cell and the average surface area of a CHO cell, scaled to the area of the simulation space.

To analyze multiple data sets containing two-color trajectories, we developed and applied a domain reconstruction algorithm (DRA). The DRA converts dynamic trajectories into static spatial data that can be used to approximate the size and contours of confinement zones occupied by ErbB3 and ErbB2 on the CHO cell membranes (Supplemental Figure S1). The algorithm is fully described in the Supplemental Material. In brief, SPT trajectory data are first sorted into two groups that reflect either the confined or the freely diffusing state. For each point, a ranking system is applied that compares the preceding and subsequent jump sizes in the trajectories against the total distribution. When these ranks are compiled and sorted into a histogram, a bimodal distribution becomes apparent (Figure 2B). The local minimum of the bimodal distribution is then used to determine a cutoff rank to separate the confined points from the freely diffusing points. The analysis was applied to 25 SPT data sets to generate the plots in Figure 2B. Results were comparable when applied to 13 SPT data sets in which the QD probes were reversed; we consider this to be an important control measure because there is a slight difference in localization accuracy for the two classes of QDs (anti–HA-Fab-QD⁶⁵⁵ and HRG-QD⁵⁸⁵; Supplemental Figure S2A). Based on these results, a cutoff score of 0.65 was used for further DRA analyses.

To estimate domain size, we next used a clustering algorithm (Espinoza et al., 2012) that assigns a reasonable length parameter as the maximum distance between two points for them to be considered in the same cluster. The average perimeter of all the clusters in a single SPT movie data set is computed over a range of clustering characteristic lengths. This average perimeter is then compared across all the SPT tracking files. Supplemental Figure S2, B and C, shows the average perimeter of domains for each characteristic length from the ErbB2 and ErbB3 tracking data, respectively. We defined the average characteristic length of the clusters for each receptor based on the local minimum in these plots. This local minimum corresponds to a minimum of domain perimeters. Padding the perimeter points in each cluster by one-half the characteristic length creates the final confinement shape and area.

On the basis of the DRA results, we are able to compare the membrane domain characteristics for ErbB2 and HRG-bound ErbB3. We used the one-way analysis of variance (ANOVA) test, which does not assume any specific distribution type, only that the data sets being compared come from the same distribution. We find that the characteristic lengths for ErbB2 and ErbB3 domains are statistically different (p = 3.46 × 10⁻⁶). Box plots of the two data sets are shown in Figure 2C, confirming that the characteristic lengths for ErbB2 and HRG-bound ErbB3 clusters on CHO membranes are 57 and 30 nm, respectively. Note that cluster size and total domain area for these receptors can vary on membranes of different cell types (Yang et al., 2007; Nagy et al., 2010).

The next important membrane characteristic to address is the density of domains on the membrane. SPT experiments require sparse labeling of receptors to allow for single-particle resolution. One method to compensate for this sparse labeling is to estimate the total area of the membrane explored by labeled receptors from a single SPT data file and compare it to the total domain area of the membrane from the same SPT data file. To calculate the area of the membrane explored by a receptor, the DRA was used to analyze the SPT data using a characteristic length equal to the average localization error of the SPT experiment (Figure 2D). Computing the ratio of total domain area to the total explored membrane area allows the sparse SPT domain reconstruction information to be applied to the full cell membrane. As shown in Figure 2E, the ratio of total domain area to total explored membrane area can be computed for each SPT data file for each receptor. This ratio is then compared between ErbB2 and ErbB3 to determine whether both receptors explore the same membrane space. Using the one-way ANOVA test, we find that this ratio is also statistically different between ErbB2 and ErbB3 (p = 1.09 × 10⁻¹⁰). The results of these two sets of tests suggest that motion of ErbB2 and ligand-bound ErbB3 is differentially constrained within the membrane landscape.

Figure 2F illustrates the landscape for 2D spatial stochastic simulations, created as an outcome of the cumulative information from the DRA analysis. We estimated the surface area of a cell by approximating the cell shape to be a sphere. On the assumption that a cell diameter is 10 μm, the approximate surface area of a cell is 314.16 μm². Flow experiments were performed to measure the number of receptors per cell for both ErbB2, ∼500,000 receptors/cell, and ErbB3, ∼250,000 receptors/cell. Using these measures, we calculate the number of receptors per square micrometer of cell surface to be 1592 and 796 receptors/μm² for ErbB2 and ErbB3, respectively. To reduce computing time, we converted the simulation space to a total surface area of ∼0.2 μm², equating to ∼317 ErbB2 receptors and ∼158 ErbB3 receptors for our simulations. Of importance, because our approach is agent based, every receptor can be tracked continuously for comparison to ensemble behavior. Note that although the domains were statistically different, analysis of the single-particle tracking data also revealed an overlap between the two types of domains. This result is consistent with the findings from our prior immuno–electron microscopy study (Yang et al., 2007). To represent these domains in the simulation landscape we used the ratio of the domain area to the explored membrane area to determine the amount of domain coverage for the desired surface area. The reconstruction of these irregular domains is depicted by blue (ErbB2) and orange (ErbB3) contours in Figure 2F. During stochastic simulations, receptor species exhibit no preference to enter their respective domains, but there is an escape penalty. Our value for the escape penalty was estimated by dividing the area of domains by the area of free simulation space. This ratio was then scaled with the fraction of receptors that are inside domains at any given time (0.65), a measure calculated during the DRA.

Differential ErbB3 and ErbB2 kinase activity and dephosphorylation kinetics influence signaling output

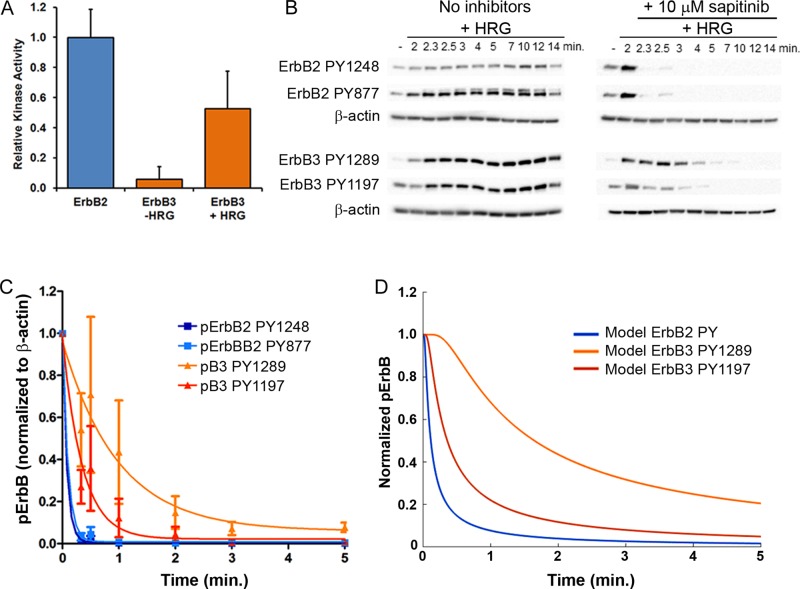
To establish essential new parameters for the model, we performed experiments to establish relative kinase activity for both receptor species, as well as dephosphorylation kinetics for specific sites on ErbB2 and ErbB3. We previously examined the catalytic activity of ErbB2 and ErbB3 receptors in immune complexes prepared from resting or HRG-stimulated cells using peptide substrates in a multiwell format (Yang et al., 2007; Steinkamp et al., 2014). These immunoprecipitation conditions for ErbB2 or ErbB3 avoid cross-contamination by the other receptor species (Yang et al., 2007; Steinkamp et al., 2014). To quantify the kinase activity of ErbB3 relative to ErbB2 for the model parameters, we analyzed each KLISA sample by Western blot probed with the phosphotyrosine 20 (PY20) pan-PY antibody. Kinase activity was then normalized to the PY20 signal from each sample. Relative kinase activity is plotted in Figure 3A. Basal ErbB3 activity is minimal, but with the addition of ligand, activity is approximately half that of ErbB2.

FIGURE 3:

(A) Comparison of the relative kinase activity of ErbB2 and ErbB3 ± HRG after normalization. ErbB2 kinase levels were set to 1. Data shown are the average of two independent trials ± SD. (B) Blots of lysates from CHO cells stably expressing ^HAErbB2 and ErbB3-mCitrine stimulated with 12 nM HRG for 2 min at 37°C and then treated with the pan-ErbB kinase inhibitor sapitinib (10 μM) for times ranging from 20 s to 12 min. (C) Plot of the normalized phosphorylation levels for two phosphorylation sites each for ErbB2 and ErbB3 over time. Values are the mean ± SEM based on the quantification of Western blots from three independent experiments. Levels of phosphoreceptors were normalized to β-actin levels. Phosphorylation levels for all sites were set to 1 for the 2-min time point (HRG stimulation with no inhibitor). Values were fitted to a one-phase exponential decay curve to determine the dephosphorylation half-life of each site. (D) Results from the BioNetGen model show good agreement of simulations with experimental measures of site-specific dephosphorylation kinetics.

Transphosphorylation of receptor tails is opposed by phosphatase activity, which can be quantified by the rapid addition of kinase inhibitors during signaling. We used the in vitro kinase assay to screen for tyrosine kinase inhibitors (TKIs) that effectively and rapidly block kinase activity of both species (Supplemental Figure S3, A and B). Results established both pan-ErbB inhibitors sapitinib (AZD8931) and afatinib (BIBW2992) as robust inhibitors of ErbB3 kinase activity (Supplemental Figure S3A). Sapitinib is known to bind to the ErbB3 kinase domain with nanomolar affinity (Hickinson et al., 2010). As expected, lapatinib, which does not bind to the ErbB3 kinase domain (Shi et al., 2010), did not inhibit ErbB3 activity.

The time course of ErbB3 (PY1289, PY1197) and ErbB2 (PY1248, PY877) phosphorylation in HRG-stimulated CHO transfectants is reported in Figure 3B, showing rapid onset (within 2–3 min). To uncover ErbB2 and ErbB3 dephosphorylation rates, cells were serum starved and stimulated for 2 min with 12 nM HRG. Sapitinib (10 μM) was then added to acutely inhibit the kinase activity of both receptors. Cells were washed and flash frozen at specific time intervals after the addition of sapitinib, and lysates were prepared for SDS–PAGE. Western blots were probed with phosphospecific antibodies to measure receptor dephosphorylation over time. The plots in Figure 3C (light and dark blue lines) show that addition of 10 μM sapitinib caused rapid dephosphorylation of both ErbB2 phosphosites (t_1/2 = 0.053–0.063 min), slightly faster than reported values using lapatinib (Kleiman et al., 2011). ErbB3 dephosphorylation at PY1289 is slower, with a half-life of ∼0.87 min (Figure 3C, orange line). Dephosphorylation of ErbB3 PY1197 was intermediate (t_1/2 = 0.19 min; red line).

These experimentally derived parameters, as well as those from the literature, are shown in Tables 1 and 2. Diffusion coefficients derived from SPT data were reported previously (Steinkamp et al., 2014). In the model, the diffusion coefficient of dimers in the absence of signaling (unphosphorylated receptors) is larger, based on faster diffusion in the presence of the ErbB2 inhibitor, lapatinib (unpublished data). ErbB2 kinase activity was based on published estimates for the basal rate (Kleiman et al., 2011), adjusted by a multiplier when phosphorylated (Shankaran et al., 2006). Basal ErbB3 activity is set at 1000-fold lower than ErbB2 basal activity. To estimate a corresponding multiplier value for phosphorylated ErbB3 in the simulation, we set phosphorylated ErbB3 kinase activity using a multiplier of 0.56 of ErbB2. Dephosphorylation rates fitted to simulation results shown in Figure 3D show a good fit to the experimentally measured dephosphorylation kinetics (Figure 3C).

TABLE 1:

Simulation parameters: diffusion and dimerization.

	Monomers			Dimers
Parameter	ErbB2	ErbB3	ErbB3E933Q	ErbB2 ErbB2	ErbB2 ErbB3	ErbB3 ErbB3	ErbB3E933QErbB3E933Q
Diffusion coefficient (μm2/s)a,b	0.0272	0.0310	0.0621	0.0150	0.0150	0.0185	0.0139
Diffusion coefficient for signaling dimers (μm2/s)a,b				0.0150	0.0046	0.0028	0.0067
Dimer on rate (μm3/s)c (active conformation)				0.00009	0.00009	0.00009	0.00009
No-ligand dimer off rate (1/s)a,b				4.4	0.44	0.44	0.44
HRG bound dimer off rate (μm3/s)b					0.41	0.13	0.13

^aExperimental data in this paper.

^bSteinkamp et al. (2014).

^cPryor et al. (2013).

TABLE 2:

Simulation parameters: phosphorylation/dephosphorylation.

	ErbB2	ErbB3
Basal phosphorylation rate (1/s)a,b	0.073	0.00007
Phosphorylation rate (1/s)a,b	0.146	0.078
Dephosphorylation rate (1/s)c	0.2	0.13
		(PY1197)
		0.06
		(PY1289)

^aKleiman et al., (2011).

^bShi et al. (2010).

^cExperimental data in this paper.

Receptors cycle repeatedly through heterodimer and homodimer reactions

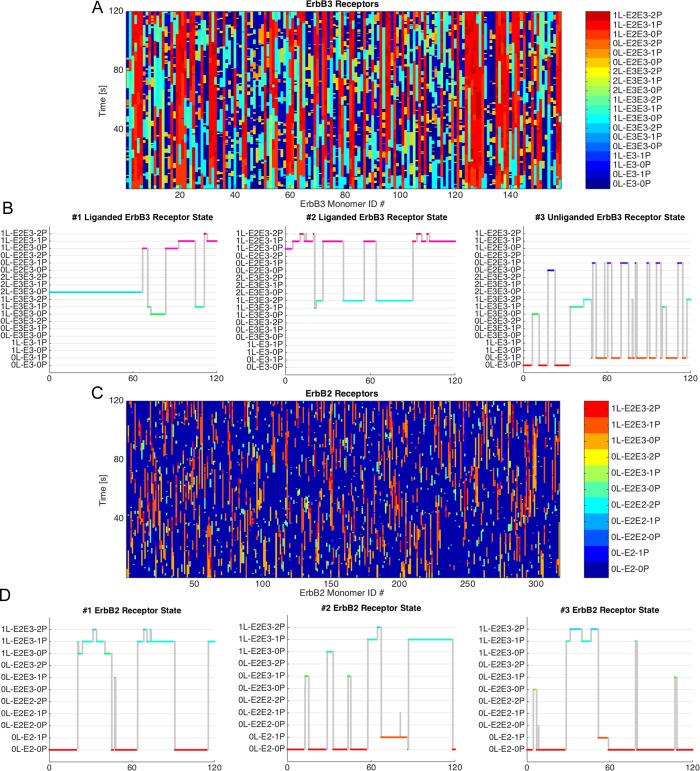
Results of spatial stochastic simulations are shown in Figure 4. In the two composites (Figure 4, A and C), the state transitions of all individual ErbB3 (A) or ErbB2 (C) receptors are shown for a single 120-s simulation initiated with 50% of the ErbB3 prebound to ligand and the ratio of receptors 2:1 (two ErbB2:one ErbB3). The colors indicate the interaction state of each receptor (monomer or dimer) and its phosphorylation state over time. The figure illustrates the stochasticity of the system achieved by using experimentally derived rates for dimer dissociation and phosphorylation/dephosphorylation.

FIGURE 4:

Receptor states occurring during a 120-s simulation populated with a ratio of 2 ErbB2:1 ErbB3 receptor. (A) Compilation of the dimerization and phosphorylation states for each simulated ErbB3 receptor over time. Individual receptors and their states are represented by vertical lines that switch color with a change in state. (B) Plots illustrating state changes over the simulation time for three representative ErbB3 receptors, two with ligand (receptors 1 and 2) and one without ligand (receptor 3). (C) Compilation of dimerization states over the simulation time for each individual ErbB2 receptor. (D) Receptor state changes over the simulation time for three individual ErbB2 receptors.

Under each composite, we show three examples representative of individual monomers as they cycle through distinct states. In Figure 4B, the first ligand-bound example is stalled as an unphosphorylated homodimer, before its dissociation and association with an ErbB2. Example 2 fluxes between a heterodimer and a homodimer state. An unliganded ErbB3 (receptor 3) spends most of the simulation time fluctuating rapidly between a monomer state and transient homodimer and heterodimer states.

Figure 4D presents a similar set of illustrations for individual ErbB2 receptors in the simulation. Each of these receptors participates in heterodimers, cycling in and out of pairs in which one or both members become phosphorylated.

The plot in Supplemental Figure S4 provides results of a 120-s stimulation performed in the BioNetGen version of our model, in which a 20-fold excess of ErbB3 to ErbB2 was considered. In the extreme case of limited ErbB2, a majority of ErbB3 receptors are sequestered in homodimers.

Steady-state analysis of ErbB phosphorylation reactions underscores the dependence of ErbB3 activation on ErbB2 and a potentially significant role for the ErbB3 kinase

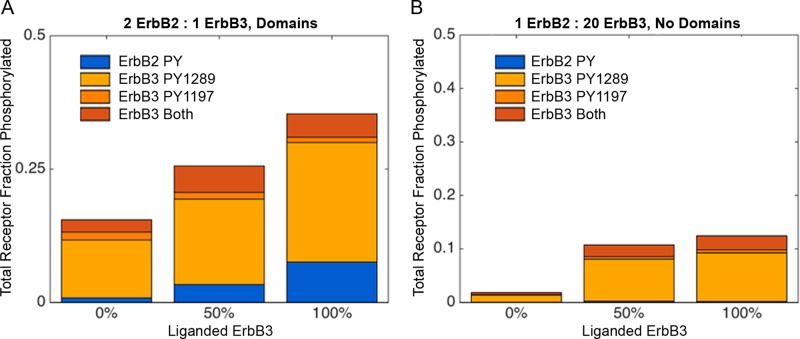
Figure 5A presents summary data for a series of spatial stochastic simulations, varying ligand occupancy for ErbB3 to 0, 50, or 100% and using a ratio of two ErbB2 to one ErbB3. For comparison, nonspatial BioNetGen results in Figure 5B show conditions in which ErbB2 is limiting (1 ErbB2:20 ErbB3). The graphs report the phosphorylation states of ErbB3 PY1197 and PY1289, as well as a single representative site for ErbB2. Results qualitatively fitted the experimental data, with a few caveats. Basal levels of ErbB2 phosphorylation are low but measurable, as noted in Figure 5D, increasing markedly with HRG addition. Monomers phosphorylated on both ErbB3 PY1197 and PY1289 are also low under basal conditions, increasing severalfold in response to HRG. The weakest fit is the relatively high basal phosphorylation of ErbB3 PY1289 in Figure 5A, which can be attributed to the short-lived dimers that occur between transiently upright ErbB3 (in the absence of ligand) and stably upright ErbB2. This suggests that an unknown regulatory mechanism exists to limit ligand-independent signaling by ErbB2-ErbB3 heterodimers. Many possibilities exist, including stronger spatial segregation of components, adaptor binding that obscures PY1289, and/or an even more restrictive probability than 0.01% for ErbB3 to assume the upright, dimer-competent conformation in the absence of ligand. Explorations of the parameter space for ErbB3 open–closed conformational flux is explored later in Figure 6E.

FIGURE 5:

Comparison of ErbB3 and ErbB2 phosphorylation at 2 min, with and without HRG. (A) Spatial stochastic simulation results for ErbB3 and ErbB2 phosphorylation, using values of 0, 50, or 100% ligand-bound ErbB3. Ratios of ErbB2:ErbB3 were set at 2:1. (B). BioNetGen results for simulations with a ratio of 1 ErbB2:20 ErbB3. The key indicates ErbB2 (blue) and ErbB3 (orange) phosphorylation sites that were tracked.

FIGURE 6:

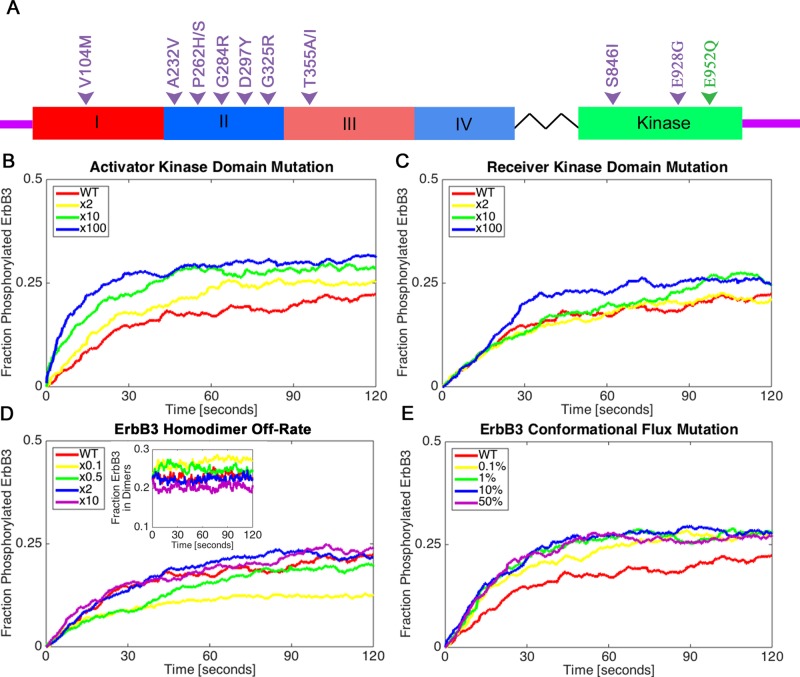
Classes of ErbB3 oncogenic mutations can differentially affect receptor phosphorylation. (A) Diagram of the ErbB3 receptor with hot spot mutations from Jaiswal et al. (2013; purple), as well as the E933Q mutation from this study (E952Q based on the alternative numbering system, green). Hot spot mutations occur in different ErbB3 domains and are potentially linked to distinct mechanistic classes. (B–E) Four possible mechanistic classes explored by varying multipliers within the simulation. All simulations were initiated with 50% ligand-bound ErbB3. The fraction of ErbB3 receptors phosphorylated over time is shown for each class of mutations. Shown are the effects of (B) an ErbB3 kinase domain mutation that causes the activator receptor to more efficiently activate its partner kinase, (C) a mutation in the kinase domain that increases kinase activity in the receiver, (D) mutations that increase or decrease the dimer off-rate (inset shows the fraction of ErbB3 receptors in dimers), and (E) a mutation that increases the stability of the extended, active conformation of ErbB3 independent of ligand binding. In E, the reported range is 0.1–50% of unliganded ErbB3 receptors in the extended conformation, by comparison to 0.01% as the original flux rate for wild-type receptors.

Computational approaches offer tractable methods to evaluate the effect of mutations on ErbB3-mediated signaling

As depicted in Figure 6A, Jaiswal et al. (2013) reported “hot spot” mutations that appear in the extracellular and cytoplasmic tail of ErbB3. We reasoned that, based on the various locations of these mutations, they might reasonably fall within several different mechanistic classes:

1. Mutations that raise the efficiency of the activator function of ErbB3 monomers. In the model, this would result in increased activity of the receiver (ErbB3 or ErbB2 as dimerizing partner).

2. Mutations that increase the intrinsic catalytic activity of the receiver (ErbB3 monomer bearing the mutation).

3. Mutations that decrease the stability of ErbB3 homodimers, resulting in a faster off-rate.

4. Mutations that increase the stability of ErbB3 homodimers, resulting in a slower off-rate.

5. Mutations that stabilize the extended conformation of ErbB3 in the absence of ligand, raising the probability that encounters of nonliganded receptors will lead to dimers.

We next extended our model to examine how these assumptions might alter ErbB3 dynamics. As a strategy, we adopted the successful modeling convention of a “multiplier” (Shankaran et al., 2006) to account for differential behavior of the receptor species. To achieve the results in Figure 6, we applied multipliers to specific reactions in the simulations. In Figure 6B, the multiplier was applied to ErbB3 monomers when acting individually as an activator. Results plotted in Figure 6B show a significant effect on overall ErbB3 phosphorylation when multipliers of 2 (yellow), 10 (green), or 100 (blue) are applied to ErbB3’s activator function. This type of mutation is expected to occur in the contact site between the C-lobe of the activator and the N-lobe of the receiver, with precedents set by critical studies reconstituting dimerization of recombinant ErbB3 with ErbB4 (Monsey et al., 2010)

When a multiplier was applied to ErbB3’s own intrinsic catalytic activity (“receiver”), improvement was also seen in overall ErbB3 phosphorylation levels—particularly using a higher multiplier of 100 (blue line)—but the effect was not as substantial as with the activator mutations (Figure 6C). The less dramatic effect is explained mechanistically, since the activity would be increased only in the ErbB3 monomer bearing the activating mutation. This type of ErbB3 mutation would not influence the ability of ErbB3 to activate ErbB2 (or ErbB4) when the latter is a receiver in the heterodimer state. Thus, hot spot mutations identified within or near the ErbB3 kinase domain (Jaiswal et al., 2013) could potentially fall into either category, with “activator” mutations having a greater effect than “receiver” mutations.

The results of simulations altering ErbB3 homodimer off-rates are shown in Figure 6D. The most significant change occurs when the dimer off-rate for a predicted mutant is 1/10 (yellow line) that of the measured value of 0.44/s for ligand-bound wild-type receptors (red line). Because a slower off-rate translates into a longer dimer lifetime, the fraction of ErbB3 in dimers increases to ∼28% at steady state. Of note, because a large number of these dimers are expected to be ErbB3 homodimers without benefit of prior ErbB2-mediated activation, the overall phosphorylation achieved by ErbB3 species is lower. Conversely, 2- to 10-fold faster off-rates (shorter ErbB3 homodimer lifetimes) have little effect on total ErbB3 phosphorylation under these conditions (a 2:1 ratio of ErbB2 to ErbB3).

Finally, Figure 6E reports results of simulations increasing the probability for unliganded ErbB3 to assume the upright state, from a set value of 0.01% over a range of 10- to 5000-fold (0.1% yellow, 1% green, 10% blue, or 50% purple). Here this applies to 50% of the receptors in the simulation (the other half are ligand bound, as for all simulations in this figure). Even under the conditions of 50% ligand, there is a measurable effect for raising the basal flux rate of ErbB3.

Substitution at ErbB3-E933 is a gain-of-function mutation that amplifies the phosphotidylinositol-3-kinase/AKT signaling pathway

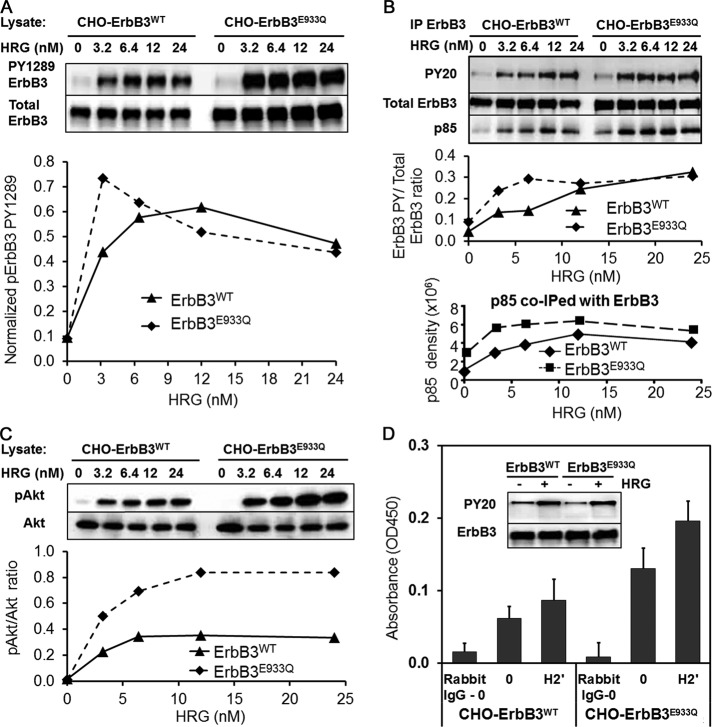
We next sought experimental validation of the predictions given in Figure 6. Independent of the site-directed engineering approach taken by Monsey et al. (2010), we discovered a naturally occurring somatic ErbB3 mutation in the widely used SKBR3 breast cancer cell line at position E933Q (E952 in Monsey’s amino acid–numbering system). This mutation has since been listed in the Cancer Cell Line Encyclopedia (Barretina et al., 2012). Our sequencing results showed that the mutation occurs in only one ErbB3 allele in SKBR3 cells (Supplemental Figure S5). To evaluate the possibility that this was an activating mutation, we transfected CHO cells with vectors for expression of mCitrine-fusion proteins bearing either ErbB3^WT or ErbB3^E933Q. After selection to ensure comparable surface expression of the two fluorescent ErbB3-fusion proteins, cells were stimulated for 2 min with HRG over a range of doses, lysed, and subjected to SDS–PAGE and Western blotting to measure levels of ErbB3 phosphorylation at PY1289. Robust phosphorylation of mutant ErbB3 was consistently detected at the lowest dose of HRG, with twofold to threefold stronger phosphorylation than for wild-type ErbB3 at suboptimal ligand concentrations (Figure 7A).

FIGURE 7:

The gain-of-function mutant ErbB3 E933Q demonstrates increased sensitivity to ligand and increased kinase activity when expressed in CHO cells. (A) CHO ErbB3^E933Q-mCitrine cells have high levels of ErbB3 phosphorylation even at the lowest dose of HRG (3.2 nM). (B) Immunoprecipitated ErbB3 samples show strong phosphorylation detected using a pan- PY antibody, PY20-HRP. ErbB3^E933Q coimmunoprecipitates more p85, a PI3K subunit, in the presence of ligand. (C) Increased levels of phosphorylated Akt downstream of PI3K indicate an overall up-regulation of the ErbB3 signaling network in CHO ErbB3^E933Q-mCitrine cells. (D) Immunoprecipitated ErbB3^E933Q has higher basal and ligand-dependent kinase activity in an in vitro kinase assay compared with ErbB3^wt. CHO cells expressing ErbB3^wt-mCitrine or ErbB3^E933Q-mCitrine were stimulated with low levels of HRG (3.2 nM) before immunoprecipitation.

We reasoned that the robust phosphorylation of ErbB3^E933Q in response to low doses of ligand might amplify downstream signaling by increased recruitment of class IA phosphotidylinositol-3-kinase (PI3K). Cells expressing ErbB3^WT or ErbB3^E933Q were stimulated over the same range of doses, followed by immunoprecipitation of ErbB3 from cell lysates and Western blotting to measure coprecipitated p85 regulatory subunits of PI3K. The amount of p85 recovered in ErbB3 immune complexes paralleled the degree of phosphorylation of ErbB3 in the CHO transfectants, with more p85 recovery at low ligand doses for ErbB3^E933Q than for ErbB3^WT (Figure 7B). Cells expressing ErbB3^E933Q also had a more robust activation of the downstream serine/threonine kinase, AKT, as measured by phosphorylation of AKT S473 (Figure 7C). The phospho-AKT/total AKT ratio was higher at times after HRG stimulation of CHO cells expressing ErbB3^E933Q than for cells expressing the wild-type receptor. Figure 7D reports results of in vitro kinase assays for ErbB3^WT and ErbB3^E933Q immune complexes isolated independently from the cell lysates of the two transfected CHO cell lines after 2-min stimulation with 3.2 nM HRG. Greater activity is shown for mutant ErbB3, despite modest differences in phosphorylation at this dose. Together with its location in the C-lobe interface with a receiver N-lobe, these results indicate that the E933Q substitution is likely to be a member of the first class of gain-of-function mutations (Figure 6B), for which the activator is more efficient at activating the receiver in the asymmetrical dimerization model.

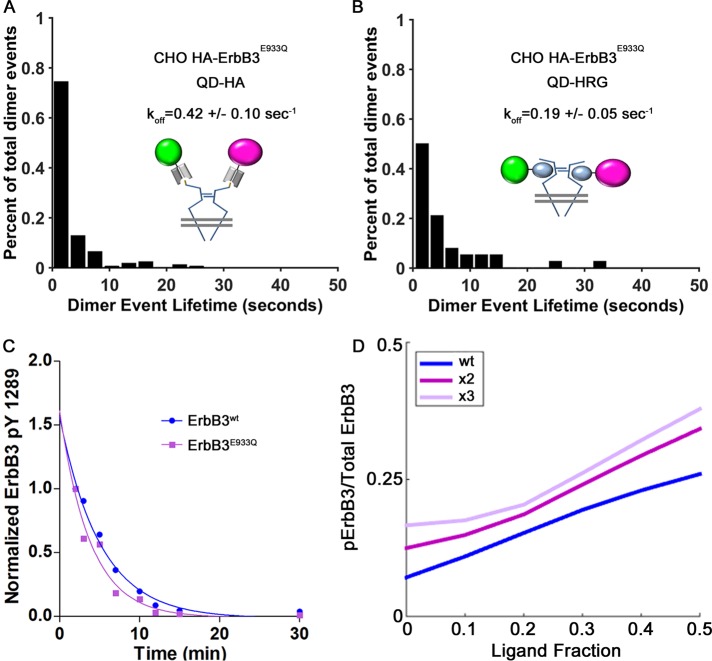
Our final objective was to use the mathematical model to estimate the relative contribution of the E933Q activating mutation, expressed as a “multiplier” value. As a prelude to simulations, we applied our existing experimental methods to determine whether the E933Q mutation might alter critical parameters such as the diffusion rate, homodimer lifetime, or dephosphorylation kinetics. Results of these experiments are shown in Figure 8, A–C, and in the Supplemental Material. We observed very slight changes in monomer diffusion coefficients for ErbB3^E933Q (Supplemental Figure S6). The off-rate of 0.41/s for unliganded ErbB3^E933Q homodimers (Figure 8A) was comparable to previously measured values for ErbB3^WT (Steinkamp et al., 2014). Liganded ErbB3^E933Q also had a similar dimer off-rate of 0.19/s (Figure 8B) compared with the ErbB3^WT off-rate of 0.13/s. The plot in Figure 8C (derived from data in Supplemental Figure S6B) shows that dephosphorylation kinetics for ErbB3^WT and ErbB3^E933Q are also comparable. These important control experiments eliminated a change in off-rate or phosphatase recruitment as a factor in this particular mutant.

FIGURE 8:

(A–C) Characterization of the E933Q ErbB3 mutant indicates that changes in off-rate or dephosphorylation do not contribute to gain of function. (A, B) Histograms of dimer lifetimes as revealed by single-particle tracking and HMM analysis of two-color QD-conjugated HA Fab (A) or HRG (B) bound to ^HAErbB3^E933Q receptors on the surface of CHO cells. Unliganded receptor pairs have an off-rate of 0.42/s, which is comparable to the wild-type value. The lifetime of liganded ^HAErbB3^E933Q receptor pairs is also comparable to wild-type receptor at 0.19/s. (C) Normalized ErbB3 PY1289 phosphorylation levels after 2-min stimulation followed by lapatinib treatment (10 μM) in CHO ErbB3^wt vs. CHO ErbB3^E933Q plotted over time. As in Figure 3, phosphorylation levels of both receptors were set to 1 for the 2-min time point after HRG stimulation. Points were fitted to a one-phase exponential decay curve to determine the dephosphorylation half-life. (D) Simulation in BioNetGen for a gain-of-function mutation applied to the activator function, as a function of ligand occupancy. Ratio of 1 ErbB2:20 ErbB3 is used here, since the data reported in Figure 7 were acquired in cells stably expressing ErbB3 in the background of low, endogenous ErbB2.

Results of simulations to evaluate the relative enhancement of the ErbB3^E933Q mutant as a better activator are shown in Figure 8D. Performed in the BioNetGen platform with ratio of 1 ErbB2:20 ErbB3, these simulations show that the progressive increase in ErbB3^WT phosphorylation levels off as a function of ligand occupancy. If we simply apply a multiplier of 2 or 3 for the activation function, we do observe an overall increase in phosphorylation. However, the lack of intersection between the slopes is not a perfect fit for the experimental data in Figure 7A, indicating that the ErbB3^E993Q mutation may have additional influence on ErbB3 behavior, possibly by affecting the recruitment of adaptor proteins.

DISCUSSION

We presented a combination of experimental and computational methods to explore the relationship between ErbB2 and ErbB3. We also established a framework for evaluating the growing list of ErbB family mutations. Our experimental portfolio captures receptor dynamics, including state-dependent diffusion coefficients and spatial analysis of receptors in confinement zones. Despite the close relationship between these receptors, the membrane features that transiently entrap ErbB2 and ErbB3 appear to occupy distinct areas and are only partially overlapping. We developed a new algorithm to estimate the area and highly variable shapes associated with these membrane features. We used the results to create a membrane landscape for our 2D spatial stochastic simulation. Our rule-based model uniquely captures the essential features of diffusion-limited dimerization reactions and considers other complex factors, such as conformation, ligand occupancy, differential dimer lifetimes, and the asymmetrical orientation of paired kinase domains within a dimer. Our simulations predict that most individual receptors cycle rapidly and continuously through monomer and dimer states. They shuffle partners and switch roles as activator and receiver through the stochastic, asymmetric orientation of their kinase domains (Pryor et al., 2013).

Until recently, it was believed that the kinase domain of ErbB3 was completely dead. Shi et al. (2010) reported weak kinase activity for recombinant ErbB3 cytoplasmic tails tethered to liposomes. In conjunction with evaluating ErbB2/3 interactions by single-molecule methods, we made the novel observation that ErbB3 kinase activity is significantly up-regulated in an ErbB2-dependent manner and linked to its phosphorylation state (Steinkamp et al. 2014). Although the putative phosphorylation site that activates ErbB3 has not yet been identified, the ErbB2-mediated activation of ErbB3 is a major assumption in our mathematical model. We specifically sought insight into important gaps in our knowledge of their complex interplay, particularly ErbB3’s unique dependence on a heterodimerizing partner such as ErbB2.

The results of our model confirm that ErbB2 is critical to ErbB3 activation, as proposed by others (Wallasch et al., 1995; Pinkas-Kramarski et al., 1996; Holbro et al., 2003; Baselga and Swain, 2009). However, the presence of ErbB2 alone does not explain the complex regulation of ErbB2-ErbB3 cosignaling. BioNetGen results in Supplemental Figure S4 show that the relative ratio of each receptor species is an important variable because it heavily weights the steady-state distributions of homodimers and heterodimers and the resulting signaling output. As receptors diffuse and collide, dimerization is restricted to pairs of conformationally competent receptors. Whereas ErbB2 is assumed to always adopt the extended conformation that exposes its dimerization arm (Garrett et al., 2003), ErbB3’s upright form must be stabilized by ligand. Indeed, to prevent a predominance of ErbB2 homodimers, we found it necessary to restrict ErbB2 self-association by imposing a very low on-rate through a probability term. Our need for a low on-rate is consistent with work by Garrett et al. (2003), who implicated electrostatic repulsion at the homodimer interface as a mechanism to restrict ErbB2 homointeractions. A high density of ErbB2 can override this restriction (Supplemental Figure S7), which is also consistent with ErbB2-driven signaling in breast and other epithelial cancers with ErbB2 gene amplification (Hynes and MacDonald, 2009; Chen et al., 2014).

One unexplored parameter is the potential for “repositioning” of the C-terminal tails to swap the receiver/activator status of monomers within dimers (Macdonald-Obermann et al., 2012). We await the development of new experimental methods to measure and validate the intriguing possibility that asymmetrically oriented kinase domains can reshuffle while their extracellular domains are engaged in dimers.

Our simulation results are in good agreement with the experimental data, motivating extension of the model to explore potential mechanisms governing ErbB3 oncogenic mutations. Our approach was to vary key model parameters and evaluate their potential to up-regulate overall ErbB3 phosphorylation levels or alter dimerization properties. Because some mutations in ErbB3 fall in the extracellular domain (Jeong et al., 2006; Jaiswal et al., 2013), which is implicated in forming and maintaining ErbB dimer contacts (Ferguson et al., 2003; Franco-Gonzalez et al., 2013), one set of simulations explored the effect that these might have on dimer dissociation rate. Because ErbB3 mutations within the cytoplasmic tail occur in both the catalytic domain and the N-lobe/C-lobe interface, we considered the potential effect of mutations that might enhance the activator and receiver functions of receptors in dimers. When compared with experimental evaluation of the ErbB3^E933Q gain-of-function mutation, our simulations suggest that one outcome of this mutation may be to render ErbB3 a better “activator.” Of interest, certain oncogenic EGFR mutants that lie within the core of the kinase domain have been shown to prefer binding as receivers or “superacceptors,” suggesting that mutations in the kinase domain may have long-range effects on conformation (Red Brewer et al., 2013). Finally, we note that mutations in an RTK kinase domain may have unexpected effects on the extracellular domain, dimer stability, or the docking of signaling partners. Members of our group have recently characterized activation mutations of EGFR associated with non–small cell lung cancer, with the discovery that these kinase domain mutations facilitate ligand-independent dimerization with an off-rate that is similar to that of ligand-bound dimers (Valley et al., 2015). A future goal is to apply the predictive power of our model to additional gain-of-function and inactivating mutations in all of the ErbB family members, providing insight into the mechanisms by which they drive carcinogenesis and contribute to drug resistance.

MATERIALS AND METHODS

Experimental

Stable coexpression of ErbB2 and ErbB3 and determination of average receptor numbers.

A hemagglutinin peptide (HA) tag was introduced after the signal peptide but 5′ of the mature ErbB2 coding sequence and cloned into the pcDNA3.1 vector using the pcDNA3.1 Directional TOPO Expression Kit (Life Technologies, Grand Island, NY). CHO cells were sequentially transfected with the pcDNA3.1-^HAErbB2 and a pcDNA6-ErbB3-mCitrine construct and selected using G418 and blasticidin. Stably transfected cells were flow sorted on the iCyt SY3200 (Sony Biotechnologies, San Jose, CA) at the University of New Mexico Shared Flow Cytometry and High Throughput Screening Resource to obtain comparable expression levels of both receptors. The average receptor number for the sorted population was determined by flow using the LSR Fortessa Flow Cytometer (BD Biosciences, San Jose, CA) after labeling of live cells with Alexa 647–labeled anti-ErbB2 or anti-ErbB3 antibodies. Quantum MESF Alexa 647 microspheres (Bangs Laboratories, Fishers, IN) were used to quantify the fluorescence of the labeled cells. Receptor number was determined based on the average of two experiments performed on separate days.

Determination of the dephosphorylation rates for ErbB2 and ErbB3.

CHO cells stably expressing ^HAErbB2 and ErbB3-mCit were seeded and incubated overnight. Cells were then serum starved for up to 4 h and stimulated for 2 min at 37°C with 12 nM (75 ng/ml) heregulin-β (US Biological, Salem, MA). Cells were then treated at 37°C with 10 μM sapitinib (Selleckchem, Houston, TX) to inhibit ErbB kinase activity and harvested 20 s to 12 min after HRG activation. Controls were harvested at the same time points plus HRG without sapitinib treatment. At each time point, medium was removed, cells were washed with ice-cold 1× phosphate-buffered saline (PBS), and the plate was floated on liquid nitrogen to snap-freeze cells. Cells were then harvested in lysis buffer, and total protein levels were determined by bicinchoninic acid (BCA) assay with the Pierce BCA Protein Assay Kit (Life technologies). A total of 20 μg of protein/sample was run on an acrylamide gel and transferred to nitrocellulose membranes using the iBlot system (Life Technologies). Phosphorylated ErbBs were detected using phosphorylation-specific polyclonal rabbit antibodies: ErbB3 PY1289 or PY1197 and ErbB2 PY1248 or PY877 (Cell Signaling, Danvers, MA). Labeling with anti–β-actin mouse monoclonal antibody (Sigma-Aldrich, St. Louis, MO) was used as a loading control. Secondary anti-rabbit and anti-mouse horseradish peroxidase (HRP) were from Santa Cruz Biotechnology (Dallas, TX). Blots were revealed using the SuperSignal West Pico Chemiluminescent Substrate (Life Technologies) and detected on a ChemiDoc XRS+ Gel Imager (Bio-Rad, Hercules, CA). Bands were quantified using ImageLab quantification software (Bio-Rad). Data were plotted and fitted to a one-phase exponential decay curve using GraphPad Prism5 (GraphPad Software, La Jolla, CA). The dephosphorylation half-life was calculated from this curve.

Constructing a homology model for the extracellular domain of ErbB3.

Studying molecular interactions between ErbB3 monomers and ErbB3 with its ligand requires a structural model of ErbB3 that represent the “proud” or upright conformation of the extracellular domain (ECD). Only the “tethered” conformation of the ErbB3-ECD has been crystalized, and it is available in the Protein Data Bank (PDB; Berman et al., 2000). Because the ErbB3-ECD has >40% sequence identity with the EGFR-ECD, we constructed a homology model for the ErbB3-ECD with the help of the known crystal structure of the upright conformation of the EGFR-ECD. We used EasyModeller (version 2.0; Kuntal et al., 2010), a graphical interface for MODELLER (Fiser and Šali, 2003), to construct a crude homology model of the ErbB3-ECD. The sequence of ErbB3-ECD was extracted from the UniProt database. The sequence used for modeling contains the ECD of ErbB3 without the signaling peptide (UniProt ID: P21860[20-643]). The source of template structure was the crystal structure of EGFR-ECD (PDB code: 3NJP), which represents a homodimer, both monomers in the upright conformation. Therefore it was necessary to separate the monomers and use each of them as a template structure in the homology model construction process. Using the ErbB3-ECD sequence and one of the template structures, EasyModeller performed the sequence alignment and generated the homology model. Accordingly, two homology models were built for the ErbB3-ECD. Note that the resultant homology models were mainly used for simulating interactions between macromolecules. Therefore the crude models were acceptable without further optimization. However, future optimization and refinement of the models might be beneficial.

Cryo-EM of recombinant HRG-bound ErbB3.

The ErbB3Δ expression vector, pcDNA3.1-ErbB3Δ-CBP-SBP, was constructed using fusion PCR. The calmodulin-binding peptide (CBP) and streptavidin-binding peptide (SBP) tags were amplified from the pCTAP vector (Agilent Technologies, Santa Clara, CA) and fused to the C-terminal of ErbB3Δ, a truncated version of ErbB3 (amino acids 1–998) lacking the unstructured C-terminal tail. The construct was transfected into HEK293 cells by electroporation using the Amaxa Nucleofector, Solution V, program Q-001 (Lonza, Basel, Switzerland). Stable transfectants were selected with G418 and sorted for surface expression of ErbB3 on the iCyt SY3200. Cell pellets from ErbB3Δ-CBP-SBP stably expressing cells were freeze/thawed and resuspended in 20 mM Tris, pH 8.0, 400 mM NaCl, 10% glycerol, 0.2% Triton X-100, and 1 mM EDTA plus protease inhibitor cocktail, incubated for 1 h on ice, and cleared by centrifugation at 25,000 × g for 30 min at 4°C based on methods described by Mi et al. (2008). ErbB3Δ-SBP was purified using the InterPlay Mammalian TAP System (Agilent) and stored at −80°C. To encourage dimerization, aliquots of thawed sample (∼2 μM ErbB3Δ-SBP) were incubated with 5 μM HRG in kinase reaction buffer (2 mM ATP) for 30 min on ice. ErbB3Δ-SBP plus HRG sample was applied to Quantifoil R 1.2/1.3 holey carbon film 400 mesh copper grids (Quantifoil Micro Tools, Jena, Germany) and manually plunge-frozen in liquid nitrogen–cooled liquefied ethane. Images of the vitrified samples suspended over holes were obtained under low-dose conditions using a 626 single-tilt liquid nitrogen cryotransfer holder (Gatan, Pleasanton, CA) on a Tecnai G2 T12 Twin transmission electron microscope (FEI, Hillsboro, OR) equipped with a Lab6 filament (Denka Corporation, Chuo-ku, Tokyo, Japan) operated at 120 kV. Micrographs were recorded on Kodak ISO-163 plates (Eastman Kodak, Rochester, NY) with a total dose of 20–50 e⁻/Ų at a nominal magnification of 67,000 and at 2.5-μm defocus. The micrographs were developed in full-strength Kodak D19 developer and digitized using a SCAI scanner (Integraph, Leica Geosystems, Norcross, GA) at 7-μm raster. In total, 7310 particles were manually picked from the micrographs. Iterative sorting and refinement procedures were applied following established protocols (Xu et al., 2012). A homogeneous subset of 3108 particles was used to obtain a three-dimensional reconstruction corresponding to an Erbb3 dimer. Twofold symmetry was apparent in the reconstruction and was applied in subsequent refinement runs to improve the reconstruction quality.

Immunoprecipitation.

CHO cells expressing ErbB constructs were serum starved for up to 4 h. CHO ErbB3^wt-mCitrine cells were stimulated with 12 nM HRG for 2 min. All cells were washed with ice-cold PBS on ice and lysed with cold NP-40 lysis buffer (Yang et al., 2007). Protein concentrations in cleared lysates were measured by BCA assay (Pierce, Rockford, IL). Supernatants were precleared with Protein A beads (Amersham GE Healthcare, Chicago, IL) and normal rabbit immunoglobulin G (Cell Signaling) followed by overnight incubation at 4°C with primary antibodies against ErbB2 (RB9040; Neomarkers) or ErbB3 (sc285 [Santa Cruz Biotechnology] or ErbB3-XP [Cell Signaling]). Proteins in immune complexes were either resuspended in reaction buffer for the in vitro kinase assay or denatured and separated by SDS–PAGE, transferred to nitrocellulose, and probed with the pan-PY antibody anti-PY20-HRP (Santa Cruz Biotechnology) to detect all phosphorylated proteins in the immunoprecipitate or with primary antibodies against ErbB2 or ErbB3 and HRP-conjugated secondary antibodies. Blots were revealed and detected as described.

Sequencing of ErbB3 from SKBR3 Cells.

mRNA was extracted from SKBR3 cells using the RNeasy Mini Kit (Qiagen, Chatsworth, CA). Pairs of primers were designed to span the ErbB3 tyrosine kinase domain: 5′-CTC TGG ACC CCA GTG AGA AG-3′ and 5′-GGG AGT ACA AAT TGC CAA GG-3′; and 5′-GGT CAG CCA CAC CAA AAT CT-3′ and 5′-CAG ATA CCG TGG TGG GTC TC-3′. After amplification using the Qiagen One-Step reverse transcription (RT)-PCR kit, PCR products were separated by agarose gel electrophoresis, extracted with the QIAquick gel extraction kit, and sequenced using the foregoing primer sets.

In vitro kinase assay.

The in vitro kinase assay was performed as detailed in Steinkamp et al. (2014). Briefly, CHO cells expressing either ErbB3^wt-mCitrine or ErbB3^E933Q-mCitrine were serum starved and then stimulated for 2 min with 3.2 nM HRG-β. Lysates were immunoprecipitated with the anti-ErbB3 polyclonal rabbit antibody sc-285 (Santa Cruz Biotechnology). Kinase activity was measured based on the ability of the immunoprecipitated ErbB3 to phosphorylate an EAY peptide substrate (Sigma-Aldrich).

Single-particle tracking.

The E933Q mutation was introduced into an expression vector pcDNA3.1-^HAErbB3 and stably transfected into CHO cells. CHO ^HAErbB3^E933Q cells were sorted for high expression after labeling with an anti–HA-Alexa 488 antibody (Cell Signaling). Single-particle tracking experiments were performed as in Steinkamp et al. (2014). Briefly, CHO ^HAErbB3^E933Q cells were plated in LabTek eight-well chambers (Life Technologies) the day before imaging. Heregulin was biotinylated using NHS-ester chemistry with Biotin-XX-SE (Life Technologies) and purified from free biotin on a G25 column by gravity flow. Biotinylated HRG and biotinylated anti–HA Fab (Sigma-Aldrich) were conjugated to streptavidin QDots (Life Technologies) QD655 and QD585 in a 1:1 M ratio in PBS plus 0.1% bovine serum albumin (BSA) by rotating for ≥1 h at 4°C. Cells were serum starved for 1 h and then moved into Tyrode’s buffer supplemented with 1% BSA and 20 mM glucose. Cells were labeled with 100 pM QD-anti-hemagglutinin peptide tag (HA) Fab for 15 min or 20 pM QD-HRG for 5 min before washing and imaging at 20 frames/s on an Olympus IX71 inverted microscope with a 60×/1.2 numerical aperture water objective. An objective heater (Bioptechs, Butler, PA) was used to stabilize chamber temperature at 34–35°C. A mercury lamp with a 436/10-nm band-pass (BP) excitation filter provided wide-field excitation. Emission was collected by an electron-multiplying charge-coupled device camera (Andor iXon 887) using an Optosplit II image splitter (Cairn Research, Kent, United Kingdom) to image both QD585 (585/20-nm BP) and QD655 (655/40-nm BP) probes. Image processing was performed using Matlab (MathWorks, Natick, MA) functions in conjunction with the image processing software DIPImage (Delft University of Technology, Delft, Netherlands). Single-molecule localization, trajectory elongation, and two-channel image registration were performed as previously described (Smith et al., 2010; Low-Nam et al., 2011; Steinkamp et al., 2014).

State determination of receptor pairs.

Receptor interactions were identified in the single-particle tracking data using a three-state hidden Markov model (HMM) in which two-color QD candidate pairs (one QD⁵⁸⁵ and one QD⁶⁵⁵) that are <1 μm apart are assigned to one of three states—separated, coconfined, or interacting (Low-Nam et al., 2011)—for each time step. Distribution of the displacements between the QDs is modeled by a zero-mean Gaussian distribution in each (x, y) dimension using σdimer and σdomain, respectively. The value σdimer for ErbB3 was estimated based on the EGFR crystal structure, erbB homology modeling, and the size of QDs (Steinkamp et al., 2014). For the separated state in the model, the probability density is calculated as a function of the observed distance in the previous frame and a characteristic diffusion constant. Rate constants are determined by maximizing the likelihood over all interactions of two QDs for a specific condition. Standard errors for parameters are calculated as (H_i,i^–1)^–0.5, where H is the Hessian matrix of the negative log-likelihood and i denotes one of the estimated rate constants. The Viterbi algorithm (Forney, 1973) is used to identify the most likely state within individual QD interactions. Diffusion by state was calculated based on the mean-squared displacement of all tracks per condition.

Modeling

Modeling biological assumptions.

Our model assumes that ErbB3 dimerization occurs through conventional interactions between dimerization arms of the extracellular domains as shown for EGFR (Yarden and Sliwkowski, 2001). This premise is supported by evidence that blockade of the ErbB2 dimerization arm with 2C4 antibodies ablates its transactivation of ErbB3 (Zhang et al., 2009; Steinkamp et al., 2014), as well as homology models of ErbB2/ErbB3 heterodimers based upon the structure of EGFR homodimers (Franco-Gonzalez et al., 2013). We do not formally consider the possibility that ErbB3 may engage in homointeractions through other interfaces (Zhang et al., 2012), due to the lack of available kinetic parameters. We also do not consider the intriguing possibility for higher-order oligomers (Kani et al., 2005; Kozer et al., 2013) because the sparse labeling of SPT renders it highly unlikely that such events can be captured and measured using our available technologies.

Nonspatial modeling in BioNetGen.

We used BioNetGen to create a nonspatial version of our model; it was used for computationally efficient exploration of parameters.

Spatial stochastic model for homodimerization and heterodimerization

Domain reconstruction algorithm.

To score each point in each trajectory from a single file and channel, the length of the jump is compared for varying step sizes. Compiling and comparing these scores against one another reveals a bimodal distribution in the scores. The local minimum of the modes is used as a cutoff score. This score separates the trajectory points into confined points and freely diffusing points. This step takes the dynamic SPT data and creates a subset of static data. The slow points are considered to be representative of confined areas on the membrane. The slow points are then clustered to determine confinement areas or domains. A characteristic length study is first done to determine the characteristic length that best describes the distance between points in a cluster. This length is varied from 0 to 1000 nm. Over this range, the average perimeter of the clusters is computed. The perimeter reaches a local minimum over this range. The characteristic length at which this minimum is reached is used as the characteristic length. The characteristic length is then used to create the clusters. Each cluster is then used to create a contour that will define the final confinement area. The contour is created by padding the cluster. Outside points of the cluster are extended outward by one-half of the characteristic length. This allows some give in the confinement area to consider that these points could have bounced off a structure and would not have sat directly next to the confining structure. The extended points are then connected to create a contour. This is the final domain structure.

Reaction network generation.

Our reaction network definition begins with the interaction model proposed by Steinkamp et al. (2014). In this model, ErbB2 receptors dimerize with ErbB3, allowing ErbB2 to activate (phosphorylate) ErbB3. These dimer interactions appear to be transient and quickly fall apart. The activated ErbB3 receptor is then free to homodimerize with another ErbB3. The activated state of the ErbB3 allows it to illicit kinase activity from the unphosphorylated ErbB3, causing activation and therefore phosphorylation. We extend this model slightly by implementing the asymmetric phosphorylation model used in our previous ErbB1 activation article (Pryor et al., 2013).

Receptor diffusion and reaction kinetics.

Receptors diffuse according to Brownian motion through a combination of specific diffusion coefficients calculated from SPT experiments and normally distributed random variables. Diffusion is interrupted when a membrane domain is encountered in the receptors path. To account for this obstacle, two tolls are considered: entrance into the domain and exit from the domain. The entrance and exit rates of the domains are converted into probabilities using the simulation time-step. When a receptor attempts to enter or exit a domain, the relevant probability is evaluated, and either the receptor is allowed to leave the domain or the receptor is reflected back into the domain.

Receptor reactions are treated differently depending on their reaction order. First-order reactions are treated similarly to the domain entrance/exit tolls. The reaction rate is converted into a probability using the time-step and evaluated. If the probability is met, the reaction occurs, and if it is not met, no reaction occurs. Second-order reactions are a bit more complicated. These reactions are diffusion limited, and therefore the spatial aspect of the model must be taken into consideration. The solution to this problem, proposed by Andrews and Bray (2004), is to use a binding radius and unbinding radius, if the reaction is reversible (Andrews and Bray, 2004). The binding radius is a function of simulation time-step, receptor diffusion coefficients, and receptor on-rates. At the end of a receptors diffusion step, the area around the receptor bounded by the binding radius is scanned for other receptors. If an available receptor is found within the binding radius, a reaction occurs. There is no probability associated with second-order reactions; likelihood of reaction is taken into consideration through the binding radius. If a reverse reaction is possible, an unbinding radius is implemented. The length of the unbinding radius is picked such that an unrealistic number of repeated interactions is minimized. Andrews and Bray (2004) suggest that the ratio of binding to unbinding radius be 20% as a starting point.

Glossary

Abbreviations used:

DRA

domain reconstruction algorithm

HRG

heregulin

PY

phosphotyrosine

QD

quantum dot

SPT

single-particle tracking

WT

wild type.