Task-Specific Stability of Multi-Finger Steady-State Action

Abstract

We explored task-specific stability during accurate multi-finger force production tasks with different numbers of instructed fingers. Subjects performed steady-state isometric force production tasks and were instructed “not to interfere voluntarily” with transient lifting-and-lowering perturbations applied to the index finger. The main results were: (1) Inter-trial variance in the space of finger modes at steady states was larger within the subspace that had no effect on the total force (the uncontrolled manifold, UCM); (2) Perturbations caused large deviations of finger modes within the UCM (motor equivalence); and (3) Deviations caused by the perturbation showed larger variance within the UCM. No significant effects of the number of task fingers were noted in any of the three indicators. The results are discussed within the frameworks of the UCM and referent configuration hypotheses. We conclude, in particular, that all the tasks were effectively four-finger tasks with different involvement of task and non-task fingers.

Introduction

At multiple levels of analysis, the human body has more elements at its disposal to enact a given task than it has task-related constraints. This design is sometimes viewed as a source of computational problems for the central nervous system (CNS) – problems of motor redundancy – that have to be solved, for example, by means of optimization (reviewed in Prilutsky and Zatsiorsky 2002). Alternatively, within the principle of abundance (Gelfand and Latash 1998; Latash 2012), this design may be viewed as crucial for the ability of the CNS to organize such sets of elements into flexible structures that ensure task-specific stability of motor actions (Schöner 1995).

In recent studies, stability of actions by abundant sets of elements has been explored using three main approaches. First, analysis of the structure of inter-trial variance during multiple repetitions of a given task assumes that each trial begins from a slightly different internal state, and that variance along less stable directions will be larger. This approach has been developed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999). Within this analysis, inter-trial variance in the space of elemental variables is partitioned into two components: variance within the UCM (V_UCM), which does not affect a task-specific performance variable, and variance orthogonal to the UCM (V_ORT), which does affect the performance variable. Task-specific stability can be characterized by an inequality V_UCM > V_ORT.

Second, if a small, transient perturbation is applied during the execution of a steady-state task, inter-trial variance of the difference in elemental variables between initial and final conditions is expected to be larger in directions of relatively low stability. As such, perturbations are expected - and have been experimentally shown - to lead to a higher inter-trial variance in elemental variables along directions that kept the task-related salient performance variable unchanged (Wilhelm et al. 2013) than in directions that led to changes in that variable.

Third, net displacements between an initial and final steady state caused by a transient perturbation may be analyzed. These displacements are expected to be large in directions within the corresponding UCM (addressed as motor equivalent, ME; Mattos et al. 2011). While there is no obligatory connection between the three methods, they may be expected to lead to consistent results reflecting task-specific stability of the system. To our knowledge, so far, no study has used all three methods applied to a single data set.

The present study was primarily motivated by an earlier experiment (Wilhelm et al. 2013) that used the “inverse piano” device (Martin et al. 2011; also see Methods) to produce a transient perturbation of a finger during accurate four-finger force production tasks. That study explored the structure of inter-trial variance in the finger force changes induced by the perturbation and showed that most variance was within the UCM. Here we used this method across tasks with different numbers of explicitly involved fingers (two, three, and four). We also used all three aforementioned methods to quantify indices of task-specific stability. Increasing the number of instructed fingers for tasks with only one task-specific performance variable (total force) affords the system more ways to vary without affecting the task performance. Hence, we hypothesized that: During steady states, V_UCM > V_ORT and the difference between the two would increase as more fingers were involved in the task (Method 1; Hypothesis-1); the same would be true for variance indices calculated using the difference in individual finger force production induced by the transient perturbation, from the beginning to the end of the trials (Method 2; Hypothesis-2); and the ME component of the four-finger displacement would increase as more fingers were involved (Method 3; Hypothesis-3).

Methods

Subjects

Eight self-reported right-handed subjects were recruited for this study. Subjects' ages ranged from 23–36 years; they included four men and four women. Subjects were healthy, had no history of hand injury, and did not participate professionally in activities likely to significantly alter their dexterity. All subjects provided informed consent in accordance with procedures approved by the Office of Research Protections at The Pennsylvania State University.

Apparatus

Data were recorded and perturbations were applied by means of the "inverse piano" apparatus (Martin et al. 2011). This custom-built piece of equipment uses four PCB 208C01 single-axis piezoelectric force transducers (PCB Piezotronics, Depew, NY) to record finger forces from four fingers. The force sensors are mounted on individual Linmot PS01-23×80 linear actuators (Linmot, Spreitenbach, Switzerland) and are controlled by a Linmote E400AT four-channel servo drive such that each sensor can move vertically with a finger during experimental procedures. Force data were sent from each transducer to its respective PCB 484B11 signal conditioner (one per sensor); the analog data were then digitized at 300 Hz using a 16-bit PCI-6052E analog-to-digital card (National Instruments Corp., Austin, Tx). Before each trial, sensor readings were zeroed while the subjects' fingers rested on the sensors, ensuring that the weight of the fingers was not included in force measurements. Visual feedback to the subjects was provided by means of a 19" monitor placed 0.8 m from the subject. Data collection, actuator control, and visual feedback to the subject and experimenter were all managed by means of a customized program running in a National Instruments LabVIEW environment. Although subjects were asked to press with varying numbers of fingers during the procedure, they were always presented with feedback on the total force they produced with all four fingers regardless of the number of fingers they were instructed to use. An illustration of the “inverse piano” is included as Panel A of Figure 1.

Figure 1.

Panel A shows the succession of experimental conditions, which each subject was assigned. While the order of the first two conditions was obligatory, the order of the succeeding four conditions was randomized; however, in I and IM pressing conditions, I-perturbation conditions always preceded R-perturbation conditions. Data from the shaded condition (I-pressing) are not presented here. Panel B shows a schematic of the Inverse Piano device, from the top (with the front of the device at the bottom of the figure), and from the front. Only the sensors (and drive shafts during perturbations) protrude through the table top; the actuators are mounted under the table.

Experimental Procedure

The full experimental procedure comprised of three main tasks. In the first task, each subject was instructed to press as hard as possible on each sensor in order for the experimenter to measure the subject's maximal voluntary contraction (MVC) force. The collection of the MVC force allowed the force levels for subsequent tasks to be adjusted according to the subjects' capacities for force production. In each MVC trial, subjects were given 6 s to produce MVC in a smoothly increasing manner. Each subject repeated the MVC task two times and was required to rest for 30 s in between trials.

In the second task, subjects produced force ramps with individual fingers. Subjects were instructed to produce force using a specific (instructed) finger and follow a target force trajectory. The subject always received feedback on total force produced by all four fingers. The target force corresponded to 5% of the instructed finger's contribution to the 4-finger MVC for 2 s, a smooth increase from 5% to 45% of the instructed finger's MVC contribution over 6 s, and finally 2 s at 45% of the instructed finger's MVC contribution. This task involved four repetitions so that each finger was the task finger for one trial. The data from these trials were used to calculate enslaving matrices (Zatsiorsky et al. 2000; discussed in more detail later).

The third task was the main experimental task for this study. Each trial in this task lasted for 12 s and had the same basic form: for the first 6 s, the subject was provided with visual feedback on total force (F_TOT) and instructed to reach and maintain a target force level. After the first 6 s, visual feedback on F_TOT was removed, so the subject could only see the line, which corresponded to the target force level. There were four combinations of fingers with which subjects were instructed to press (instructed fingers): Index only (I), Index and Middle (IM), Index, Middle, and Ring (IMR), and all fingers (IMRL). While data were collected for the I-pressing condition, they are not presented here. The task force was always set to 20% of the instructed fingers' contribution to the 4-finger MVC; for example, for the IM task, F_TOT was set at 20% of the sum of the forces of the I and M fingers at the time of peak F_TOT in the four-finger MVC task. No subjects reported fatigue during the course of the procedure.

Contemporaneously with the disappearance of visual feedback on their force production, in most trials, one of the subject's fingers was perturbed by being raised by 1.0 cm at 2.0 cm/s, held in place for 1.5 s, and then lowered to its initial position at −2.0 cm/s. The first three trials in each finger-pressing condition were controls: visual feedback on F_TOT was removed, but no finger was moved. After those initial trials, trials with perturbations were performed. Across all conditions, the perturbation was applied to the I finger. In addition, in the I and IM conditions, R finger was also perturbed, but these data are not going to be presented here. Each subject performed 24 consecutive perturbation trials for each finger-pressing condition. Subjects paced themselves through each series of 24 perturbation trials and were required to rest for 30 s after each series. Finger-pressing conditions were randomized. This sequence of experimental conditions is illustrated in Figure 1, Panel B.

Data Processing

In the MVC trials, the forces produced by individual fingers were recorded when the total four-finger force was at its peak magnitude. Although fairly infrequent, sometimes recording errors corrupted the data we collected; these trials needed to be excluded from our results. The largest number of corrupted trials for a single subject was two. In order to maintain a balanced number of observations for each subject, when a subject had fewer than two corrupt trials, we rejected the one or two trials with largest deviations from that subject’s mean performance per condition. As a result, each subject’s performance over 22 accepted trials was analyzed. For the main trials, all accepted trials for a given condition were time-aligned.

Calculation of the Enslaving Matrix and Finger Modes

Even when a person attempts to produce force with only one finger, the rest of the fingers of his or her hand also produce force; this phenomenon is called enslaving or lack of finger individuation (Kilbreath and Gandevia 1994; Li et al. 1998, Zatsiorsky et al. 2000; Schieber and Santello 2004). We quantified enslaving individually for each subject by constructing a 4 × 4 enslaving matrix [E] using the data collected from each of the force production ramp tasks. In each of these tasks, the force produced by all four fingers increased even though only one finger was instructed to produce force. Linear regression was used to quantify the contribution of each finger's force to F_TOT:

$${\mathrm{F}}_{\mathrm{i},\mathrm{j}}={{\mathrm{F}}_{\mathrm{i}}}^0+{\mathrm{k}}_{\mathrm{i},\mathrm{j}}\times {\mathrm{F}}_{\text{TOT},\mathrm{j}},$$ (1)

where i, j = {I,M,R,L}, F_TOT,j is the total force produced by all fingers when j is the instructed finger, and F_i,j is the force produced by finger i when j is the instructed finger. The constants k_i,j were taken as representing partial derivatives of total force with respect to individual finger forces and arranged into [E]. F_i⁰ is the intercept calculated from each regression; it may be thought of as the initial force level for a given enslaved finger in the ramp trial when the total force is zero; values of F_i⁰ were very close to zero and they do not appear in [E], which is composed only of the regression slopes. Subsequently, we used [E] to calculate modes, which are hypothetical commands to fingers, which can be modified by the central nervous system one at a time (Latash et al. 2001; Danion et al. 2003):

$$\mathbf{m}={[\mathbf{E}]}^{-1}\mathbf{F},$$ (2)

where m is a 4 × 1 vector of mode values and F is a 4 × 1 vector of force values. It should be noted that, according to this methodology, finger modes are expressed in newtons, and the sum of finger modes at a given time point will be identical to the sum of finger forces at the same point; the mode analysis re-apportions total force to each finger mode according to the observed interdependence of digits during ramp trials.

Analysis of multi-finger actions can be performed in both force and mode spaces. Within this study, all the methods of analysis of the main task compared finger force changes and variances in different directions within the space of elemental variables, forces or modes. We have assumed that enslaving is a robust phenomenon seen across tasks and force ranges (Li et al. 1998; Danion et al. 2003). It is expected to lead to finger force inter-dependence and, hence, to unequal magnitudes of force changes and variances in different directions in the finger force space. This could potentially lead to false positive or false negative conclusions depending on the selected performance variable with respect to which analysis is performed. Using finger modes is expected to eliminate the inter-dependence among the elemental variables and alleviate or even remove this potential problem.

Analysis of the Main Task

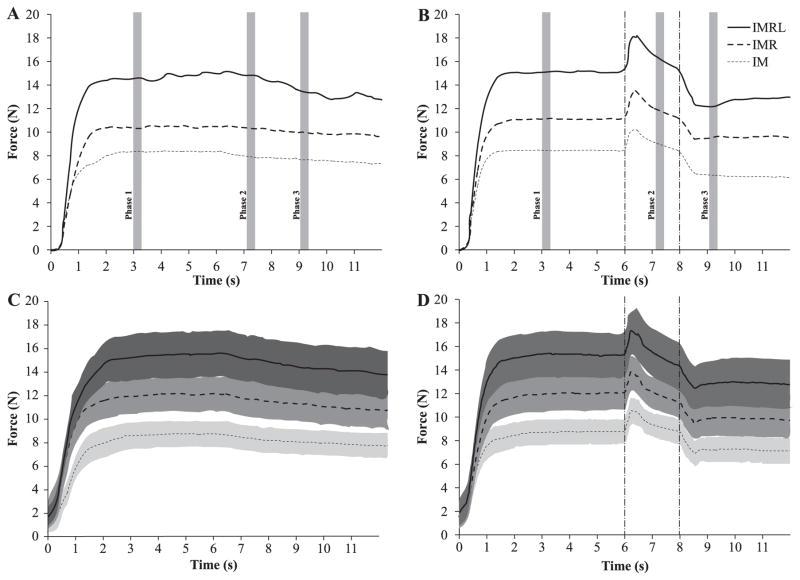
Over the course of the experimental trials - which required subjects to accurately produce and maintain a given amount of force - subjects displayed relatively consistent behavior. Panels A and B of Figure 2 show a typical subject's performance for the IM (thin dotted line), IMR (thick dotted line) and IMRL (thick solid line) tasks during control (A) and perturbation (B) trials. Panels C and D show time series of the mean performance for all subjects with shading representing the associated standard error of the means (SEM) for the same three finger-pressing conditions (identified with the same line styles as in panels A and B) for control (C) and perturbation (D) trials. It is important to note that, while each subject performed a task normalized to his or her force-production capabilities, the data in panels C and D are in newtons and are not normalized; as such, the SEM is representative of both inter-subject variance in force production during trials as well as inter-subject variance of force target levels (scaled to the corresponding MVC values) for each condition.

Figure 2.

Panels A and B show the average across trials performance of a representative subject for the IM, IMR, and IMRL tasks. Control trials (without perturbations) are shown in Panel A and C and perturbation trials in Panel B and D. Panels C and D show the mean performance across all subjects in newtons with standard error shades. Note that while subjects performed each task at a level, which corresponded to 20% of his or her MVC (with the fingers to be used in the condition), these data to not reflect this experimental normalization. The figure accurately conveys the fact, however, that target force increased with each finger added to the task. Shaded vertical stripes represent the three 250-ms phases during which subjects' performance was analyzed. Vertical dotted lines represent the time the sensors started moving upward (first line) and when they began moving downward (second line).

We chose three 250-ms phases during which to analyze subjects' behavior: phase-1 was defined to be well before the perturbation in order to define a pre-perturbation steady state and was therefore set from 3.00–3.25 s from perturbation onset. Next, phase-2 was defined to occur during the middle of the time the perturbed finger was lifted (7.23–7.48 s); note that it is not midway between the onset of the perturbation, but is rather midway between the end of the upward perturbation (when the sensor stopped moving) and when the sensor began to move downward again. Finally, phase-3 was a post-perturbation steady state (8.92–9.17 s). These phases, as well as their relations to the perturbations, can been seen in Figure 2 (vertical dotted lines represent the times at which the sensors began moving upward and downward).

Analysis of Force Change

For each condition, the difference between F_TOT produced in phase-3 and phase-1 (ΔF_TOT) was calculated for each subject. Since ΔF_TOT has been shown to depend on the initial force level (Vaillancourt and Russell 2002; Ambike et al. 2014), we also calculated ΔF_TOT as a percentage of task force.

Analysis of Variance of Finger Forces and Modes

Inter-trial variance in two spaces of elemental variables, those of finger forces (F) and finger modes (m), was analyzed for each subject within the framework of the UCM hypothesis (Scholz and Schöner 1999). According to this hypothesis, the neural control results in different stability properties in different directions within the multi-dimensional space of elemental variables. In particular, relatively high stability (reflected in low across-trials variance) is expected in directions that lead to changes in a potentially important performance variable, while relatively low stability (high variance) is expected in directions that lead to changes in this performance variable. This analysis was performed using the individual finger F (m) data averaged over each of the three phases in each trial. We also applied this analysis to the differences in the forces (modes) between phase-3 and phase-1 computed for each trial separately. This analysis quantifies variance in two spaces, the UCM (where F_TOT is constant) and the space orthogonal to the UCM (ORT, where F_TOT changes). We will refer to these two variance components as V_UCM and V_ORT. Detailed descriptions of V_UCM and V_ORT computation can be found in earlier publications (Latash et al. 2001; Scholz et al. 2002).

For analysis in the force space, the two variance components will be referred to as V_UCM,F and V_ORT,F; for analysis in the mode space, V_UCM,m and V_ORT,m will be used. Analysis of the differences in forces (modes) between phase-3 and phase-1 resulted in variance indices V_UCM,ΔF and V_ORT,ΔF in the force space, and V_UCM,Δm and V_{ORT, m} in the mode space.

An index of multi-finger synergy (ΔV) was computed reflecting the difference between V_UCM and V_ORT after normalization of each of these indices by the dimensionality of the corresponding spaces (3 for V_UCM, 1 for V_ORT). To compare these indices across subjects, they were normalized by total variance (V_TOT), also computed per dimension:

$$\mathrm{\Delta }\mathrm{V}=({\mathrm{V}}_{\text{UCM}}/3-{\mathrm{V}}_{\text{ORT}}/1)/({\mathrm{V}}_{\text{TOT}}/4)$$ (3)

For parametric statistical analysis, ΔV was log-transformed using Fisher's transformation adjusted for its computational limits (−4 ≤ ΔV ≤ 1.33). This resulted in the transformed indices of synergy, ΔV_ZF and ΔV_Zm, in force and mode spaces, respectively.

Analysis of Motor Equivalence

This analysis quantified the force and mode difference vectors (ΔF and Δm) between phase-3 and phase-1. These vectors were projected onto the UCM and ORT spaces. The vector component within the UCM does not affect F_TOT and is therefore called the Motor Equivalent (ME) component. Conversely, the component within ORT does affect F_TOT and is called the non-Motor Equivalence (nME) component (Mattos et al. 2011). As with the described analysis of variance, high deviations are expected in directions of low stability (ME), that is, parallel to the UCM. ME and nME components were computed using the across-trial average values of the ΔF and Δm vectors in each experimental condition. The ME and nME components were normalized by the square root of the dimensionality of their respective spaces.

Statistics

Unless otherwise stated, data are presented as means ± standard errors. Two-way ANOVAs with repeated measures were used to test the effects of Condition (three levels, IM, IMR, and IMRL) and Phase (three levels, phase-1, phase-2, and phase-3) on the main outcome variables such as variance components (V_UCM and V_ORT), synergy index (ΔV), and ME and nME components of force (mode) changes between phase-3 and phase-1. Statistical tests were run in SAS 9.3 (SAS Institute Inc, Cary, NC) using linear mixed models with compound symmetrical covariance structure. When necessary, data were transformed according to statistical assumptions of normality. The Kenward-Roger method was used to adjust test degrees of freedom when necessary. Statistical significance was set at p < 0.05.

Results

General Patterns of Changes in Force Production

Across all three (IM, IMR, IMRL) finger pressing conditions, lifting the index (I) finger resulted in an increase of its force. As the I finger remained in the raised position, the force it produced decreased; when the finger was lowered to its initial position, this force decreased further. Usually, after the raising-and-lowering sequence (in phase-3), the I-finger force was lower than before the perturbation (in phase-1). The fingers, which were not perturbed, showed a drop in their forces when the I finger was raised and an increase in their forces when the I finger was lowered. In general, however, changes in total force (F_TOT) were dominated by the I-finger force changes. In particular, F_TOT at the end of trials (phase-3) was usually lower than at the beginning of trial; this decrease in F_TOT can be seen in Figure 2B. During control trials, F_TOT also decreased from phase-1 to phase-3 (Figure 2A), but this force drop was smaller than in trials with perturbations. These features can also be seen in averaged across subjects force time series (panels C and D in Figure 2). The rather large standard error shades in these panels are primarily due to the differences in the task force levels scaled to the individual MVC force values.

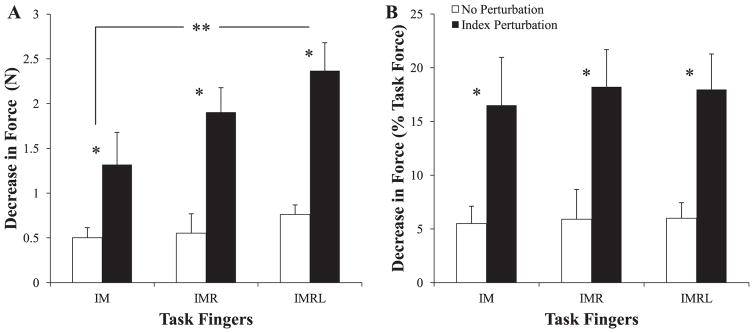
The F_TOT change (ΔF_TOT) was larger as the number of fingers pressing increased: for trials with perturbations, the average magnitude of ΔF_TOT was −1.32 ± 0.36 N, –1.90 ± 0.28 N, and –2.37 ± 0.31 N for the IM, IMR, and IMRL conditions, respectively. In control trials, the magnitudes of force changes were smaller: –0.50 ± 0.11 N, –0.55 ± 0.22 N, and –0.76 ± 0.11 N for the IM, IMR, and IMRL conditions, respectively. Two-way ANOVAs with repeated measures, using factors Condition (3 levels) and Perturbation (2 levels), showed significant effects of both Condition (F_2,35 = 5.67; p < 0.01) and Perturbation (F_1,35 = 62.7; p < 0.001) with no significant interaction. Tukey-Kramer adjusted mean comparisons on Condition showed that only IMRL was significantly different from IM (p < 0.05).

After force changes between phase-3 and phase-1 were normalized by the initial force level (ΔF_TOT.%), the two-way ANOVA showed a significant main effect of Perturbation (F_1,35 = 38.4; p < 0.001), but no effect of Condition (F_2,35 = 0.13; p > 0.8). Figure 3 shows ΔF_TOT (A) and ΔF_TOT.% (B) for perturbed trials (closed bars) and unperturbed trials (open bars) with associated significance.

Figure 3.

The magnitude of the decrease in total force, ΔF_TOT, from phase-1 to phase-3. Mean values across subjects with standard error bars and shown in panel A. Panel B shows the mean magnitudes normalized by the force subjects were instructed to produce at phase-1. * denotes significant differences in ΔF_TOT between perturbed and unperturbed trials; ** denotes significant differences in ΔF_TOT between IM- and IMRL-pressing conditions.

Structure of Variance

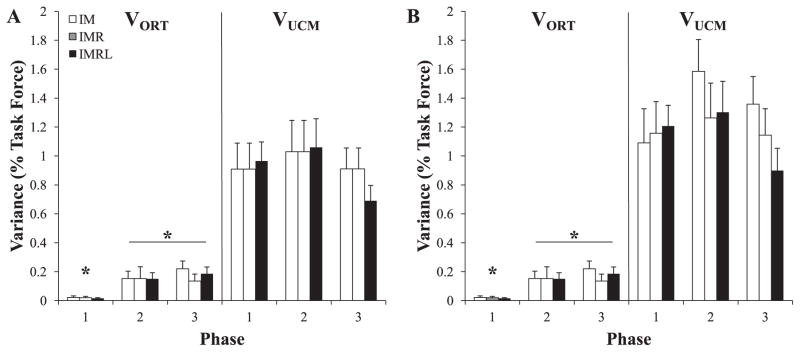
To test the effect of explicitly involved fingers on variance of elements within and orthogonal to the UCM (Hypothesis-1), we analyzed the structure of inter-trial variance using both finger forces and finger modes as elemental variables at all three data collection phases. V_UCM was of larger magnitude than V_ORT during at all phases and for all pressing conditions during both perturbed and unperturbed trials. V_ORT was especially small during phase-1; this is unsurprising because subjects had visual feedback by which they could correct deviation in the ORT direction during phase-1. In contrast, V_UCM had similar values across the phases and condition.

Figure 4 illustrates the structure of variance in force space (A) and mode space (B) with V_ORT on the left half of each panel and V_UCM on the right half. Finger pressing conditions are represented by open bars (IM), shaded bars (IMR), and filled bars (IMRL). In order to provide cross-subject comparison, each subject's V_UCM and V_ORT values were normalized by the square of each his or her target force for the associated task before these values were averaged across all subjects. The only consistent differences were between the V_ORT values in phase-1 compared to phases-2 and -3.

Figure 4.

Two components of inter-trial variance, within the UCM (V_UCM) and orthogonal to the UCM (V_ORT). The results of analysis are presented for the three phases of action in both force space (Panel A) and mode space (Panel B). Each finger-pressing condition is represented by bar style (IM = open; IMR = shaded; IMRL = filled). At each phase, V_UCM was significantly smaller than V_ORT; * signifies that V_ORT was significantly smaller during phase-1 than it was during phase-2 and phase-3. Mean data across subjects with standard error bars are shown.

To test Hypothesis-1 statistically at each steady state, three-way ANOVAs with repeated measures with factors Condition (3 levels: IM, IMR, IMRL), Phase (3 levels: 1, 2, 3), and Variance (2 levels: UCM, ORT) were run on log-transformed data in both force and mode space. In force space, there was a significant Phase × Variance interaction (F_2,119 = 5.50; p < 0.01) but no significant main effect or interaction with Condition. Tukey-Kramer comparisons confirmed that V_UCM > V_ORT for all phases. Additionally, V_ORT at phase-1 was significantly smaller than V_ORT at phase-2 and phase-3, while V_ORT was not significantly different between phase-2 and phase-3. There were no significant differences in V_UCM across the phases. These results were consistent in mode space.

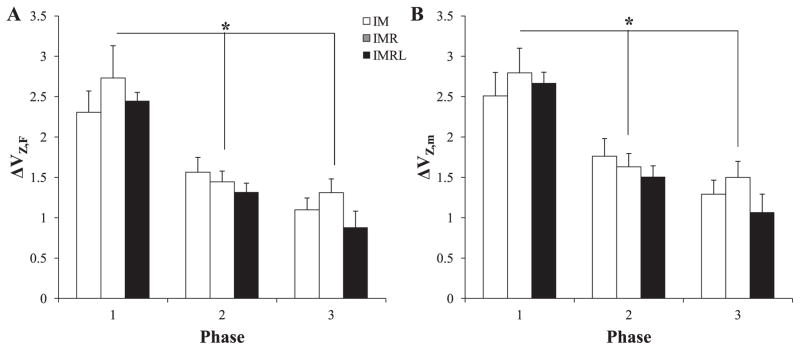
An index of synergy (ΔV) was calculated separately for each subject at each of the three phases. We observed ΔV > 0 for all phases and finger-pressing conditions, reflecting the inequality V_UCM > V_ORT described previously. Figure 5 shows ΔV_Z, the z-transformed index of synergy, for each condition (with the same shading scheme as in Figure 4) during each phase in force space (A) and mode space (B). In force space, a two-way ANOVA with repeated measures, using factors Condition and Phase, showed a significant main effect of Phase (F_2,56 = 52.97; p < 0.001) without other effects. Since there was no significant effect of Condition, Hypothesis-1 was falsified: the number of explicitly instructed fingers did not significantly affect the difference between the magnitudes of V_UCM and V_ORT. Mean comparisons with Tukey-Kramer adjustment showed that all three levels of Phase were significantly different from one another. These results were consistent in both force and mode spaces.

Figure 5.

The magnitude of the z-transformed index of synergy, ΔV_Z, at each of the three phases for each finger pressing condition. Panel A shows ΔV_Z in force space; Panel B shows ΔV_Z in mode space. * denotes significant differences between phases. Mean data across subjects with standard error bars are shown.

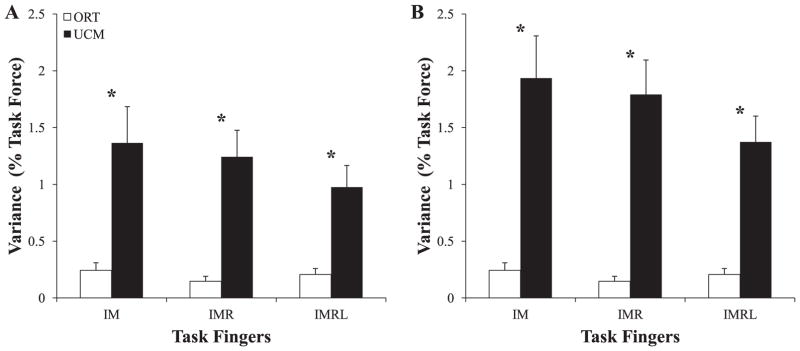
We also analyzed inter-trial variance of the difference vector between forces (and modes) produced in phase-3 and phase-1, denoted by V_UCM,ΔF and V_ORT,ΔF in force space, and V_UCM,Δm and V_ORT,Δm in mode space. These results speak to the veracity of Hypothesis-3. Again, in order to make the cross-subject comparison, these data were normalized by the associated target force squared. Figure 6 shows V_UCM (filled bars) and V_ORT (open bars) for the force-based (panel A) and mode-based analysis (panel B) for the three finger-pressing condition. The inequality V_UCM > V_ORT was observed across conditions and analyses, with no obvious difference among finger-pressing conditions (effect of Variance in two-way ANOVA with no other effects, F_1,35 = 98.8; p < 0.001). These results were consistent in mode space. The lack of a significant effect of Condition falsifies Hypothesis-3.

Figure 6.

Two components of inter-trial variance, within the UCM (V_UCM) and orthogonal to the UCM (V_ORT) computed for the difference vector calculated between phase-1 and phase-3. Both components of variance are normalized by the associated target force for each subject before being averaged across subjects. * denotes significant differences between V_UCM and V_ORT for each finger pressing condition in the space of both forces (A) and modes (B).

Analysis of Motor Equivalence

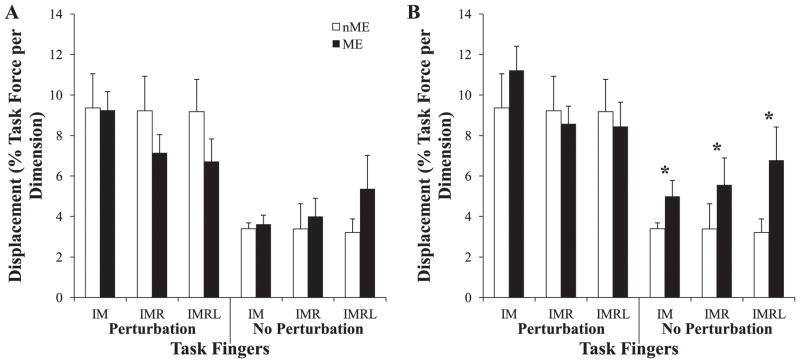
To test Hypothesis-2, two components of system displacement, motor equivalent (ME, leading to no F_TOT changes) and non-motor equivalent (nME) were computed for the differences in finger forces (and modes) between phase-3 and phase-1. Both ME and nME were normalized by the target force before their averages were computed across subjects. During trials with perturbations, the magnitude of nME changed very little across the finger-pressing condition, whereas the magnitude of ME decreased somewhat as the number of task fingers increased. In contrast, when no perturbation was applied, ME increased with the number of task fingers while nME stayed approximately consistent. Both ME and nME were larger during perturbed trials than control trials. Figure 7 shows, in both force space (A) and mode space (B), the mean magnitudes of both ME (closed bars) and nME (open bars) for each finger-pressing condition during trials with (left) and without perturbation (right).

Figure 7.

The motor equivalent (ME) and non-motor equivalent (nME) components of the difference vectors calculated between phase-1 and phase-3 in force space (A) and mode space (B). * represents the significant difference between nME and ME components in mode space in control trials (no perturbation). In trials with perturbations, the magnitudes of ME and nME were significantly different from their respective values in control trials.

A 3-way ANOVA with repeated measures utilizing the factors Condition, Perturbation, and Component (2 levels: ME, nME) was used in both force and mode spaces. Data were log-transformed for normality. In force space, the Perturbation × Component interaction was significant (F_1,77 = 5.42; p < 0.05), while neither the main effect of Condition nor any interactions including it were significant. Tukey-Kramer mean of the Perturbation × Component interaction showed that magnitudes of ME and nME were significantly different during the I-perturbed trials from their respective values during the control trials, but nME and ME were not significantly different from one another. These results were similar in mode space, except that the ME component of system displacement was significantly greater than the nME component in the control trials. As in the other tests of our specific hypotheses, the lack of a significant Condition effect falsified Hypothesis-2 because no significant difference in the magnitude of ME displacement was observed as a function of the number of explicitly involved fingers.

Discussion

Across the perturbation and finger-pressing conditions studied, the component of inter-trial variance that did not affect total force (V_UCM) was consistently larger than the component that affected total force (V_ORT). The inequality V_UCM > V_ORT held for both phases and differences between phases; it was true for analyses in both force and mode spaces. Overall, these results confirm previous observations from the application of transient perturbations to the four-finger system (Wilhelm et al. 2013). Additionally, when two components of the displacements over the trial duration in the space of finger forces (modes) were quantified, motor equivalent (ME) and non-motor equivalent (nME), the ME component was consistently large: either larger than nME (in mode space for control trials), or statistically indistinguishable from nME displacement (for other analyses). These observations are similar to those reported in earlier studies of multi-joint reaching tasks quantified in the spaces of joint configurations and muscle activations (Mattos et al. 2011, 2013).

While the main result of Wilhelm and colleagues was duplicated in tasks with different numbers of instructed fingers, our specific hypotheses were largely falsified. Increasing the number of instructed fingers involved in the task did not significantly affect distribution of inter- trial variance between V_UCM and V_ORT as reflected in the magnitude of ΔV computed over steady states (Hypothesis-1) and for the difference between phase 3 and phase 1 (Hypothesis-2), while the magnitude of the ME component also did not vary across conditions with different numbers of task fingers (Hypothesis-3).

Task-specific stability and its behavioral consequences

The idea of task-specific stability (Schöner 1995) is tightly linked to the problem of motor redundancy (Bernstein 1967). This is because the central nervous system (CNS) can only prioritize stability in some directions over others when it has a redundant set of elemental variables at its disposal. One consequence of task-specific stability is the so-called synergic structure of inter-trial variance. The word "synergy" takes on various meanings in the motor control literature (see Latash 2008 for a review), and is often taken to mean a group of variables, which scale together during a task or across tasks (d’Avela et al. 2003; Ivanenko et al. 2004; Ting and Mcpherson 2005; Tresch and Jarc 2009). This definition of synergy follows from Bernstein's (1967) hypothesis that the central nervous system must somehow reduce the number of elemental variables in redundant systems to a manageable number for control purposes. Within the theoretical framework provided by the principle of motor abundance and the UCM hypothesis (Scholz and Schöner 1999; Latash et al. 2007; Latash 2012), however, synergy refers to co-variation in a relatively high-dimensional space of elemental variables such that the relatively high variance in this space is associated with relatively low variance of a salient performance variable. This characteristic of synergy is evident in the data presented: the magnitude of V_UCM was far greater than that of V_ORT for all finger-pressing conditions, with and without perturbations. So this marker of task-specific stability is clearly seen, even in minimally redundant (two-finger) tasks (cf. Latash et al. 2001).

When a redundant system is subject to a perturbation, it is expected to deviate primarily along the directions of low stability, i.e. along the UCM. Our analysis of the differences between forces and modes in phase-1 and phase-3 confirm these predictions: inter-trial variance of deviations over the time course of each trial also displayed the signature of synergic organization: V_UCM > V_ORT. While this observation supports earlier results of studies with perturbations applied during multi-finger and multi-joint tasks (Wilhelm et al. 2013; Zhou et al. 2014), it also extends these observations to tasks with different numbers of explicitly involved elements. While redundancy is essential for the inequality V_UCM > V_ORT to exist (in non-redundant tasks, V_UCM is zero by definition), our study shows that changes in the number of explicitly involved elements has no effects on the structure of inter-trial variance (reflected in particular in the synergy index ΔV, Fig. 5).

Lastly, a system with task-specific stability may be expected to show large drift within the UCM both spontaneously and under the action of transient perturbations. This characteristic has been observed in terms of the large ME component of displacement induced by an external unidirectional perturbation and also by corrections of the deviations induced by the perturbation (Mattos et al. 2011, 2013). Our study is one of the first to demonstrate large ME deviations of a multi-finger system under a transient perturbation (see also Mattos et al. 2014). As in the case of indices of the structure of variance, a change in the number of explicitly involved fingers had no effect on the proportion of ME motion in the total motion within the four-finger force (mode) space.

A system stabilized in a task-specific way is expected to display all three aforementioned characteristics: a synergic structure of inter-trial variance, greater variance in directions that do not affect task performance in response to transient perturbations, and relatively large drift in directions that do not affect performance. The two, three, and four-finger systems we studied all exhibited these characteristics with no major differences related to the number of explicitly involved fingers. This result allows two interpretations. The first is that all the mentioned characteristics show qualitative changes between redundant and non-redundant systems (for the latter, V_UCM = 0; ΔV is negative; and ME motion = 0), while the number of extra elements has no effects on the quantitative indices of those characteristics.

This interpretation, however, seems to be at odds with earlier results, which showed that, during accurate finger force production tasks, humans preferentially stabilize the total moment of force computed with respect to the longitudinal axis of the hand/forearm (Latash et al. 2001; Scholz et al. 2002). In particular, during two-finger tasks, the structure of variance showed strong stabilization of the total moment of force (positive co-variation of finger forces and modes across trials), which was incompatible with stabilization of total force requiring negative co-variation of finger forces. In three-finger tasks, episodes of force stabilization emerged, and they became more pronounced in four-finger tasks, while stabilization of total moment of force (not instructed!) persisted over two-, three-, and four-finger tasks.

There are two important differences between the cited studies and the current one. First, the earlier studies used cyclical force production, which involved phases with relatively fast force changes, which are known to lead to large V_ORT computed for total force resulting in lower indices of force-stabilizing synergies (Goodman et al. 2005; Friedman et al. 2009). The current study used steady force production thus favoring force-stabilizing synergies. Maybe more importantly, in the earlier studies, only the explicitly involved fingers produced force, while the other fingers of the hand did not even touch force sensors. In our study, across conditions, all four fingers rested on force sensors. So, it is possible that, despite the difference in the instructions, all the tasks were effectively four-finger tasks with different involvement of task and non-task fingers. This conclusion is supported by the results of our analysis that was always performed in the four-dimensional space of finger forces (modes).

Relation to the control with referent body configurations

The referent configuration (RC) hypothesis (Feldman 2009) assumes that intentional movement begins with the motor system defining a task RC (RC_TASK): a small number of task-salient referent coordinates in the low-dimensional task space. From this RC_TASK, a sequence of few-to-many transformations occur leading to RCs at individual effector, joint, and muscle levels which eventually propagate to the level of individual pools of alpha-motoneurons. At this point, RC is equivalent to the threshold for the tonic stretch reflex (TSR), as in Feldman's lambda-model (Feldman 1986). In this context, the presence of motor redundancy becomes non-problematic: Since task performance only needs to be specified in a low-dimensional task space, the involvement of individual elements arise from this specification and physical/physiological interactions within the body and with the external force field. Within this scheme, the number of explicitly involved elements is not essential: a conclusion that fits well our results across conditions with different numbers of explicitly involved fingers.

Task-specific stability is a likely result of control with RCs. RC_TASK plays the role of an attractor for the actual values of task-salient variables. As a result, elemental variables are more constrained (show higher stability) in directions that affect those variables than in other directions (those within the UCMs for the variables). The scheme predicts all three main results of our study: the inequality V_UCM > V_ORT at steady states and for changes in elemental variables (forces or modes) in response to a transient perturbation, as well as large ME motion components.

The RC hypothesis also predicts equifinality - the return of the system to its initial state - after a transient perturbation, so long as RC_TASK remains unchanged. In fact, in both perturbed and unperturbed trials, a decrease in total force was observed. This suggests an unintentional change in RC_TASK. Similar decreases in force production have been documented previously in unperturbed trials when visual feedback was removed (Slifkin et al. 2000; Vaillancourt and Russell 2002; Shapkova et al. 2008). As in the study of Vaillancourt and Russell (2002), in our study, the amount of force drop changed in proportion with the initial force level (Fig. 2). Similar results were observed in a recent study that covered a broad range of finger forces (Ambike et al. REF) for force production above a certain threshold level. Another phenomenon that may be related to an unintentional drift in RC_TASK is the so-called phenomenon of “slacking” (Reinkensmeyer et al. 2009; Secoli et al. 2011), the property of the human motor system to attempt to decrease levels of muscle activation when movement error is small, seen in paretic patients helped by a robotic device to perform motor tasks.

All these phenomena may be driven by a hypothetical process addressed as RC-back-coupling, by which the RC tends to move toward the actual configuration of the body. This process may be viewed as complementary to the motion of actual body configuration towards the corresponding RCs. RC motion attracts the actual configuration (direct coupling), while actual configuration attracts the RC (RC-back-coupling): Both processes contribute to the overall movement of the system to a state of higher stability. The former process (direct coupling) is relatively fast, with typical times reflecting delays in neural signal propagation and the electromechanical delay on the order of 100 ms. The RC-back-coupling, in contrast, seems to be a much slower process with characteristic times ranging from about 1 s to a few seconds (Zhou et al. 2014; Ambike et al. 2014).

Concluding comments

The results presented in this study are consistent with those seen in previous iterations of similar tasks and fill in some important gaps in our understanding of the extent to which the CNS can organize the body in a synergic fashion even when redundancy is apparently reduced by instruction. Even so, the experimental design and data presented here have some limitations, specifically regarding application of perturbation, assumptions with respect to enslaving, feedback/perturbation interaction, and potentially sample size.

Effects observed from the application of perturbations to only the index finger are not necessarily indicative of the effects of perturbations to other fingers. Each finger of the hand is uniquely interrelated with each other finger, and the index finger is generally the most independent of the fingers of the hand (Li et al. 1998). While research using the same experimental paradigm showed no significant differences as a result of the finger perturbed, only the IMRL-pressing task was considered (Wilhelm et al. 2011). Additionally, during the experimental procedure, perturbation onset occurred at the same time as feedback was removed, so it is difficult to know what role each individual occurrence had - although the control trials also involved removal of visual feedback.

In a number of studies, enslaving was shown to be robust across tasks and ranges of force production (Li et al. 1998; Danion et al. 2003). On the other hand, several recent studies have provided evidence towards changes in enslaving over a relatively brief practice session (Wu et al. 2012, 2013). Our earlier study has suggested that it is next to impossible for a person to use just one finger mode in an accurate force production task when only one finger is instructed but all four fingers stay on their respective force sensors (Reschechtko et al. 2014). These recent studies suggest that enslaving may be rather volatile. In this study, we assumed that enslaving did not change over the trial duration (12 s), particularly given that the hand configuration was the same at the beginning and end of each trial. We view this as a relatively safe assumption, but it may happen to be wrong.

Finally, the relatively small sample size raises the possibility that statistical power was too low to find significance of certain observed trends.