Direct Conversion of Free Space Millimeter Waves to Optical Domain by Plasmonic Modulator Antenna

Abstract

A scheme for the direct conversion of millimeter and THz waves to optical signals is introduced. The compact device consists of a plasmonic phase modulator that is seamlessly cointegrated with an antenna. Neither high-speed electronics nor electronic amplification is required to drive the modulator. A built-in enhancement of the electric field by a factor of 35 000 enables the direct conversion of millimeter-wave signals to the optical domain. This high enhancement is obtained via a resonant antenna that is directly coupled to an optical field by means of a plasmonic modulator. The suggested concept provides a simple and cost-efficient alternative solution to conventional schemes where millimeter-wave signals are first converted to the electrical domain before being up-converted to the optical domain.

Devices that can directly convert millimeter and THz wave signals to an optical signal are of great interest for both the communications community and the sensing industry.¹⁻³ For instance, they are needed in future high data rate wireless communication systems to encode Tbit/s wireless signals onto an optical carrier.⁴ So far, millimeter-wave (MMW) to optical conversion is performed in two stages. First, the signal received by the antenna is amplified and converted to the baseband with a MMW electronic receiver.⁵ Then the signal is again electrically amplified and finally mapped onto an optical carrier by means of an electro-optic modulator.^4,6 Direct MMW-to-optical converters thus enable a significant leap forward toward low-cost wireless THz communication systems, particularly when electrical amplification and high-speed electronics are no longer required. However, they can only be of relevance if they offer sufficient sensitivity so that data with very low field amplitudes can be transmitted over a certain distance. In particular, they should feature operation up to highest speed where electronics becomes prohibitively expensive.⁷⁻⁹

The direct encoding of an RF signal onto an optical carrier has been a research topic for a while.^10,11 Recently, a 58 GHz RF carrier has been mapped onto an optical signal by means of a lithium niobate modulator with an array of patch antennas as electrodes.⁸ However, the relatively large footprint (>10 mm²) does not allow for dense integration. A strongly improved modulation efficiency was shown by taking advantage of slow light in silicon photonic crystal modulators coupled with a bowtie antenna.¹² Yet, the inherent resistive nature of silicon limited the modulation speed to a few GHz. In the past years, plasmonic technologies that are no longer subject to such RC-speed limitations have emerged.¹³⁻¹⁸ Only recently, we have demonstrated micrometer sized plasmonic modulators with flat frequency responses way beyond 70 GHz.^19,20 The small footprint in combination with highest speed, makes the plasmonic technology an ideal candidate for the realization of MMW and THz electro-optic devices.^21,22

In this paper, we demonstrate a compact high-speed and passive device that directly encodes a wireless MMW signal onto an optical carrier. The device consists of a single resonant structure featuring a millimeter-wave antenna with a built-in electro-optic plasmonic phase modulator. The plasmonic modulator-antenna strongly focuses the incident MMW electric field into the nanometer sized antenna slot. This nanometer antenna slot subsequently forms the plasmonic slot waveguide for the electro-optic phase modulator. Due to the narrow slot—as enabled by plasmonics—and the resonant design, we find an electric field enhancement by more than 35 000 within the electro-optic active section of the plasmonic modulator. Detection of an incident electric field as low as 10 V/m with a sub-mm² footprint device (0.009 mm²) is achieved. This ultimately leads to an efficient and simple MMW-to-optical receiver solution that does not require any electrical power or high speed electronics. Given that plasmonics allows operation up to highest speed, the concept offers a solution for the practical realization of future Tbit/s wireless-fiber links and THz field sensors.^3,4

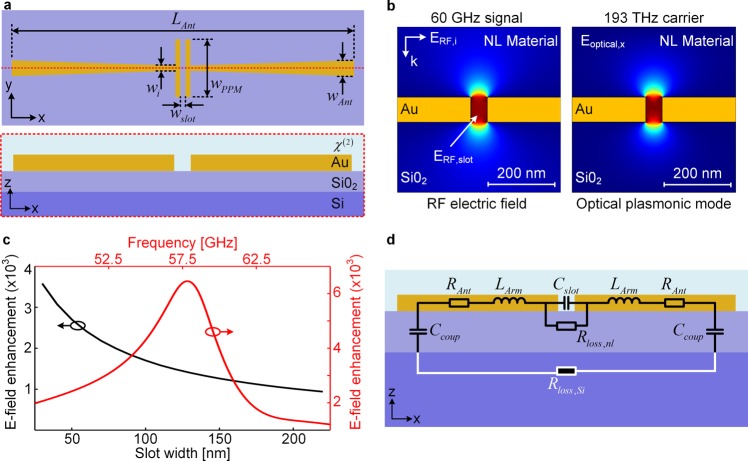
The operation principle of the device is explained by Figure 1. The device consists of two main parts, the antenna and the plasmonic phase modulator (PPM). The combination of plasmonic modulator and antenna will sometimes be referred to as “plasmotenna” throughout the manuscript. Laser light is coupled to surface plasmon polaritons (SPP) and fed into the PPM via photonic plasmonic converters.²³ The PPM is a metal–insulator–metal (MIM) slot waveguide filled with a second-order nonlinear material.¹⁷ The nonlinear material in the slot changes its refractive index linearly in the presence of an electric field (Pockels effect). The electric field is coupled in the slot through the antenna. The antenna arms are used to directly convert the energy of incident free-space MMWs to a strong electric field across the MIM slot. This way, the effective refractive index seen by the optical plasmonic mode in the MIM waveguide can be controlled by an incident wave to the antenna.

Figure 1.

Plasmotenna concept. The RF energy collected by the antenna is confined to the plasmonic slot. Light from the silicon waveguide is converted to SPPs. Their phase is modulated in the PPM section by the applied electric field.

The plasmonic modulator antenna achieves a high efficiency for three main reasons, the nanoconfinement of the electric field in the plasmonic slot, the resonant enhancement of the electric field in the device, and the strong nonlinear interaction of the optical and electrical fields in the slot. The proposed plasmotenna structure is shown in Figure 2a.

Figure 2.

(a) Geometry of the plasmotenna structure in the xy-plane (top). The xz-plane cross section of the plasmotenna (bottom). (b) The 2D simulated electric field of the RF field confinement (left) and optical plasmonic mode (right) in the optical plasmonic slot. (c) Electric field enhancement as a function of the plasmonic slot (black line, x-axis at the bottom) and field enhancement as a function of the frequency for the same structure at resonance (red line, x-axis at the top). In the latter, the slot width was fixed to 100 nm and the antenna dipole length was optimized for a resonance around 60 GHz. (d) Lumped element model of the plasmotenna device.

First, the incident RF power collected by the antenna is almost completely confined to the MIM slot, see Figure 2b (left). This is because the voltage applied to the antenna drops completely across the nanometer slot. This way, the RF electric field amplitude in the nanoscale plasmonic slot is several orders of magnitude larger than the incident field. As shown in Figure 2c (black curve), the electric field in the slot increases inversely proportional to the slot width w_slot. In practice, fabrication tolerances put a practical limit to the lower slot width achievable.

Second, in order to go beyond the achievable enhancement for a given slot width, a resonant structure is used to further increase the electric field in the gap. The device can be modeled by a RLC resonator as depicted in Figure 2d. To achieve resonance, the antenna arms should provide a complex conjugate reactance matching the PPM capacitive reactance. This way, at resonance the electric field in the slot is further enhanced. To illustrate the resonance enhancement, Figure 2c (red curve) shows the field enhancement as a function of the frequency. This enhancement is proportional to the resonator’s Q factor. In our structure the Q factor is limited by the dielectric losses (R_loss,Si and R_loss,nl), the radiation and ohmic losses (R_Ant), and defines the device’s electrical bandwidth. It should be noted that the resonant design of the antenna optimized to a carrier frequency around 60 GHz restricts the use of this particular plasmotenna to the spectral band around this frequency. However, one can design the structure to operate in a higher frequency range. This way even THz signals could be encoded onto an optical carrier.

Last, light propagating in the form of SPPs is also strongly confined to the same plasmonic slot, leading to an almost perfect overlap of the RF electric field and the optical plasmonic mode within the nonlinear material.¹⁷ The result is a highly nonlinear interaction, and the incident RF field can be efficiently encoded onto an optical carrier. Figure 2b shows the simulated 2D electric field of the RF field confinement (left) and optical plasmonic mode (right) in the plasmonic slot.

We define the electric field enhancement factor (FE) by the ratio of the electric field in the plasmonic slot (E_slot) and the field strength of the incident wave (E_i). The amount of the incident power collected by the antenna and converted into the electric field in the slot E_slot is then derived. Further explanation regarding the derivation steps can be found in the Supporting Information. This leads to the following FE expression

1

where Z_d is the device’s impedance defined as the ratio between the voltage and current seen by a port placed in the plasmonic slot, w_slot is the width of the plasmonic slot, λ_RF is the incident RF wavelength, G_R is the antenna gain, and Z₀ is the free-space impedance. As can be seen, a narrow slot width and a high device impedance increase the electric field in the slot. It is not surprising to see that the enhancement is also proportional to the square root of the antenna gain G_R. This is the enhancement of the incident field E_i provided by the antenna geometry. The factor G_R includes the losses as well.

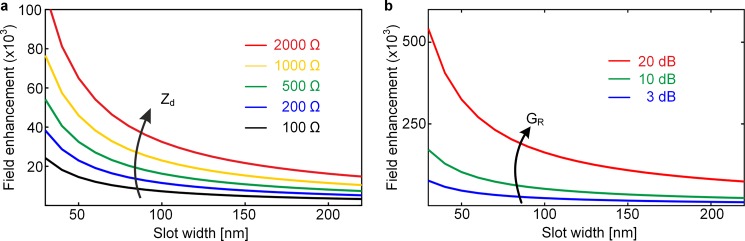
Figure 3a depicts the theoretical field enhancement factor described by eq 1 as a function of the slot width and device impedance. The incident RF wavelength is set to 5 mm and the antenna gain to 1. It is clear that the slot width has the strongest influence on the field enhancement. To illustrate the potential of the proposed concept, we plot in Figure 3b the FE as a function of the slot width for several antenna gains. The device impedance Z_d is fixed to 500 Ω. Field enhancements >10⁵ can be predicted for large antenna gains. Note that high gains require, e.g., lens structures or parabolic reflectors.

Figure 3.

Field enhancement as a function of the plasmonic slot width for an incident RF wavelength of 5 mm. (a) For a wide range of device impedances Z_d, FE factors largely above 10⁴ are predicted. (b) Field enhancement as a function of the slot width for different antenna gains with device impedance fixed to 500 Ω.

To validate the above theory, simulations were performed, and the optimum structure was then fabricated.

Simulations were carried out with a plasmotenna structure as depicted in Figure 2a. First, the dimensions of the PPM were defined. From Figure 3a, it can be derived that the PPM slot width should be as narrow as possible, yet still within fabrication tolerances. We decided for slot widths w_slot of 40, 75, and 90 nm. Next, we chose the length of the PPM. The longer an electro-optic modulator, the larger the induced phase-shift. Yet, since optical plasmonic losses increase strongly with the length, we confined the length of the PPM to 50 μm. Last, the dimensions of the antenna were optimized with a commercial FEM simulation software (CST Studio Suite) for a maximum electric field enhancement; see eq 1. It has been found that maximum enhancement is achieved when the antenna is operated near its full-wave resonance (see Supporting Information). For an antenna with 60 GHz operation we found an optimum antenna length L_Ant of 1430 μm and optimum widths w_Ant and w_i of 12.5 μm and 1 um, respectively. Predictably, the plasmotenna with the narrowest slot width of 40 nm provides the highest FE of 27 000, whereas the device with slot width of 75 nm provides a FE of 18 000. Both devices show a 3 dB bandwidth of 14 GHz. This enhancement was obtained with a G_R = −4 dB. This is the antenna gain when the plasmotenna is fabricated on a bare SOI chip. The negative gain is the result of the silicon wafer which introduces high RF losses. Of course, the gain can be improved by additionally placing the device into a reflector or lens arrangement.

Devices were fabricated to experimentally confirm the concept. Figure 4a shows a fabricated device, with the insets showing scanning electron microscope (SEM) images of the PPM. Silicon waveguides with dimensions of w_si = 450 nm and h_si = 220 nm were patterned by e-beam lithography and dry etching on a SOI wafer. The MIM plasmonic waveguides and antenna arms were fabricated by means of a gold lift-off process. The height of the gold is 150 nm. PPMs with a length of 50 μm and slot widths of 40, 75, and 90 nm have been fabricated. In a final step, the χ⁽²⁾ nonlinear material (DLD164²⁴) was applied by spin-coating. SEM images were used to verify the fabricated PPM dimensions. Figure 4a (II) shows the 40 nm wide plasmonic slot.

Figure 4.

(a) Microscope image of fabricated plasmotenna. (I) False color SEM image of a 50 μm long PPM. (II) SEM image of the 40 nm wide plasmonic slot. (b) MMW to optic characterization setup.

The devices were characterized using the experimental setup shown in Figure 4b. Light from a continuous wave laser is coupled to and from the chip by grating couplers. A MMW horn antenna with 20 dB gain is placed above the chip at a distance of 150 mm. A 60 GHz RF signal is fed from a RF synthesizer to the antenna. The RF power fed into the antenna is 5 dBm, which corresponds approximately to an incident electric field E_i of 20 V/m. The RF field incident upon the chip modulates the phase of the SPPs traveling in the plasmonic slot waveguide. The modulated light coupled out of the chip is then analyzed with an optical spectrum analyzer (OSA).

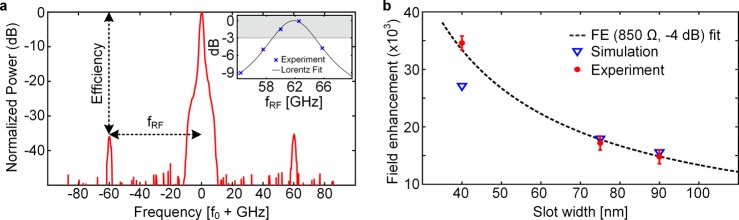
We measure the field enhancement from the electro-optic response of the devices. Figure 5a shows the measured optical spectrum of a device with a slot width of 75 nm. The optical carrier with sidebands at the transmitted MMW frequency (60 GHz) is clearly visible. The optical response gives information about the modulation efficiency, defined as the side to main lobe ratio. This can be used to calculate the achieved phase modulation index.¹⁷ The induced phase modulation is proportional to the change in the effective refractive index Δn_eff and the length L of the PPM waveguide

2

where k₀ = 2π/λ₀ with λ₀ the vacuum wavelength of the photon. In our device, we exploit the Pockels effect to induce the phase change. In the plasmonic slot waveguide the effective refractive index change is related to the electric field E_slot by¹⁹

3

where n is the refractive index of the nonlinear material, r₃₃ is the nonlinear coefficient of the material, Γ is the field energy interaction factor, and n_slow is the enhancement of nonlinear interaction due to the slow-down of SPPs in the MIM waveguide. The nonlinear coefficient r₃₃ was measured using an external Mach–Zehnder configuration.²⁰ The field interaction and slow-down factors can be obtained from simulations. Through eq 2 and 3, one then can derive E_slot and calculate the FE by taking the ratio of E_slot with the known incident field E_i.

Figure 5.

(a) Measured optical response of the device. Sidebands at the modulating frequency of 60 GHz can be observed. The inset shows the electro-optic frequency response of the device. The experimental data (blue crosses) are fitted with a Lorentzian model (black curve), indicating a 3 dB electrical bandwidth of 5 GHz. (b) Measured field enhancement for devices with 40, 75, and 90 nm slot widths. Curve fitting suggests an impedance of 850 Ω.

The measured FEs by applying the above procedure are plotted in Figure 5b (red dots) for devices with various slot widths. For the 75 nm device, an incident electric field E_i of 20 V/m induces a phase modulation Δφ of 0.0323 rad. Using eq 2 and 3 with the measured nonlinear coefficient r₃₃ of 160 pm/V,²⁰ the simulated confinement factor Γ = 0.47, and optical slow-down factor n_slow = 3.4, one can derive a field E_slot of 37 × 10⁵ V/m, which leads to a FE of 17 000. For devices with slot widths of 40 and 90 nm field enhancements as high as 35 000 and 15 000 were derived. These FE derived by measurements fit well with the FE from simulations (blue triangles). The 3D simulation for the device with a 40 nm slot width deviates quite a bit from the measured value. We ascribe this to errors that arise when performing simulations across a large domain of several millimeters where the minimum mesh size of 20 nm (limited by the computational power) is too close to the slot width. A fit of the FE eq 1 is depicted as a black dashed curve in Figure 5b as well. It was obtained by using an antenna gain of G_R = −4 dB and a device impedance of 850 Ω. It can be seen that the three experimental values follow nicely the theoretical model.

In addition, we measured the electro-optic frequency response of the device. The inset of Figure 5a shows the experimental data, indicating a 3 dB bandwidth of 5 GHz. The linear dependence of the modulation index versus the incident electric field was measured and is shown in the Supporting Information. Sensitivity measurements showed that the minimal incident electric field required to observe modulation is 10 V/m and is only limited by the noise floor of the measurement instrumentation (−90 dBm).

In conclusion, we demonstrate for the first time a wirelessly driven plasmonic phase modulator that can directly encode a MMW incident electric field on an optical carrier. A resonant plasmonic device concept is introduced to enhance the electric field in the plasmonic slot. This way, a highly efficient MMW-to-optical conversion device is implemented. This approach also enables new designs for ultrahigh-speed and power efficient plasmonic modulators and detectors.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b04025.

• Detailed derivation of the field enhancement expression, the 3D simulation results discussion and sensitivity measurement (PDF)

The authors declare no competing financial interest.