Electron Tomography: A Three-Dimensional Analytic Tool for Hard and Soft Materials Research

Abstract

Three-dimensional (3D) structural analysis is essential to understand the relationship between the structure and function of an object. Many analytical techniques, such as X-ray diffraction, neutron spectroscopy, and electron microscopy imaging, are used to provide structural information. Transmission electron microscopy (TEM), one of the most popular analytic tools, has been widely used for structural analysis in both physical and biological sciences for many decades, in which 3D objects are projected into two-dimensional (2D) images. In many cases, 2D-projection images are insufficient to understand the relationship between the 3D structure and the function of nanoscale objects. Electron tomography (ET) is a technique that retrieves 3D structural information from a tilt series of 2D projections, and is gradually becoming a mature technology with sub-nanometer resolution. Distinct methods to overcome sample-based limitations have been separately developed in both physical and biological science, although they share some basic concepts of ET. This review discusses the common basis for 3D characterization, and specifies difficulties and solutions regarding both hard and soft materials research. It is hoped that novel solutions based on current state-of-the-art techniques for advanced applications in hybrid matter systems can be motivated.

1. Introduction

1.1. The Electron Microscope: A Brief History

The development of transmission electron microscopy (TEM) started with the concept of matter waves founded by Louis de Broglie in 1924.^[1] The wave nature of the electron was later proven by electron diffraction in 1927. After Hans Busch showed that a magnetic field can deflect electrons, the concept of the electromagnetic lens was developed in 1926,^[2,3] and the first TEM was invented by Ernst Ruska in the early 1930s.^[4] TEM quickly surpassed the resolution of the light microscope due to the shorter wavelength of high-energy electrons compared to visible light (Figure 1a).^[5]

Figure 1.

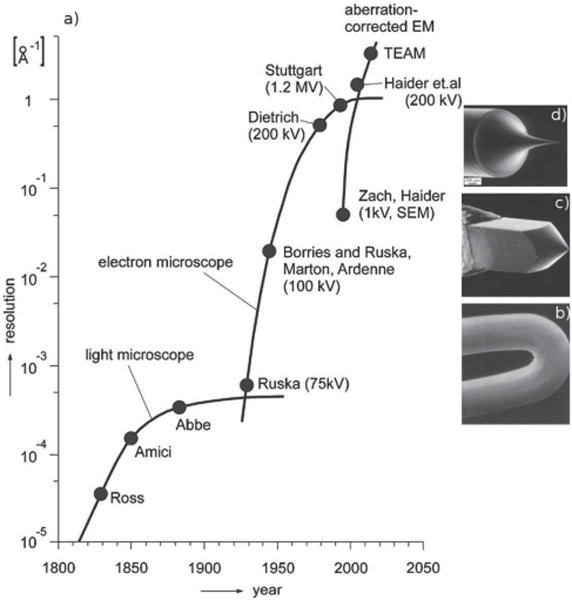
A schematic diagram of the historical resolution of visible light microscopes and transmission electron microscopes. a) The left panel shows a time line for the improvement of the resolution of microscopes versus the year of development. Reproduced with permission.^[6] Copyright 2009, Oxford University Press. b–d) Three different types of TEM electron sources: a W filament, a LaB₆ filament, and an FEG. b) Reproduced with permission.^[7] Copyright 1991, Springer; c,d) Reproduced with permission.^[8] Copyright 2009, Springer.

TEM was greatly improved with the development of electron sources exhibiting smaller energy spread and improved coherence. Early TEM instruments used heated W-cathodes consisting of a V-shaped hairpin geometry as an electron source (Figure 1b) with a ca. 100 μm tip radius.^[4] In the 1970s, a LaB₆ crystal was developed as an improved electron source with a higher brightness, lower energy width, and lower operating temperature, and ultimately improved the imaging resolution (Figure 1c). In the late 1980s, a new-generation electron source, the field-emission gun (FEG), was developed for even better resolution. Cold FEGs have a sharp W tip (Figure 1d) to concentrate the electric field and do not require heating. Their excellent electron-emission capability is offset by a short lifetime and the need for ultra-high vacuum conditions. A more recently developed source, called a Schottky FEG, utilizes a Zr coating on the sharp W tip to provide most of the advantages of field emission without the need for an ultra-high vacuum. Today, both LaB₆ and FEGs are predominately used as electron sources providing significant improvements in beam coherence, energy spread, brightness, and source lifetime. Through these improvements, TEM has achieved a resolution better than 4 Å for hard and soft materials (Figure 1a).^[9]

Despite the developments in electron sources, TEM reached a resolution limit imposed by physical lens aberrations as predicted by Scherzer.^[10] This motivated two approaches to further improve resolution. One approach was to increase the accelerating voltage to ca. 1 MeV to reach very small electron wavelengths.^[11] The other approach is to correct the lens aberrations as proposed by Scherzer.^[12] Despite numerous attempts over several decades, the implementation of a lens-aberration corrector finally achieved an improvement in resolution to 1.4 Å in the late 1990s.^[6,13,14] Recent successes in aberration correction have provided the ability to image atoms at 0.5 Å resolution (Figure 1a).^[15]

In parallel with developments in TEM, scanning transmission electron microscopy (STEM) was introduced by Crewe et al.^[16] to image heavy atoms supported on a light-atom carbon substrate. Early developments enabled STEM to provide high-contrast images of soft and hard materials.^[17,18] Recent developments have pushed STEM to atomic resolution, making it a widely used tool for nanoscale analysis.

1.2. The Need for Three-Dimensional Analysis

TEM and STEM are capable of directly imaging structures at nanometer length scales. However, the two-dimensional (2D) images produced are projections from the inherent three-dimensional (3D) structure of the sample. Early on, it was realized that retrieving the missing third dimension was required to determine the functionality of many structures.^[19] This requirement led to the development of 3D-reconstruction techniques from 2D projections.^[20] The development proceeded mostly separately in physical and biological sciences based on differences in the objects of interest, the required resolution, and the radiation tolerance.

Physical-science investigations in TEM seek to determine the morphology (size and shape) and distribution of elements in a structure to determine its functionality, which usually requires atomic resolution.^[21] As the ability to control matter at small length scales progressed, such as in microelectronics and nanotechnology, investigations at such high resolution using 2D-projection images became difficult due to the overlap of critical features in such images.^[22] Physical sciences needed to analyze nanoscale features in 3D to determine their effect on mechanical and electrical phenomena that occur at small length scales. 3D nanoscale analysis using TEM and STEM can now provide feedback to technological-development cycles in physical sciences.

Biological sciences in TEM seek to understand how biomolecules carry out their biological function through their physical structure. The structure includes the atomic spatial distributions, orientations, and interactions within and between biomolecules.^[23] However, determination of the atomic-resolution structure of biomolecules is extremely challenging by TEM. Radiation damage limits the illumination dose and signal-to-noise ratio (SNR) in TEM imaging,^[24] which usually hinders high-resolution structure analysis. Even so, low-resolution 3D structures are still valuable for answering important questions in biology. Fortunately, many biological specimens possess high symmetry,^[17] and the building blocks of structures, such as α-helices, β-sheets and amino acids, can be used to enhance the information obtained from lower-resolution 3D reconstructions of biological samples.^[25]

1.3. The Development of 3D Electron Tomography

The term tomography has been used to describe the process of “imaging by sections”.^[26] The mathematical concepts of electron tomography (ET) to reconstruct a 3D volume (or density map) from a set of 2D projections was first proposed by Radon in 1917.^[27] Despite this early mathematical foundation, it was not practically applied for 3D reconstruction until 1956 in astronomy using a set of projections of the Sun from the Earth.^[28] The first non-cosmic application was conducted by Oldendorf^[29] in 1961 for medical imaging using X-rays. The technique was further developed in the early 1970s by Hounsfield and Cormack, independently, and later improved upon by others to become what is now known as computed axial tomography (CAT).^[29–33]

The basic concepts of tomography were applied to TEM images for 3D analysis in the 1960s.^[19,34,35] In the past few decades, ET has benefited from enormous technological developments in instrumentation, computational power, and reconstruction algorithms. Examples of promising directions in both hard and soft materials include high-resolution tomography of nanoparticles,^[36] tomographic studies on single particles,^[37,38] the structural determination of very large biological complexes,^[39] and the structure of whole cells in a native environment.^[40,41] Even so, many challenges still lay ahead. The following sections will discuss the basic concepts of ET to provide readers an overview of the strategies, approaches, and tools in both the physical and biological sciences. Although the basic concept of tomography is the same, each discipline has developed a set of specific techniques according to the specific limitations inherent in the physical properties of the materials of interest. By presenting the details of the limitations, solutions, and applications of ET in both fields, we hope to benefit 3D analysis of hybrid materials consisting of both hard and soft materials.

2. Concepts of ET

2.1. Basic Data-Acquisition Concepts

In conventional TEM (simply referred to as TEM), a parallel, coherent beam of electrons is formed as a plane wave with approximately equal amplitude and phase everywhere at the top surface of the sample. As the electrons pass through the sample, they interact with the local atomic potentials modifying their phase and possibly producing scattering events. When the electron wave exits the bottom surface it contains information about the projected potential of the specimen. A post-specimen detector with high pixel density records the square magnitude (commonly called the intensity) of the transmitted electron wave irreversibly mixing the two wave components. Very thin specimens of material predominantly affect the phase of the electron wave, which is very sensitive to small changes in density, such as those in carbonaceous materials. Image contrast can be enhanced by applying a large defocus to the objective lens while also improving information transfer at low spatial frequencies.

In STEM, a focused beam of electrons (also called a probe) is formed at the sample with a sub-nanometer diameter. This probe is rastered across the sample and single-channel post-specimen detectors are used to detect the amount of electron scattering at each scanned position. An image is therefore formed by a 2D set of equally spaced positions of the probe. An STEM can be operated such that the detector collects only highly scattered electrons, producing incoherent image intensities based on mass-thickness with minimal coherent diffraction contrast. This type of scattering is weak for light atoms such as carbon, but ideal for the heavy atoms commonly found in specimens in physical science.^[42]

ET reconstructs 3D information from a tilt series of 2D images acquired at many different viewing angles.^[43] All projection images are then aligned and combined digitally to produce a faithful representation of the original object. This process requires image intensities that consistently provide a monotonic measurement of some property of the sampled volume in every tilted projection, which is known as the projection requirement. The resulting reconstruction consists of voxel (a 3D version of a pixel) intensities exhibiting the 3D distribution of the measured parameter. TEM and STEM images are known to provide monotonic projections of density in both biological and physical-science specimens under certain imaging conditions and are most often used to reconstruct 3D density.^[44] Tomography can be used to reconstruct other types of measurements, such as magnetic field lines, from projections that fulfill the projection requirement (see Section 3.6).

The single-axis tilt scheme is the most commonly used acquisition technique in ET, because it entails relatively simple methods for data acquisition and reconstruction. The specimen rotates around a fixed eucentric axis within the microscope sample chamber from one extreme tilt angle to the other, while projections are acquired at well-defined tilt increments. Ideally, a tilt series contains projections from a complete ±90° rotation of the object to include projections from all possible directions. The maximum tilt accessible for most ET experiments is limited to ±70° due to shadowing of the specimen holder and space limitations in the TEM specimen chamber.

The Fourier slice theorem (also known as the projection theorem) is the basic underlying principle of 3D tomographic reconstruction regardless of the method used to acquire the projections. It states that a projection of an object at an angle θ is equivalent to sampling a central plane of the object’s full 3D Fourier transform at the same angle θ.^[43] Figure 2 shows a diagram of this mathematical theorem, outlining the connection between the projection in real space and the corresponding plane sampled in Fourier (reciprocal) space. The Fourier transforms of a series of real-space projections acquired at many different angles can be used to fill in the object’s 3D Fourier transform, which is then inverted to produce a 3D reconstruction of the original object in real-space. Figure 3 shows the theoretical discrete sampling of Fourier space along the k_y and k_z directions of 17 projections with evenly spaced tilt increments through a tilt range of ±70°. The blue triangles around the k_z axis highlight regions of missing information in Fourier space by this incomplete tilting scheme, which distorts features along the projection direction (the z-axis) in the final reconstruction. Acquisition of projection images at the highest tilt angle possible minimizes the effect of this missing wedge of information. Detailed treatments of the mathematics involved in Fourier reconstruction are offered in Herman’s book on the subject.^[45]

Figure 2.

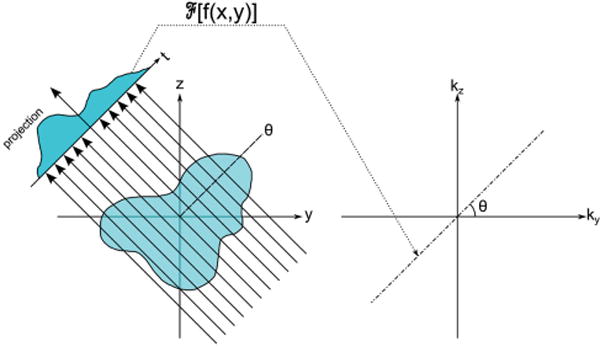
A diagram of the mathematical concept of the projection theorem in 2D (directly extendible to 3D). A projection of a 2D object in real space is reduced to a 1D measurement of the projected density. The Fourier transform of the 1D projection is equivalent to a central section at the original projection direction through the object’s full Fourier transform.

Figure 3.

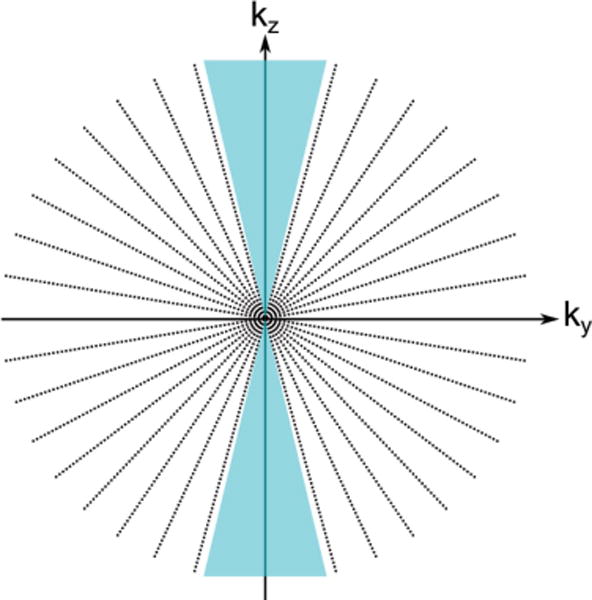
The theoretical sampling (dotted lines) of reciprocal space by a tomographic tilt series from ±70° with equal angular increments. The blue triangles indicate the missing wedge of information between 70° and 90°, which impacts resolution along the original projection direction. Notice the oversampling of information at low spatial frequencies near the zero frequency, which is compensated for in the WBP reconstruction method.

2.2. Basic Reconstruction Algorithms

2.2.1. Direct Fourier-Space Reconstruction

The Fourier transforms of all acquired projections properly combine to fill an object’s Fourier space F (k_x, k_y, k_z) and application of the 3D inverse Fourier transform f⁻¹[F(k_x, k_y, k_z)] produces a real-space approximation of the object’s shape and density. This method, known as direct Fourier space reconstruction, offers a clear description of tomography’s underlying principles but in practice presents difficult and computationally expensive complications. The inverse Fourier transform requires a continuously varying function with a Cartesian based coordinate system, but tomographic data is acquired by discrete radial sampling as seen in Figure 3. The radially sampled data require interpolation to properly map from polar to Cartesian coordinates (see Figure 4a) prior to Fourier inversion, and the specific interpolation method chosen greatly affects the quality of the final reconstruction.^[46] Furthermore, until recently computer memory was incapable of holding large data sets consisting of N_x × N_y × N_z pixels required for most reconstructions (possibly multiple gigabytes).

Figure 4.

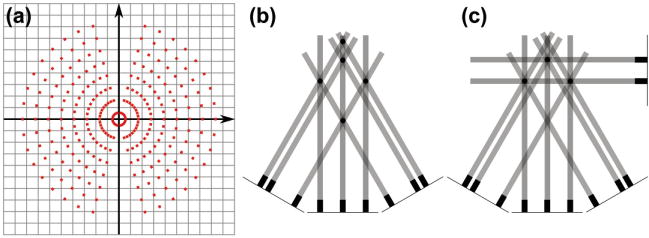
a) The mismatch between information sampled by a 17-image tilt series with equal angular increments (red dots) and a square Cartesian grid. The interpolation method used to combine this data can strongly influence the final reconstruction. Radon back-projection is used to avoid interpolation in space interpolation. b) A simplified example of Radon back-projection for a set of 3 low-tilt projections producing 5 possible object locations (black dots). c) The addition of a high-tilt projection uniquely defines the existence and location of only 3 objects.

2.2.2. Real-Space Radon Transform

To avoid the complications of direct Fourier inversion, tomography relied on the real-space Radon transform to produce 3D reconstructions.^[47,48] The forward Radon transform (R) maps a 3D object onto a 2D plane by calculating line integrals (projections) of the object’s density through all “projection rays” parallel to a given axis. Incoherent electron-scattering contrast in TEM and STEM images can be considered as a line integral of the specimen’s density, and therefore the Radon function provides a mathematical framework that closely matches the tomographic method. This algorithm drastically reduces the amount of memory required, as it does not have to hold the entire 3D volume in memory concurrently and independently operates on each subset of a tilt series (N_y × Nz) perpendicular to the tilt-axis called a sinogram. In other words, all projection information in the pixels perpendicular to the tilt-axis is independent from neighboring pixels, because an object is rotated around a single axis. Reconstruction of a tilt series using the inverse Radon transform (R⁻¹) is known as back-projection, because the projected intensity in each pixel of a projection is linearly added into a 3D volume along a ray at the correct angle to build up the 3D density. Figure 4b shows a simple example of back-projection from three low-tilt projections resulting in 5 possible object locations (round dots). The addition of a fourth back-projection at a high-tilt angle (90°) uniquely defines the existence and location of only 3 objects as shown in Figure 4c.

2.2.3. Weighted Back-Projection

A fundamental connection exists between the Radon transform and the Fourier transform, such that both theoretically offer equivalent methods for tomographic reconstruction, but the forward and reverse Radon transforms are performed completely in real space. Back-projection via the inverse Radon transform avoids the forward/inverse Fourier transforms and errors associated with the necessary interpolation steps.^[49] Back-projection reconstructions typically produce a 3D object with blurred features with poorly defined fine spatial details because, as is clear in Figure 3, the low-frequency information (corresponding to larger spatial detail) near the zero of the k-axes is oversampled, as opposed to the undersampled high frequencies (corresponding to small spatial details). The weighted back-projection (WBP) convolves the reconstruction with a simple radial weighting filter, with an amplitude that increases linearly to a maximum at a high cut-off value, and is applied after the real-space back-projection calculations are completed. The weighting filter evens out the uneven sampling distribution in Fourier space and is currently the most widely used reconstruction technique due to its simplicity and speed.^[47] More-complex techniques discussed later in Section 3.4 can be used to reduce artifacts in 3D reconstructions.

2.3. Resolution and Missing-Wedge Effects

Reconstruction from a single-axis tilt series exhibits anisotropic resolution, because the tomographic-acquisition method inherently undersamples the object’s structure. Resolution along the tilt-axis (here defined as the x-axis) is equal to the original experimental resolution assuming a perfect tilt-series alignment. Resolution along the imaging axis perpendicular to the tilt axis (here defined as the y-axis) is reduced due to the discrete number of projections, N, acquired. An estimation of the best resolution possible along the y-axis for a reconstruction of diameter D from N projections equally spaced over a full ±90° tilt range is:

$$d_{\mathit{\gamma }}=\frac{\pi D}{N}$$ (1)

which is derived from the geometrical sampling of Fourier space.^[43] In practice, the resolution is difficult to assess, because it is influenced by many other experimental factors such as image SNR and tilt-series alignment.

The missing wedge of information along the k_z axis, not sampled due to a limited maximum tilt angle α < 90°, dominates resolution along the original projection direction (here defined as the z-axis). Features along the z-axis are stretched by an elongation factor e_yz defined as:^[49]

$$d_z=e_{\mathit{\gamma }z}{d}_{\mathit{\gamma }}=d_{\mathit{\gamma }}\sqrt{\frac{\alpha +\sin \alpha \cos \alpha }{\alpha -\sin \alpha \cos \alpha }}$$ (2)

Rotation increments of finer than 1–2° are probably not necessary, and a maximum tilt angle of 70° produces an elongation factor of <1.3 to produce readily interpretable results. Resolution along the projection direction should be maximized because we specifically utilize ET to recover this information. These are simple estimations of the achievable resolution possible for the parameters of a tilt series based on the filling of Fourier space. Many other factors such as microscope stability, drift, pixel resolution, sample thickness, tilt-series alignment, and beam damage are all possible sources of reduced resolution. The resolution of iterative reconstruction techniques (see Section 3.4) is more difficult to define, although the resolution of a final reconstruction can be assessed by several techniques (see Section 4.2.5).

The missing wedge of information has the largest impact on resolution and artifacts in tilting ET. The space between the strong focusing lenses near the sample does not typically allow for large rotations of the sample holder unless the holder is specifically built for ET. Even in this case, the typical slab-like sample geometry restricts tilts to <80° due to sample shadowing or projected thickness. One solution is to rotate the sample by 90° in the specimen plane either with a tilt-rotate stage or after removing the holder from the microscope. Then, a second tilt series is acquired of the same object, reducing the missing wedge to a missing cone of information.^[50] The requirements to acquire two tilt series introduces a significant dose to the acquisition and complicates the post-processing alignment and reconstruction. This method is not typically used due to the extra complications. Work on advanced algorithms to retrieve the information in the missing wedge is based on prior knowledge of the system and will be discussed in later sections.

2.4. Differences Between Hard Materials and Soft/Biomaterials

As mentioned previously, ET is used extensively in investigations of specimens for both physical and biological science. However, very few techniques are shared between these two fields. The physical constraints imposed by the constituent materials and the functional parameters that need to be measured both lead to very different types of solutions to investigate 3D structure.

Early in the development of TEM, the biological community quickly realized that 2D projections of macromolecules were insufficient to understand their functionality, and then ET was initially developed to reconstruct biological macromolecules in 3D. Biological macromolecules generally consist of light atoms (H, C, N, O, etc.), and produce low contrast in TEM images, which can be difficult to detect above the background noise. Additionally, the structure of biological samples is sensitive to the electron beam, which mainly limits biological investigations. Electron–sample interactions lead to both elastic and inelastic scattering of the incident electrons, which either imparts momentum to atoms or deposits energy in the target material. Inelastic scattering produces free radicals with 5–100 eV energy that can damage biological samples by breaking covalent bonds and destroying their structure. Thus, biological samples can only sustain a limited dose, which results in even lower contrast images, and limits the 3D-reconstruction resolution of biological structures. Nonetheless, the low-resolution 3D structures of large macromolecules can still provide numerous insights into their function. Many techniques, as described in Section 4, have been developed to maximize resolution while keeping the biological structure intact. These techniques may also be applicable to research in physical sciences.

Unlike biology, samples in physical science often contain crystalline materials, which produce diffraction contrast that cannot be used for ET reconstruction. Recently, STEM has provided high-contrast and high-resolution images with limited diffraction contrast, providing 3D ET reconstructions of nanoscale objects. Attaining high contrast and high resolution is possible in physical-science specimens due to the radiation hardness (strong bonding) of the materials involved. Radiation damage due to elastic scattering (knock-on effects) are more relevant to hard materials, compared to radiation damage from inelastic scattering events. Since permanent knock-on displacements occur above a certain threshold energy, radiation damage in hard materials can be limited by lowering the incident electron energy, and tends to be less of a concern compared to soft materials. Thinned TEM specimens of metals, such as Au and Ag, can be imaged at relatively high doses without significantly changing their internal bulk structure. Surfaces and defects exhibit much lower damage thresholds.^[51] Carefully choosing the acceleration voltage and dose during imaging can produce much-improved results, as demonstrated recently by images of Si with much-reduced beam damage.^[52]

The separate development of ET in both physical and biological fields has led to very different techniques, which are shown in the following sections. New classes of hybrid materials are being developed, which incorporate both hard and soft materials, such as metal–organic frameworks (MOFs)^[53] and polymer/metal interfaces in solid-state battery electrodes.^[54] Current 2D and 3D analysis techniques are incapable of simultaneously imaging both hard and soft materials, especially at interfaces. There exists the opportunity to incorporate ET techniques from both biological and physical sciences to provide a robust analytical tool for a wide range of hybrid matter systems.

3. Advances in ET for Physical-Sciences Research

3.1. Nanoscale Research using TEM

The analysis of hard materials structures with reduced, or scaled, size is critical to the further advancement of technology in many fields of the physical sciences, such as integrated circuits and nanotechnology. Many materials systems derive their macroscale properties from structural elements that exist at the micro- to atomic scales. Physical sciences seek to understand the macroscopic characteristics of materials through the investigation of fundamental structural characteristics, such as morphology (size and shape), crystal type, grain size, composition, defects, and interface structure. TEM is a versatile tool to directly observe materials spanning a range of length scales in both imaging and diffraction modes. Due to the direct link between characteristics at reduced length scales and macro-scale properties, TEM investigations provide key insights into the mechanical, electrical, and magnetic properties of materials with direct application to behavior at the macroscale.

Because they are charged particles, electrons are not only easily focused by magnetic lenses, but also interact very strongly with matter, limiting their penetration depth. Sub-nanometer resolution imaging requires the preparation of <100 nm-thick lamellae of material from bulk samples to reduce the incident electron–sample interactions during transmission. The possibility of controlling materials at the nanoscale is now a challenge for TEM and STEM analysis. Still, TEM has been a very successful tool to investigate structures, despite the fact that TEM images are only 2D projections of the specimen.^[21] For example, some bulk materials can be sufficiently thinned, such that important features do not overlap in projection, and the third dimension can be considered constant during analysis. This assumption is no longer valid in many cases where precise control of material distributions with sub-10 nanometer or even atomic-scale accuracy is required. For example, feature sizes of modern integrated circuits are now so small that the overlap of many features within the thickness of a TEM sample presents problems for analysis, because the obfuscated nanoscale morphology defines their functionality. This section discusses the application of ET in physical sciences for full 3D characterization of structures including materials differentiation at the nanoscale with a lateral field of view of <1 μm.^[55] We also discuss recent advances in tomography for physical sciences, with the ultimate goal of achieving Richard Feynman’s 1959 challenge in his famous lecture “There’s Plenty of Room at the Bottom” to measure all atomic positions in 3D, and thus to provide full knowledge of a material’s properties.^[56]

3.2. Electron-Microscope Image Formation

Two different nanoscale imaging techniques typically used in the physical sciences, TEM and STEM, utilize different illumination modes, which result in very different contrast mechanisms (see the beginning of Section 2.1) with important implications for ET. Image contrast in TEM images satisfies the projection requirement at a certain size and resolution for non-crystalline materials. Unfortunately the coherent nature of TEM illumination produces non-monotonic image intensities for crystalline materials at different tilt angles. To understand the impact of TEM and STEM image formation on electron tomographic reconstruction of physical-science samples, we must examine the relevant damage mechanisms and how image formation connects to the projection theorem.

Most physical-science specimens consist of materials that are relatively radiation hard, and can withstand significantly larger irradiation doses compared with biological samples, before damage is evident.^[57] The high dose tolerance of so-called hard materials provides more flexibility in imaging conditions to directly investigate these materials even at atomic resolution.^[42,58] Beam damage in hard materials, described as loss of crystallinity or mass loss, occurs in two different ways, as described in Egerton’s review of the subject.^[59] Knock-on damage occurs when an incident electron scatters from a specimen atom transferring momentum in the process. The atom can be displaced from its location, and, if sufficiently large, the atom will be permanently displaced or sputtered away. The bulk atoms in some strongly bonded materials can withstand such elastic events at moderate doses without any evident damage, even at the atomic scale. Ionization damage (also called radiolysis) occurs when the incident electron transfers energy to an electron in the specimen. This can break bonds in the material, producing reactions, heat, and other radiation such as X-rays. Knock-on damage can be mostly eliminated if the electron-accelerating voltage is below a threshold value for a given material. For example, graphene, a single layer of carbon atoms, is not damaged by knock-on processes from 80 kV electrons. Ionization damage is much more important for weakly bonded materials at lower accelerating voltages and atoms with lower Z numbers.

Resistance to electron-beam damage in hard materials derives from the strong bonding in crystalline solids at the atomic scale, but crystals introduce a different problem for the utilization of TEM in structural investigations due to diffraction. TEM is a coherent imaging technique where the final image is produced by interference of diffracted beams at the imaging detector, and thus, for crystals, the intensity is dominated by diffraction conditions with a non-linear dependence on the projected potential. A small change in crystal structure or orientation can produce radically different intensities and patterns in the recorded image.^[44,60] This violates the projection theorem necessary for tomographic reconstruction by traditional back-projection algorithms and limits the application of ET using TEM in the physical sciences.^[22,61]

This issue was resolved with improvements and more-wide-scale use of STEM, which utilizes the pre-specimen optics to create a convergent electron probe at the sample surface focused to a small diameter. After the specimen, a convergent-beam electron diffraction (CBED) pattern is produced at each raster position, and a single-channel detector is used to integrate the electron flux within a range of scattering angles. The information in each CBED pattern is localized to the probe diameter. STEM provides a highly flexible range of operating modes with nanometer to sub-angstrom resolution, depending on the electron source, accelerating voltage, convergence angle, and lens settings. The specific collection angles of the post-specimen detector determine the dominant contrast mechanism in images acquired by STEM. The most-common detector is a high-angle annular dark-field (HAADF) detector designed to collect only highly scattered electrons, which are mostly incoherently scattered electrons.^[42] HAADF-STEM can differentiate between materials with different atomic numbers (known as Z-contrast imaging), but has poor sensitivity for low-Z elements such as C in comparison with heavier species. Other incoherent STEM imaging techniques, such as incoherent bright field (IBF), have also been utilized for 3D analysis.^[62]

Both methods, TEM and STEM, have advantages and disadvantages for use in ET. TEM is relatively more efficient compared to HAADF-STEM per unit dose, due to the low probability of high-angle scattering events required for STEM, especially for low-Z materials. Low-dose imaging is therefore a strength of TEM, hence its use for soft materials (see Section 4). STEM has the advantage that image intensities are directly interpretable due to the dominance of incoherent scattering, and is capable of distinguishing between materials without spectroscopic methods.^[63] As a focused probe technique, STEM also has a limited depth of field, which is an important consideration for recently developed advanced STEM optics, as discussed later in this review. Figure 5 shows a comparison between the information transfers (called the contrast transfer function (CTF)) of STEM and TEM at optimal defocus values for high-resolution imaging. The STEM curve (red) is monotonic and decreasing at all spatial resolutions. For TEM, the lack of transfer at low spatial frequencies, as well as the oscillatory nature, makes interpretation of images difficult especially for crystalline specimens.^[60] A large defocus is commonly applied to the TEM image to improve information transfer and contrast at low spatial frequencies, but also has the effect of increasing the oscillatory function for high spatial frequencies. This comparison does not account for the dose applied.

Figure 5.

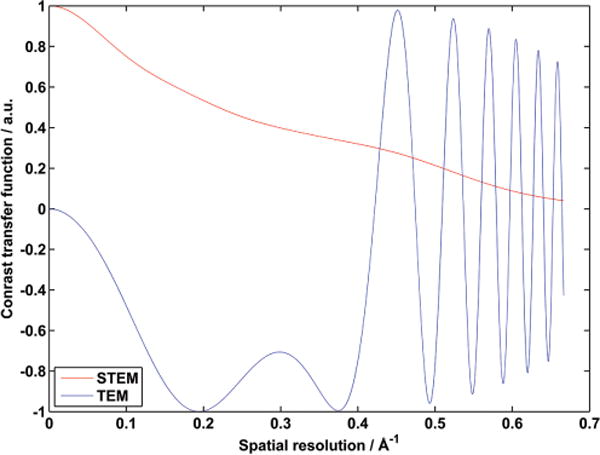
A comparison of the CTF for STEM (red) and TEM (blue). The phase portion of the CTF for TEM is plotted at Scherzer defocus (maximum resolution). STEM shows a monotonically decreasing function for increasing spatial frequency. TEM has low information transfer at low frequencies (<0.1 Å⁻¹). However, TEM provides relatively high transfer compared to STEM near the maximum linear resolution at the first zero crossing of the TEM CTF (ca. 0.32 Å⁻¹). The oscillatory nature of the TEM transfer function above the first zero crossing complicates analysis of TEM images at high resolution especially for crystalline materials. Importantly, TEM provides relatively high SNR for a given dose compared to STEM, which are not considered in this comparison.

STEM required improvements in sources, lenses, scanning electronics, and room environments to finally realize wide-spread adoption in materials research.^[64] This has led to increased availability of ET within physical sciences, long after its establishment for soft materials. Sample preparation is now seen as an important issue for more-wide-spread adoption of the technique (see Section 3.5). Also, the application of new post-processing algorithms is now possible due to the advent of powerful desktop computing as well as high-performance computing clusters (see Section 3.4). Recently, aberration correctors simultaneously improved many aspects of STEM, including resolution (lateral and depth), image contrast, and beam current. The capabilities of these new systems are still being explored (see Section 3.3) with the possibility of new acquisition schemes combined with new reconstruction algorithms. The following sections cover recent progress in state-of-the-art ET, making this an exciting time for 3D nanoscale analysis.

3.3. Benefits of Aberration-Corrected STEM

An important recent advance in STEM with direct application to ET has been the wide-scale introduction of aberration correctors. The focusing power of the round electron lenses used in STEM is intrinsically limited by their well-known spherical aberration, where the minimum probe size is defined as:

$$d_{min}=0.43{\lambda }^{3/4}{C}_3^{1/4}$$ (3)

where C₃ is the third-order spherical aberration (typically 1–2 mm, and also traditionally called C_s) and λ is the wavelength of the incident electrons.^[10] Spherical aberration causes electrons further from the center of the lens to be focused to a different point along the optical axis, and thus increases the size of the focused electron beam at the sample. STEM instruments were typically limited to electron probes with >1 Å resolution, as measured by the full width at half maximum of the focused probe intensity, making many important features at the atomic-scale unresolvable. Simple round electron lenses always exhibit positive spherical aberration coefficients, but it was known that other optical elements with non-round symmetry could be combined to produce negative spherical aberration.^[6,65] Ideally, the C₃ value of round objective lenses can be compensated by introducing such electron optical elements to the column, but this has proved extremely difficult for many years.^[66]

Essentially, non-rotationally symmetric electron lenses, such as quadrupoles, hexapoles, and octapoles, are used to modify the trajectories of electrons off the optical axis to exactly cancel the aberration of round lenses. Early correctors suffered from the effects of higher-order aberrations,^[67] which was overcome by the invention of an aplanatic design.^[68] However, the time required to align all of the extra optical elements, together with the limited stability of the system, made aberration correctors unpractical at best. Rose offers an excellent history of the development of aberration correction.^[6]

Further developments in computer control, lens power supply stability, electron–optical theory, and other concerted efforts in the field have recently led to the realization of aberration correction by two major groups, through the use of multipole elements capable of compensating for the intrinsic aberrations of an electron–optical system.^[13,69] Since then aberration correction for TEM and STEM is now in general use at many research institutions around the world. With this technology almost all aspects of electron-microscopy instrumentation have been improved: lateral resolution is reduced to 0.5–1 Å, contrast is greatly improved, and beam current is increased. These improvements now routinely allow microscopists to measure atomic distances for most crystalline materials, see individual atoms, and make atomic-resolution spectroscopic measurements.^[70,71] This ability to see the location of atoms and their species provides unprecedented knowledge of the basic buildings blocks of materials systems.

ET benefits from these improvements as well, although there is one important aspect to consider. STEM is a focused probe technique, and the semi-angle of convergence of the probe at the sample (α) is an important quality metric.^[72] The best uncorrected microscopes provide a convergence semi-angle of ca. 10 mrad, but aberration correction allows for >3× increase in this parameter. Lateral resolution scales inversely with the convergence angle (1/α), while the depth resolution scales as the inverse square of the convergence angle (1/α²).^[73,74] Thus, the depth resolution of an aberration-corrected STEM is reduced to less than 10 nm, compared with >30 nm for a C₃-limited instrument. Figure 6 shows a focused STEM probe at different defocus values to compare the depth and lateral resolutions of: an uncorrected FEI Tecnai 200 kV STEM with α = 9.6 mrad (Figure 6a), and an aberration-corrected FEI Titan 300 kV STEM with α = 30 mrad (Figure 6b). It is clear that the lateral and depth resolutions are substantially better for the aberration-corrected probe.

Figure 6.

A comparison between the lateral and depth resolution of focused STEM beams for: a) an uncorrected 200 kV FEI Tecnai STEM and b) an aberration-corrected 300 kV FEI Titan. The intensity scale shows low intensity for blue and high intensity for red. The drastically reduced probe dimensions (both lateral and depth) of aberration-corrected STEM have important implications for electron tomography because the entire object may not be in focus.

Initially, it was believed that aberration-corrected STEM would provide a confocal mode of operation that could directly measure 3D structures by simply changing the focus value. This is true for point objects such as atoms, but extended objects suffer from a very large elongation effect, and cannot be reconstructed in this manner.^[75–77] The entire beam passes through the sample at every scan position, and a typical STEM optical system does not allow for selective imaging of in-focus electrons, in comparison with out-of-focus electrons. The information transfer of such a focal series is equivalent to a tilting-tomography series with a maximum tilt angle of ±α.^[73] Figure 7 shows a cross-section in the x–z plane of a focal series of ca. 5 nm Au nanoparticles on a carbon substrate using the probe in Figure 6b, showing the clear elongation of the nanoparticles along the vertical defocus direction. A true confocal mode requires a pin-hole to reject out-of-focus electrons and a spectrometer to select inelastically scattered electrons. Such an optical system has been realized by multiple groups, although the resolution is limited to ca. 5 nm along the beam direction.^[78,79]

Figure 7.

An example of the limited 3D-reconstruction resolution achieved using only defocus in aberration-corrected HAADF-STEM. The image is a cross-section through a set of images at different defocus values of ca. 5 nm diameter gold nanoparticles on a carbon substrate using an aberration-corrected STEM at 300 kV with a 30 mrad semiconvergence angle. The depth of focus is estimated to be ca. 6 nm. The lateral extent of the nanoparticles (horizontal axis) is well defined and the thickness (vertical axis) is highly elongated due to signal from the focused and unfocused parts of electron beam.

In tilting ET, the depth of focus is important to consider with an uncorrected STEM, but aberration correction leads to a more-significant limitation in the volume that can be reconstructed at high resolution.^[80] For large (30 mrad) convergence angles, lateral resolution is sufficient to resolve small atomic distances, but objects larger than 10 nm will not be fully in focus. This places an upper limit on the size of objects that can be reconstructed using single projections acquired by aberration-corrected STEM. There are two possible methods that utilize a series of STEM images at different defocus values of an extended object at each tilt angle to overcome this limitation. In the first method, all of the images in the tilt series can be combined by a wave-packet analysis algorithm into one image with all objects in focus.^[81] Therefore, a tilt series of high-resolution images of an extended object with all features in focus is obtained at all viewing angles and reconstructed by traditional means. The dose applied to the sample is higher than a traditional tilt series, and the wave-packet algorithm essentially removes any information about the depth location of the objects. The second option utilizes the full focal series at each tilt angle to combine both high-lateral-resolution information and depth information at every tilt angle.^[82,83] The amount of information sampled about the object along the projection direction is directly related to the convergence semi-angle of the STEM (±3° for α = 30 mrad), which provides the additional advantage that fewer tilting angles are required to fully sample the object. The various tilt series are combined in Fourier space using bilinear extrapolation and per-pixel weighting of all spatial frequencies to compensate for over sampling. Direct Fourier reconstruction is used to produce the 3D density distribution in real space. This technique simultaneously utilizes the high lateral and high depth resolution of aberration-corrected STEM. This was shown to be useful for large extended systems with a range of important length scales, such as collections of nanoporous catalytic FePt particles on carbon supports. The ability to determine the large-scale distribution of the nanoparticles and their internal porosity provides statistical information relevant to catalytic properties of the system from a single tomography data set using focus and tilt.^[83]

3.4. Algorithm Development for 3D Reconstruction

The WBP technique discussed in Section 2.2.3 can now produce a reconstruction in a few minutes on a moderately powerful desktop computer. WBP is also highly parallelizable, lending itself to implementation on multicore processors and graphics cards for significantly faster reconstructions. The simplicity and speed of this method has led to its wide-scale use, but it does not take full advantage of the input data to refine the final reconstruction. The rapid advance and general availability of powerful computers with large amounts of memory has led to the implementation of more-complex reconstruction algorithms, such as the simultaneous iterative reconstruction technique (SIRT).^[84] Missing information due to the discrete number of projections acquired and the missing wedge of information introduce errors into the final reconstruction, but the original TEM images can be considered ideal projections of the original object. SIRT was developed to iteratively improve the agreement between reconstructions and experimental projections. The original projections are iteratively compared with linear re-projections of a reconstruction to remove artifacts from the final representation of the object. SIRT is now a common reconstruction technique and is known to reduce reconstruction artifacts for sets of projections with low noise and high contrast commonly found in hard-material specimens. It requires a relatively large number of projections with a small missing wedge (1–2° tilt steps and ±70°) to produce the best results. Furthermore, the reconstruction tends to converge to a local minimum after 20–30 iterations before the reconstruction quality degrades with more refinement steps. Recently, a hybrid method combining WBP and SIRT, called W-SIRT, was shown to further improve the technique.^[85] This review will briefly discuss recent advancements in post-processing beyond SIRT, which seek to improve 3D analysis by achieving atomic-scale resolution, using fewer input projections, and improving agreement with physical models.

3.4.1. Atomic-Resolution Reconstruction

A grand challenge of electron microscopy is to identify the species and location of all atoms within a system to predict its materials properties from first principles. The ca. 1 nm resolution limit of HAADF-STEM tomography is approximately 5 to 10 times larger than a high-quality STEM probe and is the result of multiple other factors. The discrete number of tilts and missing wedge degrade resolution, as described in Equation 1 and 2 of Section 2.1, regardless of the microscope resolution. Uncorrected STEM instruments have also previously provided insufficient image contrast, especially at high tilt angles, to distinguish subtle changes in projected density amounting to single-atom contrast.

Crystal-Model-Based Reconstruction

The advent of aberration correction (discussed in Section 3.3) significantly improved the resolution and contrast of STEM instrumentation to detect single atoms in 2D projections.^[63,86] To take advantage of these improvements, a novel reconstruction technique known as discrete tomography was developed, with the accurate assumption that an object is made of discrete atoms, called atomicity.^[87] This led to the first atomic-resolution 3D reconstruction of a Ag nanoparticle embedded in Al using two high-resolution projections.^[88] A statistical method was used to determine the number of atoms in each column from the projected intensity for each projection.^[89] The assumptions of a face-centered-cubic crystalline lattice and physical continuity between columns were used to solve a unique atomic arrangement that matched the two projections along the crystalline-zone axes. An additional zone-axis projection at a different angle was used to confirm the result. Since that publication, more work has been done to apply this technique to reconstruct crystalline structures from multiple zone axes or even using just one aberration-corrected TEM image.^[90,91] The amount of dose applied to the sample is less, compared with a tomographic tilt series, due to the limited number of tilts required, potentially leaving surface atoms and faceting intact for analysis. Discrete tomography uses atomicity (a physical constraint) and a crystalline structure (prior knowledge) to significantly reduce the required input data, but it produces reconstructions with atoms on a predefined lattice. These assumptions cannot be used in many other materials that would benefit from 3D knowledge of atomic positions.

Equally Sloped Tomography

A generally applicable method to reach atomic-scale resolution is called equally sloped tomography (EST). This method utilizes the pseudo-polar fast Fourier transform (pPFFT) to directly transform between real and reciprocal (Fourier) space.^[92,93] As discussed in Section 2.1, direct Fourier inversion is not ideal for a traditional tomographic tilt series acquired with equal angular increments between projections, because inverse Fourier reconstruction involves interpolation (approximations) to between polar and Cartesian coordinates (see Figure 4a). In EST, the experimental projection angles are chosen such that the tilt increments between projections have equal slope, and the pPFFT is then an exact transform between the projections in reciprocal space and a Cartesian grid in real space. Figure 8 shows how the information acquired by the EST method can be described as a linogram grid of N concentric squares, where each black dot represents a measurement (a pixel). Figure 8 also shows the relationship between a 4 × 4 Cartesian grid (real space) and a linogram grid (reciprocal space) with N = 4 connected by the pPFFT and its inverse. The dots represent a measurement of the projected density (a pixel) and the equal slope is indicated by the colored lines with equal spacing horizontally and vertically. Before reconstruction, the EST projections are aligned to high accuracy by a center-of-mass method.^[94] An iterative procedure is used to produce a 3D density through continual improvement using the following steps. First, the projections are mapped to the linogram grid via a fractional Fourier transform (FrFT), which changes the sample spacing of the projections in reciprocal space for each individual projection to match the pPFFT. These are then directly combined in reciprocal space without interpolation. Next the pPFFT⁻¹ is applied to produce a 3D density in Cartesian real space, and constraints are imposed on the density. The updated density is transformed back to reciprocal space by the pPFFT, and the original projections are used to replace the information at the corresponding angles. This iterative reconstruction procedure converges to a 3D density that best matches the projections producing higher resolution and contrast with fewer artifacts compared to traditional algorithms.^[95] EST has achieved atomic-scale resolution of an Au nanoparticle at a resolution of 2.4 Å and produced the first images of dislocations at atomic resolution in a Pt nanoparticles.^[94,96] The technique is generally applicable to projections of any unique object with the possibility of investigating amorphous materials at the atomic scale.^[97]

Figure 8.

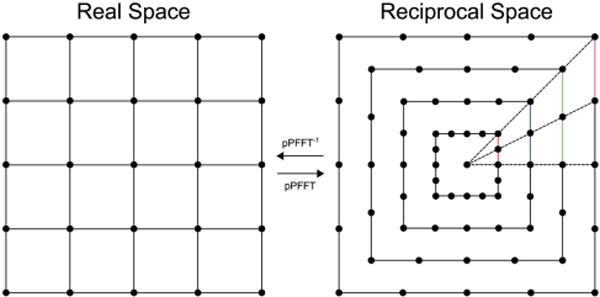
Unlike normal tilting ET, data acquisition for equally sloped tomography (EST) uses specific tilt-angles that directly map into reciprocal space on a grid of concentric squares without interpolation. The pPFFT⁻¹ accurately calculates the density map in real space on a rectangular grid. For clarity, the diagram shows a small set of 4 tilt angles with 22.5° between tilt images. Notice the colored vertical lines in reciprocal space, which mark equal slope increments between projections. Since projections acquired using EST perfectly map to reciprocal space, iterative calculations that transform the data between real and reciprocal space (used to improve the reconstruction resolution) are exact and produce no artifacts.

3.4.2. Methods for Non-linear Projections

The two traditional reconstruction algorithms (WBP and SIRT) assume a linear relationship between the projected density and the image intensity. This is a good approximation in most cases for HAADF-STEM images, but non-linear and non-monotonic deviations are known to exist.^[62] Furthermore, traditional reconstruction algorithms do not account for the noise characteristics of HAADF-STEM. Methods that compensate for non-linear scattering, originally developed for medical CAT, can incorporate the known physics of particle scattering into the reconstruction algorithm.^[98,99]

Utilizing the physics of the imaging process during reconstruction can include factors such as exponential signal attenuation inside thick specimens (known as Beer’s law) and nonlinear diffraction contrast.^[100] Intensities in HAADF-STEM images are dominated by incoherently scattered electrons, but the low flux of highly scattered electrons requires a large electron dose to achieve a good SNR. Improved dose efficiency can be achieved at the cost of a less-linear signal by using electrons scattered at lower angles (including Bragg scattering). A model-based iterative reconstruction (MBIR) technique (not to be confused with the density model used to align projection images in biology) can account for noise and non-linear intensities during a reconstruction based on the scattering processes involved in image formation.^[101] This approach has also been utilized to produce reliable reconstructions from highly non-linear imaging methods such as bright-field (BF) STEM.^[102] MBIR can also be used to produce quantitative reconstructions where the voxel intensity provides a real measure of the local material property, such as a scattering cross-section, rather than relative density. MBIR has been shown to reduce artifacts and improve contrast, even with fewer projections, using rational physical constraints imposed on the system to eliminate unphysical results.^[103]

3.4.3. Compressed Sensing

There exists great interest in the community to reduce the number of projections and the impact of the missing wedge, while maintaining the accuracy of the final reconstruction. A promising route to accomplish both of these goals simultaneously is to incorporate constraints and/or prior knowledge into the reconstruction technique. For many years, electron microscopists have designed sample preparation and experiments to project along specific crystalline zone axes that contain as much information as is needed to measure the materials property of interest. A priori information about the crystalline arrangements of solids can be used to deduce the 3D arrangement of atoms. Until recently, ET in physical sciences has endeavored to sample all possible information about a structure to ensure a faithful reconstruction, but this is not possible in all cases due to dose and time constraints.

Compressed sensing is a fairly new general technique just now being adapted to ET reconstructions. The algorithm is designed to find solutions to systems considered under-determined by the Nyquist sampling theorem.^[104,105] Compressed sensing assumes that some information contained in a digital signal or image is sparsely distributed (or compressible), and thus not all channels must be fully sampled to produce a sufficient (or even exact) representation of the object. An analogy commonly used is JPEG image compression, which significantly reduces the storage required for digital pictures while maintaining quality. Rather than reducing the information that is stored after acquisition, compressed sensing seeks to reconstruct the unknown information from a dramatically reduced set of experimental data. The concept relies on the fact that the object can be described in a domain, such as reciprocal space, where some pieces of information are important to the overall structure and other minor parts can be discarded. For ET, data acquired from fewer tilt angles can be combined with a priori information about the structure to produce a high-quality reconstruction.^[106] The projection directions may even be chosen based on the symmetry of the structure to specifically include critical information. This can mean significant reductions in the electron irradiation dose and the number of tilt angles, as well as the use of new signals (such as electron energy loss spectroscopy (EELS)) that previously were experimentally impractical.

In a recent example, the assumptions of sparsity in the Fourier domain and cubic symmetry were applied to low-loss EELS tomography to reconstruct surface plasmon resonances of cubic metal nanoparticles in 3D.^[107] The scattering cross-section for inelastic EELS signals are 10 to 100 times lower than for elastic HAADF-STEM scattering, and 2D EELS maps require significantly longer exposures to achieve a good SNR. The authors designed the experiment to acquire the necessary data from a limited number of projections in order to utilize dose and time efficiently. The sample’s known cubic symmetry was exploited to allow a reconstruction using only the positive tilt angles. Compressed sensing was used with the assumption that the artifacts introduced from the limited number of tilt angles only added noise in the final reconstruction. In other words, the acquired projections sampled the important information to define the structure, and all other information was distributed throughout the 3D reconstruction as noise. This result demonstrates the importance of an experiment designed to sample a small set of necessary information to reproduce the structure. The 3D reconstruction provides important insights into spectral modes of nanoparticles interacting with a dielectric surface.

It is important to realize the limitations of compressed sensing. Unlike the more-general WBP and SIRT algorithms, the assumptions made for one system are not generally applicable to all structures. Furthermore, the final model will directly reflect those assumptions, and the researcher must be aware of model bias, a more commonly known problem in biological sciences. Traditional tomographic reconstruction techniques are generally applicable in almost all cases where the projection requirement holds, and the artifacts are now well understood. Algorithms that are more advanced must be carefully studied and verified for each new set of applications.

3.5. Improvements in Sample Preparation by Focused Ion Beam Experiments

Sample preparation in the physical sciences has long relied on polishing by physical grinding to produce uniformly flat regions of material with minimal surface damage.^[108] Traditional polishing can prepare thin, smooth TEM specimens from large bulk materials, but cannot easily prepare a sample of a specific sample area, such as is needed in microelectronics failure analysis. The introduction of the focused ion beam (FIB) and subsequent development of in situ and ex situ lift-out techniques have enabled site-specific sample preparation for TEM.^[109,110] FIB can produce thin and flat TEM samples even for atomic-resolution investigations using low-voltage (1–3 kV) final milling. The microelectronics industry benefits greatly from FIB TEM preparation to investigate the failure of specific electronic components among the millions on a single chip. The time required to produce very high quality samples with <20 nm thickness is prohibitive in many cases, and even the thinnest FIB samples can be thicker than the electronic components themselves. Thus, the overlap of complex structures cannot be fully analyzed from a single 2D projection due to the overlap of many different features. ET and FIB lift-out sample preparation can provide a significant amount of information about specific devices (failed or intact) from relatively thick sections to investigate the failure modes and provide many measurements of critical features.^[111] FIB has also been utilized to prepare specimens of soft materials for 3D analysis that were previously difficult to analyze by TEM,^[112,113] and even for improving reconstructions of frozen-hydrated cells.^[114]

Nanoprocessing by FIB has also enabled the preparation of needle-like samples to simultaneously eliminate two problems inherent in slab-type TEM samples.^[109,115] The projected thickness of material in slab-type samples increases as (1/cosθ), where θ is the tilt angle, reaching 2.9 times the original thickness at a tilt of 70°. Subsequently, the resolution and SNR in images acquired at the high tilt angles are significantly reduced.^[80] All viewing angles of a needle sample provide projections of equivalent quality even from relatively thick samples. Also, needle samples can be mounted in a full-rotation TEM holder, which allows ±90° rotation to completely eliminate the missing wedge of information (discussed in Section 2.1). This improves the resolution and greatly reduces artifacts in the final 3D volume.^[109] Moreover, the development of FIB-prepared needle-shaped samples was a critical development for the hybrid 3D spectroscopic measurements discussed later in Section 3.6.

3.6. Beyond Density: Measurement of Intrinsic Material Properties in 3D

The main focus of ET until recently was to determine the 3D density distribution of an object, but TEM is a very versatile tool capable of measuring more than just the projected density of materials. Recent advances in hardware and software provide electron microscopists with vastly more-stable and powerful microscopes enabling STEM and TEM to achieve new milestones in analytical capabilities, such as quantitative sensitivity to spectroscopic,^[58,116] magnetic,^[117] and electronic^[118] properties of materials, even with atomic resolution. Some of these advanced TEM experiments satisfy the projection requirement for tomography, opening up the possibility of directly measuring functional properties in 3D at the nanoscale.

3.6.1. Spectroscopic Tomography

HAADF-STEM is useful to distinguish between materials with large differences in atomic number (Au and C), and has been used to determine distributions of metals in core/shell structures at high resolution.^[119] Small differences are much more difficult to detect (Co and Ni). Initial experiments that retrieved more than a single density measurement per voxel involved spectroscopic methods such as EELS^[120] and X-ray energy-dispersive spectroscopy (X-EDS)^[121] in TEM or STEM mode. Both spectroscopic methods are very powerful for measuring elemental distributions at the nanometer scale, producing signals that conform to projection theorems.^[122,123] These methods are very dose intensive because the scattering cross-sections for inelastic (energy loss) events are extremely low, leading to long acquisition times. Until recently, even 2D mapping of structures in a single projection had proved difficult due to limited stability and beam current over hour(s) long acquisitions. Advances in detectors, electron-source brightness, and collection optics have all provided sufficient beam current and collection efficiency to reduce acquisition times of 2D maps from hours to minutes. EELS and X-EDS are therefore used to unambiguously distinguish elements in 2D, even within mixtures of materials, and 3D measurements have become more practical.^[124] For example, EELS measurements of the 3D distribution of surface plasmon modes of cubic metal nanoparticles, which could not be determined without spectroscopic imaging, were recently reported.^[107]

Although neither of these spectroscopic techniques applies a low dose on the specimen during imaging, the resulting noisy tilt series could benefit from techniques developed in biological sciences for low-SNR reconstruction to improve elemental mapping in 3D at the nanoscale. The quality of a spectroscopic signal from nanostructures also greatly depends on the thickness of the specimen, and spectroscopic tomography was partially made possible by the preparation of the needle-like samples discussed in Section 3.5.^[109] For EELS, specimens much thicker than the incident electron mean-free path produces multiple scattering, which increases the signal background.^[120] For X-EDS, the spectrum intensities depend on the path of the incident electron and the path of the generated X-rays, and thickness corrections must be applied even for relatively thin samples to achieve quantitative results.^[116,125] For tomography, these corrections may need to be applied for each separate tilt angle. Reconstruction of 200 nm LiNiMnO₂ nanoparticles showed the segregation of one species (Ni in this case) to the surface of the particle even for low-contrast materials that would not be visible in a typical HAADF-STEM 3D reconstruction.^[126] Although powerful enough to unambiguously differentiate elemental species in 3D, spectroscopic tomography only produces the morphology of the object of interest. Other TEM imaging projection methods have been used to investigate materials properties, such as magnetic fields at the nanometer scale in 3D.

3.6.2. Measuring Magnetic Fields

The magnetic properties of materials are important aspects of device functionality in advanced technologies such as magnetic hard drives. Continued improvement of such devices requires quantitative measurements of magnetic fields within and around nanoscale features, which are independent of density. For example, the size of magnetic domains that define storage bits on magnetic hard drives is limited due to magnetic interactions at the nanoscale.^[127] Unfortunately, the objective lens in STEM and TEM produces a strong magnetic field of ca. 2 T perpendicular to the sample surface, which magnetizes almost all material perpendicular to the sample. Removing this strong magnetic field provides a field-free imaging condition, generally referred to as Lorentz TEM, sensitive to the intrinsic in-plane magnetization of the material, although the resolution is degraded to >1 nm.^[128] Nanoscale resolution is sufficient to analyze many magnetic structures, but generating images with contrast that can be related to measurable magnetic properties is difficult. We discuss two quantitative techniques used in Lorentz microscopy that determine the relative phase shifts of the incident electron beam, which can be related to the object’s intrinsic magnetic field. Fresnel image contrast measures effects of phase shifts in TEM image intensities, and off-axis holography accurately measures the electron phase shifts of the complex electron wave.

Fresnel Imaging Contrast

The most-common technique in Lorentz microscopy to produce magnetic contrast, called Fresnel imaging, is achieved by simply defocusing the imaging lens in field-free conditions to enhance coherent interference.^[129] Adjacent magnetic grains in a thin film are separated by a boundary called a magnetic domain wall where the in-plane magnetic field changes direction. The path of an electron traveling perpendicular to the sample surface is deflected according to the strength of the in-plane field. At a magnetic domain wall, grains with opposing magnetic fields will produce bright or dark lines according to their direction and the lens defocus. The diagram in Figure 9 shows how deflected electrons overlap in a defocused image to produce bright or dark lines according to the magnetic orientation of neighboring grains. This technique highlights the grain boundaries in a 2D projection of a thin film. For quantitative measurements, a digital phase-retrieval algorithm, such as the transport of intensity equation, is necessary to measure the projected phase change of the electrons from a series of defocused images (Figure 9a–d).^[130] The in-plane magnetic induction is then calculated from the relative phase changes at each position. The image of the magnetic field provides a measure of the projected in-plane component of a 3D magnetic vector,^[131] and a double-tilt ET experiment^[50] is required to determine the full 3D magnetic vector field.^[132] In practice, the object is removed from the microscope and rotated 90° in the holder after the acquisition of each tilt series.^[132] Further developments in equipment, image acquisition techniques, and post-processing algorithms are needed to fully realize the potential of 3D Fresnel imaging in Lorentz microscopy to study nanoscale magnetic devices.

Figure 9.

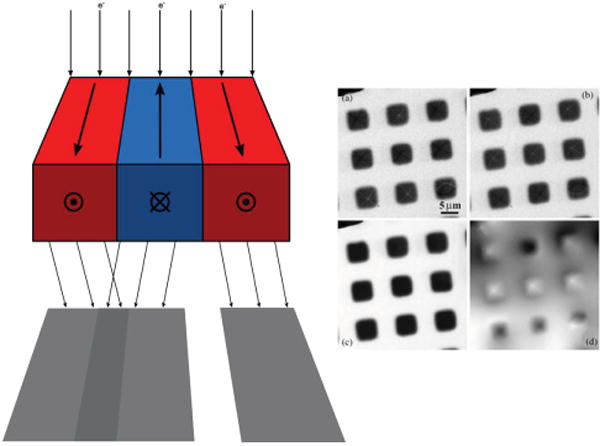
Concepts of Fresnel contrast in Lorentz (field-free) microscopy. The diagram on the left shows the paths of electrons passing through grains of a magnetic material with opposing in-plane magnetization. The paths bend according to the direction of the magnetic field yielding bright and dark contrast at domain walls. The image intensities in a series of defocused images at a) under-focus, b) over-focus and c) in-focus can be used to estimate d) the electron wave phase shifts due to the magnetic field of the sample. These relative phase shifts can be related to the magnetic properties of the object. Adapted with permission.^[130] Copyright 2014, Elsevier.

Off-Axis Electron Holography

Off-axis electron holography is a powerful technique that uses interference to measure both the amplitude and phase of the electron wave after it passes through the sample.^[133] This is unlike typical TEM, because an imaging detector measures the intensity (or magnitude squared) of the complex electron wave.^[134] The technique utilizes a post-specimen electrostatic biprism to interfere with one portion of the electron beam that passes through vacuum and a separate portion that passes through the sample. A fringe pattern is created on the imaging detector, and digital processing of the fringe pattern is used to determine the complex values of the electron wave. For most materials, the phase is directly related to the projected mean inner potential (MIP) and magnetic field of the underlying structure. The technique can quantitatively measure electrostatic and magnetic properties of materials with sub-nanometer resolution, such as the potential of pn-junctions, dopant profiles, and the magnetization distribution in and around objects.^[135] Projection measurements from off-axis holography conform to the projection theorem of ET, providing the ability to quantitatively measure 3D electrostatic potentials of core–shell nanowires and semiconductor devices.^[136,137] When used in a field-free Lorentz TEM, magnetic fields are particularly interesting to study in 3D by electron holography, because even field lines in vacuum around the sample can even be measured.^[138] However, just as with Fresnel imaging, determination of the magnitude and direction of the 3D vector field requires acquisition of two tilt series with a 90° rotation between them.^[139]

Outlook

The applications of 3D magnetic Lorentz tomography and off-axis electron holography are currently limited due to the specialized equipment required to accomplish the experiments. For both techniques, Lorentz TEM has relatively low resolution compared with normal TEM, although recent developments in aberration correction will provide higher-resolution, field-free imaging in the near future.^[140] Off-axis electron holography requires a highly coherent source (such as an FEG), a biprism, and a special electron optical setup.^[141] Other important limitations to consider are the field-of-view and hologram fringe contrast (peak to valley measurements), which have direct effects on the achievable lateral resolution and phase resolution in the reconstructed exit wave.^[142]

4. Advances in ET for Soft-Materials and Biomaterials Research

4.1. Background

ET has contributed effectively to the study of a wide variety of biological molecules, from a single macromolecule to a whole cell. Examples include the nuclear pore,^[143] viruses,^[144] micro-tubules,^[145] bacterial ultrastructure,^[146] molecular motors,^[147] and cell sections.^[148] More recently, the technique enabled the study of conformational dynamics based on the structure of a single protein.^[37,38]

Tilt series ET has several advantages over X-ray crystal diffraction and single-particle reconstruction. X-ray crystallography captures diffraction patterns from crystallized molecules and then solves for the real-space density. Single-particle reconstruction uses tens of thousands of images of immobilized particles in random orientations. Those 2D images are organized into different classes based on particle 3D orientations before being averaged into a 3D reconstruction. In ET, 3D reconstruction from a single object can avoid possible artifacts introduced through averaging a large number of images of flexible proteins in different conformations. Structurally flexible proteins show significant variability in solution, making them difficult to classify accurately prior to identifying their orientations.^[149–151] Moreover, aligning ET images is, in principle, simple compared to aligning images in single-particle reconstructions, which requires a reference model. In addition, ET enables 3D structural determinations of a wide variety of macromolecules and macromolecular processes, such as large complexes^[39] and aggregates. However, the resolution achieved directly from ET (without averaging) is rarely beyond ca. 2 nm.

Many factors need to be considered before 3D reconstruction in soft materials or biomaterials. In terms of the sample environment, the sample itself tends to lower the quality of the recorded images due to the solvent background, stain effects, temperature-related drift, sample surface charging, and beam-induced motion.^[152,153] In terms of TEM operation, limitations are related to the use of a high-defocus (trading low-resolution details for high-resolution),^[154,155] detector shot noise, and detector quantum efficiency.^[156,157] In terms of the instrument, the quality of the recorded images is affected by instabilities in the TEM source and lenses (beam coherence),^[158] lens astigmatism,^[159] spherical aberrations,^[12] energy filter distortion,^[160] and mechanical tilting. Ideally, all of the above parameters should to be adjusted, optimized, corrected, and compensated before or during ET data acquisition and 3D reconstruction.

4.2. Strategies in ET

The following section provides a brief account of selected aspects of sample preparation, data acquisition, tilt-series alignment, and 3D-reconstruction techniques.

4.2.1. Sample Preparation

Biological samples have generally poor contrast to their image background, typically amorphous carbon, and can be easily damaged by the electron beam during imaging. As a result, numerous methods have been developed to both enhance sample contrast, and improve sample integrity under illumination. For the purpose of the following discussion, we broadly categorize these methods into three groups based on the main strategy used in the sample preparation: staining-based methods, cryogenic methods (cryofixation) and combinations of both staining and cryofixation. The method of choice usually depends on the targeted resolution, the purpose of the study, and the nature of the sample, which can vary from individual molecules to whole cells or tissues.

Staining-Based Sample Preparation

Staining-based sample preparation, used to improve image contrast, includes negative staining^[161] and positive staining.^[162] Negative staining is the most-popular technique, in which the sample is surrounded with a layer of charged heavy-metal salts. The stain appears as dark regions on the edges of molecules in images, thus highlighting their shape in a “negative” contrast image.^[163] When the stain is sufficiently thin, only barely covering the sample surface, a “positive” contrast image is generated, termed positive staining. The high image contrast, in both cases, is due to the fact that the heavy-metal ions scatter more electrons compared with the lighter atoms in the sample.^[164–166] The heavy-metal coating on the sample permits a high dose with high contrast for easier determination of particle orientation in 3D reconstructions.^[167] Negative-staining reagents include phosphotungstic acid salts, ammonium molybdate, uranyl acetate, uranyl formate, and methylamine vanadate. Phosphotungstic acid is particularly widely used in standard protocols due to its near physiological pH.^[168] In general, preparation of stained samples is simple and efficient compared to cryo-electron-microscopy (cryo-EM). It therefore permits the screening of a large number of samples and conditions.

Although TEM studies that utilized negative staining were able to observe macromolecules, the fine details of those molecules remained unresolved.^[34] It was generally believed that a detailed particle structure was preserved and stabilized with negative staining.^[169] Other studies showed that the stain could introduce distortions to some molecules, such as general aggregation, molecular dissociation, and flattening.^{[167,170,171]} For example, a common artifact due to negative staining of lipid-related proteins is that particles stacked and packed together into a structure called a rouleaux.^{[163,172–176]} Recently, an optimized negative-staining (OpNS) method^[177–179] was proposed via a refined conventional protocol (Figure 10).^[180] The OpNS protocol has been validated by proteins with a known structure,^[179] including cholesterol ester transfer protein (CETP),^[162] GroEL, and proteasome (Figure 11),^[181] and applied to examine the structures of lipoproteins^[177,178] and flexible antibodies.^[37]

Figure 10.

A schematic diagram of optimized negative-staining (OpNS) procedures. a) Incubation station designed to hold a glow-discharged TEM grid pre-coated with a thin carbon film, which incubates a 3 μL sample solution above an ice bath. b) Staining workstation designed to hold water droplets and stain droplets above an ice bed while minimizing stain exposure to light. c) Overview of the staining procedure. The TEM grid with sample was prepared via 3× water washing, 3× UF stain exposure and followed by backside blotting with a filter. The grid was then dried immediately by nitrogen gas. Reproduced with permission.^[181] Copyright 2014, The Authors, published by Journal of Vizualized Experiments (JoVE).

Figure 11.

TEM images of proteins with known structure using OpNS. a) Survey view of a small and asymmetric protein, 53 kDa CETP (dashed circles) by OpNS. b) 30 representative images of CETP particles. c) Two representative images of CETP particles with particle orientation identified by their tapered tip end (N-terminal β-barrel domain) and globular tip end (C-terminal β-barrel domain), d) which is consistent with the CETP structure, obtained from X-ray crystallography (PDB: 2OBD), in size and shape. e) The high-contrast images were used to reconstruct a 3D volume at 1.4 nm resolution. f) Survey view of another protein with known structure, GroEL, and g) 9 representative particles images prepared by OpNS. h) Survey view of a third protein with known structure, proteasome, and i) 9 representative particle images prepared by OpNS. Scale bars: a) 50 nm; e) 3 nm; f) and h) 50 nm. a–e) Reproduced with permission.^[162] Copyright 2012, rights managed by Nature Publishing Group; f–i) Reproduced with permission.^[181] Copyright 2014, The Authors, published by Journal of Vizualized Experiments (JoVE).

Cryo-EM

The main advantage of cryo-EM is that the samples can be examined in their hydrated native state.^{[23,182–184]} Samples embedded in a physiological buffer or even inside cells could avoid potential artifacts induced by dehydration, chemical fixation, or staining.^[185] Unlike for hard materials, images from soft materials and biomaterials exhibit low contrast, which arises from differences between the scattering densities of the biomolecules and the solvent. Small proteins are difficult to be visualized or identified, although the image contrast of the overall shape of biomolecules can be enhanced by defocusing.^[186,187]

Cryofixation of hydrated samples is currently the most-common ET method to examine micrometer- to nanometer-scale objects, including 2D molecular crystals and helical structures. Samples are fixed by rapid freezing with liquid ethane using a plunger and then transferred to liquid nitrogen (or liquid helium) for storage. TEM imaging is accomplished while the sample is maintained at liquid-nitrogen temperature in a cryo-holder (Figure 12).^{[185,188–191]}

Figure 12.

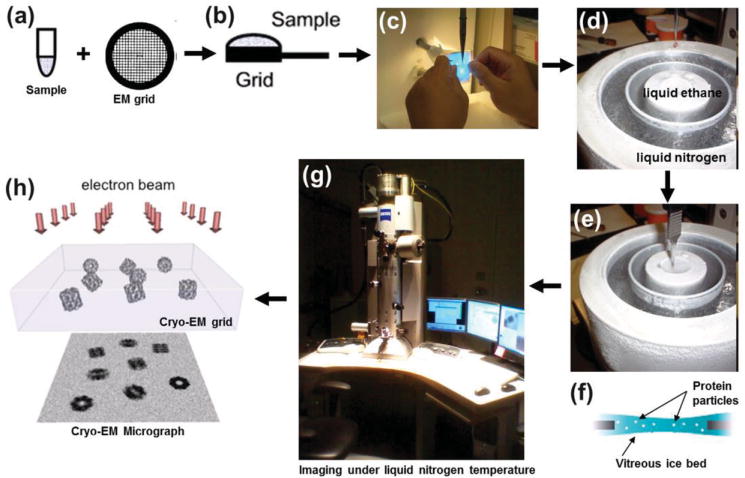
A schematic diagram of cryo-EM sample-preparation procedures. a) A 3–4 μL sample solution is deposited onto the holey carbon coated TEM grid, which was previously glow-discharged. b) The grid is then incubated for approximately one minute. c–e) Excess solution is removed by blotting with filter paper (c), and then quickly plunged into liquid ethane [(d,e) Reproduced with permission.^[192] Copyright 1999, Hanspeter Niederstrasser/Snaggled Works]. f) The frozen grid, with vitrified ice covering the carbon film holes, is then transferred to liquid nitrogen for storage. g) The grid is imaged under liquid nitrogen temperature of −170 °C to −180 °C. h) An electron beam passing through the vitrified ice projects the 3D sample into a 2D image, which is recorded by CCD. h) Reproduced with permission.^[193] Copyright 2010, Greg Pintilie.

Cryo-EM of vitrified sections (called CEMOVIS) is a method to prepare thicker samples using a high-pressure freezing machine. The machine, operating under more than 10³ bar pressure, enables rapid cooling of thick samples before the formation of ice crystals.^[194] The vitrified sample is then sectioned by a cryo-microtome to obtain a thin layer of sample, such as a thickness of ca. 50 nm. The technique has been applied to several studies, including ET of cells.^[195,196] The limitation of this method includes potential artifacts at the cutting surface, such as compressions or crevasses, which can be several nanometers deep.^[197]

Cryo-Negative and Cryo-Positive Staining

In cryo-EM, small proteins (<200 kDa) exhibit low contrast compared with the vitrified ice background, and the proteins are extremely challenging to identify. Consequently, particle orientations and classes are difficult to determine by cross-correlation calculations. This is also difficult for large proteins that are structurally flexible and naturally fluctuate in solution, because they exhibit a continuous range of conformations.^[37,162]

By combination of the advantages of both cryo-EM and negative staining, Adrian and co-workers^[198,199] reported a cryo-negative-staining (cryo-NS) method. In cryo-NS, the sample was mixed with a staining solution (16% ammonium molybdate) and then rapidly frozen to produce a thin layer of vitrified ice. Cryo-NS enables high-contrast images with a relatively higher resolution than negative staining. The image resolution from cryo-NS samples of tobacco mosaic virus (TMV) rods and catalase crystals shows information in reciprocal space up to 10 Å. Cryo-NS images have a reversed image contrast compared to that from unstained vitrified cryo-EM.

Recently, Ren and co-workers reported another combination of cryo-EM and a staining method by using 1% uranyl formate (UF)^[162] instead of 16% ammonium molybdate as the staining solution. The staining solution was mixed with the samples before cryo-EM preparation. Since the image contrast is inverted compared to the cryo-NS method,^[198–200] but consistent with images obtained from conventional cryo-EM, the method was termed cryo-positive staining (cryo-PS). Cryo-PS provides high-contrast images of small and asymmetric proteins, such as a 53 kDa cholesterol ester transfer protein (CETP). The high-contrast images contain fine-structural details of the protein, similar to the secondary structure solved by X-ray crystallography of these molecules (Figure 13). The cryo-PS made it possible to achieve a 3D reconstruction of a 53 kDa protein with 1.4 nm resolution by single-particle reconstruction, providing a new sample preparation technique for ET.^[162]

Figure 13.

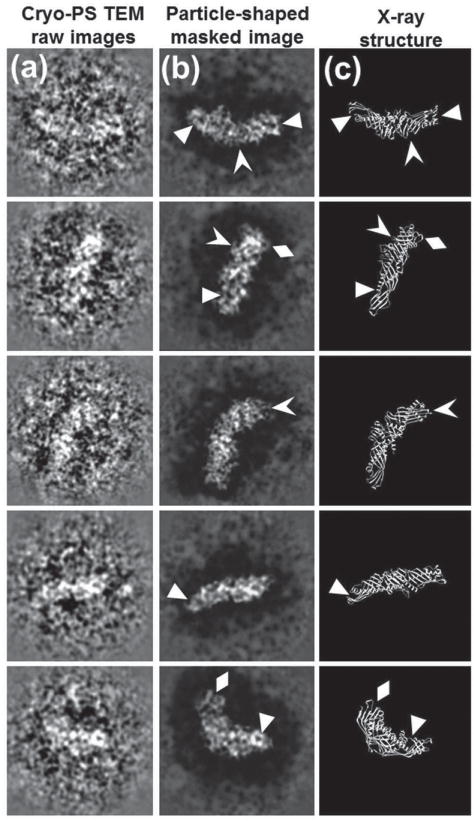
Images of a small and asymmetric protein CETP (53 kDa) imaged using cryo-positive staining (cryo-PS) showing high-resolution details. a) Five representative images of CETP particles prepared by cryo-positive staining (with reversed contrast and a circular-shaped soft mask). b) By applying particle-shaped soft masks on each particle image, the masked images are compared with (c) the structure of CETP (obtained by X-ray crystallography and shown in ribbon structure) at similar viewing angles. Similar structural features are marked by arrows. Reproduced with permission.^[162] Copyright 2012, rights managed by Nature Publishing Group.

4.2.2. Image-Acquisition Strategies

Automated Data Acquisition

The recent growth in the ET field has been fostered by automated computer control.^[201,202] During tilt-series acquisition, the sample stage suffers from various mechanical vibrations induced by gears, motors, liquid nitrogen, and thermal expansion.^[203,204] As a result, neither the specimen central position (x and y planes) nor the eucentric height (z) could be fixed throughout the collection of the tilt series. Automated data collection software attempts to compensate for these imperfections through the use of various computational algorithms. For example, x- and y-plane translational parameters can be determined by using a reference image before re-centering the specimen for the next tilt-image acquisition.^[202] Other methods attempt to predict the translational parameters using previous tilted-image positions,^[205,206] or using combination of both the predicted positions and reference images.^[201] Sequential data acquisition for single-^[202] and dual-tilt,^[207] and also random canonical tilt series have been automated.^[208,209] Facilitating program functions, such as real-time reconstruction using parallel computing and specimen autofocus, have been implemented.^[203] A number of software packages for automated data collection are currently widely used by the biological/soft material ET community, such as UCSF tomography,^[206] Leginon,^[210] SerialEM,^[201] Xplore3D,^[211] TOM software toolbox^[212] and Gatan Tomography.

Dose Limitation

The resolution of a TEM image is limited by many factors, including the SNR. Biological materials are quickly destroyed by the electron beam, which tends to break bonds between atoms in the structure. The radiation damage often destroys the fine spatial detail before the large overall structure.

Optimal exposure will depend on the target resolution. The dose limitations for both single-particle reconstruction and ET reconstruction have been discussed frequently in the literature over the years.^{[24,186,213–218]} It is usually thought that ET is more tolerant to overexposure than single-particle reconstruction methods because ET usually targets a lower resolution, and exposure is applied at a lower dose rate over a longer time.^[217] Conventionally, exposure of 5–20 e⁻ Å⁻² is often used in imaging for single-particle reconstruction to achieve a structure resolution beyond 4 Å.^[23,191,219] By ET, it has been reported that ca. 20 Å resolution is feasible for a thin sample with a total exposure of 120 e⁻ Å^−2.[40] However, in many studies, a higher dose is often used in ET imaging.^[38,179,210] It is difficult to determine the actual dose limitation for ET imaging because a quantitative method to assess the degree of radiation damage is not available.

The severity of radiation damage can be affected by sample temperature. It is well known that the rate of chemical reactions is influenced by the temperature, which affects molecular motion and hence the collision rate between molecules.^[220] Considering biological samples are sensitive to radiolysis (or ionization damage by inelastic scattering), low temperatures can slow down radiation damage. For example, catalase crystals show higher resolution in electron diffraction under frozen conditions than that under room temperature.^[186] Although cooling itself does not eliminate radiation damage (bond breaking occurs at all temperatures), the cooling can reduce the motion of irradiated molecules.^[221] Theoretically, any method of sample fixation should reduce the mobility of particles, and therefore reduce radiation damage.^[222] Currently, in cryo-EM, liquid nitrogen is used to reach a cryogenic temperature of 77 K. It has been reported that optimal cryogenic temperatures to reduce beam damage from both X-rays and electron sources is ca. 50 K.^[218,223] The cost-to-benefit ratio of this relatively small improvement is still a point of debate.^[222]

To reduce the temperature increase of the specimen in cryo-EM during illumination, Zhang and Ren^[38] proposed using a large piece of ice (ca. 7–10 μm) for ET imaging. A larger volume of ice provides more material to absorb heat and increases tolerance to radiation damage. It is usually observed that an exposure of ca. 30–40 e⁻ Å⁻² could generate bubbling in carbon-film areas that are covered with super-thin ice; however, the larger-ice areas suspended across a hole in the carbon film bubbles less (Figure 12f). Additionally, the larger piece of ice provides a larger evenly flat sample area, which provides a more-even background contrast during tilting.^[38,179]

To reduce the specimen motion during irradiation, Russo and Passmore^[224] recently developed a gold specimen substrate to increase the heat transfer rate and nearly eliminate specimen motion during irradiation. The improvement may be due to the high thermal and electron conductivity of the gold material supporting the frozen sample.

Low-Dose CCD and Direct Electron Detectors

Considering that the dose used for imaging biological samples is much lower than that used for hard materials, low-dose-sensitive charge-coupled device (CCD) detectors were specifically designed for biological applications.^[225] Today, CCD detectors have almost entirely replaced photographic film for imaging due to their fast response, low noise, easy operation, and real-time image examination.^[226] Moreover, real-time monitoring of radiation damage using CCD detectors provides an extra benefit to optimize the experimental conditions to maximize the dose on the sample.

CCD detectors are easily damaged by high-energy electrons, and are coupled with a phosphor that converts the incident electrons to photons. The electrons scatter in the phosphor blurring information between pixels. A new type of detector, called a direct electron detector (DED), produces higher-resolution images from a thin readout area that directly detects electrons without a phosphor. The detector also provides a fast rapid readout rate of 2 ms.^[227] Recently, Li et. al. showed that the combination of rapid readout and nearly-noiseless electron counting allowed image blurring to be corrected to subpixel accuracy, restoring intrinsic image information at high resolution.^[152] For example, using this camera, a 3.3 Å resolution-structure of GroEL^[152] and 3.4 Å resolution-structure mammalian transient receptor potential (TRP) channel^[23] were reconstructed by single particle reconstruction. The structure of TRP determined using a DED broke the side-chain resolution barrier for membrane proteins without crystallization.

Phase Plates

An alternative approach to enhance the low-dose image contrast is by using a phase plate. A common type of phase plate, called the Zernike phase plate, consists of a continuous amorphous carbon film with a small central hole placed in a diffraction plane after the specimen. The zero-order beam passes through the central hole, while scattered electrons are phase-shifted by −π/2, resulting in a many-fold increase in specimen contrast.^[228,229] By implementing a phase-plate with cryo-EM, visualization of small proteins with molecular mass of ca.100 kDa is promising. A phase-plate was implemented in ET by Dai et al.^[230] to visualize a cyanophage virus as it matured inside a Synechococcus cell (Figure 14).

Figure 14.

Phase-plate TEM imaging of a cyanophage virus assembling inside marine cyanobacteria. a) Sectional overview of a late-stage infected Syn5 including labeled cellular components and phages: carboxysomes (C), infecting phages (I), ribosomes (R) and thylakoid membranes (T). b–e) Higher-magnification views of sections and their corresponding 3D reconstructions of cellular components of thylakoid membrane (green) (b); carboxysome (blue) (c); ribosome (purple) (d); A Syn5 cyanophage (red) (e) on the cell’s surface during infection. Yellow: cell envelope; magenta: phage progeny. Scale bars: 50 nm (b,c); 60 nm (d,e). Reproduced with permission.^[230] Copyright 2013, Nature Publishing Group.

4.2.3. Alignment Strategies

The alignment of low-dose tilt images plays a crucial role in obtaining an accurate 3D reconstruction. Some commonly used methods in soft materials and biomaterials are described below.

Fiducial-Marker Alignmentx

The most-common method is carried out with the aid of heavy-metal markers. The markers provide high-contrast reference points for the determination of the geometric angles and positions of the tilt images. Commonly, 5–10 nm-diameter gold beads are added to the sample during sample preparation. Usually, 5–10 fiducial markers in the field of view is considered sufficient for aligning the tilt images.^[231]

Cross-Correlation Alignment

Another alignment method without using gold beads is implemented by calculating the cross-correlation coefficients among the tilt images. The advantage of this method is that it does not require any sample manipulation prior to data acquisition.^[230] However, this method depends primarily on having a high-density object (usually unique) in the image. For low-contrast imaging, the alignment has a lower accuracy compared to marker-based alignment.

4.2.4. 3D-Reconstruction Strategies

Numerous software packages and algorithms have been developed for 3D reconstruction, such as SPIDER,^[232] EMAN,^[233] IMOD,^[234] IMAGIC,^[235] EM3D,^[236,237] and UCSF Tomography.^[206] Although the software packages use different strategies, algebraic reconstruction technique (ART),^[238] SIRT^[84] or WBP are generally used. The details of the algorithms have been reviewed.^[26] Here, we briefly describe three typical strategies in improving the resolution of reconstruction of proteins by ET.

Subvolume Averaging

In subvolume averaging, a large-volume, low-resolution, high-noise 3D reconstruction containing many particles is first reconstructed from the tilt series of large-size whole microscopy images. Local regions containing only one macromolecular structure are identified and isolated into small volumes from the overall density map. Hundreds to thousands of such subvolumes are submitted for classification and 3D alignment. Similar subvolumes with high cross-correlation values are averaged together to increase the SNR and reduce reconstruction errors. By subvolume averaging, it is possible to obtain a higher resolution.^{[204,239,240]} The subvolume-averaging method is largely restricted to specimens that have some form of symmetry, with partially known orientation on the substrate, such as phages on bacteria surfaces (Figure 15).^[241–243]

Figure 15.

3D reconstruction of bacteriophage T7 virion infection of Escherichia coli minicells by cryo-electron tomography. a–c) Three selected sections of large-volume 3D reconstructions of T7 infection of E. coli. d–f) Higher-magnification views of the sections of the subvolumes. g,h) A central slice and 3D surface view of a selected sub-volume average from 3352 virions. i,j) A central slice and 3D surface view of another selected sub-volume average from 1886 virions. Reproduced with permission.^[241] Copyright 2013, American Association for the Advancement of Science (AAAS).

Individual-Particle Electron Tomography

For proteins with asymmetry, subvolume averaging is challenging, because 3D alignment by cross-correlation calculation is not sensitive to the orientation, due to low-quality and high-noise subvolumes. Therefore, obtaining a high-quality 3D reconstruction from each individual protein became essential.

Large-size whole microscopy images are often used to determine the geometric angles and translational parameters of each image in the data set.^[244–249] It is commonly believed that using maximum information from the whole image can provide the most-accurate tilt-series alignment. The 3D-reconstruction resolution from whole-image tilt series rarely exceeds 30 Å. It was believed that the resolution limitation is ca. 20 Å in theory.^[250] Zhang and Ren^[38] reported that large-scale image distortion could limit the accuracy in determining the geometric angles and translational parameters when using the whole-image. The distortion can be induced by defocus, astigmatism, projector lens, and energy filter, and even radiation-induced deformations. These large-scale distortions can induce more errors to the alignment when the structures are located near the edges of the microscopy images than when they are located near the center. Inaccurate determination of translational and tilting parameters would directly affect the 3D-reconstruction resolution, which cannot be reduced by subvolume averaging.

To reduce the influences from image distortion, Zhang and Ren^[38] reported an individual-particle electron tomography (IPET) method to reduce translational errors in a tilt-series alignment, which improved the resolution of 3D reconstructions without using subvolume averaging. Smaller selected regions containing an object of interest are isolated from the whole-image tilt series. It was estimated that the maximum translational error in the alignment of the smaller images is less than half of a pixel, much smaller than the full-size microscopy-image scale alignment. The smallest image size that can be used contains only one unique particle of interest. IPET utilizes the focused electron tomography reconstruction (FETR) algorithm. The algorithm is an iterative refinement process containing a series of automatically generated dynamic filters, soft-masks, and multiple alignment steps (using information gradually from low resolution to high resolution). IPET/FETR can compensate for certain levels of errors in the original tilt-series alignment through precisely determining the translational parameters. The 3D reconstruction of a unique particle can be achieved at an intermediate resolution (1–4 nm). IPET reconstruction does not require an initial model, class averaging of multiple molecules, nor an extended ordered lattice. This approach was validated using two negatively stained antibody particles (Figure 16a–f) and two 17 nm high-density lipoprotein particles from cryo-EM (Figure 16g–l). The method has been also used to uncover the domain conformational changes of antibodies,^[251] one of the most flexible proteins when bound to peptides.^[37] By statistically analyzing the variation of the 3D reconstructions from different particles, IPET can potentially uncover the dynamic characteristics and equilibrium fluctuations of macromolecules.

Figure 16.

IPET 3D reconstructions of two IgG antibody particles by negative-staining ET and two HDL particles by cryo-EM. a) Nine representative images from a tilt series of a single-instance IgG antibody by negative-staining (NS) ET displayed in the left-most column. The IPET method obtains the 3D model of an individual protein via an iterative refinement processes. b) The iso-surface of the final 3D reconstruction of an individual antibody particle. c) Flexible docking of the structure obtained by X-ray crystallography (PDB entry 1IGT) into each domain of IgG shows a good fit. d–f) Another example of an individual IgG antibody particle. g–i) A 17 nm nascent HDL particle embedded in ice, imaged by cryo-EM tomography and reconstructed by the IPET method. The high-density portion corresponds to the protein component, primarily consisting of apolipoprotein A-I (apoA-I), forms a discoidal shape (a ring shape). j–l) Another example of a 17 nm nascent HDL particle by cryo-EM tomography. The 3D reconstruction showed the similar structural feature to the first HDL particle. Our cryoET reconstructions are consistent with other cryoEM observations. a–l) Reproduced with permission.^[38] Copyright 2012, The Authors, Published by PLoS ONE.

Constrained Single-Particle Cryo-ET

Another method that uses small-sized images for 3D reconstruction was proposed by Bartesaghi et al.,^[252] in which a combination of ET tilted images and single-particle reconstruction is used to determine the protein structure, termed constrained single-particle tomography. The method acquires many low-dose tilt series of randomly oriented, identical particles. The set of projections of a particle in a tilt series has known orientations due to the tilting. The known tilt-angles of the particle projections are used as a constraint during refinement with a reference model. Image sets of different particles were submitted to a conventional single-particle refinement for 3D reconstruction, incorporating geometric constraints from ET. The initial model was obtained from a standard ET subvolume averaging to reduce model bias. This method also reduced over-refinement artifacts due to ET constraints of projection orientations. A protein structure at resolutions of ca. 8 Å was demonstrated. However, the 3D reconstruction is averaged from different particles that are assumed to share a homologous structure.

4.2.5. Resolution Estimation in ET 3D Reconstructions

Assessment of the resolution of TEM 3D reconstructions has been discussed for a decade.^{[231,253,254]} However, a robust standard method to determine the 3D-reconstruction resolution of TEM is not available. Several methods used in single-particle reconstruction have been introduced for estimating the ET 3D-reconstruction resolution. The first method is derived from a conventional method.^[255–257] The final aligned tilt series was split into two groups based on their even and odd tilt indexes, where each group is used to generate a 3D structure. The similarity between these two reconstructions was computed in reciprocal space in which the correlation between the Fourier components was calculated against their frequency, known as Fourier shell correlation (FSC).^[258] The value at which the FSC curve drops to 0.5 was used to estimate the resolution.^[38] The second method is derived from the so-called “gold standard” method.^[250] The raw tilt images, instead of the aligned images, were split into two groups for independent alignment to achieve their corresponding 3D reconstructions, which are less likely to contain noise correlation.^[253,259] The FSC computed from those two 3D reconstructions was plotted against their spatial frequencies.^[260] The frequency at which the FSC curve fell below 0.143 instead of 0.5^[250,260] was used to represent the final ET reconstruction resolution. This method may avoid overestimating the resolution due to noise correlation. The third method utilizes the FSC curve between the final ET 3D reconstruction and a density map calculated from the best-fit atomic model using known structures. The value at which the FSC curve (computed between these two density maps) drops to either 0.143 or 0.5 was used for resolution estimation. Another possible method compares the structural detail of an ET 3D reconstruction to the protein structures determined by X-ray crystallography, such as a domain size, “hole” diameter, α helices, β sheets, and side chains. Parts of an ET 3D reconstruction displaying those features (and their relative resolutions) can be indicative of the attained resolution.^[38]

4.2.6. Other Useful Tools for ET Research

Contrast Transfer Function (CTF) Correction

Since the cryo-EM image contrast of proteins is very low, a high defocus condition (ca. 3–6 μm) is often used to enhance the overall shape of protein particles during ET data acquisition. Usually, the defocus value is chosen at the condition where that frequency at the first minima of the CTF is higher than the targeted resolution. In such a case, the CTF does not need to be corrected. For higher resolution, the CTF correction becomes necessary. For a tilted specimen, the CTF varies across the sample perpendicular to the tilt axis because the field-of-view contains different defocus conditions.^[261] It is difficult to measure and correct the defocus gradient, especially under conditions of image drift, astigmatism, and mechanical vibration in the z-direction. Fortunately, several software packages have been developed specifically for CTF correction of ET images, including TomoCTF^[262] and CTFPLOTTER.^[263]

Molecular-Dynamics Flexible Fitting

Molecular-dynamics flexible fitting (MDFF) is a computational method that utilizes molecular-dynamics simulations to fit an atomic resolution model into a low-resolution density map determined by ET.^[264,265] MDFF has been particularly useful in studying dynamic systems that are captured in different states by single-particle reconstruction, such as a ribosome,^[264] and by tomography, such as antibodies.^[37,264] Fitting small units/domains into the 3D reconstruction of a large object shows great potential in understanding macromolecule function and mechanisms.^[266] One implementation of this method is in the software package called NAMD.^[267]

Data Management (EM Database)

The goal of ET 3D reconstruction of biological molecules is to provide a detailed understanding of biological processes through structural analysis. The published ET 3D reconstructions could benefit the research communities in a similar field. However, data management of 3D reconstructions is challenging due to the wide variety of biological samples studied (from macromolecules to cells), sample-preparation methods, TEM instruments, imaging conditions, reconstruction methods, and data formats. The Electron Microscopy Data Bank (EMDB) is a unified global portal for deposition and retrieval of EM 3D reconstructions and atomic models, as well as a resource for news, events, software tools, data standards, and validation methods for the EM community.^[268] The database currently holds ca. 3000 density maps from ca. 1200 publications,^[269] in which ca. 20% of the density maps were determined by ET related methods. The rate of deposition of density maps has increased significantly in recent years (Figure 17).

Figure 17.

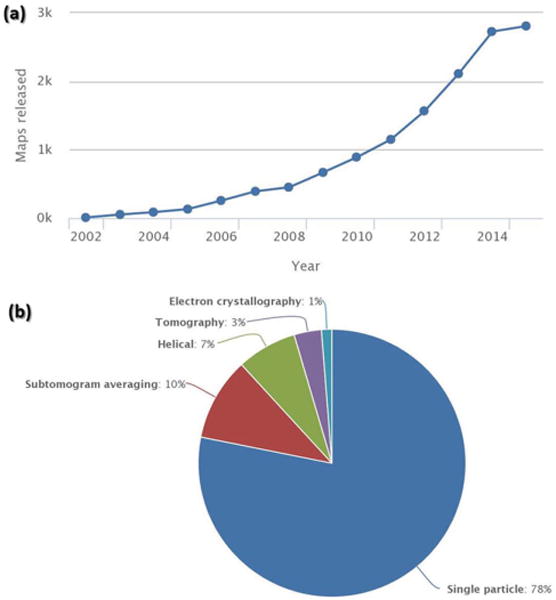
The details of the total number of 3D density maps deposited in the EM data bank (EMDB). a) Cumulative number of 3D maps released per year. The rate of deposition of density maps has increased significantly in recent years. b) Distribution of available density maps (2802 in total) as a function of technique used: single particle reconstruction (more than ca. 78%) and ET methods (ca. 20%); including subvolume averaging (ca. 10%), helical structures (ca. 7%), general ET (ca. 3%). Electron crystallography adds ca. 1% to the EMDB. Plots and pie chart were produced from data published by the EMDB.^[269]

5. Conclusion

In both the physical and biological sciences, ET is now commonly used to investigate 3D structures at the nanoscale. The technique provides a wide range of resolutions, taking full advantage of the versatile capabilities of TEM and STEM. This review discusses recent hardware and software developments that have significantly improved 3D analytical capabilities to determine morphology, shape, composition, and functionality of many different types of nanoscale structures. New research is exploring the interesting materials properties of systems that incorporate both hard and soft materials with the potential to significantly affect nanoscale functionality in applications such as plasmonics, catalysis and sensors. These hybrid systems require the development of analytical technologies that combine techniques from hard and soft matter to resolve both phases in the same 3D reconstruction. Knowledge of the limitations and solutions from both fields provides a starting point to investigate such 3D structures, especially at hard/soft matter interfaces.

Biographies

Peter Ercius is a staff scientist at the National Center for Electron Microscopy (NCEM), a facility within the Molecular Foundry (MF), Lawrence Berkeley National Laboratory, USA. He received his BS in applied and engineering physics from Cornell University in 2003 and his Ph.D. in applied and engineering physics from Cornell University in 2009. He joined NCEM as a collaborative postdoctoral fellow to develop high-resolution electron tomography. His current work focuses on 3D structural analysis for materials science using electron tomography at the sub-nanometer scale and aberration-corrected scanning transmission electron microscopy (STEM) structural analysis at atomic resolution.

Gang Ren is a staff scientist of the Molecular Foundry (MF), Lawrence Berkeley National Laboratory, USA. He received his BS and MS in theoretical physics at Lanzhou University, China in 1990 and 1993, and his Ph.D. in material physics at the University of Science and Technology Beijing in 1997. After receiving his postdoctoral training at the Scripps Research Institute (La Jolla, CA, USA) and Baylor College of Medicine (Houston, TX, USA), he joined the Department of Biophysics and Biochemistry at UCSF in 2006 as a Keck fellow, and joined MF at LBNL in 2010 for developing the individual particle electron tomography (IPET) technique.