Abstract
Studies investigating individual differences in reading ability often involve data sets containing a large number of collinear predictors and a small number of observations. In this paper, we discuss the method of Random Forests and demonstrate its suitability for addressing the statistical concerns raised by such datasets. The method is contrasted with other methods of estimating relative variable importance, especially Dominance Analysis and Multimodel Inference. All methods were applied to a dataset that gauged eye-movements during reading and offline comprehension in the context of multiple ability measures with high collinearity due to their shared verbal core. We demonstrate that the Random Forests method surpasses other methods in its ability to handle model overfitting, and accounts for a comparable or larger amount of variance in reading measures relative to other methods.
Keywords: reading ability, variable importance, Random Forests, collinearity, eye-movements, individual differences
Multivariate datasets are the chief currency of reading research. Such datasets are characterized by a large number of predictors p (usually over ten) and a relatively small number of observations n (frequently below one hundred), where each observation is an aggregate measure of an individual's behavior (e.g. mean response time or a cumulative test score). This “small n large p” problem overshadows analytical strategies for the entire field of research, since if left untreated it causes overfitting and the concomitant loss of generalizability in statistical models. One common attempt to address this problem is to reduce p through removing variables, merging of variables into composite scores, or the use of components or factor analyses. While valuable, this type of data reduction can preclude interpretation of results in terms of the relative contributions of original predictors, and often requires exclusion of hard-won data. Moreover, it minimizes the usefulness of compiling comprehensive test batteries aimed at assessing the contribution of multiple reading-related abilities, and of making theoretical advances that rely on the knowledge of which specific abilities and skills underlie reading performance for the given population.
The core of this paper is an overview of exploratory statistical techniques geared towards estimating the relative importance of variables in studies of reading performance1. This goal follows the tenets of exploratory statistics in that it uses a bottom-up data-driven approach that can guide hypothesis-building and -testing in a formal confirmatory procedure. This goal has both theoretical and practical advantages. On a practical level, this enables a more efficient choice of skill assessments in both research and clinical settings (Blalock, 1961). This is crucial when studies have resource limitations that preclude the use of multiple assessments for a single construct. Moreover, a theory-blind method can be particularly important when utilizing assessments of complex skills (e.g., Reading Comprehension, Oral Language ability, Executive Function), as any particular assessment may emphasize specific component dimensions of the skill over others (cf. Francis, Fletcher, Catts, & Tomblin, 2005; Keenan, Betiemann, & Olson, 2008; Nation & Snowling, 1997). At a theoretical level, information about the relative import of predictors provides a foundation for developing more thoroughly articulated models of reading behaviour. For example, while the construct of working memory plays a strong role in most theories of reading comprehension, there is now growing evidence that its supposed import has come about because of shared variance between typical assessments of the construct and other measures (Hamilton, Freed, & Long, 2013; Traxler, et al., 2012; cf. Van Dyke, Johns, & Kukona, 2014 for detailed discussion.)
Examination of the relative importance of variables is not new to the field of reading research and is commonly implemented through hierarchical or simultaneous regression techniques (e.g., Catts, Fey, Zhang, & Tomblin, 1999; Jenkins, Fuchs, van den Broek, Espin, & Deno, 2003). In what follows, we will contrast the Random Forests method with the family of (generalized) linear regression methods that subsume the former techniques, namely, a) Dominance Analysis (also known as Shapley value regression or hierarchical partitioning, Budescu, 1993; Chevan & Sutherland, 1991; Lipovetsky & Conklin, 2001; Shapley, 1953; Stufken, 1992), and b) Multimodel Inference (Burnham & Anderson, 2002). Random Forests is a non-parametric classification and regression method (Breiman, 2001; Strobl, Malley, & Tutz, 2009) which has so far not gained much attention in the reading field, although it has been utilized in psycholinguistic research (cf. Tagliamonte & Baayen, 2012). While the discussion of methods for obtaining a meaningful and accurate index of relative importance has been ongoing for decades (e.g., Darlington, 1968), the current consensus is that there is no single “best” solution available (Johnson, 2000; Grömping, 2009). Nevertheless, we find that these methods differ drastically in their ability to address two issues critical for the validity of statistical analyses, namely, model overfitting and collinearity (a more detailed discussion than the current space allows is available in Supplementary Materials, S1). We conclude that the Random Forests method outperforms the others in its ability to overcome statistical issues typical of reading studies.
To contrast these methods we use a dataset that includes a skills battery comprised of 15 subtests, which we will aggregate in two different ways in order to manipulate the number of predictors in the analyses. Similarly, our behavioural measure consists of eye-movements collected while reading text passages. These also will be aggregated differently for our two analyses. In so doing, we vary the parameters that influence the severity of model overfitting. In both cases, however, the issue of collinearity of predictors persists, as it must in all reading research because of the common verbal or cognitive core among reading-related skills. Thus, the extent to which the contrasted methods address the collinearity issue becomes especially important when weighing their usefulness for reading research.
Dominance Analysis and Multimodel Inference
These methods represent two examples of alternative approaches for estimating variable importance (see Supplementary Materials, S2, for a more detailed presentation). In Dominance Analysis, model variance (R2) is decomposed via a method that averages across all possible ways that the contribution of each predictor can be calculated (see Tighe & Schatschneider, 2014, for a review). In other words, Dominance Analysis subsumes methods based on both hierarchical regression and simultaneous regression. Multimodel Inference is similar in that it uses all combinations of p predictors to construct a power set of 2p linear models fitted to a dependent variable (Burnham & Anderson, 2002). Whereas Dominance Analysis gives an equal weight to each model, Multimodel Inference weighs each based on its goodness-of-fit (commonly, the Akaike Information Criterion corrected for the finite sample size). For each predictor, summing all the weights of the models in which predictor appears defines how important the predictor is. By examining the set of all possible models, both these methods work around the issue of collinearity, however the Dominance Analysis method does not address the problem of overfitting. If the ratio of model parameters to observations is too high, all models will have poor ability to generalize (i.e. predict unseen data) and their fit will be affected too strongly by random noise in the specific data set. The Multimodel Inference method does offer some protection against overfitting (Burnham & Anderson, 2002) because it takes into consideration the amount of evidence that a given model is the best-performing model in the set, however this may be insufficient to control overfitting when the majority of models have many more parameters than can be reliably estimated (see below for the case of p = 19, n = 51). Thus, while the method represents an improvement over Dominance Analysis, it is still vulnerable to overfitting in “small n large p” situations.
Random Forests
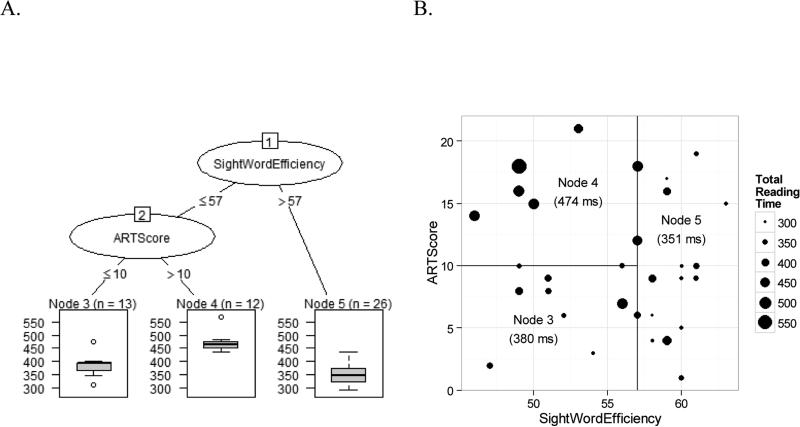
The method of Random Forests is a generalization of the decision tree method, in which the data space is recursively partitioned (usually a binary split) according to the value of one of the predictor variables, such that the observations within a partition become more and more homogeneous. Figure 1 provides an illustration of a decision tree based on Analysis 1 discussed below. Random Forests builds multiple decision trees using random samples of observations for each tree and (at each split point) random samples of predictors. The resulting forest of those trees provides fitted values, which are more accurate than those of any single tree (Breiman, 2001). Moreover, the Random Forests method comes with a built-in protection against overfitting by using part of the data that each tree in the forest has not seen to calculate its goodness-of-fit. Variable importance is assessed by randomly permuting the values of one predictor across all trees and estimating the loss in prediction accuracy of the forest: little loss implies low importance. For a detailed description of the decision tree and Random Forests method, see Supplementary Materials, S3.
Figure 1.
A decision tree fit to a random bootstrap sample of the eye-movement data (see Analysis 1). Nodes 1 and 2 represent split points that are optimal for this random sample (score of 57 in the Sight Word Efficiency test and 10 in the Author Recognition Test (ART). Terminal nodes (3-5) report the number of data points in each partition. The tree in Panel A corresponds to the partitions shown in Panel B. The box plots at the terminal nodes of the tree in Panel A display the distribution of mean total reading time of the data points that fall into the corresponding partition in panel B. The values under the node labels in Panel B represent the fitted values. The decision rule for Node 3 (the leftmost branches) corresponds to “If SightWordEfficiency ≤ 57, and if ARTScore ≤ 10, then mean total reading time = 380 ms.”
Whereas the relative importance metrics obtained from Dominance Analysis or from Multimodel Inference are independently interpretable (e.g. amount of explained variance), the metric of variable importance obtained from the Random Forests model is contingent on the scale of the dependent variables and other parameters. Thus, Random Forests’ estimates of variable importance can only be interpreted comparative to each other, rather than as absolute values (Strobl et al, 2009).
Worked Examples
In what follows we demonstrate that Dominance Analysis, Multimodel Inference and Random Forests vary in their treatment of overfitting when applied to a typical multivariate dataset collected to study individual variability in reading behavior. We report the performance of the methods in the dataset in two ways. In Analysis 1 we averaged eye-movements by participant, introducing potential overfitting due to the low number of observations and a high number of predictors. In Analysis 2, word (or passage) served as the unit of analysis and no aggregation was applied, which allowed for a direct comparison of methods unencumbered by overfitting.
Methods
The study uses data from 51 undergraduate students (40 females; age ranging from 17 to 27), who read texts from the Gray Oral Reading Test 4 (GORT; Wiederholt & Bryant, 2001) for comprehension, while their eye-movements are monitored. Participants also completed a battery of cognitive and verbal skills that assessed word-level reading, phonological processing, processing speed, reading experience and IQ. These are enumerated explicitly in Table 1; see Methods in Supplementary Materials, S4 for full details. As these tests are commonly assessed in reading research, we expected that the collinearity index among them would typify that found in many reading studies.
Table 1.
Labels and corresponding skills assessed. For complete details of instruments used, see Supplementary materials, S4.
| Label | Construct |
|---|---|
| VocabScore | Vocabulary Size |
| SightWordEfficiency | Sight Word Efficiency (TOWRE-2) |
| WordDecoding | Phonemic Decoding Efficiency (TOWRE-2_ |
| ReadEfficiency | Reading Efficiency composite score (TOWRE-2) |
| RANLetterNameTime, RANNumberNameTime | Rapid Automatized Naming |
| RANNameTime | Rapid Automatized Naming (composite of RANLetterNameTime and RANNumberNameTime) |
| MRTScore, ARTScore | Print Exposure |
| PrintExposure | Print Exposure composite of MRTScore and ARTScore |
| TimeSpentReading ReadingSpeed ComplexityMaterial UnderstandingMaterial ReadingEnjoyment |
Subjective measure of Reading Habits |
| WasiVerbalIQ WasiReasonIQ WasiFullIQ |
IQ (WASI) |
| Complex | Text Complexity (GORT) |
Dependent variables
Eye-movements provide a rich, multi-dimensional record of online reading behaviour (Rayner, 1998). For our current analyses, we only consider two of the many eye-movement measures as dependent variables, both based on the word as the unit of analysis: total reading time, which is the most general measure of word-level reading time (comprised of the summed duration of all fixations on the word) and skipping. This choice was guided by our desire to include a continuous variable (total reading time) and a binary variable (skipping) so we could illustrate the use of two different generalized linear regression modeling types, i.e., multiple regressions with a Gaussian and a binomial underlying distribution. As a third dependent variable, we consider comprehension scores, calculated as the sum of the participant's correct responses to five questions following one of five GORT passages presented for reading (maximum 5 data points per participant per passage, with a value range [0:5] of each data point). Because some passages were not completed by individual participants, the total number of available scores was 243. As comprehension scores represent count data, we use them to illustrate the use of the generalized linear regression with a Poisson distribution. Taken together, comprehension accuracy and eye-movement measures provide a detailed time-course of both online reading behavior and its end-result, i.e. comprehension of continuous text.
Independent variables
The skill test battery contained widely used standardized assessments (see Supplementary Materials, S4 for details). Table 1 presents the labels used to refer to these assessments throughout the paper.
For illustrative purposes, we confine ourselves to only considering these participant-level variables, although it is recognized that text-level variables, such as word length, frequency, and predictability also affect eye-movements. A detailed investigation of the interactions among these variables is beyond the scope of this paper.2
Results
The original data contained 33,455 data points. After trimming, we analyzed the data pool of 16,584 data points for skipping and the data pool of 12,890 data points (not skipped during reading) for fixation durations (and derivative measures like total reading time). The trimming procedure, as well as descriptive statistics and the correlation matrix for the scores obtained for the skill test battery are available in Supplemental materials, S5.
Analysis 1: Model over-fitting
The count of 14 predictor variables in the current dataset is by no means exceptional for reading research, yet it poses problems for regression modeling. The number of models to be considered in Dominance Analysis and Multimodel Inference is 2p – 1 and 2p, respectively, where p is the number of estimable parameters in the model (see Supplementary materials S2). For p = 19 (i.e. 14 parameters for individual skills, 4 for contrast coefficients of complexity, and one for intercept) this translates into half a million regression models, which is computationally demanding. This is less problematic for the Random Forests method, because the number of trees to be fitted is controlled by the user defined parameter ntree.
One notable statistical property of the linear regression model with 19 predictors is rampant collinearity (see Supplemental material S5, Figure S1, for correlations between all pairs of the 14 participant-level predictors). One common way of quantifying collinearity among predictors is referred to as condition number (Harrell, 2001). A value of 30 is held up as a threshold signalling “potentially harmful collinearity” (Baayen, 2008, p. 182; Dormann et al., 2012). In our dataset, the value of condition number is 102.94, a level that is problematic for the accuracy of all methods that rely on a single (best) regression model: the problem is alleviated for Dominance Analysis, Multimodel Inference and Random Forests (see Supplementary material S2).
An additional problem with regression models is that the large number of predictors necessitates a large number of observations to avoid overfitting. For instance, a multiple regression model with 15 estimated parameters (14 coefficients for continuous predictors and the intercept) would require 225 observations, according to Harrell's (2001) guideline. While eye-tracking data analyzed at the word-level easily meets this requirement (over 12,000 observations), and so do comprehension scores aggregated per passage (243 observations), the data averaged by participant (51 observations), as we have done for this example, would not. Yet, virtually all indices of individual differences produce a single observation per participant: either a score on a test, or an average of performance over sets of trials. Hence, a typical data set with per-participant scores like the one we present here can only be used to reliably estimate 2-3 parameters of the regression model, one of which is the model's intercept.
To illustrate this problem, we fit a linear regression model with 19 estimated parameters to total reading time aggregated by participant, which yielded 51 data points. With this model, we conducted the bootstrapping validation procedure in which a linear model with the same structure was fitted 200 times, each time to a different random training sample drawn with replacement from the 51-point dataset. The degree of model overfitting was assessed via the measure called optimism (Harrell, Lee, & Mark, 1996), which is the difference between the average R2 of the models fitted to the random training samples and the average R2 of the same models fitted to the testing set (consisting of the entire sample). While the average R2 of the training models was 0.53, the average R2 for the testing set was −0.11. The extremely high value of optimism (i.e., the discrepancy between the training set and the test set) of 0.64 indicates that linear regression models grossly overfit the data in the “small n large p” conditions and provide terrible fit to unseen data. Validated estimates of the mean squared error, intercept and slope showed a similarly large degree of optimism.
The remainder of this section demonstrates that the Random Forests method is able to provide meaningful estimates even when applied to the smallest data pool resulting from aggregation over each participant. We trained the Random Forest model using mtry (the number of predictor variables to be sampled as candidates at each split point) of 5 and ntree of 1,000 (see Supplemental Materials, S3 for further description). We assessed the optimism of the Random Forest model with the same bootstrapping validation with exactly the same bootstrap samples as described above. The average R2 of the training models was 0.12, and for the testing set it was 0.15. The optimism of −.03 suggests that, unlike linear regression models, the Random Forests method does not have the problem of overfitting in the “small n large p” setting, as its fits to testing and training datasets are stable. If anything, the method slightly underestimated its predictive power for unseen data.
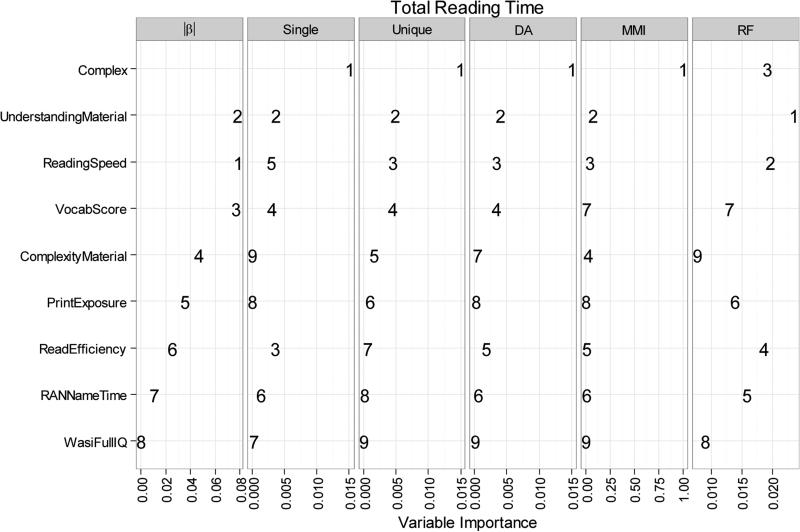
Figure 2 presents the relative importance of variables as applied to the by-participant mean total reading time, pointing to word reading measures (SightWordEfficiency, WordDecoding) and the subjective measure of reading speed as the most important predictors of mean total reading time. This result is consistent with research on eye-movement control, which has implicated word identification as a primary cause of differences between emerging and proficient readers (Kuperman & Van Dyke, 2011; Reichle et al., 2013).
Figure 2.
The relative importance of variables obtained from a Random Forests model applied to the by-participant mean total reading time in Analysis 1.
Analysis 2: Adequate predictor-to-observation ratio
To further contrast the methods under consideration, we reduced the number of predictors so that the Dominance Analysis, Multimodel Inference, and Random Forests methods can be compared directly. The reduction was done by creating composite scores from the separate subtests of standardized measures and, in the case of the subjective reading habit measures, selecting a few key predictors based on a preliminary correlational analysis (not reported). This resulted in eight participant-level variables (see Table 1 and Supplemental materials, S4 for full details): WasiFullIQ, ReadEfficiency, PrintExposure, ReadingSpeed, UnderstandingMaterial, ComplexityMaterial, VocabScore, and RANNameTime. Text complexity (Complex) was included as a ninth independent categorical variable with 5 levels. The correlations between predictors in this set were lower overall (see Supplemental material, Table S1 for the full table), with condition number of 54.18 (compared to 102.94 in Analysis 1). We note that collinearity may still be an issue for single regression models, as this value is still larger than the common threshold of 30, which signals potentially harmful collinearity.
We avoided the problem of overfitting in this analysis by choosing the word (or passage, for comprehension) as the unit of analysis for the eye-movement data, such that all eye-movements to a given word (passage) would be included in the model, rather than an average value by word. Thus, the resulting data represented both the individual differences and linguistic variability. This yielded 12,890 data points for total reading time, 16,584 for skipping, and 243 for comprehension scores. In what follows we compare the relative importance of predictors of these three dependent variables as estimated by six different metrics; the first three are derived from single regression models. The first is the absolute value of standardized beta coefficients (|β|).3 The second metric is single-R2, which is the amount of variance explained by a regression model with only one predictor. The third metric is unique-R2, which corresponds to the increase in R2 from a model with all but one predictor to a model with all the predictors. As described earlier, this way of calculating variable importance is commonly used when the simultaneous regression method is applied. The fourth metric is based on Dominance Analysis (DA). The fifth presents relative importance as obtained with the Multimodel Inference (MMI). The sixth metric is the estimate of permutation importance yielded by Random Forests using conditional inference trees (RF).
Models
To model continuous (log total reading time), binary (skipping) and count (comprehension scores) data, we used generalized linear mixed-effects regression models with Gaussian, binomial and Poisson distributions, respectively. Participant-level random intercepts were included to account for within-participant dependencies in the data: as mentioned above, we do not account for word-level variability in fixed or random effects in this paper and consider it elsewhere (Matsuki et al., in preparation). Because the Random Forests method is non-parametric, no specific distribution had to be defined (see Supplementary materials S3). The Random Forests with conditional inference trees are not currently equipped to model random effects or to accommodate clustered data (c.f. Hajjem, Bellavance, & Larocque, 2014; Karpievitch, et al., 2009). However, the type of predictors used in the current study (i.e, all but Complex are participant-level predictors) automatically makes the trees in the forests treat observations as nested under participants, such that the observations from the same participant (or at least their subsets with the same level of Complexity) would always end up in the same terminal node. All the Random Forests models in Analysis 2 were trained using mtry of 3 and ntree of 1,000. Several methods that we use are based on partitioning explained variance (i.e., Dominance Analysis, single-R2 and unique-R2). Although there are many ways to calculate R2 for mixed-effects models, we used marginal R2 (or the proportion of variance explained by fixed effects alone) introduced by Nakagawa and Schielzeth (2013) as it is easily and equally applicable to models of different distributions.
Goodness of fit
We compared the goodness of model fit using three methods of estimating predictors’ relative importance– Dominance Analysis, Multimodel Inference and Random Forests. In order to have comparable statistics across methods, we calculated proportion of explained variance as either (a) the squared coefficient of the correlation between the observed and predicted data from the model of interest (corresponding to R2) for continuous data, or (b) the squared coefficient of the correlation between the observed data and predicted probability from the model of interest (corresponding to pseudo R2 of Efron, 1978) for binary and count data. For Dominance Analysis and Multimodel Inference, we calculated the proportion of explained variance from the full regression model (a linear model in which all the predictors are used simultaneously) as the upper bound for the methods.
Predictions for unseen data
We further evaluated the ability of models to predict unseen data. Because linear regression based models do not come with a “built-in” test sample that can be used for an unbiased estimate of the goodness-of-fit, unlike Random Forests, goodness-of-fit values calculated from linear regression based methods could be biased (see our use of the optimism value in Analysis 1). In order to obtain unbiased estimates of goodness-of-fit for all the models using the identical procedure, we opted for validation through repeated random sub-sampling, where data is split into a training subset (70% of the original) and a test subset (30%); the model is trained on the training subset, and its goodness-of-fit to the test subset is calculated. The resulting goodness-of-fit is averaged over 100 splits.
Discussion
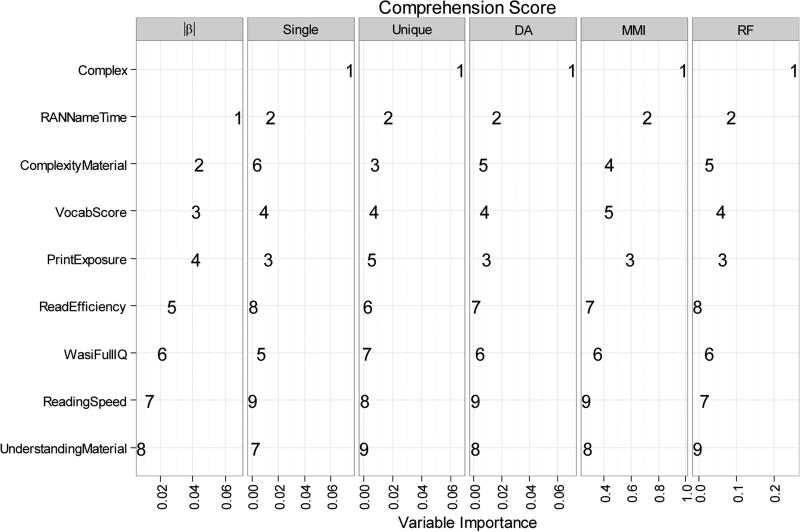
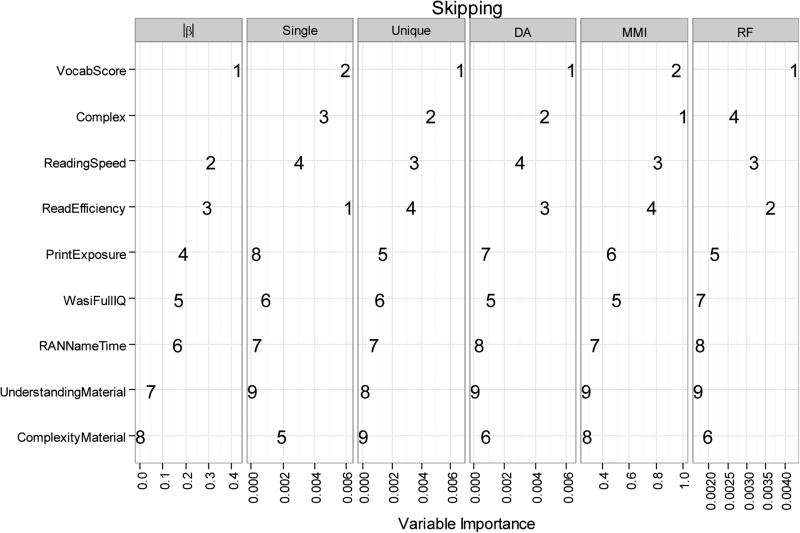
Figures 3-5 display the outcome of the six methods side by side for each dependent measure. In each Figure, the order of predictors on the y-axis follows the values of unique-R2, as this measure is commonly used to assess variable importance.
Figure 3.
Relative importance of predictors of total reading time during text reading. Six metrics compared are the absolute value of standardized beta coefficients (|β|), the amount of variance explained by a regression model with only one predictor (Single), the increase in R2 from a model with all but one predictor to a model with all the predictors (Unique), and variable importance measures from Dominance Analysis (DA), Multimodel Inference (MMI), and Random Forests (RF). Numbers inside panels indicate the predictor's importance rank within the predictor set.
Figure 5.
Relative importance of predictors of GORT comprehension scores. Six metrics compared are the absolute value of standardized beta coefficients (|β|), the amount of variance explained by a regression model with only one predictor (Single), the increase in R2 from a model with all but one predictor to a model with all the predictors (Unique), and variable importance measures from Dominance Analysis (DA), Multimodel Inference (MMI), and Random Forests (RF). Numbers inside panels indicate the predictor's importance rank within the predictor set.
Total Reading Time
As Figure 3 demonstrates, the pairwise agreement among the six metrics has some variability, but is relatively high overall (in pairwise comparisons of ranked variable orders, mean Spearman's rho=.71, ranging from .43 to .98). The metrics based on unique-R2, Dominance Analysis (DA), and Multimodel Inference (MMI) agreed with one another highly in terms of ranking, favoring Text complexity (Complex) as the most important predictor. The ranking based on Random Forests method is in modest agreement with all the other methods (mean rho = .65, ranging from .45 to .78).
Goodness-of-fit indices show that the linear mixed-effect regression based methods and Random Forests explain approximately the same amount of variance (R2 of .075 vs. .080 based on the test data), see Table 2. While amounts of explained variance are overall quite low in Analysis 2, it is worth noting that they are obtained from a very large dataset (12,890 observations) of inherently noisy eye-movement data where each predictor offers one value for all observations associated with a given participant (e.g. participant's IQ; an average of 253 observations per participant) or a given text (e.g. text complexity; an average of 2,578 per text complexity level). Moreover, strong sources of text variability have not been modeled (e.g., word length, frequency, predictability). In Analysis 1 where data are aggregated by participant, the predictor to observation ratio is 1:1, so more variance can be explained.
Table 2.
Proportion of variance accounted for by the models.
| Dependent Variable Sample used | Upper-bound for the regression based models | Random Forests |
|---|---|---|
| Total Reading Time | ||
| All | .083 | .082 |
| Test | .075 | .080 |
| Skipping | ||
| All | .029 | .027 |
| Test | .022 | .026 |
| Comprehension Score | ||
| All | .236 | .174 |
| Test | .171 | .173 |
The R2 of the full regression model with all predictors is reported as the upper bound for Dominance Analysis and Multimodel Inference. The R2 values for the All sample are based on the models trained on the entire dataset, and are calculated based either on the models’ fitted values to the entire dataset (for full regression model), or on the model's prediction to the out-of-bag samples (for Random Forests). The R2 values for the Test sample are based on the models trained on the 70% random training subsamples and are calculated using the models’ prediction to the remaining 30% testing subsamples, averaged over 100 runs.
Skipping
As Figure 4 shows, the six metrics are generally in agreement with one another (mean rho=.84, ranging from .62 to 1.0). Across all metrics, vocabulary size, text complexity, self-assessed reading speed and TOWRE reading efficiency measures appear to be particularly important determinants of an individual's skipping rate. Once again, the linear mixed-effect regression and Random Forests show similar fit to the data (R2 of .022 vs. .026 based on the test data, see Table 2).
Figure 4.
Relative importance of predictors of word skipping during text reading, estimated by six statistical methods. Six metrics compared are the absolute value of standardized beta coefficients (|β|), the amount of variance explained by a regression model with only one predictor (Single), the increase in R2 from a model with all but one predictor to a model with all the predictors (Unique), and variable importance measures from Dominance Analysis (DA), Multimodel Inference (MMI), and Random Forests (RF). Numbers inside panels indicate the predictor's importance rank within the predictor set.
Comprehension Score
All metrics converged on GORT text complexity as the most important variable in determining reading comprehension (see Figure 5). Other important predictors included RAN naming time and the print exposure score. All six metrics were generally in agreement in ranking (mean rho = .90, ranging from .69 to 1). Once again, the linear mixed-effect regression and Random Forests provided equal fits to the data (R2 of .171 vs. .173 based on test data).
General Discussion
Our findings point to the Random Forests classification method as a reliable method, capable of addressing the “small n large p” problem. Analysis 1 demonstrated this for a multivariate dataset that combines eye-movement measures and comprehension scores as dependent variables and outcomes of a large test battery of predictors, i.e. a dataset with a very low ratio of predictors (19 estimated model parameters) to observations (51). The Random Forests method evaluated the relative importance of all predictors in the dataset without data reduction and without overfitting (i.e. low optimism value): it also offered protection against the impact of rampant collinearity between predictors. Methods that we compared against Random Forests were based on linear regression and, as became evident in Analysis 1, were strongly affected by the “small n large p” problem of overfitting and further encumbered by collinearity.
Analysis 2 compared methods against non-aggregated data analyzed at the word-level and passage-level, where the large size of the dataset removed the threat of overfitting. Different methods converged on similar estimates of the relative importance of predictors of skipping rate and comprehension scores (Figures 4 and 5). Despite their inability to incorporate random effects as implemented in the mixed-effects models, Random Forests treated observations as nested under participants and consistently explained approximately the same amount of variance than the upper-bound of the linear regression-based methods (see Dilts, 2013; Hajjem et al, 2014, for similar observations). The advantage that Random Forests demonstrates in both the ability to handle the “small n large p” data set (Analysis 1) and its equally strong performance compared to other methods in a much larger dataset (Analysis 2) suggests that this method is an excellent solution for the specific statistical goal examined here, i.e. to assess variable importance among a battery of highly collinear assessments in datasets that vary in size, nature of aggregation and the predictor-to-observation ratio. In sum, we recommend the use of the Random Forests method for establishing the relative importance of variables in exploratory studies of reading behavior. We further recommend, where data allow, to avoid data reduction and use raw, non-aggregated data on the single trial level: a dramatic increase in the sample size (from 51 to over 12,000 observations) is a better solution to the “small n large p” problem than data reduction methods that diminish interpretability and generalizability of results.
While the practical utility of Random Forests is demonstrable, it is important to characterize what theoretical questions Random Forests are and are not designed to address. What can Random Forests not do? The Random Forests method considers the structure in the set of independent variables to be flat, that is, the Random Forests model does not assume (nor can it implement) any causal or correlational dependencies between those variables. In this fundamental premise, the Random Forests method differs from any method that requires an a priori theory about hierarchy in the data structure: this includes Structural Equation Modeling with its notion of latent variables, and hierarchical regression with its theoretically driven ordering of variables. In our data, most variables are individual tests, and so the outcome is the metric of relative importance of those tests. However, an approximation of latent structure is possible with the Random Forests method still, if a researcher provides composite scores that represent theoretically determined blocks of variables (e.g. composites of measures of oral comprehension, phonological awareness, RAN, etc.). In this case, relative contributions of entire components of reading ability to predicting reading behavior can be evaluated, though not the dependencies between such components.
What can Random Forests do? First, the Random Forests method is an excellent tool for data-driven identification of variables of importance that are overlooked in the literature. For instance, the present data identify subjective measures of reading habits as more influential than rapid automatized naming measures in our cohort of skilled readers, even though the latter measures are discussed in thousands of papers (cf. meta-analysis by Swanson, Trainin, Necoechea, & Hammill, 2003), while the former are hardly explored at all (Acheson et al., 2008 and references therein) but are in line with predictions of existing models of eye movement control in reading (Reichle et al., 2013). Also, Figures 3-5 reveal a strong role for the TOWRE reading efficiency measures (sight word efficiency and decoding) in predicting eye-movements in skilled undergraduate readers. This is despite the widespread assumption that word reading efficiency has reached the ceiling level for those meeting admission criteria for most 4-year universities. Second, studies of reading often represent hypothesized latent constructs by multiple redundant individual tests. The Random Forests enables reduction of this redundancy, and the selection of a subset of tests that predict the data most strongly. This is of crucial importance when testing time is limited. Finally, the Random Forests method offers the theoretically attractive possibility of an inductive process whereby latent constructs (i.e. components of reading behavior) are hypothesized by the researcher on the basis of individual tests that are identified as important predictors of reading behavior in a theory-free way. This “reverse-engineering” process is conceptually similar to one that researchers apply when considering the results of a principal components or a factor analysis, where the goal is to induce a theoretical explanation for why individual tests load on one component/factor and not another. To give an example from Analysis 1 in the present data, the fact that both decoding (non-word reading) and sight word efficiency (word reading) come out on top of the variable importance ranking, while vocabulary size is relatively low in the ranking, suggests a strong role of phonological awareness and decoding skills. If word reading and vocabulary size came out on top, with non-word reading lower in the list, that would suggest a much stronger role of word knowledge, with a reduced influence of decoding skills.
To summarize, identification of variable importance affords new insights into the structure of the data and sheds new light on extant theories of reading. The recently developed statistical method of Random Forests enables researchers to garner these insights while overcoming the typical limitations of datasets common in studies of individual variability of reading.
Supplementary Material
Acknowledgments
Funding:
National Institute of Child Health and Human Development (HD 001994,HD 073288); Natural Sciences and Engineering Research Council of Canada (RGPIN/402395-2012); Social Sciences and Humanities Research Council of Canada (430-2012-0488).
Footnotes
The term “relative importance” is used here in line with the existing statistical literature, which refers to the term “importance” as a statistic associated with a variable, rather than an interpretational value for theory building or policy making.
In Matsuki, Kuperman, and Van Dyke (in preparation) we use the Random Forests technique to establish relative variable importance in the joint pool of participant variables, which gauge individual differences and text variables at the level of word (length, frequency, contextual predictability), sentence (word position in a sentence, word's syntactic role), and passage (text complexity).
Text complexity is not included as a predictor in these models because it requires 4 regression coefficients.
Contributor Information
Dr Kazunaga Matsuki, McMaster University, Department of Linguistics and Languages, Togo Salmon Hall, 1280 Main Street West, Hamilton, Ontario, L8S 4M2 Canada, matsukik@gmail.com.
Dr Victor Kuperman, McMaster University, Department of Linguistics and Languages, Togo Salmon Hall, 1280 Main Street West, Hamilton, Ontario, L8S 4M2 Canada.
Dr Julie A Van Dyke, Haskins Laboratories, 300 George Street, New Haven, 06511 United States, jvandyke@haskins.yale.edu
References
- Baayen RH. Analyzing linguistic data: A practical introduction to statistics. Cambridge University Press; Cambridge: 2008. [Google Scholar]
- Blalock Jr HM. Evaluating the relative importance of variables. American Sociological Review. 1961;26:866–874. [Google Scholar]
- Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- Budescu DV. Dominance Analysis: A new approach to the problem of relative importance of predictors in multiple regression. Psychological Bulletin. 1993;114:542–551. [Google Scholar]
- Burnham K, Anderson D. Model selection and multimodel inference: A practical information-theoretic approach. Springer; New York, NY: 2002. [Google Scholar]
- Catts HW, Fey ME, Zhang X, Tomblin JB. Language basis of reading and reading disabilities: Evidence from a longitudinal investigation. Scientific Studies of Reading. 1999;3:331–361. [Google Scholar]
- Chevan A, Sutherland M. Hierarchical partitioning. The American Statistician. 1991;45:90–96. [Google Scholar]
- Darlington RB. Multiple regression in psychological research and practice. Psychological Bulletin. 1968;69:161–182. doi: 10.1037/h0025471. [DOI] [PubMed] [Google Scholar]
- Dilts P. Modelling phonetic reduction in a corpus of spoken English using Random Forests and Mixed-Effects Regression. University of Alberta; Canada: 2013. Unpublished doctoral dissertation. [Google Scholar]
- Dormann CF, Elith J, Bacher S, Buchmann C, Carl G, et al. Collinearity: a review of methods to deal with it and a simulation study evaluating their performance. Ecography. 2012;35:1–20. [Google Scholar]
- Efron B. Regression and ANOVA with zero-one data: measures of residual variation. Journal of the American Statistical Association. 1978;73:113–121. [Google Scholar]
- Francis DJ, Fletcher JM, Catts HW, Tomblin JB. Dimensions affecting the assessment of reading comprehension. In: Paris SG, Stahl SA, editors. Children's reading comprehension and assessment. Erlbaum; Mahwah, NJ: 2005. pp. 369–394. [Google Scholar]
- Grömping U. Variable Importance Assessment in Regression: Linear Regression versus Random Forest. The American Statistician. 2009;63:308–319. [Google Scholar]
- Hajjem A, Bellavance F, Larocque D. Mixed effects random forest for clustered data. Journal of Statistical Computation and Simulation. 2014;84:1313–1328. [Google Scholar]
- Hamilton ST, Freed EM, Long DL. Modeling reader and text interactions during narrative comprehension: A test of the lexical quality hypothesis. Discourse processes. 2013;50(2):139–163. doi: 10.1080/0163853X.2012.742001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen GS, Wernerfelt B. Determinants of firm performance: The relative importance of economic and organizational factors. Strategic Management Journal. 1989;10:399–411. [Google Scholar]
- Harrell FE, Lee KL, Mark DB. Multivariable prognostic models: Issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Statistics in Medicine. 1996;15:361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- Harrell FR. Regression Modeling Strategies. Springer; Berlin: 2001. [Google Scholar]
- Jenkins JR, Fuchs LS, van den Broek P, Espin C, Deno SL. Sources of individual differences in reading comprehension and fluency. Journal of Educational Psychology. 2003;95:719–729. [Google Scholar]
- Johnson JW. A heuristic method for estimating the relative weight of predictor variables in multiple regression. Multivariate Behavioral Research. 2000;35:1–19. doi: 10.1207/S15327906MBR3501_1. [DOI] [PubMed] [Google Scholar]
- Karpievitch YV, Hill EG, Leclerc AP, Dabney AR, Almeida JS. An introspective comparison of random forest-based classifiers for the analysis of cluster-correlated data by way of RF++. PLoS ONE. 2009;4(9):e7087. doi: 10.1371/journal.pone.0007087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keenan JM, Betjemann RS, Olson RK. Reading comprehension tests vary in the skills they assess: Differential dependence on decoding and oral comprehension. Scientific Studies of Reading. 2008;12(3):281–300. [Google Scholar]
- Kuperman V, Van Dyke JA. Effects of individual differences in verbal skills on eye-movement patterns during sentence reading. Journal of Memory and Language. 2011;65(1):42–73. doi: 10.1016/j.jml.2011.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipovetsky S, Conklin M. Analysis of regression in game theory approach. Applied Stochastic Models in Business and Industry. 2001;17:319–330. [Google Scholar]
- Nakagawa S, Schietzeth H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution. 2013;4:133–142. [Google Scholar]
- Nation K, Snowling M. Assessing reading difficulties: the validity and utility of current measures of reading skill. British Journal of Educational Psychology. 1997;67:359–370. doi: 10.1111/j.2044-8279.1997.tb01250.x. [DOI] [PubMed] [Google Scholar]
- Perfetti CA. Phonology is critical in reading-but a phonological deficit is not the only source of low reading skill. In: Brady SA, Braze D, Fowler CA, editors. Explaining Individual Differences in Reading: Theory and Evidence. Psychology Press; NY, NY: 2011. pp. 153–171. [Google Scholar]
- Rayner K. Eye movements in reading and information processing: 20 years of research. Psychological Bulletin. 1998;134:372–422. doi: 10.1037/0033-2909.124.3.372. [DOI] [PubMed] [Google Scholar]
- Reichle ED, Liversedge SP, Drieghe D, Blythe HI, Joseph HS, White SJ, Rayner K. Using EZ Reader to examine the concurrent development of eye-movement control and reading skill. Developmental Review. 2013;33(2):110–149. doi: 10.1016/j.dr.2013.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarborough HS. Predicting the future achievement of second graders with reading disabilities: Contributions of phonemic awareness, verbal memory, rapid naming, and IQ. Annals of Dyslexia. 1998;48(1):115–136. [Google Scholar]
- Shapley LS. A Value for n-person Games. In: Kuhn H, Tucker AW, editors. Contributions to the theory of games. Vol. 2. Princeton University Press; Princeton, NJ: 1953. pp. 307–317. [Google Scholar]
- Strobl C, Malley J, Tutz G. An introduction to recursive partitioning: Rationale, application, and characteristics of classification and Regression Trees, Bagging, and Random Forests. Psychological Methods. 2009;14:323–348. doi: 10.1037/a0016973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stufken J. On Hierarchical Partitioning. The American Statistician. 1992;46:70–71. [Google Scholar]
- Swanson HL, Trainin G, Necoechea DM, Hammill DD. Rapid naming, phonological awareness, and reading: A meta-analysis of the correlation evidence. Review of Educational Research. 2003;73(4):407–440. [Google Scholar]
- Tagliamonte S, Baayen RH. Models, forests and trees of York English: Was/were variation as a case study for statistical practice. Language Variation and Change. 2012;24(2):135–178. [Google Scholar]
- Traxler MJ, Johns CL, Long DL, Zirnstein M, Tooley KM, Jonathan E. Individual differences in eye-movements during reading: working memory and speed-of-processing effects. Journal of Eye Movement Research. 2012;5(1):1–16. [PMC free article] [PubMed] [Google Scholar]
- Van Dyke JA, Johns CL, Kukona A. Low working memory capacity is only spuriously related to poor reading comprehension. Cognition. 2014;131(3):373–403. doi: 10.1016/j.cognition.2014.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiederholt JL, Bryant BR. GORT 4: Gray Oral Reading Tests Examiner's manual. PRO-ED; Austin, TX: 2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.