Abstract
Free-living organisms are exposed to a wide range of stressors, all of which can disrupt components of stress-related and detoxification physiology. The subsequent accumulation of somatic damage is widely believed to play a major role in the evolution of senescence. Organisms have evolved sophisticated physiological regulatory mechanisms to maintain homeostasis in response to environmental perturbations, but these systems are likely to be constrained in their ability to optimise robustness to multiple stressors due to functional correlations among related traits. While evolutionary change can accelerate due to human ecological impacts, it remains to be understood how exposure to multiple environmental stressors could affect senescence rates and subsequently population dynamics and fitness. We used a theoretical evolutionary framework to quantify the potential consequences for the evolution of actuarial senescence in response to exposure to simultaneous physiological stressors – one versus multiple and additive versus synergistic – in a hypothetical population of avian “urban adapters”. In a model in which multiple stressors have additive effects on physiology, species may retain greater capacity to recover, or respond adaptively, to environmental challenges. However, in the presence of high synergy, physiological dysregulation suddenly occurs, leading to a rapid increase in age-dependent mortality and subsequent population collapse. Our results suggest that, if the synergistic model is correct, population crashes in environmentally-stressed species could happen quickly and with little warning, as physiological thresholds of stress resistance are overcome.
Keywords: Ageing, Senescence, Urban, Birds, Environmental stress, Evolutionary model
Highlights
-
•
Environmental stressors challenge physiological systems linked to senescence.
-
•
Various scenarios of stress exposure were simulated on a hypothetical “urban adapter”.
-
•
Actuarial senescence increased rapidly in synergistic models of stress.
-
•
Wild populations may be at greater risk of collapse than demography alone suggests.
-
•
An explicit model of how stressors affect physiology underlying ageing is required.
1. Introduction
There is now no doubt that senescent declines in fitness occur widely in free-living animals and, in recent years, a large body of empirical evidence for ageing in the wild has accumulated (e.g. Bouwhuis et al., 2010, Jones et al., 2008, Nussey et al., 2013, Nussey et al., 2007). Senescence is defined as a progressive deterioration in physiological function, widely believed to be driven by the accumulation of somatic damage and/or mutations (Beckman and Ames, 1998, Harman, 1956, Kirkwood and Holliday, 1979). Understanding how senescence – a disadvantageous trait – has evolved, has long been of interest to evolutionary biologists and the foundations of the modern evolutionary theory of ageing were laid in the mid-20th century by the likes of Haldane (1941), Medawar (1952), Williams (1957), Hamilton (1966) and Kirkwood (1977). The various non-mutually-exclusive theories do not clearly identify a proximate cause for ageing; however, given the role of physiological deterioration, factors influencing physiological defence and repair mechanisms are expected to be important in the evolution of senescence rates.
Senescence is most often studied in model organisms under controlled laboratory conditions (e.g. Klass and Hirsh, 1976, Maynard-Smith, 1958, Tatar et al., 1997a). However, free-living non-model organisms are exposed to a wide range of environmental stressors that pose a major challenge to physiological systems; these stressors can affect different components of stress-related and detoxification physiology, resulting in damage to DNA, lipids and proteins (Isaksson, 2010, Li et al., 2003). It is clear that environmental effects are particularly important in modulating expression of age-dependent mortality rates; the effects of temperature (e.g. Maynard-Smith, 1958, Pletcher and Neuhauser, 2000) and heat shock (Tatar et al., 1997b) on senescence rates in laboratory animals are well documented, while, more recently, environmental cues have also been shown to be important in influencing ageing rates in natural populations (e.g. Kawasaki et al., 2008, Mangel, 2008, Nussey et al., 2007). It is clear that senescence rates could have significant impacts on population dynamics, yet the evolutionary and ecological importance of environmentally-induced changes in senescence in wild populations is poorly understood, particularly at microevolutionary scales.
While there is evidence that evolutionary change can accelerate due to human ecological impacts (e.g. Palumbi, 2001, Yeh, 2004), it remains to be understood whether multiple anthropogenic-induced environmental stressors challenge the individual to such a degree that the rate and pattern of senescence, which would ultimately affect population demography and fitness, are altered. Most theoretical studies of senescence have only considered the effects of a single extrinsic stressor and consequences for life-history evolution at the individual level. Indeed, early theoretical models of ageing did not allow for any environmental or individual variation (see Mangel, 2001). State-dependent life-history theory has proved a useful framework for investigating optimal strategies in relation to the evolution of senescence, though studies have thus far only considered a single stressor at a time (Mangel and Munch, 2005, Mangel, 2008, Mangel, 2001, McNamara et al., 2004, Shanley and Kirkwood, 2000). However, environmental stressors rarely act in isolation and the potential for additive or synergistic effects on individual physiology, and thereby possibly the rate of senescence, needs to be taken seriously. For example, some hunter-gatherer populations show high levels of certain risk factors for cardiovascular disease, but no actual disease (Vasunilashorn et al., 2010). The modern heart-disease epidemic thus appears to result from synergistic effects of multiple lifestyle/physiological differences relative to our ancestral state. Physiological systems often show coordinated responses to changing conditions, and there is reason to expect that overall physiological regulatory mechanisms have evolved substantial robustness to normal environmental variation (Cohen et al., 2012). However, in theory, highly-optimised complex systems, such as organismal physiology, are constrained in their ability to optimise robustness to potential stressors, due to functional correlations among related traits (Kriete, 2013). This suggests that multiple simultaneous stressors might be tolerated only up to a point, beyond which an organism's tolerance is overcome and physiological condition degrades rapidly. This theoretical perspective supports a synergistic model of how stressors interact. While other authors have considered multiple mechanisms underlying senescence, including feedback loops among them (e.g. Kowald and Kirkwood, 1996), models have not been used to infer demographic consequences.
Here, we employed evolutionary simulations to investigate the potential evolutionary consequences of exposure to single and multiple external anthropogenic stressors, mediated by a trait conferring stress resistance, in a hypothetical wild animal population. To make the paper and the model biologically relevant and timely, we have envisaged the hypothetical population to be a free-living avian “urban adapter" species. While the urban environment may remove many of the ecological constraints that exist elsewhere (e.g. reduced climatic stress in temperate regions and year-round high food-availability), towns and cities present a wide range of novel environmental stressors arising from, for example, air, artificial light, water and noise pollution (McKinney, 2002, Shochat et al., 2006). Marked changes in behaviour, physiology and morphology have been widely demonstrated among organisms inhabiting urban environments (Giraudeau and McGraw, 2014, Isaksson et al., 2005, Kempenaers et al., 2010, Liker et al., 2008, Slabbekoorn and Peet, 2003) and could underlie significant evolutionary change (e.g. Yeh, 2004). Urban adapter species are considered to be those that can persist in the urban environment, even reaching very high densities in towns and cities, but typically perform less well than their rural conspecifics (Blair, 1996, McKinney, 2002, Shochat et al., 2006). Many resident (i.e. non-migratory) passerine species fall into the group of urban adapters (e.g. great tit Parus major, common blackbird Turdus merula, and American robin Turdus migratorius) and therefore offer a suitable model system for investigating the potential for evolutionary change associated with urbanisation in free-living populations. Specifically, we modelled the potential effects of exposure to stressors – single versus multiple, and in the presence of multiple stressors, whether stressors act additively versus synergistically – on the evolution of actuarial senescence, i.e. the change in the likelihood of mortality with age. Although detailed studies have now demonstrated age-related declines in organismal function in the wild (Bize et al., 2008, Broggi et al., 2010, Hruska et al., 2010), actuarial senescence continues to be a useful tool for comparing ageing rates among individuals and populations, since it directly influences population dynamics and ultimately evolution.
2. The evolutionary model framework
2.1. Overview
We simulated the evolution of stress resistance and its impacts on actuarial senescence in a closed population of 1000 individuals over 500 discrete generations subject to gradually increasing environmental stress. The hypothetical population is that of a passerine bird inhabiting an urban environment, though the results can be construed more broadly. Three core scenarios of stress exposure were simulated, involving (i) a single extrinsic stressor, (ii) two extrinsic stressors acting additively, and (iii) two extrinsic stressors acting synergistically. Parameters that were allowed to vary within models were extrinsic stress level(s), stress resistance, age-dependent mortality, lifespan and lifetime reproductive success. The model does not take into account density-dependence mechanisms, population dynamics, emigration and immigration and assumes no effects on age-independent (baseline) mortality. All data simulations were performed in R 3.1.3. The R code is available in the supplementary material (Appendix A).
2.2. Modelling extrinsic stress
Extrinsic stress levels were modelled supposing exposure to one (scenario i) or two (scenarios ii and iii) environmental stressor(s). The levels of stressors to which each individual was subject were generated by randomly sampling from a normal distribution around a variable mean (see below) and with a standard deviation fixed at 10% of the mean. Variation in extrinsic stress among individuals within the population reflects the fact that stressors are typically heterogeneous across an environment. In the single-stressor model, total extrinsic stress exposure was simply the value of a single extrinsic stressor; in the additive and synergistic models, total extrinsic stress exposure was calculated as the sum or product, respectively, of two extrinsic stressors. These different ways of calculating an individual's stress exposure reflect different hypotheses for the physiological impact of exposure to multiple simultaneous stressors. In the first generation, mean levels of each stressor were assigned an arbitrary value of 1 (scenarios i and iii) or 0.5 (scenario ii), thus the mean total stress exposure was 1 across all three scenarios. We modelled different rates of increasing environmental stress, reflecting the increasing extrinsic pressures that many urban populations are experiencing due to human population growth and associated urban development. The rate of increase of environmental stress was constant within simulations, but was allowed to vary between simulations (see Table 1). As a control, scenarios were also modelled in the absence of any change (with the exception of stochastic variation) in extrinsic stress exposure.
Table 1.
Summary of model parameters in the first and subsequent generations. The values of fixed parameters are given; where parameters were fixed within simulations, but varied across simulations, the range of values is shown.
| Parameter | First generation | Subsequent generations |
|---|---|---|
| Fixed within and across simulations | ||
| Age-independent mortality (a)1 | 0.3 | As first generation |
| Fecundity (F) | 3 | As first generation |
| Fixed within simulations, but varied across simulations | ||
| Rate of increase of ES (ESinc) | 0–0.05 | As first generation |
| Maximum stress resistance (SRmax) | 2–10 | As first generation |
| Heritability (H) | 0.1–0.99 | As first generation |
| Varied within simulations | ||
| Extrinsic stressor(s) (ES) | Randomly drawn from normal distribution with: = 0.5 or 1, σ = 0.1 ∗ |
Randomly drawn from normal distribution with: = + ESinc, σ = 0.1 ∗ |
| Stress resistance (SR) | Randomly drawn from truncated normal distribution with: = 2, σ = 0.1, min = 0.01, max = SRmax |
Sampled from previous generation, proportional to LRS, and perturbed as a function of H |
| Age-dependent mortality (b) | 0.01 ∗ e(Stotal ∗ 1/SR) | As first generation |
| Age at death (AD) | e(w ∗ e(z ∗ b)) ± stochastic variation2 | As first generation |
| Lifetime reproductive success (LRS) | F ∗ AD | As first generation |
2.3. Modelling age-dependent mortality
Stress exposure acted upon age-dependent mortality (b) and subsequently age at death (see Section 2.4) according to the exponential function:
| (1) |
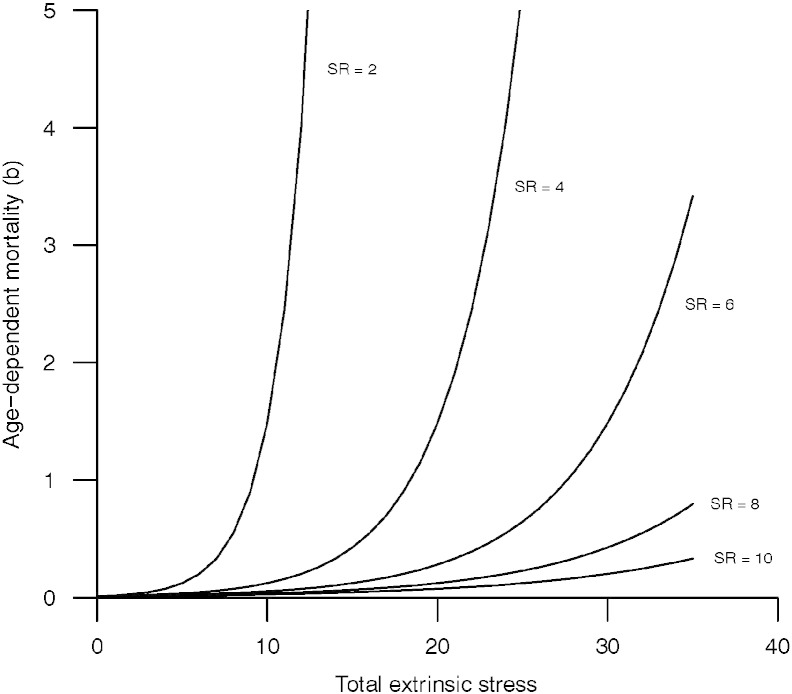
where Stotal is the total extrinsic stress exposure, SR is an individual's level of stress resistance (see Section 2.5) and c is a constant fixed at 0.01 across all simulations (see Fig. 1). As stress resistance increases, the same value of extrinsic stress results in a lower value of b, and thus a lower mortality rate. b was constrained at the lower limit, such that it could never fall below the mean of the first generation; i.e. a population cannot end up better than where it started, when both extrinsic stress and stress resistance were low. Essentially, we were constraining our simulated species to be an urban adapter rather than an urban exploiter. An upper bound was set at 10 to prevent the generation of infinite values and constrain the data to a normal distribution; an individual with b equal to 10 has a lifespan so short that it essentially dies at birth, within the context of our model.
Fig. 1.
Graphical illustration of the function relating total extrinsic stress exposure, stress resistance (SR) and age-dependent mortality (b). As stress resistance increases, the magnitude of the effect of extrinsic stress on age-dependent mortality is reduced.
2.4. Calculating lifespan and lifetime reproductive success
Mortality was modelled according to the Gompertz model, which describes the increase in mortality (μ) as a function of age (x) by the expression:
| (2) |
where a represents age-independent (baseline) mortality and b represents the age-dependent (senescent) component of mortality. The Gompertz function has been widely used to model actuarial senescence and assumes ageing-related mortality increases exponentially as a multiple of baseline mortality (Ricklefs and Scheuerlein, 2002). This implies that ageing-related mortality is not just a function of intrinsic causes of mortality, but that, as organisms age, they become more vulnerable to the same extrinsic causes of mortality to which young adults are susceptible. The Gompertz equation can be rearranged to give the probability of mortality at any age (Pμx) as follows:
| (3) |
Age at death was simulated, outside of evolutionary model simulations, for 10,000 individuals for different values of b (range: 0.01–3, in increments of 0.01), while a was fixed at 0.3. The probability of mortality at yearly intervals was calculated for each individual, according to Eq. (3). If a random number drawn from a uniform distribution between 0 and 1 was less than the probability of mortality, the individual died and age of death recorded. Using the nls() function in R, non-linear models of the form y = webz were subsequently fitted to log-transformed means and standard deviations of age at death. The estimates for the parameters w and z derived from these models were then used to calculate, with a stochastic element, age at death of each individual in the model, depending on each individual's value of b (as calculated according to Eq. (1)). In effect, we randomly sampled ages at death from an empirically-generated distribution for each possible value of b.
Individual lifetime reproductive success (LRS) was subsequently calculated as a product of fecundity (fixed at 3) and lifespan. As explained above, when b = 10, lifespan is effectively zero; therefore, in the model, when b = 10, age at death was set to zero and thus an individual's LRS was also zero. If an entire generation failed to reproduce, the population was deemed to have gone extinct and the simulation was terminated.
2.5. Modelling evolution of stress resistance
We modelled an evolvable individual parameter of "stress resistance" (SR), representing an individual's capacity to withstand stress. Individual stress resistance in the first generation was generated by randomly sampling from a truncated normal distribution with a mean of 2 and standard deviation of 0.1, using the rtruncnorm() function. Stress resistance was constrained such that it could not fall below 0.01 and was bounded at the upper limit by a maximum (SRmax), which was fixed within each simulation, but set at a different level between simulations. Unlike extrinsic stress, an individual's stress resistance was partly heritable. Individual stress resistance in each successive generation was generated by sampling with replacement from the previous generation, weighted by a probability positively correlated with an individual's lifetime reproductive success relative to the rest of the population. Each individual's probability weighting was calculated by dividing their lifetime reproductive success by the total reproductive success of the generation. These generated values were then stochastically perturbed by randomly sampling from a normal distribution with a mean equal to the absolute value of stress resistance and a standard deviation equal to 1-H, where H is the heritability. As with SRmax, heritability was fixed within each simulation, but varied between simulations.
2.6. Summary of model parameters
Model parameters are summarised in Table 1. Simulations modelled the evolution of stress resistance (SR, see Section 2.5), in response to increasing environmental stress (see Section 2.2), and the subsequent consequences for age-dependent mortality (b; Section 2.3), age at death (AD; see Section 2.4) and lifetime reproductive success (LRS; see Section 2.4). Extrinsic stressors increased as a result of a fixed rate of increase (ESinc). Age-independent mortality (a) and fecundity (F) were fixed across all simulations. SRmax and heritability (H) of stress resistance were fixed at the beginning of each simulation, but were allowed to vary across simulations. By varying heritability (range: 0.1–0.99) and SRmax (range: 2–10), we explored the breadth of parameter space to examine how these two parameters influenced rates of evolution of stress resistance and fitness effects, in terms of actuarial senescence and lifetime reproductive success, over the course of the model simulation.
3. Results
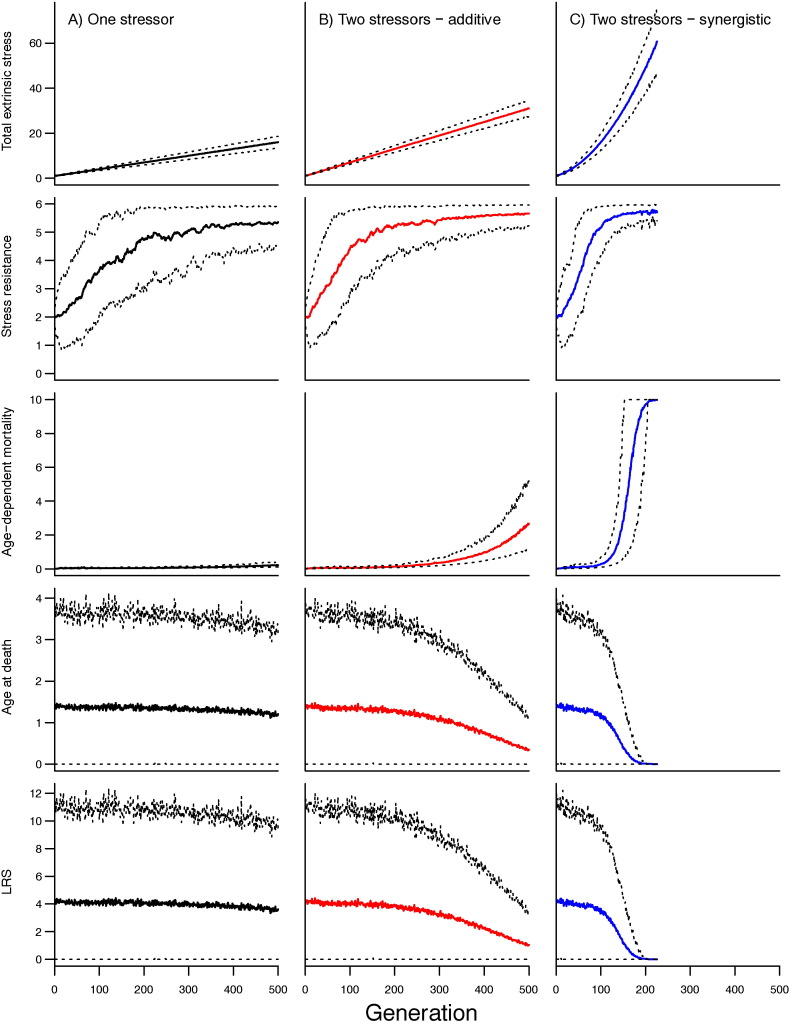
An example of a single simulation of the evolutionary model is shown in Fig. 2, in which different evolutionary outcomes were demonstrated across the three scenarios of stress exposure. Here, when heritability was fixed at 0.8 and SRmax was fixed at 6, in the single-stressor model, stress resistance was able to evolve at a rate such that there was only a small decline in mean age at death over the course of 500 generations (Fig. 2A). However, although there was little change in the mean, the variation within the population was high (Fig. 2A). Even though stress resistance initially evolved more rapidly when a population was exposed to two extrinsic stressors, this was insufficient to counter the rate of increase of environmental stress and mean age at death declined over the course of model simulations in both the additive and synergistic models (Fig. 2B & C). In the synergistic model, stress resistance evolved with greatest rapidity; in the simulations presented in Fig. 2, mean stress resistance reached within 10% of its maximum (close to the SRmax) at 100 generations (Fig. 2C), compared with 198 generations (Fig. 2B) in the additive model. Despite this, the rate of increase of environmental stress in the synergistic model soon overwhelmed the population, which went extinct after 226 generations. Outputs confirmed, as expected, that in the presence of fixed fecundity, lifetime reproductive success was directly correlated with age at death and so we do not present further outputs of reproductive success.
Fig. 2.
Model outputs illustrating variable outcomes of evolution of stress resistance and consequences for age-dependent mortality (b), age at death, and lifetime reproductive success (LRS) under three scenarios of environmental stress exposure, as labelled. Outputs were generated from a single simulation of each scenario. Parameter means (solid lines) and the 5th and 95th percentiles (dashed lines) are plotted across 500 consecutive generations. In this example, parameters were fixed as follows: rate of increase of extrinsic stressors = 0.03/generation; heritability = 0.8; and, maximum stress resistance = 6.
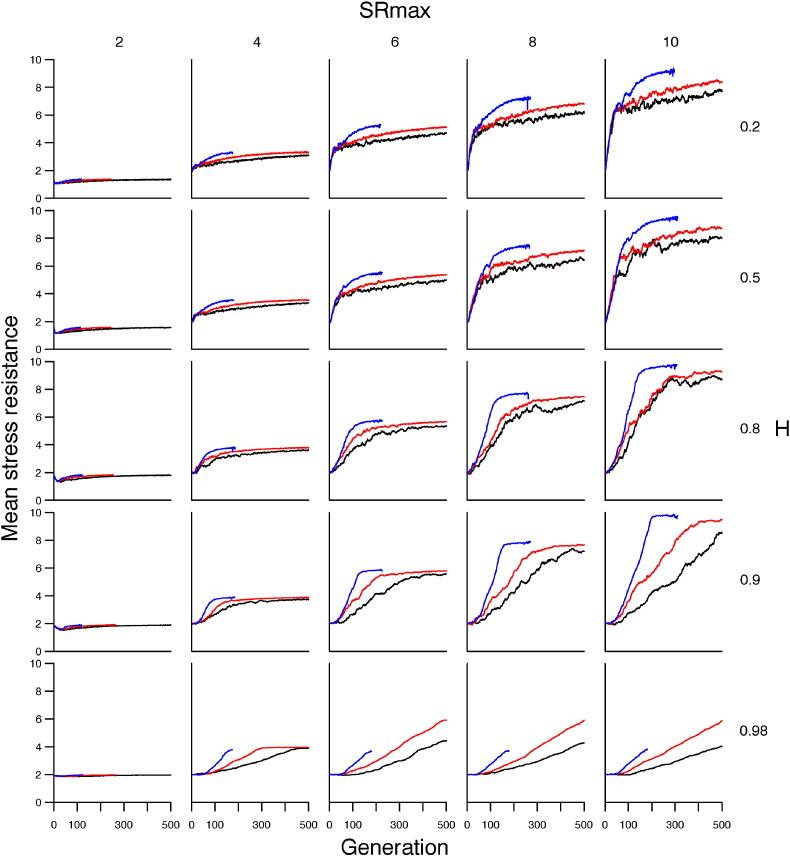
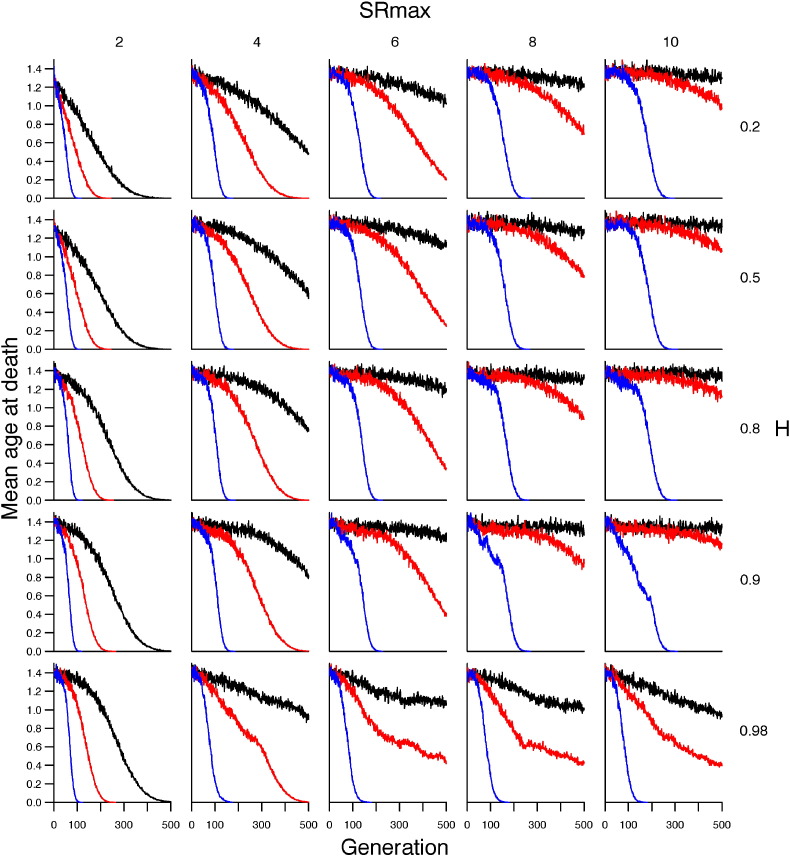
Exploring throughout parameter space revealed that when SRmax was low (e.g. 2), the evolution of stress resistance was highly constrained (Fig. 3) and mean age at death declined sharply across all scenarios of environmental stress exposure (Fig. 4). Increasing the physiological maximum (i.e. SRmax) did not affect the rate of evolution of stress resistance, but enabled mean stress resistance to reach a higher level (Fig. 3). The consequences of this for lifespan was that mean age at death did not decline so quickly and, in the single stressor and additive models, mean lifespan after 500 generations was positively correlated with SRmax (Fig. 4). As heritability increased towards an optimum of ~ 0.9, the rate of evolution of stress resistance decreased, but mean stress resistance approached closer to SRmax (Fig. 3) and, after 500 generations, mean lifespan was longer in the single stressor and additive models (Fig. 4). When heritability exceeded 0.9, populations fared markedly worse across all scenarios of environmental stress: the rate of evolution of stress resistance decreased and mean lifespan declined during the course of model simulations (Fig. 3, Fig. 4). Across all values of SRmax and heritability explored, a synergistic model of stress exposure resulted in the population going extinct long before 500 generations.
Fig. 3.
Evolution of mean stress resistance across 500 generations under different scenarios of environmental stress exposure and across a range of parameterisations of heritability (H) and maximum stress resistance (SRmax). Scenarios are: one stressor (black); two stressors acting additively (red); and, two stressors acting synergistically (blue).
Fig. 4.
Change in mean age at death across 500 generations under different scenarios of environmental stress exposure and across a range of parameterisations of heritability (H) and maximum stress resistance (SRmax). Scenarios are: one stressor (black); two stressors acting additively (red); and, two stressors acting synergistically (blue).
Varying the physiological constraints (i.e. SRmax and heritability) on the population had the greatest effect on the evolution of actuarial senescence in response to exposure to two additive stressors (Fig. 3, Fig. 4). When physiological constraints were relaxed (i.e. high heritability and SRmax), the additive model approached the single-stressor model in terms of mean age at death (Fig. 4), though mean stress resistance was higher in the additive model, compared with the single-stressor model (Fig. 3). Under tighter constraints (i.e. low SRmax and heritability), the additive model behaved similarly to the synergistic model.
The model outputs presented here are those when rate of increase of extrinsic stress was set at 0.03/generation; we have chosen to present these outputs, since they illustrate interesting variation in evolutionary responses across the parameter space (of heritability and SRmax) explored. At a lower rate of change (e.g. 0.01/generation), we see little variation in responses (see Fig. B-1A & B, Supplementary material); while at higher rates of change of environmental stress (e.g. 0.05/generation), the population is rapidly overwhelmed (see Fig. B-1C & D, Supplementary material). As a control, simulations were also performed under a scenario of constant environmental stress; the evolutionary trajectory of a trait of stress resistance was similar across all scenarios of environmental stress (Fig. B-2A, Supplementary material) and there was no change in mean age at death during the course of model simulations (Fig. B-2B, Supplementary material).
Repeated iterations of simulations, while parameterisation remained unchanged, confirmed that model outputs were consistent and repeatable. Some examples of repeated iterations are presented in Figure C-1 (Supplementary material). Given the stochastic processes involved in simulations, this process was necessary to verify that results are robust and validate the presentation of model outputs from single simulations.
4. Discussion
The rate at which physiological systems reach their limits and the rate of evolutionary change will, of course, depend on how multiple stressors interact with one another (e.g. Ezenwa, 2004, Isaksson, 2015). Here, we have demonstrated that a synergistic model of how physiological stressors interact produces much more dramatic changes in a population's mortality profile under conditions of increasing extrinsic stress than an additive or single-stressor model. Given that the absolute levels of extrinsic stress increase more quickly in the synergistic scenario, this is not unexpected; nonetheless, it is noteworthy because the observed increases in age-dependent mortality occur quite suddenly and result in rapid population collapse and subsequent extinction. Furthermore, even when physiological systems demonstrated high plasticity, populations were still rapidly pushed outside of a zone of tolerance. This suggests that, at least under some conditions, apparently stable wild populations exposed to anthropogenic stress may be at much greater risk than their demography alone suggests. Although not explicit in our models, it is likely that a trait for stress resistance would be costly to maintain (e.g. Kirkwood, 1977, Kirkwood and Holliday, 1979). If extrinsic stress heavily outweighs any advantage of having stress resistance, as in the synergistic model, the differences between individuals becomes meaningless; individuals with higher stress resistance would be expected to suffer more, in terms of fitness costs, than those with low stress resistance (Roff, 1992; Roff and Fairbairn, 2007). In the natural world, the evolutionary consequences of exposure to multiple synergistic stressors could therefore be far greater than the outcomes predicted by our model.
Our results demonstrate the importance of defining an explicit model of how environmental stressors affect the physiological mechanisms underlying ageing when conducting demographic models of senescence: the synergistic model is more biologically realistic, but without explicit consideration of the question, additive or single-stressor models have become the default (e.g. Mangel and Munch, 2005, Mangel, 2008, Shanley and Kirkwood, 2000). Though there is no consensus on the basic mechanisms of senescence, there is increasing evidence that ageing is a multi-factorial process (Kirkwood, 2011, Partridge and Barton, 1993). The present study suggests that understanding whether these multiple factors are additive or synergistic in their effects may be crucial for predicting species' abilities to tolerate stress. While there is no clear evidence as to which physiological model is more realistic for understanding how stress affects ageing, we believe that the synergistic model is more realistic. Organisms are highly-optimised complex systems that have evolved sophisticated regulatory mechanisms to maintain homeostasis (Cohen et al., 2012). In such systems, features that optimise robustness to a wide range of foreseeable conditions generally cause increased frailty for less common conditions, with overall robustness across all possible conditions remaining zero-sum (Kriete, 2013). Such a model would suggest that organisms evolve greater robustness to variation in a single stressor (a more common situation) than for simultaneous variation in multiple independent stressors (more rare). For example, if a nutrient shortage and extreme temperatures are uncorrelated environmentally, the organism may have evolved less robustness to both stresses simultaneously than would be predicted based on the resistance to each alone. Likewise, the level of resistance to stressors may not far exceed stress levels likely to be encountered. Such a principle would explain why laboratory studies often show extreme responses to endocrine disruptors at moderately high doses (Suvorov et al., 2009, Zhou et al., 2001), whereas human epidemiological studies have generally not demonstrated large effects (e.g. Abdelouahab et al., 2013).
Of course, even if the synergistic model is appropriately parameterised, we would need a detailed understanding of how important each stressor is for each species to be able make more concrete predictions of long-term impacts. Our simulations make a large number of suppositions that may or may not be realistic for some or all species, and our goal is not to suggest that the results give a clear view of what is likely to happen. Rather, the key insight is that an understanding of how stressors are integrated physiologically is necessary to understand the impacts of changing environments on the evolution of senescence, population stability, and physiological adaptation. While our simulation and discussion were conducted with a modern urban passerine species in mind, the conclusions apply much more broadly to understanding how species respond physiologically to changing environments. Furthermore, variation in physiological constraints in the model (here, being maximum stress resistance and heritability) could represent genetic or non-genetic (such as environmentally-induced changes in gene regulation, e.g. DNA-methylation) adaptations that are heritable across generations. Non-genetic mechanisms of inheritance could potentially lead to a greater robustness and a faster response towards environmental perturbations compared to strict genetic inheritance (Isaksson, 2015). However, non-genetic inheritance does not act independently of the underlying genetic structure, thus the current model does not take into account the different sources of variation.
While we have not explicitly defined stress resistance in our model, this could be thought of as one or more physiological repair mechanisms, such as those involved in the expression of heat-shock proteins or detoxification systems, with the overall level of resistance indicating the ability of the system to repair somatic damage and extend lifespan (see Gems and Partridge, 2008, Lithgow and Walker, 2002, Mangel, 2008). In this context, our model shares assumptions with the disposable soma theory of ageing (Kirkwood, 1977). Our model only considers a single trait of stress resistance, but, in reality, various physiological regulatory networks are likely to be involved in regulating responses to external cues (Cohen et al., 2012, Kirkwood, 2011). If correlations among traits are a sufficient constraint on the evolution of multiple stress resistance traits, the model considered here might be appropriate (Cohen et al., 2012), but if there is physiological canalisation or if traits evolve independently, the dramatic effects of the synergistic model might be diminished.
Variation in lifespan can, of course, arise through age-independent changes in baseline mortality as well as the ageing component of mortality (Partridge et al., 2005, Simons et al., 2013). Our model framework only considers effects of extrinsic stress on age-dependent mortality, yet baseline mortality may also be sensitive to sources of anthropogenic-induced stress. It is likely that different ecological and physiological mechanisms contribute to changes in actuarial senescence and baseline mortality and the evolution of life histories will depend on whether costs are manifested in increased baseline mortality or actuarial senescence.
The rate of senescence – the rate at which expected contributions to fitness decline – can be considered as a function of both age-specific mortality and fecundity (Hamilton, 1966). Our evolutionary model is therefore potentially limited in its ability to fully describe how selective pressures shape patterns of senescence since it does not account for age-related changes in fecundity. Indeed, physiological processes, such as oxidative stress (i.e. a surplus of pro-oxidants relative to antioxidants), have been shown to play an important role in shaping individual fecundity as well as survival, but they may also underlie complex trade-offs (Bize et al., 2008, Monaghan et al., 2009). For example, avian “urban adapters” typically have smaller clutch sizes than their non-urban counterparts (Chamberlain et al., 2009); such a reduction in reproductive output could be adaptive, enabling greater investment of resources in maintenance and survival. However, it is also quite feasible that urban environmental stress could result in positive co-variation between fecundity and survival, the extent of which will be moderated by individual variation in quality. Both physiological trade-offs and individual variation are likely to be particularly important for the shaping of senescence rates in the wild, but the relative significance of each factor is poorly understood. Thus, incorporating these two non-mutually-exclusive hypotheses into the model provides a far greater challenge and would require a wider range of scenarios to be considered.
4.1. Future directions
Identifying the precise causes and consequences of environmental variation for senescence rates in the wild presents a great challenge. In contrast to other theoretical and empirical studies of ageing, we have explored the potential for synergistic effects of exposure to multiple stressors, a mechanism recently highlighted as being of likely importance in the toxicological literature (Isaksson, 2015). As with any theoretical, or indeed empirical study, things can always be made more complicated. As a first step, our aim was to construct a simple model from which testable predictions concerning the physiological effects of multiple stressors on senescence could be generated. While we have gained much valuable knowledge on some aspects of the physiological mechanisms underlying senescence from model laboratory organisms, studies of non-model organisms are needed to reveal how environmental cues influence rates of senescence in the wild. There is a need for studies to test exposure to multiple stressors under controlled conditions to determine how different stressors interact with one another to affect age-related declines in fitness at the individual and population levels. This will require integration of carefully-designed field and laboratory experiments in non-model organisms. It is realistic to expect that stressors often do interact with a high degree of synergy in nature, but quite how commonplace this is and to what extent systems are synergistic are largely unknown. How stress resistance evolves will also be a key component of the puzzle to explore, likely through laboratory studies.
Acknowledgements
We thank Marco Klein Heerinbrink for helpful discussion concerning mathematical models. For financial support, we thank European Commission (FP7 CIG to CI, grant no: 322217) and the Swedish Research Council (VR to CI, grant no: C0361301).
Section Editor: Chennai Guest Editor
Footnotes
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.exger.2015.08.009.
Supplementary material
Appendix A - R code
Appendix B - Figs. B-1 & B-2
Appendix C - Fig. C-1
References
- Abdelouahab N., Langlois M.F., Lavoie L., Corbin F., Pasquier J.C., Takser L. Maternal and cord-blood thyroid hormone levels and exposure to polybrominated diphenyl ethers and polychlorinated biphenyls during early pregnancy. Am. J. Epidemiol. 2013;178:701–713. doi: 10.1093/aje/kwt141. [DOI] [PubMed] [Google Scholar]
- Beckman K.B., Ames B.N. The free radical theory of aging matures. Physiol. Rev. 1998;78:547–581. doi: 10.1152/physrev.1998.78.2.547. doi:OSJC0001. [DOI] [PubMed] [Google Scholar]
- Bize P., Devevey G., Monaghan P., Doligez B., Christe P. Fecundity and survival in relation to resistance to oxidative stress in a free-living bird. Ecology. 2008;89:2584–2593. doi: 10.1890/07-1135.1. [DOI] [PubMed] [Google Scholar]
- Blair R.B. Land use and avian species diversity along an urban gradient. Ecol. Appl. 1996;6:506–519. [Google Scholar]
- Bouwhuis S., Charmantier A., Verhulst S., Sheldon B.C. Individual variation in rates of senescence: natal origin effects and disposable soma in a wild bird population. J. Anim. Ecol. 2010;79:1251–1261. doi: 10.1111/j.1365-2656.2010.01730.x. [DOI] [PubMed] [Google Scholar]
- Broggi J., Hohtola E., Koivula K., Orell M., Nilsson J.Å. Idle slow as you grow old: longitudinal age-related metabolic decline in a wild passerine. Evol. Ecol. 2010;24:177–184. [Google Scholar]
- Chamberlain D.E., Cannon A.R., Toms M.P., Leech D.I., Hatchwell B.J., Gaston K.J. Avian productivity in urban landscapes: a review and meta-analysis. Ibis. 2009;151:1–18. [Google Scholar]
- Cohen A.A., Martin L.B., Wingfield J.C., McWilliams S.R., Dunne J.A. Physiological regulatory networks: ecological roles and evolutionary constraints. Trends Ecol. Evol. 2012;27:428–435. doi: 10.1016/j.tree.2012.04.008. [DOI] [PubMed] [Google Scholar]
- Ezenwa V.O. Interaction among host diet, nutritional status and gastrointestinal parasite infection in wild bovids. Int. J. Parasitol. 2004;34:535–542. doi: 10.1016/j.ijpara.2003.11.012. [DOI] [PubMed] [Google Scholar]
- Gems D., Partridge L. Stress-response hormesis and aging: “That which Does Not Kill Us Makes Us Stronger.”. Cell Metab. 2008;7:200–203. doi: 10.1016/j.cmet.2008.01.001. [DOI] [PubMed] [Google Scholar]
- Giraudeau M., McGraw K.J. Physiological correlates of urbanization in a desert songbird. Integr. Comp. Biol. 2014;4:622–632. doi: 10.1093/icb/icu024. [DOI] [PubMed] [Google Scholar]
- Haldane J.B.S. Allen & Unwin; London: 1941. New Paths in Genetics. [Google Scholar]
- Hamilton W.D. The moulding of senescence by natural selection. J. Theor. Biol. 1966;12:12–45. doi: 10.1016/0022-5193(66)90184-6. [DOI] [PubMed] [Google Scholar]
- Harman D. Aging: a theory based on free radical and radiation chemistry. J. Gerontol. 1956;11:298–300. doi: 10.1093/geronj/11.3.298. [DOI] [PubMed] [Google Scholar]
- Hruska K.A., Hinch S.G., Healey M.C., Patterson D.A., Larsson S., Farrell A.P. Influences of sex and activity level on physiological changes in individual adult sockeye salmon during rapid senescence. Physiol. Biochem. Zool. 2010;83:663–676. doi: 10.1086/652411. [DOI] [PubMed] [Google Scholar]
- Isaksson C. Pollution and its impact on wild animals: a meta-analysis on oxidative stress. EcoHealth. 2010;7:342–350. doi: 10.1007/s10393-010-0345-7. [DOI] [PubMed] [Google Scholar]
- Isaksson C. Urbanization, oxidative stress and inflammation: a question of evolving, acclimatizing or coping with urban environmental stress. Funct. Ecol. 2015;29:913–923. [Google Scholar]
- Isaksson C., Örnborg J., Stephensen E., Andersson S. Plasma glutathione and carotenoid coloration as potential biomarkers of environmental stress in great tits. EcoHealth. 2005;2:138–146. [Google Scholar]
- Jones O.R., Gaillard J.M., Tuljapurkar S., Alho J.S., Armitage K.B., Becker P.H., Bize P., Brommer J., Charmantier A., Charpentier M., Clutton-Brock T., Dobson F.S., Festa-Bianchet M., Gustafsson L., Jensen H., Jones C.G., Lillandt B.G., McCleery R., Merilä J., Neuhaus P., Nicoll M.A.C., Norris K., Oli M.K., Pemberton J., Pietiäinen H., Ringsby T.H., Roulin A., Saether B.E., Setchell J.M., Sheldon B.C., Thompson P.M., Weimerskirch H., Jean Wickings E., Coulson T. Senescence rates are determined by ranking on the fast-slow life-history continuum. Ecol. Lett. 2008;11:664–673. doi: 10.1111/j.1461-0248.2008.01187.x. [DOI] [PubMed] [Google Scholar]
- Kawasaki N., Brassil C.E., Brooks R.C., Bonduriansky R. Environmental effects on the expression of life span and aging: an extreme contrast between wild and captive cohorts of Telostylinus angusticollis (Diptera: Neriidae) Am. Nat. 2008;172:346–357. doi: 10.1086/589519. [DOI] [PubMed] [Google Scholar]
- Kempenaers B., Borgström P., Loës P., Schlicht E., Valcu M. Artificial night lighting affects dawn song, extra-pair siring success, and lay date in songbirds. Curr. Biol. 2010;20:1735–1739. doi: 10.1016/j.cub.2010.08.028. [DOI] [PubMed] [Google Scholar]
- Kirkwood T.B.L. Evolution of ageing. Nature. 1977;270:301–304. doi: 10.1038/270301a0. [DOI] [PubMed] [Google Scholar]
- Kirkwood T.B.L. Systems biology of ageing and longevity. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2011;366:64–70. doi: 10.1098/rstb.2010.0275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkwood T.B.L., Holliday F.R.S. The evolution of ageing and longevity. Proc. R. Soc. B. 1979;205:531–546. doi: 10.1098/rspb.1979.0083. [DOI] [PubMed] [Google Scholar]
- Klass M., Hirsh D. Non-ageing developmental variant of Caenorhabditis elegans. Nature. 1976;260:523–525. doi: 10.1038/260523a0. [DOI] [PubMed] [Google Scholar]
- Kowald A., Kirkwood T.B.L. A network theory of ageing: the interactions of defective mitochondria, aberrant proteins, free radicals and scavengers in the ageing process. Mutat. Res. 1996;316:209–236. doi: 10.1016/s0921-8734(96)90005-3. [DOI] [PubMed] [Google Scholar]
- Kriete A. Robustness and aging — a systems-level perspective. Biosystems. 2013;112:37–48. doi: 10.1016/j.biosystems.2013.03.014. [DOI] [PubMed] [Google Scholar]
- Li N., Sioutas C., Cho A., Schmitz D., Misra C., Sempf J., Wang M., Oberley T., Froines J., Nel A. Ultrafine particulate pollutants induce oxidative stress and mitochondrial damage. Environ. Health Perspect. 2003;111:455–460. doi: 10.1289/ehp.6000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liker A., Papp Z., Bókony V., Lendvai A.Z. Lean birds in the city: body size and condition of house sparrows along the urbanization gradient. J. Anim. Ecol. 2008;77:789–795. doi: 10.1111/j.1365-2656.2008.01402.x. [DOI] [PubMed] [Google Scholar]
- Lithgow G.J., Walker G.A. Stress resistance as a determinate of C. elegans lifespan. Mech. Ageing Dev. 2002;123:765–771. doi: 10.1016/s0047-6374(01)00422-5. [DOI] [PubMed] [Google Scholar]
- Mangel M. Complex adaptive systems, aging and longevity. J. Theor. Biol. 2001;213:559–571. doi: 10.1006/jtbi.2001.2431. [DOI] [PubMed] [Google Scholar]
- Mangel M. Environment, damage and senescence: modelling the life-history consequences of variable stress and caloric intake. Funct. Ecol. 2008;22:422–430. [Google Scholar]
- Mangel M., Munch S.B. A life-history perspective on short- and long-term consequences of compensatory growth. Am. Nat. 2005;166:E155–E176. doi: 10.1086/444439. [DOI] [PubMed] [Google Scholar]
- Maynard-Smith J. The effects of temperature and of egg-laying on the longevity of Drosophila subobscura. J. Exp. Biol. 1958;35:832–842. [Google Scholar]
- McKinney M.L. Urbanization, biodiversity and conservation. Bioscience. 2002;52:883–890. [Google Scholar]
- McNamara J.M., Welham R.K., Houston A.I., Daan S., Tinbergen J.M. The effects of background mortality on optimal reproduction in a seasonal environment. Theor. Popul. Biol. 2004;65:361–372. doi: 10.1016/j.tpb.2003.10.006. [DOI] [PubMed] [Google Scholar]
- Medawar P.B. An unsolved problem of biology. Evol. Heal. Dis. 1952 [Google Scholar]
- Monaghan P., Metcalfe N.B., Torres R. Oxidative stress as a mediator of life history trade-offs: mechanisms, measurements and interpretation. Ecol. Lett. 2009;12:75–92. doi: 10.1111/j.1461-0248.2008.01258.x. [DOI] [PubMed] [Google Scholar]
- Nussey D.H., Froy H., Lemaitre J.F., Gaillard J.M., Austad S.N. Senescence in natural populations of animals: widespread evidence and its implications for bio-gerontology. Ageing Res. Rev. 2013;12:214–225. doi: 10.1016/j.arr.2012.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussey D.H., Kruuk L.E.B., Morris A., Clutton-Brock T.H. Environmental conditions in early life influence ageing rates in a wild population of red deer. Curr. Biol. 2007;17:1000–1001. doi: 10.1016/j.cub.2007.10.005. [DOI] [PubMed] [Google Scholar]
- Palumbi S.R. Evolution — humans as the world's greatest evolutionary force. Science (80-.) 2001;293:1786–1790. doi: 10.1126/science.293.5536.1786. [DOI] [PubMed] [Google Scholar]
- Partridge L., Barton N.H. Optimality, mutation and the evolution of ageing. Nature. 1993;363:305–311. doi: 10.1038/362305a0. [DOI] [PubMed] [Google Scholar]
- Partridge L., Pletcher S.D., Mair W. Dietary restriction, mortality trajectories, risk and damage. Mech. Ageing Dev. 2005;126:35–41. doi: 10.1016/j.mad.2004.09.017. [DOI] [PubMed] [Google Scholar]
- Pletcher S.D., Neuhauser C. Biological aging-criteria for modeling and a new mechanistic model. Int. J. Mod. Phys. C. 2000;11:525–546. [Google Scholar]
- Ricklefs R.E., Scheuerlein A. Biological implications of the weibull and gompertz models of aging. J. Gerontol. A Biol. Sci. Med. Sci. 2002;57:B69–B76. doi: 10.1093/gerona/57.2.b69. [DOI] [PubMed] [Google Scholar]
- Roff D.A. Chapman and Hall; New York: 1992. The Evolution of Life Histories: Theory and Analysis. [Google Scholar]
- Roff D.A., Fairbairn D.J. The evolution of trade-offs: where are we now? J. Evol. Biol. 2007;20:433–447. doi: 10.1111/j.1420-9101.2006.01255.x. [DOI] [PubMed] [Google Scholar]
- Shanley D.P., Kirkwood T.B. Calorie restriction and aging: a life-history analysis. Evolution. 2000;54:740–750. doi: 10.1111/j.0014-3820.2000.tb00076.x. [DOI] [PubMed] [Google Scholar]
- Shochat E., Warren P.S., Faeth S.H., Mcintyre N.E., Hope D. From patterns to emerging processes in mechanistic urban ecology. Trends Ecol. Evol. 2006;21:186–191. doi: 10.1016/j.tree.2005.11.019. [DOI] [PubMed] [Google Scholar]
- Simons M.J.P., Koch W., Verhulst S. Dietary restriction of rodents decreases aging rate without affecting initial mortality rate - a meta-analysis. Aging Cell. 2013;12:410–414. doi: 10.1111/acel.12061. [DOI] [PubMed] [Google Scholar]
- Slabbekoorn H., Peet M. Birds sing at a higher pitch in urban noise. Nature. 2003;424:267. doi: 10.1038/424267a. [DOI] [PubMed] [Google Scholar]
- Suvorov A., Girard S., Lachapelle S., Abdelouahab N., Sebire G., Takser L. Perinatal exposure to low-dose BDE-47, an emergent environmental contaminant, causes hyperactivity in rat offspring. Neonatology. 2009;95:203–209. doi: 10.1159/000155651. [DOI] [PubMed] [Google Scholar]
- Tatar M., Gray D.W., Carey J.R. Altitudinal variation for senescense in Melanoplus grasshoppers. Oecologia. 1997;111:357–364. doi: 10.1007/s004420050246. [DOI] [PubMed] [Google Scholar]
- Tatar M., Khazaeli A.A., Curtsinger J.W. Chaperoning extended life. Nature. 1997;390:30. doi: 10.1038/36237. [DOI] [PubMed] [Google Scholar]
- Vasunilashorn S., Crimmins E.M., Kim J.K., Winking J., Gurven M., Kaplan H., Finch C.E. Blood lipids, infection, and inflammatory markers in the Tsimane of Bolivia. Am. J. Hum. Biol. 2010;22:731–740. doi: 10.1002/ajhb.21074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams G.C. 1957. Pleiotropy, natural selection and senescence. (pdf. Evolution (N. Y)) [Google Scholar]
- Yeh P.J. Rapid evolution of a sexually selected trait following population establishment in a novel habitat. Evolution. 2004;58:166–174. doi: 10.1111/j.0014-3820.2004.tb01583.x. [DOI] [PubMed] [Google Scholar]
- Zhou T., Ross D.G., Devito M.J., Crofton K.M. Effects of short-term in vivo exposure to polybrominated diphenyl ethers on thyroid hormones and hepatic enzyme activities in weanling rats. Toxicol. Sci. 2001;61:76–82. doi: 10.1093/toxsci/61.1.76. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix A - R code
Appendix B - Figs. B-1 & B-2
Appendix C - Fig. C-1